Abstract
The integrity parameter in vulnerability refers to a set of removed vertices and the maximum number of connected components that remain functional. A bipolar fuzzy graph (BFG) assigns membership values to both positive and negative attributes. A new parameter, integrity, is defined and discussed using an example of a BFG. The integrity value of a special type of graph is determined, and the node strength sequence (NSS) for BFG is introduced. Specific NSS values are used to discuss the integrity values of paths and cycles. The integrity of the union, join, and Cartesian product of two BFGs is presented. This parameter is then applied to a road network with both positive and negative attributes, and the findings are discussed with a conclusion.
1. Introduction
A graph can model any network, with crisp graphs assigning membership values of 1 to all vertices and edges. However, in real-world road networks, connectivity often exhibits uncertainty, where membership values range between 0 and 1. If connectivity is absent, the membership value is zero; if fully connected, it is one. A fuzzy graph accommodates such variations by accepting membership values in . Incorporating symmetry and symmetric structures into fuzzy graphs provides a novel perspective for road network analysis, enabling the identification of balanced patterns, optimizing traffic flow, and enhancing resilience against disruptions through structural harmony.
If vertex and edge membership values fall within the range , the graph is a BFG (bipolar fuzzy graph). Without diminishing the significance of any linguistic factors, fuzzy graph theory can resolve practical issues. When considering linguistic terms, it often occurs that not all nodes possess the property; some nodes are even against it. All networks have pros and cons. A transport network helps improve a country’s economy but also creates environmental issues. When modeling this type of transport network as a BFG, membership values reflecting economic growth take the form , while those indicating negative impact on the environment take the form .
L.A. Zadeh [1] proposed the mathematical concept of fuzzy sets to model uncertainty in real-life situations. Rosenfeld [2] extended this framework by introducing the theory of fuzzy graphs through fuzzy relations on fuzzy sets. Complete and strong fuzzy graphs were studied by Bhutani et al. [3,4], while Sunitha et al. [5] defined fundamental operations on fuzzy graphs such as union, join, composition, and complement. The concept of node strength sequence was introduced by Mathew et al. [6], and a comprehensive overview of fuzzy graph theory was later provided by Sunitha et al. [7]. More recently, Jamil [8] analyzed distance-based topological indices in double graphs, and Ali et al. [9] developed the notion of double resolving sets with the exchange property, emphasizing their applications in network optimization and cybersecurity, thereby extending the practical utility of graph-theoretic tools.
Akram [10] proposed BFGs and developed the concept of regular BFGs [11]. Rashmanlou et al. [12] discussed direct, semi-strong, and strong BFG; Broumi et al. [13] focused on bipolar neutrosophic graphs; and Pramanika et al. [14] introduced the concept of a bipolar fuzzy planar graph. In [11,15,16,17], regular, totally regular, irregular, highly irregular, neighborly irregular, neighborly totally irregular, and highly totally irregular BFGs are defined. Ref. [18] defines strong edge, dominating set, independent set, total dominating number, and independent number of BFGs. The concepts of ordinary order, size, and weak isomorphism of BFGs are discussed in [19,20], and refs. [21,22,23,24] covers self-complement, self-weak complement, strong isomorphism, and other properties of BFGs. Different types of BFGs, such as direct, regular, semi-strong, completely regular, and strong ones, are discussed in [12,16], while normal product and tensor product BFGs are covered in [25]. Various applications of BFGs are presented in [26,27,28,29,30].
Connectivity is a major concern in networking, and vulnerabilities that affect connectivity need to be measured using specific parameters. When disconnecting a network, each component has a certain impact. This disconnection process involves removing certain vertices or edges. The integrity parameter is linked to the set of vertices used for disconnection and the highest-order connected component that remains.
The concept of graph integrity was introduced by Goddard et al. [31], with a survey provided by Bagga et al. [32] covering weak integrity. Kirlangic et al. [33] discussed weak hub integrity, and Mahde et al. [34,35] explored hub integrity and weak hub integrity of graphs. Kilicc et al. [36] proposed edge integrity domination in graphs, and Besirik [37] presented total dominance integrity of graphs.
Saravanan et al. [38] introduced the concept of integrity in fuzzy graphs. Subsequent studies by the same authors [39,40,41] explored integrity across different contexts, including union, join, Cartesian product, domination, and efficient fuzzy graphs. Sujatha et al. [42] focused on span integrity within fuzzy graphs, while Sankar et al. [43,44,45] examined edge integrity, vertex integrity, and domination integrity specifically in signed fuzzy graphs.
1.1. Originality and Significance of Integrity in Bipolar Fuzzy Graphs
A fuzzy graph takes membership values only within the range [0, 1]. While converting profit and loss problems into a fuzzy graph, the membership value assigned to zero for non-profit does not imply a loss. It fails to indicate a loss in the fuzzy sense. Similarly, in the construction of roadways, there can be significant economic profit alongside substantial environmental issues. When converting this into a fuzzy model, traditional fuzzy models are insufficient. There is a need to take values in the range [−1, 1] and discuss determinacy and indeterminacy simultaneously. Bipolar fuzzy graphs provide these advancements.
The integrity parameter in fuzzy graphs deals only with the positive side. Integrity in bipolar fuzzy graphs addresses both positive and negative aspects. This feature allows for the discussion of not only economic growth but also environmental issues. For a single crisp graph, we can draw an infinite number of fuzzy graphs. The bounds for each parameter represent a significant improvement in the field of bipolar fuzzy graphs. The integrity parameter bounds are derived for standard bipolar fuzzy graphs.
1.2. Motivation
Integrity reveals the significance of a set of vertices when they are removed from the graph. In BFGs, it reflects both positive and negative attributes. Similar to the profit and loss network model, the integrity parameter specifies both the minimum gain, even if some nodes are not working, and the maximum loss with a set of vertices that do not contribute. Thus, integrity in BFGs is represented as a 2-tuple value, indicating both positive and negative integrity.
Integrity is the first vulnerability parameter in bipolar fuzzy graphs. Comparison with other parameters is not possible.
1.3. Organization of the Paper
This article begins with Section 1, which outlines the necessity of the parameter and offers a brief literature survey covering fuzzy graph theory, bipolar fuzzy graphs, and integrity parameters. Section 2 provides all the fundamental definitions necessary for understanding both fuzzy graphs and BFGs. Section 3.1 introduces and elucidates the vulnerability parameter, integrity, with an accompanying example. This section also presents the integrity values for some basic and standard BFGs. Section 3.2 delves into the operations of BFGs, discussing the integrity values for union, join, and Cartesian BFGs. Section 3.3 scrutinizes the integrity of BFG values and their significance, using a transport network model as an illustration. The article concludes with a discussion on potential avenues for future research.
2. Preliminaries
A crisp graph consists of a nonempty set of nodes ℑ and a set of edges . Rosenfeld extended this concept to fuzzy graphs. A fuzzy graph is defined as a pair of functions, where and . For all , we require
A subgraph of is a fuzzy graph if and for all . Furthermore, has a spanning subgraph if both fuzzy graphs share the same vertex set.
A sequence of distinct nodes such that for all i is called a path of length n in . The minimum membership value of the edges along a path determines its strength. A fuzzy graph is connected if every pair of vertices is connected by a path. The maximum strength among all paths connecting and defines their connectedness, denoted by
If, in a fuzzy graph, for all , then is called a strong fuzzy graph. A fuzzy graph is complete if for all ,
The order and size of a fuzzy graph are defined as
The complement of a fuzzy graph is given by , where and
Finally, the integrity of a fuzzy graph is defined as where denotes the maximum order of with respect to the underlying crisp graph .
To establish the framework for our analysis, we first outline the notation used in this paper. The fundamental concepts of bipolar fuzzy graphs (BFG), vertex and edge membership functions, and integrity measures are consistently represented using the symbols summarized in Table 1.

Table 1.
Summary of key symbols and notations used in this paper.
Definition 1
([46,47]). Consider the vertex set S to be non-empty. A bipolar fuzzy set on S is defined as , where and .
Definition 2
([47]). Consider the vertex set S to be non-empty. A bipolar fuzzy relation on S is defined as such that and .
Definition 3
([10]). A BFG with an underlying crisp set ℑ is defined to be a pair , where is a bipolar fuzzy set in ℑ and is a bipolar fuzzy set in such that and for all , where is the bipolar fuzzy vertex set of ℑ, and is the bipolar fuzzy edge set of . Thus is a BFG of if and for all .
Definition 4
([11]). A BFG is complete if , .
Definition 5
([10]). A BFG is strong if , .
Definition 6
([48]). Let be a BFG then the complement is defined as . Where and are defined as and .
Definition 7
([48]). Let be a strong BFG, then the complement is defined as , where and are defined as
and
.
Definition 8
([10]). Let and be bipolar fuzzy subsets on the vertex sets and , respectively. Let and be bipolar fuzzy subsets on the edge sets and , respectively. Then the union of and is defined as where
- (i)
- (ii)
- (iii)
- (iv)
Definition 9
([10]). Let and be bipolar fuzzy subsets on the vertex sets and , respectively. Let and be bipolar fuzzy subsets on the edge sets and , respectively. Then the join of and is where
- (i)
- For each ,
- (ii)
- For each edge ,
- (iii)
- For each new edge , where is the set of edges joining a vertex of with a vertex of ,
Definition 10
([10]). Let and be a bipolar fuzzy subsets of and and let and be bipolar fuzzy subsets of and , respectively. Then the cartesian BFG of and is is defined as follows.
- (i)
- ,
- (ii)
- (iii)
- .
Definition 11
([27]). Let be a Bipolar Fuzzy Graph (BFG) with an underlying crisp graph , where ℑ is the vertex set and is the edge set. For each vertex , the positive and negative membership functions of are denoted by and , respectively. For each edge , the positive and negative membership functions of are denoted by and , respectively. Then:
- 1.
- The order of Σ is defined as
- 2.
- The size of Σ is defined as
3. Results
3.1. Integrity of Bipolar Fuzzy Graph
In this section, the integrity parameter is defined and explained with an example.
Definition 12.
Let Σ be a BFG with an underlying crisp graph having a vertex set ℑ and an edge set . The integrity of Σ is represented as a tuple value, denoted by , where denotes the positive integrity, and denotes the negative integrity of Σ.
The positive integrity of a BFG is defined as , and the negative integrity is defined as , where represent the vertex cardinality of vertex subsets and , respectively. Furthermore, denotes the maximum order of the connected component after removing , and denotes the maximum order of the connected component after removing .
Definition 13.
The sets and are referred to as the positive and negative integrity sets of Σ if and .
Example 1.
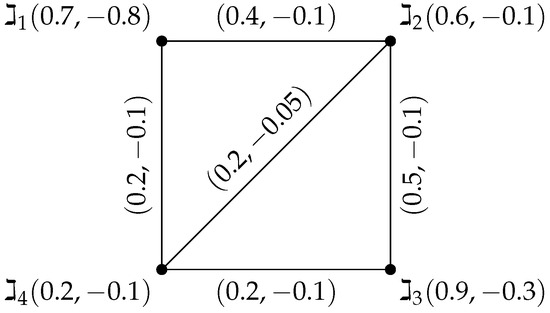

Consider a BFG such that , . Let be a bipolar fuzzy subset of as shown in Figure 1. The integrity value is calculated as shown in Table 2.

Figure 1.
BFG.

Table 2.
Integrity of BFGs.
The computation of integrity in a bipolar fuzzy graph involves systematically removing subsets of vertices and evaluating the resulting connected components. The step-by-step procedure used in this paper is outlined in Algorithm 1.
| Algorithm 1 Computation of Integrity of a BFG |
| Require: A BFG with underlying crisp graph |
| Ensure: Positive integrity , Negative integrity |
|
The evaluation of connected components, which can be completed in time for a graph with and , is the main source of computational complexity in the suggested framework. All vertex subsets are enumerated by the brute-force (exact) method, which results in a total time complexity of and space complexity of .
Theorem 1.
Let Σ be a BFG with the underlying crisp graph with n vertices. If the PVMV of Σ is and NVMV of Σ is then the integrity of Σ is
- 1.
- Null BFG is .
- 2.
- Complete BFG is .
- 3.
- Star BFG is .
- 4.
- Path BFG of length n is.
- 5.
- Cycle BFG is.
- 6.
- Complete bipartite BFG is.
Proof.
- 1.
- Consider a null BFG with constant membership values. Choosing the integrity set as empty implies and . Therefore the integrity of becomes .
- 2.
- In a complete BFG, every vertex is adjacent to all other remaining vertices. Removing a vertex set with r number of vertices leaves a single connected component with remaining vertices. Then and and hence .
- 3.
- In a star BFG, , a single vertex is adjacent to all the remaining other n vertices. Choosing that center vertex as integrity set S and removing implies all the other n vertices are isolated with constant vertex membership values. Then and implies .
- 4.
- By Theorem 2.1 in [32], if the membership values are constant, then the integrity set for both the crisp graph and fuzzy graph are same. From the definition of a BFG, it also has the same integrity set while considering constant vertex membership values. Removing a vertex set S with k vertices, at least one component will have number of vertices. The function attains its minimum at and its maximum at . Therefore .
- 5.
- Removing a vertex from a cycle with n vertices turns into a path of vertices. Including a vertex membership value with the integrity value of a path with , the integrity value of the cycle becomes .
- 6.
- Without loss of generality, assume . Let and be the vertices in . Then removing m vertices from , there are n isolated vertices each with constant positive membership value and negative membership value . Choosing the integrity set S with leaves a set of isolated vertices with each membership value , which implies and . Thus the integrity value becomes .
□
Remark 1.
For the above Theorem 1, if the membership values are the same then the integrity for the BFG, fuzzy graph, and crisp graph have same integrity set.
Remark 2.
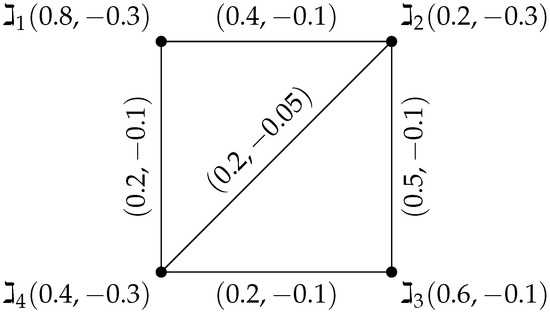

In a BFG, positive and negative integrity sets need not be same. For example, consider a BFG such that , . Let be a bipolar fuzzy subset of as shown in Figure 2. Then integrity is , as shown in Table 3.

Figure 2.
BFG.

Table 3.
Integrity of BFG.
Definition 14.
Let Σ be a bipolar fuzzy graph (BFG) with n vertices. The NSS of Σ is defined as where each , with (positive membership value) and (negative membership value). Here, denotes the vertex with the minimum membership values in the NSS, and denotes the vertex with the maximum membership values in the NSS.
Theorem 2.
Let Σ be a bipolar fuzzy path graph whose underlying crisp graph is the path on vertices. Suppose the NSS of Σ is i.e., there are vertices with positive/negative strengths , and two exceptional vertices with strengths and . Let and be the positive and negative integrity sets of Σ. Then the integrity is obtained as follows. Then the positive part is equal to one of the four quantities (depending on whether lie in ):
Similarly, the negative part equals one of the corresponding four quantities with replaced by and replaced by :
Proof.
Let Σ be a BFG with underlying crisp graph being a path with NSS where . The proof consists of two cases, where the first case deals with positive integrity and the second case discusses negative integrity.
- Case 1 Let be the positive integrity set with x vertices. Then removing from leaves or less components and at least one of them must contain vertices. Thus for a positive integrity value, the function should get a minimum value and for negative integrity, it should get a maximum value. Let ℷ be the highest order component of . The cases arise while and lies either in or ℷ or any other component. Here the vertices with membership values and are the deciding factor in finding the integrity value.
- Case 1.1 Then vertices have node strength , one vertex with node strength and another vertex with strength and ℷ have node strength . Or, if , then vertices have node strength , and one vertex with node strength and ℷ have node strength and one node with . Or, if , then vertices have node strength , and one vertex with node strength and ℷ have node strength and one node with . Or, if , then x vertices have node strength and ℷ have node strength , one node with and one vertex with node strength .Therefore and
- Case 1.2 In , then vertices have node strength and one vertex with strength and ℷ have node strength . Therefore and
- Case 1.3 If , then vertices have node strengths of and one vertex with strength and ℷ have node strength . Therefore and
- Case 1.4 If , then x vertices each have node strength and ℷ have node strength . Therefore andThe proof for is identical after replacing by and by .
□
Example 2.
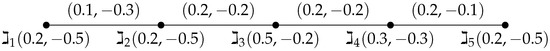
Consider a BFG such that , . Let be a bipolar fuzzy subset of as shown in Figure 3. The integrity of the path BFG is .
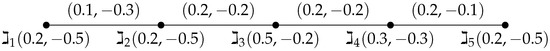
Figure 3.
Path BFG.
Theorem 3.
A bipolar fuzzy null graph integrity is defined as (maximum of the PVMV, minimum of NVMV).
Proof.
Every vertex in the given graph is an isolated vertex because it is a null bipolar graph. Let S be the empty set, then remains the same null BFG. For PVMV, is maximum. Therefore the integrity is , where maximum of PVMV and for NVMV, is minimum. Therefore the integrity is minimum of NVMV. □
Theorem 4.
In the integrity of a complete BFG is equal to (Order of the PVMV, Order of the NVMV).
Proof.
G is a complete BFG, therefore between every pair of vertex there is an edge. If any vertex is removed from then the remaining vertex will be a connected graph. For PVMV is sum of the PVMV, and for NVMV is sum of NVMV. Integrity of a complete BFG is , where = Order of the PVMV, = Order of the NVMV. □
Corollary 1.
Assume Σ is a complete BFG with n vertices and an NSS ; , where . Then integrity is .
Theorem 5.
The integrity of a bipolar star graph is , where is the centre vertex of the star graph and vertex is adjacent to .
Proof.
The centre vertex of the star bipolar graph is connected to every other vertex in . Let S be the centre vertex. When it is removed then every other vertex gets disconnected. For PVMV is the maximum value of the PVMV and for NVMV is the minimum of NVMV. Therefore integrity of a bipolar star graph is equal to , where . □
Example 3.
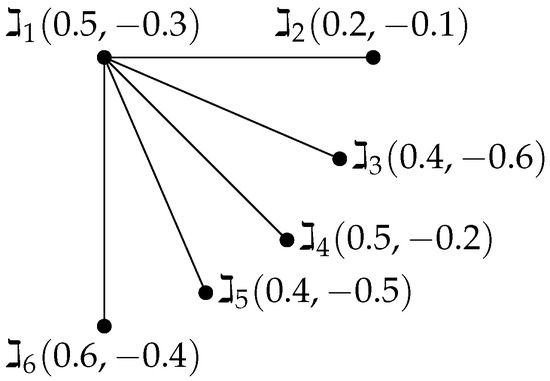
Consider a BFG such that , . Let be a bipolar fuzzy subset of as shown in Figure 4. The integrity of the star BFG is .

Figure 4.
Star BFG.
To highlight the distinction between classical and fuzzy models, we compare the integrity measures of crisp graphs, fuzzy graphs, and bipolar fuzzy graphs. The summary of these comparisons for standard graphs such as null, complete, and star graphs is presented in Table 4.

Table 4.
Comparison of integrity of crisp graph, fuzzy graph, and BFG.
3.2. Union, Join and Cartesian BFG
Integrity values for the union of BFGs, the join of BFGs, and the Cartesian product of BFGs are discussed with examples, and integrity values are found.
Theorem 6.
Let Σ be a strong BFG and be the complement of Σ. Then the integrity of BFG is .
Proof.
Let be a strong BFG and be the complement of . Then the union of and is a complete BFG. Therefore by Theorem 4, the integrity is (Order of PVMV, Order of NVMV). □
Theorem 7.
Let Σ be the union of two disjoint BFGs, with . Then , where and .
Proof.
Let Σ be the union of two disjoint BFGs with .
- Case 1: The integrity set S of a BFG is empty. Then, the integrity for PVMV of is the maximum of and and integrity for NVMV of is the minimum of and .
- Case 2: If the integrity set S is from BFG . For PVMV , then . If for any set S, , then . For NVMV , then . If for any set S, . Then .
- Case 3: If S is from and . If S is a cut vertex from or , we get at least three components in . Then the positive integrity is and negative integrity is , where and . If S does not have any cut vertex of or , it cannot be the integrity set for , since and are disjoint. Combining the above cases, integrity is and .
□
Theorem 8.
Let Σ be the union of two disjoint connected BFGs, and . Then , where is and is .
Theorem 9.
Let and be two connected BFGs, then the join with . Then , where and .
Proof.
According to the definition of the join of two BFGs, one edge connects each vertex from to .
If and are complete BFGs, then the join of and is also a complete BFG. Then the integrity for PVMV is sum of PVMV and for NVMV integrity is sum of NVMV.
If and are two disjoint connected BFGs, then the join of is a complete BFG. Then the integrity for positive vertex membership value is sum of PVMV and the integrity for NVMV is sum of NVMV. □
Example 4.
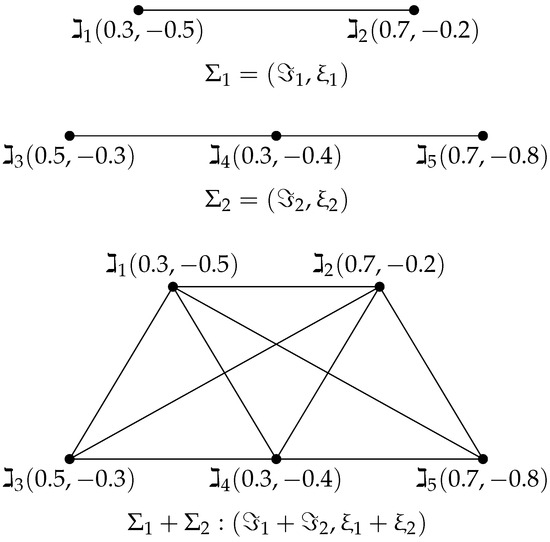
Consider two BFGs such that , and such that , . Then the join of and is shown in Figure 5.

Figure 5.
Join of two BFGs.
Theorem 10.
Let be a star BFG. Then , where maximum and minimum .
Theorem 11.
Let and be two connected BFGs with vertex set and and edges and , respectively. Let Σ be the cartesian BFG of and . Let and be two partial subgraphs of Σ. Then the integrity of is and , where is the minimal set of and .
Proof.
The BFG consists of two partial subgraphs and , which are isomorphic to . remains a single connected component after less than n vertices are removed. Therefore, in order to break the graph, we must take away at least n vertices from and . In BFG, if n vertices are removed then with minimal set is the integrity. Similarly in BFG if n vertices are removed then with minimal set is the integrity. The integrity value of is and , where is the minimal set of and . □
Example 5.

Consider two BFG such that , and such that , . Then the cartesian of and is shown in Figure 6.

Figure 6.
Cartesian product of two BFG.
Theorem 12.
Let and be two BFGs, then the cartesian BFG is . Then , where Sum of PVMV +maximum order of the PVMV in n components and Sum of NVMV +minimum order of the NVMV in n components.
Proof.
Let the vertices of be and be , where vertex u is the central vertex in with degree n. Let the minimal set , then has m components of . The integrity of is Sum of PVMV +maximum order of the PVMV in n components and Sum of NVMV +minimum order of the NVMV in n components. □
Theorem 13.
Let and be two BFGs, then the cross BFG is . Then , where +maximum order of the PVMV in m components and +minimum order of the NVMV in m components, where S is the minimal set.
Proof.
Let the vertices of be and has vertices in one partite set and are in the other partite set, respectively. Let the minimal set of be , then has m components of . The integrity of is +maximum order of the PVMV in m components and +minimum order of the NVMV in m components, where S is the minimal set. □
Example 6.
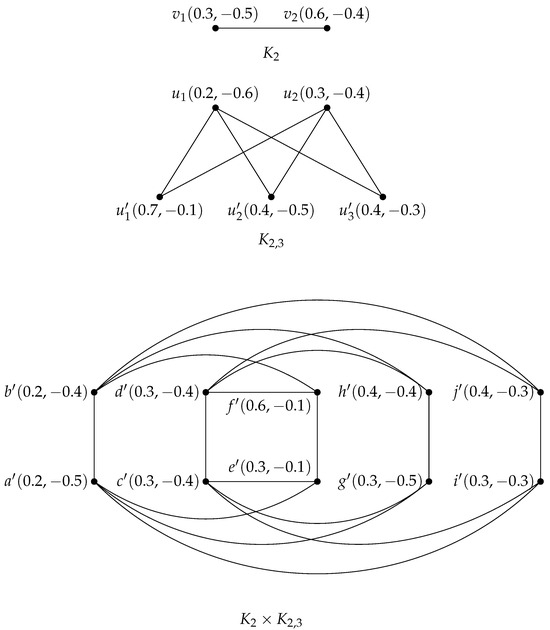
Consider two BFG of and . Then cartesian of and is shown in Figure 7.

Figure 7.
Cartesian BFG of and .
Theorem 14.
Let and be two BFGs, then the cartesian BFG is . Then , where + and + .
Proof.
Let the vertices of be and the vertices of be . Let the minimal set of be , then has only one component of . The integrity of BFG is + and + . □
3.3. Application
When modeling real-world problems with mathematical models, it is important to recognize that every model has limitations. For new projects, it is essential to consider both advantages and disadvantages. By assigning fuzzy membership values to these pros and cons, the pros receive positive membership values, while the cons are assigned negative membership values.
If these values are considered as membership values of a fuzzy graph, it transforms into a bipolar fuzzy graph (BFG). The road network serves as a fundamental transportation mode for goods and people, significantly impacting a country’s economy. When implementing a project within the road network, choosing the right path optimizes both profit and loss comprehensively. Longer road lengths directly lead to increased gasoline and diesel consumption, contributing to environmental issues. At times, the compensation cost significantly surpasses the actual cost of road construction.
As a result, road construction has both positive and negative effects on social and economic conditions. This network type can be considered as a BFG. The positive impact is represented by positive membership values, while the negative impact is represented by negative membership values on specific nodes.
Consider a road network where nodes in the graph represent specific areas, places, villages, or towns, and the edges denote proposed road routes. Each node’s positive membership value represents economic gain, while the negative membership value represents economic loss due to environmental issues for that node. The integrity parameter is particularly helpful in identifying the optimal transmission path in such problems.
The network depicted in Figure 8 illustrates all possible road routes from node to node . There are seven distinct paths between these two nodes:
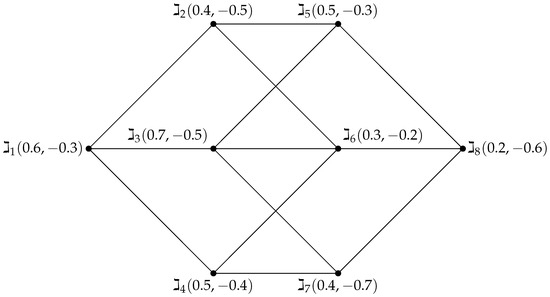
Figure 8.
Roadway from vertex to .
For each path S, the integrity set is defined as where and are the cumulative positive and negative membership values of nodes in S, is the maximum positive membership value in the complement, and is the maximum negative membership value in the complement.
From Table 5, the path achieves the minimal positive integrity, and the path achieves the maximal negative integrity. Thus, the overall integrity of the BFG is obtained as after normalization. This ensures that the transmission from to is selected based on both economic gain and environmental loss in a balanced manner.

Table 5.
Integrity of BFG.
4. Conclusions
Both advantages and disadvantages are simultaneously reflected in the study of integrity in bipolar fuzzy graphs (BFGs), which extend traditional graph theory by incorporating both positive and negative membership values. By considering vertex removal and the resulting components, the integrity parameter defined as a tuple of positive and negative integrities effectively evaluates the robustness and vulnerability of BFGs. Interestingly, as the examples demonstrate, the integrity parameter can assume both positive and negative values, reflecting the complex trade-offs observed in real-world systems modelled by BFGs.
A comprehensive understanding of the structural resilience of BFGs is obtained by investigating integrity across specific graph classes, including null, complete, star, path, cycle, and bipartite graphs, as well as under operations such as union, join, and Cartesian product. Modeling a road network as a BFG further demonstrates the practical value of the integrity measure in a real-world application. In this case, positive membership values represent financial gains, while negative values capture environmental losses, showing how the network’s integrity can guide decisions that balance ecological impact with economic profit.
Overall, the integrity parameter of bipolar fuzzy graphs serves as a valuable tool for evaluating and improving complex systems with competing criteria, thereby enabling better decision-making in real-world applications. Moreover, this concept can be extended to intuitionistic fuzzy graphs and generalized fuzzy graphs, offering broader opportunities for research and application.
Author Contributions
Funding acquisition, M.A. and S.O.H.; Conceptualization, G.V.N. and P.C.; Software, G.V.N.; Formal analysis, M.A.; Methodology, S.O.H.; Supervision, G.V.N. and M.A.; Writing—original draft, M.A. and G.V.N.; Validation, P.C. and S.O.H.; Writing—review and editing, G.V.N. and S.O.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Deanship of Research and Graduate Studies at King Khalid University, Project under grant number RGP. 2/81/46 and Deanship of Scientific Research at Northern Border University. Project Number “NBU-FFR-2025-781-14”.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through Large Research Project under grant number RGP. 2/81/46, the authors also express their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, Saudi Arabia for funding this research work through project number “NBU-FFR-2025-781-14”.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Rosenfeld, A. Fuzzy graphs. In Fuzzy Sets and Their Applications to Cognitive and Decision Processes; Academic press: Cambridge, MA, USA, 1975; pp. 77–95. [Google Scholar]
- Bhutani, K.R. On automorphisms of fuzzy graphs. Pattern Recognit. Lett. 1989, 9, 159–162. [Google Scholar] [CrossRef]
- Bhutani, K.R.; Rosenfeld, A. Strong arcs in fuzzy graphs. Inf. Sci. 2003, 152, 319–322. [Google Scholar] [CrossRef]
- Sunitha, M.; Vijayakumar, A. Complement of a fuzzy graph. Indian J. Pure Appl. Math. 2002, 33, 1451–1464. [Google Scholar]
- Mathew, S.; Sunitha, M. Node connectivity and arc connectivity of a fuzzy graph. Inf. Sci. 2010, 180, 519–531. [Google Scholar] [CrossRef]
- Sunitha, M.; Mathew, S. Fuzzy graph theory: A survey. Ann. Pure Appl. Math. 2013, 4, 92–110. [Google Scholar]
- Jamil, M.K. Distance-based topological indices and double graph, Iranian Journal of Mathematical Chemistry. Univ. Kashan 2017, 8, 83–91. [Google Scholar]
- Ali, S.; Jamil, M.K.; Azeem, M.; Zahid, M.A.; Ismail, T.A. Double resolving sets and the exchange property with applications in network optimization and cybersecurity. Mater. Chem. Phys. 2025, 346, 131289. [Google Scholar] [CrossRef]
- Akram, M. Bipolar fuzzy graphs. Inf. Sci. 2011, 181, 5548–5564. [Google Scholar] [CrossRef]
- Akram, M.; Dudek, W.A. Regular bipolar fuzzy graphs. Neural Comput. Appl. 2012, 21, 197–205. [Google Scholar] [CrossRef]
- Rashmanlou, H.; Samanta, S.; Pal, M.; Borzooei, R.A. A study on bipolar fuzzy graphs. J. Intell. Fuzzy Syst. 2015, 28, 571–580. [Google Scholar] [CrossRef]
- Broumi, S.; Smarandache, F.; Talea, M.; Bakali, A. An introduction to bipolar single valued neutrosophic graph theory. Appl. Mech. Mater. 2016, 841, 184–191. [Google Scholar] [CrossRef]
- Pramanik, T.; Pal, M.; Mondal, S.; Samanta, S. A study on bipolar fuzzy planar graph and its application in image shrinking. J. Intell. Fuzzy Syst. 2018, 34, 1863–1874. [Google Scholar] [CrossRef]
- Akram, M. Bipolar fuzzy graphs with applications. Knowl.-Based Syst. 2013, 39, 1–8. [Google Scholar] [CrossRef]
- Ghorai, G.; Pal, M. Certain types of product bipolar fuzzy graphs, International. J. Appl. Comput. Math. 2017, 3, 605–619. [Google Scholar]
- Samanta, S.; Pal, M. Irregular bipolar fuzzy graphs. arXiv 2012, arXiv:1209.1682. [Google Scholar] [CrossRef]
- Karunambigai, M.; Akram, M.; Palanivel, K.; Sivasankar, S. Domination in bipolar fuzzy graphs. In Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Hyderabad, India, 7–10 July 2013; pp. 1–6. [Google Scholar]
- Mohideen, B.A. Types of degrees in bipolar fuzzy graphs. Appl. Math. Sci. 2013, 7, 4857–4866. [Google Scholar] [CrossRef][Green Version]
- Rashmanlou, H.; Jun, Y.B.; Borzooei, R. More results on highly irregular bipolar fuzzy graphs. Ann. Fuzzy Math. Inform. 2014, 8, 149–168. [Google Scholar][Green Version]
- Akram, M.; Akmal, R. Application of bipolar fuzzy sets in graph structures. Appl. Comput. Intell. Soft Comput. 2016, 2016, 5859080. [Google Scholar] [CrossRef]
- Akram, M.; Waseem, N. Novel applications of bipolar fuzzy graphs to decision making problems. J. Appl. Math. Comput. 2018, 56, 73–91. [Google Scholar] [CrossRef]
- Rashmanlou, H.; Samanta, S.; Pal, M.; Borzooei, R.A. Bipolar fuzzy graphs with categorical properties. Int. J. Comput. Intell. Syst. 2015, 8, 808–818. [Google Scholar] [CrossRef]
- Talebi, A.A.; Rashmanlou, H. Complement and isomorphism on bipolar fuzzy graphs. Fuzzy Inf. Eng. 2014, 6, 505–522. [Google Scholar] [CrossRef]
- Rashmanlou, H.; Samanta, S.; Pal, M.; Borzooei, R.A. Product of bipolar fuzzy graphs and their degree. Int. J. Gen. Syst. 2016, 45, 1–14. [Google Scholar] [CrossRef]
- Gong, S.; Hua, G.; Zhang, X. Bipolar picture fuzzy graph based multiple attribute decision making approach-part ii. In International Conference on Machine Learning for Cyber Security; Springer: Cham, Switzerland, 2022; pp. 309–320. [Google Scholar]
- Lu, J.; Zhu, L.; Gao, W. Structured representation of fuzzy data by bipolar fuzzy hypergraphs. In International Conference on Machine Learning for Cyber Security; Springer: Cham, Switzerland, 2022; pp. 663–676. [Google Scholar]
- Pandey, S.D.; Ranadive, A.; Samanta, S. Bipolar-valued hesitant fuzzy graph and its application. Soc. Netw. Anal. Min. 2022, 12, 14. [Google Scholar] [CrossRef] [PubMed]
- Poulik, S.; Ghorai, G. Applications of graph’s complete degree with bipolar fuzzy information. Complex Intell. Syst. 2022, 8, 1115–1127. [Google Scholar] [CrossRef]
- Talebi, A.A.; Amiri, S.O. Cayley bipolar fuzzy graphs associated with bipolar fuzzy groups. Int. J. Adv. Intell. Paradig. 2023, 24, 1–11. [Google Scholar]
- Goddard, W.; Swart, H.C. Integrity in graphs: Bounds and basics. J. Combin. Math. Combin. Comput 1990, 7, 139–151. [Google Scholar]
- Bagga, K.S.; Beineke, L.W.; Goddard, W.D.; Lipman, M.J.; Pippert, R.E. A survey of integrity. Discret. Appl. Math. 1992, 37, 13–28. [Google Scholar] [CrossRef]
- Kirlangic, A. On the weak-integrity of graphs. J. Math. Model. Algorithms 2003, 2, 81–95. [Google Scholar] [CrossRef]
- Mahde, S.S.; Mathad, V. On weak hub-integrity of graphs. Gulf J. Math. 2017, 5, 14. [Google Scholar] [CrossRef]
- Mahde, S.S.; Mathad, V.; Sahal, A.M. Hub-integrity of graphs. Bull. Int. Math. Virtual Inst. 2015, 5, 57–64. [Google Scholar]
- Kılıc, E.; Besirik, A. Domination edge integrity of graphs. Adv. Math. Models Appl. 2018, 3, 234–238. [Google Scholar]
- Besirik, A. Total domination integrity of graphs. J. Mod. Technol. Eng. 2019, 4, 11–19. [Google Scholar]
- Saravanan, M.; Sujatha, R.; Sundareswaran, R. Integrity of fuzzy graphs. Bull. Int. Math. Virtual Inst. 2016, 6, 89–96. [Google Scholar]
- Mariappan, S.; Ramalingam, S.; Raman, S.; Bacak-Turan, G. Domination integrity and efficient fuzzy graphs. Neural Comput. Appl. 2020, 32, 10263–10273. [Google Scholar] [CrossRef]
- Saravanan, M.; Sujatha, R.; Sundareswaran, R.; Sahoo, S.; Pal, M. Concept of integrity and its value of fuzzy graphs. J. Intell. Fuzzy Syst. 2018, 34, 2429–2439. [Google Scholar] [CrossRef]
- Saravanan, M.; Sujatha, R.; Sundareswaran, R.; Balasubramanian, M.S. Application of domination integrity of graphs in pmu placement in electric power networks. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 2066–2076. [Google Scholar] [CrossRef]
- Sujatha, R.; Saravanan, M.; Sundareswaran, R. Brain network analysis through span integrity of fuzzy graphs. New Math. Nat. Comput. 2023, 19, 525–539. [Google Scholar] [CrossRef]
- Chakaravarthy, S.; Chandran, K.; Mariappan, S.; Ramalingam, S. Edge integrity for signed fuzzy graphs. J. Intell. Fuzzy Syst. 2022, 43, 4681–4690. [Google Scholar] [CrossRef]
- Chakaravarthy, S.; Chandran, K.; Mariappan, S.; Ramalingam, S. An algorithmic approach to signed fuzzy graph integrity: Complexity, graph operations, and metro rail network applications. Ain. Shams. Eng. J. 2025, 16, 103509. [Google Scholar]
- Sankar, C.; Kalaivani, C.; Chellamani, P.; Venkat Narayanan, G. Analyzing Network Stability via Symmetric Structures and Domination Integrity in Signed Fuzzy Graphs. Symmetry 2025, 17, 766. [Google Scholar] [CrossRef]
- Lee, K.M. Bipolar-valued fuzzy sets and their operations. In Proceedings of the International Conference on Intelligent Technologies, Bangkok, Thailand, 13–15 December 2000; pp. 307–312. [Google Scholar]
- Zhang, W.-R. Bipolar fuzzy sets and relations: A computational framework for cognitive modeling and multiagent decision analysis, in NAFIPS/IFIS/NASA’94. In Proceedings of the First International Joint Conference of the north American Fuzzy Information Processing Society Biannual Conference. The Industrial Fuzzy Control and Intellige, San Antonio, TX, USA, 18–21 December 1994; pp. 305–309. [Google Scholar]
- Akram, M.; Sarwar, M.; Dudek, W.A. Graphs for the Analysis of Bipolar Fuzzy Information; Springer: Sinapore, 2021; Volume 401. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).