The Cramér–Von Mises Statistic for Continuous Distributions: A Monte Carlo Study for Calculating Its Associated Probability ^†

Abstract

The Cramér–von Mises (CM) statistic can assess the goodness-of-fit when the null distribution is independent of the underlying distribution, provided it is continuous, resulting in a universality that supports symmetry in its application and interpretation. Along with other order statistics, it serves in a battery of tests. A key element in its use is availability of the cumulative distribution function inverse for calculating the p-value. CM does not have an explicit formula for the cumulative distribution function. Here, a Monte–Carlo experiment was deployed to generate a large amount of data resembling CM. Furthermore, regression analysis was deployed, in order to obtain the dependence of the p-value as function of the statistic and of the sample size. For two cases, one assuming Beta distribution and the other assuming Cauchy distribution, an analysis using the CM statistic was conducted.

1. Introduction

The literature is abundant on the uses of the Cramér–von Mises test in biological sciences for comparing observed distributions of biological phenomena against theoretical models [1] and for testing if certain biological data (like gene expression levels [2] and physiological measurements [3]) follows a theoretical distribution as prerequisite in applying parametric statistical methods.

In relation to complexity [4], the Cramér–von Mises statistic (CM) is used, along with other statistics, to assess the goodness of fit statistics for average yield (per acre) of Bajra in the Punjab province, having 12 alternatives for the population distribution function. This is a regular report using CM (others may be enumerated here: [5,6,7,8]). However, one should notice that the probability associated with the CM statistic is usually not provided (see [4]). In most instances, its absence is masked behind the reporting of software use. Take, for instance, ref. [9], where R (version 4.2.1) is reported in the supplementary material (of  [9]) to provide calculations for the statistic. One explanation is given at the end of the Literature survey subsection below.

Along with Anderson–Darling [10,11] and Kolmogorov–Smirnov [12,13], CM [14,15] is a well-known statistic of which applications include goodness-of-fit testing for discrete [16] and continuous [17,18] distributions and parameter estimation [19,20,21]. In goodness-of-fit testing with CM, tabulated critical values are unfortunately used [17,18,22] (explanation given at the end of Literature survey subsection below). Other applications include using CM as a metric [23].

Take a sample size of n, $\{x_1,\dots ,x_n\}$. Please note that the values in the sample are not necessarily ordered or distinct. Assume for the sample a theoretical distribution for which the cumulative distribution function (CDF) is available. Then, the cumulative probabilities $\{q_1,\dots ,q_n\}$ can be computed as in Equation (1).

$$\{q_1,\dots ,q_n\}=\mathrm{CDF}(\{x_1,\dots ,x_n\};{\alpha }_1,\dots ,{\alpha }_k),$$

(1)

where ${\alpha }_1,\dots ,{\alpha }_k$ are the parameters of the theoretical distribution.

The existence of the CDF is essential for what follows, since it is the one which brings an arbitrary distribution (of $\{x_1,\dots ,x_n\}$) to the standard continuous uniform distribution (of $\{q_1,\dots ,q_n\}$). The implicit expectation is that the identification of the parameters did not decrease from the number of the degrees of freedom (n), such as being determined from maximum likelihood estimation (MLE, see [24]). If some of the parameters are explicitly determined using values from the sample (such as using methods of moments), then their number should be decreased from the degrees of freedom of the sample (see [25]). If all of them were explicitly determined using the values from the sample, then the number of the degrees of freedom is reduced correspondingly (to $n-k$).

The next step is to sort the probabilities, in order to arrive at a permutation of them, as in Equation (2).

$$\{s_1,\dots ,s_n\}=\mathrm{Sort}\left(\{q_1,\dots ,q_n\}\right),$$

(2)

where sorting is expected to produce an ascending order ($s_1\le \dots \le s_n$).

With the sorted probabilities, the Cramér–von Mises sample statistic ($CM$) can be computed as in Equation (3).

$$\mathrm{CM}\left(\{s_1,\dots ,s_n\}\right)={\displaystyle \frac{1}{12n}}+\sum _{i=1}^n{\left({\displaystyle \frac{2i-1}{2n}}-s_i\right)}^2$$

(3)

The basic CM statistic itself is symmetric. It measures the overall squared deviation between the expected and observed CDF across the range of the data (Equation (3)), treating deviations above and below the theoretical distribution with equal importance, so the statistic itself does not favor one side of the distribution over the other.

As an alternative, one computes the Kolmogorov–Smirnov statistic ($KS$) with Equation (4).

$$\mathrm{KS}\left(\{s_1,\dots ,s_n\}\right)=\underset{i=1,\dots ,n}{max}\left(s_i-{\displaystyle \frac{i-1}{n}},{\displaystyle \frac{i}{n}}-s_i\right)$$

(4)

The final step is using a table (detailing values by sample size n and statistical significance $\alpha$) to compare the calculated value $CM\left(\{s_1,\dots ,s_n\}\right)$ with a tabulated one, for possibly rejecting the hypothesis of the distribution (distribution having CDF from Equation (1)) or of a function (feed with n and $CM\left(\{s_1,\dots ,s_n\}\right)$), which retrieves a probability to observe such a large value simply by chance. The objective is to obtain the latter.

Literature Survey

Specialized CM statistics can be constructed specifically to test whether a distribution is symmetric about zero or another center [26]. These tests use the general quadratic form of the CM statistic, but are formulated to assess whether the distribution of data is mirror-symmetric around a point. In fact, several references propose CM-type statistics where the null hypothesis is the symmetry of the distribution function, and their development ensures that, under the null, the statistic reflects symmetry [27,28,29,30].

In [31], some limited results are reported for the model of ${\mathrm{CDF}}_{\mathrm{CM}}$ as a function of n and $CM$. Thus, following their notation, if $V_n\left(CM\right)\leftarrow {\mathrm{CDF}}_{\mathrm{CM}}(CM;n)$, then:

• For $V\left(x\right)\leftarrow \underset{n\to \infty }{lim}{V}_n\left(x\right)$, with $D_v\left(u\right)$, the parabolic cylinder function of index v and argument u and $u,v\in \mathbb{R}$ (see p. 687 in [32]):

  $$V\left(x\right)={\displaystyle \frac{2}{{\pi }^{1/2}{x}^{1/4}}}\sum _{k=0}^{\infty }{\displaystyle \frac{\mathrm{\Gamma }(k+1/2)}{k!\mathrm{\Gamma }(1/2)}}{\mathrm{e}}^{-{\displaystyle \frac{{(4k+1)}^2}{16x}}}{\mathrm{D}}_{-1/2}\left({\displaystyle \frac{4k+1}{2x^{1/2}}}\right)$$

  (5)
• For $x\in \mathbb{R}$:

  $$V_n\left(x\right)=V\left(x\right)+{\displaystyle \frac{{\psi }_1\left(x\right)}{n}}+\mathcal{O}\left({\displaystyle \frac{1}{n^2}}\right)$$

  (6)
• For ${\displaystyle \frac{1}{12n}}\le CM\le {\displaystyle \frac{n+3}{12n^2}}$:

  $$V\left(x\right)={\displaystyle \frac{n!{\pi }^{n/2}}{\mathrm{\Gamma }(n/2+1)}}{\left(x-{\displaystyle \frac{1}{12n}}\right)}^{n/2}$$

  (7)
• For $x\in \mathbb{R}$:

  $$\begin{array}{c}\hfill {\psi }_1\left(x\right)={\displaystyle \frac{1}{12}}V\left(x\right)-{\displaystyle \frac{1}{9{\pi }^{1/2}{x}^{3/4}}}\sum _{k=0}^{\infty }{\displaystyle \frac{\mathrm{\Gamma }(k+3/2)}{k!\mathrm{\Gamma }(3/2)}}{\mathrm{e}}^{-{\displaystyle \frac{{(4k+3)}^2}{16x}}}{\mathrm{D}}_{1/2}\left({\displaystyle \frac{4k+3}{2x^{1/2}}}\right)\\ \hfill -{\displaystyle \frac{7}{144{\pi }^{1/2}{x}^{3/4}}}\sum _{k=0}^{\infty }{\displaystyle \frac{\mathrm{\Gamma }(k+3/2)}{k!\mathrm{\Gamma }(3/2)}}{\mathrm{e}}^{-{\displaystyle \frac{{(4k+1)}^2}{16x}}}{\mathrm{D}}_{1/2}\left({\displaystyle \frac{4k+1}{2x^{1/2}}}\right)\\ \hfill -{\displaystyle \frac{7}{144{\pi }^{1/2}{x}^{3/4}}}\sum _{k=0}^{\infty }{\displaystyle \frac{\mathrm{\Gamma }(k+3/2)}{k!\mathrm{\Gamma }(3/2)}}{\mathrm{e}}^{-{\displaystyle \frac{{(4k+5)}^2}{16x}}}{\mathrm{D}}_{1/2}\left({\displaystyle \frac{4k+5}{2x^{1/2}}}\right)\\ \hfill -{\displaystyle \frac{1}{72{\pi }^{1/2}{x}^{5/4}}}\sum _{k=0}^{\infty }{\displaystyle \frac{\mathrm{\Gamma }(k+1/2)}{k!\mathrm{\Gamma }(1/2)}}{\mathrm{e}}^{-{\displaystyle \frac{{(4k+3)}^2}{16x}}}{\mathrm{D}}_{1/2}\left({\displaystyle \frac{4k+1}{2x^{1/2}}}\right)\\ \hfill -{\displaystyle \frac{1}{72{\pi }^{1/2}{x}^{5/4}}}\sum _{k=0}^{\infty }{\displaystyle \frac{\mathrm{\Gamma }(k+5/2)}{k!\mathrm{\Gamma }(5/2)}}{\mathrm{e}}^{-{\displaystyle \frac{{(4k+3)}^2}{16x}}}{\mathrm{D}}_{1/2}\left({\displaystyle \frac{4k+5}{2x^{1/2}}}\right)\end{array}$$

  (8)

Since the above given formulas are infinite series and/or limited by a range of values, they have reduced practical usability for small samples. No progress has been reported since [31].

To alleviate the inconveniences of the absence of an analytical formula for the calculation of the p-value (named empirical level in [16]), the CM test statistic is formulated in [33] using a norm, with calibration achieved via a wild bootstrap resampling procedure. Please note that [33] does not deal with small samples, using a fixed size of $n=1000$ and bootstrapping 1500 samples.

2. Materials and Methods

The first step in obtaining a statistic-probability map for CM is to generate a large amount of data, getting as close as possible to the population of the CM (sample statistic $CM$ is given as Equation (3)). This experiment is usually called Monte–Carlo (MC).

An MC simulation requires a large number of samples drawn from the uniform continuous distribution. The question is, how many?

A (pseudo) random number generator is available in many software programs and, in most cases, it is based on Mersenne Twister [34], uniformly generating numbers from the $[0,1)$ interval.

To ensure a good quality of the simulation, simply using a random number generator is not good enough.

The question is whether the sampling can be manipulated somehow, in order to increase its quality, and the answer is yes.

What if one must extract a sample of size $n=2$ (let us extract $s_1$ and $s_2$)? By splitting the $[0,1)$ interval in two equal parts, then extracting two values from it, the analysis of the cases is as follows:

• Extracting both $s_1$ and $s_2$ from $[0,0.5)$: 25%; extracting both $s_1$ and $s_2$ from $[0.5,1)$: 25%; extracting one (either $s_1$ or $s_2$) from $[0,0.5)$ and one (either $s_1$ or $s_2$) from $[0.5,1)$: 50%.
• If four extractions are needed, both $s_1$ and $s_2$ should be from $[0,0.5)$ in one extraction, in another, both $s_1$ and $s_2$ are from $[0.5,1)$, and in two extractions, one (either $s_1$ or $s_2$) from $[0,0.5)$ and one (either $s_1$ or $s_2$) from $[0.5,1)$: 50% should be extracted.
• Going further, an extraction from $[0.5,1)$ is equivalent to an extraction from $[0,0.5)$, at which 0.5 is added.

The analysis above can be generalized for a sample of size n. Thus, if $s_1$, $s_2$, …, $s_n$ are to be taken from $[0,1)$, then one can instead extract $s_1$, $s_2$, …, $s_n$ from $[0,0.5)$ and follow

Table 1. Refining the sampling.

	Is ${\mathit{s}}_{\mathit{i}}\in [0,0.5)?$ (${\mathit{s}}_{\mathit{i}}\in [0.5,1)$ Otherwise)						Occurrence
i	1	…	j	$j+1$	…	n
$d_0$	0	…	0	0	…	0	$\left({\displaystyle \genfrac{}{}{0pt}{}{n}{0}}\right)$
…	…	…	…	…	…	…	…
$d_j$	0	…	0	1	…	1	$\left({\displaystyle \genfrac{}{}{0pt}{}{n}{j}}\right)$
…	…	…	…	…	…	…	…
$d_n$	1	…	1	1	…	1	$\left({\displaystyle \genfrac{}{}{0pt}{}{n}{n}}\right)$

$d_j=\{s_1,\dots ,s_n\}$.

to proliferate $2^n$ samples, represented in a simplified way with $n+1$ entries, using one generated sample.

According to the design given in Table 1, for n numbers to be drawn from [0, 1), a multiple of $n+1$ drawings must be made.

Now, an answer to the question of how many samples can be given: the largest multiple of $n+1$, limited only by hardware and software: the internal memory capacity and the maximum array size.

The algorithm implementing this strategy for CM is given as the Algorithm 1 below.

Algorithm 1 MC experiment for CM (MC-CM)

$$\begin{array}{cc}\hfill & MA\leftarrow \mathrm{100,000,000};//\mathrm{maximum} \mathrm{array} \mathrm{size}\hfill \\ \hfill & m\leftarrow MA-\mathrm{Remainder}(MA,n);\hfill \\ \hfill & //\mathrm{With}\mathrm{Rand}\mathrm{a}\mathrm{good}\mathrm{random}\mathrm{number}\mathrm{generator}\hfill \\ \hfill & \mathrm{For}(k=1;k\le m;k+=n+1)\hfill \\ \hfill & \mathrm{For}(i=1;i\le n;i++)q_i\leftarrow \mathrm{Rand};//q_i\in [0,1]\hfill \\ \hfill & \mathrm{For}(i=0;i\le n;i++)\hfill \\ \hfill & \mathrm{For}(j=1;j\le n;j++)s_j\leftarrow {\displaystyle \frac{q_j}{2}};//s_j\in [0,0.5]\hfill \\ \hfill & \mathrm{For}(j=i+1;j\le n;j++)s_j\leftarrow s_j+{\displaystyle \frac{1}{2}};//s_j\in [0.5,1]\hfill \\ \hfill & \mathrm{Sort}\left(\{s_1,\dots ,s_n\}\right);//\mathrm{see} \mathrm{Equation} \left(2\right)\hfill \\ \hfill & {\mathrm{CMv}}_{k+i}\leftarrow \mathrm{CM}\left(\{s_1,\dots ,s_n\}\right);//\mathrm{see} \mathrm{Equation} \left(3\right)\hfill \end{array}$$ $\begin{array}{cc}\hfill & {\mathrm{CMf}}_{k+i}\leftarrow \left({\displaystyle \genfrac{}{}{0pt}{}{n}{i}}\right);//\hfill \end{array}$see Table 1 $$\begin{array}{cc}\hfill & \mathrm{EndFor};\hfill \\ \hfill & \mathrm{EndFor};\hfill \\ \hfill & \mathrm{Sort}(\mathrm{CMv},\mathrm{CMf});//\mathrm{CDF} \mathrm{of} \mathrm{CM} \mathrm{is} \mathrm{constructed}\hfill \end{array}$$

The algorithm provides for a given sample size n the CDF for CM, as it results from the MC experiment.

Other strategies of sampling have also been reported, so one can say that the idea behind the MC-CM algorithm is not completely new. Take, for instance, $\mathtt{R}\mathtt{Software}$. According to its manuals, it implements the sampling with the Walker’s alias method, as described in [35]. The Walker’s alias method returns integer values $1\le i\le n$ according to some arbitrary discrete probability distribution [36]. Based on the two tables (one containing probabilities and the other aliases), a random outcome is obtained as an index into the two tables. In a way, the CM-MC algorithm uses tables as well, but the probability one is not internally stored since the distribution is very simple, uniform. Instead of using the second table for aliases, it is used for mirroring the sampling in its subintervals (see Table 1). The proposed method balances the sampling, resembling a stratified sampling much more than a random sampling. In the CM-MC algorithm, the variable m controls stratification, being the greatest multiple of n smaller than the amount of available memory ($MA$). Then, the m samples are generated according to the strategy illustrated in Table 1.

One alternative is to obtain the probability associated with CM statistics by MC sampling on demand [37]. Apart from the disadvantage of this alternative that two different executions produce different probabilities, the proposed CM-MC method offers other advantages, which stem from the reduction of sampling error by applying the sampling refinement illustrated in Table 1.

3. Results and Discussions

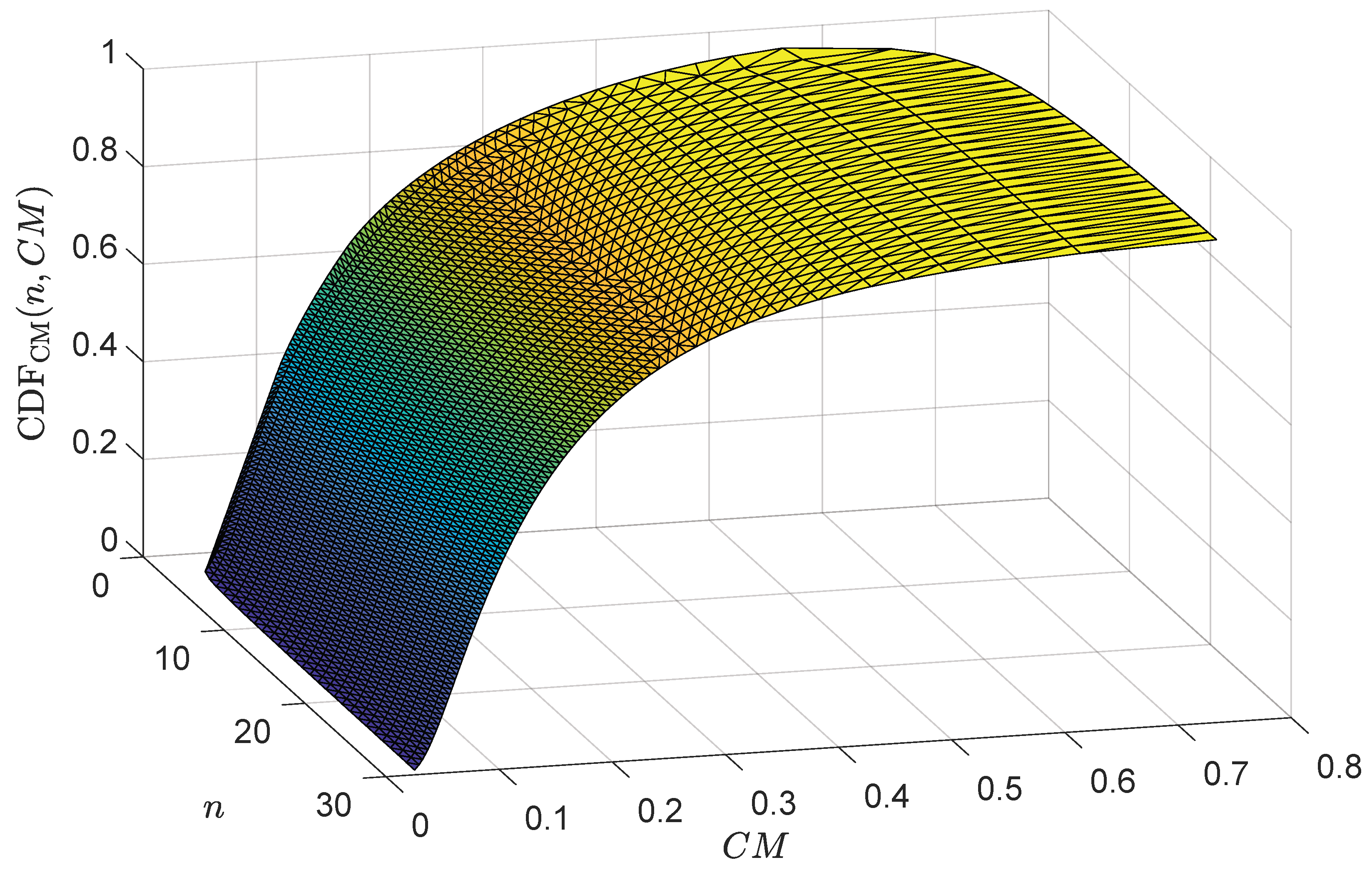
3.1. Raw Data

The MC-CM algorithm generates a very large amount of raw data for a given sample size n. This sample can be seen as close as possible to the CM population statistic (${\mathrm{CM}}_{\mathrm{P}}$). However, different percentiles (very commonly the one at 5%) or tenths of percentiles are usually preferred.

Figure 1 is obtained from the MC-CM algorithm by averaging generated data. The Matlab trisurf function was used for visual effects while the Delaunay function was used for triangulation.

A grid of percentiles (from 1% to 99%) for sample sizes from $n=2$ to $n=30$ was used to generate Figure 1. The major changes (having abrupt slopes) can be observed for small values of the sample statistic ($CM$).

Quantiles from 0.001 to 0.999 were extracted from the raw data and further investigated to be estimated by a linear or nonlinear model.

A number of 21 MC-CM experiments were run, and 21 independent samples of CM quantiles from 0.001 to 0.999 for n, ranging from 2 to 30, were generated.

3.2. A Nonlinear Model for CM: Using Its Inverse for Calculating the Associated Probability

Since the linear regression is preferred for simplicity, interpretability, and efficiency, and nonlinear regression offers flexibility for complex patterns at the expense of increased complexity and computation, the simplest way is to transform the data to a linear form, but this task is not possible every time. Nonlinear regression was chosen for this paper, since the relationship is clearly nonlinear. This was done to obtain a better fit and flexibility, in order to outweigh the costs of increased complexity and reduced interpretability.

A cubic/cubic rational on n was defined ($R_{33}$ in Equation (9)) since it was identified as a pattern in the raw data, expressing the CM population statistic (${\mathrm{CM}}_{\mathrm{P}}$) as a function of sample size n and cumulative probability q.

$$R_{33}(z;c_0,\dots ,c_6)={\displaystyle \frac{c_0+c_1{z}^{-1}+c_2{z}^{-2}+c_3{z}^{-3}}{1+c_4{n}^{-1}+c_5{n}^{-2}+c_6{n}^{-3}}}$$

(9)

A frontier between two models, one expressing better ${\mathrm{CM}}_{\mathrm{P}}$ as function of q, and the other expressing better ${\mathrm{CM}}_{\mathrm{P}}$ as function of p-value ($p=1-q$), was found (Equation (10)).

$$\begin{array}{cc}\hfill f_{\mathrm{CM}}\left(n\right)=R_{33}(n,0.10716,& -1.244,4.64,-5.66,\hfill \\ \hfill & -11.68,43.8,-53.6)\hfill \end{array}$$

(10)

The $f_{\mathrm{CM}}$ frontier depicted in Figure 2 has a vertical asymptote between 5 and 6 ($n\approx 5.4386$). When $CM$ is above the $f_{\mathrm{CM}}$ frontier, the model having q as an actual parameter is to be used. When $CM$ is below the $f_{\mathrm{CM}}$ frontier, the model having $1-q$ as an actual parameter is to be used.

Both models use a ratio of linear functions of two variables, as in Equation (11).

$$\begin{array}{cc}\hfill & R_{22}(z;c_0,\dots ,c_4)=\hfill \\ \hfill & {\displaystyle \frac{c_0+c_1{\left(\arctan \left(z^{-1}\right)\right)}^{1/8}+c_2{\left(\arctan \left(z^{-1}\right)\right)}^{1/9}}{1+c_3{\left(\arctan \left(z^{-1}\right)\right)}^{1/8}+c_4{\left(\arctan \left(z^{-1}\right)\right)}^{1/9}}}\hfill \end{array}$$

(11)

where the coefficients of the $R_{22}$ function are linear functions of $n^{-1}$ (like in Equation (12)).

$$\begin{array}{c}\hfill l(n;a_0,a_1)=a_0+a_1{n}^{-1}\end{array}$$

(12)

$R_{22}$ is an asymmetrical function, but one can notice that the argument (z in Equation (12)) is always positive.

Thus,

• The model giving the value of the CM population statistic (${\mathrm{CM}}_{\mathrm{P}}$) as a function of the cumulative probability (q) and sample size (n) uses Equation (13) (Model 1):

  $$\begin{array}{cc}\hfill & {\mathrm{CM}}_{\mathrm{P}}(q,n;a_0,\dots ,a_9)=R_{22}(q;l(n;a_0,a_9),\hfill \\ \hfill & l(n;a_1,a_5),l(n;a_2,a_6),l(n;a_3,a_7),l(n;a_4,a_8))\hfill \end{array}$$

  (13)
• the Model giving the value of the CM population statistic (${\mathrm{CM}}_{\mathrm{P}}$) as a function of the p-value ($p=1-q$) and sample size (n) uses Equation (14) (Model 2):

  $$\begin{array}{cc}\hfill & {\mathrm{CM}}_{\mathrm{P}}(q,n;b_0,\dots ,b_9)=R_{22}(1-q;l(n;b_0,b_9),\hfill \\ \hfill & l(n;b_1,b_5),l(n;b_2,b_6),l(n;b_3,b_7),l(n;b_4,b_8))\hfill \end{array}$$

  (14)

It is important to notice the presence of q as an actual parameter for $R_{22}$ in Equation (13), and the presence of $1-q$ as an actual parameter for $R_{22}$ in Equation (14). The purpose of changing from q for low values of q (in the vicinity of 0) to $1-q$ at high values of q (in the vicinity of 1) is to diminish any errors caused by computer roundoff in the vicinity of 1.0 (machine epsilon limit, see for instance [38]).

The coefficients were identified using a uniform bivariate grid of 999 values for q, from $q=0.001$ to $q=0.999$, and 29 values for n, from $n=2$ to $n=30$.

In order to obtain q (or, more often, of interest is the p-value, $p=1-q$) for given n and $CM$ (which is a sample statistic), the numerical inverse of the functions from Equations (13) and (14) must be obtained.

Distinct values for the coefficients from Equations (13) and (14) were obtained for each of the 21 MC simulations.

Table 2. Model parameters.

Coeff. Number	Model 1 (Equation (13))		Model 2 (Equation (14))
	${\mathit{a}}_{\mathit{i}}$ Value	±95% CI	${\mathit{b}}_{\mathit{i}}$ Value	±95% CI
$i=0$	$0.0000000$	$0.0000000$	$-0.052099$	$0.000012$
$i=1$	$0.0245416$	$0.0000013$	$-0.052099$	$0.000093$
$i=2$	$-0.0247069$	$0.0000013$	$0.432868$	$0.000105$
$i=3$	$-7.8481554$	$0.0000041$	$-7.453054$	$0.000018$
$i=4$	$8.8490877$	$0.0000041$	$8.450995$	$0.000018$
$i=5$	$0.0014491$	$0.0000062$	$0.027440$	$0.000430$
$i=6$	$-0.0014551$	$0.0000062$	$-0.031700$	$0.000490$
$i=7$	$-0.0603235$	$0.0000373$	$0.004058$	$0.000086$
$i=8$	$0.0603182$	$0.0000375$	$-0.004092$	$0.000087$
$i=9$	$0.0000000$	$0.0000000$	$0.004292$	$0.000055$

contains the values of the coefficients, along with their 95% confidence intervals (±95% CI).

The significance of the models is very high. In Table 2, the coefficient of variation varies from about $5·{10}^{-7}$ (at $i=4$) to about $4·{10}^{-3}$ (at $i=5$) for Model 1, and from about $2·{10}^{-6}$ (at $i=4$) to about $2·{10}^{-2}$ (at $i=8$) for Model 2. From 21 resamples, for building Model 1, 12,991.5 $\pm 0.5$ ($n,q,{\mathrm{CM}}_{\mathrm{P}}$) pairs of data were used, while for building Model 2, 15,979.5 $\pm 0.5$ ($n,q,{\mathrm{CM}}_{\mathrm{P}}$) pairs of data were used (please note that the frontier between the models is a rational function, Equation (10)). The frontier between the models was chosen in such a way that total square error (from Model 1 and Model 2) is minimized. Determination coefficients between ${\mathrm{CM}}_{\mathrm{P}}$ values calculated with Equation (13) and MC simulated ones were very high, namely $1-r^2<3·{10}^{-10}$ (standard error of the residuals was $2·{10}^{-9}$, with a standard deviation obtained from the 21 replicates of $2·{10}^{-12}$). Similarly, the determination coefficients between ${\mathrm{CM}}_{\mathrm{P}}$ values calculated with Equation (14) and MC simulated ones were even greater, namely $1-r^2<9·{10}^{-12}$ (standard error of the residuals was $3·{10}^{-9}$, with a standard deviation obtained from the 21 replicates of $3·{10}^{-12}$).

Since the first report of the calculation of p-value from the CM in [39] for the analysis of 50 samples of chemical compounds with potent property and/or activity, a series of others were communicated, and the last was in [40] for two electrochemical properties of a sample of 4-(azulen-1-yl)-2,6-divinylpyridine derivatives.

3.3. New Samples Analyzed with CM

In [41,42,43,44,45,46,47], datasets following theoretical distributions are reported. Thus, ref. [41] analyzes Beta distribution fit with the KS statistic, ref. [42] analyzes Beta distribution fit with CM, KS, and three other alternatives, ref. [43] analyzes Cauchy distribution fit with KS, and ref. [44] analyzes Cauchy distribution fit with CM, KS, and one other alternative. The others analyze generalizations of the Cauchy and Beta distributions with KS (in [45,46]), and CM, KS, and one other alternative (in [47]). Here, different alternative distributions for these data are analyzed.

3.3.1. Case Study on Beta Distribution

The PDF of the Beta distribution is given in Appendix A.1. In

Table 3. Measuring agreement for Beta distribution with Cramér–von Mises statistic.

Sample Data	a	b	c	d	$\mathbf{CM}$	${\mathit{p}}_{\mathbf{CM}}$	$\mathbf{KS}$	${\mathit{p}}_{\mathbf{KS}}$
Dozer cycle in [41]	2.3798	3.2848	0.0882	2.1199	0.036765	0.947	0.50799	0.944
Truck cycle in [41]	1.8312	3.6563	6.7852	16.746	0.080000	0.692	0.72844	0.632
May 2007 in [42]	1.5356	0.8614	0.3200	0.9700	0.207980	0.253	0.90067	0.354
May 2008 in [42]	0.4855	0.6385	0.3900	0.9800	0.043692	0.915	0.63770	0.770
First set in [43]	3.2524	8.3550	0.4614	8.3534	0.054735	0.850	0.55456	0.899
Second set in [43]	3.5028	$1.12·{10}^7$	−0.5478	$3.92·{10}^6$	0.369010	0.084	1.09460	0.169

a, b, c, d were obtained from MLE; $p_{\mathrm{CM}}=1-{\mathrm{CDF}}_{\mathrm{CM}}\left(CM\right)$; $p_{\mathrm{KS}}=1-{\mathrm{CDF}}_{\mathrm{KS}}\left(KS\right)$.

, the agreement measured by the Cramér–von Mises statistic is given.

Remarks on Table 3:

• Parameter estimation was conducted with MLE, so the number of degrees of freedom is equal to the sample size in each instance;
• The agreement between statistics is remarkable on average: ${\overline{p}}_{\mathrm{CM}}=0.624$ and ${\overline{p}}_{\mathrm{KS}}=0.628$—this is the expected result, since one should expect both statistics to perform the same on random picked datasets. Student’s t-test does not discriminate between the two series of probabilities: there is a 98% likelihood to belong to the same population (one can test for paired probabilities, when the matching probability is somewhat lower, 92%);
• At a significance level of 5%, all samples passed the hypothesis that they are possibly drawn from the Beta distribution (it was not possible to reject the null hypothesis that the Beta distribution is not the population from which they were drawn).

3.3.2. Case Study on Cauchy Distribution

The PDF of the Cauchy distribution is given in Appendix A.2. In

Table 4. Measuring agreement for Cauchy distribution with the Cramér–von Mises statistic.

Sample Data	a	b	$\mathbf{CM}$	${\mathit{p}}_{\mathbf{CM}}$	$\mathbf{KS}$	${\mathit{p}}_{\mathbf{KS}}$
Venus observations in [44]	0.0267	0.2613	0.024332	0.9962	0.3710	0.9968
Wheaton river in [45]	7.0718	6.4622	0.705420	0.0125	2.0189	0.0005
Floyd river in [45]	2878.9	1928.8	0.448170	0.0509	1.2921	0.0609
Guinea pigs survival in [46]	139.32	48.138	0.451190	0.0504	1.2017	0.1004
Nile river in [46]	879.34	103.89	0.351690	0.0945	1.3117	0.0579
Accelerated life tests in [47]	6.8426	0.8896	0.069199	0.7591	0.6465	0.7657

a and b were obtained from MLE; $p_{\mathrm{CM}}=1-{\mathrm{CDF}}_{\mathrm{CM}}\left(CM\right)$; $p_{\mathrm{KS}}=1-{\mathrm{CDF}}_{\mathrm{KS}}\left(KS\right)$.

, the agreement measured by the Cramér–von Mises statistic is given.

Remarks on Table 4:

• Parameter estimation was conducted with MLE, so the number of degrees of freedom is equal to the sample size in each instance;
• The agreement between statistics is remarkable on average: ${\overline{p}}_{\mathrm{CM}}=0.3273$ and ${\overline{p}}_{\mathrm{KS}}=0.3304$—this is the expected result since one should expect both statistics to perform the same on random picked datasets. Student’s t-test does not discriminate between the two series of probabilities: there is a 99% likelihood of belonging to the same population (one can test for paired probabilities when the matching probability is lower, 80%);
• At a significance level of 1%, there is some disagreement between the CM and KS statistics at Wheaton river sample if the hypothesis of being drawn from the Cauchy distribution must be rejected or not.

The case of the Wheaton river sample being drawn (or not) from a Cauchy population of data opens an opportunity for discussion.

There is no clear method to determine which statistic is best, even though some authors compare the statistics by power and suggest that the Anderson–Darling statistic is most powerful. However, having power is one thing, and accurately assessing the fit is another. No mathematical analysis based on power alone can dismiss the usefulness of one statistic over another, for a simple reason: the intrinsic variability of a distribution having one, two, three, four, or more parameters cannot be trapped by only one (nonparametric) statistic. Fisher recommends combining independent tests of significance [48]. A combined probability chi-squared test on 0.0125 and 0.0005 gives a probability of 2.4‰, which can be used to reject the hypothesis that the Wheaton river sample data belongs to a Cauchy distribution population of data.

If the method of estimating the parameters of the theoretical distribution uses the maximization of the likelihood, then there is no need to reduce the sample size when the probability of CM (or any other statistic) is calculated [24]. On the other hand, with the method of moments, degrees of freedom must be reduced with the number of parameters of the underlying distribution [25].

4. Conclusions

A composite model providing the CM statistic as a function of the sample size and the probability has been obtained. The model is very accurate in estimations of the CM statistic for the probability within the range [0.001, 0.999] and for the sample size within the range [2, 30]. The probability associated with the CM statistic can be obtained from the model and has been used, as given here, in testing the goodness of fit in case studies in the past and in two less common cases here (one measuring the agreement of a sample with Cauchy distribution, and one measuring the agreement of a sample with Beta distribution). Combining independent tests of significance is recommended in any instance of decision split based on individual tests.

5. Future Work

Equations (13) and (14), combined with Equation (9), represent an approximation, and a very good one, considering the obtained correlation coefficients. However, as with any other approximation, it is possible to be improved upon.

Improvement can be obtained by having even more accurate sampling from the CM population statistic (the sampling as given in Table 1 can be refined further), having more cut points (permiles has been used here, permillion quantiles can be used instead), and having more computing memory (here, one can move from internal memory to disk memory, especially since the discovery of the solid state drives with much higher speed, sometimes comparable with internal memory speed, with some additional computational time costs).

Equations (13) and (14), combined with Equation (9), are intended to be used within the applicability domain defined by the sampling: for p-values ranging from 0.001 to 0.999 and sample sizes n ranging from 2 to 30. Since the proposed model is nonlinear, the use of it outside of this domain should be made with caution and reservation, nonlinear models being known for their low predictability outside of the applicability domain. One can look to work around this issue, possibly by incorporating an asymptotic formula in it.