Abstract
Polyhedral cages (p-cages) are Euclidean geometric structures corresponding to polyhedra with holes. They are a good example of the geometry of some artificial protein cages. In this paper we identify p-cages made out of two families of equivalent polygonal faces, where the face of one family is attached to three other faces while the faces of the other family are attached to three, four, five or six other faces. To restrict ourselves to p-cages with small holes, we consider p-cages where each hole comprises at most four faces. The construction starts from planar graphs made out of two families of equivalent nodes. One can then construct the dual of the solid corresponding to that graph and tile its faces with regular or nearly regular polygons. An energy function is then defined to quantify the amount of irregularity of the p-cages which is then minimised using a simulated annealing algorithm. We have analysed nearly 100,000 possible configurations, ruling out the p-cages made out of faces with deformations exceeding 10%. We then present graphically some of the most interesting geometries.
1. Introduction
The polyhedral cage, a p-cage for short, is a relatively new concept. It was first introduced to describe the geometry of an artificial protein cage [1]. Made out of 24 seemingly regular hendecagons, the geometry of the experimentally obtained cage looked impossible, but it turned out that the faces are actually nearly regular with deformations so small that they cannot be observed with the naked eye. Nevertheless, despite this irregularity, such a structure can be made experimentally.
This observation led us to formalise the concept of polyhedral cages to identify which other geometries could be generated experimentally [2]. A p-cage consists of an assembly of regular or nearly regular, but planar, polygons with holes between them. The polygons share some of their edges with their neighbour faces, like the face of polyhedron, but some edges are adjacent to a hole. To describe objects that are cage-like, we depend upon two further requirements. First, we require that each face has at least three neighbours. This is to avoid chicken wire-like structures. We also require that of two adjacent polygon edges, at most one of them, can be shared with a neighbour face. A p-cage is said to be regular if all its faces are regular polygons. On the other hand, if some of its faces are nearly regular, the p-cage is said to be a near-miss. We also restrict ourselves to convex p-cages.
Our main aim was to identify potential geometries for artificial protein cages. All the virus capsids found in nature essentially have the structure of Platonic solids [3]. Artificial protein cages have, on the other hand, more general symmetries or near-symmetries [1,4,5,6,7]. J. Heddle has created in his laboratory several artificial protein cages made from TRAP proteins [8]. These TRAP proteins are modified so as to form so called rings made out of typically 11, 12 or 13 TRAP proteins which exhibit the geometry of polygons with 11, 12 or 13 edges [9]. These rings assemble to form several structures. For example, the 11 ring forms protein cages made out of 24 rings but also smaller ones made out of 12 rings [1,5]. While chemical and physical properties of the assembling proteins must obviously be taken into account [10,11,12], identifying the possible geometries for protein nano-cages will help the selection of protein candidates to form such cages.
The motivation for making such artificial protein cages is to develop new methods of targeted drug delivery by enclosing the desired drug inside a protein capsid which will contain, on its outer side, receptors which will in turn allow it to penetrate inside the target type of cells [13,14,15,16,17,18,19,20,21,22,23] such as cancer cells, for example [24]. Once inside the cell, the protein cage will open to release its cargo [25,26]. The advantage of using artificial capsids is that they provide a larger number of options but also reduce the risk of the protein cage being recognised by the immune system of the patient [24,27,28,29,30].
Joining proteins to form artificial cages is not easy and requires suitable geometries and binding properties between them [31,32,33,34]. Some protein cages are built using symmetry properties [35,36,37,38,39], while others break known symmetries [40].
A p-cage is homogeneous symmetric [41] if for any pair of faces there is a congruent automorphism of the p-cage that maps one face onto the other. This means that, as for Platonic solids, all the faces are equivalent. We later defined bi-symmetric p-cages as p-cages made out of two families of faces, so that for any two faces belonging to the same family, there is a congruent automorphism of the p-cage that maps one face onto the other [2]. Homogeneous bi-symmetric p-cages are made out of the same type of faces, but most bi-symmetric p-cages are made of two different types of polygons.
Polyhedral cages can be seen as a generalisation of regular polyhedra or polytopes [42]. With the restrictions which we have imposed, most p-cages are sphere-like with small holes and so are good candidates for encapsulating some cargo. Mathematically, it is interesting to compute their Euler characteristic C, which is defined as [43]
where V is the number of vertices, E the number of edges, and F the number of faces. For a polyhedron C is always 2. This implies that for a p-cage, , where H is the number of holes of the p-cages. Indeed, if a p-cage is such that each of its faces share only one edge per hole, the hole can be considered as the face of a containing polyhedron. If denotes the number of faces of the p-cage, we have
and so
To generate more general p-cages, we must add one or more vertices to the edges of the above p-cage. Doing so increases V and E by 1 for each extra vertex while keeping and H unchanged, and so, by (1), C remains unchanged, proving that for all p-cages.
All the homogeneous symmetric p-cages with deformations not exceeding 10% were identified in [2,41]. In [44], we identified all the bi-symmetric p-cages such that the faces of a given family are only adjacent to the faces of the other family. In [45,46], we have identified all the bi-symmetric p-cages with faces adjacent to four other faces that contribute to, at most, three edges to each hole. In this paper, we complete this later study by identifying all the bi-symmetric p-cages for which the faces of one family have three neighbours each, while the other faces have three, four, five or six neighbour faces. To avoid p-cages with large holes, we also restrict ourselves to p-cages where its faces contribute to at most only three of the edges to any given hole.
It is worthwhile at this point to describe how nano-bio-chemical engineers should use the results of this study, as well as those described in our previous papers. The results presented in this study are purely geometric and describe the structures that can be realised with nano-protein cages. If a research group has two types of polygon-shaped proteins with and edges, one can identify from the lists we provide which p-cage shapes can be achieved, if any. For example, there are none for and but there are quite a few for and . The Heddle lab [9] can make , , and polygons with TRAP proteins, but there is no reason why other polygons cannot be achieved with other proteins.
The 10% deformation criteria was chosen in [2] to be large enough to include all potentially realisable geometries. In [5,9] the deformations of some of the obtained protein cages were shown to be above 3%.
The large number of geometries for p-cages implies that there is potentially a very large number of different protein nano-cages that can be realised. They will have to be realised with a range of different proteins and that diversity should lead to a larger range of cargo that can be encapsulated inside these nano-cages. This will obviously require many further experimental works.
Many aspect of the protein nano-cages are bio-chemical problems well beyond the scope of our study. For example, the holes can either be plucked with receptors if left as they are, but this is for the designer to decide.
Drug encapsulation is also a bio-chemical problem related directly to the type of protein used to make nano-cages and so it is not covered at all in our study which is purely geometric. To determine the actual geometry of protein nano-cages, see the paper from the Heddle lab [4,8,9].
2. Methodology
The main method to categorise and classify p-cages is to join the faces at the centre of a p-cage with lines; these lines define a polyhedron which corresponds to the dual of the p-cage. This is illustrated for a specific p-cage made out of nanogons and decagons in Figure 1a. We call these polyhedra the hole-polyhedra and they describe the characteristics of the p-cages as follows. The faces describe the structure of the p-cage hole. So a triangle corresponds to a hole formed by 3 faces and a square to a hole made out from 4 faces…. This is represented by red lines in Figure 1a. The vertices of the hole-polyhedra correspond to the p-cage faces while the edges describe how these faces are connected together. So if a vertex joins 4 edges, it corresponds to a p-cage face, sharing 4 of its edges with neighbour faces.

Figure 1.
Graphical representation of the connectivity between the faces of a p-cage made out of 8 nanogons and 24 decagons. (a) Hole-polyhedron. The nodes correspond to the position of the p-cage faces and the red lines describe how the faces are linked together. The face hole-edges are yellow while the shared edges are black. The black numbers specify the number of edges of each face. (b) Hole-polyhedron planar graph. The numbers indicate the number of hole-edges contributed by each face to each hole. (c) Dual of the hole-polyhedron also referred to as tilling solid.
The hole-polyhedra can be projected onto a plane to obtain the corresponding planar graph, as illustrated in Figure 1b. A p-cage made out of 2 families of equivalent families will then correspond to a planar graph made out of 2 families of nodes such that each node of a given family can be mapped to any other node of the same family via an automorphism of the graph.
As we do not allow the adjacent edges of the p-cage faces to be both shared with neighbours, each face must have a number of edges adjacent to holes. A given face can contribute an arbitrary number of its edges to any hole, aside from the fact that in order for the p-cage faces to be equivalent the symmetry of the planar graph must impose some restrictions. In Figure 1b we have indicated in the corners of the planar graph the number of edges contributing to each hole for the p-cage shown in Figure 1a.
The equivalence between the p-cage faces of each family suggests that the automorphisms mapping the nodes of the planar graphs must also leave the number of hole-edges, denoted in the graph corners, as invariant.
To classify the p-cage faces with two families of equivalent faces, we must consider all the planar graphs made out of two families of equivalent nodes. Then we must assign a number of hole-edges to each corner of these planar graphs so that the equivalence between the nodes is preserved. As we will illustrate with a few examples later, this can lead to a very large number of configurations to consider.
Planar graphs where all the nodes are equivalent are called Cayley graphs [47] and Maschke proved [48] that the only planar Cayley graphs are the graphs of the regular solids, i.e., the prism, antiprism, Platonic solids, and Archimedean solids. Planar graphs made out of 2 families of equivalent nodes were classified in [49] where it was shown that there are over 400 such graphs when considering only those with faces no larger than decagons.
In [44] we have classified all the bi-symmetric p-cages where all the faces of a given family are only adjacent to faces of the other family. There were only 9 graphs to consider and most of them lead to p-cages with very large holes. In [46] we have classified all the bi-homogenous symmetric p-cages where each face has at least 4 neighbours and their holes are made out of at most 4 faces.
In this paper we complete that study by characterising all the bi-homogenous symmetric p-cages where the faces of one family has 3 neighbours faces while the others have 3, 4, 5 or 6 neighbours faces. We consider all the graphs corresponding to such p-cages [49] one by one. Each planar graph corresponds to a hole-polyhedron and we start by constructing the dual of that polyhedron which we call the tilling polyhedron. Notice that these tilling polyhedron are made out of 2 types of planar non-regular polygons. Moreover, in most cases, they are not unique as the faces can be deformed while preserving the equivalence between the faces of each family. We call this polyhedra the tilling polyhedra because the p-cage can be obtained by inserting the polygonal face onto its faces.
Because the p-cage faces belong to 2 families of equivalent faces, we only need to consider one representative for each family, which we call the reference faces, with the other faces being obtained by applying the rotation that maps these faces together.
We denote and as the number of edges for the face belonging to family I and II, respectively. Following [44,45], the family of type I is chosen to be the one with 3 neighbours.
The vertices of the reference faces are denoted for , ordered anticlockwise when seen from outside the p-cage. The normal to the reference face of type j, , is chosen to point towards the outside of the p-cage. The edges are then given by the vectors so that the edge lengths are . We can then determine the inside angles between adjacent edges, , by evaluating and
As we are only interested in convex faces we must have . For a regular P-gon, the angles between the adjacent edges are and the edges all have the same length. To minimise the deformations of the p-cage face we must evaluate all the and and adjust the coordinates of the reference face so as to minimise the difference between the and and the corresponding values for a regular polygon. We achieve this by minimising the energy
where
where , , and and weight factors which, as will be shown later, can be adjusted to obtain p-cages with different levels of deformations. In (6), the first term evaluates the deviation of the edge lengths from the target length L while the second term does the same for deviations from that of a regular P-gon. is given explicitly by
where is the Heaviside function. Notice that for a concave polygon (7) is 0.
is obtained by computing , the centre of face i and by choosing 2 adjacent faces, and , with normal vectors and , respectively. The p-cage is convex if for all pairs of adjacent faces, the distance between the centres of the 2 faces is smaller than the distance between and . This allows us to define as
where is the set of faces, of any type, adjacent to the reference face j. For convex p-cages is 0.
To obtain p-cages that are minimally irregular but convex, we used a simulated annealing algorithm [50], varying the parameters of the p-cages to minimise E and hence determine optimal configurations for each p-cage.
To ensure that the p-cage and its faces are all convex, we have taken very large values for and so that the last two terms in (5), , and dominate the energy contribution when they are non null. In (5), we divide the energy by to make the parameterisation of the numerical optimising algorithm easier to tune.
To describe the regularity of the p-cages, we use the following two quantities:
- Length: ;
- Angle: .
To balance the edge length and angle deformations, the weight and were varied but with the constraints . We started with the values and perform a full simulated annealing relaxation. We then adjusted and using a gradient algorithm to minimise , performing a full simulated annealing relaxation for each value of and . In units of energy (5), the temperature decreased from to by the multiplicative factor , using 2000 randomisations per degree of freedom for each temperature.
The reference faces can be described by a vector normal to the face, where is used to label the two faces’ families, as well as 2 orthonormal basis vectors and . Any point on the plane span by the face can then be described as . These vectors can be parameterised by the angles and as well as the length as follows:
As all the faces k of a given family are related to the corresponding reference via a rotation R, the normal and basis vectors for this plane are given by
Notice that is the unit matrix for the reference faces.
The edges of the p-cage faces are obtained by parameterising the lines intersecting the plane span by any two pairs of adjacent faces. Given , , and , , , the vectors spanning two adjacent planes, we first define
where and and the normal vectors are normalised to 1, and is a vector parallel to the line intersecting the 2 planes.
Multiplying (12) by , we identify the point on the intersecting line
which is perpendicular to . This leads to a relation between the parameters and as well as and . The values of are obtained by multiplying (12) by . Inserting the result back into (12), we obtain
Given the intersecting lines between 2 pairs of adjacent faces, we will also need to determine the intersecting point between these 2 lines:
We achieve this by imposing the condition
Then, multiplying (15) by and also leads to the following system of two linear algebraic equations
This can easily be solved to find
The most efficient way to perform the p-cage configuration optimisation is to determine the coordinates of the tilling solid so that the initial face configuration can be obtained by tilling the solid faces. The reason is that it can often be tricky to find the tilling solid coordinates from the hole-polyhedron planar graph and we only need to perform this once for every planar graph considered rather than for every possible p-cage corresponding to that planar graph (there can be a thousand of such p-cages to consider).
Some of the hole-polyhedra are regular solids or the duals of a regular solid. In this case the tilling solid is known. The other hole-polyhedra are either axially symmetric solids or their planar graphs are obtained by adding nodes to the planar graph of a regular solid [49]. The construction of the tilling solids was detailed in [46] and we shall not repeat it here.
Given a tilling solid, the normal of its reference face is used as the initial normal vector for the p-cage reference faces.
Choosing different polygons for the p-cage faces leads to a number of p-cages for each hole-polyhedron graph. When a P-gon face shares n edges with as many neighbours there remain edges to distribute between the holes. This repartition of the hole-edges must preserve the equivalence between the faces of each family. We can determine how this can be performed for each graph by labelling the number of hole-edges using the symbols a,b,c,d,e and A,D,C,D,E,F for, respectively, the type I and II families. The is carried out via construction, as illustrated in a few example below. The algorithm used to list all the hole-edge configurations for a given graph, avoiding duplications, was the same as in [46]. The python program used for this is available on zenodo as part of all the computer programs used to generate the p-cages (see the zenodo reference at the end).
We illustrate this in 3 cases shown in Figure 2. In the first case, the hole-polyhedron is a triangular pyramid where the top node is of type II while the 3 sides are of type I. The dual of the hole-polyhedron, the tilling solid, is also a triangular pyramid where the base is of type II and the side of type I. Figure 2a corresponds to the planar graph of the tilling solid, so we must place the hole-edge labels in the corner of each face. The symmetry is a rotation around the main axis of the pyramid. As a result, the hole-edge labels for the type II face must be identical so that each of the type I faces are adjacent with the same configuration. We then place an A at each corner of the base face. The type I faces are mapped onto each other by a rotation around the main pyramid axis and so they must all have the same label at the top vertex which we name a. We then place the remaining labels b and c anticlockwise around each type I face.
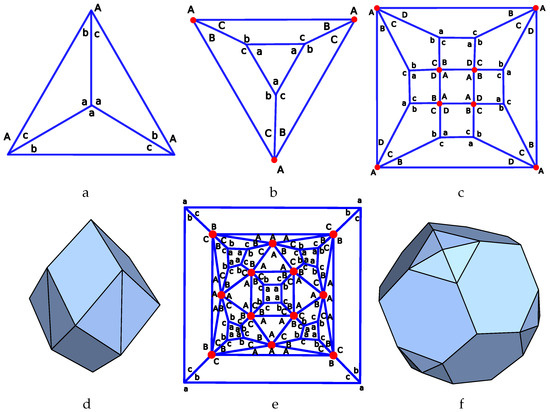
Figure 2.
Repartition of the edges holes. (a) Triangular pyramid as the tilling solid. The type II face is on the base of the tilling pyramid. The edge labels are placed on the faces. (b) Triangular prism as the hole-polyhedron. The type I and II faces are at the vertices of opposite bases. The edge labels are placed around each node. (c) The hole-polyhedron is a square prism where the side edges have been split into squares. The type II faces are the nodes of the prism and the type I faces at the nodes added to the prism. The edge labels are placed around each node. (d) Tilling solid of the hole-polyhedron shown in (c). (e) The hole-polyhedron is a cuboctahedron where a truncated pyramid has been placed on the square faces. The type II faces correspond to the nodes of the cuboctahedron while the type I face correspond to the nodes of the truncated part of the pyramids. (f) Tilling solid of the hole-polyhedron shown in (e).
The second hole-polyhedron is a triangular prism, Figure 2b. The type I and II faces cover, respectively, both bases of the prism. In this case, it is easy to see that the tilling solid consists of two triangular pyramids joined at their bases which we label in the hole-polyhedron planar graph. The symmetry is again a rotation around the main axis of the prism. The three nodes of type I must then have the same edge label on the top base of the prism, similarly for type II nodes and the bottom base. We then label them, respectively, as a and A. The other labels are then placed anticlockwise around each node.
The third hole-polyhedron has the symmetry of a square prism, Figure 2c. The type II nodes are the 8 nodes of the square prism graph while the type I faces are on the side of the prism. The symmetry is again another rotation symmetry around the main axis of the prism as well as a rotation around the centre of the prism faces. The type II faces must then have the same label on the prism base, which we call A, and we then label the other corners around these type II nodes anticlockwise. We label the three corners around one of the type I nodes anticlockwise a, b, and c. Applying the rotation around the main axis of the prism to these labels, we obtain the labelling of 3 more nodes. We can then apply the rotation to these first four nodes to obtain the labelling of the remaining four. The tilling solid corresponding to the hole-polyhedron is shown in Figure 2d.
The fourth hole-polyhedron is a cuboctahedron where a truncated pyramid has been added to the square faces; see Figure 2e. The type II and type I faces correspond, respectively, to the nodes of the cuboctahedron and the nodes of the truncated part of the pyramids. The symmetries are a rotation around the axis of the square faces/truncated pyramids and a rotation around the axis going through the triangular faces of the cuboctahedron. The labels at the top of the truncated pyramids must be the same, a, and we add the other labels anticlockwise around the type I nodes. The labels on the triangular faces must also be identical, A, and we label the other corners anticlockwise around each type II nodes. The tilling solid for that hole-polyhedron is shown in Figure 2f. It corresponds to a rhombic dodecahedron where 4 of the rhombic faces are split in 2 triangles.
Before providing some examples of p-cage derivations, it is useful to describe the naming convention which we use to refer to these p-cages. The names are of the format GRAPH_P_P_a_b_c_d[_e]-A_B_C_D[_E_F] where the italic symbols are replaced by actual values. GRAPH stands for the nickname of the hole-polyhedron graph while , and the hole-edge labels are self explanatory. We also use the following simplification to avoid excessively long names: when n successive hole-edge labels have the same values, , we replace the sequence by nx. As an example, p5-2pyr_P10_P10_1_1_2_2-1_1_1_1_1 becomes p5-2pyr_P10_P10_2x1_2x2-5x1.
The graphs that we have considered are all listed in Appendix A together with the planar graph names taken from [49], the p-cage names, the number of configurations that we have tested, as well as the number of p-cages found with deformations not exceeding 10%, 5% and regular p-cages ().
3. Results
In what follows, we will detail with some of the examples outlined above. The derivation of the other classes of bi-symmetric p-cages are detailed in the supplementary files pcage_graph_properties.pdf and Pcages-3-4-5-6neib.pdf.
The first example is derived from the planar graph 3pyr (33_F4_1-3-0_3-2-1_V3_1 in [49]). It corresponds to the planar graph of a triangular pyramid where the top vertex is of type II and the other three are of type I. The dual of that solid is also a triangular pyramid where we fit the type II face while the side faces are tilled with the type I p-cage faces. The hole-edge repartition is shown in Figure 1a. This results in 12, 6 and 3 p-cages with deformations below, respectively, 10%, 5% or equal to 0%. The regular p-cages consist in the simple embedding of hexagons, nanogons or decagons on the four faces of a tetrahedron, as shown in Figure 3a. The non-regular p-cages have a regular base, while the type II faces are non-regular polygons on the sides (Figure 3b,c).

Figure 3.
Construction of the 3pyr p-cage. (a) Regular p-cage 3pyr_P6_P6_3x1-3x1. (b) P-cage 3pyr_P8_P12_1_2x2-3x3 . (c) P-cage 3pyr_P8_P6_3_2x1-3x1.
The second example is derived from the planar graph p3-tb (33_F5_1-0-3_1-3-0_3- 2-2_V3_3 in [49]). It corresponds to the planar graph of a triangular prism where the vertices of a given base belong to the same family, as shown in Figure 1b. The dual of that solid consists of two pyramids joined at their bases where the face of a pyramid are all of the same type.
The hole-edge repartition is shown in Figure 1b. This results in 65, 20, and 5 p-cages with deformations below, respectively, 10%, 5% or equal to 0%. The regular p-cages consist in two identical pyramids (Figure 4a,b). Figure 4c shows a p-cage made of two different pyramids: three decagons and three hendecagons.
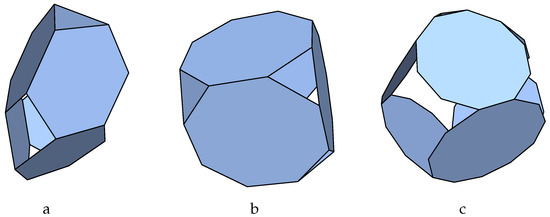
Figure 4.
Construction of the p3-tb p-cage. (a) Regular p-cage p3-tb_P6_P6_3x1-3x1. (b) Regular p-cage p3-tb_P8_P8_2x1_3-2x1_3. (c) P-cage p3-tb_P11_P10_2_2x3-1_2x3 .
The third example is derived from the planar graph p4-12sqr (34_F14_2-0-4_12-2-2_ V8_8 in [49]). It corresponds to the planar graph of a square prism where the vertical edges have been split, as shown in Figure 1c which describes the hole-edge repartition for that graph. The dual of that solid corresponds to a rhombic dodecahedron where four of the squares have been split into two triangles, as shown in Figure 1d.
This results in 25, 5 and 1 p-cages with deformations below, respectively, 10%, 5% or equal to 0%. The regular p-cage consists of a square prism where the base are tiled with four octagons and the edges with two octagons (Figure 5a). This is a degenerate p-cage as the side octagons are touching those on the adjacent side. The difference is clear when we compare it with the p-cage shown in Figure 5b. This second p-cage is made out of eight 13-gons (on the prism base) and eight decagons (on the prism sides). This p-cage has a 4.3% deformation).

Figure 5.
Construction of the p4-12sqr p-cage. (a) Regular p-cage p4-12sqr_P8_P8_1_3_1-4x1. (b) P-cage p4-12sqr_P10_P13_2_3_2-3_3x2 .
The fourth example is derived from the planar graph p4-bsplit (34_F8_4-1-2_4-2-2_ V4_4 in [49]). The graph has an axial symmetry but is not directly related to the planar graph of a regular solid. The hole-edge repartition is shown in Figure 6a. This results in 101 and 14 p-cages with deformations below, respectively, 10%, 5% and no regular p-cages. We present two examples in Figure 6b,c with deformations of 2.4% and 4.3%.

Figure 6.
Construction of the p4-bsplit p-cage. (a) Hole-polyhedron planar graph for the p4-12sqr p-cages. The edge labels are placed around each node. (b) P-cage p4-bsplit_P8_P10_1_2x2-2x1_2x2 . (c) P-cage p4-bsplit_P11_P14_2_2x3-2x2_2x3 .
The fifth example is derived from the planar graph DAco (34_F12_12-2-2_V8_6 in [49]). It corresponds to the planar graph of the rhombic dodecahedron, the dual solid of cuboctahedron. As a result, the tilling solid is the cuboctahedron and its planar graph with the hole-edge repartition is shown in Figure 7a. The symmetry of the graph imposes strong constraints on the hole-edge values. As a results this leads to nine regular p-cages and no near-miss p-cages. The simplest one, DAco_P6_P8_3x1-4x1, is shown in Figure 7b; it corresponds to the truncated cuboctahedron where the squares are the p-cage holes. The p-cage shown in Figure 7c, DAco_P9_P8_3x2-4x1, is another example.
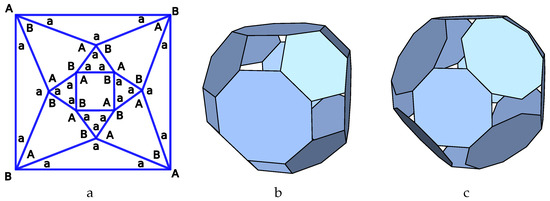
Figure 7.
Construction of the DAco p-cage. (a) Tilling solid planar graph with hole-edge repartition. The edge labels are placed around each node. (b) P-cage DAco_P6_P8_3x1-4x1 . (c) P-cage DAco_P9_P8_3x2-4x1 .
The sixth example is derived from the planar graph Da5 (35_F10_10-3-1_V10_2 in [49]). It corresponds to the planar graph of the dual of the pentagonal antiprism. As a result, the tilling solid is the pentagonal antiprism and the hole-edge repartition is shown in Figure 8a.

Figure 8.
Construction of the Da5 p-cage. (a) Tilling solid planar graph with hole-edge repartition. The edge labels are placed around each node. (b) P-cage Da5_P10_P10_3_1_3-5x1 . (c) P-cage Da5_P7_P20_1_2_1-5x3 .
This results in 4, 5 and 1 p-cages with deformations below respectively 10%, 5% or equal to 0%. The regular p-cage Da5_P10_P10_3_1_3-5x1, shown in Figure 8b is degenerate as described above. Most of the near-miss p-cages of this type look like ice cream sandwiches, as shown in Figure 8c.
The seventh example is derived from the planar graph DAid (35_F30_30-2-2 _V20_12 in [49]). It corresponds to the planar graph of the dual of the icosidodecahedron. The tilling solid is hence the icosidodecahedron and the hole-edge repartition for that planar graph shown in Figure 9a. This is another example where the hole-edge numbers are very constrained.

Figure 9.
Construction of the DAid p-cage. (a) Tilling solid planar graph with hole-edge repartition. The edge labels are placed around each node. (b) P-cage DAid_P6_P10_3x1-5x1 . (c) P-cage DAid_P9_P10_3x2-5x1 .
This results in five regular p-cages and no near-miss one. The simplest one DAid_P6 _P10_3x1-5x1, Figure 9b, corresponds to the icosidodecahedron where the square are the p-cage holes. The second example, shown in Figure 9c, is one of the few examples of a three-neighbours family p-cage which is sphere-like in shape and has small holes.
The eighth example is derived from the planar graph Aco-6tr-4pyr (36_F38_6-4-0_8-0-3_24-2-2_V24_12 in [49]). It corresponds to the planar graph of the cuboctahedron on which truncated pyramids have been placed on its square faces.
This results in no regular p-cages but seven and two p-cages with deformations below, respectively, 10% and 5%. As an example, the p-cage Aco-6tr-4pyr_P6_P18_3x1-6x2 is shown in Figure 10a.
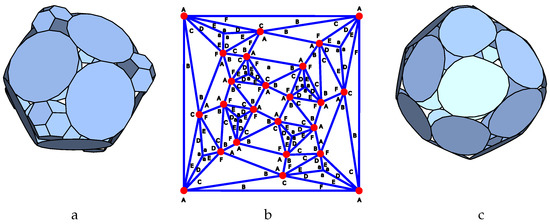
Figure 10.
Construction of the Aco-6tr-4pyr and Asc-8-3pyr p-cage. (a) P-cage Aco-6tr-4pyr_P6_P18_3x1-6x2 . (b) Tilling solid planar graph for the Asc-8-3pyr p-cages with hole-edge repartition. The edge labels are placed around each node. (c) P-cage Asc-8-3pyr_P6_P20_3x1-3x3_2x1_3 .
The ninth example is derived from the planar graph Asc-8-3pyr (36_F54_6-0-4_24-0-3_24-1-2_V8_24 in [49]). It corresponds to the planar graph of the snubcube on which triangular pyramids have been placed on the eight triangles located at the corner of the underlying cube. The hole-edge repartition is presented in Figure 10b.
This results in three p-cages with deformation below 10% but none with deformations below 5%, let alone regular p-cages. An example, Asc-8-3pyr_P6_P20_3x1-3x3_2x1_3, is presented in Figure 10c. It has a deformation exceeding 8% as is clearly seen from the shape of the icosagons.
4. Conclusions
In this paper we have determined the geometry of all bi-symmetric polyhedral cages made out of two families of equivalent faces. The first family type has three neighbour faces while the other family has three, four, five or six neighbours. We also restricted ourselves to p-cages such that each face contributes at most three edges to each holes. This was to ensure that the holes are always small. To identify all the possible connectivities between the p-cage faces, we have shown that one has to consider planar graphs which have two families of nodes each linked to the same number of nodes as the p-cage faces that have neighbours.
We have considered the 54 planar graphs with the desired properties, listed in the Appendix A, and constructed their associated solids made out of two types of irregular planar polygons. These solids were usually not unique as they can be deformed while preserving the symmetry. We also identified all the possible symmetry preserving repartitions of the hole-edges around the p-cage holes (the nodes of the planar graph considered). By fitting polygons on the faces of the solids, we have obtained p-cages which are regular or nearly regular. This was achieved by minimising the energy function (5) for all the identified configurations with respect to the solid and polygon parameters. Out of the 98,937 configurations that we have tested, we found 160 p-cages with deformations not exceeding 10%, 192 with deformations below 5%, and 53 regular p-cages. Notice also that out of the 54 graphs considered, 15 did not lead to any p-cage with deformations below 10%. Detail description of all the p-cages can be found in the supplementary material: best_p_cages_figs.pdf figures for all the p-cages with less than 5% deformation; OFFS.tar.gz files for 3d visualisation; best_table.pdf a list of tables describing the properties of all the p-cages.
The computer programs used to generate the p-cages are available on zenodo (see below). It takes from a few minutes of computer time for the p-cages which are ruled out because of very strong deformations to a day or two for the larger p-cages.
Peripherality measures [51] on the graphs corresponding to the p-cage might provide some information on the holes of the p-cages, but this is beyond the scope of this study.
We concluded the paper by providing some examples and describing some of the more interesting p-cages that we have obtained.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/sym17091537/s1. File pcage_graph_properties.pdf: graphical representation and properties of all the hole-polyhedron graphs considered. File Pcages-3-4-5-6neib.pdf: list of all the p-cages with 3 neighbours for the type I faces and 3 to 6 neighbours for the type II faces, and less than 10% deformation. File best_p_cages_figs.pdf: figure of all the p-cages with less than 5% deformation. File OFFS.tar.gz: “.off” and “.ply” files for every bi-symmetric p-cage with deformations not exceeding 10%. “.off” files can be viewed with tools such as geomview and antiview. “.ply” files can be viewed using a number of 3D visualisation tools such as ctmviewer. File best_table.pdf: a list of tables describing all the p-cages including the number of faces that they contain as well as a description of all their holes.
Funding
This research received no external funding.
Data Availability Statement
The C++ and Python programs used to generate all the data are available from https://zenodo.org/records/16900762 (accessed on 7 September 2025).
Acknowledgments
The computer simulations were performed on the Condor cluster of the Mathematical Science Department of Durham University. The figures were produced with the Geomview Software (http://www.geomview.org/, accessed on 19 August 2025) and the Inkscape Software (https://inkscape.org, accessed on 19 August 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| TRAP | trp RNA-binding attenuation protein. |
| RNA | Ribonucleic acid: a nucleic acid present in all living cells. |
Appendix A. List of Planar Graphs
This is the list of bi-symmetric graphs where the nodes of type I have three neighbours while the nodes of type II have three, four, five or six of them. This is also restricted to the graph for which the faces are either triangles or squares. In each table the first column is the name of the graph described in [49], the second column is the label for the corresponding p-cage, is the number of configurations investigated while and are, respectively, the number of p-cages found with deformations not exceeding 10% and 5%.
The following graphs did not lead to any p-cage with deformations below 10%: 35_F10_2-2-2_8-1-2_V4_4, 35_F12_6-0-3_6-1-2_V2_6, 35_F14_2-0-3_6-1-2_6-2-2_V6_6_B, 35_F14_2-3-0_6-0-3_6-2-2_V6_6, 35_F18_2-0-4_8-1-2_8-2-2_V8_8_B, 35_F18_2-4-0_8-0-3_8-2-2_V8_8, 35_F42_18-0-4_24-1-2_V8_24, 35_F50_8-3-0_18-0-4_24-2-2_V24_24, 36_F20_4-0-3_4-3-0_12-2-2_V12_6, 36_F22_2-0-4_4-2-2_16-1-2_V8_8, 36_F28_12-1-2_16-0-3_V4_12, 36_F32_4-3-0_12-2-2_16-0-3_V12_12, 36_F38_6-0-4_8-3-0_24-2-2_V24_12, 36_F62_6-0-4_8-0-3_24-1-2_24-2-2_V24_24_B, 36_F62_6-0-4_8-3-0_24-0-3_24-2-2_V24_24.
- 3-3 graphs:
| Graph Name | p-Cage Name | ||||
| 33_F4_1-3-0_3-2-1_V3_1 | 3pyr | 81 | 12 | 6 | 3 |
| 33_F4_2-1-2_2-2-1_V2_2 | Pte-22 | 405 | 15 | 4 | 3 |
| 33_F5_1-0-3_1-3-0_3-2-2_V3_3 | p3-tb | 405 | 65 | 20 | 5 |
| 33_F6_6-3-1_V6_2 | Pcu-diag | 54 | 3 | 3 | 3 |
| 33_F6_6-2-2_V4_4_A | p4-22-A | 405 | 94 | 24 | 6 |
| 33_F6_6-2-2_V4_4_B | p4-22-B | 9 | 9 | 9 | 9 |
| 33_F6_1-0-4_1-4-0_4-2-2_V4_4 | p4-tb | 405 | 106 | 25 | 5 |
- 3-4 graphs:
| Graph Name | p-Cage Name | ||||
| 34_F5_1-4-0_4-2-1_V4_1 | 4pyr | 81 | 11 | 5 | 1 |
| 34_F6_6-1-2_V2_3 | 2-3pyr | 135 | 5 | 1 | 0 |
| 34_F8_8-3-1_V8_2 | Da4 | 54 | 6 | 4 | 1 |
| 34_F8_2-3-0_6-2-2_V6_3 | 2-tr3pyr | 2187 | 2 | 0 | 0 |
| 34_F8_4-1-2_4-2-2_V4_4 | p4-bsplit | 2187 | 101 | 14 | 0 |
| 34_F9_3-0-4_6-1-2_V2_6 | p3-2pyr | 135 | 6 | 2 | 0 |
| 34_F10_2-4-0_8-2-2_V8_4 | 2-tr4pyr | 216 | 1 | 0 | 0 |
| 34_F11_2-3-0_3-0-4_6-2-2_V6_6 | p3-tr-3pyr | 1134 | 32 | 8 | 0 |
| 34_F11_2-0-3_9-2-2_V6_6 | p3-9sqr | 1215 | 46 | 8 | 0 |
| 34_F12_12-2-2_V8_6 | DAco | 27 | 9 | 9 | 9 |
| 34_F14_2-0-4_12-2-2_V8_8 | p4-12sqr | 1215 | 25 | 5 | 1 |
| 34_F14_2-4-0_4-0-4_8-2-2_V8_8 | p4-tr-4pyr | 1134 | 48 | 9 | 0 |
| 34_F16_4-0-3_12-1-3_V4_12 | Att-split | 243 | 32 | 7 | 0 |
| 34_F30_6-0-4_24-1-3_V8_24 | Ato-split | 243 | 15 | 4 | 0 |
- 3-5 graphs:
| Graph Name | p-Cage Name | ||||
| 35_F10_10-3-1_V10_2 | Da5 | 54 | 4 | 2 | 1 |
| 35_F14_2-0-3_6-1-2_6-2-2_V6_6_A | p3-2tr-3sqr-A | 3402 | 52 | 2 | 0 |
| 35_F14_2-0-3_6-1-2_6-2-2_V6_6_C | p3-2tr-3sqr-C | 3402 | 21 | 3 | 1 |
| 35_F18_2-0-4_8-1-2_8-2-2_V8_8_A | p4-2tr-3sqr-A | 3402 | 16 | 1 | 0 |
| 35_F18_2-0-4_8-1-2_8-2-2_V8_8_C | p4-2tr-3sqr-C | 3402 | 8 | 1 | 0 |
| 35_F30_30-2-2_V20_12 | DAid | 9 | 5 | 5 | 5 |
| 35_F50_6-4-0_8-0-3_12-0-4_24-2-2_V24_24 | Arco-6tr-4pyr | 3402 | 3 | 0 | 0 |
- 3-6 graphs:
| Graph Name | p-Cage Name | ||||
| 36_F12_12-3-1_V12_2 | Da6 | 54 | 6 | 3 | 0 |
| 36_F12_12-1-2_V4_4 | DAtt | 5850 | 13 | 2 | 0 |
| 36_F16_4-3-0_12-2-2_V12_4 | Pte-tr-3pyr | 10935 | 3 | 1 | 0 |
| 36_F16_4-0-3_12-1-2_V4_6 | Poc-4-3pyr | 81 | 8 | 3 | 0 |
| 36_F17_2-0-3_3-2-2_12-1-2_V6_6 | p3-4tr-1sqr | 19683 | 10 | 0 | 0 |
| 36_F30_6-0-4_24-1-2_V8_12 | Aco-8-3pyr | 81 | 3 | 0 | 0 |
| 36_F38_6-4-0_8-0-3_24-2-2_V24_12 | Aco-6tr-4pyr | 405 | 7 | 2 | 0 |
| 36_F54_6-0-4_24-0-3_24-1-2_V8_24 | Asc-8-3pyr | 2187 | 3 | 0 | 0 |
| 36_F62_6-0-4_8-0-3_24-1-2_24-2-2_V24_24_A | Arco-2tr-2sqr-A | 10206 | 81 | 0 | 0 |
| 36_F62_6-4-0_24-2-2_32-0-3_V24_24 | Asc-6tr-4pyr | 19683 | 26 | 0 | 0 |
References
- Malay, A.D.; Miyazaki, N.; Biela, A.; Chakraborti, S.; Majsterkiewicz, K.; Stupka, I.; Kaplan, C.S.; Kowalczyk, A.; Piette, B.M.A.G.; Hochberg, G.K.; et al. An ultra-stable gold-coordinated protein cage displaying reversible assembly. Nature 2019, 569, 438–442. [Google Scholar] [CrossRef] [PubMed]
- Piette, B.M.A.G.; Kowalczyk, A.; Heddle, J.G. Characterization of near-miss connectivity-invariant homogeneous convex polyhedral cages. Proc. R. Soc. A 2022, 478, 20210679. [Google Scholar] [CrossRef] [PubMed]
- Reidun, T.; Antoni, L. Structural puzzles in virology solved with an overarching icosahedral design principle. Nat. Commun. 2019, 10, 4414. [Google Scholar] [CrossRef] [PubMed]
- Majsterkiewicz, K.; Biela, A.P.; Maity, S.; Sharma, M.; Piette, B.M.A.G.; Kowalczyk, A.; Gaweł, S.; Chakraborti, S.; Roos, W.H.; Heddle, J.G. Artificial protein cage with unusual geometry and regularly embedded gold nanoparticles. Nano Lett. 2022, 22, 3187–3195. [Google Scholar] [CrossRef]
- Sharma, M.; Biela, A.P.; Kowalczyk, A.; Borzęcka-Solarz, K.; Piette, B.M.; Gaweł, S.; Bishop, J.; Kukura, P.; Benesch, J.L.; Imamura, M.; et al. Shape-Morphing of an Artificial Protein Cage with Unusual Geometry Induced by a Single Amino Acid Change. ACS Nanosci. Au 2022, 2, 404–413. [Google Scholar] [CrossRef]
- Putri, R.; Cornelissen, J.; Koay, M. Self-assembled cage-like protein structures. Chemphyschem 2015, 16, 911–918. [Google Scholar] [CrossRef]
- Blum, A.; Soto, C.; Wilson, C.; Cole, J.; Kim, M.; Gnade, B.; Chatterji, A.; Ochoa, W.; Lin, T.; Johnson, J.; et al. Cowpea Mosaic Virus as a Scaffold for 3-D Patterning of Gold Nanoparticles. Nano Lett. 2004, 4, 867–870. [Google Scholar] [CrossRef]
- Malay, A.D.; Heddle, J.G.; Tomita, S.; Iwasaki, K.; Miyazaki, N.; Sumitomo, K.; Yanagi, H.; Yamashita, I.; Uraoka, Y. Gold nanoparticle-induced formation of artificial protein capsids. Nano Lett. 2012, 12, 2056–2059. [Google Scholar] [CrossRef]
- Stupka, I.; Biela, A.P.; Piette, B.M.A.G.; Kowalczyk, A.; Majsterkiewicz, K.; Borzęcka-Solarz, K.; Naskalska, A.; Heddle, J.G. An artificial protein cage made from a 12-membered ring. J. Mater. Chem. B 2024, 12, 436–447. [Google Scholar] [CrossRef]
- Roos, W.; Gibbons, M.; Arkhipov, A.; Uetrecht, C.; Watts, N.; Wingfield, P.; Steven, A.; Heck, A.; Schulten, K.; Klug, W.; et al. Squeezing Protein Shells: How Continuum Elastic Models, Molecular Dynamics Simulations, and Experiments Coalesce at the Nanoscale. Biophys. J. 2010, 99, 1175–1181. [Google Scholar] [CrossRef]
- de Pablo, P.; Mateu, M. Mechanical Properties of Viruses. Subcell. Biochem. 2013, 68, 519–551. [Google Scholar] [CrossRef]
- Roos, W.; Bruinsma, R.; Wuite, G. Physical Virology. Nat. Phys. 2010, 6, 733–743. [Google Scholar] [CrossRef]
- Huang, P.; Boyken, S.; Baker, D. The coming of age of de novo protein design. Nature 2016, 537, 320–327. [Google Scholar] [CrossRef] [PubMed]
- Chakraborti, S.; Lin, T.Y.; Glatt, S.; Heddle, J.G. Enzyme encapsulation by protein cages. RSC Adv. 2020, 10, 13293–13301. [Google Scholar] [CrossRef] [PubMed]
- Gao, R.; Tan, H.; Li, S.; Ma, S.; Tang, Y.; Zhang, K.; Zhang, Z.; Fan, Q.; Yang, J.; Zhang, X.E.; et al. A prototype protein nanocage minimized from carboxysomes with gated oxygen permeability. Proc. Natl. Acad. Sci. USA 2022, 119, e2104964119. [Google Scholar] [CrossRef]
- Zhu, J.; Avakyan, N.; Kakkis, A.; Hoffnagle, A.M.; Han, K.; Li, Y.; Zhang, Z.; Choi, T.S.; Na, Y.; Yu, C.J.; et al. Protein assembly by design. Chem. Rev. 2021, 121, 13701–13796. [Google Scholar] [CrossRef]
- Lapenta, F.; Aupič, J.; Vezzoli, M.; Strmšek, Ž.; Da Vela, S.; Svergun, D.I.; Carazo, J.M.; Melero, R.; Jerala, R. Self-assembly and regulation of protein cages from pre-organised coiled-coil modules. Nat. Commun. 2021, 12, 939. [Google Scholar] [CrossRef]
- Percástegui, E.G.; Ronson, T.K.; Nitschke, J.R. Design and applications of water-soluble coordination cages. Chem. Rev. 2020, 120, 13480–13544. [Google Scholar] [CrossRef]
- Golub, E.; Subramanian, R.H.; Esselborn, J.; Alberstein, R.G.; Bailey, J.B.; Chiong, J.A.; Yan, X.; Booth, T.; Baker, T.S.; Tezcan, F.A. Constructing protein polyhedra via orthogonal chemical interactions. Nature 2020, 578, 172–176. [Google Scholar] [CrossRef]
- Brinkkemper, M.; Sliepen, K. Nanoparticle Vaccines for Inducing HIV-1 Neutralizing Antibodies. Vaccines 2019, 7, 76. [Google Scholar] [CrossRef]
- Chung, Y.; Cai, H.; Steinmetz, N. Viral Nanoparticles for Drug Delivery, Imaging, Immunotherapy, and Theranostic Applications. Adv. Drug Delivery Rev. 2020, 156, 214–235. [Google Scholar] [CrossRef] [PubMed]
- Lavanya, A.; Paopachapich, P.; Chheng, Y.; Joon, H.; Shee, E. Protein nanocages: A new frontier in mucosal vaccine delivery and immune activation. Hum. Vaccines Immunother. 2025, 21, 2492906. [Google Scholar] [CrossRef] [PubMed]
- Anam, Z.; Ammara, F.; Maria, K.; Muhammad, U.; Muhammad, W.; Tehreem, U.; Mohibullah, S.A.N. Two-dimensional material-based scaffolds for cell-based chip and tissue engineering and their recent progress in medical application. In Functionalization of Two-Dimensional Materials and Their Applications; Elsevier: Amsterdam, The Netherlands, 2024; pp. 177–208. [Google Scholar] [CrossRef]
- Liang, Y.; Furukawa, H.; Sakamoto, K.; Inaba, H.; Matsuura, K. Anticancer activity of reconstituted ribonuclease S-decorated artificial viral capsid. ChemBioChem 2022, 23, e202200220. [Google Scholar] [CrossRef]
- Stupka, I.; Azuma, Y.; Biela, A.P.; Imamura, M.; Scheuring, S.; Pyza, E.; Woźnicka, O.; Maskell, D.P.; Heddle, J.G. Chemically induced protein cage assembly with programmable opening and cargo release. Sci. Adv. 2022, 8, eabj9424. [Google Scholar] [CrossRef] [PubMed]
- Osiński, N.; Majsterkiewicz, K.; Pakosz-Stępień, Z.; Azuma, Y.; Biela, A.P.; Gaweł, S.; Heddle, J.G. Designed, Programmable Protein Cages Utilizing Diverse Metal Coordination Geometries Show Reversible, pH-Dependent Assembly. Macromol. Rapid Commun. 2024, 46, 2400712. [Google Scholar] [CrossRef]
- Olshefsky, A.; Richardson, C.; Pun, S.H.; King, N.P. Engineering self-assembling protein nanoparticles for therapeutic delivery. Bioconjug. Chem. 2022, 33, 2018–2034. [Google Scholar] [CrossRef]
- Luo, X.; Liu, J. Ultrasmall luminescent metal nanoparticles: Surface engineering strategies for biological targeting and imaging. Adv. Sci. 2022, 9, 2103971. [Google Scholar] [CrossRef]
- Naskalska, A.; Borzecka-Solarz, K.; Rozycki, J.; Stupka, I.; Bochenek, M.; Pyza, E.; Heddle, J.G. Artificial protein cage delivers active protein cargos to the cell interior. Biomacromolecules 2021, 22, 4146–4154. [Google Scholar] [CrossRef]
- Edwardson, T.G.; Tetter, S.; Hilvert, D. Two-tier supramolecular encapsulation of small molecules in a protein cage. Nat. Commun. 2020, 11, 5410. [Google Scholar] [CrossRef]
- Cao, S.; Peeters, S.; Michel-Souzy, S.; Hamelmann, N.; Paulusse, J.M.J.; Yang, L.l.; Cornelissen, J.J.L.M. Construction of viral protein-based hybrid nanomaterials mediated by a macromolecular glue. J. Mater. Chem. B 2023, 11, 7933–7941. [Google Scholar] [CrossRef]
- João, J.; Prazeres, D.M.F. Manufacturing of non-viral protein nanocages for biotechnological and biomedical applications. Front. Bioeng. Biotechnol. 2023, 11, 1200729. [Google Scholar] [CrossRef]
- Li, W.; Yang, H.; Stachowski, K.; Norris, A.S.; Lichtenthal, K.; Kelly, S.; Gollnick, P.; Wysocki, V.H.; Foster, M.P. Structural basis of nearest-neighbor cooperativity in the ring-shaped gene regulatory protein TRAP from protein engineering and cryo-EM. Proc. Natl. Acad. Sci. USA 2025, 122, e2409030121. [Google Scholar] [CrossRef]
- Laniado, J.; Cannon, K.A.; Miller, J.E.; Sawaya, M.R.; McNamara, D.E.; Yeates, T.O. Geometric Lessons and Design Strategies for Nanoscale Protein Cages. ACS Nano 2021, 15, 4277–4286. [Google Scholar] [CrossRef] [PubMed]
- Fatehi, F.; Twarock, R. An interaction network approach predicts protein cage architectures in bionanotechnology. Proc. Natl. Acad. Sci. USA 2023, 120, e2303580120. [Google Scholar] [CrossRef]
- Bae, J.H.; Kim, H.S.; Kim, G.; Song, J.J.; Kim, H.S. Dendrimer-like supramolecular assembly of proteins with a tunable size and valency through stepwise iterative growth. bioRxiv 2021. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Deng, P.; Gao, H.; Zhang, W.B. Systematic discovery and feature analysis of intertwined symmetric protein motifs for topology engineering. Giant 2024, 17, 100226. [Google Scholar] [CrossRef]
- Khmelinskaia, A.; Wargacki, A.; King, N.P. Structure-based design of novel polyhedral protein nanomaterials. Curr. Opin. Microbiol. 2021, 61, 51–57. [Google Scholar] [CrossRef]
- Koziej, L.; Fatehi, F.; Aleksejczuk, M.; Byrne, M.; Heddle, J.; Twarock, R.; Azuma, Y. Dynamic Assembly of Pentamer-Based Protein Nanotubes. ACS Nano 2025, 19, 8786–8798. [Google Scholar] [CrossRef]
- Gladkov, N.; Scott, E.A.; Meador, K.; Lee, E.J.; Laganowsky, A.D.; Yeates, T.O.; Castells-Graells, R. Design of a symmetry-broken tetrahedral protein cage by a method of internal steric occlusion. bioRxiv 2023. [Google Scholar] [CrossRef]
- Piette, B.M.A.G.; Lukács, Á. Near-Miss Symmetric Polyhedral Cages. Symmetry 2023, 15, 717. [Google Scholar] [CrossRef]
- Coxeter, H. Regular Polytopes, 1st ed.; Methuen: London, UK, 1949. [Google Scholar]
- Flegg, H.G. From Geometry to Topology; Dover Books on Mathematics; Dover Publications: Mineola, NY, USA, 2001. [Google Scholar]
- Piette, B.M.A.G.; Lukács, Á. Near-Miss Bi-Homogenous Symmetric Polyhedral Cages. Symmetry 2023, 15, 1804. [Google Scholar] [CrossRef]
- Piette, B.; Lukács, Á. Bi-Symmetric Polyhedral Cages with Maximally Connected Faces and Small Holes. Symmetry 2025, 17, 101. [Google Scholar] [CrossRef]
- Piette, B. Bi-Symmetric Polyhedral Cages with Nearly Maximally Connected Faces and Small Holes. Symmetry 2025, 17, 940. [Google Scholar] [CrossRef]
- Magnus, W.; Karrass, A.; Solitar, D. Combinatorial Group Theory: Presentations of Groups in Terms of Generators and Relations; Courier Corporation: Chelmsford, MA, USA, 2004. [Google Scholar]
- Maschke, H. The Representation of Finite Groups, Especially of the Rotation Gro ups of the Regular Bodies of Three-and Four-Dimensional Space, by Cayley’s Color Diagrams. Am. J. Math. 1896, 18, 156–194. [Google Scholar] [CrossRef]
- Piette, B. Biequivalent Planar Graphs. Axioms 2024, 13, 437. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Tang, L. Extremal bounds on peripherality measures. Discrete Math. Lett. 2023, 12, 201–208. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).