Functional Identities in Superalgebras: Theoretical Insights and Computational Verification

Abstract

This paper investigates functional identities in superalgebras, building on Wang’s foundational work. We study d-superfree subsets and k-supercommuting maps in prime superalgebras, both with and without superinvolution, introducing new results on symmetric and skew elements. Using SageMath, we computationally verify key properties in the finite-dimensional superalgebra $M_2\left(\mathbb{Q}\right)$, including supercommutators, superinvolutions, and k-supercommuting maps, thereby providing concrete illustrations of the abstract theory. These computations underscore the practical applicability of functional identities in finite-dimensional settings and offer fresh insights into superalgebra structures.

1. Introduction

Superalgebras arise as a natural extension of classical algebraic structures by incorporating a ${\mathbb{Z}}_2$-grading that distinguishes between even and odd elements. Historically, the concept of superalgebras emerged in the 1970s, motivated by developments in theoretical physics, particularly in supersymmetry and quantum field theory. Victor Kac’s seminal work rigorously formalized Lie superalgebras, laying a foundation for the algebraic treatment of symmetry principles that mix commuting and anticommuting variables [1].

A superalgebra $\mathcal{A}={\mathcal{A}}_0\oplus {\mathcal{A}}_1$ over a commutative ring $\mathcal{F}$ with ${\displaystyle \frac{1}{2}}\in \mathcal{F}$ is an associative algebra equipped with a ${\mathbb{Z}}_2$-grading such that

$${\mathcal{A}}_i{\mathcal{A}}_j\subseteq {\mathcal{A}}_{i+j(mod2)},$$

for $i,j\in \{0,1\}$. Elements in ${\mathcal{A}}_0$ are called even, and those in ${\mathcal{A}}_1$ are odd. Homogeneous elements $x\in {\mathcal{A}}_i$ have degree $\left|x\right|=i$. The grading automorphism $\sigma :\mathcal{A}\to \mathcal{A}$ defined by

$$\sigma (x_0+x_1)=x_0-x_1,$$

satisfies ${\sigma }^2=\mathrm{id}$, identifying

$${\mathcal{A}}_0=\{x\mid \sigma \left(x\right)=x\}\mathrm{and}{\mathcal{A}}_1=\{x\mid \sigma \left(x\right)=-x\}.$$

Superalgebras have profound applications not only in physics but also in pure mathematics, including representation theory, noncommutative geometry, and homological algebra [2,3,4,5,6,7,8,9,10].

Functional identities, first developed by Brešar for rings were adapted by Wang to the graded setting, leading to the notion of d-superfree subsets, which guarantee the existence of standard solutions to certain functional equations [11].

Building upon this foundation, our paper introduces new theorems concerning superinvolutions and k-supercommuting maps in prime superalgebras. We emphasize computational verification using SageMath [12] in the specific case of $M_2\left(\mathbb{Q}\right)$, validating theoretical results such as the behavior of supercommutators, superinvolutions, and k-supercommuting maps [13,14]. This approach bridges the gap between abstract theory and explicit finite-dimensional examples, providing novel insights into the structure and applications of superalgebras.

The paper concludes by discussing implications for Lie superalgebras and proposing open problems for further exploration.

2. Preliminaries

Definition 1.

superalgebra $\mathcal{A}={\mathcal{A}}_0\oplus {\mathcal{A}}_1$ over a field $\mathcal{F}$ with ${\displaystyle \frac{1}{2}}\in \mathcal{F}$ is a ${\mathbb{Z}}_2$-graded associative algebra satisfying

$${\mathcal{A}}_i{\mathcal{A}}_j\subseteq {\mathcal{A}}_{i+j(mod2)},$$

for $i,j\in \{0,1\}$. Elements in ${\mathcal{A}}_0\cup {\mathcal{A}}_1$ are called homogeneous with degree $\left|a\right|=i$ for $a\in {\mathcal{A}}_i$ [1].

Example 1.

The algebra $M_2\left(\mathbb{Q}\right)$ of $2\times 2$ matrices over $\mathbb{Q}$ is a superalgebra with

$${\mathcal{A}}_0=\left\{\left(\begin{array}{cc}a& 0\\ 0& b\end{array}\right):a,b\in \mathbb{Q}\right\},{\mathcal{A}}_1=\left\{\left(\begin{array}{cc}0& c\\ d& 0\end{array}\right):c,d\in \mathbb{Q}\right\}.$$

It’s supercenter $\mathcal{Z}{\left(M_2\left(\mathbb{Q}\right)\right)}_s$ consists of scalar diagonal matrices

$$\left\{\left(\begin{array}{cc}c& 0\\ 0& c\end{array}\right):c\in \mathbb{Q}\right\}.$$

Example 2.

The Clifford algebra $C\mathcal{\ell }(1,1)$ over $\mathbb{Q}$ is a superalgebra with basis $\{1,e_1,e_2,e_1{e}_2\}$ satisfying

$$e_1^2=1,e_2^2=-1,e_1{e}_2=-e_2{e}_1.$$

The even part ${\mathcal{A}}_0$ is spanned by $\{1,e_1{e}_2\}$, and the odd part ${\mathcal{A}}_1$ by $\{e_1,e_2\}$.

Definition 2.

For homogeneous elements $x,y\in \mathcal{A}$, the supercommutator is defined by

$$[x,y]=xy-{(-1)}^{\left|x\right|\left|y\right|}yx.$$

Extending bilinearly to all $x=x_0+x_1$ and $y=y_0+y_1$ with $x_i,y_i\in {\mathcal{A}}_i$, we have

$$[x,y]=[x_0,y_0]+[x_1,y_0]+[x_0,y_1]+[x_1,y_1].$$

Definition 3.

A superinvolution ‘∗’ on $\mathcal{A}$ is a graded $\mathcal{F}$-linear map satisfying

$${\left(x^{*}\right)}^{*}=x,{\left(xy\right)}^{*}={(-1)}^{\left|x\right|\left|y\right|}{y}^{*}{x}^{*},x,y\in \mathcal{A}\mathit{homogeneous}.$$

The set of symmetric elements is

$$\mathcal{S}\left(\mathcal{A}\right)=\{x\in \mathcal{A}\mid x^{*}=x\},$$

and the set of skew-symmetric elements is

$$\mathcal{K}\left(\mathcal{A}\right)=\{x\in \mathcal{A}\mid x^{*}=-x\}.$$

Definition 4.

Let $\mathcal{R}$ be a graded $\mathcal{F}$-submodule of $\mathcal{A}$. A map $f:\mathcal{R}\to \mathcal{A}$ is k-supercommuting if for all $x\in \mathcal{R}$,

$${[f\left(x\right),x]}_k=0,$$

where the iterated supercommutators ${[x,y]}_k$ are defined recursively by

$${[x,y]}_0=x,{[x,y]}_1=[x,y],{[x,y]}_k=[{[x,y]}_{k-1},y].$$

3. Functional Identities and $\mathit{d}$-Superfree Subsets

Functional identities in superalgebras extend classical ring theory to the graded setting, capturing ${\mathbb{Z}}_2$-graded behavior. Wang introduced the notion of d-superfree subsets to guarantee uniqueness of standard solutions to functional identities [15].

Definition 5

(d-Superfree Triples). Let $\mathcal{Q}={\mathcal{Q}}_0\oplus {\mathcal{Q}}_1$ be a unital superalgebra with center $\mathcal{C}={\mathcal{C}}_0\oplus {\mathcal{C}}_1$ and grading automorphism σ. Fix an element $\omega \in \mathcal{Q}$ such that

$$\omega =\left\{\begin{array}{cc}0\hfill & \mathit{if}\sigma =\mathrm{id}\mathit{or}\sigma \mathit{is}\mathit{outer},\hfill \\ \mathit{invertible}\mathit{with}\sigma \left(a\right)=\omega a{\omega }^{-1}\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

A triple $(\widehat{\mathcal{S}};\Delta ;\widehat{\mathcal{U}})$ is called d-superfree if for any subsets $\mathcal{I},\mathcal{J}\subseteq \{1,\dots ,m\}$ with

$$max\left\{\right|\mathcal{I}|,|\mathcal{J}\left|\right\}<d+1;$$

the functional identity

$$\sum _{i\in \mathcal{I}}{E}_i\left(x\right){\delta }_i\left(x\right)+\sum _{j\in \mathcal{J}}{\delta }_j\left(x\right)F_j\left(x\right)=0$$

(1)

implies the existence of ${\lambda }_i\in \mathcal{C}$ such that the standard solution

$$E_i\left(x\right)=\sum _{j\notin \mathcal{I}}{\lambda }_j{F}_j\left(x\right),F_j\left(x\right)=-\sum _{i\notin \mathcal{J}}{\lambda }_i{E}_i\left(x\right)$$

(2)

holds. Moreover, if

$$max\left\{\right|\mathcal{I}|,|\mathcal{J}\left|\right\}<d,$$

and the sum in (1) lies in $\mathcal{C}+\mathcal{C}\omega$, the same conclusion applies [15].

Example 3.

In $M_2\left(\mathbb{Q}\right)$, taking $\mathcal{R}={\mathcal{A}}_0$ and considering the functional identity $[x,f(x\left)\right]=0$ for $f:\mathcal{R}\to \mathcal{A}$, one obtains that $f\left(x\right)$ lies in the supercenter $\mathcal{Z}{\left(\mathcal{A}\right)}_s$ (cf. computations in Section 6).

Example 4.

In $M_2\left(\mathbb{Q}\right)$, consider the functional identity

$$E\left(x\right)x=0$$

for a homogeneous map E. This forces $E\left(x\right)=0$ for all $x\in {\mathcal{A}}_0\cup {\mathcal{A}}_1$, illustrating a trivial standard solution.

Theorem 1

(Uniqueness of Standard Solutions). For a d-superfree triple $(\widehat{\mathcal{S}};\Delta ;\widehat{\mathcal{U}})$, the functional identities

$$\sum _{i\in \mathcal{I}}{E}_i\left(x\right){\delta }_i\left(x\right)+\sum _{j\in \mathcal{J}}{\delta }_j\left(x\right)F_j\left(x\right)=0,$$

with

$$max\left\{\right|\mathcal{I}|,|\mathcal{J}\left|\right\}<d+1,$$

and similarly when the sum lies in $\mathcal{C}+\mathcal{C}\omega$ for

$$max\left\{\right|\mathcal{I}|,|\mathcal{J}\left|\right\}<d,$$

admit unique standard solutions given by (2) (Theorem 3.4, [15]).

Proof. 

See (Theorem 3.4, [15]).    □

4. Results in Prime Superalgebras

Theorem 2.

Let $\mathcal{A}$ be a prime superalgebra with grading automorphism σ. If σ is outer, then

$${\mathcal{M}}_{\sigma }=\left\{0\right\},$$

where

$${\mathcal{M}}_{\sigma }=\{s\in \mathcal{Q}\mid rs=s{r}^{\sigma }\mathit{for}\mathit{all}r\in \mathcal{A}\}.$$

Proof. 

See (Theorem 4.1, [15]).    □

Theorem 3.

Let $\mathcal{A}$ be a semiprime superalgebra with maximal left ring of quotients $\mathcal{Q}$. For $q_i\in {\mathcal{A}}_0\cup {\mathcal{Q}}_1$ and ${\theta }_i\in {\mathrm{Aut}}_{{\mathbb{Z}}_2}\left(\mathcal{A}\right)$, if $q_1$ is left independent over $q_2,\dots ,q_n$ relative to ${\theta }_1,\dots ,{\theta }_n$, then there exist $a_i,b_i\in {\mathcal{A}}_0\cup {\mathcal{A}}_1$ such that

$$\begin{array}{c}\hfill 0\ne \sum _{i=1}^m{a}_i^{{\theta }_i}{q}_i{b}_i\in {\mathcal{A}}_0\cup {\mathcal{Q}}_1,\mathit{and}\sum _{i=1}^m{a}_i^{{\theta }_j}{q}_i{b}_i=0\mathit{for}\mathit{all}j\ge 2.\end{array}$$

Proof. 

See (Theorem 4.2, [15]).    □

Theorem 4.

Let $\mathcal{A}$ be a prime superalgebra with superinvolution ∗. If

$$deg\left((\mathcal{S}\left(\mathcal{A}\right)\cup \mathcal{K}\left(\mathcal{A}\right))\cap {\mathcal{A}}_1\right)\ge 4d+5,$$

then $\mathcal{S}\left(\mathcal{A}\right)$ and $\mathcal{K}\left(\mathcal{A}\right)$ are d-superfree [15].

Proof. 

See (Theorem 5.10, [15]).    □

5. $\mathit{k}$-Supercommuting Maps

Theorem 5.

Let $\mathcal{Q}={\mathcal{Q}}_0\oplus {\mathcal{Q}}_1$ be a unital superalgebra with supercenter $\mathcal{Z}{\left(\mathcal{Q}\right)}_s$. Let $\mathcal{R}$ be a graded $\mathcal{F}$-submodule of $\mathcal{Q}$. Suppose $f:\mathcal{R}\to \mathcal{Q}$ is $\mathcal{F}$-linear and satisfies

$${[f\left(x\right),x]}_k=0\mathit{for}\mathit{all}x\in \mathcal{R},$$

and $\mathcal{R}$ is $(k+1)$-superfree. Then

$$f\left(\mathcal{R}\right)\subseteq \mathcal{Z}{\left(\mathcal{Q}\right)}_s.$$

Proof. 

See (Theorem 6.1, [15]).    □

Corollary 1.

Let $\mathcal{A}$ be a prime superalgebra with maximal left ring of quotients $\mathcal{Q}$. If $f:\mathcal{A}\to \mathcal{Q}$ is k-supercommuting and

$$deg\left({\mathcal{A}}_1\right)\ge 2k+3,$$

then

$$f\left(\mathcal{A}\right)\subseteq {\mathcal{C}}_0,$$

the center of the even part [15].

Corollary 2.

Let $\mathcal{A}$ be a prime superalgebra with superinvolution ∗. For $\mathcal{R}=\mathcal{S}\left(\mathcal{A}\right)$ or $\mathcal{K}\left(\mathcal{A}\right)$, if $f:\mathcal{R}\to \mathcal{Q}$ is k-supercommuting and

$$deg\left((\mathcal{S}\left(\mathcal{A}\right)\cup \mathcal{K}\left(\mathcal{A}\right))\cap {\mathcal{A}}_1\right)\ge 4k+9,$$

then

$$f\left(\mathcal{R}\right)\subseteq {\mathcal{C}}_0.$$

Theorem 6.

Let $\mathcal{A}$ be a prime superalgebra with superinvolution ∗. If $f:\mathcal{S}\left(\mathcal{A}\right)\to \mathcal{A}$ is k-supercommuting and

$$deg(\mathcal{S}\left(\mathcal{A}\right)\cap {\mathcal{A}}_1)\ge 2k+3,$$

then

$$f{\left(x\right)}^{*}=f\left(x\right)\mathit{for}\mathit{all}x\in \mathcal{S}\left(\mathcal{A}\right).$$

Proof. 

Let $x\in \mathcal{S}\left(\mathcal{A}\right)$. By hypothesis f is k-supercommuting on $\mathcal{S}\left(\mathcal{A}\right)$, so

$${[f\left(x\right),x]}_k=0.$$

The degree condition $deg(\mathcal{S}\left(\mathcal{A}\right)\cap {\mathcal{A}}_1)\ge 2k+3$ ensures that $\mathcal{S}\left(\mathcal{A}\right)$ satisfies the superfreeness hypothesis required to apply Corollary 2. Thus Corollary 2 gives

$$f\left(\mathcal{S}\left(\mathcal{A}\right)\right)\subseteq {\mathcal{C}}_0,$$

where ${\mathcal{C}}_0$ denotes the even part of the center of $\mathcal{A}$.

In a prime superalgebra equipped with a superinvolution the even central elements are invariant under the involution. Hence every $c\in {\mathcal{C}}_0$ satisfies $c^{*}=c$. Since $f\left(x\right)\in {\mathcal{C}}_0$ for all $x\in \mathcal{S}\left(\mathcal{A}\right)$, we obtain $f{\left(x\right)}^{*}=f\left(x\right)$ for every $x\in \mathcal{S}\left(\mathcal{A}\right)$, as required.    □

Theorem 7.

Let $\mathcal{A}$ be a prime superalgebra with superinvolution ∗. If $f:\mathcal{K}\left(\mathcal{A}\right)\to \mathcal{A}$ is k-supercommuting and

$$deg(\mathcal{K}\left(\mathcal{A}\right)\cap {\mathcal{A}}_1)\ge 2k+3,$$

then

$$f\left(x\right)=0\mathit{for}\mathit{all}x\in \mathcal{K}\left(\mathcal{A}\right).$$

Proof. 

Let $x\in \mathcal{K}\left(\mathcal{A}\right)$. Since f is k-supercommuting on $\mathcal{K}\left(\mathcal{A}\right)$, we have

$${[f\left(x\right),x]}_k=0.$$

The degree bound $deg(\mathcal{K}\left(\mathcal{A}\right)\cap {\mathcal{A}}_1)\ge 2k+3$ permits application of Corollary 2 to the skew subspace $\mathcal{K}\left(\mathcal{A}\right)$; hence

$$f\left(\mathcal{K}\left(\mathcal{A}\right)\right)\subseteq {\mathcal{C}}_0.$$

Therefore, for each $x\in \mathcal{K}\left(\mathcal{A}\right)$ the element $f\left(x\right)$ lies in ${\mathcal{C}}_0$, and so $f{\left(x\right)}^{*}=f\left(x\right)$.

But every $x\in \mathcal{K}\left(\mathcal{A}\right)$ satisfies $x^{*}=-x$. If $f\left(x\right)$ were also skew (i.e., $f\left(x\right)\in \mathcal{K}\left(\mathcal{A}\right)$), then $f{\left(x\right)}^{*}=-f\left(x\right)$, contradicting $f{\left(x\right)}^{*}=f\left(x\right)$ unless $f\left(x\right)=0$. Equivalently, since $\mathcal{K}\left(\mathcal{A}\right)\cap {\mathcal{C}}_0=\left\{0\right\}$ in the prime superalgebra setting, the inclusion $f\left(x\right)\in {\mathcal{C}}_0$ forces $f\left(x\right)=0$ for every $x\in \mathcal{K}\left(\mathcal{A}\right)$. This completes the proof.    □

6. Computational Examples

We verify results in $M_2\left(\mathbb{Q}\right)$, with grading:

• ${\mathcal{A}}_0$: diagonal matrices, e.g., $\left(\begin{array}{cc}a& 0\\ 0& b\end{array}\right)$.
• ${\mathcal{A}}_1$: off-diagonal matrices, e.g., $\left(\begin{array}{cc}0& c\\ d& 0\end{array}\right)$.

The supercenter $\mathcal{Z}{\left(M_2\left(\mathbb{Q}\right)\right)}_s$ consists of scalar matrices $\left(\begin{array}{cc}c& 0\\ 0& c\end{array}\right)$.

6.1. Supercommutator Implementation

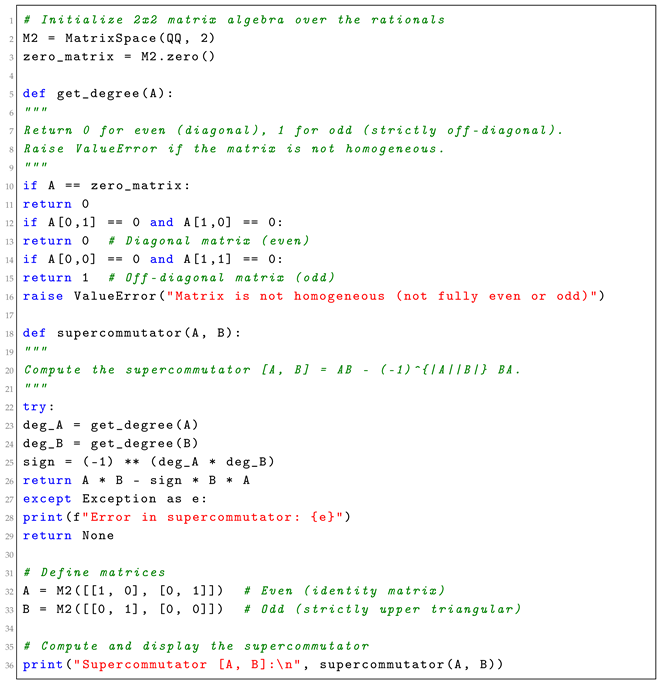
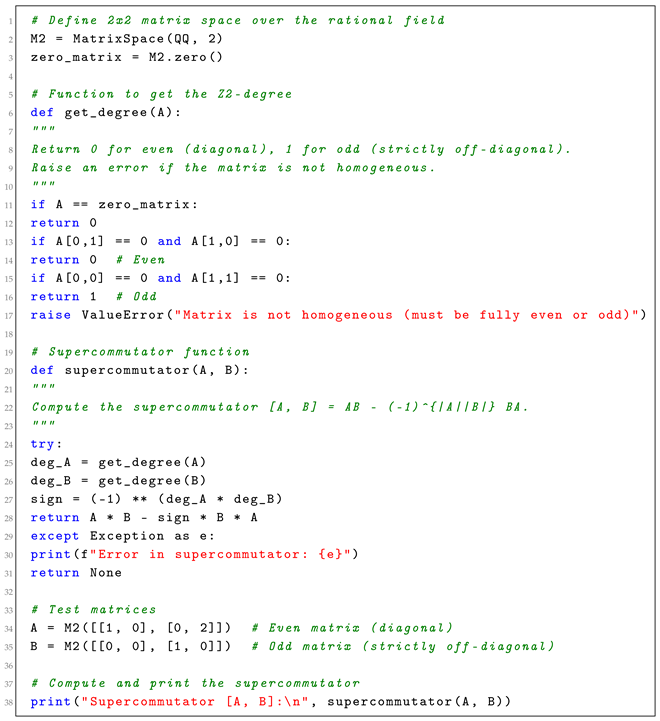
An explicit SageMath implementation of supercommutator is shown in Listing 1.

Listing 1. SageMath implementation of superalgebra operations.

6.2. Supercommutator Examples

Example 5.

For $A=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$ (even) and $B=\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right)$ (odd):

$$[A,B]=AB-BA=\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right)-\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right)=\left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right).$$

SageMath implementation for calculating supercommutator is presented in Listing 2.

Listing 2. Verification of supercommutator.

Output:

Supercommutator [A,B]:

[0 0]

[0 0]

Example 6.

For $A=\left(\begin{array}{cc}1& 0\\ 0& 2\end{array}\right)$ (even) and $B=\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right)$ (odd):

$$[A,B]=AB-BA=\left(\begin{array}{cc}0& 0\\ 2& 0\end{array}\right)-\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right)=\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right).$$

SageMath implementation for calculating an additional supercommutator is presented in Listing 3.

Listing 3. Additional supercommutator verification.

Output:

Supercommutator [A,B]:

[0  0]

[1  0]

Example 7.

For $A=\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)$ (odd) and $B=\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right)$ (odd):

$$[A,B]=AB+BA=\left(\begin{array}{cc}1& 0\\ 0& 0\end{array}\right)+\left(\begin{array}{cc}0& 0\\ 0& 1\end{array}\right)=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right).$$

SageMath code for the calculation of a odd supercommutator appears in Listing 4.

Listing 4. Odd supercommutator verification.

Output:

Supercommutator [A,B]:

[1 0]

[0 1]

6.3. Superinvolution Implementation

SageMath implementation for calculating superinvolution is presented in Listing 5.

Listing 5. Superinvolution implementation.

6.4. Superinvolution Examples

Example 8.

Let $C=\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)$, which is an odd matrix. Then the superinvolution is computed as:

$$C^{*}=-C^T=-\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right)=\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)=C.$$

Thus, C is self-adjoint under the superinvolution.

SageMath code for the calculation of a superinvolution appears in Listing 6.

Listing 6. Verification of superinvolution.

C*:

[ 0  1]

[-1  0]

Is C self-adjoint? True

Example 9.

For $D=\left(\begin{array}{cc}1& 0\\ 0& 2\end{array}\right)$, which is an even matrix:

$$D^{*}=D^T=\left(\begin{array}{cc}1& 0\\ 0& 2\end{array}\right)=D.$$

Thus, D is self-adjoint under the superinvolution.

SageMath implementation for calculating additional superinvolution is presented in Listing 7.

Listing 7. Additional superinvolution verification.

D*:

[1 0]

[0 2]

Is D self-adjoint? True

Example 10.

For $E=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$, which is an odd matrix:

$$E^{*}=-E^T=-\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)=\left(\begin{array}{cc}0& -1\\ -1& 0\end{array}\right)=-E.$$

Thus, E is not self-adjoint under the superinvolution.

SageMath implementation for calculating non-selfadjoint superinvolution is presented in Listing 8.

Listing 8. Non-selfadjoint superinvolution.

E*:

[ 0 -1]

[-1  0]

Is E self-adjoint? False

6.5. k-Supercommuting Maps

SageMath implementation for calculating k-supercommuting map is presented in Listing 9.

Listing 9. k-supercommuting map verification.

Central map [f(x_even),x_even]_1:

[0 0]

[0 0]

Central map [f(x_even),x_even]_2:

[0 0]

[0 0]

Non-central map [f(x_even),x_even]_1:

[0 0]

[0 0]

Central map [f(x_odd),x_odd]_1:

[0 0]

[0 0]

Symmetric map [f(x_skew),x_skew]_1:

[0 0]

[0 0]

Central map [f(x_skew),x_skew]_2:

[0 0]

[0 0]

Is central_map(x_even) in supercenter? True

Is noncentral_map(x_even) in supercenter? False

Is symmetric_map(x_skew) symmetric? True

6.6. Visualization of Supercommutator Norms

To quantify the behavior of supercommutators, we compute the Frobenius norm ${\left|\right|[A,B]\left|\right|}_F$ for pairs of matrices. SageMath implementation for calculating Frobenius norm of supercommutators is presented in Listing 10.

Listing 10. Frobenius norm of supercommutators.

Output:

Frobenius norms = \([0, 1, \sqrt{2}]\).

7. Applications to Lie Superalgebras

Functional identities provide deep insights into the structure of Lie superalgebras, where the supercommutator serves as the Lie bracket. The set $\mathcal{K}\left(\mathcal{A}\right)$ of skew elements relative to a superinvolution forms a Lie superalgebra. Theorems 6 and 7 indicate that k-supercommuting maps on $\mathcal{S}\left(\mathcal{A}\right)$ and $\mathcal{K}\left(\mathcal{A}\right)$ produce central elements, which are crucial for constructing central extensions.

Proposition 1.

Let $\mathcal{A}$ be a prime superalgebra equipped with a superinvolution ‘∗’. Then $\mathcal{K}\left(\mathcal{A}\right)$, the set of skew elements, forms a Lie superalgebra under the supercommutator bracket $[x,y]$. Moreover,

$$\mathcal{K}{\left(\mathcal{A}\right)}_0\subseteq {\mathcal{A}}_0\mathit{and}\mathcal{K}{\left(\mathcal{A}\right)}_1\subseteq {\mathcal{A}}_1.$$

Proof. 

For homogeneous $x,y\in \mathcal{K}\left(\mathcal{A}\right)$, we have $x^{*}=-x$ and $y^{*}=-y$. Consider

$$\begin{array}{cc}\hfill {[x,y]}^{*}& ={(xy-{(-1)}^{\left|x\right|\left|y\right|}yx)}^{*}\hfill \\ & ={(-1)}^{\left|x\right|\left|y\right|}{y}^{*}{x}^{*}-x^{*}{y}^{*}\hfill \\ & ={(-1)}^{\left|x\right|\left|y\right|}(-y)(-x)-(-x)(-y)\hfill \\ & =-[x,y].\hfill \end{array}$$

Hence, $[x,y]\in \mathcal{K}\left(\mathcal{A}\right)$. The graded Jacobi identity follows from associativity and the properties of the supercommutator.    □

Example 11.

In $M_2\left(\mathbb{Q}\right)$, the matrix

$$x=\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)\in \mathcal{K}{\left(\mathcal{A}\right)}_1$$

satisfies $x^{*}=-x$ and $[x,x]=0$, consistent with the Lie superalgebra structure.

Example 12.

Consider

$$y=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)\in \mathcal{K}{\left(\mathcal{A}\right)}_0.$$

Since $y^{*}=-y$ (where ‘∗’ is the superinvolution, here the transpose combined with a sign), the bracket $[y,x]$ lies in $\mathcal{K}{\left(\mathcal{A}\right)}_1$, illustrating the grading in the Lie superalgebra.

8. Open Problems and Future Directions

This study prompts several open questions:

• Can the degree bounds in Theorem 4 be improved specifically for matrix superalgebras?
• Under what conditions do k-supercommuting maps on non-prime superalgebras map into the supercenter?
• How can functional identities be extended to ${\mathbb{Z}}_n$-graded algebras beyond the ${\mathbb{Z}}_2$-graded case?
• Can computational and symbolic methods effectively predict the structure of d-superfree subsets in higher-dimensional superalgebras?

These questions, together with the computational evidence presented, highlight promising directions for further research into superalgebra structures via symbolic computation and functional identities.

9. Conclusions

This study advances the theory of functional identities in superalgebras by extending Wang’s framework. In particular, Theorems 6 and 7 establish that k-supercommuting maps on symmetric elements of prime superalgebras with superinvolution map into the even center, while those on skew elements vanish, under suitable degree conditions. These results highlight the deep interaction between ${\mathbb{Z}}_2$-grading and superinvolutions.

Computational experiments in $M_2\left(\mathbb{Q}\right)$ using SageMath corroborate the theoretical framework, verifying the behavior of supercommutators, superinvolutions, and k-supercommuting maps, and thereby bridging abstract results with explicit finite-dimensional examples. The implications for Lie superalgebras are significant: skew elements form a Lie superalgebra under the supercommutator, offering new insights into symmetry in algebraic structures.

Finally, the open problems posed in Section 8 including sharpening degree bounds and extending the theory to ${\mathbb{Z}}_n$-graded algebras point toward rich directions for further research. By combining rigorous theory with computational validation, this work deepens the understanding of superalgebras and reinforces their role in both mathematics and theoretical physics, in line with the interdisciplinary scope of symmetry-driven research.