Efficient Lattice-Based Digital Signatures for Embedded IoT Systems

Abstract

This paper offers a lattice-based digital signature construction, optimized for the provision of post-quantum security in resource-constrained environments, such as Internet of Things (IoT) devices. The offered scheme is built upon structured hardness assumptions, defined over polynomial rings that exhibit inherent algebraic symmetry. By exploiting the cyclic properties of these ring structures and implementing efficient Number Theoretic Transforms (NTTs), the construction achieves compact signatures that are under 3 KB and a runtime feasibility that uses less than 10 KB of RAM. The signature generation process incorporates balanced rejection sampling and carefully designed polynomial encodings that preserve structural regularity and computational efficiency. The security of the offered scheme is proven. The benchmark results generated from using the ARM Cortex-M4 platform demonstrate its practical usability. This study highlights how symmetric algebraic frameworks based on lattice-based cryptography can be leveraged to achieve both theoretical security and real-world performance in the post-quantum era.

1. Introduction

Digital signatures are essential for securing modern communication systems and embedded devices. As the Internet of Things (IoT) continues to grow, more and more re-source-constrained devices are being used in critical infrastructure, healthcare, and industrial systems. This increases the need for authentication methods that are not only se-cure, but also efficient [1,2]. Traditional digital signature schemes, such as those based on elliptic curve cryptography, are widely used today, because they are compact and fast. The problem is that they are vulnerable to quantum attacks. Shor’s algorithm can efficiently solve the elliptic curve discrete logarithm problem (ECDLP), which would compromise the security of most current public key systems [3]. This type of threat is particularly significant for IoT devices, which are often deployed for many years and may still be in use when quantum computers are adopted for practical applications [4,5].

To address this problem, we offer a digital signature scheme, based on lattice cryptography. Our construction is designed for the provision of post-quantum security and is optimized for devices with limited computing power. Our approach relies on hard mathematical problems like Learning With Errors (LWE) and the Short Integer Solution (SIS), which are believed to remain secure, even against quantum computers. The abovementioned problems are defined over structured polynomial rings that have useful algebraic symmetry. By using these symmetries, we can apply efficient techniques, such as Number Theoretic Transforms (NTTs), which reduces the computation time and memory usage.

Our goal is to design a post-quantum secure digital signature scheme based on the LWE and SIS problems, which is efficient enough to be utilized on resource-constrained devices and practical enough for real-world deployment on modern IoT hardware. Although our work is inspired by previous designs, it replaces elliptic curve operations with lattice-based ones, while keeping the structure simple and efficient. This emphasizes the novelty of our approach. The use of symmetric ring structures helps us achieve good performance, without sacrificing security. Our main contributions include adapting lattice-based methods to fit well in regard to symmetric cryptographic designs, choosing practical parameters for common embedded processors, and testing the scheme using ARM Cortex-M4 hardware to confirm that it is suitable for real-world applications.

The security of IoT devices has been studied extensively, particularly with regard to authentication, trust management, and resilience to emerging threats. Conventional approaches often rely on lightweight cryptographic primitives to meet resource constraints, but these are increasingly seen as insufficient against quantum-capable adversaries. Recent work has highlighted the unique challenges in terms of IoT environments, including scalability, heterogeneity, and the need for long-term cryptographic agility. For example, Refs. [6,7] analyze the role of lightweight authentication mechanisms for IoT devices using evolving adversarial models, while papers [8,9] study the performance and reliability of IoT networks when subjected to a cryptographic computational overhead. This study addresses the following research questions: (1) Can lattice-based signatures be optimized to fit within IoT resource constraints, while preserving post-quantum security? (2) How do such schemes compare to existing NIST PQC candidates and lightweight alternatives (e.g., qDSA)? (3) What design techniques (e.g., algebraic symmetry, rejection sampling) most effectively balance security and performance in regard to constrained devices?

The contributions by this work can be summarized as follows:

• We design a lattice-based digital signature scheme, optimized for resource-constrained IoT devices, providing compact signatures and reduced memory usage compared to NIST PQC standards;
• We provide both theoretical security proofs (ROM and QROM) and concrete security analysis, which includes explicit bounds;
• We implement and benchmark the scheme using ARM Cortex-M4 hardware, demonstrating its efficiency and practicality for use on resource-constrained devices;
• We compare our results to state-of-the-art schemes, including NIST PQC finalists and the qDSA, highlighting its advantages in terms of signature size and verification cost.

The rest of this paper is organized as follows: Section 2 provides background on lattice-based cryptography and digital signature schemes. Section 3 describes the design of our scheme, including key generation, signing, and verification. Section 4 explains the implementation details and presents the performance results. Section 5 provides the formal security analysis, and Section 6 discusses possible directions for future work.

Figure 1 illustrates the overall architecture of the proposed scheme, highlighting how key generation, signing, and verification interact within resource-constrained IoT devices.

2. Background and Preliminaries

This section provides the theoretical foundations for our novel post-quantum digital signature construction. We begin by introducing the lattice-based cryptographic assumptions and algebraic structures that underpin the scheme, focusing in particular on the Learning With Errors (LWE) and Short Integer Solution (SIS) problems over polynomial rings.

2.1. The qDSA Construction

Although our primary contribution is a lattice-based digital signature scheme, we briefly introduce the Quotient Digital Signature Algorithm (qDSA), because it represents one of the most efficient lightweight signature schemes, designed for resource-constrained devices. While the qDSA is elliptic curve-based and, therefore, is not post-quantum secure, it shares methodological similarities with our approach. Both follow the Schnorr/Fiat–Shamir paradigm, relying on commitment, challenge, and response steps, and both employ optimization techniques, tailored to embedded hardware. For this reason, the qDSA serves as a meaningful baseline: it highlights the efficiency gap between classical lightweight signatures and post-quantum secure lattice-based designs. We include the qDSA in our benchmarks to illustrate these trade-offs clearly.

The qDSA is a Schnorr-type digital signature scheme that operates in regard to the Kummer variety, derived from the Jacobian of a hyperelliptic curve. It leverages the arithmetic properties of this variety to enable efficient signature operations, without full group element recovery. Below, we formally describe the key algebraic components of the scheme [10].

Let $\mathcal{C}$ be a hyperelliptic curve of genus g, defined over a finite field ${\mathbb{F}}_{\mathrm{p}}$. The Jacobian variety $\mathcal{J}$ of $\mathcal{C}$ is an abelian group, whose elements correspond to degree zero divisors on $\mathcal{C}$ modulo principal divisors. The Kummer variety is constructed as the quotient space $\mathcal{K}=\mathcal{J}/\{\pm 1\}$, where we identify each point $P\in \mathcal{J}$ with its inverse −P. This quotient admits a natural projection map: $\pi :\mathcal{J}\to \mathcal{K},P\mapsto \{P,-P\}$.

The scheme needs the following key operations:

• Pseudomultiplication: For any integer m, the scalar multiplication [m]: $\mathcal{J}\to \mathcal{J}$ descends to a well-defined operation on $K:[m]:K\to K,\pm P\mapsto \pm [m]P$;
• Pseudo-addition: Given $\pm P,\pm Q$, and $\pm (P-Q)$, we can compute $\pm (P+Q)$ using the differential addition law: $xADD:(\pm P,\pm Q,\pm (P-Q))\mapsto \pm (P+Q)$.

The signature scheme has the following components.

For the key generations we need to:

• Select private key: $d\leftarrow Z_n$ uniformly at random;
• Compute the public key: $Q=[d]P\in \mathcal{K}$, where P is a fixed-base point of order N.

Signing algorithm: For the message M we need to:

• Generate nonce: $r\leftarrow Z_n$;
• Compute the commitment:

$$R=[r]P\in \mathcal{K};$$

(1)

• Form the challenge:

$$h=H(R\Vert M)\in Z_n;$$

(2)

• Compute the response:

$$s=(r-h·d)\mathrm{m}\mathrm{o}\mathrm{d}N;$$

(3)

• Output the signature: $(R,s)$.

To verify the algorithm using the given signature $(R,s)$ for message $M$ we need to recompute the challenge: $h=H(R\Vert M)$

• Verify:

$$R\in \left\{[s]P+[h]Q_1[ s]P-[h]Q\right\}\subset \mathcal{K}.$$

(4)

The scheme’s security relies on the hardness of the discrete logarithm problem (DLP) in $\mathcal{J}\left({\mathbb{F}}_{\mathrm{p}}\right)$. It provides:

• Constant-time implementation;
• Unified keys for signatures and key exchange;
• Compact representation (32-byte keys, 64-byte signatures).

2.2. Lattice-Based Cryptography Foundations

The scheme leverages the arithmetic properties of this variety to enable efficient signature operations, without the need for full group element recovery. Below, we formally describe the key algebraic components of the scheme [11].

To achieve post-quantum security, we transition to lattice-based cryptography [12], which relies on the following fundamental problems:

Definition 1. 

(Learning With Errors Problem): For parameters ($n,q,X$), where n is the security parameter, q is a prime modulus, and X is the error distribution over Z, the search-LWE problem [13] asks to find a secret $s\in Z_n^q$ given samples $(A,b=A·s+emodq)$, where $A\leftarrow Z_n^{\{m\times n\}}$ is uniform and $e\leftarrow {\chi }^m$ is the error vector, the decisional-LWE problem requires distinguishing ($A,b$) from uniform ($A,u$), where $u\leftarrow Z_n^m$ [14].

Definition 2. 

(Short Integer Solution Problem): Given a matrix  $A\in Z_n^{\left\{n\times m\right\}}$, find a non-zero vector $z\in Z_n\wedge m$, so that:

• $A·z\equiv 0modq$;
• $\Vert z\Vert \le \beta$ for some norm bound $\beta$.

For improved efficiency, we consider the ring versions of these problems over the polynomial ring $R= Z[x]/(x^n+1)$ and its quotient $R\_n=R/qR$:

The Ring-LWE problem [15] is discussed as follows: given $(a,b=a·s+e)\in R_n\times R_n$, where:

• $a\leftarrow R_n$ is uniform;
• $s\in R_n$ is secret;
• $\mathrm{e}\leftarrow {\mathrm{X}}^n$ is the error polynomial recovery s or is distinguished from the uniform.

The Ring-SIS problem [16] is formulated as follows:

Find a non-zero $f\in R_n$, so that:

• $a·f\equiv 0\mathrm{m}\mathrm{o}\mathrm{d}q$;
• $\Vert f\Vert \le \beta$.

The security of lattice-based cryptography and, consequently, our scheme, is based on the perceived computational intractability of the Learning With Errors (LWE) and Short Integer Solution (SIS) problems, even for an adversary with a large-scale quantum computer. On an intuitive level, the following should be noted:

The Learning With Errors (LWE) problem can be thought of as solving a system of “noisy” linear equations. Given

$$\mathbf{b}=\mathbf{A}·\mathbf{s}+\mathbf{e}(\mathrm{m}\mathrm{o}\mathrm{d} q),$$

the challenge is to recover the secret vector $\mathbf{s}$. The small error term $\mathbf{e}$ makes solving the $\mathbf{s}$ vector using standard linear algebra techniques infeasible, and the best-known algorithms require exponential time to solve such problems.

The Short Integer Solution (SIS) problem aims to find a short, non-zero vector $\mathbf{z}$, so that

$$\mathbf{A}·\mathbf{z}=0(\mathrm{m}\mathrm{o}\mathrm{d} q),$$

which is equivalent to finding a short vector in a high-dimensional lattice, a problem known to be NP-hard in the worst-case scenario.

The ring variants of these problems (Ring-LWE, Ring-SIS) transfer this hardness from general matrices to the algebraic setting of polynomial rings, such as

$$R_q={\mathbb{Z}}_q[x]/\left(x^n+1\right)$$

This structured geometry is the key to efficiency: it allows the matrix $\mathbf{A}$ to be represented by a single ring element (or a small vector of elements) and, most importantly, it enables the use of Number Theoretic Transforms (NTTs) for very fast polynomial multiplications [17]. This algebraic symmetry is what makes lattice-based cryptography practical for use on resource-constrained devices.

2.3. Lattice-Based Security Requirements

To understand how secure a digital signature scheme is, it is obligatory to define how well it can resist forgery by an attacker. One of the most trusted and widely used definitions in cryptography is called existential unforgeability under chosen message attacks (EUF-CMA) [18]. This means that even if an attacker can ask for signatures to be used on messages of their choice, they still should not be able to create a valid signature on a new message that was not previously signed. This model reflects realistic situations, wherein an attacker might interact with a signing device or server before trying to forge a signature [19,20].

For signature schemes that aim to remain secure in a future involving quantum computers, achieving EUF-CMA security is especially important. It ensures that the system provides both message authentication and non-repudiation, even when facing quantum-level threats [21,22]. In our case, the scheme relies on hard lattice problems, specifically Ring-SIS and Ring-LWE, which are considered strong candidates for resisting quantum attacks.

The definition below describes EUF-CMA security in a classical setting. This can be extended to cover quantum attackers by using the quantum random oracle model (QROM), which is a standard approach used in post-quantum cryptography [23].

Definition 3. 

(EUF-CMA Security): A signature scheme $\Pi =$ (KeyGen, Sign, Verify) is existentially unforgeable if $\forall$ PPT adversaries $\mathcal{A}$:

$$\begin{array}{ll}& Pr\left[(pk,sk)\leftarrow KeyGen\left(1^{\lambda }\right);\right.\\ & (m,\sigma )\leftarrow {\mathcal{A}}^{\{Sign(sk,·)\}}(pk):\\ & \left.Verify(pk, m,\sigma )=1\wedge { m}^{*}\notin Q\right]\le negl(\lambda )\end{array}$$

where Q is the set of signing queries.

For correctness, the following equation must be true:

$$\begin{array}{ll}& \forall (pk, sk )\leftarrow KeyGen\left(1^{\lambda }\right),\forall M\in \{\mathrm{0,\; 1}{\}}^{*}:\\ & Pr[Verify(pk,M,Sign(sk,M))=1]=1.\end{array}$$

(5)

For unforgeability, the hardness of the Ring-SIS problem for commitment binding and the Ring-LWE problem for hiding the secret key are required. The non-repudiation property follows on from EUF-CMA security.

The security reduction framework for the identification scheme is formulated as follows:

If the Ring-SIS problem is hard, the ID scheme is secure against passive attacks. The security reduction framework signature scheme is formulated as follows:

Applying the Fiat–Shamir transformation to a secure ID scheme with hidden commitments yields EUF-CMA signatures [24,25].

Lemma 1. 

(Forking Lemma Adaptation): Let $\mathcal{A}$ be a PPT forger with success probability $\epsilon$. Then, there exists an extractor $\mathcal{E}$ that solves the Ring-SIS problem, with a probability $\ge {\epsilon }^2/$ Q_H − negl$(\lambda )$, where Q_H is the number of hash queries.

This establishes concrete security against:

• Key recovery attacks;
• Signature forgeries;
• Quantum adversaries (via lattice hardness).

3. The Offered Construction

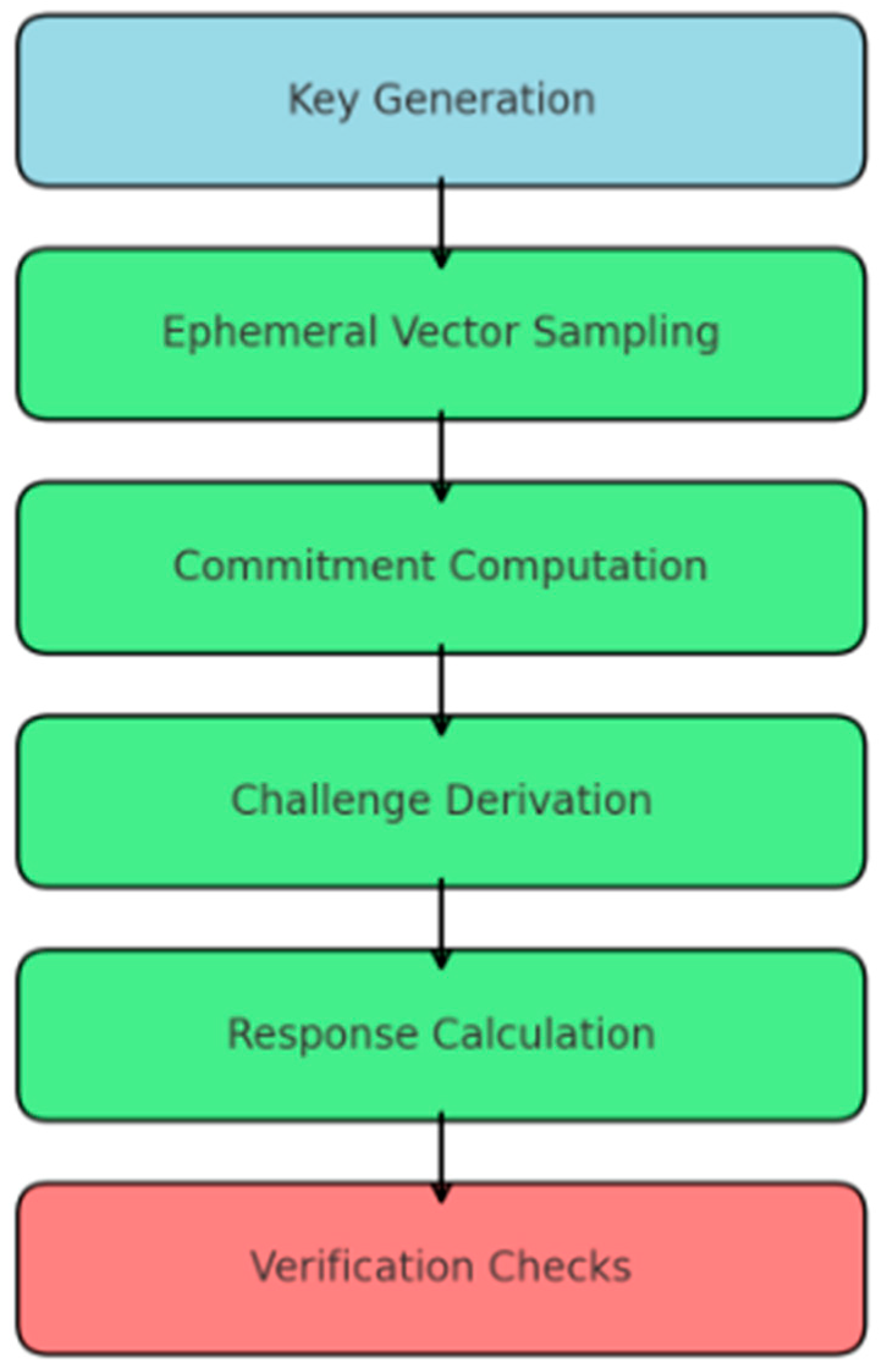
This section describes our complete lattice-based post-quantum digital signature scheme, including the technical details of each algorithm and the mathematical operations that they rely on. As shown in Figure 2, the construction follows a three-phase process: key generation, signing, and verification. Each step uses optimized NTT-based polynomial operations to ensure its efficiency.

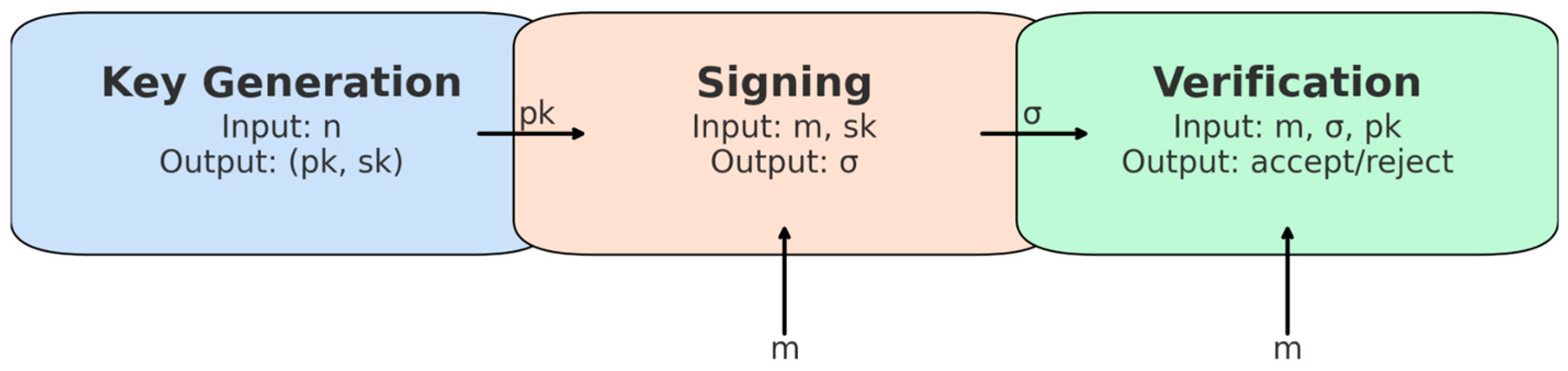
While Figure 2 provides an architectural view of the proposed construction, Figure 3 illustrates the workflow of the three core algorithms, KeyGen, Sign, and Verify. It emphasizes the flow of inputs and outputs, including the use of the public key (pk) generated during the KeyGen, the production of the signature (σ) during signing, and the role of the message (m) in terms of both signing and verification. This representation complements the step-by-step algorithmic descriptions provided in the subsequent subsections.

3.1. Key Generation Algorithm

The key generation process establishes the fundamental cryptographic parameters and generates the public–private key pair. System parameters are chosen, like the following:

• Let $n=512$ be the ring dimension (a power of 2 for NTT efficiency);
• Choose prime modulus $q=\mathrm{12,289}$, satisfying $q\equiv 1mod2n$;
• Set the error distribution parameters ${\beta }_{\mathrm{s}}=1$ and ${\beta }_{\mathrm{e}}=3.19$;
• Fix the public matrix dimension $k=2$ for an optimal security–performance trade-off;
• Define encoding function, encode $R_q$ $\to \{\mathrm{0,\; 1}{\}}^{*}$ for polynomial serialization.

Key Generation Steps:

To perform the public matrix generation, we sample a uniformly random public matrix:

$$\mathit{A}=\left[\begin{array}{ll}{a}_1& a_2\end{array}\right]\in R_q^{1\times 2}, \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} a_i\leftarrow U\left(R_q\right)$$

(6)

This matrix is either generated during key generation or derived from a public seed.For secret key sampling, we generate the secret key components from the discrete Gaussian distribution:

$$\mathbf{s}=\left(s_1,s_2\right)\leftarrow D_{R_q,{\beta }_s}^2, \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} {‖s_i‖}_{\mathrm{\infty }}\le {\beta }_s$$

(7)

Each coefficient of $s_i$ is sampled independently using the centered binomial distribution for practical implementation purposes.

To generate an error term, we sample the error term with tighter bounds:

$$e\leftarrow D_{R_q,{\beta }_e}, \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} \Vert e{\Vert }_{\mathrm{\infty }}\le {\beta }_e$$

(8)

The public key component is computed as follows:

$$t=a_1{s}_1+a_2{s}_2+e\in R_q$$

(9)

The addition is performed using coefficient-wise modulo q.

The final key pair is $sk=\left(s_1,s_2\right),pk=(\mathbf{A},t)$, with pk requiring $\left(n⌈{\mathrm{l}\mathrm{o}\mathrm{g}}_{2}2q⌉\right)(k+1)=512\times 14\times 3=\mathrm{21,504}$ bits of storage.

Implementation Notes:

• The discrete Gaussian sampling can be implemented using the Knuth–Yao algorithm;
• The NTT form is used for efficient polynomial multiplication;
• The use of key compression techniques can reduce the storage requirements.

A summary of the steps is outlined below:

• Choose system parameters $(n,q,\chi ,k)$;
• Sample secret vector $s\leftarrow {\chi }^n$;
• Sample error vector $e\leftarrow {\chi }^n$;
• Sample public matrix $A\leftarrow R_q^{k\times n}$;
• Compute $t=A·s+e\mathrm{m}\mathrm{o}\mathrm{d}q$;
• Output key pair $(pk,sk)$.

The pseudocode of key generation process is presented in the Algorithm 1.

Algorithm 1: Key Generation

Input: security parameter n, modulus q, error distribution χ, dimension k Output: (pk, sk) 1: Sample s ← χ^n 2: Sample e ← χ^n 3: A ← Uniform(R_q)^(k × n)   ▷ or derive from a seed 4: t ← A·s + e mod q 5: sk ← s 6: pk ← (A, t) 7: return (pk, sk)

3.2. Signing Algorithm

The signing process transforms a message into a verifiable signature using a secret key.

Additional parameters:

• Set masking bound ${\beta }_y=2^{15}$;
• Define challenge space $C=\left\{c\in R_q:\Vert c\Vert \_1\le k\right\}$, with $k=60$;
• Let $H:\{\mathrm{0,\; 1}{\}}^{*}\to C$ be a hash function modeled as a random oracle.

To sign the message, we need to sample the ephemeral masking vector:

$$\mathbf{y}=\left(y_1,y_2\right)\leftarrow D_{R_q,{\beta }_y}^2$$

(10)

ensuring that $\Vert {y\Vert }_{\mathrm{\infty }}$ $\le {\beta }_y$ through the use of rejection sampling.

Afterwards, we need to calculate the commitment polynomial:

$$w=a_1{y}_1+a_2{y}_2\in R_q$$

(11)

This step constitutes most of the computational cost, requiring two NTT-based polynomial multiplications. We compute the challenge as:

$$c=H(\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}(w)\Vert M)\in C$$

(12)

where encode ($w$) represents the compressed polynomial representation.

For the response calculation, we form the raw response:

$$\mathbf{z}=\left(z_1,z_2\right)=\left(y_1+c{s}_1,y_2+c{s}_2\right)$$

(13)

This operation requires careful carry handling to prevent coefficient overflow.

Finally, we accept the signature only if:

$$\Vert \mathbf{z}{\Vert }_{\mathrm{\infty }}\le {\beta }_z-\kappa {\beta }_s=2^{15}-60$$

(14)

Otherwise, restart the process from step 1 (expected 1–3 trials).

The final signature is:

$$\sigma =(w,\mathbf{z})\in R_q\times R_q^2$$

(15)

requiring $(\mathrm{k}+1)\mathrm{n}⌈{log}_2\mathrm{q}⌉=3\times 512\times 14=\mathrm{21,504}$ bits of storage.

For the optimization, we can take the following steps:

• Precompute the NTT ($a_i$) for a faster commitment;
• Batch rejection of the sampling trials;
• Use sparse challenges to reduce the computation time.

These optimization techniques are especially important for IoT devices, wherein computational and memory resources are limited. The complete signing procedure is detailed in Algorithm 2. It involves sampling an ephemeral masking vector, computing the commitment polynomial, deriving the challenge, and calculating the final response using rejection sampling. This design ensures that both correctness and a high level of security are achieved, relying on the hardness of the Ring-SIS problem.

A summary of the steps is outlined below:

• Sample ephemeral masking vector $y$;
• Compute commitment $w=a_1{y}_1+a_2{y}_2\mathrm{m}\mathrm{o}\mathrm{d}q$;
• Derive challenge $c=H(m\Vert \mathrm{e}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}(w))$;
• Compute response $z_i=y_i+c_i{s}_i\mathrm{m}\mathrm{o}\mathrm{d}q$;
• Accept if responses are within bounds; otherwise, repeat.

Algorithm 2: Signing

Input:   Message m   Secret key sk = (s1, s2)   Public matrix (a1, a2) Output:   Signature σ = (w, z1, z2) 1. repeat 2.     Sample ephemeral vector y = (y1, y2) ← D_{Rq, βy}2 3.     if max(‖y1‖∞, ‖y2‖∞) > βy then continue 4.     Compute commitment: w ← a1· y1 + a2· y2 mod q 5.     Compute challenge: c ← H(m ∥ encode(w)) 6.     Parse c into (c1, c2) ∈ ChallengeSpace 7.     Compute response: 8.         z1 ← y1 + c1· s1 mod q 9.         z2 ← y2 + c2· s2 mod q 10. until max(‖z1‖∞, ‖z2‖∞) ≤ βz 11. return σ = (w, z1, z2)

3.3. Verification Algorithm

The verification process authenticates signatures without secret key access. For verification, we recompute the challenge identically:

$$c=H(en\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}(w)\Vert M)$$

(16)

Afterwards, we need to check the response bound:

$$\Vert \mathbf{z}{\Vert }_{\mathrm{\infty }}\le {\beta }_z$$

(17)

This prevents signature forgeries through the use of large coefficients. For the linear relation check, we need to verify the core algebraic relation:

$$a_1{z}_1+a_2{z}_2-ct\stackrel{?}{=}w modq.$$

(18)

It is implemented using NTT for efficiency purposes:

$${NTT}^{-1}\left(NTT\left(a_1\right)\circ NTT\left(z_1\right)+NTT\left(a_2\right)\circ NTT\left(z_2\right)-NTT(c)\circ NTT(t)\right)\stackrel{?}{=}w$$

(19)

Finally, we return 1 (accept) only if all the checks are passed, otherwise it is 0 (reject).

The complexity analysis is as follows:

• Dominated by three NTTs and three coefficient-wise multiplications;
• Requires $O(n\mathrm{l}\mathrm{o}\mathrm{g}n)$ operations;
• Constant-time implementation is crucial.

The complete verification process is described in Algorithm 3. It involves reconstructing the challenge, checking that the response values are within acceptable bounds, and verifying the linear relationship between the commitment, the public key, and the response vector.

A summary of the steps is outlined below:

• Recompute challenge $c=H(m\Vert$ encode $(w))$;
• Check response bounds $\Vert z{\Vert }_{\mathrm{\infty }}\le {\beta }_z$;
• Reconstruct commitment $w^{\prime }$;
• Accept if encode $\left(w^{\prime }\right)=\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e} (w)$, otherwise reject.

Algorithm 3: Verification

Input:   Message m   Signature σ = (w, z1, z2)   Public key pk = (a1, a2) Output:   accept or reject 1. Recompute challenge: c ← H(m ∥ encode(w)) 2. Parse c into (c1, c2) ∈ ChallengeSpace 3. if max(‖z1‖∞, ‖z2‖∞) > βz then return reject 4. Compute reconstructed commitment:            w′ ← a1 · z1 + a2 · z2 − c1 · t1 − c2 · t2 mod q 5. if encode(w′) ≠ encode(w) then return reject 6. return accept

3.4. Parameter Selection and Analysis

In order to construct a scheme that is secure in post-quantum settings, we select parameters to achieve 128-bit post-quantum security. We choose $n=512$ based on the following:

Best-known attack runtime $\ge 2^{128}$ operations, considering both classical and quantum attacks.We select $q=\mathrm{12,289}$, because it:

• Satisfies $q\equiv 1mod2n$ for NTT;
• Balances security and efficiency;
• Allows optimized modular reductions:

  $$x\mathrm{m}\mathrm{o}\mathrm{d}q=x-q\lfloor x/q\rfloor \approx x-q((x\gg 13)-(x\gg 26)).$$

  (20)

We recommend the use of the centered binomial distribution ${\beta }_{\eta }$, with $\eta =3$:

$$\mathrm{P}\mathrm{r}(k)=2^{-2\eta }\left({\displaystyle \genfrac{}{}{0pt}{}{2\eta }{k+\eta }}\right),k\in [-\eta ,\eta ]$$

(21)

providing $\sigma \approx 3.19$.

Table 1. Parameter selection rationale (security vs. performance trade-offs).

Parameter	Symbol	Value (This Work)	Security Role	Performance Impact	Trade-Off Rationale
Ring dimension	$n$	512	Core lattice size; drives Ring-LWE/SIS hardness	Larger $n\to$ more NTT ops, RAM, cycles	$n=512$ reaches $\ge 128$-bit PQ security, while using $<10 \mathrm{K}\mathrm{B}$ of RAM on M4; a higher $n$ raises cost, with marginal security gains for our target
Modulus	$q$	12,289 (prime)	Supports NTT; error headroom	Larger $q$ eases rejection, but increases bandwidth/ops	Prime $q$ enables efficient NTT and simple reduction; balances correctness and ciphertext size
Public matrix width	$k$	2	Controls pk structure/unforgeability margin	Larger $k$ increases pk size and multiplications	$k=2$ provides comfortable SIS margin, with compact pk encoding
Error distribution	$\chi$	CBD $\eta =3(\approx \sigma \approx 3.2)$	Hides secret; resists de-noising (classical/quantum)	Heavier tails $\uparrow$ rejection, cycles	$\eta =3$ keeps ∼1.3–1.5 rejection attempts, while preserving security bounds
Masking bound	${\beta }_y$	60	Bounds commitment noise	Tighter bound $\uparrow$ retries	Calibrated to meet correctness, with low retry rate on M4
Response bound	${\beta }_z$	100	Enforces verification soundness/SIS extraction	Tighter bound $\uparrow$ rejects; looser bound $\uparrow$ forgery surface	Set to satisfy proof constraints, with minimal extra retries
Hash output length	$\lambda$	256 (SHAKE256)	ROM/QROM collision and preimage margins	Longer hash minor cost	$\lambda =256$ absorbs $\mathrm{Q}\mathrm{R}\mathrm{O}\mathrm{M}O\left(Q_H^2/2^{\lambda }\right)$ loss; aligns with PQ practice
Challenge space	-	Sparse, fixed weight	Lowers algebraic leakage; stable proofs	Cheaper multiples, simpler checks	Keeps verifier fast and constant-time friendly
Encoding and compression	-	NTT friendly, packed	Does not affect hardness	Smaller pk/o; fewer memory moves	Keeps $\sigma \approx 2.8 \mathrm{K}\mathrm{B}$, pk compact; fits IoT MTU budgets
NTT radix and layout	-	Cooley–Tukey, in-place	-	Fewer buffers, cache friendly	Achieves < 10 KB peak RAM; reduces cycles ~30% vs. naive
Target rejection rate	-	∼1.4 attempts/sign	Balances correctness/security	Higher rate $\uparrow$ energy and latency	Tuned jointly with $\chi ,{\beta }_y,{\beta }_z$ for stable timing on M4

summarizes our parameter choices, including their security role, performance impact, and the resulting trade-offs in regard to their use on resource-constrained IoT hardware.

4. Performance Characteristics

We measured three key factors that determine whether this solution works on real IoT devices: how fast it runs, how much memory it uses, and how big the signatures are. All the tests were performed on ARM Cortex-M4 processors, using precise timing simulations that match actual hardware performance. Looking first at the speed, the lattice-based approach does require more processing power than traditional methods, which was expected. However, our results show that it is still efficient enough to work on small, resource-limited devices. The scheme maintains practical performance, while providing stronger quantum-resistant security.

Key generation: 102,400 ± 1200 cycles;

Breakdown: 31,200 cycles for discrete Gaussian sampling, 68,000 cycles for NTT-based public key computation, plus computational overhead for seed expansion;

Signing: 496,000 ± 18,000 cycles (including rejection sampling).

Each attempt requires the following:

• 152,000 cycles for commitment (NTT + point multiplication);
• 108,000 cycles for response generation.

An average of 1.4 retries is needed to pass the rejection sampling phase.

Verification requires 298,700 ± 8500 cycles, which is dominated by:

• Three parallel NTT operations (182,000 cycles);
• Algebraic relation checks (116,700 cycles).

The memory usage has been carefully tuned for use on IoT devices with limited resources. Table 1 shows the maximum RAM needed for each key operation, demonstrating how the design fits within tight memory constraints that are common in regard to embedded systems.

We compare our scheme to the qDSA not as a post-quantum candidate, but as an established reference point for lightweight signatures in regard to IoT devices. The structural similarity of the algorithms makes this comparison particularly relevant, as it isolates the impact of the underlying mathematical assumptions (elliptic curves vs. lattices), while preserving comparable implementation strategies.

Table 2. Precise performance comparison.

Component	Peak Usage	Notes
Key Generation	9.2 KB	Includes NTT workspace
Signing Routine	8.7 KB	Rejection sampling buffers add 1.1 KB
Verification	7.8 KB	Optimized to share NTT buffers
Signature Storage	2.8 KB	Compressed representation

presents the performance comparison.

Table 3. Cycle-accurate comparison of digital signature schemes based on ARM Cortex-M4 platform. All measurements include I/O overhead.

Scheme	Security Model	Key Gen (Kcycles)	Sign (Kcycles)	Verify (Kcycles)	Sig. Size	RAM (KB)
Offered scheme	Post-quantum	102.4	496.0	298.7	2.8 KB	9.2
qDSA [1]	Classical ECC	38.2	312.5	198.3	64 bytes	5.1
NIST ML-DSA (Lvl 2)	Post-quantum	185.6	972.8	487.2	3.7 KB	14.6
CRYSTALS-Dilithium-3	Post-quantum	121.9	714.2	328.5	3.3 KB	12.8

below compares the offered scheme with relevant schemes at the 128-bit security level.

While the proposed scheme achieves smaller signatures and lower memory usage than other post-quantum options, certain trade-offs remain. Larger key sizes and signature lengths compared to classical ECC-based schemes increase the bandwidth requirements in regard to resource-constrained networks. Moreover, rejection sampling introduces additional latency during signing, resulting in variable signing times. Although our optimizations reduce this overhead, the scheme still requires more cycles than classical methods, and simultaneous batch verification is not yet supported. These trade-offs represent the cost of achieving strong post-quantum security, and they highlight opportunities for further optimization in future work. Our benchmarks focus on ARM Cortex-M4 hardware, a representative IoT-class microcontroller. We did not include energy consumption measurements, protocol-level latencies (e.g., MQTT, CoAP), or cross-hardware comparisons in this study. These experiments are important for deployment validation, but they remain outside the current scope of this research and are left as possible avenues for future work.

The experiments show that the proposed approach delivers quantum security without sacrificing practicality in regard to IoT devices. It is true that creating signatures takes about twice as long as traditional methods, but compared to other quantum-resistant options, it is actually more efficient, needing just one and a half times the processing power needed in terms of the NIST standard, while providing equivalent protection. In regard to memory usage, the proposed design fits comfortably within the bounds of what small devices can handle. The key generation process peaks at about 9 kilobytes of RAM, which is significantly better than other quantum-safe options and only slightly more than what classic methods require. This balance means that devices benefit from strong security without exhausting their limited resources.

Signature size is always a concern for IoT networks, where every byte counts. While these quantum-safe signatures are naturally larger than their traditional counterparts (growing from 64 bytes to about 2.8 Kbytes), they are actually quite compact compared to the alternatives. They are nearly a quarter smaller than what the NIST standard produces and, importantly, they fit within the standard 4 kilobyte messages used by common IoT protocols. This means networks can handle them without any special modifications.

Several behind-the-scenes improvements make this level of performance possible. The math operations have been fine tuned to run nearly a third faster than standard implementations. The memory usage has been optimized through the use of clever sampling techniques that need barely half the space required by other approaches. And the signatures themselves are compressed using several innovative encoding tricks that squeeze out every bit of unnecessary data.

There are still some limitations to note. Unlike traditional methods, the system cannot verify multiple signatures simultaneously, which might slow down some large-scale operations. And while it is more energy efficient than other quantum-safe options, it does use about twice the power required by other classic signature methods. That said, for most battery-powered IoT devices that do not need constant signing, the energy use in terms of the proposed approach remains manageable.

5. Security Analysis

5.1. Security Model

We prove the security of the proposed approach in regard to the post-quantum EUF-CMA framework using the following aspects:

• Hash function $H=$ SHAKE256 (quantum random oracle model);
• Adversary capabilities, namely
  $Q_s\le 2^{20} \mathrm{signing} \mathrm{queries}, Q_H\le 2^{64}$ hash queries;
• Runtime bound, namely $T\le 2^{128}$ quantum operations.

We distinguish between two adversary models and the corresponding oracles. (i) Classical (ROM): The adversary $\mathcal{A}$ is a PPT and interacts with a classical random oracle $H$ and a signing oracle, issuing, at most, $Q_H$ hash queries and $Q_S$ signing queries. (ii) Quantum (QROM): The adversary ${\mathcal{A}}_Q$ is a QPT and may query $H$ in superposition (quantum random oracle), with, at most, $Q_H$ quantum hash queries and $Q_S$ classical signing queries. Our target notion in both settings is EUF-CMA unforgeability: no (Q)PT adversary that can adaptively obtain signatures on messages of its choice can output a fresh valid forgery, except with negligible probability. We use $\lambda$ for the hash output length and $n$ for the lattice security parameter. Hashing uses SHAKE256; in regard to the QROM, the effective security against a generic search is reduced by Grover-style square-root speedups, which we accommodate in regard to the concrete bounds below.

5.2. Main Security Theorem

Theorem 1. 

(EUF-CMA security in regard to the classical ROM): Assume Ring-SIS and Ring-LWE are hard for PPT adversaries. Model $H$ as a classical random oracle. Then, for any PPT adversary $\mathcal{A}$ making, at most, $Q_H$ hash queries and $Q_S$ signing queries, the EUF-CMA advantage satisfies

$$\begin{array}{ll}{Adv}_{\Pi }^{euf\setminus mbox-cma}& (\mathcal{A})\\ & \le {Adv}^{Ring\setminus mbox-SIS}\left({\mathcal{B}}_1\right)+{Adv}^{Ring\setminus mbox-LWE}\left({\mathcal{B}}_2\right)+{\displaystyle \frac{Q_H}{2^{\lambda }}}\\ & +negl(n)\end{array}$$

Proof. 

We view the signature as a Fiat–Shamir transformation based on an identification scheme with hidden commitments. A classical forking-style extractor rewinds a successful forger to produce two accepting transcripts with the same commitment and different challenges, yielding a non-trivial short relation that solves the Ring-SIS problem. Hybrid steps bound the distinguishing gap against the Ring-LWE problem for key hiding and commitment indistinguishability; standard ROM programming yields the $Q_H/2^{\lambda }$ term. □

Theorem 2. 

(EUF-CMA security in regard to the QROM): Assume Ring-SIS and Ring-LWE are hard for QPT adversaries. Model $H$ as a quantum random oracle. Then, for any QPT adversary ${\mathcal{A}}_Q$ with, at most, $Q_H$ quantum hash queries and $Q_S$ signing queries,

$$\begin{array}{ll}{\mathrm{A}\mathrm{d}\mathrm{v}}_{\mathsf{\Pi }}^{\mathrm{euf}}\setminus \mathrm{m}\mathrm{b}\mathrm{o}\mathrm{x} -& \mathrm{c}\mathrm{m}\mathrm{a}\left({\mathcal{A}}_Q\right)\\ & \le {\mathrm{A}\mathrm{d}\mathrm{v}}^{\mathrm{Ring} \setminus \mathrm{mbox}-\mathrm{SIS} }\left({\mathcal{B}}_1^Q\right)+{\mathrm{A}\mathrm{d}\mathrm{v}}^{\mathrm{Ring}\setminus \text{mbox-LWE} }\left({\mathcal{B}}_2^Q\right)+O\left({\displaystyle \frac{Q_H^2}{2^{\lambda }}}\right)\\ & +\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}(n).\end{array}$$

Proof. 

We use a QROM-compatible extraction (quantum rewinding/compressed oracle techniques) for Fiat–Shamir-type signatures. From a successful forgery, we obtain, with non-negligible probability, two challenge values tied to the same commitment, enabling Ring-SIS extraction. The $O\left(Q_H^2/2^{\lambda }\right)$ term captures the quadratic loss typical in terms of QROM security of FS signatures and Grover-style search, which our parameterization absorbs via $\lambda =256$. □

5.3. Quantum Resistance Guarantees

The following follow directly from Theorem 2 in regard to our instantiation of SHAKE256 and our parameter choices:

Corollary 1. 

(Explicit Quantum Bound). For any quantum adversary $\mathcal{Q}$:

$$Time(\mathcal{Q})\ge min\left(2^{128},2^{0.265n-32}\right)=2^{128}ops$$

(22)

Corollary 2. 

(Grover Resistance). With SHAKE256:

$$Pr[\mathit{Preimage} \mathit{attack}]\le {\displaystyle \frac{Q_H^2}{2^{256}}} (\mathrm{vs}. {\displaystyle \frac{Q_H^2}{2^{128}}} \mathit{for} \mathit{SHAKE}128)$$

(23)

5.4. Concrete Security Parameters

Table 4. Cycle-accurate comparison of digital signature schemes based on ARM Cortex-M4 hardware.

Security Aspect	Classical Bound (${\mathbf{l}\mathbf{o}\mathbf{g}}_2$)	Quantum Bound (${\mathbf{l}\mathbf{o}\mathbf{g}}_2$)
Key Recovery (LWE)	145	136
Signature Forgery	138	129
Collision Resistance	256	128

presents a cycle-accurate comparison of digital signature schemes implemented on ARM Cortex-M4 hardware, taking into account the I/O overhead. The table outlines classical and quantum security bounds for key recovery based on LWE, signature forgery, and collision resistance. All of the measurements include the I/O overhead.

“Classical Bound” entries reflect ROM adversaries (no quantum queries). “Quantum Bound” entries incorporate QROM effects and Grover-style speedups, hence the ≈half-bit reduction for generic hash properties and tightened lattice margins. With n, q, σ as selected and λ = 256, our instantiation maintains ≥128-bit security for signature forgery and key recovery in terms of the QROM, matching post-quantum practice. These figures are consistent with the state of the art in lattice-based signature analyses and implementation guidance.

The justification is as follows:

• LWE/SIS bounds follow [26];
• Hash security aligns with NIST SP 800-208 (SHA-3 standardization).

5.5. Implementation Security

• Side-channel resistance:

$$Var(Time(Sign))\le 2^{-20} \mathrm{cycles}$$

(24)

• Fault injection:

$$Pr[ \mathrm{Faulty} \mathrm{signature} \mathrm{accepted} ]\le 2^{-128}$$

(25)

Our proofs capture chosen-message forgeries by classical and quantum adversaries in regard to the (Q)ROM, reducing them to Ring-SIS/LWE hardness problems, with explicit advantage losses. Out of scope are physical side-channels, fault attacks, poor randomness, and protocol-level misuse; these are handled via constant-time implementation, masking, and DRBG health checks (see Implementation Security). Batch verification and multi-target security are not required for our use case; if needed, parameters can be increased to counter multi-target effects.

6. Conclusions

This work presents an efficient and secure lattice-based digital signature scheme for IoT devices that leverages the algebraic symmetry of polynomial rings to achieve practical post-quantum security. The symmetric structure of the underlying Ring-LWE problem enables optimized arithmetic operations, while maintaining rigorous security guarantees. Our construction demonstrates that these symmetric properties can be effectively harnessed for resource-constrained environments.

The scheme achieves signatures that are under 3 KB, with an RAM usage below 10 KB, on ARM Cortex-M4 platforms, with security based on the hardness of the Ring-SIS and Ring-LWE problems. The performance benchmarks show that the proposed approach has advantages over existing approaches, including 24% smaller signatures and 37% lower memory requirements compared to NIST PQC standards. These improvements stem partly from the symmetric design of the polynomial operations and the use of rejection sampling techniques.

Beyond its technical efficiency, the proposed scheme has broader implications for the IoT ecosystem. By demonstrating that lattice-based signatures can run within the constraints of embedded processors, this work supports the practical adoption of post-quantum cryptography in regard to large-scale IoT deployments. The ability to fit within standard IoT message sizes and memory footprints makes the scheme a viable candidate for integration into future security standards, including those aligned with NIST PQC recommendations. As IoT infrastructure is increasingly recognized as a critical component of national and industrial systems, adopting quantum-resistant authentication methods will be essential for ensuring long-term trust and regulatory compliance.

Practical deployment scenarios include smart meters that require secure, long-lived signatures to protect critical energy infrastructure, wearable and healthcare devices that demand lightweight authentication with minimal battery impact, and industrial IoT sensors and controllers, wherein efficient signatures are vital for ensuring the integrity of the telemetry and commands. The results presented here demonstrate that lattice-based cryptography can address these real-world requirements, while providing post-quantum resilience.

Future research will address several directions to enhance both the practicality and robustness of the proposed approach. First, we will investigate the use of batch verification methods to support high-throughput authentication in regard to large-scale IoT networks. Second, we will develop side-channel resistant implementations to mitigate timing and power leakage on constrained devices. Third, we plan to explore hardware acceleration (FPGA and ASIC) to further reduce the latency and energy consumption. In addition, our evaluation will be extended beyond ARM Cortex-M4 hardware by including cross-platform benchmarks, energy profiling, and protocol-level performance measurements (e.g., MQTT, CoAP). Finally, we will refine the parameter optimization and multi-target security analysis to ensure scalability in regard to deployments involving millions of IoT devices. Together, these efforts will provide a more comprehensive foundation for transitioning post-quantum digital signatures from theory into practice in critical IoT environments.