Experimental Search for Neutron–Antineutron Oscillation with the Use of Ultra-Cold Neutrons Revisited
Abstract
1. Introduction
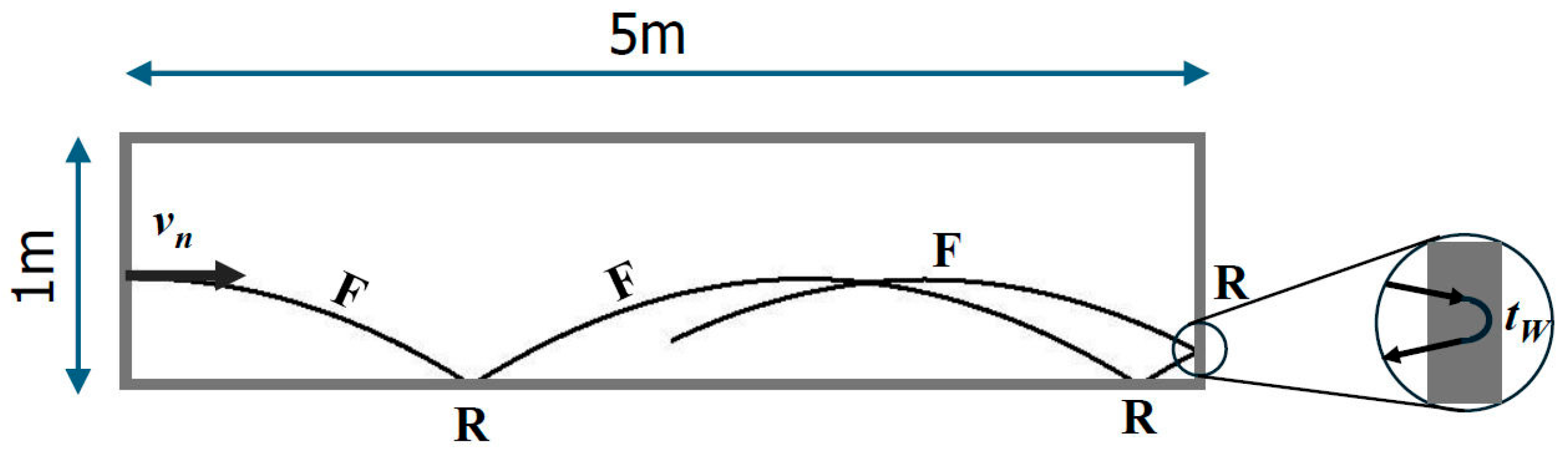
2. Method for Realistic Evaluation of
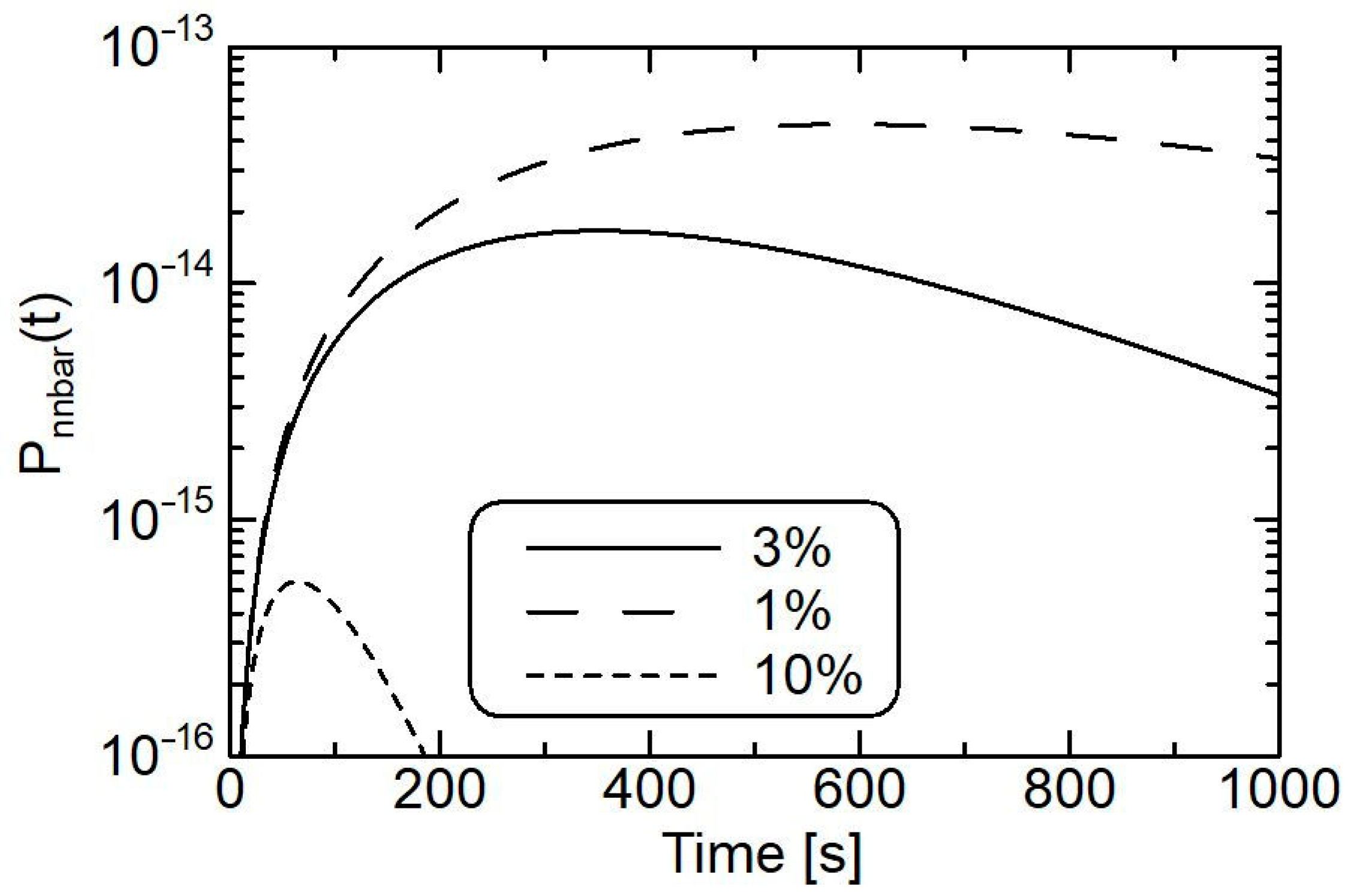
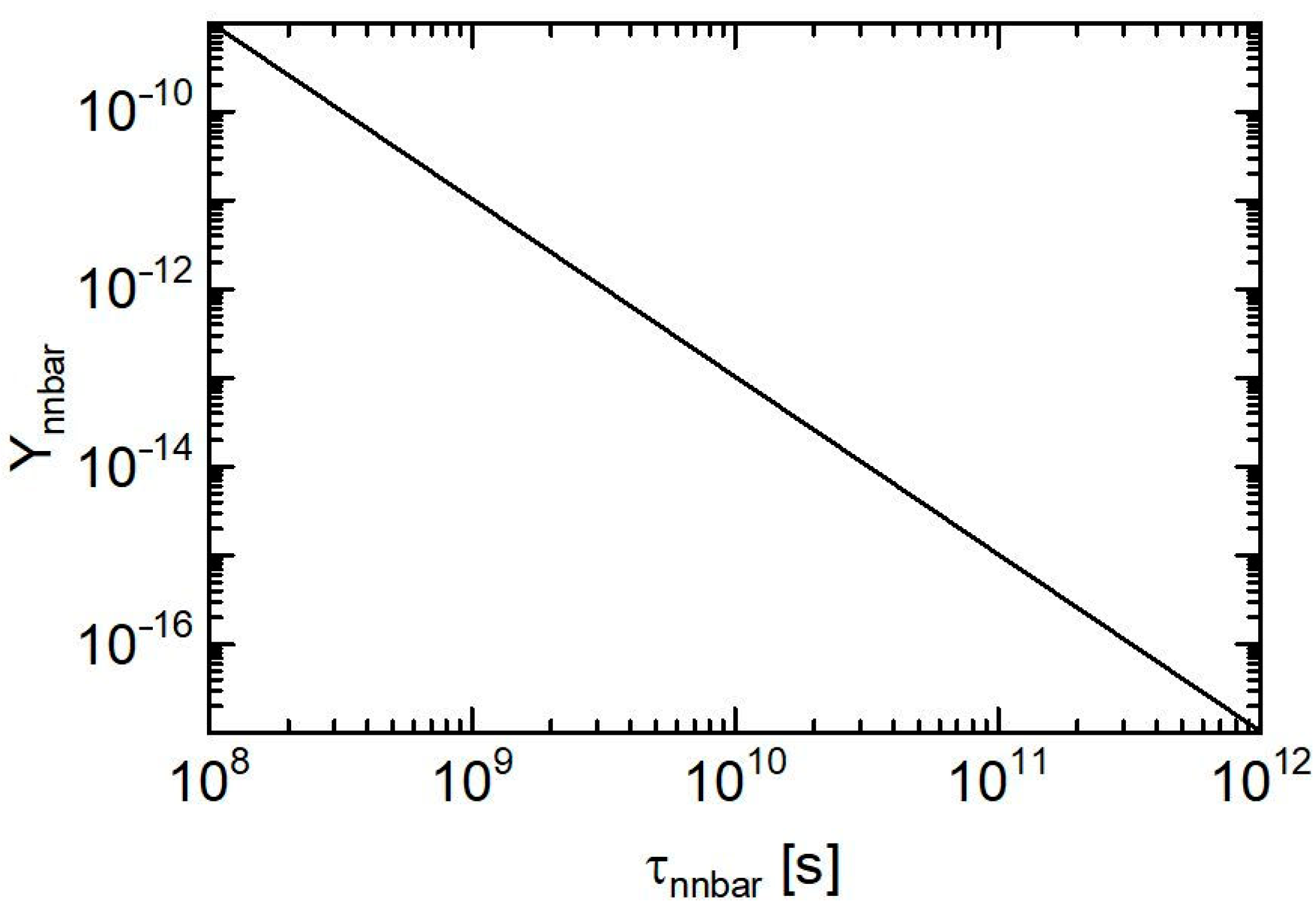
3. Results
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UCN | Ultra-cold neutron |
| VCN | Very-cold neutron |
| GUT | Grand unified theory |
| SUSY | Super symmetry |
| nnbar-osc | Neutron-antineutron oscillation |
References
- Lazarides, G.; Shafi, Q.; Wetterich, C. Proton lifetime and fermion masses in an SO(10) model. Nucl. Phys. B 1981, 181, 287–300. [Google Scholar] [CrossRef]
- Mohapatra, R.N. Neutron-antineutron oscillation in grand unified theories: An update. Nucl. Instr. Meth. in Phys. Res. A 1989, 284, 1–8. [Google Scholar] [CrossRef]
- Babu, K.S.; Dev, P.S.B.; Fortes, E.C.F.S.; Mohapatra, R.N. Post-sphaleron baryogenesis and an upper limit on the neutron-antineutron oscillation time. Phys. Rev. D 2013, 87, 115019. [Google Scholar] [CrossRef]
- Nussinov, S.; Shrock, R. n- oscillations in models with large extra dimensions. Phys. Rev. Lett. 2002, 88, 171601. [Google Scholar] [CrossRef] [PubMed]
- Girmohanta, S.; Shrock, R. Nucleon decay and n- oscillations in a left-right symmetric model with large extra dimensions. Phys. Rev. D 2020, 101, 095012. [Google Scholar] [CrossRef]
- Baldo-Ceolin, M.; Benetti, P.; Bitter, T.; Bobisut, F.; Calligarich, E. A New experimental limit on neutron-anti-neutron oscillations. Z. Phys. C 1994, 63, 409. [Google Scholar] [CrossRef]
- Addazi, A.; Anderson, K.; Ansell, S.; Babu, K.S.; Barrow, J.L.; Baxter, D.V.; Bentley, P.M.; Berezhiani, Z.; Bevilacqua, R.; Biondi, R.; et al. New high-sensitivity searches for neutrons converting into antineutrons and/or sterile neutrons at the HIBEAM/NNBAR experiment at the European Spallation Source. J. Phys. G 2021, 48, 070501. [Google Scholar] [CrossRef]
- Abe, K.; Bronner, C.; Hayato, Y.; Ikeda, M.; Imaizumi, S.; Ito, H.; Kameda, J.; Kataoka, Y.; Miura, M.; Miura, M.; et al. Neutron-antineutron oscillation search using a 0.37 megaton-years exposure of Super-Kamiokande. Phys. Rev. D 2021, 103, 012008. [Google Scholar] [CrossRef]
- Navas, S.; Amsler, C.; Gutsche, T.; Hanhart, C.; Hernández-Rey, J.; Lourenço, C.; Masoni, A.; Mikhasenko, M.; Mitchell, E.; Anderson, J.; et al. Review of Particle Physics. Phys. Rev. D 2024, 110, 030001. [Google Scholar] [CrossRef]
- Golub, R.; Pendlebury, J.M. Ultra-cold neutrons. Rep. Prog. Phys. 1979, 42, 439. [Google Scholar] [CrossRef]
- Yoshiki, H. The Ultra Cold Neutron Production at KENS. KENS Report, No. 2. In Proceedings of the 4th Meeting International Collaboration on Advanced Neutron Sources (ICANS-IV), National Laboratory for High Energy Physics, Tsukuba, Japan, 20–24 October 1980; pp. 718–722. Available online: https://www2.kek.jp/imss/kens/document/kens_report/KENS_REPORT_2_1981.pdf (accessed on 7 September 2025).
- Chetyrkin, K.G.; Kazarnovsky, M.V.; Kuzmin, V.A.; Shaposhnikov, M.E. On the possibility of an experimental search for n- oscillations. Phys. Lett. B 1981, 99, 358. [Google Scholar] [CrossRef][Green Version]
- Marsh, S.; McVoy, K.W. Theory of neutron anti-neutron oscillation using bottled ultracold neutrons. Phys. Rev. D 1983, 28, 2793–2799. [Google Scholar] [CrossRef]
- Kerbikov, B.O.; Kudryavtsev, A.E.; Lensky, V.A. Neutron-antineutron oscillations in a trap revisited. JETP 2004, 98, 417–426. [Google Scholar] [CrossRef][Green Version]
- Kerbikov, B.O. The effect of collisions with the wall on neutron-antineutron transitions. Phys. Lett. B 2019, 795, 362–365. [Google Scholar] [CrossRef]
- Protasov, K.V.; Gudkov, V.; Kupriyanova, E.A.; Nesvizhevsky, V.V.; Snow, W.M.; Voronin, A.Y. Theoretical analysis of antineutron-nucleus data needed for antineutron mirrors in neutron-antineutron oscillation experiments. Phys. Rev. D 2020, 102, 075025. [Google Scholar] [CrossRef]
- Nesvizhevsky, V.V.; Gudkov, V.; Protasov, V.; Snow, M.; Voronin, Y. Experimental Approach to Search for Free Neutron-Antineutron Oscillations Based on Coherent Neutron and Antineutron Mirror Reflection. Phys. Rev. Lett. 2019, 122, 221802. [Google Scholar] [CrossRef] [PubMed]
- Schreyer, W.; Davis, C.A.; Kikawa, T.; Mishima, K.; Okamura, T.; Picker, R. Optimizing neutron moderators for a spallation-driven ultracold-neutron source at TRIUMF. Nucl. Instr. Meth. Phys. Res. A 2020, 959, 163525. [Google Scholar] [CrossRef]
- Fujioka, H.; Higuchi, T. Impact of a Reflecting Material on a Search for Neutron-Antineutron Oscillations using Ultracold Neutrons. arXiv 2025, arXiv:2508.17725. [Google Scholar]
| Elemental Composition | ) [fm] | ) [fm] | Molar Ratio [%] |
|---|---|---|---|
| Ni | 10.3 | 5.47 | 85.2 |
| Al | 3.449 | 4.29 | 14.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shima, T. Experimental Search for Neutron–Antineutron Oscillation with the Use of Ultra-Cold Neutrons Revisited. Symmetry 2025, 17, 1524. https://doi.org/10.3390/sym17091524
Shima T. Experimental Search for Neutron–Antineutron Oscillation with the Use of Ultra-Cold Neutrons Revisited. Symmetry. 2025; 17(9):1524. https://doi.org/10.3390/sym17091524
Chicago/Turabian StyleShima, Tatsushi. 2025. "Experimental Search for Neutron–Antineutron Oscillation with the Use of Ultra-Cold Neutrons Revisited" Symmetry 17, no. 9: 1524. https://doi.org/10.3390/sym17091524
APA StyleShima, T. (2025). Experimental Search for Neutron–Antineutron Oscillation with the Use of Ultra-Cold Neutrons Revisited. Symmetry, 17(9), 1524. https://doi.org/10.3390/sym17091524






