Abstract
We establish a hierarchy of Euclidean stars according to their degree of complexity, as measured by the complexity factor and the complexity of the pattern of evolution. We consider both, non-dissipative and dissipative systems. Solutions range from the simplest one, in order of increasing complexity. Some specific models are found and analyzed in detail.
PACS:
04.40.-b; 04.40.Nr; 04.40.Dg
1. Introduction
This work deals with a family of solutions to Einstein equations for fluid distributions satisfying the heuristic assumption that the areal radius of any shell of fluid, which is the radius obtained from its area, equals the proper radial distance from the center to the shell [1], named “Euclidean stars” (see [2,3,4,5,6,7,8,9,10] for generalizations and/or applications of this idea).
Since the abovementioned assumption is obviously satisfied in the weak field (Newtonian) limit, we expect that Euclidean stars could provide simple models of evolving stars, which are relatively simple to analyze but still contain some of the essential features of a realistic situation.
In this work, we endeavor to classify all possible solutions describing “Euclidean stars”, according to the complexity of their structure and their pattern of evolution. The simplest solution satisfies the condition of vanishing complexity factor and evolves in the homologous or quasi-homologous regime. From there on, we obtain different families of solutions by relaxing the above conditions.
A rigorous definition of complexity is important since complexity, however we define it, is a physical concept deeply intertwined with fundamental aspects of the system, which we expect could provide relevant information about its behavior.
Here, we shall resort to the definition given in [11], intuitively associated to the very concept of “structure” within the fluid distribution. Such a definition is based on the assumption that the simplest system (or at least one of them) is represented by the homogeneous fluid with isotropic pressure. Having assumed this conjecture for a vanishing complexity system, the variable responsible for measuring complexity, which we call the complexity factor, appears in a natural way in the orthogonal splitting of the Riemann tensor (see [11] for details).
In the case of time-dependent systems, there is another aspect that requires our attention regarding the degree of complexity of the system. We have in mind the problem of the complexity of the patterns of evolution of the fluid.
In [12], it was shown that the homologous condition (H) may be suitable to characterize the simplest possible mode of evolution. It is worth recalling that in Newtonian physics, this condition implies that the radial velocity of any fluid element is proportional to its radial distance from the center, implying in its turn that the ratio of the radii of two comoving shells of fluid remains constant throughout the entire evolution. However, in the relativistic regime, these two properties of homologous condition are independent. Thus, we may consider a somewhat less restrictive condition by assuming only the first of the two abovementioned features. This is the so-called quasi-homologous condition () [13] (see details in Section 3.2).
Thus, we shall select solutions corresponding to Euclidean stars, and range them from the simplest one satisfying the vanishing complexity factor condition and evolving in the homologous regime, to solutions with an increasing level of complexity.
We shall consider dissipative and non-dissipative models.
The inclusion of dissipation is justified by the fact that gravitational collapse is a highly dissipative process (see [14] and references therein). This dissipation is required to account for the very large (negative) binding energy of the resulting compact object of the order of erg [15].
Non-dissipative Euclidean models are necessarily geodesic, belonging to the Lemaître–Tolman–Bondi (LTB) solutions [16,17,18] (more specifically to the parabolic subclass). They may describe evolving dust or, more generally, evolving anisotropic fluids [19].
We shall first consider the non-dissipative case, and identify the simplest model according to the criteria mentioned above. Such a solution appears to be the well-known Friedman–Robertson–Walker spacetime (FRW). Next, we shall relax the H or the conditions, keeping only the vanishing complexity factor condition. This leads to a family of solutions depending on two arbitrary functions of the radial coordinate. A specific model of this family is found and analyzed in detail.
Next, we shall consider the dissipative case. We shall first notice that we cannot impose the H condition since it would imply that the fluid is geodesic, which in the context of Euclidean stars implies that it is non-dissipative. Thus, we shall first consider the case when the vanishing complexity factor condition and hold, which leads to a large family of solutions, a specific example of which will be analyzed in detail.
Finally, we shall relax the condition, keeping only the vanishing complexity factor condition. Additionally, in order to be able to integrate the system, we shall assume the fluid to be shear-free. These two conditions lead to a large family of solutions already known in the literature [20,21,22].
2. The Euclidean Condition and Its Consequences
We shall start by defining all concepts, variables, and equations required for our discussion. This includes the definitions of complexity, the matching conditions, the Weyl tensor, and the transport equation. Next, we shall define the Euclidean condition, and the general properties of fluids satisfying this condition.
2.1. Basic Equations and Variables
Let us consider spherically symmetric distributions of fluid, bounded by a spherical surface . The fluid is assumed to be locally anisotropic with principal stresses unequal and undergoing dissipation in the form of heat flow. Choosing comoving coordinates inside , the general interior metric can be written as
where A, B, and R are functions of t and r and are assumed positive. We number the coordinates , , , and .
The matter energy momentum tensor inside has the form
where is the energy density, the radial pressure, the tangential pressure, the heat flux, the four-velocity of the fluid, and a unit four-vector along the radial direction.
It will be convenient to express the energy momentum tensor (2) in the equivalent (canonical) form
with
These quantities satisfy
Since we assumed that metric (1) is comoving then
where q is a function of t and r.
The four-acceleration and the expansion of the fluid are given by
and the shear by
where the semicolon denotes a covariant derivative, and the round brackets around the indexes denote symmetrization.
From (6) with (5), we have for the four-acceleration and its scalar a,
and for the expansion
where the prime stands for r differentiation and the dot stands for differentiation with respect to t. Using (5) and (7), we may write
where
The mass function introduced by Misner and Sharp [23] (see also [24]) reads
As it immediately follows from (1), the function R is the areal radius (i.e., the radius as measured from the area of a spherical surface). Therefore, we can define the velocity U of the evolving fluid as the variation of the areal radius with respect to proper time, i.e.,
where defines the derivative with respect to proper time. Then, (12) can be rewritten as
2.2. The Weyl Tensor
Let us recall that in the spherically symmetric case, the Weyl tensor () is defined by its “electric” part alone, since its “magnetic” part vanishes. Indeed, the magnetic part of the Weyl tensor is associated with vorticity, which of course is absent in any spherically symmetric distribution.
Thus we have
whose nontrivial components are
where
Observe that the electric part of the Weyl tensor may also be written as
2.3. The Transport Equation
In the diffusion approximation, we shall need a transport equation to evaluate the temperature and its evolution within the fluid distribution. Here, we shall resort to a transport equation derived from a causal dissipative theory (e.g., the Israel–Stewart second-order phenomenological theory for dissipative fluids [25,26,27]).
Thus, the corresponding transport equation for the heat flux reads
where denotes the thermal conductivity, and T and denote temperature and relaxation time, respectively. Observe that, due to the symmetry of the problem, Equation (19) only has one independent component, which may be written as
In the case of , we recover the Eckart–Landau equation [28,29].
For simplicity, one can consider in some cases the so-called “truncated” version, where the last term in (19) is neglected [30]:
and whose only non-vanishing independent component becomes
2.4. The Exterior Spacetime and Junction Conditions
Since our fluid distribution is bounded, we assume that, outside , the spacetime is described by the Vaidya metric, which reads as
where denotes the total mass, is a null coordinate, and v is the retarded time.
The smooth matching of the full nonadiabatic sphere to the Vaidya spacetime, on the surface where constant, requires the fulfillment of the Darmois conditions [31], i.e., the continuity of the first and second fundamental forms across (see [32] and references therein for details), which implies
and
where means that both sides of the equation are evaluated on .
When Darmois conditions are not satisfied, the boundary surface is a thin shell [33].
3. The Conditions for Classifying Euclidean Stars
As mentioned before, we endeavor to classify Euclidean stars according to their degree of complexity. Such a complexity will be measured by the complexity factor, and the complexity of the pattern of evolution. We shall next provide a brief description of the complexity factor, the homologous and the quasi-homologous regimes, which are the two modes of evolution assumed to be the simplest ones.
3.1. The Complexity Factor
The complexity factor is a scalar function that has been proposed in order to measure the degree of complexity of a given fluid distribution [11,12].
The complexity factor is identified with the scalar function , which defines the trace-free part of the electric Riemann tensor (see [12] for details).
It can be expressed in terms of physical variables as
or in terms of the metric functions
or
3.2. The Homologous (H) and the Quasi-Homologous () Condition
The condition is a generalization of the H condition. This latter condition has been assumed in [12] to represent the simplest mode of evolution of the fluid distribution. However, it appears to be too stringent, thereby excluding many potential interesting scenarios. Therefore, in [13], we have proposed to relax (H), and consider what we call the “quasi-homologous” condition (), which corresponds to a more complex pattern of evolution than H.
More specifically, the H condition implies that
and
where and denote the areal radii of two concentric shells () described by , and , respectively.
These relationships are characteristic of the homologous evolution in Newtonian hydrodynamics [34,35,36]. More so, in the latter case, (29) implies (30). However, in the relativistic case, both (29) and (30) are in general independent, and the former implies the latter only in very special cases (e.g., the geodesic case).
On the other hand, only requires (29), which, by using the field equations, may also be written as (see [13] for details)
3.3. Euclidean Stars and Their Properties
The regularity condition at the center requires that the perimeter of an infinitesimally small circle around the center be given by , where l is the proper radius of the circle, i.e., the proper radial distance from the center to the circle, given by
On the other hand, the perimeter of any circle, as it follows from (1), is given by , implying that in the neighborhood of the center, the regularity conditions imply
Euclidean stars are characterized by the fulfillment of the above condition not only at the center of symmetry, but at all points of the fluid distribution.
Thus, we shall assume that the “areal” radius (R) representing the radius as measured by its spherical surface, and the proper radius defined by , be equal. These two radii in general, in Einstein’s theory, need not be equal, unlike in Newton’s theory. Such a condition defines the Euclidean star. Hence, with this condition, we can write
implying from (14) that
Using (37) and (38) with (12), we obtain
Three interesting features of Euclidean stars deserve to be highlighted at this point:
- From (37), it follows that if the system is dissipating in the form of heat flow, the collapsing source requires , implying that because of (8), . This means that dissipation does not allow collapsing particles to follow geodesics. Inversely, of course, non-dissipative Euclidean models are necessarily geodesic since implies that, because of (8) and (37), .
- From (40), it follows that if , then and spacetime becomes Minkowskian. Therefore, all Euclidean stars are necessarily non-static. Furthermore, using (13), (40) can be rewritten asThe above equation can be interpreted as the Newtonian kinetic energy (per unit mass) of the collapsing particles being equal to their Newtonian potential energy.
- The proper radial three-acceleration of a falling particle inside can be calculated to obtainOn the other hand, due to the Euclidean condition, the dynamical Equation (43) becomesThus, it appears that the contribution of the non-gravitational force term (the last on the right-hand side) to , for any fluid element, does not depend on its inertial mass density (). Or, in other words, non-gravitational forces produce a radial three-acceleration independent on the inertial mass density of the fluid element, similarly to the gravitational force term.
4. A Hierarchy of Euclidean Stars According to Their Complexity
We shall now proceed to classify Euclidean stars by imposing different restrictions based on the notion of complexity discussed above. We shall start by considering the simplest possible model by assuming the vanishing complexity factor and the H mode of evolution. From there on, we shall relax the conditions on the complexity, thereby allowing more complex systems. We shall consider separately non-dissipative and dissipative fluids.
Let us consider first the non-dissipative case.
4.1. Evolution with
As mentioned before, for this case, we have from (37) that , which means , and by rescaling t, we can obtain without loss of generality
Of course, such models are members of the Lemaître–Tolman–Bondi (LTB) spacetimes [16,17,18]. Furthermore, they correspond to the parabolic case.
Indeed, the general metric for LTB spacetimes reads as
where is an arbitrary function of r.
Imposing the Euclidean condition (34) in (46), one obtains , which defines parabolic LTB spacetimes.
In this latter case, we know that for pure dust
where is an integration function of r.
However, the above solution is only valid for dust. For the sake of completeness, we shall consider an anisotropic fluid (we recall that LTB spacetime is compatible with an anisotropic fluid [19]).
4.1.1. Models Satisfying H Condition and
If we impose the H condition, then the shear vanishes and it follows from (27) and (11) that . Furthermore, since the fluid is geodesic, and H are equivalent. In such a case, as it has been shown in [12], the spacetime is the FRW solution.
Thus, the simplest non-dissipative Euclidean star is described by the FRW line element.
4.1.2. Models Satisfying Only
In order to find the next subfamily of solutions in terms of increasing complexity, let us consider that , but the system does not evolve in the H regime. Then, from and (34), it follows that
where is an arbitrary function of its argument.
Next, from Equations (38), (39), and (48), we find that
It is worth noticing that if we assume the fluid to be isotropic, then it follows from (49) that R is separable, i.e., , implying that the (H) condition is satisfied and we have FRW.
From the above, it follows that we have to consider anisotropic models.
In the non-dissipative case (), we have constant, and then using (42) evaluated on the boundary surface, we may write
whose solution reads
where is a constant of integration. This solution represents an ever-expanding fluid configuration. Changing t by in (51), we obtain the corresponding collapsing solution.
From the results above and the field equations, we may write
The general solution of (48) using (52) reads as
where and are two arbitrary functions of integration.
The mass function for this family of solutions reads
which asymptotically, as , becomes
It is worth noticing that, since we are considering non-vanishing pressure, then in general, m also depends on t as it follows from (41).
Also, since the system is non-dissipative, then constant, implying that
Thus, the physical variables read as
with
and .
In order to specify a model, let us propose
which satisfies the boundary condition (60), and where , and .
In this model, the variables become
where
and
Finally, for the mass function, we obtain the expression
where
and
Figure 1 and Figure 2 depict the evolution and spatial distribution of the mass function and the physical variables for this model.
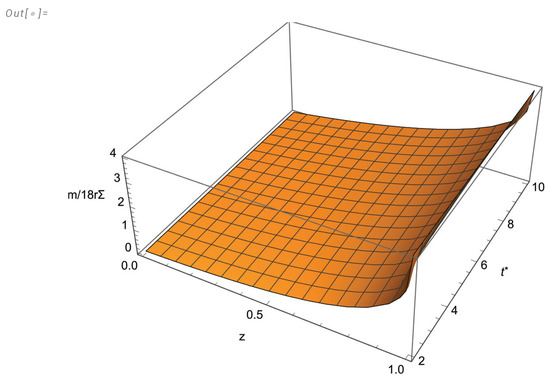
Figure 1.
as a function of z in the interval , and in the interval .
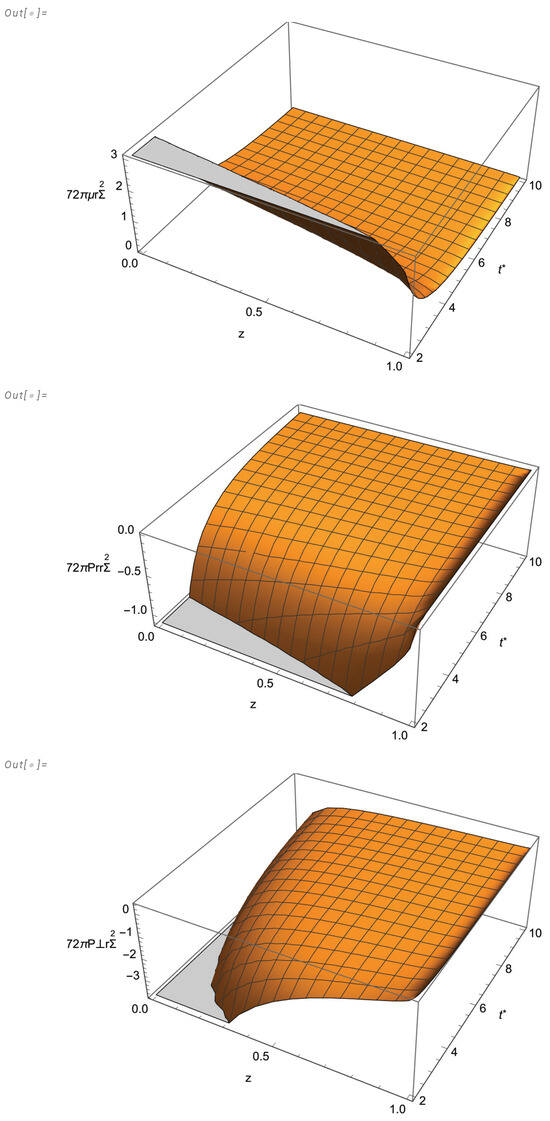
Figure 2.
, , and as functions of z in the interval , and in the interval .
4.2. Evolution with
We shall next consider the dissipative case.
Let us start by noting that the H condition (as shown in [12]) implies that the fluid is geodesic, which is incompatible with a dissipative Euclidean star. Then, concerning complexity, the lowest degree of complexity admissible for a dissipative Euclidean star would be described by the condition and .
We shall consider here two possible families of solutions with different degrees of complexity. We shall first consider fluid distributions satisfying the vanishing complexity factor condition plus the condition. Such a case, as mentioned above, represents models with the lowest degree of complexity. Next, we shall consider the family of solutions satisfying the vanishing complexity factor condition alone. In order to integrate the equations, we have complemented this latter condition with the shear-free condition.
4.2.1. Models with and Evolution
As it follows from (31), the () condition reads
where is the function of integration, with dimensions , which without lost of generality may be put equal to 1 by a reparametrization of t.
In order to find a solution to the above equation, we shall split it into a system of two equations resulting from equating to zero the expressions within each of the square brackets in (75), producing
and
where and .
Equation (77) may be solved to obtain
where are arbitrary functions of their argument. and G are dimensionless, whereas has dimensions .
Taking the r derivative of (79) and using (77), we obtain
whose solution may be written as
where is an arbitrary function of t.
Using (81) in (80) produces
or, introducing the variables
it becomes
whose solution reads
where is an arbitrary function.
Returning to the original variables, the above equation reads
with each solution corresponding to a given choice of .
Next, we may find a relationship between the time-dependent functions appearing in (78) by imposing the boundary condition (25), which now reads
whose integration produces
where and is a constant of integration.
Thus, the whole family of solutions satisfying the and evolution condition (besides de Euclidean condition), depends on one arbitrary function of t and one arbitrary function on r.
In terms of the function R, the physical variables for this family read
In order to illustrate how to find a specific model of this family, we shall present in the next subsection a toy model.
4.2.2. A Toy Model
We start the construction of this model by assuming
where b is a constant with dimensions of .
In order to fully specify the model, it remains to provide the function . For simplicity, and to avoid shell crossing singularities, we shall assume
where is a positive constant with dimensions .
Using the above expressions, the areal radius of the boundary surface becomes
whereas for the physical variables, we obtain
where ; ; , and we assume .
The temperature and the tangential pressure for this model may be calculated using (22), (98), and (92); however, the resulting expressions are cumbersome and not very illuminating. Accordingly, we will dispense with these expressions and the corresponding graphics.
Figure 3 depicts the evolution and spatial distribution of for this model, which represents an ever-expanding sphere starting from a singularity.
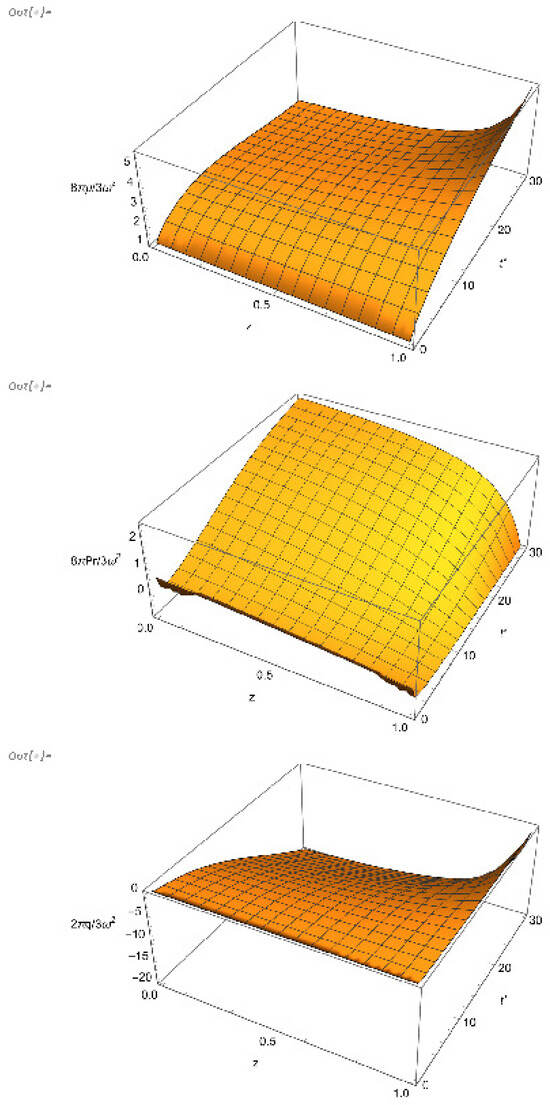
Figure 3.
, and as functions of z in the interval , and in the interval .
4.2.3. Models with
We shall now relax the condition of the evolution. In order to be able to integrate the system of field equations, we need an additional condition, which we choose to be the shear-free condition. The motivation of assuming such a restriction stems from the role played by shear in the collapse of dissipative fluid spheres (see [37,38,39] and references therein). Obviously in this case we cannot assume since that would imply, due to (31), that .
The general shear-free case for dissipative Euclidean stars has been considered in [1]. In such a case, the line element can be written as [40]
and the Euclidean condition becomes
implying
where f is an arbitrary function of t.
From (105) and (106), we have
On the other hand, using (101) and (102) in (27), the condition becomes
whose solution reads
where and are two functions of integration.
From (107) and (108), it follows that the fluid is isotropic, and from (28), it follows that it is also conformally flat.
The general form of all conformally flat and shear-free metrics is known [20] as follows:
where is an arbitrary function of t, and
where and are arbitrary functions of t.
The Euclidean condition and the vanishing complexity factor condition then imply
An approximate solution of this kind has been presented and discussed in [20]. Furthermore, an exact solution is also known [21], which in turn is a particular case of a family of solutions found in [22]. It reads (see Case III in [21])
and
where , , and are constants. The above solution satisfies junction conditions and its physical properties have been discussed in [21]. Thus we shall not elaborate any further on it. Let us also mention that its physical properties are reasonable, and using (22), it has been shown that relaxation effects play an important role in the evolution of the system.
5. Discussion and Conclusions
The family of Euclidean stars encompasses a large number of solutions to Einstein equations, describing the evolution of spherically symmetric fluid distributions, which may be dissipative or not. Research work devoted to the application of some of these solutions in the study of the structure and evolution of compact objects may be found in [1,2,3,4,5,6,7,8,9,10] and references therein.
The main interest of these solutions stems from the fact that the heuristic condition defining these models is borrowed from Euclidean geometry, thereby allowing for the analytical modeling of stellar evolution, relying on a condition which should hold at least for fields that are not very strong. Additionally, it should be pointed out that such relevant solutions as FRW and some LTB models are members of this family.
Our goal in this work has been to introduce a hierarchical structure of different subfamilies of Euclidean stars based on their degree of complexity. As a measure of complexity, we have resorted to the notion of the complexity factor defined in [11,12], and to the notion of Homologous and quasi-homologous evolution as defined in [12,13].
We have considered both the adiabatic and the dissipative case. In the former case, it appears that the fluid must be geodesic, and therefore, it belongs to the family of LTB solutions, more specifically to the parabolic case of LTB models.
The highest degree of simplicity in this case, which corresponds to the vanishing complexity factor and H evolution, leads to the FRW spacetime. We next relaxed the H condition, maintaining the vanishing of the complexity factor condition. In such a case, we found a family of solutions described by Equations (61)–(64), depending on two arbitrary functions of r.
A specific model of the above mentioned family of solutions was obtained from the additional assumptions given by Equations (65) and (66). Figure 1 and Figure 2 depict the evolution and spatial distribution of the mass function and the physical variables for this model. It is worth stressing that our motivation to present such a model was not to describe any specific astrophysical or cosmological scenario, but just to illustrate the means of obtaining models. The possible application of any model belonging to this family of solutions is out of the scope of this manuscript.
Next, we considered the dissipative case. The first family of solutions of this case satisfies the conditions and . This is the simplest family of Euclidean dissipative stars. In general, this family of solutions depends on one arbitrary function of t and one arbitrary function of r. A toy model belonging to this family was constructed by assuming for the two functions mentioned above the conditions (93) and (95). The behavior of the physical variables for this model is depicted in Figure 3. Once again, we should stress the fact that this toy model was obtained only to illustrate the means of obtaining specific solutions corresponding to this family.
Finally, as the last step in order of increasing complexity, we relaxed the condition and considered only the condition. To integrate the system, we complemented this latter condition with the shear-free condition, which prevents the system to satisfy the condition. Thus, from the point of view of complexity, this family of solutions satisfies only one of the restrictions based on the notion of complexity. However, as shown above, this family of solutions is also conformally flat, and as a matter of fact, was already known from previous works, with their properties analyzed in detail in [20,21,22].
We would like to conclude by emphasizing the main goal of our endeavor. We looked for a hierarchy of Euclidean stars according to their complexity. As a byproduct of this research, we were able to present an analytical method for the modeling of these stars. The presented examples were proposed simply to illustrate the method. In order to obtain models which could be applied to study specific astrophysical or cosmological scenarios, it would be necessary to relate the arbitrary functions involved in the different families of solutions to relevant observable variables, among which the gravitational surface redshift and the rate of emitted energy are most likely the best candidates (although not the only ones).
Author Contributions
Conceptualization, L.H.; methodology, L.H., A.D.P. and J.O.; software, J.O.; formal analysis, L.H., A.D.P. and J.O.; writing—original draft preparation, L.H.; writing—review and editing, L.H., A.D.P. and J.O.; funding acquisition, L.H. and J.O. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Grant PID2021-122938NB-I00 funded by MCIN/AEI/10.13039/501100011033 and by the ERDF—A way of making Europe, as well as the Consejería de Educación of the Junta de Castilla y León under the Research Project Grupo de Excelencia Ref.:SA097P24 (Fondos Feder y en línea con objetivos RIS3).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Herrera, L.; Santos, N.O. Collapsing spheres satisfying an Euclidean condition. Gen. Relativ. Gravit. 2010, 42, 2383–2391. [Google Scholar] [CrossRef]
- Govinder, K.S.; Govender, M. A general class of Euclidean stars. Gen. Relativ. Gravit. 2010, 44, 147. [Google Scholar] [CrossRef]
- Govender, G.; Govender, M.; Govinder, K.S. Thermal behavior of Euclidean stars. Int. J. Mod. Phys. D 2010, 19, 1773. [Google Scholar] [CrossRef]
- Abebe, G.; Maharaj, S.; Govinder, K. Generalized Euclidean stars with equation of state. Gen. Relativ. Gravit. 2014, 46, 1733. [Google Scholar] [CrossRef]
- Ivanov, B. All solutions for geodesic anisotropic spherical collapse with shear and heat radiation. Astrophys. Space Sci. 2016, 361, 18. [Google Scholar] [CrossRef]
- Maharaj, S.; Tiwari, A.; Mohanlal, R.; Narain, R. Riccati equations for bounded radiating systems. J. Math. Phys. 2016, 57, 092501. [Google Scholar] [CrossRef]
- Abebe, G.; Maharaj, S. Charged radiating stars with Lie symmetries. Eur. Phys. J. C 2019, 79, 849. [Google Scholar] [CrossRef]
- Yousaf, Z.; Bhatti, M.; Naseer, T. Evolution of the charged dynamical radiation spherical structures. Ann. Phys. 2020, 420, 168267. [Google Scholar] [CrossRef]
- Yousaf, Z.; Bhatti, M.; Naseer, T. Measure of complexity for dynamical self-gravitating structures. Int. J. Mod. Phys. D 2020, 29, 2050061. [Google Scholar] [CrossRef]
- Mumtaz, S.; Manzoor, R.; Sarwar, U. Solutions for anisotropic dissipative collapse in f(R) gravity. New Astron. 2024, 106, 102133. [Google Scholar] [CrossRef]
- Herrera, L. New definition of complexity for self–gravitating fluid distributions: The spherically symmetric static case. Phys. Rev. D 2018, 97, 044010. [Google Scholar] [CrossRef]
- Herrera, L.; Di Prisco, A.; Ospino, J. Definition of complexity for dynamical spherically symmetric dissipative self–gravitating fluid distributions. Phys. Rev. D 2018, 98, 104059. [Google Scholar] [CrossRef]
- Herrera, L.; Di Prisco, A.; Ospino, J. Quasi–homologous evolution of self–gravitating systems with vanishing complexity factor. Eur. Phys. J. C 2020, 80, 631. [Google Scholar] [CrossRef]
- Mitra, A. Why gravitational contraction must be accompanied by emission of radiation in both Newtonian and Einstein gravity. Phys. Rev. D 2006, 74, 024010. [Google Scholar] [CrossRef]
- Kazanas, D.; Schramm, D.N. Neutrino competition with gravitational radiation during collapse. In Sources of Gravitational Radiation; Cambridge University Press: New York, NY, USA, 1979. [Google Scholar]
- Lemaître, G. L’Univers en expansion. Ann. Soc. Sci. Brux. 1933, A 53, 51. [Google Scholar]
- Tolman, R.C. Effect of Inhomogeneity on Cosmological Models. Proc. Natl. Acad. Sci. USA 1934, 20, 169. [Google Scholar] [CrossRef]
- Bondi, H. Spherically symmetrical models in general relativity. Mon. Not. R. Astron. Soc. 1947, 107, 410. [Google Scholar] [CrossRef]
- Sussman, R.A. Quasilocal variables in spherical symmetry: Numerical applications to dark matter and dark energy sources. Phys. Rev. D 2009, 79, 025009. [Google Scholar] [CrossRef]
- Herrera, L.; Le Denmat, G.; Santos, N.O.; Wang, A. Shear–free radiating collapse and conformal flatness. Int. J. Mod. Phys. D 2004, 13, 583. [Google Scholar] [CrossRef]
- Maharaj, S.D.; Govender, M. Radiating collapse with vanishing Weyl stresses. Int. J. Mod. Phys. D 2005, 14, 667. [Google Scholar] [CrossRef]
- Herrera, L.; Di Prisco, A.; Ospino, J. Some analytical models of radiating collapsing spheres. Phys. Rev. D 2006, 74, 044001. [Google Scholar] [CrossRef]
- Misner, C.; Sharp, D. Relativistic Equations for Adiabatic, Spherically Symmetric Gravitational Collapse. Phys. Rev. 1964, 136, B571. [Google Scholar] [CrossRef]
- Cahill, M.; McVittie, G. Spherical Symmetry and Mass-Energy in General Relativity. I. General Theory. J. Math. Phys. 1970, 11, 1382. [Google Scholar] [CrossRef]
- Israel, W. Nonstationary irreversible thermodynamic: A causal relativistic theory. Ann. Phys. 1976, 100, 310–331. [Google Scholar] [CrossRef]
- Israel, W.; Stewart, J. Thermodynamic of nonstationary and transient effects in a relativistic gas. Phys. Lett. A 1976, 58, 213–215. [Google Scholar] [CrossRef]
- Israel, W.; Stewart, J. Transient relativistic thermodynamics and kinetic theory. Ann. Phys. 1979, 118, 341–372. [Google Scholar] [CrossRef]
- Eckart, C. The Thermodynamics of Irreversible Processes. III. Relativistic Theory of the Simple Fluid. Phys. Rev. 1940, 58, 919. [Google Scholar] [CrossRef]
- Landau, L.; Lifshitz, E. Fluid Mechanics; Pergamon Press: London, UK, 1959. [Google Scholar]
- Triginer, J.; Pavon, D. On the thermodynamics of tilted and collisionless gases in Friedmann–Robertson–Walker spacetimes. Class. Quantum Gravity 1995, 12, 199. [Google Scholar] [CrossRef]
- Darmois, G. Memorial des Sciences Mathematiques; Gauthier-Villars: Paris, France, 1927; p. 25. [Google Scholar]
- Chan, R. Collapse of a radiating star with shear. Mon. Not. R. Astron. Soc. 1997, 288, 589–595. [Google Scholar] [CrossRef]
- Israel, W. Singular hypersurfaces and thin shells in general relativity. Il Nuovo C. B 1966, 44, 1–14. [Google Scholar] [CrossRef]
- Schwarzschild, M. Structure and Evolution of the Stars; Dover: New York, NY, USA, 1958. [Google Scholar]
- Hansen, C.; Kawaler, S. Stellar Interiors: Physical Principles, Structure and Evolution; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Kippenhahn, R.; Weigert, A. Stellar Structure and Evolution; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Chan, R. Radiating gravitational collapse with shear revisited. Int. J. Mod. Phys. D 2003, 12, 1131. [Google Scholar] [CrossRef]
- Pinheiro, G.; Chan, R. Radiating gravitational collapse with shearing motion an bulk viscosity revisited. Int. J. Mod. Phys. D 2010, 19, 1797. [Google Scholar] [CrossRef]
- Govender, M.; Reddy, K.P.; Maharaj, S.D. The role of shear in dissipative gravitational collapse. Int. J. Mod. Phys. D 2014, 23, 1450013. [Google Scholar] [CrossRef]
- Glass, E.N. Shear-free gravitational collapse. J. Math. Phys. 1979, 20, 1508. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).