Stellar-Mass Black Holes
Abstract
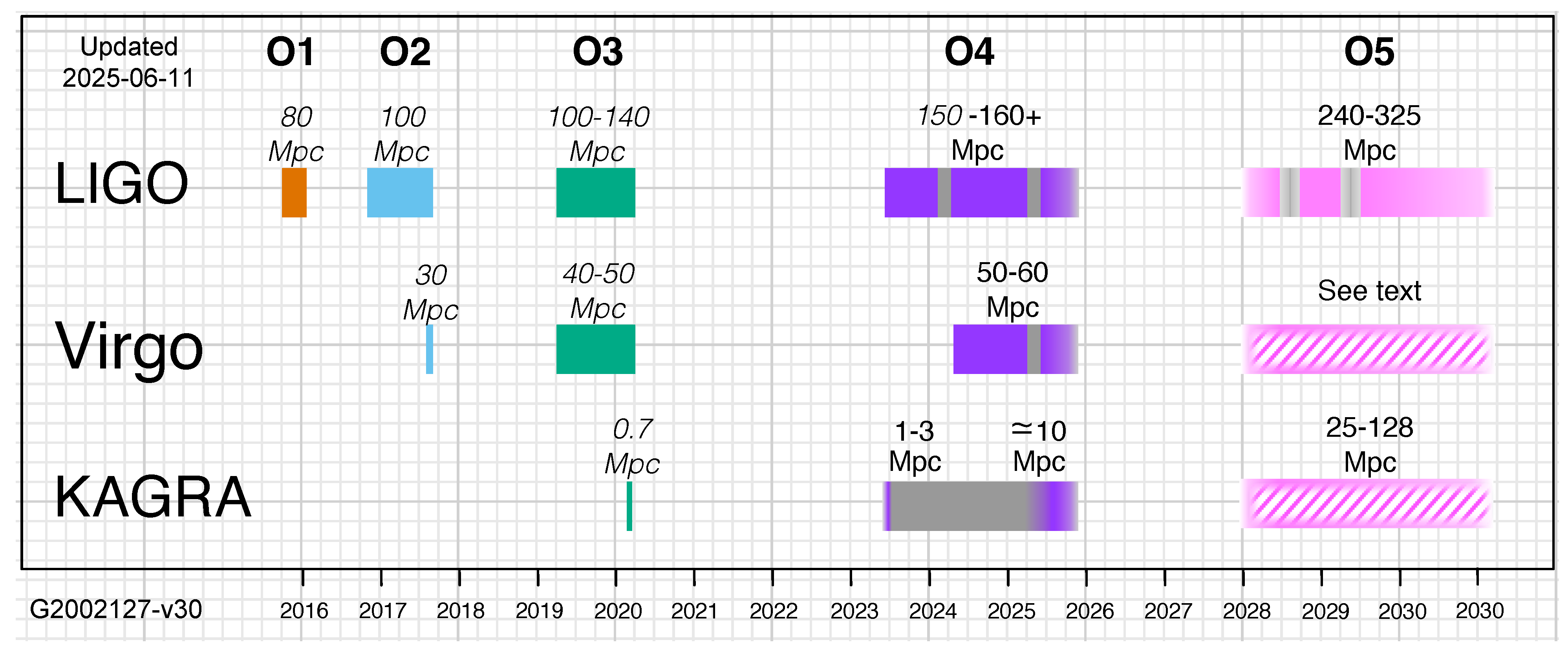
1. Introduction
- Stellar-mass black holes have masses in the range ∼3 to ∼150 . They are the natural product of the evolution of heavy stars. They are the topic of this review article and they will be discussed in the next sections.
- Supermassive black holes have masses in the range – and are found at the center of every middle-size and large galaxy ( ) [7] (exceptions may be possible: the galaxy A2261-BCG is one of the largest galaxies known but does not seem to host any supermassive black hole at its center [8]). In the case of small galaxies ( ), the situation is more controversial: some small galaxies host a supermassive black hole at their center while other small galaxies do not seem to have any supermassive black hole [9,10]. While heavy objects can naturally migrate to the center of a multi-body system, which explains why supermassive black holes are at the center of their host galaxies, we do not know exactly how they formed and evolved: for example, they could have formed as stellar-mass black holes from the collapse of heavy stars and grown later or they could have formed from the collapse of heavy clouds and been heavier than stellar-mass black holes from the very beginning.
2. Stellar-Mass Black Holes
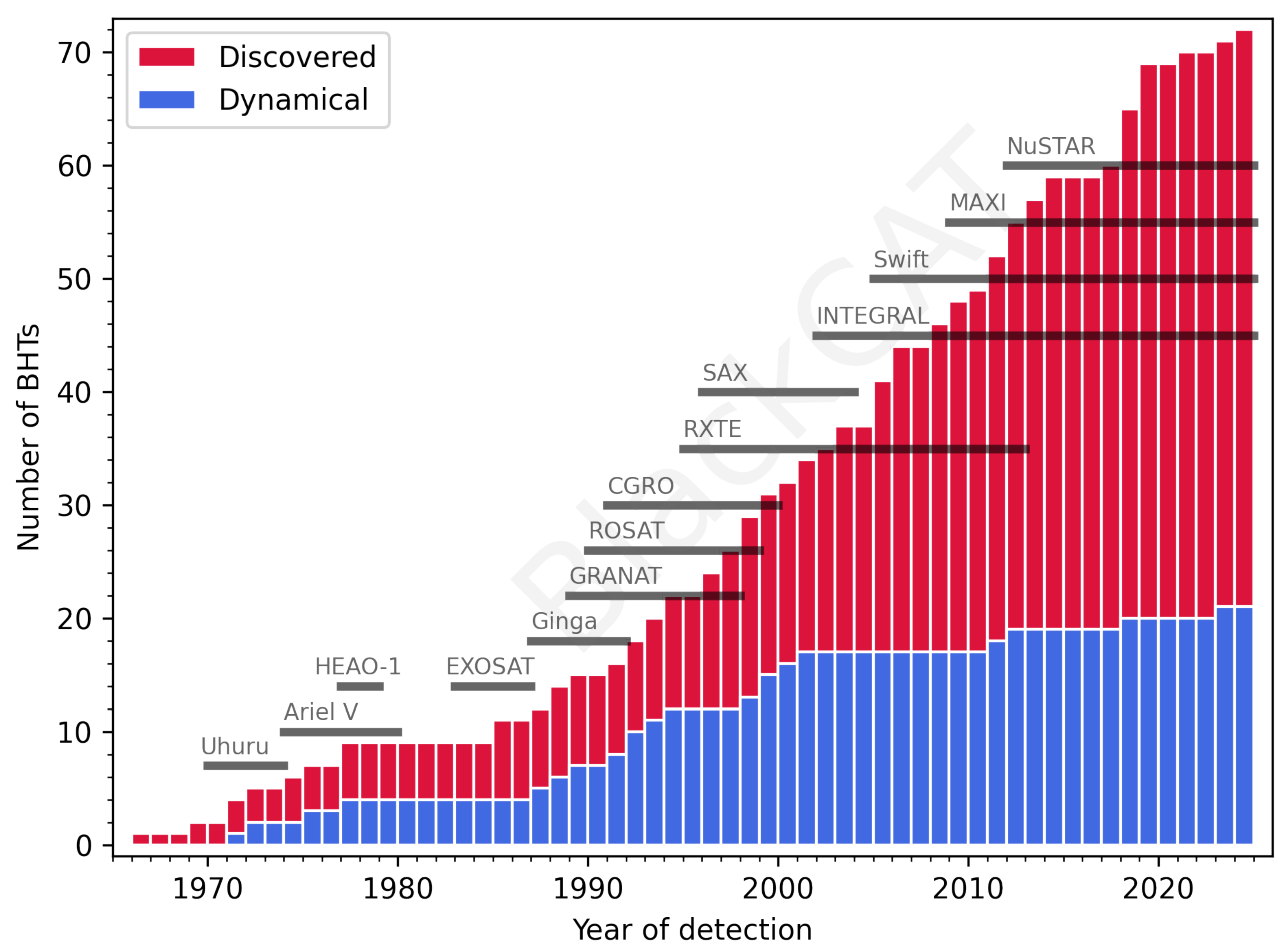
- Around seventy black holes in X-ray binaries.
- Four black holes in astrometric binaries.
- One isolated black hole.
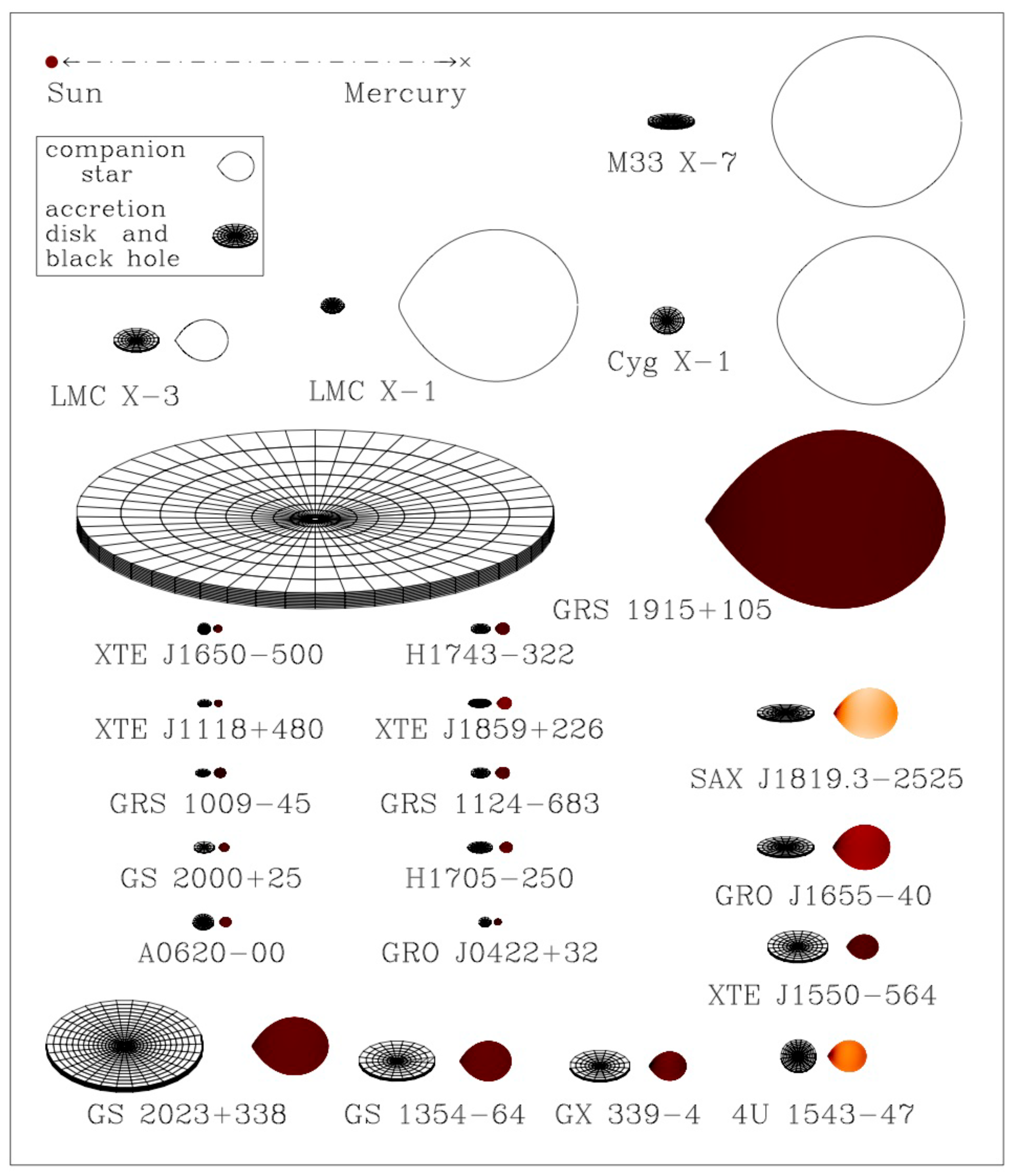
2.1. Black Holes in X-Ray Binary Systems
2.2. Black Holes in Astrometric Binary Systems
- GAIA BH3 [55] (mass ; orbital period of the binary years; distance of the source pc). As of now, this is the heaviest known stellar-mass black hole in our Galaxy and the black hole binary with the longest orbital period.
- ALS 8814 [56] (mass –58 ; orbital period of the binary days; distance of the source kpc). As of now, this is the only unambiguous binary system of a Be-star and a black hole.
2.3. Isolated Black Holes
2.4. Black Holes in Compact Binary Systems
3. Open Issues
3.1. Mass Gap
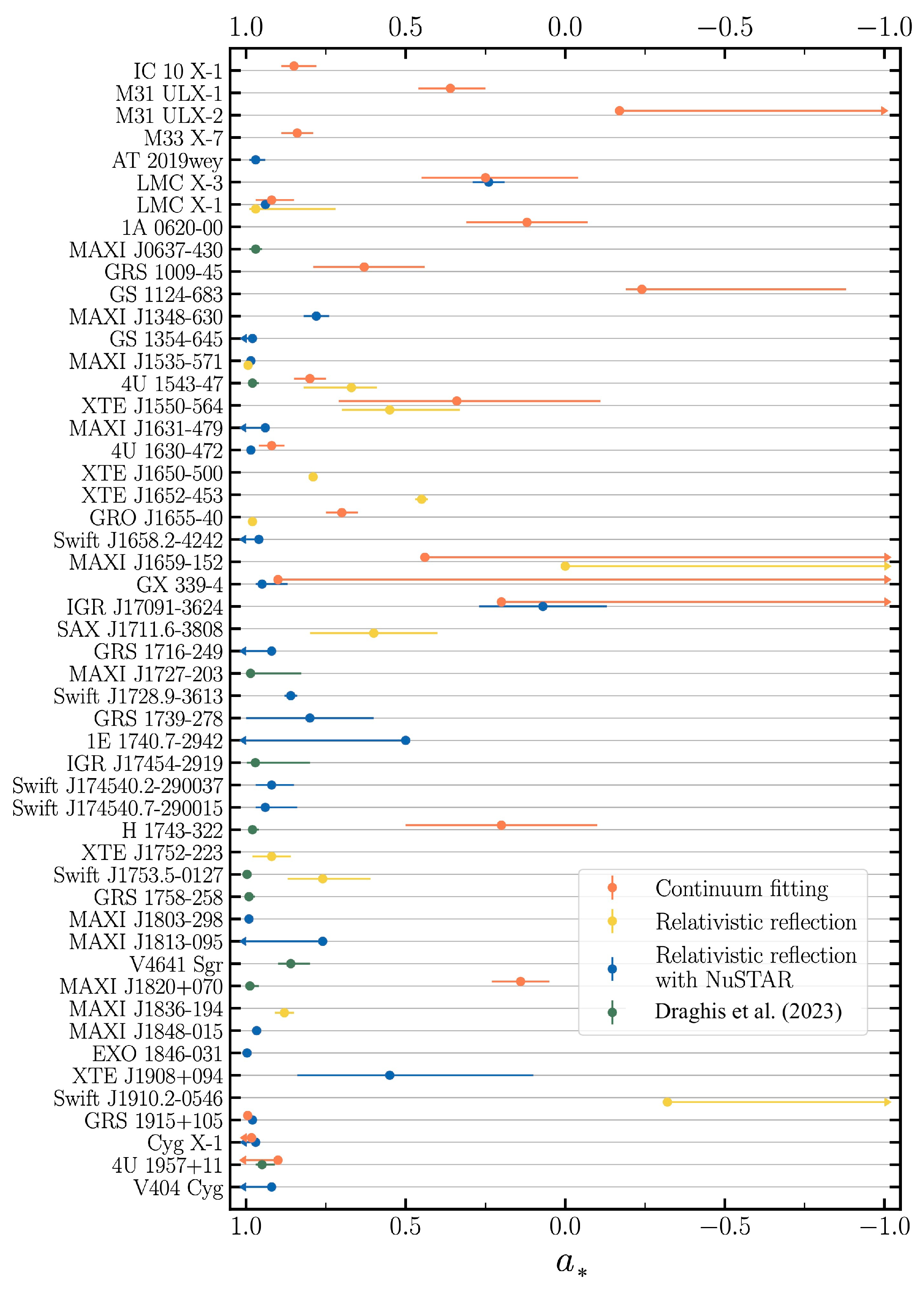
3.2. Black Hole Spins
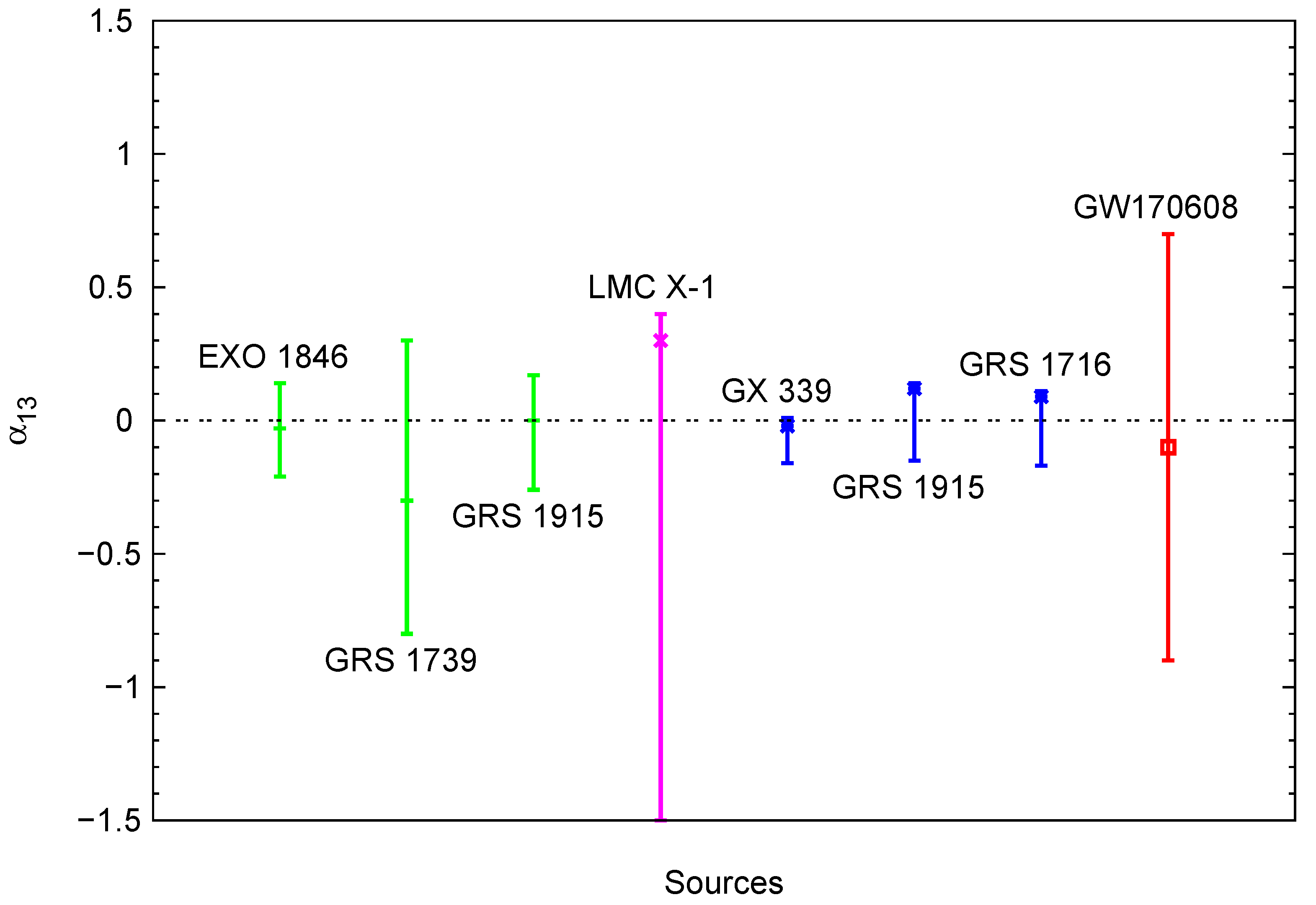
3.3. Is General Relativity Correct?
4. An Interstellar Mission to the Closest Black Hole?
5. Concluding Remarks
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: New York, NY, USA, 1973; ISBN 978-0-7167-0344-0/978-0-691-17779-3. [Google Scholar]
- Bambi, C. Black Holes: A Laboratory for Testing Strong Gravity; Springer: Singapore, 2017; ISBN 978-981-10-4523-3/978-981-13-5158-7/978-981-10-4524-0. [Google Scholar] [CrossRef]
- Carter, B. Axisymmetric Black Hole Has Only Two Degrees of Freedom. Phys. Rev. Lett. 1971, 26, 331–333. [Google Scholar] [CrossRef]
- Robinson, D.C. Uniqueness of the Kerr black hole. Phys. Rev. Lett. 1975, 34, 905–906. [Google Scholar] [CrossRef]
- Chrusciel, P.T.; Costa, J.L.; Heusler, M. Stationary Black Holes: Uniqueness and Beyond. Living Rev. Rel. 2012, 15, 7. [Google Scholar] [CrossRef] [PubMed]
- Penrose, R. Gravitational collapse: The role of general relativity. Riv. Nuovo Cim. 1969, 1, 252–276. [Google Scholar] [CrossRef]
- Kormendy, J.; Richstone, D. Inward bound: The Search for supermassive black holes in galactic nuclei. Ann. Rev. Astron. Astrophys. 1995, 33, 581. [Google Scholar] [CrossRef]
- Postman, M.; Lauer, T.R.; Donahue, M.; Graves, G.; Coe, D.; Koekemoer, A.; Bradley, L.; Ford, H.C.; Grillo, C.; Zitrin, A.; et al. A Brightest Cluster Galaxy with an Extremely Large Flat Core. Astrophys. J. 2012, 756, 159. [Google Scholar] [CrossRef]
- Ferrarese, L.; Cote, P.; Bonta, E.D.; Peng, E.W.; Merritt, D.; Jordán, A.; Blakeslee, J.P.; Haşegan, M.; Mei, S.; Piatek, S.; et al. A fundamental relation between compact stellar nuclei, supermassive black holes, and their host galaxies. Astrophys. J. Lett. 2006, 644, L21–L24. [Google Scholar] [CrossRef]
- Gallo, E.; Treu, T.; Jacob, J.; Woo, J.H.; Marshall, P.; Antonucci, R. AMUSE-Virgo. 1. Super-massive black holes in low-mass spheroids. Astrophys. J. 2008, 680, 154. [Google Scholar] [CrossRef]
- Greene, J.E.; Strader, J.; Ho, L.C. Intermediate-Mass Black Holes. Ann. Rev. Astron. Astrophys. 2020, 58, 257–312. [Google Scholar] [CrossRef]
- Dolgov, A.; Silk, J. Baryon isocurvature fluctuations at small scales and baryonic dark matter. Phys. Rev. D 1993, 47, 4244–4255. [Google Scholar] [CrossRef]
- Byrnes, C.; Franciolini, G.; Harada, T.; Pani, P.; Sasaki, M. Primordial Black Holes; Springer: Singapore, 2025; ISBN 978-981-97-8886-6/978-981-97-8889-7/978-981-97-8887-3. [Google Scholar] [CrossRef]
- Price, R.H. Nonspherical perturbations of relativistic gravitational collapse. 1. Scalar and gravitational perturbations. Phys. Rev. D 1972, 5, 2419–2438. [Google Scholar] [CrossRef]
- Bambi, C.; Dolgov, A.D.; Petrov, A.A. Black holes as antimatter factories. JCAP 2009, 09, 013. [Google Scholar] [CrossRef]
- Barausse, E.; Cardoso, V.; Pani, P. Can environmental effects spoil precision gravitational-wave astrophysics? Phys. Rev. D 2014, 89, 104059. [Google Scholar] [CrossRef]
- Bambi, C.; Malafarina, D.; Tsukamoto, N. Note on the effect of a massive accretion disk in the measurements of black hole spins. Phys. Rev. D 2014, 89, 127302. [Google Scholar] [CrossRef]
- Burrows, A.; Vartanyan, D.; Wang, T. Black Hole Formation Accompanied by the Supernova Explosion of a 40 M⊙ Progenitor Star. Astrophys. J. 2023, 957, 68. [Google Scholar] [CrossRef]
- Burrows, A.; Wang, T.; Vartanyan, D. Channels of Stellar-mass Black Hole Formation. Astrophys. J. 2025, 987, 164. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The maximum mass of ideal white dwarfs. Astrophys. J. 1931, 74, 81–82. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On massive neutron cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Rhoades, C.E., Jr.; Ruffini, R. Maximum mass of a neutron star. Phys. Rev. Lett. 1974, 32, 324–327. [Google Scholar] [CrossRef]
- Kalogera, V.; Baym, G. The maximum mass of a neutron star. Astrophys. J. Lett. 1996, 470, L61–L64. [Google Scholar] [CrossRef]
- Lattimer, J.M. The nuclear equation of state and neutron star masses. Ann. Rev. Nucl. Part. Sci. 2012, 62, 485–515. [Google Scholar] [CrossRef]
- Heger, A.; Fryer, C.L.; Woosley, S.E.; Langer, N.; Hartmann, D.H. How massive single stars end their life. Astrophys. J. 2003, 591, 288–300. [Google Scholar] [CrossRef]
- Spera, M.; Mapelli, M.; Bressan, A. The mass spectrum of compact remnants from the PARSEC stellar evolution tracks. Mon. Not. R. Astron. Soc. 2015, 451, 4086–4103. [Google Scholar] [CrossRef]
- Mapelli, M. Formation Channels of Single and Binary Stellar-Mass Black Holes. In Handbook of Gravitational Wave Astronomy; Bambi, C., Katsanevas, S., Kokkotas, K.D., Eds.; Springer: Singapore, 2022; pp. 705–769. [Google Scholar] [CrossRef]
- Heger, A.; Woosley, S.E. The nucleosynthetic signature of population III. Astrophys. J. 2002, 567, 532–543. [Google Scholar] [CrossRef]
- Belczynski, K.; Heger, A.; Gladysz, W.; Ruiter, A.J.; Woosley, S.; Wiktorowicz, G.; Chen, H.-Y.; Bulik, T.; O’Shaughnessy, R.; Holz, D.E.; et al. The Effect of Pair-Instability Mass Loss on Black Hole Mergers. Astron. Astrophys. 2016, 594, A97. [Google Scholar] [CrossRef]
- Woosley, S.E. Pulsational Pair-Instability Supernovae. Astrophys. J. 2017, 836, 244. [Google Scholar] [CrossRef]
- Woosley, S.E. The Evolution of Massive Helium Stars, Including Mass Loss. Astrophys. J. 2019, 878, 49. [Google Scholar] [CrossRef]
- Farmer, R.; Renzo, M.; de Mink, S.E.; Marchant, P.; Justham, S. Mind the gap: The location of the lower edge of the pair instability supernovae black hole mass gap. Astrophys. J. 2019, 887, 53. [Google Scholar] [CrossRef]
- Mapelli, M.; Spera, M.; Montanari, E.; Limongi, M.; Chieffi, A.; Giacobbo, N.; Bressan, A.; Bouffanais, Y. Impact of the Rotation and Compactness of Progenitors on the Mass of Black Holes. Astrophys. J. 2020, 888, 76. [Google Scholar] [CrossRef]
- Costa, G.; Bressan, A.; Mapelli, M.; Marigo, P.; Iorio, G.; Spera, M. Formation of GW190521 from stellar evolution: The impact of the hydrogen-rich envelope, dredge-up and 12C(α, γ)16O rate on the pair-instability black hole mass gap. Mon. Not. R. Astron. Soc. 2021, 501, 4514–4533. [Google Scholar] [CrossRef]
- Vink, J.S.; Higgins, E.R.; Sander, A.A.C.; Sabhahit, G.N. Maximum black hole mass across cosmic time. Mon. Not. R. Astron. Soc. 2021, 504, 146–154. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration; Virgo Collaboration; KAGRA Collaboration. GW231123: A Binary Black Hole Merger with Total Mass 190–265 M⊙. arXiv 2025, arXiv:2507.08219. [Google Scholar] [CrossRef]
- Timmes, F.X.; Woosley, S.E.; Weaver, T.A. The Neutron star and black hole initial mass function. Astrophys. J. 1996, 457, 834. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef]
- Olejak, A.; Belczynski, K.; Bulik, T.; Sobolewska, M. Synthetic catalog of black holes in the Milky Way. Astron. Astrophys. 2020, 638, A94. [Google Scholar] [CrossRef]
- Giesers, B.; Dreizler, S.; Husser, T.-O.; Kamann, S.; Escude, G.A.; Brinchmann, J.; Carollo, C.M.; Roth, M.M.; Weilbacher, P.M.; Wisotzki, L.; et al. A detached stellar-mass black hole candidate in the globular cluster NGC 3201. Mon. Not. R. Astron. Soc. 2018, 475, L15–L19. [Google Scholar] [CrossRef]
- Giesers, B.; Kamann, S.; Dreizler, S.; Husser, T.; Askar, A.; Göttgens, F.; Brinchmann, J.; Latour, M.; Weilbacher, P.M.; Wendt, M.; et al. A stellar census in globular clusters with MUSE: Binaries in NGC 3201. Astron. Astrophys. 2019, 632, A3. [Google Scholar] [CrossRef]
- Thompson, T.A.; Kochanek, C.S.; Stanek, K.Z.; Badenes, C.; Post, R.S.; Jayasinghe, T.; Covey, K. Discovery of a Candidate Black Hole-Giant Star Binary System in the Galactic Field. Science 2019, 366, 637–640. [Google Scholar] [CrossRef]
- Lam, C.Y.; Lu, J.R.; Udalski, A.; Bond, I.; Bennett, D.P.; Skowron, J.; Terry, S.K. An isolated mass gap black hole or neutron star detected with astrometric microlensing. Astrophys. J. Lett. 2022, 933, L23. [Google Scholar] [CrossRef]
- Mahy, L.; Sana, H.; Shenar, T.; Sen, K.; Langer, N.; Marchant, P.; Eldridge, C. Identifying quiescent compact objects in massive Galactic single-lined spectroscopic binaries. Astron. Astrophys. 2022, 664, A159. [Google Scholar] [CrossRef]
- Howil, K.; Kruszyńska, K.; Zieliński, P.; Bachelet, E.; Gromadzki, M.; Mikołajczyk, P.J.; Wicker, M. Uncovering the Invisible: A Study of Gaia18ajz, a Candidate Black Hole Revealed by Microlensing. Astron. Astrophys. 2025, 694, A94. [Google Scholar] [CrossRef]
- Casares, J.; Jonker, P.G. Mass Measurements of Stellar and Intermediate Mass Black-Holes. Space Sci. Rev. 2014, 183, 223–252. [Google Scholar] [CrossRef]
- Corral-Santana, J.M.; Casares, J.; Munoz-Darias, T.; Bauer, F.E.; Martinez-Pais, I.G.; Russell, D.M. BlackCAT: A catalogue of stellar-mass black holes in X-ray transients. Astron. Astrophys. 2016, 587, A61. [Google Scholar] [CrossRef]
- Laycock, S.G.T.; Maccarone, T.J.; Christodoulou, D.M. Revisiting the Dynamical Case for a Massive Black Hole in IC10 X-1. Mon. Not. R. Astron. Soc. 2015, 452, L31–L35. [Google Scholar] [CrossRef]
- Yungelson, L.R.; Lasota, J.P.; Nelemans, G.; Dubus, G.; Heuvel, E.P.J.v.; Dewi, J.; Zwart, S.P. The origin and fate of short-period low-mass black-hole binaries. Astron. Astrophys. 2006, 454, 559. [Google Scholar] [CrossRef]
- Kiel, P.D.; Hurley, J.R. Populating the Galaxy with low-mass X-ray binaries. Mon. Not. R. Astron. Soc. 2006, 369, 1152–1166. [Google Scholar] [CrossRef]
- El-Badry, K.; Rix, H.W.; Quataert, E.; Howard, A.W.; Isaacson, H.; Fuller, J.; Wojno, J. A Sun-like star orbiting a black hole. Mon. Not. R. Astron. Soc. 2023, 518, 1057–1085. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Simon, J.D.; Craig, P.A.; Reggiani, H.; Brandt, T.D.; Guhathakurta, P.; Dalba, P.A.; Kirby, E.N.; Chang, P.; Hey, D.R.; et al. A Noninteracting Galactic Black Hole Candidate in a Binary System with a Main-sequence Star. Astron. J. 2023, 166, 6. [Google Scholar] [CrossRef]
- Tanikawa, A.; Hattori, K.; Kawanaka, N.; Kinugawa, T.; Shikauchi, M.; Tsuna, D. Search for a Black Hole Binary in Gaia DR3 Astrometric Binary Stars with Spectroscopic Data. Astrophys. J. 2023, 946, 79. [Google Scholar] [CrossRef]
- El-Badry, K.; Rix, H.W.; Cendes, Y.; Rodriguez, A.C.; Conroy, C.; Quataert, E.; Faigler, S. A red giant orbiting a black hole. Mon. Not. R. Astron. Soc. 2023, 521, 4323–4348. [Google Scholar] [CrossRef]
- Panuzzo, P.; Mazeh, T.; Arenou, F.; Holl, B.; Caffau, E.; Jorissen, A.; Babusiaux, C.; Gavras, P.; Sahlmann, J.; Bastian, U.; et al. Discovery of a dormant 33 solar-mass black hole in pre-release Gaia astrometry. Astron. Astrophys. 2024, 686, L2. [Google Scholar] [CrossRef]
- An, Q.Y.; Huang, Y.; Gu, W.M.; Shao, Y.; Zhang, Z.X.; Yi, T.; Liu, J. A Be star-black hole binary with a wide orbit from LAMOST time-domain survey. arXiv 2025, arXiv:2505.23151. [Google Scholar] [CrossRef]
- Mashian, N.; Loeb, A. Hunting Black Holes with Gaia. Mon. Not. R. Astron. Soc. 2017, 470, 2611–2616. [Google Scholar] [CrossRef]
- Breivik, K.; Chatterjee, S.; Larson, S.L. Revealing black holes with Gaia. Astrophys. J. Lett. 2017, 850, L13. [Google Scholar] [CrossRef]
- Wiktorowicz, G.; Lu, Y.; Wyrzykowski, L.; Zhang, H.; Liu, J.; Justham, S.; Belczynski, K. Noninteracting Black Hole Binaries with Gaia and LAMOST. Astrophys. J. 2020, 905, 134. [Google Scholar] [CrossRef]
- Janssens, S.; Shenar, T.; Sana, H.; Faigler, S.; Langer, N.; Marchant, P.; Mazeh, T.; Schürmann, C.; Shahaf, S. Uncovering astrometric black hole binaries with massive main-sequence companions with Gaia. Astron. Astrophys. 2022, 658, A129. [Google Scholar] [CrossRef]
- Chawla, C.; Chatterjee, S.; Shah, N.; Breivik, K. Detecting Detached Black Hole Binaries through Photometric Variability. Astrophys. J. 2024, 975, 163. [Google Scholar] [CrossRef]
- Sahu, K.C.; Anderson, J.; Casertano, S.; Bond, H.E.; Udalski, A.; Dominik, M.; Steele, I.A. An Isolated Stellar-mass Black Hole Detected through Astrometric Microlensing. Astrophys. J. 2022, 933, 83. [Google Scholar] [CrossRef]
- Bennett, D.P.; Becker, A.C.; Quinn, J.L.; Tomaney, A.B.; Alcock, C.; Allsman, R.A.; Welch, D. Gravitational microlensing events due to stellar mass black holes. Astrophys. J. 2002, 579, 639–659. [Google Scholar] [CrossRef]
- Poindexter, S.; Afonso, C.; Bennett, D.P.; Glicenstein, J.F.; Gould, A.; Szymanski, M.K.; Udalski, A. Systematic analysis of 22 microlensing parallax candidates. Astrophys. J. 2005, 633, 914–930. [Google Scholar] [CrossRef]
- Wyrzykowski, L.; Mandel, I. Constraining the masses of microlensing black holes and the mass gap with Gaia DR2. Astron. Astrophys. 2020, 636, A20. [Google Scholar] [CrossRef]
- Shvartsman, V.F. Halos around “Black Holes”. Soviet Astron. 1971, 15, 377. [Google Scholar]
- Meszaros, P. Radiation from spherical accretion onto black holes. Astron. Astrophys. 1975, 44, 59–68. [Google Scholar]
- McDowell, J. Accretion radiation from nearby isolated black holes. Mon. Not. R. Astron. Soc. 1985, 217, 77–85. [Google Scholar] [CrossRef]
- Campana, S.; Pardi, M.C. Do molecular clouds contain accreting black holes? Astron. Astrophys. 1993, 277, 477. [Google Scholar]
- Fujita, Y.; Inoue, S.; Nakamura, T.; Manmoto, T.; Nakamura, K.E. Emission from isolated black holes and MACHOs accreting from the interstellar medium. Astrophys. J. Lett. 1998, 495, L85. [Google Scholar] [CrossRef]
- Tsuna, D.; Kawanaka, N.; Totani, T. X-ray Detectability of Accreting Isolated Black Holes in Our Galaxy. Mon. Not. R. Astron. Soc. 2018, 477, 791–801. [Google Scholar] [CrossRef]
- Kimura, S.S.; Kashiyama, K.; Hotokezaka, K. Multiwavelength Emission from Magnetically Arrested Disks around Isolated Black Holes. Astrophys. J. Lett. 2021, 922, L15. [Google Scholar] [CrossRef]
- Murchikova, L.; Sahu, K. Observability of Isolated Stellar-mass Black Holes. Astrophys. J. Lett. 2025, 988, L12. [Google Scholar] [CrossRef]
- Petrich, L.I.; Shapiro, S.L.; Stark, R.F.; Teukolsky, S.A. Accretion onto a Moving Black Hole: A Fully Relativistic Treatment. Astrophys. J. 1989, 336, 313–349. [Google Scholar] [CrossRef]
- Kaaz, N.; Murguia-Berthier, A.; Chatterjee, K.; Liska, M.T.P.; Tchekhovskoy, A. Jet Formation in 3D GRMHD Simulations of Bondi–Hoyle–Lyttleton Accretion. Astrophys. J. 2023, 950, 31. [Google Scholar] [CrossRef]
- Galishnikova, A.; Philippov, A.; Quataert, E.; Chatterjee, K.; Liska, M. Strongly Magnetized Accretion with Low Angular Momentum Produces a Weak Jet. Astrophys. J. 2025, 978, 148. [Google Scholar] [CrossRef]
- Kim, Y.; Most, E.R. General relativistic magnetized Bondi-Hoyle-Lyttleton accretion with a spin-field misalignment: Jet nutation, polarity reversals, and Magnus drag. Phys. Rev. D 2025, 111, 083025. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Cavalieri, R. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Bossilkov, V. GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo during the Second Part of the Third Observing Run. Phys. Rev. X 2023, 13, 041039. [Google Scholar] [CrossRef]
- Bailyn, C.D.; Jain, R.K.; Coppi, P.; Orosz, J.A. The Mass distribution of stellar black holes. Astrophys. J. 1998, 499, 367. [Google Scholar] [CrossRef]
- Ozel, F.; Psaltis, D.; Narayan, R.; McClintock, J.E. The Black Hole Mass Distribution in the Galaxy. Astrophys. J. 2010, 725, 1918–1927. [Google Scholar] [CrossRef]
- Farr, W.M.; Sravan, N.; Cantrell, A.; Kreidberg, L.; Bailyn, C.D.; Mandel, I.; Kalogera, V. The Mass Distribution of Stellar-Mass Black Holes. Astrophys. J. 2011, 741, 103. [Google Scholar] [CrossRef]
- Fryer, C.L.; Belczynski, K.; Wiktorowicz, G.; Dominik, M.; Kalogera, V.; Holz, D.E. Compact Remnant Mass Function: Dependence on the Explosion Mechanism and Metallicity. Astrophys. J. 2012, 749, 91. [Google Scholar] [CrossRef]
- Belczynski, K.; Wiktorowicz, G.; Fryer, C.; Holz, D.; Kalogera, V. Missing Black Holes Unveil The Supernova Explosion Mechanism. Astrophys. J. 2012, 757, 91. [Google Scholar] [CrossRef]
- Fryer, C.L.; Olejak, A.; Belczynski, K. The Effect of Supernova Convection On Neutron Star and Black Hole Masses. Astrophys. J. 2022, 931, 94. [Google Scholar] [CrossRef]
- Podsiadlowski, P.; Langer, N.; Poelarends, A.J.T.; Rappaport, S.; Heger, A.; Pfahl, E. The effects of binary evolution on the dynamics of core collapse and neutron-star kicks. Astrophys. J. 2004, 612, 1044–1051. [Google Scholar] [CrossRef]
- Mandel, I.; Müller, B. Simple recipes for compact remnant masses and natal kicks. Mon. Not. R. Astron. Soc. 2020, 499, 3214–3221. [Google Scholar] [CrossRef]
- Burrows, A.; Wang, T.; Vartanyan, D.; Coleman, M.S.B. A Theory for Neutron Star and Black Hole Kicks and Induced Spins. Astrophys. J. 2024, 963, 63. [Google Scholar] [CrossRef]
- Fryer, C.L.; Kalogera, V. Theoretical black hole mass distributions. Astrophys. J. 2001, 554, 548–560. [Google Scholar] [CrossRef]
- Siegel, J.C.; Kiato, I.; Kalogera, V.; Berry, C.P.; Maccarone, T.J.; Breivik, K.; Zapartas, E. Investigating the Lower Mass Gap with Low-mass X-Ray Binary Population Synthesis. Astrophys. J. 2023, 954, 212. [Google Scholar] [CrossRef]
- Kreidberg, L.; Bailyn, C.D.; Farr, W.M.; Kalogera, V. Mass Measurements of Black Holes in X-Ray Transients: Is There a Mass Gap? Astrophys. J. 2012, 757, 36. [Google Scholar] [CrossRef]
- Farah, A.M.; Fishbach, M.; Essick, R.; Holz, D.E.; Galaudage, S. Bridging the Gap: Categorizing Gravitational-wave Events at the Transition between Neutron Stars and Black Holes. Astrophys. J. 2022, 931, 108. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Bose, N. Population of Merging Compact Binaries Inferred Using Gravitational Waves through GWTC-3. Phys. Rev. X 2023, 13, 011048. [Google Scholar] [CrossRef]
- Abac, A.G.; Abbott, R.; Abouelfettouh, I.; Acernese, F.; Ackley, K.; Adhicary, S.; Blagg, L.A. Observation of Gravitational Waves from the Coalescence of a 2.5–4.5 M ⊙ Compact Object and a Neutron Star. Astrophys. J. Lett. 2024, 970, L34. [Google Scholar] [CrossRef]
- Ray, A.; Farr, W.; Kalogera, V. Hiding Out at the Low End: No Gap and a Peak in the Black-Hole Mass Spectrum. arXiv 2025, arXiv:2507.09099. [Google Scholar] [CrossRef]
- Fishbach, M.; Breivik, K.; Willcox, R.; van Son, L.A.C. Where are Gaia’s small black holes? arXiv 2025, arXiv:2508.08986. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, X.; Feng, F.; Ge, H.; Shao, Y.; Cui, Y.; Liu, J. A potential mass-gap black hole in a wide binary with a circular orbit. Nat. Astron. 2024, 8, 1583–1591. [Google Scholar] [CrossRef]
- Novikov, I.D.; Thorne, K.S. Astrophysics of black holes. In Black Holes; De Witt, C., De Witt, B., Eds.; Gordon and Breach: New York, NY, USA, 1973; pp. 343–450. [Google Scholar]
- Page, D.N.; Thorne, K.S. Disk-Accretion onto a Black Hole. Time-Averaged Structure of Accretion Disk. Astrophys. J. 1974, 191, 499–506. [Google Scholar] [CrossRef]
- Thorne, K.S. Disk accretion onto a black hole. 2. Evolution of the hole. Astrophys. J. 1974, 191, 507–520. [Google Scholar] [CrossRef]
- Li, L.X.; Zimmerman, E.R.; Narayan, R.; McClintock, J.E. Multi-temperature blackbody spectrum of a thin accretion disk around a Kerr black hole: Model computations and comparison with observations. Astrophys. J. Suppl. 2005, 157, 335–370. [Google Scholar] [CrossRef]
- Agol, E.; Krolik, J. Magnetic stress at the marginally stable orbit: Altered disk structure, radiation, and black hole spin evolution. Astrophys. J. 2000, 528, 161–170. [Google Scholar] [CrossRef]
- Mummery, A. Black hole-disc coevolution in the presence of magnetic fields: Refining the Thorne limit with emission from within the plunging region. Mon. Not. R. Astron. Soc. 2025, 537, 1963–1972. [Google Scholar] [CrossRef]
- Woosley, S.E.; Bloom, J.S. The Supernova Gamma-Ray Burst Connection. Ann. Rev. Astron. Astrophys. 2006, 44, 507–556. [Google Scholar] [CrossRef]
- Yoon, S.C.; Langer, N.; Norman, C. Single star progenitors of long gamma-ray bursts. 1. Model grids and redshift dependent GRB rate. Astron. Astrophys. 2006, 460, 199. [Google Scholar] [CrossRef]
- King, A.R.; Kolb, U. The evolution of black hole mass and angular momentum. Mon. Not. R. Astron. Soc. 1999, 305, 654. [Google Scholar] [CrossRef]
- Valsecchi, F.; Glebbeek, E.; Farr, W.M.; Fragos, T.; Willems, B.; Orosz, J.A.; Liu, J.; Kalogera, V. Formation of the black-hole binary M33 X-7 via mass-exchange in a tight massive system. Nature 2010, 468, 77. [Google Scholar] [CrossRef] [PubMed]
- Wong, T.W.; Valsecchi, F.; Fragos, T.; Kalogera, V. Understanding Compact Object Formation and Natal Kicks. III. The case of Cygnus X-1. Astrophys. J. 2012, 747, 111. [Google Scholar] [CrossRef]
- Fragos, T.; McClintock, J.E. The Origin of Black Hole Spin in Galactic Low-Mass X-ray Binaries. Astrophys. J. 2015, 800, 17. [Google Scholar] [CrossRef]
- Qin, Y.; Marchant, P.; Fragos, T.; Meynet, G.; Kalogera, V. On the Origin of Black-Hole Spin in High-Mass X-ray Binaries. Astrophys. J. Lett. 2019, 870, L18. [Google Scholar] [CrossRef]
- Zhang, S.N.; Cui, W.; Chen, W. Black hole spin in X-ray binaries: Observational consequences. Astrophys. J. Lett. 1997, 482, L155. [Google Scholar] [CrossRef]
- McClintock, J.E.; Narayan, R.; Steiner, J.F. Black Hole Spin via Continuum Fitting and the Role of Spin in Powering Transient Jets. Space Sci. Rev. 2014, 183, 295–322. [Google Scholar] [CrossRef]
- Brenneman, L.W.; Reynolds, C.S. Constraining Black Hole Spin via X-ray Spectroscopy. Astrophys. J. 2006, 652, 1028–1043. [Google Scholar] [CrossRef]
- Dauser, T.; Garcia, J.; Wilms, J.; Bock, M.; Brenneman, L.W.; Falanga, M.; Fukumura, K.; Reynolds, C.S. Irradiation of an Accretion Disc by a Jet: General Properties and Implications for Spin Measurements of Black Holes. Mon. Not. R. Astron. Soc. 2013, 430, 1694. [Google Scholar] [CrossRef]
- Bambi, C.; Brenneman, L.W.; Dauser, T.; Garcia, J.A.; Grinberg, V.; Ingram, A.; Zdziarski, A.A. Towards Precision Measurements of Accreting Black Holes Using X-Ray Reflection Spectroscopy. Space Sci. Rev. 2021, 217, 65. [Google Scholar] [CrossRef]
- Draghis, P.A.; Miller, J.M.; Zoghbi, A.; Reynolds, M.; Costantini, E.; Gallo, L.C.; Tomsick, J.A. A Systematic View of Ten New Black Hole Spins. Astrophys. J. 2023, 946, 19. [Google Scholar] [CrossRef]
- Fishbach, M.; Kalogera, V. Apples and Oranges: Comparing Black Holes in X-Ray Binaries and Gravitational-wave Sources. Astrophys. J. Lett. 2022, 929, L26. [Google Scholar] [CrossRef]
- Zdziarski, A.A.; Marcel, G.; Veledina, A.; Olejak, A.; Lancova, D. Spins of Black Holes in X-ray Binaries and the Tension with the Gravitational Wave Measurements. arXiv 2025, arXiv:2506.00623. [Google Scholar] [CrossRef]
- Draghis, P.A.; Miller, J.M.; Costantini, E.; Gallo, L.C.; Reynolds, M.; Tomsick, J.A.; Zoghbi, A. Systematically Revisiting All NuSTAR Spins of Black Holes in X-Ray Binaries. Astrophys. J. 2024, 969, 40. [Google Scholar] [CrossRef]
- Shashank, S.; Abdikamalov, A.B.; Liu, H.; Nosirov, A.; Bambi, C.; Dihingia, I.K.; Mizuno, Y. Measuring black hole spins with X-ray reflection spectroscopy: A GRMHD outlook. arXiv 2025, arXiv:2507.02583. [Google Scholar] [CrossRef]
- Bambi, C. Testing black hole candidates with electromagnetic radiation. Rev. Mod. Phys. 2017, 89, 025001. [Google Scholar] [CrossRef]
- Bambi, C.; Cardenas-Avendano, A. Recent Progress on Gravity Tests. Challenges and Future Perspectives; Springer: Singapore, 2024; ISBN 978-981-97-2870-1/978-981-97-2873-2/978-981-97-2871-8. [Google Scholar] [CrossRef]
- Bambi, C.; Cardenas-Avendano, A.; Dauser, T.; Garcia, J.A.; Nampalliwar, S. Testing the Kerr black hole hypothesis using X-ray reflection spectroscopy. Astrophys. J. 2017, 842, 76. [Google Scholar] [CrossRef]
- Abdikamalov, A.B.; Ayzenberg, D.; Bambi, C.; Dauser, T.; Garcia, J.A.; Nampalliwar, S. Public Release of RELXILL_NK: A Relativistic Reflection Model for Testing Einstein’s Gravity. Astrophys. J. 2019, 878, 91. [Google Scholar] [CrossRef]
- Abdikamalov, A.B.; Ayzenberg, D.; Bambi, C.; Dauser, T.; Garcia, J.A.; Nampalliwar, S.; Tripathi, A.; Zhou, M. Testing the Kerr black hole hypothesis using X-ray reflection spectroscopy and a thin disk model with finite thickness. Astrophys. J. 2020, 899, 80. [Google Scholar] [CrossRef]
- Zhou, M.; Abdikamalov, A.B.; Ayzenberg, D.; Bambi, C.; Liu, H.; Nampalliwar, S. XSPEC model for testing the Kerr black hole hypothesis using the continuum-fitting method. Phys. Rev. D 2019, 99, 104031. [Google Scholar] [CrossRef]
- Tripathi, A.; Zhang, Y.; Abdikamalov, A.B.; Ayzenberg, D.; Bambi, C.; Jiang, J.; Liu, H.; Zhou, M. Testing General Relativity with NuSTAR data of Galactic Black Holes. Astrophys. J. 2021, 913, 79. [Google Scholar] [CrossRef]
- Tripathi, A.; Abdikamalov, A.B.; Ayzenberg, D.; Bambi, C.; Grinberg, V.; Zhou, M. Testing the Kerr Black Hole Hypothesis with GX 339–4 by a Combined Analysis of Its Thermal Spectrum and Reflection Features. Astrophys. J. 2021, 907, 31. [Google Scholar] [CrossRef]
- Tripathi, A.; Abdikamalov, A.B.; Ayzenberg, D.; Bambi, C.; Grinberg, V.; Liu, H.; Zhou, M. Testing the Kerr black hole hypothesis with the continuum-fitting and the iron line methods: The case of GRS 1915+105. JCAP 2022, 01, 019. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, H.; Abdikamalov, A.B.; Ayzenberg, D.; Bambi, C.; Zhou, M. Testing the Kerr Black Hole Hypothesis with GRS 1716-249 by Combining the Continuum Fitting and the Iron-line Methods. Astrophys. J. 2022, 924, 72. [Google Scholar] [CrossRef]
- Bambi, C. Testing Gravity with Black Hole X-Ray Data. In Recent Progress on Gravity Tests. Challenges and Future Perspectives; Bambi, C., Cardenas-Avendano, A., Eds.; Springer: Singapore, 2024; pp. 149–182. [Google Scholar] [CrossRef]
- Shashank, S.; Bambi, C. Constraining the Konoplya-Rezzolla-Zhidenko deformation parameters III: Limits from stellar-mass black holes using gravitational-wave observations. Phys. Rev. D 2022, 105, 104004. [Google Scholar] [CrossRef]
- Das, D.; Shashank, S.; Bambi, C. Non-Kerr constraints using binary black hole inspirals considering phase modifications up to 4 PN order. Eur. Phys. J. C 2024, 84, 1237. [Google Scholar] [CrossRef]
- Yunes, N.; Yagi, K.; Pretorius, F. Theoretical Physics Implications of the Binary Black-Hole Mergers GW150914 and GW151226. Phys. Rev. D 2016, 94, 084002. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Cerretani, G. Tests of general relativity with GW150914. Phys. Rev. Lett. 2016, 116, 221101, Erratum in Phys. Rev. Lett. 2018, 121, 129902. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Cahillane, C. Tests of General Relativity with the Binary Black Hole Signals from the LIGO-Virgo Catalog GWTC-1. Phys. Rev. D 2019, 100, 104036. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Brillet, A. Tests of general relativity with binary black holes from the second LIGO-Virgo gravitational-wave transient catalog. Phys. Rev. D 2021, 103, 122002. [Google Scholar] [CrossRef]
- Abbott, R.; Abe, H.; Acernese, F.; Ackley, K.; Adhikari, N.; Adhikari, R.X.; Boër, M. Tests of General Relativity with GWTC-3. arXiv 2021, arXiv:2112.06861. [Google Scholar] [CrossRef]
- Das, D.; Roy, S.; Sengupta, A.S.; Bambi, C. Probing missing physics from inspiralling compact binaries via time-frequency tracks. arXiv 2025, arXiv:2507.21566. [Google Scholar] [CrossRef]
- Colleoni, M.; Krishnendu, N.V.; Mourier, P.; Bera, S.; Jiménez-Forteza, X. Testing Gravity with Binary Black Hole Gravitational Waves. In Recent Progress on Gravity Tests. Challenges and Future Perspectives; Bambi, C., Cardenas-Avendano, A., Eds.; Springer: Singapore, 2024; pp. 239–274. [Google Scholar] [CrossRef]
- Bambi, C. An interstellar mission to test astrophysical black holes. iScience 2025, 28, 113142. [Google Scholar] [CrossRef]
- Lubin, P. A Roadmap to Interstellar Flight. J. Br. Interplanet. Soc. 2016, 69, 40–72. [Google Scholar]
- Lubin, P. The Path to Transformational Space Exploration; World Scientific Publishing Company: Singapore, 2022; ISBN 978-981-12-4903-7/978-981-12-4828-3. [Google Scholar] [CrossRef]
- Lin, J.Y.; de Sterke, C.M.; Ilic, O.; Kuhlmey, B.T. Photonic Lightsails: Fast and Stable Propulsion for Interstellar Travel. arXiv 2025, arXiv:2502.17828. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bambi, C. Stellar-Mass Black Holes. Symmetry 2025, 17, 1393. https://doi.org/10.3390/sym17091393
Bambi C. Stellar-Mass Black Holes. Symmetry. 2025; 17(9):1393. https://doi.org/10.3390/sym17091393
Chicago/Turabian StyleBambi, Cosimo. 2025. "Stellar-Mass Black Holes" Symmetry 17, no. 9: 1393. https://doi.org/10.3390/sym17091393
APA StyleBambi, C. (2025). Stellar-Mass Black Holes. Symmetry, 17(9), 1393. https://doi.org/10.3390/sym17091393






