Symmetry-Aware Short-Term Load Forecasting in Distribution Networks: A Synergistic Enhanced KMA-MVMD-Crossformer Framework
Abstract
1. Introduction
- The proposed EnKMA-MVMD modal decomposition method, which considers the minimum average envelope entropy, effectively extracts periodic and symmetric characteristics of state changes. It demonstrates higher accuracy in corresponding prediction models compared to other modal decomposition methods, validating the effectiveness of the EnKMA-MVMD approach in preserving symmetry.
- The MVRapidMIC feature extraction algorithm used in this paper not only speeds up training but also further enhances prediction accuracy by capturing symmetric feature correlations.
- Introducing the Crossformer prediction model into power distribution network short-term load forecasting significantly improves the accuracy and robustness of load predictions by leveraging its symmetry-aware mechanisms for capturing feature and temporal correlations.
- In simulations, the method proposed in this paper has been proven effective and demonstrates strong generalizability in preserving and utilizing symmetry patterns.
2. Enhanced Komodo Mlipir Algorithm Optimization
2.1. Komodo Mlipir Algorithm Optimization
- Setting the number of Komodo dragon individuals , the proportion of adult males , and the mlipir rate;
- Randomly creating Komodo dragon individuals, which then evolve. Evolution stops once the predetermined criteria are met;
- All individuals are evaluated and ranked based on body mass and optimization objectives. They are divided into three groups according to Equations (1) and (2): high-mass adult males, one medium-mass female, and low-mass juvenile males [30];
- Each adult male moves according to (3), retaining optimal positions for survival in the next generation [30].where and represent the fitness of the jth and ith large male individuals, respectively; represents the movement distance from the ith to the jth large male individual; and represent the position vectors of the jth and ith large male individuals, respectively; and are random numbers from a normal distribution in the interval (0, 1); q represents the number of large male individuals; represents the new position of the large male individual after movement.
- 5.
- Finally, population size is adaptively updated via Equation (7). The algorithm terminates by returning the highest-quality individuals as the global optimal solution upon meeting convergence criteria. This social stratum-based dynamic division of labor and collaborative optimization mechanism implies symmetrical balance in population structure—through complementary behaviors of high-, middle-, and low-stratum individuals, it achieves symmetrical regulation of global exploration and local development, supporting stable algorithm convergence [30].where represents the number of individuals to be removed or generated; represents the number of newly generated individuals; and are the differences in fitness between the consecutive ith and (i − 1)th generations, respectively. Here, the value of is set to 5, indicating a smaller population size used in the first stage. Additionally, the initial value, minimum value, and maximum value of should also be determined accordingly.
2.2. Logistic Chaotic Mapping for Particle Initialization
2.3. Introducing Time-Varying Inertia Weight Strategy and Female Movement
2.4. Tent Chaos Mapping Perturbation Strategy
- Set the chaos search count t to a starting value of 0 and a maximum value k. Generate a random number m within (0, d] to indicate chaos search in the mth dimension, and a random variable within (0, 1);
- Use Tent chaos mapping to generate a chaotic variable , creating a local solution around the ith individual in the jth dimension;
- Check if meets constraint conditions, ensuring it falls within the specified range;
- Calculate the fitness of . If the local solution is better than the original, replace the original solution with the local solution; otherwise, return to step 2. If t reaches the maximum chaos count (t < k) without producing a solution better than the original, discard the local solution and keep the original solution.
2.5. Hyperparameter Tuning for EnKMA
- Logistic Chaotic Mapping Parameter: The control parameter μ in the Logistic chaotic mapping (8 is set to 3.9, a value widely recognized to ensure strong chaotic behavior and uniform traversal of the solution space [32]. Sensitivity analysis shows that μ < 3.5 leads to premature convergence due to insufficient randomness, while μ > 4.0 causes excessive chaos, disrupting the symmetry of population distribution.
- Time-Varying Inertia Weights: The initial and final values of inertia weights (w1, w2, w3) in Equations (9)–(11) are critical for adaptive search. w1 is tuned to decrease from 1.0 to 1/3, while w2 and w3 increase from 0 to 1/3, ensuring global exploration in early iterations and local refinement in later stages. Deviations from this range result in premature trapping in local optima, increasing the average envelope entropy by up to 12% in validation experiments.
- Population Adaptation Parameters: The parameter λ in Equation (7) (set to 5) regulates population size dynamics. A smaller λ (e.g., λ = 2) slows population adaptation, prolonging training time by 30% without accuracy gains, while a larger λ (e.g., λ = 8) causes unstable population fluctuations, reducing decomposition stability.
3. EnKMA-MVMD for Power Distribution Network Load Decomposition and MVRapidMIC Feature Analysis/Data Preprocessing Method
3.1. MVMD Algorithm
3.2. MVMD Decomposition Algorithm for Power Distribution Network Load Sequences Based on EnKMA
3.3. Feature Analysis Method Based on MVRapidMIC
4. EnKMA-MVMD-Crossformer Based Method for Short-Term Load Forecasting in Power Distribution Networks
4.1. Crossformer Prediction Model
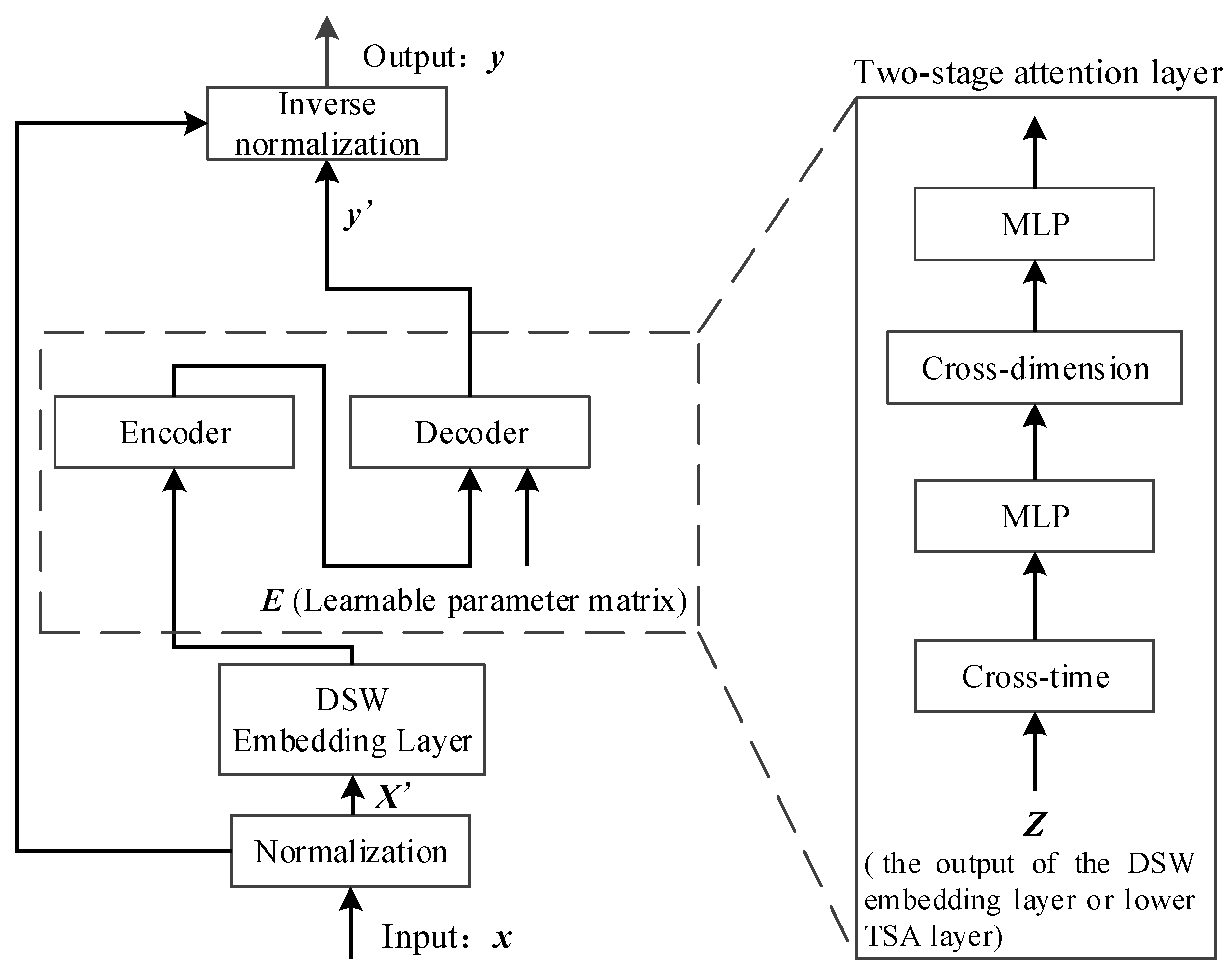
4.1.1. DSW Embedding Layer
4.1.2. TSA Layer
- A.
- Cross-Time Stage
- B.
- Cross-Dimension Stage
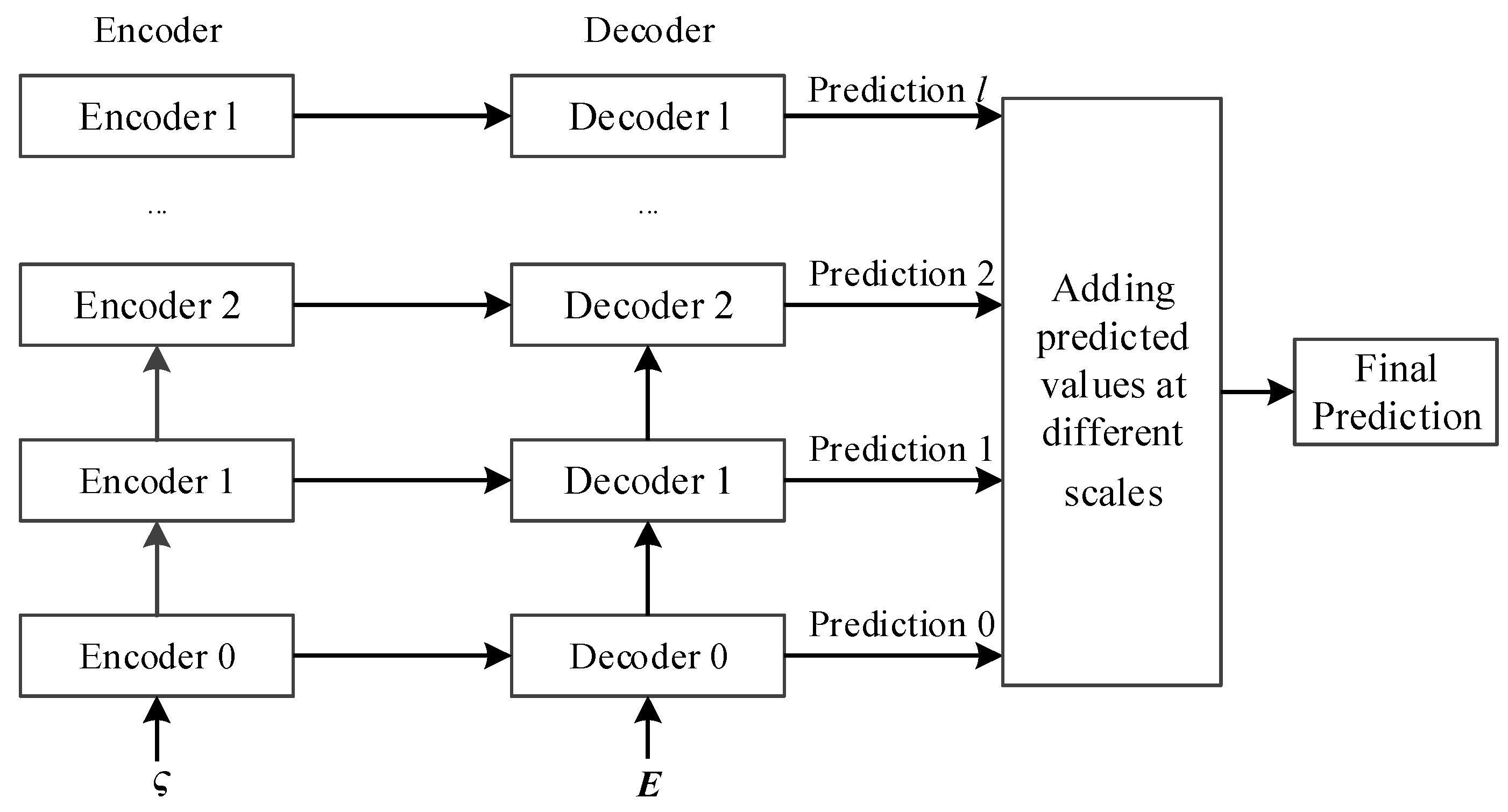
4.1.3. Hierarchical Encoder–Decoder
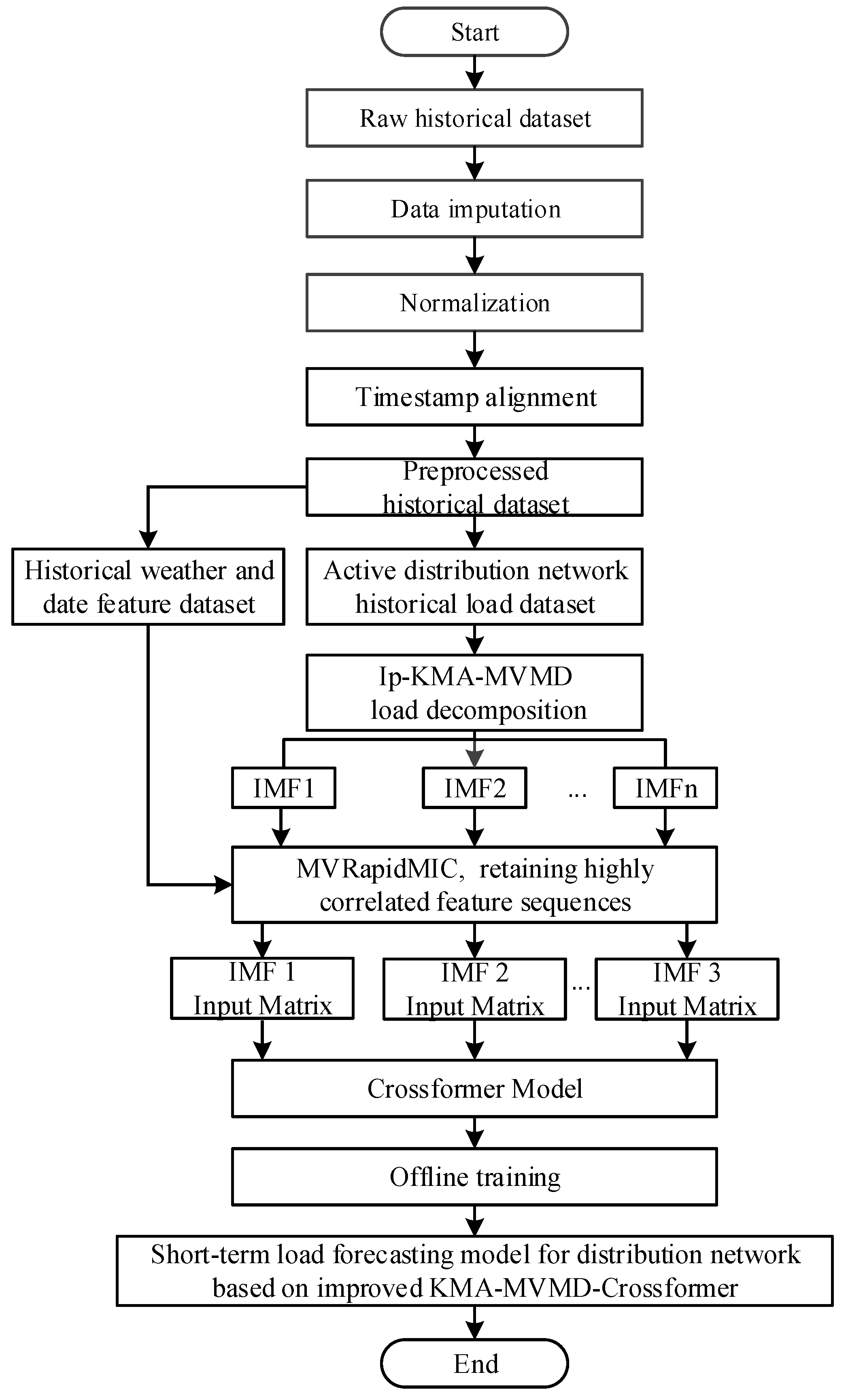
4.2. Short-Term Load Forecasting Method for Power Distribution Networks Based on EnKMA-MVMD-Crossformer
- Firstly, for missing data in the power distribution network load dataset, the average value of six data points before and after the sampling point is taken for completion.
- The Z-score algorithm [39] is used for normalization to ensure balanced data distribution.
- For the alignment of timestamps in the dataset, spline interpolation is employed.
- The En-KMA-MVMD algorithm is used to decompose the power distribution network load sequence into a series of relatively stable IMFs.
- The mutual information coefficients between weather, date features, and the power distribution network load sequence are calculated. Strongly correlated features are retained, and the remaining features are filtered out. Weather features include temperature, cumulative temperature effect, relative humidity, visibility, atmospheric pressure, wind speed, cloud cover, wind direction, and precipitation intensity (nine categories in total); date features include month, day, hour, week type, and holidays (five categories in total). The definition of the input feature sequence is shown in Table 1. For feature sequences H2~H11, the MVRapidMIC algorithm’s multivariate-single variable mode is used for correlation analysis, while for other features, the MVRapidMIC algorithm’s single variable-single variable mode is used.
- The decomposed load IMFs are combined with weather and date features. A feature matrix is established for each mode of the load sequence, and the feature matrices are independently input into the Crossformer model for offline training.
- Finally, a short-term load forecasting model for power distribution networks based on the EnKMA-MVMD-Crossformer is obtained.
4.3. Discussion on AI Model Architectures
4.3.1. LSTM Architecture
4.3.2. Analysis of Transformer Architecture
4.3.3. Discussion on En—Crossformer Architecture
5. Simulations
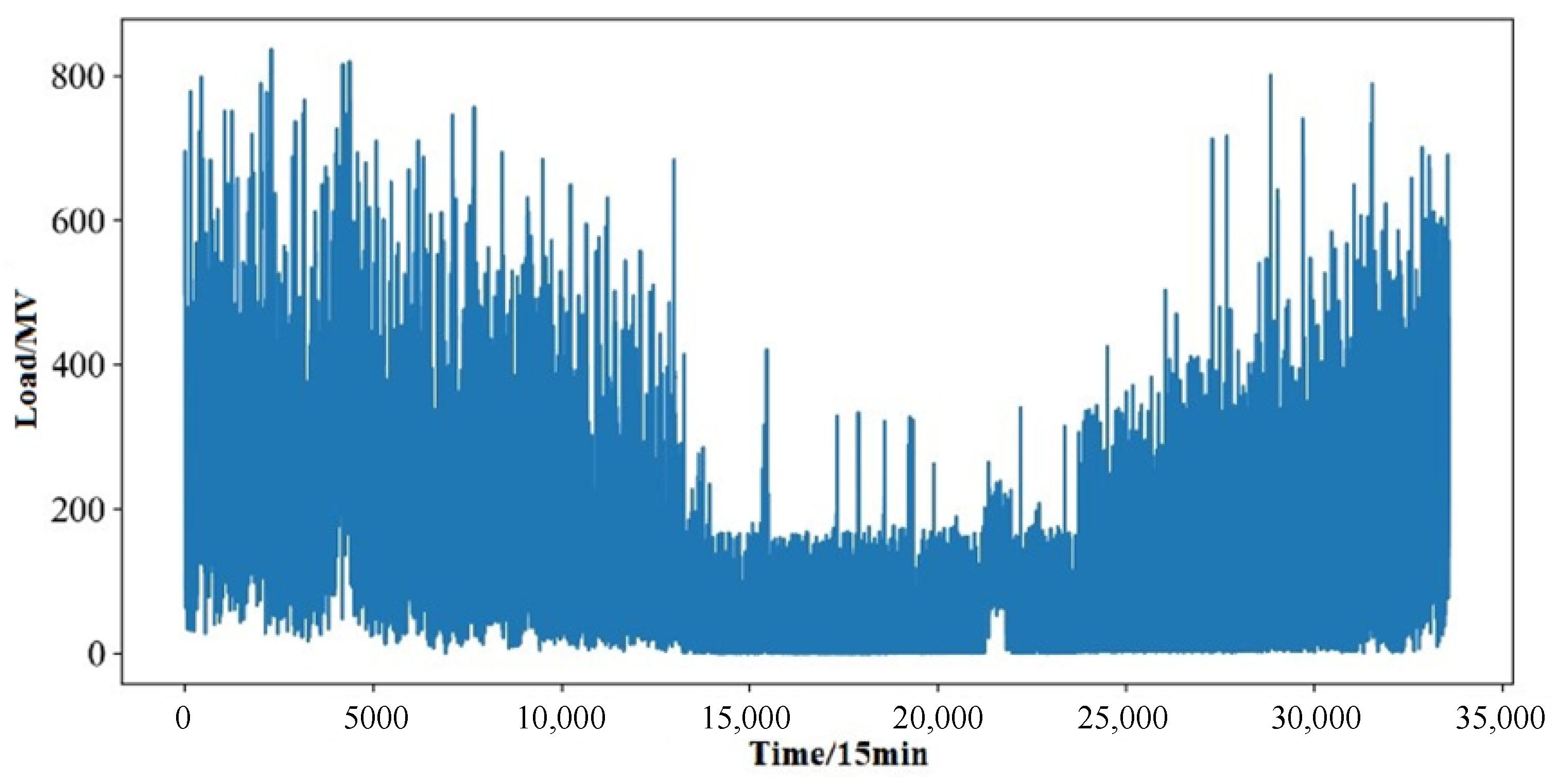
5.1. Decomposition Results of Power Distribution Network Load Sequence
5.2. Dimensionality Reduction in Weather and Date Features
5.3. Comparison with Different Forecasting Models
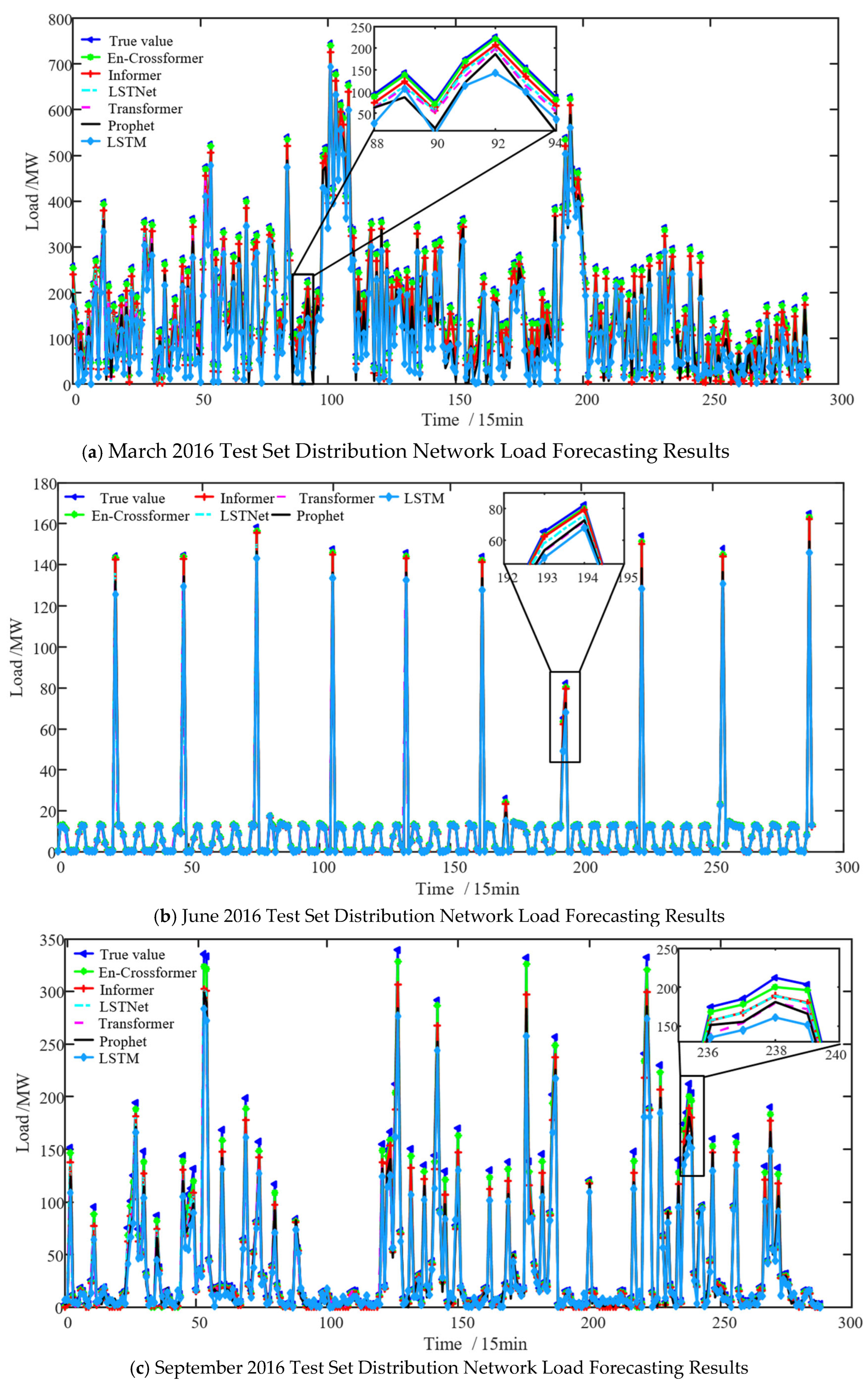
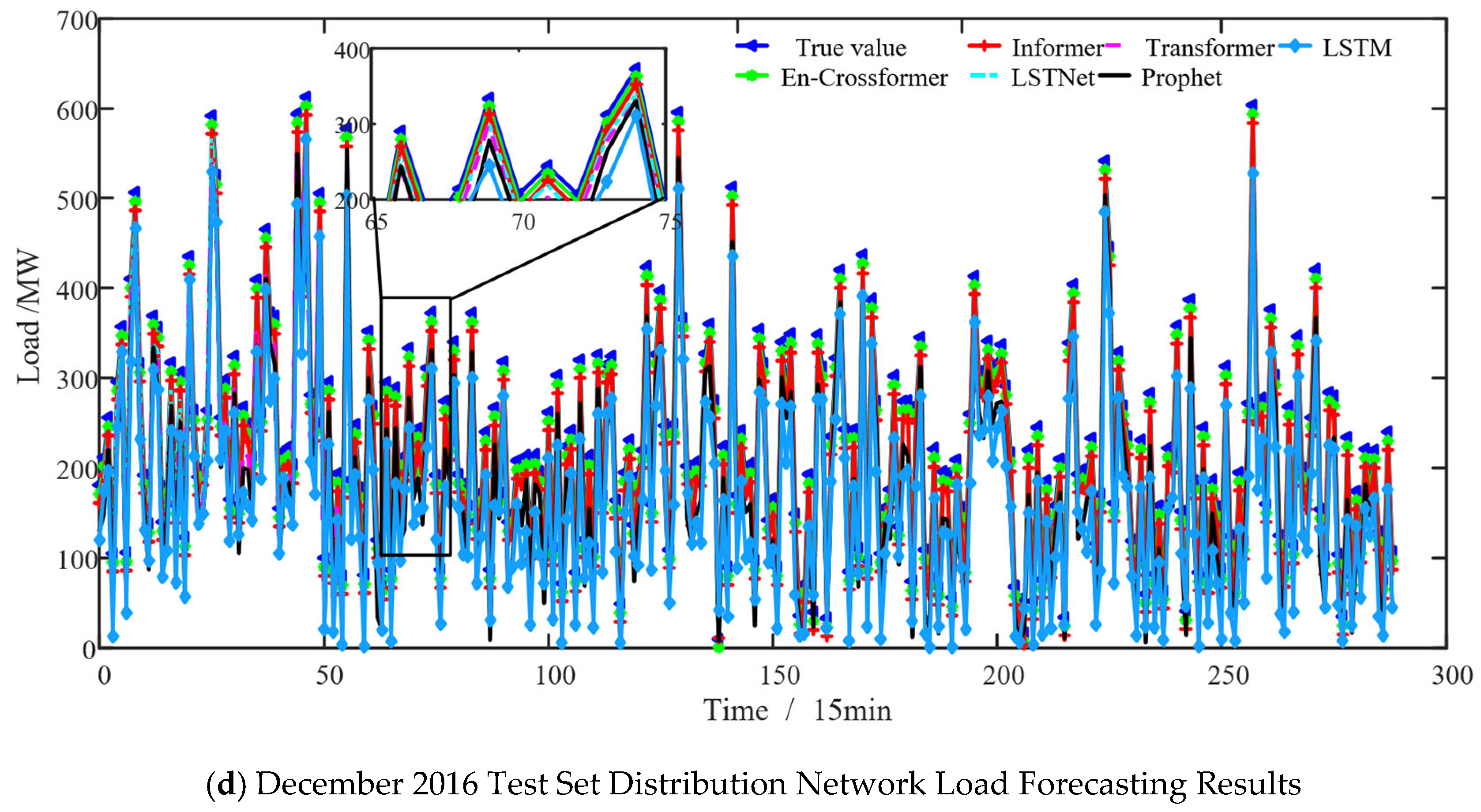
5.3.1. Comparison with Baseline Models
- Training set: RMSE = 12.36 MW, MAE = 11.52 MW, MAPE = 4.21%, R2 = 0.9965. The low errors indicate effective learning of load patterns, including symmetric temporal correlations and multi-scale features.
- Validation set: RMSE = 13.89MkW, MAE = 12.75 MW, MAPE = 4.58%, R2 = 0.9952. Performance is slightly lower than the training set but stable, confirming the model avoids overfitting through hyperparameter tuning (e.g., dropout rate = 0.2).
- Test set: RMSE = 14.76 MW, MAE = 13.97 MW, MAPE = 4.89%, R2 = 0.9942. The small gap between validation and test results demonstrates strong generalization, validating the model’s robustness in unseen scenarios.
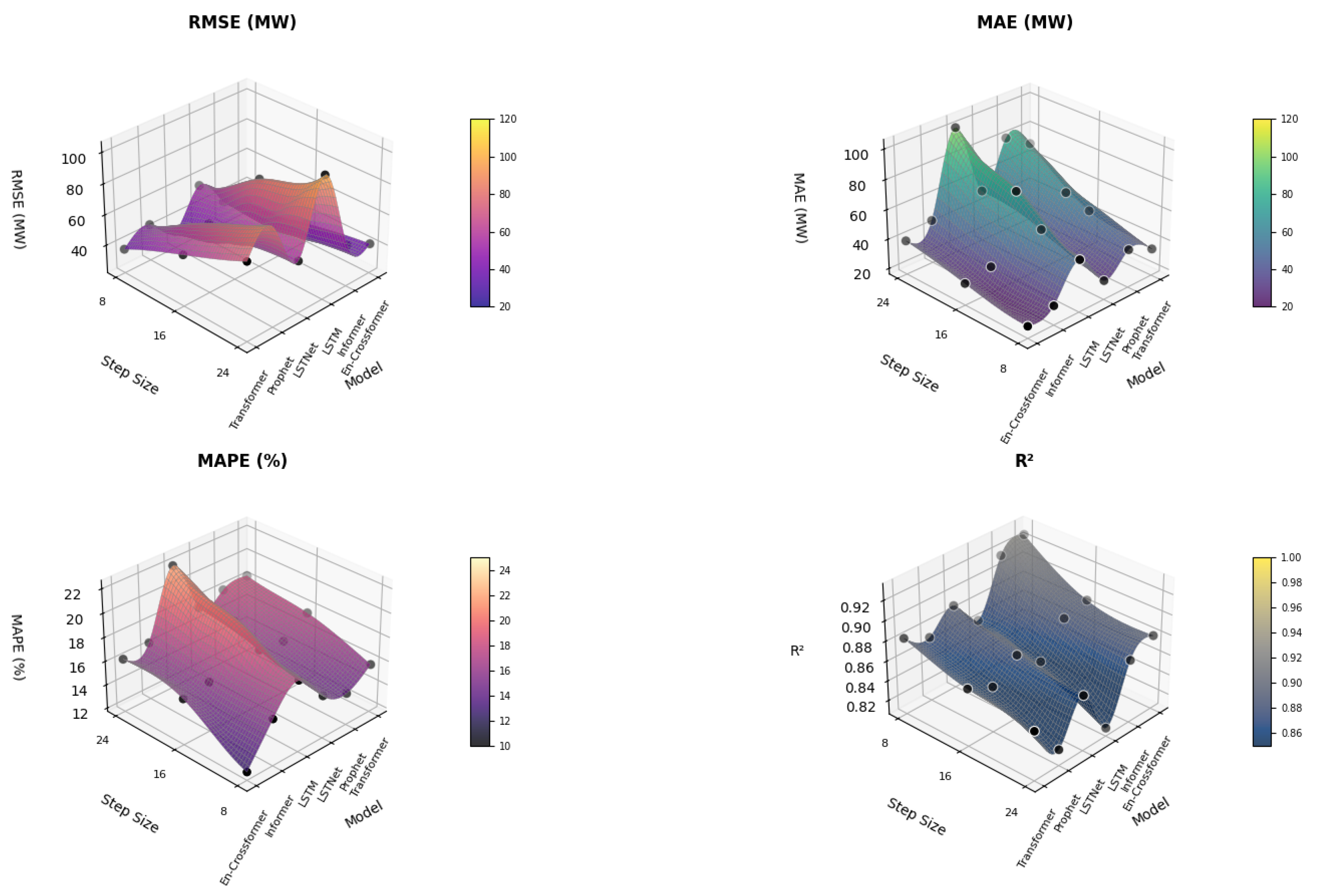
5.3.2. Comparison of Different Prediction Step Lengths
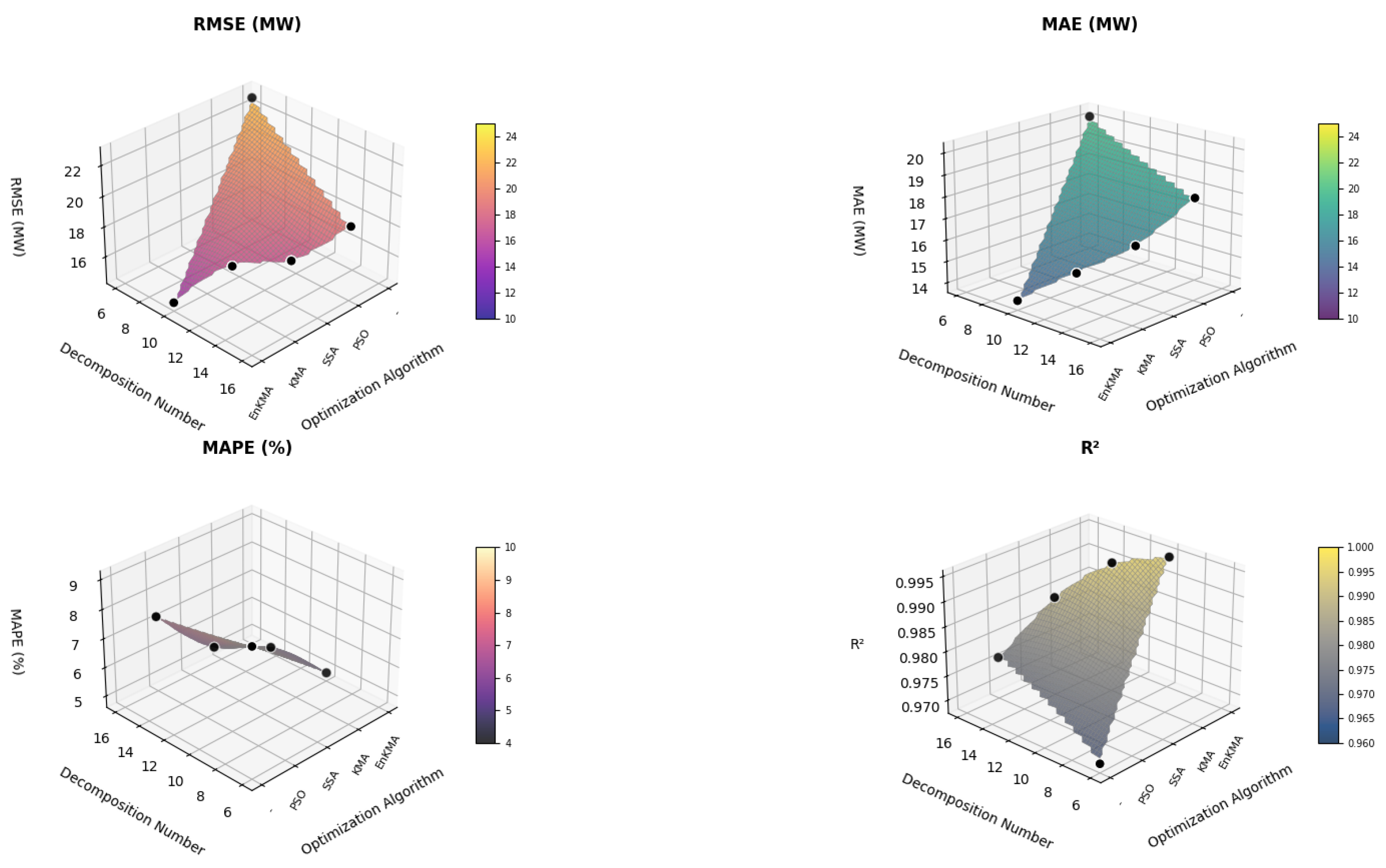
5.4. Comparison of Prediction Results Using Different Optimization Algorithms
5.5. Comparison of Prediction Results Using Different Decomposition Algorithms
5.6. Comparison of Prediction Results Using Different Feature Analysis Algorithms
5.7. Ablation Experiments
- A sole Transformer prediction model (baseline model);
- DSW-Transformer prediction model;
- DSW-TSA-Transformer prediction model;
- DSW-HED-Transformer prediction model;
- Crossformer (DSW-TSA-HED-Transformer) prediction model.
5.8. Hyperparameter Sensitivity Analysis
5.9. Empirical Validation of EnKMA Innovations
5.10. Benchmark Model Testing
5.10.1. Compare with Advanced Algorithms
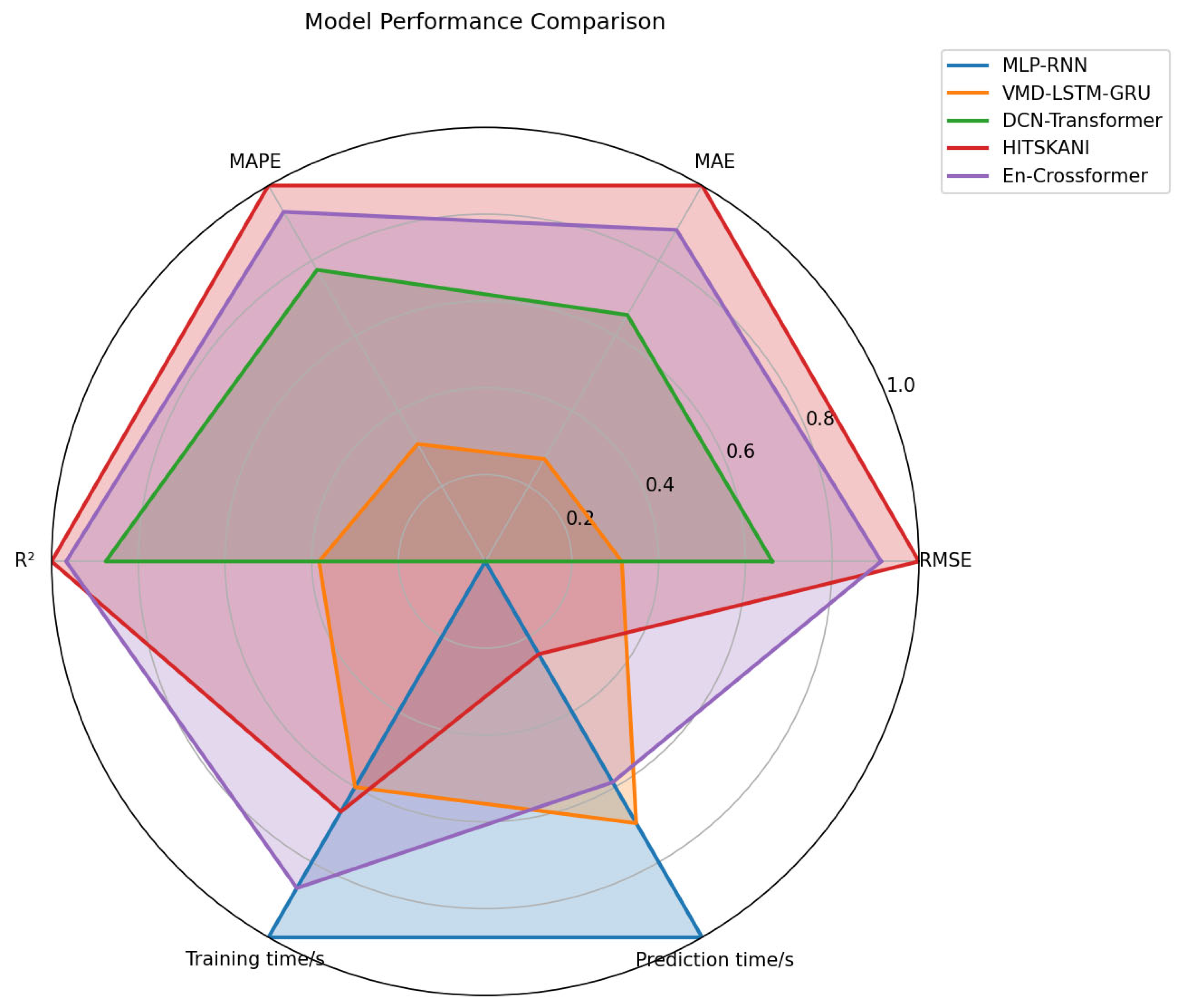
- Error index: The vRMSE of the proposed model is 10.2387 MW, which is reduced by more than 62% compared with MLP-RNN (38.2181 MW), but there is still a certain gap compared with HITSKANI (7.4641 MW). The vMAE was 9.3228 MW, which was reduced by more than 50% compared with VMD-LSTM-GRU (29.2939 MW). The vape is 4.74%, which is much better than that of traditional models (such as MLP-RNN being 16.49%), and the relative deviation is controllable.
- Fit degree: R2 reaches 0.9946, which can explain over 99.4% of load fluctuations, but there is still a certain gap in the level of HITSKANI (0.9945).
- The training time: EnKMA-MVMD-Crossformer is only 182.28 s, which is over 71% less than that of DCN-Transformer (605.92 s). This is because EnKMA optimizes MVMD parameters and Crossformer effectively handles long sequences, balancing accuracy and efficiency.
- Prediction time: The prediction time is 23.34 s, which is nearly 50% shorter than that of DCN-Transformer (41.97 s), meeting the high-efficiency requirements of real-time dispatching in power systems.
- Compared with traditional models, it has significant advantages in accuracy indicators and solves the fitting problem of complex loads.
- On the USD dataset used in this study (2016, 50 randomly selected apartments, 15 min resolution), the En-Crossformer model achieves an MAE of 9.3228 MW and a MAPE of 4.74%. Although there is a gap between these results and HITSKAN’s performance on its test dataset (2015–2016, 114 apartments, 1 h resolution: MAE = 5.8343 MW, MAPE = 4.01%), considering the differences in time range, sample size, and resolution between the two datasets, the En-Crossformer still demonstrates effective predictive ability for complex distribution network loads while ensuring a short training time of 182.39 s (35.2% shorter than HITSKAN).
5.10.2. Test on a General Benchmark Dataset
6. Conclusions
- Among various prediction models, the proposed En-Crossformer model achieved optimal prediction accuracy at different prediction steps, demonstrating good accuracy and robustness. This unity of high precision and robustness is attributed to the model’s in-depth mining of the symmetrical features of the load sequence—from the frequency symmetry of modal decomposition to the symmetrical capture of feature correlation, achieving symmetrical optimization of prediction performance in different scenarios.
- Compared to other modal decomposition methods, the proposed KMA-MVMD method considering minimum average envelope entropy effectively extracted cyclical features of state changes, leading to higher prediction model accuracy and validating the effectiveness of the EnKMA-MVMD modal decomposition method. The superiority of the Crossformer prediction model, when combined with various state decomposition methods, was also demonstrated, EnKMA-MVMD extracts periodic features through symmetric decomposition, while Crossformer captures cross-temporal and cross-feature correlations through the symmetric attention mechanism. The two form a symmetric collaborative framework of “data preprocessing—model prediction”, jointly enhancing the prediction performance, further validating the applicability of the En-Crossformer prediction model.
- Compared to the traditional RapidMIC algorithm, the MVRapidMIC algorithm used in this study not only improved training speed but also further enhanced prediction accuracy. Lastly, the ablation experiments proved that each module within the Crossformer model leverages its advantages, addressing the issue of traditional Transformer prediction models failing to consider the correlations between different feature sequences.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- 1.
- Set each mode ϕ(t) have C channels, i.e., ϕ(t) = [ϕ1(t), ϕ2(t), … ϕC(t)]. Let there be κ multivariate modulated oscillations uκ(t).
- 2.
- Each element in the sequence uκ(t) undergoes Hilbert transformation, denoted as , then exponentiation adjusts it to the corresponding central frequency ωκ(t). ωκ(t) is utilized as the harmonic mixing frequency of , and the L2 norm of the gradient function of after harmonic transformation is used to estimate the bandwidth of each mode uκ(t). The variational constrained problem can be represented as follows.
- 3.
- While solving multiple variational problems, the number of equations in the linear equation system corresponds to the total number of channels. Simultaneously, an augmented Lagrangian equation is constructed:
- 4.
- The multiplier alternating direction method is employed to solve the transformed unconstrained variational problem for uκ(t) and ωκ(t) to obtain the decomposed components. The mode update of MVMD is given by:
Appendix B
Appendix C
| Prediction Model | Parameter Name | Parameter Value |
|---|---|---|
| LSTNet | skip | 5 |
| Highway window | 3 | |
| Dropout rate | 0.2 | |
| LSTM batch size | 64 | |
| Long pattern | Disabled | |
| Number of iterations | 300 | |
| Initial learning rate | 0.1 | |
| Transformer | Feature size | 8 |
| Number of layers | 5 | |
| Initial learning rate | 0.1 | |
| Dropout rate | 0.2 | |
| Number of iterations | 300 | |
| Prophet | Change point prior scale | 0.05 |
| Seasonal pattern | Additive mode | |
| Seasonal prior scale | 10 | |
| Change point range | 0.8 | |
| Annual seasonality | Enabled | |
| Monthly seasonality | Enabled | |
| Informer | Input sequence length | 384 |
| Label sequence length | 192 | |
| Prediction sequence length | 4 | |
| Model dimension | 512 | |
| Number of attention heads | 8 | |
| Dropout rate | 0.05 | |
| Initial learning rate | 0.0001 | |
| Crossformer | Input sequence length | 384 |
| Label sequence length | 192 | |
| Prediction sequence length | 4 | |
| Segmentation window size for merging | 2 | |
| Number of routers in TSA cross-dimensional stages | 10 | |
| Number of attention heads | 4 | |
| Dropout rate | 0.2 | |
| Initial learning rate | 0.0001 |
Appendix D
| Prediction Model | Parameter Name | Parameter Value |
|---|---|---|
| KMA | Maximum adaptive population size | 200 |
| Number of mature males | 6 | |
| Mlipir rate | 0.75 | |
| Female mutation rate | 0.5 | |
| Radius limiting female mutation steps | 0.5 | |
| SSA | Population size | 20 |
| Number of iterations | 50 | |
| Ratio of explorers | 10 | |
| Number of sentinels | 5 | |
| Safety threshold | 0.8 | |
| Monthly seasonality | Enabled | |
| PSO | Population size | 20 |
| Number of iterations | 50 | |
| Individual learning factor | 4 | |
| Social learning factor | 512 |
References
- Zhang, Z.; Hui, H.; Song, Y. Response Capacity Allocation of Air Conditioners for Peak-Valley Regulation Considering In-teraction with Surrounding Microclimate. IEEE Trans. Smart Grid 2024, 16, 1155–1167. [Google Scholar] [CrossRef]
- Wang, K.; Wang, C.; Yao, W.; Zhang, Z.; Liu, C.; Dong, X.; Yang, M.; Wang, Y. Embedding P2P transaction into demand response exchange: A cooperative demand response management framework for IES. Appl. Energy 2024, 367, 123319. [Google Scholar] [CrossRef]
- Su, T.; Zhao, J.; Pei, Y.; Ding, F. Probabilistic Physics-Informed Graph Convolutional Network for Active Distribution System Voltage Prediction. IEEE Trans. Power Syst. 2023, 38, 5969–5972. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Zhao, Y.; Wang, X. Implementation of Chaotic Reverse Slime Mould Algorithm Based on the Dandelion Optimizer. Biomimetics 2023, 8, 482. [Google Scholar] [CrossRef]
- Guo, Y.; Li, Y.; Qiao, X.; Zhang, Z.; Zhou, W.; Mei, Y.; Lin, J.; Zhou, Y.; Nakanishi, Y. BiLSTM Multitask Learning-Based Combined Load Forecasting Considering the Loads Coupling Relationship for Multienergy System. IEEE Trans. Smart Grid 2022, 13, 3481–3492. [Google Scholar] [CrossRef]
- Sarajcev, P.; Kunac, A.; Petrovic, G.; Despalatovic, M. Artificial Intelligence Techniques for Power System Transient Stability Assessment. Energies 2022, 15, 507. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, X.; Dai, J.; Zhang, T. Photovoltaic Power Prediction Technology Based on Multi-Source Feature Fusion. Symmetry 2025, 17, 414. [Google Scholar] [CrossRef]
- Li, Y.; Yang, N.; Bi, G.; Chen, S.; Luo, Z.; Shen, X. Carbon Price Forecasting Using a Hybrid Deep Learning Model: TKMixer-BiGRU-SA. Symmetry 2025, 17, 962. [Google Scholar] [CrossRef]
- Karpagam, T.; Kanniappan, J. Symmetry-Aware Multi-Dimensional Attention Spiking Neural Network with Optimization Techniques for Accurate Workload and Resource Time Series Prediction in Cloud Computing Systems. Symmetry 2025, 17, 383. [Google Scholar] [CrossRef]
- L’Heureux, A.; Grolinger, K.; Capretz, M.A.M. Transformer-Based Model for Electrical Load Forecasting. Energies 2022, 15, 4993. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30, 6000–6010. [Google Scholar]
- Zhou, H.Y.; Zhang, S.H.; Peng, J.Q.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. In Proceedings of the 35th AAAI Conference on Artificial Intelligence; Association for the Advancement of Artificial Intelligence, Online, 2–9 February 2021; pp. 11106–11115. [Google Scholar]
- Zhu, Q.; Han, J.; Chai, K.; Zhao, C. Time Series Analysis Based on Informer Algorithms: A Survey. Symmetry 2023, 15, 951. [Google Scholar] [CrossRef]
- Zhou, N.; Zheng, Z.; Zhou, J. Prediction of the RUL of PEMFC Based on Multivariate Time Series Forecasting Model. In Proceedings of the 2023 3rd International Symposium on Computer Technology and Information Science (ISCTIS), Chengdu, China, 20–22 May 2023; pp. 87–92. [Google Scholar]
- Wang, W.; Chen, W.; Qiu, Q.; Chen, L.; Wu, B.; Lin, B.; He, X.; Liu, W. Crossformer++: A Versatile Vision Transformer Hinging on Cross-Scale Attention. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 46, 3123–3136. [Google Scholar] [CrossRef]
- Zhou, J.; Yu, X.; Jin, B. Short-Term Wind Power Forecasting: A New Hybrid Model Combined Extreme-Point Symmetric Mode Decomposition, Extreme Learning Machine and Particle Swarm Optimization. Sustainability 2018, 10, 3202. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, H.; Hu, M.; Jiang, A.; Zhang, L.; Xu, F.; Hao, G. An Adaptive CEEMDAN Thresholding Denoising Method Optimized by Nonlocal Means Algorithm. IEEE Trans. Instrum. Meas. 2020, 69, 6891–6903. [Google Scholar] [CrossRef]
- Tang, J.; Chien, Y.-R. Research on Wind Power Short-Term Forecasting Method Based on Temporal Convolutional Neural Network and Variational Modal Decomposition. Sensors 2022, 22, 7414. [Google Scholar] [CrossRef]
- Cao, R.; Tian, H.; Li, D.; Feng, M.; Fan, H. Short-Term Photovoltaic Power Generation Prediction Model Based on Improved Data Decomposition and Time Convolution Network. Energies 2024, 17, 33. [Google Scholar] [CrossRef]
- Liu, Y.; Zeng, Y.; Li, R.; Zhu, X.; Zhang, Y.; Li, W.; Li, T.; Zhu, D.; Hu, G. A Random Particle Swarm Optimization Based on Cosine Similarity for Global Optimization and Classification Problems. Biomimetics 2024, 9, 204. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Shi, Y.; Eberhart, R. A Modified Particle Swarm Optimizer. In Proceedings of the IEEE International Conference on Evolutionary Computation, Anchorage, AK, USA, 4–9 May 1998; IEEE: Piscataway, NJ, USA, 1998; pp. 69–73. [Google Scholar]
- An, G.; Jiang, Z.; Chen, L.; Cao, X.; Li, Z.; Zhao, Y.; Sun, H. Ultra Short-Term Wind Power Forecasting Based on Sparrow Search Algorithm Optimization Deep Extreme Learning Machine. Sustainability 2021, 13, 10453. [Google Scholar] [CrossRef]
- Mirjalili, S.M.; Mirjalili, S.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, Y.; Wang, K.; Chen, Y. Particle Swarm Optimization (PSO) for the Constrained Portfolio Optimization Problem. Expert Syst. Appl. 2011, 38, 10161–10169. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An Improved Grey Wolf Optimizer for Solving Engineering Problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Aljarah, I.; Faris, H.; Mirjalili, S. Optimizing Connection Weights in Neural Networks Using the Whale Optimization Algorithm. Soft Comput. 2018, 22, 1–15. [Google Scholar] [CrossRef]
- Available online: https://traces.cs.umass.edu/docs/traces/smartstar/#umass-smart-dataset--2017-release (accessed on 2 September 2025).
- Suyanto, S.; Ariyanto, A.A.; Ariyanto, A.F. Komodo Mlipir Algorithm. Appl. Soft Comput. 2022, 114, 108043. [Google Scholar] [CrossRef]
- Zhao, Q.; Li, C.; Zhu, D.; Xie, C. Coverage Optimization of Wireless Sensor Networks Using Combinations of PSO and Chaos Optimization. Electronics 2022, 11, 853. [Google Scholar] [CrossRef]
- Wang, L.; Cheng, H. Pseudo-Random Number Generator Based on Logistic Chaotic System. Entropy 2019, 21, 960. [Google Scholar] [CrossRef]
- Huang, X.; Li, C.; Chen, H.; An, D. Task Scheduling in Cloud Computing Using Particle Swarm Optimization with Time Varying Inertia Weight Strategies. Clust. Comput. 2020, 23, 1137–1147. [Google Scholar] [CrossRef]
- Li, Y.; Han, M.; Guo, Q. Modified Whale Optimization Algorithm Based on Tent Chaotic Mapping and Its Application in Structural Optimization. KSCE J. Civ. Eng. 2020, 24, 3703–3713. [Google Scholar] [CrossRef]
- Ur Rehman, N.; Aftab, H. Multivariate Variational Mode Decomposition. IEEE Trans. Signal Process. 2019, 67, 6039–6052. [Google Scholar] [CrossRef]
- Yu, Y.; Jin, Z.; Ćetenović, D.; Ding, L.; Levi, V.; Terzija, V. A robust distribution network state estimation method based on enhanced clustering Algorithm: Accounting for multiple DG output modes and data loss. Int. J. Electr. Power Energy Syst. 2024, 157, 109797. [Google Scholar] [CrossRef]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting Novel Associations in Large Data Sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef]
- Tang, D.; Wang, M.; Zheng, W.; Wang, H. RapidMic: Rapid Computation of the Maximal Information Coefficient. Evol. Bioinform. 2014, 10, EBO.S13121. [Google Scholar] [CrossRef] [PubMed]
- Curtis, A.E.; Smith, T.A.; Ziganshin, B.A.; Elefteriades, J.A. The Mystery of the Z-Score. Aorta 2016, 4, 124–130. [Google Scholar] [CrossRef] [PubMed]
- National Weather Service. Available online: https://www.weather.gov/ (accessed on 1 September 2025).
- Muqtadir, A.; Li, B.; Ying, Z.; Songsong, C.; Kazmi, S.N. Day—Ahead demand response potential prediction in residential buildings with HITSKAN: A fusion of Kolmogorov—Arnold networks and N—HiTS. Energy Build. 2025, 332, 115455. [Google Scholar] [CrossRef]
- Sarah, Y.; Rabea, G.; Amirouche, N.S. Harnessing Deep Learning for Enhanced Energy Consumption Forecasting in smart Home: A comparative Study of MLP and RNN Architectures. In Proceedings of the 2025 3rd International Conference on Electronics, Energy and Measurement (IC2EM), Algiers, Algeria, 6–8 May 2025; pp. 1–5. [Google Scholar]
- Natarajan, K.P.; Singh, J.G. Day—Ahead Residential Load Forecasting based on Variational Mode Decomposition and Hybrid Deep Networks with Granger Causality Feature Selection. In Proceedings of the 2024 IEEE 3rd Industrial Electronics Society Annual Online Conference (ONCON), Beijing, China, 8–10 December 2024; pp. 1–6. [Google Scholar]
- Zhang, K.; Wang, J.; Zhu, Y.; Zhu, T. Ensemble Learning—Based Electricity Theft Detection: Combining Deep & Cross Network and Transformer. In Proceedings of the 2025 IEEE 5th International Conference on Power, Electronics and Computer Applications (ICPECA), Shenyang, China, 17–19 January 2025; pp. 633–638. [Google Scholar]
- Available online: https://github.com/zhouhaoyi/ETDataset (accessed on 1 September 2025).
- Available online: https://archive.ics.uci.edu/dataset/321/electricityloaddiagrams20112014 (accessed on 1 September 2025).
- Nie, X.; Zhou, X.; Li, Z.; Wang, L.; Lin, X.; Tong, T. Logtrans: Providing efficient local-global fusion with transformer and cnn parallel network for biomedical image segmentation. In Proceedings of the IEEE 24th Int Conf on High Performance Computing & Communications; 8th Int Conf on Data Science & Systems; 20th Int Conf on Smart City; 8th Int Conf on Dependability in Sensor, Cloud & Big Data Systems & Application (HPCC/DSS/SmartCity/DependSys), Hainan, China, 18–20 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 769–776. [Google Scholar]
- Kitaev, N.; Kaiser, Ł.; Levskaya, A. Reformer: The efficient transformer. arXiv 2020, arXiv:2001.04451. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
- Ariyo, A.A.; Adewumi, A.O.; Ayo, C.K. Stock price prediction using the ARIMA model. In Proceedings of the 2014 UKSim-AMSS 16th International Conference on Computer Modelling and Simulation, Cambridge, UK, 26–28 March 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 106–112. [Google Scholar]

| Input Feature Sequence | Variable Indices | Input Feature Sequence | Variable Indices |
|---|---|---|---|
| Temperature | H1 | Wind direction | H17 |
| Cumulative temperature effect 1 | H2, H3, H4, H5, H6, H7, H8, H9, H10, H11 | Precipitation amount | H18 |
| Relative humidity | H12 | Month | H19 |
| Visibility | H13 | Day | H20 |
| Atmospheric pressure | H14 | Hour | H21 |
| Wind speed | H15 | Day of the week | H22 |
| Cloud coverage | H16 | Holiday | H23 |
| Input Feature Sequence | MVRapidMIC | Input Feature Sequence | MVRapidMIC |
|---|---|---|---|
| H1 | 0.81 | H17 | 0.22 |
| H2~H11 | 0.77 | H18 | 0.68 |
| H12 | 0.35 | H19 | 0.72 |
| H13 | 0.50 | H20 | 0.36 |
| Prediction Model | Load Forecasting Evaluation Metrics | Time/s | ||||
|---|---|---|---|---|---|---|
| vRMSE/(MW) | vMAE/(MW) | vMAPE | R2 | Training Time | Prediction Time | |
| LSTM | 35.7969 | 31.4123 | 15.69% | 0.8823 | 256.71 | 16.23 |
| Prophet | 29.4507 | 26.3463 | 12.56% | 0.9274 | 315.96 | 18.97 |
| Transformer | 25.8336 | 23.2294 | 10.82% | 0.9409 | 504.42 | 37.36 |
| LSTNet | 22.3816 | 20.9563 | 8.97% | 0.9677 | 368.40 | 29.51 |
| Informer | 18.4891 | 17.6506 | 6.74% | 0.9815 | 242.26 | 27.56 |
| En-Crossformer | 14.7597 | 13.9728 | 4.89% | 0.9942 | 171.28 | 21.18 |
| Prediction Model | Step Size | Load Forecasting Evaluation Metrics | |||
|---|---|---|---|---|---|
| vRMSE/(MW) | vMAE/(MW) | vMAPE | R2 | ||
| LSTM | 8 | 55.5209 | 51.0952 | 17.66% | 0.8619 |
| 16 | 79.2543 | 76.4207 | 19.85% | 0.8497 | |
| 24 | 101.2694 | 100.5158 | 21.99% | 0.8142 | |
| Prophet | 8 | 45.3835 | 41.6667 | 16.37% | 0.8703 |
| 16 | 66.7176 | 60.8309 | 18.14% | 0.8516 | |
| 24 | 85.1479 | 80.0743 | 20.06% | 0.8219 | |
| Transformer | 8 | 37.3619 | 34.2263 | 15.74% | 0.8825 |
| 16 | 55.1108 | 43.8107 | 17.55% | 0.8635 | |
| 24 | 72.5263 | 69.3337 | 18.33% | 0.8551 | |
| LSTNet | 8 | 32.4565 | 28.9410 | 15.28% | 0.8896 |
| 16 | 47.4929 | 43.1873 | 16.45% | 0.8698 | |
| 24 | 55.4632 | 50.5857 | 17.52% | 0.8613 | |
| Informer | 8 | 29.6550 | 27.0331 | 14.62% | 0.9159 |
| 16 | 38.8328 | 33.7901 | 15.88% | 0.8806 | |
| 24 | 48.5686 | 45.1626 | 16.53% | 0.8687 | |
| En-Crossformer | 8 | 28.3780 | 24.1907 | 12.41% | 0.9255 |
| 16 | 33.7545 | 30.7733 | 15.58% | 0.8864 | |
| 24 | 41.0055 | 39.0086 | 16.19% | 0.8801 | |
| Optimization Algorithm | Load Forecasting Evaluation Metrics | Decomposition Number | Penalty Factor | Decomposition Loss /MW | |||
|---|---|---|---|---|---|---|---|
| vRMSE/(MW) | vMAE/MW) | vMAPE | R2 | ||||
| - | 22.6119 | 20.0316 | 8.99% | 0.9691 | 6 | 1246 | 5.51 |
| PSO | 19.1239 | 18.2746 | 7.22% | 0.9758 | 16 | 2897 | 3.43 |
| SSA | 17.0925 | 16.2173 | 6.04% | 0.9874 | 14 | 2530 | 2.83 |
| KMA | 16.9635 | 15.0975 | 5.92% | 0.9937 | 12 | 2085 | 1.69 |
| EnKMA | 14.7597 | 13.9728 | 4.89% | 0.9942 | 10 | 1850 | 1.37 |
| Test Samples | Prediction Model | Load Forecasting Evaluation Metrics | |||
|---|---|---|---|---|---|
| vRMSE/(MW) | vMAE/(MW) | vMAPE | R2 | ||
| - | LSTM | 50.0781 | 46.9592 | 17.42% | 0.8647 |
| Prophet | 45.4147 | 38.6275 | 16.39% | 0.8701 | |
| Transformer | 40.3611 | 32.9509 | 16.15% | 0.8794 | |
| LSTNet | 36.7190 | 32.1820 | 15.70% | 0.8817 | |
| Informer | 32.7509 | 29.6262 | 15.37% | 0.8872 | |
| Crossformer | 27.4124 | 24.3565 | 11.89% | 0.9377 | |
| EnKMA-MVMD | LSTM | 35.7969 | 31.4123 | 15.69% | 0.8823 |
| Prophet | 29.4507 | 26.3463 | 12.56% | 0.9274 | |
| Transformer | 25.8336 | 23.2294 | 10.82% | 0.9409 | |
| LSTNet | 22.3816 | 20.9563 | 8.97% | 0.9677 | |
| Informer | 18.4891 | 17.6506 | 6.74% | 0.9815 | |
| Crossformer | 14.7597 | 13.9728 | 4.89% | 0.9942 | |
| CEEMDAN | LSTM | 40.5979 | 35.6253 | 16.08% | 0.8805 |
| Prophet | 38.5173 | 34.4572 | 15.86% | 0.8809 | |
| Transformer | 34.0976 | 30.8089 | 15.61% | 0.8812 | |
| LSTNet | 30.2598 | 28.3787 | 15.21% | 0.8899 | |
| Informer | 26.4883 | 23.5827 | 11.74% | 0.9372 | |
| Crossformer | 23.4385 | 20.5829 | 9.55% | 0.9567 | |
| Prediction Model | Load Forecasting Evaluation Metrics | Time/s | ||||
|---|---|---|---|---|---|---|
| vRMSE/(MW) | vMAE/(MW) | vMAPE | R2 | Training Time | Prediction Time | |
| AF-Crossformer | 29.4561 | 27.9854 | 12.57% | 0.9272 | 867.97 | 28.97 |
| MIC-Crossformer | 17.4035 | 15.6387 | 6.43% | 0.9866 | 674.16 | 23.64 |
| RapidMIC-Crossformer | 16.9157 | 15.4622 | 5.86% | 0.9931 | 393.54 | 21.59 |
| En-Crossformer | 14.7597 | 13.9728 | 4.89% | 0.9942 | 171.28 | 21.18 |
| Prediction Model | Load Forecasting Evaluation Metrics | |||
|---|---|---|---|---|
| vRMSE/(MW) | vMAE/(MW) | vMAPE | R2 | |
| Transformer | 25.8336 | 23.2294 | 10.82% | 0.9409 |
| DSW-Transformer | 17.9163 | 16.4578 | 6.58% | 0.9806 |
| DSW-TSA-Transformer | 15.4396 | 14.4395 | 5.51% | 0.9940 |
| DSW-HED-Transformer | 16.1643 | 15.2661 | 5.73% | 0.9939 |
| Crossformer | 14.7597 | 13.9728 | 4.89% | 0.9942 |
| Hyperparameter | Baseline Value | The Changed Value | vRMSE/(MW) | vMAE/(MW) | vMAPE | R2 | Training Time |
|---|---|---|---|---|---|---|---|
| EnKMA λ | 5 | 6 | 15.2320 | 14.3638 | 5.49% | 0.9941 | 313.87 |
| MVMD K | 8 | 6 | 16.6046 | 15.5515 | 5.79% | 0.9935 | 249.58 |
| Crossformer Dropout | 0.2 | 0.24 | 15.6010 | 14.6573 | 5.53% | 0.9940 | 260.43 |
| TSA Attention Heads | 4 | 3 | 15.9552 | 15.0205 | 5.54% | 0.9939 | 238.73 |
| Algorithm | Function | Avg. Convergence Accuracy | Convergence Iterations |
|---|---|---|---|
| Standard KMA | Sphere | 2.36 × 10−3 | 85 |
| Griewank | 1.89 × 10−2 | 112 | |
| EnKMA (Full Innovations) | Sphere | 1.69 × 10−4 | 68 |
| Griewank | 2.15 × 10−3 | 89 | |
| Ablation (w/o Tent perturbation) | Sphere | 5.23 × 10−4 | 75 |
| Griewank | 5.87 × 10−3 | 103 | |
| Ablation (w/o TVIW) | Sphere | 8.11 × 10−4 | 82 |
| Griewank | 7.34 × 10−3 | 115 | |
| PSO | Sphere | 3.12 × 10−3 | 92 |
| Griewank | 2.56 × 10−2 | 125 | |
| TSA Attention Heads | Sphere | 2.88 × 10−3 | 88 |
| Griewank | 2.23 × 10−2 | 118 |
| Prediction Model | Load Forecasting Evaluation Metrics | Time/s | ||||
|---|---|---|---|---|---|---|
| vRMSE/(MW) | vMAE/(MW) | vMAPE | R2 | Training Time | Prediction Time | |
| MLP-RNN [42] | 38.2181 | 35.3831 | 16.59% | 0.8821 | 118.55 | 10.26 |
| VMD-LSTM-GRU [43] | 29.2939 | 27.3281 | 12.66% | 0.9267 | 313.32 | 19.89 |
| DCN-Transformer [44] | 18.2342 | 16.011 | 6.83% | 0.9840 | 605.92 | 41.97 |
| HITSKAN [41] | 7.4641 | 5.8343 | 4.01% | 0.9985 | 281.46 | 34.15 |
| En-Crossformer | 10.2387 | 9.3228 | 4.74% | 0.9946 | 182.39 | 23.34 |
| Methods | En-Crossformer | Informer+ [12] | LogTrans [47] | Reformer [48] | LSTMa [49] | DeepAR [50] | ARIMA [51] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | |
| ETTh1 | 24 | 0.089 | 0.0244 | 0.092 | 0.246 | 0.103 | 0.259 | 0.222 | 0.389 | 0.114 | 0.272 | 0.107 | 0.280 | 0.108 | 0.284 |
| 48 | 0.156 | 0.317 | 0.161 | 0.322 | 0.167 | 0.328 | 0.284 | 0.445 | 0.193 | 0.358 | 0.162 | 0.327 | 0.175 | 0.424 | |
| 168 | 0.181 | 0.343 | 0.187 | 0.355 | 0.207 | 0.375 | 1.522 | 1.191 | 0.236 | 0.392 | 0.239 | 0.422 | 0.396 | 0.504 | |
| 336 | 0.212 | 0.367 | 0.215 | 0.369 | 0.230 | 0.398 | 1.860 | 1.124 | 0.590 | 0.698 | 0.445 | 0.552 | 0.468 | 0.593 | |
| 720 | 0.255 | 0.417 | 0.257 | 0.421 | 0.273 | 0.463 | 2.112 | 1.436 | 0.683 | 0.768 | 0.658 | 0.707 | 0.659 | 0.766 | |
| ETTm1 | 24 | 0.027 | 0.135 | 0.034 | 0.160 | 0.102 | 0.255 | 0.263 | 0.437 | 0.155 | 0.307 | 0.098 | 0.280 | 3.554 | 0.445 |
| 48 | 0.067 | 0.200 | 0.066 | 0.194 | 0.169 | 0.348 | 0.458 | 0.545 | 0.190 | 0.348 | 0.163 | 0.327 | 3.190 | 0.474 | |
| 168 | 0.192 | 0.371 | 0.187 | 0.384 | 0.246 | 0.422 | 1.029 | 0.879 | 0.385 | 0.514 | 0.255 | 0.422 | 2.800 | 0.595 | |
| 336 | 0.399 | 0.546 | 0.409 | 0.548 | 0.267 | 0.437 | 1.668 | 1.228 | 0.558 | 0.606 | 0.604 | 0.552 | 2.753 | 0.738 | |
| 720 | 0.508 | 0.641 | 0.519 | 0.665 | 0.303 | 0.493 | 2.030 | 1.721 | 0.640 | 0.681 | 0.429 | 0.707 | 2.878 | 1.044 | |
| ECL | 24 | 0.201 | 0.355 | 0.238 | 0.368 | 0.280 | 0.429 | 0.971 | 0.884 | 0.493 | 0.539 | 0.204 | 0.357 | 0.879 | 0.764 |
| 48 | 0.313 | 0.433 | 0.442 | 0.514 | 0.454 | 0.529 | 1.671 | 1.587 | 0.723 | 0.655 | 0.315 | 0.436 | 1.032 | 0.833 | |
| 168 | 0.411 | 0.517 | 0.501 | 0.552 | 0.514 | 0.563 | 3.528 | 2.196 | 1.212 | 0.898 | 0.414 | 0.519 | 1.136 | 0.876 | |
| 336 | 0.539 | 0.568 | 0.543 | 0.578 | 0.558 | 0.609 | 4.891 | 4.047 | 1.511 | 0.966 | 0.563 | 0.595 | 1.251 | 0.933 | |
| 720 | 0.579 | 0.605 | 0.594 | 0.638 | 0.624 | 0.645 | 7.019 | 5.105 | 1.545 | 1.006 | 0.657 | 0.683 | 1.370 | 0.982 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Liu, K.; You, Q.; Bai, L.; Zhang, S.; Guo, H.; Liu, H. Symmetry-Aware Short-Term Load Forecasting in Distribution Networks: A Synergistic Enhanced KMA-MVMD-Crossformer Framework. Symmetry 2025, 17, 1512. https://doi.org/10.3390/sym17091512
Zhao J, Liu K, You Q, Bai L, Zhang S, Guo H, Liu H. Symmetry-Aware Short-Term Load Forecasting in Distribution Networks: A Synergistic Enhanced KMA-MVMD-Crossformer Framework. Symmetry. 2025; 17(9):1512. https://doi.org/10.3390/sym17091512
Chicago/Turabian StyleZhao, Jingfeng, Kunhua Liu, Qi You, Lan Bai, Shuolin Zhang, Huiping Guo, and Haowen Liu. 2025. "Symmetry-Aware Short-Term Load Forecasting in Distribution Networks: A Synergistic Enhanced KMA-MVMD-Crossformer Framework" Symmetry 17, no. 9: 1512. https://doi.org/10.3390/sym17091512
APA StyleZhao, J., Liu, K., You, Q., Bai, L., Zhang, S., Guo, H., & Liu, H. (2025). Symmetry-Aware Short-Term Load Forecasting in Distribution Networks: A Synergistic Enhanced KMA-MVMD-Crossformer Framework. Symmetry, 17(9), 1512. https://doi.org/10.3390/sym17091512





