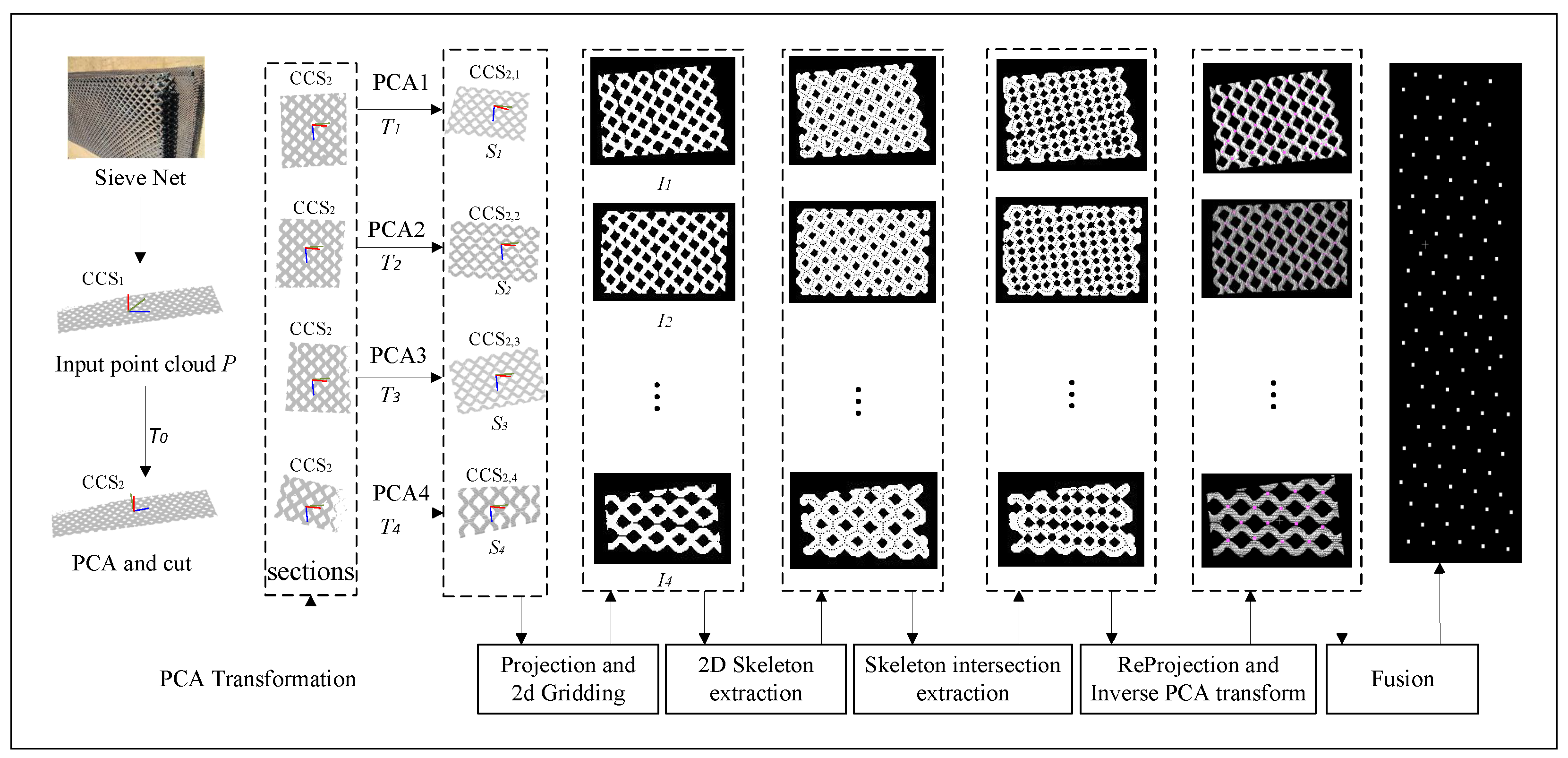
3.1. Projection and 2D Gridding
To preserve structural details in 3D-to-2D projection by automatically aligning the sieve net to an optimal orientation, the point cloud acquired from arbitrarily angled scans is transformed into a fixed XYZ coordinate system via PCA transformation in the proposed method. The following is an analogical description of PCA transformation.
A piece of crumpled paper, when spread on a table, is automatically rotated by PCA so that its shadow covers the largest possible area, capturing most details.
The original point cloud is denoted as
. The covariance matrix of data is computed by
and is decomposed by singular value decomposition (SVD).
where
U consists of three eigenvectors
,
, and
arranged in the descending order with respect to their eigenvalues, representing the principal geometric directions of the point cloud. In the case where the sieve net can be approximated as a plane,
and
are dominant, corresponding to the in-plane extension directions, while
is minor, corresponding to the plane’s normal direction. These eigenvectors are aligned with the three principal axes (x, y, and z) of the local coordinate system, thereby enabling dimensionality reduction and structural preservation during the two-dimensional projection process.
Thus, the point cloud of sieve net is decentered and rotationally transformed along the projection with minimal loss of information, and it is formulated as follows:
where
C is the center coordinate of sieve-net point cloud. The point cloud
P is transformed into a new coordinate system and is denoted as
. In this paper, the new coordinate system has the same dimensions as the original one.
Real-world sieve nets are not ideally horizontal and may be uneven, the principal component projections selected in the PCA transformation is not sufficiently spread to support high-accuracy detection. Therefore, large deviations can occur when processed directly. The original point cloud can be segmented and divided into multiple partitions. A second PCA transformation can then be performed so that the subsequent identification of the solder joint can have greater accuracy. Partitioning the point cloud involves dividing the original point cloud into a plane parallel to the surfaces formed by the second and third principal components. Each partition should allow some degree of area overlap between them. This is to prevent the partition from causing the solder joints at the partition boundary to be severed, which can lead to incorrect detection in the subsequent solder joint identification. The principal component matrix is recorded for the subsequent conversion of the solder joint results into 3D space.
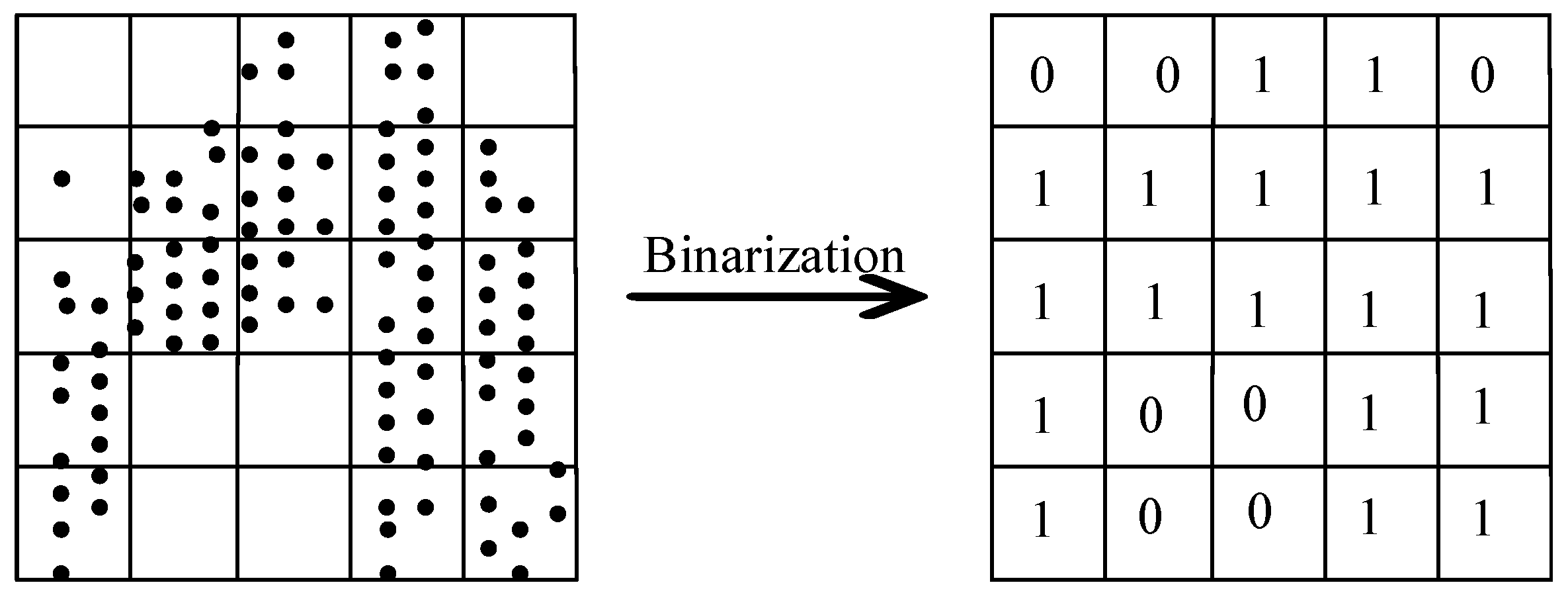
In order to stably extract the welded points of the sieve net, we consider extracting the weld trajectory points based on the characteristics of the 2D image of the sieve net. Firstly, the point cloud is projected to a 2D plane. Then, 2D gridding is achieved on the projected image to generate a 2D binarized image
I. The 2D gridded processing is shown in
Figure 2, the grid occupied by dots is marked as 1, which is the corresponding pixel value of the image; the others are marked as 0.
3.2. Two-Dimensional Skeleton and Intersection Extraction
After generating the 2D binarized image of sieve net, the weld points are generated by the intersection of skeletons. First of all, the 2D skeleton of sieve net needs to be extracted. In fact, the points where the sieve net needs to be welded are not connected, which means that the 2D image of the sieve net generated by the projection has some gaps. Therefore, in order to extract the welded points of the sieve net using the skeleton intersections, it is necessary to carry out swelling and corrosion operations on the sieve-net image. Thus, the gap can be connected in the skeleton intersections, which generates the coherent image I.
Inspired by the method of reference [
33], we extract the 2D skeleton of sieve net. The key idea is that the deletion of pixels in the current iteration of the algorithm depends only on the result of the previous iteration. Each iteration marks the target pixels that meet the deletion conditions. After iterating through the whole image, all marked points are deleted until no pixel is marked in a given iteration. Then, the iteration is completed, and the image obtained after deleting the marked points is the refined skeleton image.
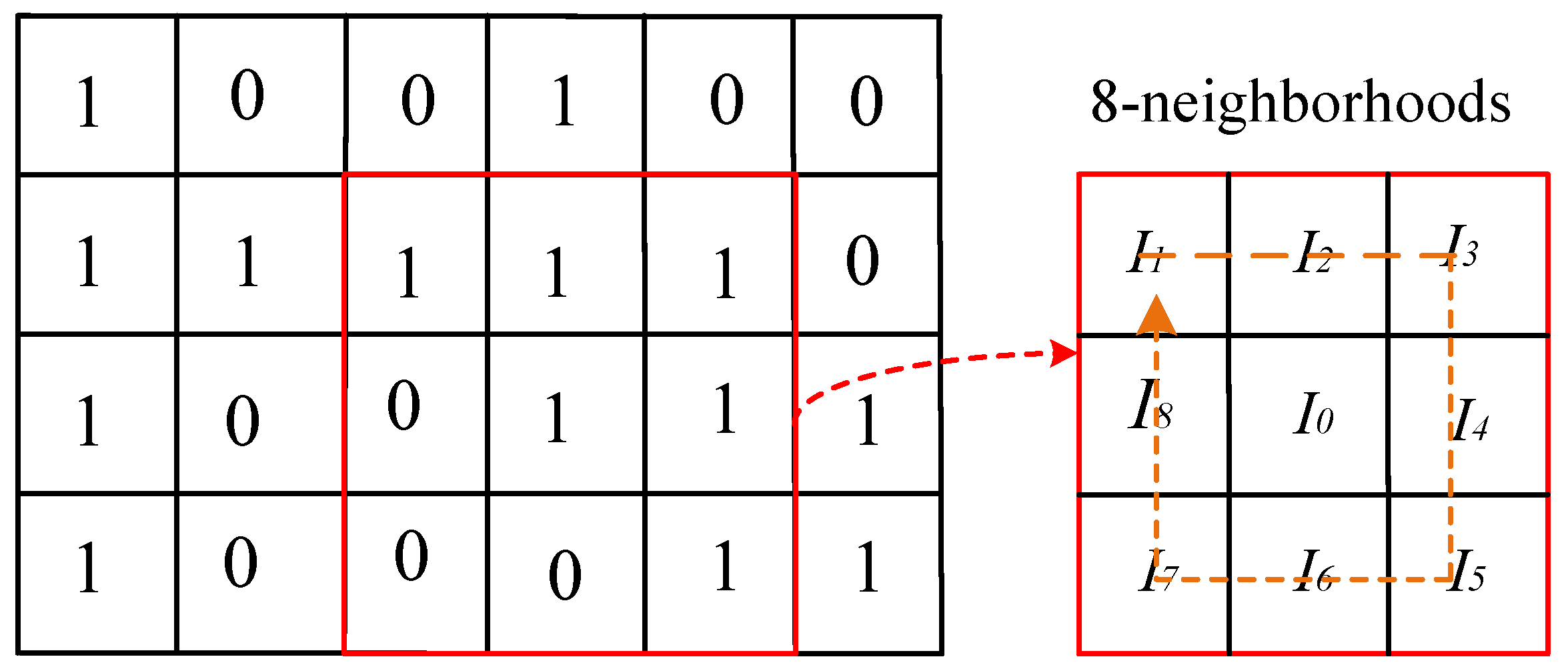
Here, the following basic concepts are first defined. As shown in
Figure 3, given an image
, each pixel
with a value of 1 has 8 neighborhoods. Then, the pixels in the neighborhood are arranged clockwise around
. The pixel points with value 1 in the binarized image correspond to target points, and pixel points with a pixel value of 0 correspond to background points.The target points in the 8 neighborhoods where at least one background point exists are treated as boundary points. The number of 1-to-0 conversions around the pixel
in the image is denoted as
. The number of pixels with a value of 0 in the 8 neighborhoods of
is denoted as
.
The refinement algorithm of the 2D skeleton is performed in two steps per iteration by continuously executing logical operations to remove non-skeleton points that meet the conditions. The two steps are described as follows.
In the first step, given a target point
, when it is a boundary point, judge whether the point
satisfies the following conditions in turn.
In the first equation of Equation (
4), when
g(
) ≐ 0, there is no pixel equal to 1 around
, and
is an isolated point. When
g(
) ≐ 1, there is one and only one pixel around
equal to the gray value of 1, and
is an endpoint. Neither isolated points nor endpoints can be deleted.
g(
)
2 can guarantee that it is neither an isolated point nor an endpoint, and
guarantees that
is a boundary point not an interior point. In the second equation of Equation (
4), a connected graph is guaranteed after the current pixel is deleted. In the last two equations of Equation (
4), ensure that
≐ 0 or
≐ 0 or both
and
are 0. That is,
will be marked only if it is an east or south boundary point or a northwest corner point.
In the second step, similarly to the first two conditions of the first step, there are connected target points ensured in the 8 neighborhoods of the target point
. And it is also ensured that the basis for skeletal formation still exists even after the target point
is deleted. The last two equations of Equation (
5) are the same as Equation (
4), but a little difference exists in that
is only marked if it is a western or northern boundary point or a southeast corner point.
The refinement algorithm of the 2D skeleton undergoes the aforementioned two steps to continuously mark pixels that meet the specified conditions. Iteration ceases when no further pixels are marked within a given iteration. Subsequently, all marked pixels are deleted, leaving the remaining pixels to form the refined skeleton image.
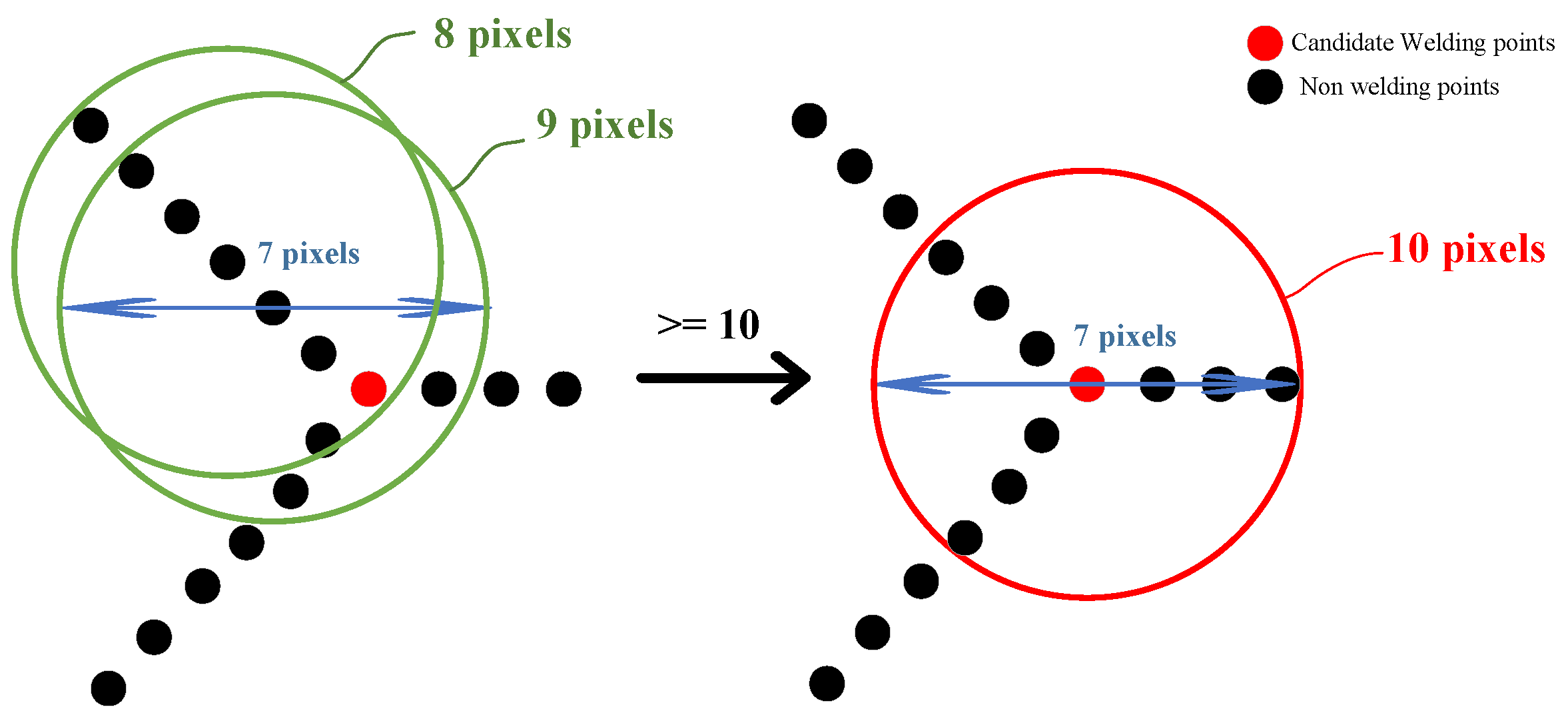
To pinpoint the exact positions of welded joints, skeleton intersections within the image must be extracted subsequent to the skeleton extraction. As illustrated in
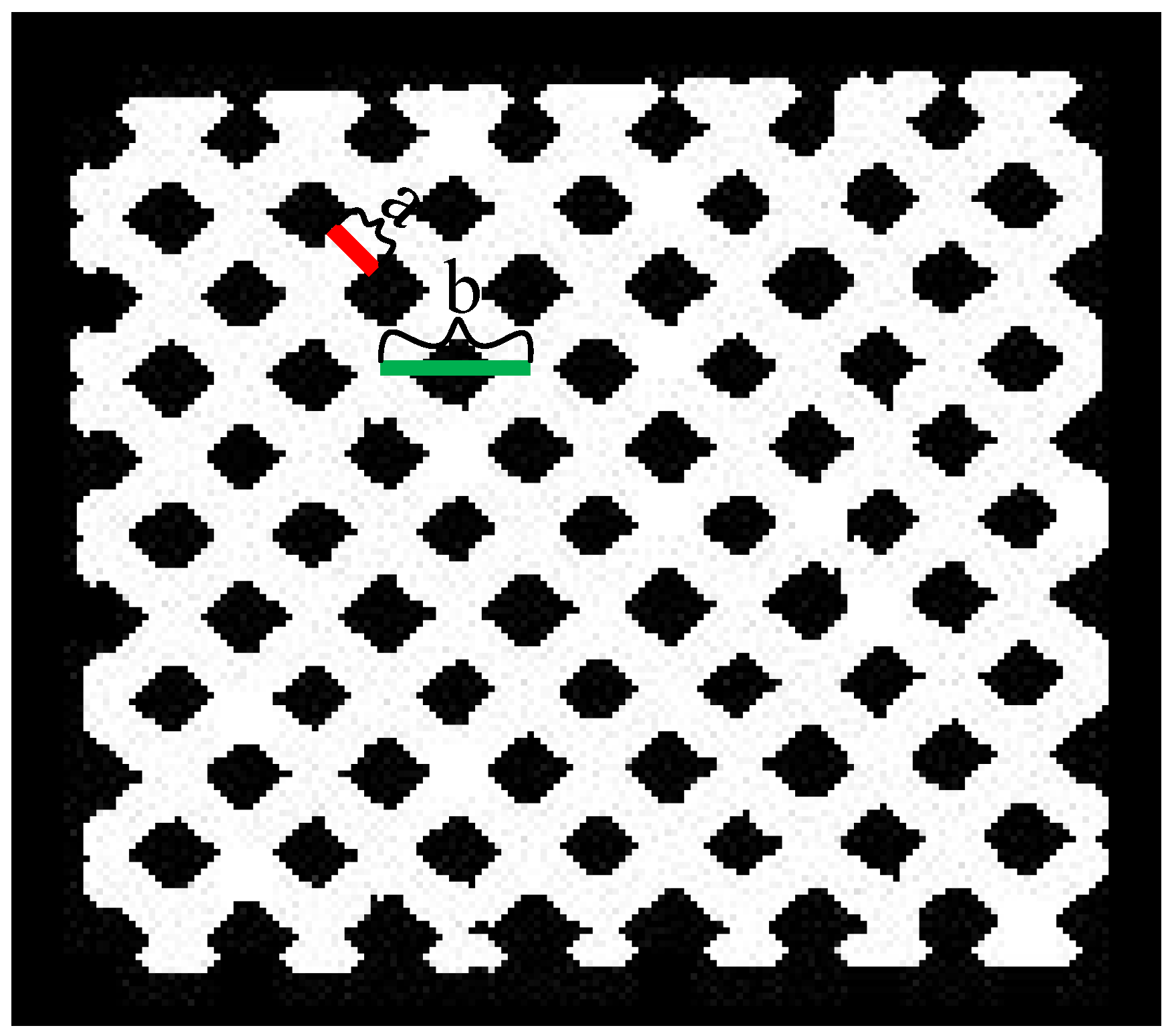
Figure 4, a circular neighborhood with a diameter of 7 pixels is employed, with the origin of this neighborhood traversing each pixel point sequentially. When the origin of the neighborhood coincides with a skeleton intersection, the neighborhood encompasses at least 10 pixel points. Conversely, if it does not align with a skeleton intersection, the number of pixel points within the neighborhood falls below 10. The neighborhood pixel count, denoted as N(I0), is calculated using brute force methods. Between two reinforcement columns, multiple skeleton intersections may be extracted along the edges. Ideally, the welding point should be centered within the gaps between reinforcements, necessitating the merging of skeleton intersections.
At the gap between every two bars, a circular neighborhood is selected based on the location of the extracted skeleton intersections, ensuring that it encompasses all intersections. The center of this circle is then designated as the final welding point, as depicted in
Figure 5, which illustrates the diameters of the reinforcing steel and mesh.
The time complexity of Algorithm 1 is established as
, where
n denotes the total number of pixels in the input image. This linear complexity indicates that the algorithm’s performance is linearly proportional to the image size, thereby ensuring its efficiency and feasibility in processing large-scale datasets.
| Algorithm 1 Two-dimensional skeleton intersection extraction |
| Require: Given a coherent image , maximum number of iteration rounds , sieve net diameter b. |
| Ensure: 2D skeleton intersection set W. |
| //2D skeleton extraction. |
| while iteration rounds do |
| for each pixel ∈ image do |
| if satisfies Equation (4) or Equation (5) then //[Extract a 2D skeleton point set of the mesh] |
| mark . |
| end if |
| end for |
| Delete all marked pixels. |
| end while |
| //Weld joint extraction based on skeleton intersection method. |
| while any pixel in image do |
| if then |
| . //[Extract the intersection points of the skeleton] |
| end if |
| end while |
| return the set W. |
3.3. Reprojection and Inverse PCA Transform
After the 2D skeleton intersection is merged, the 2D welded joints are obtained in a binarized image. Subsequently, inverse PCA transformation is applied to transform these 2D welded joints back into the original 3D point cloud data. Since the PCA transformation was initially performed in two stages, the inverse transformation process must also be executed in two corresponding stages: once for the inverse transformation of each partitioned chunk and once for the final inverse transformation of the entire assembled point cloud. This ensures that the welded joints, initially identified in 2D, are accurately mapped back to their respective 3D coordinates.
Because the sieve net is an irregular surface, it is not possible to determine the 3D coordinates of the weld joints. To further extract the weld points accurately, we will merge and fuse the skeleton intersections. Specifically, a skeleton intersection
is selected and used as the center point to search the set of skeleton intersections
in the field with the diameter of the screen mesh
. Then, the center
of
is calculated and treated as the point for welding. Finally, proceeding similarly in sequence, traversing and merging are carried out on all sets of skeleton intersections to obtain a set of welded points with respect to the sieve net. Although the coordinates of the weld joints in the binarized image were recognized and the inverse PCA transformation of the sieve-net coordinates was implemented, the coordinates at this time are
,
, where
m is the number of weld points in the binarized image. The welds at the original sieve-net coordinates are
,
, where
n is the number of sieve-net points. The corresponding welding point
with the smallest value of Equation (
6) is found, which is the 3D coordinate of the weld point.
The extracted steps of 3D weld points are described in Algorithm 2, which provides a description of the 3D weld point extraction method.
| Algorithm 2 Three-dimensional weld point extraction |
Require: PCA-processed 3D pixels set P, 2D skeleton intersection set W, sieve-net diameter b, PCA-transformation matrices U and . Ensure: 3D welding point .
- 1:
//Merge and extract intersections. - 2:
Given two pixels sets C and V. - 3:
for each ∈ W do - 4:
- 5:
for each , do - 6:
- 7:
end for - 8:
, and - 9:
end for - 10:
//Converting 2D pixels to 3D. - 11:
Extract 3D welding point by the Equation ( 6). - 12:
, , and . - 13:
. - 14:
return .
|
The time complexity of Algorithm 2 is determined to be , where denotes the size of the 2D skeleton intersection set, and represents the size of the PCA-processed 3D pixel set. Although the intersection’s merging step may theoretically exhibit the worst-case complexity of , practical efficiency is significantly improved due to the sparse distribution of intersections and the limited search radius.
With the algorithmic framework defined,
Section 4 will validate its performance through experiments on seven datasets, emphasizing accuracy, robustness, and computational efficiency.