A Trace Recognition of Rock Mass Point Clouds by the Fusion of Normal Tensor Voting and a Minimum Spanning Tree
Abstract
1. Introduction
2. Proposed Methods
- Step 1: Detect trace feature points on the triangulated point cloud surfaces by using the normal tensor voting method;
- Step 2: Group neighboring feature points;
- Step 3: Connect feature points belonging to the same grouping to form a trace segment using a growth algorithm;
- Step 4: Connect the trace segments that may belong to one trace;
- Step 5: Calculate an estimate of the final trace length. The overall flow of the method is shown in Figure 1.
2.1. Trace Feature Point Detection by Normal Tensor Voting Method
- (1)
- If is dominant and when and can be neglected, the vertex is the face type;
- (2)
- If and are dominant and when can be neglected and not remembered, the vertex is of the sharp edge type;
- (3)
- If , , and are approximately equal, then the vertices are of the angular type.
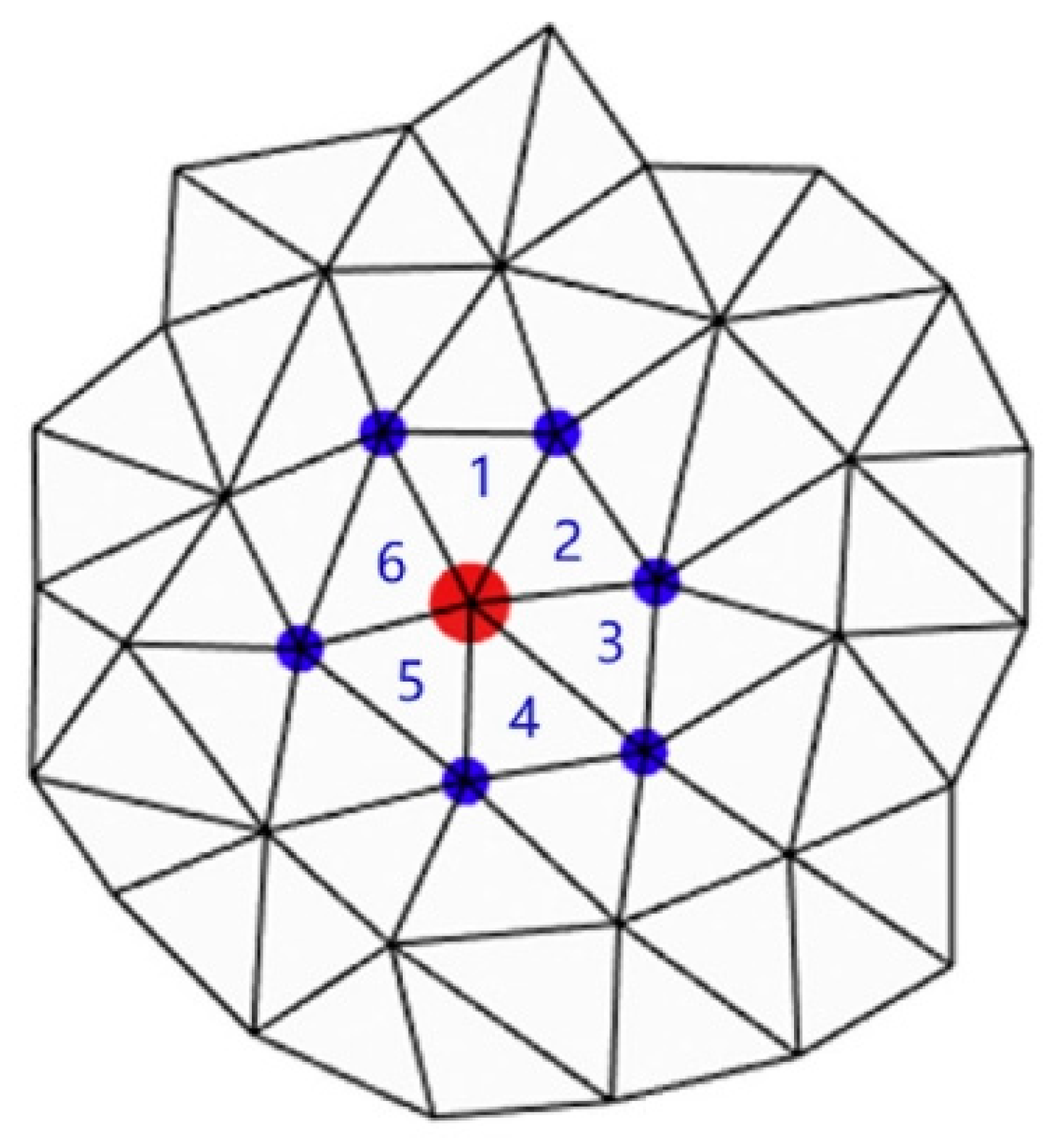
2.2. Grouping of Trace Feature Points
- (1)
- Place the angular and acute-edge points of the feature points into a separate set. One feature point is randomly selected as the initial point;
- (2)
- Calculate the angle between the current feature point and the normal vectors of the neighboring points, and compare it with the threshold value, and finally divide it into the same group;
- (3)
- Compare all the points found until there is no feature point that satisfies the threshold condition. Then, the current grouping is completed, and the next group is started;
- (4)
- Repeat the above steps for the remaining feature points until all the feature points are grouped.
2.3. Grouping of Traces Growth
- (1)
- Process each grouping using the MST algorithm to find the possible endpoints in the group;
- (2)
- Select the endpoints of the group that are furthest apart, specifying the direction of the line between the two points as the direction of the subject’s connecting line;
- (3)
- Find the surrounding neighboring feature points using one of the subject endpoints as the starting point, which is also the current connecting point;
- (4)
- Calculate the angle between the connecting line between the current point and the neighboring points and the main body connecting line, give an angle threshold of θ2, and connect the line if the angle is within the threshold;
- (5)
- The body’s connecting lines are connected according to the Euclidean distance, and its connecting lines will be used as the body part of the current grouping;
- (6)
- Since groupings containing multiple traces exist, after the subject is identified, the remaining endpoints are connected with the subject as the target until they are merged into the subject.
2.4. Trace Segments Connection
2.5. Calculation of Mean Trace Length
3. Results
3.1. The Effect of Different Parameters
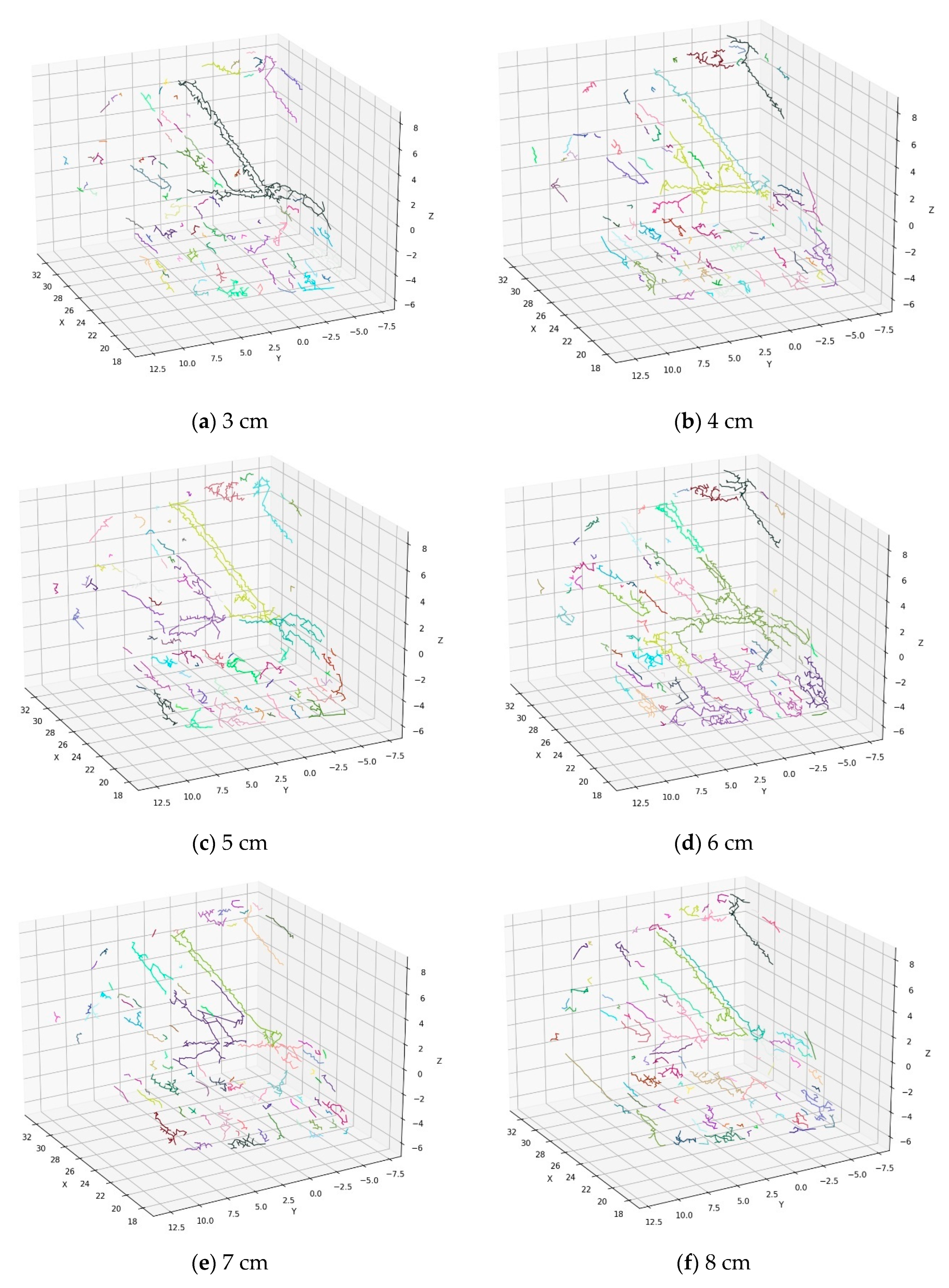
3.1.1. The Effect of Resampled Triangular Grid Cell Sizes
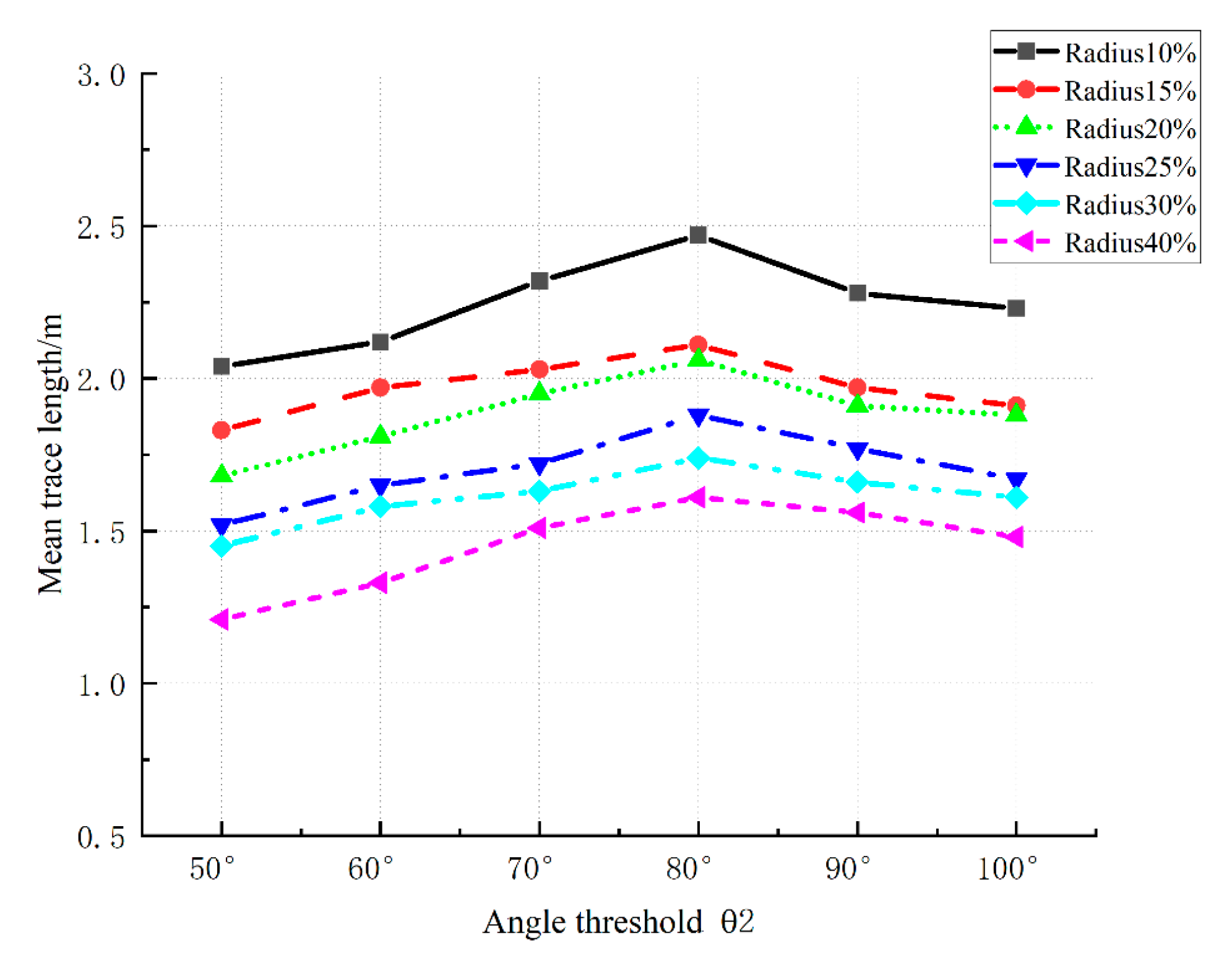
3.1.2. The Effect of the Angular Threshold
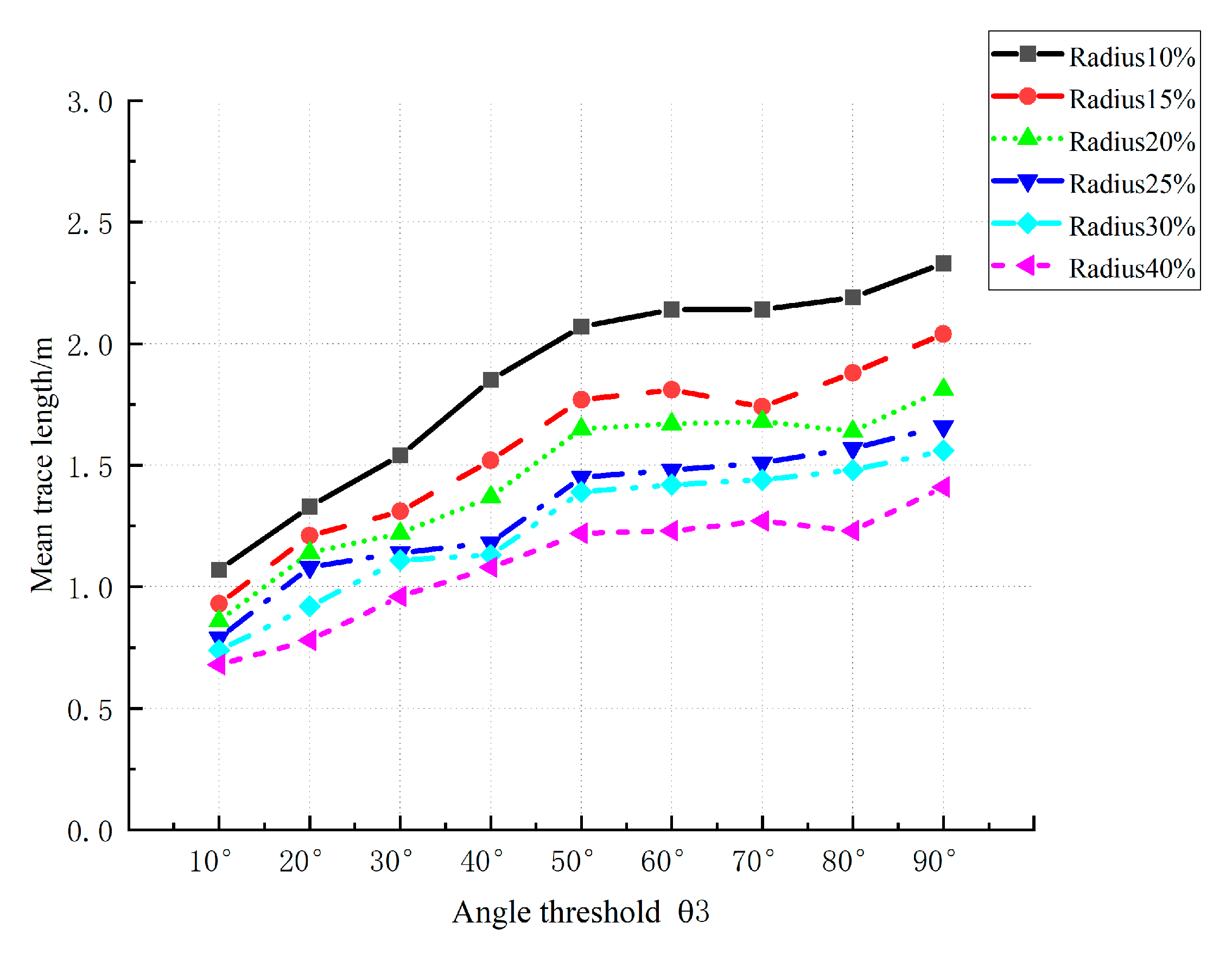
3.1.3. The Effect of the Distance Threshold d
3.1.4. The Effect of the Angular Threshold
3.2. Comparative Analysis
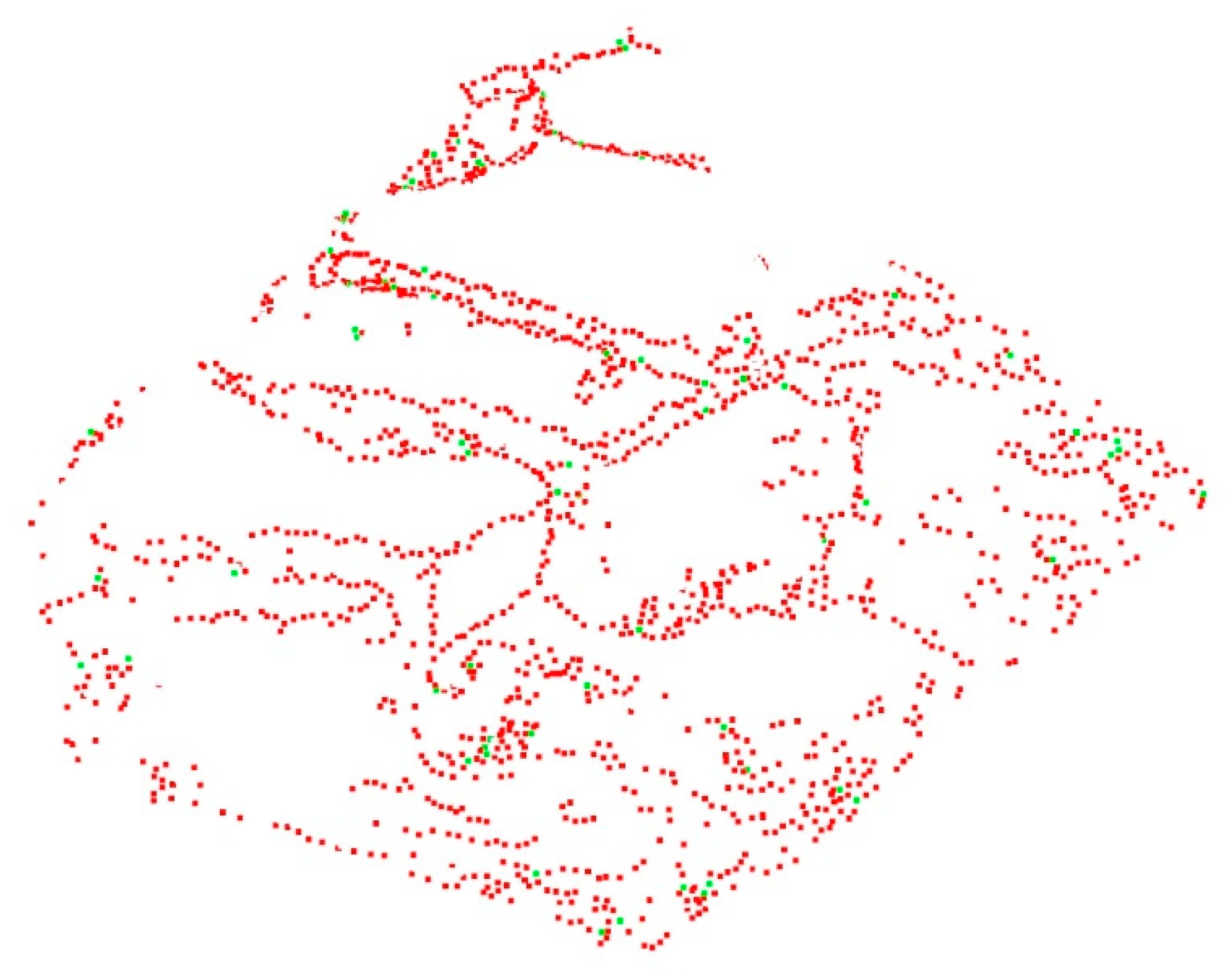
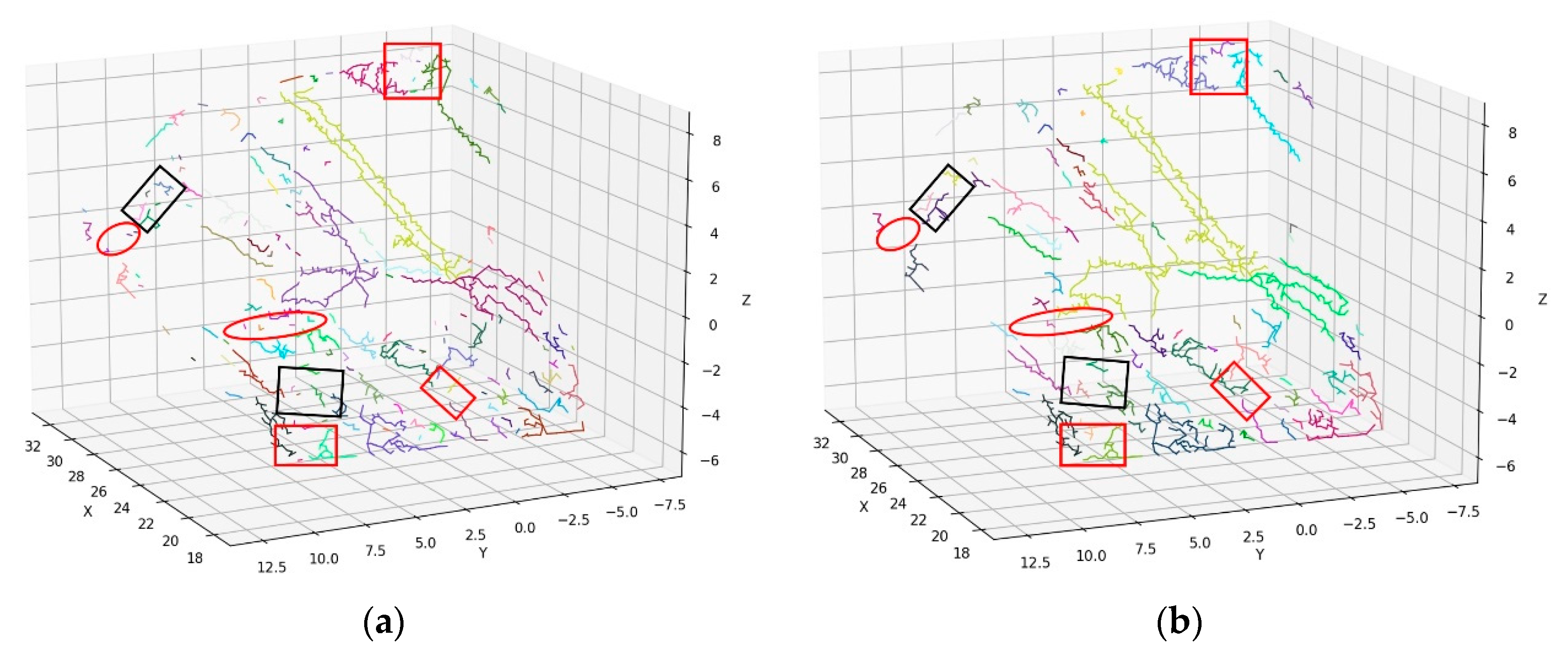
3.3. Noise Resistance Analysis
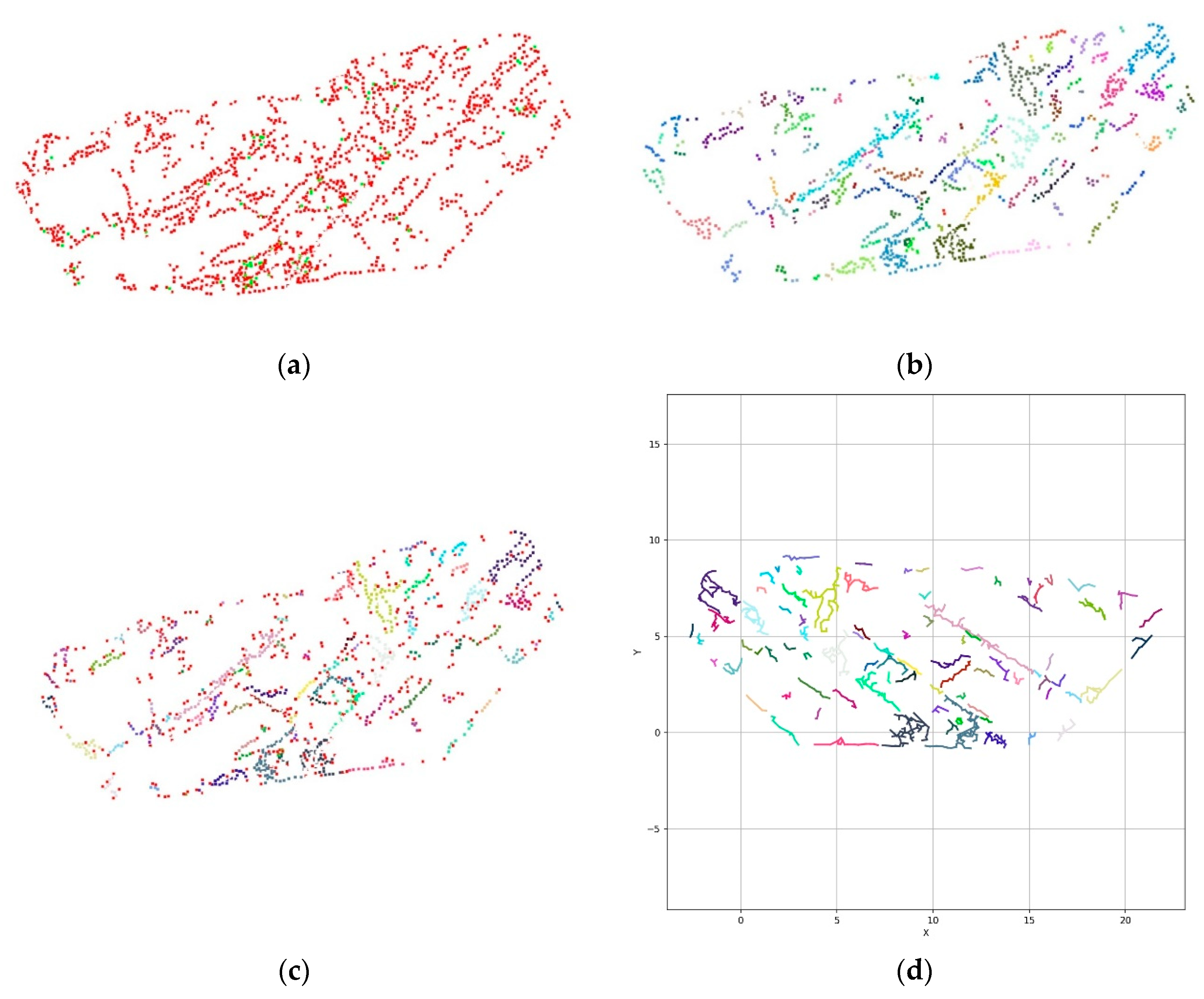
3.4. Case Study
3.5. Discussion
- (1)
- A reliability assessment of the discontinuities’ spatial persistence in stability analysis.
- (2)
- The statistical determination of representative elementary volumes (REVs) for numerical modeling.
- (3)
- An objective evaluation of rock mass quality indices (e.g., RQD and GSI).
- (1)
- The linear extension of the detected traces is obvious, robust to noise points, and better matches the main trend of the real traces;
- (2)
- The proposed method is more stable, and is able to overcome the segmentation problem of trace extraction and obtain linear and continuous traces.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, Q.; Ma, C.; Bai, Y.; He, L.; Tan, J.; Cai, Q.; Zeng, J. A Rapid Method of the Rock Mass Surface Reconstruction for Surface Deformation Detection at Close Range. Sensors 2020, 20, 5371. [Google Scholar] [CrossRef] [PubMed]
- Mehrishal, S.; Kim, J.; Song, J.J.; Sainoki, A. A semi-automatic approach for joint orientation recognition using 3D trace network analysis. Eng. Geol. 2024, 332, 107462. [Google Scholar] [CrossRef]
- Lemy, F.; Hadjigeorgiou, J. Discontinuity Trace Map Construction Using Photographs of Rock Exposures. Int. J. Rock Mech. Min. Sci. 2003, 40, 903–917. [Google Scholar] [CrossRef]
- Ferrero, A.M.; Forlani, G.; Roncella, R.; Voyat, H. Advanced Geostructural Survey Methods Applied to Rock Mass Characterization. Rock Mech. Rock Eng. 2009, 42, 631–665. [Google Scholar] [CrossRef]
- Li, X.; Chen, J.; Zhu, H. A New Method for Automated Discontinuity Trace Mapping on Rock Mass 3d Surface Model. Comput. Geosci. 2016, 89, 118–131. [Google Scholar] [CrossRef]
- Cao, T.; Xiao, A.; Wu, L.; Mao, L. Automatic Fracture Detection Based on Terrestrial Laser Scanning Data: A New Method and Case Study. Comput. Geosci. 2017, 106, 209–216. [Google Scholar] [CrossRef]
- Pan, D.; Li, Y.; Wang, X.; Xu, Z. Intelligent Image-Based Identification and 3-D Reconstruction of Rock Fractures: Implementation and Application. Tunn. Undergr. Space Technol. 2024, 145, 105582. [Google Scholar] [CrossRef]
- Gigli, G.; Casagli, N. Semi-Automatic Extraction of Rock Mass Structural Data from High Resolution Lidar Point Clouds. Int. J. Rock Mech. Min. Sci. 2011, 48, 187–198. [Google Scholar] [CrossRef]
- Lu, F.; Fu, C.; Shi, J.; Zhang, G. Attention Based Deep Neural Network for Micro-Fracture Extraction of Sequential Coal Rock Ct Images. Multimed. Tools Appl. 2022, 81, 26463–26482. [Google Scholar] [CrossRef]
- Umili, G.; Ferrero, A.; Einstein, H. A New Method for Automatic Discontinuity Traces Sampling on Rock Mass 3d Model. Comput. Geosci. 2013, 51, 182–192. [Google Scholar] [CrossRef]
- Vöge, M.; Lato, M.J.; Diederichs, M.S. Automated Rockmass Discontinuity Mapping from 3-Dimensional Surface Data. Eng. Geol. 2013, 164, 155–162. [Google Scholar] [CrossRef]
- Taghizadeh, M.; Kakaee, R.K.; Nasirabad, H.M.; Alenizi, F.A. Automatic Detection of Discontinuity Trace Maps: A Study of Image Processing Techniques in Building Stone Mines. Geomech. Eng. 2024, 36, 205. [Google Scholar]
- Chudasama, B.; Ovaskainen, N.; Tamminen, J.; Nordbäck, N.; Engström, J.; Aaltonen, I. Automated Mapping of Bedrock-Fracture Traces from Uav-Acquired Images Using U-Net Convolutional Neural Networks. Comput. Geosci. 2024, 182, 105463. [Google Scholar] [CrossRef]
- He, Y.; Hu, Z.; Wang, R.; Zhu, H.; Fu, G. Features Extraction of Point Clouds Based on Otsu’s Algorithm. Meas. Sci. Technol. 2024, 35, 065205. [Google Scholar] [CrossRef]
- Guo, J.; Wu, L.; Zhang, M.; Liu, S.; Sun, X. Towards Automatic Discontinuity Trace Extraction from Rock Mass Point Cloud without Triangulation. Int. J. Rock Mech. Min. Sci. 2018, 112, 226–237. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, Z.; Mao, Y.; Liu, S.; Zhu, W.; Yang, T. Automatic Extraction of Discontinuity Traces from 3d Rock Mass Point Clouds Considering the Influence of Light Shadows and Color Change. Remote Sens. 2022, 14, 5314. [Google Scholar] [CrossRef]
- Gézero, L.; Antunes, C. Automated Road Curb Break Lines Extraction from Mobile Lidar Point Clouds. ISPRS Int. J. Geo-Inf. 2019, 8, 476. [Google Scholar] [CrossRef]
- Ge, Y.; Cao, B.; Tang, H. Rock Discontinuities Identification from 3d Point Clouds Using Artificial Neural Network. Rock Mech. Rock Eng. 2022, 55, 1705–1720. [Google Scholar] [CrossRef]
- Mehrishal, S.; Kim, J.; Shao, Y.; Song, J.J. Artificial intelligence-aided semi-automatic joint trace detection from textured three-dimensional models of rock mass. J. Rock Mech. Geotech. Eng. 2024; in press. [Google Scholar] [CrossRef]
- Alseid, B.; Chen, J.; Huang, H.; Seo, H. Automatic Detection of Traces in 3d Point Clouds of Rock Tunnel Faces Using a Novel Roughness: Canupo Method. J. Civ. Struct. Health Monit. 2024, 17, 1703–1718. [Google Scholar] [CrossRef]
- Page, D.L.; Sun, Y.; Koschan, A.F.; Paik, J.; Abidi, M.A. Normal Vector Voting: Crease Detection and Curvature Estimation on Large, Noisy Meshes. Graph. Models 2002, 64, 199–229. [Google Scholar] [CrossRef]
- Phan, T.D.K. A Triangle Mesh-Based Corner Detection Algorithm for Catadioptric Images. Imaging Sci. J. 2018, 66, 220–230. [Google Scholar] [CrossRef]
- Kim, H.S.; Choi, H.K.; Lee, K.H. Feature Detection of Triangular Meshes Based on Tensor Voting Theory. Comput. Aided Des. 2009, 41, 47–58. [Google Scholar] [CrossRef]
- Zhang, L.; Einstein, H. Estimating the Mean Trace Length of Rock Discontinuities. Rock Mech. Rock Eng. 1998, 31, 217–235. [Google Scholar] [CrossRef]
- Zhang, K.; Wu, W.; Zhu, H.; Zhang, L.; Li, X.; Zhang, H. A Modified Method of Discontinuity Trace Mapping Using Three-Dimensional Point Clouds of Rock Mass Surfaces. J. Rock Mech. Geotech. Eng. 2020, 12, 571–586. [Google Scholar] [CrossRef]








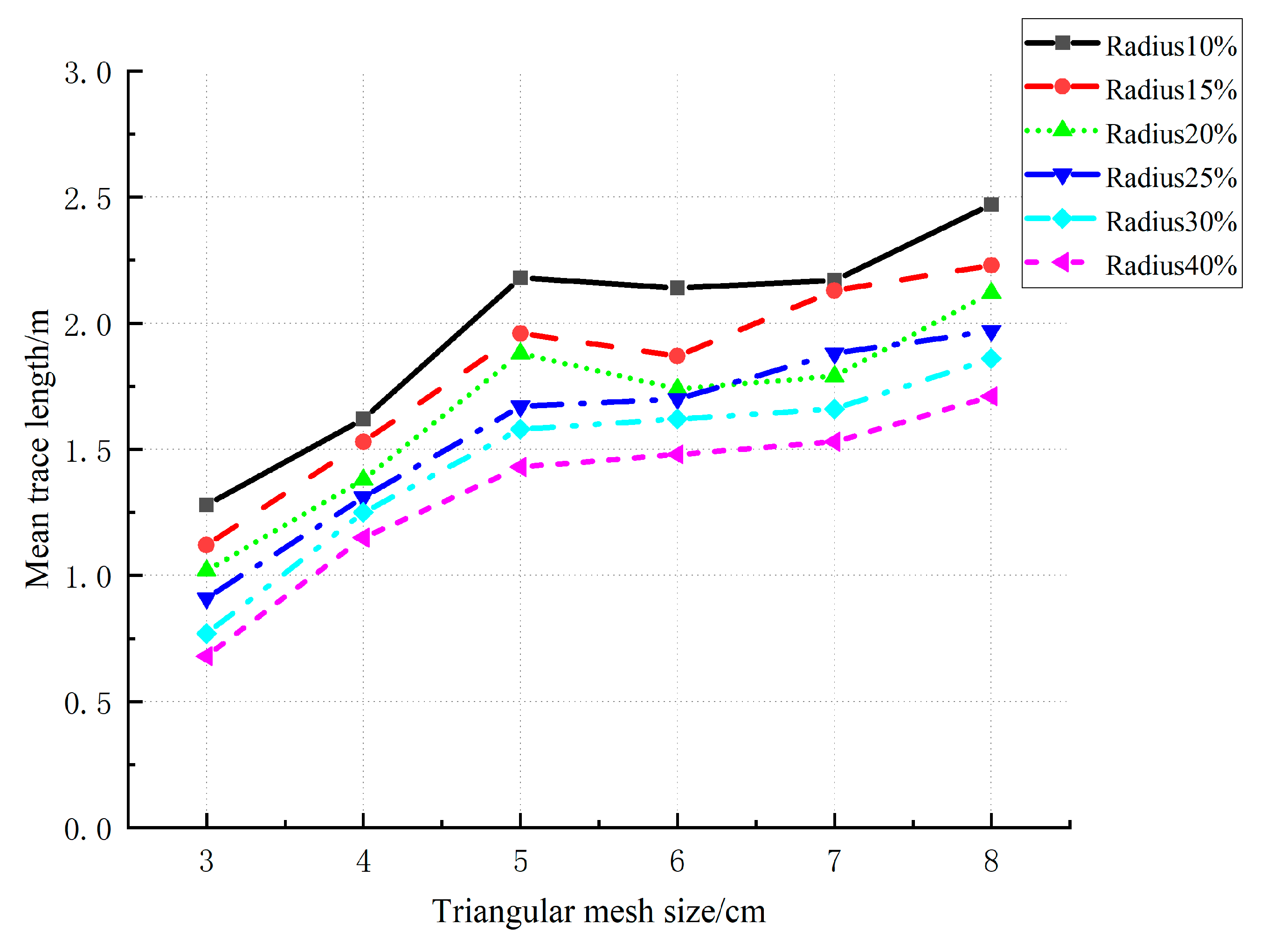






| Sampling Radii/m | Mesh Size/cm | Angle Threshold θ2 | Angle Threshold θ3 | Distance Threshold d | Mean Trace Lengths/m |
|---|---|---|---|---|---|
| 10% | 5 | 80° | 60° | 0.83 | |
| 15% | 5 | 80° | 60° | 0.97 | |
| 20% | 5 | 80° | 60° | 1.34 | |
| 25% | 5 | 80° | 60° | 1.18 | |
| 30% | 5 | 80° | 60° | 1.04 | |
| 35% | 5 | 80° | 60° | 0.92 | |
| 40% | 5 | 80° | 60° | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Yang, Y.; An, Q.; Han, X. A Trace Recognition of Rock Mass Point Clouds by the Fusion of Normal Tensor Voting and a Minimum Spanning Tree. Symmetry 2025, 17, 415. https://doi.org/10.3390/sym17030415
Chen X, Yang Y, An Q, Han X. A Trace Recognition of Rock Mass Point Clouds by the Fusion of Normal Tensor Voting and a Minimum Spanning Tree. Symmetry. 2025; 17(3):415. https://doi.org/10.3390/sym17030415
Chicago/Turabian StyleChen, Xijiang, Yi Yang, Qing An, and Xianquan Han. 2025. "A Trace Recognition of Rock Mass Point Clouds by the Fusion of Normal Tensor Voting and a Minimum Spanning Tree" Symmetry 17, no. 3: 415. https://doi.org/10.3390/sym17030415
APA StyleChen, X., Yang, Y., An, Q., & Han, X. (2025). A Trace Recognition of Rock Mass Point Clouds by the Fusion of Normal Tensor Voting and a Minimum Spanning Tree. Symmetry, 17(3), 415. https://doi.org/10.3390/sym17030415







