Favorable Symmetric Structures of Radiopharmaceutically Important Anionic (2-) Cyclen-Based Ligands
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Characteristic Conformational Properties of Cyclen-Based Ligands
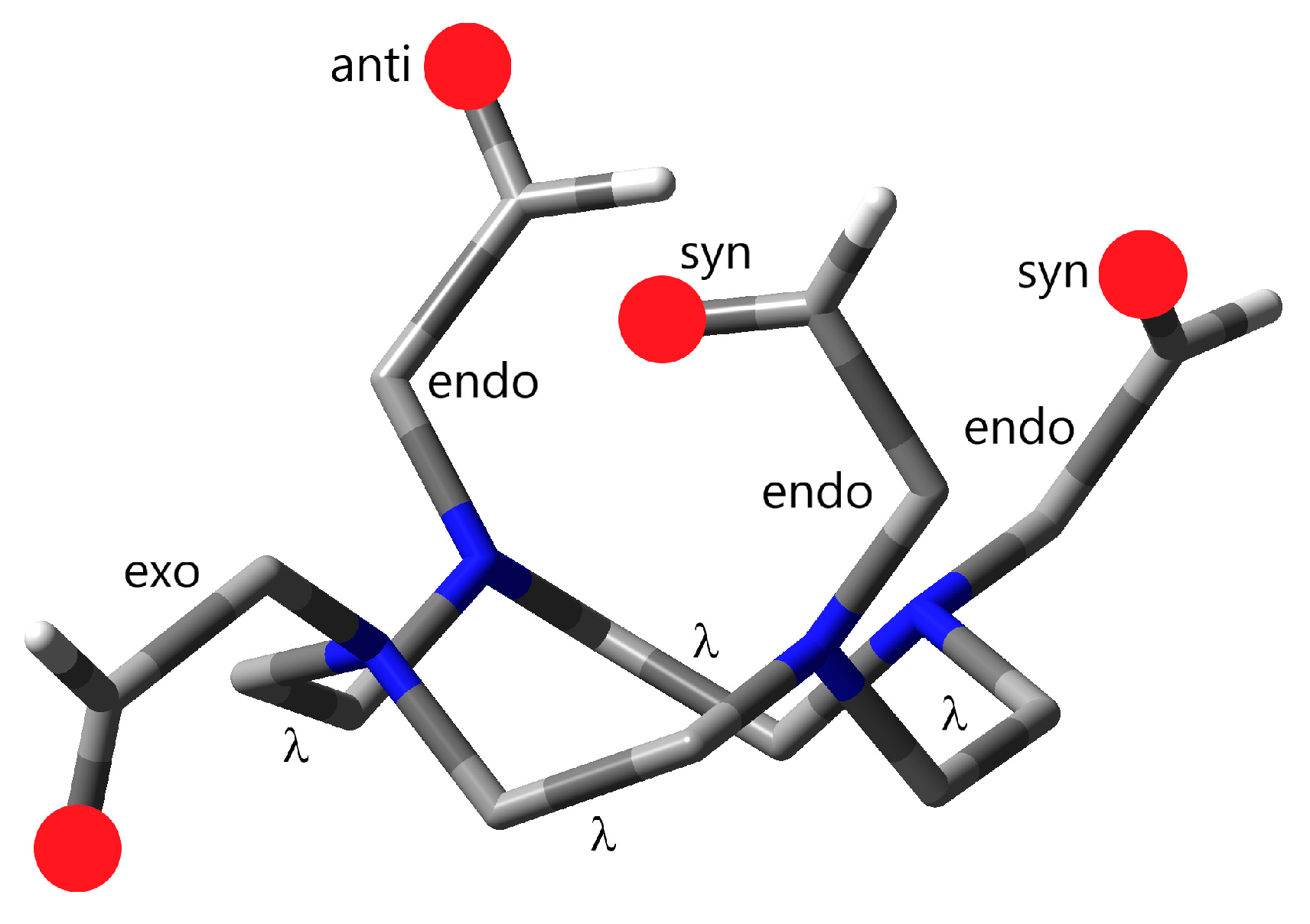
- The conformation of the cyclen ring is determined by the four-ring N–C–C–N torsional angles. They can occur as δ- or λ-gauche arrangements (positive or negative sign, respectively, according to Corey and Bailar [49]). In the metal complexes of cyclen-based ligands, generally uniform cyclen conformations—clockwise (δδδδ) or equivalent enantiomeric anticlockwise (λλλλ)—have been found [15,22,50].
- The pendant arms at the cyclen N-s can turn towards the cavity of the cyclen ring or away from the cavity (endo or exo orientation, respectively; Figure 2).
- Similarly, the donor groups of the pendant arms can point towards the cavity (in the complexes coordinating to the encapsulated metal ions in this way, syn orientation) or can turn outside for interactions with solvent molecules (anti orientation; Figure 2). The syn/anti orientations are relevant only for endo pendant arms.
3.2. MeDO2PA
3.3. H2DO2PA
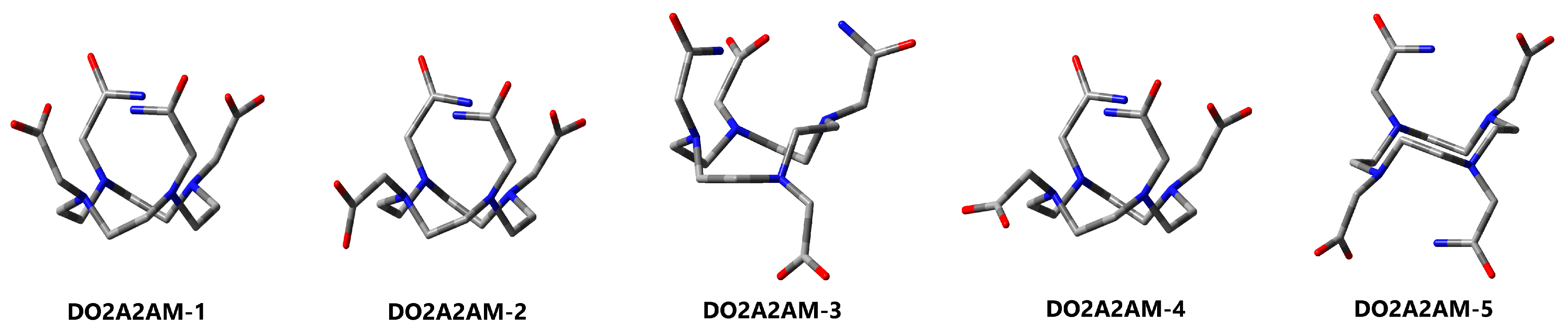
3.4. DO2A2AM
3.5. DO2A2Py
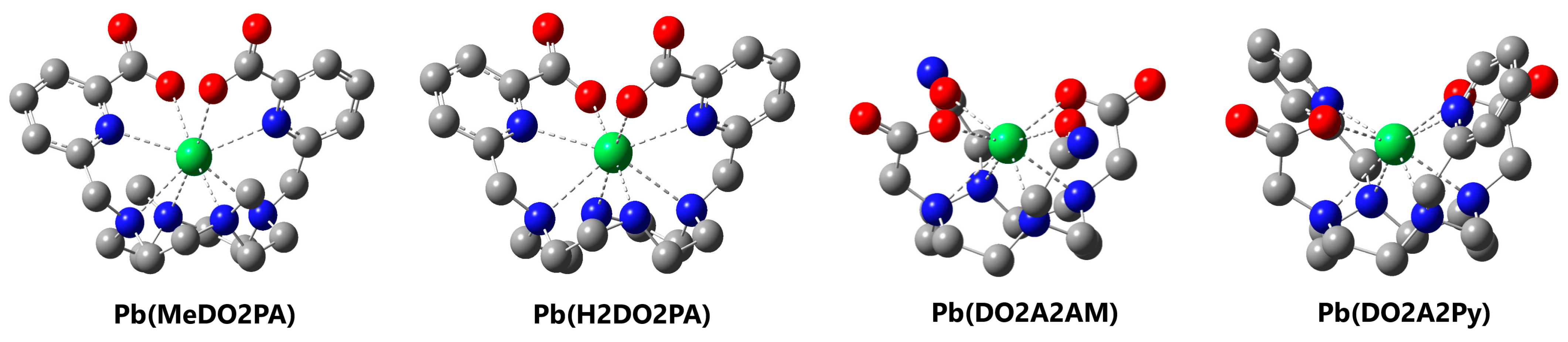
3.6. Stabilities of Complexes with Pb2+
4. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Driggers, E.M.; Hale, S.P.; Lee, J.; Terrett, N.K. The exploration of macrocycles for drug discovery—An underexploited structural class. Nat. Rev. Drug Discov. 2008, 7, 608–624. [Google Scholar] [CrossRef] [PubMed]
- Giordanetto, F.; Kihlberg, J. Macrocyclic Drugs and Clinical Candidates: What Can Medicinal Chemists Learn from Their Properties? J. Med. Chem. 2014, 57, 278–295. [Google Scholar] [CrossRef]
- Wei, W.; Rosenkrans, Z.T.; Liu, J.; Huang, G.; Luo, Q.-Y.; Cai, W. ImmunoPET: Concept, Design, and Applications. Chem. Rev. 2020, 120, 3787–3851. [Google Scholar] [CrossRef]
- Mota, F.; Ordonez, A.A.; Firth, G.; Ruiz-Bedoya, C.A.; Ma, M.T.; Jain, S.K. Radiotracer Development for Bacterial Imaging. J. Med. Chem. 2020, 63, 1964–1977. [Google Scholar] [CrossRef]
- Kręcisz, P.; Czarnecka, K.; Królicki, L.; Mikiciuk-Olasik, E.; Szymański, P. Radiolabeled Peptides and Antibodies in Medicine. Bioconjug. Chem. 2021, 32, 25–42. [Google Scholar] [CrossRef]
- Llop, J.; Lammers, T. Nanoparticles for Cancer Diagnosis, Radionuclide Therapy and Theranostics. ACS Nano 2021, 15, 16974–16981. [Google Scholar] [CrossRef]
- Sgouros, G.; Bodei, L.; McDevitt, M.R.; Nedrow, J.R. Radiopharmaceutical therapy in cancer: Clinical advances and challenges. Nat. Rev. Drug Discov. 2020, 19, 589–608. [Google Scholar] [CrossRef]
- St. James, S.; Bednarz, B.; Benedict, S.; Buchsbaum, J.C.; Dewaraja, Y.; Frey, E.; Hobbs, R.; Grudzinski, J.; Roncali, E.; Sgouros, G.; et al. Current Status of Radiopharmaceutical Therapy. Int. J. Radiat. Oncol. Biol. Phys. 2021, 109, 891–901. [Google Scholar] [CrossRef]
- Rondon, A.; Rouanet, J.; Degoul, F. Radioimmunotherapy in Oncology: Overview of the Last Decade Clinical Trials. Cancers 2021, 13, 5570. [Google Scholar] [CrossRef]
- Zhang, T.; Lei, H.; Chen, X.; Dou, Z.; Yu, B.; Su, W.; Wang, W.; Jin, X.; Katsube, T.; Wang, B.; et al. Carrier systems of radiopharmaceuticals and the application in cancer therapy. Cell Death Discov. 2024, 10, 16. [Google Scholar] [CrossRef]
- Bazak, R.; Houri, M.; El Achy, S.; Hussein, W.; Refaat, T. Passive targeting of nanoparticles to cancer: A comprehensive review of the literature. Mol. Clin. Oncol. 2014, 2, 904–908. [Google Scholar] [CrossRef]
- Kleynhans, J.; Grobler, A.F.; Ebenhan, T.; Sathekge, M.M.; Zeevaart, J.-R. Radiopharmaceutical enhancement by drug delivery systems: A review. J. Control. Release 2018, 287, 177–193. [Google Scholar] [CrossRef]
- Kostelnik, T.I.; Orvig, C. Radioactive Main Group and Rare Earth Metals for Imaging and Therapy. Chem. Rev. 2019, 119, 902–956. [Google Scholar] [CrossRef]
- Peltek, O.O.; Muslimov, A.R.; Zyuzin, M.V.; Timin, A.S. Current outlook on radionuclide delivery systems: From design consideration to translation into clinics. J. Nanobiotechnol. 2019, 17, 90. [Google Scholar] [CrossRef]
- Price, E.W.; Orvig, C. Matching chelators to radiometals for radiopharmaceuticals. Chem. Soc. Rev. 2014, 43, 260–290. [Google Scholar] [CrossRef]
- Csajbók, É.; Baranyai, Z.; Bányai, I.; Brucher, E.; Király, R.; Muller-Fahrnow, A.; Platzek, J.; Raduchel, B.; Schäfer, M. Equilibrium, 1H and 13C NMR spectroscopy, and X-ray diffraction studies on the complexes Bi(DOTA)− and Bi(DO3A-Bu). Inorg. Chem. 2003, 42, 2342–2349. [Google Scholar] [CrossRef]
- Tosato, M.; Lazzari, L.; Marco, V.D. Revisiting Lead(II)-1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetic Acid Coordination Chemistry in Aqueous Solutions: Evidence of an Underestimated Thermodynamic Stability. ACS Omega 2022, 7, 15596–15602. [Google Scholar] [CrossRef]
- Deal, K.A.; Davis, I.A.; Mirzadeh, S.; Kennel, S.J.; Brechbiel, M.W. Improved in vivo stability of actinium-225 macrocyclic complexes. J. Med. Chem. 1999, 42, 2988–2992. [Google Scholar] [CrossRef]
- Kovács, A. Favorable symmetric structures of radiopharmaceutically important neutral cyclen-based ligands. Symmetry 2024, 16, 1668. [Google Scholar] [CrossRef]
- Lima, L.M.P.; Beyler, M.; Oukhatar, F.; Le Saec, P.; Faivre-Chauvet, A.; Platas-Iglesias, C.; Delgado, R.; Tripier, R. H2Me-do2pa: An attractive chelator with fast, stable and inert natBi3+ and 213Bi3+ complexation for potential a-radioimmunotherapy applications. Chem. Commun. 2014, 50, 12371–12374. [Google Scholar] [CrossRef]
- Lima, L.M.P.; Beyler, M.; Delgado, R.; Platas-Iglesias, C.; Tripier, R. Investigating the Complexation of the Pb2+/Bi3+ Pair with Dipicolinate Cyclen Ligands. Inorg. Chem. 2015, 54, 7045–7057. [Google Scholar] [CrossRef]
- Kovács, A.; Varga, Z. Theoretical Study of Metal–Ligand Interactions in Lead Complexes with Radiopharmaceutical Interest. Molecules 2024, 29, 4198. [Google Scholar] [CrossRef]
- Glendening, E.D.; Streitwieser, A. Natural energy decomposition analysis: An energy partitioning procedure for molecular interactions with application to weak hydrogen bonding, strong ionic, and moderate donor–acceptor interactions. J. Chem. Phys. 1994, 100, 2900–2909. [Google Scholar] [CrossRef]
- Glendening, E.D. Natural Energy Decomposition Analysis: Extension to Density Functional Methods and Analysis of Cooperative Effects in Water Clusters. J. Phys. Chem. A 2005, 109, 11936–11940. [Google Scholar] [CrossRef]
- Gutten, O.; Bím, D.; Řezáč, J.; Rulíšek, L. Macrocycle Conformational Sampling by DFT-D3/COSMO-RS Methodology. J. Chem. Inf. Model. 2018, 58, 48–60. [Google Scholar] [CrossRef]
- Mohamadi, F.; Richards, N.G.J.; Guida, W.C.; Liskamp, R.; Lipton, M.; Caufield, C.; Chang, G.; Hendrickson, T.; Still, W.C. Macromodel—An integrated software system for modeling organic and bioorganic molecules using molecular mechanics. J. Comput. Chem. 1990, 11, 440–467. [Google Scholar] [CrossRef]
- Watts, K.S.; Dalal, P.; Tebben, A.J.; Cheney, D.L.; Shelley, J.C. Macrocycle Conformational Sampling with MacroModel. J. Chem. Inf. Model. 2014, 54, 2680–2696. [Google Scholar] [CrossRef]
- Shivakumar, D.; Harder, E.; Damm, W.; Friesner, R.A.; Sherman, W. Improving the Prediction of Absolute Solvation Free Energies Using the Next Generation OPLS Force Field. J. Chem. Theory Comput. 2012, 8, 2553–2558. [Google Scholar] [CrossRef]
- Still, W.C.; Tempczyk, A.; Hawley, R.C.; Hendrickson, T. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc. 1990, 112, 6127–6129. [Google Scholar] [CrossRef]
- Schrödinger Release 2024-1; Schrödinger, LLC.: New York, NY, USA, 2024.
- Olanders, G.; Alogheli, H.; Brandt, P.; Karlén, A. Conformational analysis of macrocycles: Comparing general and specialized methods. J. Comput. Aided Mol. Des. 2020, 34, 231–252. [Google Scholar] [CrossRef]
- Polak, E.; Ribiere, G. Note sur la convergence de méthodes de directions conjuguées. ESAIM 1969, 3, 35–43. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M. Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Brandenburg, J.G.; Bannwarth, C.; Hansen, A.; Grimme, S. B97-3c: A revised low-cost variant of the B97-D density functional method. J. Chem. Phys. 2018, 148, 064104. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868, Errata in Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Orca, Input Library Webpage. Available online: https://sites.google.com/site/orcainputlibrary/numerical-precision (accessed on 20 June 2025).
- Caldeweyher, E.; Bannwarth, C.; Grimme, S. Extension of the D3 dispersion coefficient model. J. Chem. Phys. 2017, 147, 034112. [Google Scholar] [CrossRef]
- Caldeweyher, E.; Ehlert, S.; Hansen, A.; Neugebauer, H.; Spicher, S.; Bannwarth, C.; Grimme, S. A generally applicable atomic-charge dependent London dispersion correction. J. Chem. Phys. 2019, 150, 154122. [Google Scholar] [CrossRef]
- Dunlap, B.I. Robust and variational fitting. Phys. Chem. Chem. Phys. 2000, 2, 2113–2116. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Chen, X.-Y.; Landis, C.R.; Neese, F. All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms. J. Chem. Theory Comput. 2008, 4, 908–919. [Google Scholar] [CrossRef]
- van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic total energy using regular approximations. J. Chem. Phys. 1994, 101, 9783–9792. [Google Scholar] [CrossRef]
- Martin, R.L.; Hay, P.J.; Pratt, L.R. Hydrolysis of Ferric Ion in Water and Conformational Equilibrium. J. Phys. Chem. A 1998, 102, 3565–3573. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Corey, E.J.; Bailar, J.C. The Stereochemistry of Complex Inorganic Compounds. XXII. Stereospecific Effects in Complex Ions. J. Am. Chem. Soc. 1959, 81, 2620–2629. [Google Scholar] [CrossRef]
- Viola-Villegas, N.; Doyle, R.P. The coordination chemistry of 1,4,7,10-tetraazacyclododecane-N,N′,N″,N‴-tetraacetic acid (H4DOTA): Structural overview and analyses on structure-stability relationships. Coord. Chem. Rev. 2009, 253, 1906–1925. [Google Scholar] [CrossRef]
- Kovács, A.; Varga, Z. Metal–ligand interactions in complexes of cyclen-based ligands with Bi and Ac. Struct. Chem. 2021, 32, 1719–1731. [Google Scholar] [CrossRef]
- Martinez, C.R.; Iverson, B.L. Rethinking the term “pi-stacking”. Chem. Sci. 2012, 3, 2191–2201. [Google Scholar] [CrossRef]
- Lewis, M.; Bagwill, C.; Hardebeck, L.; Wireduaah, S. Modern Computational Approaches to Understanding Interactions of Aromatics. In Aromatic Interactions: Frontiers in Knowledge and Application; Johnson, D.W., Hof, F., Eds.; The Royal Society of Chemistry: Cambridge, UK, 2016; pp. 1–17. [Google Scholar] [CrossRef]




| 1 (C2) | 2 | 3 (C2) | 4 | 5 | ||
|---|---|---|---|---|---|---|
| Pendants 2 | Arm | 2 × endo | 2× endo | 2 × endo | 1 × endo 1 × exo | 2 × endo |
| PA | 2 × syn | 1 × anti 1 × syn | 2 × syn | 1 × syn | 2 × anti | |
| ∆ECPCM | 0.0 | 2.5 | 4.4 | 10.4 | 6.2 | |
| ∆GCPCM | 0.0 | 0.4 | 4.9 | 4.2 | 1.7 | |
| ∆GSMD | 0.0 | 4.0 | 9.9 | 10.9 | 11.0 |
| 1 (C2) | 2 | 3 | 4 | 5 | ||
|---|---|---|---|---|---|---|
| Pendants 2 | Arm | 2 × endo | 2 × endo | 2 × endo | 2 × endo | 2 × endo |
| PA | 2 × anti | 1 × anti 1 × syn | 1 × anti 1 × syn | 2 × anti | 2 × anti | |
| ∆ECPCM | 1.0 | 0.0 | 2.1 | 6.0 | 6.5 | |
| ∆GCPCM | 0.0 | 0.3 | 2.3 | 4.3 | 4.7 | |
| ∆GSMD | 0.0 | 1.8 | 2.6 | 4.6 | 4.9 |
| 1 (C2) | 2 | 3 | 4 | 5 (Ci) | ||
|---|---|---|---|---|---|---|
| Pendants 2 | COO-Arm | 2 × endo | 1 × endo 1 × exo | 1 × endo 1 × exo | 1 × endo 1 × exo | 2 × endo |
| CONH2-Arm | 2 × endo | 2 × endo | 2 × endo | 2 × endo | 2 × endo | |
| C=OCOO | 2 × anti | 1 × anti | 1 × syn | 1 × anti | 2 × anti | |
| C=OCONH2 | 2 × anti | 2 × anti | 2 × anti | 2 × anti | 2 × anti | |
| ∆ECPCM | 0.0 | 10.4 | 17.1 | 16.7 | 16.1 | |
| ∆GCPCM | 0.0 | 8.5 | 11.5 | 15.4 | 12.7 | |
| ∆GSMD | 0.0 | 9.0 | 11.8 | 11.9 | 12.0 | |
| Cyclen conformation 3 | δδδδ | δδδδ | δδδλ | δδδδ | δδλλ | |
| Hydrogen bonding | N-H···O | 4× | 2× | 3× | 2× | 4× |
| N-H···N | 4× | 4× | 3× | 4× | 4× | |
| C-H···O | 4× | 4× | 2× | 5× | 2× | |
| C-H···N | 2× | 3× | 2× | 3× | 4× | |
| Σ | 14 | 13 | 10 | 14 | 14 |
| 1 (C2) | 2 (C2) | 3 | 4 | 5 (C2) | ||
|---|---|---|---|---|---|---|
| Pendants 2 | COO-Arm | 2 × endo | 2 × endo | 1 × endo 1 × exo | 2 × endo | 2 × exo |
| Py-Arm | 2 × endo | 2 × endo | 2 × endo | 1 × endo 1 × exo | 2 × endo | |
| C=O | 2 × anti | 2 × anti | 1 × anti | 2 × anti | - | |
| NPy | 2 × anti | 2 × syn | 2 × anti | 1 × anti | 2 × syn | |
| ∆ECPCM | 0.0 | 6.6 | 6.1 | 13.6 | 14.0 | |
| ∆GCPCM | 0.0 | 6.1 | 2.0 | 9.7 | 10.9 | |
| ∆GSMD | 0.0 | 3.1 | 4.9 | 11.4 | 12.7 |
| Complex (PbL) | ∆Eint 1 | ∆Gdiss 2 | log KPbL 3 |
|---|---|---|---|
| Pb(MeDO2PA) | −2523 | 326.1 | 18.44(2) |
| Pb(H2DO2PA) | −2471 | 313.1 | 16.44(2) |
| Pb(DO2A2AM) | −2520 | 335.0 | - |
| Pb(DO2A2Py) | −2513 | 342.0 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovács, A. Favorable Symmetric Structures of Radiopharmaceutically Important Anionic (2-) Cyclen-Based Ligands. Symmetry 2025, 17, 1466. https://doi.org/10.3390/sym17091466
Kovács A. Favorable Symmetric Structures of Radiopharmaceutically Important Anionic (2-) Cyclen-Based Ligands. Symmetry. 2025; 17(9):1466. https://doi.org/10.3390/sym17091466
Chicago/Turabian StyleKovács, Attila. 2025. "Favorable Symmetric Structures of Radiopharmaceutically Important Anionic (2-) Cyclen-Based Ligands" Symmetry 17, no. 9: 1466. https://doi.org/10.3390/sym17091466
APA StyleKovács, A. (2025). Favorable Symmetric Structures of Radiopharmaceutically Important Anionic (2-) Cyclen-Based Ligands. Symmetry, 17(9), 1466. https://doi.org/10.3390/sym17091466









