Abstract
A single circular DNA or polypeptide strand can be used to construct nanostructures based on the mathematical concept of strong traces. It is known that if a special face graph of a 2-connected plane graph G is a tree, then G has a thickened graph with only one boundary component. However, to ensure that this thickened graph contains only a single boundary component, it is not necessary for the special face graph of G to be a tree. In this paper, we summarize a combinatorial method, called the flat-based operations, for obtaining a matrix where determines whether associated with G contains just one boundary component. By applying this method, we can easily determine if the number of boundary components of some is one. Further, we characterize a type of 2-connected plane graph whose thickened graph has more than one boundary component and then has no antiparallel strong trace.
1. Introduction
DNA and polypeptides are two types of biomolecules that can self-assemble into complex three-dimensional shapes. One common shape is the polyhedron, which is a closed spatial graph composed of several plane polygons. DNA polyhedra have important applications in biology and biochemistry, such as drug delivery and disease treatment. To achieve these applications, researchers have developed and synthesized various polyhedral structures, such as DNA tetrahedra, cubes, hexahedra, dodecahedra, etc. [1,2,3,4,5,6,7,8,9,10]. These structures can be described by mathematical language, namely DNA polyhedral cages. To construct a specific DNA polyhedral structure, a specific arrangement of junctions is required at the vertices of the polyhedral graph, which can be realized by biological engineering methods.
By using orthogonal segments that form coiled-coils, a method is proposed to design self-assembled polypeptide nanostructures that have polyhedral shapes. A tetrahedral cage, TET12, can be folded from a single polypeptide chain with 12 coiled-coil segments [11], which is shown in Figure 1. Some other polyhedral shapes are also designed by using this method, such as triangular prisms and trigonal bipyramids [12,13]. Fijavž described these polypeptides [14] by using strong traces. How polypeptide nanostructures are modeled by antiparallel strong traces were studied by Klazara and Rus, respectively [14,15].
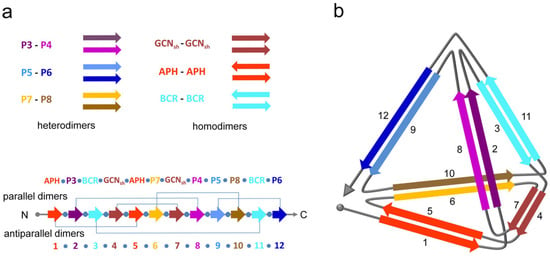
Figure 1.
(a) 12 coiled-coil segments which can be self-assembled into a single polypeptide chain; (b) Self-assembly of polypeptides into a tetrahedral shape [11].
Based on biologically stable configurations, strong trace is a good mathematical model for designing polypeptide and DNA nanostructures. Fijavž et al. [14] provided a necessary and sufficient condition for a graph G to have an antiparallel or parallel strong trace. Jonoska and Saito found that the quantity and shape of DNA structures are influenced by the boundary components of a thickened graph. Specifically, the number of circular DNA strands is linked to the boundary curves of the thickened graph [16]. Jonoska and Twarock designed nucleic acid dodecahedral molecules, and drew blueprints of DNA dodecahedra with only two strands by using 3-arms as building blocks [17]. Using only one or two strands, Cheng and Diao designed DNA structures by 3-arms, and figured out the smallest number and position of these 3-arms [18]. Subsequently, they also created more complex DNA cages with a single branch on a 2-connected planar graph, using junctions of odd-crossing curves and 0-crossing curves, where the construction of a special face graph is a tree [19]. They obtained a necessary and sufficient condition for the special face graph of a 2-connected plane graph G to be a tree. They also noted that, if the special face graph is not a tree, the number of components of the constructed DNA or polypeptide cage may be one or greater than one.
The components of DNA or polypeptide cages are of significant importance for the design and adaptation of increasingly complex cage-like structures and functions, which play an important role in catalysis, materials science, and medicine. The number of these components can alter the morphology, stability, and assembly/disassembly characteristics of protein cages. Furthermore, these components of protein cages can be modified through methods such as supercharging, cyclic permutation, direct evolution, and genetic fusion of biologically orthogonal functional groups, thereby enhancing their efficiency in drug encapsulation and release [20,21,22]. Notably, recent research highlights the relevance of this component-related exploration in the context of broader studies on DNA and polypeptide nanostructures. In 2022, Edwardson highlighted that the number of components within protein cages from a biological perspective, which is related to the boundary components we study, directly impacts drug encapsulation efficiency. He emphasized that understanding these components is essential for optimizing the functions of cages in biological applications [20]. In 2023, Majsterkiewicz et al. mathematically pointed out that topological features like boundary components play a decisive role in determining the connectability and the functional modifiability of cages [21].
In this paper, we continue the work of Diao et al., and provide a new combinatorial method called the flat-based operations for obtaining the target matrix denoted by , where the determinant only equals to 0 or 1. If , then the number of components of the constructed DNA or polypeptide cage is greater than one. If , then the number of components of the constructed DNA or polypeptide cage is equal to one. Further, we also characterize a type of 2-connected plane graph whose thickened graph has more than one boundary component and then has no antiparallel strong trace. Our research provides new perspectives and tools for understanding and designing new polypeptide nanostructures.
2. Preliminaries
2.1. Double Trace and Its Properties
All graphs considered in this paper are finite and contain no loops or multiple edges. Some basic terminologies in graph theory can be found in [23], while some terminologies in algebraic topology can be found in [24]. Let G be a graph with and as its vertex set and edge set, respectively. Let and denote the number of vertices and edges of G, respectively. Let W be a closed walk that traverses every edge of G twice. Then W is called a double trace of G. If W traverses an edge e of G in opposite (or the same) direction, then e is called an antiparallel (or parallel) edge with respect to W. A double trace W is called an antiparallel (or parallel) trace if all the edges of G are traversed in the opposite (or the same) directions.
Proposition 1
([14]). Any connected graph G contains a double trace.
Let be a double trace of G of length l. Let v be a vertex of G and N be a subset of , where denotes the set of all vertices adjacent to v. We say that W has an N-repetition at v if the following holds: For every , if , then if and only if , where i is under modulo l. Intuitively, whenever we enter v from a vertex in N, we also exit to a vertex in N from v. If , the repetition is also called a k-repetition. Figure 2 gives an example of 3- and 4-repetition at v where . The N-repetition is called trivial if N is either ∅ or . A double trace is called a strong trace if it has only trivial repetitions. Then we have the following theorem.
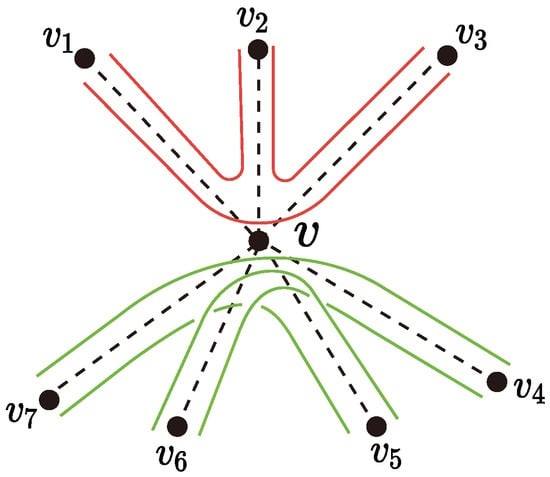
Figure 2.
A 4-repetition (marked in green) and a 3-repetition (marked by in red) at the vertex v where the drawing of the solid lines is the visualization of a part of W.
Theorem 1
([14]). Any connected graph G contains a strong trace.
A cellularly embedded graph G means that G is embedded in a closed surface such that every connected component of the complement of the union of the points and arcs associated with the vertices and edges of G, denoted by , is homeomorphic to an open disk, called a face. Furthermore, if the number of faces is k, we say that G has a k-face embedding. A thickened graph (of G) is defined as a compact orientable surface such that G is topologically embedded (as a 1-complex) in as a deformation retract (see [24] for examples of deformation retract). By capping each boundary component of the thickened graph with a topological disk, we obtain a closed orientable surface without boundary. It implies that G is cellularly embedded in . Then we have the following theorem.
Theorem 2
([14]). A graph G can be cellularly embedded in an orientable surface with a single face if and only if it admits an antiparallel strong trace.
2.2. Some Basic Results in Knot Theory
The boundary of the thickened graph can also be seen as a link in . Then we outline some basic terminologies and results in knot theory below. Some basic terminologies in knot theory can be found in [25,26].
Theorem 3
([25]). Let L be an arbitrary oriented knot (or link) in . Then there is an orientable connected surface F in with L as its boundary.
The surface F is called a Seifert surface of L. Let D be a regular oriented diagram of L. A method called Seifert decomposition can be used to construct the Seifert surface and it is dependent on the choice of D. The knot book [25] explains how to construct the Seifert surface by Seifert decomposition where all types of crossings in D are smoothed out as illustrated in Figure 3.
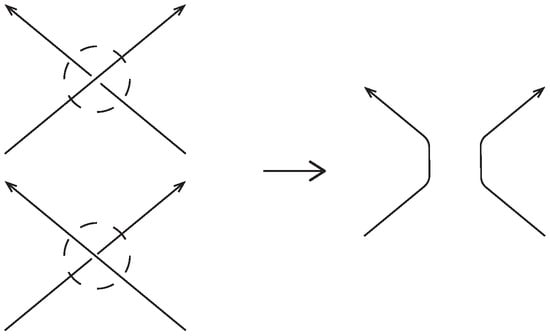
Figure 3.
Smoothing the crossings by Seifert decomposition where the arrows represent the orientations for arcs.
Then we obtain a collection of circles that do not intersect each other, which are called Seifert circles. Each Seifert circle can be spanned by a topological disk. By attaching positive or negative bands as shown in Figure 4 among these Seifert circles according to the types of crossings of D, we can obtain a connected and orientable surface F. This surface is known as the Seifert surface and is constructed by Seifert decomposition. The boundary of F is the original L. Figure 5 gives an example of the Seifert decomposition of the Hopf link with its Seifert graph. Moreover, if we contrast each disk to a point, and narrow each band to an edge, then we obtain the Seifert graph of D. Denote the Seifert graph by . Note that is bipartite and plane.
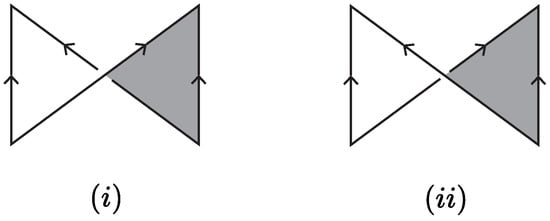
Figure 4.
Two types of half-twisted bands. In each band the grey and white regions represent distinct sides of the band. (i) The positive band corresponding to a positive crossing; (ii) the negative band corresponding to a negative crossing.
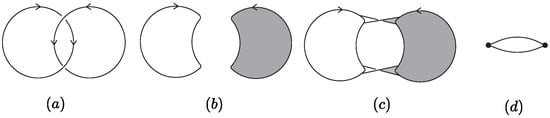
Figure 5.
(a) A Hopf link diagram D with orientation assigned; (b) the Seifert circles of D spanned by topological disks; (c) the Seifert surface F of D; (d) the Seifert graph of F.
There are two types of crossings, positive and negative crossings, as shown in Figure 4. When we come across a crossing c of D as shown in Figure 4i, we assign a value of , while in the case shown in Figure 4ii, we assign a value of . Then we consider a 2-component link L, consisting of components and , and the link is represented by an oriented regular diagram D. The crossings between the projections of and are labeled as , . In this case, we are only considering the intersections between the two components, not the self-intersections of each component. The linking number of and , denoted by , is defined as half the sum of the signs of these crossings. In mathematical terms,
This linking number provides valuable information about the topological relationship between and in the link L.
A matrix called Seifert matrix created from the Seifert surface F can be used to obtain a link invariant called the Alexander polynomial. There are several closed curves on F corresponding to the bounded face boundaries in . The orientation of these closed curves are arbitrarily given. Let be a closed curve on F corresponding to a bounded face boundary of . Since F is orientable, we can thicken (or lift) F slightly by the right-hand rule, in other words, construct . Then we denote , . Suppose is another closed curves on F corresponding to a bounded face boundary of . Then the element of the Seifert matrix corresponding to is defined as , where is the linking number of and . Then the number of closed cuvers corresponding to face boundaries in the Seifert graph (excluding the unbounded face) is equal to the number of bounded face boundaries in , which is the order of the constructed Seifert matrix. For more information about Seifert matrix, refer to [25]. Then we have the following theorem.
Theorem 4
([25]). Suppose and are two Seifert matrices of a knot (or link) L. Let r and s be the orders of and , respectively. Then we have
Thus, if we suppose M is a Seifert matrix of L and k is the order of M, is an invariant, called the Alexander polynomial.
Then we have the following proposition.
Proposition 2
([25]). The link L is a knot (or a link with at least two components) if and only if (or ).
3. π-Junction, the Special Face Graph, and the Flat-Based Operations
In this section, we will use -junction and -junction to construct , as the thickened graph of a 2-connected plane graph G, and establish a combinatorial method for obtaining the matrix from G, where M is the Seifert matrix derived from the boundary of the thickened graph , denoted by , of G. Then by Proposition 2, we have access to determining whether has more than one boundary component by computing .
3.1. π-Junction and Special Face Graph
Suppose G is a plane graph (without loops) and v is a vertex of G which is not an isolated vertex. Let be the set of the edges incident with v as shown in Figure 6.
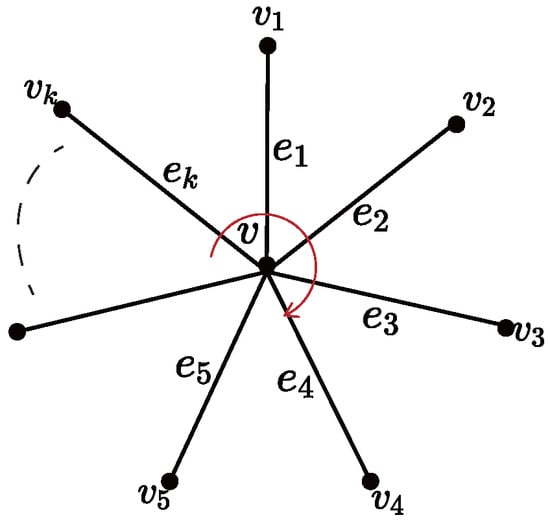
Figure 6.
The vertex v and its incident edges emanating from v in a clock-wise orientation which is marked in red.
Then the (or )-junction at v is defined as a cyclic permutation of in the clock-wise ordering around v, denoted by (or ), which satisfies (or ), where i is under modulo k.
Note that the degree of v, denoted by , must be odd if a -junction is assigned to v, since is a cyclic permutation. The thickened graph that we want to construct can now be described through the two junctions. As for -junction at a vertex v, we rearrange the edges incident with v as shown in Figure 7a, where the -junction . The local thickened graph is constructed from Figure 7a where each vertex is replaced with a vertex-disc and each edge is replaced with an edge-ribbon, as shown in Figure 7b. Figure 7c shows the crossing form realized by the -junction, which is also the boundary curves shown in Figure 7b up to homeomorphism. We shall assign the orientation to the boundary of as shown in Figure 7b. Similarly, Figure 7e shows the local thickened graph of with -junction. This type of junction is also called the 0-crossing junction.
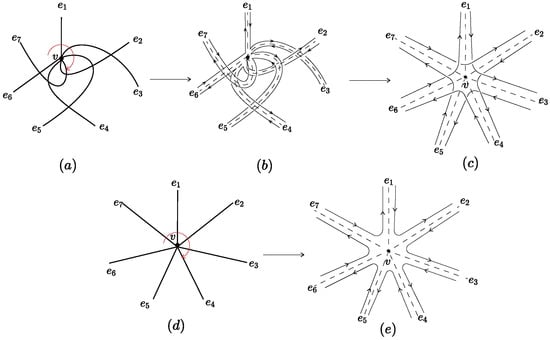
Figure 7.
(a) The rearrangement of edges according to -junction; (b) a locally thickened graph according to Figure (a); (c) the crossing from of the boundary as shown in Figure (b); (d) the rearrangement of edges according to -junction; (e) based on Figure (d), a locally thickened graph is created.
Note that how to arrange the crossing types as shown Figure 7c is not essential, since we consider the boundary of the thickened graph, as shown in Figure 7b, up to homeomorphism. The vertex v is also called a -vertex (or -vertex) if a -junction (or -junction) is assigned to it. By connecting these bands along the edges of G in a natural way, we obtain the thickened graph denoted by . An example is shown in Figure 8b where the vertices in red are -vertices and the vertices in black are -vertices.
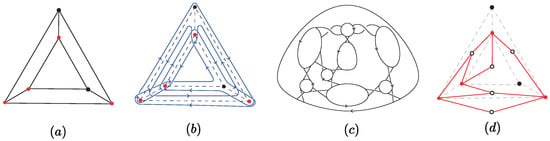
Figure 8.
(a) A 3-prism graph G with four -vertices assigned in red; (b) the boundary D of the thickened graph marked by blue lines; (c) the Seifert surface of D by Seifert decomposition; (d) the special face graph of a graph G where the edges are marked in red.
We can also regard the boundary of the thickened graph as a link. Let D denote the regular oriented diagram of . By Seifert decomposition and smoothing all the crossings in D, the Seifert surface F and the Seifert graph are constructed. Nevertheless, the Seifert graph can also be obtained by constructing the graph which is induced from G as defined below. This alternative way to construct the Seifert graph is more convenient once the -vertices are given.
Definition 1.
Let G be a 2-connected plane graph where some vertices are π-vertices. If we place a vertex called face vertex in each face of G (including the unbounded face), and connect each of the π-vertices and its corresponding adjacent face vertices by single edges. Then the graph constructed by the π-vertices and face vertices with the new added edges is called the special face graph of G, denoted by .
Note that is a simple and bipartite plane graph. Figure 8d gives an example of the construction of the special face graph where consists of those in red. It is not difficult to verify that the construction of the Seifert graph of D can be replaced by , we recommend readers refer to [19].
3.2. The Flat-Based Operations
By Seifert decomposition, as shown in Figure 8c, only one disk corresponding to the unbounded face of G in the Seifert surface F is not on the same level (plane) as the other disks of F. If all disks of a Seifert surface stay on the same level, we say that it is a flat. Then the surface as shown in Figure 8c is not flat.
Although F is not a flat, we can still obtain a flat Seifert surface from F. Without loss of generality, we suppose the disk corresponding to the unbounded face is at the bottom. The strategy is to use Reidemeister moves (refer to [25]) to replace the bottom disk with a narrow disk, as shown in Figure 9. Then by Seifert decomposition, we obtain the flat Seifert surface, denoted by . Let be the link diagram of as shown in Figure 9 and be the corresponding Seifert graph of . Since is flat, we can construct directly from by thickening the vertices into disks and widening the edges into bands corresponding to the crossings in (see also Figure 9).
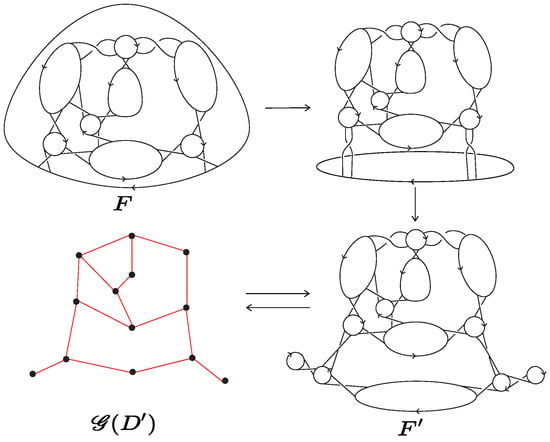
Figure 9.
An example of the construction of the flat Seifert surface and the corresponding Seifert graph .
Then we have the following proposition.
Proposition 3
([25]). Let denote the Seifert matrix of the flat Seifert surfaces . Then is -equivalent to M, where , and P represents an invertible integer matrix with a determinant of .
As Proposition 3 indicates,
If we want to calculate , we just need to calculate the linking numbers directly from by using the bounded face boundaries in and without considering the spacial structure of since is flat. In addition, the pendent edges are not essential. Then in the following discussion, we only consider the graphs induced from the special face graph and by deleting all 1-degree vertices, denoted by and , respectively. is also called the reduced special face graph (briefly RSF graph) of G.
Let , be the two different closed curves on corresponding to two bounded face boundaries A and B of , respectively. Let , (or ), respectively, denote the pair of the linking numbers of and . If a and b have no common edges, then the linking numbers , are both zeros, where , are the lifts of , respectively. If A and B have edges in common, then we establish a combinatorial method to compute the linking numbers , .
Further, and are isomorphic according to the construction. Then we can calculate the Seifert matrix of directly from . It does not change the number of components of the regular diagram D of when we exchange the overcrossing and undercrossing relationship of a crossing point. Thus, we suppose D is alternating, which refers to a specific arrangement where the crossings alternate between overcrossings and undercrossings. Besides, all the crossings in D are supposed to be positive (see Figure 4i).
When we lift from to , accordingly, we also lift from to . Then the face boundaries in corresponding to the closed curves in F should also be lifted. To calculate the linking numbers, we assume that the orientations of all face boundaries in the RSF graph are anti-clockwise.
Let be a closed curve that travels along the band of the Seifert surface as shown in Figure 10i. When we lift (including the band), then there is a point in such that the lift direction of that point is as shown in Figure 10i marked in blue. The edges in the RSF graph correspond to positive bands of as shown in Figure 10ii where the point marked in red is a -vertex, and the other is a face vertex. Accordingly, we attach a small arrow to each edge of as shown in Figure 10iii, which is vertical with the edge according to Figure 10ii. The direction of the arrow represents the direction of the lift of the local point of the edge.
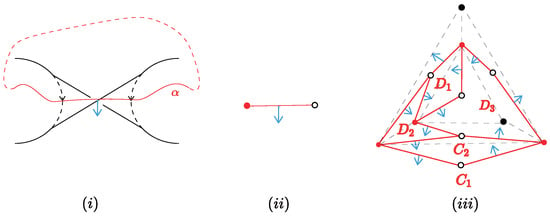
Figure 10.
(i) The direction marked in blue of the lift of a local point in a closed curve ; (ii) the direction of the lift of a local point in an edge; (iii) the RSF graph of a 3-prism graph (marked by broken dashed line) with arrows assigned (marked in blue).
Let and be two bounded face boundaries of as shown in Figure 11. Without loss of generality, suppose is a path of length k, denoted by . If is a -vertex, when we lift , can be illustrated as shown in Figure 11i, then the linking number of and is
If is a face vertex, can be illustrated as shown in Figure 11ii, then the linking number of and is
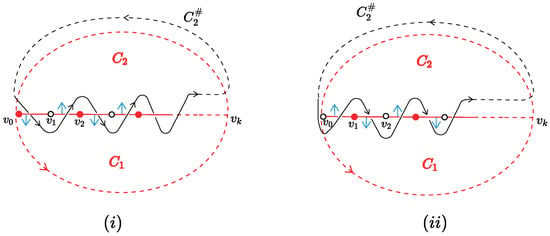
Figure 11.
The two cases of lifting . (i) Lifting when is a -vertex; (ii) Lifting when is a face vertex.
In general, equals to the number of the arrows (marked in blue) on which are not contained in the exterior of . These arrows are also called edge-arrows.
Thus we can calculate the linking number by counting the number of the arrows. For instance, in Figure 10iii, since the number of the arrows on that are not contained in the exterior of is one. Similarly, . This RSF graph as illustrated in Figure 10 is also called the reduced special face graph with edge-arrows, denoted by . We have the following definition for constructing .
Definition 2.
Let be an RSF graph with edge-arrows of a 2-connected plane graph G. Let C be a face boundary of and let S be any subset of . We define as the number of the arrows on that are not contained in the exterior of C. Let . Then is called the arrow-value of C restricted by S.
Note that the arrow-value of C is the difference between the number of the arrows on that are not contained in the exterior of C and the number of the arrows on that are contained in the exterior of C, since . If or , then .
Since , where M denote the corresponding Seifert matrix of by Seifert decomposition. Let and be two bounded face boundaries of . Then we have
which is the element of corresponding to the row of and column of .
Note that is a skew-symmetric matrix, all diagonal elements of the matrix are zeros. The order of the matrix is the number of the bounded face boundaries in . For example, as shown in Figure 10, we consider the element corresponding to and . Then and . Similarly, . We have the matrix is -equivalent to
Proposition 2 implies that , the boundary of the thickened graph , has only one component as shown in Figure 8b, since . It also tells us, if we choose the -vertices as Figure 10iii shows, an antiparallel strong trace can be obtained according to Theorem 2.
This method for obtaining the matrix contains several operations on . Since the concept of flat plays an important role in the above discussion, we name this method the flat-based operations.
4. A Theorem on 2-Connected and Plane Graphs
As a Seifert graph of , the construction of is more convenient. If has at least two boundary components, then the determinant of the target matrix of is zero. This implies that can not be a tree and then contains a face boundary. As we know, it is also possible that has one component even when the is not a tree. In this section, we characterize a type of 2-connected plane graph whose special face graph contains at least one face boundary, which is not a tree.
Theorem 5 provides a method for finding a graph G that is 2-connected and plane such that its thickened graph contains at least two boundary components. It implies that G admits no antiparallel strong trace according to Theorem 2. In the proof of Theorem 5, we use the flat-based operations to determine the number of boundary components of the corresponding thickened graph.
Lemma 1.
Let G be a 2-connected plane graph and be an RSF graph with edge-arrows of G. Let S be the edge set of a subgraph of and be a face boundary of . Then , where denotes the symmetric difference between S and .
Proof.
We have
since and contain all edges in and have no common edges. Similarly,
Since and have no common edges, then . Thus,
Then . □
Theorem 5.
Let G be a 2-connected plane graph and be an RSF graph with edge-arrows of G. Suppose m bounded face boundaries of , denoted by for some integer m, and let be the symmetric difference among . For any arbitrary bounded face boundary C of , if , then the corresponding thickened graph has at least two boundary components.
Proof.
We claim that . If , then the result holds. We assume that the result holds if for some . Then we prove by induction when . For all , if , then we have
since any of the arrows attached in is not attached in . By the assumption, we have
thus .
If for some . Then we discuss two cases.
Case 1.
contains an edge for some . Since is simple and is only contained in two face boundaries, then is identical to either or . Without loss of generality, suppose . Let , then according to Lemma 1, we have
Then by the assumption, we have
Since , then
Case 2.
For all , contains no edges in . Then
Thus, .
Let be the target matrix of , and let be the row vector of corresponding to . Since the element of corresponding to equals to , then . Then we have
Thus are linearly dependent, and the determinant of the target matrix is equal to 0. By Proposition 2, the thickened of G has at least two boundary components. □
Example 1.
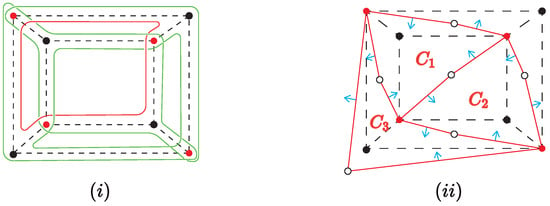
As an application of Theorem 5, we have the following example as shown in Figure 12.

Figure 12.
(i) A 4-prism with -vertices assigned in red and the resulting boundary components (marked by red and green lines) of ; (ii) the graph of G where the letters in red represent the face boundaries of .
Figure 12i shows the 4-prism with four -vertices assigned, and Figure 12ii shows the RSF graph with edge-arrows of G. Let . As we can see, . Similarly, . Then by Theorem 5, the number of the boundary components of is more than one. According to Theorem 2, it also implies that the graph G as shown in Figure 12 contains no antiparallel strong trace by these -vertices.
Example 2.
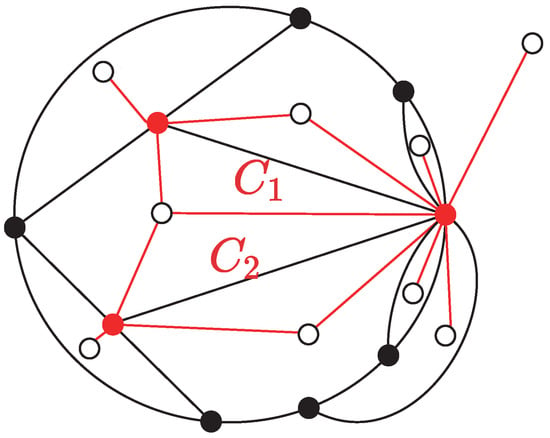
The authors Cheng et al. pointed out that their method for obtaining the thickened graph with one boundary component is by no means the only approach in [19] and they gave an example, as shown in Figure 13, where the special face graph marked in red is not a tree.

Figure 13.
A graph G with -vertices marked in red dots whose is not a tree but the thickened graph has only one boundary component [19].
By the discussion of Section 3, we can use the flat-based operation to obtained the target matrix corresponding to this special face graph. Obviously, is -equivalent to
Then . The graph as shown in Figure 13 (marked in black) must admit a thickened graph with one boundary component although its special face graph is not a tree. Then this graph admits an antiparallel strong trace. By Theorem 5 in Section 4, we know that, if it has a thickened graph with only one boundary component, then we can not find some bounded face boundaries in to construct D and any bounded face boundary C of such that . Figure 13 shows only two bounded face boundaries and , then D can only be or or . Then any is not equal to 0.
5. Conclusions
In this study, we extend the research framework of DNA and polypeptide cage construction based on Diao et al., focusing on developing combinatorial methods to analyze the topological properties of thickened graphs associated with 2-connected plane graphs G. The core objective is to determine the number of boundary components of , which directly influences nanostructure design.
The main contribution is the flat-based operations, a method for obtaining the target matrix . Its determinant classifies topology: indicates a single boundary component (enabling single-strand cages via antiparallel strong traces), while indicates multiple components. This overcomes previous limitations that required the special face graph to be a tree. For example, can have a single component with a non-tree (e.g., Figure 13).
We also characterize the thickened graph with multiple components using Theorem 5: if the bounded face boundaries in yield for some symmetric difference D, then . The 4-prism example (Figure 12) confirms this, with 4 -vertices leading to 4 face boundaries and .
Topologically, single-component (e.g., 3-prism, Figure 8) supports single-strand cages, while multi-component structures (e.g., 4-prism) require multi-strand designs. This links algebraic topology to biomolecular engineering, allowing strand requirements to be predicted via graph theory. Functionally, single-component cages (e.g., DNA tetrahedrons) are suitable for uniform applications like drug delivery, while multi-component cages offer flexibility for complex interactions. Manipulating -junctions in the 2-connected plane graph G enables control over and nanostructure architecture.
In summary, our work not only enriches the mathematical modeling of DNA and polypeptide nanostructures, but also lays a theoretical foundation for their design and synthesis. Future research may explore the potential of the flat-based operations in broader classes of graphs and their applications in biophysical contexts.
Author Contributions
Conceptualization, J.N. and X.-S.C.; methodology, J.N.; software, X.-S.C.; validation, J.N. and X.-S.C.; formal analysis, J.N.; investigation, X.-S.C.; resources, X.-S.C.; data curation, J.N.; writing—original draft preparation, J.N.; writing review and editing, J.N. and X.-S.C.; visualization, X.-S.C.; supervision, X.-S.C.; project administration, X.-S.C.; funding acquisition, X.-S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Huizhou City Basic Education educational science research project (No. 2023hzkt193), Teaching Quality and Teaching Reform Project of Huizhou University (No. 158 [2023]), and National Natural Science Foundation of China (No. 12171402). The APC was funded by Huizhou City Basic Education educational science research project (No. 2023hzkt193).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RSF graph | Reduced special face graph |
References
- Aldaye, F.A.; Palmer, A.L.; Sleiman, H.F. Assembling materials with DNA as the guide. Science 2008, 321, 1795–1799. [Google Scholar] [CrossRef]
- Seeman, N.C. Nanomaterials based on DNA. Annu. Rev. Biochem. 2010, 79, 65–87. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Tian, T.; Zhang, T.; Cai, X.; Lin, Y. Advances in biological applications of self-assembled DNA tetrahedral nanostructures. Mater. Today 2019, 24, 57–68. [Google Scholar] [CrossRef]
- Sadowski, J.P.; Calvert, C.R.; Zhang, D.Y.; Pierce, N.A.; Yin, P. Developmental self-assembly of a DNA tetrahedron. ACS Nano. 2014, 8, 3251–3259. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, Z.; Zhang, H.; Li, M.; Hou, Z.; Luo, X.; Xue, X. Development of DNA tetrahedron-based drug delivery system. Drug Deliv. 2017, 24, 1295–1301. [Google Scholar] [CrossRef]
- Li, J.B.; Wang, X.C.; Wang, X.M. Radiolabeling and preliminary evaluation of DNA cube nanoparticles in vivo & in vitro. J. Nucl. Med. 2018, 59, 1069. [Google Scholar]
- Bujold, K.E.; Fakhoury, J.; Edwardson, T.G.W.; Carneiro, K.M.M.; Briard, J.N.; Godin, A.G.; Amrein, L.; Hamblin, G.D.; Panasci, L.C.; Wiseman, P.W.; et al. Sequence-responsive unzipping DNA cubes with tunable cellular uptake profiles. Chem. Sci. 2014, 5, 2449–2455. [Google Scholar] [CrossRef]
- Liu, L.; Li, Z.; Li, Y.; Mao, C.D. Rational design and self-assembly of two-dimensional, dodecagonal DNA quasicrystals. J. Am. Chem. Soc. 2019, 141, 4248–4251. [Google Scholar] [CrossRef]
- Hu, G.; Zhai, X.; Lu, D.; Qiu, W.-Y. The architecture of Platonic polyhedral links. J. Math. Chem. 2009, 46, 592–603. [Google Scholar] [CrossRef]
- Duan, J.; Li, W.; Li, X.W.; Hu, G.; Qiu, W.-Y. Molecular design of DNA polyhedra based on genus. J. Math. Chem. 2014, 52, 2380–2394. [Google Scholar] [CrossRef]
- Gradišar, H.; Božič, S.; Doles, T.; Vengust, D.; Hafner-Bratkovič, I.; Mertelj, A.; Webb, B.; Šali, A.; Klǎzar, S.; Jerala, R. Design of a single-chain polypeptide tetrahedron assembled from coiled-coil segments. Nat. Chem. Biol. 2013, 9, 362–366. [Google Scholar] [CrossRef]
- Ljubetič, A.; Lapenta, F.; Gradišar, H.; Drobnak, I.; Aupič, J.; Strmšek, Ž.; Lainšček, D.; Hafner-Bratkovič, I.; Majerle, A.; Krivec, N.; et al. Design of coiled-coil protein-origami cages that self-assemble in vitro and in vivo. Nat. Biotechnol. 2017, 35, 1094–1101. [Google Scholar] [CrossRef]
- Majerle, A.; Hadži, S.; Aupič, J. A nanobody toolbox targeting dimeric coiled-coil modules for functionalization of designed protein origami structures. Proc. Natl. Acad. Sci. USA 2021, 118, e2021899118. [Google Scholar] [CrossRef] [PubMed]
- Fijavž, G.; Pisanski, T.; Rus, J. Strong traces model of self-assembly polypeptide structures. MATCH Commun. Math. Comput. Chem. 2014, 71, 199–212. [Google Scholar]
- Klavzˇar, S.; Rus, J. Stable traces as a model for self-assembly of polypeptide nanoscale polyhedrons. MATCH Commun. Math. Comput. Chem. 2013, 70, 317–330. [Google Scholar]
- Jonoska, N.; Saito, M. Boundary components of thickened graphs. Lect. Notes Comput. Sci. 2002, 2340, 70–81. [Google Scholar] [CrossRef]
- Jonoska, N.; Twarock, R. Blueprints for dodecahedral DNA cages. J. Phys. A Math. Theor. 2008, 41, 304043–304057. [Google Scholar] [CrossRef]
- Cheng, X.S.; Diao, Y. Configurations of DNA cages based on plane graphs and vertex junctions. J. Phys. Math. Theor. 2020, 52, 395601–395623. [Google Scholar] [CrossRef]
- Cheng, X.S.; Deng, Q.; Diao, Y. Constructions of DNA and polypeptide cages based on plane graphs and odd crossing π-junctions. Appl. Math. Comput. 2023, 443, 127773–127788. [Google Scholar] [CrossRef]
- Edwardson, T.G.W.; Levasseur, M.D.; Tetter, S.; Steinauer, A.; Hori, M.; Hilvert, D. Protein cages: From fundamentals to advanced applications. Chem. Rev. 2022, 122, 9145–9197. [Google Scholar] [CrossRef]
- Majsterkiewicz, K.; Azuma, Y.; Heddle, J.G. Connectability of protein cages. Nanoscale Adv. 2020, 2, 2255–2264. [Google Scholar] [CrossRef] [PubMed]
- Tupe, C.; Chakraborti, S. Bioinspired and Green Synthesis of Nanostructures: A Sustainable Approach; Scrivener Publishing LLC: Beverly, MA, USA, 2023. [Google Scholar]
- West, D.B. Introduction to Graph Theory; Prentice Hall: Upper Saddle River, NJ, USA, 1996; Volume 2. [Google Scholar]
- Hatcher, A. Algebraic Topology; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Murasugi, K. Knot Theory and Its Applications; Birkhauser Boston: Boston, MA, USA, 1996. [Google Scholar]
- Livingston, C. Knot Theory; The Mathematical Association of America: Washington, DC, USA, 1993. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).