Lie Symmetries, Solitary Waves, and Noether Conservation Laws for (2 + 1)-Dimensional Anisotropic Power-Law Nonlinear Wave Systems

Abstract

This study presents the complete analysis of a (2 + 1)-dimensional nonlinear wave-type partial differential equation with anisotropic power-law nonlinearities and a general power-law source term, which arises in physical domains such as fluid dynamics, nonlinear acoustics, and wave propagation in elastic media, yet their symmetry properties and exact solution structures remain largely unexplored for arbitrary nonlinearity exponents. To fill this gap, a complete Lie symmetry classification of the equation is performed for arbitrary values of m and n, providing all admissible symmetry generators. These generators are then employed to systematically reduce the PDE to ordinary differential equations, enabling the construction of exact analytical solutions. Traveling wave and soliton solutions are derived using Jacobi elliptic function and sine-cosine methods, revealing rich nonlinear dynamics and wave patterns under anisotropic conditions. Additionally, conservation laws associated with variational symmetries are obtained via Noether’s theorem, yielding invariant physical quantities such as energy-like integrals. The results extend the existing literature by providing, for the first time, a full symmetry classification for arbitrary m and n, new families of soliton and traveling wave solutions in multidimensional settings, and associated conserved quantities. The findings contribute both computationally and theoretically to the study of nonlinear wave phenomena in multidimensional cases, extending the catalog of exact solutions and conserved dynamics of a broad class of nonlinear partial differential equations.

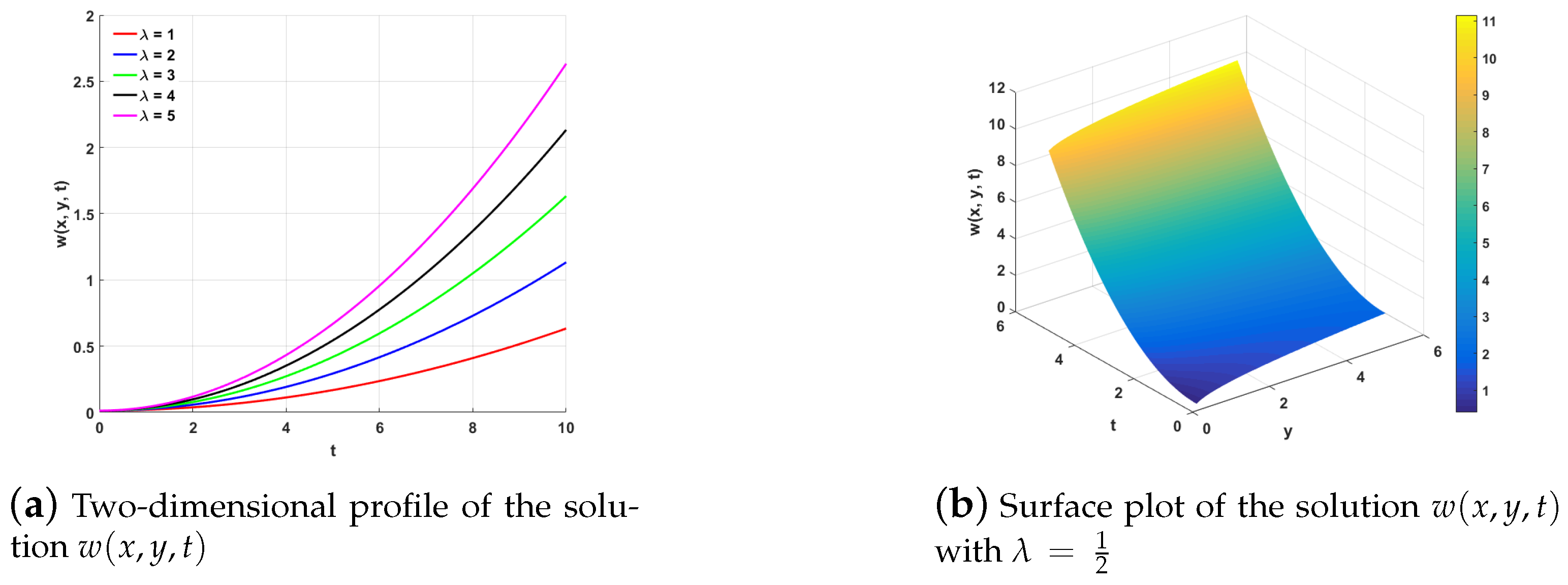
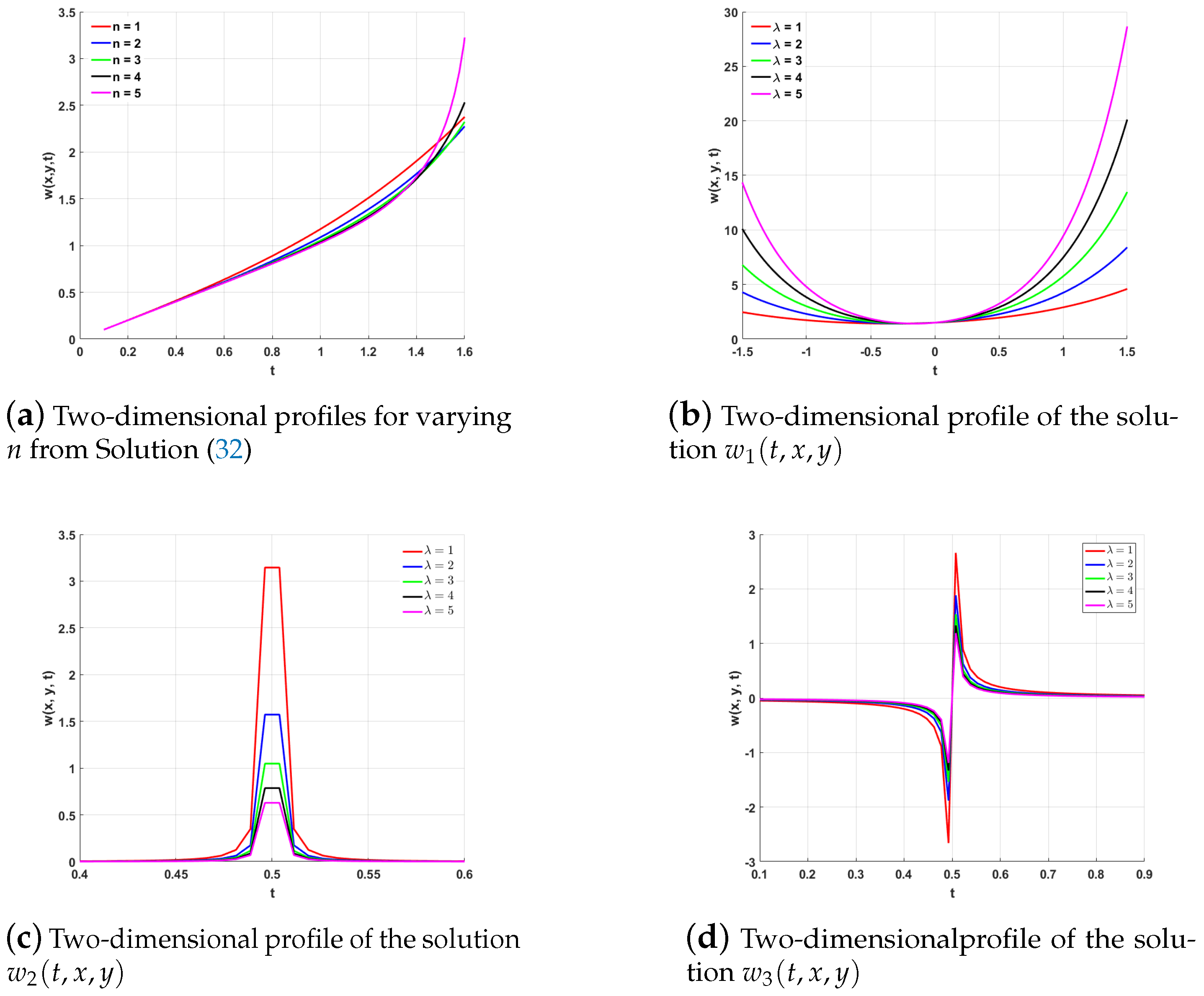
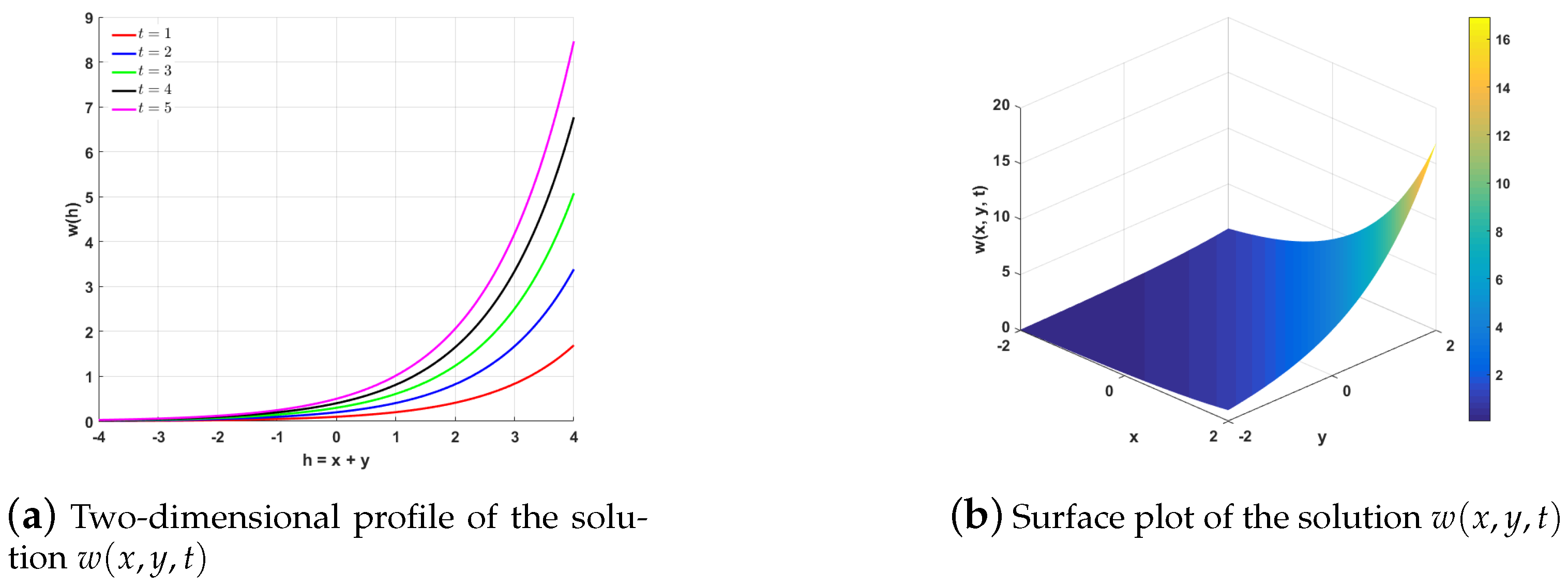
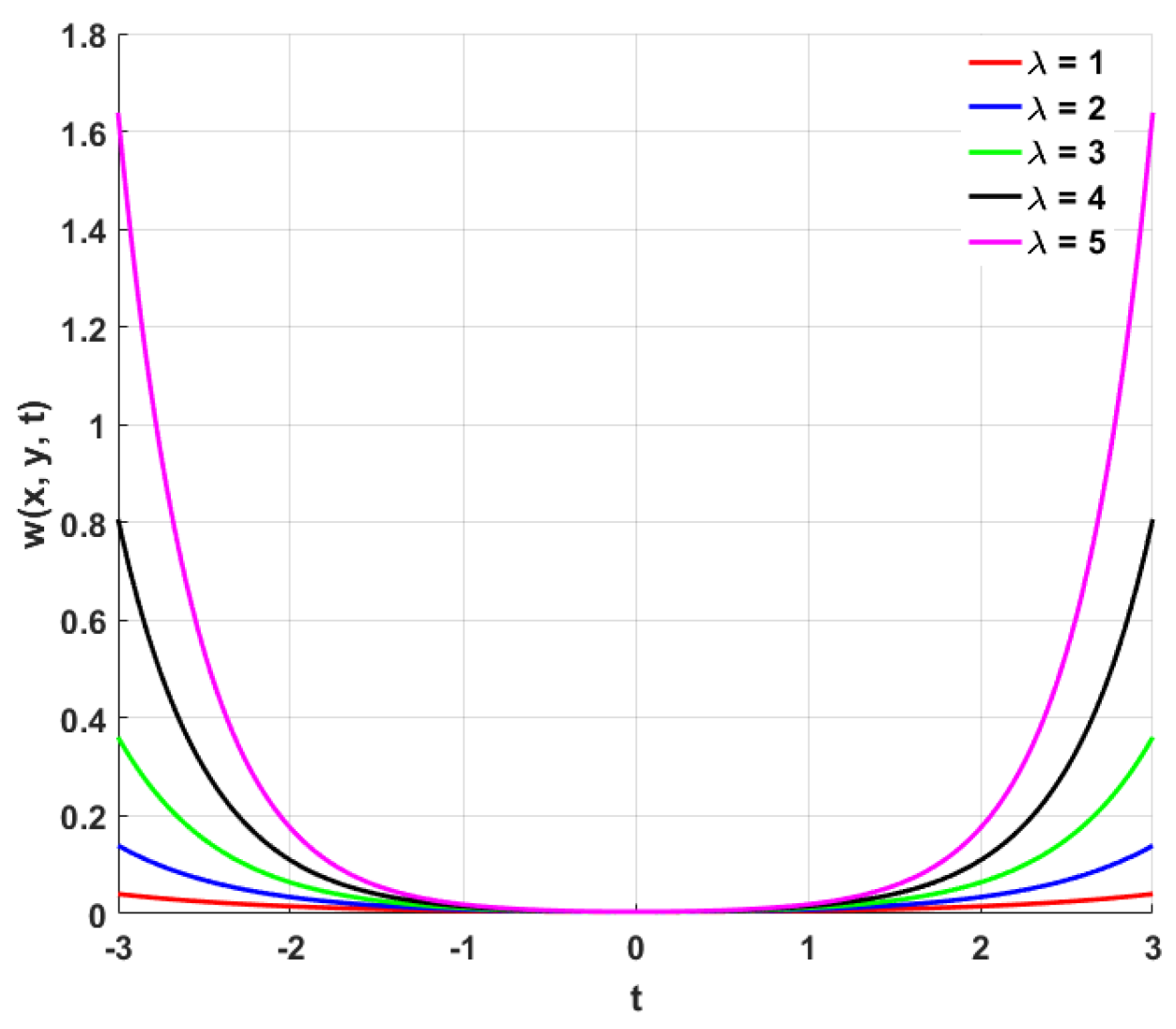
1. Introduction

Partial differential equations (PDEs) exhibiting power-law nonlinearity and anisotropic spatial behavior are fundamental in describing a wide array of physical processes, such as modeling phenomena in gas dynamics, wave propagation in shallow water, and nonlinear acoustics. Among such equations, the nonlinear wave-type equation

$$w_{tt}-w_{xx}{w}_x^m-f\left(w\right)=0,$$

(1)

with spatial nonlinearities was extensively analyzed by Arrigo, who obtained its Lie symmetries, constructed reduced forms through symmetry reductions, and derived exact analytical solutions for some particular cases of the source term [1]. Motivated by the aim to explore richer multidimensional and nonlinear behaviors, we generalize this equation by introducing a power-law source term and an additional spatial direction, leading us to consider the following extended form of the equation:

$$w_{tt}-w_{xx}{w}_x^m-w_{yy}{w}_y^m=\lambda w^n.$$

(2)

This generalization enables the modeling of systems with nonlinear source behaviors and spatially symmetric diffusion along multiple directions.

Equation (2) serves as a prototypical model for wave propagation and diffusion in nonlinear media where both the transport and reaction mechanisms exhibit state-dependent behavior. Its structure captures situations in which the spreading of a quantity is not purely linear but is instead modulated by the local gradient, while a nonlinear source term drives growth or decay within the system. Such formulations naturally arise in the study of nonlinear acoustics, elastic wave motion, and heat or mass transfer in heterogeneous and reactive environments. The generalized form of Equation (2) enables the modeling of systems with nonlinear source behaviors and spatially symmetric diffusion along multiple spatial directions. The dispersive terms ${\left(w_x\right)}^m{w}_{xx}$ and ${\left(w_y\right)}^m{w}_{yy}$, with $m\in \mathbb{R}$, represent a class of nonlinear spatial dispersions in which the wave or diffusion speeds depend on the magnitudes of the local gradients. These effects are encountered in diverse contexts, such as non-Newtonian fluid flows, wave motion in nonlinear elastic solids, and porous media transport where the effective diffusivity changes with the state of the system [2,3,4]. On the other hand, the source term $\lambda w^n$ encapsulates nonlinear reaction dynamics, encountered in fields such as chemical kinetics, pattern formation, and heat transfer in reactive media and population biology [5,6,7]. The combination of reactive forcing and directionally nonlinear transport gives rise to rich mathematical behaviors, including finite-time blow-up, the emergence of dispersive wave trains, the formation of shock waves, and self-similarity structures. These features make Equation (2) a rich and physically grounded model for studying nonlinear PDE phenomena.

Finding exact solutions to such nonlinear PDEs is essential for understanding the qualitative behavior and long-term dynamics of complex systems. These solutions often serve as canonical models, providing tools for validating numerical algorithms, guiding the interpretation of physical phenomena, and uncovering underlying mathematical structures. However, due to their highly nonlinear structures, these types of equations rarely yield general solution methods. To handle such equations, one powerful method is the Lie symmetry method, which offers a constructive approach to reduce the dimensionality of these equations and generate exact group-invariant solutions. In the context of nonlinear wave equations, this methodology yields important solution types: such as solitons, traveling waves, and shock-like profiles which are crucial in disciplines like plasma physics, optics, and biological transport.

Lie symmetry analysis offers a powerful method for analyzing nonlinear differential equations, as it identifies continuous transformation groups that leave the equation form invariant. These symmetries enable systematic reduction of PDEs to ordinary differential equations (ODEs), which are often easier to solve analytically or numerically. In this context, Noether’s theorem serves as a fundamental bridge between conservation laws and the symmetries of variational systems: every continuous symmetry of the action functional corresponds to a conservation law. The connection between Lie group theory and variational principles thus facilitates not only the classification of invariant solutions but also the construction of conserved physical or geometric structures intrinsic to the system [8,9,10].

This method has been continuously applied in recent years to a broad range of nonlinear systems. For instance, Ghanbari et al. [11] carried out a complete Lie symmetry analysis of a nonlinear wave equation with non-homogeneous coefficients and obtained similarity reductions leading to exact invariant solutions. Khan et al. [12] analyzed the generalized Korteweg–de Vries equations using Lie symmetries and derived the corresponding conserved quantities using Noether’s theorem. Their method, combining symmetry analysis with conservation laws, aligns closely with our approach to equations involving power-law sources and anisotropic diffusion. Vali et al. [13] studied the Lie symmetries of a two-dimensional Burgers-type equation, revealing how commuting vector fields lead to simplified reductions. Their approach parallels with our use of commutator algebra for symmetry reductions. Yurushev [14] employed symmetry methods for nonlinear optical wave equations, demonstrating the role of wave-type PDEs in modeling spatial-temporal field evolution in dispersive media. Ahmad et al. [15] combined Jacobi elliptic function expansions with Lie reductions to obtain soliton and periodic solutions to nonlinear evolution equations, highlighting the strength of hybrid analytical techniques. Debnath et al. [16] carried out symmetry analysis and invariant quantities for nonlinear field equations emerging in mathematical physics, revealing the broad applicability of Lie symmetry methods to nonlinear PDEs. Next, Samina et al. performed a detailed symmetry analysis and derived conservation laws of the Monge–Ampère equation, and they also obtained its traveling wave and soliton-type solutions, complementing our study of nonlinear wave phenomena [17]. Finally, Singhal et al. conducted a Lie symmetry analysis of a (3+1)-dimensional nonlinear dispersive soliton equation, obtaining exact invariant solutions and conservation laws [18]. Gou et al. studied solitary waves in anisotropic nonlinear Schrödinger models, emphasizing the impact of directional anisotropy on localized wave behavior. These studies highlight the importance of symmetry methods and anisotropic effects in analyzing complex nonlinear wave phenomena [19].

Our central objective (See

Table 1. Comparison between Arrigo (1991) [1] and the present study.

Aspect	Arrigo (1991) [1]	Present Work
Model Studied	$w_{tt}-w_{xx}{w}_x^m=f\left(w\right)$	$w_{tt}-w_{xx}{\left(w_x\right)}^m-w_{yy}{\left(w_y\right)}^m=\lambda w^n$
Source Term	General $f\left(w\right)$	Power-law $\lambda w^n$
Dimensions	Two-dimensional	Two spatial (x, y) + time (t)
Symmetry Classification	Uses infinitesimal method	Carried out for all possible $(m,n)$ values
Reductions Obtained	In some cases	For all cases based on commutator table
Exact Solutions	Some reduced ODEs solved	Full set of reduced ODEs solved
Soliton/Traveling Solutions	Not identified	Derived using sine–cosine and Jacobi methods
Conservation Laws	Not derived	Fully derived using Noether’s theorem

) is to perform a complete symmetry analysis of the generalized Equation (2) for all possible values of the parameters m and n. We exploit the algebraic structure of the admitted Lie symmetries to classify and reduce the equation into various simplified forms. In addition to deriving group-invariant solutions, we use the sine–cosine and Jacobi elliptic function methods to obtain exact traveling wave and soliton-type solutions. Furthermore, we apply the Noether symmetry approach to derive conservation laws, determining specific conditions under which the equation admits variational formulations and the corresponding conserved quantities.

The structure of the paper is as follows: Section 2 outlines the Lie symmetry analysis for various values of m and n. Section 3 presents the symmetry reductions and exact invariant solutions and also obtains soliton- and wave-type solutions, supported by graphical visualizations. Moreover, Section 4 derives conservation laws using the Noether theorem. Lastly, Section 6 presents a discussion of the results.

2. Lie Group Analysis

To derive the Lie point symmetries of Equation (2), we consider a one-parameter Lie group of infinitesimal transformations acting on the space of dependent and independent variables $(w,y,x,t)$; the corresponding infinitesimal generator is represented as

$$\mathcal{X}=\eta (w,y,x,t){\displaystyle \frac{\partial }{\partial w}}+{\varphi }^1(w,y,x,t){\displaystyle \frac{\partial }{\partial x}}+{\varphi }^2(w,y,x,t){\displaystyle \frac{\partial }{\partial y}}+{\varphi }^3(w,y,x,t){\displaystyle \frac{\partial }{\partial t}}.$$

(3)

To derive the Lie symmetries, we require that the prolonged vector field ${\mathrm{pr}}^{\left(2\right)}\mathcal{X}$ annihilates Equation (2) on its solution manifold, i.e.,

$${\mathrm{pr}}^{\left(2\right)}\mathcal{X}\left[w_{tt}-w_{xx}{\left(w_x\right)}^m-w_{yy}{\left(w_y\right)}^m-\lambda w^n\right]{|}_{w_{tt}=w_{xx}{\left(w_x\right)}^m+w_{yy}{\left(w_y\right)}^m+\lambda w^n}=0.$$

(4)

The second prolongation ${\mathrm{pr}}^{\left(2\right)}\mathcal{X}$ of the vector field $\mathcal{X}$ is represented as follows:

$${\mathrm{pr}}^{\left(2\right)}\mathcal{X}=\mathcal{X}+{\eta }^t{\displaystyle \frac{\partial }{\partial w_t}}+{\eta }^x{\displaystyle \frac{\partial }{\partial w_x}}+{\eta }^y{\displaystyle \frac{\partial }{\partial w_y}}+{\eta }^{tt}{\displaystyle \frac{\partial }{\partial w_{tt}}}+{\eta }^{xx}{\displaystyle \frac{\partial }{\partial w_{xx}}}+{\eta }^{yy}{\displaystyle \frac{\partial }{\partial w_{yy}}}+\cdots ,$$

where the extended infinitesimal are explicitly defined in the following form:

$$\begin{array}{c}\hfill {\eta }^i=D_i\left(\eta \right)-w_j{D}_i\left({\varphi }^j\right),\\ \hfill {\eta }^{ij}=D_j\left({\eta }^i\right)-w_{ik}{D}_j\left({\varphi }^k\right),\end{array}$$

and $D_i$ represents the total derivative with respect to $i,j\in \{x,y,t\}$.

Substituting the prolongation expressions into the invariance condition stated in (4) and simplifying yields an overdetermined system of PDEs in the unknowns ${\varphi }^1,{\varphi }^2,{\varphi }^3,\mathrm{and}\eta$, these equations are known as the determining equations and are given as

$${\varphi }_w^1=0,{\varphi }_w^2=0,{\varphi }_w^3=0,{\eta }_{ww}=0,$$

(5)

$${\eta }_y=0,{\eta }_x=0,$$

(6)

$${\varphi }_t^1=0,{\varphi }_y^1=0,$$

(7)

$${\varphi }_t^2=0,{\varphi }_x^2=0,$$

(8)

$${\varphi }_x^3=0,{\varphi }_y^3=0,$$

(9)

$${\varphi }_{xx}^1=0,$$

(10)

$${\varphi }_{yy}^2=0,$$

(11)

$$2{\eta }_{wt}-{\varphi }_{tt}^3=0,$$

(12)

$$-m{\eta }_w-2{\varphi }_t^3+(m+2){\varphi }_x^1=0,$$

(13)

$$-m{\eta }_w-2{\varphi }_t^3+(m+2){\varphi }_y^2=0,$$

(14)

$$-n\lambda \eta w^{n-1}+\lambda ({\eta }_w-2{\varphi }_t^3)w^n+{\eta }_{tt}=0.$$

(15)

It follows from Equations (13) and (14), that

$$(m+2)({\varphi }_x^1-{\varphi }_y^2)=0.$$

(16)

Consequently, the equation splits into the following two cases.

2.1. Case 1: ${\varphi }_x^1-{\varphi }_y^2=0$ Provided $m\ne -2$

Differentiation of Equation (13) with respect to t and substitution of the resulting expression into Equation (12), yields

$$(m+4){\varphi }_{tt}^3=0.$$

(17)

From this equation, two additional subcases can be identified as follows:

2.1.1. Subcase 1.1: $m\ne -4$ Provided ${\varphi }_{tt}^3=0$

This case results in the following infinitesimals:

$$\begin{array}{cc}\hfill {\varphi }^1& =c_{1}x+c_2,{\varphi }^2=c_{1}y+c_3,\hfill \\ \hfill {\varphi }^3& ={\displaystyle \frac{(1-n)(m+2)}{2m+2-2n}}{c}_{1}t+c_4,\eta ={\displaystyle \frac{m+2}{m+1-n}}{c}_{1}w.\hfill \end{array}$$

These infinitesimals constitute a four-dimensional Lie symmetry algebra associated with Equation (2), represented as follows:

$$\begin{array}{cc}\hfill {\mathcal{X}}_1& =x{\displaystyle \frac{\partial }{\partial x}}+y{\displaystyle \frac{\partial }{\partial y}}-{\displaystyle \frac{(n-1)(m+2)}{2m+2-2n}}t{\displaystyle \frac{\partial }{\partial t}}+{\displaystyle \frac{m+2}{m+1-n}}w{\displaystyle \frac{\partial }{\partial w}},\hfill \\ \hfill {\mathcal{X}}_2& ={\displaystyle \frac{\partial }{\partial x}},{\mathcal{X}}_3={\displaystyle \frac{\partial }{\partial y}},{\mathcal{X}}_4={\displaystyle \frac{\partial }{\partial t}}.\hfill \end{array}$$

2.1.2. Subcase 1.2: $m=-4$ provided ${\varphi }_{tt}^3\ne 0$

In this case, Equation (13), takes the following form:

$$2{\eta }_w-{\varphi }_t^3-{\varphi }_x^1=0.$$

(18)

Moreover, from Equations (10), (11), and (16), we obtain

$${\varphi }^1=c_{1}x+c_2\mathrm{and}{\varphi }^2=c_{1}y+c_3.$$

Equation (5) yields

$$\eta =\mathcal{A}\left(t\right)w+\mathcal{B}\left(t\right).$$

(19)

By substituting Equation (19) into Equation (18), and subsequently applying Equation (12), we get the following relation:

$$2\mathcal{A}\left(t\right)={\varphi }_t^3+c_1.$$

(20)

Next, inserting this result along with Equation (19) into Equation (15), and equating the coefficients of like powers of w, we derive the following system of equations:

$$\mathcal{B}\left(t\right)=0,$$

(21)

$$\mathcal{A}{\left(t\right)}_{tt}=0,$$

(22)

$$(1-n)\mathcal{A}\left(t\right)-2{\varphi }_t^3=0.$$

(23)

Solving Equations (22) and (23), we obtain

$${\varphi }^3={\displaystyle \frac{1}{2}}{d}_1{t}^2+d_{2}t+d_3.$$

(24)

Subsequently, Equations (23) and (20), result in

$$(n+3)d_{1}t+(n+3)d_2-(1-n)c_1=0,$$

now, equating the coefficients of like powers of t, we obtain the following constraints:

$$(n+3)d_1=0,$$

(25)

$$d_2={\displaystyle \frac{1-n}{n+3}}{c}_1.$$

(26)

Based on Equation (25), we consider the following two distinct subcases.

2.1.3. Subcase 1.2.1: $d_1=0$ provided $n\ne -3$

Thus, in this case, the expressions given in Equations (19) and (24) take the following form:

$${\varphi }^3={\displaystyle \frac{1-n}{n+3}}{c}_{1}t+d_3\mathrm{and}\eta ={\displaystyle \frac{2}{n+3}}{c}_{1}w.$$

As a result, these infinitesimals form a four-dimensional Lie algebra of symmetries admitted by Equation (2), represented by the following basis:

$$\begin{array}{c}{\mathcal{X}}_1=x{\displaystyle \frac{\partial }{\partial x}}+y{\displaystyle \frac{\partial }{\partial y}}+{\displaystyle \frac{(1-n)}{(n+3)}}t{\displaystyle \frac{\partial }{\partial t}}+{\displaystyle \frac{2}{(n+3)}}w{\displaystyle \frac{\partial }{\partial w}},\hfill \\ {\mathcal{X}}_2={\displaystyle \frac{\partial }{\partial x}},{\mathcal{X}}_3={\displaystyle \frac{\partial }{\partial y}},{\mathcal{X}}_4={\displaystyle \frac{\partial }{\partial t}}.\hfill \end{array}$$

2.1.4. Subcase 1.2.2: $d_1\ne 0$ provided $n=-3$

In this case, a constraint is imposed on $c_1$ requiring $c_1=0$, and leads to the following five-dimensional Lie algebra admitted by Equation (2):

$$\begin{array}{cc}\hfill {\mathcal{X}}_1& ={\displaystyle \frac{1}{2}}tw{\displaystyle \frac{\partial }{\partial w}}+{\displaystyle \frac{1}{2}}{t}^2{\displaystyle \frac{\partial }{\partial t}},{\mathcal{X}}_2={\displaystyle \frac{1}{2}}w{\displaystyle \frac{\partial }{\partial w}}+t{\displaystyle \frac{\partial }{\partial t}},\hfill \\ \hfill {\mathcal{X}}_3& ={\displaystyle \frac{\partial }{\partial x}},{\mathcal{X}}_4={\displaystyle \frac{\partial }{\partial y}},{\mathcal{X}}_5={\displaystyle \frac{\partial }{\partial t}}.\hfill \end{array}$$

2.2. Case 2: ${\varphi }_x^1-{\varphi }_y^2\ne 0$ provided $m=-2$

In this case, Equations (13) and (14) reduce to

$${\eta }_w-{\varphi }_t^3=0.$$

(27)

Differentiating it with respect to t and inserting the resulting equation into Equation (12), and then integration of the resulting equation with respect to t, yields the following result:

$${\varphi }^3=a_{1}t+a_2,$$

and additionally, from Equations (10) and (11), we get the following forms of ${\varphi }^1$ and ${\varphi }^2$:

$${\varphi }^1=c_{1}x+c_2\mathrm{and}{\varphi }^2=c_{3}y+c_4.$$

Ultimately, Equation (19) now takes the form

$$\eta =a_{1}w+\mathcal{B}\left(t\right).$$

Next, substituting the above results into Equation (15) and matching the coefficients of the corresponding powers of w, we obtain $\mathcal{B}\left(t\right)=0,$ along with the following two additional cases.

2.2.1. Subcase 2.1: $n\ne -1$ provided $a_1=0$

This case results in the following five-dimensional Lie algebra:

$$\begin{array}{c}{\mathcal{X}}_1=x{\displaystyle \frac{\partial }{\partial x}},{\mathcal{X}}_2=y{\displaystyle \frac{\partial }{\partial y}},\hfill \\ {\mathcal{X}}_3={\displaystyle \frac{\partial }{\partial x}},{\mathcal{X}}_4={\displaystyle \frac{\partial }{\partial y}},{\mathcal{X}}_5={\displaystyle \frac{\partial }{\partial t}}.\hfill \end{array}$$

2.2.2. Subcase 2.2: $n=-1$ provided $a_1\ne 0$

Accordingly, the resulting Lie symmetry algebra in this case is six-dimensional and expressed in the form

$$\begin{array}{cc}\hfill {\mathcal{X}}_1& =w{\displaystyle \frac{\partial }{\partial w}}+t{\displaystyle \frac{\partial }{\partial t}},{\mathcal{X}}_2=x{\displaystyle \frac{\partial }{\partial x}},{\mathcal{X}}_3=y{\displaystyle \frac{\partial }{\partial y}},\hfill \\ \hfill {\mathcal{X}}_4& ={\displaystyle \frac{\partial }{\partial x}},{\mathcal{X}}_5={\displaystyle \frac{\partial }{\partial y}},{\mathcal{X}}_6={\displaystyle \frac{\partial }{\partial t}}.\hfill \end{array}$$

The resulting infinitesimal generators form a Lie algebra under the Lie bracket or the commutator bracket. These symmetries are fundamental in constructing exact solutions through symmetry reductions and in deriving associated conservation laws. For each of the cases discussed above, the commutator tables, which are essential for performing symmetry reductions, are presented below.

The commutator table (

Table 2. Lie bracket table for Subcases 1.1 and 1.2.1.

$[{\mathcal{X}}_i,{\mathcal{X}}_j]$	${\mathcal{X}}_1$	${\mathcal{X}}_2$	${\mathcal{X}}_3$	${\mathcal{X}}_4$
${\mathcal{X}}_1$	0	−${\mathcal{X}}_2$	0	p${\mathcal{X}}_4$
${\mathcal{X}}_2$	${\mathcal{X}}_2$	0	0	0
${\mathcal{X}}_3$	0	0	0	0
${\mathcal{X}}_4$	−p${\mathcal{X}}_4$	0	0	0

) is valid for both Subcase 1.1 and Subcase 1.2.1, where p takes the value $p={\displaystyle \frac{(m+1)(n-1)}{2m-2n+2}}$ for Subcase 1.1 and $p={\displaystyle \frac{n-1}{n+3}}$ for Subcase 1.2.1. While the commutator table for Subcase 1.2.2 is given in

Table 3. Lie bracket table for Subcase 1.2.2.

$[{\mathcal{X}}_i,{\mathcal{X}}_j]$	${\mathcal{X}}_1$	${\mathcal{X}}_2$	${\mathcal{X}}_3$	${\mathcal{X}}_4$	${\mathcal{X}}_5$
${\mathcal{X}}_1$	0	−${\mathcal{X}}_1$	0	0	−${\mathcal{X}}_2$
${\mathcal{X}}_2$	${\mathcal{X}}_1$	0	0	0	−${\mathcal{X}}_5$
${\mathcal{X}}_3$	0	0	0	0	0
${\mathcal{X}}_4$	0	0	0	0	0
${\mathcal{X}}_5$	${\mathcal{X}}_2$	${\mathcal{X}}_5$	0	0	0

, Subcase 2.1 is mentioned in

Table 4. Lie bracket table for Subcase 2.1.

$[{\mathcal{X}}_i,{\mathcal{X}}_j]$	${\mathcal{X}}_1$	${\mathcal{X}}_2$	${\mathcal{X}}_3$	${\mathcal{X}}_4$	${\mathcal{X}}_5$
${\mathcal{X}}_1$	0	0	−${\mathcal{X}}_3$	0	0
${\mathcal{X}}_2$	0	0	0	−${\mathcal{X}}_4$	0
${\mathcal{X}}_3$	${\mathcal{X}}_3$	0	0	0	0
${\mathcal{X}}_4$	0	${\mathcal{X}}_4$	0	0	0
${\mathcal{X}}_5$	0	0	0	0	0

and Subcase 2.2 is mentioned in

Table 5. Lie bracket table for Subcase 2.2.

$[{\mathcal{X}}_i,{\mathcal{X}}_j]$	${\mathcal{X}}_1$	${\mathcal{X}}_2$	${\mathcal{X}}_3$	${\mathcal{X}}_4$	${\mathcal{X}}_5$	${\mathcal{X}}_6$
${\mathcal{X}}_1$	0	0	0	0	0	−${\mathcal{X}}_6$
${\mathcal{X}}_2$	0	0	0	−${\mathcal{X}}_4$	0	0
${\mathcal{X}}_3$	0	0	0	0	−${\mathcal{X}}_5$	0
${\mathcal{X}}_4$	0	${\mathcal{X}}_4$	0	0	0	0
${\mathcal{X}}_5$	0	0	${\mathcal{X}}_5$	0	0	0
${\mathcal{X}}_6$	${\mathcal{X}}_6$	0	0	0	0	0

.

3. Reduction to Ordinary Differential Equations

Reduction techniques play an important role in the analysis of nonlinear PDEs, as they enable the transformation of complex systems into simpler forms, often ODEs, by using underlying symmetries. This simplification not only facilitates the solution process but also reveals hidden structural features, invariant solutions, and connections to established solvable models. Each reduced form can correspond to a physically relevant situation, such as traveling wave propagation or self-similar evolution, thereby linking abstract formulations to observable phenomena. This section outlines the reductions of Equation (2) using two-dimensional subalgebras of its obtained Lie symmetry algebra. The process consists of the following main steps:

1.

Identify the Lie symmetry generators of the given PDE.

2.

For reduction, choose a two-dimensional subalgebra $\left[{\mathcal{X}}_i,{\mathcal{X}}_j\right]$ from the commutator table.

3.

Derive the invariants under both generators to define new similarity variables.

4.

Rewrite the original equation in terms of the obtained invariants or similarity variables, reducing it to a simpler PDE or an ODE.

5.

Solve the resulting reduced equation and revert to the original variables to find invariant solutions, if necessary.

3.1. Reductions for Subcase 1.1

3.1.1. Reduction Under $\left[{\mathcal{X}}_1,{\mathcal{X}}_2\right]$

To initiate the reduction of Equation (2) under $\left[{\mathcal{X}}_1,{\mathcal{X}}_2\right]$, we consider the symmetry generator

$${\mathcal{X}}_2={\displaystyle \frac{\partial }{\partial x}},$$

The associated characteristic equation takes the form

$${\displaystyle \frac{dw}{0}}={\displaystyle \frac{dx}{1}}={\displaystyle \frac{dy}{0}}={\displaystyle \frac{dt}{0}},$$

and, after certain simplifications, we obtain the following similarity transformations:

$$z=y,\rho =t,w=g(z,\rho ).$$

Under these transformations, Equation (2) reduces to a following lower-dimensional PDE:

$$g_{\rho \rho }-g_z^m{g}_{zz}-\lambda g^n=0.$$

(28)

Next, we apply the generator ${\mathcal{X}}_1$, which in terms of the new variables, takes the following form:

$${\tilde{\mathcal{X}}}_1=z{\displaystyle \frac{\partial }{\partial z}}-{\displaystyle \frac{(n-1)(m+2)}{2m-2n+2}}\rho {\displaystyle \frac{\partial }{\partial \rho }}+{\displaystyle \frac{m+2}{m-n+1}}g{\displaystyle \frac{\partial }{\partial g}}.$$

The invariants under ${\tilde{\mathcal{X}}}_1$ are

$$\alpha =z^{{\displaystyle \frac{(n-1)r}{2}}}\rho ,g(z,\rho )=u\left(\alpha \right)z^r.$$

Here, $r={\displaystyle \frac{m+2}{m-n+1}}.$ Inserting these into Equation (2), we obtain the following reduced ODE associated with Equation (2):

$$u^{″}-r^{m+2}{(u-{\displaystyle \frac{(1-n)}{2}}\alpha u^{\prime })}^m\left((r-1)u-2{\displaystyle \frac{(1-n)}{2}}\alpha u^{\prime }+{\displaystyle \frac{(1-n)}{2}}({\displaystyle \frac{(1-n)r}{2}}+1){\alpha }^2{u}^{″}\right)-\lambda u^n=0,$$

(29)

and this represents a second-order nonlinear ODE with the dependent variable u and independent variable $\alpha .$

3.1.2. Reduction Under $\left[{\mathcal{X}}_1,{\mathcal{X}}_3\right]$

In this case, we begin with the symmetry generator

$${\mathcal{X}}_3={\displaystyle \frac{\partial }{\partial y}},$$

The corresponding similarity variables are given as

$$z=x,\rho =t,w=g(z,\rho ).$$

Subject to these invariants, Equation (2) simplifies to the same lower-dimensional PDE as given in Equation (28), which further reduces to the same ODE presented in Equation (29).

3.1.3. Reduction Under $\left[{\mathcal{X}}_1,{\mathcal{X}}_4\right]$

To begin the reductions in this case, we first choose

$${\mathcal{X}}_4={\displaystyle \frac{\partial }{\partial t}}.$$

This results in the following transformations:

$$z=x,\rho =y,w=g(z,\rho ).$$

Subject to these similarity variables, we obtain the following reduction of Equation (2):

$$g_{\rho }^m{g}_{\rho \rho }+g_z^m{g}_{zz}+\lambda g^n=0.$$

(30)

We now consider the application of the symmetry generator ${\mathcal{X}}_1$, which transforms in the similarity variables $(z,\rho ,g)$ as

$${\tilde{\mathcal{X}}}_1=z{\displaystyle \frac{\partial }{\partial z}}+\rho {\displaystyle \frac{\partial }{\partial \rho }}+{\displaystyle \frac{m+2}{m-n+1}}g{\displaystyle \frac{\partial }{\partial g}}.$$

Transformations associated with ${\tilde{\mathcal{X}}}_1$ are as follows:

$$\alpha ={\displaystyle \frac{z}{\rho }}g(z,\rho )=z^{r}u\left(\alpha \right),$$

where the similarity exponent is defined by $r={\displaystyle \frac{m+2}{m-n+1}}$. Substituting these expressions into the Equation (30), we obtain the following reduced nonlinear differential equation:

$${\alpha }^m{u^{\prime }}^m(2\alpha u^{\prime }+{\alpha }^2{u}^{″})+{(ru+\alpha u^{\prime })}^m\left((r-1)((ru+\alpha u^{\prime })+\alpha (r{u}^{\prime }+u^{\prime }+\alpha u^{″})\right)+\lambda u^n=0.$$

3.1.4. Reduction Under $\left[{\mathcal{X}}_2,{\mathcal{X}}_3\right]$

Starting with the generator ${\mathcal{X}}_2$, we recover the same reduction as previously obtained in Equation (28). Next, consider the generator ${\mathcal{X}}_3$, which, in terms of the similarity variables $(z,\rho ,g)$, takes the simplified form

$${\tilde{\mathcal{X}}}_3={\displaystyle \frac{\partial }{\partial z}}.$$

This shows that z is a cyclic variable, and hence the reduced Equation (28) can be further transformed using the invariants:

$$\alpha =\rho ,g=u\left(\alpha \right).$$

Substituting these into the Equation (28) results in the following second-order nonlinear ODE:

$$u^{″}-\lambda u^n=0,$$

(31)

which admits the following solution:

$$\alpha -{\alpha }_0=\int {\displaystyle \frac{du}{\sqrt{2\left({\displaystyle \frac{\lambda }{n+1}}{u}^{n+1}+b\right)}}}.$$

Reverting to the original variables, we obtain the following implicit solution of Equation (2):

$$t-{\alpha }_0=\int {\displaystyle \frac{dw}{\sqrt{2\left({\displaystyle \frac{\lambda }{n+1}}{w}^{n+1}+b\right)}}},$$

where in b and ${\alpha }_0$ are the constants. Alternatively, an implicit solution to (31) is given by

$${\displaystyle \frac{u{\left(\alpha \right)}^2\left({\displaystyle \frac{2\lambda u{\left(\alpha \right)}^{n+1}}{c_1(n+1)}}+1\right)[{}_{2}F_1\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{n+1}};1+{\displaystyle \frac{1}{n+1}};-{\displaystyle \frac{2\lambda u{\left(\alpha \right)}^{n+1}}{c_1(n+1)}}\right){]}^2}{\left({\displaystyle \frac{2\lambda u{\left(\alpha \right)}^{n+1}}{n+1}}+c_1\right)}}={(\alpha +c_2)}^2,$$

where ${}_{2}F_1$ is the Gaussian hypergeometric function and $c_1$, $c_2$ represent the integration constants.

In the original variables, this solution takes the following form:

$${\displaystyle \frac{w{(x,y,t)}^2\left({\displaystyle \frac{2\lambda w{(x,y,t)}^{n+1}}{c_1(n+1)}}+1\right)[{}_{2}F_1\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{n+1}};1+{\displaystyle \frac{1}{n+1}};-{\displaystyle \frac{2\lambda w{(x,y,t)}^{n+1}}{c_1(n+1)}}\right){]}^2}{\left({\displaystyle \frac{2\lambda w{(x,y,t)}^{n+1}}{n+1}}+c_1\right)}}={(t+c_2)}^2,$$

(32)

We consider the following different values of n in order to solve the resulting elliptic integral in an explicit form:

• $n=1$: $w_1(t,x,y)=A{e}^{\sqrt{\lambda }t}+B{e}^{-\sqrt{\lambda }t}$.
• $n=2$: $w_2(t,x,y)={\left({\displaystyle \frac{3\sqrt{\lambda }}{2}}(t-{\alpha }_0)\right)}^{-2}$.
• $n=3$: $w_3(t,x,y)={\left(\sqrt{\lambda }(t-{\alpha }_0)\right)}^{-1}$.

Graphically, these solutions can be represented as follows:

The solution (32) represents the nonlinear evolution of a wave influenced by nonlinear forcing effects and spatial diffusion. It shows how the wave profile changes over time. The appearance of a hypergeometric function denotes a self-similar structure in the solution. Subplots Figure 1a–d describe how the variation of n affects the temporal and spatial evolution of the wave profile. Increasing n intensifies the nonlinear source term, leading to steeper growth or decay in the amplitude, depending on the sign of the exponent in the analytical form. In Figure 1a,b, a larger n produces faster growth rates in the solution due to enhanced nonlinear effects, while in Figure 1c the wave becomes more sharply localized in time, indicating a stronger focusing behavior. In Figure 1d, the oscillatory pattern shows higher peaks and sharper transitions for larger n, reflecting the stronger influence of nonlinearity on wave steepening.

3.1.5. Reduction Under $\left[{\mathcal{X}}_2,{\mathcal{X}}_4\right]$

Take the generator ${\mathcal{X}}_4$, which simplifies in the similarity variables $(z,\rho ,g)$ as

$${\tilde{\mathcal{X}}}_4={\displaystyle \frac{\partial }{\partial \rho }}.$$

As a result, this yields the following invariants:

$$\alpha =z,g=u\left(\alpha \right).$$

Inserting these into Equation (28) results in

$${u^{\prime }}^m{u}^{″}+\lambda u^n=0.$$

(33)

Associated with this reduction, the solution to Equation (2) can be expressed as

$$\int {\left[(m+2)\left(c_1-{\displaystyle \frac{\lambda }{n+1}}{w}^{n+1}\right)\right]}^{-{\displaystyle \frac{1}{m+2}}}dw=y+c_2,$$

in an alternate form:

$$y+c_2={\displaystyle \frac{w(x,y,t)}{{\left((m+2)c_1\right)}^{\frac{1}{m+2}}}}·{}_{2}F_1\left({\displaystyle \frac{1}{n+1}},{\displaystyle \frac{1}{m+2}};{\displaystyle \frac{n+2}{n+1}};{\displaystyle \frac{\lambda w{(x,y,t)}^{n+1}}{(n+1)c_1}}\right),$$

where in $c_1$, $c_2$ denote constants of integration and ${}_{2}F_1$ represents the Gaussian hypergeometric function.

3.1.6. Reduction Under $\left[{\mathcal{X}}_3,{\mathcal{X}}_4\right]$

In this case, we consider the symmetry generator

$${\mathcal{X}}_3={\displaystyle \frac{\partial }{\partial y}}.$$

The associated similarity variables are

$$z=x,\rho =t,w=g(z,\rho ).$$

Subject to these invariants, Equation (2) reduces to the same lower-dimensional PDE expressed in Equation (28), which further transforms to the ODE given in Equation (33). Consequently, the solution to Equation (2) can be represented as

$$x+c_2={\displaystyle \frac{w(x,y,t)}{{\left((m+2)c_1\right)}^{\frac{1}{m+2}}}}·{}_{2}F_1\left({\displaystyle \frac{1}{n+1}},{\displaystyle \frac{1}{m+2}};{\displaystyle \frac{n+2}{n+1}};{\displaystyle \frac{\lambda w{(x,y,t)}^{n+1}}{(n+1)c_1}}\right),$$

(34)

For various values of n, we obtain

• $n=1$: $w(x,y,t)={\left((m+2)c_1\right)}^{{\displaystyle \frac{1}{m+2}}}·(x+c_2)·[{}_{2}F_1\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{m+2}};{\displaystyle \frac{3}{2}};{\displaystyle \frac{\lambda w^2}{2c_1}}\right){]}^{-1}$.
• $n=2$: $w(t,x,y)={\left((m+2)c_1\right)}^{{\displaystyle \frac{1}{m+2}}}·(x+c_2)·[{}_{2}F_1\left({\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{m+2}};{\displaystyle \frac{4}{3}};{\displaystyle \frac{\lambda w^3}{3c_1}}\right){]}^{-1}.$
• $n=3$: $w(t,x,y)={\left((m+2)c_1\right)}^{{\displaystyle \frac{1}{m+2}}}·(x+c_2)·[{}_{2}F_1\left({\displaystyle \frac{1}{4}},{\displaystyle \frac{1}{m+2}};{\displaystyle \frac{5}{4}};{\displaystyle \frac{\lambda w^4}{4c_1}}\right){]}^{-1}$.

3.2. Reductions for Subcase 1.2.1:

In this case, Equation (2) takes the following form:

$$w_{tt}-w_{xx}{w}_x^{-4}-w_{yy}{w}_y^{-4}=\lambda w^n.$$

(35)

3.2.1. Reduction Under $\left[{\mathcal{X}}_1,{\mathcal{X}}_2\right]$

To carry out the symmetry reduction of Equation (35) using the vector fields $\left[{\mathcal{X}}_1,{\mathcal{X}}_2\right]$, we start with the generator

$${\mathcal{X}}_2={\displaystyle \frac{\partial }{\partial x}},$$

which leads to the following set of similarity variables:

$$z=y,\rho =t,w=g(z,\rho ).$$

Substituting these expressions into Equation (35), we obtain its lower-dimensional form, given by

$$g_{\rho \rho }-g_z^{-4}{g}_{zz}-\lambda g^n=0.$$

(36)

We now utilize the generator ${\mathcal{X}}_1$, which transforms in the new variables to

$${\tilde{\mathcal{X}}}_1=z{\displaystyle \frac{\partial }{\partial z}}-{\displaystyle \frac{n-1}{n+3}}\rho {\displaystyle \frac{\partial }{\partial \rho }}+{\displaystyle \frac{2}{n+3}}g{\displaystyle \frac{\partial }{\partial g}}.$$

The invariants associated with this operator are

$$\alpha =z^{{\displaystyle \frac{(n-1)s}{2}}}\rho ,g(z,\rho )=u\left(\alpha \right)z^{2s},$$

where the exponent is given as $s={\displaystyle \frac{1}{n+3}}$. Plugging these transformations into the reduced Equation (36), we arrive at the following nonlinear ODE:

$$u^{″}-s^{-4}{\left(2u-(1-n)s\alpha u^{\prime }\right)}^{-4}\left[f_{1}u+f_2\alpha u^{\prime }+f_3{\alpha }^2{u}^{″}\right]-\lambda u^n=0.$$

(37)

where $f_1=-{\displaystyle \frac{2(n+1)}{{(n+3)}^2}}$, $f_2={\displaystyle \frac{(n-1)(2-n)}{{(n+3)}^2}}$, and $f_3={\displaystyle \frac{{(1-n)}^2}{{(n+3)}^2}}$. Equation (35) admits the following power-series solution:

$$w(x,y,t)=a_0{y}^{{\displaystyle \frac{2}{5}}}+({\displaystyle \frac{1}{2}}({\displaystyle \frac{6}{25}}{a}_0+\lambda a_0^2))t^2,$$

and this solution is valid for $n=2.$ Graphically, this solution can be seen in Figure 2.

This reflects a phenomenon in which the wave amplitude increases with time under the influence of both its initial profile and external forcing. The graphs represent a system in which the wave amplitude w varies with the spatial coordinate y and evolves quadratically in time t. The first term, $y^{2/5}$, describes the initial spatial distribution, while the second term captures the time-dependent growth of the amplitude. As the parameter $\lambda$ increases, the coefficient of $t^2$ increases, indicating that the amplitude grows more rapidly, highlighting the effect of the nonlinear contribution in the system.

Figure 2. Graphical representations of the solution $w(x,y,t)=y^{{\displaystyle \frac{2}{5}}}+\left({\displaystyle \frac{1}{2}}({\displaystyle \frac{6}{25}}+\lambda )\right)t^2$.

Figure 2. Graphical representations of the solution $w(x,y,t)=y^{{\displaystyle \frac{2}{5}}}+\left({\displaystyle \frac{1}{2}}({\displaystyle \frac{6}{25}}+\lambda )\right)t^2$.

3.2.2. Reduction Under $\left[{\mathcal{X}}_1,{\mathcal{X}}_4\right]$

To carry out the reduction for this case, we begin by selecting the symmetry generator

$${\mathcal{X}}_4={\displaystyle \frac{\partial }{\partial t}}.$$

This choice leads to the following similarity variables:

$$z=y,\rho =x,w=g(z,\rho ).$$

By substituting these into Equation (35), we obtain the reduced form:

$$g_{\rho }^{-4}{g}_{\rho \rho }+g_z^{-4}{g}_{zz}+\lambda g^n=0.$$

(38)

Next, we apply the generator ${\mathcal{X}}_1$, which transforms into new variables as follows:

$${\tilde{\mathcal{X}}}_1=z{\displaystyle \frac{\partial }{\partial z}}+\rho {\displaystyle \frac{\partial }{\partial \rho }}+{\displaystyle \frac{2}{n+3}}g{\displaystyle \frac{\partial }{\partial g}}.$$

The associated invariants are given by

$$\alpha ={\displaystyle \frac{z}{\rho }},g(z,\rho )=z^{\nu }u\left(\alpha \right),$$

where the exponent $\nu$ is defined as $\nu ={\displaystyle \frac{2}{n+3}}$. Inserting in Equation (38), we obtain

$$u^{\prime -4}{u}^{″}+{(\nu u-\alpha u^{\prime })}^{-4}\left((\nu -1)(\nu u-\alpha u^{\prime })-\alpha u^{\prime }+{\alpha }^2{u}^{″}\right)+\lambda u^n=0.$$

3.2.3. Reduction Under $\left[{\mathcal{X}}_2,{\mathcal{X}}_4\right]$

Initiating with the symmetry ${\mathcal{X}}_2$, we recover the same reduction as derived previously in Equation (36). We now apply the generator ${\mathcal{X}}_4$, which reduces to the following simplified form:

$${\tilde{\mathcal{X}}}_4={\displaystyle \frac{\partial }{\partial \rho }}.$$

This leads to the invariants

$$\alpha =z,g=u\left(\alpha \right).$$

By substituting these into the previously reduced Equation (36), we obtain the following:

$$u^{\prime -4}{u}^{″}+\lambda u^n=0.$$

(39)

The general solution admitted by this equation can be implicitly represented by the quadrature

$$\alpha +c_1=\pm \int {\displaystyle \frac{du}{\sqrt{2\left({\displaystyle \frac{\lambda u^{n+1}}{n+1}}-c_2\right)}}}$$

Reverting to original variables

$$y+c_1=\pm \int {\displaystyle \frac{dw}{\sqrt{2\left({\displaystyle \frac{\lambda w{(x,y,t)}^{n+1}}{n+1}}-c_2\right)}}}$$

(40)

3.2.4. Reduction Under $\left[{\mathcal{X}}_3,{\mathcal{X}}_4\right]$

To initiate the symmetry reduction of Equation (35), we first utilize the generator

$${\mathcal{X}}_3={\displaystyle \frac{\partial }{\partial y}},$$

which implies the following similarity variables:

$$z=x,\rho =t,w=g(z,\rho ).$$

These similarity variables yield the same reduction as stated in Equation (36). Now, associated with ${\tilde{\mathcal{X}}}_4$, we obtain the same reduced ODE as given in Equation (39), subject to

$$\alpha =z,g=u\left(\alpha \right).$$

The corresponding solution is as follows, reverting to original variables:

$$x+c_1=\pm \int {\displaystyle \frac{dw}{\sqrt{2\left({\displaystyle \frac{\lambda w{(x,y,t)}^{n+1}}{n+1}}-c_2\right)}}}$$

3.3. Reductions for Subcase 1.2.2:

In this case, Equation (2) transforms into the following form:

$$w_{tt}-w_{xx}{w}_x^{-4}-w_{yy}{w}_y^{-4}=\lambda w^{-3}.$$

(41)

Reduction Under $\left[{\mathcal{X}}_{\mathbf{1}},{\mathcal{X}}_{\mathbf{2}}\right]$

To perform the symmetry reduction of Equation (41), we begin by applying the generator

$${\mathcal{X}}_1=-{\displaystyle \frac{1}{2}}tw{\displaystyle \frac{\partial }{\partial w}}-{\displaystyle \frac{1}{2}}{t}^2{\displaystyle \frac{\partial }{\partial t}},$$

which results in the following similarity invariants:

$$z=y,\rho =x,w=tg(z,\rho ).$$

These variables produce the following reduction:

$$g_{\rho }^{-4}{g}_{\rho \rho }+g_z^{-4}{g}_{zz}+\lambda g^{-3}=0.$$

(42)

Furthermore, employing the generator ${\tilde{\mathcal{X}}}_2$ yields the following reduced ODE:

$$2u^{″}+\lambda u^{-3}{u}^{\prime 4}=0,$$

(43)

under the transformations

$$\alpha =\rho +z,g=u\left(\alpha \right).$$

Equation (47) admits the following implicit solution:

$$\sqrt{-\lambda -4c_2{u}^2}-\sqrt{-\lambda }ln\left|{\displaystyle \frac{\sqrt{-\lambda -4c_2{u}^2}+\sqrt{-\lambda }}{\sqrt{-\lambda -4c_2{u}^2}-\sqrt{-\lambda }}}\right|=\pm \alpha +c_1.$$

Equation (47) has the explicit solution (for $\lambda =-4$) represented by

$$u\left(\alpha \right)=c_1{e}^{\pm {\displaystyle \frac{\alpha }{\sqrt{2}}}},$$

where $c_1$ is an arbitrary nonzero constant. In original variables

$$w(x,y,t)=t{c}_1{e}^{\pm {\displaystyle \frac{x+y}{\sqrt{2}}}}.$$

This solution can be seen as follows.

Figure 3 and Figure 4 represent a wave profile that increases linearly with time and indicates exponential behavior along the diagonal direction $x+y$. The sign in the exponent determines whether the wave decays or amplifies as it moves through space. This form suggests a directed wave propagation without oscillations, where the amplitude increases uniformly over time due to the linear dependence on time t. The multiplicative factor of t modulates this growth over time so that both spatial position and temporal evolution contribute to the increase in amplitude. Higher values of t result in a proportional vertical shift of the surface, whereas the exponential term mainly controls the steepness along the diagonal $x=-y$. Physically, this represents a wave that faces simultaneous temporal amplification and spatially exponential growth. In Figure 4, the negative exponent in the spatial term causes amplitude decay along the $x+y$ direction, producing a damped profile. The linear time dependence still drives uniform temporal growth, but spatially the solution diminishes, suggesting wave attenuation in a specific direction. This behavior is typical in dissipative systems where temporal forcing is counteracted by spatial damping.

3.3.1. Reduction Under $\left[{\mathcal{X}}_1,{\mathcal{X}}_3\right]$

In this case, we start with the symmetry generator ${\mathcal{X}}_1$, under which Equation (41) simplifies to the same reduced PDE as derived in Equation (42). Proceeding further, the implementation of the transformed symmetry ${\tilde{\mathcal{X}}}_3$ leads to the following similarity variables:

$$\alpha =z,g=u\left(\alpha \right),$$

and under these invariants, Equation (42) further reduces to the same ODE presented as

$$u^{″}+\lambda u^{-3}{u}^{\prime 4}=0.$$

(44)

The solution for $\lambda =1$ can be expressed as

$$\sqrt{{\left(u\left(\alpha \right)\sqrt{2k}\right)}^2-1}-{sec}^{-1}\left(u\sqrt{2k}\right)=\pm \alpha +c_2.$$

The general solution to Equation (44) is

$$u\left(\alpha \right)=c_1{e}^{\pm {\displaystyle \frac{\alpha }{\sqrt{-\lambda }}}},$$

rewriting into the original variables, we obtain

$$w(x,y,t)=t{c}_1{e}^{\pm {\displaystyle \frac{y}{\sqrt{-\lambda }}}}.$$

3.3.2. Reduction Under $\left[{\mathcal{X}}_1,{\mathcal{X}}_4\right]$

Proceeding with the symmetry generator ${\mathcal{X}}_1$, we derive the same reduced PDE as given in Equation (42). Next, using the transformed symmetry ${\tilde{\mathcal{X}}}_4$ results in the following invariants:

$$\alpha =\rho ,g=u\left(\alpha \right),$$

with these similarity variables, Equation (42) transforms to the same ODE expressed in Equation (44). The corresponding solution is

$$w(x,y,t)=t{c}_1{e}^{\pm {\displaystyle \frac{x}{\sqrt{-\lambda }}}}.$$

This solution describes a spatially uniform state in the y-direction, whose variation occurs only along the x-axis. Such a pattern can represent wavefronts or fields that maintain their shape in x while either increasing or decreasing uniformly in time, arising from a balance between the nonlinear spatial fluxes in the governing equation and the source term.

3.3.3. Reduction Under $\left[{\mathcal{X}}_1,{\mathcal{X}}_5\right]$

To carry out the symmetry reduction of Equation (41), we begin the process by using the generator

$${\mathcal{X}}_2=t{\displaystyle \frac{\partial }{\partial t}}+{\displaystyle \frac{1}{2}}w{\displaystyle \frac{\partial }{\partial w}},$$

which introduces the following similarity transformations:

$$z=y,\rho =x,w=t^{{\displaystyle \frac{1}{2}}}g(z,\rho ).$$

Plugging these variables transforms the Equation (41) into the reduced form

$$g_{\rho }^{-4}{g}_{\rho \rho }+g_z^{-4}{g}_{zz}+\lambda g^{-3}+{\displaystyle \frac{1}{4}}g=0.$$

(45)

Next, applying the symmetry generator ${\tilde{\mathcal{X}}}_5$ leads to a further reduction, resulting in the following ODE:

$$2u^{″}+\lambda u^{-3}{\left(u^{\prime }\right)}^4+{\displaystyle \frac{1}{4}}u(u^{\prime }{)}^4=0,$$

(46)

where the transformation is defined by

$$\alpha =\rho +z,g=u\left(\alpha \right).$$

The solution to Equation (46) is given as follows:

$$\alpha +c_1=\int \sqrt{{\displaystyle \frac{u^4-16c_2{u}^2-4\lambda }{8u^2}}}du.$$

3.3.4. Reduction Under $\left[{\mathcal{X}}_2,{\mathcal{X}}_3\right]$

Carrying out the reduction of Equation (41) through

$${\mathcal{X}}_2=t{\displaystyle \frac{\partial }{\partial t}}+{\displaystyle \frac{1}{2}}w{\displaystyle \frac{\partial }{\partial w}},$$

leads to invariants

$$z=y,\rho =x,w=t^{{\displaystyle \frac{1}{2}}}g(z,\rho ).$$

These transformations result in the same reduction presented in Equation (45). Next, applying the symmetry generator ${\tilde{\mathcal{X}}}_3$ leads to the following transformations:

$$\alpha =z,g=u\left(\alpha \right),$$

resulting in the following reduction:

$$u^{″}+\lambda u^{-3}(u^{\prime }{)}^4+{\displaystyle \frac{1}{4}}u(u^{\prime }{)}^4=0.$$

(47)

Equation (47) has the following implicit solution:

$$\alpha +c_1=\int {\displaystyle \frac{udu}{\sqrt{\lambda -\frac{1}{4}{u}^4-2c_2{u}^2}}}.$$

3.3.5. Reduction Under $\left[{\mathcal{X}}_2,{\mathcal{X}}_4\right]$

In this case, the reduction results in the same form as stated in Equation (47), corresponding to the following invariants:

$$\alpha =\rho ,g=u\left(\alpha \right).$$

3.3.6. Reduction Under $\left[{\mathcal{X}}_2,{\mathcal{X}}_5\right]$

Reducing Equation (41) using the symmetry generator

$${\mathcal{X}}_5={\displaystyle \frac{\partial }{\partial t}},$$

yields the following similarity transformations:

$$z=y,\rho =x,w=g(z,\rho ).$$

These invariants lead to the reduced form shown in Equation (42). Subsequently, employing the generator ${\tilde{\mathcal{X}}}_2$ introduces the new variables

$$\alpha =z+\rho ,g=u\left(\alpha \right),$$

which transform the equation into the following ODE:

$$2u^{″}+\lambda u^{-3}(u^{\prime }{)}^4=0.$$

(48)

Equation (48) admits the solution of the form

$$u\left(\alpha \right)=c_1{e}^{\pm {\displaystyle \frac{\alpha }{\sqrt{2}}}},$$

where $c_1$ represents a nonzero constant. Expressing into original variables, we have

$$w(x,y,t)=c_1{e}^{\pm {\displaystyle \frac{x+y}{\sqrt{2}}}},$$

subject to $\lambda =-4.$ This solution is independent of time, representing a stationary spatial configuration. The dependence on the combined coordinate $(x+y)$ indicates a field that varies uniformly along the diagonal direction in the $(x,y)$-plane, corresponding to propagation or structure aligned with the line $x+y=\mathrm{constant}$. The exponential factor $e^{\pm (x+y)/\sqrt{2}}$ describes either amplification (+ sign) or attenuation (− sign) along this diagonal, with $\sqrt{2}$ serving as a characteristic scaling length.

3.3.7. Reduction Under $\left[{\mathcal{X}}_3,{\mathcal{X}}_4\right]$

First, apply the symmetry generator ${\mathcal{X}}_3$, and Equation (41) reduces to

$$g_{zz}-g_{\rho }^{-4}{g}_{\rho \rho }-\lambda g^{-3}=0,$$

(49)

under the following transformations:

$$z=t,\rho =y,w=g(z,\rho ).$$

Next, using the generator ${\tilde{\mathcal{X}}}_4$ leads to invariants

$$\alpha =z,g=u\left(\alpha \right),$$

which provide the following ODE:

$$u^{″}-\lambda u^{-3}=0.$$

(50)

Equation (50) has the following solution:

$$u\left(\alpha \right)=\pm \sqrt{2c_1{(\alpha +{\alpha }_0)}^2+{\displaystyle \frac{\lambda }{2c_1}}},$$

represented in original variables, and we obtain the following solution of Equation (2):

$$w(x,y,t)=\pm \sqrt{2c_1{(t+c_2)}^2+{\displaystyle \frac{\lambda }{2c_1}}}.$$

This solution can be visualized graphically as follows.

Figure 5 describes a time-dependent behavior in which the wave amplitude increases or decreases uniformly, depending on the chosen sign. The graphs show that the magnitude of w increases with time through a quadratic dependence inside the square root. The parameter $\lambda$ introduces a constant positive shift in the amplitude. As $\lambda$ increases, this change increases, leading to a higher baseline value of w at all times. Consequently, the wave profile is elevated uniformly, while temporal variation continues to govern the rate of growth. The $pm$ sign indicates two symmetric states with equal magnitude but opposite sign, corresponding to different propagation directions or phases.

3.3.8. Reduction Under $\left[{\mathcal{X}}_3,{\mathcal{X}}_5\right]$

Applying the symmetry generator ${\mathcal{X}}_3$ to Equation (41) yields the same reduced partial differential equation as given in Equation (49). Following this, the use of the generator ${\tilde{\mathcal{X}}}_4$ introduces the following transformations:

$$\alpha =\rho ,g=u\left(\alpha \right),$$

which further reduces the equation to the ODE

$$u^{″}+\lambda u^{-3}(u^{\prime }{)}^4=0.$$

(51)

3.3.9. Reduction Under $\left[{\mathcal{X}}_4,{\mathcal{X}}_5\right]$

First, employing the generator ${\mathcal{X}}_4$, Equation (41) is transformed to the same form as given in Equation (49), corresponding to the similarity variables

$$z=t,\rho =x,w=g(z,\rho ).$$

Subsequently, applying the symmetry ${\tilde{\mathcal{X}}}_5$ yields the following transformations:

$$\alpha =\rho ,g=u\left(\alpha \right),$$

which transforms Equation (49) into the same reduction as stated in Equation (43).

3.4. Reductions for Subcase 2.1

Equation (2) now becomes

$$w_{tt}-w_{xx}{w}_x^{-2}-w_{yy}{w}_y^{-2}=\lambda w^n.$$

(52)

3.4.1. Reduction Under $\left[{\mathcal{X}}_1,{\mathcal{X}}_2\right]$

The symmetry generator ${\mathcal{X}}_1$ yields the following:

$$\rho =t,z=y,w=g(\rho ,z),$$

which transforms Equation (52) into the following lower-dimensional form:

$$g_{\rho \rho }-g_z^{-2}{g}_{zz}-\lambda g^n=0,$$

(53)

Following this, the use of the transformed symmetry ${\mathcal{X}}_2$ reduces Equation (53) into the equation

$$u^{″}-\lambda u^n=0,$$

(54)

under the similarity variables

$$\alpha =\rho ,g=u\left(\alpha \right).$$

Equation (54) results in the following:

$$\int {\displaystyle \frac{du}{\sqrt{{\displaystyle \frac{2\lambda }{n+1}}{u}^{n+1}+2c_2}}}=\pm \alpha +c_1,$$

where $c_1$ is the constant of integration.

3.4.2. Special case: $n=1$

In this case, Equation (54) reduces to

$$u^{\prime \prime }-\lambda u=0,$$

which is a second-order linear ODE with constant coefficients.

• For $\lambda >0$, the characteristic equation has real and distinct roots, yielding the following general solution of Equation (52) and represented in Figure 6:

  $$w(x,y,t)=A{e}^{\sqrt{\lambda }t}+B{e}^{-\sqrt{\lambda }t}.$$
• For $\lambda <0$, let $\lambda =-{\mu }^2$, where $\mu >0$. The roots of the characteristic equation are imaginary, resulting in the oscillatory solution

  $$w(x,y,t)=Acos\left(\mu t\right)+Bsin\left(\mu t\right).$$
  The curves in Figure 7 show periodic oscillations with frequency $\mu$, where changes in the phase and amplitude are determined by the sine and cosine contributions. Variations in $\mu$ modify the oscillation period, with higher $\mu$ producing more frequent oscillations over the same time window. Physically, this represents a purely oscillatory mode of the system without damping or growth, where the dynamics are dominated by harmonic time variations.
• When $\lambda =0$, the equation becomes $u^{\prime \prime }=0$, and the general solution is a linear function

  $$u\left(\alpha \right)=A\alpha +B.$$

  which gives

  $$w(x,y,t)==At+B.$$

3.4.3. Reduction Under $\left[{\mathcal{X}}_1,{\mathcal{X}}_5\right]$

First, using the generator ${\mathcal{X}}_1$, Equation (52) is transformed into the same reduced form as presented in Equation (53). Next, applying the symmetry generator ${\tilde{\mathcal{X}}}_5$ leads to the following transformations:

$$\alpha =z,g=u\left(\alpha \right),$$

which reduces Equation (49) to the ordinary differential equation, given as

$$u^{″}+\lambda u^n{u}^{\prime 2}=0.$$

(55)

The solution to this equation is given by

$$\int exp\left({\displaystyle \frac{\lambda }{n+1}}{u}^{n+1}\right)du=c_1\alpha +c_2,$$

and rewriting into the original form, we find

$$\int exp\left({\displaystyle \frac{\lambda }{n+1}}w{(x,y,t)}^{n+1}\right)dw=c_{1}y+c_2.$$

3.4.4. Reduction Under $\left[{\mathcal{X}}_2,{\mathcal{X}}_3\right]$

The application of the symmetry generator ${\mathcal{X}}_2$ results in the transformations

$$\rho =x,z=t,w=g(\rho ,z),$$

which reduces Equation (52) to the following lower-dimensional form:

$$g_{zz}-g_{\rho }^{-2}{g}_{\rho \rho }-\lambda g^n=0.$$

(56)

Subsequently, employing the transformed generator ${\mathcal{X}}_3$ further reduces Equation (56) to Equation (54), based on similarity variables.

$$\alpha =z,g=u\left(\alpha \right).$$

3.4.5. Reduction Under $\left[{\mathcal{X}}_3,{\mathcal{X}}_4\right]$

The symmetry generator ${\mathcal{X}}_3$ leads to invariants

$$\rho =t,z=y,w=g(\rho ,z),$$

which produces the same reduction as given in Equation (53).

Following this, using the transformed generator ${\mathcal{X}}_4$ further transforms Equation (53) to Equation (54), subject to similarity transformations.

$$\alpha =\rho ,g=u\left(\alpha \right).$$

3.5. Reductions for Subcase 2.2

Accordingly, Equation (2) reduces to the following expression:

$$w_{tt}-w_{xx}{w}_x^{-2}-w_{yy}{w}_y^{-2}=\lambda w^{-1}.$$

(57)

3.5.1. Reduction Under $\left[{\mathcal{X}}_1,{\mathcal{X}}_2\right]$

The symmetry generator ${\mathcal{X}}_1$ leads to the introduction of the similarity variables

$$\rho =x,z=y,w=tg(\rho ,z),$$

which transforms Equation (57) into the reduced form:

$$g_{\rho }^{-2}{g}_{\rho \rho }+g_z^{-2}{g}_{zz}+\lambda g^{-1}=0.$$

(58)

Next, the use of the transformed generator ${\mathcal{X}}_2$ yields a further reduction of Equation (58) into

$$u^{″}+\lambda u^{-1}{u}^{\prime 2}=0,$$

(59)

with the corresponding similarity variables

$$\alpha =z,g=u\left(\alpha \right).$$

To obtain the solution of Equation (59), we consider the following two cases.

3.5.2. Case a: $\lambda \ne -1$

This case yields the following:

$$u\left(\alpha \right)={\left((\lambda +1)(c_1\alpha +c_2)\right)}^{{\displaystyle \frac{1}{\lambda +1}}},$$

represented in the original variables, and we have

$$w(x,y,t)=t{\left((\lambda +1)(c_{1}y+c_2)\right)}^{{\displaystyle \frac{1}{\lambda +1}}}.$$

This solution can be graphically shown as follows.

Figure 8 indicates that the amplitude w grows linearly with time t, meaning that the temporal increase directly scales the amplitude without altering its spatial profile. The spatial dependence is governed by the term ${\left((\lambda +1)(y+1)\right)}^{1/(\lambda +1)}$, which is sensitive to variations in $\lambda$. As $\lambda$ increases, the exponent $1/(\lambda +1)$ decreases, flattening the spatial variation and reducing sensitivity to changes in y. In contrast, smaller values of $\lambda$ enhance spatial gradients.

3.5.3. Case b: $\lambda =-1$

For this case, we obtain the following solution:

$$u\left(\alpha \right)=c_1{e}^{c\alpha },$$

and substituting back into the original variables yields the following:

$$w(x,y,t)=c_{1}t{e}^{cy}.$$

Graphically, it can be seen as follows.

Figure 9 shows that the wave amplitude w increases linearly with time t, implying that temporal growth directly amplifies the overall magnitude without altering the shape of the spatial profile. The exponential term $e^{3y}$ dictates the spatial variation, causing rapid growth along the positive y direction and decay in the negative y direction. As t increases, the entire spatial profile is uniformly scaled upward, reflecting a proportional amplification over time while preserving its exponential spatial structure.

3.5.4. Reduction Under $\left[{\mathcal{X}}_1,{\mathcal{X}}_3\right]$

The symmetry generator ${\mathcal{X}}_1$ yields the same reduced form as given in Equation (58). Subsequently, applying the transformed generator ${\mathcal{X}}_3$ further reduces Equation (58) to Equation (59), under the similarity transformations

$$\alpha =\rho ,g=u\left(\alpha \right).$$

3.5.5. Reduction Under $\left[{\mathcal{X}}_1,{\mathcal{X}}_6\right]$

Using the symmetry generator ${\mathcal{X}}_6$, we derive the following similarity variables:

$$\rho =x,z=y,w=g(\rho ,z),$$

which reduces Equation (57) to the same lower-dimensional form given in Equation (58). Following this, the application of the transformed generator ${\mathcal{X}}_1$ further simplifies Equation (58), resulting in the reduced equation

$$2u^{″}{\left(u^{\prime }\right)}^{-2}+\lambda u^{-1}=0,$$

(60)

using similarity invariants

$$\alpha =z+\rho ,g=u\left(\alpha \right).$$

To obtain its solution, we consider the following:

3.5.6. Case a: $\lambda \ne -2$

In this case, the solution to Equation (60) can be expressed as follows:

$$u\left(\alpha \right)={\left(({\displaystyle \frac{\lambda }{2}}+1)(c_1\alpha +c_2)\right)}^{{\displaystyle \frac{1}{\lambda /2+1}}}.$$

In the original variables:

$$w(x,y,t)={\left(({\displaystyle \frac{\lambda }{2}}+1)(c_1(x+y)+c_2)\right)}^{{\displaystyle \frac{1}{\lambda /2+1}}}.$$

3.5.7. Case b: $\lambda =-2$

This case results in the following:

$$u\left(\alpha \right)=c_1{e}^{c\alpha }.$$

Rewriting in the original form, we obtain the following:

$$w(x,y,t)=c_1{e}^{c(x+y)}.$$

3.5.8. Reduction Under $\left[{\mathcal{X}}_2,{\mathcal{X}}_3\right]$

Applying the generator ${\mathcal{X}}_2$, we obtain the following invariants:

$$\rho =y,z=t,w=g(\rho ,z),$$

which converts Equation (57) into the simplified form

$$g_{zz}-g_{\rho }^{-2}{g}_{\rho \rho }-\lambda g^{-1}=0.$$

(61)

Subsequently, the implementation of the transformed generator ${\mathcal{X}}_3$ allows for a further reduction of Equation (61) to the equation

$$u^{″}-\lambda u^{-1}=0,$$

(62)

subject to the similarity variables

$$\alpha =z,g=u\left(\alpha \right).$$

The implicit solution can be represented as follows:

$$\int {\displaystyle \frac{du}{\sqrt{2\lambda ln\left|u\right|+c}}}=\pm \alpha +c_1.$$

In the original variables, it is given by

$$\int {\displaystyle \frac{dw}{\sqrt{2\lambda ln\left|w\right(x,y,t\left)\right|+c}}}=\pm t+c_1.$$

3.5.9. Reduction Under $\left[{\mathcal{X}}_2,{\mathcal{X}}_6\right]$

The symmetry ${\mathcal{X}}_2$ results in the same reduced form as that given in Equation (61). Consequently, the generator ${\mathcal{X}}_6$ reduces Equation (61) to Equation (59), subject to the following:

$$\alpha =\rho ,g=u\left(\alpha \right).$$

3.5.10. Reduction Under $\left[{\mathcal{X}}_3,{\mathcal{X}}_4\right]$

Using symmetry ${\mathcal{X}}_3$, we derive similarity transformations

$$\rho =x,z=t,w=g(\rho ,z),$$

which reduces Equation (57) to the same form as given in Equation (61). Then, by applying the transformed generator ${\mathcal{X}}_4$, Equation (61) is further simplified to Equation (62), subject to the similarity invariants

$$\alpha =z,g=u\left(\alpha \right).$$

3.5.11. Reduction Under $\left[{\mathcal{X}}_3,{\mathcal{X}}_6\right]$

The use of the generator ${\mathcal{X}}_6$ leads to the same reduced equation as presented in (58). Following this, the use of the transformed symmetry ${\mathcal{X}}_3$ provides a further reduction of Equation (58) to the ordinary differential Equation (59), through the similarity transformations

$$\alpha =\rho ,g=u\left(\alpha \right).$$

3.6. Traveling Wave or Soliton Solutions

This section focuses on traveling wave and soliton solutions, which are examined independently from the Lie symmetry reductions. Although Lie symmetry methods provide a systematic approach for reducing the number of independent variables and obtaining invariant solutions, they do not always capture certain localized or periodic wave structures that are of significant physical interest. Traveling wave and soliton solutions, on the other hand, are derived using specific ansatz forms that inherently account for coherent patterns, such as solitary pulses or periodic wave trains. By treating these solutions separately, we are able to highlight their distinct analytical characteristics and emphasize their relevance in modeling nonlinear phenomena in various physical domains.

To obtain exact traveling wave or soliton solutions of Equation (2), we apply two analytical methods: the Jacobi elliptic function method and the sine–cosine approach [20,21].

3.6.1. Sine–Cosine Method

The sine–cosine method is an effective approach for obtaining periodic solutions to nonlinear differential equations. It assumes the solution in terms of trigonometric functions, which often transform the nonlinear PDEs into simplified and solvable forms after a traveling wave reduction. This method consists of the following steps:

1.

Introduce a transforming variable $\alpha ={\mu }_{1}x+{\mu }_{2}y-ct$ and assume $w(x,y,t)=u\left(\alpha \right)$. Inserting in Equation (2) yields

$${\omega }^2{u}^{″}-{\mu }_1^{m+2}{\left(u^{\prime }\right)}^m{u}^{″}-{\mu }_2^{m+2}{\left(u^{\prime }\right)}^m{u}^{″}=\lambda u^n.$$

2.

Let $\zeta ={\mu }_1^{m+2}+{\mu }_2^{m+2}$, then the reduced equation takes the form

$$u^{″}\left(c^2-\zeta {\left(u^{\prime }\right)}^m\right)=\lambda u^n.$$

(63)

3.

Assume a solution of the form

$$u\left(\alpha \right)=A{cos}^p\left(\alpha v\right)\mathrm{or}u\left(\alpha \right)=A{sin}^p\left(\alpha v\right),$$

with constants $A,v,p$ to be determined.

4.

Use classical identities to evaluate

$$u^{\prime }=-Apv{cos}^{p-1}\left(\alpha v\right)sin\left(\alpha v\right),$$

$$u^{″}=Ap{v}^2{cos}^{p-2}\left(\alpha v\right)\left((p-1){sin}^2\left(\alpha v\right)-{cos}^2\left(\alpha v\right)\right).$$

5.

Insert u, $u^{\prime }$, and $u^{″}$ into the obtained ODE and match powers of $cos\left(\alpha v\right)$ and $sin\left(\alpha v\right)$.

6.

Solving the resulting algebraic equations yields

$$p={\displaystyle \frac{2+m}{1+m-n}}.$$

This results in the following exact traveling wave solution of Equation (2):

$$w(x,y,t)=A{cos}^p\left(v({\mu }_{1}x+{\mu }_{2}y-ct)\right),p={\displaystyle \frac{2+m}{1+m-n}}.$$

Its graphical representation is shown in Figure 10.

The derived solution emphasizes the nonlinear wave profile propagating through a two-dimensional medium. The trigonometric solution describes periodic waves with frequency and amplitude influenced by nonlinearity parameters m and n. Such waves resemble nonlinear harmonics and often arise in elastic media.

3.6.2. Jacobi Elliptic Function Method

The Jacobi elliptic function method generalizes the sine–cosine method by introducing the class of Jacobi elliptic functions, such as $\mathrm{cn}(\alpha ,r)$, $\mathrm{sn}(\alpha ,r)$, and $\mathrm{dn}(\alpha ,r)$. These functions enable modeling of more intricate wave behaviors, transitioning from periodic to solitary waves as the modulus r varies. This approach includes the consideration of the following essential steps:

1.

As mentioned above, consider $\alpha ={\mu }_{1}x+{\mu }_{2}y-ct$ and $w(x,y,t)=u\left(\alpha \right)$, transforming Equation (2) into Equation (63).

2.

Choose a trial function.

$$u\left(\alpha \right)=A{\mathrm{sn}}^p(v\alpha ,r),$$

where $r\in (0,1)$ represents the elliptic modulus.

3.

Compute the associated derivatives.

$$u^{\prime }=Apv{\mathrm{sn}}^{p-1}(v\alpha ,r)\mathrm{cn}(v\alpha ,r)\mathrm{dn}(v\alpha ,r),$$

$$u^{″}=Ap{v}^2{\mathrm{sn}}^{p-2}(v\alpha ,r)\left[(p-1){\mathrm{cn}}^2(v\alpha ,r){\mathrm{dn}}^2(v\alpha ,r)-{\mathrm{sn}}^2(v\alpha ,r)\left({\mathrm{dn}}^2(v\alpha ,r)+r^2{\mathrm{cn}}^2(v\alpha ,r)\right)\right]$$

4.

Plug into the Equation (63) and match coefficients of similar powers of elliptic functions.

5.

The resulting constraints result in

$$p={\displaystyle \frac{2+m}{1+m-n}},$$

and additional relations for $A,v,\omega$, and r.

Thus, the obtained Jacobi elliptic solution can be expressed as

$$w(x,y,t)=A{\mathrm{sn}}^p\left(v({\mu }_{1}x+{\mu }_{2}y-ct),r\right),p={\displaystyle \frac{2+m}{1+m-n}}.$$

Graphically, it is represented as shown in Figure 11.

The Jacobi elliptic solution describes a wider range of wave phenomena. For a small modulus r, the solution approximates a sinusoidal wave, while as $r\to 1$, it transforms into a soliton. This characteristic models systems where both pulse-like wave profiles and oscillatory waves coexist, for example, in shallow water dynamics. Herein, m governs the degree of nonlinear dispersive steepening, n modulates the nonlinear energy supply, and r dictates the transition from purely periodic to solitary waveforms. Their combined influence shapes the waveform profile, stability, and energy distribution, with r serving as the principal shape-controlling parameter and m and n refining its nonlinear robustness.

Furthermore, when $r=0$, the Jacobi elliptic function simplifies, and the solution corresponds to the exact traveling wave form, obtained earlier. However, for $r=1$, the above solution reduces to

$$w(x,y,t)=A{tanh}^p\left(v({\mu }_{1}x+{\mu }_{2}y-ct)\right),$$

and its visualization is given in Figure 12, it is a solitary wave solution, particularly of the pulse type. The solution is localized in space and asymptotically approaches a constant value as $\alpha \to \pm \infty$. Such waveforms arise in nonlinear mediums where there is a balance between dispersion and nonlinear effects, enabling the wave to maintain its shape and speed over time.

Moreover, the Jacobi elliptic function solution

$$w(x,y,t)=A{\mathrm{sn}}^p\left(v({\mu }_{1}x+{\mu }_{2}y-ct),r\right),$$

exhibits a smooth transition from spatially periodic waveforms to solitary pulse structures. This transition is jointly influenced by the nonlinear parameters m and n in the governing PDE (2), together with the elliptic modulus r from the solution form. The parameter m determines the intensity of the anisotropic dispersive effects represented by the terms ${\left(w_x\right)}^m{w}_{xx}$ and ${\left(w_y\right)}^m{w}_{yy}$. Larger values of m enhance nonlinear steepening, producing sharper gradients and promoting the formation of localized solitary-like profiles, even for intermediate r. When m is smaller, the dispersive sloping is weaker, resulting in smoother, nearly sinusoidal periodic waves. The term $\lambda w^n$ controls the rate of nonlinear energy input or reaction within the system. Higher n values channel more energy into regions of large amplitude, amplifying the wave peaks and encouraging the shift toward pulse-type solitary forms. Lower n values distribute the input energy more evenly, preserving periodic oscillations over time. The modulus r determines the inherent geometry of the Jacobi $\mathrm{sn}$ function. When $0<r\ll 1$, the function closely resembles a sine wave, yielding evenly distributed low-amplitude periodic oscillations. As $r\to 1$, the function approaches a hyperbolic tangent, giving rise to a single, well-localized soliton with concentrated energy at its center and exponentially decaying tails. From a stability perspective, periodic solutions associated with small r are generally more resistant to small disturbances when m and n remain moderate due to the uniform spread of energy. As r approaches unity (see

Table 6. Parameter effects on wave characteristics.

Parameter	Effect on Energy Distribution	Effect on Stability
m	Large m values concentrate energy in narrow regions; small m spreads energy more evenly	Large m can stabilize localized structures; small m supports stable periodic forms
n	High n concentrates energy at maxima; low n keeps distribution uniform	Excessively large n may cause instability; moderate n supports robust waves
r	Small r yields evenly spread energy; large r localizes energy in the core	Small r solutions are more stable; large r waves are sensitive to m and n changes

), the localization of energy increases and the solitary state becomes more sensitive to nonlinear effects, and larger m can stabilize the soliton, while excessively high n can trigger amplitude blow-up or instability due to extreme energy concentration.

4. Noether’s Theorem and Conservation Laws

This section focuses on the derivation of conservation laws for Equation (2) using the variational symmetry approach provided by the Noether theorem [22]. It establishes a profound connection between conservation laws and symmetries in systems governed by variational principles. Conservation laws are fundamental in understanding the qualitative behavior of solutions to nonlinear PDEs. They often correspond to physically meaningful quantities such as energy, momentum, or mass, which remain conserved throughout the evolution dictated by the system. These conserved quantities serve multiple purposes; for example, they provide tools for verifying the correctness of analytical solutions, guide the development of stable and accurate numerical methods, and offer insights in assessing long-term dynamics or stability properties of nonlinear wave phenomena. In models exhibiting anisotropic diffusion and nonlinear source terms, identifying such invariants is particularly important because they shed light on the mechanisms governing wave propagation, energy distribution, and interaction within complex mediums. The implementation of Noether’s theorem typically proceeds through two essential steps:

1.

Derivation of the appropriate Lagrangian for the system;

2.

Application of Noether’s symmetry condition to derive conservation laws.

For the nonlinear Equation (2), the corresponding Lagrangian that satisfies the underlying Euler–Lagrange condition,

$${\displaystyle \frac{\delta \mathcal{L}}{\delta w}}=0,$$

is given by

$$\mathcal{L}={\displaystyle \frac{1}{2}}{w}_t^2-{\displaystyle \frac{1}{(m+1)(m+2)}}\left(w_x^{m+2}+w_y^{m+2}\right)+{\displaystyle \frac{\lambda }{n+1}}{w}^{n+1}.$$

(64)

The operator defined in Equation (3) is referred to as the Noether operator associated with Equation (2) in the context of the Lagrangian (64), provided it satisfies the Noether identity,

$${\mathcal{X}}^{\left[1\right]}\mathcal{L}+\left({\mathcal{D}}_x{\varphi }^1+{\mathcal{D}}_y{\varphi }^2++{\mathcal{D}}_t{\varphi }^3\right)\mathcal{L}={\mathcal{D}}_x{\mathcal{G}}^1+{\mathcal{D}}_y{\mathcal{G}}^2+{\mathcal{D}}_t{\mathcal{G}}^3,$$

(65)

where ${\mathcal{G}}^1$, ${\mathcal{G}}^2$, and ${\mathcal{G}}^3$ are gauge terms that may depend on the variables $(x,y,t,w)$. Condition (65) yields a following system of determining equations, which can be solved to derive the variational symmetries and the corresponding conserved quantities:

$$\begin{array}{cc}\hfill {\varphi }_w^1=0,{\varphi }_w^2=0,{\varphi }_w^3& =0,\hfill \end{array}$$

(66)

$$\begin{array}{cc}\hfill {\eta }_y=0,{\eta }_x& =0,\hfill \end{array}$$

(67)

$$\begin{array}{cc}\hfill {\varphi }_t^1=0,{\varphi }_y^1& =0,\hfill \end{array}$$

(68)

$$\begin{array}{cc}\hfill {\varphi }_t^2=0,{\varphi }_x^2& =0,\hfill \end{array}$$

(69)

$$\begin{array}{cc}\hfill {\varphi }_x^3=0,{\varphi }_y^3& =0,\hfill \end{array}$$

(70)

$$\begin{array}{cc}\hfill {\mathcal{G}}_w^1=0,{\mathcal{G}}_w^2& =0,\hfill \end{array}$$

(71)

$$\begin{array}{cc}\hfill {\mathcal{G}}_w^3-{\eta }_t& =0,\hfill \end{array}$$

(72)

$$\begin{array}{cc}\hfill 2{\eta }_w-{\varphi }_t^3+{\varphi }_x^1+{\varphi }_y^2& =0,\hfill \end{array}$$

(73)

$$\begin{array}{cc}\hfill (m+2){\eta }_w+{\varphi }_t^3-(m+1){\varphi }_x^1+{\varphi }_y^2& =0,\hfill \end{array}$$

(74)

$$\begin{array}{cc}\hfill (m+2){\eta }_w+{\varphi }_t^3+{\varphi }_x^1-(m+1){\varphi }_y^2& =0,\hfill \end{array}$$

(75)

$$\begin{array}{cc}\hfill (n+1)\eta w^n+w^{n+1}\left({\varphi }_t^3+{\varphi }_x^1+{\varphi }_y^2\right)+{\displaystyle \frac{n+1}{\lambda }}\left({\mathcal{G}}_x^1+{\mathcal{G}}_y^2+{\mathcal{G}}_t^3\right)& =0.\hfill \end{array}$$

(76)

We employ the following formula to extract the conservation laws associated with Equation (2):

$${\mathcal{C}}^i={\mathcal{G}}^i-{\varphi }^i\mathcal{L}-\left(\eta -{\varphi }^1{w}_x-{\tau }^2{w}_y-{\varphi }^3{w}_t\right){\displaystyle \frac{\partial \mathcal{L}}{\partial w_i}},$$

(77)

where $i\in \{1,2,3\}\equiv \{x,y,t\}$. Accordingly, the conserved quantities can be derived using the following expanded forms of Equation (77):

$$\begin{array}{cc}\hfill {\mathcal{C}}^x& ={\mathcal{G}}^1-{\varphi }^1\mathcal{L}+{\displaystyle \frac{1}{m+1}}\left(\eta -{\varphi }^1{w}_x-{\varphi }^2{w}_y-{\varphi }^3{w}_t\right)w_x^{m+1},\hfill \end{array}$$

(78)

$$\begin{array}{cc}\hfill {\mathcal{C}}^y& ={\mathcal{G}}^2-{\varphi }^2\mathcal{L}+{\displaystyle \frac{1}{m+1}}\left(\eta -{\varphi }^1{w}_x-{\varphi }^2{w}_y-{\varphi }^3{w}_t\right)w_y^{m+1},\hfill \end{array}$$

(79)

$$\begin{array}{cc}\hfill {\mathcal{C}}^t& ={\mathcal{G}}^3-{\varphi }^3\mathcal{L}-\left(\eta -{\varphi }^1{w}_x-{\varphi }^2{w}_y-{\varphi }^3{w}_t\right)w_t.\hfill \end{array}$$

(80)

Equation (73) implies that

$$\eta =\mathcal{A}\left(t\right)w+\mathcal{B}\left(t\right).$$

(81)

Subsequently, Equations (73)–(75) yield the following result:

$$(m+2)({\varphi }_y^2-{\varphi }_x^1)=0.$$

(82)

Next, we consider the following two cases:

4.1. Case 1:    ${\varphi }_y^2-{\varphi }_x^1=0$ provided $m\ne -2$

Using Equations (74) and (75) and (81), we obtain the following.

$$\eta =-{\displaystyle \frac{2-m}{m+4}}{c}_{1}w+\mathcal{B}\left(t\right),$$

and consequently, this branches into two additional subcases.

4.1.1. Subcase 1.1: $m\ne -4$

In this case, we obtain the following infinitesimals:

$$\begin{array}{cc}\hfill {\varphi }^1=& c_{1}x+c_2,{\varphi }^2=c_{1}y+c_3,\hfill \\ \hfill {\varphi }^3=& {\displaystyle \frac{4(m+1)}{m+4}}{c}_{1}t+c_4,\eta ={\displaystyle \frac{m-2}{m+4}}{c}_{1}w+\mathcal{B}\left(t\right),\hfill \end{array}$$

subject to

$$\begin{array}{cc}\hfill \mathcal{B}\left(t\right)& =0,\hfill \\ \hfill (n+1)\left({\mathcal{G}}_x^1+{\mathcal{G}}_y^2+{\mathcal{G}}_t^3\right)& =0.\hfill \end{array}$$

This leads to two further subcases.

4.1.2. Subcase 1.1.1: $n\ne -1$

This case results in the following conditions:

$$n={\displaystyle \frac{7m+10}{2-m}},{\mathcal{G}}^1=b_{1}x+b_2,{\mathcal{G}}^2=-b_{1}y+b_3,{\mathcal{G}}^3=b_0,$$

leading to the following conserved quantities:

$$\begin{array}{cc}\hfill {\mathcal{C}}^x& =-(c_{1}x+c_2)\mathcal{L}+{\displaystyle \frac{1}{m+1}}\left({\displaystyle \frac{m-2}{m+4}}{c}_{1}w-(c_{1}x+c_2)w_x-(c_{1}y+c_3)w_y-({\displaystyle \frac{4m+4}{m+4}}{c}_{1}t+c_4)w_t\right)w_x^{m+1},\hfill \\ \hfill {\mathcal{C}}^y& =-(c_{1}y+c_3)\mathcal{L}+{\displaystyle \frac{1}{m+1}}\left({\displaystyle \frac{m-2}{m+4}}{c}_{1}w-(c_{1}x+c_2)w_x-(c_{1}y+c_3)w_y-({\displaystyle \frac{4m+4}{m+4}}{c}_{1}t+c_4)w_t\right)w_y^{m+1},\hfill \\ \hfill {\mathcal{C}}^t& =-({\displaystyle \frac{4m+4}{m+4}}{c}_{1}t+c_4)\mathcal{L}-\left({\displaystyle \frac{m-2}{m+4}}{c}_{1}w-(c_{1}x+c_2)w_x-(c_{1}y+c_3)w_y-({\displaystyle \frac{4m+4}{m+4}}{c}_{1}t+c_4)w_t\right)w_t.\hfill \end{array}$$

Here, the parameters $c_i$ represent arbitrary constants for $i=1,2,3,4$. Consequently, one can identify four distinct conserved quantities corresponding to the specific selections $(c_1=1,c_j=0,\mathrm{for}j=2,3,4), (c_2=1,c_j=0,\mathrm{for}j=1,3,4), (c_3=1,c_j=0,\mathrm{for}j=1,2,4), \mathrm{and} (c_4=1,c_j=0,\mathrm{for}j=1,2,3).$ This yields

$$\begin{array}{cc}\hfill {\mathcal{C}}_1^x& =-x\mathcal{L}+{\displaystyle \frac{1}{m+1}}\left({\displaystyle \frac{m-2}{m+4}}w-x{w}_x-y{w}_y-({\displaystyle \frac{4m+4}{m+4}}t)w_t\right)w_x^{m+1},\hfill \\ \hfill {\mathcal{C}}_1^y& =-y\mathcal{L}+{\displaystyle \frac{1}{m+1}}\left({\displaystyle \frac{m-2}{m+4}}w-x{w}_x-y{w}_y-({\displaystyle \frac{4m+4}{m+4}}t)w_t\right)w_y^{m+1},\hfill \\ \hfill {\mathcal{C}}_1^t& =-\left({\displaystyle \frac{4m+4}{m+4}}t\right)\mathcal{L}-\left({\displaystyle \frac{m-2}{m+4}}w-x{w}_x-y{w}_y-({\displaystyle \frac{4m+4}{m+4}}t)w_t\right)w_t.\hfill \end{array}$$

For $c_2=1$, we obtain

$$\begin{array}{cc}\hfill {\mathcal{C}}_2^x& ={\displaystyle \frac{1}{2}}{w}_t^2-{\displaystyle \frac{1}{(m+1)(m+2)}}\left(w_x^{m+2}+w_y^{m+2}\right)+{\displaystyle \frac{\lambda }{n+1}}{w}^{n+1}-{\displaystyle \frac{1}{m+1}}{w}_x{w}_x^{m+1},\hfill \\ \hfill {\mathcal{C}}_2^y& =-{\displaystyle \frac{1}{m+1}}{w}_x{w}_y^{m+1},\hfill \\ \hfill {\mathcal{C}}_2^t& =w_x{w}_t.\hfill \end{array}$$

This corresponds to the conservation of momentum along the x-axis. The principle of translational symmetry in the x-direction ensures that the total momentum in that direction does not change over time.

Similarly, for $c_3=1$, we have

$$\begin{array}{cc}\hfill {\mathcal{C}}_3^x& =-{\displaystyle \frac{1}{m+1}}{w}_y{w}_x^{m+1},\hfill \\ \hfill {\mathcal{C}}_3^y& =-({\displaystyle \frac{1}{2}}{w}_t^2-{\displaystyle \frac{1}{(m+1)(m+2)}}\left(w_x^{m+2}+w_y^{m+2}\right)+{\displaystyle \frac{\lambda }{n+1}}{w}^{n+1})-{\displaystyle \frac{1}{m+1}}{w}_y{w}_y^{m+1},\hfill \\ \hfill {\mathcal{C}}_3^t& =w_y{w}_t.\hfill \end{array}$$

This represents the conservation of momentum along the y-axis. The principle of translational symmetry in the y-direction confirms that the total momentum in that direction remains conserved.

Lastly, $c_4=1$ results in

$$\begin{array}{cc}\hfill {\mathcal{C}}_4^x& =-{\displaystyle \frac{1}{m+1}}{w}_t{w}_x^{m+1},\hfill \\ \hfill {\mathcal{C}}_4^y& =-{\displaystyle \frac{1}{m+1}}{w}_t{w}_y^{m+1},\hfill \\ \hfill {\mathcal{C}}_4^t& =-({\displaystyle \frac{1}{2}}{w}_t^2-{\displaystyle \frac{1}{(m+1)(m+2)}}\left(w_x^{m+2}+w_y^{m+2}\right)+{\displaystyle \frac{\lambda }{n+1}}{w}^{n+1})+w_t{w}_t.\hfill \end{array}$$

This conservation law arises due to the invariance of the system under time translations, indicating that, in the absence of external influences or dissipation, the total energy remains conserved over time. Such energy conservation is fundamental in physics and provides an important tool for studying the stability and long-term behavior of solutions to nonlinear PDEs.

4.1.3. Subcase 1.1.2: $n=-1$

This case yields the following infinitesimals:

$$\begin{array}{cc}\hfill {\varphi }^1=& c_1,{\varphi }^2=c_2,{\varphi }^3=c_3,\eta =0,\hfill \end{array}$$

which, in turn, result in the following conserved quantities:

$$\begin{array}{cc}\hfill {\mathcal{C}}^x& =-c_1\left({\displaystyle \frac{1}{2}}{w}_t^2-{\displaystyle \frac{1}{(m+1)(m+2)}}\left(w_x^{m+2}+w_y^{m+2}\right)+{\displaystyle \frac{\lambda }{n+1}}{w}^{n+1}\right)-{\displaystyle \frac{1}{m+1}}\left(c_1{w}_x+c_2{w}_y+c_3{w}_t\right)w_x^{m+1},\hfill \\ \hfill {\mathcal{C}}^y& =-c_2\left({\displaystyle \frac{1}{2}}{w}_t^2-{\displaystyle \frac{1}{(m+1)(m+2)}}\left(w_x^{m+2}+w_y^{m+2}\right)+{\displaystyle \frac{\lambda }{n+1}}{w}^{n+1}\right)-{\displaystyle \frac{1}{m+1}}\left(c_1{w}_x+c_2{w}_y+c_3{w}_t\right)w_y^{m+1},\hfill \\ \hfill {\mathcal{C}}^t& =-c_3\left({\displaystyle \frac{1}{2}}{w}_t^2-{\displaystyle \frac{1}{(m+1)(m+2)}}\left(w_x^{m+2}+w_y^{m+2}\right)+{\displaystyle \frac{\lambda }{n+1}}{w}^{n+1}\right)+\left(c_1{w}_x+c_2{w}_y+c_3{w}_t\right)w_t.\hfill \end{array}$$

When $c_1=1$ with $c_2=c_3=0$, the corresponding conservation law stems from invariance under translations in the x-direction and represents the conservation of linear momentum along the x–axis. Setting $c_2=1$ with $c_1=c_3=0$ gives the analogous conservation law for momentum in the y-direction, arising from y-translation invariance. Finally, taking $c_3=1$ with $c_1=c_2=0$ corresponds to invariance under time translations, yielding the conservation of energy. In this case, the conserved quantity describes the total energy, including kinetic and potential components as well as the contribution from the nonlinear source term, while the associated flux terms represent the spatial transport of this energy.

4.1.4. Subcase 1.2: $m=-4$

We obtain the same conservation laws as those identified in Subcase 1.1.2 for Case 1.2.

4.2. Case 2: ${\varphi }_y^2-{\varphi }_x^1\ne 0$ Provided $m=-2$

This case leads to the derivation of the following infinitesimals:

$$\begin{array}{cc}\hfill {\varphi }^1=& c_{1}x+c_2,{\varphi }^2=c_{3}y+c_4,{\varphi }^3=-(c_1+c_3)t+c_5,\eta =-(c_1+c_3)w,\hfill \end{array}$$

which, in turn, yield the associated conserved quantities:

$$\begin{array}{cc}\hfill {\mathcal{C}}^x& =-(c_{1}x+c_2)\mathcal{L}-{\displaystyle \frac{1}{m+1}}\left((c_1+c_3)w+(c_{1}x+c_2)w_x+(c_{3}y+c_4)w_y+(-(c_1+c_3)t+c_5)w_t\right)w_x^{m+1},\hfill \\ \hfill {\mathcal{C}}^y& =-(c_{3}y+c_4)\mathcal{L}-{\displaystyle \frac{1}{m+1}}\left((c_1+c_3)w+(c_{1}x+c_2)w_x+(c_{3}y+c_4)w_y+(-(c_1+c_3)t+c_5)w_t\right)w_y^{m+1},\hfill \\ \hfill {\mathcal{C}}^t& =((c_1+c_3)t-c_5)\mathcal{L}-\left((c_1+c_3)w+(c_{1}x+c_2)w_x+(c_{3}y+c_4)w_y+(-(c_1+c_3)t+c_5)w_t\right)w_t,\hfill \end{array}$$

provided $n=-1.$ This set of conservation laws emerge from a symmetry structure that includes scaling, translations, and dilations in both space and time, as well as transformations involving the dependent variable w. The parameter $c_1$ controls a combined scaling in x and t together with a proportional change in w, while $c_3$ governs a similar scaling in y and t. The constants $c_2$ and $c_4$ correspond to translations in the x and y directions, respectively, and $c_5$ represents time translations. By activating these parameters individually, one recovers conservation laws for linear momenta, energy, or scaling invariants. When scaling parameters are nonzero, the conserved quantities mix contributions from the field itself, its spatial derivatives, and its time derivative, reflecting the interplay between field amplitude changes and geometric transformations of the coordinates. However, for $n\ne -1,$ we obtain

$$\begin{array}{cc}\hfill {\varphi }^1=& c_{1}x+c_2,{\varphi }^2=-c_{1}y+c_3,{\varphi }^3=c_4,\eta =0,\hfill \end{array}$$

which consequently yields the following conserved quantities:

$$\begin{array}{cc}\hfill {\mathcal{C}}^x& =-(c_{1}x+c_2)\mathcal{L}-{\displaystyle \frac{1}{m+1}}\left((c_{1}x+c_2)w_x+(-c_{1}y+c_3)w_y+c_4{w}_t\right)w_x^{m+1},\hfill \\ \hfill {\mathcal{C}}^y& =-(c_{1}y+c_3)\mathcal{L}-{\displaystyle \frac{1}{m+1}}\left((c_{1}x+c_2)w_x+(-c_{1}y+c_3)w_y+c_4{w}_t\right)w_y^{m+1},\hfill \\ \hfill {\mathcal{C}}^t& =-c_4\mathcal{L}+\left((c_{1}x+c_2)w_x+(-c_{1}y+c_3)w_y+c_4{w}_t\right)w_t.\hfill \end{array}$$

Herein, $c_i$ ($i=1,2,\dots ,5$) are arbitrary constants. Associated with Equation (2), these conservation laws, particularly those involving spatial derivatives such as $w_x^{m+1}$ and $w_y^{m+1}$, are fundamental to understanding the important properties of the underlying system. These conserved quantities signify the invariance of physical quantities such as momentum flow, directional wave propagation, and energy distribution. Their existence ensures the mathematical consistency of the model and aids in symmetry-based reductions and analytical solution methods. Moreover, these conservation laws provide a foundation for developing stable and physically consistent numerical schemes to simulate the nonlinear wave dynamics governed by the PDE.

5. Discussion

The generalized form of Equation (2) is particularly significant because it allows for a systematic exploration of how multidirectional nonlinearities interact with nonlinear sources. Previous studies, such as Arrigo [1], were limited to a single spatial direction and arbitrary source terms or specific functional forms, which restricted the ability to uncover soliton and traveling wave behaviors in higher-dimensional settings. Our analysis fills this gap by providing a full Lie symmetry classification for arbitrary m and n, thereby revealing all possible invariant reductions and associated exact solutions.

The present work provides a complete Lie symmetry analysis and classification of the nonlinear PDE (2), which generalizes previously studied wave-type equations by including power-law source terms and anisotropic spatial nonlinearities. The choice of this equation is motivated by both physical and mathematical considerations. Nonlinear wave-type equations with gradient-dependent diffusion, such as ${\left(w_x\right)}^m{w}_{xx}$ and ${\left(w_y\right)}^m{w}_{yy}$, naturally appear in diverse phenomena, including non-Newtonian fluid flows, nonlinear elastic media, and transport in porous materials [2,3,4]. Moreover, power-law source terms $\lambda w^n$ represent essential nonlinear reactions or forcing mechanisms present in chemical kinetics, pattern formation, population dynamics, and reactive heat transfer [5,6,7]. By combining these nonlinear dispersive and reactive effects in two spatial dimensions, Equation (2) captures a level of complexity and richness that simpler one-dimensional or linear models cannot.

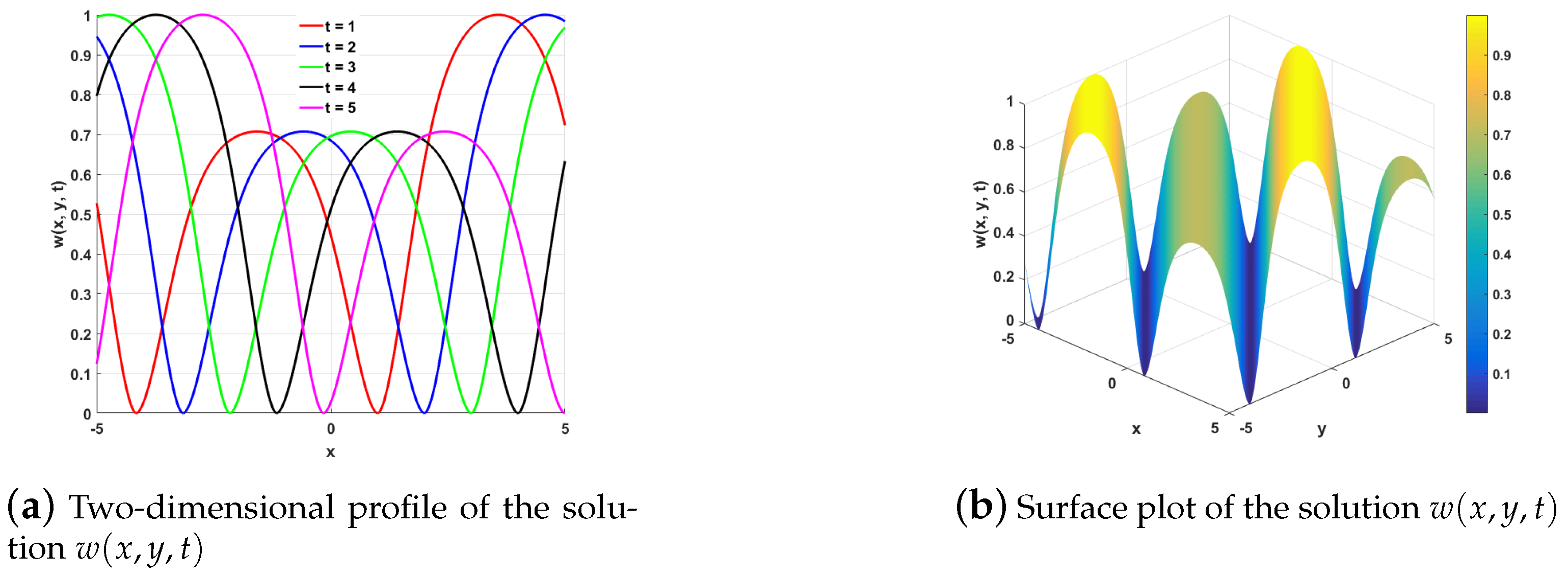
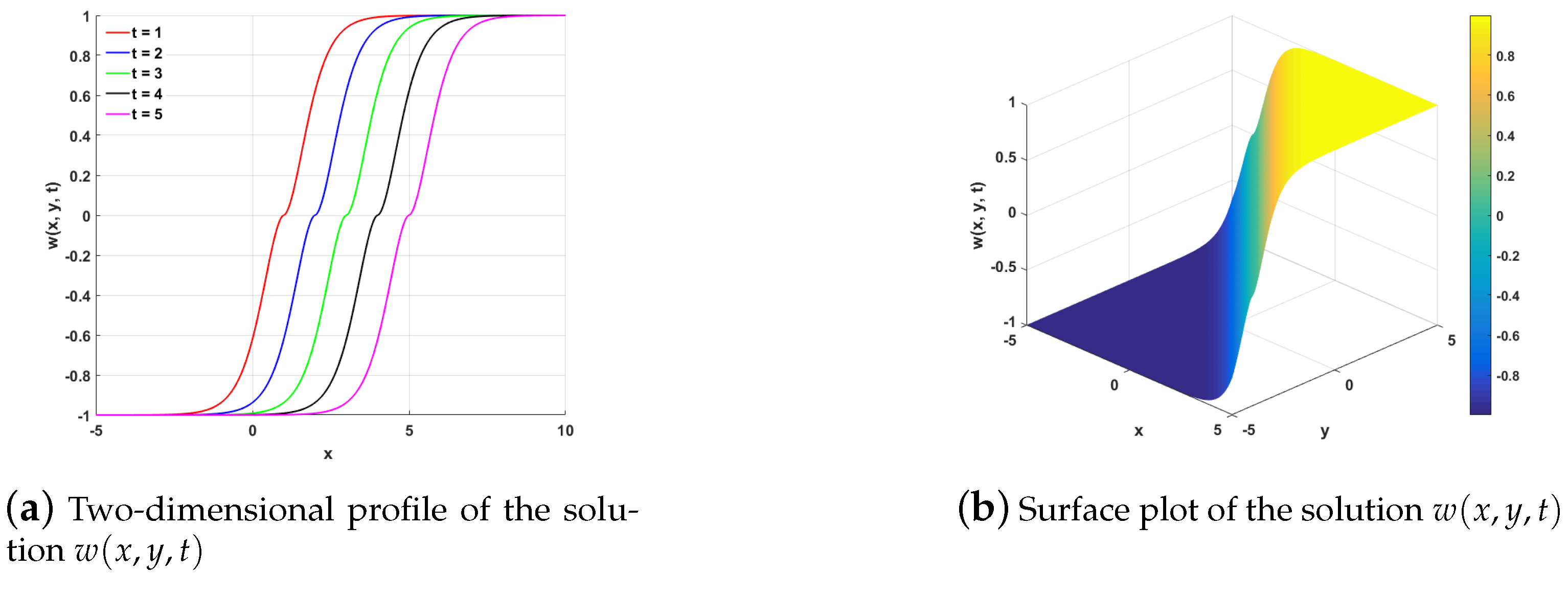
The derivation of exact solutions using sine–cosine and Jacobi elliptic function methods is a significant contribution. These solutions capture traveling wave and soliton behaviors that are intrinsic to nonlinear wave dynamics but were previously unaddressed in similar two-dimensional systems. The richness of these solution families highlights the intricate interplay between nonlinear dispersive terms and the power-law source, providing insight into phenomena such as wave steepening, self-focusing, and periodic pattern formation in anisotropic media.

Another notable advancement is the systematic derivation of conservation laws via Noether’s theorem. By identifying infinitesimal symmetries associated with variational structures, we established intrinsic invariants of the system, which serve dual purposes: first, as analytical checks for the correctness of exact solutions, and second, as guides for developing energy-preserving numerical schemes. Unlike prior studies that focused mainly on symmetry reductions or specific solution forms, our approach integrates symmetry classification, exact solutions, and conservation laws into a single setup.

In terms of novelty, this work goes beyond previous literature in several ways.

1.

The generalized PDE (2), featuring both anisotropic nonlinear diffusion in multiple spatial directions and a power-law source term, enables modeling of more complex physical processes.

2.

The complete Lie symmetry classification for arbitrary m and n values provides a systematic and exhaustive approach for further analytical and numerical investigations.

3.

The combination of Jacobi elliptic and sine–cosine methods with symmetry reductions yields a rich spectrum of traveling and soliton-type solutions, revealing behaviors that were inaccessible in earlier studies.

4.

The explicit derivation of conservation laws via Noether’s theorem complements the construction of the solution, offering a set of tools to validate analytical and computational results.

The analytical traveling wave solutions obtained in this study are not purely theoretical; they correspond closely to waveforms observed in various physical systems. For example, in nonlinear acoustics, typical parameter values are $m=2$, $n=1$, and $\lambda$ in the range $0.1$–$1.0$, representing quadratic nonlinearities with moderate dispersion [23,24]. In shallow water wave theory, cubic-type nonlinearities ($m\approx 3$) with $n=2$ and $\lambda$ proportional to the square of the undisturbed water depth have been reported in the framework of Boussinesq- and KdV-type models [25].

These outcomes have multiple potential applications. In physical sciences, the derived traveling waves and soliton solutions can model nonlinear wave propagation in elastic media, shallow water, and non-Newtonian fluids. In applied mathematics and computational physics, conservation laws provide benchmarks for developing energy-conservation numerical algorithms. Furthermore, the methodology developed here is adaptable to more complex systems, including multi-dimensional PDEs with variable coefficients, generalized damping, and coupled nonlinear interactions.

6. Conclusions

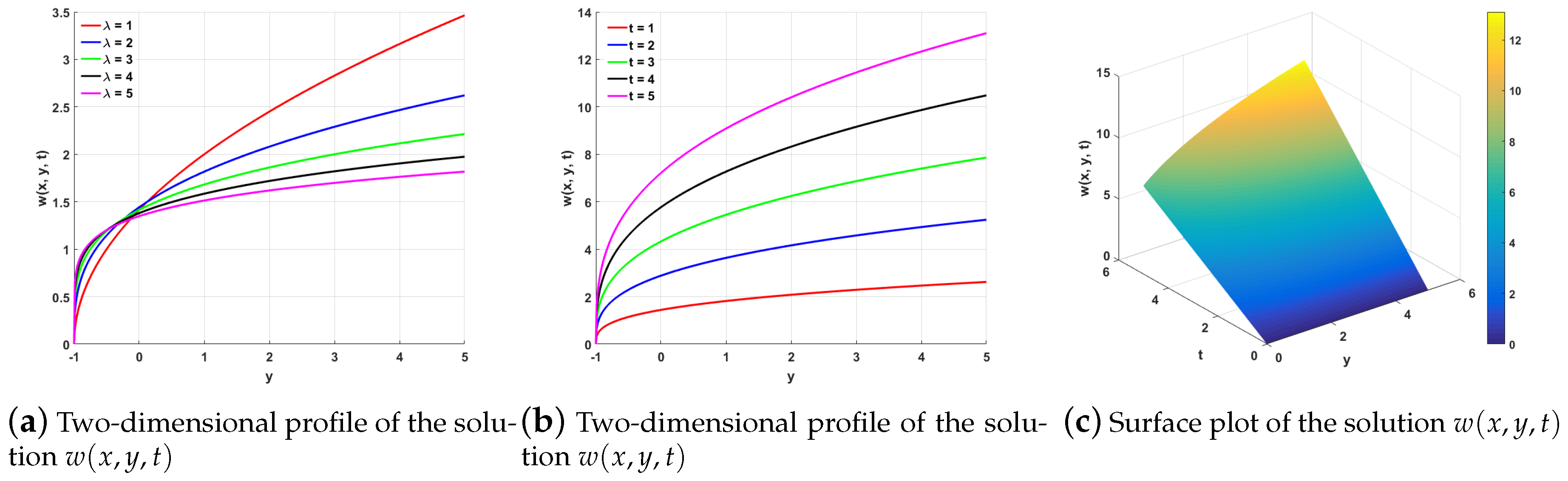
In this work, we carried out a detailed Lie symmetry analysis and classification of a nonlinear partial differential equation involving power-law spatial derivatives. Based on our understanding of the existing literature, this work provides what we believe to be the first comprehensive Lie symmetry classification of Equation (2) for general values of m and n, together with the associated explicit invariant solutions and derived conservation laws. Exact analytical solutions are constructed, including, for instance, $w(x,y,t)=t{c}_1{e}^{\pm {\displaystyle \frac{x+y}{\sqrt{2}}}}$ for $m=-4$, $n=-3$, $\lambda =-4$, and $w(x,y,t)=t{\left((\lambda +1)(c_{1}y+c_2)\right)}^{{\displaystyle \frac{1}{\lambda +1}}}$ for $m=-2$, $n=-1$. The results extend and unify earlier partial classifications by covering the full parameter space without imposing restrictive assumptions. This comprehensive treatment not only enriches the theoretical understanding of the symmetry structure of the equation but also lays a solid foundation for further analytical and numerical investigations. This study enables an understanding of the symmetry properties and solution structure of Equation (2) with anisotropic and power-law nonlinearities. The obtained symmetries enabled reductions to ODEs and the derivation of exact solutions, including traveling and soliton waves via Jacobi elliptic and sine-cosine methods. The construction of traveling and soliton wave solutions through Jacobi’s elliptic and sine-cosine methods revealed the rich nonlinear behavior of the system. The solutions presented here can be applied to model nonlinear wave phenomena in practical systems. For example, in nonlinear acoustics, they can represent the propagation of high-intensity sound waves in anisotropic materials, while in fluid dynamics, they describe dispersive wave motion in layered or direction-dependent media. By adjusting the model parameters, the framework can capture both periodic and localized wave patterns relevant to real-world engineering and physical applications. Furthermore, by determining infinitesimal symmetries and employing Noether’s theorem, we systematically derived associated conservation laws that reveal intrinsic invariants of the system. These conserved quantities aid in both analytical reduction and numerical validation. These findings deepen the analytical understanding of nonlinear wave models and provide a foundation for future studies involving generalized damping, variable coefficients, and multi-dimensional systems.

The results obtained in this work are broadly relevant to physical systems where the nonlinear wave dynamics are significant. The generalized equation, together with its exact traveling wave and soliton solutions, can model phenomena such as nonlinear acoustic propagation in media with quadratic or cubic nonlinearities, dispersive–nonlinear interactions in shallow water dynamics, deformation waves in anisotropic elastic solids, and nonlinear transport in porous or heterogeneous media. These findings are also applicable to reaction–diffusion processes in chemical kinetics and biological systems. The conservation laws derived alongside the solutions provide analytical benchmarks, supporting both theoretical studies and the development of energy-preserving numerical schemes for practical engineering and scientific applications. By connecting the mathematical structure of the equation to these real-world contexts, the present work offers both theoretical insight and a foundation for further applied investigations.