Design and Analysis of Reliability Sampling Plans Based on the Topp–Leone Generated Weibull Distribution
Abstract
1. Introduction
1.1. Topp–Leone Generated Weibull Distribution
1.2. Why the Topp–Leone Generator (vs. Other Generators Such as Weibull–G)?
2. Reliability Sampling Plan
2.1. Consumer’s Risk and Minimum Sample Size
2.2. Operating Characteristic Function
2.3. Producer’s Risk
3. Numerical Results and Discussion
Illustrative Examples
- Designing a Sampling Plan. Consider a product whose lifetime follows the TLGW distribution. Suppose the specified average life is h. We choose a consumer confidence level and plan to truncate the life test at h (so that ).If we select an acceptance number , Table 1 (binomial model) indicates that the minimum required sample size is . The Poisson approximation in Table 2 gives a similar suggestion of . Let us use the plan . For this plan, the OC values can be obtained from Table 3. In particular, when the true mean life is twice the specified value (), the acceptance probability is about . If the true mean is four times the specified value (), the acceptance probability rises to , and it is essentially for . Thus, the lot has a very high chance of being accepted as long as the product’s actual mean life is significantly better than the requirement.From Table 4, for and at , the minimum ratio that guarantees a producer’s risk of is approximately . In other words, if the true mean life is about h or more, the probability of rejecting such a good lot is 5% or less under this plan.
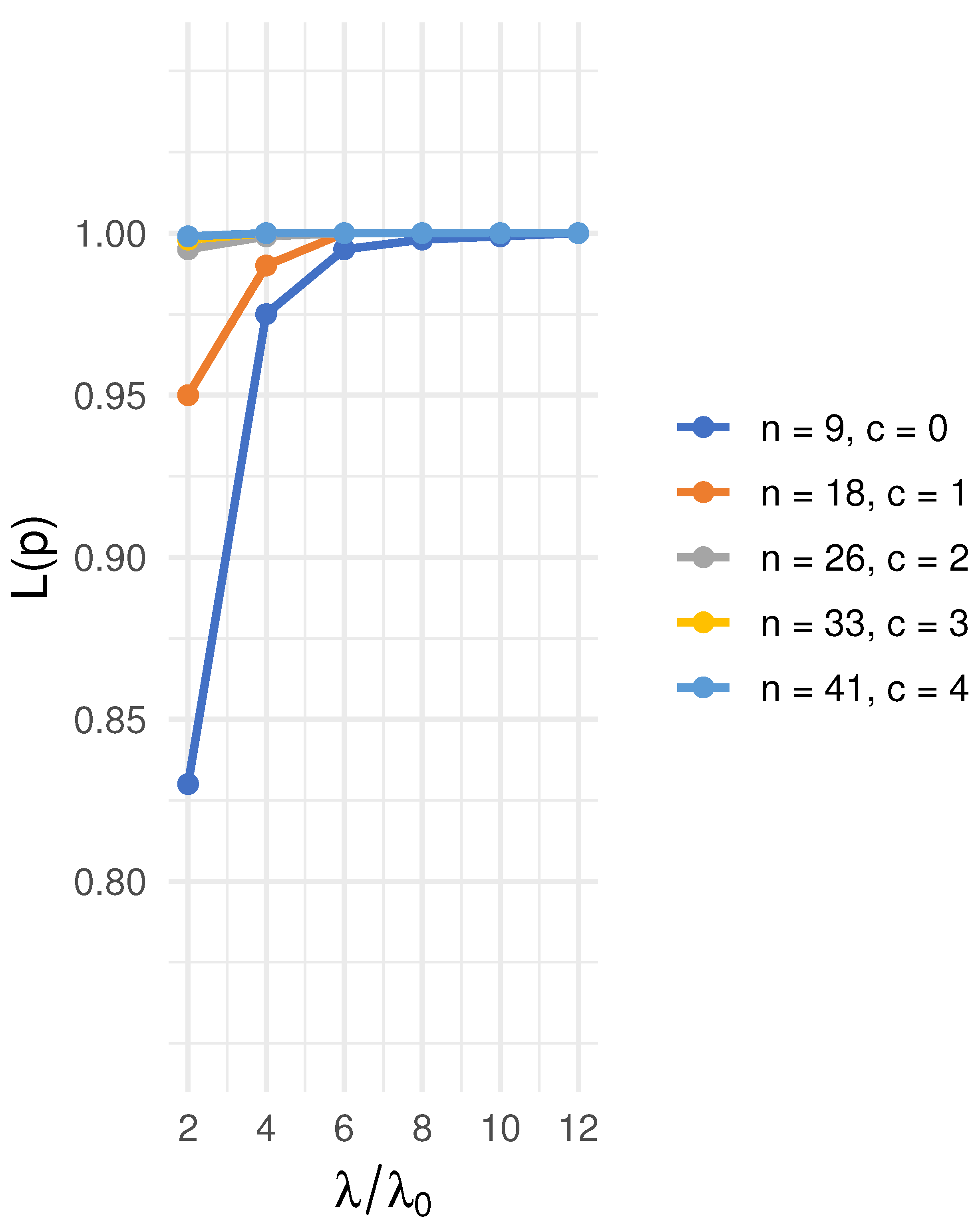
2 4 6 8 10 12 OC 0.9446 0.9998 0.9999 1 1 1 Figure 1 illustrates the OC curves for this sampling plan under various acceptance numbers. The plot shows the probability of acceptance versus for different values of c. Such a graph helps in visualizing the stringency of the plan; a smaller acceptance number c leads to a lower curve (meaning the plan is more stringent and less likely to accept lots unless is much larger than ), whereas a larger c makes the plan more lenient (higher acceptance probability for a given ). By examining these curves, a practitioner can choose an acceptance number that provides an appropriate balance between consumer and producer protection for their specific situation. - Application to Real Data. We now consider a real dataset of failure times to illustrate how the sampling plan can be applied. The dataset, reported by Wood [21], consists of 16 ordered failure times (in hours) of a software system:Assume that the lifetime of this software follows the TLGW distribution. Let the specified mean life be h, and set the consumer’s risk at (so ). We choose a test truncation time of h (as before, ). Based on the earlier results, a reasonable plan is since our sample size is 16 and allowing two failures meets the desired confidence level (indeed, from Table 1, the minimum n for and at was 13, so is adequate).By the time the test reached h, only one failure had occurred in the sample (the first failure was at 519 h; the second failure was at 968 h, which is just beyond t). Because the observed number of failures (1) does not exceed the acceptance number , the lot (software) would be accepted. In summary, using this reliability sampling plan, the software passes the test, providing at least 90% confidence that its mean lifetime is not below the specified 1000 h.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Gupta, S.S.; Groll, P.A. Gamma distribution in acceptance sampling based on life tests. J. Am. Stat. Assoc. 1961, 56, 942–970. [Google Scholar] [CrossRef]
- Subba Rao, R.; Prasad, G.; Kantam, R.R.L. Acceptance sampling based on life tests: Pareto-Rayleigh model. Int. J. Adv. Res. Sci. Eng. 2016, 5, 427–436. [Google Scholar]
- Balakrishnan, N.; Leiva, V.; Lopez, J. Acceptance sampling plans from truncated life tests based on the generalized Birnbaum–Saunders distribution. Commun. Stat. Simul. Comput. 2007, 36, 643–656. [Google Scholar] [CrossRef]
- Baklizi, A.; El Masri, A.E.Q.; Al-Nasser, A. Acceptance sampling plans in the Rayleigh model. Commun. Stat. Simul. Comput. 2005, 34, 603–611. [Google Scholar] [CrossRef]
- Rosaiah, K.; Kantam, R.R.L. Acceptance sampling based on the inverse Rayleigh distribution. Econ. Qual. Control 2005, 20, 277–286. [Google Scholar] [CrossRef]
- Aslam, M.; Kundu, D.; Ahmad, M. Time truncated acceptance sampling plans for generalized exponential distribution. J. Appl. Stat. 2010, 37, 555–566. [Google Scholar] [CrossRef]
- Rao, G.S.; Kantam, R.R.L. Acceptance sampling plans from truncated life tests based on the log-logistic distribution for percentiles. Stoch. Qual. Control 2010, 25, 153–167. [Google Scholar] [CrossRef]
- Jose, K.K.; Sivadas, R. Negative binomial Marshall–Olkin Rayleigh distribution and its applications. Econ. Qual. Control 2015, 30, 89–98. [Google Scholar] [CrossRef]
- Ravikumar, M.S.; Kantam, R.R.L.; Durgamamba, A.N. Acceptance sampling plans for Burr Type X distribution. Int. J. Adv. Technol. Eng. Sci. 2016, 4, 36–44. [Google Scholar]
- Gillariose, J.; Tomy, L. A new lifetime model: The generalized Rayleigh-truncated negative binomial distribution. Int. J. Sci. Res. Math. Stat. Sci. 2018, 5, 1–12. [Google Scholar]
- Jose, K.K.; Joseph, J. Reliability test plan for the Gumbel-Uniform distribution. Stoch. Qual. Control 2018, 33, 71–81. [Google Scholar] [CrossRef]
- Shahbaz, S.H.; Khan, K.; Shahbaz, M.Q. Acceptance sampling plans for finite and infinite lot size under power Lindley distribution. Symmetry 2018, 10, 496. [Google Scholar] [CrossRef]
- Singh, N.; Singh, N.; Kaur, H. A repetitive acceptance sampling plan for generalized inverted exponential distribution based on truncated life test. Int. J. Sci. Res. Math. Stat. Sci. 2018, 5, 58–64. [Google Scholar] [CrossRef]
- Aryal, G.R.; Ortega, E.M.; Hamedani, G.G.; Yousof, H.M. The Topp–Leone generated Weibull distribution: Regression model, characterizations and applications. Int. J. Stat. Probab. 2016, 6, 126–141. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Lee, C.; Famoye, F. A new method for generating families of continuous distributions. Metron 2013, 71, 63–79. [Google Scholar] [CrossRef]
- da Silva, R.; Bourguignon, M.; da Motta Singer, J.; Cordeiro, G. A new lifetime model: The gamma extended Fréchet distribution. J. Stat. Theory Appl. 2013, 12, 39–54. [Google Scholar] [CrossRef]
- Chhikara, R.S.; Folks, J.L. The Inverse Gaussian Distribution: Theory, Methodology, and Applications; Marcel Dekker: New York, NY, USA, 1989. [Google Scholar]
- Efron, B. Logistic regression, survival analysis, and the Kaplan–Meier curve. J. Am. Stat. Assoc. 1988, 83, 414–425. [Google Scholar] [CrossRef]
- Bourguignon, M.; Silva, R.B.; Cordeiro, G.M. The Weibull–G Family of Probability Distributions. J. Data Sci. 2014, 12, 53–68. [Google Scholar] [CrossRef]
- Gillariose, J.; Tomy, L. Reliability Test Plan for an Extended Birnbaum–Saunders Distribution. J. Reliab. Stat. Stud. 2021, 14, 353–372. [Google Scholar] [CrossRef]
- Wood, A. Predicting software reliability. IEEE Trans. Softw. Eng. 1996, 22, 69–77. [Google Scholar] [CrossRef]
| c | 0.628 | 0.942 | 1.257 | 1.571 | 2.356 | 3.141 | 3.972 | 4.712 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 9 | 4 | 2 | 2 | 1 | 1 | 1 | 1 | |
| 1 | 18 | 7 | 4 | 3 | 2 | 2 | 2 | 2 | |
| 2 | 26 | 10 | 6 | 5 | 3 | 3 | 3 | 3 | |
| 3 | 33 | 13 | 8 | 6 | 4 | 4 | 4 | 4 | |
| 4 | 41 | 16 | 10 | 8 | 6 | 5 | 5 | 5 | |
| 0.75 | 5 | 49 | 19 | 12 | 9 | 7 | 6 | 7 | 6 |
| 6 | 56 | 22 | 14 | 10 | 8 | 7 | 8 | 7 | |
| 7 | 64 | 25 | 16 | 12 | 9 | 8 | 9 | 8 | |
| 8 | 71 | 28 | 17 | 13 | 10 | 9 | 10 | 9 | |
| 9 | 78 | 31 | 19 | 15 | 11 | 10 | 11 | 10 | |
| 10 | 86 | 34 | 21 | 16 | 12 | 11 | 12 | 11 | |
| 0 | 15 | 6 | 3 | 2 | 1 | 1 | 1 | 1 | |
| 1 | 25 | 10 | 6 | 4 | 3 | 2 | 2 | 2 | |
| 2 | 34 | 13 | 8 | 6 | 4 | 3 | 3 | 3 | |
| 3 | 43 | 17 | 10 | 7 | 5 | 4 | 4 | 4 | |
| 4 | 52 | 20 | 12 | 9 | 6 | 5 | 5 | 5 | |
| 0.90 | 5 | 60 | 23 | 14 | 10 | 7 | 6 | 6 | 6 |
| 6 | 68 | 27 | 16 | 12 | 8 | 7 | 7 | 7 | |
| 7 | 76 | 30 | 18 | 13 | 10 | 9 | 8 | 8 | |
| 8 | 84 | 33 | 20 | 15 | 11 | 10 | 9 | 10 | |
| 9 | 92 | 36 | 22 | 16 | 12 | 11 | 10 | 11 | |
| 10 | 100 | 40 | 24 | 18 | 13 | 12 | 11 | 11 | |
| 0 | 19 | 7 | 4 | 3 | 2 | 1 | 1 | 1 | |
| 1 | 30 | 11 | 7 | 5 | 3 | 2 | 2 | 2 | |
| 2 | 40 | 15 | 9 | 6 | 4 | 3 | 3 | 3 | |
| 3 | 50 | 19 | 11 | 8 | 5 | 5 | 4 | 4 | |
| 4 | 59 | 23 | 13 | 9 | 6 | 6 | 5 | 5 | |
| 0.95 | 5 | 68 | 26 | 15 | 12 | 7 | 7 | 6 | 6 |
| 6 | 76 | 30 | 17 | 13 | 8 | 8 | 7 | 7 | |
| 7 | 85 | 33 | 20 | 14 | 9 | 9 | 8 | 8 | |
| 8 | 93 | 36 | 22 | 16 | 11 | 10 | 9 | 9 | |
| 9 | 102 | 40 | 24 | 17 | 12 | 11 | 10 | 10 | |
| 10 | 110 | 43 | 26 | 19 | 13 | 12 | 11 | 11 | |
| 0 | 29 | 11 | 6 | 4 | 2 | 2 | 1 | 1 | |
| 1 | 42 | 16 | 9 | 6 | 4 | 3 | 2 | 2 | |
| 2 | 53 | 20 | 11 | 8 | 5 | 4 | 3 | 3 | |
| 3 | 64 | 24 | 14 | 10 | 6 | 5 | 5 | 4 | |
| 4 | 74 | 28 | 16 | 12 | 7 | 6 | 6 | 5 | |
| 0.99 | 5 | 84 | 32 | 18 | 13 | 9 | 7 | 7 | 6 |
| 6 | 93 | 36 | 21 | 15 | 10 | 8 | 8 | 7 | |
| 7 | 102 | 39 | 23 | 16 | 11 | 9 | 9 | 8 | |
| 8 | 111 | 42 | 25 | 18 | 12 | 10 | 10 | 9 | |
| 9 | 120 | 46 | 27 | 20 | 13 | 12 | 11 | 10 | |
| 10 | 129 | 50 | 29 | 21 | 15 | 13 | 12 | 11 | |
| c | 0.628 | 0.942 | 1.257 | 1.571 | 2.356 | 3.141 | 3.972 | 4.712 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 10 | 4 | 3 | 2 | 2 | 2 | 2 | 2 | |
| 1 | 18 | 8 | 5 | 4 | 3 | 3 | 3 | 3 | |
| 2 | 27 | 11 | 7 | 6 | 5 | 5 | 4 | 4 | |
| 3 | 35 | 14 | 9 | 7 | 6 | 6 | 6 | 6 | |
| 4 | 42 | 18 | 11 | 9 | 7 | 7 | 7 | 7 | |
| 0.75 | 5 | 50 | 21 | 13 | 11 | 8 | 8 | 8 | 8 |
| 6 | 57 | 24 | 15 | 12 | 10 | 9 | 9 | 9 | |
| 7 | 65 | 27 | 17 | 14 | 11 | 10 | 10 | 10 | |
| 8 | 72 | 30 | 19 | 15 | 12 | 12 | 11 | 11 | |
| 9 | 80 | 33 | 21 | 17 | 13 | 13 | 13 | 12 | |
| 10 | 87 | 36 | 23 | 18 | 14 | 14 | 14 | 14 | |
| 0 | 16 | 7 | 4 | 4 | 3 | 3 | 3 | 3 | |
| 1 | 26 | 11 | 7 | 6 | 5 | 4 | 4 | 4 | |
| 2 | 36 | 15 | 10 | 8 | 6 | 6 | 6 | 6 | |
| 3 | 45 | 19 | 12 | 10 | 8 | 7 | 7 | 7 | |
| 4 | 54 | 22 | 14 | 11 | 9 | 9 | 9 | 8 | |
| 0.90 | 5 | 62 | 26 | 16 | 13 | 10 | 10 | 10 | 10 |
| 6 | 71 | 29 | 19 | 15 | 12 | 11 | 11 | 11 | |
| 7 | 79 | 33 | 21 | 16 | 13 | 12 | 12 | 12 | |
| 8 | 87 | 36 | 23 | 18 | 14 | 14 | 14 | 14 | |
| 9 | 95 | 39 | 25 | 20 | 16 | 15 | 15 | 15 | |
| 10 | 103 | 42 | 27 | 21 | 17 | 16 | 16 | 16 | |
| 0 | 20 | 9 | 6 | 5 | 4 | 4 | 4 | 3 | |
| 1 | 32 | 13 | 9 | 7 | 6 | 5 | 5 | 5 | |
| 2 | 42 | 18 | 11 | 9 | 7 | 7 | 7 | 7 | |
| 3 | 52 | 22 | 14 | 11 | 9 | 8 | 8 | 8 | |
| 4 | 61 | 25 | 16 | 13 | 10 | 10 | 10 | 10 | |
| 0.95 | 5 | 70 | 29 | 19 | 15 | 12 | 11 | 11 | 11 |
| 6 | 79 | 33 | 21 | 17 | 13 | 13 | 12 | 12 | |
| 7 | 88 | 36 | 23 | 18 | 15 | 14 | 14 | 14 | |
| 8 | 97 | 40 | 25 | 20 | 16 | 15 | 15 | 15 | |
| 9 | 105 | 43 | 28 | 22 | 17 | 16 | 16 | 16 | |
| 10 | 113 | 47 | 30 | 23 | 19 | 18 | 18 | 17 | |
| 0 | 31 | 13 | 8 | 7 | 5 | 5 | 5 | 5 | |
| 1 | 45 | 19 | 12 | 9 | 8 | 7 | 7 | 7 | |
| 2 | 56 | 23 | 15 | 12 | 9 | 9 | 9 | 9 | |
| 3 | 67 | 28 | 18 | 14 | 11 | 11 | 11 | 11 | |
| 4 | 78 | 32 | 20 | 16 | 13 | 12 | 12 | 12 | |
| 0.99 | 5 | 88 | 36 | 23 | 18 | 15 | 14 | 14 | 14 |
| 6 | 97 | 40 | 26 | 20 | 16 | 16 | 15 | 15 | |
| 7 | 107 | 44 | 28 | 22 | 18 | 17 | 17 | 17 | |
| 8 | 116 | 48 | 30 | 24 | 19 | 18 | 18 | 18 | |
| 9 | 125 | 52 | 33 | 26 | 21 | 20 | 20 | 19 | |
| 10 | 135 | 55 | 35 | 28 | 22 | 21 | 21 | 21 | |
| n | ||||||||
|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 6 | 8 | 10 | 12 | |||
| 26 | 0.628 | 0.9860 | 0.9999 | 1 | 1 | 1 | 1 | |
| 10 | 0.942 | 0.9729 | 0.9999 | 0.9999 | 1 | 1 | 1 | |
| 6 | 1.257 | 0.9521 | 0.9998 | 0.9999 | 1 | 1 | 1 | |
| 5 | 1.571 | 0.8917 | 0.9994 | 0.9999 | 0.9999 | 1 | 1 | |
| 0.75 | 3 | 2.356 | 0.8504 | 0.9979 | 0.9999 | 0.9999 | 1 | 1 |
| 3 | 3.141 | 0.5922 | 0.9836 | 0.9992 | 0.9999 | 0.9999 | 0.9999 | |
| 3 | 3.972 | 0.3333 | 0.9340 | 0.9949 | 0.9994 | 0.9999 | 0.9999 | |
| 3 | 4.712 | 0.1804 | 0.8504 | 0.9835 | 0.9979 | 0.9996 | 0.9999 | |
| 34 | 0.628 | 0.9713 | 0.9999 | 1 | 1 | 1 | 1 | |
| 13 | 0.942 | 0.9446 | 0.9998 | 0.9999 | 1 | 1 | 1 | |
| 8 | 1.257 | 0.8938 | 0.9996 | 0.9999 | 1 | 1 | 1 | |
| 6 | 1.571 | 0.8234 | 0.9988 | 0.9999 | 0.9999 | 1 | 1 | |
| 0.90 | 4 | 2.356 | 0.6399 | 0.9925 | 0.9997 | 0.9999 | 0.9999 | 1 |
| 3 | 3.141 | 0.5922 | 0.9835 | 0.9992 | 0.9999 | 0.9999 | 0.9999 | |
| 3 | 3.972 | 0.3333 | 0.9341 | 0.9949 | 0.9994 | 0.9999 | 0.9999 | |
| 3 | 4.712 | 0.1804 | 0.8504 | 0.9835 | 0.9979 | 0.9996 | 0.9999 | |
| 40 | 0.628 | 0.9565 | 0.9999 | 0.9999 | 1 | 1 | 1 | |
| 15 | 0.942 | 0.9204 | 0.9998 | 0.9999 | 1 | 1 | 1 | |
| 9 | 1.257 | 0.8579 | 0.9994 | 0.9999 | 1 | 1 | 1 | |
| 0.95 | 6 | 1.571 | 0.8234 | 0.9988 | 0.9999 | 0.9999 | 1 | 1 |
| 4 | 2.356 | 0.6399 | 0.9925 | 0.9997 | 0.9999 | 0.9999 | 1 | |
| 3 | 3.141 | 0.5922 | 0.9935 | 0.9992 | 0.9999 | 0.9999 | 0.9999 | |
| 3 | 3.972 | 0.3333 | 0.9940 | 0.9949 | 0.9994 | 0.9999 | 0.9999 | |
| 3 | 4.712 | 0.1804 | 0.8504 | 0.9835 | 0.9979 | 0.9996 | 0.9999 | |
| 53 | 0.628 | 0.9143 | 0.9998 | 0.9999 | 1 | 1 | 1 | |
| 20 | 0.942 | 0.8448 | 0.9995 | 0.9999 | 1 | 1 | 1 | |
| 11 | 1.257 | 0.7770 | 0.9988 | 0.9999 | 0.9999 | 1 | 1 | |
| 8 | 1.571 | 0.6673 | 0.9969 | 0.9999 | 0.9999 | 1 | 1 | |
| 0.99 | 5 | 2.356 | 0.4423 | 0.9830 | 0.9994 | 0.9999 | 0.9999 | 0.9999 |
| 4 | 3.141 | 0.2760 | 0.9467 | 0.9970 | 0.9997 | 0.9999 | 0.9999 | |
| 3 | 3.972 | 0.3333 | 0.9340 | 0.9949 | 0.9994 | 0.9999 | 0.9999 | |
| 3 | 4.712 | 0.1804 | 0.8504 | 0.9835 | 0.9979 | 0.9996 | 0.9999 | |
| c | 0.628 | 0.942 | 1.257 | 1.571 | 2.356 | 3.141 | 3.972 | 4.712 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 2.985 | 3.476 | 3.761 | 4.7 | 5.573 | 7.43 | 9.395 | 11.145 | |
| 1 | 1.987 | 2.185 | 2.363 | 2.647 | 3.202 | 4.269 | 5.398 | 6.404 | |
| 2 | 1.717 | 1.842 | 2.003 | 2.325 | 2.528 | 3.37 | 4.262 | 5.056 | |
| 3 | 1.598 | 1.691 | 1.819 | 1.946 | 2.167 | 2.89 | 3.654 | 4.335 | |
| 4 | 1.495 | 1.587 | 1.708 | 1.913 | 2.386 | 2.634 | 3.331 | 3.952 | |
| 0.75 | 5 | 1.448 | 1.513 | 1.628 | 1.726 | 2.144 | 2.435 | 3.615 | 3.653 |
| 6 | 1.397 | 1.467 | 1.576 | 1.607 | 2.005 | 2.274 | 3.38 | 3.412 | |
| 7 | 1.374 | 1.427 | 1.536 | 1.614 | 1.9 | 2.164 | 3.203 | 3.247 | |
| 8 | 1.346 | 1.398 | 1.456 | 1.532 | 1.826 | 2.077 | 3.079 | 3.116 | |
| 9 | 1.319 | 1.375 | 1.433 | 1.543 | 1.743 | 2.002 | 2.939 | 3.003 | |
| 10 | 1.319 | 1.354 | 1.416 | 1.483 | 1.683 | 1.941 | 2.837 | 2.912 | |
| 0 | 3.445 | 3.913 | 4.179 | 4.641 | 5.573 | 7.43 | 9.395 | 11.145 | |
| 1 | 2.213 | 2.48 | 2.766 | 2.953 | 3.912 | 4.243 | 5.366 | 6.366 | |
| 2 | 1.879 | 2.029 | 2.256 | 2.484 | 3.035 | 3.34 | 4.224 | 5.011 | |
| 3 | 1.717 | 1.865 | 2.003 | 2.114 | 2.605 | 2.886 | 3.649 | 4.329 | |
| 4 | 1.625 | 1.732 | 1.856 | 2.02 | 2.326 | 2.607 | 3.297 | 3.911 | |
| 0.90 | 5 | 1.561 | 1.636 | 1.758 | 1.841 | 2.142 | 2.416 | 3.055 | 3.624 |
| 6 | 1.495 | 1.596 | 1.691 | 1.806 | 2.005 | 2.274 | 2.876 | 3.412 | |
| 7 | 1.457 | 1.542 | 1.634 | 1.706 | 2.102 | 2.533 | 2.737 | 3.247 | |
| 8 | 1.422 | 1.501 | 1.59 | 1.688 | 2.013 | 2.419 | 2.626 | 3.116 | |
| 9 | 1.397 | 1.463 | 1.554 | 1.611 | 1.922 | 2.324 | 2.531 | 3.487 | |
| 10 | 1.382 | 1.456 | 1.525 | 1.611 | 1.853 | 2.244 | 2.455 | 2.912 | |
| 0 | 3.584 | 4.067 | 4.571 | 5.32 | 6.96 | 7.43 | 9.395 | 11.145 | |
| 1 | 2.377 | 2.575 | 2.973 | 3.222 | 3.912 | 4.243 | 5.366 | 6.366 | |
| 2 | 1.987 | 2.158 | 2.372 | 2.484 | 3.035 | 3.34 | 4.224 | 5.011 | |
| 3 | 1.811 | 1.941 | 2.087 | 2.264 | 2.597 | 3.462 | 3.649 | 4.329 | |
| 4 | 1.7 | 1.842 | 1.928 | 2.013 | 2.601 | 3.128 | 3.297 | 3.911 | |
| 0.95 | 5 | 1.611 | 1.72 | 1.819 | 2.035 | 2.386 | 2.859 | 3.055 | 3.624 |
| 6 | 1.549 | 1.668 | 1.74 | 1.89 | 2.227 | 2.673 | 2.876 | 3.412 | |
| 7 | 1.516 | 1.606 | 1.719 | 1.778 | 2.102 | 2.533 | 2.737 | 3.247 | |
| 8 | 1.476 | 1.555 | 1.669 | 1.758 | 2.005 | 2.419 | 2.626 | 3.116 | |
| 9 | 2.985 | 3.476 | 3.761 | 4.7 | 5.573 | 7.43 | 9.395 | 11.145 | |
| 10 | 1.422 | 1.501 | 1.59 | 1.666 | 1.853 | 2.244 | 2.455 | 2.912 | |
| 0 | 4.029 | 4.584 | 5.131 | 5.7 | 6.935 | 9.245 | 9.395 | 11.145 | |
| 1 | 2.563 | 2.875 | 3.174 | 3.453 | 4.429 | 5.216 | 5.366 | 6.366 | |
| 2 | 2.147 | 2.36 | 2.554 | 2.81 | 3.417 | 4.076 | 4.224 | 5.011 | |
| 3 | 1.941 | 2.108 | 2.312 | 2.503 | 2.913 | 3.462 | 4.378 | 4.329 | |
| 4 | 1.813 | 1.959 | 2.106 | 2.32 | 2.601 | 3.102 | 3.922 | 3.906 | |
| 0.99 | 5 | 1.734 | 1.865 | 1.971 | 2.119 | 2.601 | 2.859 | 3.615 | 3.624 |
| 6 | 1.667 | 1.798 | 1.933 | 2.05 | 2.42 | 2.673 | 3.38 | 3.412 | |
| 7 | 1.611 | 1.714 | 1.835 | 1.919 | 2.273 | 2.533 | 3.203 | 3.247 | |
| 8 | 1.563 | 1.657 | 1.773 | 1.878 | 2.162 | 2.419 | 3.059 | 3.116 | |
| 9 | 1.538 | 1.626 | 1.736 | 1.678 | 2.072 | 2.57 | 2.947 | 3.003 | |
| 10 | 1.505 | 1.597 | 1.678 | 1.769 | 2.116 | 2.47 | 2.837 | 2.912 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gillariose, J.; Abdelwahab, M.M.; Venkatesan, R.; Joseph, J.; Abdelkawy, M.A.; Hasaballah, M.M. Design and Analysis of Reliability Sampling Plans Based on the Topp–Leone Generated Weibull Distribution. Symmetry 2025, 17, 1439. https://doi.org/10.3390/sym17091439
Gillariose J, Abdelwahab MM, Venkatesan R, Joseph J, Abdelkawy MA, Hasaballah MM. Design and Analysis of Reliability Sampling Plans Based on the Topp–Leone Generated Weibull Distribution. Symmetry. 2025; 17(9):1439. https://doi.org/10.3390/sym17091439
Chicago/Turabian StyleGillariose, Jiju, Mahmoud M. Abdelwahab, Rakshana Venkatesan, Joshin Joseph, Mohamed A. Abdelkawy, and Mustafa M. Hasaballah. 2025. "Design and Analysis of Reliability Sampling Plans Based on the Topp–Leone Generated Weibull Distribution" Symmetry 17, no. 9: 1439. https://doi.org/10.3390/sym17091439
APA StyleGillariose, J., Abdelwahab, M. M., Venkatesan, R., Joseph, J., Abdelkawy, M. A., & Hasaballah, M. M. (2025). Design and Analysis of Reliability Sampling Plans Based on the Topp–Leone Generated Weibull Distribution. Symmetry, 17(9), 1439. https://doi.org/10.3390/sym17091439







