Proper Total Domination in Trees

Abstract

A vertex u in a graph G totally dominates a vertex v if u is adjacent to v. A set S of vertices in a graph G is a total dominating set of G if every vertex of G is totally dominated by at least one vertex of S. For a total dominating set S of a graph G and a vertex v of G, let ${\sigma }_S\left(v\right)$ denote the number of vertices in S that totally dominate v. A total dominating set S in a graph G is a proper total dominating set if ${\sigma }_S\left(u\right)\ne {\sigma }_S\left(v\right)$ for every two adjacent vertices u and v of G. While proper total dominating sets in trees have been previously studied, the primary goal here is to extend this study to classes of trees with a symmetric structure or that possess subtrees with a symmetric structure. Those trees belonging to several of the most-studied classes of trees that possess a proper total dominating set are determined. Graphical structures of proper total dominating sets in these trees are investigated. The minimum cardinality of a proper total dominating set in a graph G is the proper total domination number of G. Characterizations are obtained for all trees T with a small proper total domination number. Other results and problems are also presented on proper total dominating sets in trees in general.

1. Introduction

The concept of domination in graph theory originally started with the work of Berge [1] in 1958 and Ore [2] in 1962. After the publication of a survey paper [3] by Cockayne and Hedetniemi in 1977, much research on domination in graphs has surfaced, and this subject has become an active area of research. Furthermore, numerous variations of domination have been introduced and studied (see [4,5,6], for example). One of the best known of these is total domination. A vertex u in a graph G totally dominates a vertex v if u is adjacent to v. A set S of vertices in G is called a total dominating set in [7] if every vertex of G is totally dominated by at least one vertex of S. A graph G has a total dominating set if and only if G contains no isolated vertices. In recent years, the concept of total domination has been studied extensively with many interesting results and applications (see [6,8], for example). Various domination concepts have been introduced that connect total domination with other popular areas in graph theory, including irregularity and graph coloring (see [6,9,10,11,12,13,14] for example).

Let G be a graph with a total dominating set S. Then every vertex of G is totally dominated by one or more vertices of S. The number of vertices in S that totally dominate a vertex v of G is denoted by ${\sigma }_S\left(v\right)$. While no total dominating set S in a graph G has the property that ${\sigma }_S\left(u\right)\ne {\sigma }_S\left(v\right)$ for every two vertices u and v of G, it is possible that ${\sigma }_S\left(u\right)\ne {\sigma }_S\left(v\right)$ for every two adjacent vertices u and v of G. A total dominating set S in a graph G is called proper if ${\sigma }_S\left(u\right)\ne {\sigma }_S\left(v\right)$ for every two adjacent vertices u and v of G. Therefore, a proper total dominating set S in a graph gives rise to a proper vertex coloring ${\sigma }_S$ of the graph. This concept was introduced and studied in [12] and studied further in [13,15] and is related to topics studied in [9,14,16,17].

In recent decades, domination has received increased attention due to its many applications in modern society and various fields such as network security, wireless sensor placement, facility location problems, and finding representative sets as well as in chemical sciences (see [6,8,18,19], for example). On the other hand, there is no doubt that graph coloring is one of the most popular areas of graph theory because of its intriguing history, many fascinating problems, and the sheer mathematical beauty of the subject. Furthermore, there are many practical applications in real life that can be analyzed and sometimes solved by modeling the situation described in a problem using a graph and defining a vertex coloring of the graph in an appropriate manner. These applications include scheduling, communication, and packaging (see [20,21] for example). As we mentioned, every proper total dominating set in a graph gives rise to a proper vertex coloring of the graph. Consequently, the concept of a proper total dominating set combines the features of colorings and dominations in graphs, which are two of the most popular areas of research in graph theory. This combination will broaden the scope of colorings and domination in graphs and suggest rich directions for future exploration and potentially important applications.

First, we present some preliminary information on proper total domination in graphs. A graph G is sometimes called locally irregular if $degu\ne degv$ for every two adjacent vertices u and v of G (see [22]). If G is locally irregular, then the vertex set $V\left(G\right)$ of G is a total dominating set of G. In fact, locally irregular graphs are the only graphs G for which $V\left(G\right)$ is a proper total dominating set. For a set S of vertices of G, let $G\left[S\right]$ denote the subgraph of G induced by S.

Proposition 1.

Let G be a nontrivial connected graph. If S is a proper total dominating set of G, then $G\left[S\right]$ is a locally irregular subgraph without isolated vertices in G. Consequently,

(a)

$\left|S\right|\ge 3$ and $\left|S\right|=3$ if and only if $G\left[S\right]=P_3$ and

(b)

$V\left(G\right)$ is a proper total dominating set of G if and only if G is locally irregular.

Proof. 

Since S is a total dominating set of G, it follows that $H=G\left[S\right]$ has no isolated vertices. Furthermore, ${\sigma }_S\left(v\right)={deg}_{H}v$ for every vertex of H. Since S is a proper total dominating set of G, it follows that if u and v are adjacent vertices in H, then ${\sigma }_S\left(u\right)\ne {\sigma }_S\left(v\right)$ and so ${deg}_{H}u\ne {deg}_{H}v$. Therefore, H is a locally irregular subgraph without isolated vertices in G. Furthermore, there is no locally irregular graph of order 2, and $P_3$ is the only locally irregular graph of order 3. Thus, (a) holds. Furthermore, if $S=V\left(G\right)$ is a proper total dominating set of G, then ${\sigma }_S\left(v\right)={deg}_{G}v$ for every vertex of G. Consequently, $V\left(G\right)$ is a proper total dominating set of G if and only if G is locally irregular, and so (b) holds. □

By Proposition 1, if G is a graph of order n having a proper total dominating set, then $n\ge 3$. Furthermore, G has a proper total dominating set if and only if each component of G has a proper total dominating set. Consequently, we only consider connected graphs of order 3 or more.

While every graph G without isolated vertices possesses a total dominating set, it is those total dominating sets of minimum cardinality that are of greatest interest. The minimum cardinality of a total dominating set in G is the total domination number ${\gamma }_t\left(G\right)$ of G. A total dominating set S with $\left|S\right|={\gamma }_t\left(G\right)$ is called a ${\gamma }_t$-set of G. We now turn our attention to the corresponding parameter for graphs possessing proper total dominating sets. The minimum cardinality of a proper total dominating set in a graph G is its proper total domination number or more simply the $pt$-domination number ${\gamma }_{pt}\left(G\right)$ of G. That is,

$${\gamma }_{pt}\left(G\right)=min\left\{\left|S\right|:S\mathrm{is}\mathrm{a}\mathrm{proper}\mathrm{total}\mathrm{dominating}\mathrm{set}\mathrm{of}G\right\}.$$

A proper total dominating set S with $\left|S\right|={\gamma }_{pt}\left(G\right)$ is referred to as a ${\gamma }_{pt}$-set of G. By Proposition 1, every proper total dominating set must contain at least three vertices.

Observation 1

([12]). If a graph G has a proper total dominating set, then ${\gamma }_{pt}\left(G\right)\ge 3$.

Proper total dominating sets in trees with symmetric structure have been previously studied. Among the results obtained in [12] are the following.

Proposition 2

([12]). For each integer $n\ge 3$, the star $K_{1,n-1}$ of order n has a proper total dominating set. Furthermore, ${\gamma }_{pt}\left(K_{1,n-1}\right)=3$ for $n\ge 3$.

Proposition 3

([12]). For an integer $n\ge 3$, the path $P_n$ of order n has a proper total dominating set if and only if $n\equiv 3\left(\mathrm{mod}4\right)$. Furthermore, ${\gamma }_{pt}\left(P_n\right)={\displaystyle \frac{3(n+1)}{4}}$ if $n\ge 3$ and $n\equiv 3\left(\mathrm{mod}4\right)$.

By Proposition 3, not all connected graphs of order at least 3 contain proper total dominating sets. Our primary interest is in graphs that possess such sets. In particular, the goal here is to investigate those trees with a symmetric structure or possessing subtrees with a symmetric structure as well as having a proper total dominating set. We refer to the books [6,20] for notation and terminology not defined here.

2. Trees of Diameter at Most 4

By Observation 1 and Proposition 2, every star (a tree of diameter 2) of order at least 3 has a proper total dominating set. Furthermore, stars have the smallest possible $pt$-dominating number 3. In fact, stars are the only trees with $pt$-domination number 3.

Proposition 4.

A tree T has ${\gamma }_{pt}\left(T\right)=3$ if and only if T is a star of order 3 or more.

Proof. 

By Proposition 2, if T is a star of order 3 or more, then ${\gamma }_{pt}\left(T\right)=3$. In fact, any set of three vertices containing the center of a star T of order 3 or more is a proper total dominating set of T. For the converse, suppose that T is a tree of order 3 or more with ${\gamma }_{pt}\left(T\right)=3$. Assume, to the contrary, that T is not a star. Let $S=\{x,y,z\}$ be a proper total dominating set of T. We may assume that $(x,y,z)$ is a path in T. Then ${\sigma }_S\left(x\right)={\sigma }_S\left(z\right)=1$ and ${\sigma }_S\left(y\right)=2$. Since T is not a star, there is a vertex $v\in V\left(T\right)-S$ that is adjacent to exactly one of x and z but not to y, say $vx$ is an edge of T. However then, ${\sigma }_S\left(v\right)={\sigma }_S\left(x\right)=1$, which is impossible. □

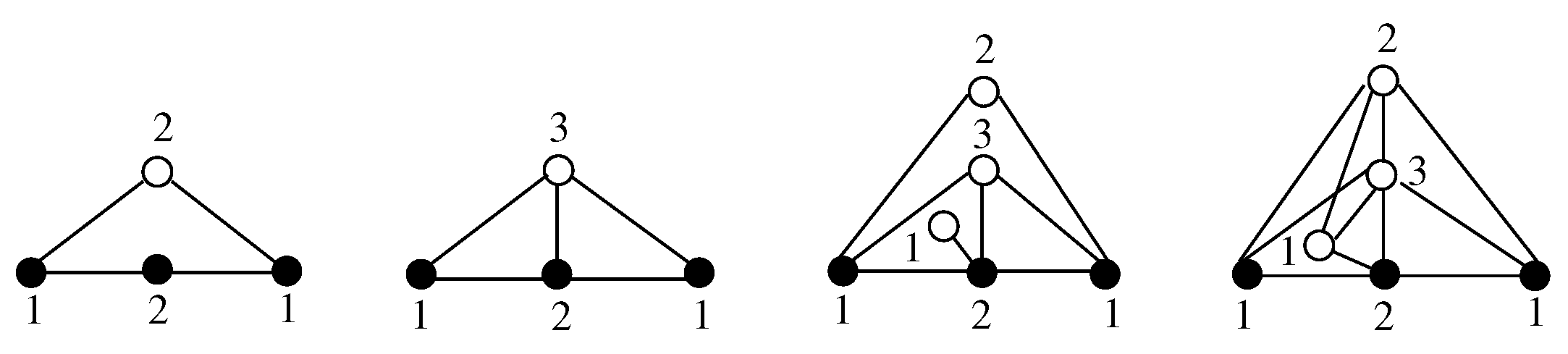
While stars are the only trees having $pt$-domination number 3, there are graphs that are not trees with $pt$-domination number 3. In fact, each graph in Figure 1 has $pt$-domination number 3, where the three solid vertices in each graph G form a $pt$-set S of G and $G\left[S\right]=P_3$.

There are also connected graphs G with ${\gamma }_{pt}\left(G\right)=4$. One such graph is shown in Figure 2, where the four solid vertices form a $pt$-set. Of course, this graph is not a tree. In fact, no tree has $pt$-dominating number 4. Before verifying this, we present a lemma. The diameter $\mathrm{diam}\left(G\right)$ of a connected graph G is the greatest distance between two vertices of G.

Lemma 1.

Let T be a tree with a proper total dominating set S. If $T\left[S\right]$ is a tree, then each vertex of $V\left(T\right)-S$ is an end-vertex of T that is adjacent to a non-end-vertex of $T\left[S\right]$. Furthermore, $\mathrm{diam}\left(T\right)=\mathrm{diam}\left(T\right[S\left]\right)$.

Proof. 

Let S be a a proper total dominating set of a tree T such that $T\left[S\right]$ is a tree and let $v\in V\left(T\right)-S$. Since $T\left[S\right]$ is a tree, it follows that v is adjacent to exactly one vertex of $T\left[S\right]$ and so ${\sigma }_S\left(v\right)=1$. Furthermore, ${\sigma }_S\left(u\right)=1$ for every end-vertex u of $T\left[S\right]$ and so v is adjacent to a non-end-vertex of $T\left[S\right]$.

It remains to show that $\mathrm{diam}\left(T\right)=\mathrm{diam}\left(T\right[S\left]\right)$. Since the statement is true if T is a star, we may assume that $\mathrm{diam}\left(T\right)\ge 3$. Furthermore, $\mathrm{diam}\left(T\right)\ge \mathrm{diam}\left(T\right[S\left]\right)$ and so it suffices to show that $\mathrm{diam}\left(T\right)\le \mathrm{diam}\left(T\right[S\left]\right)$. Let u and v be two vertices of T such that $d_T(u,v)=\mathrm{diam}\left(T\right)$. Let $P_{uv}$ be the unique $u-v$ path in T.

🟉

First, suppose that $u,v\in S$. Since $T\left[S\right]$ is a subtree of T, it follows that P is also a $u-v$ path in $T\left[S\right]$. Thus, $\mathrm{diam}\left(T\left[S\right]\right)\ge d_{T\left[S\right]}(u,v)=d_T(u,v)=\mathrm{diam}\left(T\right)$.

🟉

Next, suppose that $u,v\notin S$. Then u is adjacent to a non-end-vertex $u^{\prime }$ in $T\left[S\right]$ and v is adjacent to a non-end-vertex $v^{\prime }$ in $T\left[S\right]$. Since $d_T(u,v)\ge 3$, it follows that $u^{\prime }\ne v^{\prime }$. Let $P^{\prime }$ be the unique $u^{\prime }-v^{\prime }$ path in $T\left[S\right]$. Then $P-\{u,v\}=P^{\prime }$. Since $u^{\prime }$ and $v^{\prime }$ are non-end-vertices of $T\left[S\right]$, there are two vertices $u^{″},v^{″}\in S$ that do not belong to P such that $u^{″}$ is adjacent to $u^{\prime }$ and $v^{″}$ is adjacent to $v^{\prime }$. Let $P^{″}$ be the unique $u^{″}-v^{″}$ path in $T\left[S\right]$. Then $P^{″}-\{u^{″},v^{″}\}=P^{\prime }$. Hence, $\mathrm{diam}\left(T\left[S\right]\right)\ge d_{T\left[S\right]}(u^{″},v^{″})=d_T(u,v)=\mathrm{diam}\left(T\right)$.

🟉

Finally, suppose that exactly one of u and v belongs to S, say $u\in S$ and $v\notin S$. Then v is adjacent to a non-end-vertex $v^{\prime }$ in $T\left[S\right]$. Let $v^{″}\in S$ be a neighbor of $v^{\prime }$ that does not belong to P. Then $\mathrm{diam}\left(T\left[S\right]\right)\ge d_{T\left[S\right]}(u,v^{″})=d_T(u,v)=\mathrm{diam}\left(T\right)$.

□

Proposition 5.

There is no tree T with ${\gamma }_{pt}\left(T\right)=4$.

Proof. 

Assume, to the contrary, that there is a tree T with ${\gamma }_{pt}\left(T\right)=4$ where $S=\{u,v,w,x\}$ is a proper total dominating set of T. By Proposition 1, $T\left[S\right]$ is a locally irregular forest of order 4 without isolated vertices. Since $2K_2,P_4,$ and $K_{1,3}$ are the only forests of order 4 without isolated vertices and $2K_2$ and $P_4$ are not locally irregular, it follows that $T\left[S\right]=K_{1,3}$. It then follows by Lemma 1 that $\mathrm{diam}\left(T\right)=\mathrm{diam}\left(T\right[S\left]\right)=3$ and so T is a star, which contradicts Proposition 4. □

While no tree has $pt$-dominating number 4, there are trees with $pt$-domination number 5. In fact, as we show next, only trees of diameter 3 can have $pt$-dominating number 5. A double star is a tree of diameter 3. Every double star T has exactly two vertices that are not leaves. These are the central vertices of T. For integers a and b with $2\le a\le b$, let $S_{a,b}$ denote the double star of order $a+b$ and size $a+b-1$ whose central vertices u and v have degrees a and b, respectively. Thus, $P_4=S_{2,2}$ is a double star of smallest order. By Proposition 3, the path $P_4$ does not have a proper total dominating set. With regard to double stars having a proper total dominating set, the path $P_4$ is the exceptional double star.

Proposition 6.

The path $P_4$ is the only double star without a proper total dominating set.

Proof. 

Let T be a double star. We show that T has a proper total dominating set if and only if $T\ne P_4$. We saw in Proposition 3 that $P_4$ does not have a proper total dominating set. Thus, it remains only to verify the converse. Let $T=S_{a,b}$ be a double star with central vertices u and v, where $degu=a$, $degv=b$, and $T\ne P_4$. If $a\ne b$, then T is locally irregular and so T has a proper total dominating set. We may therefore assume that $a=b\ge 3$. Let S be the set consisting of five vertices of T, namely $u,v$, two end-vertices adjacent to u, and one end-vertex adjacent to v. Since ${\sigma }_S\left(u\right)=3$, ${\sigma }_S\left(v\right)=2$, and ${\sigma }_S\left(w\right)=1$ for each end-vertex w of T, it follows that S is a proper total dominating set of T. □

By the proof of Proposition 6, if T is a double star having a proper total dominating set, then ${\gamma }_{pt}\left(T\right)\le 5$. In fact, more can be said. Next, we determine all those trees T with ${\gamma }_{pt}\left(T\right)=5$. For two vertex-disjoint graphs G and H, the union $G+H$ is the graph with vertex set $V(G+H)=V\left(G\right)\cup V\left(H\right)$ and edge set $E(G+H)=E\left(G\right)\cup E\left(H\right)$.

Proposition 7.

A tree T has ${\gamma }_{pt}\left(T\right)=5$ if and only if T is a double star of order 5 or more.

Proof. 

First, let T be a double star of order 5 or more. Then $T\ne P_4$ and so ${\gamma }_{pt}\left(T\right)\le 5$ as we mentioned earlier. Since ${\gamma }_{pt}\left(T\right)\ge 5$ by Propositions 4 and 5, it follows that ${\gamma }_{pt}\left(T\right)=5$.

For the converse, let T be a tree with ${\gamma }_{pt}\left(T\right)=5$ where $S=\{x_1,x_2,\dots ,x_5\}$ is a ${\gamma }_{pt}$-set of T. Then $T\left[S\right]$ is a locally irregular forest of order 5 without isolated vertices by Lemma 1. Since $K_{1,4}$, $S_{3,2}$, $P_5$, and $K_2+P_3$ are the only forests of order 5 without isolated vertices and $P_5$ and $K_2+P_3$ are not locally irregular, it follows that $T\left[S\right]=K_{1,4}$ or $T\left[S\right]=S_{3,2}$. First, suppose that $T\left[S\right]=K_{1,4}$ is a star of order 5. However then, $\mathrm{diam}\left(T\right)=\mathrm{diam}\left(K_{1,4}\right)=3$ and so T is a star by Lemma 1, which is impossible. Next, suppose that $T\left[S\right]=S_{3,2}$ is the double star of order 5. Then $\mathrm{diam}\left(T\right)=\mathrm{diam}\left(S_{3,2}\right)=3$ and so T is a double star by Lemma 1. □

We now turn our attention to trees of diameter 4. First, we present some useful information on proper total dominating sets in graphs with at least one end-vertex.

Observation 2.

Let G be a connected graph with at least one end-vertex, let $V^{\prime }$ be the set of vertices of G that are adjacent to an end-vertex of G, and let S be a proper total dominating set of G. Then $V^{\prime }\subseteq S$ and ${\sigma }_S\left(v\right)\ge 2$ for each $v\in V^{\prime }$.

A path $P_k=(v_1,v_2,\dots ,v_k)$ of order $k\ge 3$ in a graph G is a pendant k-path at the vertex $v_k$ in G if $v_1$ is an end-vertex in G and $v_i$ has degree 2 in G for $2\le i\le k-1$. In this case, $v_k$ is referred to as the terminal vertex of $P_k$.

Lemma 2.

Let $P_k=(v_1,v_2,\dots ,v_k)$ be a pendant k-path of order $k\ge 3$ in a graph G. If S is a proper total dominating set of G, then $v_i\in S$ if $i\not\equiv 0\left(\mathrm{mod}4\right)$ and $v_i\notin S$ if $i\equiv 0\left(\mathrm{mod}4\right)$. In particular, every vertex of a pendant 3-path belongs to S, and the terminal vertex of a pendant 4-path is the only vertex in the path that does not belong to S.

Proof. 

Let S be a proper total dominating set of G. Then ${\sigma }_S\left(v_1\right)=1$ and $1\le {\sigma }_S\left(v_i\right)\le 2$ for $2\le i\le k-1$. Since S is a proper total dominating set of G, it follows that ${\sigma }_S\left(v_i\right)=1$ if i is odd and $1\le i\le k-1$ and ${\sigma }_S\left(v_i\right)=2$ if i is even and $2\le i\le k-1$. Therefore, $v_i\in S$ if and only if $i\not\equiv 0\left(\mathrm{mod}4\right)\}$ for $1\le i\le k$. □

By Proposition 6, a double star T has a proper total dominating set if and only if $T\ne P_4$. We now determine all trees of diameter 4 having a proper total dominating set. A broom is a tree obtained by joining the central vertex of a star to an end-vertex of a path. In particular, $P_5$ is a broom of diameter 4. With regard to trees of diameter 4 having a proper total dominating set, we show that brooms are the exceptional trees of diameter 4.

Proposition 8.

A tree T of diameter 4 has a proper total dominating set if and only if T is not a broom.

Proof. 

First, suppose that T is a broom of diameter 4. Let $P_5=(u_1,u_2,u_3,u_4,u_5)$ be a longest path in T, where $deg{u}_1=deg{u}_5=1$, $deg{u}_2\ge 2$, and $deg{u}_3=deg{u}_4=2$. Assume, to the contrary, that T has a proper total dominating set S. Since T contains a pendant 4-path at $u_2$, it follows that $u_2\notin S$ by Lemma 2. On the other hand, $u_2$ is adjacent to the end-vertex $u_1$ in T and so $u_2\in S$ by Observation 2. This is impossible.

For the converse, let T be a tree of diameter 4 that is not broom. Let $P_5=(v_1,v_2,v_3,v_4,v_5)$ be a longest path in T. Thus, either (i) ${deg}_T{v}_3\ge 3$ or (ii) ${deg}_T{v}_3=2$ and both $v_2$ and $v_4$ have degree at least 3.

🟉

First, suppose that (i) occurs. Let $v_6$ be a vertex not on $P_5$ that is adjacent to $v_3$. If $v_6$ is an end-vertex of T, then let $S=\{v_1,v_2,\dots ,v_6\}$. Since each vertex not in S is an end-vertex of T that is adjacent to exactly one of $v_2,v_3,v_4$, it follows that ${\sigma }_S\left(v_3\right)=3$, ${\sigma }_S\left(v_2\right)={\sigma }_S\left(v_4\right)=2$, and ${\sigma }_S\left(v\right)=1$ for each remaining vertex v of T. Hence, S is a proper total dominating set of T. If $v_6$ is not an end-vertex of T, then $v_6$ is adjacent to an end-vertex $v_7$ (since $\mathrm{diam}\left(T\right)=4$). In that case, let $S=\{v_1,v_2,\dots ,v_6,v_7\}$. Since each vertex not in S is an end-vertex of T that is adjacent to exactly one of $v_2,v_3,v_4,v_6$, it follows that ${\sigma }_S\left(v_3\right)=3$, ${\sigma }_S\left(v_2\right)={\sigma }_S\left(v_4\right)={\sigma }_S\left(v_6\right)=2$, and ${\sigma }_S\left(v\right)=1$ for each remaining vertex v of T. Hence, S is a proper total dominating set of T.

🟉

Next, suppose that (ii) occurs. Let $v_6$ be a vertex not on $P_5$ that is adjacent to $v_2$, let $v_7$ be a vertex not on $P_5$ that is adjacent to $v_4$, and let $S=\{v_1,v_2,\dots ,v_6,v_7\}$ be a proper total dominating set of T. Since each vertex not in S is an end-vertex of T and is adjacent to exactly one of $v_2,v_3,v_4$, it follows that ${\sigma }_S\left(v_2\right)={\sigma }_S\left(v_4\right)=3$, ${\sigma }_S\left(v_3\right)=2$, and ${\sigma }_S\left(v\right)=1$ for each remaining vertex v of T. Hence, S is a proper total dominating set of T.

□

The $pt$-dominating number of a tree of diameter 4 can be arbitrarily large. For example, for each integer $k\ge 3$, let $S\left(K_{1,k}\right)$ be the tree of order $2k+1$ and diameter 4 that is obtained from the star $K_{1,k}$ of order $k+1$ by subdividing each edge of $K_{1,k}$ exactly one. By Proposition 2, the vertex set of $S\left(K_{1,k}\right)$ is the only proper total dominating set of $S\left(K_{1,k}\right)$ and so ${\gamma }_{pt}\left(S\left(K_{1,k}\right)\right)=2k+1$ for each integer $k\ge 3$.

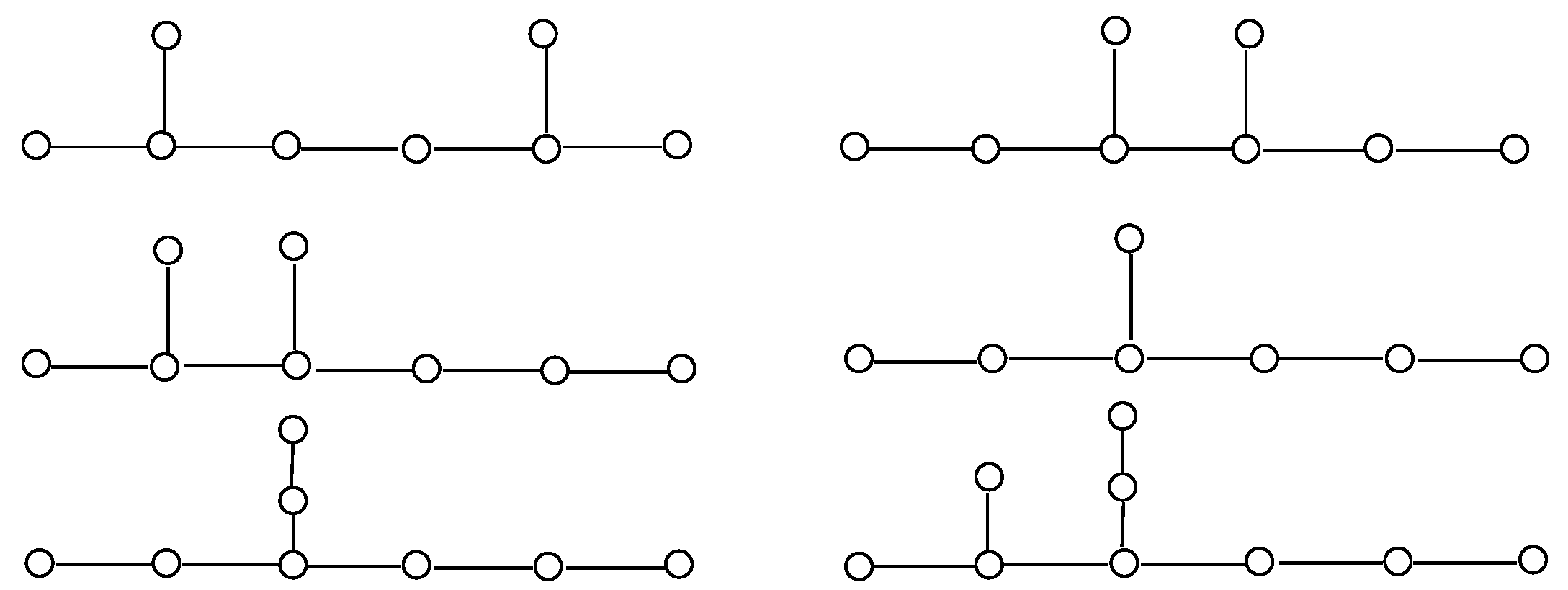
By Proposition 8, every tree of diameter 4 that is not a broom has a proper total dominating set. Such is not the case for trees of greater diameter. With the aid of Observation 2 and Proposition 2, it can be shown that none of the trees of diameter 5 in Figure 3 have a proper total dominating set.

3. Starlike Trees

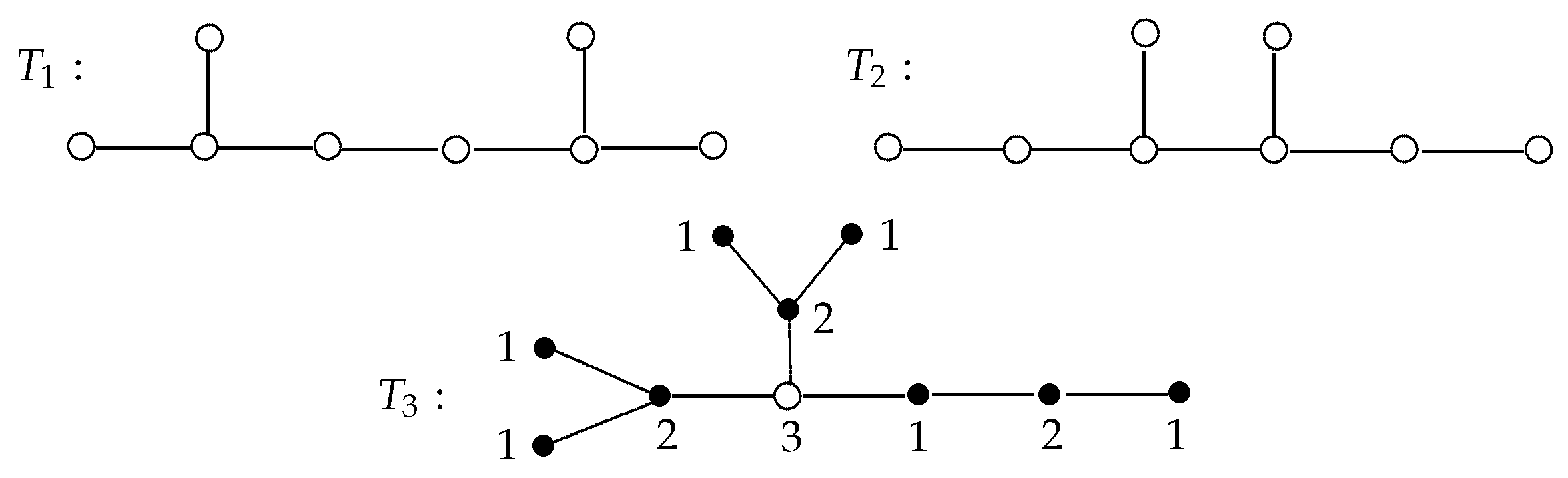
A tree T is starlike if T is obtained by subdividing the edges of a star of order 4 or more. Equivalently, a tree T is starlike if T has exactly one vertex whose degree is greater than 2. This vertex is referred to as the center of T. The branches of T at its center are called the arms of T. An arm is even if its length is even, while an arm is odd if its length is odd. For example, the tree T shown in Figure 4 is a starlike tree obtained by subdividing the edges of the star $K_{1,4}$, whose center is indicated by the solid vertex. This tree T has two even arms of lengths 2 and 4 and two odd arms of lengths 1 and 3.

With the aid of Lemma 2, all starlike trees possessing a proper total dominating set can be determined.

Theorem 1.

Let T be a starlike tree.

(i)

If T has an arm whose length is congruent to 3 mod 4, then T has a proper total dominating set if and only if the length of every arm of T is congruent to 3 mod 4.

(ii)

If T has no arm whose length is congruent to 3 mod 4, then T has a proper total dominating set if and only if T satisfies one of the following two conditions:

(a)

T has at least three arms whose lengths are not congruent to 0 mod 4,

(b)

T has exactly one arm whose length is not congruent to 0 mod 4 and this length is congruent to 2 mod 4.

Proof. 

Let v be the center of T with $N\left(v\right)=\{v_1,v_2,\dots ,v_t\}$ where $t\ge 3$. For $1\le i\le t$, let

$$A_i=(v,v_i=u_{i,{\mathsf{\ell }}_i},u_{i,{\mathsf{\ell }}_i-1},\dots ,u_{i,2},u_{i,1})$$

(1)

be the ith arm of T at v having length ${\mathsf{\ell }}_i$ and let

$$S=\bigcup _{i=1}^t\{u_{i,j}:j\not\equiv 0\left(\mathrm{mod}4\right)\mathrm{and}1\le j\le {\mathsf{\ell }}_i\}.$$

(2)

First, we verify (i). Suppose that T has an arm $A_1$ whose length ${\mathsf{\ell }}_1$ is congruent to 3 mod 4. Then v does not belong to any proper total dominating set of T by Lemma 2. If T has an arm $A_2$ such that ${\mathsf{\ell }}_2\not\equiv 3\left(\mathrm{mod}4\right)$, then v must belong to every proper total dominating set of T by Lemma 2. Hence, T has no proper total dominating set.

For the converse, suppose that ${\mathsf{\ell }}_i\equiv 3\left(\mathrm{mod}4\right)$ for $1\le i\le t$. Then ${\sigma }_S\left(v\right)=t\ge 3$. Since ${\sigma }_S\left(u_{i,j}\right)=1$ if j is odd and $1\le j\le {\mathsf{\ell }}_i$ while ${\sigma }_S\left(u_{i,j}\right)=2$ if j is even and $2\le i\le {\mathsf{\ell }}_i-1$ where $1\le i\le t$, it follows that $\{{\sigma }_S\left(x\right),{\sigma }_S\left(y\right)\}=\{1,2\}$ for every two adjacent vertices x and y in $T-v$. Hence, S is a proper total dominating set of T.

Next, we verify (ii). In this case, T has no arms whose lengths are congruent to 3 mod 4. Hence, the length of each arm of T is congruent to 0, 1 or 2 mod 4. Thus, the center vertex v of T belongs to every proper total dominating set of T. First, suppose that T has a proper total dominating set. It then follows by Lemma 2 that $S^{*}=S\cup \left\{v\right\}$ is a proper total dominating set of T. For $1\le i\le t$, if $j\equiv 0\left(\mathrm{mod}4\right)$, then $u_{i,j}\notin S^{*}$; while if $j\not\equiv 0\left(\mathrm{mod}4\right)$, then $u_{i,j}\in S^{*}$. Consequently, for $1\le i\le t$, if ${\mathsf{\ell }}_i\equiv 0\left(\mathrm{mod}4\right)$, then $v_i=u_{i,{\mathsf{\ell }}_i}\notin S^{*}$; while if ${\mathsf{\ell }}_i\not\equiv 0\left(\mathrm{mod}4\right)$, then $v_i=u_{i,{\mathsf{\ell }}_i}\in S^{*}$. Suppose that T has q arms whose lengths are not congruent to 0 mod 4. Then v is totally dominated by q vertices of $S^{*}$ and ${\sigma }_{S^{*}}\left(v\right)=q\ge 1$. If $q\ge 3$, then (a) holds. Thus, we may assume that $q=1,2$.

First, suppose that $q=1$. Thus, T has exactly one arm whose length is not congruent to 0 mod 4. We may assume that ${\mathsf{\ell }}_1\not\equiv 0\left(\mathrm{mod}4\right)$. Since ${\mathsf{\ell }}_1\not\equiv 3\left(\mathrm{mod}4\right)$ as well, it follows that ${\mathsf{\ell }}_1\equiv 1\left(\mathrm{mod}4\right)$ or ${\mathsf{\ell }}_1\equiv 2\left(\mathrm{mod}4\right)$. If ${\mathsf{\ell }}_1\equiv 1\left(\mathrm{mod}4\right)$, then ${\sigma }_{S^{*}}\left(v\right)={\sigma }_{S^{*}}\left(v_1\right)=1$, which is impossible. Thus, ${\mathsf{\ell }}_1\equiv 2\left(\mathrm{mod}4\right)$ and so (b) holds when $q=1$. It remains to show that $q\ne 2$. Assume, to the contrary, that $q=2$, say ${\mathsf{\ell }}_i\not\equiv 0\left(\mathrm{mod}4\right)$ for $i=1,2$. Then ${\sigma }_{S^{*}}\left(v\right)=2$. Since T is not a path, there is an arm $A_3$ such that ${\mathsf{\ell }}_3\equiv 0\left(\mathrm{mod}4\right)$. Thus, ${\sigma }_{S^{*}}\left(v_3\right)=2$. Since v and $v_3$ are adjacent, this is impossible and so $q\ne 2$.

For the converse, suppose that T satisfies one of the conditions (a) and (b). We show that $S^{*}=S\cup \left\{v\right\}$ is a proper total dominating set of T. Let x and y be two adjacent vertices of T. If $x,y\in V\left(T\right)-\left\{v\right\}$, then $\{{\sigma }_{S^{*}}\left(x\right),{\sigma }_{S^{*}}\left(y\right)\}=\{1,2\}$. Thus, we may assume that $x=v$ and $y\in N\left(v\right)$.

• If T has at least three arms whose lengths are not congruent to 0 mod 4, then ${\sigma }_{S^{*}}\left(x\right)={\sigma }_{S^{*}}\left(v\right)=3$ and ${\sigma }_{S^{*}}\left(y\right)\in \{1,2\}$.
• If T has exactly one arm whose length is not congruent to 0 mod 4 and this length is congruent to 2 mod 4, then ${\sigma }_{S^{*}}\left(x\right)={\sigma }_{S^{*}}\left(v\right)=1$ and ${\sigma }_{S^{*}}\left(y\right)=2$.

Hence, $S^{*}$ is a proper total dominating set of T. □

As a consequence of Lemma 2 and Theorem 1, if a starlike tree T has a proper total dominating set, then T has a unique proper total dominating set and so ${\gamma }_{pt}\left(T\right)$ can be determined.

Corollary 1.

Let T be a starlike tree with center v and $N\left(v\right)=\{v_1,v_2,\dots ,v_t\}$ where $t\ge 3$. For $1\le i\le t$, let $A_i$ be the ith arm of T of length ${\mathsf{\ell }}_i$ at v defined in $\left(1\right)$ and let S be the set of vertices of T defined in $\left(2\right)$. If T has a proper total dominating set $S^{*}$, then either $\left(i\right)$ $S^{*}=S$ and ${\gamma }_{pt}\left(T\right)=\left|S\right|$ or $\left(ii\right)$ $S^{*}=S\cup \left\{v\right\}$ and ${\gamma }_{pt}\left(T\right)=\left|S\right|+1$.

To illustrate Theorem 1 and Corollary 1, we consider two special classes of starlike trees.

• For integers $d,\hspace{0.17em}\Delta$ where $d\ge 5$ and $\Delta \ge 3$, let $B_{d,\Delta }$ be the broom of order $d+\Delta -1$ with diameter d and maximum degree $\Delta$. By Corollary 1, if $B_{d,\Delta }$ has a $pt$-set S, then S is unique.

  🟉

  For odd integers $d\ge 5$, $B_{d,\Delta }$ has a proper total dominating set if and only if $\Delta \ge 4$. Suppose that $d=4q+1$ or $d=4q+3$ for some integer $q\ge 1$ and $\Delta \ge 4$. If $d=4q+1$, then ${\gamma }_{pt}\left(B_{d,\Delta }\right)=3(q+1)+1$ and $B\left[S\right]=K_{1,3}+q{P}_3$. If $d=4q+3$, then ${\gamma }_{pt}\left(B_{d,\Delta }\right)=3(q+2)$ and $B\left[S\right]=S_{4,2}+q{P}_3$.

  🟉

  For even integers $d\ge 6$, $B_{d,\Delta }$ has a proper total dominating set if and only if $d\equiv 2\left(\mathrm{mod}4\right)$. Furthermore, if $d=4q+2$ for some integer $q\ge 1$, then ${\gamma }_{pt}\left(B_{d,\Delta }\right)=3(q+1)$ and $B\left[S\right]=(q+1)P_3$.

• For integers t and k where $t\ge 1$ and $k\ge 3$, let $K_{1,k}$ be the star centered at a vertex v and let $S_t\left(K_{1,k}\right)$ be the starlike tree of order $n=(t+1)k+1$ obtained by subdividing each edge of $K_{1,k}$ exactly t times. In particular, $S\left(K_{1,k}\right)=S_1\left(K_{1,k}\right)$. If $T=S\left(K_{1,k}\right)$, then $V\left(T\right)$ is the only proper total dominating set of T and so ${\gamma }_{pt}\left(T\right)=2k+1$. If $T=S_2\left(K_{1,k}\right)$, then $V\left(T\right)-\left\{v\right\}$ is the only proper total dominating set of T and so ${\gamma }_{pt}\left(T\right)=3k$. If $T=S_3\left(K_{1,k}\right)$, then no neighbor of v can belong to any proper total dominating set of T and so v is not dominated by any vertex, which implies that T has no proper total dominating set. If $T=S_4\left(K_{1,k}\right)$, then let $N_2\left(v\right)$ be the set of vertices at distance 2 from v. Then $V\left(T\right)-N_2\left(v\right)$ is a proper total dominating set of T and so ${\gamma }_{pt}\left(T\right)=(4k+1)-k=3k+1$. In general, for integers t and k with $t\ge 1$ and $k\ge 3$, the starlike tree $S_t\left(K_{1,k}\right)$ has a proper total dominating set if and only if $t\not\equiv 3\left(\mathrm{mod}4\right)$. Furthermore,

  $${\gamma }_{pt}\left(S_t\left(K_{1,k}\right)\right)=\left\{\begin{array}{cc}k(t+1-q)+1& \mathrm{if}t=4q+1\mathrm{or}t=4q\hfill \\ k(t+1-q)& \mathrm{if}t=4q+2.\hfill \end{array}\right.$$

4. Caterpillars

Another familiar class of trees that is closely related to stars and paths is the class of caterpillars. A caterpillar is a tree of order 3 or more, the removal of whose end-vertices results in a path called the spine of the caterpillar. A star is therefore a caterpillar with a trivial spine and a double star is a caterpillar with spine $P_2$.

The non-leaf minimum degree ${\delta }^{*}\left(T\right)$ of a tree T is the minimum degree of a non-leaf of T. A tree T is r-regular for some integer $r\ge 2$ if every non-end-vertex of T has degree r. Thus a path of order 3 or more is 2-regular and the star $K_{1,n}$ of size n is n-regular. Every caterpillar T with ${\delta }^{*}\left(T\right)\ge 3$ has a proper total dominating set. Before showing this, we first make an observation.

Observation 3.

Let $G^{\prime }$ be a graph with a proper total dominating set S. If G is a graph obtained by adding pendant edges at those vertices v of $G^{\prime }$ for which $v\in S$ and ${\sigma }_S\left(v\right)\ne 1$, then S is a proper total dominating set of G.

Theorem 2.

Each caterpillar T with ${\delta }^{*}\left(T\right)\ge 3$ has a proper total dominating set. In particular, every r-regular caterpillar $(r\ge 3)$ has a proper total dominating set.

Proof. 

Let d be the diameter of T. Since every star has a proper total dominating set, we may assume that $d\ge 3$. Let $(u_0,u_1,\dots ,u_{d-1},u_d)$ be a path of length d in T. First, we show that T has a proper total dominating set. We consider two cases.

Case 1. T is a cubic caterpillar. For $1\le i\le d-1$, let $v_i$ be the end-vertex adjacent to $u_i$. Let S be a set of vertices of T such that $x\in S$ if $x=u_i$ for $0\le i\le d$ or $x=v_j$ for an odd integer j with $1\le j\le d-1$. Since ${\sigma }_S\left(x\right)=1$ if x is an end-vertex of T, ${\sigma }_S\left(u_i\right)=2$ if i is even and $2\le i\le d-1$, and ${\sigma }_S\left(u_i\right)=3$ if i is odd and $1\le i\le d-1$, it follows that S is a proper total dominating set of T.

Case 2. T is not a cubic caterpillar. Since ${\delta }^{*}\left(T\right)\ge 3$, it follows that T contains a 3-regular (cubic) caterpillar $T_0$ as a subtree as described in Case 1. Let S be the proper total dominating set of $T_0$ defined in Case 1. Then S is also a proper total dominating set of T by Observation 3. □

Theorem 2 cannot be improved in general. For example, by Proposition 3 every path $P_n$ of order $n\ge 4$ where $n\not\equiv 3\left(\mathrm{mod}4\right)$ is a caterpillar that does not have a proper total dominating set.

By Theorem 2, it remains to consider caterpillars T that are not locally irregular and ${\delta }^{*}\left(T\right)=2$. With the aid of Observation 3, another class of such caterpillars having a proper total dominating set can be constructed. First, let $P_n=(v_1,v_2,\dots ,v_n)$ where $n\ge 3$ and $n\equiv 3\left(\mathrm{mod}4\right)$. Then $P_n$ has a unique proper total dominating set $S=\{v_i:i\not\equiv 0\left(\mathrm{mod}4\right)\}$ and each component of $T\left[S\right]$ is $P_3$. Furthermore, ${\sigma }_S\left(v_i\right)=1$ if i is odd and ${\sigma }_S\left(v_i\right)=2$ if i is even. if i is even with $i\equiv 2\left(\mathrm{mod}4\right)$, then $v_i\in S$ and ${\sigma }_S\left(v_i\right)=2$. Let T be the caterpillar obtained by adding pendant edges at a vertex $v_i$ with $i\equiv 2\left(\mathrm{mod}4\right)$. Then S is also a proper total dominating set of T by Observation 3.

Next, we show that if T is a tree with ${\gamma }_{pt}\left(T\right)\le 8$, then T is a caterpillar with the one exception where $S\left(K_{1,3}\right)\subseteq T$.

Proposition 9.

Let T be a tree. Then ${\gamma }_{pt}\left(T\right)=6$ if and only if

(a)

T is a caterpillar of diameter 4 whose central vertex has degree at least 3 or

(b)

T is a caterpillar of diameter 6 such that all three interior vertices on its spine have degree 2.

Proof. 

First, let T be a caterpillar satisfying condition (a). Let $P_5$= ($x_1$, $x_2$, $x_3$, $x_4$, $x_5$) be a longest path in T and let $S=V\left(P_5\right)\cup \left\{x\right\}$ where x is an end-vertex adjacent to the central vertex $x_3$ in T. Then $T\left[S\right]$ is a caterpillar of order 6 and diameter 4 whose central vertex $x_3$ has degree 3. Since ${\sigma }_S\left(x_3\right)=3$, ${\sigma }_S\left(x_i\right)=2$ for $i=2,4$ and ${\sigma }_S\left(v\right)=1$ for each remaining vertex v of T, it follows that S is a proper total dominating set of T and so ${\gamma }_{pt}\left(T\right)\le \left|S\right|=6$. On the other hand, ${\gamma }_{pt}\left(T\right)\ge 6$ by Propositions 4–7. Therefore, ${\gamma }_{pt}\left(T\right)=6$.

Next, suppose that T is a caterpillar satisfying condition (b). Let $P_7=(x_1,x_2,\dots ,x_7)$ be a longest path in T and let $S=V\left(P_7\right)-\left\{x_4\right\}$. Then $T\left[S\right]=2P_3$. Since ${\sigma }_S\left(x_i\right)=2$ for $i=2,4,6$ and ${\sigma }_S\left(v\right)=1$ for each remaining vertex v of T, it follows that S is a proper total dominating set of T and so ${\gamma }_{pt}\left(T\right)\le \left|S\right|=6$. On the other hand, ${\gamma }_{pt}\left(T\right)\ge 6$ by Propositions 4–7. Therefore, ${\gamma }_{pt}\left(T\right)=6$.

To verify the converse, let T be a tree with ${\gamma }_{pt}\left(T\right)=6$. Let $S=\{x_1,x_2,\dots ,x_6\}$ be a $pt$-dominating set of T. Since (i) $T\left[S\right]$ is a locally irregular forest of order 6 without isolated vertices and (ii) $T\left[S\right]$ is neither a star nor a double star, it follows that $T\left[S\right]$ is either the caterpillar $T_0$ of order 6 and diameter 4 whose central vertex has degree 3 or $T\left[S\right]=2P_3$.

🟉

First, suppose that $T\left[S\right]=T_0$. We may assume that $(x_1,x_2,x_3,x_4,x_5)$ is a path in $T\left[S\right]$ and $x_6$ is adjacent to $x_3$. Then ${\sigma }_S\left(x_3\right)=3$, ${\sigma }_S\left(x_2\right)={\sigma }_S\left(x_4\right)=2$, and ${\sigma }_S\left(x\right)=1$ for each remaining vertex x of $T\left[S\right]$. Thus, either $T=T_0$ or $T\ne T_0$ and each vertex of $V\left(T\right)-S$ is an end-vertex of T that is adjacent to exactly one of $x_2,x_3,x_4$ in T. This implies that T is a caterpillar satisfying condition (a).

🟉

Next, suppose that $T\left[S\right]=2P_3$. We may assume that $(x_1,x_2,x_3)$ and $(x_4,x_5,x_6)$ are two copies of $P_3$ in $T\left[S\right]$. Thus, ${\sigma }_S\left(x_2\right)={\sigma }_S\left(x_5\right)=2$ and ${\sigma }_S\left(x\right)=1$ for each remaining vertex x of $T\left[S\right]$. Since T is a tree, there is exactly one vertex $y\in V\left(T\right)-S$ that is adjacent to exactly one vertex $x_i\in \{x_1,x_2,x_3\}$ and adjacent to exactly one vertex $x_j\in \{x_1,x_2,x_3\}$. Thus, ${\sigma }_S\left(y\right)=2$. Since ${\sigma }_S\left(x_2\right)={\sigma }_S\left(x_5\right)=2$, it follows that $x_i\ne x_2$ and $x_j\ne x_5$ and so $x_i\in \{x_1,x_3\}$ and $x_j\in \{x_4,x_6\}$. We may assume that $x_i=x_3$ and $x_j=x_4$. Hence, T contains $P_7=(x_1,x_2,x_3,y,x_4,x_5,x_6)$ as a subgraph. Again, since T is a tree, if $T\ne P_7$, then each vertex in $V\left(T\right)-\left(\right\{y\}\cup S)$ is an end-vertex of T that is adjacent to exactly one of $x_2$ and $x_4$. Therefore, T is a caterpillar satisfying condition (b).

□

Proposition 10.

Let T be a tree. Then ${\gamma }_{pt}\left(T\right)=7$ if and only if

(a)

T has diameter 4 such that either $T=S\left(K_{1,3}\right)$ or T is obtained by adding pendant edges at non-end-vertices of $S\left(K_{1,3}\right)$,

(b)

T is a caterpillar of diameter 4 such that its central vertex has degree 2 and the two neighbors of the central vertex have degree at least 3, or

(c)

T is a caterpillar of order at least 8 and diameter 5 such that its two central vertices have degree 2 and one of the two end-vertices of its spine has degree at least 4 in T.

Consequently, a tree T has ${\gamma }_{pt}\left(T\right)=7$ if and only if T is a tree of diameter 4 or 5.

Proof. 

By Propositions 4–9, if T is a tree satisfying one of conditions (a)–(c), then ${\gamma }_{pt}\left(T\right)\ge 7$. Thus, it remains to show that ${\gamma }_{Pt}\left(T\right)\le 7$.

First, suppose that T is a tree satisfying condition (a). Let $S=V\left(S\left(K_{1,3}\right)\right)$, where u is the center of $K_{1,3}$ and $u_1,u_2,u_3$ are the neighbors of u. Since ${\sigma }_S\left(u\right)=3$, ${\sigma }_S\left(u_i\right)=2$ for $i=1,2,3$ and ${\sigma }_S\left(v\right)=1$ for each remaining vertex v of T, it follows that S is a proper total dominating set of T and so ${\gamma }_{pt}\left(T\right)\le \left|S\right|=7$.

Next, suppose that T is a caterpillar satisfying condition (b). Let $P_5=(x_1,x_2,x_3,x_4,x_5)$ be a longest path in T, where $deg{x}_2\ge 3$, $deg{x}_4\ge 3$, and $deg{x}_3=2$. For $i=2,4$, let $x_i^{\prime }$ be an end-vertex adjacent to $x_i$. Now, let $S=V\left(P_5\right)\cup \{x_2^{\prime },x_4^{\prime }\}$. Since ${\sigma }_S\left(x_i\right)=3$ for $i=2,4$, ${\sigma }_S\left(x_3\right)=2$, and ${\sigma }_S\left(v\right)=1$ for each remaining vertex v of T, it follows that S is a proper total dominating set of T and so ${\gamma }_{pt}\left(T\right)\le \left|S\right|=7$.

Finally, suppose that T is a caterpillar satisfying condition (c). Let $P_6=(x_1,x_2,\dots ,x_6)$ be a longest path in T. Since the order of T is at least 8, it follows that $deg{x}_2\ge 3$ or $deg{x}_5\ge 3$. If $deg{x}_2=deg{x}_5=3$, then T has no proper total dominating set. Thus, we may assume that $deg{x}_2\ge 4$. Let $x_{2,1},x_{2,2},x_{2,3}$ be three end-vertices of T adjacent to $x_2$ and $S=(V\left(P_6\right)-\left\{x_3\right\})\cup \{x_{2,1},x_{2,2},x_{2,3}\}$. Since ${\sigma }_S\left(x_2\right)=3$, ${\sigma }_S\left(x_3\right)={\sigma }_S\left(x_5\right)=2$ and ${\sigma }_S\left(v\right)=1$ for each remaining vertex v of T, it follows that S is a proper total dominating set of T and so ${\gamma }_{pt}\left(T\right)\le \left|S\right|=7$.

To verify the converse, let T be a tree with ${\gamma }_{pt}\left(T\right)=7$ and let $S=\{x_1,x_2,\dots ,x_7\}$ be a $pt$-dominating set of T. Since (i) $T\left[S\right]$ is a locally irregular forest of order 7 without isolated vertices and (ii) $T\left[S\right]$ is neither a star nor a double star, it follows that either $T\left[S\right]$ is a locally irregular tree of diameter 4 or $T\left[S\right]=K_{1,3}+P_3$.

🟉

First, suppose that $T\left[S\right]$ is a locally irregular tree of diameter 4. Thus, $T\left[S\right]$ is either $S\left(K_{1,3}\right)$ or one of two caterpillars. All three of these trees are shown in Figure 5. If $T\left[S\right]=S\left(K_{1,3}\right)$, then T satisfies condition (a). Thus, we may assume that $T\left[S\right]$ is one of the two caterpillars shown in Figure 5. Let $P_5=(x_1,x_2,x_3,x_4,x_5)$ be a longest path in T. If $deg{x}_3\ge 3$, then ${\gamma }_{pt}\left(T\right)=6$ by Proposition 9. Thus, we may assume that $deg{x}_3=2$. This implies that $deg{x}_2\ge 3$ and $deg{x}_4\ge 3$. Hence, T satisfies condition (b).

🟉

Next, suppose that $T\left[S\right]=K_{1,3}+P_3$. We may assume that $V\left(K_{1,3}\right)=\{x_1,x_2,x_3,x_4\}$ where $x_4$ is the central vertex and $P_3=(x_5,x_6,x_7)$ is in $T\left[S\right]$. Thus, ${\sigma }_S\left(x_4\right)=3$, ${\sigma }_S\left(x_6\right)=2$, and ${\sigma }_S\left(x\right)=1$ for each remaining vertex x of $T\left[S\right]$. Since T is a tree, there is exactly one vertex $y\in V\left(T\right)-S$ that is adjacent to exactly one vertex $x_i\in \{x_1,x_2,x_3,x_4\}$ and exactly one vertex $x_j\in \{x_5,x_6,x_7\}$. Thus, ${\sigma }_S\left(y\right)=2$. Since ${\sigma }_S\left(x_6\right)=2$, it follows that $x_j\ne x_6$ and so $x_j\in \{x_5,x_7\}$, say $y{x}_5\in E\left(T\right)$. If $x_i\in \{x_1,x_2,x_3\}$, then the diameter of T is 6 and ${\gamma }_{pt}\left(T\right)=6$ by Proposition 9, producing a contradiction. Therefore, y is adjacent to $x_4$ and so T satisfies condition (c).

□

The following is a consequence of the proofs of Propositions 9 and 10.

Corollary 2.

Let T be a tree of diameter 4. Then ${\gamma }_{pt}\left(T\right)\in \{6,7\}$ where ${\gamma }_{Pt}\left(T\right)=6$ if and only if T is a caterpillar of diameter 4 whose central vertex has degree at least 3.

Proposition 11.

Let T be a tree. Then ${\gamma }_{pt}\left(T\right)=8$ if and only if

(a)

T is a caterpillar of diameter 5 such that two nonadjacent vertices on its spine have degree at least 3 one of which is a central vertex,

(b)

T is a caterpillar of diameter 6 such that two adjacent interior vertices on its spine have degree 2, or

(c)

T is a caterpillar of diameter 7 such that there is a 3-path $(u,v,w)$ on its spine where ${deg}_{T}u={deg}_{T}v={deg}_{T}w=2$ and u and w are the central vertices of T.

Consequently, a tree T has ${\gamma }_{pt}\left(T\right)=8$ if and only if T is a caterpillar of diameter $5,6$, or 7.

Proof. 

First, if T is a caterpillar that satisfies (a), (b), or (c), then it can be shown that ${\gamma }_{pt}\left(T\right)=8$. For the converse, suppose that T is a tree with ${\gamma }_{pt}\left(T\right)=8$. Let $S=\{x_1,x_2,\dots ,x_8\}$ be a ${\gamma }_{pt}$-set of T. Since (i) $T\left[S\right]$ is a locally irregular forest of order 8 without isolated vertices, (ii) $T\left[S\right]$ is neither a star nor a double star, and (iii) $T\left[S\right]$ is not a tree of diameter 4, it follows that either $T\left[S\right]$ is a tree of diameter at least 5 or $T\left[S\right]\in \{2K_{1,3},K_{1,4}+P_3,S_{2,3}+P_3\}$. We consider these four cases.

Case 1. $T\left[S\right]$ is a tree of order 8 having diameter at least 5. Since $T\left[S\right]$ is a locally irregular tree of order 8, it follows that $\mathrm{diam}\left(T\right[S\left]\right)\le 5$ and so $\mathrm{diam}\left(T\right)\le 5$ by Lemma 1. Thus, $\mathrm{diam}\left(T\right)=5$. Let $P_6=(v_1,v_2,\dots ,v_6)$ be a longest path in $T\left[S\right]$. Then exactly two nonadjacent interior vertices of $P_6$ have degree 3, say ${deg}_{T\left[S\right]}{v}_2={deg}_{T\left[S\right]}{v}_4=3$. Thus, either (i) $T=T\left[S\right]$ or (ii) $T\ne T\left[S\right]$ and each vertex $y\in V\left(T\right)-S$ is an end-vertex adjacent to exactly one vertex in $\{v_2,v_3,v_4,v_5\}$. Therefore, T is a caterpillar satisfying (a).

Case 2. $T\left[S\right]=2K_{1,3}$. Let $F_1$ and $F_2$ be the two copies of $K_{1,3}$ in $T\left[S\right]$. We may assume that $V\left(F_1\right)=\{x_1,x_2,x_3,x_4\}$ and $V\left(F_2\right)=\{x_5,x_6,x_7,x_8\}$ where $F_1$ is centered at $x_1$ and $F_2$ is centered at $x_5$. Thus, ${\sigma }_S\left(x_1\right)={\sigma }_S\left(x_5\right)=3$ and ${\sigma }_S\left(x\right)=1$ for each remaining vertex x of S. Since T is a tree, there is exactly one vertex $y\in V\left(T\right)-S$ such that ${deg}_{T}y=2$ and y is adjacent to exactly one vertex $x_i\in \{x_1,x_2,x_3,x_4\}$ and adjacent to exactly one vertex $x_j\in \{x_5,x_6,x_7,x_8\}$. If $x_i\ne x_1$ and $x_j\ne x_5$, then T is a caterpillar of diameter 6 whose three interior vertices on the spine have degree 2. However then, ${\gamma }_{pt}\left(T\right)=6$ by Proposition 9, a contradiction. If (i) $x_i=x_1$ and $x_j\ne x_5$ or (ii) $x_i\ne x_1$ and $x_j{x}_5$, then T is a caterpillar of diameter 5 whose two interior vertices on the spine have degree 2. However then, ${\gamma }_{pt}\left(T\right)=7$ by Proposition 10, a contradiction. Hence, we may assume that $x_i=x_1$ and $x_j=x_5$. Thus, $\mathrm{diam}\left(T\right)=4$ and so ${\gamma }_{pt}\left(T\right)\le 7$ by Corollary 2, which is a contradiction. Therefore, Case 2 cannot occur.

Case 3. $T\left[S\right]=K_{1,4}+P_3$. We may assume that $V\left(K_{1,4}\right)=\{x_1,x_2,x_3,x_4,x_5\}$, where $x_1$ is the central vertex and $P_3=(x_6,x_7,x_8)$. Thus, ${\sigma }_S\left(x_1\right)=4$, ${\sigma }_S\left(x_7\right)=2$, and ${\sigma }_S\left(x\right)=1$ for each remaining vertex x of S. Since T is a tree and ${\sigma }_S\left(x_7\right)=2$, there is exactly one vertex $y\in V\left(T\right)-S$ such that ${deg}_{T}y=2$ where y is adjacent to exactly one vertex $x_i\in \{x_1,x_2,x_3,x_4,x_5\}$ and adjacent to exactly one vertex in $\{x_6,x_8\}$. If $x_i\ne x_1$, then T is a caterpillar of diameter 6 whose three interior vertices on the spine have degree 2. However then, ${\gamma }_{pt}\left(T\right)=6$ by Proposition 9, which is a contradiction. If $x_i=x_1$, then T is a caterpillar of diameter 5 whose two interior vertices on the spine have degree 2. However then, ${\gamma }_{pt}\left(T\right)=7$ by Proposition 10, which is a contradiction. Hence, Case 3 cannot occur.

Case 4. $T\left[S\right]=S_{2,3}+P_3$. We may assume that $V\left(S_{2,3}\right)=\{x_1,x_2,x_3,x_4,x_5\}$, where $x_1$ has degree 3 in $T\left[S\right]$, the vertex $x_2$ has degree 2 in $T\left[S\right]$, and $P_3=(x_6,x_7,x_8)$. Thus, ${\sigma }_S\left(x_1\right)=3$, ${\sigma }_S\left(x_2\right)={\sigma }_S\left(x_7\right)=2$, and ${\sigma }_S\left(x\right)=1$ for each remaining vertex x of S. There is exactly one vertex $y\in V\left(T\right)-S$ that is adjacent to exactly one vertex $x_i\in \{x_1,x_3,x_4,x_5\}$ and adjacent to exactly one vertex in $\{x_6,x_8\}$. If $x_i\ne x_1$, then T is a caterpillar of diameter 7 satisfying condition (c). If $x_i=x_1$, then T is a caterpillar of diameter 6 satisfying condition (b). □

Corollary 3.

Let T be a tree of diameter 5 and ${\gamma }_{pt}\left(T\right)\le 8$. Then T has a proper total dominating set if and only if T is a caterpillar in which either $\left(i\right)$ two nonadjacent vertices on its spine have degree at least 3 or $\left(ii\right)$ two central vertices have degree 2 and at least one of the end-vertices of its spine has degree at least 4 in T. Furthermore, if $\left(i\right)$ occurs, then ${\gamma }_{pt}\left(T\right)=8$; while if $\left(ii\right)$ occurs, then ${\gamma }_{pt}\left(T\right)=7$.

By Corollary 3, the two trees $T_1$ and $T_2$ of diameter 5 in Figure 6 have no proper total dominating sets. The condition ${\gamma }_{pt}\left(T\right)\le 8$ is necessary in Corollary 3. For example, the tree $T_3$ of order 10 and diameter 5 in Figure 6 has a proper total dominating set but $T_3$ is not a caterpillar. It can be shown that ${\gamma }_{pt}\left(T_3\right)=9$.

5. In Closing

Finally, we summarize what has been presented here. As we mentioned, our goal was to investigate those trees with a symmetric structure or possessing subtrees with a symmetric structure and having a proper total dominating set. All trees of diameter at most 4 that possess a proper total dominating set are characterized. All starlike trees having a proper total dominating set are determined as well as their proper total domination numbers. It is shown that if a starlike tree has a proper total dominating set, then it has a unique proper total dominating set with a fixed graphical structure. Sufficient conditions are established for caterpillars to possess a proper total dominating set. Furthermore, by investigating proper total dominating sets in caterpillars, all trees with proper total domination number at most 8 are determined.

The results obtained on proper total domination in trees suggest other questions, including the following.

Question 1.

Is there a characterization of caterpillars possessing a proper total dominating set?

Question 2.

Is there a sufficient or a necessary condition for a tree to have a proper total dominating set?

Since proper total domination is more restrictive than total domination, it follows that $2\le {\gamma }_t\left(G\right)\le {\gamma }_{pt}\left(G\right)$ for every graph G with a proper total dominating set. A pair $a,b$ of integers with $2\le a\le b$ is realizable if there is a connected graph G such that ${\gamma }_t\left(G\right)=a$ and ${\gamma }_{pt}\left(G\right)=b$. All realizable pairs were determined in [12].

Theorem 3

([12]). For each pair $a,b$ of integers with $2\le a\le b$, there exists a connected graph G such that ${\gamma }_t\left(G\right)=a$ and ${\gamma }_{pt}\left(G\right)=b$ if and only if $\left(1\right)$ $a\in \{2,3,4\}$ and $b\ge a+1$ or $\left(2\right)$ $5\le a\le b$.

In the proof of Theorem 3, none of the graphs G is a tree. This leads to the following question.

Question 3.

For which pairs $a,b$ of positive integers with $a\le b$, does there exist a tree T such that ${\gamma }_t\left(T\right)=a$ and ${\gamma }_{pt}\left(T\right)=b$?

While many problems on this topic remain unsolved, there are some related and potentially intriguing concepts that are worthy of further investigation. For example, recall that the proper total domination number ${\gamma }_{pt}\left(G\right)$ of a graph G is the minimum cardinality of a proper total dominating set in G. A related parameter is the maximum cardinality of a proper total dominating set in a graph G, which we refer to as the upper proper total domination number ${\Gamma }_{pt}\left(G\right)$ of G. For every graph G having a proper total dominating set, it follows that ${\gamma }_{pt}\left(G\right)\le {\Gamma }_{pt}\left(G\right)$. While there are infinitely many graphs G having a proper total dominating set such that ${\gamma }_{pt}\left(G\right)={\Gamma }_{pt}\left(G\right)$, there are also graphs G having proper total dominating sets for which the difference ${\Gamma }_{pt}\left(G\right)-{\gamma }_{pt}\left(G\right)$ can be arbitrarily large. This observation gives rise to the following question.

Question 4.

For which pairs $a,b$ of positive integers with $a\le b$, does there exist a graph G such that ${\gamma }_{pt}\left(G\right)=a$ and ${\Gamma }_{pt}\left(G\right)=b$?