Modeling Uncertainty with Interval-Valued Intuitionistic Fuzzy Filters in Hoop Algebras

Abstract

This paper systematically investigates interval-valued intuitionistic fuzzy (IVIF) sets and filters within the framework of hoop algebras, unifying and extending classical fuzzy set theory and intuitionistic fuzzy sets (IFS) in algebraic logic. We clarify the foundational relationships among fuzzy sets, IFS, and hoop algebras, and introduce novel characterizations of IVIF filters, including necessary and sufficient conditions for their existence and structure. Theoretical advancements include the demonstration that IVIF filters can be described via their endpoint functions, the establishment of a bounded distributive lattice of IVIF filters, and the identification of congruence relations induced by these filters. Algorithmic and numerical aspects are addressed through explicit pseudocode and detailed examples, illustrating how the verification and construction of IVIF filters can be performed in finite hoop algebras. Practical implications are highlighted in decision-making scenarios where modeling uncertainty and vagueness with interval-valued membership and non-membership degrees offers enhanced flexibility and robustness. Our results lay a rigorous foundation for further applications of IVIF filters in fuzzy logic, artificial intelligence, and multi-criteria decision analysis.

1. Introduction

Hoop algebras, introduced by Bosbach [1,2], are naturally ordered commutative residuated integral monoids [3]. These structures play a crucial role in fuzzy logic and various algebraic frameworks [4,5]. Residuated structures, as explored by Blok and Ferreirim [6], serve as a foundation for modeling logical systems through operations such as multiplication and residuation, which represent conjunction and implication.

The connection between hoop algebras and BL-algebras is well-established, particularly in the context of continuous t-norms [7,8,9]. Esteva and Godo’s work on monoidal t-norm based logic [10] further highlights the applicability of these structures in logical systems, focusing on left-continuous t-norms and their algebraic counterparts, MTL-algebras. These algebras capture the essence of Hájek’s basic fuzzy logic, addressing the tautologies of continuous t-norms and their residua [10].

The introduction of fuzzy sets by Zadeh [11] established a foundation for contemporary fuzzy logic frameworks. This innovation enables the modeling of uncertainty and vagueness, which is further advanced through the creation of interval-valued intuitionistic fuzzy (IVIF) filters [12]. Singh and Garg contributed to this area by developing type-2 intuitionistic fuzzy sets [13]. IVIF filters offer a sophisticated method for representing both membership and non-membership degrees, thereby improving the ability of hoop algebras to handle intricate decision-making processes.

The integration of IVIF filters into hoop algebras enriches the algebraic structure and bridges classical properties with modern fuzzy systems [4,5]. Borzooei and Kologani’s exploration of local and perfect semihoops [14] adds depth to this exploration, introducing concepts such as primary and perfect filters and their connections to semihoop structures. Furthermore, the study of obstinate filters and their relationships with other types of filters, like fantastic and positive implicative filters, expands the understanding of hoop algebras [5].

Despite the growing interest in interval-valued intuitionistic fuzzy (IVIF) sets and their applications in algebraic structures, the study of IVIF filters within the framework of hoop algebras remains largely unexplored. Hoop algebras, as generalizations of certain logical and algebraic systems, provide a rich environment for modeling uncertainty and vagueness. However, there is a lack of systematic investigation into how IVIF filters behave in hoop algebras, what properties they possess, and how they can be characterized and applied.

The main problem addressed in this paper is to develop a comprehensive theory of IVIF filters in hoop algebras. Specifically, we aim to achieve the following:

• Define and characterize IVIF filters in the context of hoop algebras.
• Investigate the relationships between IVIF filters and other types of filters in hoop algebras.
• Explore the algebraic properties and potential applications of IVIF filters in this setting.

By addressing these issues, we seek to fill a gap in the literature and provide new tools for the study of fuzzy logic, algebraic structures, and their applications.

While interval-valued intuitionistic fuzzy (IVIF) sets and their associated filters have been studied in various algebraic structures such as lattices [15,16], BL-algebras [17], UP-algebras [18] and MV-algebras [19], the literature reveals several limitations. Most notably, there is a scarcity of research focusing on the behavior and structure of IVIF filters specifically within hoop algebras. Existing works often overlook the unique properties of hoop algebras and do not provide comprehensive characterizations or systematic frameworks for IVIF filters in this context.

Furthermore, prior studies have not thoroughly explored the relationships between IVIF filters and other types of filters in hoop algebras, nor have they addressed the potential implications for fuzzy logic and its applications.

This paper aims to fill these gaps by

• Introducing and systematically studying IVIF filters in hoop algebras.
• Providing new characterizations and properties of IVIF filters tailored to hoop algebras.
• Establishing connections between IVIF filters and existing filter concepts in this algebraic setting.
• Highlighting possible directions for future research and applications.

The results established in this paper provide a rigorous foundation for representing and manipulating uncertainty in algebraic logic systems. Interval-valued intuitionistic fuzzy (IVIF) filters in hoop algebras allow for a nuanced encoding of both membership and non-membership degrees with intervals, which is essential for modelling complex forms of vagueness and incomplete information.

In particular, the following contributions are relevant for logical inference and automated reasoning:

• Enhanced Uncertainty Representation: IVIF filters extend classical fuzzy filters by capturing a range of possible membership and non-membership values, rather than single points. This enables more robust reasoning in systems where data or expert knowledge is imprecise or variable.
• Logical Inference Mechanisms: The algebraic properties and closure conditions of IVIF filters mirror deductive structures found in logic, such as modus ponens, but with interval-valued uncertainty. The residuation-style criteria and lattice-theoretic results enable the construction of inference engines that can propagate uncertainty through logical rules.
• Automated Reasoning: The congruence relations and quotient structures induced by IVIF filters allow for the reduction and simplification of complex reasoning tasks. Automated reasoning systems can utilize these algebraic tools to handle uncertain premises, aggregate evidence, and derive conclusions with quantified confidence intervals.
• Practical Example: For example, in multi-criteria decision-making or expert systems, each criterion or rule can be evaluated using IVIF sets, and the overall inference can be performed within the hoop algebraic framework, ensuring consistency and transparency in uncertainty propagation.

Overall, the theoretical developments in IVIF filters not only advance the mathematical understanding of uncertainty in algebraic logic, but also provide concrete tools for the design of intelligent systems capable of reasoning under uncertainty.

As a conclusion, this paper aims to explore the properties and applications of IVIF filters within hoop algebras, building on the foundational work of previous researchers. By examining these filters and other algebraic structures, we seek to provide a comprehensive framework for understanding their role in modeling uncertainty and enhancing logical reasoning. The study contributes to the growing body of research in fuzzy logic by extending the notion of filters to interval-valued settings, paving the way for applications in decision-making, data analysis, and artificial intelligence.

2. Preliminaries

In this section, we recall basic definitions, propositions and notations that will be used throughout the paper. Due to the complex use of symbols and algebraic terms, we summarize the main notations in Table 1 for the reader’s convenience.

Table 1. Table of notation.

Symbol	Description
$\mathcal{H}$	Hoop algebra
⊙	Binary operation (multiplication) on hoop algebra
→	Binary operation (residuation/implication) on hoop algebra
1	Identity element of $\mathcal{H}$
${\le }_{\mathcal{H}}$	Partial order on $\mathcal{H}$ defined by $x{\le }_{\mathcal{H}}y\iff x\to y=1$
$\mathcal{F}$	Filter of a hoop algebra
$\mathcal{S}$	Sub-hoop of a hoop algebra
$\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$	Interval-valued intuitionistic fuzzy (IVIF) set on $\mathcal{H}$
${\mu }_{\mathcal{A}}\left(x\right)$	Interval-valued membership degree of x in $\mathcal{A}$
${\gamma }_{\mathcal{A}}\left(x\right)$	Interval-valued non-membership degree of x in $\mathcal{A}$
$\mathcal{D}[0,1]$	Set of all closed subintervals of $[0,1]$
$rmin({\mathcal{D}}_1,{\mathcal{D}}_2)$	$[min(m_1,m_2),min(n_1,n_2)]$ for ${\mathcal{D}}_1=[m_1,n_1],{\mathcal{D}}_2=[m_2,n_2]$
$rmax({\mathcal{D}}_1,{\mathcal{D}}_2)$	$[max(m_1,m_2),max(n_1,n_2)]$ for ${\mathcal{D}}_1=[m_1,n_1],{\mathcal{D}}_2=[m_2,n_2]$
$\overline{{\mu }_{\mathcal{A}}}\left(x\right)$	Complement of ${\mu }_{\mathcal{A}}\left(x\right)$, i.e., $[1-{\mu }_{\mathcal{A}}^u\left(x\right),1-{\mu }_{\mathcal{A}}^l\left(x\right)]$
$\overline{{\gamma }_{\mathcal{A}}}\left(x\right)$	Complement of ${\gamma }_{\mathcal{A}}\left(x\right)$, i.e., $[1-{\gamma }_{\mathcal{A}}^u\left(x\right),1-{\gamma }_{\mathcal{A}}^l\left(x\right)]$
$\mathcal{A}\cup \mathcal{B}$	Union of two IVIF sets
$\mathcal{A}\cap \mathcal{B}$	Intersection of two IVIF sets
$\mathcal{U}({\mu }_{\mathcal{A}},[m,n])$	Upper level set: $\{x\in \mathcal{H}\mid {\mu }_{\mathcal{A}}\left(x\right)\ge [m,n]\}$
$\mathcal{L}({\gamma }_{\mathcal{A}},[m,n])$	Lower level set: $\{x\in \mathcal{H}\mid {\gamma }_{\mathcal{A}}\left(x\right)\le [m,n]\}$

Definition 1 

([9]). A hoop (also referred to as a hoop algebra) is an algebraic structure denoted as $(\mathcal{H},\odot ,\to ,1)$, where the triple $(\mathcal{H},\odot ,1)$ forms a commutative monoid, and the following axioms are satisfied:

• (H1) ${\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_x}=1$,
• (H2) ${\hslash }_{{\mathfrak{a}}_x}\odot ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})={\hslash }_{{\mathfrak{a}}_y}\odot ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})$,
• (H3) ${\hslash }_{{\mathfrak{a}}_x}\to ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})=({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_z}$

• for all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H}$.

We define a relation ${\le }_{\mathcal{H}}$ on a hoop $\mathcal{H}$ as follows:

$$\begin{array}{c}\hfill (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H})\left({\hslash }_{{\mathfrak{a}}_x}{\le }_{\mathcal{H}}{\hslash }_{{\mathfrak{a}}_y}\iff {\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}=1\right).\end{array}$$

(1)

It is clear that $(\mathcal{H},{\le }_{\mathcal{H}})$ constitutes a partially ordered set.

Definition 2 

([20]). A non-empty subset $\mathcal{S}$ of a hoop algebra $\mathcal{H}$ is called a sub-hoop of $\mathcal{H}$ if it satisfies the following condition:

$$\begin{array}{c}\hfill (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{S})\left({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}\in \mathcal{S}\mathit{and}{\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}\in \mathcal{S}\right).\end{array}$$

(2)

Furthermore, every sub-hoop must contain the element 1.

Proposition 1 

([20]). Let $(\mathcal{H},\odot ,\to ,1)$ be a hoop algebra. For any ${\hslash }_{\mathfrak{a}},{\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H}$, the following conditions hold

• (a1) $(\mathcal{H},{\le }_{\mathcal{H}})$ is a meet-semilattice with ${\hslash }_{{\mathfrak{a}}_x}\wedge {\hslash }_{{\mathfrak{a}}_y}={\hslash }_{{\mathfrak{a}}_x}\odot ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})$,
• (a2) ${\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}{\le }_{\mathcal{H}}{\hslash }_{{\mathfrak{a}}_z}$ if and anly if ${\hslash }_{{\mathfrak{a}}_x}{\le }_{\mathcal{H}}{\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z}$,
• (a3) ${\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}{\le }_{\mathcal{H}}{\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}$ and ${\hslash }_{{\mathfrak{a}}_x}^{\mathfrak{n}}{\le }_{\mathcal{H}}{\hslash }_{{\mathfrak{a}}_x}$ for any $\mathfrak{n}\in N$,
• (a4) ${\hslash }_{{\mathfrak{a}}_x}{\le }_H{\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x}$,
• (a5) $1\to {\hslash }_{\mathfrak{a}}={\hslash }_{\mathfrak{a}}$ and ${\hslash }_{\mathfrak{a}}\to 1=1$,
• (a6) ${\hslash }_{{\mathfrak{a}}_x}\odot ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}){\le }_{\mathcal{H}}{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}{\le }_{\mathcal{H}}{\hslash }_{{\mathfrak{a}}_x}\wedge {\hslash }_{{\mathfrak{a}}_y}{\le }_{\mathcal{H}}{\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}$,
• (a7) ${\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}{\le }_{\mathcal{H}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})$,
• (a8) ${\hslash }_{{\mathfrak{a}}_x}{\le }_{\mathcal{H}}{\hslash }_{{\mathfrak{a}}_y}$ implies ${\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z}{\le }_{\mathcal{H}}{\hslash }_{{\mathfrak{a}}_y}\odot {\hslash }_{{\mathfrak{a}}_z},{\hslash }_{{\mathfrak{a}}_z}\to {\hslash }_{{\mathfrak{a}}_x}{\le }_{\mathcal{H}}{\hslash }_{{\mathfrak{a}}_z}\to {\hslash }_{{\mathfrak{a}}_y}$ and ${\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z}{\le }_{\mathcal{H}}{\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z}$,
• (a9) ${\hslash }_{{\mathfrak{a}}_x}\to ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})={\hslash }_{{\mathfrak{a}}_y}\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})$.

Definition 3 

([20]). A non-empty subset $\mathcal{F}$ of a hoop algebra $\mathcal{H}$ is referred to as a filter of $\mathcal{H}$ if the following conditions hold

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H})\left({\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{F}\Rightarrow {\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}\in \mathcal{F}\right),\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H})\left({\hslash }_{{\mathfrak{a}}_x}\in \mathcal{F},{\hslash }_{{\mathfrak{a}}_x}\le {\hslash }_{{\mathfrak{a}}_y}\Rightarrow {\hslash }_{{\mathfrak{a}}_y}\in \mathcal{F}\right).\hfill \end{array}$$

(4)

Definition 4 

([21]). A non-empty subset $\mathcal{F}$ of a hoop algebra $\mathcal{H}$ is termed an implicative filter of $\mathcal{H}$ if it satisfies the following conditions:

$$\begin{array}{cc}\hfill & 1\in \mathcal{F},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H})\left({\hslash }_{{\mathfrak{a}}_x}\to (({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to {\hslash }_{{\mathfrak{a}}_y})\in \mathcal{F},{\hslash }_{{\mathfrak{a}}_x}\in \mathcal{F}\Rightarrow {\hslash }_{{\mathfrak{a}}_y}\in \mathcal{F}\right).\hfill \end{array}$$

(6)

Note that the conditions (3) and (4) imply that $\mathcal{F}$ is closed under the operation ⊙ and is upward closed, respectively. Additionally, a subset $\mathcal{F}$ of a hoop algebra $\mathcal{H}$ is a filter of $\mathcal{H}$ if and only if it satisfies condition (5) and the following:

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H})\left({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}\in \mathcal{F},{\hslash }_{{\mathfrak{a}}_x}\in \mathcal{F}\Rightarrow {\hslash }_{{\mathfrak{a}}_y}\in \mathcal{F}\right).\hfill \end{array}$$

(7)

Definition 5 

([22]). Let A be a non-empty set. The intuitionistic fuzzy set on A is defined as the structure

$$\begin{array}{c}\hfill \mathcal{A}:=\{⟨{\hslash }_{{\mathfrak{a}}_x},{\mu }_A\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_A\left({\hslash }_{{\mathfrak{a}}_x}\right)\mid {\hslash }_{{\mathfrak{a}}_x}\in A\},\end{array}$$

(8)

where ${\mu }_{\mathcal{A}}:\mathcal{A}\to [0,1]$ denotes the degree of membership of ${\hslash }_{{\mathfrak{a}}_x}$ to $\mathcal{A}$, and  ${\gamma }_{\mathcal{A}}:\mathcal{A}\to [0,1]$ denotes the degree of non-membership of ${\hslash }_{{\mathfrak{a}}_x}$ to $\mathcal{A}$, with the condition $0\le {\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)+{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\le 1$. The intuitionistic fuzzy set in (8) is simply denoted by $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$.

Let $\mathcal{D}[0,1]$ denote the set of all closed subintervals of the interval $[0,1]$. Consider two elements ${\mathcal{D}}_1,{\mathcal{D}}_2\in \mathcal{D}[0,1]$. If ${\mathcal{D}}_1=[{\mathfrak{m}}_1,{\mathfrak{n}}_1]$ and ${\mathcal{D}}_2=[{\mathfrak{m}}_2,{\mathfrak{n}}_2]$, then we define

$$rmin({\mathcal{D}}_1,{\mathcal{D}}_2)=[min({\mathfrak{m}}_1,{\mathfrak{m}}_2),min({\mathfrak{n}}_1,{\mathfrak{n}}_2)]$$

and

$$rmax({\mathcal{D}}_1,{\mathcal{D}}_2)=[max({\mathfrak{m}}_1,{\mathfrak{m}}_2),max({\mathfrak{n}}_1,{\mathfrak{n}}_2)].$$

Thus, if ${\mathcal{D}}_{\mathfrak{j}}=[{\mathfrak{m}}_{\mathfrak{j}},{\mathfrak{n}}_{\mathfrak{j}}]\in \mathcal{D}[0,1]$ for $\mathfrak{j}=1,2,\dots$, we define

$$r\underset{\mathfrak{j}}{sup}\left({\mathcal{D}}_{\mathfrak{j}}\right)=[\underset{\mathfrak{j}}{sup}\left({\mathfrak{m}}_{\mathfrak{j}}\right),\underset{\mathfrak{j}}{sup}\left({\mathfrak{n}}_{\mathfrak{j}}\right)].$$

Similarly, we define

$$r\underset{\mathfrak{j}}{inf}\left({\mathcal{D}}_{\mathfrak{j}}\right)=[\underset{\mathfrak{j}}{inf}\left({\mathfrak{m}}_{\mathfrak{j}}\right),\underset{\mathfrak{j}}{inf}\left({\mathfrak{n}}_{\mathfrak{j}}\right)].$$

We say that ${\mathcal{D}}_1\ge {\mathcal{D}}_2$ if and only if ${\mathfrak{m}}_1\ge {\mathfrak{m}}_2$ and ${\mathfrak{n}}_1\le {\mathfrak{n}}_2$. Similarly, the relations ${\mathcal{D}}_1\le {\mathcal{D}}_2$ and ${\mathcal{D}}_1={\mathcal{D}}_2$ are defined.

Definition 6. 

An interval-valued intuitionistic fuzzy (IVIF) set $\mathcal{A}$ over a set $\mathcal{X}$ is an object of the form

$$\mathcal{A}=\{⟨\mathfrak{x},{\mu }_{\mathcal{A}}\left(\mathfrak{x}\right),{\gamma }_{\mathcal{A}}\left(\mathfrak{x}\right)⟩:\mathfrak{x}\in \mathcal{X}\},$$

where ${\mu }_{\mathcal{A}}\left(\mathfrak{x}\right):\mathcal{X}\to \mathcal{D}[0,1]$ and ${\gamma }_{\mathcal{A}}\left(\mathfrak{x}\right):\mathcal{X}\to \mathcal{D}[0,1]$. The intervals ${\mu }_{\mathcal{A}}\left(\mathfrak{x}\right)$ and ${\gamma }_{\mathcal{A}}\left(\mathfrak{x}\right)$ represent the degree of belongingness and non-belongingness of the element $\mathfrak{x}$ to the set $\mathcal{A}$, respectively, where ${\mu }_{\mathcal{A}}\left(\mathfrak{x}\right)=[{\mu }_{\mathcal{A}}^{\mathfrak{l}}\left(\mathfrak{x}\right),{\mu }_{\mathcal{A}}^{\mathfrak{u}}\left(\mathfrak{x}\right)]$ and ${\gamma }_{\mathcal{A}}\left(\mathfrak{x}\right)=[{\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left(\mathfrak{x}\right),{\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left(\mathfrak{x}\right)]$ for all $\mathfrak{x}\in \mathcal{X}$, subject to the condition

$$0\le {\mu }_{\mathcal{A}}^{\mathfrak{l}}\left(\mathfrak{x}\right)+{\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left(\mathfrak{x}\right)\le 1.$$

For convenience, we denote the IVIF set as $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$. Additionally, the complement of $\mathfrak{x}$ in $\mathcal{A}$ is represented by

$$\overline{{\mu }_{\mathcal{A}}}\left(\mathfrak{x}\right)=[1-{\mu }_{\mathcal{A}}^{\mathfrak{u}}\left(\mathfrak{x}\right),1-{\mu }_{\mathcal{A}}^{\mathfrak{l}}\left(\mathfrak{x}\right)]\mathit{and}\overline{{\gamma }_{\mathcal{A}}}\left(\mathfrak{x}\right)=[1-{\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left(\mathfrak{x}\right),1-{\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left(\mathfrak{x}\right)],$$

where $[\overline{{\mu }_{\mathcal{A}}}\left(\mathfrak{x}\right),\overline{{\gamma }_{\mathcal{A}}}\left(\mathfrak{x}\right)]$ denotes the complement of $\mathfrak{x}$ in $\mathcal{A}$.

3. IVIF Filters in Hoop Algebra

In this section, we systematically develop the theory of interval-valued intuitionistic fuzzy (IVIF) filters within hoop algebras. We first introduce the formal definitions and axiomatic conditions that characterize IVIF filters, and present algorithmic procedures for their verification. The section proceeds to establish fundamental properties and alternative criteria for IVIF filters, including their closure under intersection and their relationships with sub-hoops and classical fuzzy filters. Through detailed examples and proofs, we illustrate the construction and behavior of IVIF filters and their various subclasses, such as implicative IVIF filters. Additionally, we investigate the lattice-theoretic structure of IVIF filters, congruence relations induced by filter properties, and the connections between interval-valued fuzzy sets, sub-hoops, and generated filters. The results in this section provide a comprehensive framework for understanding and analyzing uncertainty propagation in hoop algebras under interval-valued intuitionistic fuzzy logic.

Definition 7. 

An IVIF set $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ in a hoop $\mathcal{H}$ is defined as an IVIF filter of $\mathcal{H}$ if the following conditions hold for any operation $\diamond \in \{\odot ,\to \}$:

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H})\left(\begin{array}{c}{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})\ge rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}\hfill \\ {\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})\le rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}\hfill \end{array}\right),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H})\left(\begin{array}{c}{\hslash }_{{\mathfrak{a}}_x}\le {\hslash }_{{\mathfrak{a}}_y}\Rightarrow \left\{\begin{array}{c}{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\le {\mu }_A\left({\hslash }_{{\mathfrak{a}}_y}\right)\hfill \\ {\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\ge {\gamma }_A\left({\hslash }_{{\mathfrak{a}}_y}\right)\hfill \end{array}\right.\hfill \end{array}\right).\hfill \end{array}$$

(10)

Now, we provide a pseudocode to determine whether a given IVIF set $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ in a hoop $\mathcal{H}$ fulfills the criteria to be an IVIF filter of $\mathcal{H}$.

Algorithm 1 systematically verifies whether a given pair of functions $({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ defines an IVIF filter on the hoop $\mathcal{H}$. The algorithm operates as follows:

• For every pair of elements ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$ and for each operation $\diamond \in \{\odot ,\to \}$, it checks the filter conditions:

  $${\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})\ge min\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\},{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})\le max\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}.$$
  If either condition fails for any pair or operation, the algorithm returns False.
• Additionally, for every pair ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$ such that ${\hslash }_{{\mathfrak{a}}_x}\le {\hslash }_{{\mathfrak{a}}_y}$, it verifies the monotonicity conditions:

  $${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\le {\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\ge {\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right).$$
  If either monotonicity condition fails, the algorithm returns False.

If all conditions are satisfied for all relevant elements and operations, the algorithm concludes that $({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ constitutes an IVIF filter of $\mathcal{H}$ and returns True. This procedure provides a rigorous and efficient means for confirming the IVIF filter property in the context of hoops.

Proposition 2. 

Let $(\mathcal{H},\odot ,\to ,1)$ be a hoop algebra. For every element ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$, the condition ${\hslash }_{{\mathfrak{a}}_x}\le 1$ holds.

Proof. 

By using the relation ${\le }_{\mathcal{H}}$ in (1) and Proposition 1$\left(a4\right)$, we conclude that the inequality ${\hslash }_{{\mathfrak{a}}_x}\le 1$ is satisfied for all elements ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$.    □

Algorithm 1: Verifying an IVIF filter in a hoop

This elementary ordering fact justifies repeated use of the unit element as a universal upper benchmark when deriving monotonicity constraints on interval membership and non-membership functions in later theorems.

Definition 8. 

An IVIF set $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ in $\mathcal{H}$ is called an IVIF sub-hoop of $\mathcal{H}$ if for any $\diamond \in \{\odot ,\to \}$

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H})\left(\begin{array}{c}{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})\ge rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}\hfill \\ {\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})\le rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}\hfill \end{array}\right).\hfill \end{array}$$

(11)

Proposition 3. 

For every IVIF sub-hoop $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ of $\mathcal{H}$, the following holds:

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}){\mu }_{\mathcal{A}}\left(1\right)\ge {\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left(1\right)\le {\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right).\hfill \end{array}$$

(12)

Proof. 

Since ${\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_x}=1$ for all ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$, the result follows directly from (12).    □

Example 1. 

Let $\mathcal{H}=\{0,1,2,3,4,5,6\}$ be a set with two binary operations, ⊙ and →, defined by the following Table 2 and Table 3.

Table 2. Cayley table of the binary operation →.

→	0	1	2	3	4	5	6
0	1	1	2	1	1	1	1
1	0	1	2	3	4	5	6
2	1	1	1	1	1	1	1
3	0	1	2	1	4	5	1
4	5	1	2	1	1	4	1
5	4	1	2	1	1	1	1
6	0	1	2	3	4	5	1

Table 3. Cayley table of the binary operation ⊙.

⊙	0	1	2	3	4	5	6
0	0	0	2	0	0	0	0
1	0	1	2	3	4	5	6
2	2	2	2	2	2	2	2
3	0	3	2	3	4	5	3
4	0	4	2	4	5	0	4
5	0	5	2	5	0	0	5
6	0	6	2	3	4	5	6

The binary operation → on $\mathcal{H}$ is given by the Cayley table below, where the entry in the i-th row and j-th column corresponds to the value of $x_i\to x_j$ for $x_i,x_j\in \mathcal{H}$.

Similarly, the binary operation ⊙ on $\mathcal{H}$ is defined by the following Cayley table, where the entry in the i-th row and j-th column is $x_i\odot x_j$.

Then $(\mathcal{H},\odot ,\to ,1)$ is a hoop algebra.

Let $\mathcal{A}=(\mathcal{H},{\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ in H be an IVIF set in $\mathcal{H}$ given by Table 4.

Table 4. Tabular representation of $\mathcal{A}=(\mathcal{H},{\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$.

$\mathcal{H}$	0	1	2	3	4	5	6
${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$	$[0.4,0.7]$	$[0.7,0.8]$	$[0.4,0.6]$	$[0.6,0.8]$	$[0.4,0.7]$	$[0.4,0.7]$	$[0.6,0.8]$
${\nu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$	$[0.2,0.3]$	$[0.1,0.2]$	$[0.2,0.3]$	$[0.1,0.2]$	$[0.2,0.3]$	$[0.2,0.3]$	$[0.1,0.2]$

Table 4 presents the IVIF set $\mathcal{A}$ on $\mathcal{H}$. For each $x\in \mathcal{H}$, the table lists the corresponding interval-valued membership degree ${\mu }_{\mathcal{A}}\left(x\right)$ and non-membership degree ${\gamma }_{\mathcal{A}}$. Each entry is an interval in $[0,1]$, reflecting the degree of membership and non-membership of each element in the set $\mathcal{A}$.

Let $\mathcal{A}=(\mathcal{H},{\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ in H be an IVIF set in $\mathcal{H}$ given by Table 4.

Then it is easy to check that the IVIF set $\mathcal{A}=(\mathcal{H},{\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ in $\mathcal{H}$ is an IVIF filter of $\mathcal{H}$.

Theorem 1. 

An IVIF set $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$ if and only if it satisfies (12) and the following condition:

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H})\left(\begin{array}{c}{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\},\hfill \\ {\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le rmax\{{\gamma }_A\left(x\right),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}.\hfill \end{array}\right)\hfill \end{array}$$

(13)

Proof. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ be an IVIF filter of $\mathcal{H}$. Since ${\hslash }_{{\mathfrak{a}}_x}\le 1$ for all ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$, it follows from (10) that (12) is satisfied. For any ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$, we know that ${\hslash }_{{\mathfrak{a}}_x}\odot ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\le {\hslash }_{{\mathfrak{a}}_y}$. By using (9) and (10), we obtain the following:

$${\mu }_A\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge {\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}))\ge rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\},$$

and

$${\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le {\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}))\le rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_A({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\},$$

which proves (13).

Conversely, suppose that an IVIF set $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ satisfies both (12) and (13). Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$. Since

$${\hslash }_{{\mathfrak{a}}_x}\to ({\hslash }_{{\mathfrak{a}}_y}\to ({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}))=({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})\to ({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})=1\in \mathcal{H},$$

it follows from (12) and (13) that

$$\begin{array}{ccc}{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})& \ge & rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to ({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}))\}\hfill \\ & \ge & rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),min\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to ({\hslash }_{{\mathfrak{a}}_y}\to ({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})))\}\}\hfill \\ & \ge & rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),min\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}\left(1\right))\}\}\hfill \\ & \ge & rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\},\hfill \end{array}$$

and similarly,

$$\begin{array}{ccc}{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})& \le & rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to ({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}))\}\hfill \\ & \le & rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),max\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to ({\hslash }_{{\mathfrak{a}}_y}\to ({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})))\}\}\hfill \\ & \le & rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),max\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left(1\right))\}\}\hfill \\ & \le & rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}.\hfill \end{array}$$

Next, suppose that ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$ such that ${\hslash }_{{\mathfrak{a}}_x}\le {\hslash }_{{\mathfrak{a}}_y}$. Then ${\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}=1\in \mathcal{H}$, and we have

$${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}=rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}\left(1\right)\}={\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),$$

$${\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}=rmax\{{\gamma }_A\left(x\right),{\gamma }_{\mathcal{A}}\left(1\right)\}={\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right).$$

Thus, $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ satisfies the conditions to be an IVIF filter of $\mathcal{H}$.    □

The above theorem furnishes a residuation-style criterion for IVIF filters, reducing global closure requirements to a local implicational inequality. This facilitates both algorithmic verification (by testing pairs) and a logical reading: membership propagation mirrors modus ponens–like reasoning under interval uncertainty.

Theorem 2. 

Every IVIF filter is a sub-hoop of the IVIF.

Proof. 

This result is straightforward.    □

This embeds the fuzzy deductive layer into the underlying algebraic skeleton: any uncertainty-resilient deductive structure (IVIF filter) simultaneously preserves the binary operations. Hence, classification of IVIF filters can exploit sub-hoop invariants and structural decompositions.

The Converse of Theorem 2 may not be true as seen in the following example.

Example 2. 

Let $(\mathcal{H},\odot ,\to ,1)$ be Consider a Hoop algebra in Example 1. Let $A=(H,{\mu }_A,{\gamma }_A)$ in H be an IVIF set in H given by the Table 5:

Table 5. Tabular representation of $A=(H,{\mu }_A,{\gamma }_A)$.

H	0	1	2	3	4	5	6
${\mu }_A\left(x\right)$	$[0.6,0.7]$	$[0.7,0.8]$	$[0.4,0.6]$	$[0.6,0.8]$	$[0.4,0.7]$	$[0.4,0.7]$	$[0.6,0.8]$
${\nu }_A\left(x\right)$	$[0.2,0.3]$	$[0.1,0.2]$	$[0.2,0.3]$	$[0.1,0.2]$	$[0.2,0.3]$	$[0.2,0.3]$	$[0.1,0.2]$

Then the IVIF set $A=(H,{\mu }_A,{\gamma }_A)$ in H is an IVIF sub-hoop of H but it is not an IVIF filter of $\mathcal{H}$ since

$${\mu }_{\mathcal{A}}\left(4\right)=[0.4,0.7]\ngeqq [0.6,0.7]=[min\{0.6,0.7\},min\{0.7,0.8\}]$$

$$=rmin\left\{\right[0.6,0.7],[0.7,0.8\left]\right\}$$

$$=rmin\{{\mu }_{\mathcal{A}}\left(0\right),{\mu }_{\mathcal{A}}(0\to 4)\}$$

This counterexample delineates the strictness of the hierarchy “IVIF sub-hoop” vs. “IVIF filter” preventing overgeneralization and clarifying which closure axioms truly encode deductive propagation.

Definition 9. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ be an interval-valued intuitionistic fuzzy (IVIF) set in $\mathcal{H}$. We say that $\mathcal{A}$ is an intuitionistic fuzzy filter of $\mathcal{H}$ if, for all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$ and for every binary operation $\diamond \in \{\odot ,\to \}$, the following conditions are satisfied:

(i) 

${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\le {\mu }_{\mathcal{A}}\left(1\right)$ and ${\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\ge {\gamma }_{\mathcal{A}}\left(1\right)$,

(ii) 

${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge min\left\{{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\right\}$,

(iii) 

${\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le max\left\{{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\right\}$.

The following pseudocode determines whether a given IVIF set $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ on a hoop $\mathcal{H}$ fulfills the axiomatic conditions of an intuitionistic fuzzy filter of $\mathcal{H}$.

Algorithm 2 systematically checks whether a given pair of functions $({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ defines an intuitionistic fuzzy filter on the hoop $\mathcal{H}$. The procedure is as follows:

• For each element ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$, the algorithm first verifies the normalization conditions:

  $${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\le {\mu }_{\mathcal{A}}\left(1\right)\mathrm{and}{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\ge {\gamma }_{\mathcal{A}}\left(1\right).$$
  If either condition fails, the algorithm returns False.
• Then, for every pair ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$ and for each operation $\diamond \in \{\odot ,\to \}$, it checks the filter conditions:

  $${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge min\left\{{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\right\},{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le max\left\{{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\right\}.$$
  If either of these is not satisfied for any combination, the algorithm returns False.

Algorithm 2: Verifying an intuitionistic fuzzy filter in a hoop

If all conditions are met for all elements and operations, the algorithm concludes that $({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an intuitionistic fuzzy filter of $\mathcal{H}$ and returns True. This approach provides a precise and reliable method for verifying the intuitionistic fuzzy filter property in hoops.

Theorem 3. 

Let $\mathcal{A}=\left\{[{\mu }_{\mathcal{A}}^{\mathfrak{l}},{\mu }_{\mathcal{A}}^{\mathfrak{u}}],[{\gamma }_{\mathcal{A}}^{\mathfrak{l}},{\gamma }_{\mathcal{A}}^{\mathfrak{u}}]\right\}$ be an interval-valued intuitionistic fuzzy (IVIF) set in $\mathcal{H}$. Then, $\mathcal{A}$ is an IVIF filter of $\mathcal{H}$ if and only if each of ${\mu }_{\mathcal{A}}^{\mathfrak{l}}$, ${\mu }_{\mathcal{A}}^{\mathfrak{u}}$, ${\gamma }_{\mathcal{A}}^{\mathfrak{l}}$, and ${\gamma }_{\mathcal{A}}^{\mathfrak{u}}$ is an intuitionistic fuzzy filter of $\mathcal{H}$.

Proof. 

$(\Rightarrow :)$ Since ${\mu }_{\mathcal{A}}^{\mathfrak{l}}\left(1\right)\ge {\mu }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$, ${\mu }_{\mathcal{A}}^{\mathfrak{u}}\left(1\right)\ge {\mu }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$, ${\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left(1\right)\le {\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$ and ${\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left(1\right)\le {\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$, ${\mu }_A\left(1\right)\ge {\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$ and ${\gamma }_{\mathcal{A}}\left(1\right)\le {\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$.

Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$. Then for any $\diamond \in \{\odot ,\to \}$, we have

$$\begin{array}{ccc}{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)& =& [{\mu }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\mu }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_y}\right)]\hfill \\ & \ge & [min\{{\mu }_{\mathcal{A}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\},min\{{\mu }_{\mathcal{A}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}]\hfill \\ & =& rmin\{[{\mu }_{\mathcal{A}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})],[{\mu }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_A^u\left(x\right)]\}\hfill \\ & =& rmin\{{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_A{\hslash }_{{\mathfrak{a}}_x})\},\hfill \end{array}$$

and

$$\begin{array}{ccc}{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)& =& [{\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_y}\right)]\hfill \\ & \le & [max\left\{{\gamma }_{\mathcal{A}}^{\mathfrak{l}}\right(x\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\},max\{{\gamma }_{\mathcal{A}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}]\hfill \\ & =& rmax\{[{\gamma }_{\mathcal{A}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})],[{\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)]\}\hfill \\ & =& rmax\{{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}.\hfill \end{array}$$

Hence, $\mathcal{A}=\{[{\mu }_{\mathcal{A}}^{\mathfrak{l}},{\mu }_{\mathcal{A}}^{\mathfrak{u}}],[{\gamma }_{\mathcal{A}}^{\mathfrak{l}},{\gamma }_{\mathcal{A}}^{\mathfrak{u}}]\}$ is an IVIF filter of H.

$(\Leftarrow :)$ Conversely, assume that $\mathcal{A}=\{[{\mu }_{\mathcal{A}}^{\mathfrak{l}},{\mu }_{\mathcal{A}}^{\mathfrak{u}}],[{\gamma }_{\mathcal{A}}^{\mathfrak{l}},{\gamma }_{\mathcal{A}}^{\mathfrak{u}}]\}$ is an IVIF filter of $\mathcal{H}$. Let ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$. Then, $[{\mu }_{\mathcal{A}}^{\mathfrak{l}}\left(1\right),{\mu }_{\mathcal{A}}^{\mathfrak{u}}\left(1\right)]={\mu }_A\left(1\right)\ge {\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)=[{\mu }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)]$; hence, ${\mu }_{\mathcal{A}}^{\mathfrak{l}}\left(1\right)\ge {\mu }_{\mathcal{A}}^{\mathfrak{l}}\left(x\right)$ and ${\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left(1\right)\le {\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left(x\right)$. Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$. Then

$$\begin{array}{ccc}[{\mu }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\mu }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_y}\right)]& =& {\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\hfill \\ & \ge & rmin\{{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}\hfill \\ & =& rmin\{[{\mu }_{\mathcal{A}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})],[{\mu }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\mu }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_y}\right)]\}\hfill \\ & =& [min\{{\mu }_{\mathcal{A}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\},min\{{\mu }_{\mathcal{A}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}].\hfill \end{array}$$

Hence, ${\mu }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge min\{{\mu }_{\mathcal{A}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}$ and ${\mu }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge min\{{\mu }_{\mathcal{A}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}$. Also

$$\begin{array}{ccc}[{\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_y}\right)]& =& {\gamma }_A\left(y\right)\hfill \\ & \le & rmax\{{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}\hfill \\ & =& rmax\{[{\gamma }_{\mathcal{A}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})],[{\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)]\}\hfill \\ & =& [max\{{\gamma }_{\mathcal{A}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\},max\{{\gamma }_{\mathcal{A}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}].\hfill \end{array}$$

Then we have ${\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le max\{{\gamma }_{\mathcal{A}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}$ and ${\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le max\{{\gamma }_{\mathcal{A}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}.$ Therefore, ${\mu }_{\mathcal{A}}^{\mathfrak{l}},{\mu }_{\mathcal{A}}^{\mathfrak{u}},{\gamma }_{\mathcal{A}}^{\mathfrak{l}}$ and ${\gamma }_{\mathcal{A}}^{\mathfrak{u}}$ are fuzzy filters of $\mathcal{H}$.    □

By reducing the interval-valued intuitionistic constraints to four scalar fuzzy filters, this result enables modular verification and translation of existing fuzzy filter theory into the IVIF framework, improving both implementability and reuse of classical results.

Definition 10. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ and $\mathcal{B}=({\mu }_{\mathcal{B}},{\gamma }_{\mathcal{B}})$ be two IVIF filters of $\mathcal{H}$. The union of these filters, denoted as $\mathcal{A}\cup \mathcal{B}$, is defined by:

$${\mu }_{\mathcal{A}\cup \mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)=max\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\},{\gamma }_{\mathcal{A}\cup \mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)=min\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}$$

for all ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$.

Similarly, the intersection of the filters, denoted as $\mathcal{A}\cap \mathcal{B}$, is defined by

$${\mu }_{\mathcal{A}\cap \mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)=min\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\},{\gamma }_{\mathcal{A}\cap \mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)=max\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}$$

for all ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$.

Proposition 4. 

If $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ and $\mathcal{B}=({\mu }_{\mathcal{B}},{\gamma }_{\mathcal{B}})$ are IVIF filters of $\mathcal{H}$, then $\mathcal{A}\cap \mathcal{B}$ is an IVIF filter of $\mathcal{H}$.

Proof. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ and $\mathcal{B}=({\mu }_{\mathcal{B}},{\gamma }_{\mathcal{B}})$ be IVIF filters of $\mathcal{H}$.

Let ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$. Then we have

$$\begin{array}{ccc}{\mu }_{\mathcal{A}\cap \mathcal{B}}\left(1\right)& =& [{\mu }_{\mathcal{A}\cap \mathcal{B}}^l\left(1\right),{\mu }_{\mathcal{A}\cap \mathcal{B}}^u\left(1\right)]\hfill \\ & =& [min\{{\mu }_{\mathcal{A}}^{\mathfrak{l}}\left(1\right),{\mu }_{\mathcal{B}}^{\mathfrak{l}}\left(1\right)\},min\{{\mu }_{\mathcal{A}}^{\mathfrak{u}}\left(1\right),{\mu }_{\mathcal{B}}^{\mathfrak{u}}\left(1\right)\}]\hfill \\ & \ge & [min\{{\mu }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{B}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\},min\{{\mu }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{B}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}]\hfill \\ & =& [{\mu }_{\mathcal{A}\cap B}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}\cap \mathcal{B}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)]\hfill \\ & =& {\mu }_{\mathcal{A}\cap \mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}{\gamma }_{\mathcal{A}\cup \mathcal{B}}\left(1\right)& =& [{\gamma }_{\mathcal{A}\cup \mathcal{B}}^l\left(1\right),{\gamma }_{\mathcal{A}\cup \mathcal{B}}^{\mathfrak{u}}\left(1\right)]\hfill \\ & =& [max\{{\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left(1\right),{\gamma }_{\mathcal{B}}^{\mathfrak{l}}\left(1\right)\},max\{{\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left(1\right),{\gamma }_{\mathcal{B}}^u\left(1\right)\}]\hfill \\ & \le & [max\{{\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{B}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\},max\{{\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{B}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}]\hfill \\ & =& [{\gamma }_{\mathcal{A}\cup \mathcal{B}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}\cup \mathcal{B}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)]\hfill \\ & =& {\gamma }_{\mathcal{A}\cup \mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right).\hfill \end{array}$$

Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$. Then we get

$$\begin{array}{ccc}{\mu }_{\mathcal{A}\cap \mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_y}\right)& =& [{\mu }_{\mathcal{A}\cap \mathcal{B}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\mu }_{\mathcal{A}\cap \mathcal{B}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_y}\right)]\hfill \\ & =& [min\{{\mu }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\mu }_{\mathcal{B}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\},min\{{\mu }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\mu }_{\mathcal{B}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}]\hfill \\ & \ge & \left[min\{min\{{\mu }_{\mathcal{A}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\},min\{{\mu }_{\mathcal{B}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{B}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}\},\right.\hfill \\ & & \left.min\{min\{{\mu }_{\mathcal{A}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\},min\{{\mu }_{\mathcal{B}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{B}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}\}\right]\hfill \\ & =& \left[min\{min\{{\mu }_{\mathcal{A}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{B}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})\},min\{{\mu }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{B}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}\},\right.\hfill \\ & & \left.min\{min\{{\mu }_{\mathcal{A}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{B}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})\},min\{{\mu }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{B}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}\}\right]\hfill \\ & =& [min\{{\mu }_{\mathcal{A}\cap \mathcal{B}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}\cap \mathcal{B}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\},min\{{\mu }_{\mathcal{A}\cap \mathcal{B}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}\cap \mathcal{B}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}]\hfill \\ & =& rmin\{{\mu }_{\mathcal{A}\cap \mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}\cap \mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\},\hfill \end{array}$$

and

$$\begin{array}{ccc}{\gamma }_{\mathcal{A}\cup \mathcal{B}}{\left({\hslash }_{{\mathfrak{a}}_y}\right)}^{\mathfrak{l}}& =& [{\gamma }_{\mathcal{A}\cup \mathcal{B}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\gamma }_{\mathcal{A}\cup \mathcal{B}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_y}\right)]\hfill \\ & =& [max\{{\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\gamma }_{\mathcal{B}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\},max\{{\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\gamma }_{\mathcal{B}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}]\hfill \\ & \le & \left[max\{min\{{\gamma }_{\mathcal{A}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\},min\{{\gamma }_{\mathcal{B}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{B}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}\},\right.\hfill \\ & & \left.max\{min\{{\gamma }_{\mathcal{A}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\},min\{{\gamma }_{\mathcal{B}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{B}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}\}]\right]\hfill \\ & =& \left[max\{min\{{\gamma }_{\mathcal{A}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{B}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})\},min\{{\gamma }_{\mathcal{A}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{B}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}\}\right.,\hfill \\ & & \left.max\{min\{{\gamma }_{\mathcal{A}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{B}}^{\mathfrak{u}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})\},min\{{\gamma }_{\mathcal{A}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{B}}^{\mathfrak{u}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}\}\right]\hfill \\ & =& [max\{{\gamma }_{\mathcal{A}\cap \mathcal{B}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}\cap \mathcal{B}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\},max\{{\gamma }_{\mathcal{A}\cap \mathcal{B}}^{\mathfrak{l}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}\cap \mathcal{B}}^{\mathfrak{l}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}]\hfill \\ & =& rmax\{{\gamma }_{\mathcal{A}\cap \mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}\cap \mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}.\hfill \end{array}$$

Hence $\mathcal{A}\cap \mathcal{B}$ is an IVIF filter of $\mathcal{H}$.    □

Closure under intersection shows that the IVIF filters form a complete meet-semilattice, allowing construction of the least filter containing a given family—essential for generated filters and lattice-theoretic semantics.

In contrast, the union of two IVIFFs need not be an IVIFF in general. This is because the union operation, which uses the maximum for the membership function and the minimum for the non-membership function, may fail to preserve the required filter conditions. In particular, the following filter condition may fail for the union:

$${\mu }_{\mathcal{A}\cup \mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge min\{{\mu }_{\mathcal{A}\cup \mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}\cup \mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}$$

for some ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$ and $\diamond \in \{\odot ,\to \}$.

To illustrate an counterexample, consider two IVIFFs $\mathcal{A}$ and $\mathcal{B}$ on $\mathcal{H}$ such that for some ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$,

$${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)<{\mu }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)>{\mu }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})<{\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}).$$

Then,

$${\mu }_{\mathcal{A}\cup \mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)={\mu }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}\cup \mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_y}\right)={\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\mu }_{\mathcal{A}\cup \mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})={\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}).$$

It is possible that

$${\mu }_{\mathcal{A}\cup \mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_y}\right)<min\{{\mu }_{\mathcal{A}\cup \mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}\cup \mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\},$$

thus violating the filter condition.

Therefore, the set of all IVIFFs on $\mathcal{H}$ is closed under intersection but not necessarily under union. This set forms a complete meet-semilattice, but not a lattice, with respect to the pointwise-defined intersection operation.

Corollary 1. 

If $\mathcal{A}=\{⟨{\hslash }_{{\mathfrak{a}}_x},{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)⟩:{\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}\}$ is an IVIF filter of $\mathcal{H}$, then $\overline{\mathcal{A}}$ is also an IVIF filter of $\mathcal{H}$.

Complement stability provides a dualization principle, ensuring that reasoning about acceptance (membership) and rejection (non-membership) can be symmetrically interchanged without loss of algebraic fidelity.

Theorem 4. 

If $\mathcal{A}=\{⟨{\hslash }_{{\mathfrak{a}}_x},{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)⟩:{\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}\}$ is an IVIF filter of $\mathcal{H}$, then both $\oplus \mathcal{A}$ and $\otimes \mathcal{A}$ are IVIF filters.

Proof. 

Assume that $\mathcal{A}=\{⟨{\hslash }_{{\mathfrak{a}}_x},{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)⟩:{\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}\}$ is an IVIF filter of $\mathcal{H}$. Let ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$. Then $\overline{{\mu }_{\mathcal{A}}}\left(1\right)=1-{\mu }_{\mathcal{A}}\left(1\right)\le 1-{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\le \overline{{\mu }_{\mathcal{A}}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$.

Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$. Then

$$\begin{array}{ccc}\overline{{\mu }_{\mathcal{A}}}\left({\hslash }_{{\mathfrak{a}}_y}\right)& =& 1-{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\hfill \\ & \le & 1-rmin\{{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}\hfill \\ & =& rmax\{1-{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),1-{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}\hfill \\ & =& rmax\{\overline{{\mu }_{\mathcal{A}}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),\overline{{\mu }_{\mathcal{A}}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}.\hfill \end{array}$$

Hence $\oplus A$ is an IVIF filter of $\mathcal{H}$.

Let $x\in H$. Then $\overline{{\gamma }_{\mathcal{A}}}\left(1\right)=1-{\gamma }_{\mathcal{A}}\left(1\right)\ge 1-{\gamma }_A\left({\hslash }_{{\mathfrak{a}}_x}\right)\ge \overline{{\gamma }_{\mathcal{A}}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$. Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$. Then

$$\begin{array}{ccc}\overline{{\gamma }_A}\left({\hslash }_{{\mathfrak{a}}_y}\right)& =& 1-{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\hfill \\ & \ge & 1-rmax\{{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}\hfill \\ & =& rmin\{1-{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),1-{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}\hfill \\ & =& rmin\{\overline{{\gamma }_{\mathcal{A}}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),\overline{{\gamma }_{\mathcal{A}}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}.\hfill \end{array}$$

Hence $\otimes \mathcal{A}$ is an IVIF filter of $\mathcal{H}$.    □

These operations formalize two dual uncertainty transformations—attenuation vs. reinforcement—while preserving filterhood. They model controlled revisions of evidence intervals in dynamic inference settings.

Theorem 5. 

An IVIF set $\mathcal{A}=\{⟨{\hslash }_{{\mathfrak{a}}_x},{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)⟩:{\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}\}$ is an IVIF filter of $\mathcal{H}$ if and only if, for every $[{\mathfrak{m}}_1,{\mathfrak{n}}_1],[{\mathfrak{m}}_2,{\mathfrak{n}}_2]\in \mathcal{D}[0,1]$, the sets $\mathcal{U}({\mu }_A,[{\mathfrak{m}}_2,{\mathfrak{n}}_2])$ and $\mathcal{L}({\gamma }_{\mathcal{A}},[{\mathfrak{m}}_1,{\mathfrak{n}}_1])$ are either empty or filters of $\mathcal{H}$.

Proof. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ be an IVIF filter of $\mathcal{H}$, and suppose $[{\mathfrak{m}}_1,{\mathfrak{n}}_1],[{\mathfrak{m}}_2,{\mathfrak{n}}_2]\in \mathcal{D}[0,1]$ are such that $\mathcal{U}({\mu }_A,[{\mathfrak{m}}_2,{\mathfrak{n}}_2])$ and $\mathcal{L}({\gamma }_A,[{\mathfrak{m}}_1,{\mathfrak{n}}_1])$ are non-empty sets of H. Then, $1\in \mathcal{U}({\mu }_{\mathcal{A}},[{\mathfrak{m}}_2,{\mathfrak{n}}_2])\cap \mathcal{L}({\gamma }_{\mathcal{A}},[{\mathfrak{m}}_1,{\mathfrak{n}}_1])$, since ${\mu }_{\mathcal{A}}\left(1\right)\ge [{\mathfrak{m}}_2,{\mathfrak{n}}_2]$ and ${\gamma }_{\mathcal{A}}\left(1\right)\le [{\mathfrak{m}}_1,{\mathfrak{n}}_1]$.

Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$ such that ${\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_x}\in \mathcal{U}({\mu }_{\mathcal{A}},[{\mathfrak{m}}_2,{\mathfrak{n}}_2])$. Then, we have ${\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})\ge [{\mathfrak{m}}_2,{\mathfrak{n}}_2]$ and ${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\ge [{\mathfrak{m}}_2,{\mathfrak{n}}_2]$. Hence, ${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge min\{{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}\ge [{\mathfrak{m}}_2,{\mathfrak{n}}_2]$, which implies ${\hslash }_{{\mathfrak{a}}_y}\in \mathcal{U}({\mu }_{\mathcal{A}},[{\mathfrak{m}}_2,{\mathfrak{n}}_2])$. Therefore, $\mathcal{U}({\mu }_{\mathcal{A}},[{\mathfrak{m}}_2,{\mathfrak{n}}_2])$ is a filter of $\mathcal{H}$.

Now, let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$ and ${\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_x}\in \mathcal{L}({\gamma }_{\mathcal{A}},[{\mathfrak{m}}_1,{\mathfrak{n}}_1])$. Then, ${\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})\le [{\mathfrak{m}}_1,{\mathfrak{n}}_1]$ and ${\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\le [{\mathfrak{m}}_1,{\mathfrak{n}}_1]$. Thus, ${\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le max\{{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}\le [{\mathfrak{m}}_1,{\mathfrak{n}}_1]$, so ${\hslash }_{{\mathfrak{a}}_y}\in \mathcal{L}({\gamma }_{\mathcal{A}},[{\mathfrak{m}}_1,{\mathfrak{n}}_1])$. Consequently, $\mathcal{L}({\gamma }_{\mathcal{A}},[{\mathfrak{m}}_1,{\mathfrak{n}}_1])$ is a filter of $\mathcal{H}$.

Next, assume that every non-empty set $\mathcal{U}({\mu }_{\mathcal{A}},[{\mathfrak{m}}_2,{\mathfrak{n}}_2])$ and $\mathcal{L}({\gamma }_{\mathcal{A}},[{\mathfrak{m}}_1,{\mathfrak{n}}_1])$ are filters of $\mathcal{H}$. If ${\mu }_{\mathcal{A}}\left(1\right)\ge {\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$ does not hold for all ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$, then there exists ${\mathfrak{x}}_0\in \mathcal{H}$ such that ${\mu }_{\mathcal{A}}\left(1\right)<{\mu }_{\mathcal{A}}\left({\mathfrak{x}}_0\right)$. In this case, take $[{\mathfrak{m}}_1,{\mathfrak{n}}_1]={\displaystyle \frac{1}{2}}({\mu }_{\mathcal{A}}\left(1\right)+{\mu }_{\mathcal{A}}\left({\mathfrak{x}}_0\right))$. Then, ${\mathfrak{x}}_0\in \mathcal{U}({\mu }_{\mathcal{A}},[{\mathfrak{m}}_1,{\mathfrak{n}}_1])$, which means $\mathcal{U}({\mu }_{\mathcal{A}},[{\mathfrak{m}}_1,{\mathfrak{n}}_1])\ne \varnothing$. Since $\mathcal{U}({\mu }_{\mathcal{A}},[{\mathfrak{m}}_1,{\mathfrak{n}}_1])$ is a filter of $\mathcal{H}$, we must have ${\mu }_{\mathcal{A}}\left(1\right)\ge [{\mathfrak{m}}_1,{\mathfrak{n}}_1]$, a contradiction. Therefore, ${\mu }_{\mathcal{A}}\left(1\right)\ge {\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$ for all ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$.

If ${\gamma }_{\mathcal{A}}\left(1\right)\le {\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$ is not true, then there exists ${\mathfrak{y}}_0\in \mathcal{H}$ such that ${\gamma }_{\mathcal{A}}\left(1\right)<{\gamma }_{\mathcal{A}}\left({\mathfrak{y}}_0\right)$. In this case, take $[{\mathfrak{m}}_1^{\prime },{\mathfrak{n}}_1^{\prime }]={\displaystyle \frac{1}{2}}({\gamma }_{\mathcal{A}}\left(1\right)+{\gamma }_{\mathcal{A}}\left({\mathfrak{y}}_0\right))$. Then, ${\mathfrak{y}}_0\in \mathcal{L}({\gamma }_{\mathcal{A}},[s_1^{\prime },s_2^{\prime }])$, meaning $\mathcal{L}({\gamma }_{\mathcal{A}},[{\mathfrak{m}}_1^{\prime },{\mathfrak{n}}_1^{\prime }])\ne \varnothing$. Since $\mathcal{L}({\gamma }_{\mathcal{A}},[{\mathfrak{m}}_1^{\prime },{\mathfrak{n}}_1^{\prime }])$ is a filter of $\mathcal{H}$, it must hold that ${\gamma }_{\mathcal{A}}\left(1\right)\le [{\mathfrak{m}}_1^{\prime },{\mathfrak{n}}_1^{\prime }]$, which leads to a contradiction. Hence, ${\gamma }_{\mathcal{A}}\left(1\right)\le {\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$ for all ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$.

Now, assume that ${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge rmin\{{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}$ is not true for all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$. Then there exist $\mathfrak{u},\mathfrak{v}\in \mathcal{H}$ such that ${\mu }_{\mathcal{A}}\left(\mathfrak{v}\right)<rmin\{{\mu }_{\mathcal{A}}(\mathfrak{u}\diamond \mathfrak{v}),{\mu }_{\mathcal{A}}\left(\mathfrak{u}\right)\}$. Taking $[{\mathfrak{p}}_1^{\prime },{\mathfrak{p}}_2^{\prime }]={\displaystyle \frac{1}{2}}({\mu }_{\mathcal{A}}\left(\mathfrak{v}\right)+rmin\{{\mu }_{\mathcal{A}}(\mathfrak{u}\diamond \mathfrak{v}),{\mu }_{\mathcal{A}}\left(\mathfrak{u}\right)\})$, we have ${\mu }_{\mathcal{A}}\left(\mathfrak{v}\right)<[{\mathfrak{p}}_1^{\prime },{\mathfrak{p}}_2^{\prime }]<rmin\{{\mu }_{\mathcal{A}}(\mathfrak{u}\diamond \mathfrak{v}),{\mu }_{\mathcal{A}}\left(\mathfrak{u}\right)\}$, which shows that $\mathfrak{u}\diamond \mathfrak{v},\mathfrak{u}\in \mathcal{U}({\mu }_{\mathcal{A}},[{\mathfrak{p}}_1^{\prime },{\mathfrak{p}}_2^{\prime }])$. Since $\mathcal{U}({\mu }_{\mathcal{A}},[{\mathfrak{p}}_1^{\prime },{\mathfrak{p}}_2^{\prime }])$ is a filter of $\mathcal{H}$, we obtain $\mathfrak{v}\in \mathcal{U}({\mu }_{\mathcal{A}},[{\mathfrak{p}}_1^{\prime },{\mathfrak{p}}_2^{\prime }])$, a contradiction. Thus, ${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge rmin\{{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_A\left({\hslash }_{{\mathfrak{a}}_x}\right)\}$ for all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$.

Finally, suppose that ${\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le rmax\{{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}$ is not true for all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$. Then there exist $\mathfrak{u},\mathfrak{v}\in \mathcal{H}$ such that ${\gamma }_{\mathcal{A}}\left(\mathfrak{v}\right)>rmax\{{\gamma }_{\mathcal{A}}(\mathfrak{u}\diamond \mathfrak{v}),{\gamma }_{\mathcal{A}}\left(\mathfrak{u}\right)\}$. Taking $[{\mathfrak{p}}_1^{″},{\mathfrak{p}}_2^{″}]={\displaystyle \frac{1}{2}}({\gamma }_{\mathcal{A}}\left(\mathfrak{v}\right)+rmax\{{\gamma }_{\mathcal{A}}(\mathfrak{u}\diamond \mathfrak{v}),{\gamma }_{\mathcal{A}}\left(\mathfrak{u}\right)\})$, we find ${\gamma }_{\mathcal{A}}\left(\mathfrak{v}\right)>[{\mathfrak{p}}_1^{″},{\mathfrak{p}}_2^{″}]>rmax\{{\gamma }_{\mathcal{A}}(\mathfrak{u}\diamond \mathfrak{v}),{\gamma }_{\mathcal{A}}\left(\mathfrak{u}\right)\}$, which shows that $\mathfrak{u}\diamond \mathfrak{v},\mathfrak{u}\in \mathcal{L}({\gamma }_{\mathcal{A}},[{\mathfrak{p}}_1^{″},{\mathfrak{p}}_2^{″}])$. Since $\mathcal{L}({\gamma }_{\mathcal{A}},[{\mathfrak{p}}_1^{″},{\mathfrak{p}}_2^{″}])$ is a filter of $\mathcal{H}$, we conclude $\mathfrak{v}\in L({\gamma }_{\mathcal{A}},[p_1^{\prime 0},p_2^{‴}])$, a contradiction. Therefore, ${\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le rmax\{{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}$ holds for all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$.

Hence, $\mathcal{A}=\{⟨{\hslash }_{{\mathfrak{a}}_x},{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)⟩:{\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}\}$ is an intuitionistic fuzzy filter of $\mathcal{H}$.    □

A cut-based criterion links the graded (interval-valued) semantics with classical crisp filters, enabling a bridge between quantitative uncertainty representations and qualitative logical abstraction; useful for threshold-driven decision systems.

Theorem 6. 

For any IVIF set $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$ if and only if it satisfies (12) and

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H})\left(\begin{array}{c}{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})=rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}\hfill \\ {\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})=rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}\hfill \end{array}\right).\hfill \end{array}$$

(14)

Proof. 

($\Rightarrow :$) Assume that $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$, and let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$.

Since ${\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}\le {\hslash }_{{\mathfrak{a}}_x}$ and ${\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}\le {\hslash }_{{\mathfrak{a}}_y}$, by the monotonicity property (10), we have

$${\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})\le {\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})\le {\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),$$

so

$${\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})\le min\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}.$$

Similarly,

$${\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})\ge {\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})\ge {\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),$$

and hence

$${\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})\ge max\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}.$$

Multiplying both sides by r (where $0<r\le 1$), we obtain

$${\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})\le rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\},$$

$${\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})\ge rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}.$$

On the other hand, since ${\hslash }_{{\mathfrak{a}}_x}\le {\hslash }_{{\mathfrak{a}}_y}\to ({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})$, by properties (13) and (10), we have

$${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\le {\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to ({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})).$$

By the filter property (12), we get

$${\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})\ge rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to ({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}))\}\ge rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}.$$

Similarly, for the non-membership function,

$${\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\ge {\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to ({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})),$$

and hence

$${\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})\le rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to ({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}))\}\le rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\}.$$

Combining the above inequalities, we deduce

$${\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})=rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\},$$

$${\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})=rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\},$$

which is exactly (14).

($\Leftarrow :$) Conversely, suppose that $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ satisfies (12) and (14). For any ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$, since ${\hslash }_{{\mathfrak{a}}_x}\odot ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\le {\hslash }_{{\mathfrak{a}}_y}$, by the monotonicity property (12), we have

$${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge {\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})).$$

By (14),

$${\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}))=rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}.$$

Thus,

$${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}.$$

Similarly,

$${\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le {\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}))=rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}.$$

Therefore, by Theorem 1, $\mathcal{A}$ is an IVIF filter of $\mathcal{H}$.    □

Replacing inequalities by equalities isolates “tight” IVIF filters where conjunctive aggregation is maximally information-preserving. This subclass is important for canonical representations and extremal model analysis.

Theorem 7. 

An IVIF set $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$ if and only if it satisfies (12) and

$$\begin{array}{c}\hfill (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H})\left(\begin{array}{c}{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})\ge rmin\{{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to z)\}\hfill \\ {\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})\le rmax\{{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\}\hfill \end{array}\right).\end{array}$$

(15)

Proof. 

Assume that $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$ and let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H}$. Since $({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\odot ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\le {\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z}$, we have

$${\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})\ge {\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\odot ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z}))=rmin\{{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\},$$

and

$${\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})\le {\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\odot ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z}))=rmax\{{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\},$$

by (10) and (14).

Conversely, suppose that $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ satisfies (12) and (15). If we set ${\hslash }_{{\mathfrak{a}}_x}=1$ in (15), we obtain (13). Therefore, $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$ by Theorem 1.    □

This theorem provides a practical criterion for identifying IVIF filters based on their behavior under implication operations. It simplifies the classification and analysis of filters, enhancing their applicability in modeling and reasoning with interval-valued intuitionistic fuzzy information.

Theorem 8. 

An IVIF set $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of H if and only if it satisfies (12) and

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H})\left(\begin{array}{c}{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\odot {\hslash }_{{\mathfrak{a}}_z})\ge rmin\{{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z}),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}\hfill \\ {\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\odot {\hslash }_{{\mathfrak{a}}_z})\le rmax\{{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z}),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}\hfill \end{array}\right).\hfill \end{array}$$

(16)

Proof. 

Assume that $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$ and let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H}$. Note that $({\hslash }_{{\mathfrak{a}}_z}\odot {\hslash }_{{\mathfrak{a}}_x})\odot ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})={\hslash }_{{\mathfrak{a}}_z}\odot ({\hslash }_{{\mathfrak{a}}_x}\odot ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}))\le {\hslash }_{{\mathfrak{a}}_z}\odot {\hslash }_{{\mathfrak{a}}_y}$. Using (10) and (14), we get

$${\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_z}\odot {\hslash }_{{\mathfrak{a}}_y})\ge {\mu }_{\mathcal{A}}\left(({\hslash }_{{\mathfrak{a}}_z}\odot {\hslash }_{{\mathfrak{a}}_x})({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\right)=rmin\{{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_z}\odot {\hslash }_{{\mathfrak{a}}_x}),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\},$$

and

$${\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_z}\odot {\hslash }_{{\mathfrak{a}}_y})\le {\gamma }_{\mathcal{A}}\left(({\hslash }_{{\mathfrak{a}}_z}\odot {\hslash }_{{\mathfrak{a}}_x})({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\right)=rmax\{{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_z}\odot {\hslash }_{{\mathfrak{a}}_x}),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}.$$

Conversely, suppose that $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ satisfies (12) and (16). If we take ${\hslash }_{{\mathfrak{a}}_z}=1$ in (16), we obtain (13). Therefore, $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$ by Theorem 1.    □

This theorem offers an alternative criterion for characterizing IVIF filters using both the product and implication operations, making filter identification more systematic. It thus aids in the efficient analysis and application of IVIF filters in fuzzy modeling and reasoning contexts.

Theorem 9. 

An IVIF set $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of H if and only if it satisfies

$$\begin{array}{c}\hfill (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H})\left(\begin{array}{c}{\hslash }_{{\mathfrak{a}}_x}\le {\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z}\Rightarrow \left\{\begin{array}{c}{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_z}\right)\ge rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}\hfill \\ {\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_z}\right)\le rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}\hfill \end{array}\right.\hfill \end{array}\right).\end{array}$$

(17)

Proof. 

Assume that $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$ and let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H}$ be such that ${\hslash }_{{\mathfrak{a}}_x}\le {\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z}$. Then ${\hslash }_{{\mathfrak{a}}_x}\to ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})=1$, and so

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})& \ge rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z}))\}=rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}\left(1\right)\}={\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),\hfill \\ \hfill {\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})& \le rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z}))\}=rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left(1\right)\}={\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right).\hfill \end{array}\end{array}$$

(18)

It follows that

$${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_z}\right)\ge rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\}\ge rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\},$$

and

$${\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_z}\right)\le rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\}\le rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}.$$

Conversely, suppose that $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ satisfies (12) and (17). Since ${\hslash }_{{\mathfrak{a}}_x}\le ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_y}$ for all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$, it follows from (17) that

$${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\},{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}.$$

Hence, $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$ by Theorem 1.    □

This theorem presents a useful order-based criterion for IVIF filter characterization, linking the structure of the set to its membership and non-membership functions. It streamlines the process of identifying filters, supporting more effective modeling and reasoning in interval-valued intuitionistic fuzzy environments.

Theorem 10. 

An IVIF set $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$ if and only if it satisfies (12) and

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H})\left(\begin{array}{c}{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})\ge rmin\{{\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_z}),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}\hfill \\ {\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})\le rmax\{{\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_z}),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}\hfill \end{array}\right).\hfill \end{array}$$

(19)

Proof. 

Suppose that $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$. Since $({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_z}\le {\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z}$ and ${\hslash }_{{\mathfrak{a}}_y}\odot (({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_z})\le {\hslash }_{{\mathfrak{a}}_y}\odot ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\le {\hslash }_{{\mathfrak{a}}_z}\le {\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z}$ for all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H}$, we have

$$\begin{array}{ccc}{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})& \ge & {\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_z}\right)\hfill \\ & \ge & {\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\odot ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z}))\hfill \\ & =& rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\}\hfill \\ & \ge & rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_z})\},\hfill \end{array}$$

and

$$\begin{array}{ccc}{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})& \le & {\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_z}\right)\hfill \\ & \le & {\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\odot ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z}))\hfill \\ & =& rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\}\hfill \\ & \le & rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right),{\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_z})\}.\hfill \end{array}$$

Conversely, assume that $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ satisfies (12) and (19). If we take ${\hslash }_{{\mathfrak{a}}_x}=1$ in (19), we obtain (13). Therefore, $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$ by Theorem 1.    □

The above theorem provides another implication-based criterion for identifying IVIF filters, focusing on the relationships between nested implications and membership functions. It further simplifies the recognition and analysis of filters in interval-valued intuitionistic fuzzy frameworks.

Definition 11. 

An IVIF set $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is called an implicative IVIF filter of $\mathcal{H}$ if it satisfies the condition (12) and

$$\begin{array}{c}\hfill (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H})\left(\begin{array}{c}{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to (({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to {\hslash }_{{\mathfrak{a}}_y}))\}\hfill \\ {\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to (({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to {\hslash }_{{\mathfrak{a}}_y}))\}\hfill \end{array}\right).\end{array}$$

(20)

This definition introduces the concept of an implicative IVIF filter, characterized by a specific implication-based condition involving three elements. It establishes a framework for studying more specialized filter structures in interval-valued intuitionistic fuzzy sets.

Now, we give a psudecode for above definition as follows:

Algorithm 3 provides a step-by-step procedure to verify if a given IVIF set $({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an implicative IVIF filter of the hoop $\mathcal{H}$. The verification process is as follows:

• For every triple ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H}$, the algorithm computes the element $\mathrm{temp}={\hslash }_{{\mathfrak{a}}_x}\to (({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to {\hslash }_{{\mathfrak{a}}_y})$ and checks the following conditions:

  $${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge min\left\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}\left(\mathrm{temp}\right)\right\},{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le max\left\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left(\mathrm{temp}\right)\right\}.$$
  If either condition fails for any triple, the algorithm returns False.
• After checking the above, the algorithm verifies that Condition (12) (as referenced in the definition) is also satisfied. If not, it returns False.

Algorithm 3: Verifying an implicative IVIF filter in a hoop

If all these conditions are met, the algorithm concludes that $({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an implicative IVIF filter of $\mathcal{H}$ and returns True. This approach ensures rigorous verification of the implicative property for IVIF filters in hoops.

Example 3. 

Let $\mathcal{H}=\{0,1,2,3,4,5\}$ be a set with the binary operations ⊙ and → defined as follows.

The binary operation → on $\mathcal{H}$ is specified by the Cayley Table 6 below. In this table, the entry in the i-th row and j-th column gives the result of $x_i\to x_j$, where $x_i,x_j\in \mathcal{H}$.

Table 6. Cayley table of the binary operation →.

→	0	1	2	3	4	5
0	1	1	1	4	4	5
1	0	1	2	3	4	5
2	0	1	1	3	4	5
3	1	1	1	1	1	5
4	0	1	1	0	1	5
5	1	1	1	1	1	1

Similarly, the binary operation $\mathsf{\odot }$ on $\mathcal{H}$ is defined by the following Cayley Table 7. Each entry in the i-th row and j-th column represents the value $x_i\odot x_j$.

Table 7. Cayley table of the binary operation ⊙.

⊙	0	1	2	3	4	5
0	0	0	0	3	3	5
1	0	1	2	3	4	5
2	0	2	2	3	4	5
3	3	3	3	3	3	5
4	3	4	4	3	4	5
5	5	5	5	5	5	5

Then $(\mathcal{H},\odot ,\to ,1)$ is a hoop algebra.

Table 8 presents the IVIF set $\mathcal{A}$ on $\mathcal{H}$. For each $x\in \mathcal{H}$, the table lists the interval-valued membership degree ${\mu }_{\mathcal{A}}\left(x\right)$ and non-membership degree ${\gamma }_{\mathcal{A}}$. These intervals indicate the degree to which each element belongs or does not belong to the set $\mathcal{A}$.

Table 8. Tabular representation of $\mathcal{A}=(\mathcal{H},{\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$.

$\mathcal{H}$	0	1	2	3	4	5
${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$	$[0.6,0.7]$	$[0.6,0.7]$	$[0.6,0.7]$	$[0.6,0.7]$	$[0.6,0.7]$	$[0.5,0.6]$
${\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$	$[0.1,0.2]$	$[0.1,0.2]$	$[0.1,0.2]$	$[0.1,0.2]$	$[0.1,0.2]$	$[0.2,0.3]$

It is easy to check that the IVIF set $\mathcal{A}=(\mathcal{H},{\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ in $\mathcal{H}$ is an implicative IVIF filter of $\mathcal{H}$.

Theorem 11. 

Every implicative IVIF filter is an IVIF filter.

Proof. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ be an implicative IVIF filter of $\mathcal{H}$. If we take ${\hslash }_{{\mathfrak{a}}_z}=1$ in (20) and use Proposition 1$\left(a5\right)$, then we obtain (13). Therefore, $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$ by Theorem 1.  □

This theorem shows that every implicative IVIF filter automatically satisfies the conditions of an IVIF filter. Thus, the class of implicative IVIF filters forms a subclass within the broader family of IVIF filters.

The converse of Theorem 11 may not be true as seen in the following example.

Example 4. 

Consider the IVIF filter $\mathcal{A}=(\mathcal{H},{\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ of the hoop algebra $(\mathcal{H},\odot ,\to ,1)$ given in Example 1. We now show, by explicit calculation, that $\mathcal{A}$ is not an implicative IVIF filter of $\mathcal{H}$.

Recall from Table 4 the values:

$${\mu }_{\mathcal{A}}\left(4\right)=[0.4,0.7],{\gamma }_{\mathcal{A}}\left(4\right)=[0.2,0.3]$$

and

$${\mu }_{\mathcal{A}}\left(3\right)=[0.6,0.8],{\gamma }_{\mathcal{A}}\left(3\right)=[0.1,0.2]$$

Let us compute ${\mu }_{\mathcal{A}}(3\to ((4\to 0)\to 4))$ and ${\gamma }_{\mathcal{A}}(3\to ((4\to 0)\to 4))$ step by step using Table 2. First, we determine the value of $4\to 0$ by referring to the entry in the row corresponding to 4 and the column corresponding to 0; according to the table, this yields $4\to 0=5$. Next, we evaluate $(4\to 0)\to 4$, which is equivalent to $5\to 4$. Consulting Table 2, we find that the entry in row 5 and column 4 gives $5\to 4=1$. Finally, we compute $3\to (5\to 4)$, which reduces to $3\to 1$. Again, referencing Table 2, the entry in row 3 and column 1 is $3\to 1=1$. Thus, we attain the following:

$$3\to \left(\right(4\to 0)\to 4)=3\to 1=1.$$

Now, from Table 4, we obtain

$${\mu }_{\mathcal{A}}\left(1\right)=[0.7,0.8],{\gamma }_{\mathcal{A}}\left(1\right)=[0.1,0.2]$$

Now,

$$\begin{array}{cc}\hfill {\mu }_{\mathcal{A}}\left(4\right)=[0.4,0.7]& \ngeqq [0.6,0.8]\hfill \\ \hfill & =rmin\left\{\right[0.6,0.8],[0.7,0.8\left]\right\}\hfill \\ \hfill & =rmin\{{\mu }_{\mathcal{A}}\left(3\right),{\mu }_{\mathcal{A}}\left(1\right)\}\hfill \\ \hfill & =rmin\{{\mu }_{\mathcal{A}}\left(3\right),{\mu }_{\mathcal{A}}(3\to ((4\to 0)\to 4))\},\hfill \end{array}$$

so the condition fails for μ.

Also,

$$\begin{array}{cc}\hfill {\gamma }_{\mathcal{A}}\left(4\right)=[0.2,0.3]& \nleqq [0.1,0.2]\hfill \\ \hfill & =rmax\left\{\right[0.1,0.2],[0.1,0.2\left]\right\}\hfill \\ \hfill & =rmax\{{\gamma }_{\mathcal{A}}\left(3\right),{\gamma }_{\mathcal{A}}\left(1\right)\}\hfill \\ \hfill & =rmax\{{\gamma }_{\mathcal{A}}\left(3\right),{\gamma }_{\mathcal{A}}(3\to ((4\to 0)\to 4))\},\hfill \end{array}$$

so the condition fails for γ.

Therefore, the IVIF filter $\mathcal{A}$ is not an implicative IVIF filter of $\mathcal{H}$.

Proposition 5. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ be an implicative IVIF filter of H. Recall that ${\mu }_{\mathcal{A}}$ and ${\gamma }_{\mathcal{A}}$ denote the interval-valued membership and non-membership functions of $\mathcal{A}$, respectively. For all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$, the following properties hold independently for ${\mu }_{\mathcal{A}}$ and ${\gamma }_{\mathcal{A}}$:

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H})\left(\begin{array}{c}{\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to x)\le {\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\hfill \\ {\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to x)\ge {\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\hfill \end{array}\right).\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H})\left(\begin{array}{c}{\mu }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})={\mu }_{\mathcal{A}}\left(1\right)\hfill \\ {\gamma }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})={\gamma }_{\mathcal{A}}\left(1\right)\hfill \end{array}\right).\hfill \end{array}$$

(22)

These assertions express that the membership and non-membership functions satisfy analogous algebraic properties in the context of implicative IVIF filters, and should not be mixed within a single statement without explicit clarification.

Proof. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ be an implicative IVIF filter of $\mathcal{H}$. If we set ${\hslash }_{{\mathfrak{a}}_y}={\hslash }_{{\mathfrak{a}}_x}$, ${\hslash }_{{\mathfrak{a}}_x}=1$, and ${\hslash }_{{\mathfrak{a}}_z}={\hslash }_{{\mathfrak{a}}_y}$ in (20) and use (a5) and (12), then we obtain (21). Using (21), (H1), (a5), (a7), (a9), and (10), we derive

$$\begin{array}{ccc}{\mu }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})& \ge & {\mu }_{\mathcal{A}}((((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_y})\to \hfill \\ & & ((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x}))\hfill \\ & =& {\mu }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to \hfill \\ & & ((((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x}))\hfill \\ & \ge & {\mu }_{\mathcal{A}}((((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_y})\to \hfill \\ & & ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}))\hfill \\ & \ge & {\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to ((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x}))\hfill \\ & =& {\mu }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_x}))\hfill \\ & =& {\mu }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to 1)\hfill \\ & =& {\mu }_{\mathcal{A}}\left(1\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}{\gamma }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})& \le & {\gamma }_{\mathcal{A}}((((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_y})\to \hfill \\ & & ((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x}))\hfill \\ & =& {\gamma }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to \left(\right(\left(\right(({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to \hfill \\ & & {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x}\left)\right)\hfill \\ & \le & {\gamma }_{\mathcal{A}}((((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_y})\to \hfill \\ & & ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}))\hfill \\ & \le & {\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to ((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x}))\hfill \\ & =& {\gamma }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_x}))\hfill \\ & =& {\gamma }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to 1)\hfill \\ & =& {\gamma }_{\mathcal{A}}\left(1\right),\hfill \end{array}$$

for all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$. It follows from (12) that we have (22).  □

This proposition reveals that implicative IVIF filters possess special monotonicity and idempotency properties with respect to their membership and non-membership functions. These properties further distinguish implicative IVIF filters within the interval-valued intuitionistic fuzzy filter framework.

Proposition 6. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ be an implicative IVIF-filter of $\mathcal{H}$, where ${\mu }_{\mathcal{A}}$ and ${\gamma }_{\mathcal{A}}$ denote the interval-valued membership and non-membership functions of $\mathcal{A}$, respectively. Then, for all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H}$, the following conditions hold separately for each function:

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H})\left(\begin{array}{c}{\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})={\mu }_A\left(1\right)\hfill \\ {\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})={\gamma }_A\left(1\right),\hfill \end{array}\right),\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H})\left(\begin{array}{c}{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\ge {\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}^{\prime })\to {\hslash }_{{\mathfrak{a}}_y})\hfill \\ {\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\le {\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}^{\prime })\to {\hslash }_{{\mathfrak{a}}_y})\hfill \end{array}\right),\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H})\left(\begin{array}{c}{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})\ge rmin\{{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z}),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to ({\hslash }_{{\mathfrak{a}}_z}^{\prime }\to {\hslash }_{{\mathfrak{a}}_y}))\}\hfill \\ {\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})\le rmax\{{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z}),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to ({\hslash }_{{\mathfrak{a}}_z}^{\prime }\to {\hslash }_{{\mathfrak{a}}_y}))\}\hfill \end{array}\right).\hfill \end{array}$$

(25)

These properties describe the algebraic relationships satisfied by the membership and non-membership functions in implicative IVIF-filters. Note that each assertion is stated independently for ${\mu }_{\mathcal{A}}$ and ${\gamma }_{\mathcal{A}}$, in accordance with their respective definitions.

Proof. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ be an implicative IVIF filter of a bounded hoop algebra $\mathcal{H}$. By Theorem 11, $\mathcal{A}$ is also an IVIF filter of $\mathcal{H}$.

If we set ${\hslash }_{{\mathfrak{a}}_y}=0$ in (22), we obtain for all ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$:

$${\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})={\mu }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to 0)\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})={\mu }_A\left(1\right),$$

$${\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})={\gamma }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to 0)\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})={\gamma }_A\left(1\right).$$

Thus, assertion (23) holds.

For all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$, observe that ${\hslash }_{{\mathfrak{a}}_y}^{\prime }\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\le {({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})}^{\prime }\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})$. From $\left(H3\right)$ in Definition 1, and (10), we deduce:

$$\begin{array}{cc}\hfill & \begin{array}{c}\hfill {\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}^{\prime })\to {\hslash }_{{\mathfrak{a}}_y})={\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}^{\prime }\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}))\le {\mu }_{\mathcal{A}}({({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})}^{\prime }\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})),\\ \hfill {\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}^{\prime })\to {\hslash }_{{\mathfrak{a}}_y})={\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}^{\prime }\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}))\ge {\gamma }_{\mathcal{A}}({({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})}^{\prime }\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})).\end{array}\hfill \end{array}$$

(26)

By combining Proposition 1$\left(a5\right)$, (12), (20), and (26), we obtain:

$$\begin{array}{ccc}{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})& \ge & rmin\{{\mu }_{\mathcal{A}}\left(1\right),{\mu }_{\mathcal{A}}(1\to ((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to 0)\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})))\}\hfill \\ & =& {\mu }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to 0)\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}))\hfill \\ & =& {\mu }_{\mathcal{A}}({({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})}^{\prime }\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}))\hfill \\ & \ge & {\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}^{\prime })\to {\hslash }_{{\mathfrak{a}}_y}),\hfill \end{array}$$

$$\begin{array}{ccc}{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})& \le & rmax\{{\gamma }_{\mathcal{A}}\left(1\right),{\gamma }_{\mathcal{A}}(1\to ((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to 0)\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})))\}\hfill \\ & =& {\gamma }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to 0)\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}))\hfill \\ & =& {\gamma }_{\mathcal{A}}({({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})}^{\prime }\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}))\hfill \\ & \le & {\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}^{\prime })\to {\hslash }_{{\mathfrak{a}}_y}).\hfill \end{array}$$

This proves (24).

Finally, using $\left(H3\right)$ in Definition 1, (15) and (24), for all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H}$, we have

$$\begin{array}{ccc}{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})& \ge & {\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z}^{\prime })\to {\hslash }_{{\mathfrak{a}}_z})\hfill \\ & \ge & rmin\{{\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z}^{\prime })\to {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\}\hfill \\ & =& rmin\{{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to ({\hslash }_{{\mathfrak{a}}_z}^{\prime }\to {\hslash }_{{\mathfrak{a}}_y})),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\},\hfill \end{array}$$

$$\begin{array}{ccc}{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})& \le & {\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z}^{\prime })\to {\hslash }_{{\mathfrak{a}}_z})\hfill \\ & \le & rmax\{{\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z}^{\prime })\to {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\}\hfill \\ & =& rmax\{{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to ({\hslash }_{{\mathfrak{a}}_z}^{\prime }\to {\hslash }_{{\mathfrak{a}}_y})),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\}.\hfill \end{array}$$

Thus, assertion (25) is established.  □

The above proposition demonstrates that implicative IVIF filters satisfy several additional algebraic properties, including idempotency and certain monotonicity relations involving implication and negation. These results further clarify the structural behavior of implicative IVIF filters in bounded hoop algebras.

Theorem 12. 

Let $\mathcal{A}=\{⟨{\hslash }_{{\mathfrak{a}}_x},{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)⟩:{\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}\}$ be an IVIF set. Then, $\mathcal{A}$ is an implicative filter of $\mathcal{H}$ if and only if for all $[{\mathfrak{m}}_1,{\mathfrak{n}}_1],[{\mathfrak{m}}_2,{\mathfrak{n}}_2]\in \mathcal{D}[0,1]$, the sets $U({\mu }_{\mathcal{A}},[{\mathfrak{m}}_2,{\mathfrak{n}}_2)$ and $L({\gamma }_{\mathcal{A}},[{\mathfrak{m}}_1,{\mathfrak{n}}_1])$ are either empty or are implicative filters of $\mathcal{H}$.

Proof. 

The proof follows closely the reasoning outlined in Theorem 5.  □

This theorem provides a characterization of implicative IVIF filters in terms of their level sets, stating that such a filter exists if and only if all its upper and lower level sets are either empty or implicative filters themselves. This result connects the interval-valued intuitionistic fuzzy structure with classical filter theory via level set analysis.

Theorem 13. 

If the IVIF filter $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ of $\mathcal{H}$ satisfies the condition (22), then it is an implicative IVIF filter of $\mathcal{H}$.

Proof. 

Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H}$. Then

$$\begin{array}{ccc}{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)& \ge & rmin\{{\mu }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to {\hslash }_{{\mathfrak{a}}_y})\}\hfill \\ & =& rmin\{{\mu }_{\mathcal{A}}\left(1\right),{\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to {\hslash }_{{\mathfrak{a}}_y})\}\hfill \\ & =& {\mu }_{\mathcal{A}}((y\to z)\to y)\hfill \\ & \ge & rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_A({\hslash }_{{\mathfrak{a}}_x}\to (({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to {\hslash }_{{\mathfrak{a}}_y}))\},\hfill \end{array}$$

and

$$\begin{array}{ccc}{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)& \le & rmax\{{\gamma }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to {\hslash }_{{\mathfrak{a}}_y})\to y),{\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to {\hslash }_{{\mathfrak{a}}_y})\}\hfill \\ & =& rmax\{{\gamma }_{\mathcal{A}}\left(1\right),{\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to {\hslash }_{{\mathfrak{a}}_y})\}\hfill \\ & =& {\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to {\hslash }_{{\mathfrak{a}}_y})\hfill \\ & \le & rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_A({\hslash }_{{\mathfrak{a}}_x}\to (({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to {\hslash }_{{\mathfrak{a}}_y}))\}\hfill \end{array}$$

by (12), (13) and (22). Then, $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an implicative IVIF filter of $\mathcal{H}$.  □

This theorem states that if an IVIF filter satisfies the specific idempotency condition given in (22), then it necessarily possesses the stronger structure of an implicative IVIF filter. Thus, condition (22) serves as a sufficient criterion for an IVIF filter to be implicative.

Theorem 14. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},\gamma \mathcal{A})$ be an IVIF filter of $\mathcal{H}$. If $\mathcal{A}$ satisfies the condition (21), then it is an implicative IVIF filter of $\mathcal{H}$.

Proof. 

Assume that $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$ satisfying condition (21). From Proposition 5, we know that (21) implies (22). Therefore, by Theorem 13, it follows that $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an implicative IVIF filter of $\mathcal{H}$.  □

Theorem 15. 

If an IVIF filter $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ of $\mathcal{H}$ satisfies the condition (23), then $\mathcal{A}$ is an implicative IVIF filter of $\mathcal{H}$.

Proof. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ be an IVIF filter of $\mathcal{H}$ that satisfies (23). Observe that for all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$, we have $({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x}\le (({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x}$. From the conditions in (12), (10), and (23), it follows that

$$\begin{array}{ccc}{\mu }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})& \le & {\mu }_{\mathcal{A}}\left(1\right)\hfill \\ & =& {\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})\hfill \\ & \le & {\mu }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x}),\hfill \end{array}$$

and

$$\begin{array}{ccc}{\gamma }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})& \ge & {\gamma }_{\mathcal{A}}\left(1\right)\hfill \\ & =& {\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})\hfill \\ & \ge & {\gamma }_{\mathcal{A}}((({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x}).\hfill \end{array}$$

Thus, (22) holds, and consequently, $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an implicative IVIF filter of H by Theorem 13.  □

This theorem asserts that if an IVIF filter satisfies the idempotency property stated in (23), then it must be an implicative IVIF filter. Therefore, condition (23) provides another sufficient criterion for an IVIF filter to be implicative.

Theorem 16. 

If an IVIF filter $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ of $\mathcal{H}$ satisfies the condition (24), then $\mathcal{A}$ is an implicative IVIF filter of $\mathcal{H}$.

Proof. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ be an IVIF filter of $\mathcal{H}$ that satisfies (24). For arbitrary elements ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$, we have the following sequence of inequalities:

$$\begin{array}{ccc}{\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})& \le & {\mu }_{\mathcal{A}}\left(1\right)\hfill \\ & =& {\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to ({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x}))\hfill \\ & =& {\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\odot ({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x}))\to {\hslash }_{{\mathfrak{a}}_x})\hfill \\ & \le & {\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x}).\hfill \end{array}$$

Similarly, for ${\gamma }_A$ we have

$$\begin{array}{ccc}{\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})& \ge & {\gamma }_{\mathcal{A}}\left(1\right)\hfill \\ & =& {\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to ({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x}))\hfill \\ & =& {\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\odot ({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x}))\to {\hslash }_{{\mathfrak{a}}_x})\hfill \\ & \ge & {\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x}).\hfill \end{array}$$

These inequalities follow from (H1), (H3), (12), and (24). Thus, Equation (23) holds, and therefore, by Theorem 15, $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an implicative IVIF filter of $\mathcal{H}$.  □

This theorem states that if an IVIF filter satisfies the condition given in (24), then it is necessarily an implicative IVIF filter. Thus, Equation (24) provides yet another sufficient condition ensuring the implicative nature of an IVIF filter.

Theorem 17. 

If an IVIF filter $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ of H satisfies the condition (25), then it is an implicative IVIF filter of $\mathcal{H}$.

Proof. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ be an IVIF filter of H satisfying (25). From the condition (25), we have the following inequalities:

$$\begin{array}{ccc}{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})& \ge & rmin\{{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to ({\hslash }_{{\mathfrak{a}}_y}^{\prime }\to {\hslash }_{{\mathfrak{a}}_y}))\}\hfill \\ & =& rmin\{{\mu }_{\mathcal{A}}\left(1\right),{\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}^{\prime })\to {\hslash }_{{\mathfrak{a}}_y})\}\hfill \\ & =& {\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}^{\prime })\to {\hslash }_{{\mathfrak{a}}_y}),\hfill \end{array}$$

and similarly,

$$\begin{array}{ccc}{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})& \le & rmax\{{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to ({\hslash }_{{\mathfrak{a}}_y}^{\prime }\to {\hslash }_{{\mathfrak{a}}_y}))\}\hfill \\ & =& rmax\{{\gamma }_{\mathcal{A}}\left(1\right),{\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}^{\prime })\to {\hslash }_{{\mathfrak{a}}_y})\}\hfill \\ & =& {\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}^{\prime })\to {\hslash }_{{\mathfrak{a}}_y}).\hfill \end{array}$$

These hold for all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$. Therefore, Equation (24) is satisfied, and by Theorem 16, $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an implicative IVIF filter of $\mathcal{H}$.  □

The above theorem shows that if an IVIF filter satisfies the condition in (25), then it is necessarily an implicative IVIF filter. Therefore, Equation (25) offers a further sufficient condition for an IVIF filter to be implicative.

Theorem 18. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ and $\mathcal{B}=({\mu }_{\mathcal{B}},{\gamma }_{\mathcal{B}})$ be IVIF filters of H such that

$$\begin{array}{cc}\hfill & {\mu }_{\mathcal{A}}\left(1\right)={\mu }_{\mathcal{B}}\left(1\right),{\gamma }_{\mathcal{A}}\left(1\right)={\gamma }_{\mathcal{B}}\left(1\right),\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H})({\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\le {\mu }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\ge {\gamma }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)).\hfill \end{array}$$

(28)

If $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an implicative IVIF filter of $\mathcal{H}$, then $\rho =({\mu }_{\mathcal{B}},{\gamma }_{\mathcal{B}})$ is also an implicative IVIF filter of $\mathcal{H}$.

Proof. 

Assume that $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an implicative IVIF filter of $\mathcal{H}$. This implies that $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$ (see Theorem 11). For any ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$, we have the following:

$${\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})\ge {\mu }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})={\mu }_{\mathcal{A}}\left(1\right)={\mu }_{\mathcal{B}}\left(1\right),$$

and

$${\gamma }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})\le {\gamma }_{\mathcal{A}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})={\gamma }_{\mathcal{A}}\left(1\right)={\gamma }_{\mathcal{B}}\left(1\right),$$

where the equalities and inequalities hold by (27), (28) and (23). Since $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$, from (12) it follows that

$${\mu }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})\le {\mu }_{\mathcal{B}}\left(1\right),{\gamma }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})\ge {\gamma }_{\mathcal{B}}\left(1\right).$$

Thus, we obtain

$${\mu }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to {\hslash }_{{\mathfrak{a}}_x})\to {\hslash }_{{\mathfrak{a}}_x})={\mu }_{\mathcal{B}}\left(1\right),{\gamma }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_x}^{\prime }\to x)\to x)={\gamma }_B\left(1\right),$$

for all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$. Therefore, $\mathcal{B}=({\mu }_{\mathcal{B}},{\gamma }_{\mathcal{B}})$ is an implicative IVIF filter of $\mathcal{H}$ by Theorem 15.  □

The above theorem establishes that if an implicative IVIF filter $\mathcal{A}$ is dominated by another IVIF filter $\mathcal{B}$ in the sense of conditions (27) and (28), then $\mathcal{B}$ is also implicative. Thus, the implicative property is preserved under these comparative conditions between IVIF filters.

In this part of this paper, we address the converses of Theorems 16–18; which provide essential insights into the relationships between IVIF filters and implicative IVIF filters. Understanding these converses will enhance the theoretical foundation of our study and clarify the conditions under which certain properties hold.

Theorem 16 states: An IVIF set $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an implicative IVIF filter of $\mathcal{H}$ if and only if it satisfies specific properties related to the membership and non-membership functions.

Converse Statement: If an IVIF set $\mathcal{A}$ satisfies the conditions outlined in Theorem 16, does it necessarily imply that $\mathcal{A}$ is an implicative IVIF filter?

The converse holds true under the following conditions:

• The membership function ${\mu }_{\mathcal{A}}$ must satisfy the condition ${\mu }_{\mathcal{A}}\left(1\right)\ge {\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$ for all ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$.
• The non-membership function ${\gamma }_{\mathcal{A}}$ must satisfy ${\gamma }_{\mathcal{A}}\left(1\right)\le {\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$ for all ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$.

If these conditions are met, then the implications defined in Theorem 16 can be reversed, confirming that $\mathcal{A}$ is indeed an implicative IVIF filter.

Theorem 17 states: An IVIF set $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an implicative IVIF filter of $\mathcal{H}$ if it satisfies certain conditions regarding the relationships between its membership and non-membership functions.

Converse Statement: If an IVIF set $\mathcal{A}$ is an implicative IVIF filter, does it necessarily satisfy the conditions outlined in Theorem 17? The converse of Theorem 17 holds true. If $\mathcal{A}$ is an implicative IVIF filter, then it must satisfy the properties defined in Theorem 17. This is due to the inherent definitions of implicative filters, which require specific relationships between the membership and non-membership functions.

Theorem 18 states: An IVIF set $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$ if and only if it meets certain criteria related to its structural properties.

Converse Statement: If an IVIF set $\mathcal{A}$ meets the conditions specified in Theorem 18, does it imply that $\mathcal{A}$ is an implicative IVIF filter? The converse of Theorem 18 is valid under the same structural conditions outlined in the theorem. Specifically, if an IVIF set meets the criteria for being an IVIF filter, it must also satisfy the additional properties required for it to be classified as an implicative IVIF filter.

The exploration of the converses of Theorems 16–18 provides valuable insights into the relationships between IVIF filters and implicative IVIF filters. By establishing these connections, we enhance the theoretical framework of our study and clarify the conditions under which various properties hold. This deeper understanding is crucial for future applications and research in the field of interval-valued intuitionistic fuzzy logic.

Proposition 7. 

Let $\{{\mathcal{A}}_{\mathfrak{k}}=({\mu }_{{\mathcal{A}}_{\mathfrak{k}}},{\gamma }_{{\mathcal{A}}_{\mathfrak{k}}}):\mathfrak{k}\in \mathrm{\Delta }\}$ be a family of IVIF filters of $\mathcal{H}$, where each ${\mu }_{{\mathcal{A}}_{\mathfrak{k}}}$ and ${\gamma }_{{\mathcal{A}}_{\mathfrak{k}}}$ denote the interval-valued membership and non-membership functions, respectively. Define the intersection ${\displaystyle \underset{\mathfrak{k}\in \mathrm{\Delta }}{\bigwedge }}{\mathcal{A}}_{\mathfrak{k}}$ by

$$\left(\underset{\mathfrak{k}\in \mathrm{\Delta }}{\bigwedge }{\mathcal{A}}_{\mathfrak{k}}\right)\left(x\right)=\left(\underset{\mathfrak{k}\in \mathrm{\Delta }}{inf}{\mu }_{{\mathcal{A}}_{\mathfrak{k}}}\left(x\right),\underset{\mathfrak{k}\in \mathrm{\Delta }}{sup}{\gamma }_{{\mathcal{A}}_{\mathfrak{k}}}\left(x\right)\right)$$

for all $x\in \mathcal{H}$. Then, ${\displaystyle \underset{\mathfrak{k}\in \mathrm{\Delta }}{\bigwedge }{\mathcal{A}}_{\mathfrak{k}}}$ is an IVIF filter of $\mathcal{H}$.

Proof. 

Let $A_i=\{({\mu }_{A_i},{\gamma }_{A_i}):i\in \mathrm{\Delta }\}$ be a family of IVIF filters of a hoop H.

Let ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$, we have

$$\left({\displaystyle \underset{\mathfrak{k}\in \mathrm{\Delta }}{\bigwedge }}{\mu }_{{\mathcal{A}}_{\mathfrak{k}}}\right)\left(1\right)=\underset{\mathfrak{k}\in \mathrm{\Delta }}{inf}\left\{{\mu }_{{\mathcal{A}}_{\mathfrak{k}}}\left(1\right)\right\}\ge \underset{\mathfrak{k}\in \mathrm{\Delta }}{inf}\left\{{\mu }_{{\mathcal{A}}_{\mathfrak{k}}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\right\}=\left({\displaystyle \underset{\mathfrak{k}\in \mathrm{\Delta }}{\bigwedge }}{\mu }_{{\mathcal{A}}_{\mathfrak{k}}}\right)\left({\hslash }_{{\mathfrak{a}}_x}\right),$$

$$\left({\displaystyle \underset{\mathfrak{k}\in \mathrm{\Delta }}{\bigwedge }}{\gamma }_{{\mathcal{A}}_{\mathfrak{k}}}\right)\left(1\right)=\underset{\mathfrak{k}\in \mathrm{\Delta }}{sup}\left\{{\gamma }_{{\mathcal{A}}_{\mathfrak{k}}}\left(1\right)\right\}\le \underset{\mathfrak{k}\in \mathrm{\Delta }}{sup}\left\{{\gamma }_{{\mathcal{A}}_{\mathfrak{k}}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\right\}=\left({\displaystyle \underset{\mathfrak{k}\in \mathrm{\Delta }}{\bigwedge }}{\gamma }_{{\mathcal{A}}_{\mathfrak{k}}}\right)\left({\hslash }_{{\mathfrak{a}}_x}\right).$$

Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$. Then we have

$$\begin{array}{ccc}\left({\displaystyle \underset{\mathfrak{k}\in \mathrm{\Delta }}{\bigwedge }}{\mu }_{{\mathcal{A}}_{\mathfrak{k}}}\right)\left({\hslash }_{{\mathfrak{a}}_y}\right)& =& \underset{\mathfrak{k}\in \mathrm{\Delta }}{inf}\left\{{\mu }_{{\mathcal{A}}_{\mathfrak{k}}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\right\}\hfill \\ & \ge & \underset{\mathfrak{k}\in \mathrm{\Delta }}{inf}\{rmin\{{\mu }_{{\mathcal{A}}_{\mathfrak{k}}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{{\mathcal{A}}_{\mathfrak{k}}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}\}\hfill \\ & =& rmin\{\underset{\mathfrak{k}\in \mathrm{\Delta }}{inf}{\mu }_{{\mathcal{A}}_{\mathfrak{k}}}\left({\hslash }_{{\mathfrak{a}}_x}\right),\underset{\mathfrak{k}\in \mathrm{\Delta }}{inf}{\mu }_{{\mathcal{A}}_{\mathfrak{k}}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}\hfill \\ & =& rmin\{\left({\displaystyle \underset{\mathfrak{k}\in \mathrm{\Delta }}{\bigwedge }}{\mu }_{{\mathcal{A}}_{\mathfrak{k}}}\right)\left({\hslash }_{{\mathfrak{a}}_x}\right),\left({\displaystyle \underset{\mathfrak{k}\in \mathrm{\Delta }}{\bigwedge }}{\mu }_{{\mathcal{A}}_{\mathfrak{k}}}\right)({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}\hfill \end{array}$$

and

$$\begin{array}{ccc}\left({\displaystyle \underset{\mathfrak{k}\in \mathrm{\Delta }}{\bigwedge }}{\gamma }_{A_{\mathfrak{k}}}\right)\left({\hslash }_{{\mathfrak{a}}_y}\right)& =& \underset{\mathfrak{k}\in \mathrm{\Delta }}{sup}\left\{{\gamma }_{{\mathcal{A}}_{\mathfrak{k}}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\right\}\hfill \\ & \le & \underset{\mathfrak{k}\in \mathrm{\Delta }}{sup}\{rmax\{{\gamma }_{{\mathcal{A}}_{\mathfrak{k}}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{{\mathcal{A}}_{\mathfrak{k}}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}\}\hfill \\ & =& rmax\{\underset{\mathfrak{k}\in \mathrm{\Delta }}{sup}{\gamma }_{{\mathcal{A}}_{\mathfrak{k}}}\left({\hslash }_{{\mathfrak{a}}_x}\right),\underset{\mathfrak{k}\in \mathrm{\Delta }}{sup}{\gamma }_{{\mathcal{A}}_{\mathfrak{k}}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}\hfill \\ & =& rmax\{\left({\displaystyle \underset{\mathfrak{k}\in \mathrm{\Delta }}{\bigwedge }}{\gamma }_{{\mathcal{A}}_{\mathfrak{k}}}\right)\left({\hslash }_{{\mathfrak{a}}_x}\right),\left({\displaystyle \underset{\mathfrak{k}\in \mathrm{\Delta }}{\bigwedge }}{\gamma }_{{\mathcal{A}}_{\mathfrak{k}}}\right)({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}.\hfill \end{array}$$

Hence ${\displaystyle \underset{\mathfrak{k}\in \mathrm{\Delta }}{\bigwedge }}{\mathcal{A}}_{\mathfrak{k}}$ is an IVIF filter of $\mathcal{H}$.  □

This proposition shows that the infimum of any family of IVIF filters is itself an IVIF filter. Thus, the class of IVIF filters of $\mathcal{H}$ is closed under arbitrary intersections.

Lemma 1. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ be an IVIF filter of $\mathcal{H}$ if and only if ${\mu }_{\mathcal{A}}$ and $\overline{{\gamma }_{\mathcal{A}}}$ are interval-valued fuzzy filters of $\mathcal{H}$.

Proof. 

Assume that $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$. Then, it is clear that ${\mu }_{\mathcal{A}}$ is an interval-valued fuzzy filter of $\mathcal{H}$. Consider, for every $x\in H$, we have

$$\overline{{\gamma }_{\mathcal{A}}}\left(1\right)=-1-{\gamma }_{\mathcal{A}}\left(1\right)\ge -1-{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)=\overline{{\gamma }_{\mathcal{A}}}\left({\hslash }_{{\mathfrak{a}}_x}\right).$$

Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$. Then, we have the following inequality:

$$\begin{array}{ccc}\overline{{\gamma }_{\mathcal{A}}}\left({\hslash }_{{\mathfrak{a}}_y}\right)& =& -1-{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\hfill \\ & \ge & -1-rmax\{{\gamma }_{\mathcal{A}}\left(x\right),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}\hfill \\ & =& rmin\{-1-{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),-1-{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}\hfill \\ & =& rmin\{\overline{{\gamma }_{\mathcal{A}}}\left({\hslash }_{{\mathfrak{a}}_x}\right),\overline{{\gamma }_{\mathcal{A}}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}.\hfill \end{array}$$

Thus, $\overline{{\gamma }_{\mathcal{A}}}$ is an interval-valued fuzzy filter of $\mathcal{H}$.

Conversely, assume that ${\mu }_{\mathcal{A}}$ and $\overline{{\gamma }_{\mathcal{A}}}$ are interval-valued fuzzy filters of $\mathcal{H}$. Then, for every ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$, we have ${\mu }_{\mathcal{A}}\left(1\right)\ge {\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$ and

$$-1-{\gamma }_{\mathcal{A}}\left(1\right)=\overline{{\gamma }_{\mathcal{A}}}\left(1\right)\ge \overline{{\gamma }_{\mathcal{A}}}\left({\hslash }_{{\mathfrak{a}}_x}\right)=-1-{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),$$

which implies that ${\gamma }_{\mathcal{A}}\left(1\right)\le {\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$. Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$. Then, it follows that

$${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\ge rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}.$$

Additionally,

$$\begin{array}{ccc}-1-{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)& =& \overline{{\gamma }_{\mathcal{A}}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\hfill \\ & \ge & rmin\{\overline{{\gamma }_{\mathcal{A}}}\left({\hslash }_{{\mathfrak{a}}_x}\right),\overline{{\gamma }_{\mathcal{A}}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}\hfill \\ & =& rmin\{-1-{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),-1-{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}\hfill \\ & =& -1-rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}.\hfill \end{array}$$

Hence, we obtain ${\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le max\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\}$.

Therefore, $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of H.  □

Remark 1. 

The characterization in Lemma 1 directly implies that the corresponding pairs $({\mu }_{\mathcal{A}},\overline{{\mu }_{\mathcal{A}}})$ and $({\gamma }_{\mathcal{A}},\overline{{\gamma }_{\mathcal{A}}})$ inherit the interval-valued fuzzy filter property.

Proof. 

If $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$, then by Lemma 1, ${\mu }_{\mathcal{A}}=\overline{\overline{{\mu }_{\mathcal{A}}}}$ and ${\gamma }_{\mathcal{A}}$ are interval-valued fuzzy filters of $\mathcal{H}$. Hence, $({\mu }_{\mathcal{A}},\overline{{\mu }_{\mathcal{A}}})$ and $(\overline{{\gamma }_{\mathcal{A}}},{\gamma }_{\mathcal{A}})$ are IVIF filters of H.

Conversely, if $({\mu }_{\mathcal{A}},\overline{{\mu }_A})$ and $({\gamma }_{\mathcal{A}},\overline{{\gamma }_{\mathcal{A}}})$ are IVIF filters of $\mathcal{H}$, then ${\mu }_{\mathcal{A}}$ and $\overline{{\gamma }_A}$ are IVF filters of $\mathcal{H}$. Therefore, $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF filter of $\mathcal{H}$.  □

Definition 12. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ be an IVIF set in $\mathcal{H}$. We define a subset ${\psi }^{-1}(1,1)$ of A by

$${\psi }^{-1}(1,1)=\{{\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}\mid {\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)={\gamma }_{\mathcal{A}}\left(1\right)\mathit{and}{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)={\mu }_{\mathcal{A}}\left(1\right)\}.$$

This definition introduces the subset ${\psi }^{-1}(1,1)$, which consists of all elements in $\mathcal{H}$ whose membership and non-membership degrees are equal to those of the unit element. Thus, ${\psi }^{-1}(1,1)$ characterizes elements that are maximally similar to 1 in terms of both degrees in the IVIF set $\mathcal{A}$.

Theorem 19. 

If $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ is an IVIF sub-hoop of $\mathcal{H}$, then ${\psi }^{-1}(1,1)$ is a sub-hoop of $\mathcal{H}$.

Proof. 

Clearly, $1\in {\psi }^{-1}(1,1)$. Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in {\psi }^{-1}(1,1)$. Then we have ${\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)={\gamma }_{\mathcal{A}}\left(1\right)$, ${\mu }_{\mathcal{A}}\left(x\right)={\mu }_{\mathcal{A}}\left(1\right)$, ${\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)={\gamma }_{\mathcal{A}}\left(1\right)$, and ${\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)={\mu }_{\mathcal{A}}\left(1\right)$. Therefore, for $\diamond \in \{\odot ,\to \}$, we obtain

$${\gamma }_{\mathcal{A}}\left(1\right)\le {\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})\le rmax\{{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}=rmax\{{\gamma }_{\mathcal{A}}\left(1\right),{\gamma }_{\mathcal{A}}\left(1\right)\}={\gamma }_{\mathcal{A}}\left(1\right),$$

and

$${\mu }_{\mathcal{A}}\left(1\right)\ge {\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})\ge rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}=rmin\{{\mu }_{\mathcal{A}}\left(1\right),{\mu }_{\mathcal{A}}\left(1\right)\}={\mu }_{\mathcal{A}}\left(1\right).$$

Hence, ${\gamma }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})={\gamma }_{\mathcal{A}}\left(1\right)$ and ${\mu }_{\mathcal{A}}({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})={\mu }_{\mathcal{A}}\left(1\right)$, which implies that ${\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}\in {\psi }^{-1}(1,1)$. Thus, ${\psi }^{-1}(1,1)$ is a sub-hoop of $\mathcal{H}$.  □

For any fixed interval numbers ${\tilde{\mathfrak{a}}}^{+}$, ${\tilde{\mathfrak{a}}}^{-}$, ${\tilde{\mathfrak{b}}}^{+}$, and ${\tilde{\mathfrak{b}}}^{-}$ in $\left[\right[0,1\left]\right]$ such that ${\tilde{\mathfrak{a}}}^{+}\succ {\tilde{\mathfrak{a}}}^{-}$, ${\tilde{\mathfrak{b}}}^{+}\succ {\tilde{\mathfrak{b}}}^{-}$, and a nonempty subset $\mathcal{G}$ of $\mathcal{H}$, the IVIS is defined as

$${\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{cc}{\tilde{\mathfrak{a}}}^{+},& {\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{a}}}^{-},& {\tilde{\mathfrak{b}}}^{+}\end{array}\right]=\left(\mathcal{H},{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right],{\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\right)$$

in $\mathcal{H}$, where

$${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)=\left\{\begin{array}{cc}{\tilde{\mathfrak{a}}}^{+}& \mathrm{if}{\hslash }_{{\mathfrak{a}}_x}\in \mathcal{G}\\ {\tilde{\mathfrak{a}}}^{-}& otherwise,\end{array}\right.$$

$${\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{b}}^{+}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)=\left\{\begin{array}{cc}{\tilde{\mathfrak{b}}}^{-}& \mathrm{if}{\hslash }_{{\mathfrak{a}}_x}\in \mathcal{G}\\ {\tilde{\mathfrak{b}}}^{+}& otherwise.\end{array}\right.$$

Lemma 2. 

If the constant 1 of $\mathcal{H}$ is in a nonempty subset $\mathcal{G}$ of $\mathcal{H}$, then the IVIS

$${\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{cc}{\tilde{\mathfrak{a}}}^{+}& {\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{a}}}^{-}& {\tilde{\mathfrak{b}}}^{+}\end{array}\right]$$

in $\mathcal{H}$ satisfies the conditions (3).

Proof. 

If $1\in \mathcal{G}$, then ${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left(1\right)={\tilde{\mathfrak{a}}}^{+}$, and ${\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left(1\right)={\tilde{\mathfrak{b}}}^{-}$. Thus

$$\begin{array}{cc}\hfill & (\forall {\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H})\left(\begin{array}{c}{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left(1\right)={\tilde{\mathfrak{a}}}^{+}⪰{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)\hfill \\ {\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left(1\right)={\tilde{b}}^{-}⪯{\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)\hfill \end{array}\right).\hfill \end{array}$$

(29)

Hence ${\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{cc}{\tilde{\mathfrak{a}}}^{+},& {\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{a}}}^{-},& {\tilde{\mathfrak{b}}}^{+}\end{array}\right]$ satisfies the conditions (3).  □

Lemma 3. 

If the IVIS

$${\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{cc}{\tilde{\mathfrak{a}}}^{+}& {\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{a}}}^{-}& {\tilde{\mathfrak{b}}}^{+}\end{array}\right]$$

in $\mathcal{H}$ satisfies the conditions (3), then the constant 1 of $\mathcal{H}$ is in a nonempty subset $\mathcal{G}$ of $\mathcal{H}$.

Proof. 

Assume that the IVIS

$${\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{cc}{\tilde{\mathfrak{a}}}^{+}& {\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{a}}}^{-}& {\tilde{\mathfrak{b}}}^{+}\end{array}\right]$$

in $\mathcal{H}$ satisfies the condition (3). Then, we have

$${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left(1\right)⪰{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)\mathrm{for}\mathrm{all}{\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}.$$

Since $\mathcal{G}$ is nonempty, there exists some $\mathfrak{g}\in \mathcal{G}$. Therefore,

$${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left(\mathfrak{g}\right)={\tilde{\mathfrak{a}}}^{+}.$$

From this, we get

$${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left(1\right)⪰{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left(\mathfrak{g}\right)={\tilde{a}}^{+}⪰{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left(1\right).$$

Thus, we conclude that

$${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left(1\right)={\tilde{\mathfrak{a}}}^{+}.$$

Hence, $1\in \mathcal{G}$.  □

Theorem 20. 

The IVIS

$${\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{cc}{\tilde{\mathfrak{a}}}^{+}& {\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{a}}}^{-}& {\tilde{\mathfrak{b}}}^{+}\end{array}\right]$$

in $\mathcal{H}$ is an IVIF sub-hoop of $\mathcal{H}$ if and only if a nonempty subset $\mathcal{G}$ of $\mathcal{H}$ is a sub-hoop of $\mathcal{H}$.

Proof. 

Assume that $A^G\left[\begin{array}{cc}{\tilde{\mathfrak{a}}}^{+},& {\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{a}}}^{-},& {\tilde{\mathfrak{b}}}^{+}\end{array}\right]$ is an IVIF sub-hoop of $\mathcal{H}$. Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{G}$. Then ${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)={\tilde{\mathfrak{a}}}^{+}={\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)$. Thus

$$\begin{array}{ccc}{\mu }_A^G\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})& ⪰& rmin\left\{{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)\right\}\hfill \\ & =& rmin\{{\tilde{\mathfrak{a}}}^{+},{\tilde{\mathfrak{a}}}^{+}\}\hfill \\ & =& {\tilde{\mathfrak{a}}}^{+}\hfill \\ & ⪰& {\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})\hfill \end{array}$$

and so ${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})={\tilde{\mathfrak{a}}}^{+}$. Thus ${\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}\in \mathcal{G}$. Hence $\mathcal{G}$ is a sub-hoop of $\mathcal{H}$.

Conversely, assume that $\mathcal{G}$ is a sub-hoop of $\mathcal{H}$. Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in H$.

Case (1): Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{G}$. Then

$${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)={\tilde{\mathfrak{a}}}^{+}={\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right),$$

$${\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left(x\right)={\tilde{b}}^{-}={\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right).$$

Since $\mathcal{G}$ is a sub-hoop of $\mathcal{H}$, ${\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}\in \mathcal{G}$ and so ${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right](x\diamond y)={\tilde{\mathfrak{a}}}^{+},{\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\widetilde{\mathfrak{ba}}}^{+}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})={\tilde{\mathfrak{b}}}^{-}$.

• Then

$${\mu }_A^G\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})={\tilde{\mathfrak{a}}}^{+}⪰{\tilde{\mathfrak{a}}}^{+}=rmin\{{\tilde{\mathfrak{a}}}^{+},{\tilde{\mathfrak{a}}}^{+}\}=rmin\left\{{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left(y\right)\right\},$$

$${\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{b}}^{+}\\ {\tilde{b}}^{-}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})={\tilde{\mathfrak{b}}}^{-}⪯{\tilde{\mathfrak{b}}}^{-}=rmax\{{\tilde{\mathfrak{b}}}^{-},{\tilde{\mathfrak{b}}}^{-}\}=rmax\left\{{\gamma }_A^G\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{+}\\ {\tilde{\mathfrak{b}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{+}\\ {\tilde{\mathfrak{b}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)\right\}.$$

Case 2: Let ${\hslash }_{{\mathfrak{a}}_x}\notin \mathcal{G}$ or ${\hslash }_{{\mathfrak{a}}_y}\notin \mathcal{G}$. Then

$${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)={\tilde{\mathfrak{a}}}^{-}or\mu \text{\_}{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\widetilde{\mathfrak{a}a}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)={\tilde{\mathfrak{a}}}^{-},$$

$${\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)={\tilde{\mathfrak{b}}}^{+}or{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)={\tilde{\mathfrak{b}}}^{+}.$$

Then

$$rmin\left\{{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)\right\}=rmin\left\{{\tilde{\mathfrak{a}}}^{+},{\tilde{\mathfrak{a}}}^{-}\right\}={\tilde{\mathfrak{a}}}^{-},$$

$$rmax\left\{{\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right),{\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)\right\}=rmax\{{\tilde{\mathfrak{b}}}^{+},{\tilde{\mathfrak{b}}}^{+}\}={\tilde{\mathfrak{b}}}^{+}.$$

Therefore,

$${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right](x\diamond y)⪰{\tilde{\mathfrak{a}}}^{-}=rmin\left\{{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left(x\right),{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)\right\}$$

$${\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right](x\diamond y)⪯{\tilde{\mathfrak{b}}}^{+}=rmax\left\{{\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left(x\right),{\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)\right\}$$

Hence ${\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{cc}{\tilde{\mathfrak{a}}}^{+},& {\tilde{\mathfrak{b}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-},& {\tilde{\mathfrak{b}}}^{-},\end{array}\right]$ is an IVIF sub-hoop of $\mathcal{H}$.  □

This theorem provides a characterization of IVIF sub-hoops in terms of their underlying crisp structure. Specifically, it shows that an IVIF sub-hoop of $\mathcal{H}$ corresponds exactly to an ordinary sub-hoop of $\mathcal{H}$ determined by the nonempty subset $\mathcal{G}$.

Theorem 21. 

TThe IVIS ${\mathcal{A}}^{\mathcal{G}}$

$$\left[\begin{array}{cc}{\tilde{\mathfrak{a}}}^{+}& {\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{a}}}^{-}& {\tilde{\mathfrak{b}}}^{+}\end{array}\right]$$

in $\mathcal{H}$ is an IVIF filter of $\mathcal{H}$ if and only if a nonempty subset $\mathcal{G}$ of $\mathcal{H}$ is a filter of $\mathcal{H}$.

Proof. 

Assume that ${\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{cc}{\tilde{\mathfrak{a}}}^{+}& {\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{a}}}^{-}& {\tilde{\mathfrak{b}}}^{+}\end{array}\right]$ is an IVIF filter of $\mathcal{H}$. Since ${\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{cc}{\tilde{\mathfrak{a}}}^{+}& {\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{a}}}^{-}& {\tilde{\mathfrak{b}}}^{+}\end{array}\right]$ satisfies the condition (29), it follows from Lemma 3 that $1\in \mathcal{G}$.

Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$ and ${\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_x}\in \mathcal{G}$. We have

$${\mu }_A^G\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right](x\diamond y)={\tilde{\mathfrak{a}}}^{+}={\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right).$$

Now, consider

$$\begin{array}{ccc}{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)& ⪰& rmin\left\{{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)\right\}\hfill \\ & =& rmin\{{\tilde{\mathfrak{a}}}^{+},{\tilde{\mathfrak{a}}}^{+}\}\hfill \\ & =& {\tilde{\mathfrak{a}}}^{+}\hfill \\ & ⪰& {\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)\hfill \end{array}$$

Thus, ${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)={\tilde{\mathfrak{a}}}^{+}$. Therefore, ${\hslash }_{{\mathfrak{a}}_y}\in \mathcal{G}$. Hence, $\mathcal{G}$ is a filter of $\mathcal{H}$.

Conversely, assume that $\mathcal{G}$ is a filter of $\mathcal{H}$. Since $1\in \mathcal{G}$, it follows from Lemma 2 that $A^{\mathcal{G}}\left[\begin{array}{cc}{\tilde{\mathfrak{a}}}^{+}& {\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{a}}}^{-}& {\tilde{\mathfrak{b}}}^{+}\end{array}\right]$ satisfies the conditions (29).

Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$.

Case 1: Suppose ${\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_x}\in \mathcal{G}$. Then

$${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})={\tilde{\mathfrak{a}}}^{+}={\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)$$

$${\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})={\tilde{\mathfrak{b}}}^{-}={\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)$$

Since $\mathcal{G}$ is a filter of $\mathcal{H}$, ${\hslash }_{{\mathfrak{a}}_y}\in \mathcal{G}$, and so

$${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)={\tilde{\mathfrak{a}}}^{+},{\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)={\tilde{\mathfrak{b}}}^{-}.$$

Then

$${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)={\tilde{\mathfrak{a}}}^{+}⪰{\tilde{\mathfrak{a}}}^{+}=rmin\left\{{\tilde{\mathfrak{a}}}^{+},{\tilde{\mathfrak{a}}}^{+}\right\}=rmin\left\{{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)\right\}$$

$${\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)={\tilde{\mathfrak{b}}}^{-}⪯{\tilde{\mathfrak{b}}}^{-}=rmax\left\{{\tilde{\mathfrak{b}}}^{-},{\tilde{\mathfrak{b}}}^{-}\right\}=rmax\left\{{\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)\right\}$$

Case 2: Suppose ${\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}\notin \mathcal{G}$ or ${\hslash }_{{\mathfrak{a}}_x}\notin \mathcal{G}$. Then

$${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})={\tilde{\mathfrak{a}}}^{-}\mathrm{or}{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)={\tilde{\mathfrak{a}}}^{-}$$

$${\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y})={\tilde{\mathfrak{b}}}^{+}\mathrm{or}{\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)={\tilde{\mathfrak{b}}}^{+}.$$

Then

$$rmin\left\{{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)\right\}=rmin\left\{{\tilde{\mathfrak{a}}}^{-},{\tilde{\mathfrak{a}}}^{-}\right\}={\tilde{\mathfrak{a}}}^{-}$$

$$rmax\left\{{\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)\right\}=rmax\left\{{\tilde{\mathfrak{b}}}^{-},{\tilde{\mathfrak{b}}}^{-}\right\}={\tilde{\mathfrak{b}}}^{-}$$

Therefore,

$${\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)⪰{\tilde{\mathfrak{a}}}^{-}=rmin\left\{{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\mu }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{a}}}^{+}\\ {\tilde{\mathfrak{a}}}^{-}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)\right\}$$

$${\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_y}\right)⪯{\tilde{\mathfrak{b}}}^{-}=rmax\left\{{\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]({\hslash }_{{\mathfrak{a}}_x}\diamond {\hslash }_{{\mathfrak{a}}_y}),{\gamma }_{\mathcal{A}}^{\mathcal{G}}\left[\begin{array}{c}{\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{b}}}^{+}\end{array}\right]\left({\hslash }_{{\mathfrak{a}}_x}\right)\right\}$$

Hence, $A^{\mathcal{G}}\left[\begin{array}{cc}{\tilde{\mathfrak{a}}}^{+}& {\tilde{\mathfrak{b}}}^{-}\\ {\tilde{\mathfrak{a}}}^{-}& {\tilde{\mathfrak{b}}}^{+}\end{array}\right]$ is an IVIF filter of $\mathcal{H}$.  □

The above theorem establishes a direct correspondence between IVIF filters and crisp filters in the hoop $\mathcal{H}$. In particular, it shows that an IVIF filter of $\mathcal{H}$ is determined by a nonempty subset $\mathcal{G}$ that is itself a filter of $\mathcal{H}$.

We define the operations ∨ and ∧ on the interval-valued fuzzy set $\mu$ of $\mathcal{H}$ in this way:

$$rmin\{{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right),{\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\}=\mu \left({\hslash }_{{\mathfrak{a}}_x}\right)\wedge \mu \left({\hslash }_{{\mathfrak{a}}_y}\right)$$

and

$$krmax\{\mu \left({\hslash }_{{\mathfrak{a}}_x}\right),\mu \left({\hslash }_{{\mathfrak{a}}_y}\right)\}={\mu }_{\mathcal{A}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\vee \mu \left({\hslash }_{{\mathfrak{a}}_y}\right)$$

for all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}.$

Remark 2. 

Let $\mathcal{A}$ be an IVIF-set on $\mathcal{H}$. The intersection of all IVIF-filters containing $\mathcal{A}$ is called the generated IVIF-filter by $\mathcal{A}$, denoted as $⟨\mathcal{H}⟩$.

Theorem 22. 

Let $\mathcal{A}=({\mu }_{\mathcal{A}},{\gamma }_{\mathcal{A}})$ be an IVIF-set on $\mathcal{H}$, and let $\mathcal{B}=({\mu }_{\mathcal{B}},{\gamma }_{\mathcal{B}})$ be an IVIF-set defined on $\mathcal{H}$ by:

$${\mu }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)=\underset{{\mathfrak{a}}_1\odot {\mathfrak{a}}_2\odot \cdots \odot {\mathfrak{a}}_n\le \mathfrak{d}}{\bigvee }\left\{{\mu }_{\mathcal{A}}\left({\mathfrak{a}}_1\right)\wedge {\mu }_{\mathcal{A}}\left({\mathfrak{a}}_2\right)\wedge \cdots \wedge {\mu }_{\mathcal{A}}\left({\mathfrak{a}}_n\right)\right\},$$

and

$${\gamma }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)=\underset{{\mathfrak{a}}_1\odot {\mathfrak{a}}_2\odot \cdots \odot {\mathfrak{a}}_{\mathfrak{n}}\le \mathfrak{d}}{\bigwedge }\left\{{\mu }_{\mathcal{A}}\left({\mathfrak{a}}_1\right)\wedge {\mu }_{\mathcal{A}}\left({\mathfrak{a}}_2\right)\wedge \cdots \wedge {\mu }_{\mathcal{A}}\left({\mathfrak{a}}_{\mathfrak{n}}\right)\right\},$$

for all ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$, where ${\mathfrak{a}}_i\in \mathcal{H}$ for $1\le i\le n$ and $n\in \mathbb{N}$. Then $\mathcal{B}=⟨\mathcal{L}⟩$.

Proof. 

First, we verify that $\mathcal{B}$ is an IVIF-filter. For all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$, such that ${\hslash }_{{\mathfrak{a}}_x}\le {\hslash }_{{\mathfrak{a}}_y}$, the definition of $\mathcal{B}$ yields the following:

$${\mu }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\le {\mu }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\mathrm{and}{\gamma }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le {\gamma }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right).$$

For all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\mathfrak{a}}_{\mathfrak{i}},{\mathfrak{b}}_{\mathfrak{j}},{\mathfrak{c}}_{\mathfrak{l}}\in \mathcal{H}$, $1\le i\le n$, $1\le \mathfrak{j}\le \mathfrak{m}$, $1\le l\le k$ and $\mathfrak{n},\mathfrak{m},\mathfrak{k}\in \mathbb{N}$, we have

$${\mu }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\le {\mu }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\mathrm{and}{\gamma }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_y}\right)\le {\gamma }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)$$

for all appropriate values of ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}.$

For all elements ${\mathfrak{a}}_i,{\mathfrak{b}}_j,{\mathfrak{c}}_l\in \mathcal{H}$, the following operations hold:

$${\mu }_{\mathcal{B}}\left({\mathfrak{a}}_1\right)\wedge {\mu }_{\mathcal{B}}\left({\mathfrak{a}}_2\right)\wedge \cdots \wedge {\mu }_{\mathcal{B}}\left({\mathfrak{a}}_{\mathfrak{n}}\right)\mathrm{and}\mathrm{similarly}\mathrm{for}\mathrm{the}{\gamma }_{\mathcal{B}}\left({\mathfrak{b}}_1\right)\wedge {\gamma }_{\mathcal{B}}\left({\mathfrak{b}}_2\right)\wedge \cdots \wedge {\gamma }_{\mathcal{B}}\left({\mathfrak{b}}_{\mathfrak{m}}\right).$$

This establishes the necessary properties for $\mathcal{B}$ to satisfy the IVIF-filter conditions.

$$\begin{array}{ccc}{\mu }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\wedge {\mu }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_y}\right)& =& {\displaystyle \underset{{\mathfrak{a}}_1\odot {\mathfrak{a}}_2\odot \cdots \odot {\mathfrak{a}}_{\mathfrak{n}}\le {\hslash }_{{\mathfrak{a}}_x}}{\bigvee }}\{{\mu }_{\mathcal{A}}\left({\mathfrak{a}}_1\right)\wedge {\mu }_{\mathcal{A}}\left({\mathfrak{a}}_2\right)\wedge \cdots \wedge {\mu }_{\mathcal{A}}\left({\mathfrak{a}}_{\mathfrak{n}}\right)\}\hfill \\ & & \wedge {\displaystyle \underset{{\mathfrak{b}}_1\odot {\mathfrak{b}}_2\odot \cdots \odot {\mathfrak{b}}_{\mathfrak{m}}\le {\hslash }_{{\mathfrak{a}}_y}}{\bigvee }}\{{\mu }_{\mathcal{A}}\left({\mathfrak{b}}_1\right)\wedge {\mu }_{\mathcal{A}}\left({\mathfrak{b}}_2\right)\wedge \cdots \wedge {\mu }_{\mathcal{A}}\left({\mathfrak{b}}_{\mathfrak{m}}\right)\}\hfill \\ & =& {\displaystyle \underset{{\mathfrak{a}}_1\odot {\mathfrak{a}}_2\odot \cdots \odot {\mathfrak{a}}_{\mathfrak{n}}\le {\hslash }_{{\mathfrak{a}}_x}}{\bigvee }}{\displaystyle \underset{{\mathfrak{b}}_1\odot {\mathfrak{b}}_2\odot \cdots {\mathfrak{b}}_{\mathfrak{m}}\le y}{\bigvee }}{\mu }_{\mathcal{A}}\left({\mathfrak{a}}_1\right)\wedge {\mu }_{\mathcal{A}}\left({\mathfrak{a}}_2\right)\wedge \cdots \wedge {\mu }_{\mathcal{A}}\left({\mathfrak{a}}_n\right)\wedge \hfill \\ & & {\mu }_{\mathcal{A}}\left({\mathfrak{b}}_1\right)\wedge {\mu }_{\mathcal{A}}\left({\mathfrak{b}}_2\right)\wedge \cdots \wedge {\mu }_{\mathcal{A}}\left({\mathfrak{b}}_{\mathfrak{m}}\right)\hfill \\ & \le & {\displaystyle \underset{{\mathfrak{c}}_1\odot {\mathfrak{c}}_2\odot \cdots \odot {\mathfrak{c}}_{\mathfrak{n}}\le {\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}}{\bigvee }}{\mu }_{\mathcal{A}}\left({\mathfrak{c}}_1\right)\wedge {\mu }_{\mathcal{A}}\left({\mathfrak{c}}_2\right)\wedge \cdots \wedge {\mu }_{\mathcal{A}}\left({\mathfrak{c}}_{\mathfrak{k}}\right)\hfill \\ & =& {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y})\hfill \end{array}$$

and

$$\begin{array}{ccc}{\gamma }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\vee {\gamma }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_y}\right)& =& {\displaystyle \underset{{\mathfrak{a}}_1\odot {\mathfrak{a}}_2\odot \cdots \odot {\mathfrak{a}}_{\mathfrak{n}}\le {\hslash }_{{\mathfrak{a}}_x}}{\bigwedge }}\{{\gamma }_{\mathcal{A}}\left({\mathfrak{a}}_1\right)\vee {\gamma }_{\mathcal{A}}\left(a_2\right)\vee \cdots \vee {\gamma }_{\mathcal{A}}\left({\mathfrak{a}}_{\mathfrak{n}}\right)\}\hfill \\ & & \vee {\displaystyle \underset{{\mathfrak{b}}_1\odot {\mathfrak{b}}_2\odot \cdots {\mathfrak{b}}_{\mathfrak{m}}\le {\hslash }_{{\mathfrak{a}}_y}}{\bigwedge }}\{{\gamma }_{\mathcal{A}}\left({\mathfrak{b}}_1\right)\vee {\gamma }_{\mathcal{A}}\left({\mathfrak{b}}_2\right)\vee \cdots \vee {\gamma }_{\mathcal{A}}\left({\mathfrak{b}}_{\mathfrak{m}}\right)\}\hfill \\ & =& {\displaystyle \underset{{\mathfrak{a}}_1\odot {\mathfrak{a}}_2\odot \cdots \odot {\mathfrak{a}}_{\mathfrak{n}}\le {\hslash }_{{\mathfrak{a}}_x}}{\bigwedge }}{\displaystyle \underset{{\mathfrak{b}}_1\odot {\mathfrak{b}}_2\odot \cdots {\mathfrak{b}}_{\mathfrak{m}}\le {\hslash }_{{\mathfrak{a}}_y}}{\bigwedge }}{\gamma }_{\mathcal{A}}\left({\mathfrak{a}}_1\right)\vee {\gamma }_{\mathcal{A}}\left({\mathfrak{a}}_2\right)\vee \cdots \vee {\gamma }_{\mathcal{A}}\left({\mathfrak{a}}_{\mathfrak{n}}\right)\vee \hfill \\ & & {\gamma }_{\mathcal{A}}\left({\mathfrak{b}}_1\right)\vee {\gamma }_{\mathcal{A}}\left({\mathfrak{b}}_2\right)\vee \cdots \vee {\gamma }_{\mathcal{A}}\left({\mathfrak{b}}_{\mathfrak{m}}\right)\hfill \\ & \ge & {\displaystyle \underset{{\mathfrak{c}}_1\odot {\mathfrak{c}}_2\odot \cdots \odot {\mathfrak{c}}_{\mathfrak{n}}\le {\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}}{\bigwedge }}{\gamma }_{\mathcal{A}}\left({\mathfrak{c}}_1\right)\vee {\gamma }_{\mathcal{A}}\left({\mathfrak{c}}_2\right)\vee \cdots \vee {\gamma }_{\mathcal{A}}\left({\mathfrak{c}}_{\mathfrak{k}}\right)\hfill \\ & =& {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}).\hfill \end{array}$$

Thus, $\mathcal{B}$ is an IVIF-filter. Secondly, let $\mathfrak{C}$ be an IVIF-filter such that $\mathcal{A}\subseteq \mathfrak{C}$. By the definition of an IVIF-filter, for all ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\mathfrak{a}}_{\mathfrak{i}}\in \mathcal{H}$, where $1\le \mathfrak{i}\le \mathfrak{n}$ and $\mathfrak{n}\in \mathbb{N}$, it holds that

$$\begin{array}{ccc}{\mu }_B\left({\hslash }_{{\mathfrak{a}}_x}\right)& =& {\displaystyle \underset{{\mathfrak{a}}_1\odot {\mathfrak{a}}_2\odot \cdots \odot {\mathfrak{a}}_{\mathfrak{n}}\le {\hslash }_{{\mathfrak{a}}_x}}{\bigvee }}\{{\mu }_{\mathcal{A}}\left({\mathfrak{a}}_1\right)\wedge {\mu }_{\mathcal{A}}\left({\mathfrak{a}}_2\right)\wedge \cdots \wedge {\mu }_{\mathcal{A}}\left({\mathfrak{a}}_{\mathfrak{n}}\right)\}\hfill \\ & \le & {\displaystyle \underset{{\mathfrak{a}}_1\odot {\mathfrak{a}}_2\odot \cdots \odot {\mathfrak{a}}_{\mathfrak{n}}\le {\hslash }_{{\mathfrak{a}}_x}}{\bigvee }}\{{\mu }_{\mathfrak{C}}\left({\mathfrak{a}}_1\right)\wedge {\mu }_{\mathfrak{C}}\left({\mathfrak{a}}_2\right)\wedge \cdots \wedge {\mu }_{\mathfrak{C}}\left({\mathfrak{a}}_{\mathfrak{n}}\right)\}\hfill \\ & \le & {\displaystyle \underset{{\mathfrak{a}}_1\odot {\mathfrak{a}}_2\odot \cdots \odot {\mathfrak{a}}_{\mathfrak{n}}\le {\hslash }_{{\mathfrak{a}}_x}}{\bigvee }}{\mu }_{\mathfrak{C}}({\mathfrak{a}}_1\odot {\mathfrak{a}}_2\odot \cdots \odot {\mathfrak{a}}_{\mathfrak{n}})\hfill \\ & \le & {\mu }_{\mathfrak{C}}\left({\hslash }_{{\mathfrak{a}}_x}\right)\hfill \end{array}$$

and

$$\begin{array}{ccc}{\gamma }_{\mathcal{B}}\left({\hslash }_{{\mathfrak{a}}_x}\right)& =& {\displaystyle \underset{{\mathfrak{a}}_1\odot {\mathfrak{a}}_2\odot \cdots \odot {\mathfrak{a}}_{\mathfrak{n}}\le {\hslash }_{{\mathfrak{a}}_x}}{\bigwedge }}\{{\gamma }_{\mathcal{A}}\left({\mathfrak{a}}_1\right)\vee {\gamma }_{\mathcal{A}}\left({\mathfrak{a}}_2\right)\vee \cdots \vee {\gamma }_{\mathcal{A}}\left({\mathfrak{a}}_{\mathfrak{n}}\right)\}\hfill \\ & \ge & {\displaystyle \underset{{\mathfrak{a}}_1\odot {\mathfrak{a}}_2\odot \cdots \odot {\mathfrak{a}}_{\mathfrak{n}}\le x}{\bigwedge }}\{{\gamma }_{\mathfrak{C}}\left({\mathfrak{a}}_1\right)\vee {\gamma }_{\mathfrak{C}}\left({\mathfrak{a}}_2\right)\vee \cdots \vee {\gamma }_{\mathfrak{C}}\mathfrak{C}\left({\mathfrak{a}}_{\mathfrak{n}}\right)\}\hfill \\ & \ge & {\displaystyle \underset{{\mathfrak{a}}_1\odot {\mathfrak{a}}_2\odot \cdots \odot {\mathfrak{a}}_{\mathfrak{n}}\le {\hslash }_{{\mathfrak{a}}_x}}{\bigwedge }}{\gamma }_{\mathfrak{C}}({\mathfrak{a}}_1\odot {\mathfrak{a}}_2\odot \cdots \odot {\mathfrak{a}}_{\mathfrak{a}})\hfill \\ & \ge & {\gamma }_{\mathfrak{C}}\left({\hslash }_{{\mathfrak{a}}_x}\right).\hfill \end{array}$$

and hence, $\mathcal{B}\subseteq \mathfrak{C}$. Thus, $\mathcal{B}=⟨\mathcal{H}⟩$.  □

This theorem demonstrates that the IVIF-set $\mathcal{B}$ constructed via the given supremum and infimum operations is the IVIF-filter generated by $\mathcal{A}$. In other words, $\mathcal{B}$ is the smallest IVIF-filter in $\mathcal{H}$ containing $\mathcal{A}$.

Now, we define the operations ⊓ and ⊔ on IVIF-filters of $\mathcal{H}$ in this way, $\mathcal{B}\sqcap \mathfrak{C}=\mathcal{B}\cap \mathfrak{C}$ and $\mathcal{B}\bigsqcup \mathfrak{C}=\mathcal{B}\cup \mathfrak{C}$, for any $\mathcal{B},\mathfrak{C}\in IVIFF\left(\mathcal{H}\right)$.

Theorem 23. 

$\left(IVIFF\right(\mathcal{H}),\sqcap ,\bigsqcup ,\varnothing ,\mathcal{H})$ is a bounded distributive lattice.

Proof. 

The proof can be established using techniques similar to those employed in the proofs of (Ref. [23], Theorems 10–12).  □

Theorem 24. 

Let $\mathcal{B}=({\mu }_{\mathcal{B}},{\gamma }_{\mathcal{B}})$ be an IVIF-filter on the set $\mathcal{H}$, and let the fuzzy relation ${\approx }_{\mathcal{B}}$ on $\mathcal{H}$ be defined as follows: for any ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$,

$$\begin{array}{c}\hfill {\hslash }_{{\mathfrak{a}}_x}{\approx }_{\mathcal{B}}{\hslash }_{{\mathfrak{a}}_y}\iff \left\{\begin{array}{c}{\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\wedge {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})={\mu }_{\mathcal{B}}\left(1\right),\hfill \\ {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\vee {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})={\gamma }_{\mathcal{B}}\left(1\right)\hfill \end{array}\right.\end{array}$$

(30)

Then, the relation ${\approx }_{\mathcal{B}}$ is a congruence relation on $\mathcal{H}$.

Proof. 

First, we show that ${\approx }_{\mathcal{B}}$ is an equivalence relation.

Reflexivity: For any ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$, clearly ${\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_x})={\mu }_{\mathcal{B}}\left(1\right)$ and ${\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_x})={\gamma }_{\mathcal{B}}\left(1\right)$. Thus,

$${\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_x})\wedge {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_x})={\mu }_{\mathcal{B}}\left(1\right),$$

$${\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_x})\vee {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_x})={\gamma }_{\mathcal{B}}\left(1\right),$$

which means ${\hslash }_{{\mathfrak{a}}_x}{\approx }_{\mathcal{B}}{\hslash }_{{\mathfrak{a}}_x}$.

Symmetry: The definition of ${\approx }_{\mathcal{B}}$ is symmetric in ${\hslash }_{{\mathfrak{a}}_x}$ and ${\hslash }_{{\mathfrak{a}}_y}$, so ${\hslash }_{{\mathfrak{a}}_x}{\approx }_{\mathcal{B}}{\hslash }_{{\mathfrak{a}}_y}$ implies ${\hslash }_{{\mathfrak{a}}_y}{\approx }_{\mathcal{B}}{\hslash }_{{\mathfrak{a}}_x}$.

Transitivity: Suppose ${\hslash }_{{\mathfrak{a}}_x}{\approx }_{\mathcal{B}}{\hslash }_{{\mathfrak{a}}_y}$ and ${\hslash }_{{\mathfrak{a}}_y}{\approx }_{\mathcal{B}}{\hslash }_{{\mathfrak{a}}_z}$ for some ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H}$. Then,

$${\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\wedge {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})={\mu }_{\mathcal{B}}\left(1\right),{\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\wedge {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_z}\to {\hslash }_{{\mathfrak{a}}_y})={\mu }_{\mathcal{B}}\left(1\right),$$

$${\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\vee {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})={\gamma }_{\mathcal{B}}\left(1\right),{\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\vee {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_z}\to {\hslash }_{{\mathfrak{a}}_y})={\gamma }_{\mathcal{B}}\left(1\right).$$

Using the properties of IVIF-filters (see Proposition 1$\left(a7\right)$, Equations (13) and (12)), we have

$$\begin{array}{ccc}& & {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})\wedge {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_z}\to {\hslash }_{{\mathfrak{a}}_x})\hfill \\ & \ge & {\mu }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\odot ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z}))\wedge {\mu }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_z}\to {\hslash }_{{\mathfrak{a}}_y})\odot ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x}))\hfill \\ & \ge & [{\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\wedge {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})]\wedge [{\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_z}\to {\hslash }_{{\mathfrak{a}}_y})\wedge {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})]\hfill \\ & =& {\mu }_{\mathcal{B}}\left(1\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}& & {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})\vee {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_z}\to {\hslash }_{{\mathfrak{a}}_x})\hfill \\ & \le & {\gamma }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\odot ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z}))\vee {\gamma }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_z}\to {\hslash }_{{\mathfrak{a}}_y})\odot ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x}))\hfill \\ & \le & [{\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\vee {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})]\vee [{\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_z}\to {\hslash }_{{\mathfrak{a}}_y})\vee {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})]\hfill \\ & =& {\gamma }_{\mathcal{B}}\left(1\right).\hfill \end{array}$$

Hence, ${\hslash }_{{\mathfrak{a}}_x}{\approx }_{\mathcal{B}}{\hslash }_{{\mathfrak{a}}_z}$, and ${\approx }_{\mathcal{B}}$ is transitive.

Thus, ${\approx }_{\mathcal{B}}$ is an equivalence relation.

Now, we show that ${\approx }_{\mathcal{B}}$ is a congruence relation. Let ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H}$ such that ${\hslash }_{{\mathfrak{a}}_x}{\approx }_{\mathcal{B}}{\hslash }_{{\mathfrak{a}}_y}$. Then,

$${\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\wedge {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})={\mu }_{\mathcal{B}}\left(1\right),{\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\vee {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})={\gamma }_{\mathcal{B}}\left(1\right).$$

Using the properties of IVIF-filters (see Proposition 2.1 (a2), (a8), and (H3)), we have

$${\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}\le ({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_y}\odot {\hslash }_{{\mathfrak{a}}_z}).$$

Thus, we obtain

$${\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\ge {\mu }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_y}\odot {\hslash }_{{\mathfrak{a}}_z})),$$

and

$${\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\le {\gamma }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_y}\odot {\hslash }_{{\mathfrak{a}}_z})).$$

Similarly, we get

$${\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})\ge {\mu }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_y}\odot {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z})),$$

and

$${\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})\le {\gamma }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_y}\odot {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z})).$$

Therefore, we attain

$$\begin{array}{ccc}{\mu }_{\mathcal{B}}\left(1\right)& =& {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\wedge {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})\hfill \\ & \ge & {\mu }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_y}\odot {\hslash }_{{\mathfrak{a}}_z}))\wedge {\mu }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_y}\odot {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z})),\hfill \end{array}$$

and

$$\begin{array}{ccc}{\gamma }_{\mathcal{B}}\left(1\right)& =& {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\vee {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})\hfill \\ & \le & {\gamma }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_y}\odot {\hslash }_{{\mathfrak{a}}_z}))\vee {\gamma }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_y}\odot {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z})).\hfill \end{array}$$

Thus, we reach ${\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_z}{\approx }_{\mathcal{B}}{\hslash }_{{\mathfrak{a}}_y}\odot {\hslash }_{{\mathfrak{a}}_z}$.

Similarly, using Proposition 1$\left(a7\right)$, for any ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y},{\hslash }_{{\mathfrak{a}}_z}\in \mathcal{H}$, we have

$${\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}\le ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z}),$$

so

$${\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\ge {\mu }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})),$$

and

$${\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\le {\gamma }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})),$$

and similarly for the reverse direction. Hence, we achieve

$$\begin{array}{ccc}{\mu }_{\mathcal{B}}\left(1\right)& =& {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\wedge {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})\hfill \\ & \ge & {\mu }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z}))\wedge {\mu }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})),\hfill \end{array}$$

and

$$\begin{array}{ccc}{\gamma }_{\mathcal{B}}\left(1\right)& =& {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\vee {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})\hfill \\ & \le & {\gamma }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z}))\vee {\gamma }_{\mathcal{B}}(({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z})\to ({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z})).\hfill \end{array}$$

Thus, ${\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_z}{\approx }_{\mathcal{B}}{\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_z}$. Similarly, ${\hslash }_{{\mathfrak{a}}_z}\to {\hslash }_{{\mathfrak{a}}_x}{\approx }_{\mathcal{B}}{\hslash }_{{\mathfrak{a}}_z}\to {\hslash }_{{\mathfrak{a}}_y}$.

Therefore, ${\approx }_{\mathcal{B}}$ is a congruence relation on $\mathcal{H}$.  □

This theorem shows that the fuzzy relation ${\approx }_{\mathcal{B}}$, defined in terms of the IVIF-filter $\mathcal{B}$, is not only an equivalence relation but also compatible with the operations on $\mathcal{H}$. Therefore, ${\approx }_{\mathcal{B}}$ forms a congruence relation on the structure $\mathcal{H}$.

For any ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$, ${\left[{\hslash }_{{\mathfrak{a}}_x}\right]}_{\mathcal{B}}$ denotes the equivalence class of ${\hslash }_{{\mathfrak{a}}_x}$ with respect to ${\approx }_{\mathcal{B}}$. Clearly,

$$\begin{array}{ccc}{\left[{\hslash }_{{\mathfrak{a}}_x}\right]}_{\mathcal{B}}& =& \{{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}\mid {\hslash }_{{\mathfrak{a}}_x}{\approx }_{\mathcal{B}}{\hslash }_{{\mathfrak{a}}_y}\}\hfill \\ & =& \{{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}\mid {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\wedge {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})={\mu }_{\mathcal{B}}\left(1\right),\hfill \\ & & {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\vee {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})={\gamma }_{\mathcal{B}}\left(1\right)\}\hfill \end{array}$$

For any ${\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}$, ${\left[{\hslash }_{{\mathfrak{a}}_x}\right]}_{\mathcal{B}}$ denotes the equivalence class of ${\hslash }_{{\mathfrak{a}}_x}$ with respect to ${\approx }_{\mathcal{B}}$. Clearly,

$$\begin{array}{ccc}{\left[{\hslash }_{{\mathfrak{a}}_x}\right]}_{\mathcal{B}}& =& \{{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}\mid {\hslash }_{{\mathfrak{a}}_x}{\approx }_{\mathcal{B}}{\hslash }_{{\mathfrak{a}}_y}\}\hfill \\ & =& \{{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}\mid {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\wedge {\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})={\mu }_{\mathcal{B}}\left(1\right),\hfill \\ & & {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})\vee {\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_y}\to {\hslash }_{{\mathfrak{a}}_x})={\gamma }_{\mathcal{B}}\left(1\right)\}\hfill \end{array}$$

Theorem 25. 

Let ${\displaystyle \frac{\mathcal{H}}{{\approx }_{\mathcal{B}}}}=\{{\left[{\hslash }_{{\mathfrak{a}}_x}\right]}_{\mathcal{B}}\mid {\hslash }_{{\mathfrak{a}}_x}\in \mathcal{H}\}$, and let the operations ⊙ and → on ${\displaystyle \frac{\mathcal{H}}{{\approx }_{\mathcal{B}}}}$ be defined as follows:

$${\left[{\hslash }_{{\mathfrak{a}}_x}\right]}_{\mathcal{B}}\odot {\left[{\hslash }_{{\mathfrak{a}}_y}\right]}_{\mathcal{B}}={[{\hslash }_{{\mathfrak{a}}_x}\odot {\hslash }_{{\mathfrak{a}}_y}]}_{\mathcal{B}}\mathit{and}{\left[{\hslash }_{{\mathfrak{a}}_x}\right]}_{\mathcal{B}}\to {\left[{\hslash }_{{\mathfrak{a}}_y}\right]}_{\mathcal{B}}={[{\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y}]}_{\mathcal{B}}.$$

Also, we define a binary relation on ${\displaystyle \frac{\mathcal{H}}{{\approx }_{\mathcal{B}}}}$ by

$${\left[{\hslash }_{{\mathfrak{a}}_x}\right]}_{\mathcal{B}}\le {\left[{\hslash }_{{\mathfrak{a}}_y}\right]}_{\mathcal{B}}\mathit{if}\mathit{and}\mathit{only}\mathit{if}{\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})={\mu }_B\left(1\right)\mathit{and}{\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to y)={\gamma }_{\mathcal{B}}\left(1\right),$$

for any ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}.$ Clearly, $({\displaystyle \frac{\mathcal{H}}{{\approx }_{\mathcal{B}}}},⪯)$ is a poset. Then, $({\displaystyle \frac{\mathcal{H}}{{\approx }_{\mathcal{B}}}},\odot ,\to ,{\left\{1\right\}}_{\mathcal{B}})$ is a hoop.

Proof. 

We have ${\left[{\hslash }_{{\mathfrak{a}}_x}\right]}_{\mathcal{B}}={\left[{\hslash }_{{\mathfrak{a}}_y}\right]}_{\mathcal{B}}$ and ${\left[\mathfrak{p}\right]}_{\mathcal{B}}={\left[\mathfrak{q}\right]}_{\mathcal{B}}$ if and only if ${\hslash }_{{\mathfrak{a}}_x}{\approx }_{\mathcal{B}}{\hslash }_{{\mathfrak{a}}_y}$ and $\mathfrak{p}{\approx }_{\mathcal{B}}\mathfrak{q}$. Since ${\approx }_{\mathcal{B}}$ is the congruence relation on $\mathcal{H}$, it follows that all the above operations are well-defined. Thus, by routine calculations, we can conclude that ${\displaystyle \frac{\mathcal{H}}{{\approx }_{\mathcal{B}}}}$ is a hoop.

Now, we define a binary relation on ${\displaystyle \frac{\mathcal{H}}{{\approx }_{\mathcal{B}}}}$ by ${\left[{\hslash }_{{\mathfrak{a}}_x}\right]}_{\mathcal{B}}\le {\left[y\right]}_B$ if and only if ${\mu }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})={\mu }_{\mathcal{B}}\left(1\right)$ and ${\gamma }_{\mathcal{B}}({\hslash }_{{\mathfrak{a}}_x}\to {\hslash }_{{\mathfrak{a}}_y})={\gamma }_B\left(1\right)$, for any ${\hslash }_{{\mathfrak{a}}_x},{\hslash }_{{\mathfrak{a}}_y}\in \mathcal{H}$.

We can clearly see that $({\displaystyle \frac{\mathcal{H}}{{\approx }_{\mathcal{B}}}},⪯)$ is a partial order monoid.  □

This theorem establishes that the quotient structure ${\displaystyle \frac{\mathcal{H}}{{\approx }_{\mathcal{B}}}}$, formed by the congruence relation ${\approx }_{\mathcal{B}}$, inherits the hoop structure from $\mathcal{H}$ with well-defined operations. Moreover, the induced order on the quotient set makes $({\displaystyle \frac{\mathcal{H}}{{\approx }_{\mathcal{B}}}},\odot ,\to ,{\left\{1\right\}}_{\mathcal{B}})$ a partially ordered hoop.

As a result, to clarify the relationships between the main structures discussed in this study, Figure 1 visually summarizes the connections among hoop algebras, sub-hoops, filters, IVIF sets, and implicative filters.

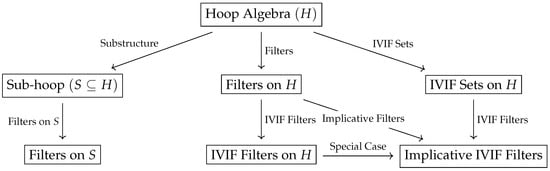
Figure 1. Diagram showing the relationships between hoop algebras, sub-hoops, filters, IVIF sets, and implicative filters.

4. Conclusions

In this manuscript, we have developed a comprehensive and systematic framework for the study of interval-valued intuitionistic fuzzy (IVIF) filters within the context of hoop algebras. Our investigation has deepened the understanding of the algebraic and logical properties of IVIF filters, extending classical fuzzy and intuitionistic fuzzy set theory into the more expressive interval-valued intuitionistic domain.

A key contribution of our work is the detailed characterization of IVIF filters, including their structural properties and their relationships with sub-hoops, implicative filters, and deductive systems. We have established necessary and sufficient conditions for the existence and classification of IVIF filters, and demonstrated how these filters can be constructed and analyzed via membership and non-membership functions. The interplay between IVIF filters and other algebraic structures, such as residuated lattices and MV-algebras, has been explored to highlight both their theoretical richness and practical versatility.

Additionally, we introduced and analyzed implicative IVIF filters, providing a nuanced classification and extending the theoretical landscape of filter theory in fuzzy algebraic systems. The study of operations—including intersections, unions, and generated filters—has yielded a robust toolkit for the manipulation of IVIF filters in both theoretical and applied contexts.

As part of our discussion, we have contextualized these findings by illustrating how IVIF filters enhance the modeling and handling of uncertainty, particularly in logical inference and automated reasoning systems. The integration of interval-valued intuitionistic fuzzy sets into hoop algebras offers a powerful formalism for representing vagueness and incomplete information, which is essential for advanced applications in decision-making, data analysis, and artificial intelligence. For example, IVIF filters can provide more flexible and robust reasoning mechanisms in multi-criteria decision analysis, risk assessment, and resource allocation, where uncertainty is inherent.

Looking ahead, several promising directions for future research emerge from our results. These include the study of IVIF filters in dynamic and temporal extensions of hoop algebras, which could facilitate novel applications in temporal logic, dynamic systems, and quantum logic. Investigating probabilistic and fuzzy measures on IVIF filters may yield new insights into the probabilistic interpretation of logical operations and their applications in uncertainty modeling. Furthermore, extending the theory of IVIF filters to other algebraic frameworks, such as Heyting algebras, Gödel algebras, and other systems in intuitionistic and many-valued logics, could unify filter theory across diverse logical systems and foster interdisciplinary research.

In summary, our findings establish the foundational theory of IVIF filters in hoop algebras, provide a thorough discussion of their significance and applications, and identify clear avenues for future exploration. We hope that this work will stimulate further research and practical advancements in the modeling of uncertainty and the development of intelligent systems capable of reasoning under vagueness and imprecision.