Secure Computation Schemes for Mahalanobis Distance Between Sample Vectors in Combating Malicious Deception

Abstract

In the context of rapid advancements in big data and artificial intelligence, similarity measurement methods between samples have been widely applied in data mining, pattern recognition, medical diagnosis, financial risk control, and other fields. The Mahalanobis distance, due to its effectiveness in capturing correlations within high-dimensional data, has become a crucial tool in many practical scenarios. However, sample data often contains sensitive privacy information, making it essential to achieve secure and privacy-preserving computation of Mahalanobis distance. This paper proposes a secure Mahalanobis distance calculation scheme tailored for sample vectors that effectively resists malicious cheating behaviors. The designed multi-party computation algorithms ensure privacy protection while maintaining computational efficiency and minimizing communication overhead. The experimental results compare three algorithms in terms of execution time and communication delay across varying sample sizes and vector dimensions. The results demonstrate that our proposed scheme achieves a favorable balance between security and performance. This research provides a practical and robust solution for similarity measurement under privacy constraints and lays a theoretical and practical foundation for secure data collaboration in multi-party computing environments, offering significant application potential.

1. Introduction

With the rapid development of new-generation information technologies, global data volumes have experienced explosive growth, and data has become a critical strategic resource for competition across all fields worldwide. To fully unleash the value of data, cross-departmental, cross-regional, and cross-system multi-source data sharing is essential. However, data security and compliance issues pose significant challenges to data sharing. As one of the core technologies of privacy computing, secure multi-party computation (MPC) enables the realization of data value while ensuring data security and compliance. MPC is an interdisciplinary technology system covering cryptography, artificial intelligence, big data, blockchain, and other fields. It provides a solution to the contradiction between data privacy and sharing and has demonstrated enormous potential in practical applications [1,2,3].

Secure multi-party computation is a privacy-preserving computation method that allows multiple participants to compute results without disclosing their private data. MPC can be applied in finance, healthcare, e-commerce, and other fields to protect user privacy and data security. MPC originated from the “millionaire problem” proposed by Professor Andrew Chi-Chih Yao, a computer scientist, in 1982 [4]. Subsequently, researchers such as Goldreich conducted in-depth studies on MPC [5,6,7]. The research areas of secure multi-party computation include private data mining, private computational geometry and set problems [8,9,10,11,12,13], private scientific computation [14,15,16,17,18], private statistical analysis [19,20,21,22], and private database query [23,24,25,26]. These studies have continuously advanced the development of secure multi-party computation and successfully solved many practical problems.

The Mahalanobis distance is a measure used to quantify the difference between samples. By performing linear transformations on data and calculating covariance, it effectively handles data correlation. In the fields of statistics and machine learning, the Mahalanobis distance is widely applied in clustering, classification, outlier detection, and pattern recognition [27,28,29,30,31]. Privately computing the Mahalanobis distance holds significant theoretical and practical value.

Mahalanobis distance, as an effective tool for measuring correlations and differences among multivariate data, has demonstrated significant value in a variety of real-world applications. For example:

(1)

Healthcare: In gene expression analysis and disease diagnosis, Mahalanobis distance enables accurate classification and anomaly detection of pathological samples, contributing to improved diagnostic precision and personalized medical care.

(2)

Financial Risk Control: Financial institutions utilize Mahalanobis distance to identify abnormal transactions and potential fraud. This facilitates enhanced risk management and credit evaluation, thus ensuring the stability and security of financial systems.

(3)

Pattern Recognition and Computer Vision: In areas such as face recognition and image matching, Mahalanobis distance effectively captures distribution differences in feature spaces, leading to improved algorithm robustness and recognition accuracy.

(4)

Secure Collaborative Computing Environments: In scenarios where multiple organizations need to share data without compromising privacy—such as joint diagnoses by medical institutions or cross-department financial risk analysis—secure computation algorithms integrated with Mahalanobis distance become essential. They enable collaborative analysis while protecting sensitive information.

However, given the high sensitivity of data involved in these applications, achieving efficient and secure distance computation under privacy preservation remains a critical challenge. In response to the threats posed by malicious attacks and cheating behaviors, this paper presents a multi-party secure computation scheme that both protects data privacy and ensures trustworthy Mahalanobis distance evaluation, thus providing technical support for the above-mentioned practical applications.

1.1. Related Work

In recent years, scholars have achieved some research results on the private computation of the Mahalanobis distance, but no solutions resistant to malicious deception have been found. Reference [32] proposes a disease diagnosis scheme based on a secure Mahalanobis distance evaluation model under the semi-honest model, suitable for scenarios with large sample sizes. This scheme utilizes the Okamoto–Uchiyama homomorphic encryption algorithm and Homomorphic Re-Encryption Scheme (HRES) and integrates outsourced cloud computing technology. Reference [33] designs a private comparison method for Mahalanobis distances to improve the accuracy of medical image retrieval, proposing a scheme that combines a Mahalanobis distance-based fuzzy algorithm to achieve precise and privacy-preserving medical image retrieval on encrypted data. Reference [34] presents a private distance evaluation method based on the Mahalanobis distance for measuring the correlation between workers and tasks in perturbed locations. Reference [35] proposes a cloud-assisted medical pre-diagnosis scheme based on private computation of the Mahalanobis distance, allowing patients to securely query outsourced models and obtain pre-diagnosis results. Reference [36] addresses the privacy protection of user diagnostic data in disease diagnosis services by proposing a disease diagnosis scheme based on a secure Mahalanobis distance evaluation model. All the above schemes are designed under the semi-honest model and do not consider how to detect or resist malicious deception by malicious participants.

In terms of Mahalanobis distance applications, Reference [37] proposes a robust multi-source fusion robust estimation method based on the Mahalanobis distance, which constructs a robust Mahalanobis distance test statistic from adjacent sequences based on an analysis of the fault propagation characteristics of observations and typical variance inflation robust estimation models. Reference [38] develops a Mahalanobis distance-based outlier filtering algorithm that performs a statistical analysis on the neighborhood of each point, calculates its Mahalanobis distance to nearby points, and removes substantial random noise in train car point clouds. Reference [39] uses the Mahalanobis distance method to calculate the similarity between the measured current–voltage data of a photovoltaic array and the output data of a simulation model for fault monitoring. Reference [40] employs a Mahalanobis distance-based similarity matrix to identify equipment operating environments and invokes corresponding equipment deduction models to achieve precise deduction of equipment status under complex working conditions. These schemes only use the Mahalanobis distance to solve practical application problems but do not address how to compute it privately.

In summary, while some progress has been made in Mahalanobis distance research, studies on its private computation remain limited. Existing schemes are adapted to scenarios different from those in this paper, and no solutions resistant to malicious deception have been identified. The schemes proposed in this paper are suitable for small-sample scenarios and do not require outsourced computation. This paper presents efficient two-party and multi-party private computation algorithms for the Mahalanobis distance under the semi-honest model and further proposes a multi-party protocol that prevents malicious participants from cheating in critical steps. This research further expands the field of secure computational geometry.

1.2. Motivation and Novelty of the Proposed Method

With the rapid development of big data and artificial intelligence technologies, similarity measurement methods between samples have been widely applied in various fields, including data mining, pattern recognition, medical diagnosis, and financial risk control. Among them, Mahalanobis distance has become a fundamental tool in many real-world applications due to its effectiveness in modeling correlations within high-dimensional data. However, as the scale of data and the depth of applications continue to expand, the need to protect data privacy and ensure security has become increasingly prominent. In practice, sample data often contain sensitive personal or institutional information. Computing with such data directly in an unprotected environment may lead to significant privacy leakage risks and may also open the door for adversarial attacks such as data injection and tampering. Therefore, there is an urgent need to design secure Mahalanobis distance computation schemes that can preserve data privacy and resist malicious behaviors.

In response to the limitations of existing solutions—such as low computational efficiency, high communication overhead, and poor resilience against adversarial behavior—this paper proposes a novel approach for secure Mahalanobis distance computation over sample vectors. Specifically, we design a multi-party secure computation protocol that enables different parties to jointly compute the Mahalanobis distance without revealing their private data. Furthermore, through innovative mechanisms, the proposed scheme effectively defends against dishonest participants during the computation process. Compared with traditional secure distance computation methods, our scheme not only theoretically guarantees privacy and security but also optimizes communication and computation resources, significantly improving overall practicality and scalability. This approach provides an innovative solution for the secure processing of high-dimensional correlated data in collaborative data analysis and distributed intelligent decision-making scenarios and holds substantial theoretical and practical significance.

1.3. Contributions

(1) Based on the fully homomorphic NTRU (Nth-degree Truncated Polynomial Ring Unit) encryption algorithm and randomization techniques, this paper first proposes a two-party private computation protocol for the Mahalanobis distance under the semi-honest model. Suitable for scenarios with few sample vectors, it eliminates the need for outsourced computation. The protocol’s correctness is analyzed, and its security is proven using the simulation paradigm.

(2) Building on the two-party private computation protocol, a multi-party private computation protocol is proposed by integrating the fully homomorphic NTRU encryption algorithm and randomization techniques. This protocol allows multiple users to jointly compute the Mahalanobis distance, expanding the application scenarios of the two-party protocol and providing a foundation for designing multi-party algorithms resistant to malicious deception. The protocol simplifies multi-party interactive computation into five processes: multi-party encryption of plaintexts, computation of the inverse covariance matrix, computation of the ciphertext of the Mahalanobis distance, single-party decryption of the ciphertext, and multi-party restoration of plaintexts. The protocol’s correctness is analyzed, and its security is proven using the simulation paradigm.

(3) Aiming at potential malicious behaviors in multi-party algorithms, this paper, for the first time, proposes a multi-party secure computation protocol for the Mahalanobis distance against malicious deception by integrating zero-knowledge proof techniques. This ensures that multi-party participants have equal status in critical steps, fairly obtain the final result, and can verify the outcome. The protocol’s correctness is analyzed, and its security is proven. Through performance analysis, experimental simulation, and comparison with related schemes, the efficiency of the proposed algorithms is validated.

Figure 1 is the flowchart of the research methodology in this paper.

1.4. Structure

Section 2 introduces preliminary knowledge, including the fully homomorphic NTRU encryption algorithm, security definitions under the semi-honest model, and an overview of the Mahalanobis distance, providing a foundation for the protocol design in subsequent sections. Section 3 presents a two-party secure computation protocol for the Mahalanobis distance under the semi-honest model, analyzes its correctness, and proves its security using the simulation paradigm. Section 4 proposes a multi-party secure computation protocol for the Mahalanobis distance under the semi-honest model, analyzes its correctness, and proves its security via simulation. Section 5 introduces a multi-party private computation protocol for the Mahalanobis distance in anti-deception scenarios, analyzes its correctness, and proves its security using the simulation paradigm. Section 6 evaluates the performance of the proposed algorithms and compares them with existing schemes. Finally, Section 7 concludes the paper.

2. Preliminary Knowledge

2.1. Fully Homomorphic NTRU Encryption Algorithm

The NTRU encryption algorithm is strongly related to the shortest vector problem on computational lattices. This algorithm possesses quantum-resistant capabilities and demonstrates excellent performance in terms of speed and security [41]. Reference [42] proposes a fully homomorphic NTRU encryption scheme, which exhibits full homomorphic properties, i.e., it simultaneously supports additive and multiplicative homomorphisms.

The following introduces the $BitDecomp$, $BitDecom{p}^{-1}$, and $Flatten$ functions [43].

The $BitDecomp$ function decomposes a vector $a=(a_0, \cdots , a_{k-1})$ into its bitwise representation as follows:

$$BitDecomp(a)=(a_{0,0}, \cdots , a_{0,l-1}, \cdots , a_{k-1,0}, \cdots , a_{k-1,l-1})$$

(1)

The $BitDecom{p}^{-1}$ function recovers the vector from its bitwise representation:

$$BitDecom{p}^{-1}(a)=({\displaystyle \sum 2^j{a}_{0,j}}, \cdots , {\displaystyle \sum 2^j{a}_{k-1,j}})$$

(2)

The $Flatten$ function is defined as

$$Flatten(a)=BitDecomp(BitDecom{p}^{-1}(a))$$

(3)

Key Generation:

Input: $n,q\in R$, $p\in R_q^{*}$, $\sigma \in ℝ$, where $R_q^{*}$ is the set of invertible elements in $R_q=R/qR=Z_q[x]/\Phi$.

Output: A key pair $(sk,pk)\in R\times R_q^{*}$.

Encryption:

Select a plaintext $m$. Run the improved NTRU encryption algorithm to encrypt 0, obtaining a ciphertext vector $c$ of length $l=\log q$, where $c=(c_{l-1},c_{l-2},\cdots ,c_0)$. Each $c_i$ is a ciphertext generated by encrypting 0 using the improved NTRU encryption scheme [42].

Convert $c$ into an $l\times l$ matrix $C$: $C=BitDecomp(c^T)=(c_{l-1}^T,c_{l-2}^T,\cdots ,c_0^T)$, where $c_i^T$ is a binary polynomial.

Compute $C^{\prime }=Flatten(I_l·m+C)$ where $I_l$ is the $l\times l$ identity matrix. $C^{\prime }$ is the ciphertext matrix corresponding to the message $m$.

Decryption:

Take the last row of the matrix $C^{\prime }$, and perform the following calculation:

$$BitDecom{p}^{-1}({C^{\prime }}_{(0,l-1)},{C^{\prime }}_{(0,l-2)},\cdots ,{C^{\prime }}_{(0,0)})=C_0$$

(4)

Recover the plaintext: $m=⌊C_{0}f⌋=\mathrm{mod}p$

Additive Homomorphism: $E(m_1)+E(m_2)==E(m_1+m_2)$, where $E$ denotes encryption and $m_1$, $m_2$ are plaintexts.

Multiplicative Homomorphism: $E(m_1)·E(m_2)==E(m_1·m_2)$, where $E$ denotes encryption and $m_1$, $m_2$ are plaintexts.

Handling Decimal Encryption:

The NTRU encryption system is based on polynomial operations, all performed in integer or binary environments. Therefore, to encrypt decimals, they are typically converted to integers or binary form first. In this study, the strategy is to multiply decimals by a predetermined factor (e.g., ${10}^4$) during encryption and restore the decrypted integers to their decimal form during decryption.

2.2. Security Definition Under Semi-Honest Model

Semi-Honest Model: In a semi-honest protocol, participants strictly follow every step of the protocol, do not provide false information, do not interrupt the execution of the protocol, and do not collude with other participants to attack the protocol. However, they will record the public information in the protocol to attempt to deduce the information of other participants [44,45,46].

Suppose the two parties involved in the secure computation are Steven and Tom, where Steven has the data $x$ and Tom has the data $y$. The goal is to collaboratively compute a probabilistic polynomial–time function $f(x,y)=(f_1(x,y),f_2(x,y))$ while ensuring the privacy of $x$ and $y$. Let $\pi$ be the protocol for computing $f$. $vie{w}_1^{\pi }(x,y)=(x,r_1,m_1^1,\cdots ,m_1^t,f_1(x,y))$ is the sequence of information obtained by Steven during the execution of the protocol, where $r_1$ is the random number chosen by Steven and $m_1^i$ ($i=1,\cdots ,t$) is the $i$-th message received by Steven. After the execution of the protocol $\pi$, Steven obtains the result $f_1(x,y)$. The definition for Tom can be made similarly.

Definition 1.

Suppose  $f(x,y)=(f_1(x,y),f_2(x,y))$ is a two-party computation function, where  $x$ and $y$ represent the input values of the two participants, respectively; $f_1(x,y)$ and $f_2(x,y)$ represent the function values obtained by the two parties; and $\pi$ is a secure protocol for computing $f$. If there exist probabilistic polynomial–time algorithms $S_1$ and $S_2$ satisfying

$${\{S_1(x,f_1(x,y))\}}_{x,y}\stackrel{c}{\equiv }{\{vie{w}_1^{\pi }(x,y)\}}_{x,y}$$

(5)

$${\{S_2(y,f_2(x,y))\}}_{x,y}\stackrel{c}{\equiv }{\{vie{w}_2^{\pi }(x,y)\}}_{x,y}$$

(6)

then $\pi$ securely computes the function $f$ and $\stackrel{c}{\equiv }$ denotes computational indistinguishability.

2.3. Mahalanobis Distance

The Mahalanobis distance is a method used to measure the dissimilarity between samples. It was first proposed by Indian statistician P. C. Mahalanobis in 1936 [27]. The Mahalanobis distance takes into account the correlation between data features, making it significant for handling data with different scales and correlations. This measurement method has a wide range of applications in fields such as statistics and machine learning and is often used in tasks like clustering, classification, pattern recognition, and anomaly detection. The Mahalanobis distance can quantify the similarity or dissimilarity between two samples—the smaller the distance, the more similar the data.

Covariance between vectors:

Let $A$ and $B$ represent two $n$-dimensional column vectors, where $A={(a_1,a_2, \cdots , a_n)}^T$ and $B={(b_1,b_2, \cdots , b_n)}^T$. The covariance between $A$ and $B$ is

$$Cov(A,B)={\displaystyle \frac{{\displaystyle {\sum }_{\mathrm{i}=1}^n(a_i-\overline{a})(b_i-\overline{b})}}{n-1}}$$

(7)

Mahalanobis distance between vectors:

Suppose two $n$-dimensional column vectors $A={(a_1,a_2, \cdots , a_n)}^T$ and $B={(b_1,b_2, \cdots , b_n)}^T$ follow the same distribution, and $\Sigma$ denotes their covariance matrix. The Mahalanobis distance between vectors $A$ and $B$ is

$$MD(A,B)=\sqrt{{(A-B)}^T{\Sigma }^{-1}(A-B)}$$

(8)

where $\Sigma$ is a matrix symmetric about the main diagonal, and ${\Sigma }^{-1}$ represents the inverse of the covariance matrix $\Sigma$.

2.4. Zero-Knowledge Proof

Zero-knowledge proof is a critical tool in secure multi-party computation, used to prove that a statement is true without disclosing detailed information about the statement [45]. In zero-knowledge proof, a prover can demonstrate to a verifier that they know a secret without revealing the content of the secret.

The following introduces the zero-knowledge proof scheme proposed in this paper and used in the multi-party secure computation protocol for Mahalanobis distance between sample vectors against malicious deception.

Using the homomorphic NTRU encryption algorithm in Section 2.1, assume participant $P_1$ holds the ciphertext $E(x)$ (where the symbol $E$ denotes encryption and $x$ represents the encrypted data), and $P_1$ does not know any information about $x$. $P_1$ possesses the public encryption key $pk$ of the encryption system, while participant $P_2$ holds the private decryption key $sk$.

(1)

$P_1$ selects two sets of random numbers $r_1$, $r_2$ and $t_1$, $t_2$ and then performs the following calculations:

$$E(d_1)=r_{1}E(x)+E(t_1)$$

(9)

$$E(d_2)=r_{2}E(x)+E(t_2)$$

(10)

$P_1$ sends $E(d_1)$ and $E(d_2)$ to $P_2$.

(2)

$P_2$ decrypts $E(d_1)$ and $E(d_2)$ into $d_1$ and $d_2$, respectively, and then sends $d_1$ and $d_2$ to $P_1$.

(3)

$P_1$ verifies whether $d_1=r_1((d_2-t_2)/r_2)+t_1$ holds to determine whether $P_2$ is correctly decrypted and sends $E(d_1)$ and $E(d_2)$ (the proof is omitted). After successful verification, $P_1$ can obtain the information for $x$ by calculating $x=(d_1-t_1)/r_1$ or $x=(d_2-t_2)/r_2$. Specific applications and explanations are provided in Section 5 of this paper.

3. Two-Party Secure Computation Protocol for Mahalanobis Distance Under Semi-Honest Model

Problem Description: Suppose two participants $P_1$ and $P_2$, respectively, hold private sample vectors $x_i^1$ and $x_j^2$ that follow the same distribution, where $i=1,2, \cdots , m_1$, $j=1,2, \cdots , m_2$. Both $x_i^1$ and $x_j^2$ are $n$-dimensional vectors ($n>\max (m_1,m_2)$), i.e., $x_i^1=(x_{i1}^1, x_{i2}^1, \cdots , x_{in}^1)$, $x_j^2=(x_{j1}^2, x_{j2}^2, \cdots , x_{jn}^2)$. Each party wants to confidentially compute the Mahalanobis distance $M{D}_{ij}$ between each pair of sample vectors $x_i^1$ and $x_j^2$ without disclosing their private sample vectors.

Solution Approach: Participant $P_1$ runs the NTRU encryption scheme to generate a public/private key pair $pk/sk$ and sends the public key $pk$ to $P_2$; $P_1$ and $P_2$ jointly compute the covariance matrix; $P_2$ computes the Mahalanobis distance between the two vectors in the ciphertext state; and $P_1$ decrypts the final computation result to obtain the Mahalanobis distance between the two vectors and notifies $P_2$.

3.1. Specific Protocol

Based on the calculation principle of Mahalanobis distance and combining the homomorphic NTRU encryption algorithm with randomized methods, a two-party secure computation protocol for Mahalanobis distance between sample vectors under the semi-honest model (Algorithm 1) is designed. Figure 2 shows the flowchart of Algorithm 1.

Algorithm 1: Two-party secure computation protocol for Mahalanobis distance between sample vectors under semi-honest model.

Input: Multiple $n$-dimensional private sample vectors $x_i^1$ and $x_j^2$ owned by participants $P_1$ and $P_2$, respectively, where $i=1,2,\cdots ,m_1$, $j=1,2,\cdots ,m_2$, $m_1>1$, $m_2>1$, and $n>\max (m_1,m_2)$.

Output: The Mahalanobis distance $f(x_i^1,x_j^2)=M{D}_{ij}=\sqrt{{(x_i^1-x_j^2)}^T{\Sigma }^{-1}(x_i^1-x_j^2)}$ between each pair of sample vectors $x_i^1$ and $x_j^2$.

Preparation: Participant $P_1$ runs the NTRU encryption scheme to generate a public/private key pair $pk/sk$ and sends the public key $pk$ to $P_2$.

(1) $P_1$ uses the public key $pk$ to encrypt each element of its sample vectors $x_1^1,x_2^1,\cdots ,x_{m_1}^1$ and the negated sample vectors $-x_1^1,-x_2^1,\cdots ,-x_{m_1}^1$ term by term, obtaining $$E_{pk}(x_i^1)=\left(E(x_{i1}^1),E(x_{i2}^1),\cdots ,E(x_{in}^1)\right)$$ (11) $$E_{pk}(-x_i^1)=\left(E(-x_{i1}^1),E(-x_{i2}^1),\cdots ,E(-x_{in}^1)\right)$$ (12) where $i=1,2,\cdots ,m_1$. Then, $P_1$ $\mathrm{sends} E_{pk}(x_i^1)$ and $E_{pk}(-x_i^1)$ to $P_2$.

(2) $P_2$ uses the public key $pk$ to encrypt each element of its sample vectors $x_1^2,x_2^2,\cdots ,x_{m_2}^2$ and the negated sample vectors $-x_1^2,-x_2^2,\cdots ,-x_{m_2}^2$ term by term, obtaining $$E_{pk}(x_j^2)=\left(E(x_{j1}^2),E(x_{j2}^2),\cdots ,E(x_{jn}^2)\right)$$ (13) $$E_{pk}(-x_j^2)=\left(E(-x_{j1}^2),E(-x_{j2}^2),\cdots ,E(-x_{jn}^2)\right)$$ (14) where $j=1,2,\cdots ,m_2$.

(3) $P_2$ combines all $E_{pk}(x_i^1)$ and $E_{pk}(x_j^2)$ into a ciphertext matrix $E(A)$ of size $(m_1+m_2)\times n$ and combines all $E_{pk}(-x_i^1)$ and $E_{pk}(-x_j^2)$ into a ciphertext matrix $E(B)$ of size $(m_1+m_2)\times n$: $$E(A)=\left(\begin{array}{cccc}E(x_{11}^1)& E(x_{12}^1)& \cdots & E(x_{1n}^1)\\ \cdots & \cdots & \cdots & \cdots \\ E(x_{m_{1}1}^1)& E(x_{m_{1}2}^1)& \cdots & E(x_{m_{1}n}^1)\\ E(x_{11}^2)& E(x_{12}^2)& \cdots & E(x_{1n}^2)\\ \cdots & \cdots & \cdots & \cdots \\ E(x_{m_{2}1}^2)& E(x_{m_{2}2}^2)& \cdots & E(x_{m_{2}n}^2)\end{array}\right) E(B)=\left(\begin{array}{cccc}E(-x_{11}^1)& E(-x_{12}^1)& \cdots & E(-x_{1n}^1)\\ \cdots & \cdots & \cdots & \cdots \\ E(-x_{m_{1}1}^1)& E(-x_{m_{1}2}^1)& \cdots & E(-x_{m_{1}n}^1)\\ E(-x_{11}^2)& E(-x_{12}^2)& \cdots & E(-x_{1n}^2)\\ \cdots & \cdots & \cdots & \cdots \\ E(-x_{m_{2}1}^2)& E(-x_{m_{2}2}^2)& \cdots & E(-x_{m_{2}n}^2)\end{array}\right)$$ (15) $P_2$ performs the following calculation: $$E(-Y_k)=E(-x_{1k}^1)+\cdots +E(-x_{m_{1}k}^1)+E(-x_{1k}^2)+\cdots +E(-x_{m_{2}k}^2)$$ (16) where $k=1,2,\cdots ,n$. $P_2$ $\mathrm{sends} E(-Y_k)$ to $P_1$.

(4) $P_1$ $\mathrm{decrypts} E(-Y_k)$ to obtain $-Y_k$, then performs the following calculation, $$-{\overline{Y}}_k={\displaystyle \frac{1}{m_1+m_2}}(-Y_k)$$ (17) and sends $-{\overline{Y}}_k$ $\mathrm{to} P_2$.

(5) $P_2$ encrypts $-{\overline{Y}}_k$ with the public key $pk$ to obtain $E(-{\overline{Y}}_k)$, and performs the following calculation: $$E(c_{kl})={\displaystyle \sum _{i=1}^{m_1}\left(\left(E(x_{ik}^1)+E(-{\overline{Y}}_k)\right)\left(E(x_{il}^1)+E(-{\overline{Y}}_l)\right)\right)}+{\displaystyle \sum _{j=1}^{m_2}\left(\left(E(x_{jk}^2)+E(-{\overline{Y}}_k)\right)\left(E(x_{jl}^2)+E(-{\overline{Y}}_l)\right)\right)}$$ (18) where $k=1,2,\cdots ,n$, $l=1,2,\cdots ,n$. $P_2$ $\mathrm{sends} E(c_{kl})$ to $P_1$.

(6) $P_1$ $\mathrm{decrypts} E(c_{kl})$ to obtain $c_{kl}$ and performs the following calculation: $${\mathrm{cov}}_{kl}={\displaystyle \frac{1}{m_1+m_2-1}}{c}_{kl}$$ (19) where $k=1,2,\cdots ,n$, $l=1,2,\cdots ,n$, and $k\le l$. $P_1$ constructs a main diagonal symmetric covariance matrix $\Sigma$ of size $n\times n$ from all ${\mathrm{cov}}_{kl}$: $$\Sigma =\left(\begin{array}{cccc}{\mathrm{cov}}_{11}& {\mathrm{cov}}_{12}& \cdots & {\mathrm{cov}}_{1n}\\ {\mathrm{cov}}_{21}& {\mathrm{cov}}_{22}& \cdots & {\mathrm{cov}}_{2n}\\ \cdots & \cdots & \cdots & \cdots \\ {\mathrm{cov}}_{n1}& {\mathrm{cov}}_{n2}& \cdots & {\mathrm{cov}}_{nn}\end{array}\right)$$ (20) where $\Sigma$ is the plaintext covariance matrix of $E(A)$. $P_1$ computes the inverse matrix ${\Sigma }^{-1}$ of $\Sigma$$(\mathrm{size} n\times n$) and sends ${\Sigma }^{-1}$ to $P_2$.

(7) $P_2$ performs the following calculation: $$E(d_{ij})={\left(E_{pk}(x_i^1)+E_{pk}(-x_j^2)\right)}^T{\Sigma }^{-1}\left(E_{pk}(x_i^1)+E_{pk}(-x_j^2)\right)$$ (21) where $i=1,2,\cdots ,m_1$, $j=1,2,\cdots ,m_2$. $P_2$ forms the calculation results $E(d_{ij})$ into a ciphertext vector, $$V=\left(E(d_{ij})\right)=\left(E(d_{11}),\cdots ,E(d_{1m_2}),\cdots ,E(d_{m_{1}1}),\cdots ,E(d_{m_1{m}_2})\right)$$ (22) and sends $V$$\mathrm{to} P_1$.

(8) $P_1$ decrypts each element $E(d_{ij})$ in the ciphertext vector $V$ in sequence to obtain $d_{ij}$, then takes the square root of $d_{ij}$, i.e., computes $M{D}_{ij}=\sqrt{d_{ij}}$, and forms a vector $MD$ from $M{D}_{ij}$: $$MD=\left(M{D}_{ij}\right)=\left(M{D}_{11},\cdots ,M{D}_{1m_2},\cdots ,M{D}_{m_{1}1},\cdots ,M{D}_{m_1{m}_2}\right)$$ (23)

(9) Each element $M{D}_{ij}$ in $MD$ is the Mahalanobis distance $f(x_i^1,x_j^2)$ between the sample vectors $x_i^1$ and $x_j^2$ of the two participants. $P_1$ sends $MD$ to $P_2$.

End of Algorithm 1.

3.2. Correctness Analysis

(1) In Steps (1) and (2) of Algorithm 1, since the homomorphic NTRU encryption algorithm cannot directly perform subtraction on ciphertexts, each participant encrypts their sample vectors $x_i^1$ and $x_j^2$ as well as their negated versions $-x_i^1$ and $-x_j^2$, and sends them to $P_2$ for subsequent calculations.

(2) In Steps (3) and (5), because the NTRU encryption scheme used in this paper has additive and multiplicative homomorphic properties, the computations of $E(-Y_k)$ and $E({\mathrm{c}}_{kl})$ in ciphertext form are correct. $E(-Y_k)$ and $E({\mathrm{c}}_{kl})$ are decrypted by $P_1$. Given $m_1>1$ and $m_2>1$, $P_1$ cannot deduce $P_2$’s private information from the plaintexts $-Y_k$ and ${\mathrm{c}}_{kl}$, and vice versa, $P_2$ cannot deduce $P_1$’s private information from these values. In Step (5), $P_2$ uses the ciphertext $E(-{\overline{Y}}_k)$ of $-{\overline{Y}}_k$ to compute $E({\mathrm{c}}_{kl})$, ensuring the homomorphic operations are feasible.

(3) In Steps (4) and (6), $P_1$ calculates the plaintext means $-{\overline{Y}}_k$ for each column in matrix $E(B)$ and the plaintext covariances ${\mathrm{cov}}_{kl}$ for each column in $E(A)$. Since these division operations are performed on plaintexts rather than ciphertexts, the computations in Steps (4) and (6) are correct. Additionally, due to $m_1>1$ and $m_2>1$, $P_1$ cannot infer $P_2$’s private sample vector data from the column means $-{\overline{Y}}_k$ and covariances ${\mathrm{cov}}_{kl}$, nor can $P_2$ infer $P_1$’s private data.

(4) In Step (6), since the covariance matrix $\Sigma$ for each column in the ciphertext matrix $E(A)$ is symmetric about the main diagonal, it is sufficient to compute ${\mathrm{cov}}_{kl}$ for $k\le l$ (where $k=1, 2, \cdots , n$, $l=1, 2, \cdots , n$). The ${\mathrm{cov}}_{kl}$ values are then constructed into a main diagonal symmetric matrix, satisfying ${\mathrm{cov}}_{kl}={\mathrm{cov}}_{lk}$.

(5) In Step (7), $P_2$ computes the squared Mahalanobis distances $E(d_{ij})$ between sample vectors. In Step (8), $P_1$ takes the square root of $d_{ij}$ to obtain the Mahalanobis distances $M{D}_{ij}$.

(6) In Step (8), although $P_1$ can decrypt each element in $U$, the condition $n>\max (m_1,m_2)$ ensures that $P_1$ cannot derive $P_2$’s private vector $x_j^2$ and $P_2$ cannot infer $P_1$’s private vector $x_i^1$ from the results in $MD$.

3.3. Security Proof

Theorem 1.

Algorithm 1 securely computes the Mahalanobis distance between two sample vectors.

Proof of Theorem 1.

This theorem is proven by constructing simulators $S_1$ and $S_2$ that satisfy Equations (1) and (2).

Simulation Process of $S_1$:

(1)

After receiving the input $(x_i^1,f_1(x_i^1,x_j^2))$, $S_1$ randomly selects ${x_j^2}^{\prime }$ such that $f_1(x_i^1,{x_j^2}^{\prime })=f_1(x_i^1,x_j^2)$.

(2)

$S_1$ encrypts each element of vectors $x_1^1, x_2^1, \cdots , x_{m_1}^1$ and their negated versions $-x_1^1,-x_2^1, \cdots , -x_{m_1}^1$ using the public key $pk$, obtaining $E_{pk}(x_i^1)$ and $E_{pk}(-x_i^1)$ $(i=1,2, \cdots , m_1)$. Similarly, $S_1$ encrypts ${x_1^2}^{\prime }, {x_2^2}^{\prime }, \cdots , {x_{m_2}^2}^{\prime }$ and their negated versions, obtaining $E_{pk}({x_j^2}^{\prime })$ and $E_{pk}(-{x_j^2}^{\prime })$ $(i=1,2, \cdots , m_2)$.

(3)

$S_1$ combines all $E_{pk}(x_i^1)$ and $E_{pk}({x_j^2}^{\prime })$ into a ciphertext matrix $E(A^{\prime })$ of size $((m_1+m_2)\times n)$ and all $E_{pk}(-x_i^1)$ and $E_{pk}(-{x_j^2}^{\prime })$ into a ciphertext matrix $E(B^{\prime })$ of the same size:

$$E(A^{\prime })=\left(\begin{array}{cccc}E(x_{11}^1)& E(x_{12}^1)& \cdots & E(x_{1n}^1)\\ \cdots & \cdots & \cdots & \cdots \\ E(x_{m_{1}1}^1)& E(x_{m_{1}2}^1)& \cdots & E(x_{m_{1}n}^1)\\ E({x_{11}^2}^{\prime })& E({x_{12}^2}^{\prime })& \cdots & E({x_{1n}^2}^{\prime })\\ \cdots & \cdots & \cdots & \cdots \\ E({x_{m_{2}1}^2}^{\prime })& E({x_{m_{2}2}^2}^{\prime })& \cdots & E({x_{m_{2}n}^2}^{\prime })\end{array}\right)E(B^{\prime })=\left(\begin{array}{cccc}E(-x_{11}^1)& E(-x_{12}^1)& \cdots & E(-x_{1n}^1)\\ \cdots & \cdots & \cdots & \cdots \\ E(-x_{m_{1}1}^1)& E(-x_{m_{1}2}^1)& \cdots & E(-x_{m_{1}n}^1)\\ E(-{x_{11}^2}^{\prime })& E(-{x_{12}^2}^{\prime })& \cdots & E(-{x_{1n}^2}^{\prime })\\ \cdots & \cdots & \cdots & \cdots \\ E(-{x_{m_{2}1}^2}^{\prime })& E(-{x_{m_{2}2}^2}^{\prime })& \cdots & E(-{x_{m_{2}n}^2}^{\prime })\end{array}\right)$$

$S_1$ computes $E(-Y_k^{\prime })=E(-x_{1k}^1)+ \cdots + E(-x_{m_{1}k}^1)+E(-{x_{1k}^2}^{\prime })+ \cdots + E(-{x_{m_{2}k}^2}^{\prime })$

for $k=1, 2, \cdots , n$.

(4)

$S_1$ computes $-{\overline{Y}}_k^{\prime }={\displaystyle \frac{1}{m_1+m_2}}(-Y_k^{\prime })$

(5)

$S_1$ computes

$$E(c_{kl}^{\prime })={\displaystyle \sum _{i=1}^{m_1}((E(x_{ik}^1)+E(-{\overline{Y}}_k))(E(x_{il}^1)+E(-{\overline{Y}}_l))})+{\displaystyle \sum _{j=1}^{m_2}((E({x_{jk}^2}^{\prime })+E^{\prime }(-{\overline{Y}}_k))(E({x_{jl}^2}^{\prime })+E^{\prime }(-{\overline{Y}}_l))})$$

(6)

$S_1$ decrypts $E(c_{kl}^{\prime })$ to obtain $c_{kl}^{\prime }$ and computes ${\mathrm{cov}}_{kl}^{\prime }={\displaystyle \frac{1}{m_1+m_2-1}}(c_{kl}^{\prime })$

for $l=1, 2, \cdots , n$ and $k\le l$. $S_1$ constructs a main diagonal symmetric plaintext matrix ${\Sigma }^{\prime }$ of size $(n\times n)$:

$${\Sigma }^{\prime }=\left(\begin{array}{cccc}{\mathrm{cov}}_{11}^{\prime }& {\mathrm{cov}}_{12}^{\prime }& \cdots & {\mathrm{cov}}_{1n}^{\prime }\\ {\mathrm{cov}}_{12}^{\prime }& {\mathrm{cov}}_{22}^{\prime }& \cdots & {\mathrm{cov}}_{2n}^{\prime }\\ \cdots & \cdots & \cdots & \cdots \\ {\mathrm{cov}}_{1n}^{\prime }& {\mathrm{cov}}_{2n}^{\prime }& \cdots & {\mathrm{cov}}_{nn}^{\prime }\end{array}\right)$$

$S_1$ computes the inverse matrix ${{\Sigma }^{\prime }}^{-1}$

(7)

$S_1$ computes $E(d_{ij}^{\prime })={(E_{pk}(x_i^1)+E_{pk}(-{x_j^2}^{\prime }))}^T{{\Sigma }^{\prime }}^{-1}(E_{pk}(x_i^1)+E_{pk}(-{x_j^2}^{\prime }))$

for $i=1,2, \cdots , m_1$ and $j=1,2, \cdots , m_2$. $S_1$ forms the results into a ciphertext vector:

$V^{\prime }=(E(d_{ij}^{\prime }))=(E(d_{11}^{\prime }), \cdots , E(d_{1m_2}^{\prime }), \cdots , E(d_{m_{1}1}^{\prime }), \cdots , E(d_{m_1{m}_2}^{\prime }))$

(8)

$S_1$ decrypts each element $E(d_{ij}^{\prime })$ in $V^{\prime }$ to obtain $d_{ij}^{\prime }$, computes ${MD}_{ij}^{\prime }=\sqrt{d_{ij}^{\prime }}$, and forms the vector $M{D}^{\prime }=({MD}_{11}^{\prime }, \cdots , {MD}_{1m_2}^{\prime }, \cdots , {MD}_{m_{1}1}^{\prime }, \cdots , {MD}_{m_1{m}_2}^{\prime })$

During the execution of the protocol, $vie{w}_1^{\pi }(x_i^1, x_j^2)=\{x_i^1,E(A),E(B),E(-Y_k),E({\mathrm{c}}_{kl}),{\Sigma }^{-1},V,f_1(x_i^1, x_j^2)\}$ while $S_1(x_i^1,f_1(x_i^1, {x_j^2}^{\prime }))=\{x_i^1,E(A^{\prime }),E(B^{\prime }),E(-Y_k^{\prime }),E(c_{kl}^{\prime }),{{\Sigma }^{-1}}^{\prime },V^{\prime },f_1(x_i^1, {x_j^2}^{\prime })\}$

Due to the semantic security of the homomorphic NTRU encryption system, we have $E(A) \stackrel{c}{\equiv } E(A^{\prime })$, $E(B) \stackrel{c}{\equiv } E(B^{\prime })$, $E(-Y_k) \stackrel{c}{\equiv } E(-Y_k^{\prime })$, $E({\mathrm{c}}_{kl}) \stackrel{c}{\equiv } E(c_{kl}^{\prime })$, and $V\stackrel{c}{\equiv }{V}^{\prime }$. Since no private information can be derived from ${\Sigma }^{-1}$, we have ${\Sigma }^{-1}\stackrel{c}{\equiv }{{\Sigma }^{\prime }}^{-1}$ (where $\stackrel{c}{\equiv }$ denotes computational indistinguishability). Additionally, because $f_1(x_i^1,x_j^2)=f_1(x_i^1,{x_j^2}^{\prime })$, it follows that

$${\{S_1(x_i^1,f_1(x_i^1, x_j^2))\}}_{(x_i^1, x_j^2)}\stackrel{c}{\equiv } {\{vie{w}_1^{\pi }(x_i^1, x_j^2)\}}_{(x_i^1, x_j^2)}$$

After receiving the input $(x_j^2,f_1(x_i^1,x_j^2))$, $S_2$ randomly selects ${x_i^1}^{\prime }$ such that $f_1({x_i^1}^{\prime },x_j^2)=f_1(x_i^1,x_j^2)$. By performing a similar simulation process to $S_1$, $S_2$ can show that

$${\{S_2(x_j^2,f_1(x_i^1, x_j^2))\}}_{(x_i^1, x_j^2)}\stackrel{c}{\equiv } {\{vie{w}_2^{\pi }(x_i^1, x_j^2)\}}_{(x_i^1, x_j^2)}$$

Therefore, Algorithm 1 securely computes the Mahalanobis distance between the two parties’ sample vectors. □

4. Multi-Party Secure Computation Protocol for Mahalanobis Distance Between Sample Vectors Under Semi-Honest Model

Problem Description: Suppose there are $m$ ($m>2$) participants $P_1, P_2, \cdots , P_m$, each holding private sample vectors $x_1, x_2, \cdots , x_m$ that follow the same distribution. Each sample vector $x_i$ is an $n$-dimensional vector, i.e., $x_i=(x_{i1}, x_{i2}, \cdots , x_{in})$ $(i=1, 2, \cdots , m)$. Each participant $P_i$ wants to confidentially compute the Mahalanobis distance $M{D}_{ij}$ $( j=1, 2, \cdots , m)$ between each pair of sample vectors $x_i$ and $x_j$ without disclosing their private sample vectors.

Solution Approach: Participant $P_m$ runs the NTRU encryption scheme to generate a public/private key pair $pk/sk$. $P_1, P_2, \cdots , P_m$ use the public key $pk$ to encrypt their sample vectors $x_1, x_2, \cdots , x_m$ term by term. Then, the encrypted sample vectors $E_{pk}(x_2)$, $\cdots$, $E_{pk}(x_m)$ and $E_{pk}(-x_2)$, $\cdots$, $E_{pk}(-x_m)$ are sent to $P_1$. $P_1$ and $P_m$ jointly and confidentially compute the covariance ${\mathrm{cov}}_{kl}$ between each pair of sample vectors $k,l\in [1, \mathrm{n}]$. $P_m$ constructs these covariances into a plaintext covariance matrix $\Sigma$, computes its inverse matrix ${\Sigma }^{-1}$ $(n\times n)$, and publishes it. Each participant $P_s$ $(s=1, 2, \cdots , m-1 )$ selects a secret random number $r_{sj}$ to compute the squared Mahalanobis distance $E(d_{sj}^2)$ between each pair of sample vectors $(j=1, 2, \cdots , m)$. $P_s$ combines these results into a ciphertext vector $E(V_s)=(E(d_{sj}^2))$ and sends it to $P_m$. $P_m$ decrypts each element $E(d_{sj}^2)$ in the $m-1$ ciphertext vectors $E(V_s)$ to obtain $d_{sj}^2$, forms these into a matrix $D_{sj}^2$ $((m-1)\times m)$, $(s=1, 2, \cdots , m-1 ; j=1, 2, \cdots , m)$, and publishes it. $P_s$ divides each $d_{sj}^2$ in the $s$-th row of $D_{sj}^2$ by their chosen random number $r_{sj}$, takes the square root to obtain $M{D}_{sj}=\sqrt{d_{sj}^2/r_{sj}}$, and forms a vector $M{D}_s=(M{D}_{s1},M{D}_{s2}, \cdots , M{D}_{sm})$. Each element $M{D}_{sj}$ in $M{D}_s$ is the Mahalanobis distance $f(x_s,x_j)$ between $P_s$’s vector $x_s$ and other participants’ vectors $x_j$. $P_s$ sends $M{D}_{sm}$ to $P_m$, allowing $P_m$ to obtain the Mahalanobis distances $M{D}_{mj}$ between its vector and other participants’ vectors.

4.1. Specific Protocol

Based on Algorithm 1 and combining the homomorphic NTRU encryption algorithm with randomized methods, a multi-party secure computation protocol for Mahalanobis distance between sample vectors under the semi-honest model (Algorithm 2) is designed.

Algorithm 2: Multi-party secure computation protocol for Mahalanobis distance between sample vectors under semi-honest model.

Input: Each participant $P_1, P_2, \cdots , P_m$ holds a sample vector $x_1, x_2, \cdots , x_m$ $(m>2$).

Output: The Mahalanobis distance $f(x_i,x_j)=M{D}_{ij}=\sqrt{{(x_i-x_j)}^T{\sum }^{-1}(x_i-x_j)}$ between each pair of vectors $x_1, x_2, \cdots , x_m$ $(i=1, 2, \cdots , m ; j=1, 2, \cdots , m)$.

Preparation: Participant $P_m$ runs the NTRU encryption scheme to generate a public/private key pair $pk/sk$ and publishes the public key $pk$.

(1) Encryption by All Participants: Each participant $P_i$ $(i=1, 2, \cdots , m$) encrypts their sample vector $x_i$ and its negation $-x_i$ element-wise using $pk$: $$E_{pk}(x_i)=(E(x_{i1}), E(x_{i2}), \cdots , E(x_{in}))$$ (24) $$E_{pk}(-x_i)=(E(-x_{i1}), E(-x_{i2}), \cdots , E(x_{in}))$$ (25) $\mathrm{Participants} P_2, \cdots , P_m$ send their encrypted vectors $E_{pk}(x_2), \cdots , E_{pk}(x_m)$ and $E_{pk}(-x_2), \cdots , E_{pk}(-x_m)$ to $P_1$.

(2) Matrix Construction by $P_1$: $P_1$ constructs ciphertext matrices $E(A)$ $(m\times n)$ and $E(B)$ $(m\times n)$ from the received encrypted vectors: $$E(A)=\left(\begin{array}{cccc}E(x_{11})& E(x_{12})& \cdots & E(x_{1n})\\ E(x_{21})& E(x_{22})& \cdots & E(x_{2n})\\ \cdots & \cdots & \cdots & \cdots \\ E(x_{m1})& E(x_{m2})& \cdots & E(x_{mn})\end{array}\right) E(B)=\left(\begin{array}{cccc}E(-x_{11})& E(-x_{12})& \cdots & E(-x_{1n})\\ E(-x_{21})& E(-x_{22})& \cdots & E(-x_{2n})\\ \cdots & \cdots & \cdots & \cdots \\ E(-x_{m1})& E(-x_{m2})& \cdots & E(-x_{mn})\end{array}\right)$$ (26) $P_1$ $\mathrm{sends} E(A)$ and $E(B)$ to $P_2, \cdots , P_{m-1}$. $P_1$ computes $$E(-Y_k)=E(-x_{1k})+E(-x_{2k})+ \cdots + E(-x_{mk})$$ (27) and sends $E(-Y_k)$ to $P_m$.

(3) Decryption and Mean Calculation by $P_m$: $P_m$ $\mathrm{decrypts} E(-Y_k)$ to obtain $-Y_k$ and computes $$-{\overline{Y}}_k={\displaystyle \frac{1}{m}}(-Y_k)$$ (28) $P_m$ $\mathrm{sends} -{\overline{Y}}_k$ $\mathrm{to} P_1$.

(4) Covariance Calculation by $P_1$: $P_1$ $\mathrm{encrypts} -{\overline{Y}}_k$ to obtain $E(-{\overline{Y}}_k)$ and computes $$E({\mathrm{c}}_{kl})={\displaystyle \sum _{i=1}^m(E(x_{ik})+E(-{\overline{Y}}_k))(E(x_{il})+E(-{\overline{Y}}_l))}$$ (29) $P_1$ $\mathrm{sends} E({\mathrm{c}}_{kl})$ to $P_m$.

(5) Covariance Matrix Construction by $P_m$: $P_m$ $\mathrm{decrypts} E({\mathrm{c}}_{kl})$ to obtain ${\mathrm{c}}_{kl}$ and computes $${\mathrm{cov}}_{kl}={\displaystyle \frac{1}{m-1}}({\mathrm{c}}_{kl})$$ (30) $P_m$ constructs the covariance matrix $\Sigma$ $(n\times n)$: $$\Sigma =\left(\begin{array}{cccc}{\mathrm{cov}}_{11}& {\mathrm{cov}}_{12}& \cdots & {\mathrm{cov}}_{1n}\\ {\mathrm{cov}}_{21}& {\mathrm{cov}}_{22}& \cdots & {\mathrm{cov}}_{2n}\\ \cdots & \cdots & \cdots & \cdots \\ {\mathrm{cov}}_{n1}& {\mathrm{cov}}_{n2}& \cdots & {\mathrm{cov}}_{nn}\end{array}\right)$$ (31) $P_m$ computes the inverse matrix ${\Sigma }^{-1}$ and sends it to $P_2, \cdots , P_{m-1}$.

(6) Randomized Distance Calculation by $P_s$: Each participant $P_s$ $(s=1, 2, \cdots , m-1$) selects secret random numbers $r_{sj}$ $(j=1, 2, \cdots , m$) and computes $$E(d_{sj}^2)=r_{sj}(({(E_{pk}(x_s)+E_{pk}(-x_j))}^T{\Sigma }^{-1}(E_{pk}(x_s)+E_{pk}(-x_j)))$$ (32) $P_s$ constructs a ciphertext vector $E(V_s)$: $$E(V_1)=(E(d_{12}^2),E(d_{13}^2), \cdots , E(d_{1m}^2))$$ $$E(V_2)=(E(d_{21}^2),E(d_{22}^2), \cdots , E(d_{2m}^2))$$ (33) $$\cdots$$ $$E(V_{m-1})=(E(d_{(m-1)1}^2),E(d_{(m-1)2}^2), \cdots , E(d_{(m-1)m}^2))$$ $P_s$ $\mathrm{sends} E(V_s)$ to $P_m$.

(7) Matrix Construction and Publication by $P_m$: $P_m$ decrypts each $E(d_{sj}^2)$ to obtain $d_{sj}^2$ and constructs a matrix $D_{sj}^2$ $((m-1)\times m)$: $$D_{sj}^2=\left(\begin{array}{cccc}{d}_{11}^2& d_{12}^2& \cdots & d_{1m}^2\\ d_{21}^2& d_{22}^2& \cdots & d_{2m}^2\\ \cdots & \cdots & \cdots & \cdots \\ d_{(m-1)1}^2& d_{(m-1)2}^2& \cdots & d_{(m-1)m}^2\end{array}\right)$$ (34) $P_m$ publishes $D_{sj}^2$.

(8) $\mathrm{Final} \mathrm{Distance} \mathrm{Calculation} \mathrm{by} P_s$: Each $P_s$ $(s=1, 2, \cdots , m-1 )$ retrieves $D_{sj}^2$, divides each element $d_{sj}^2$ in the $s$-th row by $r_{sj}$, and computes $$M{D}_{sj}=\sqrt{d_{sj}^2/r_{sj}}$$ (35) $P_s$ constructs the vector: $$M{D}_s=(M{D}_{s1},M{D}_{s2}, \cdots , M{D}_{sm})$$ (36) $P_s$ $\mathrm{sends} M{D}_{sm}$ $\mathrm{to} P_m$, allowing $P_m$ to obtain $M{D}_{mj}$.

End of Algorithm 2.

4.2. Correctness Analysis

(1) In Step (1) of Algorithm 2, since the homomorphic NTRU encryption algorithm cannot directly perform subtraction on ciphertexts, each participant encrypts their sample vectors $x_1, x_2, \cdots , x_m$ and their negated versions $-x_1, -x_2, \cdots , -x_m$ and sends them to $P_1$ for calculation.

(2) In Steps (2) and (4), due to the additive and multiplicative homomorphic properties of the NTRU encryption scheme, the computations of $E(-Y_k)$ and $E({\mathrm{c}}_{kl})$ in ciphertext form are correct. $E(-Y_k)$ and $E({\mathrm{c}}_{kl})$ are decrypted by $P_m$. Given $m>2$, $P_m$ cannot deduce other participants’ private information from the plaintexts $-Y_k$ and ${\mathrm{c}}_{kl}$, and vice versa, other participants cannot deduce $P_m$’s private information from these values. In Step (4), $P_1$ uses the ciphertext $E(-{\overline{Y}}_k)$ of $-{\overline{Y}}_k$ to compute $E({\mathrm{c}}_{kl})$, ensuring the feasibility of homomorphic operations.

(3) In Steps (3) and (5), $P_m$ calculates the plaintext means $-{\overline{Y}}_k$ for each column in matrix $E(B)$ and the plaintext covariances ${\mathrm{cov}}_{kl}$ for each column in $E(A)$. Since these division operations are performed on plaintexts rather than ciphertexts, the computations in Steps (3) and (5) are correct. Additionally, due to $m>2$, neither $P_m$ nor other participants can infer private sample vector data from the column means $-{\overline{Y}}_k$ and covariances ${\mathrm{cov}}_{kl}$.

(4) In Step (5), since the covariance matrix $\Sigma$ for each column in the ciphertext matrix $E(A)$ is symmetric about the main diagonal, it is sufficient to compute ${\mathrm{cov}}_{kl}$ for $k\le l$ (where $k,l=1, 2, \cdots , n$). The ${\mathrm{cov}}_{kl}$ values are then constructed into a main diagonal symmetric matrix, satisfying ${\mathrm{cov}}_{kl}={\mathrm{cov}}_{lk}$.

(5) In Step (6), after computing the squared Mahalanobis distances between sample vectors, $P_s$ multiplies each squared distance by a selected random number $r_{sj}$ before sending it to $P_m$ for decryption. This ensures that no single participant can derive the Mahalanobis distances between other participants’ vectors.

(6) In Step (7), although $P_m$ can decrypt each element in $V_s$, the values in $V_s$ do not reveal the private vectors $x_s$ of $P_1, P_2, \cdots , P_{m-1}$.

(7) In Step (8), $P_s$ divides the data $d_{sj}^2$ in the $s$-th row of $D_{sj}^2$ by the corresponding random number $r_{ij}$ and takes the square root of the result, thereby progressively computing the Mahalanobis distances $M{D}_{sj}$ between their sample vectors and those of other participants. $P_s$ sends the computed Mahalanobis distance $M{D}_{sm}$ between their own vector and $P_m$’s vector to $P_m$, ensuring that $P_m$ ultimately obtains the correct results.

4.3. Security Analysis

Regarding the security of the protocol, the following conclusion holds.

Theorem 2.

Algorithm 2 securely computes the Mahalanobis distances between sample vectors of multiple participants.

Proof of Theorem 2.

It is worth noting that the most severe threat to a participant’s privacy is collusion among all other participants attempting to obtain their private information. This set of attackers is referred to as the maximum attacker set. If a participant’s privacy is secure against the maximum attacker set, it is also secure against any subset of this set, as any subset can only access less information than the maximum set. Therefore, it suffices to prove that a participant’s privacy is secure against the maximum attacker set.

Assume $K=\{P_2,P_3, \cdots , P_m\}$ is the attacker set, and we prove the security of $P_1$’s information. Let $X_K=\{x_2,x_3, \cdots , x_m\}$.

Given the input $(K,X_K,M{D}_{ij})$, the simulator $S_K$ randomly selects a vector $x_1^{\prime }$ such that ${MD}_{ij}^{\prime }=M{D}_{ij}$ and uses ${MD}_{ij}^{\prime }$ to simulate the protocol execution.

During the simulation of Algorithm 2, $S_K$ generates a simulated process copy:

$$E^{\prime }(A),E^{\prime }(B),E(-Y_k^{\prime }),E(c_{kl}^{\prime }),{{\Sigma }^{-1}}^{\prime },E^{\prime }(V_s),{D_{sj}^2}^{\prime },{MD}_{ij}^{\prime }$$

That is, $S_K(K,X_K,M{D}_{ij})=\{K,X_K,E(A^{\prime }),E(B^{\prime }),E(-Y_k^{\prime }),E(c_{kl}^{\prime }),{{\Sigma }^{-1}}^{\prime },E(V_s^{\prime }),{D_{sj}^2}^{\prime },{MD}_{ij}^{\prime }\}$ In the actual execution of the protocol,

$$vie{w}_K^{\pi }(x_1,X_K)=\{K,X_K,E(A),E(B),E(-Y_k),E({\mathrm{c}}_{kl}),{\Sigma }^{-1},E(V_s),D_{sj}^2,M{D}_{ij}\}$$

Due to the semantic security of the homomorphic NTRU encryption system,

$$E(A) \stackrel{c}{\equiv } E(A^{\prime })), E(B) \stackrel{c}{\equiv } E(B^{\prime }), E(-Y_k) \stackrel{c}{\equiv } E(-Y_k^{\prime }), E({\mathrm{c}}_{kl}) \stackrel{c}{\equiv } E(c_{kl}^{\prime }).$$

No private information can be derived from ${\Sigma }^{-1}$, so ${\Sigma }^{-1}\stackrel{c}{\equiv }{{\Sigma }^{\prime }}^{-1}$.

$E(V_s)$ is computed in ciphertext using different random numbers $r_{1j},r_{2j}, \cdots , r_{(m-1)j}$ selected by $P_1, P_2, \cdots , P_{m-1}$, ensuring randomness; thus, $E(V_s)\stackrel{c}{\equiv }{E}^{\prime }(V_s)$.

By the security of the homomorphic NTRU encryption system, $D_{sj}^2\stackrel{c}{\equiv }{D_{sj}^2}^{\prime }$.

Since $M{D}_{ij}={MD}_{ij}^{\prime }$ (where $\stackrel{c}{\equiv }$ denotes computational indistinguishability), we have

$$S_K(K,X_K,M{D}_{ij})\stackrel{c}{\equiv } vie{w}_K^{\pi }(x_1,X_K)$$

Thus, $P_1$’s private information is secure. Using a similar approach, it can be proven that the information of $P_2,P_3, \cdots , P_m$ is also secure. Therefore, Algorithm 2 is secure. □

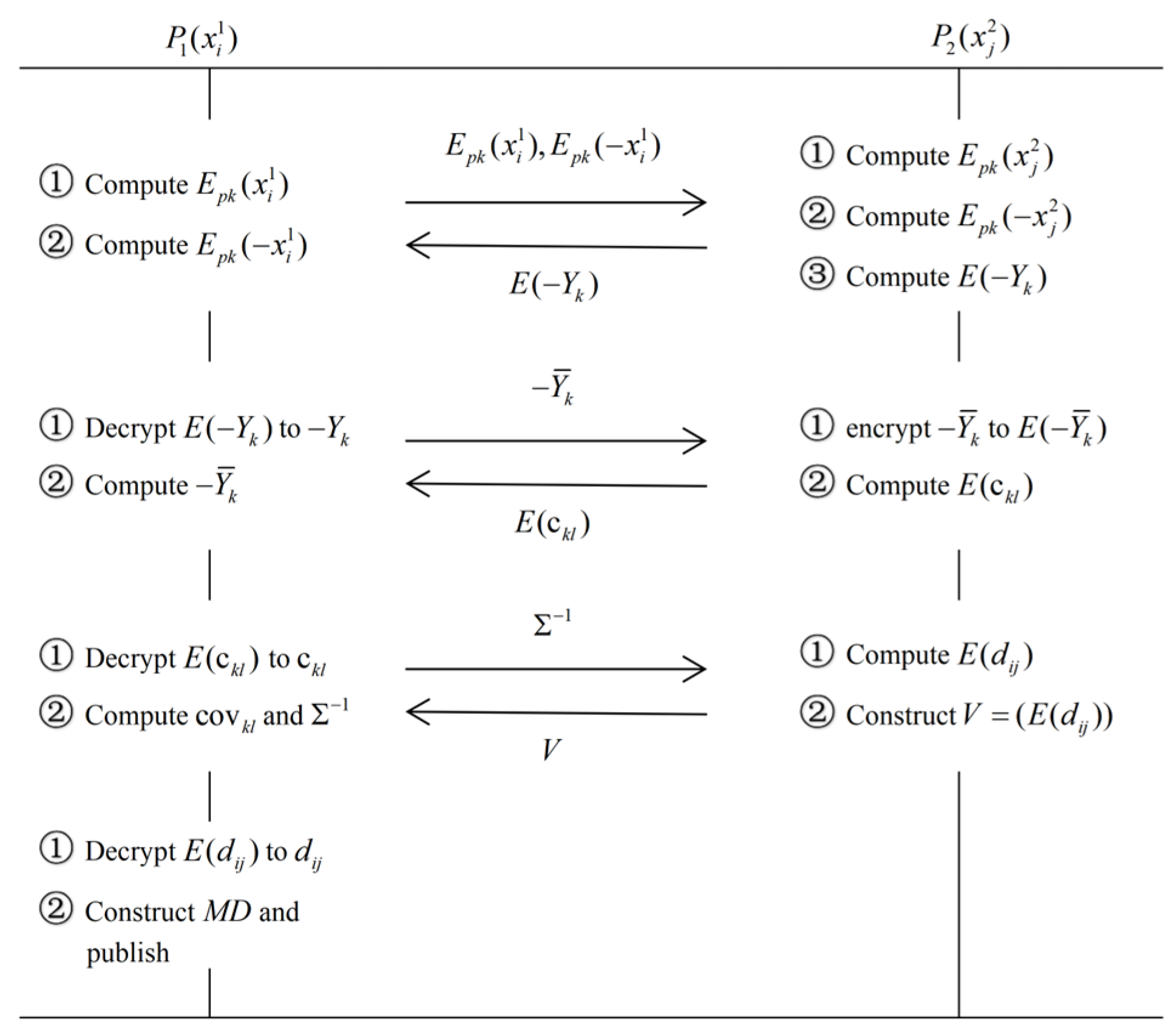
5. Multi-Party Secure Computation Protocol for Mahalanobis Distance Against Malicious Deception

Problem Description: Suppose there are $m$ ($m>2$) participants $P_1, P_2, \cdots , P_m$, each holding private sample vectors $x_1, x_2, \cdots , x_m$ that follow the same distribution. Each sample vector $x_i$ is an $n$-dimensional vector, i.e., $x_i=(x_{i1}, x_{i2}, \cdots , x_{in})$ $(i=1, 2, \cdots , m)$. All participants $P_i$ want to confidentially compute the Mahalanobis distance $M{D}_{ij}$ $( j=1, 2, \cdots , m)$ between each pair of sample vectors $x_i$ and $x_j$ without disclosing their private sample vectors.

In Step (7) of Algorithm 2, $P_m$ may publish incorrect results $D_{sj}^2$, preventing other participants $P_s$ $(s=1, 2, \cdots , m-1 )$ from obtaining correct computations. In Step (8) of Algorithm 2, $P_s$ may send incorrect results $M{D}_{sm}$ to $P_m$, causing $P_m$ to receive erroneous outcomes. To address these issues, designing a multi-party secure computation protocol for Mahalanobis distance against malicious deception is essential.

Solution Approach: Each participant $P_i$ can use zero-knowledge proof methods to verify the computation results $M{D}_{ij}$ $(i=1, 2, \cdots , m$; $j=1, 2, \cdots , m)$. Specifically, $P_s$ $(s=1, 2, \cdots , m-1 )$ can verify whether $P_m$’s computation result $D_{sj}^2$ is correct, and $P_m$ can verify whether the $M{D}_{sm}$ sent by $P_s$ is correct. Participant $P_1$ has its own public key $p{k}_1$ and private key $s{k}_1$, while participant $P_m$ has its own public key $p{k}_m$ and private key $s{k}_m$. $P_m$ also computes the Mahalanobis distances between its vector $x_m$ and the vectors $x_1, \cdots , x_{m-1}$ of other participants in ciphertext form.

5.1. Specific Protocol

Based on Algorithm 2 and combined with zero-knowledge proof methods, a multi-party secure computation protocol for Mahalanobis distance between sample vectors against malicious deception (Algorithm 3) is designed. Figure 3 shows the flowchart of Algorithm 3.

Algorithm 3: Multi-party secure computation protocol for Mahalanobis distance against malicious deception.

Input: Private sample vectors $x_1, x_2, \cdots , x_m$ held by participants $P_1, P_2, \cdots , P_m$ $(m>2$).

Output: The Mahalanobis distance $f(x_i,x_j)=M{D}_{ij}=\sqrt{{(x_i-x_j)}^T{\sum }^{-1}(x_i-x_j)}$ between each pair of vectors $x_i$ and $x_j$ $(i=1, 2, \cdots , m ; j=1, 2, \cdots , m)$.

Preparation: Participant $P_1$ runs the NTRU encryption scheme to generate a public/private key pair $p{k}_1/s{k}_1$ and sends $p{k}_1$ to $P_m$$. \mathrm{Participant} P_m$ runs the NTRU encryption scheme to generate a public/private key pair $p{k}_m/s{k}_m$ and sends $P_m$ $\mathrm{to} P_1, P_2, \cdots , P_{m-1}$.

(1) Encryption by All Participants Using $p{k}_m$: Each participant $P_i$ $(i=1, 2, \cdots , m$) encrypts their sample vector $x_i$ and its negation $-x_i$ element-wise using $p{k}_m$: $$E_{p{k}_m}(x_i)=(E(x_{i1}), E(x_{i2}), \cdots , E(x_{in}))$$ (37) $$E_{p{k}_m}(-x_i)=(E(-x_{i1}), E(-x_{i2}), \cdots , E(x_{in}))$$ (38) $\mathrm{Participants} P_2, \cdots , P_m$ send their encrypted vectors $E_{p{k}_m}(x_2), \cdots , E_{p{k}_m}(x_m)$ and $E_{p{k}_m}(-x_2), \cdots , E_{p{k}_m}(-x_m)$ to $P_1$.

(2) Matrix Construction and Summation by $P_1$: $P_1$ constructs ciphertext matrices $E(A)$ $(m\times n)$ and $E(B)$ $(m\times n)$ from the received encrypted vectors: $$E(A)=\left(\begin{array}{cccc}E(x_{11})& E(x_{12})& \cdots & E(x_{1n})\\ E(x_{21})& E(x_{22})& \cdots & E(x_{2n})\\ \cdots & \cdots & \cdots & \cdots \\ E(x_{m1})& E(x_{m2})& \cdots & E(x_{mn})\end{array}\right) E(B)=\left(\begin{array}{cccc}E(-x_{11})& E(-x_{12})& \cdots & E(-x_{1n})\\ E(-x_{21})& E(-x_{22})& \cdots & E(-x_{2n})\\ \cdots & \cdots & \cdots & \cdots \\ E(-x_{m1})& E(-x_{m2})& \cdots & E(-x_{mn})\end{array}\right)$$ (39) $P_1$ $\mathrm{sends} E(A)$ and $E(B)$ to $P_2, \cdots , P_{m-1}$. $P_1$ computes $$E(-Y_k)=E(-x_{1k})+E(-x_{2k})+ \cdots + E(-x_{mk})$$ (40) where $k=1, 2, \cdots , n$, and sends $E(-Y_k)$ to $P_m$.

(3) Decryption and Mean Calculation by $P_m$: $P_m$ $\mathrm{decrypts} E(-Y_k)$ using $s{k}_m$ to obtain $-Y_k$ and computes $$-{\overline{Y}}_k={\displaystyle \frac{1}{m}}(-Y_k)$$ (41) $P_m$ $\mathrm{sends} -{\overline{Y}}_k$ $\mathrm{to} P_1$.

(4) Covariance Calculation by $P_1$: $P_1$ $\mathrm{encrypts} -{\overline{Y}}_k$ using $p{k}_m$ to obtain $E(-{\overline{Y}}_k)$ and computes, $$E({\mathrm{c}}_{kl})={\displaystyle \sum _{i=1}^m(E(x_{ik})+E(-{\overline{Y}}_k))(E(x_{il})+E(-{\overline{Y}}_l))}$$ (42) where $k=1, 2, \cdots , n$ and $l=1, 2, \cdots , n$, and sends $E({\mathrm{c}}_{kl})$ to $P_m$.

(5) Covariance Matrix Construction by $P_m$: $P_m$ $\mathrm{decrypts} E({\mathrm{c}}_{kl})$ using $s{k}_m$ to obtain ${\mathrm{c}}_{kl}$ and computes: $${\mathrm{cov}}_{kl}={\displaystyle \frac{1}{m-1}}({\mathrm{c}}_{kl})$$ (43) $P_m$ constructs the covariance matrix $\Sigma$ $(n\times n)$: $$\Sigma =\left(\begin{array}{cccc}{\mathrm{cov}}_{11}& {\mathrm{cov}}_{12}& \cdots & {\mathrm{cov}}_{1n}\\ {\mathrm{cov}}_{21}& {\mathrm{cov}}_{22}& \cdots & {\mathrm{cov}}_{2n}\\ \cdots & \cdots & \cdots & \cdots \\ {\mathrm{cov}}_{n1}& {\mathrm{cov}}_{n2}& \cdots & {\mathrm{cov}}_{nn}\end{array}\right)$$ (44) $P_m$ computes the inverse matrix ${\Sigma }^{-1}$ and sends it to $P_2, \cdots , P_{m-1}$.

(6) Zero-Knowledge Proof-Based Computation by $P_s$: Each $P_s$ $(s=1, 2, \cdots , m-1$) selects secret random numbers $r_{sj}^1$$, r_{sj}^2$$, t_{sj}^1$, and $t_{sj}^2$ $(j=1, 2, \cdots , m$) and computes: $$W_{sj}={(E_{p{k}_m}(x_s)+E_{p{k}_m}(-x_j))}^T{\Sigma }^{-1}(E_{p{k}_m}(x_s)+E_{p{k}_m}(-x_j))$$ $$E^1(d_{sj})=r_{sj}^1{W}_{sj}+E_{p{k}_m}(t_{sj}^1)$$ (45) $$E^2(d_{sj})=r_{sj}^2{W}_{sj}+E_{p{k}_m}(t_{sj}^2)$$ Each $P_s$ sequentially combines their computation results $E^1(d_{sj})$ into a ciphertext vector $E^1(V_s)=(E^1(d_{sj}))$ $(s=1, 2, \cdots , m-1 )$, i.e., $$E^1(V_1)=(E^1(d_{11}),E^1(d_{12}), \cdots , E^1(d_{1m}))$$ $$E^1(V_2)=(E^1(d_{21}),E^1(d_{22}), \cdots , E^1(d_{2m}))$$ $$\cdots$$ (46) $$E^1(V_{m-1})=(E^1(d_{(m-1)1}),E^1(d_{(m-1)2}), \cdots , E^1(d_{(m-1)m}))$$ Each $P_s$ sequentially combines their computation results $E^2(d_{sj})$ into a ciphertext vector $E^2(V_s)=(E^2(d_{sj}))$ $(s=1, 2, \cdots , m-1 )$, i.e., $$E^2(V_1)=(E^2(d_{11}),E^2(d_{12}), \cdots , E^2(d_{1m}))$$ $$E^2(V_2)=(E^2(d_{21}),E^2(d_{22}), \cdots , E^2(d_{2m}))$$ $$\cdots$$ (47) $$E^2(V_{m-1})=(E^2(d_{(m-1)1}),E^2(d_{(m-1)2}), \cdots , E^2(d_{(m-1)m}))$$ Each $P_s$ $\mathrm{sends} E^1(V_s)$ and $E^2(V_s)$ to participant $P_m$.

(7) Encryption by All Participants Using $p{k}_1$: Each participant $P_i$ $(i=1, 2, \cdots , m$) encrypts their sample vector $x_i$ and its negation $-x_i$ element-wise using $p{k}_1$: $$E_{p{k}_1}(x_i)=(E(x_{i1}), E(x_{i2}), \cdots , E(x_{in}))$$ (48) $$E_{p{k}_1}(-x_i)=(E(-x_{i1}), E(-x_{i2}), \cdots , E(x_{in}))$$ (49) $\mathrm{Participants} P_1, P_2, \cdots , P_{m-1}$ send their encrypted vectors $E_{p{k}_1}(x_i)$ and $E_{p{k}_1}(-x_i)$ to $P_m$.

(8) Zero-Knowledge Proof-Based Computation by $P_m$: $P_m$ selects secret random numbers $r_{mj}^1$$, r_{mj}^2$$, t_{mj}^1$, and $t_{mj}^2$ and computes: $$W_{mj}={(E_{p{k}_1}(x_m)+E_{p{k}_1}(-x_j))}^T{\Sigma }^{-1}(E_{p{k}_1}(x_m)+E_{p{k}_1}(-x_j))$$ $$E^1(d_{mj})=r_{mj}^1{W}_{mj}+E_{p{k}_1}(t_{mj}^1)$$ (50) $$E^2(d_{mj})=r_{mj}^2{W}_{mj}+E_{p{k}_1}(t_{mj}^2)$$ $P_m$ combines its calculation result $E^1(d_{mj})$ into a ciphertext vector $E^1(V_m)=(E^1(d_{mj}))$, namely $$E^1(V_m)=(E^1(d_{m1}),E^1(d_{m2}), \cdots , E^1(d_{mm}))$$ (51) and combines its calculation result $E^2(d_{mj})$ into a ciphertext vector $E^2(V_m)=(E^2(d_{mj}))$, namely $$E^2(V_m)=(E^2(d_{m1}),E^2(d_{m2}), \cdots , E^2(d_{mm}))$$ (52) and then sends $E^1(V_m)$ and $E^2(V_m)$ to participant $P_1$.

(9) Decryption and Matrix Publication by $P_m$: $P_m$ decrypts $E^1(V_s)$ and $E^2(V_s)$ to obtain $d_{sj}^1$ and $d_{sj}^2$ $(s=1, 2, \cdots , m-1 ; j=1, 2, \cdots , m)$, constructs matrices $D_{sj}^1$ and $D_{sj}^2$ $((m-1)\times m)$, and publishes them: $$D_{sj}^1=\left(\begin{array}{cccc}{d}_{11}^1& d_{12}^1& \cdots & d_{1m}^1\\ d_{21}^1& d_{22}^1& \cdots & d_{2m}^1\\ \cdots & \cdots & \cdots & \cdots \\ d_{(m-1)1}^1& d_{(m-1)2}^1& \cdots & d_{(m-1)m}^1\end{array}\right) D_{sj}^2=\left(\begin{array}{cccc}{d}_{11}^2& d_{12}^2& \cdots & d_{1m}^2\\ d_{21}^2& d_{22}^2& \cdots & d_{2m}^2\\ \cdots & \cdots & \cdots & \cdots \\ d_{(m-1)1}^2& d_{(m-1)2}^2& \cdots & d_{(m-1)m}^2\end{array}\right)$$ (53)

(10) Verification by $P_s$: Each $P_s$ verifies whether $d_{sj}^1=r_{sj}^1((d_{sj}^2-t_{sj}^2)/r_{sj}^2)+t_{sj}^1$ $(s=1, 2, \cdots , m-1 ; j=1, 2, \cdots , m)$. If verified, $P_s$ computes $$M{D}_{sj}=\sqrt{(d_{sj}^1-t_{sj}^1)/r_{sj}^1}$$ (54) and obtains the vector $M{D}_s=(M{D}_{s1},M{D}_{s2}, \cdots , M{D}_{sm})$. If verification fails, $P_s$ identifies incorrect results from $P_m$.

(11) Decryption by $P_1$: $P_1$ $\mathrm{decrypts} E^1(V_m)$ and $E^2(V_m)$ to obtain $d_{mj}^1$ and $d_{mj}^2$ and sends them to $P_m$: $$d_{mj}^1=(d_{m1}^1, d_{m2}^1, \cdots , d_{mm}^1)$$ (55) $$d_{mj}^2=(d_{m1}^2, d_{m2}^2, \cdots , d_{mm}^2)$$ (56)

(12) Verification by $P_m$: $P_m$ verifies whether $d_{mj}^1=r_{mj}^1((d_{mj}^2-t_{mj}^2)/r_{mj}^2)+t_{mj}^1$ $(j=1, 2, \cdots , m)$. If verified, $P_m$ computes: $$M{D}_{mj}=\sqrt{(d_{mj}^1-t_{mj}^1)/r_{mj}^1}$$ (57) to obtain the Mahalanobis distances. If verification fails, $P_m$ identifies incorrect results from $P_1$.

End of Algorithm 3.

5.2. Correctness Analysis

(1) In Steps (1) and (7) of Algorithm 3, since the fully homomorphic NTRU encryption algorithm cannot directly perform subtraction on ciphertexts, each participant $P_i$ encrypts their respective sample vectors $x_1, x_2, \cdots , x_m$ and the negated sample vectors $-x_1, -x_2, \cdots , -x_m$ and then sends them to $P_1$ or $P_m$ for further computation.

(2) In Steps (2) and (4), leveraging the NTRU encryption scheme with additive and multiplicative homomorphic properties, the computations of $E(-Y_k)$ and $E({\mathrm{c}}_{kl})$ in ciphertext form are correct. $E(-Y_k)$ and $E({\mathrm{c}}_{kl})$ are decrypted by $P_m$. Given $m>2$, $P_m$ cannot deduce other participants’ private information from the plaintexts $-Y_k$ and ${\mathrm{c}}_{kl}$, and vice versa. In Step (4), $P_2$ uses the ciphertext $E({\mathrm{c}}_{kl})$ to compute $E({\mathrm{c}}_{kl})$, ensuring homomorphic operations.

(3) In Steps (3) and (5), $P_m$ computes the plaintext means $-{\overline{Y}}_k$ of each column in matrix $E(B)$ and the plaintext covariances ${\mathrm{cov}}_{kl}$ of each column in $E(A)$. Since divisions are performed on plaintexts rather than ciphertexts, these computations are correct. Additionally, given $m>2$, $P_m$ cannot deduce other participants’ private sample data from $-{\overline{Y}}_k$ and ${\mathrm{cov}}_{kl}$, and vice versa.

(4) In Step (5), because the covariance matrix $\Sigma$ of columns in ciphertext matrix $E(A)$ is symmetric, only ${\mathrm{cov}}_{kl}$ for $k\le l$ (where $k=1, 2, \cdots , n$ and $l=1, 2, \cdots , n$) needs to be computed. The matrix is then constructed symmetrically, i.e., ${\mathrm{cov}}_{kl}={\mathrm{cov}}_{lk}$.

Resistance to Malicious Deception:

For potential deceptions in Algorithm 2:

In Step (7), $P_m$ might publish incorrect $D_{sj}^2$, preventing other participants $P_s$ $(s=1, 2, \cdots , m-1 )$ from obtaining correct results.

In Step (8), $P_s$ might send incorrect $M{D}_{sm}$ to $P_m$, leading to invalid results for $P_m$.

Steps (6)–(12) of Algorithm 3 effectively mitigate these issues:

(5) In Step (6), after computing $W_{sj}$, $P_s$ randomizes it using two sets of random numbers $r_{sj}^1$, $r_{sj}^2$ and $t_{sj}^1$, $t_{sj}^2$ before sending it to $P_m$ for decryption. This ensures $P_m$ cannot infer the true $W_{sj}$ from $E^1(V_s)$ and $E^2(V_s)$. Using zero-knowledge proofs in Step (10), $P_s$ verifies $P_m$’s decryption via $d_{sj}^1=r_{sj}^1((d_{sj}^2-t_{sj}^2)/r_{sj}^2)+t_{sj}^1$.

(6) In Step (7), participants encrypt their vectors with $p{k}_1$ before sending them to $P_m$, enabling $P_m$ to compute Mahalanobis distances between its and others’ vectors.

(7) In Step (8), after computing $W_{mj}$, $P_m$ randomizes it using $r_{mj}^1$, $r_{mj}^2$ and $t_{mj}^1$, $t_{mj}^2$ before sending it to $P_1$ for decryption. This prevents $P_1$ from learning the true $W_{mj}$. Using zero-knowledge proofs in Step (12), $P_m$ verifies $P_1$’s decryption via $d_{mj}^1=r_{mj}^1((d_{mj}^2-t_{mj}^2)/r_{mj}^2)+t_{mj}^1$.

5.3. Security Analysis

Regarding the security of the protocol, the following conclusion holds.

Theorem 3.

Algorithm 3 can securely compute the Mahalanobis distances between sample vectors of multiple participants.

Proof of Theorem 3.

If a participant’s privacy is secure against the maximum attacker set, it is also secure against any subset of the maximum attacker set. Therefore, it suffices to prove that a participant’s privacy is secure against the maximum attacker set.

Assume $K=\{P_2,P_3, \cdots , P_m\}$ is the attacker set, and we prove the security of $P_1$’s information. Let $X_K=\{x_2,x_3, \cdots , x_m\}$.

Given the input $(K,X_K,M{D}_{ij})$, the simulator $S_K$ randomly selects a vector $x_1^{\prime }$ such that ${MD}_{ij}^{\prime }=M{D}_{ij}$ and uses ${MD}_{ij}^{\prime }$ to simulate the protocol execution.

During the simulation of Algorithm 3, $S_K$ generates the following simulated copies:

$$\begin{array}{c}{E}_{p{k}_m}(x_i^{\prime }),E_{p{k}_m}(-x_i^{\prime }),E(-Y_k^{\prime }),E(c_{kl}^{\prime }),{{\Sigma }^{-1}}^{\prime },E^1(V_s^{\prime }),E^2(V_s^{\prime }),E_{p{k}_1}(x_i^{\prime }),E_{p{k}_1}(-x_i^{\prime }),{E^1}^{\prime }(V_m),\\ {E^2}^{\prime }(V_m),{D_{sj}^1}^{\prime },{D_{sj}^2}^{\prime },{d_{mj}^1}^{\prime },{d_{mj}^2}^{\prime },{MD}_{ij}^{\prime }\end{array}$$

That is,

$$\begin{array}{c}{S}_K(K,X_K,M{D}_{ij})=\{K,X_K,E_{p{k}_m}(x_i^{\prime }),E_{p{k}_m}(-x_i^{\prime }),E(-Y_k^{\prime }),E(c_{kl}^{\prime }),{{\Sigma }^{-1}}^{\prime },E^1(V_s^{\prime }),E^2(V_s^{\prime }),E_{p{k}_1}(x_i^{\prime }),E_{p{k}_1}(-x_i^{\prime }),\\ {E^1}^{\prime }(V_m),{E^2}^{\prime }(V_m),{D_{sj}^1}^{\prime },{D_{sj}^2}^{\prime },{d_{mj}^1}^{\prime },{d_{mj}^2}^{\prime },{MD}_{ij}^{\prime }\}\end{array}$$

In the actual execution of the protocol,

$$\begin{array}{c}vie{w}_K^{\pi }(x_1,X_K)=\{K,X_K,E_{p{k}_m}(x_i),E_{p{k}_m}(-x_i),E(-Y_k),E({\mathrm{c}}_{kl}),{\Sigma }^{-1},E^1(V_s),E^2(V_s),E_{p{k}_1}(x_i),E_{p{k}_1}(-x_i),\\ E^1(V_m),E^2(V_m),D_{sj}^1,D_{sj}^2,d_{mj}^1,d_{mj}^2,M{D}_{ij}\}\end{array}$$

Due to the semantic security of the fully homomorphic NTRU encryption system, we have

$$\begin{gathered} E_{p{k}_m}(x_i) \stackrel{c}{\equiv } E_{p{k}_m}^{\prime }(x_i), E_{p{k}_m}(-x_i) \stackrel{c}{\equiv } E_{p{k}_m}^{\prime }(-x_i), E_{p{k}_1}(x_i) \stackrel{c}{\equiv } E_{p{k}_1}^{\prime }(x_i), E_{p{k}_1}(-x_i) \stackrel{c}{\equiv } E_{p{k}_1}^{\prime }(-x_i), \\ E(-Y_k) \stackrel{c}{\equiv } E(-Y_k^{\prime }), E({\mathrm{c}}_{kl}) \stackrel{c}{\equiv } E(c_{kl}^{\prime }) \end{gathered}$$

$\stackrel{c}{\equiv }$ denotes computational indistinguishability.

Since privacy information cannot be inferred from ${\Sigma }^{-1}$, we have ${\Sigma }^{-1}\stackrel{c}{\equiv }{{\Sigma }^{\prime }}^{-1}$.

Because $E^1(V_s)$, $E^2(V_s)$, $E^1(V_m)$, and $E^2(V_m)$ are computed under ciphertext using different random numbers selected by $P_i$ $(i=1, \cdots , m)$, they are random. Thus,

$$E^1(V_s)\stackrel{c}{\equiv }{E^1}^{\prime }(V_s), E^2(V_s)\stackrel{c}{\equiv }{E^2}^{\prime }(V_s), E^1(V_m)\stackrel{c}{\equiv }{E^1}^{\prime }(V_m), E^2(V_m)\stackrel{c}{\equiv }{E^2}^{\prime }(V_m)$$

Due to the security of the fully homomorphic NTRU encryption system:

$$D_{sj}^1\stackrel{c}{\equiv }{D_{sj}^1}^{\prime }, D_{sj}^2\stackrel{c}{\equiv }{D_{sj}^2}^{\prime }, d_{mj}^1\stackrel{c}{\equiv }{d_{mj}^1}^{\prime }, d_{mj}^2\stackrel{c}{\equiv }{d_{mj}^2}^{\prime }$$

Since $M{D}_{ij}={MD}_{ij}^{\prime }$, we have $S_K(K,X_K,M{D}_{ij})\stackrel{c}{\equiv } vie{w}_K^{\pi }(x_1,X_K)$ Therefore, the information of $P_1$ is secure.

Using the same method, it can be proven that the information of $P_2,P_3, \cdots , P_m$ is secure. Hence, Algorithm 3 can securely compute the Mahalanobis distances between sample vectors of multiple participants. □

6. Performance Analysis

6.1. Computational Complexity

The scheme in Reference [32] is suitable for scenarios with large sample sizes. It uses the OU homomorphic encryption algorithm and the HRES homomorphic re-encryption scheme to achieve secure outsourced diagnosis. The participants include three parties: the user (QU), the classification cloud server (CCS), and the auxiliary cloud server (ACS). The main diagnostic process is outsourced to two non-colluding cloud servers (CCS and ACS). By using simulated datasets and varying different variables, the computational overheads of QU, CCS, and ACS are analyzed. The computational overhead of this scheme is mainly affected by the feature dimension $l$ of the data to be diagnosed and the number of class labels $k$. Increasing $l$ or $k$ leads to an upward trend in the average execution time of ACS and CCS. When the security parameter $\tau$ is set to 1024 and the dimension $l$ of the data to be diagnosed is 18, the average diagnostic time does not exceed 20 s. It is worth noting that Algorithms 1–3 in this paper are suitable for scenarios with small sample sizes, which differ from the application scenarios of Reference [32]. Therefore, their computational complexity, communication complexity, and the algorithms proposed in this paper are not directly comparable, and only rough comparisons can be made. Additionally, since the algorithms proposed in this paper adopt the NTRU algorithm, which is resistant to quantum attacks, they offer higher security and computational efficiency.

Computational Complexity of Algorithm 1:

Let $m_1$ be the number of vectors $x_i^1$ owned by participant $P_1$, $m_2$ be the number of vectors $x_j^2$ owned by participant $P_2$, and $n$ be the dimension of the vectors of $P_1$ and $P_2$. Algorithm 1 uses a fully homomorphic NTRU encryption system with two participants, $P_1$ and $P_2$.

$P_1$ needs to encrypt $2m_{1}n$ times in Step (1), decrypt $n$ times in Step (4), decrypt $n^2$ times in Step (6), and decrypt $m_1{m}_2$ times in Step (8). In total, $P_1$ performs $m_1{m}_2+2m_{1}n+n^2+n$ encryption/decryption operations.

$P_2$ needs to encrypt $2m_{2}n$ times in Step (2), perform $n$ homomorphic computations in Step (3), encrypt $n$ times and perform $n^2$ homomorphic computations in Step (5), and perform $m_1{m}_2$ homomorphic computations in Step (7). In total, $P_2$ performs $m_1{m}_2+2m_{2}n+n^2+2n$ operations.

Overall, the computational complexity of Algorithm 1 is $2n^2+2m_1{m}_2+2m_{1}n+2m_{2}n+3n$.

Computational Complexity of Algorithm 2:

Let $m$ be the number of vectors (equal to the number of participants) and $n$ be the dimension of each participant’s vector. Algorithm 2 has $m$ participants $P_1, P_2, \cdots , P_m$.

Step (1): $2mn$ encryptions.

Step (2): $n$ homomorphic computations.

Step (3): $n$ decryptions.

Step (4): $n$ encryptions and $n^2$ homomorphic computations.

Step (5): $n^2$ decryptions.

Step (6): $m(m-1)$ homomorphic computations.

Step (7): $m(m-1)$ decryptions.

Overall, the computational complexity of Algorithm 2 is $2m^2+2n^2+2mn-2m+3n$.

Computational Complexity of Algorithm 2:

Let $m$ be the number of vectors (equal to the number of participants) and $n$ be the dimension of each participant’s vector. Algorithm 3 has $m$ participants $P_1, P_2, \cdots , P_m$.

Step (1): $2mn$ encryptions.

Step (2): $n$ homomorphic computations.

Step (3): $n$ decryptions.

Step (4): $n$ encryptions and $n^2$ homomorphic computations.

Step (5): $n^2$ decryptions.

Step (6): $m(m-1)$ homomorphic computations and $2m(m-1)$ encryptions.

Step (7): $2mn$ encryptions.

Step (8): $m$ homomorphic computations and $2m$ encryptions.

Step (9): $2m(m-1)$ decryptions.

Step (11): $2m$ decryptions.

Overall, the computational complexity of Algorithm 3 is $5m^2+2n^2+4mn+3n$.

6.2. Communication Complexity

The communication complexity of the algorithms is measured by the number of communication rounds.

Communication Complexity of Algorithm 1:

Algorithm 1 involves communication between two participants, $P_1$ and $P_2$:

Step (1): $P_1$ sends $E_{pk}(x_i^1)$ and $E_{pk}(-x_i^1)$ to $P_2$.

Step (3): $P_2$ sends $E(-Y_k)$ to $P_1$.

Step (4): $P_1$ sends $-{\overline{Y}}_k$ to $P_2$.

Step (5): $P_2$ sends $E({\mathrm{c}}_{kl})$ to $P_1$.

Step (6): $P_1$ sends ${\Sigma }^{-1}$ to $P_2$.

Step (7): $P_2$ sends $V$ to $P_1$.

Step (8): $P_1$ sends $MD$ to $P_2$.

In total, $P_1$ and $P_2$ require four rounds of communication.

Communication Complexity of Algorithm 2:

Algorithm 2 involves $m$ participants $P_1, P_2, \cdots , P_m$:

Step (1): $P_2, \cdots , P_m$ send their $E_{pk}(x_2), \cdots , E_{pk}(x_m)$ and $E_{pk}(-x_2), \cdots , E_{pk}(-x_m)$ to $P_1$.

Step (2): $P_1$ sends $E(-Y_k)$ to $P_m$ and sends $E(A)$ and $E(B)$ to $P_2, \cdots , P_{m-1}$.

Step (3): $P_m$ sends $-{\overline{Y}}_k$ to $P_1$.

Step (4): $P_1$ sends $E({\mathrm{c}}_{kl})$ to $P_m$.

Step (5): $P_m$ sends ${\Sigma }^{-1}$ to $P_2, \cdots , P_{m-1}$.

Step (6): $P_s$ $(s=1, 2, \cdots , m-1 )$ sends $E(V_s)$ to $P_m$.

Step (7): $P_m$ publishes $D_{sj}^2$.

Step (8): $P_s$ sends $M{D}_{sm}$ to $P_m$.

In total, $P_1, P_2, \cdots , P_m$ require four rounds of communication.

Communication Complexity of Algorithm 3:

Algorithm 3 involves $m$ participants $P_1, P_2, \cdots , P_m$:

Step (1): $P_2, \cdots , P_m$ send their $E_{p{k}_m}(x_2), \cdots , E_{p{k}_m}(x_m)$ and $E_{p{k}_m}(-x_2), \cdots , E_{p{k}_m}(-x_m)$ to $P_1$.

Step (2): $P_1$ sends $E(-Y_k)$ to $P_m$ and sends $E(A)$ and $E(B)$ to $P_2, \cdots , P_{m-1}$.

Step (3): $P_m$ sends $-{\overline{Y}}_k$ to $P_1$.

Step (4): $P_1$ sends $E({\mathrm{c}}_{kl})$ to $P_m$.

Step (5): $P_m$ sends ${\Sigma }^{-1}$ to $P_2, \cdots , P_{m-1}$.

Step (6): $P_s$ $(s=1, 2, \cdots , m-1 )$ send $E^1(V_s)$ and $E^2(V_s)$ to $P_m$.

Step (7): $P_1, P_2, \cdots , P_{m-1}$ send $E_{p{k}_1}(x_i)$ and $E_{p{k}_1}(-x_i)$ to $P_m$.

Step (8): $P_m$ sends $E^1(V_m)$ and $E^2(V_m)$ to $P_1$.

Step (9): $P_m$ publishes $D_{sj}^1$ and $D_{sj}^2$.

Step (11): $P_1$ sends $d_{mj}^1$ and $d_{mj}^2$ to $P_m$.

In total, $P_1, P_2, \cdots , P_m$ require five rounds of communication.

Table 1. Performance analysis.

Protocol	Computational Complexity	Communication Complexity
Algorithm 1	$2n^2+2m_1{m}_2+2m_{1}n+2m_{2}n+3n$	4
Algorithm 2	$2m^2+2n^2+2mn-2m+3n$	4
Algorithm 3	$5m^2+2n^2+4mn+3n$	5

and

Table 2. Performance comparison.

Protocol	Number of Participants	Outsourced	Requires Auxiliary Cloud Server	Security Model	Encryption System	Quantum Attack-Resistant
Algorithm 1	2	No	No	Semi-honest	NTRU	Yes
Algorithm 2	m	No	No	Semi-honest	NTRU	Yes
Algorithm 3	m	No	No	Enhanced semi-honest	NTRU	Yes

present the performance analysis of Algorithms 1–3 in this paper. Overall, these algorithms exhibit low computational complexity, high computational efficiency, and high communication efficiency. Since Algorithms 2 and 3 involve $m$ participants, their computational and communication complexities are slightly higher than those of the two-party Algorithm 1. As Algorithm 3 is designed for deception-resistant scenarios, it includes additional steps for computing Mahalanobis distances and verification, leading to slightly higher computational and communication complexities than Algorithm 2 under the semi-honest model.

6.3. Experimental Simulation

To further evaluate the efficiency of the algorithms in this paper, experimental simulations of Algorithms 1–3 were conducted using Python (3.10.18) on the PyCharm platform, with Algorithm 1 compared against related algorithms. Since Algorithms 1–3 are suitable for small sample sizes, their computational performance is not directly comparable, and only rough comparisons can be made.

Experimental Environment:

Windows 10 64-bit system;

Intel^® Core^TM i5-8400 CPU @ 2.80GHz;

16GB RAM.

Experimental Parameter Settings:

Key length: 512 bits;

Random number length: 64 bits.

(1) Experiment 1: Execution Time Comparison Between Algorithm 1 and Related algorithms

Experimental Method:

Randomly select the number of sample vectors $x_i^1$ and $x_j^2$ for participants $P_1$ and $P_2$ as $m_1$ and $m_2$, with the total number $m=m_1+m_2$.

When the vector dimension $n=5$, $m$ takes values sequentially as $6, 8, \cdots , 14$. For each $m$, 1000 simulated experiments were performed to statistically analyze the average execution time of Algorithm 1 and the related algorithms, taking the average of the results of 1000 experiments as the result. The results are shown in Figure 4.

When the total number of vectors $m=12$, $n$ takes values sequentially as $2, 4, \cdots , 10$. For each $n$, 1000 simulated experiments were performed to statistically analyze the average execution time of Algorithm 1 and related algorithms, taking the average of the results of 1000 experiments as the result. The results are shown in Figure 5.

Figure 4 illustrates the variation in execution time of Algorithms 1–3 and the related algorithms as the number of sample vectors $m$ increases when the vector dimension $n=5$. When $n$ is fixed, the execution time of both the two-party Algorithm 1 and related algorithms increase with $m$. The execution time of Algorithm 1 grows almost linearly. Compared with related algorithms, under the same $m$, Algorithm 1 has a shorter execution time, a lower growth rate, and better computational efficiency.

Figure 5 illustrates the variation in execution time of Algorithms 1–3 and the related algorithms as the vector dimension $n$ increases when the total number of sample vectors $m=12$. When $m$ is fixed, the execution time of both the two-party Algorithm 1 and related algorithms increase with $n$. Compared with related algorithms, under the same $n$, Algorithm 1 has a shorter execution time, a lower growth rate, and better computational efficiency.

(2) Experiment 2: Latency Time Test

The performance of the proposed schemes was further evaluated through communication experiments. Simulated experiments were conducted using Python programs (with a bandwidth of 100 Mbps) on the Pycharm platform to determine the possible latency times when executing Algorithms 1–3. In practice, latency times vary across different networks, which may affect protocol performance; however, such influencing factors were not considered in this performance evaluation.

When the dimension $n=5$, the variation in latency times of Algorithms 1–3, and related algorithms with increasing $m$ is shown in Figure 6.

When the total number of sample vectors $m=12$, the variation in latency times of Algorithms 1–3, and related algorithms with increasing $n$ is shown in Figure 7.

The experimental results show that the latency times of Algorithms 1–3 are generally low. They increase with the total number of sample vectors $m$ and the dimension $n$, but at a low growth rate, indicating high communication efficiency. As shown in Figure 6, under the same total number of sample vectors $m$, the latency time of Algorithm 1 is lower than that of Algorithms 2 and 3, while the latency time of Algorithm 3 is higher than that of Algorithms 1 and 2. As shown in Figure 7, under the same sample vector dimension $n$, the latency time of Algorithm 1 is lower than that of Algorithms 2 and 3, and the latency time of Algorithm 3 is higher than that of Algorithms 1 and 2. Due to the participation of $m$ parties in the deception-resistant Algorithm 3 and the added functions of result computation and verification by each party, its latency time is the highest. As a two-party protocol under the semi-honest model, Algorithm 1 has the lowest latency time. Algorithm 2, as an $m$-party protocol under the semi-honest model, has a moderate latency time.

Figure 6 and Figure 7 present the latency time trends of Algorithms 1–3, and related schemes under different parameter settings.

Figure 6 demonstrates the changes in latency time when the vector dimension n is fixed and the total number of sample vectors m increases. The experimental results show that as the sample size increases, the latency time of all algorithms rises accordingly; however, the rate of increase remains relatively low, indicating good scalability of the algorithms. Similarly, Algorithm 1 consistently achieves the lowest latency, Algorithm 2 ranks in the middle, and Algorithm 3 shows the highest latency. This trend suggests that when the system needs to process larger datasets, the choice of protocol will significantly impact communication efficiency.

Figure 7 illustrates the changes in latency time when the total number of sample vectors m is fixed and the vector dimension n increases. It can be observed that the latency time of all algorithms increases as the vector dimension grows, but the rate of increase is relatively slow, which indicates that the proposed algorithms maintain high communication efficiency when dealing with high-dimensional data. Among the three algorithms, Algorithm 1, due to its structure as a two-party scheme with a simple workflow and less data exchange, consistently achieves the lowest latency across all dimensions. Algorithm 2, as a multi-party semi-honest protocol, has slightly higher latency. Algorithm 3, designed with fraud-resistance features, requires each participant to perform additional result computation and verification, resulting in higher latency than Algorithms 1 and 2.

If the vector dimension or sample size increases further, both theoretical analysis and experimental results suggest that the latency of all algorithms will rise accordingly, especially in scenarios involving more participants and complex security mechanisms (such as Algorithm 3), which will lead to further increases in communication and computational overhead. In practical applications, the choice of protocol should be balanced according to data scale and security requirements to achieve optimal performance and security.

The results obtained from this study have significant implications for the field of medical research. The proposed privacy-preserving algorithms enable secure computation and analysis of sensitive medical data without compromising patient privacy. This not only ensures compliance with data protection regulations but also fosters collaboration and data sharing between medical institutions. By supporting efficient and accurate diagnosis in a privacy-aware manner, these algorithms can accelerate large-scale clinical research, facilitate the development of personalized medicine, and enhance the reliability of multi-center studies. Ultimately, the adoption of such secure computational approaches is expected to drive innovation in medical data analysis, improve patient outcomes, and contribute to the advancement of precision healthcare.

In this manuscript, we clearly state that the proposed secure Mahalanobis distance protocol is primarily applicable to scenarios with a “small number of sample vectors.” Specifically, our experiments—conducted on an Intel i5-8400 CPU with 16GB RAM and a key length of 512 bits—demonstrate that the protocol performs efficiently when the number of samples ranges from several tens to a few hundred, and the vector dimensionality ranges from around ten to several tens. For example, when the sample size is approximately 10~100 and the dimension is 5~40, the protocol achieves average execution times from a few seconds up to about ten seconds, with communication delays remaining acceptable.

This limitation is due to several technical reasons:

(1)

Encryption and Decryption Overhead: The protocol relies on NTRU-based homomorphic encryption. While NTRU offers high security and quantum resistance, the computational cost for encryption and homomorphic operations increases sharply with both the number of samples and the vector dimensionality, leading to linear or even superlinear growth in computation time and memory usage.

(2)

Communication Complexity: Secure multi-party computation schemes require multiple rounds of interaction between parties. As the sample size and the number of participants increase, the number of communication rounds and the amount of data transmitted rapidly scale up, easily causing network bottlenecks.

(3)

Resource Constraints: Under current hardware configurations, large-scale datasets may result in memory overflows or significant delays, severely affecting practical usability.

At present, the scalability of the protocol for large-scale datasets—such as those containing thousands of samples or high-dimensional feature spaces—remains unclear for the following reasons:

(1)

Experiments have not covered large-scale datasets (e.g., >1000 samples, >100 dimensions).

(2)

Encryption operations and communication costs increase too rapidly with scale, and no efficient distributed optimization has been developed.

To further investigate the impact of dataset size on method performance, we supplement our analysis as follows:

(1)

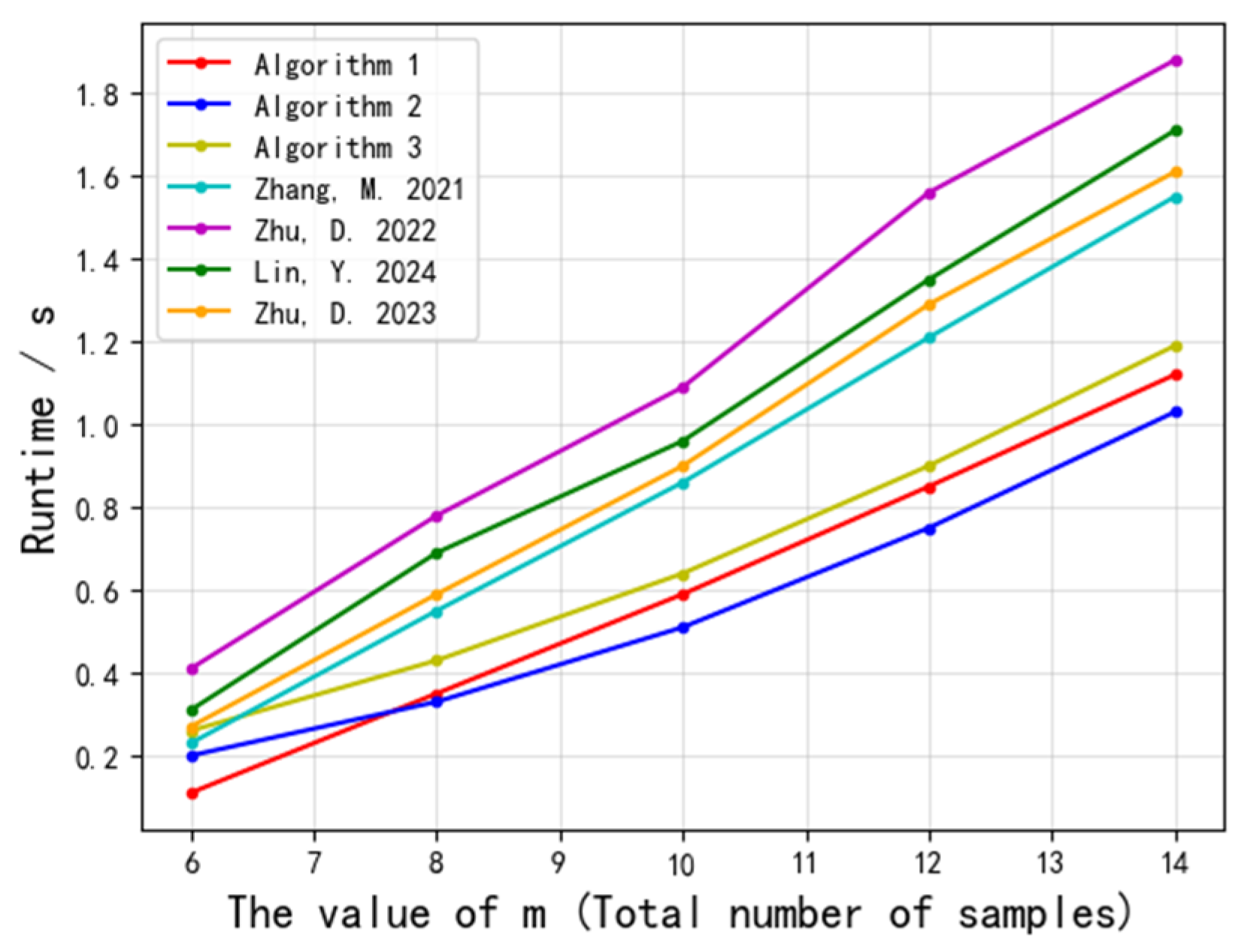
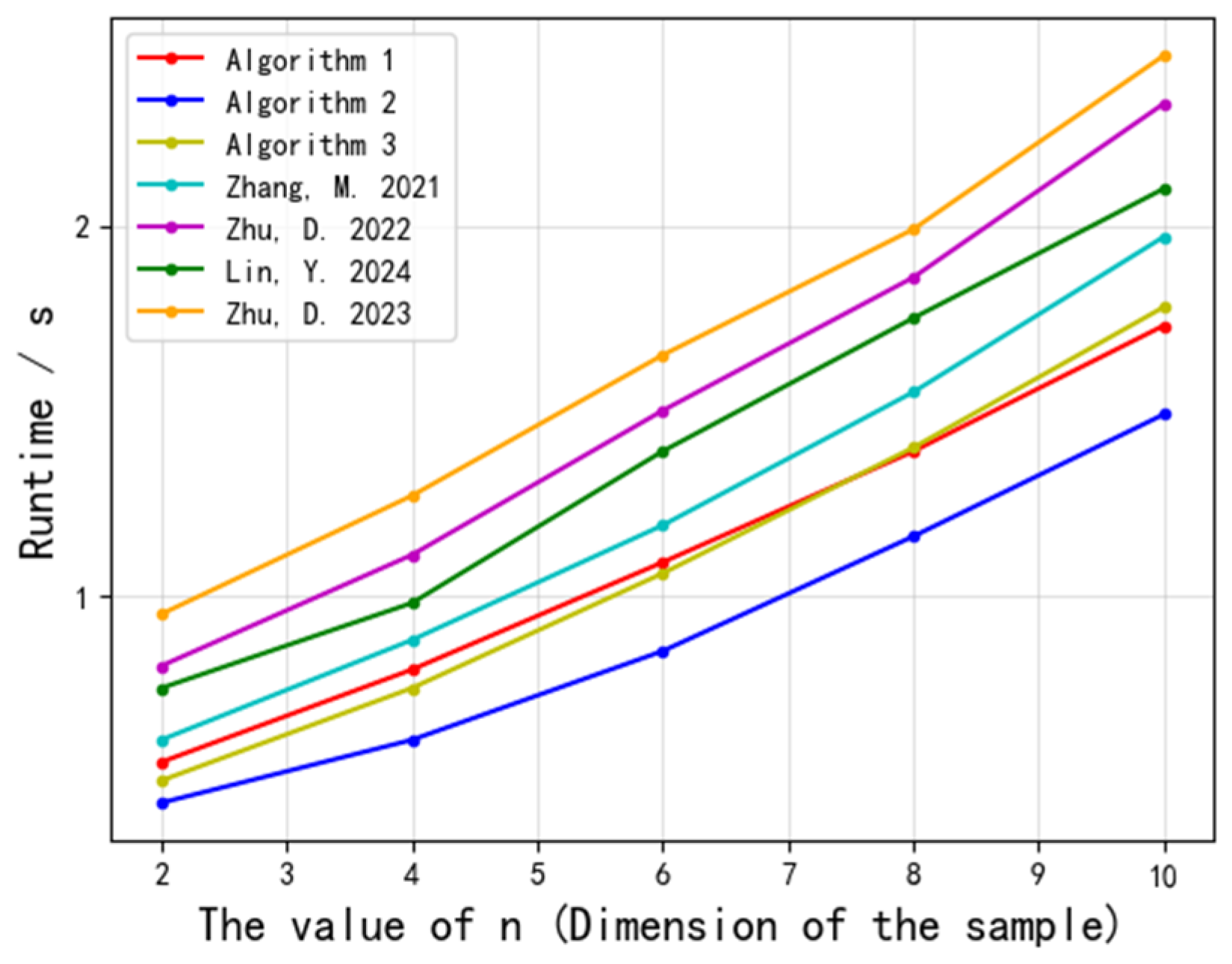
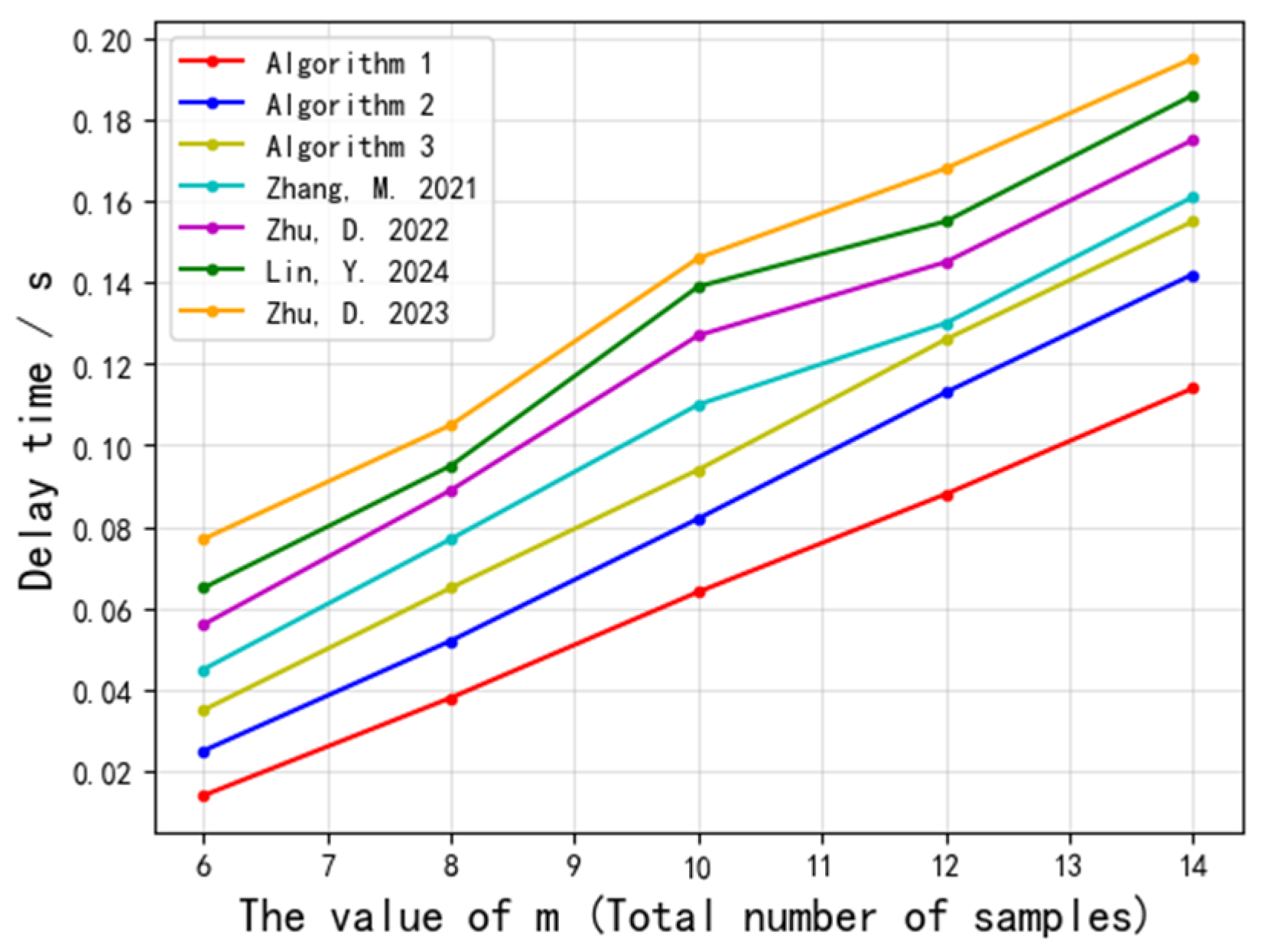
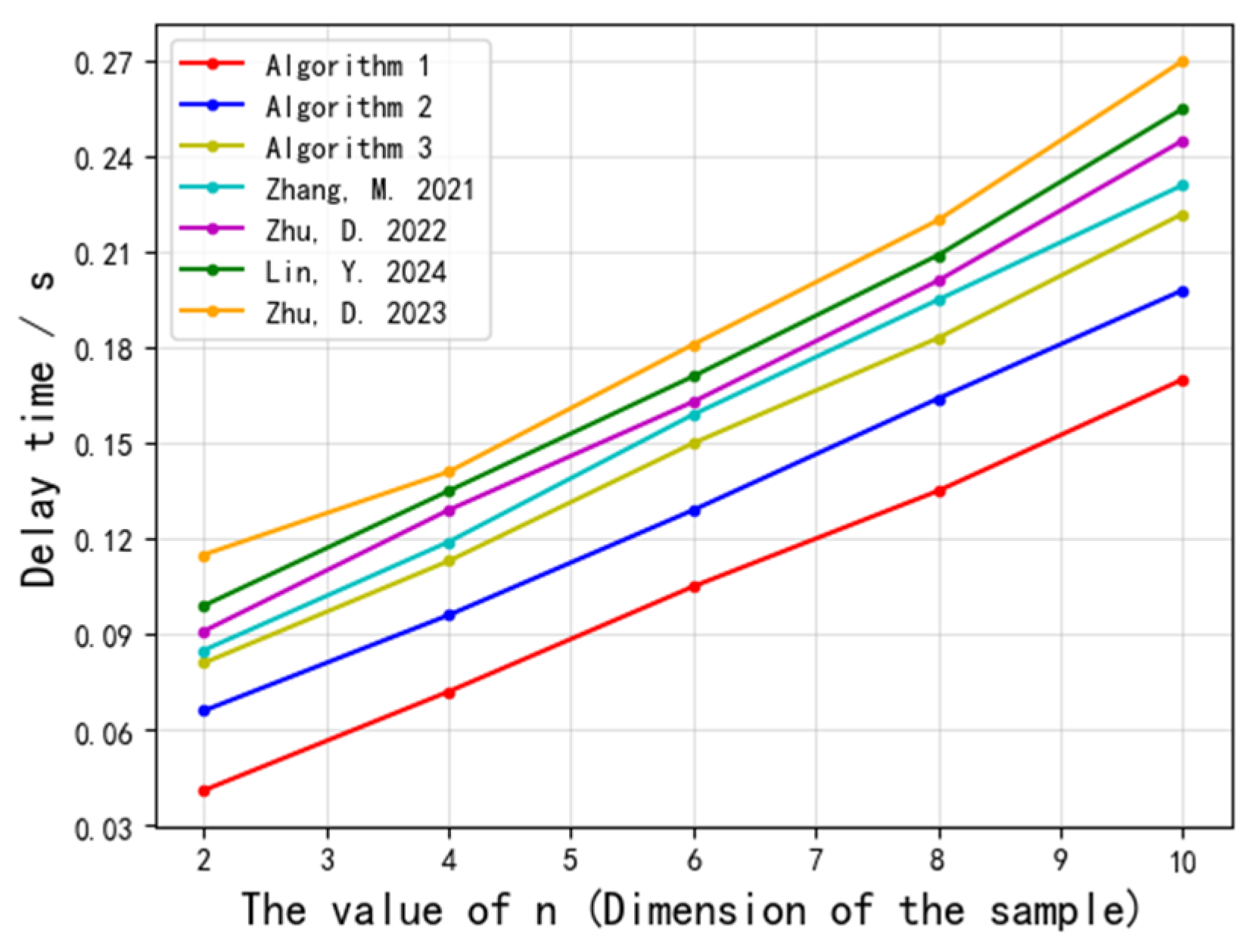
Execution Time Trends: As shown in Figure 4 and Figure 5, increasing either the number of samples or the dimensionality leads to linear (in sample size) and polynomial (in dimensionality) growth in execution time. While Algorithm 1 exhibits nearly linear growth in execution time with fixed dimensions, it still cannot accommodate extremely large-scale scenarios.

(2)

Communication Latency: Our experimental results indicate that communication latency is tied to both the number of participants and the sample size. When the sample size reaches several hundred, the communication overhead becomes significant; in large-scale settings, network costs may become unacceptable.

(3)

Scalability Outlook: To support larger datasets, protocol design enhancements such as distributed computation, batch processing, or the adoption of more efficient encryption schemes (e.g., block-based homomorphic encryption or multi-core parallelism) are needed to reduce individual node overhead and improve overall throughput.

In summary, our protocol is currently suited for collaborative scenarios with ≤hundreds of samples and ≤tens of dimensions. Processing large-scale datasets remains challenging due to technical constraints and is an important direction for future research. We plan to conduct large-scale experiments and protocol optimizations to further assess and improve the scalability of our approach.

7. Conclusions

This paper proposes a multi-party secure computation protocol for Mahalanobis distance, addressing the growing need for privacy preservation in high-dimensional collaborative data scenarios. Compared with existing solutions, our approach enables efficient and fair joint computation of the Mahalanobis distance without disclosing the original data of each participant and incorporates mechanisms to effectively defend against malicious behavior. Theoretical analysis and experimental simulations demonstrate the superiority of the proposed protocol in terms of security, correctness, and practical efficiency, providing a robust technical foundation for distributed data analysis and intelligent decision-making. A key novel insight of this work lies in the introduction of anti-malicious modeling into privacy-preserving Mahalanobis distance computation and a systematic optimization of communication and computation resources, which significantly enhances scalability and practical applicability.

Nevertheless, due to the current state of secure multi-party computation and homomorphic encryption technologies, our protocol still encounters certain computational and communication overheads when dealing with large-scale samples and high-dimensional data. Moreover, the current implementation is primarily based on the semi-honest and partially malicious adversary models and requires further improvement to handle more sophisticated real-world attacks. Future work will focus on several directions: first, exploring more efficient encryption and parallel computation mechanisms to further reduce system overhead for large datasets; second, extending protocol security under fully malicious models; and third, promoting practical deployment and optimization in real-world applications such as healthcare and finance.