The Three-Body Problem: The Ramsey Approach and Symmetry Considerations in the Classical and Quantum Field Theories

Abstract

The graph theory-based approach to the three-body problem is introduced. Vectors of linear and angular momenta of the particles form the vertices of the graph. Scalar products of the vectors of the linear and angular momenta define the colors of the links connecting the vertices. The bi-colored, complete graph emerges. This graph is called the “momenta graph”. According to the Ramsey theorem, this graph contains at least one mono-chromatic triangle. This is true even for chaotic motion of three bodies; thus, illustrating the idea supplied by the Ramsey theory, total chaos is impossible. Coloring of the graph is independent on the rotation of frames; however, it is sensitive to Galilean transformations. The coloring of the momenta graph remains the same for general linear transformations of vectors with a positive-definite matrix. For a given motion, changing the order of the vertices does not change the number and distribution of monochromatic triangles. Symmetry of the momenta graph is addressed. The symmetry group remains the same for general linear transformation of vectors of the linear and angular momenta with a positive-definite matrix. Conditions defining conservation of the coloring of the momenta graph are addressed. The notion of the stereographic momenta graph is introduced. Shannon entropy of the momenta graph is calculated. The particular configurations of bodies are addressed, including the Lagrange configuration and the figure eight-shaped motion. The suggested approach is generalized for the quantum field theory with the Pauli–Lubanski pseudo-vector. The suggested coloring procedure is the Lorenz invariant.

1. Introduction

The three-body problem remains one of the fascinating “evergreen” problems of fundamental physics. In an extended modern sense, a three-body problem is any problem in classical mechanics or quantum mechanics that models the motion of three particles. We call this problem the “general three-body problem”. In the more restricted, classical meaning, the three-body problem emerges when three bodies/masses move in 3D space under their gravitational interactions as described by Newton’s law of gravity [1]. Solutions of this problem require that future and past motions of the bodies should be uniquely determined based solely on their present positions and velocities [1,2]. Even when bodies interact via gravitational (or other $U\left(r\right)~{\displaystyle \frac{1}{r}}$ potential), no general closed-form solution of the three-body problem exists. In other words, it does not have a general solution that can be expressed in terms of a finite number of standard mathematical operations. Behavior of three-body dynamical systems is chaotic for most initial conditions, and numerical methods are generally required for deriving the exact trajectories of involved masses. In a restricted number of special configurations of the bodies, the exact solutions of the problem do exist. Special, tractable cases of the three-body problem were analyzed by Euler and Lagrange [1,2,3]. The essential progress in the development of the classical three-body problem is related to the fundamental studies by Henri Poincaré [4]. We demonstrate that certain “hidden” structures may be revealed in the three-body dynamics with the Ramsey graph theory.

Ramsey theory is a branch of discrete mathematics/combinatorics that studies order and structure that inevitably must appear in large, complex, or chaotic systems [5,6,7,8,9,10,11,12,13]. In simple terms, it says that if some set of objects is large enough, the prescribed patterns are guaranteed to emerge [10,11,12,13]. A very important, general conclusion emerging from the Ramsey theory appears as follows: “Complete disorder is impossible.” Ramsey’s theorem, formulated in the simplest possible way, states that in any group of six people, there will always be either a group of three people who all know each other or a group of three people who are complete strangers to each other. More generally, Ramsey theory deals with questions like, “how large does a system have to be before a certain structure must appear?” or, “what is the minimal number of elements needed to guarantee a particular pattern?” We apply the Ramsey theorem for the analysis of patterns inherent for the three-body problem. Thus, we suggest the novel approach, which is not focused on the exact solution of the differential equations, describing the motion of the particles. In contrast, it exploits the graph representation of the motion, revealing the hidden structures in the momenta graph, which appear even when the motion of three bodies is chaotic.

2. Results and Discussion

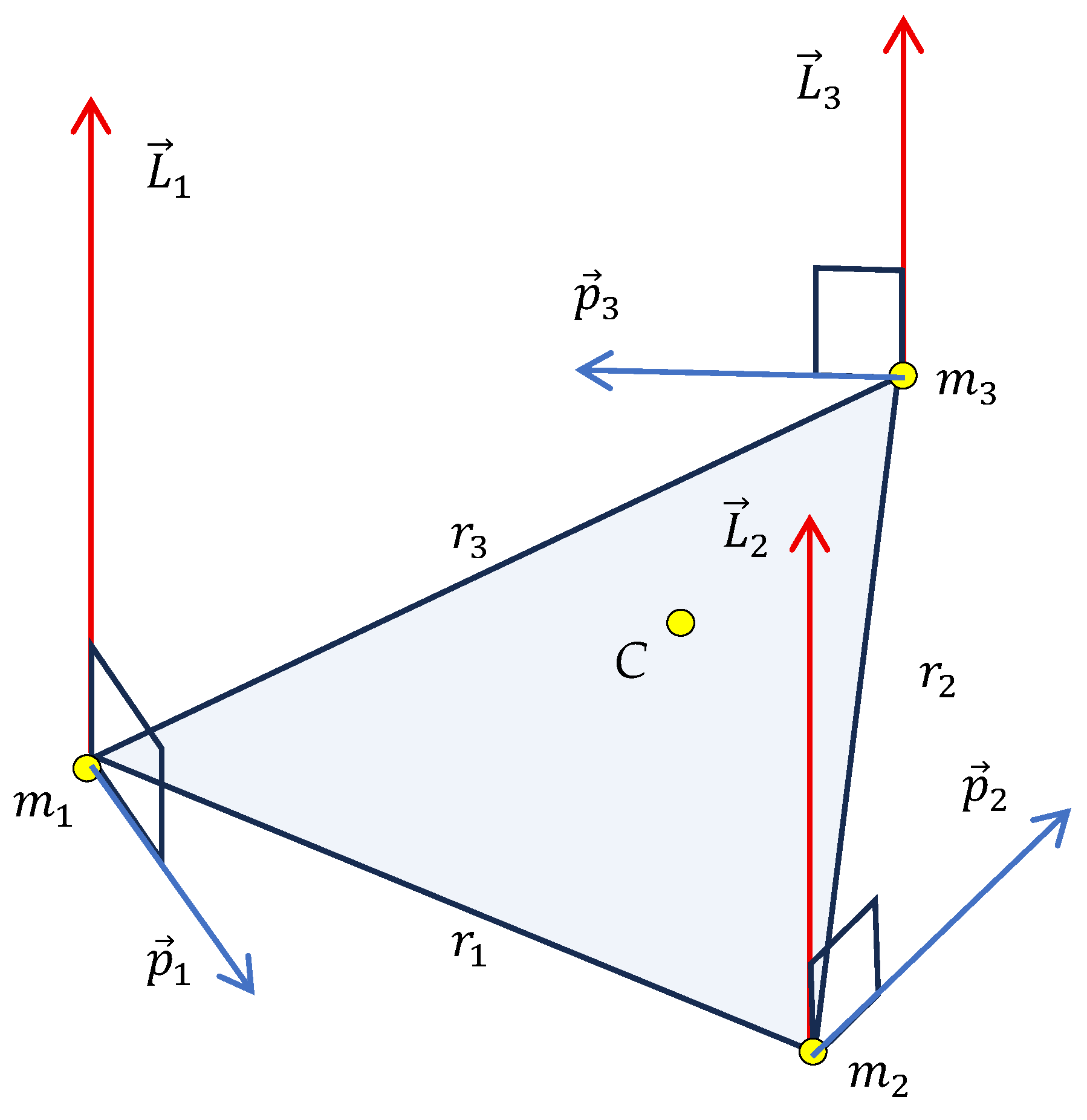
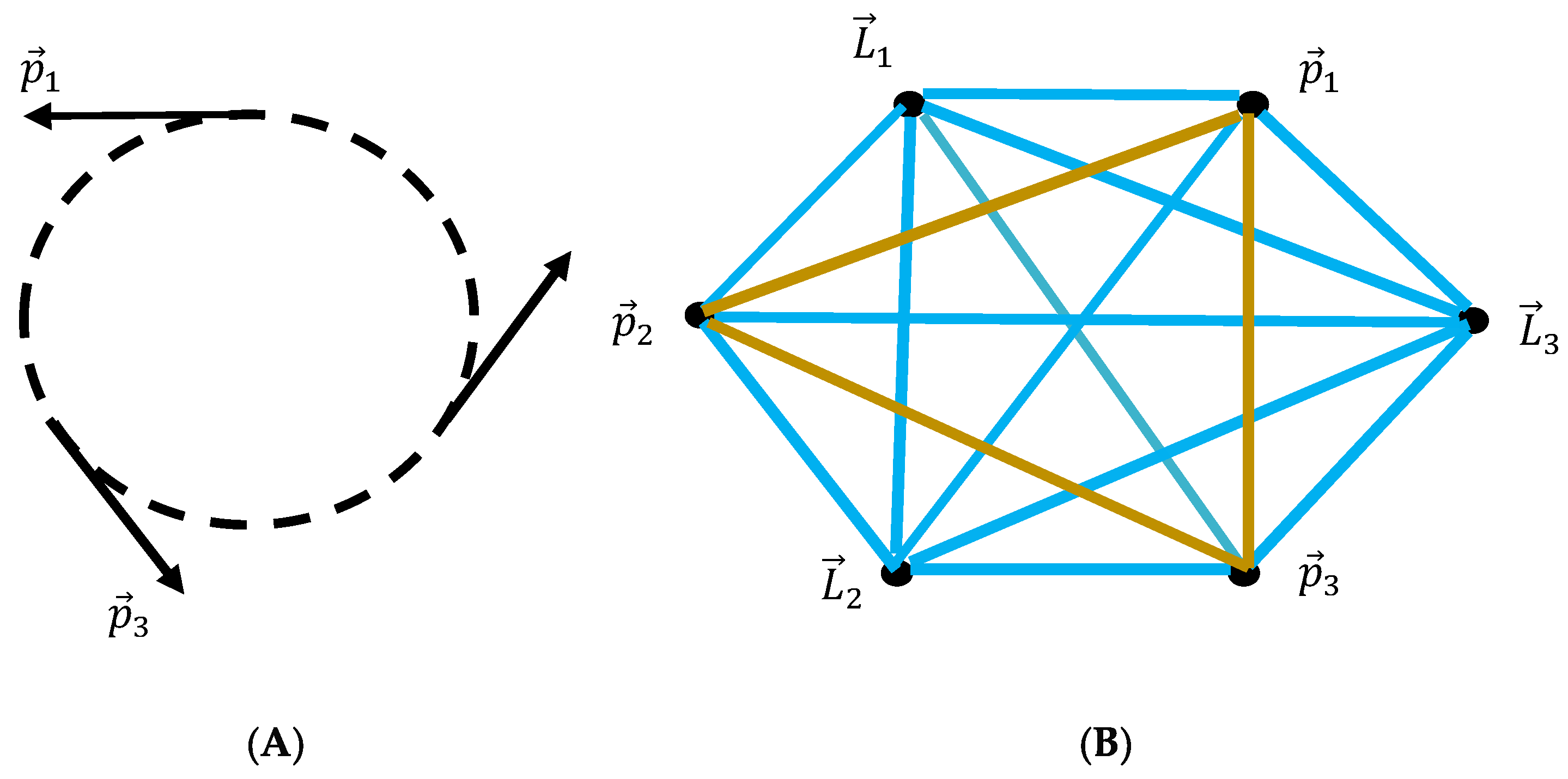
2.1. Ramsey Momenta Graph Emerging from the Motion of the Three-Body System

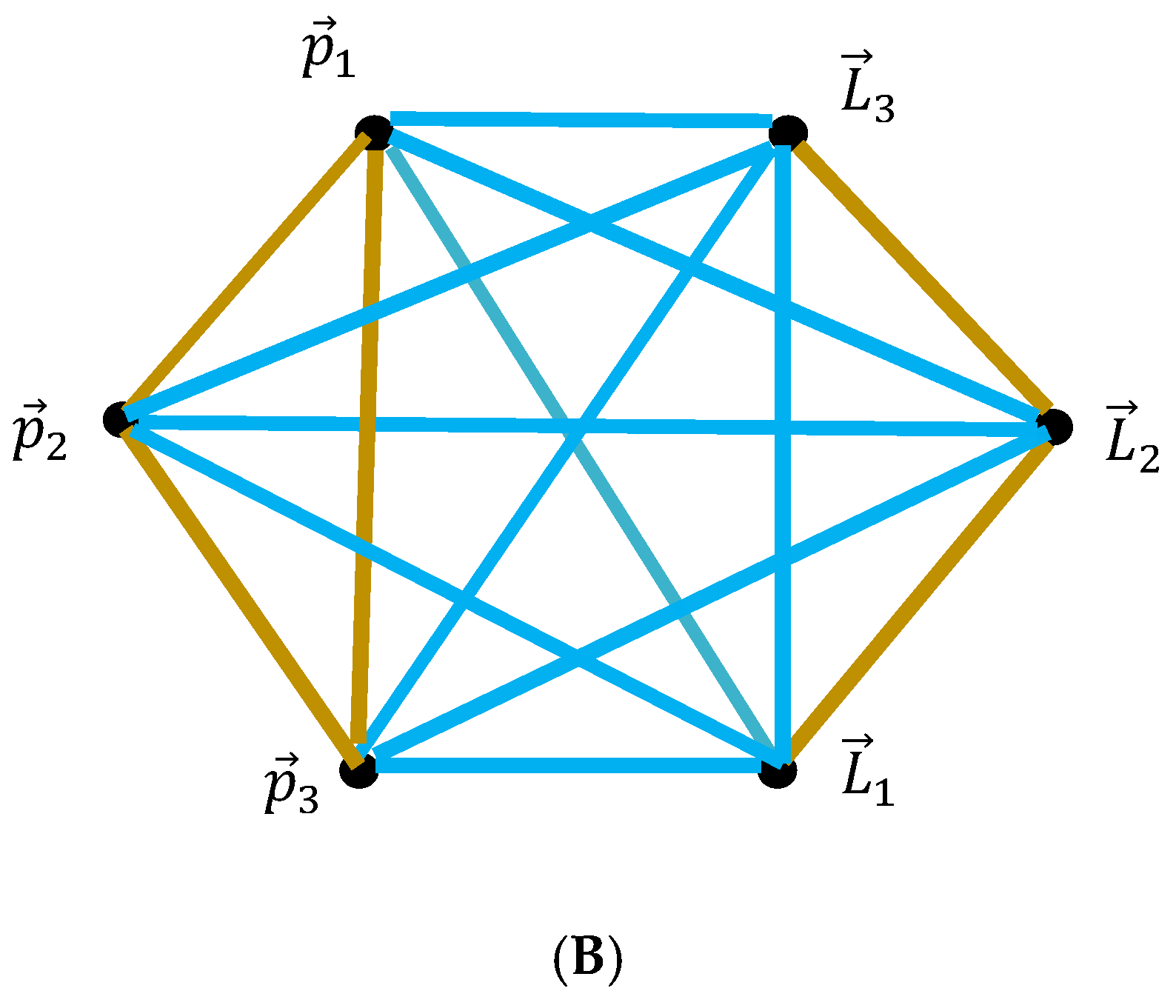
Consider the general three-body problem. We address motion of three point particles $m_{i, }(i=1,\dots 3)$. which interact via an arbitrary potential. The momenta of the particles are denoted ${\overrightarrow{p}}_i, i=1,\dots ,3$; the angular momenta of the particles are labeled ${\overrightarrow{L}}_i, i=1,\dots ,3$. We make a snapshot of the particles’ motion made in an arbitrary frame. This snapshot gives rise to the bi-colored, complete graph, built according to the mathematical procedure, introduced below. The linear and angular momenta of the particles serve as the vertices of the graph. The vertices are connected with the colored links. The colors of the links are established, as follows. The vertices are connected with the turquoise link if Equation (1) takes place (see Figure 1):

$$\left({\overrightarrow{p}}_i·{\overrightarrow{p}}_j\right)\ge 0;\left({\overrightarrow{L}}_i·{\overrightarrow{L}}_j\right)\ge 0; \left({\overrightarrow{p}}_i·{\overrightarrow{L}}_j\right)\ge 0, i,j=1,\dots ,3;i\ne j$$

(1)

The vertices are connected with the mustard link, if Equation (2) is true:

$$\left({\overrightarrow{p}}_i·{\overrightarrow{p}}_j\right)<0;\left({\overrightarrow{L}}_i·{\overrightarrow{L}}_j\right)<0;\left({\overrightarrow{p}}_i·{\overrightarrow{L}}_j\right)<0,i,j=1,\dots ,3;i\ne j$$

(2)

This similar coloring procedure was already introduced for the graphs emerging from the motion of the particles [14]. Now we extend the procedure for the analysis of the three-body problem.

It seems, at first glance, that the scalar products $\left({\overrightarrow{p}}_i·{\overrightarrow{L}}_j\right)$ are physically senseless; however, we will demonstrate below that these scalar products enable the elegant generalization in the realm of the quantum relativistic theory, exploiting the Pauli–Lubansky pseudo-vectors.

Let us address some general combinatorics properties of the momenta graph. It is noteworthy that it is different from the conventional Ramsey complete bi-colored graph due to the fact that it is built of two distinguishable groups of vertices, namely ${\overrightarrow{p}}_i=\left({\overrightarrow{p}}_1,\dots ,{\overrightarrow{p}}_3\right)$ and ${\overrightarrow{L}}_i=\left({\overrightarrow{L}}_1,\dots ,{\overrightarrow{L}}_3\right)$. Thus, no triangle (monochromatic or bi-chromatic) built of the edges ${\overrightarrow{p}}_i;{\overrightarrow{L}}_j$ is possible. Let us explain it: consider the edges ${\overrightarrow{p}}_1;{\overrightarrow{L}}_2$ and ${\overrightarrow{p}}_1;{\overrightarrow{L}}_3$. The edge closing the triangle is necessarily ${\overrightarrow{L}}_2;{\overrightarrow{L}}_3$, and it is built from the vectors of the angular momenta only. This is easily expanded to any of edges ${\overrightarrow{p}}_i;{\overrightarrow{L}}_j, i,j=1,\dots ,3$. Thus, no triangle (mono-chromatic or bi-chromatic) built only of the vertices ${\overrightarrow{p}}_i;{\overrightarrow{L}}_j, i,j=1,\dots 3$ is possible. Also, triangles built of mixed edges ${\overrightarrow{p}}_i;{\overrightarrow{p}}_j$ and ${\overrightarrow{L}}_i;{\overrightarrow{L}}_j$ only are impossible. This is easily checked.

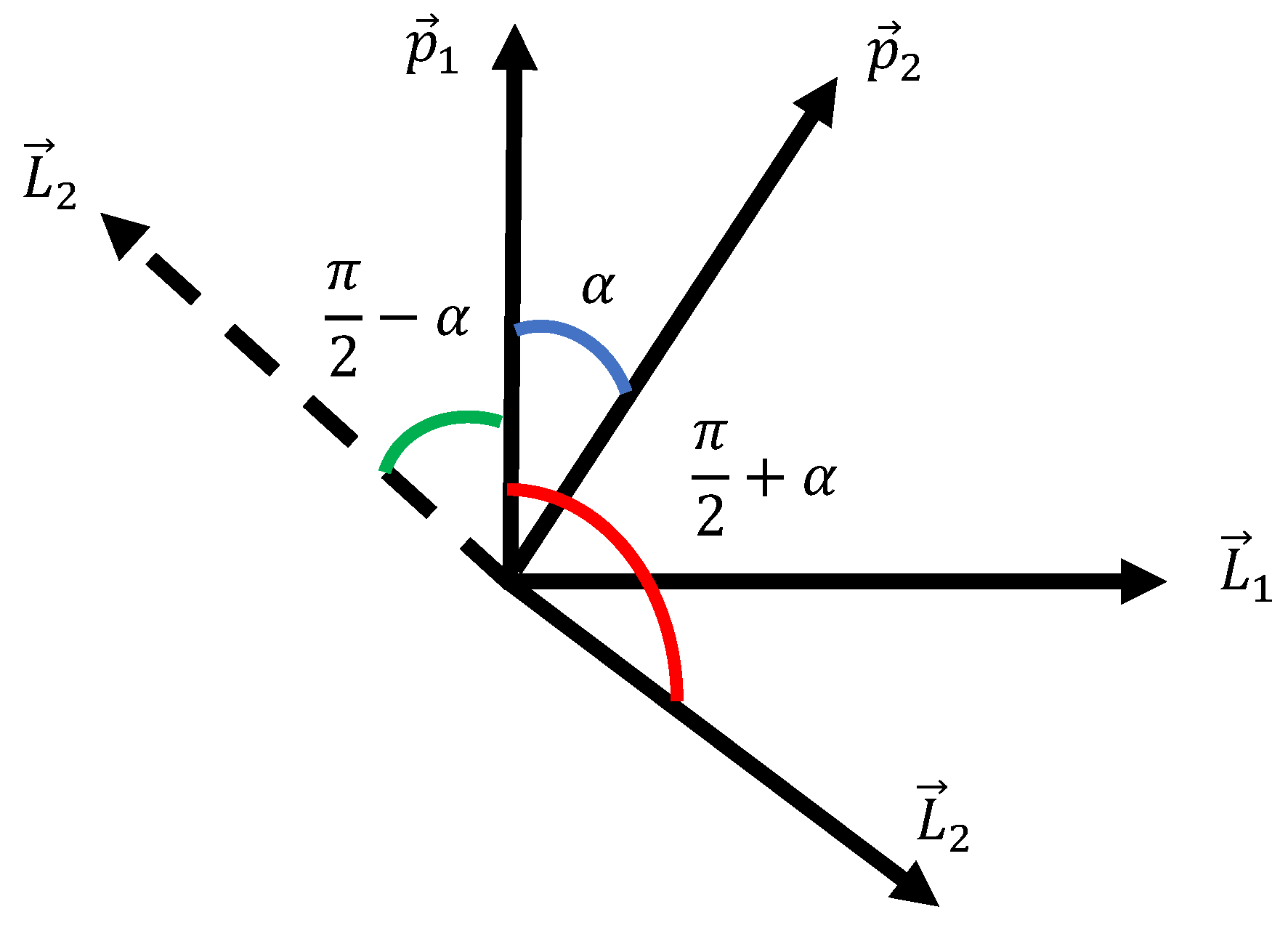
Now let us discuss the coloring of the emerging momenta graph. Obviously, vertices linking vertices corresponding to the ${\overrightarrow{p}}_i, i=1,\dots ,3$ and ${\overrightarrow{L}}_i, i=1,\dots ,3$ are always connected with the turquoise link; indeed, $\left({\overrightarrow{p}}_i·{\overrightarrow{L}}_i\right)=0$. This is true for 1D, 2D and 3D systems of vectors of linear and angular momenta and it remains correct in any frames. The sign of the scalar product of the linear and angular momenta of two different moving point masses is not fixed. It can be positive, negative, or zero depending on their relative positions and velocities. For linear momenta it is obvious; for the angular momenta it follows from Equation (3):

$$\left({\overrightarrow{L}}_i·{\overrightarrow{L}}_j\right)=r^2\left({\overrightarrow{p}}_i·{\overrightarrow{p}}_j\right)-\left(\overrightarrow{r}·{\overrightarrow{p}}_i\right)\left(\overrightarrow{r}·{\overrightarrow{p}}_j\right)$$

(3)

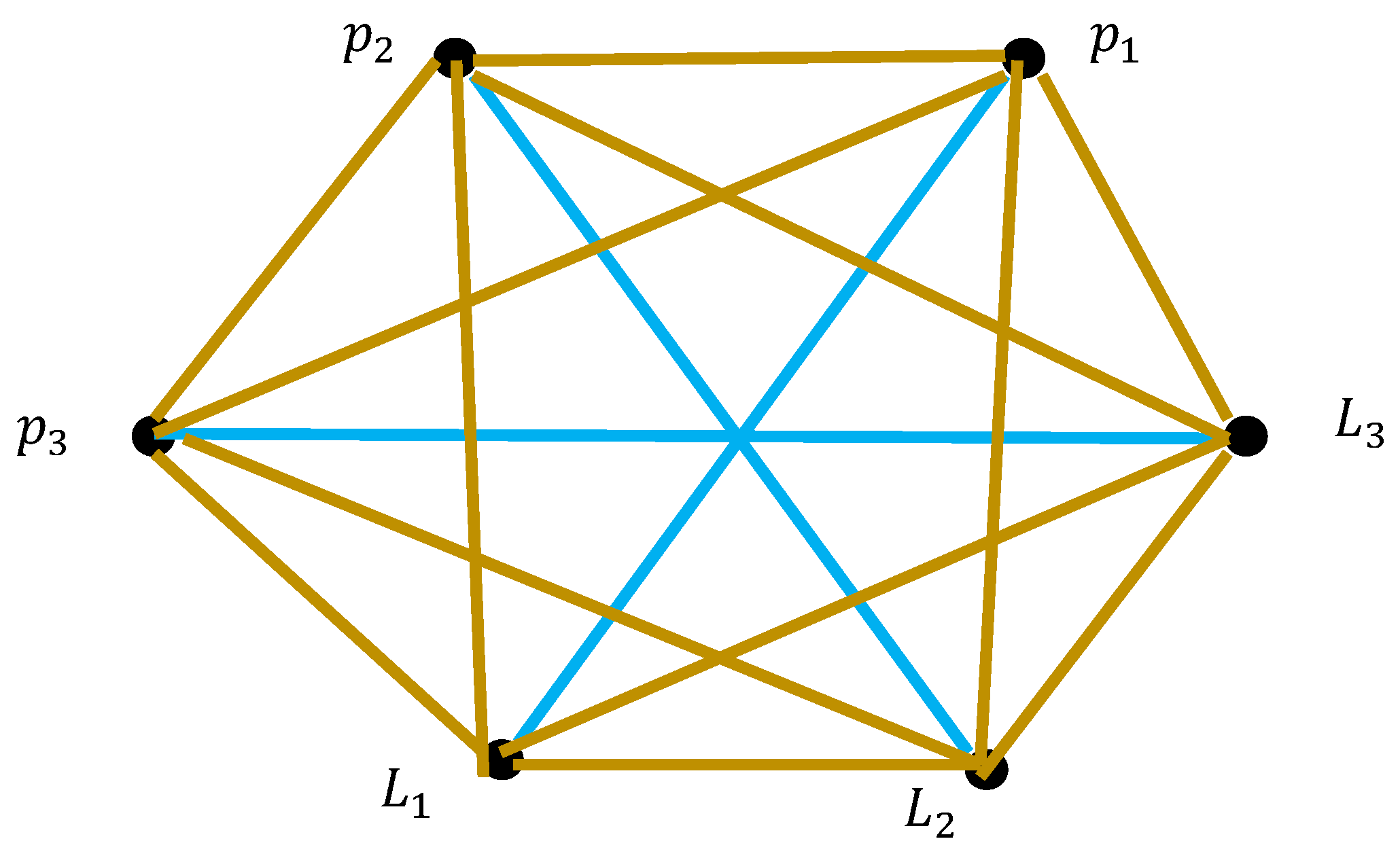
It is immediately recognized from Equation (3) that the sign of the scalar product of the angular momenta of two moving point masses can be positive, negative, or zero, depending on their relative positions and velocities. The sign of the scalar product $\left({\overrightarrow{p}}_i·{\overrightarrow{L}}_j\right)$ is also not fixed. This is illustrated with Figure 2.

According to the Ramsey theorem, the bi-colored, complete Ramsey graph built of the six vertices will inevitably contain at least one mono-colored triangle. For the sake of brevity, we call the graph built according the aforementioned procedure the “momenta graph”. Thus, we demonstrate the following theorem:

Theorem 1. 

Consider arbitrary motion of six point particles. The particles interact via arbitrary interactions. Linear and angular momenta serve as the vertices of the graph. The vertices are connected with the turquoise link if $\left({\overrightarrow{p}}_i·{\overrightarrow{p}}_j\right)\ge 0;\left({\overrightarrow{L}}_i·{\overrightarrow{L}}_j\right)\ge 0; \left({\overrightarrow{p}}_i·{\overrightarrow{L}}_j\right)\ge 0, i,j=1,\dots ,3;i\ne j$ take place. The vertices are connected with the mustard link if $\left({\overrightarrow{p}}_i·{\overrightarrow{p}}_j\right)<0;\left({\overrightarrow{L}}_i·{\overrightarrow{L}}_j\right)<0; \left({\overrightarrow{p}}_i·{\overrightarrow{L}}_j\right)<0, i,j=1,\dots ,3;i\ne j$ is true. The momenta graph will inevitably contain at least one mono-chromatic triangle.

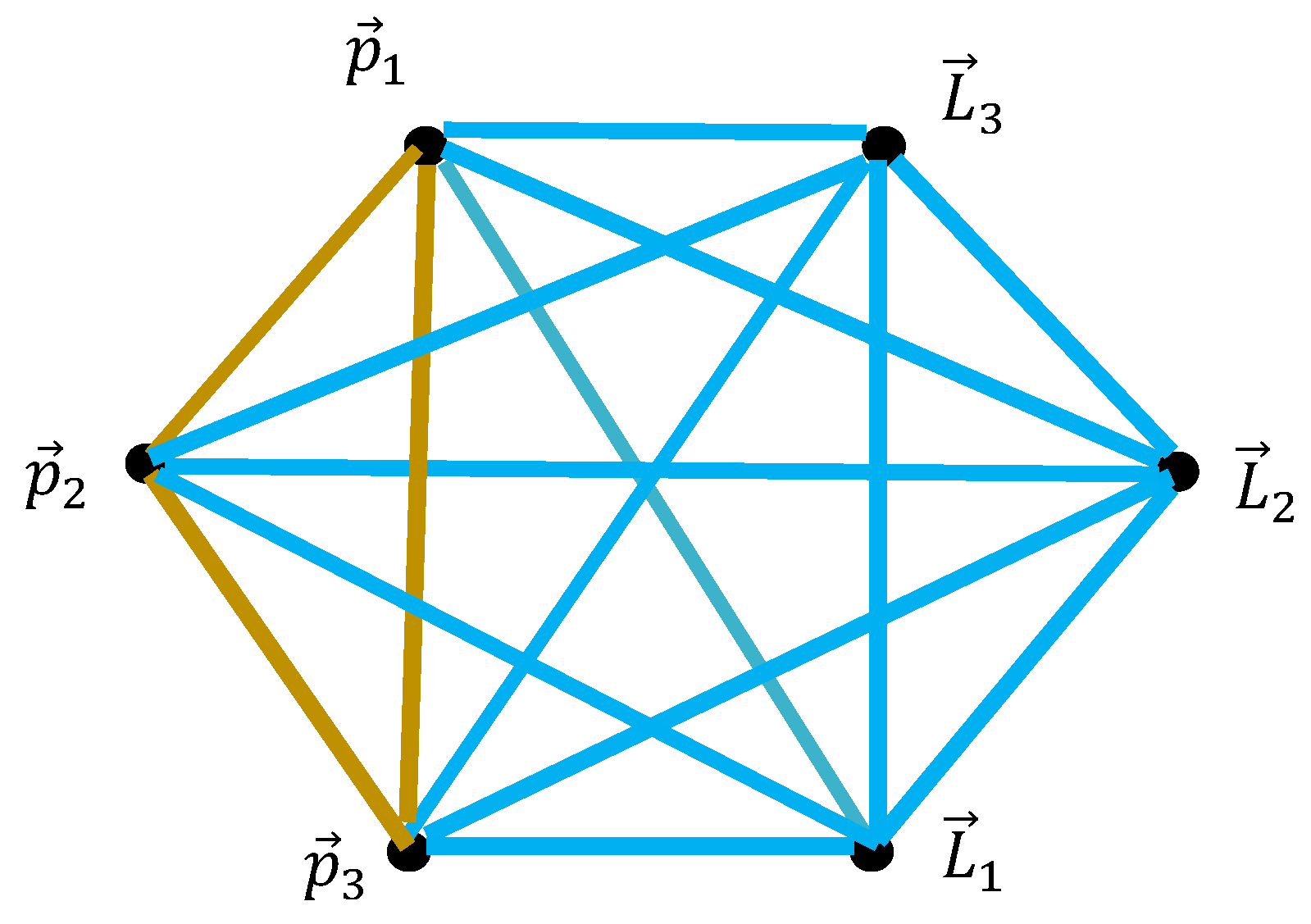
Consider now the momenta graph shown in Figure 1. It contains three turquoise triangles, namely:$\left\{{\overrightarrow{p}}_2,{\overrightarrow{L}}_1,{\overrightarrow{L}}_3\right\}$, $\left\{{\overrightarrow{p}}_2,{\overrightarrow{p}}_3,{\overrightarrow{L}}_1\right\}$, $\left\{{\overrightarrow{p}}_2,{\overrightarrow{L}}_2,{\overrightarrow{L}}_3\right\}$, and one mustard triangle, namely: $\left\{{\overrightarrow{p}}_1,{\overrightarrow{p}}_3,{\overrightarrow{L}}_2\right\}$.

Now we discuss the general properties of the momenta graph. First of all, we note that the Ramsey theorem does not define, what kind of mono-colored triangle will necessarily appear in the momenta graph [5,6,7,8,9,10,11,12,13]. The second fact is very important: the coloring of the graph will remain the same when frames are rotated relatively to the origin of the frames. Indeed, scalar products given by Equations (1) and (2) are invariant relatively to the rotation of frames relatively to origin. The coloring of the graph remains untouched also for uniform scaling of vectors (i.e., the same scalar multiplication for vectors of linear and angular momenta and reflection of axes). Generally speaking, the coloring of the graph remains the same for general linear transformation of vectors ${\overrightarrow{p}}_i, {\overrightarrow{L}}_i, i=1\dots 3$ with a positive-definite matrix A:

$$\overrightarrow{p_i^{\prime }}\to A{\overrightarrow{p}}_i; \overrightarrow{L_i^{\prime }}=A{\overrightarrow{L}}_i, i=1,\dots ,3$$

(4)

Let us demonstrate it:

$$\left(A{\overrightarrow{p}}_i\right)·\left(A{\overrightarrow{p}}_j\right)={\overrightarrow{p}}_i^T{A}^{T}A{\overrightarrow{p}}_j,i\ne j,$$

(5)

and since $A^{T}A$ is also positive-definite, the sign is preserved. The same is true for the vectors of the angular momenta and mixed scalar products. Thus, we demonstrate that the coloring of the graph, depicted in Figure 1, remains the same for general linear transformations of vectors with a positive-definite matrix A. It is noteworthy that the coloring of the graph is not Lorentz invariant.

Now we consider the distribution of the colored links within the momenta graph. The total number of the links in this graph is $N_{tot}={\displaystyle \frac{6\left(6-1\right)}{2}}=15.$ This number is built from the turquoise links, denoted $N_t$ and the mustard links denoted $N_m.$

$$N_{tot}=N_t+N_m$$

(6)

It is noteworthy that numbers $N_t \mathrm{a}\mathrm{n}\mathrm{d} N_m$ are independent of the location of vectors/vertices within the graph; the order of the vectors/vertices of the linear and angular momenta is not important and is arbitrary. These numbers remain untouched under the rotation of the origin of the frames. However, they are sensitive to Galileo transformations.

Now we address the distribution of the mono-colored triangles within the momenta graph. For a given motion, changing the order of the vertices does not change the number or distribution of monochromatic triangles. When we permute the vertices, we are simply relabeling them. This does not affect the actual connections or edge colors, it just changes their names. Therefore, the structure of the graph remains the same, and so does the number and type of monochromatic triangles. Again, the number and type of monochromatic triangles is insensitive to rotation of frames but it is sensitive to Galileo transformations.

It should be emphasized that the aforementioned Theorem 1 remains true for any motion of three bodies, including the chaotic motion, i.e., deterministic but unpredictable behavior emerging in a three-body system [1]. We mean the situation, when small differences in initial locations and velocities of bodies lead to vastly different outcomes over time, making long-term prediction practically impossible. The motion may be chaotic; however, at least one mono-colored triangle, predicted by Theorem 1, will be kept in any momenta graph. Thus, certain order will be necessarily recognized in any momenta graph. The quantification of orderliness of the graph will be discussed below. However, the coloring procedure defined by Equations (1) and (2), is sensitive to Galilean transformations [14].

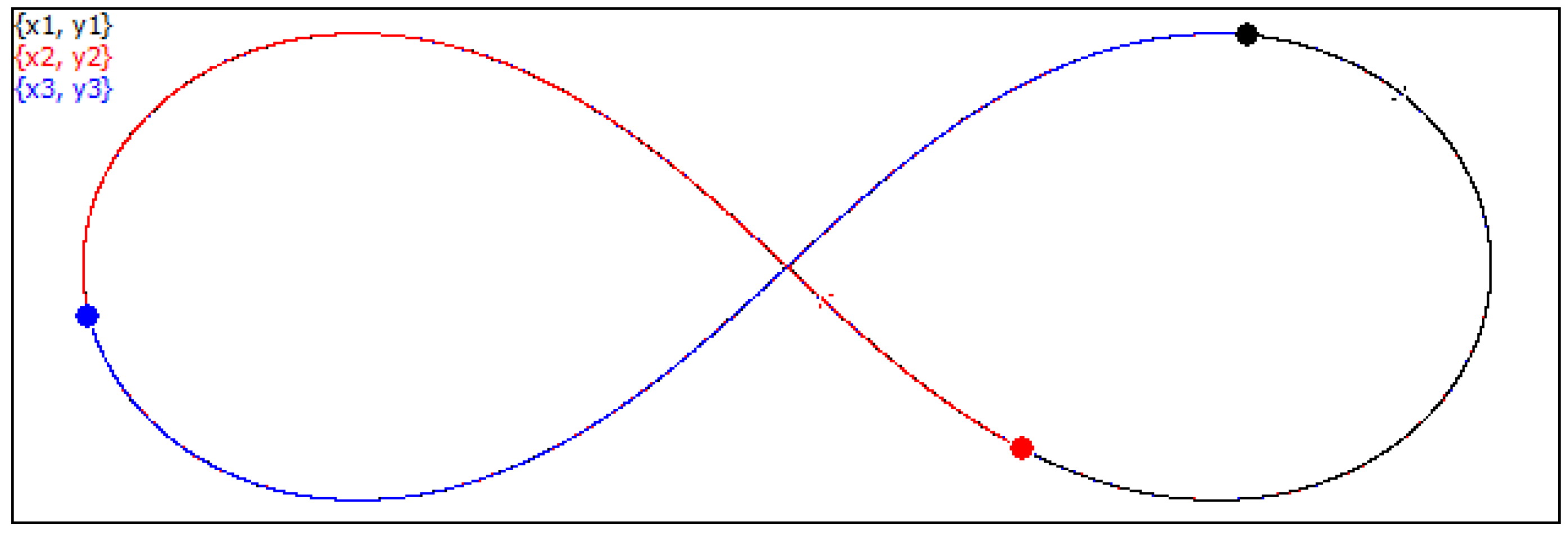
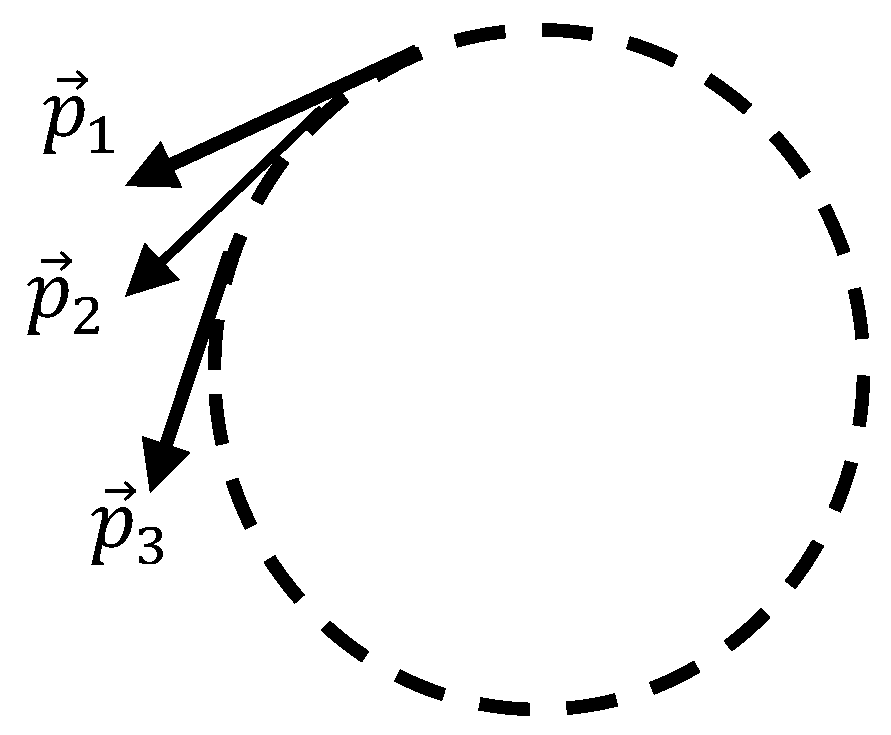
Now we introduce the notion of the “trivial motion graph”. The motion graph is defined as trivial when all of the scalar products given by Equations (1) and (2) are zero. Consider that in 3-dimensional space, the maximum number of mutually orthogonal vectors is three. Our graph is built of six vectors; thus, it is clear that the trivial motion graph is impossible. This is obviously also true for 2D and 1D motions of three bodies. The only exception is the degenerated case, when two or all of three particles are in rest. In this situation, all of the scalar products given by Equations (1) and (2) are zero. The graph is defined as “monochromatic” when all of the links are colored with the same color. The sketch depicted in Figure 3 gives rise to the mono-chromatic motion graph. The sketch illustrates the circular, planar motion of three non-interacting bodies.

All of the angles between the linear momenta of the particles are acute. It is easily seen from Equation (1) that the entire motion graph is colored with turquoise.

2.2. Conservation of Coloring of the Motion Graph

The coloring of the motion graph may change in a course of the motion of the particles. The reasonable question is when will the coloring graph remain the same? The trivial case occurs when there is no interaction between particles. In this case, the coloring of the motion graph defined by Equations (1) and (2) will be conserved. The more rich in its physical content example emerges when all internal forces are central and act pairwise in the isolated system built of three particles. In addition, we restrict ourselves with the situation when motions remain coplanar and the interactions are symmetric enough to prevent rotation of the momentum triangle (formed by the momentum vectors). The coloring of the motion graph will be kept untouched when the relative directions of momenta remain fixed, which happens when the particles exchange momentum in such a way that only magnitudes change, not directions. The necessary and sufficient condition for this to happen is that the forces acting between the particles must be central and directed along the line joining the particles, and the ratio of the magnitudes of the momenta must remain constant.

2.3. The Momenta Graph and Symmetry Considerations

Consider the motion of three particles, depicted in Figure 4A. Inset Figure 4A depicts the circular motion of three particles. The angles between the momenta in a course of motion remain constant and they are equal to ${\displaystyle \frac{2\pi }{3}}$. This kind of motion gives rise to the momenta graph depicted in inset B of Figure 4. Now we assume that the vertices of the graph form a regular hexagon, shown in Figure 4B. The graph depicted in Figure 4B obviously does not keep the true angles between the momenta vectors (we suggest below the stereographic graph which keeps these angles untouched).

It is easily seen that the momenta graph depicted in Figure 4B demonstrates the following elements of symmetry: axes of rotation: $R_2, R_4$ ($R_n$ denotes the rotation by angle $n{\displaystyle \frac{2\pi }{6}}$) and reflection $r_0$ $r_0$ denotes the reflection in the line connecting vertices ${\overrightarrow{p}}_2$ and ${\overrightarrow{L}}_3$.

Thus, the order of the symmetry group is four; the symmetry group includes the identity element ($R_0$), axes of rotation, $R_2, R_4$, and the reflection axis $r_0$. Due to the coloring, the order of the symmetry group of the motion graph is lower than that of the regular hexagon.

Five important features of the symmetry group of the momenta graph should be emphasized:

(i)

The symmetry of the graph does not coincide with the spatial symmetries of the motion of the particles.

(ii)

The symmetry of the momenta graph remains invariant relatively to the rotation of frames relatively to origin.

(iii)

The symmetry group remains the same for general linear transformation of vectors ${\overrightarrow{p}}_i, {\overrightarrow{L}}_i, i=1,\dots ,3$ with a positive-definite matrix A (see Section 2.1).

(iv)

The symmetry group of the momenta graph is sensitive to the Galileo transformations.

(v)

The order of the symmetry group of the momenta graph is equal to (for monochromatic motion graphs) or lower (for bi-colored motion graphs) than that of the regular hexagon.

2.4. Shannon Entropy of the Momenta Graphs

The Ramsey theorem states that the total chaos is impossible; ordered structures appear in the systems of a certain size, which is larger than a given value. Mono-chromatic triangles necessarily appear in the bi-colored complete graphs with the number of vertices larger than six. The very question is how the order emerging in the complete graph may be quantified. It may be quantified with the Shannon entropy [15,16,17]. The Shannon entropy of the bi-colored Ramsey complete graph is labeled S and it is introduced with Equation (7):

$$S=-{\sum }_k{P}_{k}ln{P}_k,k\ge 3,$$

(7)

where $P_k$ is the fraction of monochromatic k-polygons/polygons with k sides (whether turquoise or mustard ones) in the given complete graph [15]. The sampling takes place over the entire set of monochromatic polygons, whatever their colors. The momenta graph shown in Figure 1 contains three turquoise triangles and one mustard triangle (see Section 2.1). The total number of monochromatic triangles is four. No monochromatic quadrangles, pentagons or hexagons are recognized in the graph. We calculate $S=-\left({\displaystyle \frac{1}{4}}ln{\displaystyle \frac{1}{4}}+{\displaystyle \frac{3}{4}}ln{\displaystyle \frac{3}{4}}\right)=0.55.$ What is the meaning of S? S is adequately interpreted as the average uncertainty to find the monochromatic polygon (whatever its color) within the set of monochromatic polygons appearing in the given complete bi-colored graph. The value of the Shannon entropy is exhaustively defined by the distribution of polygons in the given complete graph, and it is independent of the exact shapes of the polygons.

The Shannon measure of the graph may be introduced in an alternative way with a pair of Shannon entropies: namely, $S_t$ and $S_m$, which are interpreted as follows: $S_t$ is interpreted as an average uncertainty to find the turquoise polygon in the given graph, $S_m$ is, in turn, an average uncertainty to find the mustard polygon in the same graph [15]. In this case, sampling of polygons is carried out separately from the turquoise and mustard subsets of convex polygons. Thus, a pair of Shannon entropies $\left(S_{\alpha },S_{\beta }\right)$ corresponds to any momenta graph. The pair of Shannon entropies is introduced as follows:

$$S_{\alpha }=-{\sum }_n{P}_{n\alpha }ln{P}_{na}, n\ge 3$$

(8)

$$S_{\beta }=-{\sum }_i{P}_{i\beta }ln{P}_{i\beta }, i\ge 3$$

(9)

where $P_{n\alpha }$ is the fraction of monochromatic turquoise ($\alpha$-colored) convex polygons with n α-sides or edges (turquoise edges), and $P_{i\beta }$ is the fraction of monochromatic convex mustard ($\beta -\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{d}$) polygons with i $\beta$-sides or edges (mustard edges) in a given complete graph. Sampling of polygons is carried out separately from the turquoise and mustard subsets of convex polygons. Thus, a pair of Shannon entropies $\left(S_{\alpha },S_{\beta }\right)$ corresponds to any momenta graph. Only mono-colored triangles appear in the graph, thus $P_{3\alpha }=1$; $P_{3\beta }=1$ and we calculate $\left(S_{\alpha },S_{\beta }\right)=\left(0,0\right)$.

2.5. The Momenta Graph in the Center of Masses Frame

Consider an isolated system built of three interacting particles. We do not restrict the potentials of interaction. Now we analyze the momenta graph as it is seen in the center of mass frame. The scalar product of the total linear ${\overrightarrow{P}}_{tot}$ and angular momenta ${\overrightarrow{L}}_{tot}$ is given by Equation (10):

$${\overrightarrow{P}}_{tot}·{\overrightarrow{L}}_{tot}={\sum }_{i=1}^3{\overrightarrow{p}}_i·{\sum }_{k=1}^3{\overrightarrow{L}}_k=0$$

(10)

Equation (10) emerges from the fact that in the center of masses frame ${\overrightarrow{P}}_{tot}=0$ (${\overrightarrow{L}}_{tot}$ is not necessarily zero). The sum in Equation (10) equals zero in two cases:

(i)

All of scalar products $\left({\overrightarrow{p}}_i·{\overrightarrow{L}}_k\right)=0,i,k=1,\dots ,3.$ This is the situation of the “trivial momenta graph” (see Section 2.1).

(ii)

Some of the scalar products $\left({\overrightarrow{p}}_i·{\overrightarrow{L}}_k\right)$ are positive and some of them are negative.

We already mentioned that in 3-dimensional space, the maximum number of mutually orthogonal vectors is three and the trivial momenta graph is impossible. Thus, necessarily, we conclude that some of the scalar products $\left({\overrightarrow{p}}_i·{\overrightarrow{L}}_k\right)$ are positive and some of them are negative and consequently the momenta graph in the center of masses frame is necessarily multi-colored. The only exception is the degenerated case when two or all of three particles are in rest in the center mass frame.

Thus, we demonstrate the following theorem:

Theorem 2. 

Consider an arbitrary motion of six point particles seen in the center of masses frame. The particles interact via arbitrary interactions. Linear and angular momenta serve as the vertices of the graph. The vertices are connected with the turquoise link if $\left({\overrightarrow{p}}_i·{\overrightarrow{p}}_j\right)\ge 0;\left({\overrightarrow{L}}_i·{\overrightarrow{L}}_j\right)\ge 0; \left({\overrightarrow{p}}_i·{\overrightarrow{L}}_j\right)\ge 0, i,j=1,\dots ,3;i\ne j$ take place. The vertices are connected with the mustard link if $\left({\overrightarrow{p}}_i·{\overrightarrow{p}}_j\right)<0;\left({\overrightarrow{L}}_i·{\overrightarrow{L}}_j\right)<0; \left({\overrightarrow{p}}_i·{\overrightarrow{L}}_j\right)<0, i,j=1,\dots ,3;i\ne j$ is true. The momenta graph is necessarily multi-colored. The only exception is the degenerated case when two or all of three particles are in rest.

We illustrate the introduced graph approach with the graphs emerging from the Lagrange three-body problem [1,2,3] in Appendix A and the graph analysis of the recently discovered eight-figure orbits [1,18,19,20] in Appendix B.

It is also instructive to build the stereographic projection of the momenta vectors. We propose to put the center of the stereographic sphere on the center mass of the three-body- system. Thus, in the isolated system the center of the stereographic sphere is in rest in a course of motion of the bodies. Hence, vectors of linear and angular momenta are analogous to poles in crystallography (poles are the directions normal to a specific crystallographic plane within a crystal lattice). Stereographic projection of the momenta vectors yields six points. These points serve now as the vertices of the graph. The coloring of the graph is prescribed with Equations (1) and (2). Thus, the complete, bi-colored, stereographic graph emerges. We label this graph as the stereographic, bi-colored graph. Stereographic projection preserves both directions and symmetry [21]. Stereographic projection is a conformal mapping technique that accurately preserves angular relationships between momenta vectors [21]. This means that the angles between momenta vectors are maintained in the two-dimensional projection. Symmetry of the system of momenta vectors will be kept within the stereographic momenta graph. Again, orderliness of the stereographic momenta graph may be quantified with the Shannon entropy

2.6. Quantum Field Generalization of the Momenta Graph

An elegant generalization of the suggested method for the quantum field theory is possible. Consider three particles possessing linear momenta four-vectors $p_i, i=1,\dots ,3$, $p=({\displaystyle \frac{E}{c}},p_x,p_y,p_z)$ and angular momenta tensors $L_{i\rho \sigma }, i=1,\dots ,3$. Consider that in relativity the angular momentum is already tensor, defined as follows:

$$L_{i\rho \sigma }=X_{\rho }{p}_{\sigma }-p_{\sigma }{X}_{\rho }$$

(11)

where $X_{\rho }=\left(ct,\overrightarrow{x}\right)$ is four-vector. Three vectors of linear momenta and three tensors of the angular momenta serve now as the vertices of the graph. Coloring of the momenta graph is now defined with the Pauli–Lubanski structures denoted $W_{ik}^{\mu }, i=1,\dots ,3;k=1,\dots ,3$, indices $i,k$ denote the number of the particles. The Pauli–Lubanski pseudo-vector is defined for quantum relativistic particles with Equation (12):

$$W^{\mu }={\displaystyle \frac{1}{2}}{ϵ}^{\mu \nu \rho \sigma }{p}_{\upsilon }{L}_{\rho \sigma },$$

(12)

where ${ϵ}^{\mu \nu \rho \sigma }$ is the four-dimensional totally antisymmetric Levi-Civita symbol [22]. The mass m and spin s of a particle are defined in terms of two quadratic invariants (Casimir operators of the Poincaré group) as follows [22]:

$$p^2=p_{\mu }{p}^{\mu }=m^2;W^2=W_{\mu }{W}^{\mu }=-m^{2}s\left(s+1\right)$$

(13)

In Equation (13) the natural units $c=\hslash =1$ are used. It is noteworthy that Equation (13) works for both bosons and fermions. We use Equation (12) for the elaboration of the momenta graph for three quantum relativistic particles. For the linear and angular momenta related to the same particle $(i=k)$ the Pauli–Lubanski formula yields

$$W_{ii}^{\mu }={\displaystyle \frac{1}{2}}{ϵ}^{\mu \nu \rho \sigma }{p}_{i\upsilon }{L}_{i\rho \sigma }$$

(14)

For the angular and linear momenta related to different particles $\left(i\ne k\right)$ we define the symmetrically shaped $\left(W_{ik}^{\mu }=W_{ki}^{\mu }\right)$ Pauli–Lubanski-like structure as follows:

$$W_{ik}^{\mu }={\displaystyle \frac{1}{8}}{ϵ}^{\mu \nu \rho \sigma }(p_{i\nu }+p_{kv})\left(L_{i\rho \sigma }+L_{k\rho \sigma }\right)$$

(15)

This Pauli–Lubanski-like structure, given by Equation (15), describes the total spin content of the two-particle system in a form that respects the exchange symmetry. The key properties of this structure are that it is invariant under Lorentz transformations and it is reduced to the standard Pauli–Lubanski vector when the system consists of a single particle $\left(i=k\right)$, given by Equation (14). Now we define the coloring of the graph as follows: we denote the links connecting the vertices numbered $i$ and $k$ with ${\zeta }_{ik}$. The link ${\zeta }_{ik}$ is colored with turquoise, when $W_{ik}^{\mu }$ is timelike or null, namely Equation (16) is true.

$$W_{ik}^{\mu }{W}_{\mu }^{ik}\ge 0$$

(16)

The link ${\zeta }_{ik}$ is colored with mustard, when $W_{ik}^{\mu }$ is space-like, namely Equation (17) holds

$$W_{ik}^{\mu }{W}_{\mu }^{ik}<0$$

(17)

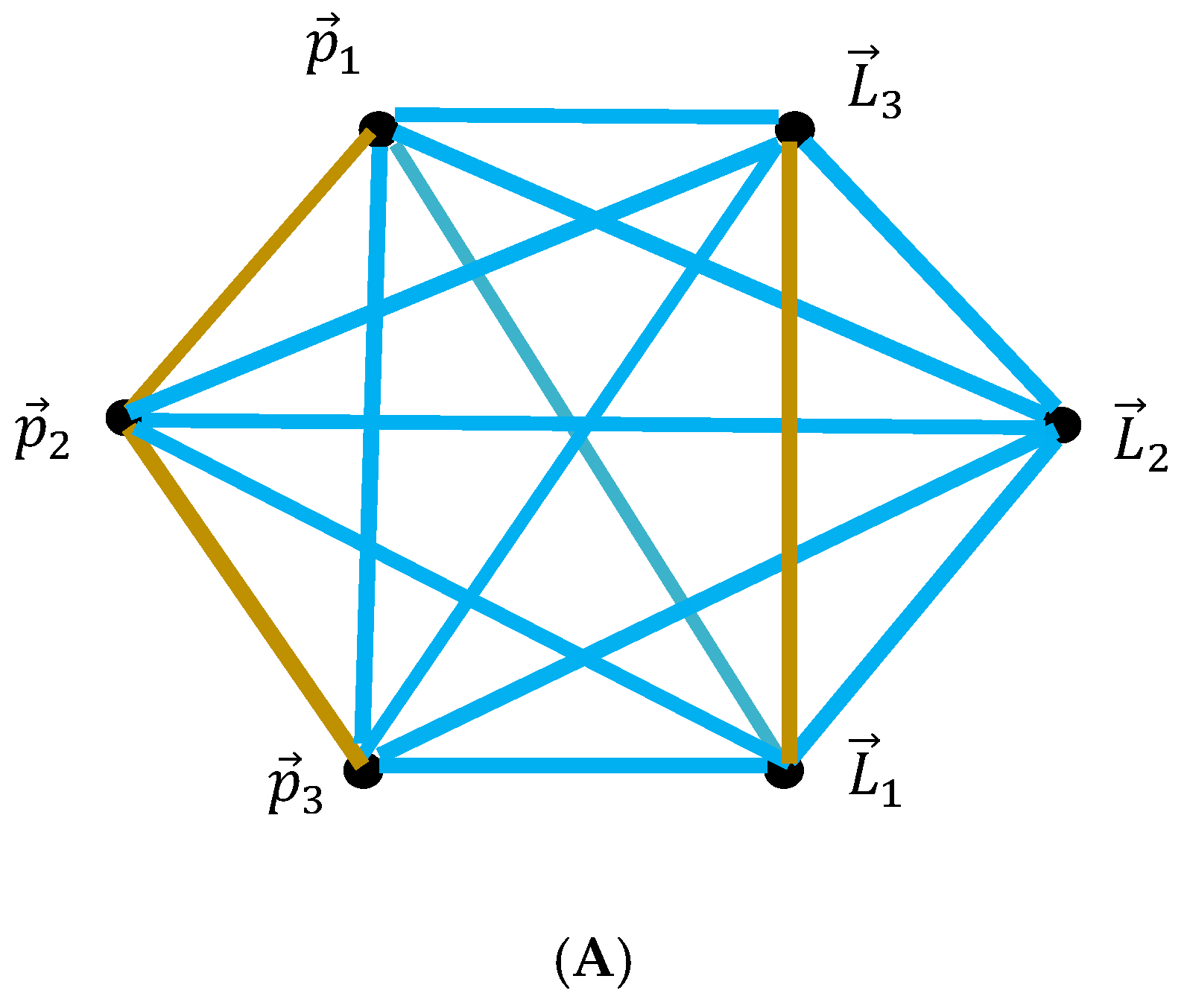
The possible momenta graph is illustrated with Figure 5. The emerging graph is the complete, bi-colored, Ramsey graph. This graph should necessarily contain at least one mono-colored triangle Indeed, the triangles $\left\{p_1,p_2,p_3\right\}$, $\left\{p_1,p_3,L_2\right\}$, $\left\{p_2,L_1,L_3\right\}$, $\left\{L_1,L_2,L_3\right\}$, $\left\{p_1,L_2,L_3\right\} \mathrm{a}\mathrm{n}\mathrm{d}$ $\left\{p_2,p_3,L_1\right\}$ are mono-colored, mustard. There are no mono-colored turquoise triangles in the graph.

Again, the Ramsey theory does not predict what kind of mono-colored triangles (mustard or turquoise) will necessarily appear in the graph. It should be emphasized that the coloring of the graph is Lorenz-covariant. Thus, the number of the turquoise links, denoted $N_t$ and the mustard links denoted $N_m$ are Lorentz invariant, and the mono-chromatic triangles appearing in the momenta graph are Lorentz invariant. Thus, we revealed the new kinds of Lorenz-invariant structures, inherent for momenta graph, built for quantum relativistic particles. Moreover, the symmetry of the momenta graph in this case is Lorenz invariant.

2.7. Three-Color Momenta Graphs and Their Properties

Bi-coloring of the momenta graphs defined with Equations (1) and (2) and Equations (16) and (17) is not unique. We introduce now three-colored graphs, as explained below. We start from the classical mechanics paradigm.

The vertices are connected with the turquoise link if Equation (18) takes place:

$$\left({\overrightarrow{p}}_i·{\overrightarrow{p}}_j\right)>0;\left({\overrightarrow{L}}_i·{\overrightarrow{L}}_j\right)>0; \left({\overrightarrow{p}}_i·{\overrightarrow{L}}_j\right)>0, i,j=1,\dots ,3;i\ne j$$

(18)

The vertices are connected with the mustard link, if Equation (19) is true:

$$\left({\overrightarrow{p}}_i·{\overrightarrow{p}}_j\right)<0;\left({\overrightarrow{L}}_i·{\overrightarrow{L}}_j\right)<0; \left({\overrightarrow{p}}_i·{\overrightarrow{L}}_j\right)<0, i,j=1,\dots ,3;i\ne j$$

(19)

The vertices are connected with the black link if Equation (20) takes place:

$$\left({\overrightarrow{p}}_i·{\overrightarrow{p}}_j\right)=0;\left({\overrightarrow{L}}_i·{\overrightarrow{L}}_j\right)=0;\left({\overrightarrow{p}}_i·{\overrightarrow{L}}_j\right)=0,i,j=1,\dots ,3;i\ne j$$

(20)

The coloring of this three-colored graph remains the same for general linear transformation of vectors supplied by Equations (4) and (5).

A similar three-colored procedure may be introduced for quantum relativistic particles with the Pauli–Lubanski-like structure defined by Equation (15). We define the coloring of the graph as follows: we denote the links connecting the vertices numbered $i$ and $k$ with ${\zeta }_{ik}$. The link ${\zeta }_{ik}$ is colored with turquoise, when $W_{ik}^{\mu }$ is time-like; namely, Equation (16) is true.

$$W_{ik}^{\mu }{W}_{\mu }^{ik}>0$$

(21)

The link ${\zeta }_{ik}$ is colored with mustard, when $W_{ik}^{\mu }$ is space-like, i.e., Equation (22) holds $W_{ik}^{\mu }{W}_{\mu }^{ik}<0$.

The link ${\zeta }_{ik}$ is colored with black, when $W_{ik}^{\mu }$ is null, i.e., Equation (22) holds:

$$W_{ik}^{\mu }{W}_{\mu }^{ik}=0$$

(22)

The coloring and symmetry of the three-colored graph defined by Equations (21) and (22) is Lorentz invariant. The aforementioned three-colored graphs do not necessarily contain monochromatic triangle due to the fact that the Ramsey number is $R\left(3,3,3\right)=17.$ The same is true for the momenta graphs defined by Equations (18)–(20).

3. Discussion

The graph theory supplies a very general framework for the description of the physical systems. The mathematical graph is a structure used to represent/model relationships between objects/elements of the set. In general, graphs represent a set of objects and a set of pairwise relations between these objects [5]. It consists of vertices/nodes, which are the fundamental units of the graph and edges/links, which are the connections between the vertices, representing mutual relationships between the vertices/nodes [5]. The graphs demonstrate a potential for physics; however, their applications for physical problems remain exotic [23,24,25,26,27]. We apply the theory of bi-colored, complete graphs for the analysis of the general three-body problem [28,29,30,31,32,33,34]. The Ramsey theorem states that in any complete graph with six vertices, if each edge is colored either turquoise or mustard, then, there must exist a monochromatic triangle—that is, a set of three vertices all of whose connecting edges are the same color [10,11,12,13,14]. In other, words, no matter how you color the edges of a complete graph with six vertices using two colors (say, red and blue), you are guaranteed to find a triangle where all the edges are turquoise or all the edges are mustard [10,11,12,13,14]. We introduce the graph in which vectors of linear and angular of momenta of the triad of particles serve as vertices. Scalar products of these vectors define the color of the links. Thus, the bi-colored, complete graph emerges, which makes possible the application of the Ramsey theorem, which in turn predicts the existence of at least one mono-chromatic triangle in the graph. The orderliness of the graph may be quantified with Shannon entropy.

The introduced graph evolves with time. In our future investigations we plan to bridge between the classical Hamiltonian/Lagrangian analysis of the three-body problem and the Ramsey analysis of the momenta graph.

4. Conclusions

We conclude that the graph theory approach is fruitful for the analysis of the general three-body problem. We considered the motion of the three particles/bodies system. We did not restrict interaction between the bodies with the certain potential. Vectors of linear and angular momenta of the particles form the vertices of the graph. Signs of the scalar products of the vectors of the linear and angular momenta define the colors of the links, connecting the vertices. Thus, the bi-colored, complete Ramsey graph emerges. This complete graph, containing six vertices, connected with bi-colored links, is labeled as the “momenta graph”. According to the Ramsey theorem, this graph inevitably contains at least one mono-chromatic triangle. The momenta graph contains at least one monochromatic triangle even for a chaotic motion of the particles. The Ramsey theorem does not predict the exact color of the monochromatic triangle. The coloring of the graph is independent on the rotation of frames; however, it is sensitive to Galilean transformations. Distribution of the colored links and colored triangles is independent on the rotation of frames. The coloring of the momenta graph remains the same for general linear transformations of vectors with a positive-definite matrix. For a given motion, changing the order of the vertices does not change the number and distribution of monochromatic triangles. The symmetry of the momenta graph is addressed. The symmetry group remains the same for general linear transformation of vectors of the linear and angular momenta with a positive-definite matrix. Conditions defining conservation of the coloring of the motion graph are addressed.

We investigated the properties of the momenta graph emerging in the frame system of the center of mass. The momenta graph is necessarily multi-colored. The only exception is the degenerated case when two or all of three particles are in rest. It is instructive to build the stereographic projection of the momenta vectors in this system, when the center of the stereographic sphere is placed on the center mass of the three-body system. Stereographic projection of the momenta vectors yields six points. Thus, the complete, bi-colored, stereographic graph emerges. Stereographic projection preserves both direction and symmetry. Symmetry of the system of momenta vectors will be kept within the stereographic momenta graph. We illustrated the developed graph approach with the particular examples of Lagrangian three-body configuration and plane eight-figure-shaped motion of the three bodies. Shannon entropy of the momenta graph, quantifying its orderliness, is reported.

Orderliness of the momenta graph may be quantified with the Shannon entropy. Three-colored momenta graphs are addressed. The suggested approach is generalized for the quantum field theory with the Pauli–Lubanski pseudo-vector. Coloring of the momenta graph is defined by the space-like/time-like nature of the Pauli–Lubanski pseudo-vector. The suggested coloring procedure is Lorenz invariant. Bridging between the suggested graph approach and Hamiltonian mechanics remains an unsolved problem.