Propagation of Tensor Perturbation in Horndeski-like Gravity
Abstract
1. Introduction
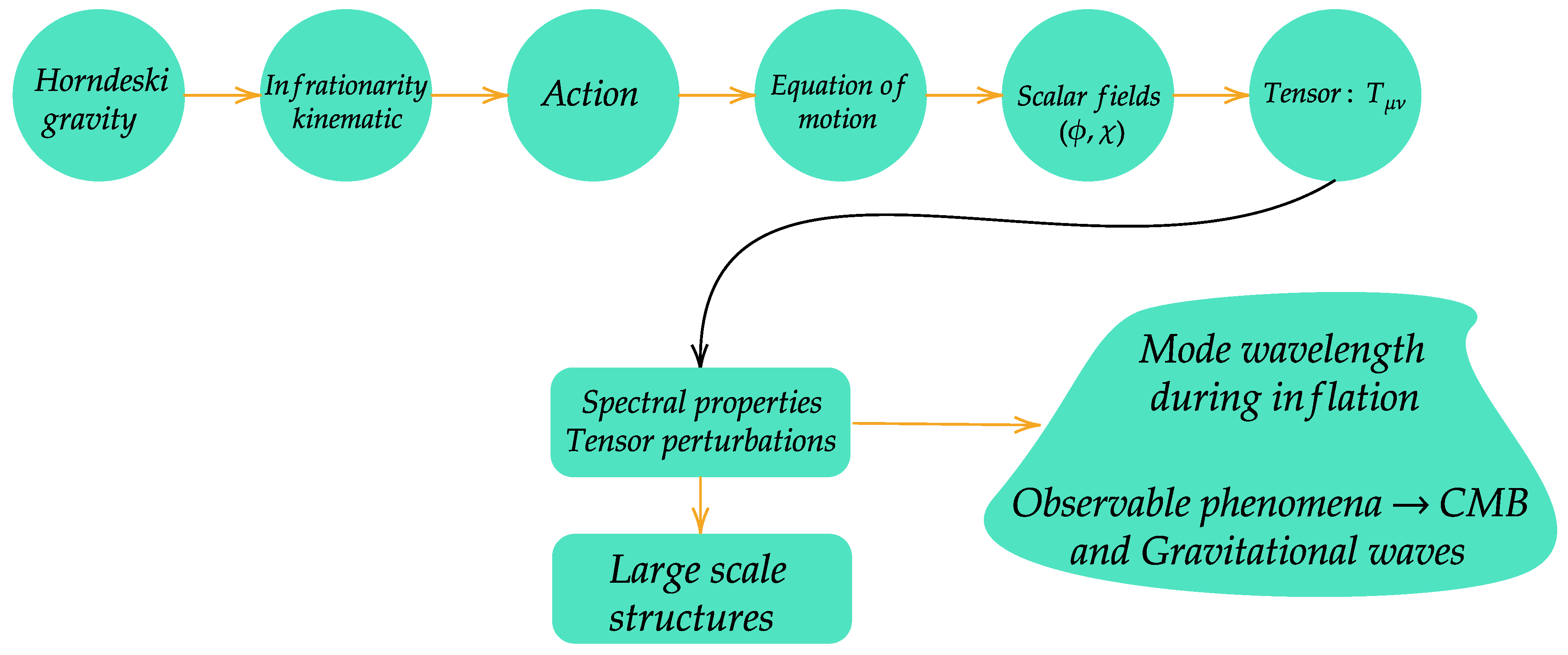
2. The Overarching Theory
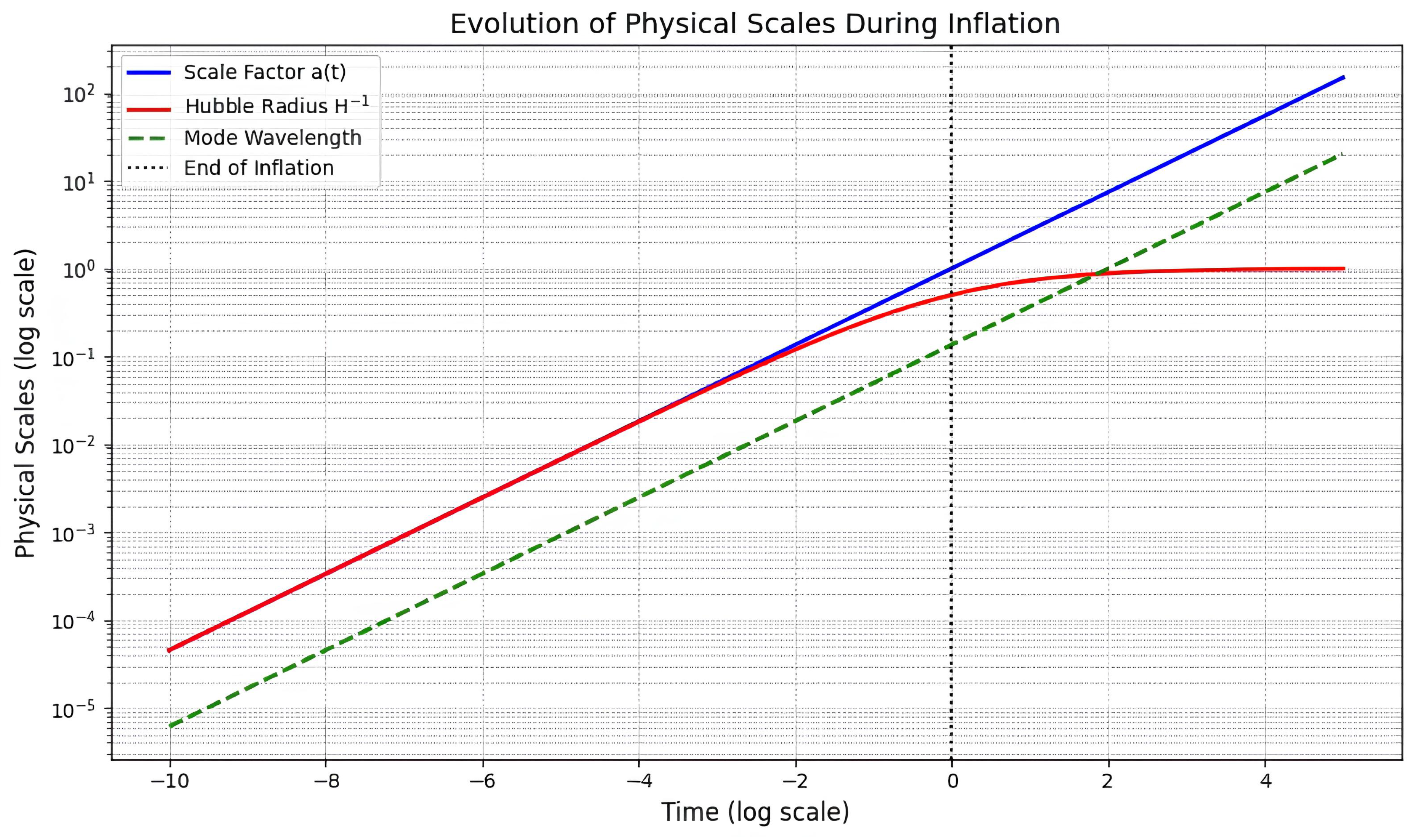
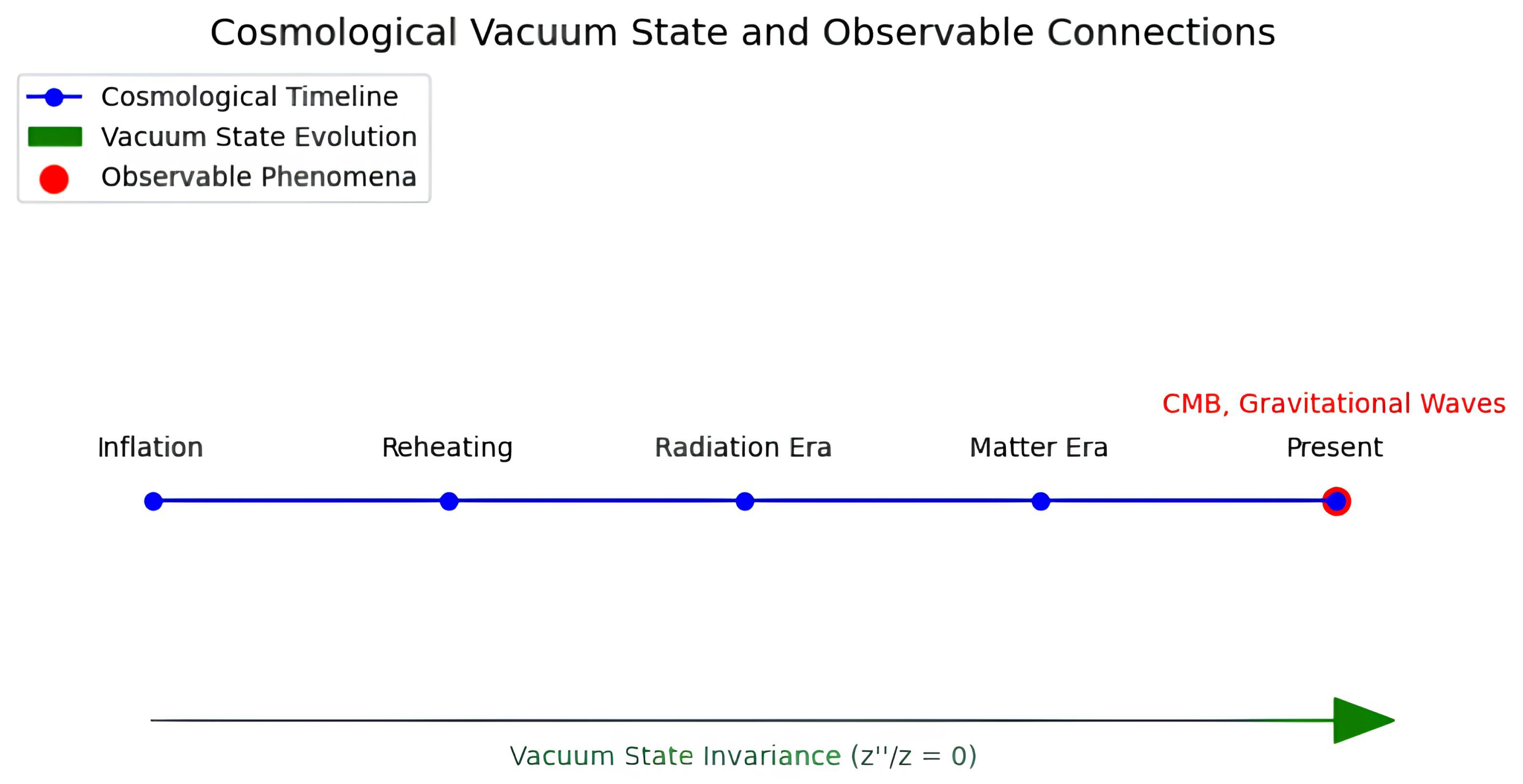
3. Propagation of Tensor Perturbations
4. Conclusions and Discussions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Haco, S.; Hawking, S.W.; Perry, M.J.; Strominger, A. Black Hole Entropy and Soft Hair. J. High Energy Phys. 2018, 12, 98. [Google Scholar] [CrossRef]
- Haco, S.; Perry, M.J.; Strominger, A. Kerr-Newman Black Hole Entropy and Soft Hair. arXiv 2019, arXiv:1902.02247. [Google Scholar]
- Haco, S. Large Gauge Transformations and Black Hole Entropy. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Hubble, E.P. A relation between distance and radial velocity among extra-galactic nebulae. Proc. Natl. Acad. Sci. USA 1929, 15, 168–173. [Google Scholar] [CrossRef] [PubMed]
- Penzias, A.A.; Wilson, R.W. A Measurement of excess antenna temperature at 4080-Mc/s. Astrophys. J. 1965, 142, 419–421. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef]
- Auclair, P.; Blanco-Pillado, J.J.; Figueroa, D.G.; Jenkins, A.C.; Lewicki, M.; Sakellariadou, M.; Sanidas, S.; Sousa, L.; Steer, D.A.; Wachter, J.M.; et al. Probing the gravitational wave background from cosmic strings with LISA. J. Cosmol. Astropart. Phys. 2020, 4, 34. [Google Scholar] [CrossRef]
- Gasperini, M. On the initial regime of pre-big bang cosmology. J. Cosmol. Astropart. Phys. 2017, 9, 1. [Google Scholar] [CrossRef]
- Sberna, L. Early-universe cosmology in Einstein-scalar-Gauss-Bonnet gravity. arXiv 2017, arXiv:1708.01150. [Google Scholar]
- Papallo, G. Causality and the Initial Value Problem in Modified Gravity. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2018. [Google Scholar] [CrossRef]
- Santos, F.F.; Sokoliuk, O.; Baransky, A. Holographic Complexity of Braneworld in Horndeski Gravity. Fortschr. Phys. 2023, 71, 2200141. [Google Scholar] [CrossRef]
- Santos, F.F.; Pourhassan, B.; Saridakis, E.N. de Sitter Versus Anti-de Sitter in Horndeski-Like Gravity. Fortschr. Phys. 2024, 72, 2300228. [Google Scholar] [CrossRef]
- Santos, F.F.; Brito, F.A. Domain walls in Horndeski gravity. arXiv 2004, arXiv:2105.00343. [Google Scholar] [CrossRef]
- Santos, F.F. Rotating black hole with a probe string in Horndeski Gravity. Eur. Phys. J. Plus 2020, 135, 810. [Google Scholar] [CrossRef]
- Santos, F.F.; Neves, R.M.P.; Brito, F.A. Modeling dark sector in Horndeski gravity at first-order formalism. Adv. High Energy Phys. 2019, 2019, 3486805. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Saridakis, E.N.; Tsoukalas, M. Cosmological models in modified gravity theories with extended nonminimal derivative couplings. Phys. Rev. D 2017, 95, 044019. [Google Scholar] [CrossRef]
- Horndeski, G.W.; Silvestri, A. 50 Years of Horndeski Gravity: Past, Present and Future. Int. J. Theor. Phys. 2024, 63, 38. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Breuval, L.; Brink, T.G.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s−1 Mpc−1 Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Abbott, T.M.; Aguena, M.; Alarcon, A.; Allam, S.; Alves, O.; Amon, A.; Andrade-Oliveira, F.; Annis, J.; Avila, S.; Bacon, D.; et al. Dark Energy Survey Year 3 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2022, 105, 023520. [Google Scholar] [CrossRef]
- Byrnes, C.T.; Wands, D. Curvature and isocurvature perturbations from two-field inflation in a slow-roll expansion. Phys. Rev. D 2006, 74, 043529. [Google Scholar] [CrossRef]
- Linde, A.D. Particle Physics and Inflationary Cosmology; Contemporary Concepts in Physics; CRC Press: Boca Raton, FL, USA, 1990; Volume 5, pp. 1–362. [Google Scholar]
- Rinaldi, M. Mimicking dark matter in Horndeski gravity. Phys. Dark Univ. 2017, 16, 14. [Google Scholar] [CrossRef]
- Brito, F.A.; Santos, F.F. Braneworlds in Horndeski gravity. Eur. Phys. J. Plus 2022, 137, 1051. [Google Scholar] [CrossRef]
- Namikawa, T.; Naruko, A.; Saito, R.; Taruya, A.; Yamauchi, D. Unified approach to secondary effects on the CMB B-mode polarization. J. Cosmol. Astropart. Phys. 2021, 2021, 29. [Google Scholar] [CrossRef]
- Kobayashi, T. Horndeski theory and beyond: A review. Rept. Prog. Phys. 2019, 82, 086901. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Fontanini, M.; Penco, R.; Trodden, M. Where does Cosmological Perturbation Theory Break Down? Class. Quantum Gravity 2009, 26, 185002. [Google Scholar] [CrossRef]
- Flanagan, E.E.; Hughes, S.A. The Basics of gravitational wave theory. New J. Phys. 2005, 7, 204. [Google Scholar] [CrossRef]
- Kubota, K.i.; Arai, S.; Mukohyama, S. Propagation of scalar and tensor gravitational waves in Horndeski theory. Phys. Rev. D 2023, 107, 064002. [Google Scholar] [CrossRef]
- Hu, W.; Sugiyama, N.; Silk, J. The Physics of microwave background anisotropies. Nature 1997, 386, 37–43. [Google Scholar] [CrossRef]
- Page, D.N. No superluminal expansion of the universe. Class. Quantum Gravity 2009, 26, 127001. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. New Astron. Rev. 2022, 95, 101659. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Smith, T.L.; Poulin, V.; Amin, M.A. Oscillating scalar fields and the Hubble tension: A resolution with novel signatures. Phys. Rev. D 2020, 101, 063523. [Google Scholar] [CrossRef]
- Givans, J.J.; Hirata, C.M. Redshift-space streaming velocity effects on the Lyman-α forest baryon acoustic oscillation scale. Phys. Rev. D 2020, 102, 023515. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, F.F.; Said, J.L. Propagation of Tensor Perturbation in Horndeski-like Gravity. Symmetry 2025, 17, 675. https://doi.org/10.3390/sym17050675
Santos FF, Said JL. Propagation of Tensor Perturbation in Horndeski-like Gravity. Symmetry. 2025; 17(5):675. https://doi.org/10.3390/sym17050675
Chicago/Turabian StyleSantos, Fabiano F., and Jackson Levi Said. 2025. "Propagation of Tensor Perturbation in Horndeski-like Gravity" Symmetry 17, no. 5: 675. https://doi.org/10.3390/sym17050675
APA StyleSantos, F. F., & Said, J. L. (2025). Propagation of Tensor Perturbation in Horndeski-like Gravity. Symmetry, 17(5), 675. https://doi.org/10.3390/sym17050675







