A Large-Span Ring Deployable Perimeter Truss for the Mesh Reflector Deployable Antenna
Abstract
1. Introduction
2. Design and Evaluation of the Large-Span Ring Deployable Perimeter Truss
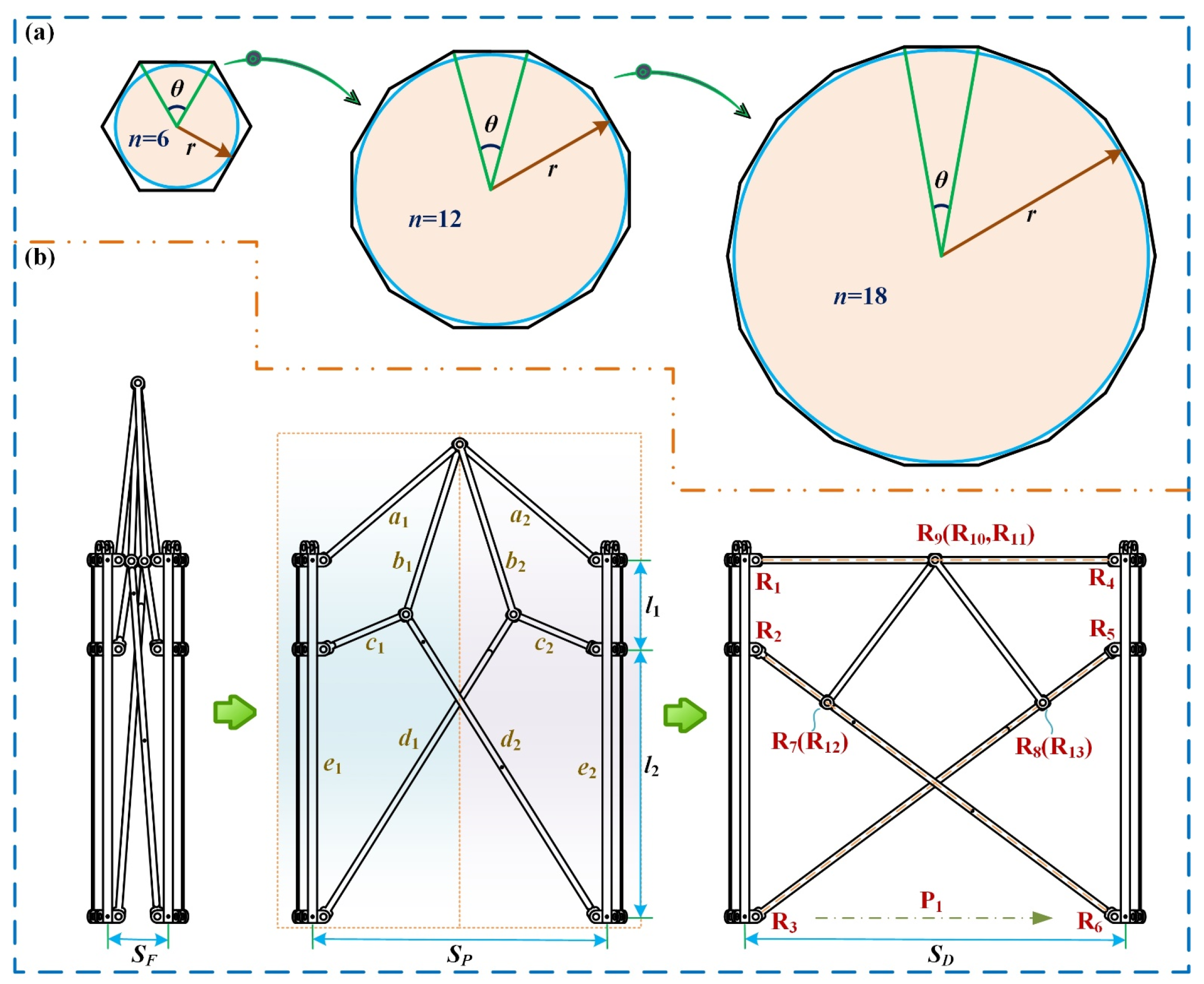
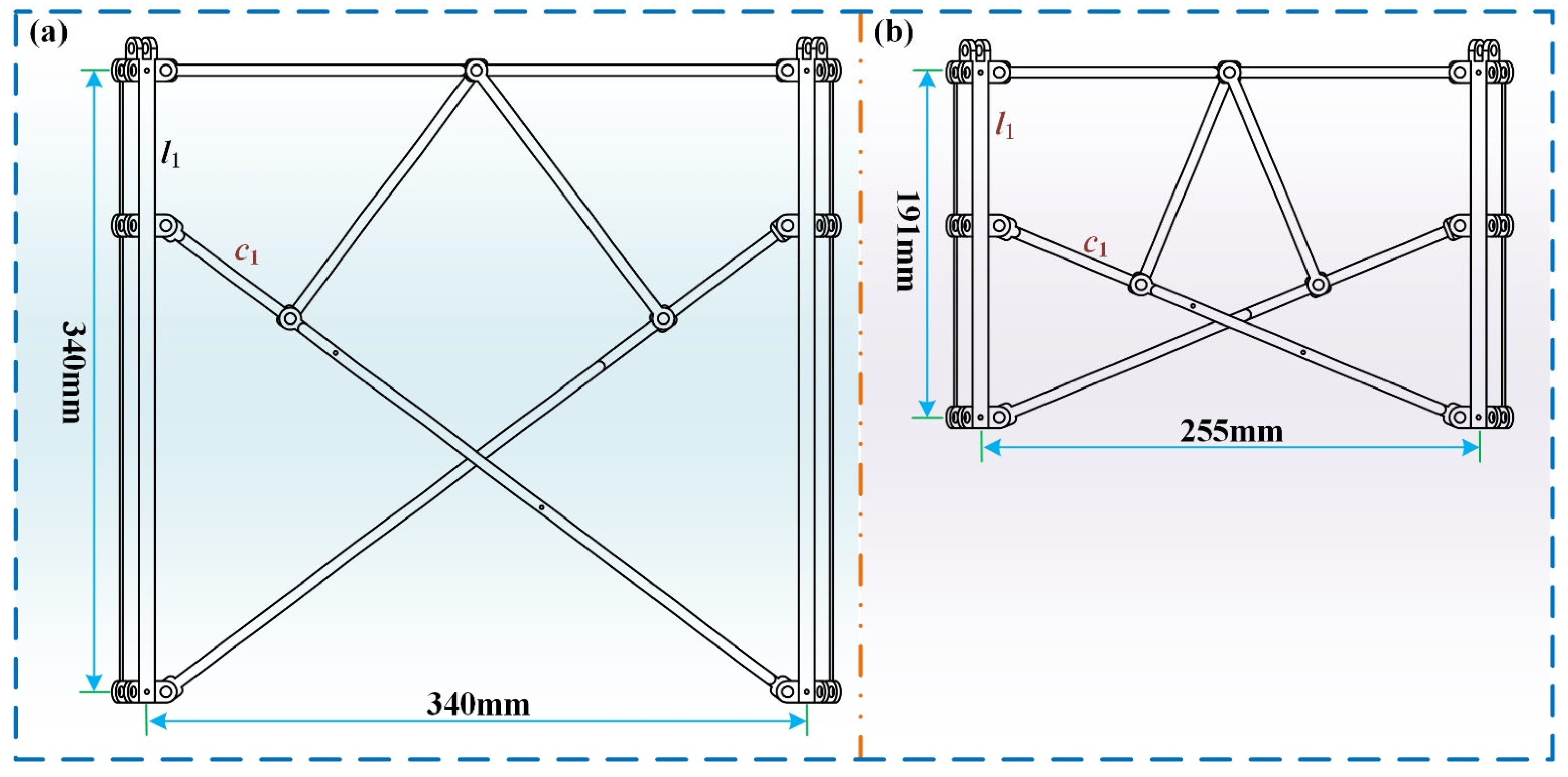
2.1. Design of the Deployable Basic Unit
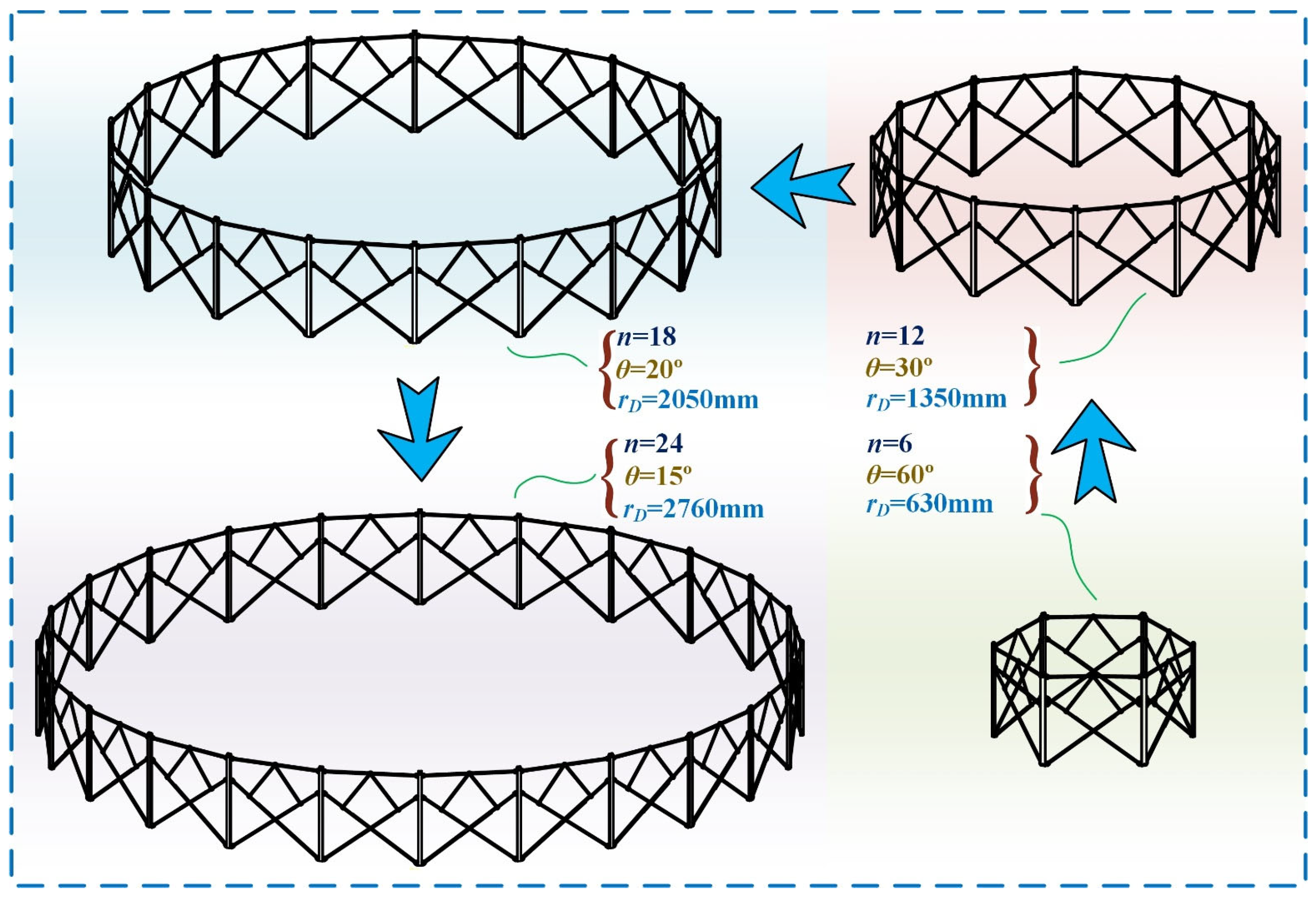
2.2. Geometric Modeling of the Ring Deployable Metamorphic Mechanism and Driving Method
2.3. Structural Analysis and Evaluation Method
3. Key Performance Analysis of the Large-Span Ring Deployable Perimeter Truss
3.1. Kinematic Analysis of the Large-Span Ring Deployable Perimeter Truss
3.2. Dynamic Analysis of the Large-Span Ring Deployable Perimeter Truss
4. Design of Cable-Net Structure Used for the Large-Span Ring Deployable Perimeter Truss
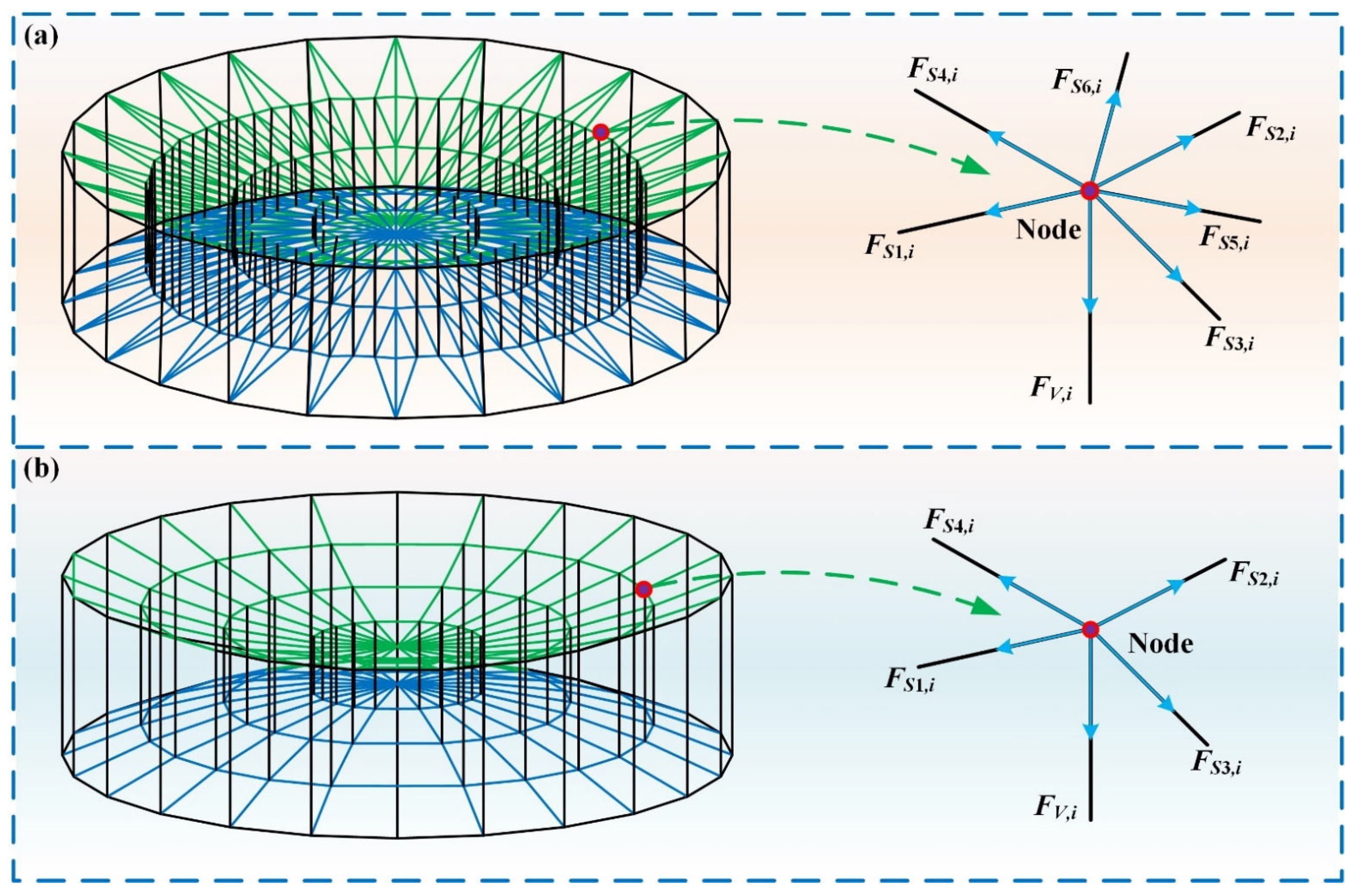
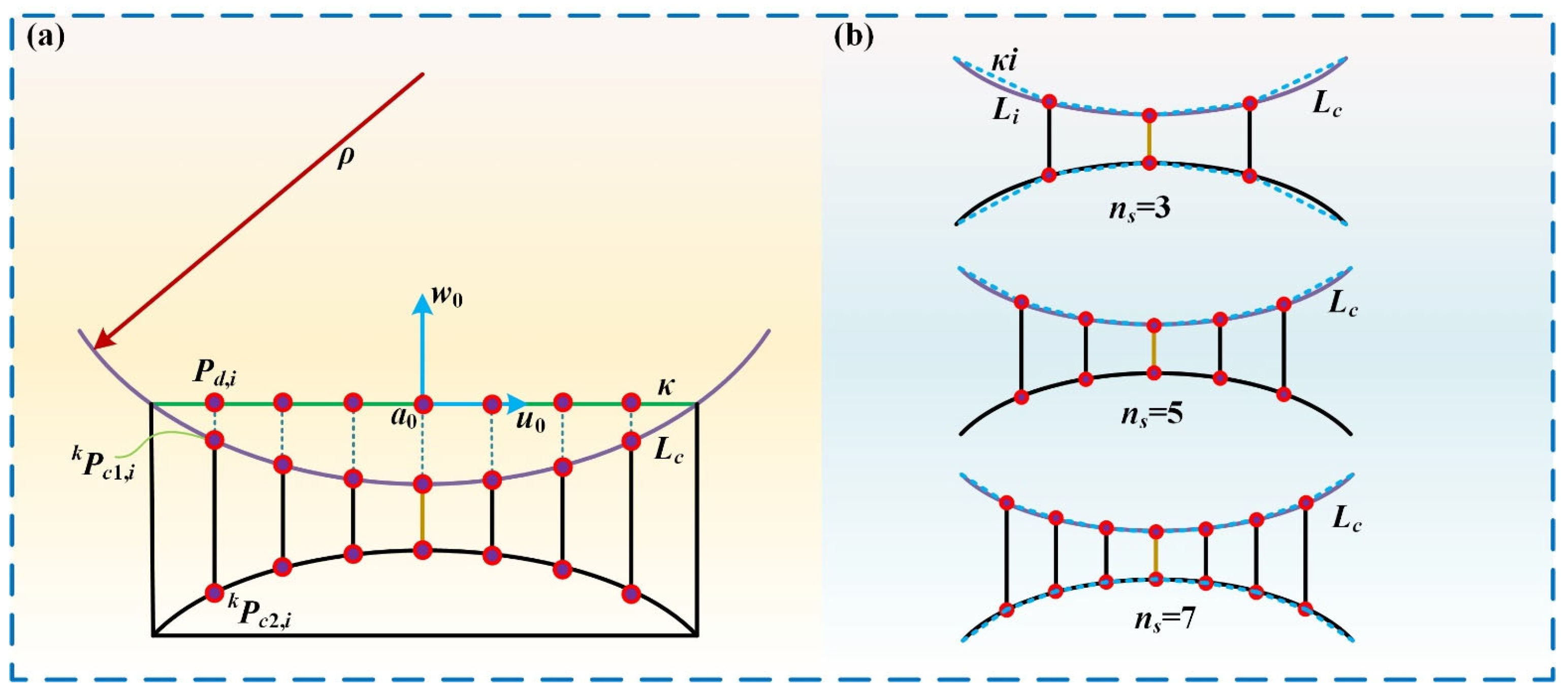
4.1. Mathematical Modeling and Prestressing Analysis for Cable-Net Structure
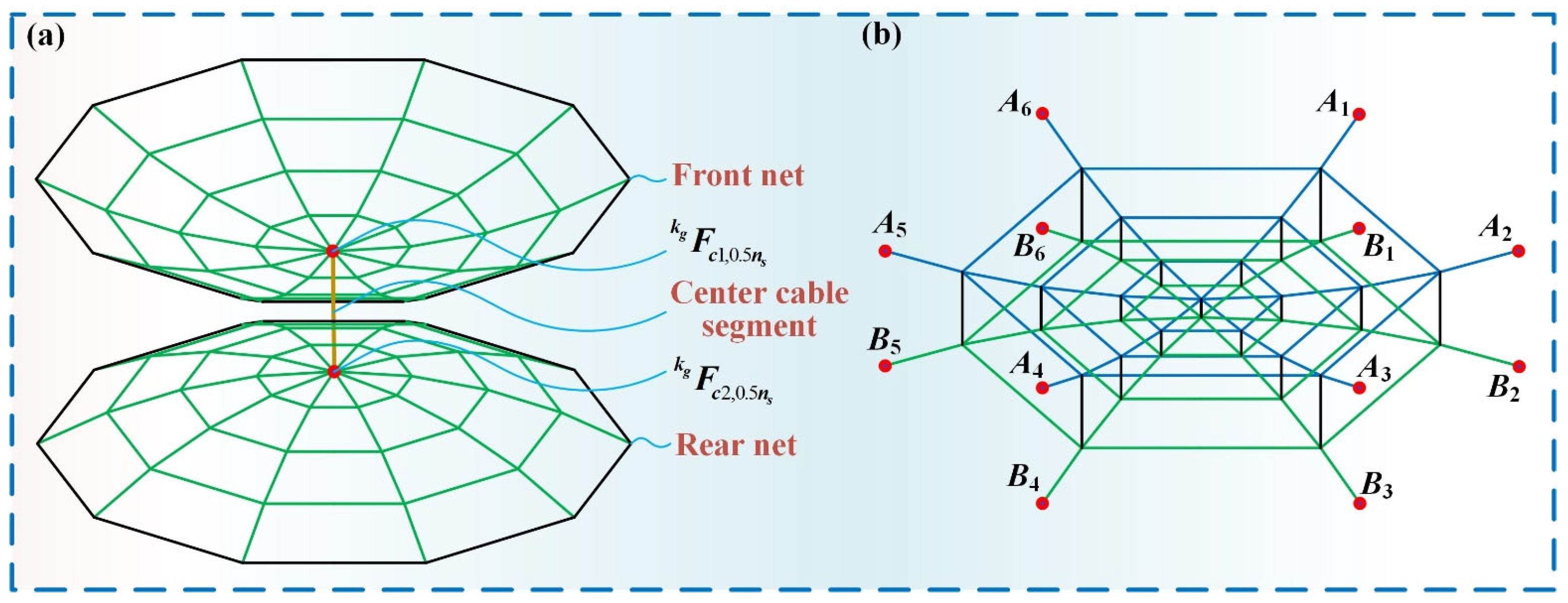
4.2. Connection Method of the Cable-Net Structure and the Large-Span Ring Deployable Perimeter Truss
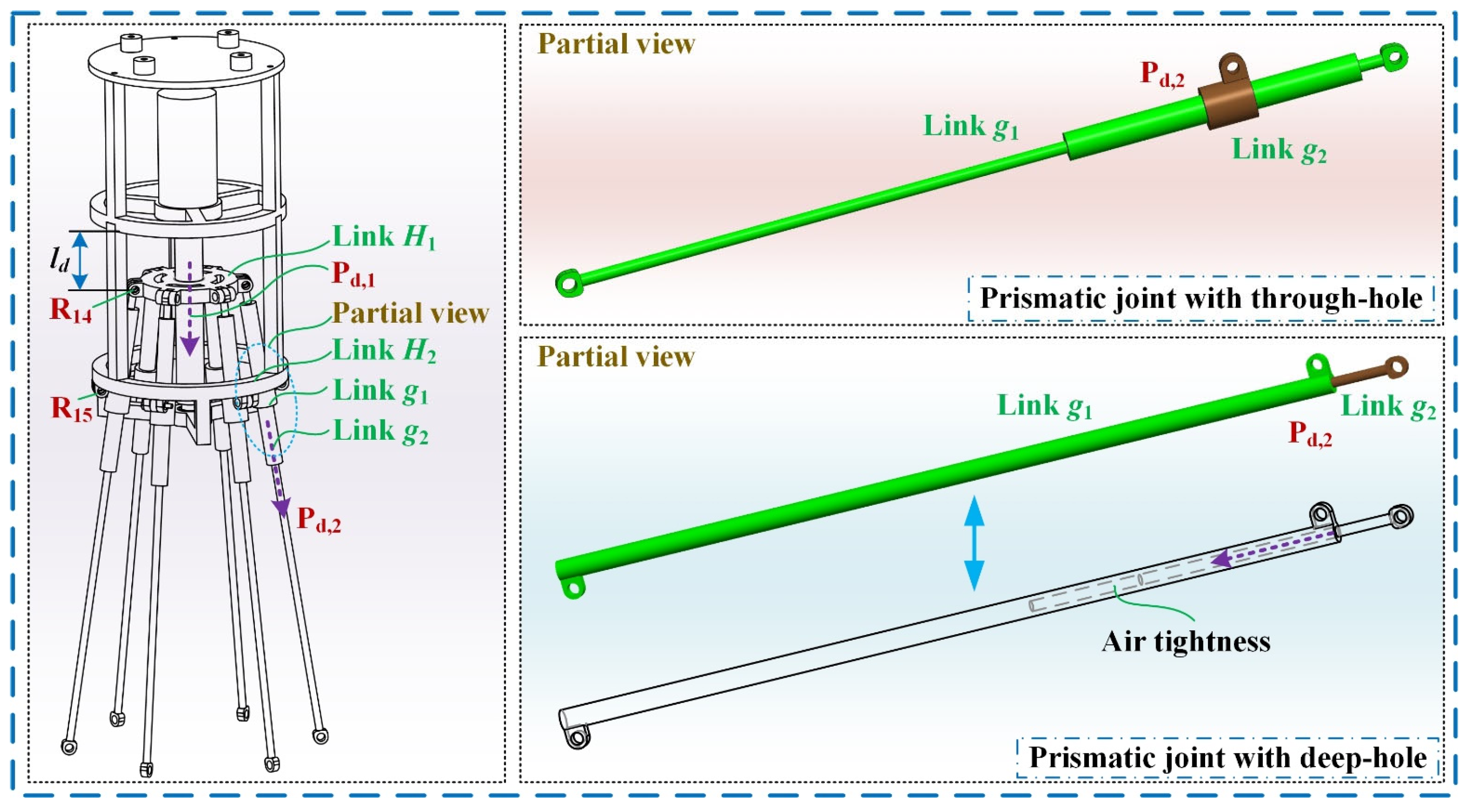
5. Physical Prototype, Control System, and Deployable Experiment
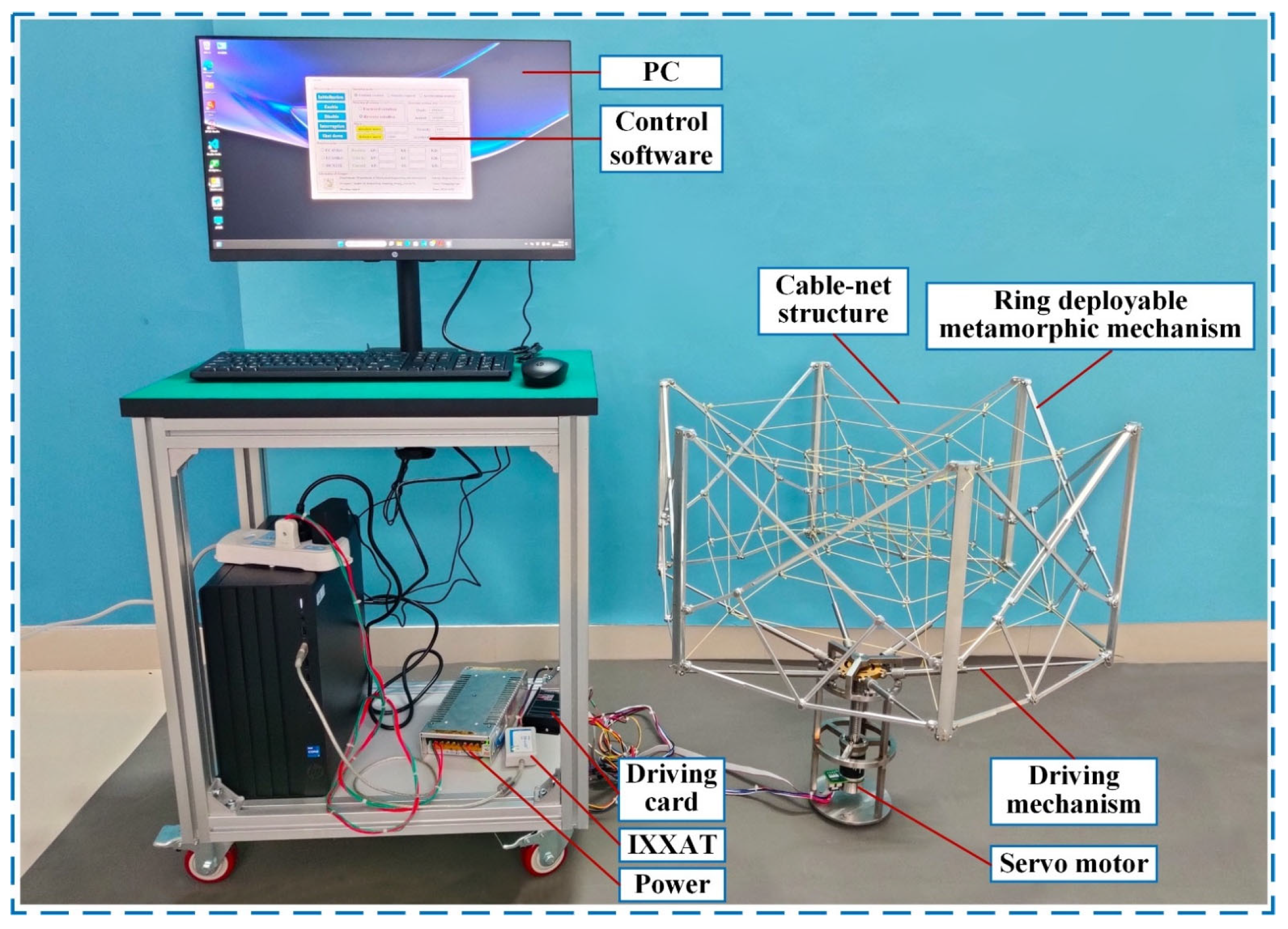
5.1. Design of the Physical Prototype and Mesh Structure
5.2. Establishment of Control System
5.3. Deployable Experimental Verification
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, Z.; Qiu, H.; Li, X.; Yang, S. Review of large spacecraft deployable membrane antenna structures. Chin. J. Mech. Eng. 2017, 30, 1447–1459. [Google Scholar] [CrossRef]
- Zheng, F.; Chen, M. New conceptual structure design for affordable space large deployable antenna. IEEE Trans. Antennas Propag. 2015, 63, 1351–1358. [Google Scholar] [CrossRef]
- Puig, L.; Barton, A.; Rando, N. A review on large deployable structures for astrophysics missions. Acta Astronaut. 2010, 67, 12–26. [Google Scholar] [CrossRef]
- Santiago-Prowald, J.; Baier, H. Advances in deployable structures and surfaces for large apertures in space. CEAS Space J. 2013, 5, 89–115. [Google Scholar] [CrossRef]
- Ma, X.; Li, T.; Ma, J.; Wang, Z.; Shi, C.; Zheng, S.; Cui, Q.; Li, X.; Liu, F.; Guo, H.; et al. Recent advances in space-deployable structures in China. Engineering 2022, 17, 207–219. [Google Scholar] [CrossRef]
- Thomson, M. The AstroMesh deployable reflector. IEEE Trans. Antennas Propag. 1999, 3, 1516–1519. [Google Scholar]
- Tserodze, S.; Medzmariashvili, E.; Klooster, C.; Muchaidze, K.C.M.; Nikoladze, M.; Chapodze, A.; Sigua, I.; Sanikidze, M. New design modifications of the supporting ring for a large deployable space reflector. CEAS Space J. 2021, 13, 175–182. [Google Scholar] [CrossRef]
- Qi, X.; Huang, H.; Li, B.; Deng, Z. A large ring deployable mechanism for space satellite antenna. Aerosp. Sci. Technol. 2016, 58, 498–510. [Google Scholar] [CrossRef]
- Qi, X.; Miao, Z.; Huang, H.; Li, B. Design and mobility analysis of large deployable mechanisms based on plane-symmetric Bricard linkage. In Proceedings of the ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016. [Google Scholar]
- Qi, X.; Li, S.; Li, B.; Huang, H. Design of a deployable ring mechanism using V-fold bars and scissor mechanisms. In Proceedings of the 6th Annual IEEE International Conference on Cyber Technology in Automation, Control and Intelligent Systems, Chengdu, China, 19–22 June 2016. [Google Scholar]
- Lu, S.; Qi, X.; Hu, Y.; Li, B.; Zhang, J. Deployment dynamics of large space antenna and supporting arms. IEEE Access 2019, 7, 69922–69935. [Google Scholar] [CrossRef]
- Li, B.; Qi, X.; Huang, H.; Xu, W. Modeling and analysis of deployment dynamics for a novel ring mechanism. Acta Astronaut. 2016, 120, 59–74. [Google Scholar] [CrossRef]
- Knight, B.; Duffy, J.; Crane, C. Optimization of ring trusses for antenna structures using line geometry. J. Spacecr. Rocket. 2003, 40, 565–569. [Google Scholar] [CrossRef]
- Xu, Y.; Guan, F.; Xu, X.; Wang, H.; Zheng, Y. Development of a novel double-ring deployable mesh antenna. Int. J. Antennas Propag. 2012, 2012, 375463. [Google Scholar] [CrossRef]
- Xu, Y.; Guan, F.; Chen, J.; Zheng, Y. Structural design and static analysis of a double-ring deployable truss for mesh antennas. Acta Astronaut. 2012, 81, 545–554. [Google Scholar] [CrossRef]
- Feng, C.; Liu, T. A graph-theory approach to designing deployable mechanism of reflector antenna. Acta Astronaut. 2013, 87, 40–47. [Google Scholar] [CrossRef]
- Han, B.; Xu, Y.; Yao, J.; Zheng, D.; Li, Y.; Zhao, Y. Design and analysis of a scissors double-ring truss deployable mechanism for space antennas. Aerosp. Sci. Technol. 2019, 93, 105357. [Google Scholar] [CrossRef]
- Han, B.; Zhou, Y.; Zhao, Y. Kinematics and dynamics characteristics analysis of a double-ring truss deployable mechanism based on rectangular scissors unit. Eng. Struct. 2024, 307, 117900. [Google Scholar] [CrossRef]
- Han, B.; Xu, Y.; Yao, J.; Zheng, D.; Zhao, Y. Kinematic characteristics analysis of a double-ring truss deployable antenna mechanism. In Proceedings of the 12th International Conference of Intelligent Robotics and Applications, Shenyang, China, 8–11 August 2019. [Google Scholar]
- Han, B.; Xu, Y.; Yao, J.; Zheng, D.; Guo, L.; Zhao, Y. Type synthesis of deployable mechanism for ring truss antenna based on constraint-synthesis method. Chin. J. Aeronaut. 2020, 33, 2445–2460. [Google Scholar] [CrossRef]
- Cao, W.; Xi, S.; Ding, H.; Chen, Z. Design and kinematics of a novel double-ring truss deployable antenna mechanism. J. Mech. Des. 2021, 143, 124502. [Google Scholar] [CrossRef]
- He, B.; Jia, L.; Li, K.; Nie, R.; Fan, Y.; Wang, G. Deployment dynamic modeling and driving schemes for a ring-truss deployable antenna. Chin. J. Mech. Eng. 2024, 37, 79. [Google Scholar] [CrossRef]
- Sun, Z.; Yang, D.; Duan, B.; Kong, L.; Zhang, Y. Structural design, dynamic analysis, and verification test of a novel double-ring deployable truss for mesh antennas. Mech. Mach. Theory 2021, 165, 104416. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, Y.; Yang, D. Structural design, analysis, and experimental verification of an H-style deployable mechanism for large space-borne mesh antennas. Acta Astronaut. 2021, 178, 481–498. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, D.; Sun, Z.; Li, N.; Du, J. Winding strategy of driving cable based on dynamic analysis of deployment for deployable antennas. J. Mech. Sci. Technol. 2019, 33, 5147–5156. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, D.; Li, S. An integrated control and structural design approach for mesh reflector deployable space antennas. Mechatronics 2016, 35, 71–81. [Google Scholar] [CrossRef]
- Gao, C.; Kang, X.; Lei, H.; Xu, P.; Li, B. Design and analysis of a novel large-span two-fold deployable mechanism. Mech. Mach. Theory 2023, 186, 105352. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, Y.; Tang, A.; Li, Y. A design approach for AstroMesh-type contoured-beam reflector antennas. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 951–955. [Google Scholar] [CrossRef]
- Zhang, Y.; Ru, W.; Yang, G.; Li, N. Deployment analysis considering the cable-net tension effect for deployable antennas. Aerosp. Sci. Technol. 2016, 48, 193–202. [Google Scholar] [CrossRef]
- Du, X.; Du, J.; Bao, H.; Chen, X.; Wu, X. Dynamic analysis of the deployment for mesh reflector antennas driven with variable length cables. J. Comput. Nonlinear Dyn. 2019, 14, 111006. [Google Scholar] [CrossRef]
- Wu, R.; Zhang, W.; Behdinan, K. Vibration frequency analysis of beam-ring structure for circular deployable truss antenna. Int. J. Struct. Stab. Dyn. 2019, 19, 1950012. [Google Scholar] [CrossRef]
- Xu, Y.; Guo, J.; Guo, L.; Liu, W.; Yao, J.; Zhao, Y. Design and analysis of a truss deployable antenna mechanism based on a 3UU-3URU unit. Chin. J. Aeronaut. 2019, 32, 2743–2754. [Google Scholar] [CrossRef]
- Shi, C.; Guo, H.; Cheng, Y.; Liu, R.; Deng, Z. Design and multi-objective comprehensive optimization of cable-strut tensioned antenna mechanism. Acta Astronaut. 2021, 178, 406–422. [Google Scholar] [CrossRef]
- Dai, L.; Guan, F.; Guest, J. Structural optimization and model fabrication of a double-ring deployable antenna truss. Acta Astronaut. 2014, 94, 843–851. [Google Scholar] [CrossRef]
- Dai, J.; Wang, D. Orientation and workspace analysis of the multi-fingered metamorphic hand-metahand. IEEE Trans. Robot. 2009, 25, 942–947. [Google Scholar] [CrossRef]
- Dai, J.; Cui, L. Posture, workspace, and manipulability of the metamorphic multifingered hand with an articulated palm. ASME Trans. J. Mech. Robot. 2011, 3, 021001. [Google Scholar]
- Wei, G.; Dai, J.; Wang, S.; Luo, H. Kinematic analysis and prototype of a metamorphic anthropomorphic hand with a reconfigurable palm. Int. J. Humanoid Robot. 2011, 8, 459–479. [Google Scholar] [CrossRef]
- Gao, Z.; Wei, G.; Dai, J. Inverse kinematics and workspace analysis of the metamorphic hand. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2015, 229, 965–975. [Google Scholar] [CrossRef]
- Wang, R.; Sun, J.; Dai, J. Design analysis and type synthesis of a petal-inspired space deployable-foldable mechanism. Mech. Mach. Theory 2019, 141, 151–170. [Google Scholar] [CrossRef]
- Gao, C.; Huang, H.; Li, B.; Jia, G. Design of a truss-shaped deployable grasping mechanism using mobility bifurcation. Mech. Mach. Theory 2019, 139, 346–358. [Google Scholar] [CrossRef]










| Link | a1, a2 | b1, b2 | c1, c2 | d1, d2 | e1, e2 | g1 | g2 |
|---|---|---|---|---|---|---|---|
| Length | 170 mm | 170 mm | 85 mm | 340 mm | 340 mm | 340 mm | 20 mm |
| Cable | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
|---|---|---|---|---|---|---|---|---|
| Length | 12 mm | 12 mm | 12 mm | 12 mm | 12 mm | 12 mm | 12 mm | 12 mm |
| Item | Rated Torque | Pole Pairs | Maximum Speed | Reduction Ratio | Sensor |
|---|---|---|---|---|---|
| Value | 128 mNm | 8 | 10,000 rpm | 26:1 | Mile 2048 cpt |
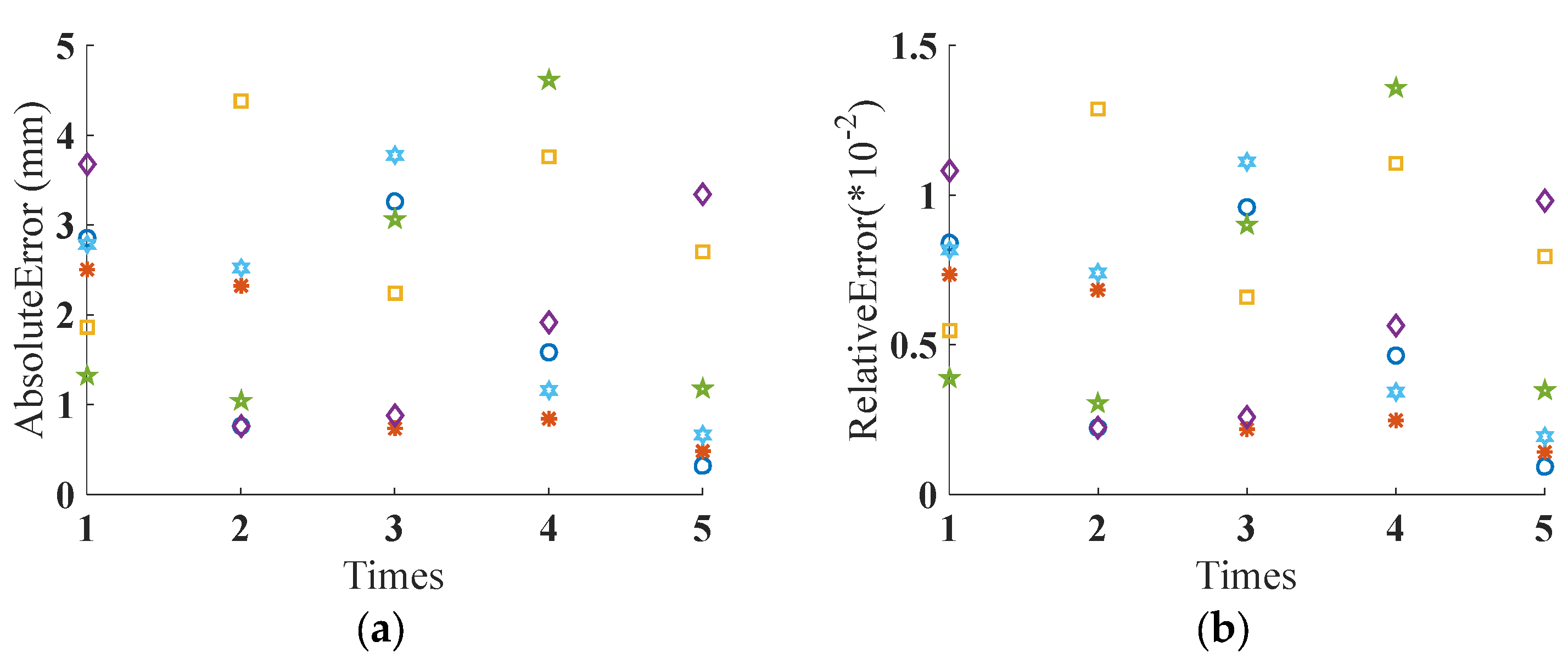
| Adjacent Key Points | Times | A1–A2 | A2–A3 | A3–A4 | A4–A5 | A5–A6 | A6–A1 |
|---|---|---|---|---|---|---|---|
| Absolute errors (mm) | First time | 2.86 mm | 2.50 mm | 1.86 mm | 3.68 mm | 1.32 mm | 2.78 mm |
| Second time | 0.76 mm | 2.32 mm | 4.38 mm | 0.76 mm | 1.04 mm | 2.52 mm | |
| Third time | 3.26 mm | 0.74 mm | 2.24 mm | 0.88 mm | 3.06 mm | 3.78 mm | |
| Forth time | 1.58 mm | 0.84 mm | 3.76 mm | 1.92 mm | 4.62 mm | 1.16 mm | |
| Fifth time | 0.32 mm | 0.48 mm | 2.70 mm | 3.34 mm | 1.18 mm | 0.66 mm | |
| Relative errors (%) | First time | 0.841% | 0.735% | 0.547% | 1.082% | 0.388% | 0.818% |
| Second time | 0.224% | 0.682% | 1.288% | 0.224% | 0.306% | 0.741% | |
| Third time | 0.959% | 0.218% | 0.659% | 0.259% | 0.900% | 1.112% | |
| Forth time | 0.465% | 0.247% | 1.106% | 0.565% | 1.359% | 0.241% | |
| Fifth time | 0.094% | 0.141% | 0.794% | 0.982% | 0.347% | 0.194% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, C.; Wang, H.; Yang, N.; Guo, J.; Liu, F.; Du, J. A Large-Span Ring Deployable Perimeter Truss for the Mesh Reflector Deployable Antenna. Symmetry 2025, 17, 1388. https://doi.org/10.3390/sym17091388
Gao C, Wang H, Yang N, Guo J, Liu F, Du J. A Large-Span Ring Deployable Perimeter Truss for the Mesh Reflector Deployable Antenna. Symmetry. 2025; 17(9):1388. https://doi.org/10.3390/sym17091388
Chicago/Turabian StyleGao, Changqing, Hanlin Wang, Nan Yang, Jianan Guo, Fei Liu, and Jingli Du. 2025. "A Large-Span Ring Deployable Perimeter Truss for the Mesh Reflector Deployable Antenna" Symmetry 17, no. 9: 1388. https://doi.org/10.3390/sym17091388
APA StyleGao, C., Wang, H., Yang, N., Guo, J., Liu, F., & Du, J. (2025). A Large-Span Ring Deployable Perimeter Truss for the Mesh Reflector Deployable Antenna. Symmetry, 17(9), 1388. https://doi.org/10.3390/sym17091388






