Abstract
To address the logistical challenges of traffic congestion and environmental concerns associated with carbon emissions in last-mile delivery, this paper explores the potential of vehicle–drone cooperative delivery. The existing studies are predominantly confined to single-drone scenarios, failing to simultaneously consider the constraints of drone payload capacity and endurance. This limitation leads to task allocation imbalance in large-scale customer deliveries and low distribution efficiency. Firstly, a mathematical model for vehicle–multi-drone collaborative delivery with payload and endurance constraint (VMDCD-PEC) is proposed. Secondly, an improved genetic algorithm (IGA) is developed, as follows: 1. designing a hybrid selection strategy to achieve symmetrical equilibrium between exploration and exploitation by adjusting the weights of dynamic fitness–distance balance, greedy selection, and random selection; and 2. introducing the local search operator composed of gene sequence reversal, single-gene slide-down, and random half-swap to improve the neighborhood quality solution mining efficiency. Finally, the experimental results show that compared with a traditional genetic algorithm (GA) and adaptive large neighborhood search (ALNS), the IGA requires less time to find solutions in various test cases and reduces the average cost of the optimal solution by up to 30%. In addition, an analysis of drone payload sensitivity showed that drone payload capacity is negatively correlated with delivery time, and that larger customer sizes corresponded to higher sensitivity.
1. Introduction
With the global e-commerce boom, the efficiency and sustainability of “last-mile” distribution have become increasingly important. The transportation sector already accounts for 21% of the global CO2 emissions, and the “last mile”, although only a small fraction of the total mileage of the commodities transported, is disproportionately responsible for transportation carbon emissions due to frequent short-distance transportation and inefficient route planning. This high-carbon model presents a double dilemma in both urban and rural areas. In cities, traffic congestion extends delivery times by 30–50%, with labor costs accounting for more than 40% of the total; in rural areas, dispersed settlements make a single delivery 2–3 times more expensive than in cities, and blind spots in coverage are common. It is predicted that by 2030, greenhouse gas emissions from delivery vehicles in the world’s top 10 most densely populated cities could increase by 21% to 32%, and the environmental and operational pressures on traditional logistics models will reach a tipping point [1,2]. Critically, such challenges necessitate policy-driven interventions. Recent research has confirmed that carbon emission policies (e.g., carbon tax and cap-and-trade) can reshape transport path decisions by internalizing environmental costs, forcing logistics operators to adopt low-carbon routing strategies even under operational uncertainties [3]. As a result, more and more studies are optimizing logistics networks from multiple perspectives [4,5].
Under such industry dilemmas, intelligent logistics solutions have become an inevitable trend, and the vehicle–drone cooperative delivery model has emerged. With its unique advantages, drone delivery shows great potential. It is able to bypass ground traffic congestion and complete deliveries at a faster speed, with low energy consumption and low carbon emissions, helping to reduce distribution costs and environmental impact. However, there are obvious shortcomings in the drone itself due to its smaller cargo capacity and shorter range, its distribution range, and the types of goods it carries are greatly restricted [6,7]. Traditional vehicle transportation has strong load-carrying capacity and endurance, enabling it to transport large quantities of goods and travel long distances. However, it faces issues such as high labor costs and low efficiency in complex road conditions.
A vehicle–drone cooperative delivery mode can precisely realize complementary advantages. Vehicles can be used as a mobile base for drones, providing range support and cargo supply and expanding the distribution range of drones; drones can go deeper into areas that are difficult for vehicles to reach to complete the last section of the distribution, improving the overall distribution efficiency and coverage capacity. This innovative model can not only effectively solve the “last-kilometer” distribution problem but also reduce logistics costs and carbon emissions, providing new opportunities for the sustainable development of the logistics industry [8].
Although the vehicle–multi-drone collaborative delivery model has demonstrated advantages in both theory and practice, the existing research has mostly focused on simplified scenarios of “single drone assisting vehicles”, including symmetrical combinations of single vehicles and single drones and multiple sets of single vehicles and single drones. In order to reduce carbon emissions and the proportion of vehicles, drones can serve customers who were originally served by vehicles [9]. In addition, in practical applications, drone service customer nodes need to meet the dual constraints of payload and endurance. To this end, this paper proposes a vehicle–multi-drone collaborative delivery with payload and endurance constraint (VMDCD-PEC) model, which reduces the overall delivery time of vehicles and drones by optimizing the delivery network. To address this optimization problem, this study designed an improved genetic algorithm for an efficient solution. Through the construction of test cases of different scales (30–100 customer nodes) and covering three typical scenarios of dispersed distribution, clustered distribution, and mixed distribution, we conducted a systematic verification. The research results provide a theoretical basis and practical reference for the optimization and development of vehicle–multi-drone collaborative delivery systems.
2. Literature Review
The optimization problem of cooperative delivery between drones and vehicles can be modeled as the “traveling salesman problem with drones” (TSP-D) [10]. This cooperative model can significantly improve the efficiency and flexibility of the delivery system and has obvious advantages over traditional vehicle-only delivery. Murray and Chu [11] first proposed the flying sidekick traveling salesman problem (FSTSP) and established a mixed-integer linear programming (MILP) model that minimizes the total completion time. The core scenario is cooperative delivery between a truck and its onboard drone. Wang et al. [12] demonstrated that a synergistic combination of truck and drone transportation reduces delivery times compared to unimodal trucking, even in multiple worst-case scenarios.
The simultaneous delivery model involving coordinated vehicle–drone operations presents significant routing challenges due to the stringent spatiotemporal synchronization requirements between both vehicles. Exact methods [13,14] (e.g., integer linear programming) guarantee optimality but are only adapted to small-scale instances; for larger-scale problems, metaheuristic algorithms [15,16,17] are more commonly used to obtain an approximate optimal solution in a shorter time.
The literature has proposed a large number of drone-based services and delivery applications in recent years. Ha et al. [18] proposed two heuristics, greedy random adaptation and local search, for the traveling salesman problem with drone (TSP-D) to minimize delivery costs. Both heuristics first generate vehicle delivery routes and then convert the optimal vehicle routes into feasible truck–drone cooperative routes. Liu et al. [19] focused on a single drone model carried by a truck. They designed a two-stage heuristic algorithm based on simulated annealing to alleviate the complexity of the MILP model. The algorithm follows the idea of “routing first, clustering later” to achieve coordinated optimization of truck and drone routes. Yu et al. [20] proposed an adaptive large neighborhood search (ALNS) algorithm to solve large-scale instances of the vehicle–drone collaborative delivery problem. In the destruction operator, they introduced a removal heuristic to eliminate customer nodes. Ha et al. [21] proposed a hybrid genetic search algorithm with dynamic population management and adaptive diversity control for the TSP-D problem, integrating a split algorithm, crossover, and local search operators. There are also variants of cooperative delivery involving vehicles and drones. For example, Duan et al. [22] studied the problem of a vehicle carrying a drone to simultaneously pick up and deliver goods. The drone can fly to multiple customer locations, and the maximum payload of the drone is taken into consideration. Mahmoudinazlou et al. [23] proposed a hybrid genetic algorithm (HGA) for the TSP-D problem, integrating local search and dynamic programming (DP). The algorithm achieves extensive exploration and effective exploitation through complex chromosome design and efficient DP. Petr et al. [24] considered a multi-vehicle, multi-drone delivery scenario involving multiple depots, with multiple groups of vehicles each carrying a drone dispatched from different depots. The drones were dispatched from the trucks along their flight paths to perform last-mile deliveries. In summary, most current research has focused on the delivery problem of a single drone carried by a vehicle or multiple drones carried by multiple vehicles. However, the number of drones on a route plays a crucial role in sharing truck loads and optimizing routes. Furthermore, existing models do not adequately address the coupled effects of load and range constraints, leading to imbalances in large-scale task allocation.
In the field of cooperative delivery using drones, researchers have proposed a variety of solution approaches. Gu et al. [25] designed a two-stage heuristic algorithm: first, an ant colony algorithm (ACO) based on ensemble covering is used to select vehicle stops; then a customized hybrid genetic search algorithm (HGSADC) is used to schedule drone missions; finally, the stops are fine-tuned by local optimization. Bian et al. [26] introduced a population-based micro-evolutionary algorithm (MEA) to address hybrid vehicle–drone delivery. Cakmak et al. [27] proposed a hybrid heuristic algorithm based on genetic algorithms and ant colony algorithms for the traveling salesman problem with drones (TSP-D), which generates both vehicle and drone routes simultaneously. Zhan et al. [28] proposed a dynamic optimization ACO algorithm that enhances the pheromone update rules. These parameters are updated based on the optimization results, and a sorting factor is introduced to prevent the optimal path from being ignored. Metaheuristic algorithms are widely used in path optimization problems. By combining metaheuristic algorithms and advanced strategies, the performance of the algorithm can be effectively improved [29]. Therefore, in this paper, in order to better solve the problem of cooperative delivery between vehicles and drones, a two-stage hybrid selection strategy (HSS) and local search are introduced into the genetic algorithm, and exploration and exploitation at different stages are weighted and coordinated through the algorithm. The proposed metaheuristic algorithm constructs both truck and drone routes simultaneously, preventing potential high-quality solutions from being overlooked due to neglecting the complex interactions between vehicles and drones.
3. Mathematical Model
To mathematically characterize the cooperative delivery mode involving vehicles and drones, this section first establishes the problem parameters and operational constraints, followed by formalizing the mathematical model. Section 3.1 details the differential delivery capabilities of drones and vehicles, while Section 3.2 translates these operational constraints into a graph-based optimization framework. This structured approach establishes clear linkages between the practical problem specifications and their theoretical representation.
3.1. Problem Description
The cooperative delivery mode refers to a system where drones and vehicles collaborate to accomplish delivery tasks. This mode can be subdivided based on whether both agents physically participate in the last-mile delivery [30]. The model studied in this paper belongs to a type of vehicle–drone cooperative delivery in which both the drone and the vehicle are involved in the actual delivery task. In the common vehicle–drone cooperative delivery mode, the drone can serve any customer point (as shown in Figure 1a). However, this paper focuses on the cooperative delivery mode due to the payload capacity and endurance limitation of drones: for overweight or remote customer nodes, a drone cannot independently complete the delivery service. The distribution schematic is shown in Figure 1b. Specifically, the distribution scenario is as follows: the vehicle departs from the distribution center and carries M drones; the drones can take off from any customer point already served by the vehicle to carry out the distribution tasks and then retrieve them at the customer nodes served by the vehicle; the vehicle does not need to wait at the same place and will return to the distribution center after completing all distribution tasks.
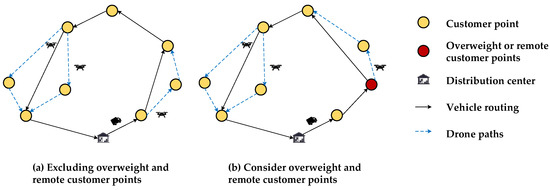
Figure 1.
Schematic diagram of vehicle–multi-drone cooperative delivery.
In the drone delivery process, it is essential to ensure that each drone launches in a fully charged state, with synchronized payload and endurance. This establishes symmetrical initial operating conditions for all drone deployments. Compared to vehicles, drones exhibit asymmetrical delivery capabilities due to constraints on overweight customer nodes and long-range customer nodes. This inherent operational asymmetry necessitates distinct collaborative strategies in the delivery system.
When optimizing the overall distribution path, priority should be given to arranging the drone to perform as many distribution tasks as possible within its capacity. This approach fully exploits the drone’s efficiency and speed advantages, effectively reducing vehicle distribution pressure and improving overall system efficiency. By reasonably coordinating the task allocation between the drone and vehicle, the advantages of both delivery agents are complementary of each other to achieve the goal of synergistic optimization.
Consider a set of n customers where each customer must be served once by a vehicle or a drone and a vehicle. Based on this problem, the following assumptions are made:
- (1)
- Both the vehicle and drone are moving at a constant speed, and the drone is flying faster than the vehicle.
- (2)
- The drone is required to return to the vehicle to pick up the packages and ensure sufficient power after each delivery.
- (3)
- When the vehicle and the drone meet at the designated customer point, the earlier arriving agent must wait for the other.
- (4)
- To simplify the definition of the problem, time for pickup/delivery and drone recharging is ignored.
3.2. Model Formulation
The VMDCD-PEC problem is defined on a complete directed graph . The vertex set is , where nodes 0 and n+1 represent warehouses, while denotes the set of n customer nodes to be served. The arcs set . The vehicle carries M drones to service all nodes. Let and represent travel time of the vehicle and drone m between node i and j with , where m is the drone number, V denotes the vehicle, and D denotes the drone. A drone voyage is defined as a triad where i is the takeoff node, j is the service node, and k is the landing node. The set of feasible paths is . Drone constraints: e is the max flight time; v is the max load capacity; u is the total number of drones initially carried by the vehicle; and denotes the number of drones carried by the vehicle on arc (i, j). The VMDCD-PEC problem can be represented as shown below:
- (1)
- Objective function
The objective function aims to find the optimal path such that the vehicle and drone depart from the warehouse and return to the warehouse after serving all the customers in the shortest time. Here, an+1 represents the time for the vehicle to return to the warehouse after serving all the customers. The decision variables xij, yi, zijk jointly determine the execution order and time of the delivery task through conditions such as flow balance constraints, arc-variable and node-variable association constraints, time constraints for the vehicle and drone, and drone takeoff and landing position constraints. Constraints (11) to (13) establish a dynamic association between decision variables and time variables to generate the arrival time series {ai} at the nodes. The time series ai characterizes the arrival moments of the vehicle at each node on the trunk path, specifically covering the time when the vehicle arrives at the customer point according to the planned route and the updated arrival time when the drone lands at the vehicle service node according to the constraints. Since the vehicle and drone work together, the generation of ai needs to satisfy the drone flight time constraint: if a node is set as a drone landing point, the arrival time of the vehicle at that node must be corrected to max(its original arrival moment, the drone landing moment). This mechanism reflects the dynamic coupling effect impact of drone flights on the vehicle time series through the time-stamp, ensuring ai strictly reflects the actual time trajectory of the vehicle on the trunk path.
- (2)
- Distribution constraints
Constraint (2) is a vehicle flow balance constraint, ensuring that the flow of vehicles entering a node equals the flow leaving the node.
Constraint (3) associates arc variables with node variables, ensuring that if a vehicle visits node i, an arc must enter the node.
Constraint (4) ensures that the vehicle departs from and returns to the warehouse.
Constraint (5) ensure that each customer node is serviced once by a vehicle or drone.
Constraint (6) constraints the number of drones departing from the warehouse.
Constraint (7) maintains node drone inventory equilibrium, where the number of drones carried by the vehicle at node i plus the number of drones landing at node i equals the number of vehicle leaving node i plus the number of drones taking off from node i.
Constraint (8) requires that all drones are recovered when the vehicle returns to the warehouse.
Constraints (9) and (10) ensure that the vehicle can carry drones only when an arc is selected.
Constraint (11) sets the initial departure time of the vehicle from the warehouse to 0.
Constraints (12) and (13) define the time constraints for the truck and drone to arrive at customer node i. If node j is visited after node i, the start time of service at node j must be greater than the service time at node i, which also acts as a sub-loop elimination constraint.
Constraint (14) specifies the drone takeoff position constraint, ensuring that the takeoff location of the drone must be a node served by the vehicle.
Constraint (15) defines the drone landing location constraint, guaranteeing that the landing location of the drone must also be a node served by the vehicle.
Constraint (16) ensure that the drone does not exceed maximum flight time while serving the customer node.
Constraint (17) guarantees that the drone’s payload capacity is not exceeded during customer service.
Constraints (18) to (20) define the decision variables: is a binary variable equal to 1 if a path exists from customer node i to j, and 0 otherwise; is a binary variable indicating whether node i ∈ N is served by the vehicle (1 if served, 0 otherwise); and is a binary variable denoting whether node j is served by the drone (1 if served, 0 otherwise).
4. Solution Methods
VMDCD-PEC is an NP-hard problem, which is too complex to be solved by exact algorithms, and it is difficult to obtain the result in a reasonable time. Although the genetic algorithm has strong global exploration ability, it is prone to premature convergence and insufficient local search capability when dealing with complex problems. The selection operation of traditional GA can easily cause the algorithm to converge to a local optimum, which affects the solution quality.
In view of the above problems, this paper proposes an improved genetic algorithm (IGA). The flow chart of the improved algorithm is shown in Figure 2. It introduces a hybrid selection strategy based on dynamic fitness distance balance after chromosome initialization to achieve the dynamic balance between global exploration and local exploitation of the algorithm. Additionally, the local search mechanism integrates three types of neighborhood operations to refine the solution, further improving solution qualities. Meanwhile, the local search mechanism integrating three types of neighborhood operations can be fine-tuned to improve the quality of solutions and the convergence speed of the algorithm, thereby optimizing distribution path planning for the VMDCD-PEC problem.
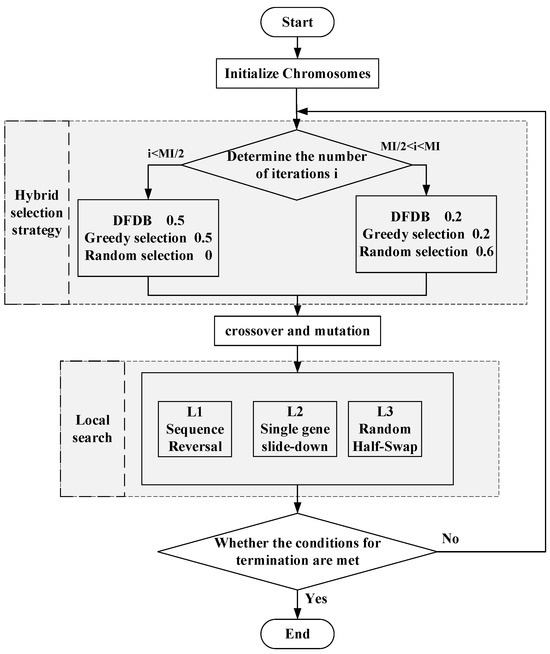
Figure 2.
IGA algorithm flow diagram.
4.1. Genetic Algorithms
The genetic algorithm (GA) is mainly used to solve complex optimization problems. The following are its basic steps:
- (1)
- Initialization of population
The initial population is constructed with reference to the hybrid initialized population strategy [31]. Through this strategy, the diversity of the population is fully guaranteed, while the quality of the initial solution is improved. Analysis shows that among the individuals of the initial population, about 90% of the individuals use the random ordering method to generate the path order of vehicle and drones, and the remaining 10% apply the greedy strategy to optimize path order.
- (2)
- Calculate individual fitness
The fitness function quantifies the quality of each individual; a higher fitness value increases the likelihood of the individual being retained in the population. Calculate the fitness values of all individuals in the population.
- (3)
- Selection operation
Roulette selection is used to calculate the fitness values of all individuals, summing them to obtain the total fitness value of the population. Then the probability of each individual being selected in the population is determined according to the proportion of its fitness value to the total fitness value. The higher the fitness value of an individual, the larger its proportion in the population, and thus the greater its chance of being selected during the selection process.
- (4)
- Crossover and mutation operations
Crossover and mutation operations are performed on individuals within a population to increase diversity. Crossover uses order crossover [32], which randomly selects two crossover points on the chromosome, copies the complete gene sequence of the middle segment of the parent individual to the corresponding position of the offspring, and cyclically traverses from the second crossover point of the other parent after the second crossover point, skipping the genes already present in the middle segment, to fill the remaining positions sequentially. Mutations are performed using random mutations [33], which randomly change one or some genes on the chromosome.
4.2. Improved Genetic Algorithm
4.2.1. Hybrid Selection Strategy
At different stages of the evolutionary algorithm, the focus of exploration and exploitation varies. In the early stage, the algorithm focuses on extensive exploration of the solution space to find a variety of potential solutions. In the later stage, as more high-quality solutions emerge, the algorithm shifts to exploiting existing information for local optimization while maintaining the ability to escape local optima. The core innovation of the IGA is its symmetry-driven hybrid selection strategy, which aims to effectively balance the conflicting needs between exploration and exploitation in the whole search process. strategy aims to effectively balance the conflicting demands between exploration and exploitation throughout the search process.
- (1)
- Components of a hybrid selection strategyThe hybrid selection strategy consists of the following three methods:
- a.
- DFDB selection combines the individual’s fitness value with the population’s spatial distribution to calculate a composite score. This balances exploitation and exploration, facilitating the selection of a more efficient candidate solution.
- b.
- Greedy selection chooses the optimal individual based on fitness value, promoting localized exploitation.
- c.
- Random selection randomly samples individuals from the population with uniform probability to maintain population diversity.
- (2)
- Two-stage weight assignment
To accommodate the different search process, the process is divided into two stages. The weights of these three methods are controlled by the parameters a, b, and c, representing the utilization ratios of DFDB selection, greedy selection, and random selection, respectively, where a + b + c = 1. The algorithm divides the maximum number of iterations (MI) into two stages, and the optimal weight coefficients obtained from repeated experiments are listed in Table 1.

Table 1.
Assignment of weights for hybrid selection strategies.
Stage 1: Initial exploration phase (). The weights are assigned as a = 0.5, b = 0.5, and c = 0. At the beginning of the search, the population diversity is high, so no random selection is required. A balanced application of greedy selection and DFDB selection is used to locate potential high-quality solution regions quickly.
Stage 2: . Weights are assigned as a = 0.2, b = 0.2, and c = 0.6. In the later stages of the search, population diversity may decrease significantly. Avoiding the population from falling into a local optimum is achieved by significantly increasing the proportion of random selection, while retaining a certain proportion of greedy selection and DFDB selection to maintain local exploitation capacity.
- (3)
- DFDB Implementation Process
The DFDB strategy is a selection method developed to efficiently manage the exploration–exploitation balance of metaheuristic optimization algorithms (MOAs) [34]. The key steps of DFDB selection are as follows:
Step 1: Calculate the distance.
Calculate the Euclidean distance between individual and the current optimal solution xbest, as shown in the following equation:
Transform the distance vector:
Step 2: Calculate the degree of adaptation.
Ti is the service time.
Step 3: Calculate individual scores.
and are the normalized values of fitness and distance and is a weighting coefficient with values in the range (0, 1) used to balance the contributions of fitness and distance.
The weighting coefficients are updated throughout the iteration as follows:
where i denotes the current number of iterations; maxi denotes the maximum number of adaptation evaluations; and is the lower bound value of the weight coefficient (0 < < 0.5, ∈ R).
Step 4: Transform into a vector of scores for the population.
4.2.2. Local Search
IGA enhances the optimization performance of the offspring individuals by introducing a local search mechanism. Specifically, we design three neighborhood search operators, denoted as L1, L2, and L3, in this study. These operators effectively enhance the local search capability of the algorithm by fine-tuning the perturbation of the parent individuals. The specific implementation of each operator is as follows (see Figure 3):
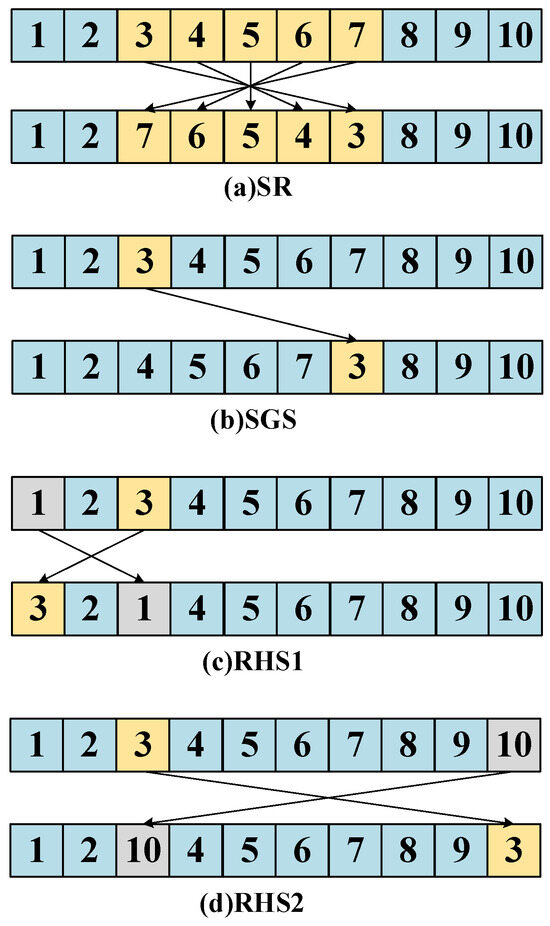
Figure 3.
Schematic diagram of neighborhood operation.
L1: Sequence reversal (SR), in which a segment of a continuous gene sequence from a parent individual is randomly selected and its order is reversed, as shown in Figure 3a.
L2: Single gene slide-down (SGS), which randomly selects a gene in a parent individual and slides it backward by k positions, as shown in Figure 3b.
L3: Random half-Swap (RHS) involves random selection of a gene position in the parent individual with 50% probability of swapping the selected gene with the first gene and a 50% probability of swapping the selected gene with the last gene, as shown in Figure 3c,d.
5. Experimental Studies
The experimental results of the proposed improved genetic algorithm are compared and analyzed with the traditional genetic algorithm and the adaptive large neighborhood search algorithm (ALNS) in solving the VMDCD-PEC problem. The sensitivity of key parameters related to drones is discussed in depth to provide more targeted and effective guidance for the optimization and practical application of the algorithm.
The ALNS algorithm is an effective metaheuristic algorithm. Its main steps are as follows:
- (1)
- Initialization: Generate an initial solution, typically using a greedy algorithm or random generation.
- (2)
- Selection operation: Select destruction and repair operators for generating neighboring solutions.
- (3)
- Local search: Search within the neighborhood to improve the current solution.
- (4)
- Update operation: Update the selection probabilities of the destruction and repair operators based on their historical performance.
- (5)
- Iteration: Repeat the selection, local search, and update operations until the stopping condition is met (maximum number of iterations or stagnation solution quality).
5.1. Settings
Experimental setup: The ALNS, IGA, and GA were implemented using MATLAB. The software version used was R2024b.
Test instances: Based on the Solomon standard test dataset, adjustments are made to ensure that the demand of all customers is between 2 kg and 30 kg, following a random distribution. The speed ratio of drones to the vehicle is 2:1, with its speed being 1 distance unit per second.
Parameter settings: To verify algorithm performance, the algorithm parameters are set as shown in Table 2. The population size Npop for both the proposed IGA and the GA was set to ten times the number of customer nodes. The maximum number of iterations M was 600, the crossover probability Pc was 0.8, and the mutation probability Pm was 0.05. For the ALNS algorithm, the initial temperature T0 was 100, the cooling rate f was 0.95, the minimum temperature Tmin was 10, and the maximum number of iterations was also set at 600.

Table 2.
Parameters of the comparison algorithm.
5.2. Experimental Results
In order to fully evaluate the performance of IGA, experiments were conducted based on 15 sets of instances from the Solomon test set, which includes R-class (dispersed distribution), C-class (clustered distribution), and RC-class (mixed distribution) data. The number of customer nodes n was set to 30, 50, 60, 80, and 100. The experiments were run through 20 independent repetitions to find the mean and minimum values, and the GAP values [35] were introduced to quantify the gap between the comparison algorithms and the IGA, which is calculated as shown in the following equation:
where x represents the instance number for each combination; denotes the average delivery time obtained after 20 independent repeated experiments for a certain method on instance x; and denotes the optimal delivery time obtained by averaging the results after 20 independent repeated experiments on instance x.
To verify the performance of the IGA in scenarios where vehicles carry multiple drones for collaborative delivery, different scales of customer nodes were selected, with the number of drones M = 2, the maximum load capacity of drones v = 20 kg, and the maximum flight time of drones e = 20 min. The experimental results are shown in Table 3, where the IGA algorithm demonstrates superior performance over the GA and ALNS algorithms in all test instances.

Table 3.
Comparison of experimental results (time unit: minutes).
Analysis indicates that in the VMDCD-PEC problem scenarios with varying scales of customer nodes, the IGA outperforms both GA and ALNS in terms of both the best and average values. Particularly in the R-class instances where customer nodes are dispersed, the optimization effect of the IGA on delivery time is the most pronounced. When the scale of customer nodes increases from 30 to 100, the optimal delivery time of IGA is reduced by 21% to 32% compared to GA, and by 19% to 28% compared to ALNS, marking the largest reduction among the three types of customer nodes.
In dispersed scenarios, where customer nodes are sparsely distributed spatially, the optimization of path planning has a more significant impact on overall delivery efficiency. The IGA, through its dynamic fitness–distance balance selection strategy, prioritizes assigning customer nodes that meet the endurance and payload constraints of drones to be serviced. By leveraging the speed advantage of drones over ground vehicles, it effectively reduces the frequency of long-distance detours by the vehicle, thereby shortening the total time consumption of the collaborative delivery system.
In the C-class instances where customer nodes are clustered, the optimization margin of the IGA was relatively balanced. When the scale of customer nodes is 30, the average delivery time of IGA was reduced by 9% compared to GA. This is because in clustered scenarios, the distance between customer nodes were already relatively close, and the routes of vehicle and drones overlap significantly, limiting the scope for the IGA algorithm to compress delivery time.
In the RC-class instances that exhibit both dispersed and clustered characteristics, the optimization effect of the IGA fell between that of the R-class and C-class. This is due to the composite distribution pattern of these instances, which is “locally clustered—globally dispersed.” The dispersed, long-distance customer nodes and the dense clustered areas created a complementary optimization space. Drones can efficiently handle long-distance orders, while vehicle focus on deliveries within clusters. The collaborative operation of the two reduces the system’s sensitivity to a single distribution pattern, making the optimization effect of the IGA more stable.
To visually characterize the algorithms’ performance traits, three representative instances with customer point scales of 30, 50, and 100 from the RC101 case were meticulously selected, and their convergence trajectories are depicted in Figure 4. A detailed analysis of the algorithm convergence profiles in Figure 4 across these multi-scale instances reveals that the IGA demonstrates pronounced advantages in convergence velocity, solution optimality, and stability.
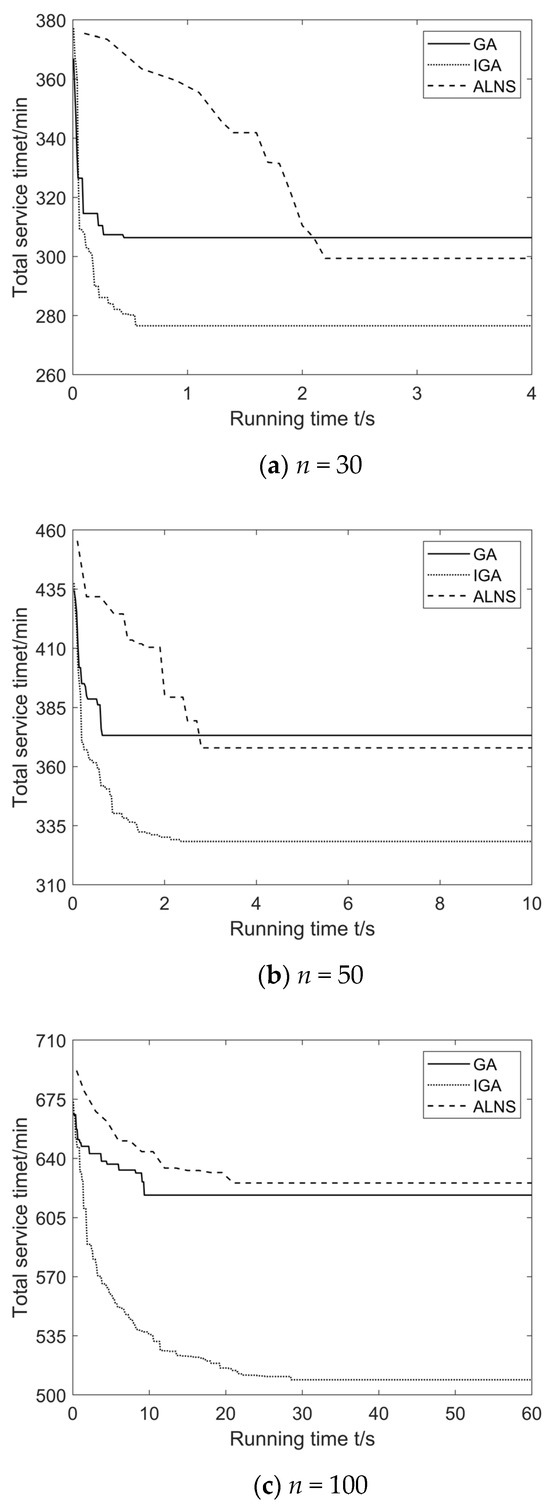
Figure 4.
Algorithmic iteration curves for different sizes of arithmetic cases.
By analyzing the convergence curves of the algorithms for different sizes of cases in Figure 4, it can be seen that the IGA shows advantages in convergence speed, solution quality, and stability. In terms of convergence speed, no matter whether it is a case of 30, 50, or 100 customer nodes, IGA’s objective function value decreases more steeply with the running time; especially in the small-scale (30 customer nodes) scenario, where it decreased rapidly in the early stage. IGA surpasses GA and ALNS, entering the convergence stage earlier. Even in large-scale scenarios (100 nodes), it maintains an efficient downward trend without stagnation. It does not stagnate due to the increase in the complexity of the problem. In the large-scale scenario, IGA still maintains an efficient downward trend without any stagnation due to the increase in problem complexity, which reflects the good adaptability to scale-up. In terms of convergence stability, the curve fluctuation of IGA is smoother after convergence, and it can lock the high-quality solution stably in the late stage of optimization, mitigating the oscillatory behavior typical of standard GA, demonstrating the enhanced convergence stability of IGA. In conclusion, IGA has realized the comprehensive performance breakthrough of “fast convergence, excellent solution quality and stable output” in multi-scale cases through the improvement of the core strategy, which effectively verifies the rationality and effectiveness of the improved algorithm.
5.3. Sensitivity Analysis
In order to test the performance of the algorithm under different drone-loading capacities, the instance RC101 is chosen as a typical representative. v is the maximum loading capacity of the drone, which is set to be 5, 10, 15, 20, and 25 kg, the IGA is averaged over 20 runs on the RC101 algorithm, and the results are plotted in Figure 5.
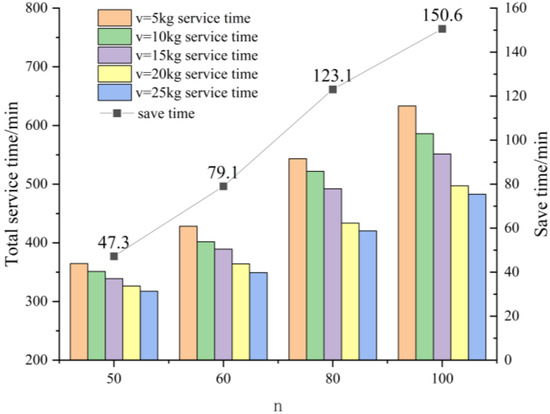
Figure 5.
Experimental results of different maximum load capacities of the drone. Among them, the data in the line chart shows that the total service time saved increased from 5 kg to 25 kg of drone payload.
The data show that when the maximum load capacity of the drone is increased from 5 kg to 25 kg, the total service time is reduced by 47.3 min, 79.1 min, 123.1 min, and 150.6 min in the cases of 50, 60, 80, and 100 customer locations. This shows a pattern of the larger the size of the customer location, the larger the reduction in the service time and indicates that the optimization effect of the increase in load capacity on the delivery efficiency increases with the increase in customer location size, which is positively correlated with the increase in delivery efficiency.
These results demonstrate that the optimization benefit of load capacity improvement on distribution efficiency increases with the increase in customer point size, showing a positive correlation. This is due to the fact that in large-scale distribution scenarios, the drone’s load capacity directly determines its effective service scope: if the drone’s load capacity is limited, it will be forced to give up its service in the face of orders from customer nodes that exceed its carrying capacity, and the ground vehicle will take on that part of the distribution task instead; then, the ground vehicle will be subject to the constraints of route planning, stopping efficiency, and other factors, which will lengthen the distribution cycle. By increasing the drone payload, it effectively expands the number of customer nodes it can serve in a single flight, reduces the inability to service due to insufficient load, and reduces the density of customer nodes to be covered by the ground vehicle. This optimization of task allocation allows the ground vehicle to focus on long-distance and large-scale cargo transportation, levering their scale transportation advantages, and ultimately reducing the total service time of cooperative delivery.
6. Conclusions
This paper focuses on the path optimization problem of collaborative delivery using vehicles and multiple drones. In large-scale customer node scenarios, vehicles must carry multiple drones to execute delivery tasks, while accounting for real-world constraints such as drone flight range and payload capacity. We propose a collaborative delivery problem between vehicles and multiple drones that considers payload and flight range constraints. A mathematical model was constructed, and the IGA was designed to solve it, effectively addressing the problems of premature convergence and imbalance between exploration and exploitation that traditional algorithms often encounter. This study aims to significantly improve the efficiency of collaborative delivery in large-scale customer point scenarios by optimizing task allocation and path planning, especially when considering the actual physical constraints of drones. The research content and main conclusions are as follows:
- Validation of algorithm effectiveness: Experiments based on the Solomon dataset show that the improved genetic algorithm (IGA), with different scales (n = 30, 50, 60, 80, 100) and customer distribution characteristics (R class, C class, RC class), achieves the optimization effect of shortening the distribution time by 19–32% on average compared with the traditional GA, and reducing the time by 28% compared with ALNS. Its core advantage is reflected in the adaptability to large-scale decentralized scenarios, through the task coordination between the drone and the vehicle on the ground, effectively reducing the frequency of vehicle meandering deliveries, which verifies the significant advantages of the cooperative delivery mode over traditional path optimization.
- Load constraint mechanism: The load capacity of the drone is significantly negatively correlated with the delivery time, and when the load capacity is increased from 5 kg to 25 kg, the delivery time of 50–100 customer locations is reduced by 47.3–150.6 min, and the larger the size of the customer locations, the higher the sensitivity is. This phenomenon reveals the dual mechanism of load enhancement by expanding the service range of a single flight of the drone and reducing the delivery density of the ground vehicle, which proves the key role of drone load parameter optimization in cooperative delivery.
In summary, the VMDCD-PEC model and IGA solution algorithm proposed in this study provide an effective theoretical framework and practical tools for solving the vehicle–multi-drone collaborative delivery path optimization problem under large-scale, multi-constraint conditions. The research results not only verify the importance of load capacity in improving delivery efficiency, but also provide an important basis for decision-making for logistics companies to deploy drone collaborative delivery systems in actual operations and optimize resource allocation to reduce costs and improve timeliness.
Although this study has achieved certain results, there are still several limitations that warrant further exploration:
- This paper mainly focuses on the impact of drone payload and flight duration limitations on delivery time. In the future, further research can be conducted on the mechanism of its impact on delivery costs. For example, logistics companies can choose drones with different configurations (such as flight duration and payload specifications) based on different cost budgets to optimize overall operational efficiency.
- This study focuses on the optimization of single-vehicle–multi-drone collaborative delivery, while the path optimization of multi-vehicle–multi-drone is a more realistic research direction. In the future, clustering algorithms can be used to divide customer nodes into multiple groups, transforming the problem into the optimization of vehicle–multi-drone collaborative delivery, thereby expanding to larger-scale logistics scenarios.
- In the actual delivery process, uncertain factors such as weather changes, traffic conditions, and fluctuations in customer demand may affect delivery efficiency. Future research can introduce robust optimization or stochastic planning methods to enhance the adaptability of vehicle–drone cooperative delivery systems in complex real-world environments and promote their wider application.
Author Contributions
Conceptualization, J.L. and M.W.; formal analysis, M.W.; methodology, M.W.; software, M.W.; validation, M.W.; visualization, M.W.; writing—original draft, M.W.; writing—review and editing, J.L. All authors will be informed about each step of the manuscript processing, including submission, revision, revision reminder, etc., via emails from our system or assigned Assistant Editor. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the school–enterprise cooperation project (Grant No. heng20250110).
Data Availability Statement
The data are part of an ongoing study, so it is not currently convenient to publish the code and data. However, we welcome other researchers discussing this with us.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Beck, K.; Esquillor, J.; Zarei, M.M.; Froes, I.; Hauswald, I.; Giannakopoulou, A.; Flämig, H. Making Last Mile Logistics Models Aware of Customer Choices, Demand Sustainability and Data Economy. Eur. Transp. Res. Rev. 2025, 17, 29. [Google Scholar] [CrossRef]
- González-Romero, I.; Ortiz-Bas, Á.; Prado-Prado, J.C. Decarbonizing the Last Mile. Innovations from an Online Retailers’ Perspective. Transp. Res. Part D Transp. Environ. 2025, 143, 104752. [Google Scholar] [CrossRef]
- Zhu, C.; Zhu, X. Multi-Objective Path-Decision Model of Multimodal Transport Considering Uncertain Conditions and Carbon Emission Policies. Symmetry 2022, 14, 221. [Google Scholar] [CrossRef]
- Zhou, J.; Wei, H.; Zhao, Y.; Ma, Y. China-Europe Container Multimodal Transport Path Selection Based on Multi-Objective Optimization. MITS 2023, 2, 72–88. [Google Scholar] [CrossRef]
- Chen, L.; Su, S. Optimization of the Trust Propagation on Supply Chain Network Based on Blockchain Plus. JIMD 2022, 1, 17–27. [Google Scholar] [CrossRef]
- Mohamed, A.; Mohamed, M. Unmanned Aerial Vehicles in Last-Mile Parcel Delivery: A State-of-the-Art Review. Drones 2025, 9, 413. [Google Scholar] [CrossRef]
- Wu, G.; Lu, J.; Hou, D.; Zheng, L.; Han, D.; Meng, H.; Long, F.; Luo, L.; Peng, K. Dynamic Task Allocation for Collaborative Data Collection: A Vehicle–Drone Approach. Symmetry 2025, 17, 67. [Google Scholar] [CrossRef]
- Xia, Y.; Wu, T.; Xia, B.; Zhang, J. Truck-Drone Pickup and Delivery Problem with Drone Weight-Related Cost. Sustainability 2023, 15, 16342. [Google Scholar] [CrossRef]
- Brown, J.R.; Bushuev, M.A. Last Mile Delivery with Drones: A Carbon Emissions Comparison. Int. J. Sustain. Transp. 2024, 18, 791–802. [Google Scholar] [CrossRef]
- Agatz, N.; Bouman, P.; Schmidt, M. Optimization Approaches for the Traveling Salesman Problem with Drone. Transp. Sci. 2018, 52, 965–981. [Google Scholar] [CrossRef]
- Murray, C.C.; Chu, A.G. The Flying Sidekick Traveling Salesman Problem: Optimization of Drone-Assisted Parcel Delivery. Transp. Res. Part C Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
- Wang, X.; Poikonen, S.; Golden, B. The Vehicle Routing Problem with Drones: Several Worst-Case Results. Results. Optim. Lett. 2017, 11, 679–697. [Google Scholar] [CrossRef]
- Lu, D.; Gzara, F. The Robust Vehicle Routing Problem with Time Windows: Solution by Branch and Price and Cut. Eur. J. Oper. Res. 2019, 275, 925–938. [Google Scholar] [CrossRef]
- Camm, J.D.; Magazine, M.J.; Kuppusamy, S.; Martin, K. The Demand Weighted Vehicle Routing Problem. Eur. J. Oper. Res. 2017, 262, 151–162. [Google Scholar] [CrossRef]
- Liu, W.; Liu, L.; Qi, X. Drone Resupply with Multiple Trucks and Drones for On-Time Delivery along given Truck Routes. Eur. J. Oper. Res. 2024, 318, 457–468. [Google Scholar] [CrossRef]
- Bai, X.; Ye, Y.; Zhang, B.; Ge, S.S. Efficient Package Delivery Task Assignment for Truck and High Capacity Drone. IEEE Trans. Intell. Transp. Syst. 2023, 24, 13422–13435. [Google Scholar] [CrossRef]
- De Freitas, J.C.; Penna, P.H.V. A Variable Neighborhood Search for Flying Sidekick Traveling Salesman Problem. Int. Trans. Oper. Res. 2020, 27, 267–290. [Google Scholar] [CrossRef]
- Ha, Q.M.; Deville, Y.; Pham, Q.D.; Ha, M.H. On the Min-Cost Traveling Salesman Problem with Drone. Transp. Res. Part C Emerg. Technol. 2018, 86, 597–621. [Google Scholar] [CrossRef]
- Liu, Y.-Q.; Han, J.; Zhang, Y.; Li, Y.; Jiang, T. Multivisit Drone-Vehicle Routing Problem with Simultaneous Pickup and Delivery Considering No-Fly Zones. Discret. Dyn. Nat. Soc. 2023, 2023, 1183764. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, P.; Yu, Y.; Sun, W.; Huang, M. An Adaptive Large Neighborhood Search for the Larger-Scale Instances of Green Vehicle Routing Problem with Time Windows. Complexity 2020, 2020, 8210630. [Google Scholar] [CrossRef]
- Ha, Q.M.; Deville, Y.; Pham, Q.D.; Hà, M.H. A Hybrid Genetic Algorithm for the Traveling Salesman Problem with Drone. J. Heuristics 2020, 26, 219–247. [Google Scholar] [CrossRef]
- Duan, H.; Li, X.; Zhang, G.; Feng, Y.; Lu, Q. Elite-Based Multi-Objective Improved Iterative Local Search Algorithm for Time-Dependent Vehicle-Drone Collaborative Routing Problem with Simultaneous Pickup and Delivery. Eng. Appl. Artif. Intell. 2025, 139, 109608. [Google Scholar] [CrossRef]
- Mahmoudinazlou, S.; Kwon, C. A Hybrid Genetic Algorithm with Type-Aware Chromosomes for Traveling Salesman Problems with Drone. Eur. J. Oper. Res. 2024, 318, 719–739. [Google Scholar] [CrossRef]
- Stodola, P.; Kutěj, L. Multi-Depot Vehicle Routing Problem with Drones: Mathematical Formulation, Solution Algorithm and Experiments. Expert Syst. Appl. 2024, 241, 122483. [Google Scholar] [CrossRef]
- Gu, Q.; Fan, T.; Han, W. Optimization of Hybrid Delivery by Vehicle and Drones. Electron. Commer. Res. Appl. 2024, 66, 101411. [Google Scholar] [CrossRef]
- Bian, J.; Song, R.; He, S.; Chi, J. Truck-Drone Hybrid Delivery Routing: A Mathematical Model and Micro- Evolutionary Algorithm. IEEE Trans. Intell. Transp. Syst. 2024, 25, 12187–12202. [Google Scholar] [CrossRef]
- Gunay-Sezer, N.S.; Cakmak, E.; Bulkan, S. A Hybrid Metaheuristic Solution Method to Traveling Salesman Problem with Drone. Systems 2023, 11, 259. [Google Scholar] [CrossRef]
- Zhang, L. Tea Leaf Picking Path Planning Based on an Improved Ant Colony Optimization Algorithm. IJKIS 2025, 3, 12–25. [Google Scholar] [CrossRef]
- Mbah, O.; Zeeshan, Q. Optimizing Path Planning for Smart Vehicles: A Comprehensive Review of Metaheuristic Algorithms. JEMSE 2023, 2, 231–271. [Google Scholar] [CrossRef]
- Madani, B.; Ndiaye, M. Hybrid Truck-Drone Delivery Systems: A Systematic Literature Review. IEEE Access 2022, 10, 92854–92878. [Google Scholar] [CrossRef]
- Qing-dao-er-ji, R.; Wang, Y.; Si, X. An Improved Genetic Algorithm for Job Shop Scheduling Problem. In Proceedings of the 2010 International Conference on Computational Intelligence and Security, Nanning, China, 16 December 2010. [Google Scholar]
- Nawaz, M.S.; Noor, S.; Fournier-Viger, P. Reasoning About Order Crossover in Genetic Algorithms. In Proceedings of the Lecture Notes in Computer Science, Advances in Swarm Intelligence, Xi’an, China, 15–19 July 2022. [Google Scholar]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A Review on Genetic Algorithm: Past, Present, and Future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Bakir, H. Dynamic Fitness-Distance Balance-Based Artificial Rabbits Optimization Algorithm to Solve Optimal Power Flow Problem. Expert Syst. Appl. 2024, 240, 122460. [Google Scholar] [CrossRef]
- Liu, Y.; Luo, Z.; Liu, Z.; Shi, J.; Cheng, G. Cooperative Routing Problem for Ground Vehicle and Unmanned Aerial Vehicle: The Application on Intelligence, Surveillance, and Reconnaissance Missions. IEEE Access 2019, 7, 63504–63518. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).