Abstract
The growing participation of elderly individuals in cruise tourism introduces asymmetry in passenger mobility and perception, posing challenges for onboard emergency evacuation. To address this, an interactive cellular automata model that enables dynamic human–signage interaction, incorporating age-dependent variations in walking speed and visual field. The model simulates passenger behavior during evacuation by integrating a static potential field, signage attraction, and directional guidance mechanisms. A bi-objective optimization framework is proposed to determine the optimal signage layout for symmetrical cruise ship theaters, balancing evacuation effectiveness across age groups with design constraints such as economic considerations. The optimization uses a genetic algorithm through simulation experiments under varying age compositions and smoke concentration levels. Results indicate that age-sensitive and interactive signage design substantially enhances evacuation efficiency, particularly for elderly passengers and under limited visibility conditions. This study offers practical insights into signage layout strategies for enhancing shipboard evacuation safety in diverse demographic and environmentally complex scenarios.
1. Introduction
The cruise industry has experienced continuous expansion in recent years, with global passenger volumes reaching tens of millions annually. In 2023, the number of cruise passengers reached 31.7 million, representing 107% of the 2019 level and reflecting a net increase of nearly 2 million compared to 2019 [1]. Simultaneously, demographic shifts are reshaping the demand for cruise tourism. Global population aging has become a growing concern in many developed and developing countries. In China, for instance, the number of individuals aged 60 and above reached 297 million by the end of 2023 [2], and this number is projected to exceed 400 million by 2035, accounting for approximately 30% of the national population [3]. This aging trend presents challenges and opportunities, positioning older adults as a key consumer segment in the cruise market.
Modern cruise ships are enclosed, multifunctional environments that integrate hospitality, entertainment, and transport functions, where limited evacuation alternatives amplify the critical importance of efficient and comprehensive emergency planning. Ensuring the safety of all passengers, particularly during emergencies, is paramount, and is complicated by the asymmetrical characteristics of the onboard population. Passengers differ in mobility, perceptual abilities, walking speeds, and cognitive response, all of which influence evacuation performance. The spatial environment of cruise ships, however, is often symmetrical by design, especially in public spaces such as theaters and atria, highlighting the tension between environmental symmetry and passenger heterogeneity. Bridging this asymmetry-symmetry gap is a fundamental challenge in evacuation planning.
Evacuation simulation has emerged as a widely adopted tool for assessing emergency response in complex environments such as buildings, airports, and ships. With advances in computational technologies, evacuation analysis has evolved from retrospective investigations to predictive modeling. In the maritime domain, simulation evacuation models are recognized by the International Maritime Organization (IMO) as effective tools for analyzing passenger movement and developing improved evacuation strategies.
Evacuation modeling methods are typically categorized into two types: macroscopic models and microscopic models. Macroscopic models treat crowd movement as continuous fluid-like flows, offering computational efficiency but lacking the capacity to account for individual behavioral variability [4,5,6]. Microscopic models, on the other hand, consider each passenger as an autonomous agent with specific attributes, enabling a more accurate representation of decision-making and interactions in evacuation scenarios [7,8,9].
Within the category of microscopic models, cellular automata (CA) models [10] and social force models [11,12] are widely adopted. While the social force model captures human dynamics through continuous force interactions, CA models discretize time, space, and movement states, offering higher computational efficiency and scalability for large-crowd simulations [13,14]. To enhance the simulation of passenger behavior in confined spaces, numerous extensions of cellular automata (CA) have been proposed over time, including multi-grid, fine mesh, floor field, and lattice gas models [15,16,17,18].
In ship evacuation research, environmental variables and passenger characteristics have been given attention. For example, fire-related factors (such as carbon monoxide concentration, temperature, and visibility [19,20]) have been incorporated into CA models to simulate fire evacuation more accurately [21]. Other studies have addressed congestion caused by reverse movement in narrow corridors [22], rapid smoke spread in flat, large spaces [23], and the influence of ship motion, including list and trim [24,25,26]. Furthermore, agent-based models have also been utilized to examine how ship swaying influences passenger movement [27].
While prior studies have incorporated certain environmental and behavioral aspects, many still treat passengers as homogeneous entities, neglecting the influence of individual differences on evacuation outcomes. In the real evacuation process, factors such as age, gender, mobility, and cognitive ability can substantially affect evacuation performance. Capturing these heterogeneities is essential for reliable evacuation modeling.
To address this need, the IMO’s Maritime Safety Committee issued guidelines recommending both simple and advanced evacuation analyses [23]. The former assumes identical characteristics for all passengers, while the latter accounts for individual variability, producing more realistic but also more complex and stochastic results. In addition, the IMO further issued MSC.1/Circ1533 [28], which outlines key personal attributes—such as age, gender, reaction time, and walking speed—necessary for simulating evacuation on passenger ships. Building on these frameworks, recent research has introduced behavior-based models that distinguish passengers by type [29], simulate collaborative search behavior [30], incorporate interaction effects such as friction and repulsion [31], and further extend to heterogeneous populations characterized by multi-type mobility speed and avoidance strategies [32].
Despite these advances, limited research has focused on the role of evacuation signage, especially within the context of cruise ships. Most studies emphasize architectural elements, focusing on stair design [33], evacuation route planning [34], or the timing of evacuation orders [35], while signage layout optimization has often been overlooked. Signage serves as a primary guidance system in maritime environments, where the unfamiliarity of layouts and the absence of alternative escape routes make effective signage layout strategies critical for passenger safety during emergencies. A few efforts have modeled signage placement as a maximum coverage location problem [36], incorporating occlusion effects and assuming a fixed number of signs. These studies, applied in single-floor supermarkets, demonstrated improvements in evacuation efficiency using CA model validation. Others have developed multi-objective signage models that jointly optimize economic costs and visibility coverage [37], validated in exhibition halls using AnyLogic simulations with gender-specific speed parameters. However, most of these approaches employ a two-stage framework—signage layout optimization followed by separate evacuation validation—and often neglect dynamic passenger-signage interactions or comprehensive cost-performance integration.
To overcome these limitations, this study proposes a bi-objective signage optimization model that simultaneously considers cost and visibility coverage across heterogeneous age groups. A cellular automata-based evacuation simulation is developed to capture dynamic interactions between passengers and signage, with a specific emphasis on visibility reductions under smoke-filled conditions. Through this integrated framework, the study explores how the asymmetry of passenger behavior interacts with the symmetry of cruise ship layouts to affect evacuation outcomes.
The remainder of the paper proceeds as follows: Section 2 introduces the cellular automata modeling framework, including static potential field construction, signage attraction mechanisms, and evacuation rules. Section 3 presents an improved signage layout optimization model, which integrates heterogeneous passenger features to identify the respective optimal results. Section 4 describes the simulation experiments designed to assess evacuation performance under various scenarios. Finally, Section 5 presents a summary of the key results, discusses the study’s limitations, and suggests directions for future research.
2. Evacuation Simulation
2.1. Cellular Automata Model
The Cellular Automata (CA) model is widely utilized in evacuation simulations due to its discrete and structured nature. It divides the simulation area into uniform square grids, each called a cell. A passenger, an obstacle, or evacuation signage may occupy a cell. Typical cell sizes employed in existing models are either 0.4 m × 0.4 m or 0.5 m × 0.5 m. Research shows that passenger movement becomes severely constrained when crowd density reaches 4 to 5.5 persons per square meter, and movement becomes nearly impossible at higher densities. Passengers typically require additional space to avoid direct physical contact. Therefore, a cell size of 0.5 m × 0.5 m is employed in this study.
In the CA model, each cell exists in one of two states: vacant or occupied. Time advances in discrete steps, and at each time step, a passenger can either move to a neighboring cell or remain stationary, based on a probabilistic rule. As illustrated in Figure 1, the green cell indicates the current position of a passenger, and the arrows denote the eight possible movement directions within the Moore neighborhood. Movement decisions are made using a roulette wheel selection approach.
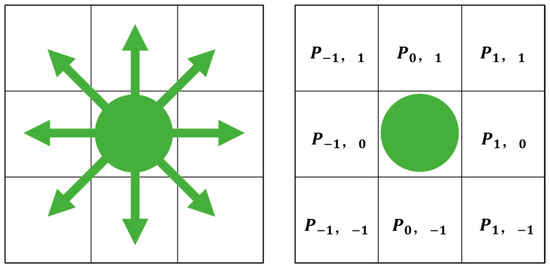
Figure 1.
Possible directions of movement in the Moore Neighborhood.
In Equations (1) and (2), represents the probability of passengers moving to the surrounding neighborhood, which is affected by four factors: the static potential field , the signage attraction field , the direction guidance factor , and the occupancy status .
where shows the cell coordinate; is the normalized coefficient; and denote the respective weights of the static potential field and signage influence; represents the state of the neighborhood cell, if the cell is occupied, and 0 otherwise. The parameter values for and are listed in Table 1.

Table 1.
Experimental parameter settings.
2.1.1. Static Potential Field
The static potential field models the ship’s layout and is held constant over the course of the evacuation [38,39]. Cells closer to exits exhibit stronger static potential values. The Dijkstra algorithm is employed for its computation [31]:
Step (1) Define exit positions: The exit is defined as , where shows the coordinates of the n-th exit.
Step (2) Initialize the static potential field values of all cells, according to Equation (3):
Step (3) Field propagation: Starting from all exit positions, for each cell where , the static potential field values of adjacent cells are updated iteratively using Equation (4):
where represents the neighborhood cell of .
Step (4) Iterative update: repeat step (3) until all cells have been assigned finite static potential field values, and no cell remains with .
Step (5) Final calculation and obstacle handling: for each cell , update its static potential field value as , and assign to all obstacle cells. This concludes the static potential field calculation. Figure 2 presents the static potential field distribution, where obstacles are denoted by gray areas.

Figure 2.
Static potential field value .
Passenger movement is influenced by the gradient of the static potential field, defined as the difference between the highest potential value within a cell’s neighborhood and the value of a given adjacent cell. This gradient is calculated using Equation (5).
2.1.2. Signage Attraction Field
Evacuation is a dynamic and high-stress process, particularly in unfamiliar environments where passengers tend to rely on signage to guide their movement. In such contexts, effective information interaction between signage and passengers plays a critical role. The signage’s influence is modeled as a circular field centered on the signage itself, with its radius defining the range within which it can affect passenger behavior. Similarly, each passenger has a circular visual field, and meaningful interaction can occur only when the signage falls within this field of vision.
To ensure mutual detectability, the signage’s service radius and the passenger’s visual radius are assumed to be equal and are jointly denoted as R. This geometric relationship is illustrated in Figure 3.
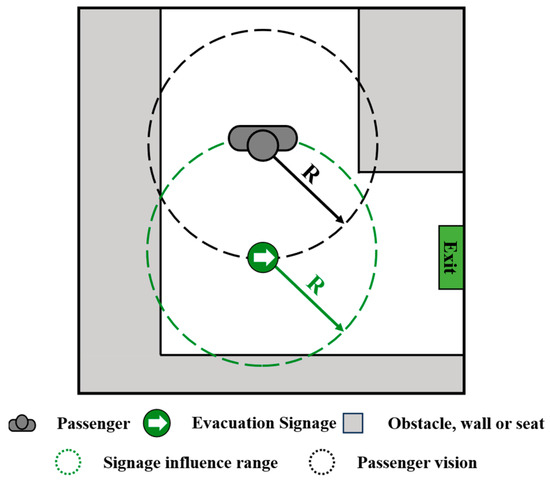
Figure 3.
Signage influence range and passenger’s vision.
When signage is visible within a passenger’s field of vision, it draws attention and exerts an attractive influence. The strength of this attraction is inversely related to the distance between the passenger and the signage—closer proximity results in greater influence. Conversely, signage located outside the visual range has no impact on the passenger’s behavior. The specific computational steps and formulas for determining the signage attraction field are provided in Equations (6)–(9):
Step (1) Calculate the Euclidean distance between the passenger’s current location and each signage location (). This is given in Equation (6).
where represents the distance from the passenger to the m-th signage.
Step (2) Identify the minimum distance to the nearest signage:
Step (3) Determine the visibility and compute the attraction field. First, calculate the distance from each neighborhood () to the nearest signage. Then, compare with the passenger’s field of vision radius If the signage is within the visual range (), the signage attraction field is defined as:
2.1.3. Direction Guidance Factor
When signage appears within a passenger’s field of view, the passenger is not only attracted by it, but also able to interact with it to obtain directional guidance. Upon perceiving this guidance, passengers tend to move in the direction indicated by the signage. As shown in Figure 4a, when signage pointing to the right enters the passenger’s visual field, the directional guidance factor increases the probability of selecting neighborhood cells aligned with the signage’s direction, thereby enhancing the likelihood of movement along the indicated path. On the contrary, as shown in Figure 4b, when signage is not visible, no visual interaction occurs, and the direction guidance factor exerts no influence on the passenger’s movement [40]. Therefore, the direction guidance factor effectively captures behavioral differences in movement based on the presence or absence of signage within the field of view. The computation of the direction guidance factor is defined as follows:
where is the direction guidance factor, ranging from 0 to 1; is the passenger’s visual radius; and denotes the distance to the nearest signage. The vector represents the direction from the current cell to a neighboring cell, and is a unit vector indicating the signage’s direction. For instance, if the signage points to the right, then . The angle formed between these vectors determines the effectiveness of directional alignment, as depicted in Figure 4a.
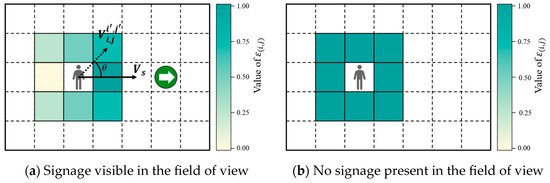
Figure 4.
Directional guidance factor effect.
Figure 4 demonstrates that passengers are more likely to move in the signage-indicated direction when signage is visible, reflecting a realistic behavioral response during emergency evacuation scenarios.
2.2. Simulation Experiment Settings
2.2.1. Passenger Setting
According to the UNESCO age classification [41], passengers are divided into three groups: young (15–24 years), middle-aged (25–64 years), and elderly (65 years and above). As specified in the IMO guidelines MSC.1/Circ.1533 [28], passengers in different age groups exhibit varying movement speeds. Considering these differences is essential for enhancing the accuracy of evacuation simulations on large cruise ships.
To simulate group-specific evacuation behaviors more accurately, this study assigns different neighborhood types based on mobility characteristics. According to MSC.1/Circ.1533 [28], the maximum walking speeds for different age groups are defined as follows: 1.1–1.6 m/s for young adults, 0.7–1.5 m/s for middle-aged individuals, and 0.6–1.2 m/s for the elderly. In this model, the lower bound of each speed range is adopted to reflect the worst-case mobility conditions during emergency evacuations.
In this study, the cell size is set to 0.5 m by 0.5 m [36], as shown in Table 1, enabling the calculation of discrete passenger movement speeds under different neighborhoods [32]. Due to mobility limitations, elderly passengers are modeled using the Von Neumann neighborhood, which allows movement in the four cardinal directions (up, down, left, and right), with discrete effective velocities {0,0.5} m/s, including the possibility of immobility under crowding conditions. Middle-aged passengers, with more flexibility, adopt the Moore neighborhood that supports movement in eight directions and corresponds to discrete velocities {0,0.5,0.7} m/s. Young passengers, possessing the highest mobility, utilize the extended Moore neighborhood to reflect their dynamic range, with discrete velocities {0,0.5,0.7,1.0} m/s [32]. The parameter values for , , and are listed in Table 1. This differentiation improves the representation of behavior patterns across age groups. Figure 5 shows these neighborhood types, where the green area indicates the reachable zones for each group.
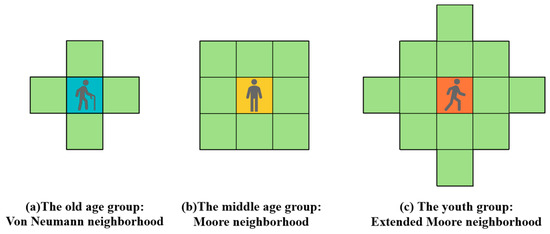
Figure 5.
The three age groups corresponding to the three types of neighborhoods.
Additionally, visual perception is also age-sensitive. As individuals age, their field of vision narrows. Thus, the elderly possess the smallest visual range, followed by the middle-aged group, with the youth exhibiting the broadest range. To quantify this, the study assigns circular visual fields with age-specific radii, as illustrated in Figure 6 [42].
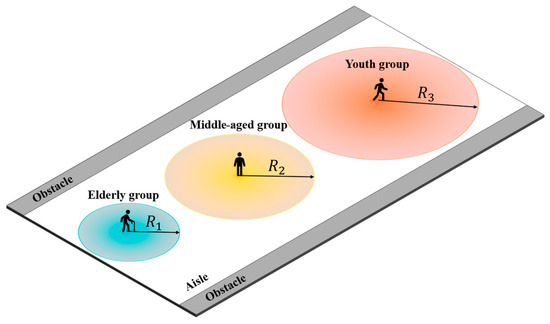
Figure 6.
Three types of passenger’s field of vision.
2.2.2. Map Setting
Due to the unique internal structure of ships and the specific behavioral patterns of passengers during evacuation, many land-based indoor evacuation approaches cannot be directly applied to passenger ships. Moreover, accidents on passenger vessels often result in severe consequences. As a result, compared to the well-developed research on land-based evacuation, studies on shipboard evacuation remain relatively limited [43]. Therefore, investigating evacuation strategies for cruise ships holds significant practical and theoretical value.
Deck 4 includes spacious public areas and a theater, with the layout shown in Figure 7. Most areas on the deck—excluding the theater—are generally spacious and flat, with a wide distribution and abundance of exits. In contrast, the theater section exhibits a higher level of complexity, characterized by narrow passageways and a limited number of exits. This study selects the Grand Theater of the Adora Magic City cruise ship as the simulation map. As a high-density gathering area on cruise ships, the theater has the characteristics of a dark environment, high noise, tight seating arrangement, and a high concentration of personnel. Furthermore, constrained by the hull structure, the cruise theater offers a narrower and more compact space compared to land-based theaters, resulting in more intricate evacuation pathways. From the passenger perspective, theater attendees are typically transient and less familiar with the vessel’s layout, leading to a heightened reliance on signage during evacuation. These factors collectively establish the cruise theater as a quintessential complex space within a cruise ship context. Investigating evacuation strategies for such environments is therefore of significant value for maritime safety engineering.
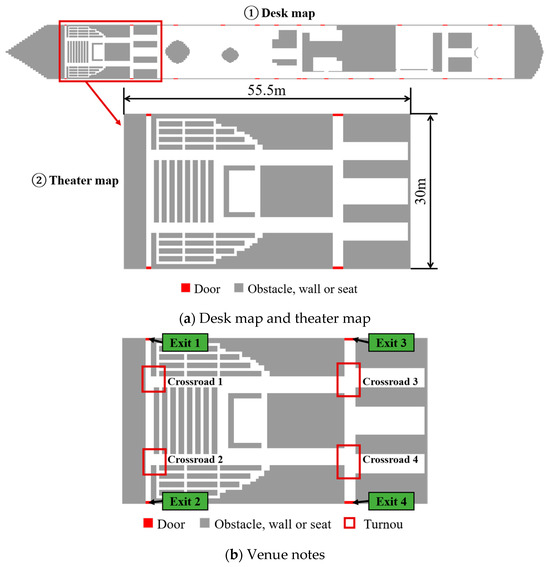
Figure 7.
Theater map and venue notes [44].
As shown in Figure 7a, the theater covers approximately , with a length of , and a width of . The layout of the theater is symmetrical. Figure 7b marks key locations, including four exits (Exit 1–Exit 4) and four crossroads (Crossroad 1–Crossroad 4).
The Grand Theater on the Adora Magic City cruise ship spans two levels and has a total capacity of 920 passengers. For simplicity, only the first floor is considered in this simulation, assumed to accommodate up to 65% of the maximum capacity, or approximately 600 passengers. These passengers include all three age groups.
Following Jeon et al. [45], three scenarios are defined: smoke-free, mild smoke, and heavy smoke. The corresponding smoke concentrations and visual ranges are assumed to be constant over time in all scenarios. The corresponding visual ranges for each age group under different conditions are shown in Table 2.

Table 2.
Visual range of the three age groups under different environments.
To evaluate how age group proportions influence evacuation outcomes, three population distributions are considered. Control group 1 is predominantly composed of middle-aged passengers. Experimental group 1 features a higher proportion of elderly passengers, while Experimental group 2 emphasizes a youth majority. The details are presented in Table 3.

Table 3.
Proportion of people in different age groups.
2.2.3. Evacuation Rules
The CA model operates using a parallel update rule during simulation. The specific evacuation consists of the following steps:
Step (1) Initialization: Compute the static potential field as described in Section 2.1.1. Populate the environment with randomly placed passengers from each age group, ensuring spatially valid placement.
Step (2) Visual field detection: At each time step, passengers perceive their surroundings within their assigned visual radius. Environmental states fall into two categories: (1) signage is visible, or (2) signage is not visible. These conditions determine the signage attraction field and direction guidance factor . Together with the static potential field , these parameters define the movement probabilities for all valid neighborhood cells via Equations (1) and (2).
Step (3) Mobility decision: Based on computed probabilities, the “roulette wheel” method is applied to select the final movement direction for each passenger.
Step (4) Conflict resolution: When multiple passengers target the same cell, conflicts are resolved by comparing their movement probabilities . The passenger with the highest probability gains movement priority. Others are reverted to their previous positions and await the next opportunity.
Step (5) Update and Termination Check: Once movements are finalized, all passenger positions are updated. Two termination conditions are checked:
- If a passenger reaches an exit, they are removed from the simulation.
- If no passengers remain in the domain, the simulation ends. Otherwise, it proceeds to the next step.
Step (6) Loop: Step (2) to Step (5) are repeated until all passengers have exited the simulation area.
The evacuation flow chart is shown in Figure 8.
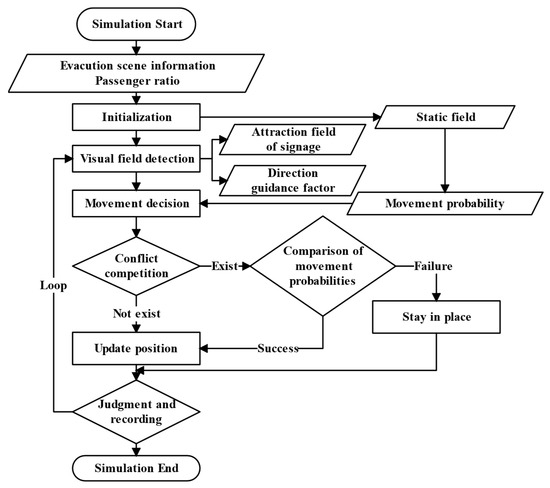
Figure 8.
Flowchart of the evacuation process.
3. Signage Layout Optimization
3.1. Selection of Candidate Points for Signage
In complex evacuation environments, installing signage at every location is impractical. Excessive signage may result in cognitive overload for passengers and even induce psychological discomfort. Identifying the appropriate number and placement of signage candidate points becomes a critical aspect of layout optimization. Based on the strategy proposed by Wan et al. [37], three typical layout scenarios for signage candidate points are illustrated in Figure 9.
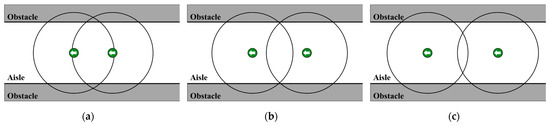
Figure 9.
Impact range under different signage spacing scenarios. (a) Signage placement achieves complete coverage of the evacuation area; (b) Maintains full coverage while minimizing redundant overlap; (c) Spans a broader area but fails to adequately cover certain corridor sections.
In Figure 9a, signage placement achieves complete coverage of the evacuation area. However, the overlapping influence ranges lead to resource wastage and reduced efficiency. Figure 9b maintains full coverage while minimizing redundant overlap, thereby enhancing utilization efficiency. Figure 9c, despite having a broader spatial span, fails to effectively cover certain corridor sections, which could impair visibility and guidance during evacuation.
Given these considerations, Figure 9b provides the best balance between coverage integrity and resource efficiency. Accordingly, the layout interval for signage candidate points is determined based on Figure 9b, with a spacing distance estimated to be approximately 7–8 m.
The cruise environment includes distinct structural components, i.e., exits, corners, and promenades. Candidate points are thus selected using the following two-step process:
Step (1): Set candidate points at all exits and corners and number each point.
Step (2): In corridors, divide the space evenly into sections so that the distance between points does not exceed .
The resulting symmetric candidate point distribution for the theater is illustrated in Figure 10, in which the candidate points are duly numbered.
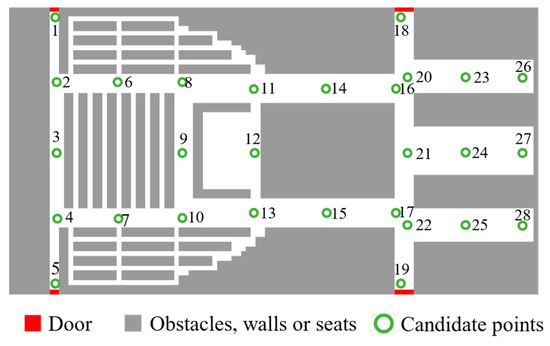
Figure 10.
Theater candidate point layout.
3.2. Light Occlusion Effect Caused by Obstacles
In practice, signage visibility is often hindered by physical obstructions such as walls (see Figure 11). These occlusions limit the effective range of signage and weaken its guidance performance. For this problem, consider signage point , three passengers , , and , and three obstacles , , and . Taking Figure 11a as an example, represents the straight-line distance between the obstacle and the line segment formed by the passenger and the signage. Let denote the vector between the signage and the passenger, and the direction from the signage to an obstacle. The following Equations are used:
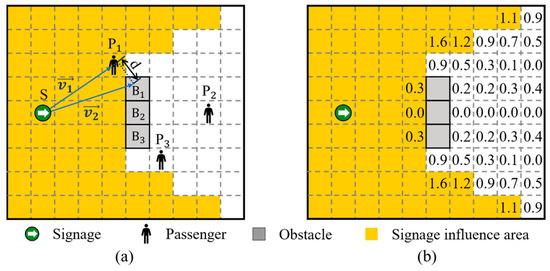
Figure 11.
(a) Schematic of signage, passengers, and obstacles. (b) Visibility calculation results based on projection analysis.
Step (1): Calculate the projection coefficient and projection vector of on .
where is the projection vector of on ; and the projection coefficient is used to determine the position of the projection point of on . If , the obstacle lies between the signage and the passenger, potentially causing occlusion. If or , the obstacle is outside the segment.
Step (2): Calculate the perpendicular distance from to the projection point.
Step (3): Determine the minimum vertical distance across all obstacles.
According to Chen et al. [36,46], an occlusion is considered significant if m. Whether occlusion affects signage visibility depends on both and . Combined with Figure 11b, there are three cases: (1) If , no occlusion occurs. (2) If and or , the influence range of the signage is occluded. (3) If and , no occlusion occurs.
The involved vectors are computed as
3.3. Objective Function and Constraint Conditions
3.3.1. Objective Function
In evacuation environments, one of the primary objectives in signage layout design is to maximize the effective coverage area of signage to ensure passengers receive timely and coherent guidance. However, this objective must be balanced against economic considerations and potential impacts on the passenger experience. Excessive placement of signage not only incurs unnecessary costs but may also cause cognitive overload and reduce evacuation clarity. The number of signages is adopted in the model as a quantitative indicator of the cost objective. Therefore, this study formulates a bi-objective optimization model that balances guidance effectiveness with layout efficiency. To integrate the two objectives, the bi-objective problem is reformulated as a single-objective optimization using a weighted sum approach.
where correspond to the elderly, middle-aged, and young groups, respectively. is the number of signage actually placed. is the total number of candidate signage points. is the area of signage influence for the i-th age group. is the total evacuation area. And is the weight coefficient. The corresponding values of the parameters are presented in Table 1.
Considering that the effective influence range of signage varies across different age groups, the model constructs age-specific objective functions. These functions are then integrated into a comprehensive objective function weighted by the population proportion of each group.
where denotes the proportion of the population in group , with = 1.
3.3.2. Constraint Conditions
Currently, there are no standardized regulations governing signage placement in cruise ship environments, especially in developing countries. National fire safety codes for high-rise buildings typically outline the general principles, such as placing exit signs at exits and limiting the distance between signs in corridors to a maximum of 20 m [47]. To meet the requirement that exit signs should be set at the exits of large public buildings, the constraint conditions are set; see Equation (21). Additionally, to ensure symmetry constraints based on the ship theater layout, we add Equation (22).
Subject to
where , if is placed at the i-th candidate position, otherwise 0. .
3.4. Signage Layout Optimization Algorithm
The genetic algorithm (GA) is a global optimization algorithm based on natural selection and genetic mechanisms. It simulates the principle of “survival of the fittest” in biological evolution. The GA evolves candidate solutions to identify optimal layouts via the following steps:
Step (1) Encoding: Binary encoding is used to represent the signage layout, where 1 means the signage is placed at a candidate point, and 0 means no signage is placed.
Step (2) Initial population: Multiple layout schemes are randomly generated to form the initial population.
Step (3) Fitness function: Layout fitness is evaluated by
Step (4) Selection: Roulette wheel selection ensures that better layouts are more likely to be retained.
Step (5) Crossover: New individuals are generated via single-point crossover between gene strings.
Step (6) Variation: Genes are randomly flipped (0 ↔ 1) with a mutation rate of 0.03.
To ensure solution robustness, the GA is executed multiple times. Convergence of optimal layouts across runs indicates good stability.
3.5. Optimization Results and Analysis of Signage Layout
Given the complex structure of cruise ships, the theater area is chosen as the case scenario. Signage plays a critical role during emergency evacuation, especially under smoky conditions where clear guidance is crucial. This study utilizes MATLAB R2022a to optimize the layout across scenarios with and without smoke concentrations. Figure 12 illustrates the results of 5000 iterations for Control group 1, Experimental group 1, and Experimental group 2 under different evacuation scenarios. The red lines in the graphs indicate the iteration results. Notably, all cases achieved convergence within 1500 iterations, demonstrating the efficiency of the algorithm and its applicability to the problem.
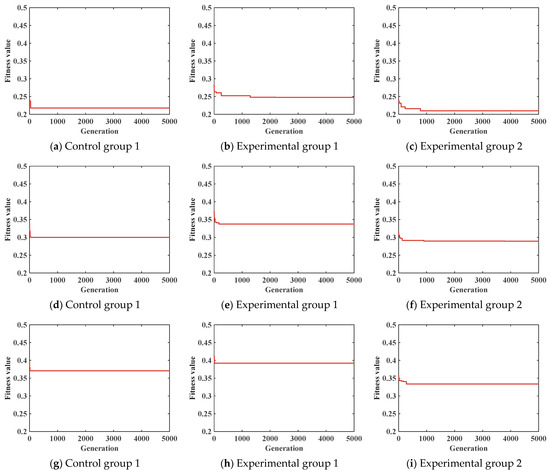
Figure 12.
Genetic algorithm iteration results: (a–c) correspond to scenario 1; (d–f) correspond to scenario 2; (g–i) correspond to scenario 3.
Figure 13 presents signage layouts for smoke-free, mild-smoke, and heavy-smoke scenarios. As smoke concentration increases, signage tends to cluster around intersections and long corridors, as these locations offer broader guidance coverage. Furthermore, under the same smoke conditions, a higher proportion of elderly passengers leads to denser signage placement, improving directional continuity. Though the layouts of experimental group 2 and control group 1 appear similar, the average spacing in group 2 is smaller, reflecting the elderly’s greater need for frequent visual cues. Conversely, fewer signs are needed when the majority are younger due to their broader field of vision. This also reflects the similarity between the young group and the middle-aged group in guiding the demand during the evacuation process, while the elderly group is the focus that needs more attention.
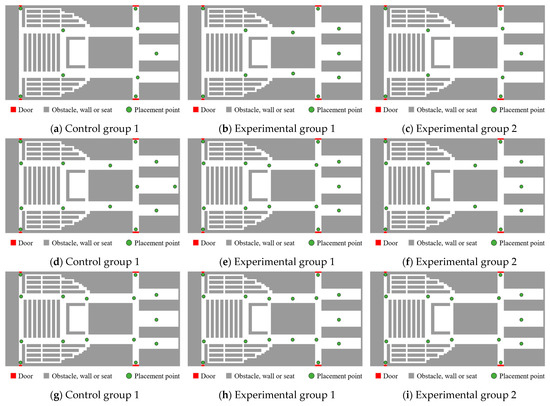
Figure 13.
Different scenario signage layouts; (a–c) correspond to scenario 1 (smoke-free); (d–f) correspond to scenario 2 (mild smoke); (g–i) correspond to scenario 3 (heavy smoke).
Table 4 summarizes signage counts across scenarios. As the smoke concentration increases, the number of signage will also increase. This shows that when the smoke affects the passenger’s vision, more signage is needed to guide the evacuation direction. In addition, in the same scenario, the increase in the proportion of the elderly group will lead to an increase in the number of signage required to ensure the continuity of direction guidance during the evacuation of the elderly. When the proportion of the young group increases, the number of signage decreases due to their wider vision.

Table 4.
Number of signage placements in different scenarios and groups, (pcs).
4. Simulation Experiments
Real-world experiments under emergency evacuation scenarios are often infeasible. Section 3 identified the optimal layout of evacuation signage and validated its effectiveness through simulation. Building upon these results, this section conducts a sensitivity analysis of key parameters in the optimization model, including weight coefficients, proportion of different populations, and field of view ranges. In particular, to account for variations in passengers’ visual range, this paper simulates the effects of different smoke concentrations under emergency conditions on visibility.
4.1. Validation of Optimization Results
To verify the effectiveness of the signage layout for the evacuation process, three groups were established: one group was the control group without the signage layout (control group 2), and the other two groups were randomly generated signage layout groups (experimental group 4, experimental group 5). To minimize the impact of outliers, each scenario was simulated 100 times under consistent conditions, as detailed in Table 5. The aim was to evaluate whether signage deployment leads to improved evacuation efficiency. The results of the comparative experiment are shown in Figure 14, and the median values of the time steps of the three groups of experiments are 231, 210, and 213.5, respectively. The time step median values of experimental group 4 and experimental group 5 are lower than those of control group 2, and the maximum and minimum values of experimental group 4 and experimental group 5 are also smaller than those of control group 2. These findings confirm that the presence of signage significantly enhances evacuation performance.

Table 5.
Experimental variable settings.
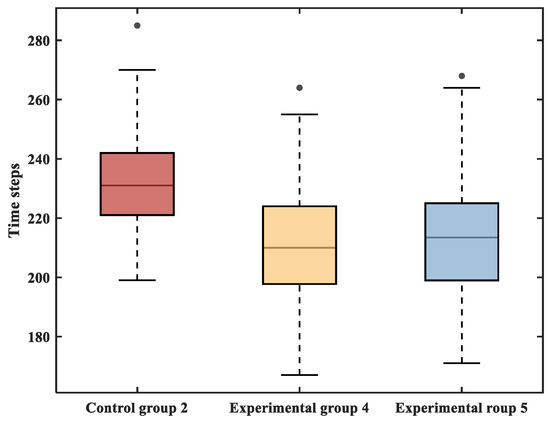
Figure 14.
Comparison experiment of cases with and without signage.
4.2. Sensitivity Analysis
4.2.1. Sensitivity Analysis of Weight Coefficient in the Objective Function
The weight coefficient in the objective function plays a critical role in balancing the trade-off between signage effectiveness and cost efficiency. A higher emphasizes cost-efficiency, whereas a lower prioritizes evacuation performance. To explore this sensitivity, simulations were conducted with three values of α: 0.8 (Experimental group 6), 0.5 (Control group 1), and 0.2 (Experimental group 7), with all other parameters held constant (Table 6). Using a genetic algorithm, the optimal signage layouts for the three scenarios were determined, and the results are illustrated in Figure 15. The number of signs deployed in Experimental group 6, Control group 1, and Experimental group 7 were 6, 9, and 14, respectively. Signage quantity is highly sensitive to α, but this sensitivity decreases as increases.

Table 6.
Experimental variable settings.
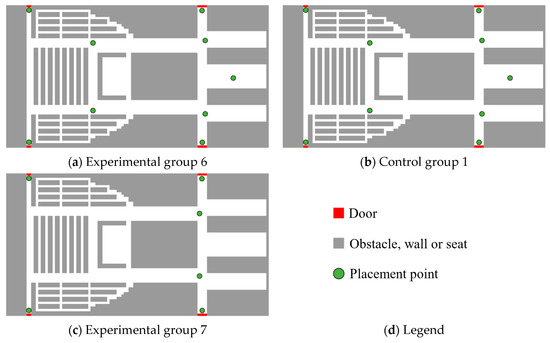
Figure 15.
Signage layout of each group.
Building on the optimal layouts, simulation experiments were performed to assess evacuation efficiency under different weight coefficients. As shown in Figure 16, the evacuation completion times were 219, 206, and 198 time steps for Experimental group 6, Control group 1, and Experimental group 7, respectively. These results show that lowering enhances evacuation efficiency. However, as decreases, further improvements in evacuation efficiency become increasingly difficult.
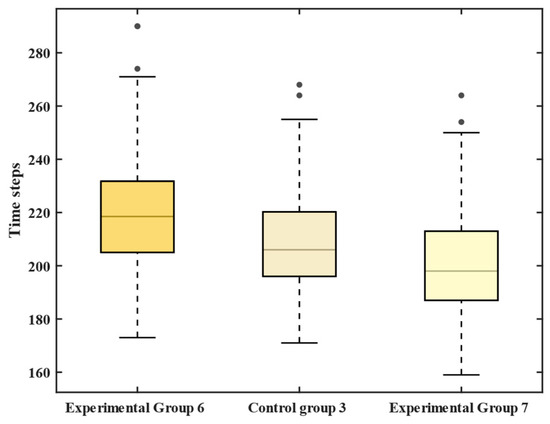
Figure 16.
ET of each group.
In summary, moderately reducing the weight coefficient α and increasing the number of evacuation signs can enhance evacuation efficiency. Nevertheless, as decreases further, marginal improvements become more difficult to achieve. In practice, it is challenging to simultaneously minimize cost and maximize evacuation efficiency. Therefore, a reasonable compromise should be made based on the safety requirements of the specific environment.
4.2.2. Sensitivity Analysis of the Proportion of Different Populations
To investigate the effect of the demographic composition on evacuation dynamics, three groups were designed with different age distributions: Control group 1, Experimental group 1, and Experimental group 2. Their performance in scenario 1 was analyzed at three critical time points—, , and —to capture evolving congestion patterns (Figure 17).
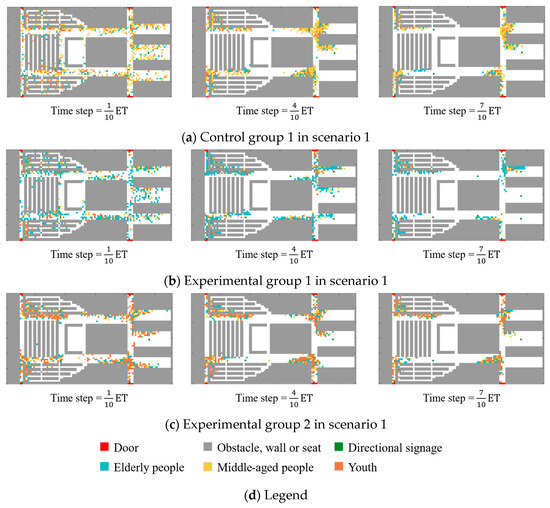
Figure 17.
Distribution of different age groups in scenario 1.
When the time step is ET, it can be found that the number of young groups in Figure 17c is larger. Although it moves faster and can go farther at the same time, it has the shortest congestion time at each crossroad. When the time step is ET, the congestion is significantly aggravated compared with the previous moment in Figure 17a,c, and the crowd gradually presents an “arched” distribution. Especially in crossroad 3 and crossroad 4, “arched” congestion is particularly prominent. In contrast, Figure 17b has no obvious “arched” congestion phenomenon, but there is a phenomenon where the elderly group queues to leave. This phenomenon suggests that due to the inconvenience of the legs and feet of the elderly group, they cannot immediately move to the left front or the right front. The influence of dense crowds and the choice of the shortest path result in the queue evacuation of the elderly group. The resulting orderly queueing behavior aligns with real-world elderly evacuation dynamics.
At ET, the “arched” congestion in Figure 17c is significantly reduced. In Figure 17a, although the “arched” congestion of crossroad 3 and crossroad 4 has been reduced, it still maintains a certain existence. In contrast, there was no obvious “arched” congestion in the experimental group 2.
Figure 18 and Table 7 show that the longest time step required for the experimental group 1 to complete the evacuation is 218 steps, followed by 206 steps for the control group 1, and the shortest evacuation time step for the experimental group 2 is 186 steps. These results indicate that a higher proportion of young passengers accelerates overall movement. Although arched congestion appears earlier in this group, it resolves more quickly. Conversely, a higher proportion of elderly passengers reduces the severity of congestion through queuing behavior, but extends the total evacuation time. Compared with Experimental group 2, evacuation duration increased by 5.82% and 17.20% for Control group 1 and Experimental group 1, respectively.
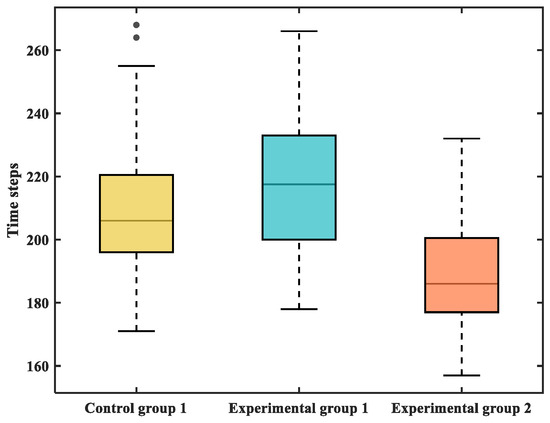
Figure 18.
Evacuation time steps of different groups in scenario 1.

Table 7.
Time steps to complete evacuation, ET (time steps).
Simulation results for other scenarios exhibit similar patterns and trends. Scenario 1 is selected as the most representative case for detailed analysis, as illustrated in Figure 19.
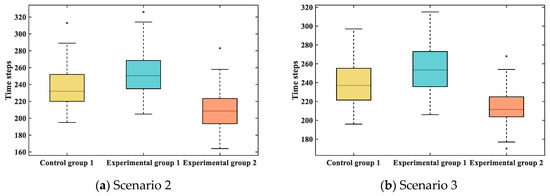
Figure 19.
Evacuation time steps of different groups in scenario 2 and scenario 3.
4.2.3. Sensitivity Analysis of Different Smoke Concentrations
Variations in smoke concentration influence passengers’ visual range and, consequently, evacuation dynamics. This section explores the effects of visual range under three smoke scenarios (Scenario 1, 2, and 3). The analysis focuses on two key time points—ET and ET—which effectively illustrate the progression of evacuation congestion (Figure 20).
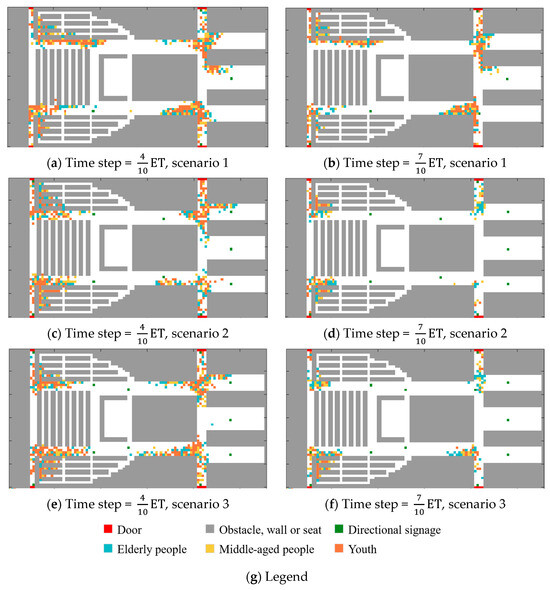
Figure 20.
Experimental group 2 in different scenarios.
As shown in Figure 20, when the time step is ET, the passenger field of view has a significant impact on the degree of evacuation congestion. In scenario 1 (Figure 20a), where the visual range is relatively large, passengers receive more signage information. Although enhanced guidance provides clearer movement directions and reduces disorganized behavior, it also results in faster movement. This accelerates the convergence of passenger flow, particularly at key intersections such as Intersection 3 and Intersection 4, thereby intensifying congestion. At the same time, Figure 20b also reveals a similar pattern: the convergence of high-speed passenger flow increases the proportion of total evacuation time occupied by congestion during evacuation.
In contrast, scenario 2 (Figure 20c,d) presents a reduced visual range due to mild smoke conditions. With less signage information available, passengers receive directional cues only within a limited range. Upon exiting this range, the lack of additional guidance results in irregular or suboptimal movement paths, increasing detours, and travel distance. This phenomenon mimics a deceleration effect. Particularly at Intersections 3 and 4, slower and more dispersed movement forms a moderate flow convergence, reducing the severity of congestion compared to scenario 1.
In the heavy smoke environment shown in Figure 20e,f, the influence range of the visual field and signage is extremely limited, and the opportunity for passengers to enter the guidance range of signage during evacuation is also greatly reduced. In such a situation of a lack of information, passengers lack clear direction guidance. Although passengers still have the basic trend of moving to the exit, their movements become disorderly due to the lack of clear guidance information. This lack of directionality leads to a decrease in efficiency during the evacuation process, notably at Intersections 3 and 4.
These results underscore that the visual range plays a decisive role in determining congestion levels. A wide field of view facilitates faster movement, which may inadvertently worsen bottlenecks at intersections. Conversely, an overly restricted visual field impairs directional awareness, slows down evacuation speed, increases detour likelihood, and ultimately contributes to congestion. The underlying mechanism lies in the passengers’ reliance on signage: when visible, signage enables efficient movement; when absent, passengers hesitate, scan for cues, and move more cautiously. This mirrors real-world behavior where individuals slow down to search for visual guidance and only accelerate after confirming the correct direction.
In addition, as shown in Figure 21, as the smoke concentration in the scenario increases, that is, the passenger’s field of view shrinks, the time step required to complete the evacuation gradually increases, and the evacuation efficiency also decreases. As shown in Figure 21a, the time steps required to complete the evacuation in scenarios 1–3 are 206, 232, and 237, respectively. The average field of view in scenario 2 is reduced by approximately 69.0% compared to scenario 1, resulting in a 12.6% increase in evacuation time. A further 23.6% reduction in visual range from scenario 2 to scenario 3 leads to a 2.2% increase in time steps.
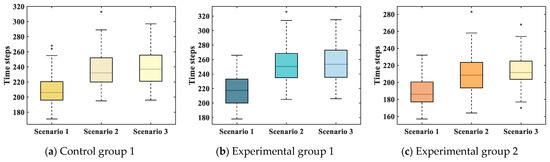
Figure 21.
Evacuation time steps of different groups under different scenarios.
This trend is consistent across all groups, as shown in Table 7. Experimental group 1 and group 2 also exhibit increased evacuation time with decreasing visual range. The findings confirm that a reduced visual field impairs evacuation performance, primarily by delaying passengers’ access to directional cues. Although wide visual fields may increase localized congestion, the enhanced directional efficiency they afford ultimately results in faster overall evacuation. This indicates that the impact of visual field on evacuation efficiency outweighs that of congestion alone.
5. Conclusions
This study proposes a cellular automata model that incorporates the age structure of passengers to simulate evacuation dynamics in enclosed ship environments. The model accounts for variations in passengers’ visual field ranges and signage influence zones across different age groups. It quantitatively integrates the static potential field, signage attraction field, and direction guidance factor to reflect realistic evacuation behavior. An optimal signage layout strategy is explored to achieve a balance between economic cost and evacuation effectiveness. The model further investigates the influence of passenger age composition and smoke concentration on evacuation performance. A simulation experiment is conducted using the main theater of the Adora Magic City cruise ship as a case scenario, incorporating varying proportions of age groups and smoke visibility conditions. The proposed model provides a practical decision-support tool for onboard signage layout by incorporating passenger mobility and visual asymmetries. This approach offers valuable guidance for improving signage design and enhancing evacuation efficiency in ship environments, thus supporting safety managers’ decision-making.
Based on the simulation results, the following conclusions can be drawn:
(1) A cellular automata model considering the age structure of passengers is successfully constructed. Passengers are categorized into three age-based groups, each defined by distinct movement speeds and visual field ranges. The model integrates static terrain features, signage attraction, and directional guidance, enabling the quantification of signage effectiveness across different passenger types. This enhances the model’s capacity to represent asymmetrical evacuation behavior in a symmetrical spatial environment.
(2) The study incorporates the light occlusion effect on signage visibility and formulates an optimization model aimed at maximizing guidance effectiveness while minimizing signage costs. Differences in signage recognition across age groups are embedded in the model, and the optimal signage layout is obtained using a genetic algorithm. The validity of this strategy is demonstrated through simulation.
(3) Evacuation experiments based on the cruise ship theater show that, under a constant age distribution, evacuation efficiency decreases as smoke concentration increases. At the same smoke level, scenarios with a higher proportion of elderly passengers exhibit lower evacuation efficiency, whereas scenarios dominated by younger passengers perform better. The proposed model effectively captures how differences in movement speed, visual range, and signage response across age groups influence evacuation outcomes. It is particularly applicable for evaluating emergency evacuation capacity in complex, smoke-filled environments such as cruise ships and terminals.
Although the simulation results validate the effectiveness of the proposed framework, several limitations remain, which provide avenues for future development. The current model focuses on a single-level theater and does not incorporate vertical evacuation routes or multi-deck configurations commonly found on cruise ships. Psychological and behavioral aspects, such as panic, stress, cognitive hesitation, or gender-based responses, are also not explicitly modeled, despite their potential influence during emergencies. Environmental dynamics, including fire spread, heat, toxic gases, ship motion, turbulence, and evolving smoke conditions, are simplified through static assumptions, limiting the model’s ability to reflect real-time degradation of visibility. Although signage occlusion by static obstacles is considered, the model does not yet simulate dynamic line-of-sight disruptions caused by moving crowds or physical interactions. Moreover, signage is assumed to be perfectly visible and interpretable whenever within a passenger’s field of vision, without accounting for recognition errors or guidance failures under stress. The cost model also adopts a simplified proxy, using the total number of signs as a stand-in for real-world economic factors such as installation, maintenance, and operational overhead. These simplifications may limit the model’s applicability in real-world scenarios.
Future work will aim to incorporate multi-deck layouts and vertical circulation, integrate cognitive behavior modeling, and adopt dynamic fire-smoke simulations to improve realism. Further, more detailed economic assessments and empirical validation, potentially through virtual reality-based human experiments, will be conducted to support the development of robust and adaptive signage layout strategies. Such improvements will support a more comprehensive assessment of evacuation efficiency in complex maritime environments.
Author Contributions
Conceptualization, Y.K. and K.J.; methodology, Y.K. and K.J.; software, K.J. and Y.K.; investigation, Y.K., K.J. and B.Y.; resources, Y.K., K.J. and R.L.; writing—original draft preparation, Y.K. and K.J.; writing—review and editing, Y.K., K.J. and H.X.; supervision, Y.K., K.J., B.Y. and H.X.; funding acquisition, Y.K. and K.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Shanghai Sailing Program (No. 23YF1416300).
Data Availability Statement
For data requests, please contact the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NE | Neighborhood cell |
| CA | Cellular automata |
| GA | Genetic algorithm |
| IMO | International Maritime Organization |
| MSC | Maritime Safety Committee |
| ET | Evacuation completion time steps |
References
- Cruise Lines International Association. 2024 State of the Cruise Industry Report. Cruise Lines International Association. Available online: https://cruising.org (accessed on 24 June 2025).
- The State Council of the People’s Republic of China. Over One Fifth of Chinese Population Older than 60, Says Official Report. The State Council of the People’s Republic of China. 2024. Available online: http://english.www.gov.cn/news/202410/12/content_WS6709cb9ac6d0868f4e8ebbda.html (accessed on 24 June 2025).
- AP News. China’s Aging Population Fuels ‘Silver Economy’ Boom, But Profits Can Prove Elusive. AP News, 2023. Available online: https://apnews.com/article/b81916bc8fea7b9f251ec8565941e692 (accessed on 24 June 2025).
- Moussaïd, M.; Helbing, D.; Theraulaz, G. How simple rules determine pedestrian behavior and crowd disasters. Proc. Natl. Acad. Sci. USA 2011, 108, 6884–6888. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Guo, F.; Kuang, H.; Geng, Z.; Fan, Y. An extended cost potential field cellular automaton model for pedestrian evacuation considering the restriction of visual field. Phys. A Stat. Mech. Appl. 2019, 515, 47–56. [Google Scholar] [CrossRef]
- Chraibi, M.; Steffen, B.; Tordeux, A. Analysis of pedestrian motion using Voronoi diagrams in complex geometries. In Traffic and Granular Flow 2019; Zuriguel, I., Garcimartin, A., Cruz, R., Eds.; Springer Proceedings in Physics; Springer: Cham, Switzerland, 2020; Volume 252, pp. 35–48. [Google Scholar] [CrossRef]
- Borsche, R.; Meurer, A. Microscopic and macroscopic models for coupled car traffic and pedestrian flow. J. Comput. Appl. Math. 2019, 348, 356–382. [Google Scholar] [CrossRef]
- Aljamal, M.A.; Rakha, H.A.; Du, J.; El Shawarby, I. Comparison of microscopic and mesoscopic traffic modeling tools for evacuation analysis. In Proceedings of the 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; IEEE: New York, NY, USA, 2018; pp. 2321–2326. [Google Scholar]
- Huang, K.; Zheng, X.; Cheng, Y.; Yang, Y. Behavior-based cellular automaton model for pedestrian dynamics. Appl. Math. Comput. 2017, 292, 417–424. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Sun, C. Cellular Automaton Model for Pedestrian Evacuation Considering Impacts of Fire Products. Fire 2023, 6, 320. [Google Scholar] [CrossRef]
- Han, Y.; Liu, H. Modified social force model based on information transmission toward crowd evacuation simulation. Phys A Stat. Mech. Appl. 2017, 469, 499–509. [Google Scholar] [CrossRef]
- Benseghir, H.; Ibrahim, A.B.; Siddique, M.N.I.; Kabir, M.N.; Alginahi, Y.M. Modelling emergency evacuation from an industrial building under spreading fire using a social force model with fire dynamics. Mater. Today Proc. 2021, 41, 38–42. [Google Scholar] [CrossRef]
- Li, Y.; Chen, M.; Dou, Z.; Zheng, X.; Cheng, Y.; Mebarki, A. A review of cellular automata models for crowd evacuation. Phys. A Stat. Mech. Appl. 2019, 526, 120752. [Google Scholar] [CrossRef]
- Ha, S.; Ku, N.K.; Roh, M.I.; Lee, K.Y. Cell-based evacuation simulation considering human behavior in a passenger ship. Ocean Eng. 2012, 53, 138–152. [Google Scholar] [CrossRef]
- Hu, M.; Cai, W.; Zhao, H. Simulation of Passenger Evacuation Process in Cruise Ships Based on A Multi-Grid Model. Symmetry 2019, 11, 1166. [Google Scholar] [CrossRef]
- Zhong, G.; Zhai, G.; Chen, W. Evacuation simulation of multi-story buildings during earthquakes based on improved cellular automata model. J. Asian Archit. Build. Eng. 2023, 22, 1007–1027. [Google Scholar] [CrossRef]
- Lu, L.; Chan, C.Y.; Wang, J.; Wang, W. A study of pedestrian group behaviors in crowd evacuation based on an extended floor field cellular automaton model. Transp. Res. Part C Emerg. Technol. 2017, 81, 317–329. [Google Scholar] [CrossRef]
- Wang, G.N.; Chen, T.; Chen, J.W.; Deng, K.; Wang, R.D. Simulation of crowd dynamics in pedestrian evacuation concerning panic contagion: A cellular automaton approach. Chin. Phys. B 2022, 31, 060402. [Google Scholar] [CrossRef]
- Tao, R.; Ren, H.; Yang, X.; Wang, D.; Sun, J. Smoke Simulation with Detail Enhancement in Ship Fires. J. Mar. Sci. Eng. 2025, 13, 101. [Google Scholar] [CrossRef]
- Ventikos, N.P.; Sotiralis, P.; Annetis, M.; Podimatas, V.C.; Boulougouris, E.; Stefanidis, F.; Chatzinikolaou, S.; Maccari, A. The Development and Demonstration of an Enhanced Risk Model for the Evacuation Process of Large Passenger Vessels. J. Mar. Sci. Eng. 2023, 11, 84. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, H.; Shi, J.; Geng, J. Evacuation simulation of a passenger ship fire based on a modified cellular automaton. Adv. Theory Simul. 2023, 6, 2300141. [Google Scholar] [CrossRef]
- Chen, M.; Wu, K.; Zhang, H.; Han, D.; Guo, M. A ship evacuation model considering the interaction between pedestrians based on cellular automata. Ocean Eng. 2023, 281, 114644. [Google Scholar] [CrossRef]
- Chen, M.; Guo, M.; Han, D.; Yuan, L.; Li, Y.; Wu, K. A pedestrian evacuation model for a ship’s flat multi-exit large space under fire environment. Ocean Eng. 2024, 309, 118570. [Google Scholar] [CrossRef]
- Sun, J.; Guo, Y.; Li, C.; Lo, S.; Lu, S. An experimental study on individual walking speed during ship evacuation with the combined effect of heeling and trim. Ocean Eng. 2018, 166, 396–403. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Loughney, S.; Yang, Z.; Wang, Y.; Wang, J. An experimental analysis of evacuees’ walking speeds under different rolling conditions of a ship. Ocean Eng. 2021, 233, 108997. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Wang, J.; Loughney, S.; Yang, Z.; Gao, X. Experimental study on individual walking speed during emergency evacuation with the influence of ship motion. Phys. A Stat. Mech. Appl. 2021, 562, 125369. [Google Scholar] [CrossRef]
- Chen, J.; Ma, J.; Lo, S. Modelling pedestrian evacuation movement on a swaying ship. In Traffic and Granular Flow’15; Springer: Cham, Switzerland, 2016; pp. 297–304. [Google Scholar] [CrossRef]
- International Maritime Organization (IMO). Guidelines for Evacuation Analysis for New and Existing Passenger Ships; MSC.1/Circ.1533; IMO: London, UK, 2016. [Google Scholar]
- Couasnon, P.; de Magnienville, Q.; Wang, T.; Claramunt, C. A multi-agent system for the simulation of ship evacuation. In Web and Wireless Geographical Information Systems; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; pp. 63–74. [Google Scholar] [CrossRef]
- Li, Y.; Cai, W.; Kana, A.A.; Atasoy, B. Modelling route choice in crowd evacuation on passenger ships. Int. J. Marit. Eng. 2021, 163, A2. [Google Scholar] [CrossRef]
- Chen, C.; Lu, T. An extended model for crowded evacuation considering stampede on inclined staircases. Simul. Model. Pract. Theory 2024, 135, 102978. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, B. Ageing vision and falls on Multi-Speed Heterogeneous Crowd Evacuation with Asymmetric Competitiveness. Symmetry 2025, 17, 298. [Google Scholar] [CrossRef]
- Han, H.; Lan, G.; Song, H.; Yi, C.; Gu, D.; Du, J. Evacuation efficiency and survival rate of bent-over walking during horizontal cabin fire evacuation. Ocean Eng. 2024, 313, 119590. [Google Scholar] [CrossRef]
- Ng, C.T.; Cheng, T.C.E.; Levner, E.; Kriheli, B. Optimal bi-criterion planning of rescue and evacuation operations for marine accidents using an iterative scheduling algorithm. Ann. Oper. Res. 2021, 296, 407–420. [Google Scholar] [CrossRef]
- Xie, Q.; Zhang, S.; Wang, J.; Lo, S.; Guo, S.; Wang, T. A surrogate-based optimization method for the issuance of passenger evacuation orders under ship fires. Ocean Eng. 2020, 209, 107456. [Google Scholar] [CrossRef]
- Chen, C.; Li, Q.; Kaneko, S.; Liu, Y. Location optimization algorithm for emergency signs in public facilities and its application to a single-floor supermarket. Fire Saf. J. 2009, 44, 113–120. [Google Scholar] [CrossRef]
- Wan, Z.; Zhou, T.; Tang, Z.; Pan, Y.; Zhang, L. Smart design for evacuation signage layout for exhibition halls in exhibition buildings based on visibility. ISPRS Int. J. Geo-Inf. 2021, 10, 806. [Google Scholar] [CrossRef]
- Xu, H.H.; Guo, R.Y. Passenger emergency evacuation from bus carriage: Results from realistic data and modeling simulations. J. Manag. Sci. Eng. 2022, 7, 530–549. [Google Scholar] [CrossRef]
- Xu, H.H.; Guo, R.Y.; Wu, P.Y. Pedestrian evacuation dynamics considering information guidance. Int. J. Mod. Phys. C 2023, 34, 2350063. [Google Scholar] [CrossRef]
- Zhang, Z.; Jia, L.; Qin, Y. Optimal number and location planning of evacuation signage in public space. Saf. Sci. 2017, 91, 132–147. [Google Scholar] [CrossRef]
- UNESCO Institute for Statistics. Percentage of Persons in a Specific Age Group That Are Employed in Cultural Occupations. UIS Glossary, 2025. Available online: https://uis.unesco.org/en/glossary-term/percentage-persons-specific-age-group-are-employed-cultural-occupations (accessed on 16 June 2025).
- Saftari, L.N.; Kwon, O.S. Ageing vision and falls: A review. J. Physiol. Anthropol. 2018, 37, 11. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Ma, Y.; Chen, M.; Wang, K.; Zheng, K. A survey of crowd evacuation on passenger ships: Recent advances and future challenges. Ocean Eng. 2022, 263, 112403. [Google Scholar] [CrossRef]
- Adora Cruises. About Adora Cruises. Adora Cruises. 2025. Available online: https://www.adoracruises.com/adora (accessed on 24 July 2025).
- Jeon, G.-Y.; Kim, J.-Y.; Hong, W.-H.; Augenbroe, G. Evacuation performance of individuals in different visibility conditions. Build. Environ. 2011, 46, 1094–1103. [Google Scholar] [CrossRef]
- Chu, J.C.; Yeh, C.Y. Emergency evacuation guidance design for complex building geometries. J. Infrastruct. Syst. 2012, 18, 288–296. [Google Scholar] [CrossRef]
- Ministry of Public Security of the People’s Republic of China. Code for Fire Protection Design of Tall Buildings (GB50045-2015); China Planning Press: Beijing, China, 2015. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).