PSO-Driven Scalable Dual-Adaptive PV Array Reconfiguration Under Partial Shading
Abstract
1. Introduction
1.1. Motivation
1.2. Problem Statement
1.3. Related Works
1.4. Proposed Approach
1.5. Contributions
- PSO-Based Optimization Approach for Dual-Adaptive PV Arrays: This study introduces the application of PSO to the reconfiguration problem of dual-adaptive PV arrays for the first time, enabling fast and efficient optimization in an exponentially expanding solution space. It also marks the initial demonstration that GA becomes infeasible for large-scale dual-adaptive configurations due to excessive convergence times, and proposes a PSO-based alternative that meets real-time applicability requirements.
- Fast Convergence and Efficient Optimization in Large Solution Spaces with PSO: Against the exponentially expanding connection possibilities as the number of rows increases, PSO’s particle-based and accelerated convergence capabilities enable efficient optimization in larger solution spaces.
- Enhanced Adaptive Panel-Fixed Panel Matching Efficiency: In dual-adaptive structures, the expanded matching space is more effectively explored through PSO’s flexible solution search mechanism. This leads to more balanced row currents across various shading scenarios, unlocking the potential for higher power efficiency.
- Scalable and Real-Time Reconfiguration Time for Large PV Arrays: With the PSO-based optimization approach, the reconfiguration time for large-scale PV arrays remains at real-time applicable levels, even in the exponentially growing solution space caused by an increasing number of rows in dual-adaptive PV arrays. This enhances the practical applicability of reconfiguration methods in large PV systems and allows faster adaptation to dynamic shading conditions.
- Adaptability of Metaheuristic Approaches to Solution Space Expansion: This study highlights the potential of fast-converging metaheuristic algorithms like PSO to provide scalable reconfiguration solutions for large-scale PV arrays, addressing the solution space expansion inherent in dual-adaptive structures.
1.6. Paper Organization
2. Materials and Methods
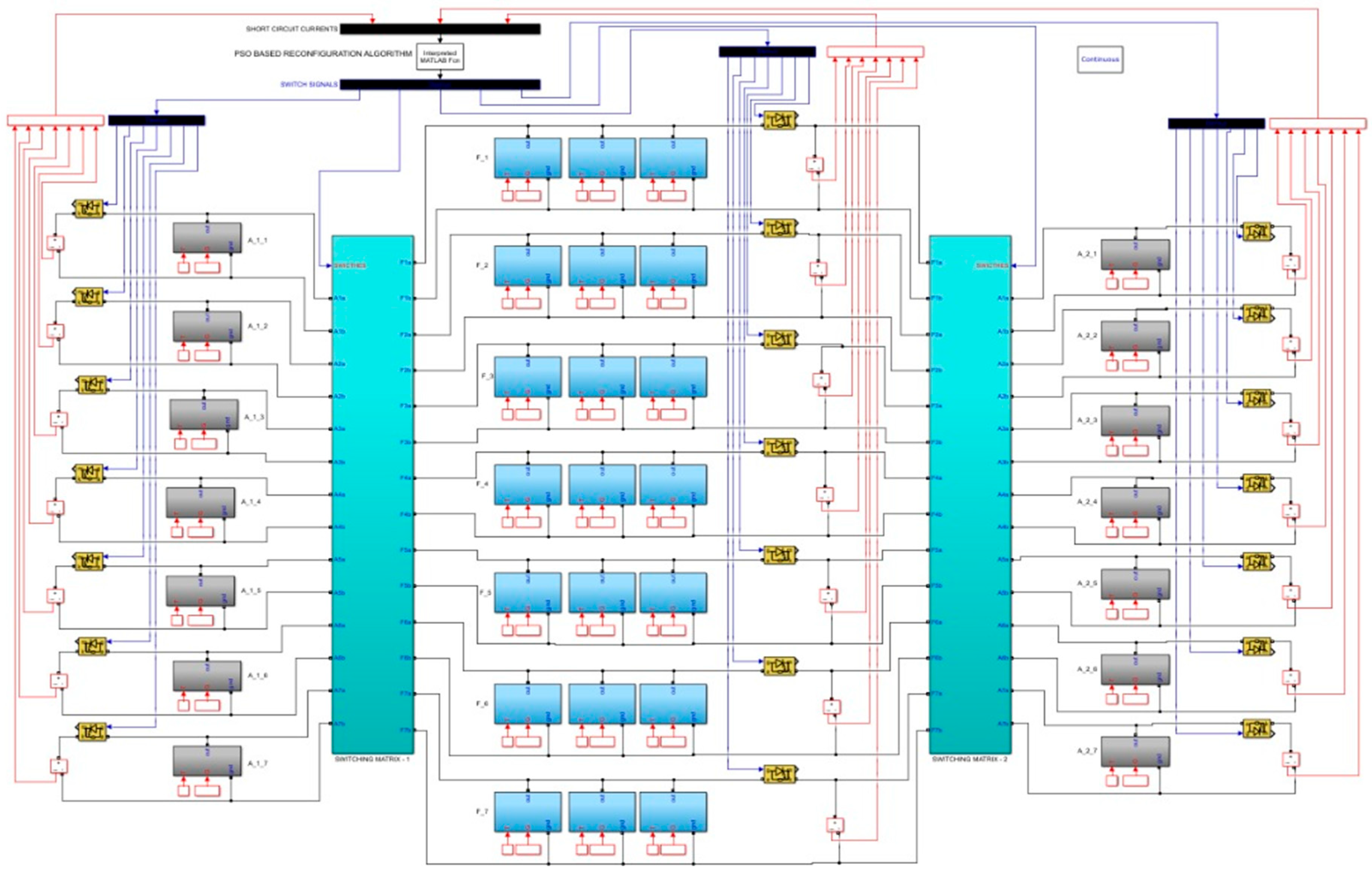
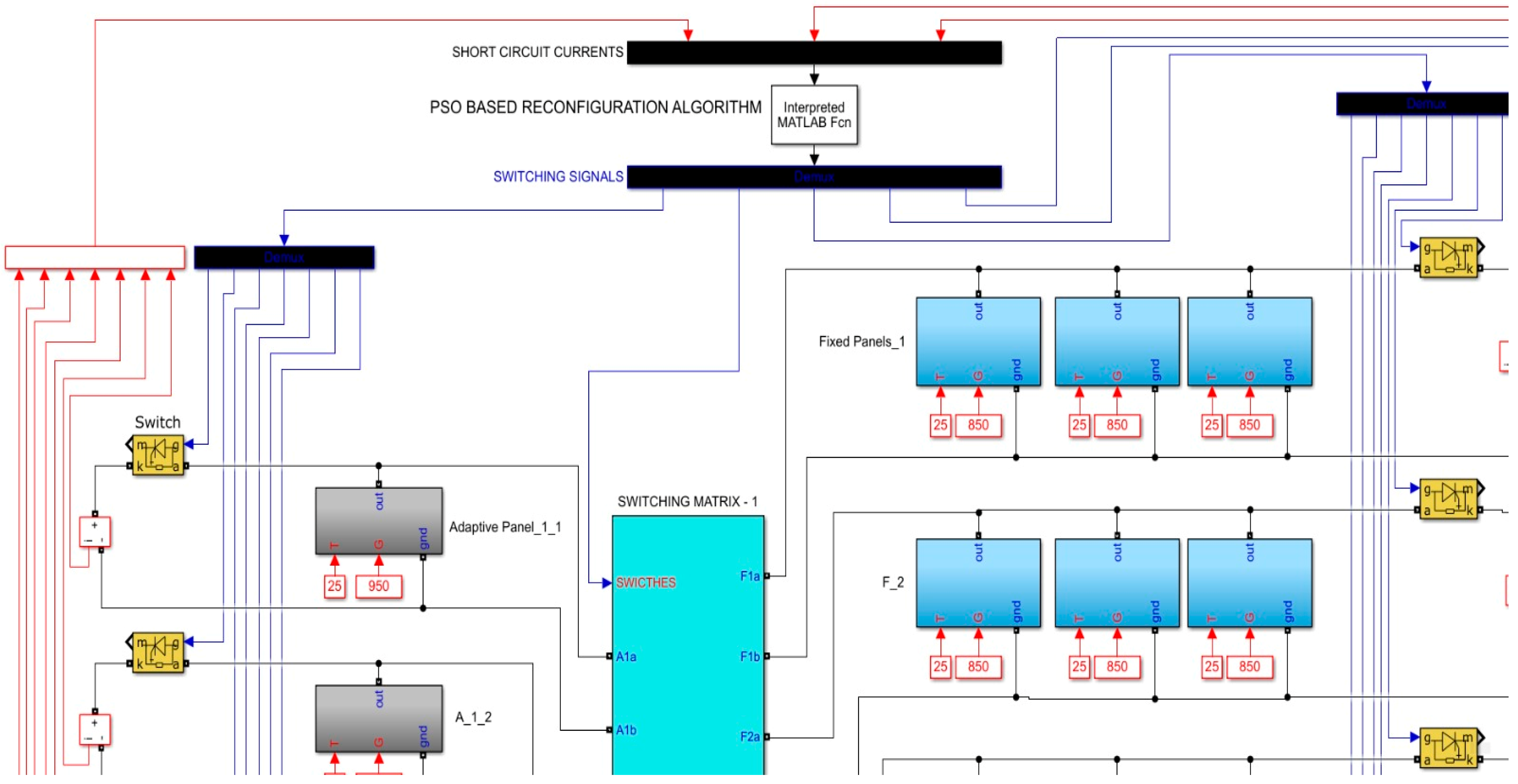
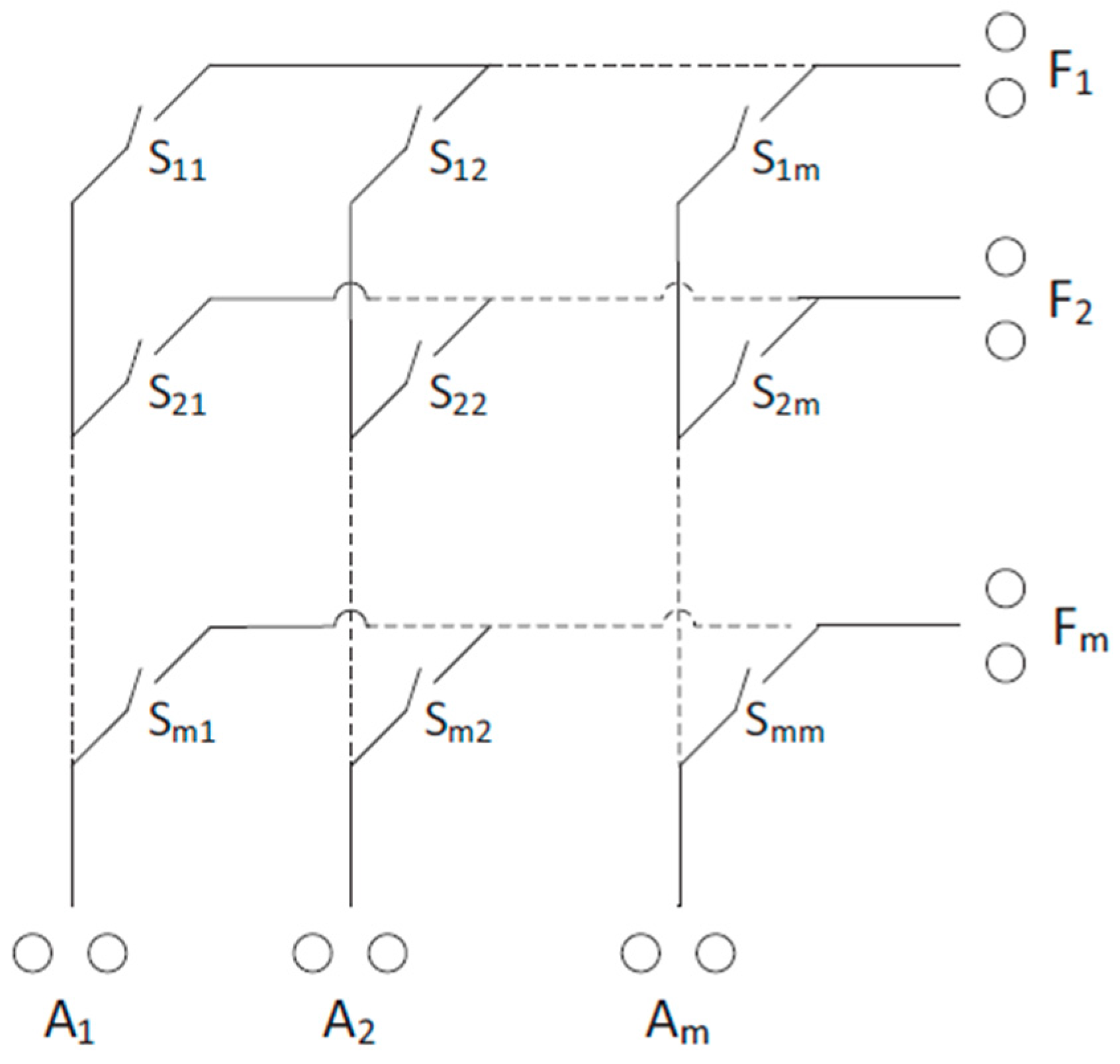
2.1. Dual-Adaptive PV Panel Architecture
2.2. Reconfiguration Process of PV Arrays Involving Adaptive Parts
- The current of each row is determined (according to the minimum current in the row).
- The voltages of all panels in each row are summed.
- The total power output of the array is obtained by multiplying the current of each row by the sum of the row voltages.
- The short-circuit currents of each row are measured using sensors.
- For each connection configuration, the row currents are determined.
- The differences between the row currents are calculated, and the minimum of these differences is taken as the CVI value.
2.3. Particle Initialization and Encoding
2.3.1. Binary Representation of All Feasible Connection Combinations Between Fixed and Adaptive Panels
2.3.2. Representation of Connections with Bit Strings
2.3.3. Exponential Growth of the Solution Space in Dual-Adaptive Structures
2.4. Particle Swarm Space Generator Unit
2.5. Particle Validity Check and Elimination of Invalid Configurations
| Algorithm 1. check_validity() |
| Input: x: particle, N: adaptive panel array length, ROW: fixed panel array length Output: valid (1: valid, 0: invalid) 1: set fixed_array ← zero_array(N), k ← 1 2: for i = 1 to N×ROW 3: fixed_array (k) ← fixed_array (k)+ x(i) 4: k ← k + 1 5: if k > N then k ← 1 endif 6: endfor 7: set product ← 1 8: for t = 1 to N 9: product = product*fixed_array(t) 10: endfor 11: if product = 1 then valid ← 1 12: else valid ← 0 endif 13: return valid |
2.6. PSO-Controller: Optimization of the Connection Configuration
2.6.1. Particle Representation and Position-Velocity Updates
2.6.2. PSO-Based Controller Module
| Algorithm 2. PSO-Based Controller |
| Inputs: fixed_panel_array, adaptive_panel_array, numParticles, maxiteration, w, c1, c2 Output: optimum_configuration, best_particle, best_fitness (CVI ← max-min) 1: N ← length(adaptive_panel_array) 2: ROW ← length(fixed_panel_array) 3: particleLength ← NxROWx2 4: foreach particle i = 1 to numParticles //particleLength-dimensional cartesian product of binary values 5: ← randomly initialize from {0, 1}^particleLength //particleLength-dimensional real-valued vector space 6: ← randomly initialize from ℝ^particleLength 7: ← 8: ← evaluate_fitness (, N, ROW, adaptive_panel_array, fixed_panel_array) 9: endforeach 10: gbest ← argmax() 11: for iter = 1 to maxiteration 12: for particle i = 1 to numParticles 13: foreach dimension d in particleLength 14: [d] ← w × [d] + //update velocity 15: c1 × rand() × ([d] − [d]) + 16: c2 × rand() × (gbest[d] − [d]) 17: s ← 1/(1 + exp(-[d])) //sigmoid 18: if rand() < s then [d] ← 1 //update position 19: else [d] ← 0 endif 20: endforeach 21: if check_validity(, N, ROW) then 22: ←evaluate_fitness(, N, ROW, adaptive_panel_array, fixed_panel_array) 23: if > fitness() then ← endif 24: if > fitness(gbest) then gbest ← endif 25: endif 26: endfor 27: endfor 28: optimum_configuration ← gbest 29: best_particle ← gbest 30: best_fitness ← fitness(gbest) 31: return optimum_configuration, best_particle, CVI ← best_fitness |
2.7. Current Variation Index (CVI)
| Algorithm 3. evaluate_fitness(): CVI calculation |
| Input: particle, A: Adaptive array, F: Fixed array, N: length of A, ROW: length of F, Output: fitness_value (CVI) 1: set k ← 0, Fk ← 0, n ← 1 2: initialize FA ← zero_array(ROW) 3: for i = 1 to NxROW 4: k ← k + 1 5: Fk ← Fk+ particle(i)xA(k) 6: if k equal N then 7: FA(n) ← Fk + F(n) 8: k ← 0, Fk ← 0, n ← n + 1 9: endif 10: endfor 11: rowSum ← sum(FA), smallest ← min(FA) 12: largest ← max(FA), fitness ← (largest − smallest)//best fitness 13: return CVI ← fitness |
[A1 A2 A3 A4 A5 A6] [A1 A2 A3 A4 A5 A6] [A1 A2 A3 A4 A5 A6]
6-bit + 6-bit + 6-bit
[A1 A2 A3 A4 A5 A6] [A1 A2 A3 A4 A5 A6] [A1 A2 A3 A4 A5 A6]
1 0 1 0 0 1 0 1 0 1 0 0 0 0 0 0 1 0
3. Simulation Results
3.1. Structural Properties of Simulation Scenarios and Hardware Environment
3.2. Core Simulation Results of PSO-Based Reconfiguration for Dual-Adaptive PV Systems
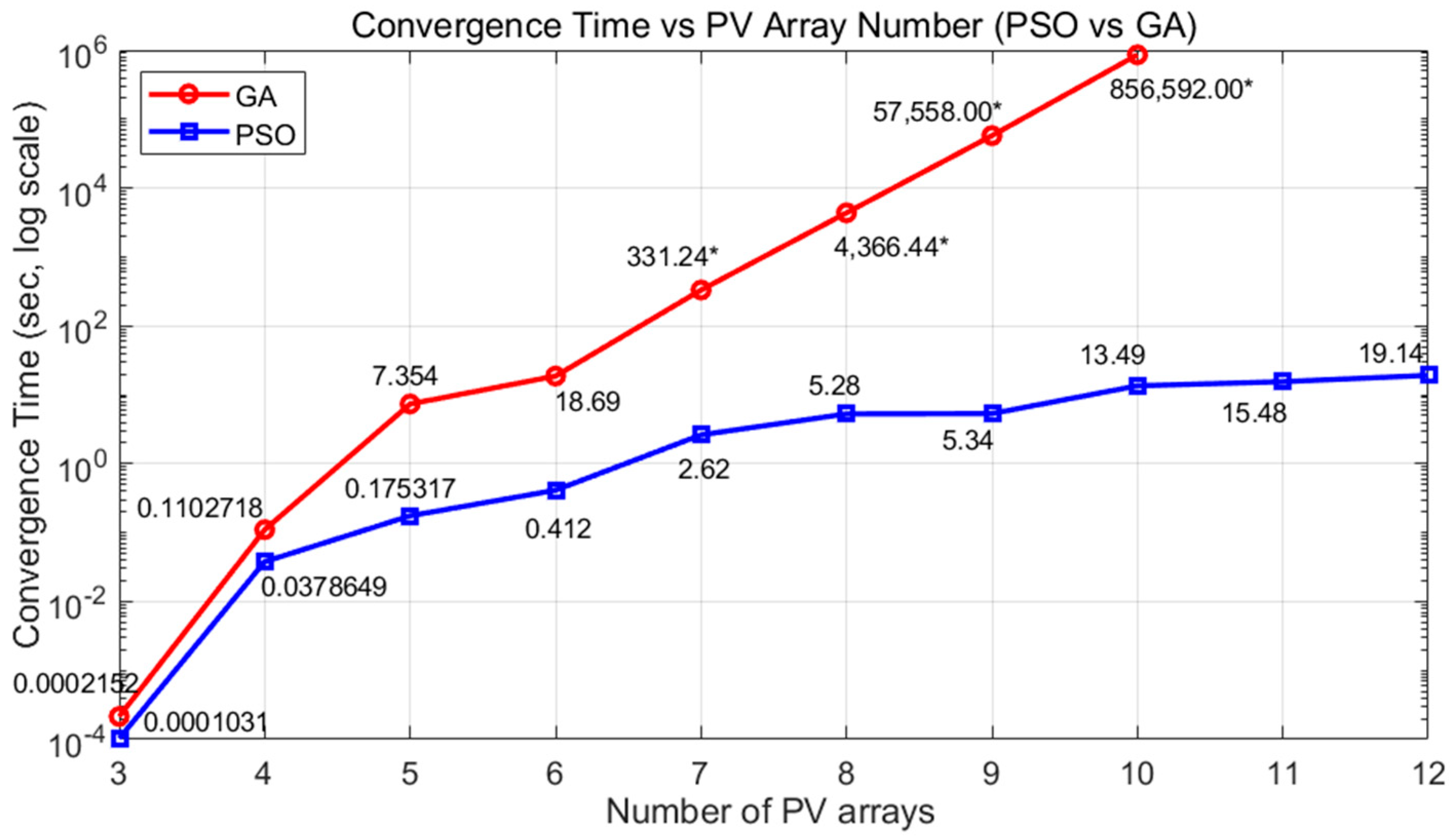
3.3. Scalability Comparison of PSO and GA Based on Reconfiguration Times in Large-Scale Dual-Adaptive PV Arrays
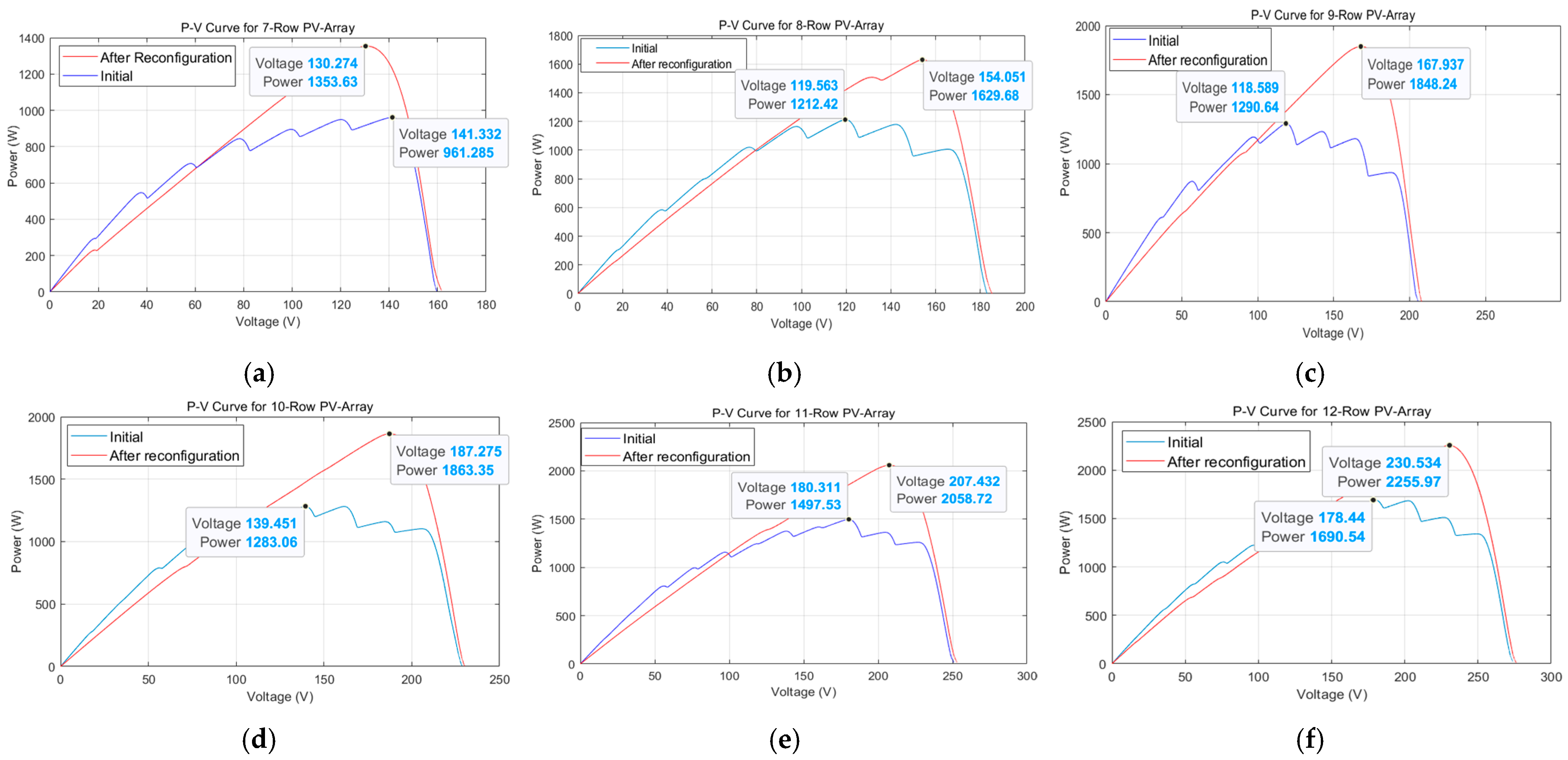
3.4. Power Efficiency Improvement After PSO-Based Reconfiguration for High-Row PV Arrays
4. Discussion
4.1. Limitations/Trade-Offs with the PSO-Based Dual-Adaptive Reconfiguration Method
4.2. Evaluation of Efficiency, Reliability, Cost and Scalability of Dual-Adaptive PV Arrays
4.3. Optimization Parameters and Strategy for Real-Time Reconfiguration Applications
4.4. Tracking Time and Dynamic Efficiency
4.5. Algorithm Selection and Optimization Strategy
4.6. Real-World Deployment Considerations of PSO-Based Reconfiguration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Pulido-Mancebo, J.S.; López-Luque, R.; Fernández-Ahumada, L.M.; Ramírez-Faz, J.C.; Gómez-Uceda, F.J.; Varo-Martínez, M. Spatial distribution model of solar radiation for agrivoltaic land use in fixed PV plants. Agronomy 2022, 12, 2799. [Google Scholar] [CrossRef]
- Malathy, S.; Ramaprabha, R. Reconfiguration strategies to extract maximum power from photovoltaic array under partially shaded conditions. Renew. Sustain. Energy Rev. 2018, 81, 2922–2934. [Google Scholar] [CrossRef]
- Parlak, K.S. FPGA based new MPPT (maximum power point tracking) method for PV (photovoltaic) array system operating partially shaded conditions. Energy 2014, 68, 399–410. [Google Scholar] [CrossRef]
- Rani, B.I.; Ilango, G.S.; Nagamani, C. Enhanced power generation from pv array under partial shading conditions by shade dispersion using sudoku configuration. IEEE Trans. Sustain. Energy 2013, 4, 594–601. [Google Scholar] [CrossRef]
- El-Dein, M.S.; Kazerani, M.; Salama, M. An optimal total cross tied interconnection for reducing mismatch losses in photovoltaic arrays. IEEE Trans. Sustain. Energy 2012, 4, 99–107. [Google Scholar] [CrossRef]
- Ajmal, A.M.; Babu, T.S.; Ramachandaramurthy, V.K.; Yousri, D.; Ekanayake, J.B. Static and dynamic reconfiguration approaches for mitigation of partial shading influence in photovoltaic arrays. Sustain. Energy Technol. Assess. 2020, 40, 100738. [Google Scholar] [CrossRef]
- Nguyen, D.; Lehman, B. An adaptive solar photovoltaic array using model-based reconfiguration algorithm. IEEE Trans. Ind. Electron. 2008, 55, 2644–2654. [Google Scholar] [CrossRef]
- Velasco-Quesada, G.; Guinjoan-Gispert, F.; Piqué-López, R.; Román-Lumbreras, M.; Conesa-Roca, A. Electrical pv array reconfiguration strategy for energy extraction improvement in grid-connected pv systems. IEEE Trans. Ind. Electron. 2009, 56, 4319–4331. [Google Scholar] [CrossRef]
- Anjum, S.; Mukherjee, V. Static and dynamic reconfiguration strategies for reducing partial shading effects in photovoltaic array: A comprehensive review. Energy Technol. 2022, 10, 2200098. [Google Scholar] [CrossRef]
- Bapurao, K.A.; Mikkili, S.; Bonthagorla, P.K. A review on static reconfiguration techniques of solar PV to mitigate Mismatch loss and minimize partial shading effect. IETE J. Res. 2023, 69, 6356–6386. [Google Scholar] [CrossRef]
- Zeeshan, M.; Islam, N.U.; Faizullah, F.; Khalil, I.U.; Park, J. A novel row index mathematical procedure for the mitigation of PV output power losses during partial shading conditions. Symmetry 2023, 15, 768. [Google Scholar] [CrossRef]
- Anjum, S.; Mukherjee, V.; Mehta, G. Hyper SuDoKu-based solar photovoltaic array reconfiguration for maximum power enhancement under partial shading conditions. J. Energy Resour. Technol. 2022, 144, 031302. [Google Scholar] [CrossRef]
- Pendem, S.R.; Sudhakar, A.V.V. Enhancement of Maximum Power in TCT PV Array through SuDoKU-based Reconfiguration Techniques under Partial Shading Conditions. In Proceedings of the IEEE IAS Global Conference on Renewable Energy and Hydrogen Technologies (GlobConHT), Male, Maldives, 11–12 March 2023; pp. 1–7. [Google Scholar]
- Fang, X.; Yang, Q. Dynamic reconfiguration of photovoltaic array for minimizing mismatch loss. Renew. Sustain. Energy Rev. 2024, 191, 114160. [Google Scholar] [CrossRef]
- Krishna, G.S.; Moger, T. A novel adaptive dynamic photovoltaic reconfiguration system to mitigate mismatch effects. Renew. Sustain. Energy Rev. 2021, 141, 110754. [Google Scholar] [CrossRef]
- Murugesan, P.; David, P.W.; Murugesan, P.; Solaisamy, N.K. One-step adaptive reconfiguration technique for partial shaded photovoltaic array. Sol. Energy 2023, 263, 111949. [Google Scholar] [CrossRef]
- Solaisamy, N.K.; David, P.W.; Murugesan, P. Performance improvement of partial shaded solar PV system using unbalanced adaptive dynamic reconfiguration technique. Renew. Energy 2025, 246, 122883. [Google Scholar] [CrossRef]
- Jazayeri, M.; Jazayeri, K.; Uysal, S. Adaptive photovoltaic array reconfiguration based on real cloud patterns to mitigate effects of non-uniform spatial irradiance profiles. Sol. Energy 2017, 155, 506–516. [Google Scholar] [CrossRef]
- Rao, P.S.; Ilango, G.S.; Nagamani, C. Maximum power from pv arrays using a fixed configuration under different shading conditions. IEEE J. Photovolt. 2014, 4, 679–686. [Google Scholar]
- Karaduman, Ö.; Parlak, K.Ş. A Dual-adaptive perspective on PV array reconfiguration with genetic algorithms under partial shading conditions. Appl. Sci. 2025, 15, 1762. [Google Scholar] [CrossRef]
- Merino, S.; Martinez, J.; Guzman, F.; Lara, J.d.D.; Guzman, R.; Sanchez, F.; Heredia, J.R.; Sidrach de Cardona, M. Dynamic reconfiguration to optimize energy production on moving photovoltaic panels. Sustainability 2023, 15, 10858. [Google Scholar] [CrossRef]
- Ajmal, A.M.; Ramachandaramurthy, V.K.; Naderipour, A.; Ekanayake, J.B. Comparative analysis of two-step GA-based PV array reconfiguration technique and other reconfiguration techniques. Energy Convers. Manag. 2021, 230, 113806. [Google Scholar] [CrossRef]
- Durango-Flórez, M.; González-Montoya, D.; Trejos-Grisales, L.A.; Ramos-Paja, C.A. PV array reconfiguration based on genetic algorithm for maximum power extraction and energy impact analysis. Sustainability 2022, 14, 3764. [Google Scholar] [CrossRef]
- Candela, R.; Di Dio, V.; Sanseverino, E.R.; Romano, P. Reconfiguration techniques of partial shaded PV systems for the maximization of electrical energy production. In Proceedings of the IEEE International Conference on Clean Electrical Power, Capri, Italy, 21–23 May 2007; pp. 716–719. [Google Scholar]
- Hou, S.; Zhu, W. Dynamic reconfiguration method of photovoltaic array based on improved HPSO combined with coefficient of variation. Electronics 2023, 12, 2744. [Google Scholar] [CrossRef]
- Parlak, K.S. PV array reconfiguration method under partial shading conditions. Int. J. Electr. Power Energy Syst. 2014, 63, 713–721. [Google Scholar] [CrossRef]
- Babu, T.S.; Ram, J.P.; Dragičević, T.; Miyatake, M.; Blaabjerg, F.; Rajasekar, N. Particle swarm optimization based solar PV array reconfiguration of the maximum power extraction under partial shading conditions. IEEE Trans. Sustain. Energy 2017, 9, 74–85. [Google Scholar] [CrossRef]
- Yousri, D.; Thanikanti, S.B.; Balasubramanian, K.; Osama, A.; Fathy, A. Multi-objective grey wolf optimizer for optimal design of switching matrix for shaded PV array dynamic reconfiguration. IEEE Access 2020, 8, 159931–159946. [Google Scholar] [CrossRef]
- Rajan, N.A.; Shrikant, K.D.; Dhanalakshmi, B.; Rajasekar, N. Solar PV array reconfiguration using the concept of Standard deviation and Genetic Algorithm. Energy Procedia 2017, 117, 1062–1069. [Google Scholar] [CrossRef]
- Zhang, J. ACP-MO: A novel metaheuristic optimization algorithm based on an advanced ceramic processing metaphor for optimization. Appl. Eng. Lett. 2025, 10, 109–124. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; pp. 4104–4108. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization: An overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Spampinato, C.; Valastro, S.; Calogero, G.; Smecca, E.; Mannino, G.; Arena, V.; Balestrini, R.; Sillo, F.; Ciná, L.; La Magna, A.; et al. Improved radicchio seedling growth under CsPbI3 perovskite rooftop in a laboratory-scale greenhouse for agrivoltaics application. Nat. Commun. 2025, 16, 2190. [Google Scholar] [CrossRef]

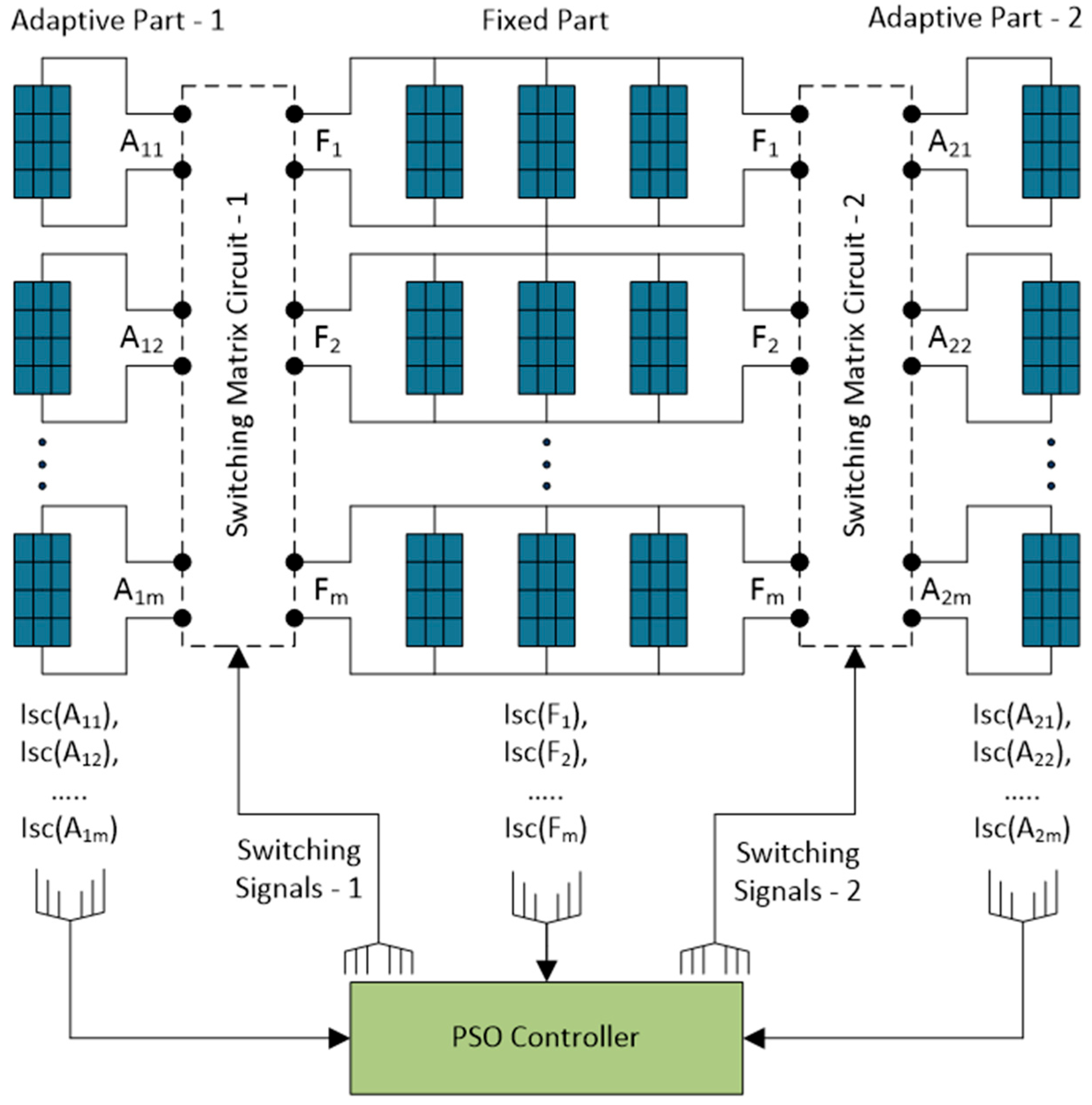
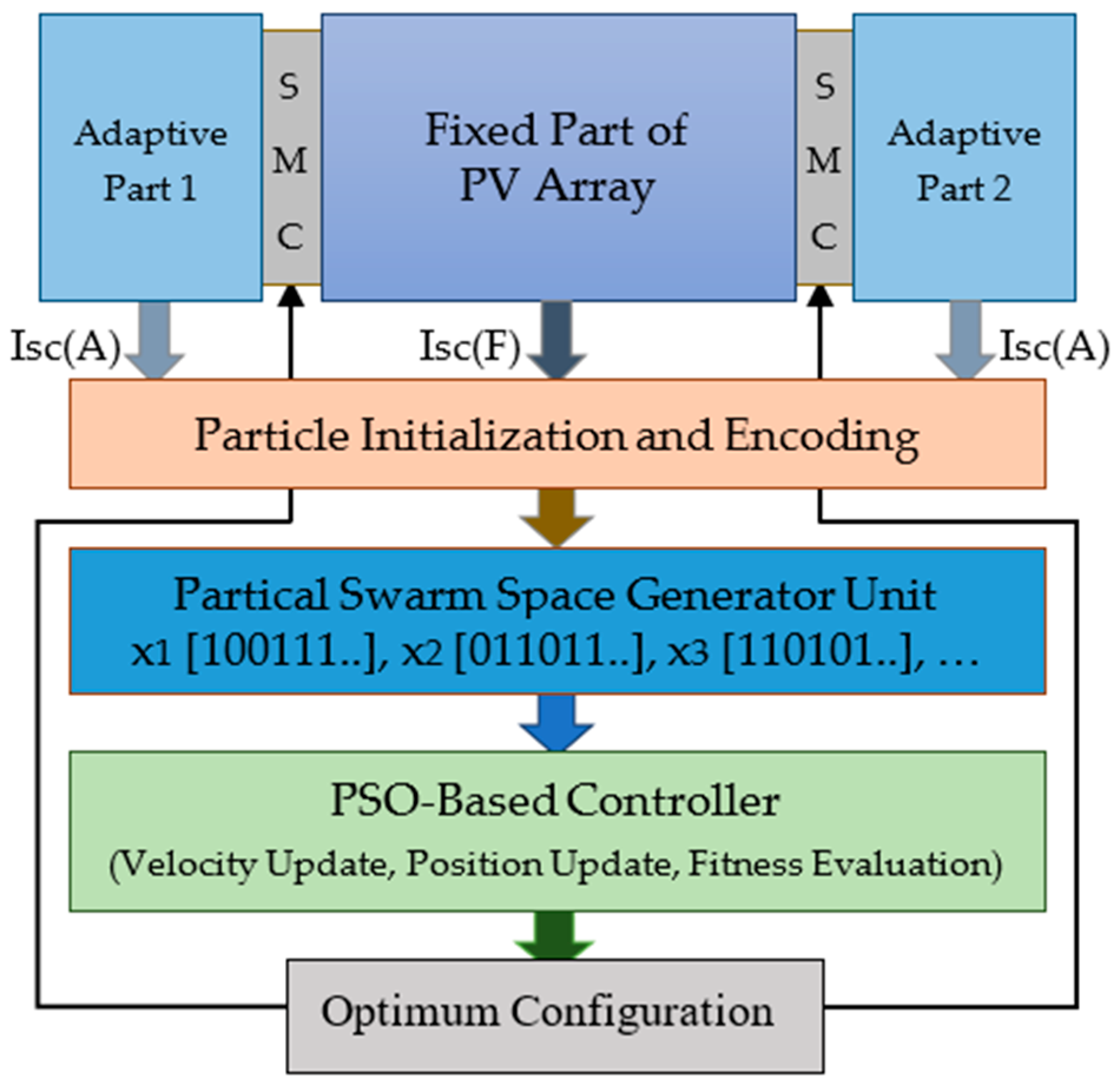
| Number of Array (m) | Calculation of All Connection Combinations for Single-Adaptive and Dual-Adaptive Structures |
|---|---|
| Single-Adaptive PV Array | |
| 3 | P= = 336 |
| 4 | P= P= 43,680 |
| 5 | P= P= 24,165,120 = 2.41 × |
| 6 | P= P= 751,408,320 = 7.51 × |
| 7 | P= P= 476,410,007,808,000 = 4.76 × |
| 12 | P= P= 21,943,955,209,199,862,746,410,706,867,184,116,563,968,000 = 2.19 × |
| Dual-Adaptive PV Array → P | |
| 3 | P= 249,984 = 2.49 × |
| 4 | P= 4,195,023,360 = 4.19 × |
| 5 | P1,114,942,319,124,480 = 1.114 × |
| 6 | P4,705,096,570,216,277,114,880 = 4.705 × |
| 7 | P316,506,657,532,245,270,854,601,277,440 = 3.165 × |
| 8 | P340,137,008,117,998,448,138,762,147,145,370,828,800 = 3.401 × |
| 9 | P5,845,203,768,943,535,666,720,547,888,464,255,925,327,904,112,640 = 5.845 × |
| 10 | P1,606,869,083,231,144,563,727,692,524,981,029,623,181,969,415,830,539,075,584,000 = 1.606 × |
| 11 | P7,067,295,584,827,156,804,193,336,349,785,776,849,625,446,302,806,824,559,065,457,296,932,864,000 = 7.067 × |
| 12 | P497,321,279,990,048,065,620,092,436,093,689,431,382,691,241,367,964,575,894,503,459,741,655,295,254,637,576,192,000 = 4.973 × |
| Fixed Panels | Adaptive Panels (for F1) | Adaptive Panels (for F2) | Adaptive Panels (for F3) |
|---|---|---|---|
| F1-F2-F3 | A1 A2 A3 A4 A5 A6 | A1 A2 A3 A4 A5 A6 | A1 A2 A3 A4 A5 A6 |
| 1 0 1 0 0 1 | 0 1 0 0 0 0 | 0 0 0 1 1 0 |
| Fixed Rows (F) | Adaptive Panels (A) | Length of Particle (bit) | Possible Assignments per F | Total Configurations |
|---|---|---|---|---|
| 3 | 6 | 18 | 26 = 64 | 643 = 262,144 |
| 4 | 8 | 32 | 28 = 256 | 2564 = ~4.2 × 109 |
| 5 | 10 | 50 | 210 = 1024 | 10245 = ~1.1 × 1015 |
| 6 | 12 | 72 | 212 = 4096 | 40966 = ~7.9 × 1021 |
| Config. Scenario | PV Array Number | Adaptive Part 1 (Iscn (A)) | Fixed Part (Iscn (F)) | Adaptive Part 2 (Iscn (A)) |
|---|---|---|---|---|
| Scen. 1 | 3 | A1 A2 A3 | F1 F2 F3 | A4 A5 A6 |
| [1.51, 1.51, 1.7] | [7, 9.06, 10.04] | [3.41, 3.79, 3.79] | ||
| Scen. 2 | 4 | A1 A2 A3 A4 | F1 F2 F3 F4 | A5 A6 A7 A8 |
| [1.13, 1.89, 2.65, 3] | [6.81, 7.92, 10.2, 11.37] | [2.65, 3.22, 3.79, 3.79] | ||
| Scen. 3 | 5 | A1 A2 A3 A4 A5 | F1 F2 F3 F4 F5 | A1 A2 A3 A4 A5 |
| [1.51, 1.89, 2.65, 3, 3.79] | [3.39, 5.29, 6.43, 7.16, 10.2] | [1.51, 2.27, 2.65, 2.65, 3.41] | ||
| Scen. 4 | 6 | A1 A2 A3 A4 A5 A6 | F1 F2 F3 F4 F5 F6 | A1 A2 A3 A4 A5 A6 |
| [1.13, 1.13, 1.51, 1.89, 3, 3.41] | [4.91, 7.19, 7.54, 9.41, 10.61, 10.99] | [1.13, 1.89, 1.89, 2.65, 3, 3.41] | ||
| Scen. 5 | 7 | A1 A2 A3 A4 A5 A6 A7 | F1 F2 F3 F4 F5 F6 F7 | A1 A2 A3 A4 A5 A6 A7 |
| [3, 3, 2.27, 1.89, 1.51, 1.13, 0.75] | [11.37, 10.99, 9.99, 8.3, 7.95, 6.05, 5.67] | [3.41, 3, 3, 2.27, 1.89, 1.51, 1.13] | ||
| Scen. 6 | 8 | A1 A2 A3 A4 A5 A6 A7 A8 | F1 F2 F3 F4 F5 F6 F7 F8 | A1 A2 A3 A4 A5 A6 A7A8 |
| [3.79, 3.79, 3, 3, 2.65, 2.65, 2.27, 1.51] | [10.61, 9.4, 8.65, 7.95, 8.65, 5.29, 4.15, 3.39] | [3.79, 3.41, 3, 3, 2.27, 1.51, 1.13, 1.13] | ||
| Scen. 7 | 9 | A1 A2 A3 A4 A5 A6 A7 A8 A9 | F1 F2 F3 F4 F5 F6 F7 F8 F9 | A1 A2 A3 A4 A5 A6 A7 A8 A9 |
| [0.75, 1.13, 1.51, 1.51, 1.89, 1.89, 3, 3.4, 3.41] | [3.77, 4.91, 6.05, 7.57, 8.3, 8.65, 10.23, 10.99, 11.37] | [0.75, 1.51, 1.51, 2.27, 2.65, 2.65, 3, 3.41, 3.41] | ||
| Scen. 8 | 10 | A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 | F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 | A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 |
| [0.75, 0.75, 1.13, 1.13, 1.13, 1.32, 1.89, 1.8, 2.27, 2.65] | [4.15, 5.1, 6.05, 6.92, 7.76, 8.84, 9.63, 10.8, 10.42, 10.99] | [0.75, 0.75, 1.13, 1.51, 1.51, 1.89, 2, 2.65, 2.84, 3] | ||
| Scen. 9 | 11 | A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 | F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 | A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 |
| [0.75, 0.75, 1.1, 3, 1.13, 1.51, 1.7, 2.27, 2.65, 2.84, 3, 3] | [4.34, 5.1, 6.05, 6.35, 7.19, 7.38, 7.95, 8.3, 9.63, 9.79, 10.11] | [0.75, 1.13, 1.51, 1.7, 1.7, 1.89, 2.27, 2.65, 2.84, 3, 3.22] | ||
| Scen. 10 | 12 | A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 | F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 | A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 |
| [0.75, 0.75, 1.13, 1.32, 1.7, 1.7, 2, 2.27, 2.65, 2.84, 3, 3] | [4.15, 5.1, 6.05, 6.73, 7.19, 7.38, 8.11, 8.4, 8.81, 9.82, 10.42, 10.8] | [0.75, 1.13, 1.51, 1.7, 1.89, 2, 2.27, 2.46, 2.65, 2.84, 3, 3.22] |
| Pop. Num. | w | c1 | c2 | CVI-Best Fitness | Conver. Time (s) | Configuration (F: Fixed, A: Adaptive Panels) | Expr. No |
|---|---|---|---|---|---|---|---|
| 50 | 0.5 | 1.6 | 1.6 | 1.65 | 3.287553 | F1->A13 F2->A14 F3->A5A11 F4->A1A12 F5->A4A9 F6->A3A7A8 F7->A2A6A10 | 1 |
| 50 | 0.5 | 1.6 | 1.8 | 1.48 | 1.522706 | F1->A13 F2->A7A14 F3->A11 F4->A1A12 F5->A6A9 F6->A3A5A8 F7->A2A4A10 | 2 |
| : | : | : | : | : | |||
| 50 | 0.5 | 2 | 2.2 | 1.92 | 0.187516 | F1->A7 F2->A14 F3->A4A13 F4->A1A12 F5->A6A9 F6->A3A8A11 F7->A2A5A10 | 12 |
| 50 | 0.5 | 2.2 | 1.6 | 1.86 | 0.903937 | F1->A7A13 F2->A14 F3->A1 F4->A4A12 F5->A6A9 F6->A5A8A11 F7->A2A3A10 | 13 |
| 50 | 0.5 | 2.2 | 1.8 | 0.95 | 1.674407 | F1->A13 F2->A4 F3->A11 F4->A3A7A12 F5->A6A9A14 F6->A1A8 F7->A2A5A10 | 14 |
| 50 | 0.5 | 2.2 | 2 | 2.06 | 1.458493 | F1->A14 F2->A3 F3->A4 F4->A5A12A13 F5->A6A7A9 F6->A1A8 F7->A2A10A11 | 15 |
| : | : | : | : | : | |||
| 50 | 0.9 | 1.6 | 1.6 | 1.86 | 0.101289 | F1->A7 F2->A3 F3->A4A13 F4->A1A14 F5->A6A9 F6->A5A8A12 F7->A2A10A11 | 33 |
| 50 | 0.9 | 1.6 | 1.8 | 1.38 | 2.908571 | F1->A13 F2->A3 F3->A4 F4->A1A12 F5->A6A9A14 F6->A5A8A11 F7->A2A7A10 | 34 |
| 50 | 0.9 | 1.6 | 2 | 1.29 | 0.481379 | F1->A13 F2->A3 F3->A11A14 F4->A2A12 F5->A4A9 F6->A5A6A8 F7->A1A7A10 | 35 |
| : | : | : | : | : | |||
| 50 | 0.9 | 2 | 2 | 0.98 | 1.371237 | F1->A13 F2->A4 F3->A11 F4->A1A12 F5->A6A7A9 F6->A3A5A8 F7->A2A10A14 | 43 |
| 50 | 0.9 | 2 | 2.2 | 1.65 | 1.641608 | F1->A7 F2->A14 F3->A5A11 F4->A1A12 F5->A4A9 F6->A3A6A8 F7->A2A10A13 | 44 |
| 50 | 0.9 | 2.2 | 1.6 | 0.8 | 2.191894 | F1->A6 F2->A3 F3->A1 F4->A4A7A12 F5->A9A13 F6->A5A8A11 F7->A2A10A14 | 45 |
| 50 | 0.9 | 2.2 | 1.8 | 1.14 | 1.395587 | F1->A7 F2->A3 F3->A11 F4->A1A12 F5->A6A9A14 F6->A4A8A13 F7->A2A5A10 | 46 |
| 50 | 0.9 | 2.2 | 2 | 1.83 | 1.924575 | F1->A7 F2->A14 F3->A4A13 F4->A3A11 F5->A1A9 F6->A6A8A12 F7->A2A5A10 | 47 |
| 50 | 0.9 | 2.2 | 2.2 | 1.87 | 2.273356 | F1->A13 F2->A11 F3->A3 F4->A1A12 F5->A4A6A9 F6->A5A8A14 F7->A2A7A10 | 48 |
| 80 | 0.5 | 1.6 | 1.6 | 1.57 | 5.212509 | F1->A13 F2->A4 F3->A6A7A14 F4->A9A12 F5->A1A11 F6->A3A5A8 F7->A2A10 | 49 |
| 80 | 0.5 | 1.6 | 1.8 | 1.1 | 0.678701 | F1->A6 F2->A13 F3->A5A7A14 F4->A2A4 F5->A3A11 F6->A1A8 F7->A9A10A12 | 50 |
| : | : | : | : | : | |||
| 80 | 0.5 | 2 | 2 | 0.78 | 1.945908 | F1->A13 F2->A12 F3->A2 F4->A5A9 F5->A3A7A11 F6->A1A8 F7->A4A6A10A14 | 59 |
| 80 | 0.5 | 2 | 2.2 | 1.18 | 1.257685 | F1->A6 F2->A7A12 F3->A5A14 F4->A4A9 F5->A2A11 F6->A1A8 F7->A3A10A13 | 60 |
| 80 | 0.5 | 2.2 | 1.6 | 1.09 | 2.858244 | F1->A6 F2->A12 F3->A5A13 F4->A2A4 F5->A3A11 F6->A1A8 F7->A7A9A10A14 | 61 |
| 80 | 0.5 | 2.2 | 1.8 | 1.15 | 4.205788 | F1->A6 F2->A13 F3->A4A14 F4->A3A9 F5->A1A11 F6->A5A8A12 F7->A2A7A10 | 62 |
| : | : | : | : | : | |||
| 80 | 0.7 | 2.2 | 2.2 | 1.39 | 1.320409 | F1->A3 F2->A5 F3->A7A13 F4->A2A12 F5->A9A11 F6->A1A8 F7->A4A6A10A14 | 80 |
| 80 | 0.9 | 1.6 | 1.6 | 1.52 | 3.085355 | F1->A6 F2->A11 F3->A4A13 F4->A5A9 F5->A1A7A12 F6->A2A8 F7->A3A10A14 | 81 |
| 80 | 0.9 | 1.6 | 1.8 | 2.22 | 0.967264 | F1->A6 F2->A7 F3->A5A13 F4->A2A12 F5->A3A9 F6->A1A8 F7->A4A10A11A14 | 82 |
| 80 | 0.9 | 1.6 | 2 | 1.1 | 1.256684 | F1->A13 F2->A12 F3->A5A6 F4->A7A9A14 F5->A3A11 F6->A1A8 F7->A2A4A10 | 83 |
| 80 | 0.9 | 1.6 | 2.2 | 1.1 | 2.573879 | F1->A6 F2->A12 F3->A10 F4->A5A9 F5->A3A11 F6->A1A8A14 F7->A2A4A7A13 | 84 |
| : | : | : | : | : | |||
| 80 | 0.9 | 2.2 | 1.6 | 1.85 | 3.252322 | F1->A5 F2->A7 F3->A12 F4->A3A9 F5->A11A13A14 F6->A1A6A8 F7->A2A4A10 | 93 |
| 80 | 0.9 | 2.2 | 1.8 | 1.13 | 0.577279 | F1->A6 F2->A12 F3->A5A13 F4->A2A14 F5->A3A11 F6->A1A7A8 F7->A4A9A10 | 94 |
| 80 | 0.9 | 2.2 | 2 | 1.59 | 0.484637 | F1->A6A13 F2->A4 F3->A5A14 F4->A9A12 F5->A3A11 F6->A1A8 F7->A2A7A10 | 95 |
| 80 | 0.9 | 2.2 | 2.2 | 1.84 | 0.885317 | F1->A6 F2->A12 F3->A5A14 F4->A2A9 F5->A3A11 F6->A1A8 F7->A4A7A10A13 | 96 |
| 100 | 0.5 | 1.6 | 1.6 | 0.8 | 6.119977 | F1->A14 F2->A3 F3->A9 F4->A4A11 F5->A1A7A13 F6->A5A8A12 F7->A2A6A10 | 97 |
| 100 | 0.5 | 1.6 | 1.8 | 0.75 | 1.641237 | F1->A14 F2->A12 F3->A9 F4->A3A4A7 F5->A1A13 F6->A5A10A11 F7->A2A6A8 | 98 |
| : | : | : | : | : | |||
| 100 | 0.5 | 2.2 | 2 | 0.8 | 2.999429 | F1->A14 F2->A3 F3->A9 F4->A5A6A11 F5->A10A13 F6->A1A8 F7->A2A4A7A12 | 111 |
| 100 | 0.5 | 2.2 | 2.2 | 0.81 | 1.385247 | F1->A4 F2->A12 F3->A9 F4->A6A7A11 F5->A1A13 F6->A3A5A8 F7->A2A10A14 | 112 |
| 100 | 0.7 | 1.6 | 1.6 | 0.84 | 1.117886 | F1->A4 F2->A3 F3->A9 F4->A6A11A14 F5->A1A13 F6->A5A8A12 F7->A2A7A10 | 113 |
| 100 | 0.7 | 1.6 | 1.8 | 1.87 | 0.780059 | F1->A14 F2->A3 F3->A9 F4->A6A11A12 F5->A1A13 F6->A5A7A8 F7->A2A4A10 | 114 |
| : | : | : | : | : | |||
| 100 | 0.9 | 2 | 1.6 | 0.8 | 2.080138 | F1->A13 F2->A5 F3->A9 F4->A4A6A12 F5->A1A3 F6->A8A11A14 F7->A2A7A10 | 137 |
| 100 | 0.9 | 2 | 1.8 | 0.69 | 2.619923 | F1->A14 F2->A12 F3->A9 F4->A1A6A7 F5->A3A11 F6->A4A5A8 F7->A2A10A13 | 138 |
| 100 | 0.9 | 2 | 2 | 1.49 | 2.688837 | F1->A4 F2->A14 F3->A9 F4->A2A11 F5->A1A6 F6->A3A5A8 F7->A7A10A12A13 | 139 |
| 100 | 0.9 | 2 | 2.2 | 1.86 | 0.76399 | F1->A14 F2->A3 F3->A9 F4->A6A7A11 F5->A4A5A13 F6->A1A10A12 F7->A2A8 | 140 |
| 100 | 0.9 | 2.2 | 1.6 | 0.84 | 2.399468 | F1->A4 F2->A3 F3->A9 F4->A6A11A14 F5->A1A12 F6->A5A8A13 F7->A2A7A10 | 141 |
| 100 | 0.9 | 2.2 | 1.8 | 1.22 | 1.160882 | F1->A11 F2->A12 F3->A1 F4->A6A9 F5->A3A13A14 F6->A4A5A8 F7->A2A7A10 | 142 |
| 100 | 0.9 | 2.2 | 2 | 1.54 | 1.450744 | F1->A4 F2->A3 F3->A9 F4->A5A6A11 F5->A1A12 F6->A7A8A13 F7->A2A10A14 | 143 |
| 100 | 0.9 | 2.2 | 2.2 | 1.92 | 5.65964 | F1->A4 F2->A1 F3->A9 F4->A5A6A11 F5->A2A13 F6->A7A8A12 F7->A3A10A14 | 144 |
| Configuration Scenario | Number of PV Array | Best Fitness (CVI) | Best Configuration |
|---|---|---|---|
| Scenario 1 | 3 | 0.17 | F1->A1A3A6 F2->A2A4 F3->A5 |
| Scenario 2 | 4 | 0.35 | F1->A7A8 F2->A1A3A4 F3->A2A5 F4->A6 |
| Scenario 3 | 5 | 0.37 | F1->A1A5A8 F2->A3A10 F3->A4A7 F4->A2A9 F5->A6 |
| Scenario 4 | 6 | 0.37 | F1->A4A5A11 F2->A1A9A10 F3->A8A12 F4->A6 F5->A2A7 F6->A3 |
| Scenario 5 | 7 | 0.69 | F1->A14 F2->A12 F3->A9 F4->A1A6A7 F5->A3A11 F6->A4A5A8 F7->A2A10A13 |
| Scenario 6 | 8 | 0.81 | F1->A13 F2->A4 F3->A5A8 F4->A9A15 F5->A1 F6->A3A12A16 F7-> A6A7A11 F8->A2A10A14 |
| Scenario 7 | 9 | 1.55 | F1->A4A8A11A16 F2->A9A17 F3->A1A13A14 F4->A7A15 F5->A18 F6->A2A6A10 F7->A3 F8->A12 F9->A5 |
| Scenario 8 | 10 | 1.74 | F1->A7A9A19 F2->A10A15A18 F3->A4A14A16 F4->A6A12A20 F5->A5A13A17 F6->A8 F7->A1 F8->A11 F9->A2 F10->A3 |
| Scenario 9 | 11 | 1.92 | F1->A6A8A22 F2->A7A21 F3->A9A15A16 F4->A10A18 F5->A2A20 F6-> A11 F7->A4A17 F8->A5A12A13 F9->A19 F10->A1A14 F11->A3 |
| Scenario 10 | 12 | 3.96 | F1->A6A10A20 F2->A9A11A21 F3->A12A19 F4->A4A15A16 F5->A3A17 F6->A24 F7->A8A18 F8->A7A22 F9->A5A13 F10->A1 F11->A2A23 F12->A14 |
| PV Array Configuration | Number of PV Array | Convergence Time by Best Fitness (GA) (s) | Convergence Time by Best Fitness (PSO) (s) |
|---|---|---|---|
| Scenario 1 | 3 | 0.0002152 | 0.0001031 |
| Scenario 2 | 4 | 0.1102718 | 0.0378649 |
| Scenario 3 | 5 | 7.354132 | 0.1753172 |
| Scenario 4 | 6 | 18.68502 | 0.4122550 |
| Scenario 5 | 7 | 331.241 * | 2.6199226 |
| Scenario 6 | 8 | 4366.437 * | 5.2776048 |
| Scenario 7 | 9 | ~57,000 * | 5.3355047 |
| Scenario 8 | 10 | ~850,000 * | 13.494531 |
| Scenario 9 | 11 | ~10,000,000 * | 15.484648 |
| Scenario 10 | 12 | ~100,000,000 * | 19.142176 |
| PV Array Configuration | Number of PV Array | Best Fitness (CVI) | Convergence Time by Best Fitness (s) | Increased Power Efficiency Ratio | ||
|---|---|---|---|---|---|---|
| Initial Power (W) | Power After Reconfiguration (W) | Power Efficiency (%) | ||||
| Scenario 5 | 7 | 0.69 | 2.619 | 961.28 | 1353.63 | 40.74 |
| Scenario 6 | 8 | 0.81 | 5.277 | 1212.42 | 1629.68 | 34.41 |
| Scenario 7 | 9 | 1.55 | 5.335 | 1290.64 | 1848.24 | 43.20 |
| Scenario 8 | 10 | 1.74 | 13.494 | 1283.06 | 1863.35 | 45.22 |
| Scenario 9 | 11 | 1.92 | 15.484 | 1497.53 | 2058.72 | 37.47 |
| Scenario 10 | 12 | 3.96 | 19.142 | 1692.71 | 2255.98 | 33.27 |
| Number of PV Array | Convergence Times of Algorithms (s) | ||||
|---|---|---|---|---|---|
| GA | DE | BAT | QPSO | PSO | |
| 7 | 331.241 | 9.33675250 | 4.82014190 | 5.38766820 | 2.6199226 |
| 8 | 4366.437 | 10.40745000 | 5.22518400 | 6.40975730 | 5.2776048 |
| 9 | ~57,000 | 11.22065790 | 5.81700080 | 7.50478160 | 5.3355047 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karaduman, Ö.; Parlak, K.Ş. PSO-Driven Scalable Dual-Adaptive PV Array Reconfiguration Under Partial Shading. Symmetry 2025, 17, 1365. https://doi.org/10.3390/sym17081365
Karaduman Ö, Parlak KŞ. PSO-Driven Scalable Dual-Adaptive PV Array Reconfiguration Under Partial Shading. Symmetry. 2025; 17(8):1365. https://doi.org/10.3390/sym17081365
Chicago/Turabian StyleKaraduman, Özgür, and Koray Şener Parlak. 2025. "PSO-Driven Scalable Dual-Adaptive PV Array Reconfiguration Under Partial Shading" Symmetry 17, no. 8: 1365. https://doi.org/10.3390/sym17081365
APA StyleKaraduman, Ö., & Parlak, K. Ş. (2025). PSO-Driven Scalable Dual-Adaptive PV Array Reconfiguration Under Partial Shading. Symmetry, 17(8), 1365. https://doi.org/10.3390/sym17081365







