Decarbonizing China’s Express Freight Market Using High-Speed Rail Services and Carbon Taxes: A Bi-Level Optimization Approach
Abstract
1. Introduction
2. Literature Review
| Reference | Measures to Promote Modal Shift | Model |
|---|---|---|
| Wang et al. [12] | Carbon tax on shippers | Two-stage Stackelberg gaming model |
| Bouchery et al. [13] | Control total carbon emissions | Multi-objective optimization |
| Tao et al. [14] | Fix subsidy to shippers | Random coefficient logit model |
| Choi et al. [15] | Containerization and taxes | System dynamics model |
| Kundu and Sheu [16] | Subsidy to shippers | Sequential game-theoretic model |
| Chen et al. [17] | Joint tax–subsidy policy | Mathematical program with complementarity constraints |
| Guo et al. [18] | Pricing, road construction, increasing railway service level, and railway subsidy | System dynamic modeling and Monte Carlo simulation |
| Nassar et al. [19] | Fiscal and regulatory measures and infrastructure investments | System Dynamics approach |
| Takman and Gonzalez-Aregall [20] | Subsidies and regulations | Ex post evaluations |
| Masone et al. [7] | Incentive schemes | Simulate shipper’s mode choice behavior |
| Shen et al. [21] | Pricing of railway | Mixed logit model |
3. Methodology
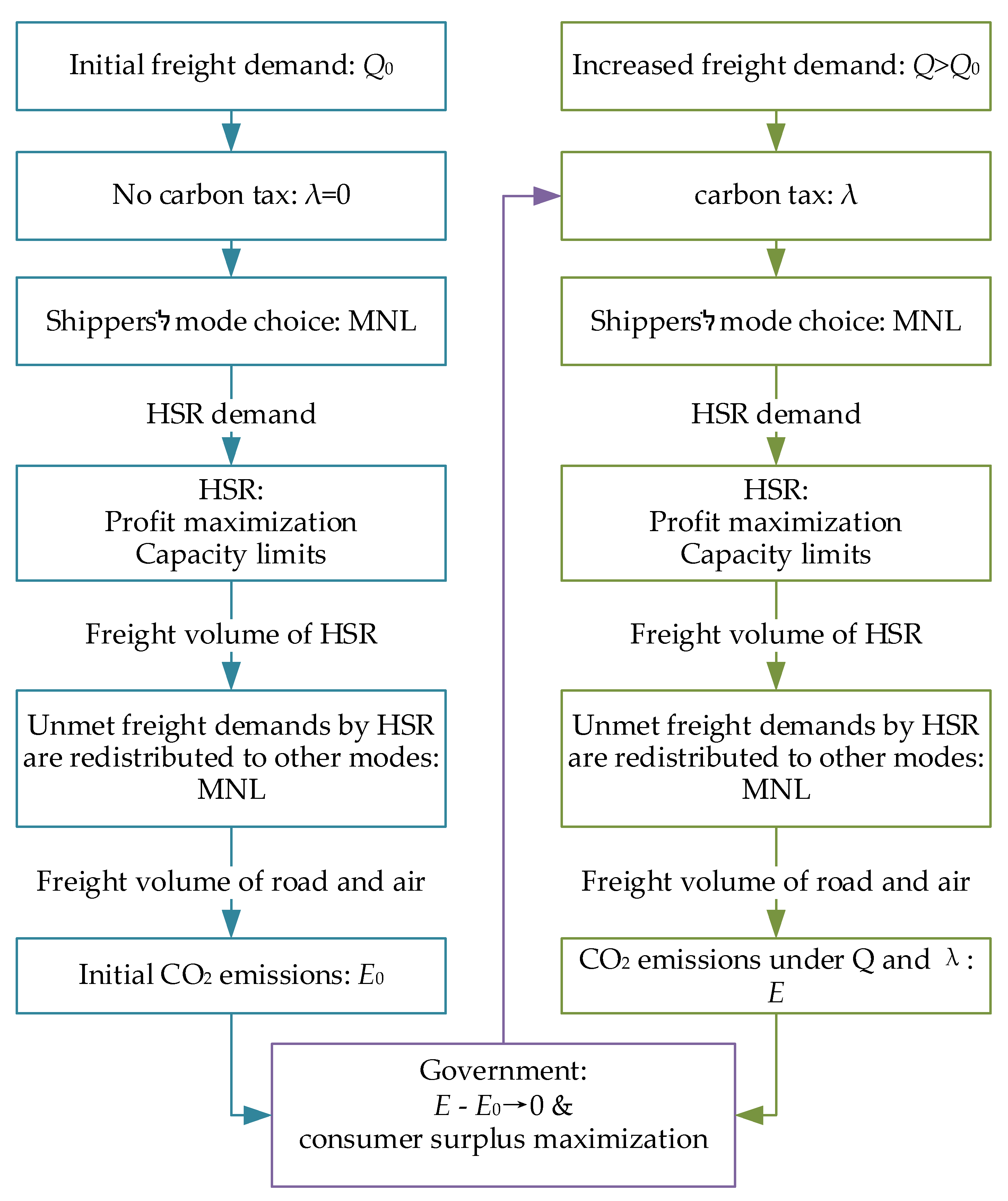
3.1. Problem Description
3.2. HSR Operator: Profit Maximization
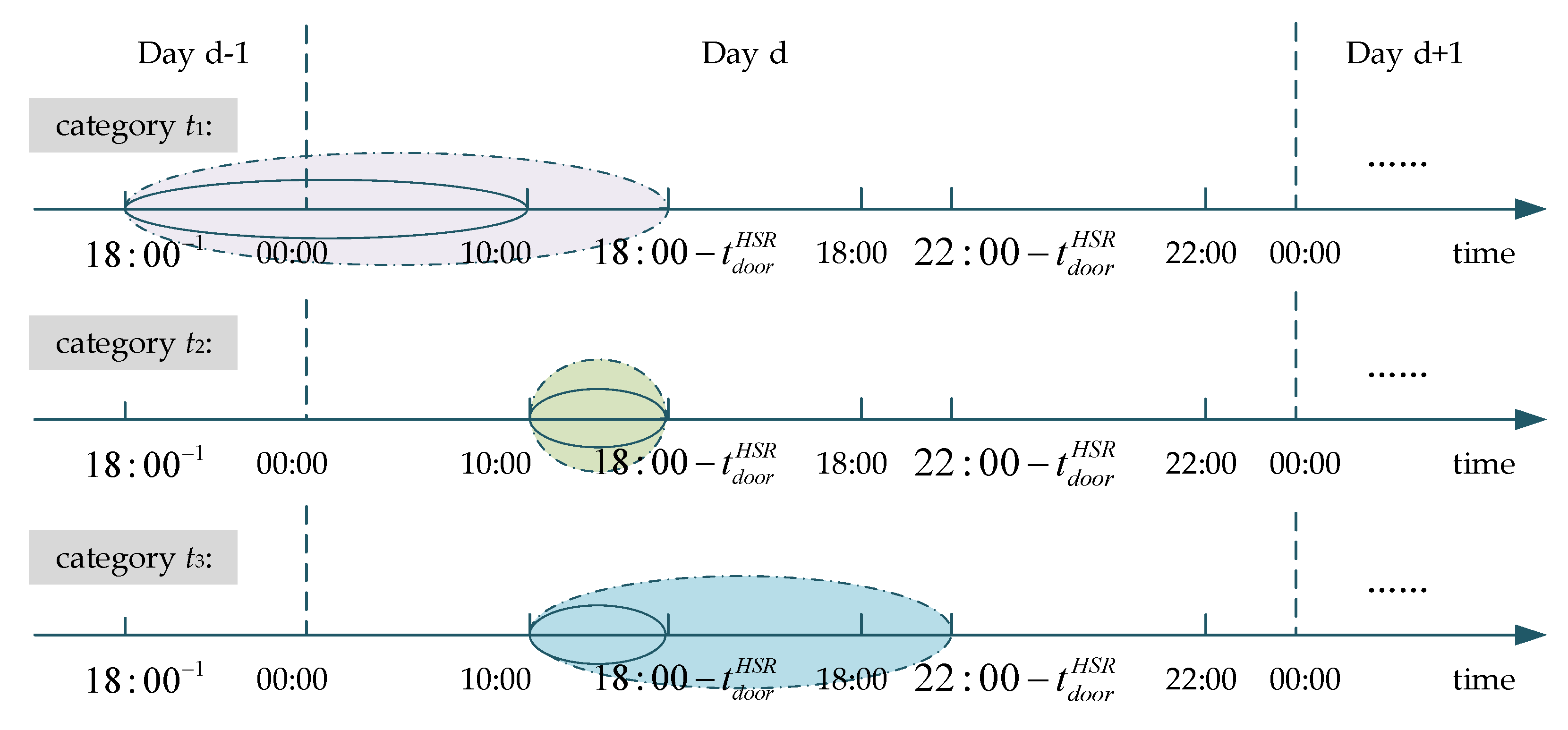
- Type one consists of transportation demands that require delivery within 12 h (n = n1).
- Type two consists of transportation demands that require delivery within 24 h (n = n2).
3.3. Shipper: Mode Choice
- (1)
- Economy
- (2)
- Timeliness
- (3)
- Reliability
- (4)
- Safety
- (5)
- Environmental externality
3.4. Government: Decarbonization and Consumer Surplus Maximization
3.5. Bi-Level Model
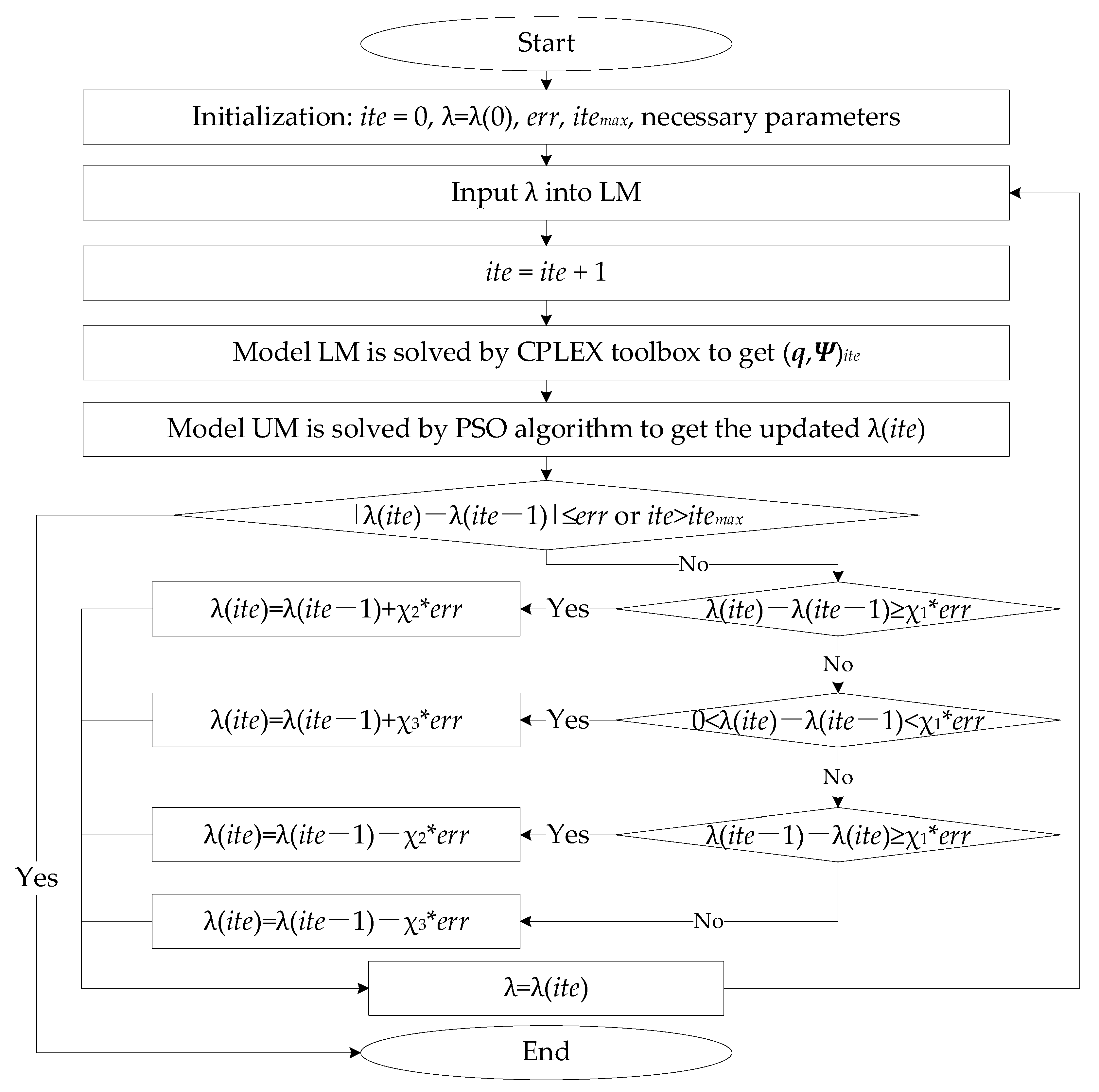
3.6. Algorithm Design
| Algorithm 1 CT algorithm |
| 1: Initialize 2: Set initial carbon tax rate λ(0) 3: Set relative error threshold err, maximum number of iterations itemax 4: Set iteration counter ite ← 0 5: Repeat 6: Input λ(ite) into LM 7: Update ite ← ite+1 8: Solve LM to obtain the freight volume of HSR , 9: and other HSR service decision variables 10: Substitute into UM 11: Solve UM to obtain the updated carbon tax rate λ(ite), 12: and freight volumes of road and air 13: Until 14: |λ(ite) -λ(ite-1) | ≤ err or ite > itemax 15: Return optimal solution |
| Algorithm 2 PSO |
| 1: Begin 2: for each particle i = 1, 2, …, N 3: Initializing velocity Vi and position Xi 4: Evaluating the fitting value of particle i and setting Pi = Xi 5: end for 6: Pg = min { Pi } 7: while terminal condition not met 8: for each particle i = 1, 2, …, N 9: Updating velocity by Equation (40) 10: Updating position by Equation (41) 11: Evaluating the fitting value of particle i 12: If fit(Xi) ≤ fit(Pi) 13: Pi = Xi 14: If fit(Pi) ≤ fit(Pg) 15: Pg = Pi 16: end for 17: end while 18: output Pg 19: End |
- (1)
- If λ(ite) < λopt, then λ(ite + 1) > λopt and λ(ite − 1) > λopt.
- (2)
- If λ(ite) > λopt, then λ(ite + 1) < λopt and λ(ite − 1) < λopt.
- (1)
- If λ(ite) > λ(ite − 1), then λ(ite − 1) < λopt;
- (2)
- If λ(ite) < λ(ite − 1), then λ(ite − 1) > λopt;
- (1)
- λ(ite) > λ(ite − 1)
- (2)
- λ(ite) < λ(ite − 1)
- (1)
- If λ(ite) − λ(ite − 1) > err, then let λ(ite) = λ(ite − 1) + χ.
- (2)
- If λ(ite − 1) − λ(ite) > err, then let λ(ite) = λ(ite − 1) − χ.
- (3)
- If |λ(ite) − λ(ite − 1)| ≤ err, the algorithm terminates and outputs the result λ(ite).
- (1)
- If λ(ite) − λ(ite − 1) ≥ χ1*err, then let λ(ite) = λ(ite − 1) + χ2*err;If 0 < λ(ite) − λ(ite − 1) < err, then let λ(ite) = λ(ite − 1) + χ3*err.
- (2)
- If λ(ite − 1) − λ(ite) ≥ χ1*err, then let λ(ite) = λ(ite − 1) − χ2*err;If 0 < λ(ite − 1) − λ(ite) < χ1*err, then let λ(ite) = λ(ite − 1) − χ3*err.
- (3)
- If |λ(ite) − λ(ite − 1)| ≤ err, the algorithm terminates and outputs the result λ(ite).
4. Numerical Experiments
4.1. The Input Data
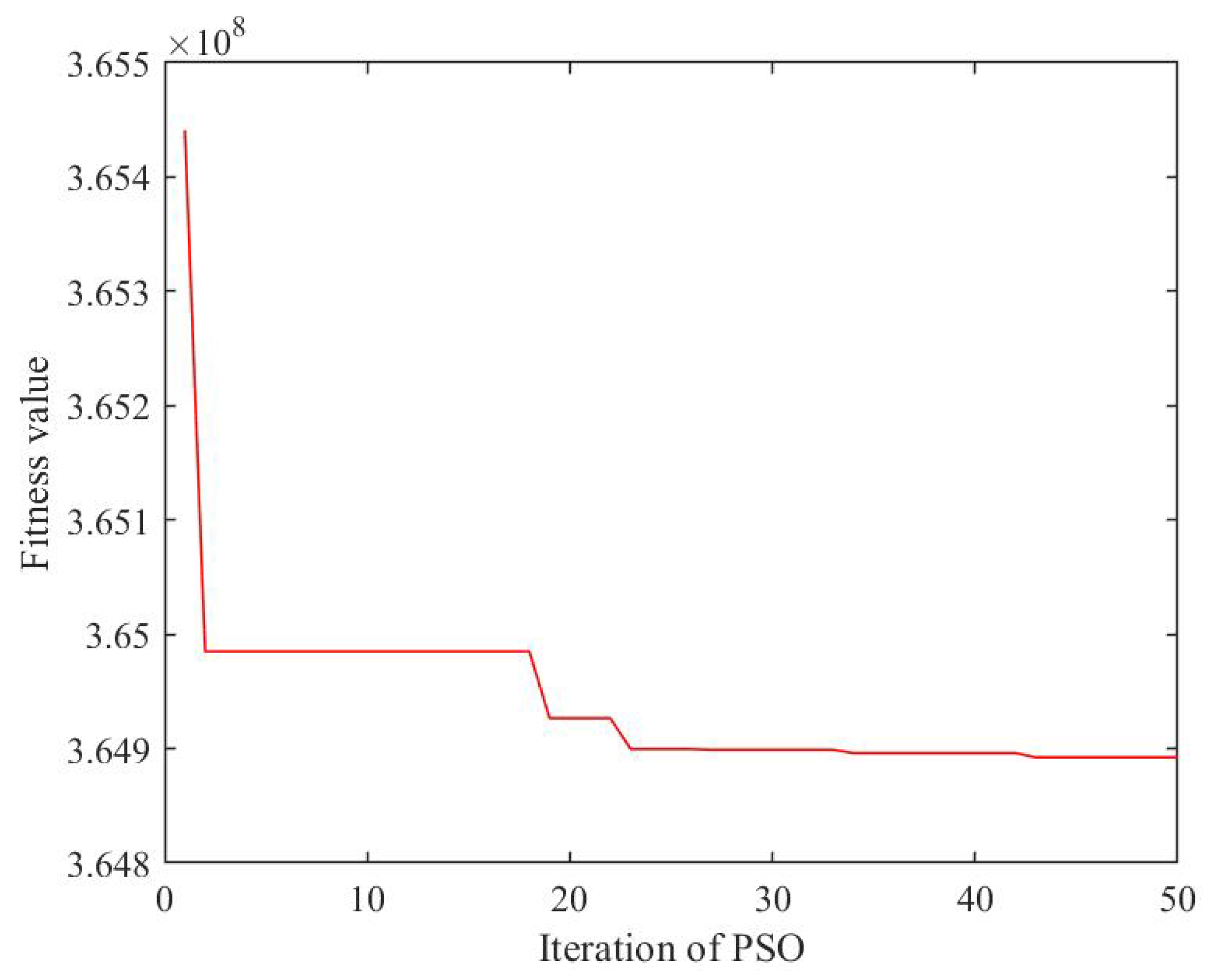
4.2. Results Analysis
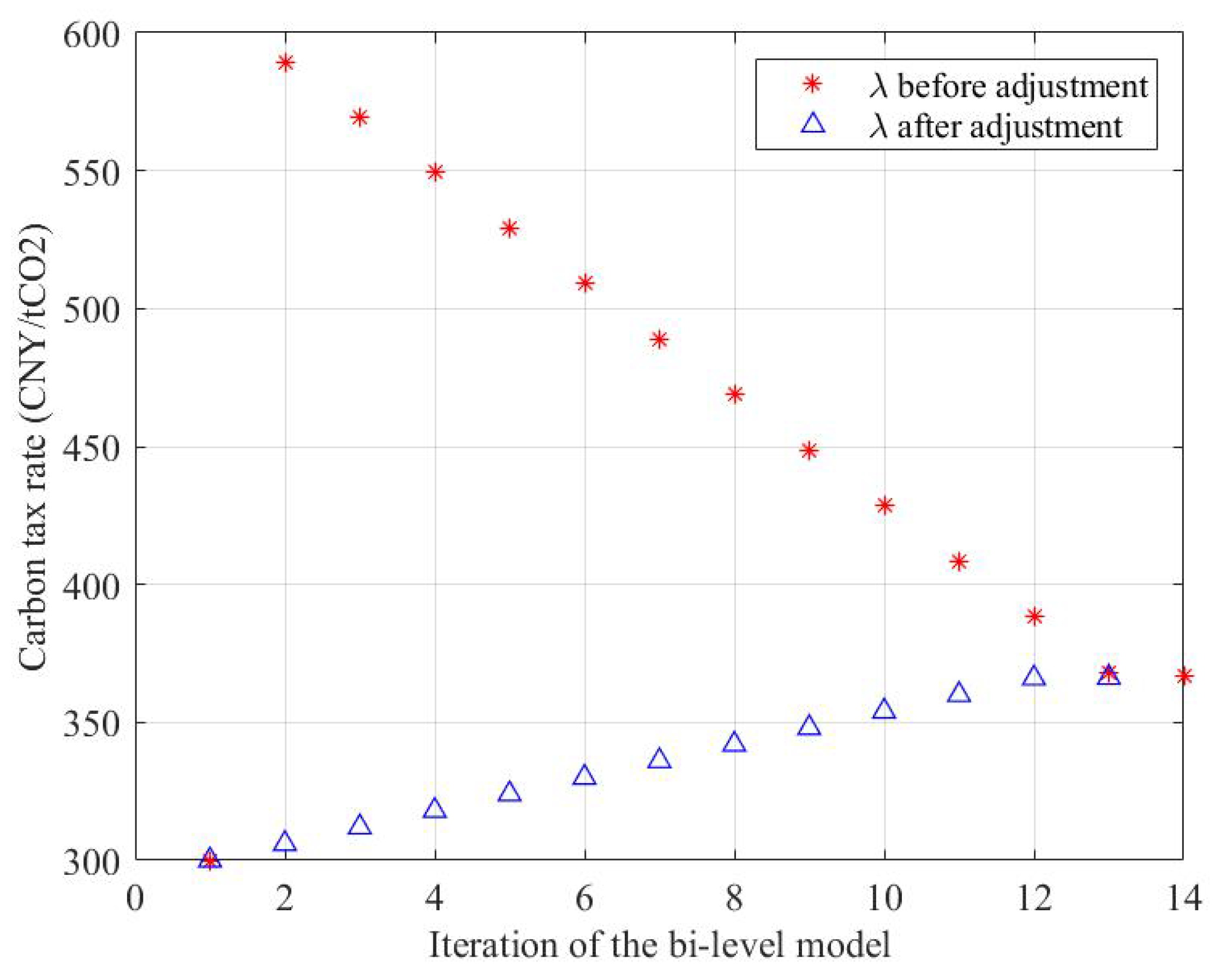
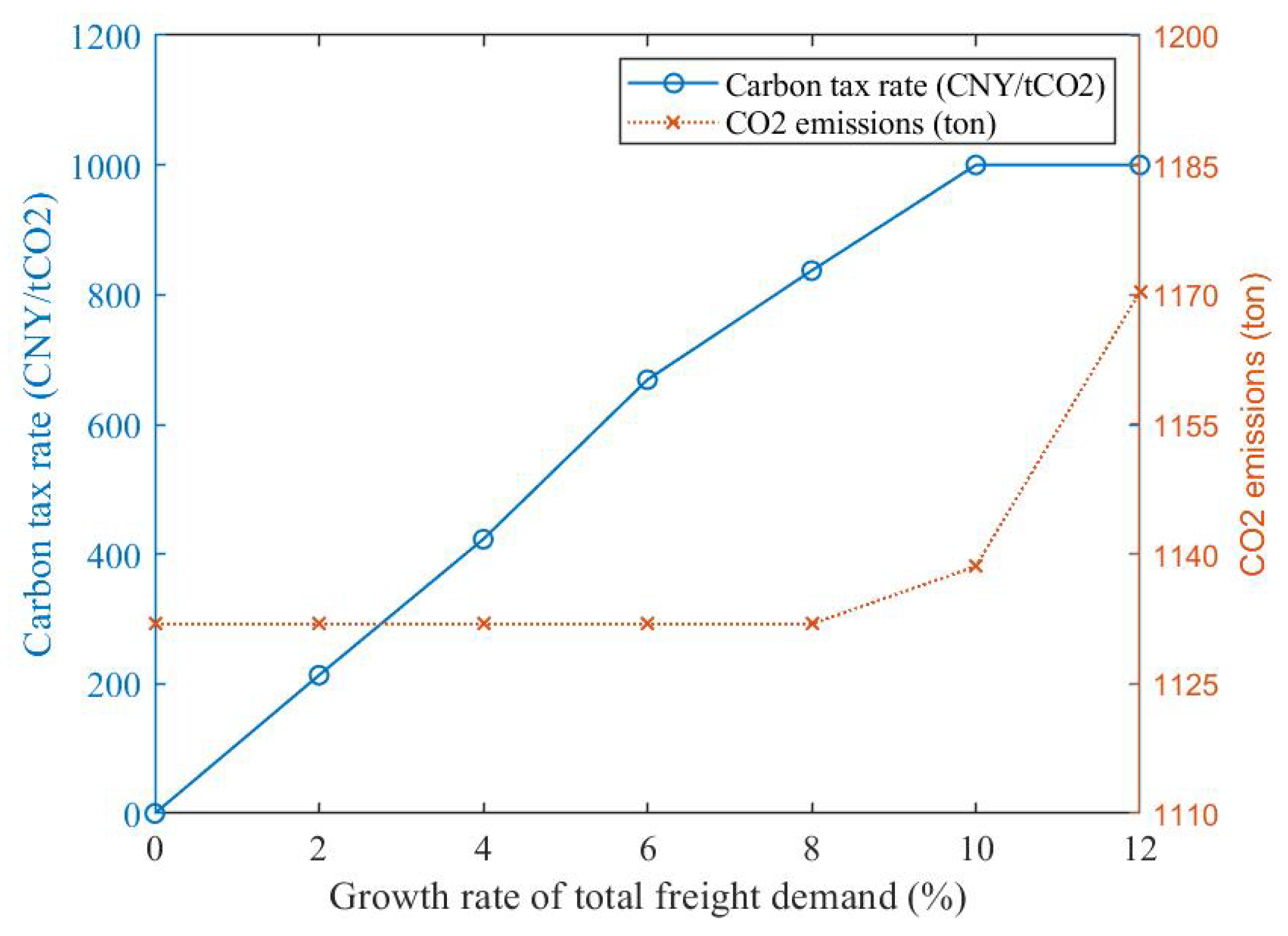
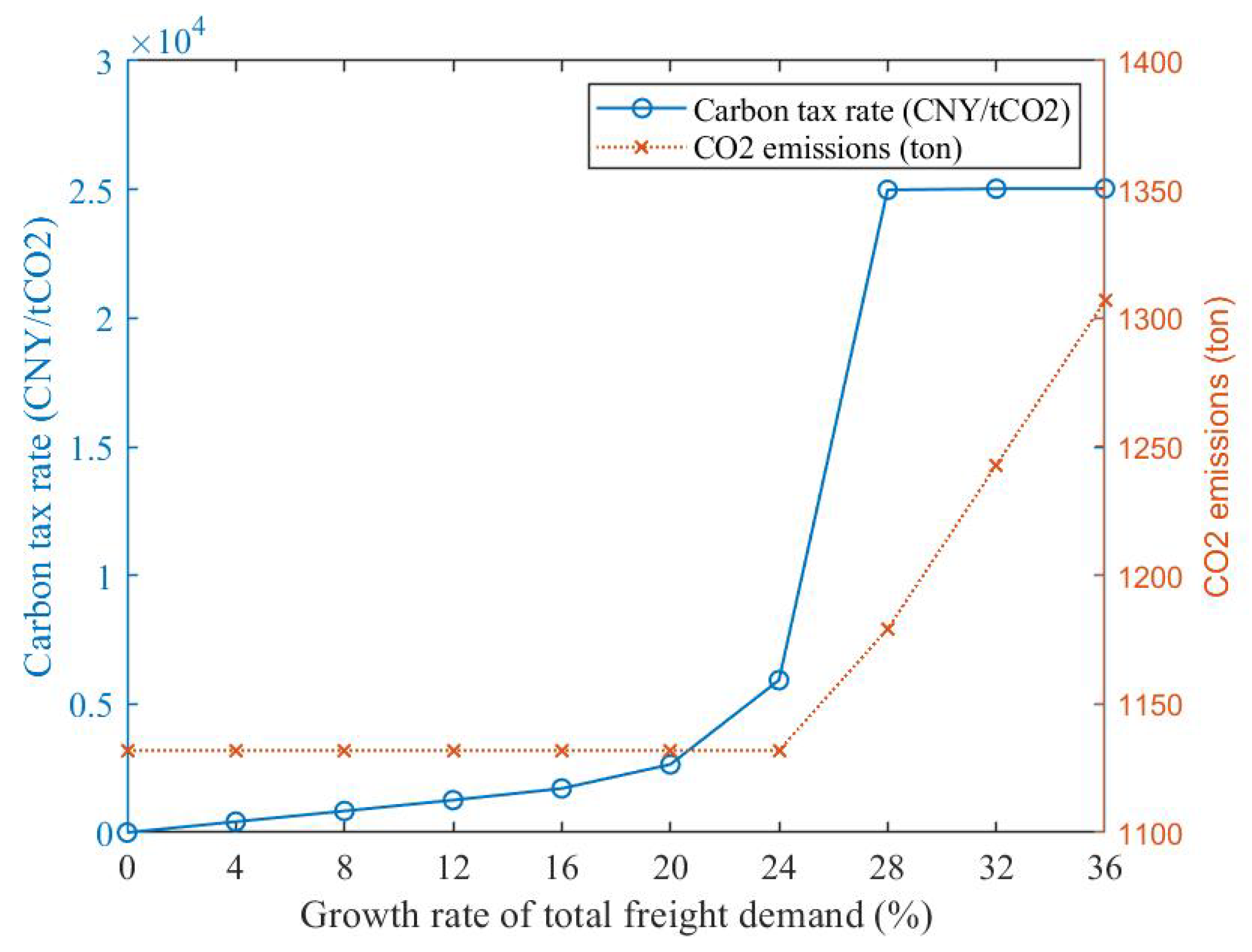
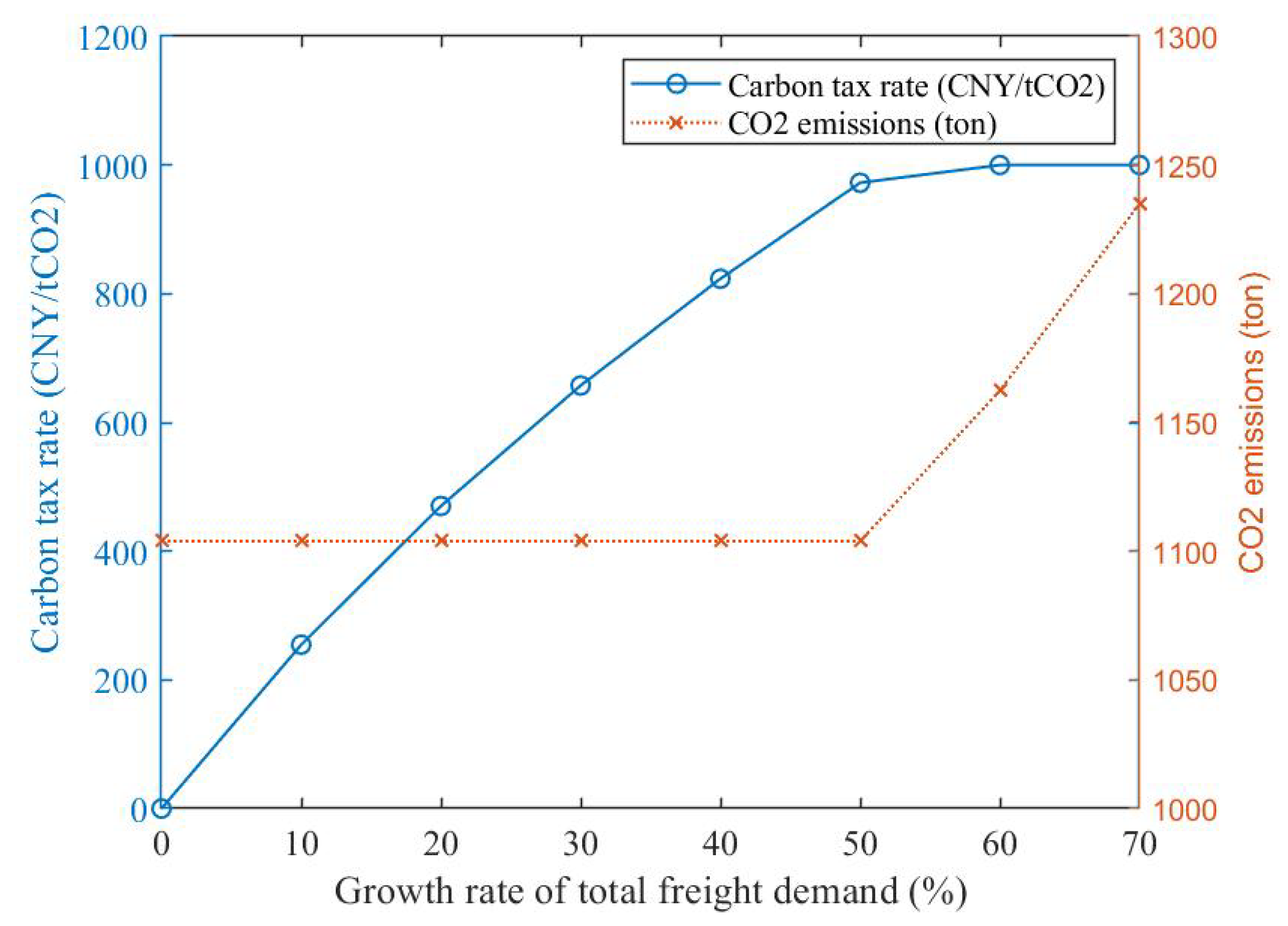
4.3. Sensitivity Analysis
5. Discussion
5.1. Management Insights
5.2. Limitations
5.3. Future Research
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HSR | High-speed rail |
| OD | Origin–destination |
| MNL | Multinomial Logit |
| UM | Upper-level model |
| LM | Lower-level model |
| PSO | Particle swarm optimization |
| CT | Carbon tax rate decision algorithm |
References
- Kaack, L.H.; Vaishnav, P.; Morgan, M.G.; Azevedo, I.L.; Rai, S. Decarbonizing intraregional freight systems with a focus on modal shift. Environ. Res. Lett. 2018, 13, 083001. [Google Scholar] [CrossRef]
- Tattini, J.; Gargiulo, M.; Karlsson, K. Reaching carbon neutral transport sector in Denmark—Evidence from the incorporation of modal shift into the TIMES energy system modeling framework. Energy Policy 2018, 113, 571–583. [Google Scholar] [CrossRef]
- NBS National Data. Available online: https://data.stats.gov.cn/easyquery.htm?cn=C01 (accessed on 1 May 2025).
- Zhao, C.; Zhou, B. Impact of Express Delivery Industry’s Development on Transportation Sector’s Carbon Emissions: An Empirical Analysis from China. Sustainability 2021, 13, 8908. [Google Scholar] [CrossRef]
- Bi, M.; He, S.; Xu, W. Express delivery with high-speed railway: Definitely feasible or just a publicity stunt. Transp. Res. Part A-Policy Pract. 2019, 120, 165–187. [Google Scholar] [CrossRef]
- To, W.M. Greenhouse gases emissions from the logistics sector: The case of Hong Kong, China. J. Clean. Prod. 2015, 103, 658–664. [Google Scholar] [CrossRef]
- Masone, A.; Marzano, V.; Simonelli, F.; Sterle, C. Exact and heuristic approaches for the Modal Shift Incentive Problem. Socio-Econ. Plan. Sci. 2024, 93, 101874. [Google Scholar] [CrossRef]
- Paladugula, A.L.; Kholod, N.; Chaturvedi, V.; Ghosh, P.P.; Pal, S.; Clarke, L.; Evans, M.; Kyle, P.; Koti, P.N.; Parikh, K.; et al. A multi-model assessment of energy and emissions for India’s transportation sector through 2050. Energy Policy 2018, 116, 10–18. [Google Scholar] [CrossRef]
- Liu, P.; Mu, D.; Gong, D. Eliminating overload trucking via a modal shift to achieve intercity freight sustainability: A system dynamics approach. Sustainability 2017, 9, 398. [Google Scholar] [CrossRef]
- Zhou, Y.; Fang, W.; Li, M.; Liu, W. Exploring the impacts of a low-carbon policy instrument: A case of carbon tax on transportation in China. Resour. Conserv. Recycl. 2018, 139, 307–314. [Google Scholar] [CrossRef]
- Qiu, R.; Xu, J.; Xie, H.; Zeng, Z.; Lv, C. Carbon tax incentive policy towards air passenger transport carbon emissions reduction. Transport. Res. Part D-Transport. Environ. 2020, 85, 102441. [Google Scholar] [CrossRef]
- Wang, M.; Liu, K.; Choi, T.-M.; Yue, X. Effects of Carbon Emission Taxes on Transportation Mode Selections and Social Welfare. IEEE Trans. Syst. Man Cybern.-Syst. 2015, 45, 1413–1423. [Google Scholar] [CrossRef]
- Bouchery, Y.; Ghaffari, A.; Jemai, Z.; Fransoo, J. Sustainable transportation and order quantity: Insights from multiobjective optimization. Flex. Serv. Manuf. J. 2016, 28, 367–396. [Google Scholar] [CrossRef]
- Tao, X.; Wu, Q.; Zhu, L. Mitigation potential of CO2 emissions from modal shift induced by subsidy in hinterland container transport. Energy Policy 2017, 101, 265–273. [Google Scholar] [CrossRef]
- Choi, B.; Park, S.-i.; Lee, K.-D. A System Dynamics Model of the Modal Shift from Road to Rail: Containerization and Imposition of Taxes. J. Adv. Transp. 2019, 2019, 7232710. [Google Scholar] [CrossRef]
- Kundu, T.; Sheu, J.-B. Analyzing the effect of government subsidy on shippers’ mode switching behavior in the Belt and Road strategic context. Transp. Res. Part E-Logist. Transp. Rev. 2019, 129, 175–202. [Google Scholar] [CrossRef]
- Chen, K.; Xin, X.; Niu, X.; Zeng, Q. Coastal transportation system joint taxation-subsidy emission reduction policy optimization problem. J. Clean. Prod. 2020, 247, 119096. [Google Scholar] [CrossRef]
- Guo, T.; Liu, P.; Wang, C.; Xie, J.; Du, J.; Lim, M.K. Toward sustainable port-hinterland transportation: A holistic approach to design modal shift policy mixes. Transp. Res. Part A-Policy Pract. 2023, 174, 103746. [Google Scholar] [CrossRef]
- Nassar, R.F.; Ghisolfi, V.; Annema, J.A.; van Binsbergen, A.; Tavasszy, L.A. A system dynamics model for analyzing modal shift policies towards decarbonization in freight transportation. Res. Transp. Bus. Manag. 2023, 48, 100966. [Google Scholar] [CrossRef]
- Takman, J.; Gonzalez-Aregall, M. Public policy instruments to promote freight modal shift in Europe: Evidence from evaluations. Transp. Rev. 2024, 44, 612–633. [Google Scholar] [CrossRef]
- Shen, J.Q.; Liu, H.; Zhang, R. Railway pricing for automobile transport based on discrete choice model and cost accounting. Res. Transp. Bus. Manag. 2025, 59, 101295. [Google Scholar] [CrossRef]
- Hoffrichter, A.; Silmon, J.; Iwnicki, S.; Hillmansen, S.; Roberts, C. Rail freight in 2035-traction energy analysis for high-performance freight trains. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2012, 226, 568–574. [Google Scholar] [CrossRef]
- Jia, X.; He, R.; Chai, H. Optimizing the Number of Express Freight Trains on a High-speed Railway Corridor by the Departure Period. IEEE Access 2020, 8, 100058–100072. [Google Scholar] [CrossRef]
- Yu, X.; Lang, M.; Gao, Y.; Wang, K.; Su, C.-H.; Tsai, S.-B.; Huo, M.; Yu, X.; Li, S. An Empirical Study on the Design of China High-Speed Rail Express Train Operation Plan-From a Sustainable Transport Perspective. Sustainability 2018, 10, 2478. [Google Scholar] [CrossRef]
- Yu, X.; Lang, M.; Zhang, W.; Li, S.; Zhang, M.; Yu, X. An Empirical Study on the Comprehensive Optimization Method of a Train Diagram of the China High Speed Railway Express. Sustainability 2019, 11, 2141. [Google Scholar] [CrossRef]
- Li, S.; Zhu, M.; Zuo, D.; Guo, C.; Shi, L. A robust optimisation approach of train timetabling for freight transportation using high-speed railway. Transp. A-Transp. Sci. 2024, 2385874. [Google Scholar] [CrossRef]
- Li, S.; Zuo, D.; Li, W.; Zhang, Y.; Shi, L. Freight train line planning for large-scale high-speed rail network: An integer Benders decomposition-based branch-and-cut algorithm. Transp. Res. Part E-Logist. Transp. Rev. 2024, 192, 103750. [Google Scholar] [CrossRef]
- Wang, X.; Zhen, L.; Wang, S. Optimizing an express delivery mode based on high-speed railway and crowd-couriers. Transp. Policy 2024, 159, 157–177. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, F.-R.; Ao, W.K.; Guo, Z.-H.; Chen, Z.-W. Optimization of cargo distribution for high-speed freight trains to overcome strong wind conditions. Eng. Appl. Comput. Fluid Mech. 2024, 18, 2434008. [Google Scholar] [CrossRef]
- Li, S.; Chen, X.; Lang, M. A hybrid heuristic algorithm for high-speed rail line planning problem with multiple transport organization modes. Res. Transp. Bus. Manag. 2025, 60, 101328. [Google Scholar] [CrossRef]
- Liang, X.-H.; Tan, K.-H. Market potential and approaches of parcels and mail by high speed rail in China. Case Stud. Transp. Policy 2019, 7, 583–597. [Google Scholar] [CrossRef]
- Small, K.A.; Rosen, H.S. Applied welfare economics with discrete choice models. Econom. J. Econom. Soc. 1981, 49, 105–130. [Google Scholar] [CrossRef]
- Yang, H.; Ma, W.; Wang, Q.; Wang, K.; Zhang, Y. Welfare implications for air passengers in China in the era of high-speed rail. Transp. Policy 2020, 95, A1–A13. [Google Scholar] [CrossRef]
- Vaze, V.; Luo, T.; Harder, R. Impacts of airline mergers on passenger welfare. Transp. Res. Part E Logist. Transp. Rev. 2017, 101, 130–154. [Google Scholar] [CrossRef]
- IPCC. Global Warming of 1.5 °C; IPCC: Geneva, Switzerland, 2015. [Google Scholar]
- Benayed, O.; Blair, C.E. Computational Difficulties of Bilevel Linear Programming. Oper. Res. 1990, 38, 556–560. [Google Scholar] [CrossRef]
- Bard, J.F. Some properties of the bilevel programming problem. J. Optim. Theory Appl. 1991, 68, 371–378. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the Proceedings of ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Chao, C.-C. Assessment of carbon emission costs for air cargo transportation. Transport. Res. Part D-Transport. Environ. 2014, 33, 186–195. [Google Scholar] [CrossRef]
- Lin, B.L.; Liu, C.; Wang, H.J.; Lin, R.X. Modeling the railway network design problem: A novel approach to considering carbon emissions reduction. Transport. Res. Part D-Transport. Environ. 2017, 56, 95–109. [Google Scholar] [CrossRef]
- Van Fan, Y.; Perry, S.; Klemes, J.J.; Lee, C.T. A review on air emissions assessment: Transportation. J. Clean. Prod. 2018, 194, 673–684. [Google Scholar] [CrossRef]
- Song, H.; Gao, S.; Li, Y.; Liu, L.; Dong, H. Train-Centric Communication Based Autonomous Train Control System. IEEE Trans. Intell. Veh. 2023, 8, 721–731. [Google Scholar] [CrossRef]



| Sets: | |
| set of transportation nodes. | |
| set of origin-destination (OD) pairs. | |
| set of express freight demand types, differentiated by their distinct transportation time requirements. | |
| set of freight modes in the express transport market. | |
| set of HSR freight organization modes. | |
| set of HSR passenger train classifications capable of meeting freight demand. | |
| Parameters: | |
| freight rate for demand between OD transported by mode (CNY/kg) | |
| fixed operating cost of HSR mode (CNY) | |
| distance-related cost of HSR mode (CNY/km) | |
| transportation distance for goods transported by mode between OD (km) | |
| volume-related cost of HSR mode (CNY/kg) | |
| transportation time of demand between OD transported by mode (h) | |
| en-route transportation time for goods transported by mode between OD (h) | |
| fixed station-to-door delivery time of mode (h) | |
| waiting time for demand transported by mode (h) | |
| average transportation speed of mode (km/h) | |
| delivery time limit for demand (h) | |
| maximum service frequency of HSR freight trains between OD | |
| maximum service frequency of HSR passenger trains with classification between OD | |
| maximum freight capacity of a single train in HSR mode (kg) | |
| total demand of between OD (kg) | |
| demand of between OD that selects mode (kg) | |
| probability of demand of between OD selecting mode | |
| the perceived utility of demand for mode between OD | |
| deterministic part of the utility | |
| random component of the utility | |
| punctuality rate of mode (%) | |
| safety of mode (%) | |
| cargo damage rate of mode (%) | |
| unit CO2 emissions of mode (tCO2/kg-km) | |
| carbon tax per unit of goods transported by mode between OD (CNY/kg) | |
| weight of each attribute in the utility function | |
| minimum and maximum allowable values for the carbon tax rate (CNY/tCO2) | |
| Decision variables: | |
| freight volume of demand between OD transported by HSR mode (kg) | |
| freight volume transported by HSR mode for OD (kg) | |
| required service frequency for HSR mode between OD | |
| freight volume of demand between OD transported by HSR mode using trains classified as | |
| required service frequency for HSR mode using trains classified as | |
| freight volume of demand between OD transported by mode (kg) | |
| carbon tax rate (CNY/tCO2) | |
| Parameter | Value | |||
|---|---|---|---|---|
| HSR | Road | Air | ||
| (CNY/kg) | demand type n1 | 25 | 10 | 30 |
| demand type n2 | 10 | 5 | 15 | |
| (h) | demand type n1 | 2 | 1 | 2 |
| demand type n2 | 12 | 9 | 12 | |
| (km/h) | 250 | 65 | - | |
| (h) | 4 | 1 | 5 | |
| (%) | 1 | 2 | 0.5 | |
| (%) | 95 | 75.5 | 76.7 | |
| (tCO2/kg-km) | 1.19 × 10−8 | 4.79 × 10−8 | 5.64 × 10−7 | |
| OD | NO | (km) | (h) | (ton) | |||
|---|---|---|---|---|---|---|---|
| HSR | Road | Air | n1 | n2 | |||
| Beijing → Tianjin | OD1 | 137 | 137 | - | - | 145 | 752 |
| Beijing → Jinan | OD2 | 406 | 410 | - | - | 43 | 225 |
| Beijing → Nanjing | OD3 | 1023 | 1010 | 981 | 2.08 | 117 | 604 |
| Beijing → Shanghai | OD4 | 1318 | 1209 | 1178 | 2.50 | 320 | 1654 |
| Tianjin → Jinan | OD5 | 269 | 328 | - | - | 14 | 74 |
| Tianjin → Nanjing | OD6 | 886 | 891 | 907 | 2.08 | 27 | 140 |
| Tianjin → Shanghai | OD7 | 1181 | 1082 | 1133 | 2.08 | 72 | 371 |
| Jinan → Nanjing | OD8 | 617 | 622 | - | - | 30 | 155 |
| Jinan → Shanghai | OD9 | 912 | 829 | 852 | 1.58 | 86 | 448 |
| Nanjing → Shanghai | OD10 | 295 | 307 | - | - | 235 | 1215 |
| OD | Alternative Modes | |
|---|---|---|
| Demand Type n1 | Demand Type n2 | |
| OD1 | HSR, road | HSR, road |
| OD2 | HSR, road | HSR, road |
| OD3 | HSR, air | HSR, air |
| OD4 | HSR, air | HSR, air |
| OD5 | HSR, road | HSR, road |
| OD6 | HSR, air | HSR, road, air |
| OD7 | HSR, air | HSR, air |
| OD8 | HSR, road | HSR, road |
| OD9 | HSR, air | HSR, road, air |
| OD10 | HSR, road | HSR, road |
| Attributes | Estimate | Standard Error | Wald Chi-Square | Pr > ChiSq | Standardized Estimate |
|---|---|---|---|---|---|
| Economy | −0.041 | 0.0235 | 3.0485 | 0.0808 | −0.1972 |
| Timeliness | −0.165 | 0.1007 | 2.6848 | 0.1013 | −0.497 |
| Environmental negative externality | −1.2826 | 0.5916 | 4.7 | 0.0302 | −0.1699 |
| Parameter | Values of Different HSR Modes | |||
|---|---|---|---|---|
| r1 | r2 | r3 | r4 | |
| (CNY) | 5263 | 152.2 | 2346 | 18,770 |
| (CNY/km) | - | - | 18.6 | 148.9 |
| (CNY/ton) | 34.7 | 35.5 | 58.8 | 49.7 |
| (ton) | 27.6 | 2.4 | 12.6 | 120 |
| OD | HSR Mode r1 | HSR Mode r2 and r3 | HSR Mode r4 | ||
|---|---|---|---|---|---|
| OD1 | 0 | 51 | 18 | 19 | 1 |
| OD2 | 1 | 4 | 0 | 0 | 2 |
| OD3 | 0 | 1 | 0 | 0 | 5 |
| OD4 | 0 | 9 | 0 | 8 | 5 |
| OD5 | 1 | 0 | 0 | 0 | 2 |
| OD6 | 0 | 0 | 0 | 0 | 2 |
| OD7 | 0 | 0 | 0 | 1 | 5 |
| OD8 | 1 | 0 | 0 | 0 | 2 |
| OD9 | 0 | 2 | 0 | 1 | 5 |
| OD10 | 1 | 28 | 5 | 12 | 2 |
| Item | Scenario #0 | Scenario #1 | Scenario #2 |
|---|---|---|---|
| optimal carbon tax rate (CNY/tCO2) | - | - | 367.03 |
| CO2 emissions (ton) | 1131.914 | 1181.727 | 1131.913 |
| Increase to Scenario #0 | - | +4.40% | +0% |
| Increase to Scenario #1 | - | - | −4.22% |
| HSR freight profits (CNY) | 27,641,787.78 | 28,306,561.22 | 29,740,030.87 |
| Increase to Scenario #0 | - | +2.41% | +7.59% |
| Increase to Scenario #1 | - | - | +5.06% |
| change in consumer surplus (CNY) | - | - | −11,628,746.67 |
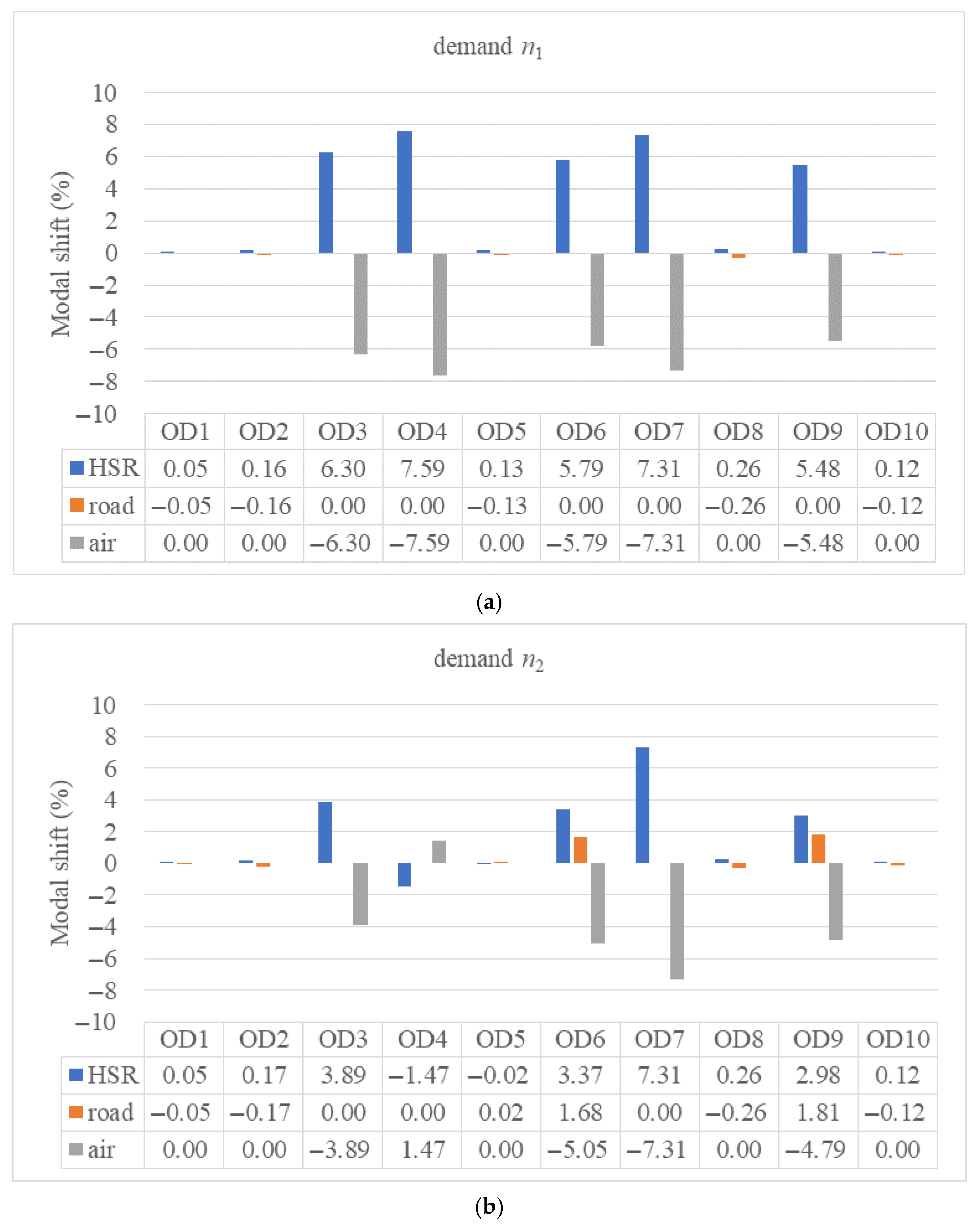
| Freight Mode | Freight Volume (ton) | Increase to Scenario #1 | |
|---|---|---|---|
| Scenario #1 | Scenario #2 | ||
| HSR | 2536.924 | 2621.67 | +3.34% |
| road | 1927.163 | 1934.053 | +0.36% |
| air | 1825.093 | 1733.431 | −5.02% |
| OD | HSR Mode r1 | HSR Mode r2 | HSR Mode r3 | HSR Mode r4 | ||||
|---|---|---|---|---|---|---|---|---|
| Trains in t1 | Trains in t2 | Trains in t3 | Trains in t1 | Trains in t2 | Trains in t3 | |||
| OD1 | 0 | 47 | 16 | 14 | 2 | 2 | 0 | 0 |
| OD2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| OD3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 3 |
| OD4 | 0 | 0 | 0 | 0 | 9 | 0 | 8 | 5 |
| OD5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| OD6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| OD7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 |
| OD8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| OD9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 |
| OD10 | 1 | 23 | 0 | 12 | 5 | 5 | 0 | 2 |
| Demand Type | OD | HSR Mode r1 | HSR Mode r2 | HSR Mode r3 | HSR Mode r4 | ||||
|---|---|---|---|---|---|---|---|---|---|
| Trains in t1 | Trains in t2 | Trains in t3 | Trains in t1 | Trains in t2 | Trains in t3 | ||||
| n1 | OD1 | 0 | 0 | 2.28 | 33.60 | 0 | 0 | 0 | 0 |
| OD2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15.21 | |
| OD3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 62.51 | |
| OD4 | 0 | 0 | 0 | 0 | 0 | 0 | 100.80 | 64.71 | |
| OD5 | 4.34 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| OD6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14.58 | |
| OD7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 37.26 | |
| OD8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13.26 | |
| OD9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 45.15 | |
| OD10 | 27.60 | 0 | 0 | 28.80 | 0 | 0 | 0 | 17.12 | |
| n2 | OD1 | 0 | 112.80 | 36.12 | 0 | 24.16 | 25.20 | 0 | 0 |
| OD2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 83.56 | |
| OD3 | 0 | 0 | 0 | 0 | 12.60 | 0 | 0 | 297.49 | |
| OD4 | 0 | 0 | 0 | 0 | 113.40 | 0 | 0 | 535.29 | |
| OD5 | 23.26 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| OD6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 56.79 | |
| OD7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 193.19 | |
| OD8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 71.640 | |
| OD9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 167.37 | |
| OD10 | 0 | 55.20 | 0 | 0 | 60.52 | 63.00 | 0 | 222.88 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L. Decarbonizing China’s Express Freight Market Using High-Speed Rail Services and Carbon Taxes: A Bi-Level Optimization Approach. Symmetry 2025, 17, 1364. https://doi.org/10.3390/sym17081364
Li L. Decarbonizing China’s Express Freight Market Using High-Speed Rail Services and Carbon Taxes: A Bi-Level Optimization Approach. Symmetry. 2025; 17(8):1364. https://doi.org/10.3390/sym17081364
Chicago/Turabian StyleLi, Lin. 2025. "Decarbonizing China’s Express Freight Market Using High-Speed Rail Services and Carbon Taxes: A Bi-Level Optimization Approach" Symmetry 17, no. 8: 1364. https://doi.org/10.3390/sym17081364
APA StyleLi, L. (2025). Decarbonizing China’s Express Freight Market Using High-Speed Rail Services and Carbon Taxes: A Bi-Level Optimization Approach. Symmetry, 17(8), 1364. https://doi.org/10.3390/sym17081364




