Remarks on the Simple Equations Method (SEsM) for Obtaining Exact Solutions of Nonlinear Differential Equations: Selected Simple Equations

Abstract

We present a short review of the methodology and applications of the Simple Equations Method (SEsM) for obtaining exact solutions to nonlinear differential equations. The applications part of the review is focused on the simple equations used, with examples of the use of the differential equations for exponential functions, for the function ${\left[{\displaystyle \frac{1}{p+exp\left(q\xi \right)}}\right]}^r$, for the function $1/{cosh}^n$, and for the function ${tanh}^n$. We list several propositions and theorems that are part of the SEsM methodology. We show how SEsM can lead to multisoliton solutions of integrable equations. Furthermore, we note that each exact solution to a nonlinear differential equation can, in principle, be obtained by the methodology of SEsM. The methodology of SEsM can be based on different simple equations. Numerous methods exist for obtaining exact solutions to nonlinear differential equations, which are based on the construction of a solution using certain known functions. Many of these methods are specific cases of SEsM, where the simple differential equation used in SEsM is the equation whose solution is the corresponding function used in these methodologies. We note that the exact solutions obtained by SEsM can be used as a basis for further research on exact solutions to corresponding differential equations by the application of methods that use the symmetries of the solved equation.

1. Short Overview of the Literature and Research on SEsM

Complex systems are everywhere [1,2,3,4,5,6] and their study is complicated by their nonlinearity [7,8,9]. In many cases, time series analysis and differential or difference equations are used in the study of such systems [10,11,12,13,14,15,16]. The focus of this review is on one aspect of the use of nonlinear differential equations for modeling such systems: obtaining exact solutions to model nonlinear differential equations. This research has a long history [17,18,19,20,21,22]. One reason for this sustained attention are the exact solutions connected to nonlinear waves [23,24,25,26,27,28,29,30,31,32]. Several areas of occurrence of nonlinear waves are fluids [33,34,35,36,37], interaction of nonlinear waves and offshore structures [38], nonlinear optical waves [39], nonlinear waves in chemical systems [40], nonlinear waves in plasmas [41], etc. A special class of nonlinear waves are the solitons [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57]. They are observed in numerous systems such as plasmas [58] and helium films [59], and can be used, for example, in long-distance communications [60].

Below we discuss the SEsM (Simple Equations Method) for obtaining exact solutions to nonlinear differential equations. the SEsM is connected to other much-used methods such as the Inverse Scattering Transform Method and the Method of Hirota.

• The most famous method in the list of methods for obtaining the exact solutions of nonlinear differential equations is the Inverse Scattering Transform Method [61]. An introduction to the method is given in [62,63]. We note

  (a)

  The work of Lax [64], who proposed a general principle for associating nonlinear equations evolutions with linear operators so that the eigenvalues of the linear operator are integrals of the nonlinear equation.

  (b)

  The contribution of Zakharov and Shabat [65,66]

  (c)

  The results of Fokas and Ablowitz [67]; Dod and Bullough [68]; Ablowitz, Kruskal, and Segur [69]; and Kaup and Newell [70,71].

• The Inverse Scattering Transform Method has many applications to

  (a)

  Nonlinear waves in dispersive systems [72].

  (b)

  Solitons [73,74,75,76,77,78].

  (c)

  Integrability of evolution equations [79,80,81,82,83].

  (d)

  Construction of higher-dimensional integrable systems [84].

  (e)

  Spectral transformation method for solving nonlinear evolution equations [85], etc. [86].

• A classic example of another method for obtaining exact solutions of nonlinear partial differential equations is the method of Hirota [87,88,89,90].

Exact solutions to many nonlinear partial differential equations are obtained by these methods. Examples of such equations are

• Korteweg–de Vries equation [91,92,93,94,95,96,97,98,99,100,101,102,103,104,105].
• Sh–Gordon equation and Benney–Newell equation [106,107].
• Sine–Gordon equation [108,109,110,111].
• Nonlinear Schrödinger equation [112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136].
• Boussinesq equation [137,138,139].
• Kadomtsev–Petviashvili equation [140,141].
• Benjamin–Ono equation [142].
• Camassa–Holm equation [143,144,145].
• Nonlinear Klein–Gordon equations [146], Degasperis –Processi equation [147], internal wave equation [148], etc. [149].

The obtained exact solutions are used for the description of various phenomena. Selected examples include

• Optical pulses [150,151,152,153,154], propagation of optical solitons in fibers [155,156,157,158,159,160,161], discrete solitons in optical systems [162].
• Solitons in lattices [163,164,165,166,167,168,169,170,171,172,173].
• Solitons in a sea [174], internal waves in the atmosphere and atmospheric solitons [175], water waves [176,177,178,179,180,181], solitary waves in large blood vessels [182].
• Dissipative solitons [183], breaking solitons [184], solitons in Heisenberg chains [185,186,187,188,189].
• Solitons in liquid crystals [190], solitons in film flows [191], solitons and collapses [192], solitary waves and liquid drops [193].
• Spin wave solitons in magnetic films [194], solitons in non-uniform media [195], nonlinear soliton wave–beach interaction [196], bifurcations of solitons [197], long internal waves in deep fluids [198].
• Dynamics of solitons under random perturbations [199], solitary excitations in muscle proteins [200].
• Ocean waves [201], solitary waves in a two-fluid medium [202], collisions of solitary waves [203], propagation of bores [204,205], interaction between short and long waves [206].
• Solitons under perturbations [207], Peregrine soliton [208], solitons connected to Thirring model [209].

This very short survey of the literature shows the interest and the importance of the research into exact solutions to nonlinear differential equations. Next, we will focus our attention on the research on the SEsM methodology and its applications.

It is well known that at the beginning of studies on exact solutions to nonlinear differential equations, researchers tried to remove the nonlinearity of the studied equation by a transformation.

• The classic example is the Hopf–Cole transformation [210,211].
• Another such transformation connected the nonlinear Korteweg–de Vries equation to the linear Schrödinger equation, and thus the method of Inverse Scattering Transform [212] emerged.
• Transformations are also used within the scope of the method of Hirota [87,88,89,90].
• Another line of research was connected to the truncated Painleve expansions [213,214,215].

An important step in the development of the methodology for obtaining exact solutions to nonlinear differential equations was the Method of Simplest Equation (MSE) formulated by Kudryashov [216]. For a description of this method and its applications, see [217,218,219,220,221,222,223,224,225,226,227,228,229,230].

Fifteen years ago, we started intensive work on a methodology for obtaining exact and approximate solutions of nonlinear differential equations. Nowadays, the methodology is called SEsM (Simple Equations Method) [231,232,233,234,235,236,237,238,239,240,241,242,243,244,245,246,247,248].

• Elements of this methodology can be shown in our early articles. [249,250,251,252].
• The systematic development of the methodology was initiated in 2009 and 2010 [253,254]: the ODE of Bernoulli was used as the simplest equation [255], and this version of the method was called Modified Method of Simplest Equation (MMSE). An application of the methodology to population dynamics and ecology followed. [256]. The MMSE [257,258] has two main points:
  • It uses the concept of the balance equation for fixation of the simplest equation. Note that, in MMSE, one uses a single balance equation.
  • The solution of the solved equation is represented as a truncated power series of the solution of the simplest equation.
• In contemporary notation, MMSE is denoted as SEsM(1,1) (SEsM for obtaining an exact solution to a single nonlinear differential equation by means of a single simplest equation).
• We note that SEsM(1,1), where the solution is searched as a power series of the solution of the simple equation, leads to results equivalent to those that can be obtained by the Method of Simplest Equation.
• SEsM(1,1) (MMSE) was widely used till 2018 [259,260,261,262,263,264]. The main extension of the methodology in this period was described in [263]. There, the methodology was extended by the use of a class of simple equations ${\left({\displaystyle \frac{d^{k}g}{d{\xi }^k}}\right)}^l={\displaystyle \sum _{j=0}^m}{d}_j{g}^j,$ where $k=1,\dots$, $l=1,\dots$, and m and $d_j$ are parameters. The solution to this equation contains as specific cases many well-known functions, such as
  • exponential functions,
  • hyperbolic functions,
  • trigonometric functions,
  • elliptic functions of Weierstrass,
  • elliptic functions of Jacobi,
  etc.
• The methodology has been extended in the last 7 years, as follows:

  (a)

  The current version of the SEsM can use more than one simple equation. An example of the use of two simple equations can be seen in [265].

  (b)

  The first discussion of SEsM was presented in [231].

  (c)

  Further discussion on SEsM can be seen in [233,234,235,236,237].

  (d)

  Applications of specific cases of SEsM are presented in [266,267,268,269,270,271,272,273,274,275,276].

The text below is organized in the following manner: In Section 2, we describe the methodology of SEsM. In Section 3, we give several notes on the transformations that can be used in SEsM, as well as notes on a result connected to the use of composite functions in SEsM. Section 4 is devoted to a discussion of opportunities connected to the use of selected simple equations in SEsM. A discussion of the obtained results is presented in Section 5. Several concluding remarks are summarized in Section 6.

2. Simple Equations Method (SEsM)

In this section, we present a brief description of the Simple Equations Method (SEsM). By means of SEsM, we can obtain exact solutions to nonlinear differential equations. The notation of SEsM is SEsM(n,m). This means that we solve a system of n nonlinear differential equations by means of known solutions of m more simple differential equations [232,247]. For simplicity, we mention below the specific case of SEsM denoted as SEsM(1,m), where we solve a more complicated nonlinear differential equation by construction of a solution that is a composite function of the solutions of m more simple equations. This specific case will be used below when solutions of the more simple equations for exponential functions re discussed. Further, we will discuss an even more specific case: $m=1$. This case will be used for the construction of solutions to more complicated equations when the solutions of the simple equations are more complicated than exponential functions.

The idea of SEsM is very simple: we transform the solved nonlinear differential equation(s) to a system of nonlinear algebraic equations—Figure 1.

We solve the complicated nonlinear differential equation

$$\mathcal{D}\left[u\right(x,\dots ,t\left)\right]=0.$$

(1)

$\mathcal{D}\left[u\right(x,\dots ,t\left)\right)]$ depends on the function $u(x,\dots ,t)$ and some of its derivatives. The function u can depend on several spatial coordinates. We solve (1) by SEsM, which transforms it to the form

$$\sum r_i(\dots ){\mathcal{A}}_i=0.$$

(2)

Here, ${\mathcal{A}}_i$ are functions. $r_i$ are nonlinear algebraic relationships between the parameters of the solved equation and the parameters of the solution. We set

$$r_i=0.$$

(3)

Thus, a system of nonlinear algebraic equations is obtained. Each nontrivial solution of (3) leads to a solution of (1).

There are four steps for transitioning from (1) to (3). They are as follows:

• Step 1.
  We apply the transformation

  $$u(x,\dots ,t)=T\left[F\right(x,\dots ,t),G(x,\dots ,t),\dots ],$$

  (4)

  to (1). $T(F,G,\dots )$ is a composite function of other functions $F,G,\dots$. The functions $F,G,\dots$ can be functions of several spatial variables and time. In the most used specific case of SEsM, the functions $F,G,\dots$ are functions of a spatial coordinate and the time. The transformation (4) has two goals.

  (a)

  If possible, (4) removes the nonlinearity of the solved equation and transforms it to a linear differential equation. The classic example of such a transformation is the Hopf–Cole transformation [210,211].

  (b)

  The removal of nonlinearity is rarely achieved. Then, the goal of the transformation (4) is to transform the nonlinearity of the solved equation to a more treatable kind of nonlinearity. The most treatable kind of nonlinearity is the polynomial nonlinearity.

  The determination of the transformation T can be performed at Step 1. Another possibility is to perform the determination of T in Step 3.
• Step 2.
  Selection of the functions $F(x,\dots ,t)$, $G(x,\dots ,t)$, …. They are composite functions of known solutions to more simple differential equations. We can
  • Fix these functions at this step.
  • Leave the fixing for Step 3.
  Let us mention two much-used examples of fixing the composite function for the specific case $F(x,\dots ,t)$.

  (a)

  The first example is as follows:

  $$F=\alpha +\sum _{i_1=1}^N{\beta }_{i_1}{f}_{i_1}+\sum _{i_1=1}^N\sum _{i_2=1}^N{\gamma }_{i_1,i_2}{f}_{i_1}{f}_{i_2}+\sum _{i_1=1}^N\dots \sum _{i_N=1}^N{\sigma }_{i_1,\dots ,i_N}{f}_{i_1}\dots f_{i_N}.$$

  (5)

  $\alpha ,{\beta }_{i_1},{\gamma }_{i_1,i_2},{\sigma }_{i_1,\dots ,i_N}\dots$ are parameters. $f_{ij}$ are solutions to some simple equations. The relationship used by Hirota [90] is a specific case of (5).

  (b)

  A specific case of (5), where F is the power series

  $$F=\sum _{i=0}^N{\mu }_n{f}^n.$$

  (6)

  $\mu$ is a parameter, and f is a solution of a simpler equation. Below, we use (5) in SEsM(1,m) and (6) in SEsM(1,1).

• Step 3.
  At this step, we have to determine

  (a)

  The form of the simple equations used.

  (b)

  The form of the composite function T,

  if these have not been determined in the previous two steps of SEsM. The idea of the determination of T is to reach the form (2) for the solved equation. An additional requirement is that the relationships $r_i$ in (2) must contain at least two terms in order to obtain a nontrivial solution to the solved equation. This additional requirement usually leads to one, or more than one, relationship among the parameters, participating in the relationships for $r_i$. These relationships are called balance equations.
• Step 4.
  Finally, we have to solve (2). This is made by setting the relationships for $r_i$ to $r_i=0$ as in (2). This leads to a system of nonlinear algebraic equations. Each nontrivial solution of the obtained system of nonlinear algebraic equations leads to a nontrivial solution of the solved Equation (1).

3. Short Overview of Some Important Work on the Methodology of SEsM

In this section, we mention several developments in the methodology of SEsM. We discuss the transformations that can convert the nonlinearity of the solved equation to a more treatable nonlinearity. Then, we mention the use of composite functions in SEsM and note two theorems connected with different forms of the used simple equations.

3.1. Transformations of Nonlinearity for Step 1 of SEsM

• Case of polynomial nonlinearity in solved Equation (1):
  There is no need for transformation. One can proceed to the next steps of SEsM.
• Case of nonpolynomial nonlinearity in (1):
  A transformation can be used in order to remove the nonlinearity or to reduce the nonlinearity to a polynomial nonlinearity. In ref. [246], we proved the following proposition:

Proposition 1.

Let us consider a differential equation for the function $u(x,\dots ,t)$ that contains terms of two kinds:

(a) 

Terms containing only derivatives of u;

(b) 

Terms containing one or several non-polynomial nonlinearities of the function u and where these nonpolynomial nonlinearities are of the same kind.

Let $u=T\left(F\right)$ be a transformation with the following properties:

(a) 

Property 1: The transformation T transforms any of the nonpolynomial nonlinearity to a function that contains only polynomials of F.

(b) 

Property 2: The transformation T transforms the derivatives of u to terms containing only polynomials of derivatives of F or polynomials of derivatives of F multiplied or divided by polynomials of F.

Then, the transformation T transforms the studied differential equation into a differential equation containing only polynomial nonlinearity of F.

• A list of some nonpolynomial nonlinearities that can be transformed into polynomial nonlinearities is presented in [246]. Two examples of non-linearities $N\left(u\right)$ that can be transformed are (m is an integer below)

Case 1: 

$N\left(u\right)={[exp\left(u\right)]}^m$. The transformation is $u=ln\left(F\right)$.

Case 2: 

$N\left(u\right)={[sin\left(u\right)]}^m$. The transformation is $u=4{tan}^{-1}\left(F\right)$.

3.2. Composite Functions and SEsM

Composite functions are important for Steps 2 and 3 of the algorithm of SEsM. They represent the solution of the solved complicated nonlinear differential equation by means of known exact solutions of simpler differential equations. The theory of the application of composite functions in SesM can be seen in [247,263]. We only mention two theorems from these studies that will be of interest to us below in the text. Let us denote the function $h(x_1,\dots ,x_d)$ of d independent variables $x_1,\dots ,x_d$, which is a composite function of m other functions $g_1^{\left(1\right)},\dots ,g^{\left(m\right)}$

$$h(x_1,\dots ,x_d)=f[g^{\left(1\right)}(x_1,\dots ,x_d),\dots ,g^{\left(m\right)}(x_1,\dots ,x_d)].$$

(7)

For the derivatives below, we will use the notations

• $g_{\left(k\right)}$: k-th derivative of the function $g\left(\xi \right)$ of the single variable $\xi$
• $g_{\left({\xi }_k\right)}$: Derivation with respect to the variable ${\xi }_k$ of the function of many variables $g({\xi }_1\dots ,{\xi }_k,\dots )$. A second derivative of such a kind will be denoted as $g_{({\xi }_k,{\xi }_l)}$, etc.

The theorems are

Theorem 1.

Let us consider a nonlinear partial differential equation that contains a polynomial P of the function $h(x_1,x_2)$ and its derivatives. We search for a solution of the above equation in the form

$$h(x_1,x_2)=f[g^{\left(1\right)}(x_1,x_2),\dots ,g^{\left(m\right)}(x_1,x_2)]$$

where h is the polynomial of the functions $g^{\left(1\right)}(x_1,x_2),\dots ,g^{\left(m\right)}(x_1,x_2)$. Let each function $g^{\left(i\right)}(x_1,x_2)$ satisfy the simple equation

$$g_{\left(x_j\right)}^{\left(i\right)}={\alpha }_{i,j}{g}^{\left(i\right)}$$

(8)

where ${\alpha }_{i,j}$ is a constant parameter. Then, the solved nonlinear PDE is reduced to a polynomial of the functions $g^{\left(1\right)}(x_1,x_2),\dots ,g^{\left(m\right)}(x_1,x_2)$ containing monomials multiplied by certain coefficients. These coefficients are nonlinear algebraic relations between the parameters of the solved equation and parameters ${\alpha }_{i,j}$. We set the above coefficients to 0. The result is a system of nonlinear algebraic equations. Any nontrivial solution to this system leads to a solution to the solved nonlinear PDE.

The second theorem is connected to the use of a composite function of a function of a single variable. We will use the following notation:

1.

We want to obtain an exact solution to a nonlinear partial differential equation with nonlinearities, which are polynomials of the unknown function $h(x,t)$ and its derivatives.

2.

The search solution is of the kind

$$h(x,t)=h\left(\xi \right);\xi =\mu x+\nu t,$$

(9)

where $\mu$ and $\nu$ are parameters.

3.

h is a composite function of another function g:

$$h=f\left[g\right(\xi \left)\right].$$

(10)

4.

We assume that f is a polynomial of g:

$$f=\sum _{r=0}^q{b}_r{g}^r,$$

(11)

5.

The general form of the simple equation is

$$g_{\left(k\right)}^l={\left({\displaystyle \frac{d^{k}g}{d{\xi }^k}}\right)}^l=\sum _{j=0}^m{a}_j{g}^j.$$

(12)

Equation (12) defines the function $V_{a_0,a_1,\dots ,a_m}(\xi ;k,l,m)$, where k is the order of derivative of g, l is the degree of derivative, and m is the highest degree of the polynomial of g in the defining ODE. V has as specific cases the exponential, trigonometric, hyperbolic, elliptic functions of Weierstrass and Jacobi, etc.

(6)

The result of Theorem 2 is for the specific case of the simple equation

$$g_{\left(1\right)}^2={\left({\displaystyle \frac{dg}{d\xi }}\right)}^2=\sum _{j=0}^m{a}_j{g}^j.$$

(13)

The theorem is

Theorem 2.

If $g_{\left(1\right)}^2$ is given by Equation (13) and f is a polynomial of g given by Equation (28), then for $h\left[f\right(g\left)\right]$ the following relationship holds:

$$h_{\left(n\right)}=K_n(q,m)\left(g\right)+g_{\left(1\right)}{Z}_n(q,m)\left(g\right)$$

where $K_n(q,m)\left(g\right)$ and $Z_n(q,m)\left(g\right)$ are polynomials of the function $g\left(\xi \right)$.

The following notes are in order here:

• For some values of n, one of the polynomials $K_n(q,m)$ or $Z_n(q,m)$ can be equal to 0.
• The polynomials can be calculated using recurrence relationships [263]

  $$K_{n+1}={\displaystyle \frac{Z_n}{2}}\sum _{j=0}^{m}j{a}_j{g}^{j-1}+{\displaystyle \frac{d{Z}_n}{dg}}\sum _{j=0}^m{a}_j{g}^j;Z_{n+1}={\displaystyle \frac{d{K}_n}{dg}},$$

  (14)

  with $K_0={\displaystyle \sum _{r=0}^q}{b}_r{g}^r$ and $Z_0=0$.

The simple equation can have the specific form

$$g_{\left(1\right)}=\sum _{j=0}^n{c}_j{g}^j.$$

(15)

For the case when the simple equation has the specific form (15), we have a simpler situation. Instead of the two kinds of polynomials $Z_n$ and $K_n$, we have a single kind of polynomial $L_n$. In other words, for the case when the simple equation is of kind (15), $h_{\left(n\right)}$ is a polynomial of g: $h_{\left(n\right)}=L_n\left(g\right)$. These polynomials can be calculated as follows: We start with $L_0={\displaystyle \sum _{r=0}^q}{b}_r{g}^r$. Then, we use the recurrence relationship

$$L_{i+1}={\displaystyle \frac{d{L}_i}{dg}}\sum _{j=0}^m{c}_j{g}^j.$$

(16)

4. Selected Simple Equations Used in SEsM

The focus of this article is on simple equations. Below we show several results connected to four simple equations. We illustrate how SEsM can lead to multisoliton solutions when the simple equations used are equations for exponential functions. In addition, we present results for the cases when the used simple equations are differential equations for the functions ${\left[{\displaystyle \frac{1}{p+exp\left(q\xi \right)}}\right]}^r$, $1/{cosh}^n\left(\xi \right)$, and ${tanh}^n\left(\xi \right)$.

4.1. Simple Equation for the Exponential Function

This is one of the most simple differential equations:

$${\displaystyle \frac{dg}{d\xi }}=\mu g\left(\xi \right),$$

(17)

where $\mu$ is a parameter. The solution is $g\left(\xi \right)=exp\left(\mu \xi \right)$. We can use many simple equations of the kind (17) in order to obtain multisoliton solutions of various integrable equations. Let us illustrate this in the case of the Korteweg–de Vries equation.

Proposition 2.

The SEsM methodology allows obtaining a multi-soliton solution to the Korteweg–de Vries equation. The used specific case of SEsM is when N simple equations for exponential functions are used, and the solution is constructed by using of the composite function (5).

Proof. 

Let us consider the following version of the Korteweg–de Vries equation:

$$u_t-6u{u}_x+u_{xxx}=0.$$

(18)

• In Step 1 of SesM, we use the transformation

  $$u(x,t)=-2{\displaystyle \frac{{\mathsf{\partial }}^2}{\mathsf{\partial }{x}^2}}lnF(x,t).$$

  (19)
• In Step 2 of SEsM, we use as a composite function a specific case of Equation (5), where $\alpha =1$, ${\beta }_i=1$, ${\gamma }_{ij}\ne 0$ for $i\ne j$, ${\delta }_{ijk}\ne 0$ for $i\ne j\ne k$,…. We obtain

  $$F=1+\sum _{i=1}^N{f}_i+\sum _{(i\ne j),i,j=1}^N{\gamma }_{i,j}{f}_i{f}_j+\sum _{(i\ne j\ne k),i,j,k=1}^N{\delta }_{i,j,k}{f}_i{f}_j{f}_k+\dots +{\sigma }_{1,\dots ,N}{f}_1\dots f_N.$$

  (20)
• In Step 3 of SEsM, we choose the simple equations as equations for exponential functions:

  $${\displaystyle \frac{d{f}_i}{d{\xi }_i}}=f_i,{\xi }_i=p_{i}x-{\omega }_{i}t-{\xi }_{i0}.$$

  (21)
  The solution of these simple equations is $f_i\left({\xi }_i\right)=exp\left({\xi }_i\right)$.
• We substitute Equations (21) into Equation (20). Then, we select the coefficients $\gamma ,\delta ,\dots ,\sigma$ appropriately in order to obtain the relationship

  $$F=1+\sum _{n=1}^N\sum _{\left({\displaystyle \genfrac{}{}{0pt}{}{N}{n}}\right)}\left[exp({\xi }_{i_1}+\dots +{\xi }_{i_N})\prod _{k<l}^{\left(n\right)}{\displaystyle \frac{{(p_{ik}-p_{il})}^2}{{(p_{ik}+p_{il})}^2}}\right].$$

  (22)
  Above ${\displaystyle \sum _{\left({\displaystyle \genfrac{}{}{0pt}{}{N}{n}}\right)}}$ is the sum of all combinations of n elements taken from the set of N elements, and ${\displaystyle \prod _{k<l}^{\left(n\right)}}$ is the product of all possible combinations of the n elements with the condition $k<l$.
• We complete Step 3 of SEsM by substitution of

  $$u(x,t)=-2{\displaystyle \frac{{\mathsf{\partial }}^2}{\mathsf{\partial }{x}^2}}ln\left\{1+\sum _{n=1}^N\sum _{\left({\displaystyle \genfrac{}{}{0pt}{}{N}{n}}\right)}\left[exp({\xi }_{i_1}+\dots +{\xi }_{i_N})\prod _{k<l}^{\left(n\right)}{\displaystyle \frac{{(p_{ik}-p_{il})}^2}{{(p_{ik}+p_{il})}^2}}\right]\right\},$$

  (23)

  into Equation (18). This substitution converts this equation to a system of algebraic relationships:

  $$\begin{array}{c}\hfill {\displaystyle \sum _{l=0}^n}{\displaystyle \sum _{\left({\displaystyle \genfrac{}{}{0pt}{}{l}{n}}\right)}}\left[{\prod }_{k<m}^{\left(l\right)}{\displaystyle \frac{{(p_{ik}-p_{im})}^2}{{(p_{ik}+p_{im})}^2}}\right]\left[{\displaystyle \prod _{k>l,k<m}^{\left(n\right)}}{\displaystyle \frac{{(p_{ik}-p_{im})}^2}{{(p_{ik}+p_{im})}^2}}\right]\left[\right(-p_{i_1}-\dots -p_{i_l}+p_{i_{(l+1)}}+\dots +\\ \hfill p_{i_n}){(-p_{i_1}-\dots -p_{i_l}+p_{i_{(l+1)}}+\dots +p_{i_n})}^3-(-p_{i_1}^3-\dots -p_{i_l}^3+p_{i_{(l+1)}}^3+\dots +\\ \hfill p_{i_n}^3\left)\right]=0.\\ \hfill {\omega }_i=p_i^3,\end{array}$$

  (24)

  for $n=1,\dots ,N$.
• In Step 4 of SEsM, we have to solve the nonlinear algebraic system (24). Each nontrivial solution leads to solitary or multisoliton solution of the Korteweg–de Vries equation.

□

As an example, let us obtain the two-soliton solution of the Korteweg–de Vries equation. We obtain this two-soliton solution for the case when we do not fix the value of $\sigma$ ($\sigma \ne 0$).

• In Step 1 of SEsM, we set $u=p_x$ in Equation (18). The obtained relationship is integrated. Then, we apply the transformation $p={\displaystyle \frac{12}{\sigma }}{(lnF)}_x$. Thus, we arrive at the equation

  $$F{F}_{tx}+F{F}_{xxxx}-F_t{F}_x+3F_{xx}^2-4F_x{F}_{xxx}=0.$$

  (25)
• In Step 2 of SesM, we select the composite function $F(x,t)$, which is constructed by two functions $f_{1,2}$ (these functions will be connected below to solutions of two simple equations:

  $$F(x,t)=1+f_1(x,t)+f_2(x,t)+c{f}_1(x,t)f_2(x,t)$$

  (26)
• The substitution of Equation (26) into Equation (25) leads to

  $$\begin{array}{c}{f}_{1xxxx}+f_{2xxxx}+3f_{1xx}^2+c{f}_{1xt}{f}_2+f_{1xt}-f_{1t}{f}_{1x}-f_{1t}{f}_{2x}-4f_{1x}{f}_{1xxx}-\hfill \\ f_{1x}{f}_{2t}-4f_{1x}{f}_{2xxx}+6f_{1xx}{f}_{2xx}-4f_{1xxx}{f}_{2x}-f_{2t}{f}_{2x}-4f_{2x}{f}_{2xxx}+f_2{f}_{1xt}+f_2{f}_{1xxxx}+\hfill \\ f_2{f}_{2xt}+f_2{f}_{2xxxx}+f_1{f}_{1xt}+f_1{f}_{1xxxx}+f_1{f}_{2xt}+f_1{f}_{2xxxx}+f_{2xt}+c^2{f}_2^2{f}_1{f}_{1xt}+c^2{f}_2^2{f}_1{f}_{1xxxx}-\hfill \\ c^2{f}_2^2{f}_{1t}{f}_{1x}-4f_2^2{c}^2{f}_{1x}{f}_{1xxx}+c^2{f}_2{f}_1^2{f}_{2xt}+c^2{f}_2{f}_1^2{f}_{2xxxx}-12c^2{f}_2{f}_{1x}^2{f}_{2xx}-c^2{f}_1^2{f}_{2t}{f}_{2x}-\hfill \\ 4c^2{f}_1^2{f}_{2x}{f}_{2xxx}-12c^2{f}_1{f}_{1xx}{f}_{2x}^2+2c{f}_2{f}_1{f}_{1xt}+2c{f}_2{f}_1{f}_{1xxxx}+2c{f}_2{f}_1{f}_{2xt}+2c{f}_2{f}_1{f}_{2xxxx}-\hfill \\ 2c{f}_2{f}_{1t}{f}_{1x}-8c{f}_2{f}_{1x}{f}_{1xxx}+12c{f}_2{f}_{1xx}{f}_{2xx}+12c{f}_1{f}_{1xx}{f}_{2xx}-2c{f}_1{f}_{2t}{f}_{2x}-8c{f}_1{f}_{2x}{f}_{2xxx}+\hfill \\ 12c^2{f}_{1x}^2{f}_{2x}^2-12c{f}_{1x}^2{f}_{2xx}-12c{f}_{1xx}{f}_{2x}^2+3c^2{f}_2^2{f}_{1xx}^2+3c^2{f}_1^2{f}_{2xx}^2+c{f}_2^2{f}_{1xt}+c{f}_2^2{f}_{1xxxx}+\hfill \\ 6c{f}_2{f}_{1xx}^2+c{f}_1^2{f}_{2xt}+c{f}_1^2{f}_{2xxxx}+6c{f}_1{f}_{2xx}^2+c{f}_1{f}_{2xt}+c{f}_1{f}_{2xxxx}+6c{f}_{1xx}{f}_{2xx}+4c{f}_{1x}{f}_{2xxx}+\hfill \\ c{f}_{1x}{f}_{2t}+c{f}_{1xxxx}{f}_2+12c^2{f}_2{f}_1{f}_{1xx}{f}_{2xx}+c{f}_{1t}{f}_{2x}+4c{f}_{1xxx}{f}_{2x}+3f_{2xx}^2=0.\hfill \end{array}$$

  (27)
• At Step 3 of SEsM, we select the simple equations for $f_{1.2}$:

  $$\begin{array}{ccc}{\displaystyle \frac{\mathsf{\partial }{f}_1}{\mathsf{\partial }x}}& =& {\alpha }_1{f}_1;{\displaystyle \frac{\mathsf{\partial }{f}_1}{\mathsf{\partial }t}}={\beta }_1{f}_1;\\ {\displaystyle \frac{\mathsf{\partial }{f}_2}{\mathsf{\partial }x}}& =& {\alpha }_2{f}_2;{\displaystyle \frac{\mathsf{\partial }{f}_2}{\mathsf{\partial }t}}={\beta }_2{f}_2.\end{array}$$

  (28)
  This choice will transform Equation (27) to a polynomial of $f_1$ and $f_2$. Further, we assume that $\xi ={\alpha }_{1}x+{\beta }_{1}t+{\gamma }_1$ and $\zeta ={\alpha }_{2}x+{\beta }_{2}t+{\gamma }_2$ (${\alpha }_{1,2}$, ${\beta }_{1,2}$ and ${\gamma }_{1,2}$ are parameters). In addition,

  $$f_1(x,t)=a\left(\xi \right);f_2(x,t)=b\left(\zeta \right);a\left(\xi \right)=q_{1}v\left(\xi \right);b\left(\zeta \right)=r_{1}w\left(\zeta \right).$$

  (29)
  The simple equations for $v\left(\xi \right)$ and $w\left(\zeta \right)$ are ${\displaystyle \frac{dv}{d\xi }}=v;{\displaystyle \frac{dw}{d\zeta }}=w$, and the corresponding solutions are $v\left(\xi \right)={\omega }_{1}exp\left(\xi \right);w\left(\zeta \right)={\omega }_{2}exp\left(\zeta \right)$. Below we assume that

  (a)

  The parameters ${\omega }_{1,2}$ are included in the parameters $q_1$ and $r_1$, respectively.

  (b)

  $q_1$ and $r_1$ can be included in $\xi$ and $\zeta$.

• At Step 4 of SEsM, we complete the conversion of the solved nonlinear differential equation to a system of nonlinear algebraic equations. We substitute Equations (28), (29) into Equation (27). The result is a sum of exponential functions and each exponential function is multiplied by a coefficient. Each of these coefficients is a relationship containing the parameters of the solution, and all the relationships contain more than one term. Thus, we do not need to perform a balance procedure.
  The system of algebraic equations is obtained by setting the abovementioned relationships to 0. The system is

  $$\begin{array}{c}{\alpha }_1^3+{\beta }_1=0,\hfill \\ {\alpha }_2^3+{\beta }_2=0,\hfill \\ (c+1){\alpha }_1^4+4{\alpha }_2(c-1){\alpha }_1^3+6{\alpha }_2^2(c+1){\alpha }_1^2+[(4c-4){\alpha }_2^3+({\beta }_1+{\beta }_2)c+\hfill \\ {\beta }_1-{\beta }_2]{\alpha }_1+[(c+1){\alpha }_2^3+({\beta }_1+{\beta }_2)c-{\beta }_1+{\beta }_2]{\alpha }_2=0.\hfill \end{array}$$

  (30)
  We can obtain a non-trivial solution of this system. This is

  $${\beta }_1=-{\alpha }_1^3;{\beta }_2=-{\alpha }_2^3;c={\displaystyle \frac{{({\alpha }_1-{\alpha }_2)}^2}{{({\alpha }_1+{\alpha }_2)}^2}}.$$

  (31)
  The corresponding solution of Equation (18) is

  $$\begin{array}{ccc}u(x,t)& =& {\displaystyle \frac{12}{\sigma }}{\displaystyle \frac{{\mathsf{\partial }}^2}{\mathsf{\partial }{x}^2}}[1+exp\left({\alpha }_{1}x-{\alpha }_1^{3}t+{\gamma }_1\right)+exp\left({\alpha }_{2}x-{\alpha }_2^{3}t+{\gamma }_2\right)+\\ & & {\displaystyle \frac{{({\alpha }_1-{\alpha }_2)}^2}{{({\alpha }_1+{\alpha }_2)}^2}}exp\left(({\alpha }_1+{\alpha }_2)x-({\alpha }_1^3+{\alpha }_2^3)t+{\gamma }_1+{\gamma }_2\right)].\end{array}$$

  (32)
  This is the bisoliton solution of the Korteweg–de Vries equation.

We can formulate

Proposition 3.

Each analytical exact solution of a nonlinear differential equation that can be obtained by other methodologies can also be obtained in principle using the methodology of SEsM.

Proof. 

Let us consider an analytical exact solution of a nonlinear differential equation

• The analytical exact solution of a nonlinear differential equation is constructed using certain functions, which can be elementary or special functions.
• Thus, the exact solution is a composite function of certain more simple functions. Each of these more simple functions is a solution of a certain simple differential equation.
• We choose for composite function in Step 2 of SEsM the abovementioned composite function.
• As simple equations in Step 3 of SEsM, we choose the differential equations for the functions that participate in the considered analytical exact solution.
• Thus, by means of SEsM we can construct the corresponding exact solution of the nonlinear differential equation.

□

The multisolition solutions of many nonlinear partial differential equations obtained by the method of Hirota and by the Method of Inverse Scattering Transform contain exponential functions. According to Proposition 3, these solutions can also be obtained by SEsM on the basis of the choice of an appropriate composite function at Step 2 of SEsM and the use of a sufficient number of simple equations for exponential functions at Step 3 of SEsM.

4.2. Simple Equation for the Function ${\left[{\displaystyle \frac{1}{p+exp\left(q\xi \right)}}\right]}^r$

Simple equations for functions containing exponential functions can also be used for obtaining specific solutions of nonintegrable equations. Let us consider the simple equation

$${\displaystyle \frac{dv}{d\xi }}=v^2-v.$$

(33)

It has the solution

$$v\left(\xi \right)={\displaystyle \frac{1}{1+exp\left(\xi \right)}}$$

(34)

We can search for solutions to the solved nonlinear partial differential equations $\mathcal{D}u\left(\xi \right)=0$ as

$$u\left(\xi \right)=\sum _{i=0}^N{a}_i{v}^i.$$

(35)

This was proposed by Kudryashov in 2012 [220].

Proposition 4.

The above approach of Kudryashov is a specific case of the SEsM methodology for the case of the use of one simple equation and representation of the searched solution as a polynomial of the solution of a simple equation of specific form (33).

Proof. 

Let us consider the SEsM methodology.

• In Step 2 of SEsM, we choose the form of the composite function to be (35).
• In Step 3 of SEsM, we choose the equation for the simple equation to be (33).
• Thus, the above approach of Kudryashov is a specific case of the SEsM methodology.

□

Of course, within the scope of SEsM, we can consider a simple equation that contains (33) as a specific case. This simple equation is

$${\displaystyle \frac{dv}{d\xi }}=qr[p{v}^{1+1/r}-v],$$

(36)

where $p,q,r$ are real numbers that are different from 0. (36) has the solution

$$v\left(\xi \right)={\left[{\displaystyle \frac{1}{p+exp\left(q\xi \right)}}\right]}^r.$$

(37)

The simple Equation (36) contains the case studied by Kudryashov as a specific case for $p=q=r=1$.

The simple Equation (36) can lead to numerous exact solutions to nonlinear differential equations containing polynomial nonlinearities. This feature is based on the following:

Proposition 5.

Let us consider the power series $u\left(\xi \right)={\displaystyle \sum _{i=0}^N}{a}_i{v}^i$, where $a_i$ are real numbers and $v\left(\xi \right)$ is a solution of the Equation (36). Then, the derivatives of $u\left(\xi \right)$ are power series of $v\left(\xi \right)$.

Proof. 

We will use the method of mathematical induction.

• First, we prove that the statement of the proposition is true for the first derivative ${\displaystyle \frac{du}{d\xi }}$. We have

  $${\displaystyle \frac{du}{d\xi }}=\sum _{i=0}^{N}i{a}_i{v}^{i-1}{\displaystyle \frac{dv}{d\xi }}=\sum _{i=0}^{N}i{a}_i\left[p{v}^{i+1/r}-r{v}^{i-1}\right].$$
  The statement of the proposition is true.
• Let the statement be true for $n=k\ne 1$. In other words, ${\displaystyle \frac{d^{k}u}{d{\xi }^k}}$ is a power series of $v\left(\xi \right)$.
• Then, for $n=k+1$

  $${\displaystyle \frac{d^{k+1}u}{d{\xi }^{k+1}}}={\displaystyle \frac{d\frac{d^{k}u}{d{\xi }^k}}{dv}}{\displaystyle \frac{dv}{d\xi }}$$

  is again a power series of $v\left(\xi \right)$, as it is a product of the power series occurring from ${\displaystyle \frac{d\frac{d^{k}u}{d{\xi }^k}}{dv}}$ and the relation ${\displaystyle \frac{dv}{d\xi }}$ which contains only powers of $v\left(\xi \right)$.

□

The Proposition 5 allows us to reduce many nonlinear differential equations to power series, containing powers of v multiplied by coefficients that are nonlinear algebraic relationships of the parameters of the problem and parameters of the solution. Then, we can proceed to Step 4 of SEsM, and each nontrivial solution of the obtained system of nonlinear algebraic equations will lead to a solution of the corresponding nonlinear differential equation.

Let us give several examples of equations which have exact solutions constructed on the basis of the composite function (35) and the simple Equation (36). We consider the equation

$$u^{\alpha }{\left({\displaystyle \frac{du}{d\xi }}\right)}^{\beta }=\sum _{j=0}^M{b}_j{u}^j.$$

(38)

We consider the case where $\alpha ,\beta ,s$ are integers and $r=1/s$ in (36). The steps of SEsM are as follows:

• Step 1: We do not need a transformation, as the nonlinearities in (38) are of polynomial kind.
• Step 2: As a composite function for the solution $u\left(\xi \right)$, we use (35)
• Step 3: As a simple equation, we use (36). All the above leads to the reduction of (38) to a polynomial of v:

  $$P\left(v\right)={\left({\displaystyle \frac{q}{s}}\right)}^{\beta }{\left(\sum _{i=0}^N{a}_i{v}^i\right)}^{\alpha }{\left[\sum _{k=0}^{N}k{a}_k{v}^k(p{v}^s-1)\right]}^{\beta }-\sum _{j=0}^M{b}_j{\left(\sum _{i=0}^N{a}_i{v}^i\right)}^j.$$

  (39)
  We have to ensure that the coefficient for each power of $P\left(v\right)$ has at least two terms. In order to achieve this, we have to balance the maximum powers of the term of $P\left(v\right)$. This operation leads to the balance equation

  $$\beta s=N(M-\alpha -\beta ).$$

  (40)
• Step 4: We set $P\left(v\right)=0$. This leads to a system of nonlinear algebraic equations. Each nontrivial solution of this system leads to a solution of (38) of the kind

  $$u\left(\xi \right)=\sum _{i=0}^{{\displaystyle \frac{\beta s}{M-\alpha -\beta }}}{a}_i{\left[{\displaystyle \frac{1}{p+exp\left(q\xi \right)}}\right]}^{i/s}.$$

  (41)

Let us obtain several solutions to (38). We will consider the specific case $\alpha =0$. The balance equation is $\beta s=N(M-\beta )$. We solve the differential equation ${\left({\displaystyle \frac{du}{d\xi }}\right)}^{\beta }={\displaystyle \sum _{j=0}^M}{b}_j{u}^j$, and search for a solution of the kind $u\left(\xi \right)={\displaystyle \sum _{i=0}^{\frac{\beta s}{M-\beta }}}{a}_i{\left[{\displaystyle \frac{1}{p+exp\left(q\xi \right)}}\right]}^{i/s}$. The case of Kudryashov is for $\beta =1,s=1,N=1,M=2$, and $a_0=0$, $a_1=-1$, $a_2=1$.

• We let $\beta =1$. The balance equation becomes $s=N(M-1)$. Let $s=2$. Then, $M=1+2/N$. ${\displaystyle \frac{du}{d\xi }}={\displaystyle \sum _{j=0}^{1+2/N}}{b}_j{u}^j$, and search for a solution of the kind $u\left(\xi \right)={\displaystyle \sum _{i=0}^N}{a}_i{\left[{\displaystyle \frac{1}{p+exp\left(q\xi \right)}}\right]}^{i/2}$, $p>0$. We consider two cases:

  –

  Case $N=1$ The equation is

  $${\displaystyle \frac{du}{d\xi }}=b_0+b_{1}u+b_2{u}^2+b_3{u}^3.$$

  (42)

  SEsM reduces this equation to a system of nonlinear algebraic equations:

  $$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{2}}pq-b_3{a}_1^2& \hfill =& \hfill 0,\\ \hfill b_2+3b_3{a}_0& \hfill =& \hfill 0,\\ \hfill {\displaystyle \frac{1}{2}}q{a}_1-3b_3{a}_0^2-2b_2{a}_0{a}_1-b_1{a}_1& \hfill =& \hfill 0,\\ \hfill b_3{a}_0^3+b_2{a}_0^2+b_0+b_1{a}_0& \hfill =& \hfill 0.\end{array}$$

  (43)

  One solution to this system is

  $$a_0=-{\displaystyle \frac{b_2}{3b_3}};a_1={\displaystyle \frac{{[-p(3b_1{b}_3-b_2^2)]}^{1/2}}{3^{1/2}{b}_3}};q=-{\displaystyle \frac{2(3b_1{b}_3-b_2^2)}{3b_3}};b_0={\displaystyle \frac{b_2(2b_2^2-9b_1{b}_3)}{27b_3^2}}$$

  (44)

  The corresponding solution to (42) is

  $$u\left(\xi \right)=-{\displaystyle \frac{b_2}{3b_3}}+{\displaystyle \frac{{[-p(3b_1{b}_3-b_2^2)]}^{1/2}}{3^{1/2}{b}_3}}{\left[{\displaystyle \frac{1}{p+exp\left(-\frac{2(3b_1{b}_3-b_2^2)}{3b_3}\xi \right)}}\right]}^{1/2}.$$

  (45)

  –

  Case $N=2$ The equation is

  $${\displaystyle \frac{du}{d\xi }}=b_0+b_{1}u+b_2{u}^2.$$

  (46)

  This is a version of the Riccati equation. We know the general solution of this equation, but for completeness, we write the specific solution, which can be obtained by SEsM. SEsM reduces this equation to a system of nonlinear algebraic equations:

  $$\begin{array}{ccc}\hfill pq-b_2{a}_2& \hfill =& \hfill 0,\\ \hfill a_1(-2a_2{b}_2+{\displaystyle \frac{1}{2}}qp)& \hfill =& \hfill 0,\\ \hfill a_2{b}_1+b_2(2a_0{a}_2+a_1^2)+a_{2}q& \hfill =& \hfill 0,\\ \hfill a_1(b_1+2b_2{a}_0+{\displaystyle \frac{1}{2}}q)& \hfill =& \hfill 0,\\ \hfill b_0+a_0{b}_1+a_0^2{b}_2& \hfill =& \hfill 0.\end{array}$$

  (47)

  One solution to this system is

  $$a_0=-{\displaystyle \frac{b_1+{(b_1^2-4b_0{b}_2)}^{1/2}}{2b_2}};a_1=0;a_2=-{\displaystyle \frac{p{(b_1^2-4b_0{b}_2)}^{1/2}}{b_2}};q={(b_1^2-4b_0{b}_2)}^{1/2}.$$

  (48)

  The corresponding solution to (46) is

  $$u\left(\xi \right)=-{\displaystyle \frac{b_1-{(b_1^2-4b_0{b}_2)}^{1/2}}{2b_2}}-{\displaystyle \frac{p{(b_1^2-4b_0{b}_2)}^{1/2}}{b_2}}\left[{\displaystyle \frac{1}{p+exp\left[{(b_1^2-4b_0{b}_2)}^{1/2}\xi \right]}}\right].$$

  (49)

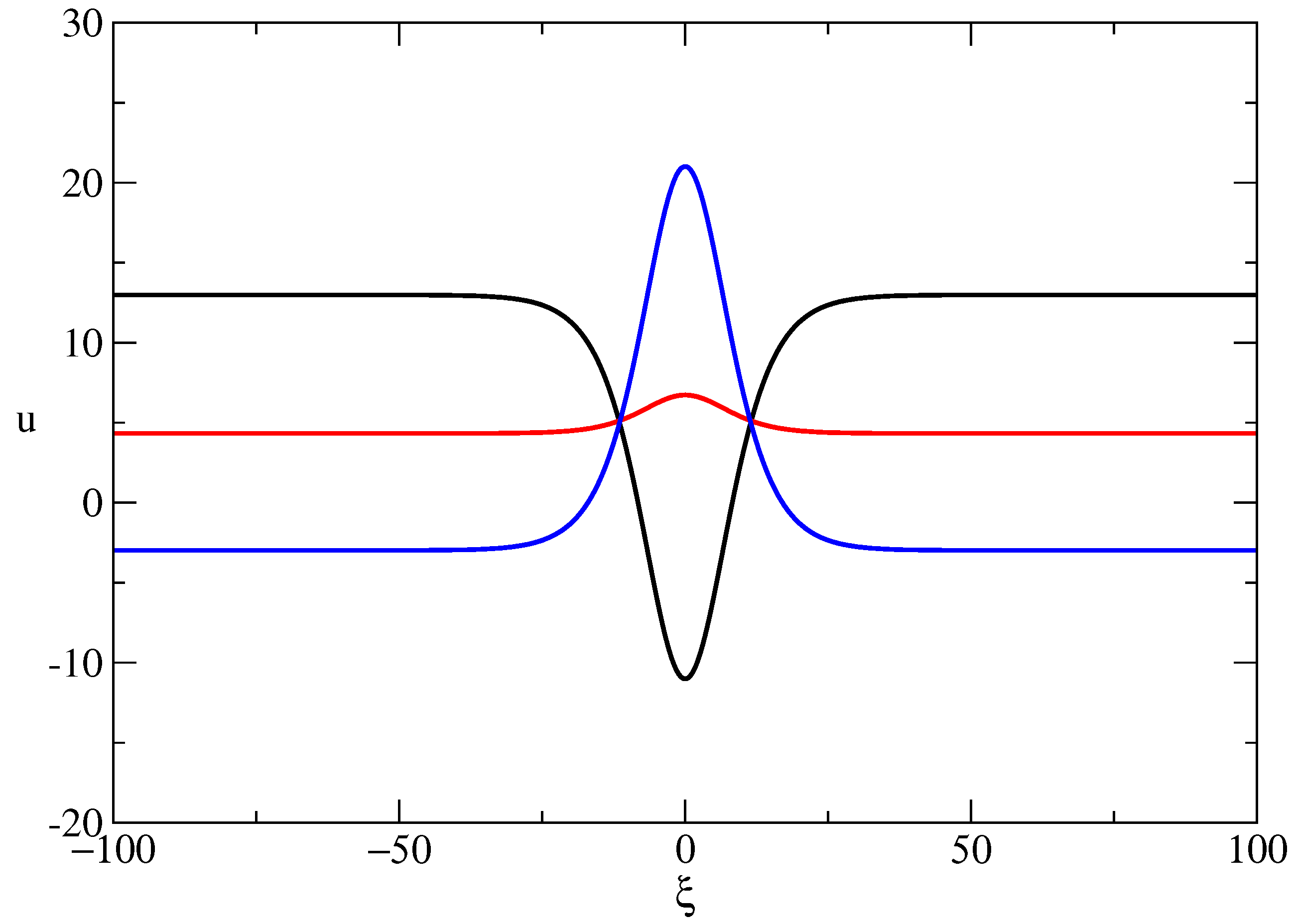
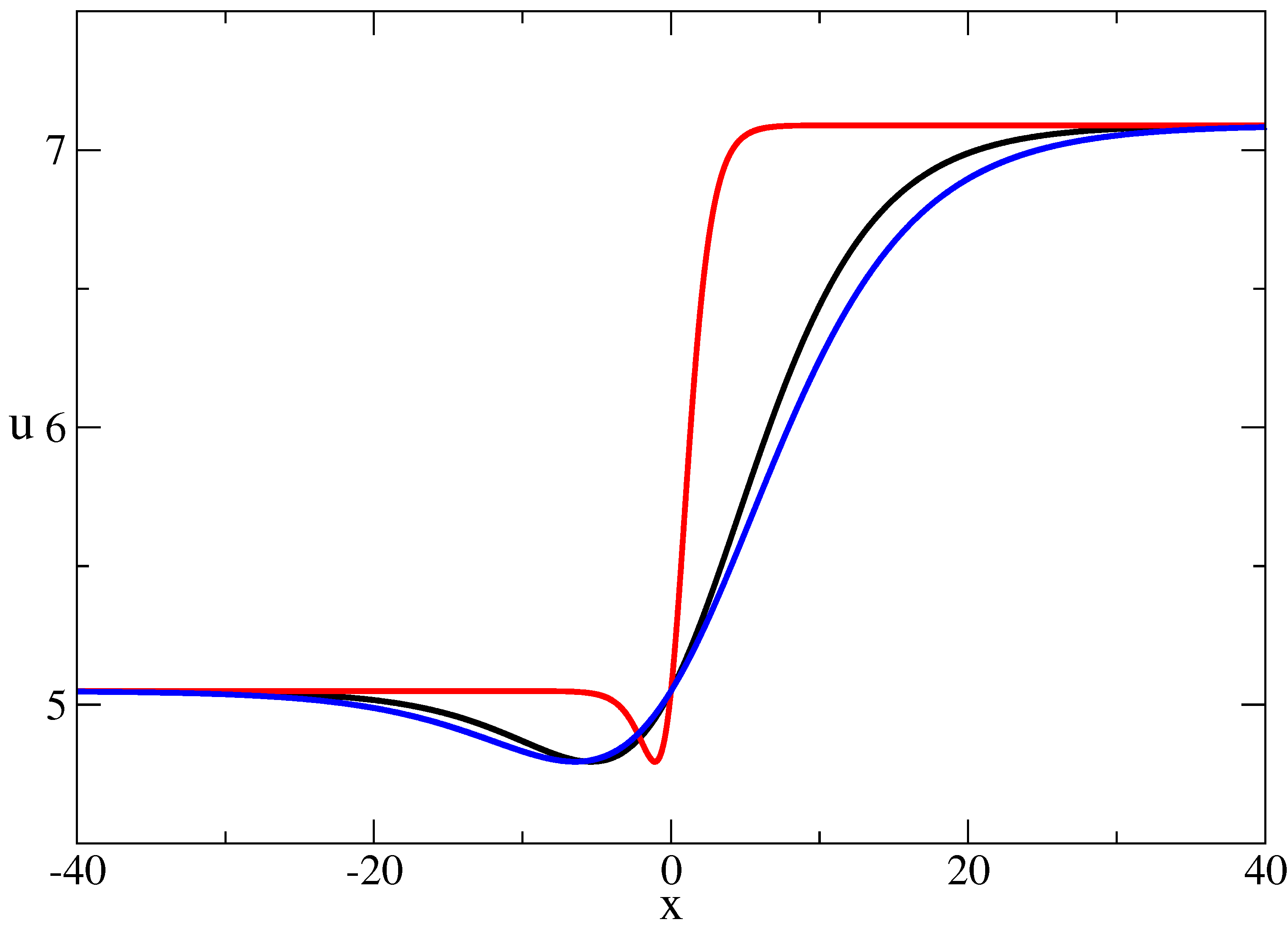
• Let now $\beta =2$. The balance equation becomes $s=N(M-2)/2$. Let us again consider the case $s=2$. Then $M=2+4/N$ We solve the equation ${\left({\displaystyle \frac{du}{d\xi }}\right)}^2={\displaystyle \sum _{j=0}^{2+4/N}}{b}_j{u}^j$, and search for a solution of the kind $u\left(\xi \right)={\displaystyle \sum _{i=0}^N}{a}_i{\left[{\displaystyle \frac{1}{p+exp\left(q\xi \right)}}\right]}^{i/2}$, $p>0$.
  We have the possibilities $N=1,2,4$. For $N=4$ and $N=2$, we obtain equations which are equations for the elliptic functions of Weierstrass and Jacobi. Then, the solutions obtained by means of SEsM will be specific cases of these functions. Because of this, we consider here the case $N=1$. Then, $M=6$, and we will obtain an exact solution to the equation

  $${\left({\displaystyle \frac{du}{d\xi }}\right)}^2=b_0+b_{1}u+b_2{u}^2+b_3{u}^3+b_4{u}^4+b_5{u}^5+b_6{u}^6.$$

  (50)
  SEsM transforms the solved equation into the following system of nonlinear differential equations:

  $$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{4}}{q}^2{p}^2-b_6{a}_1^4& \hfill =& \hfill 0,\\ \hfill b_5+6b_6{a}_0& \hfill =& \hfill 0,\\ \hfill -15b_6{a}_0^2{a}_1^2-{\displaystyle \frac{1}{2}}{q}^{2}p-b_4{a}_1^2-5b_5{a}_0{a}_1^2& \hfill =& \hfill 0,\\ \hfill 10b_5{a}_0^2+b_3+20b_6{a}_0^3+4b_4{a}_0& \hfill =& \hfill 0,\\ \hfill -b_2+{\displaystyle \frac{1}{4}}{q}^2-6b_4{a}_0^2-10b_5{a}_0^3-15b_6{a}_0^4-3b_3{a}_0& \hfill =& \hfill 0,\\ \hfill -3b_3{a}_0^2-6b_6{a}_0^5-4b_4{a}_0^3-b_1-2b_2{a}_0-5b_5{a}_0^4& \hfill =& \hfill 0,\\ \hfill -b_4{a}_0^2-b_5{a}_0^4-b_2{a}_0{b}_0-b_1-b_3{a}_0^2-b_6{a}_0^5& \hfill =& \hfill 0.\end{array}$$

  (51)
  One solution to this system is

  $$\begin{array}{c}\hfill a_0=-{\displaystyle \frac{1}{6}}{\displaystyle \frac{b_5}{b_6}};a_1={\displaystyle \frac{1}{2^{3/2}{3}^{1/2}{b}_6}}{\left[p^2(12b_4{b}_6-5b_5^2)\right]}^{1/4};\\ \hfill b_0={\displaystyle \frac{b_5^2}{186624b_6^5}}(-936b_5^2{b}_4{b}_6+169b_5^4+1296b_4^2{b}_6^2);\\ \hfill b_1={\displaystyle \frac{b_5}{1728b_6^4}}(13b_5^4-88b_4{b}_5^2{b}_6+144b_4^2{b}_6^2);\\ \hfill b_2={\displaystyle \frac{1}{1728b_6^3}}(432b_4^2{b}_6^2-25b_5^4-72b_4{b}_5^2{b}_6);\\ \hfill b_3={\displaystyle \frac{b_5}{27b_6^2}}(18b_4{b}_6-5b_5^2);q={\displaystyle \frac{12b_4{b}_6-5b_5^2}{12b_6^{3/2|}}}.\end{array}$$

  (52)
  The corresponding solution to (50) is

  $$u\left(\xi \right)=-{\displaystyle \frac{1}{6}}{\displaystyle \frac{b_5}{b_6}}+{\displaystyle \frac{{\left[p^2(12b_4{b}_6-5b_5^2)\right]}^{1/4}}{2^{3/2}{3}^{1/2}{b}_6}}{\left[{\displaystyle \frac{1}{p+exp\left(\frac{12b_4{b}_6-5b_5^2}{12b_6^{3/2|}}\xi \right)}}\right]}^{1/2}.$$

  (53)
  Figure 2 shows several profiles for the solution (53) for different values of the parameter $b_5$. The solution describes a kink wave. The wave becomes larger with decreasing value of $b_5$ and, at the same time, the area of the kink becomes smaller.

We can obtain exact solutions to more complicated equations. Let us consider, for example, the equation

$${\gamma }_{1}u{\displaystyle \frac{{\mathsf{\partial }}^{2}u}{\mathsf{\partial }{x}^2}}-{\gamma }_2{u}^2{\displaystyle \frac{{\mathsf{\partial }}^{2}u}{\mathsf{\partial }{t}^2}}=\sum _{j=0}^M{b}_j{u}^j.$$

(54)

${\gamma }_{1,2}$ are parameters. The search for traveling wave solutions of the kind $u(x,t)=u\left(\xi \right)=u(x-\nu t)$ leads to a need for a solution to an equation of the kind $({\gamma }_1+{\gamma }_2{\nu }^2){\displaystyle \frac{d^{2}u}{d{\xi }^2}}={\displaystyle \sum _{j=0}^M}{b}_j{u}^j.$ We will consider a more general version of this equation, namely

$$\left(\sum _{k=0}^L{\gamma }_k{u}^k\right){\displaystyle \frac{d^{2}u}{d{\xi }^2}}=\sum _{j=0}^M{b}_j{u}^j.$$

(55)

The solution will be of the kind $u\left(\xi \right)={\displaystyle \sum _{i=0}^N}{a}_i{v}^i$ and the simple equation will be of the kind (36). The steps of SEsM lead to the following balance equation ($s=1/r$):

$$N(M-L-1)=2s\to N={\displaystyle \frac{2s}{M-L-1}}.$$

(56)

For example, we consider the specific case $M=3,L=1$. Here, $N=2s$. Let $s=1$. Then, $N=2$. The solved equation is $\left({\gamma }_0+{\gamma }_{1}u\right){\displaystyle \frac{d^{2}u}{d{\xi }^2}}={\displaystyle \sum _{j=0}^2}{b}_j{u}^j$. The steps of SEsM transform this equation into a system of seven nonlinear algebraic equations. One solution to this system is

$$\begin{array}{ccc}{a}_0\hfill & =\hfill & -{\displaystyle \frac{1}{2{\gamma }_1{b}_3}}\left[{\gamma }_1{b}_2-{\gamma }_0{b}_3-{\left(-{\displaystyle \frac{{\gamma }_0{b}_3^2+2b_2{\gamma }_1{b}_3{\gamma }_0^2+4b_3{b}_0{\gamma }_1^3-b_2^2{\gamma }_0{\gamma }_1^2}{{\gamma }_0}}\right)}^{1/2}\right],\hfill \\ a_1\hfill & =\hfill & -{\displaystyle \frac{6p}{{\gamma }_1{b}_2}}{\left(-{\displaystyle \frac{{\gamma }_0{b}_3^2+2b_2{\gamma }_1{b}_3{\gamma }_0^2+4b_3{b}_0{\gamma }_1^3-b_2^2{\gamma }_0{\gamma }_1^2}{{\gamma }_0}}\right)}^{1/2},\hfill \\ a_2\hfill & =\hfill & {\displaystyle \frac{6p^2}{{\gamma }_1{b}_3}}{\left(-{\displaystyle \frac{{\gamma }_0{b}_3^2+2b_2{\gamma }_1{b}_3{\gamma }_0^2+4b_3{b}_0{\gamma }_1^3-b_2^2{\gamma }_0{\gamma }_1^2}{{\gamma }_0}}\right)}^{1/2},\hfill \\ b_1\hfill & =\hfill & {\displaystyle \frac{{\gamma }_0^2{\gamma }_1{b}_2-{\gamma }_0^3{b}_3+{\gamma }_1^3{b}_0}{{\gamma }_0{\gamma }_1^2}},\hfill \\ q\hfill & =\hfill & {\displaystyle \frac{1}{{\gamma }_1}}{\left(-{\displaystyle \frac{{\gamma }_0{b}_3^2+2b_2{\gamma }_1{b}_3{\gamma }_0^2+4b_3{b}_0{\gamma }_1^3-b_2^2{\gamma }_0{\gamma }_1^2}{{\gamma }_0}}\right)}^{1/4}.\hfill \end{array}$$

(57)

The corresponding solution to (55) is

$$\begin{array}{c}\hfill u\left(\xi \right)=-{\displaystyle \frac{1}{2{\gamma }_1{b}_3}}\left[{\gamma }_1{b}_2-{\gamma }_0{b}_3-{\left(-{\displaystyle \frac{{\gamma }_0{b}_3^2+2b_2{\gamma }_1{b}_3{\gamma }_0^2+4b_3{b}_0{\gamma }_1^3-b_2^2{\gamma }_0{\gamma }_1^2}{{\gamma }_0}}\right)}^{1/2}\right]+\\ \hfill -{\displaystyle \frac{6p}{{\gamma }_1{b}_2}}{\left(-{\displaystyle \frac{{\gamma }_0{b}_3^2+2b_2{\gamma }_1{b}_3{\gamma }_0^2+4b_3{b}_0{\gamma }_1^3-b_2^2{\gamma }_0{\gamma }_1^2}{{\gamma }_0}}\right)}^{1/2}{\displaystyle \frac{1}{p+exp\left[\frac{1}{{\gamma }_1}{\left(-\frac{{\gamma }_0{b}_3^2+2b_2{\gamma }_1{b}_3{\gamma }_0^2+4b_3{b}_0{\gamma }_1^3-b_2^2{\gamma }_0{\gamma }_1^2}{{\gamma }_0}\right)}^{1/4}\xi \right]}}+\\ \hfill {\displaystyle \frac{6p^2}{{\gamma }_1{b}_3}}{\left(-{\displaystyle \frac{{\gamma }_0{b}_3^2+2b_2{\gamma }_1{b}_3{\gamma }_0^2+4b_3{b}_0{\gamma }_1^3-b_2^2{\gamma }_0{\gamma }_1^2}{{\gamma }_0}}\right)}^{1/2}{\left[{\displaystyle \frac{1}{p+exp\left[\frac{1}{{\gamma }_1}{\left(-\frac{{\gamma }_0{b}_3^2+2b_2{\gamma }_1{b}_3{\gamma }_0^2+4b_3{b}_0{\gamma }_1^3-b_2^2{\gamma }_0{\gamma }_1^2}{{\gamma }_0}\right)}^{1/4}\xi \right]}}\right]}^2.\end{array}$$

(58)

We see that SEsM can lead to many solutions of nonlinear differential equations on the basis of the simple Equation (36). Let us now consider another interesting simple equation.

4.3. Simple Equation for $1/{cosh}^n$ Function

We consider a nonlinear partial differential equation and search for exact solutions on the basis of SEsM methodology. We consider the traveling wave solutions $u(x,t)=u\left(\xi \right)=u(\alpha x+\beta t)$, and we will use the simple equation

$$f_{\xi }^2=n^2(f^2-f^{{\displaystyle \frac{2n+2}{n}}}),$$

(59)

where n is an arbitrary positive real number. The solution of this equation is $f\left(\xi \right)={\displaystyle \frac{1}{{cosh}^n\left(x\right)}}$. We prove the following theorem about the exact solutions that can be obtained using this simple equation [264].

Theorem 3.

Let $\mathcal{P}$ be a polynomial of the function $u(x,t)$ and its derivatives. $u(x,t)$ belongs to the differentiability class $C^k$, where k is the highest order of derivative participating in $\mathcal{P}$. $\mathcal{P}$ can contain some or all of the following parts: (A) polynomial of u; (B) monomials that contain derivatives of u with respect to x and/or products of such derivatives. Each such monomial can be multiplied by a polynomial of u; (C) monomials that contain derivatives of u with respect to t and/or products of such derivatives. Each such monomial can be multiplied by a polynomial of u; (D) monomials that contain mixed derivatives of u with respect to x and t, and/or products of such derivatives. Each such monomial can be multiplied by a polynomial of u; (E) monomials that contain products of derivatives of u with respect to x and derivatives of u with respect to t. Each such monomial can be multiplied by a polynomial of u; (F) monomials that contain products of derivatives of u with respect to x and mixed derivatives of u with respect to x and t. Each such monomial can be multiplied by a polynomial of u; (G) monomials that contain products of derivatives of u with respect to t and mixed derivatives of u with respect to x and t. Each such monomial can be multiplied by a polynomial of u; (H) monomials that contain products of derivatives of u with respect to x, derivatives of u with respect to t and mixed derivatives of u with respect to x and t. Each such monomial can be multiplied by a polynomial of u.

Let us consider the nonlinear partial differential equation:

$$\mathcal{P}=0$$

(60)

We search for solutions to this equation of the kind $u\left(\xi \right)=\gamma f\left(\xi \right),\xi =\alpha x+\beta t$. γ is a parameter and $f\left(\xi \right)$ is a solution of the simple equation $f_{\xi }^2=n^2{f}^2-n^2{f}^{{\displaystyle \frac{2n+2}{n}}}$, where n is a real positive number. The substitution of this solution into (60) leads to a relationship R of the kind

$$R=\sum _{i=0}^{N_1}\sum _{j=0}^{M_1}{C}_{ij}f{\left(\xi \right)}^{(in+2j)/n}+f_{\xi }\sum _{k=-N_2^{\ast }}^{N_2}\sum _{l=0}^{M_2}{D}_{kl}f{\left(\xi \right)}^{(kn+2l)/n},$$

(61)

where $N_1,N_2,N_2^{\ast },M_1$ and $M_2$ are natural numbers depending on the form of the polynomial P. The coefficients $C_{ij}$ and $D_{kl}$ depend on the parameters of Equation (60) and on $\alpha ,\beta ,\gamma$. The sum ${\displaystyle \sum _{i=0}^{N_1}}{\displaystyle \sum _{j=0}^{M_1}}{C}_{ij}f{\left(\xi \right)}^{(in+2j)/n}$ consists of terms of the kind $C_p^{\ast }f{\left(\xi \right)}^{{\alpha }_p}$, where ${\alpha }_p$ is a certain number and $p=1,\dots$. The sum ${\displaystyle \sum _{k=0}^{N_2}}{\displaystyle \sum _{l=0}^{M_2}}{D}_{kl}f{\left(\xi \right)}^{(kn+2l)/n}$ consists of terms of the kind $D_q^{\ast }f{\left(\xi \right)}^{{\beta }_q}$, where ${\beta }_q$ is a certain number and $q=1,\dots$. The coefficients $C_p^{\ast }$ and $D_q^{\ast }$ depend on the parameters of Equation (60) and on $\alpha ,\beta ,\gamma$ Then, any nontrivial solution of the algebraic system

$$C_p^{\ast }=0;D_q^{\ast }=0,$$

(62)

leads to a solitary wave solution of the nonlinear PDE (60).

Let us again consider the Equation (55). We will discuss the specific case $n=1$. We will use the simple equation

$$f_{\xi }^2={\displaystyle \frac{q^2}{p^2}}\left(p^2{f}^2-f^4\right),$$

(63)

where the solution is $f=p/cosh\left(q\xi \right)$. The composite function that we will use in the application of SEsM will be $u\left(\xi \right)={\displaystyle \sum _{i=0}^N}{a}_{i}f{\left(\xi \right)}^i$. This leads to the balance equation $N(M-L-1)=2$. We consider the specific case $M=L+2$. Then, $N=2$. The application of SEsM transforms the solved equation into a system of nine nonlinear algebraic equations. One nontrivial solution to this system is

$$\begin{array}{c}\hfill a_0={\displaystyle \frac{{\gamma }_2{b}_3+{\gamma }_1{b}_4-4q^2{\gamma }_2^2}{2{\gamma }_2{b}_4}};a_1=0;a_2={\displaystyle \frac{6{\gamma }_2{q}^2}{b_4{p}^2}};\\ \hfill {\gamma }_0={\displaystyle \frac{4b_0{b}_4{\gamma }_2^3}{(-{\gamma }_2{b}_3-{\gamma }_1{b}_4+4q^2{\gamma }_2^2)({\gamma }_1{b}_4+{\gamma }_2{b}_3+4q^2{\gamma }_2^2)}};\\ \hfill b_1={\displaystyle \frac{16b_3{\gamma }_2^5{q}^4+3b_3{\gamma }_2{b}_2^4{\gamma }_1^2-4b_2{\gamma }_2^3{b}_3{b}_4-4b_2{\gamma }_2^2{\gamma }_1{b}_4^2+32b_4{\gamma }_1{\gamma }_2^4{q}^4-b_3^3{\gamma }_2^3+2b_4^3{\gamma }_1^3}{4{\gamma }_2^3{b}_4^2}};\\ \hfill b_2={\displaystyle \frac{-16b_0{b}_4^3{\gamma }_2^4-32b_3^2{\gamma }_2^6{q}^4-3b_3^4{\gamma }_1^4+b_4^4{\gamma }_2^4-6b_3^2{\gamma }_2^2{b}_4^2{\gamma }_1^2-8b_3{\gamma }_2{b}_4^3{\gamma }_1^3+32b_4^2{\gamma }_1^2{\gamma }_2^4{q}^4+256{\gamma }_2^8{q}^8}{4{\gamma }_2{b}_4(-{\gamma }_2{b}_3-{\gamma }_1{b}_4+4q^2{\gamma }_2^2)({\gamma }_1{b}_4+{\gamma }_2{b}_3+4q^2{\gamma }_2^2)}}.\end{array}$$

(64)

The corresponding solution of the solved equation is

$$u\left(\xi \right)={\displaystyle \frac{{\gamma }_2{b}_3+{\gamma }_1{b}_4-4q^2{\gamma }_2^2}{2{\gamma }_2{b}_4}}+{\displaystyle \frac{6{\gamma }_2{q}^2}{b_4{cosh}^2\left(q\xi \right)}}.$$

(65)

which describes a solitary wave.

Figure 3 shows several profiles connected to the solution (65). This solution describes a solitary wave. The height of the wave and its position with respect to the values of the solution for large absolute values of $\xi$ depend on the parameters of the solution. Figure 3 shows three profiles of the solitary wave for different values of the parameter ${\gamma }_2$. We see that with increasing values of ${\gamma }_2$, the solitary wave changes its orientation: the peak of the wave (which has a negative value for smaller values of ${\gamma }_2$) becomes positive when the value of ${\gamma }_2$ increases.

4.4. Simple Equation for ${tanh}^n$ Function

Below we shall consider traveling-wave solutions $u(x,t)=u\left(\xi \right)=u(\alpha x+\beta t),$ constructed on the basis of the simple equation

$$f_{\xi }=n\left[f^{(n-1)/n}-f^{(n+1)/n}\right],$$

(66)

where n is an appropriate positive real number. The solution of this equation is $f\left(\xi \right)={tanh}^n\left(\xi \right)$. n must be such a real number that ${tanh}^n\left(\xi \right)$ exists for $\xi \in (-\infty ,+\infty )$ ($n=1/3$ is an appropriate value for n and $n=1/2$ is not an appropriate value for n).

We formulate the following

Theorem 4.

Let $\mathcal{P}$ be a polynomial of the function $u(x,t)$ and its derivatives. $u(x,t)$ can be differentiated k times, where k is the highest order of derivative participating in $\mathcal{P}$. $\mathcal{P}$ can contain some or all of the following parts: (A) polynomial of u; (B) monomials that contain derivatives of u with respect to x and/or products of such derivatives. Each such monomial can be multiplied by a polynomial of u; (C) monomials that contain derivatives of u with respect to t and/or products of such derivatives. Each such monomial can be multiplied by a polynomial of u; (D) monomials that contain mixed derivatives of u with respect to x and t and/or products of such derivatives. Each such monomial can be multiplied by a polynomial of u; (E) monomials that contain products of derivatives of u with respect to x and derivatives of u with respect to t. Each such monomial can be multiplied by a polynomial of u; (F) monomials that contain products of derivatives of u with respect to x and mixed derivatives of u with respect to x and t. Each such monomial can be multiplied by a polynomial of u; (G) monomials that contain products of derivatives of u with respect to t and mixed derivatives of u with respect to x and t. Each such monomial can be multiplied by a polynomial of u; (H) monomials that contain products of derivatives of u with respect to x, derivatives of u with respect to t and mixed derivatives of u with respect to x and t. Each such monomial can be multiplied by a polynomial of u.

Let us consider the nonlinear partial differential equation:

$$\mathcal{P}=0.$$

(67)

We search for solutions to this equation of the kind $u\left(\xi \right)=\gamma +\delta f\left(\xi \right),\xi =\alpha x+\beta t$. γ and δ are parameters, and $f\left(\xi \right)$ is a solution of the simple equation $f_{\xi }=n\left[f^{(n-1)/n}-f^{(n+1)/n}\right]$ where n is an appropriate real positive number. The substitution of this solution in Equation (67) leads to a relationship R of the kind

$$R=\sum _{{\sigma }_i}{\kappa }_{{\sigma }_i}{f}^{{\sigma }_i},$$

(68)

where ${\sigma }_i$ are certain real numbers and ${\kappa }_{{\sigma }_i}$ are algebraic relationships containing the parameters of the solved equation and the parameters of the solution. Any nontrivial solution of the system of (nonlinear) algebraic equations ${\kappa }_{{\sigma }_i}=0$, $i=1,\dots$ leads to a solution of the solved nonlinear partial differential equation.

Let us prove the theorem.

Proof. 

Let us denote the k-th derivative of $f\left(\xi \right)$ as $f_{\xi }^{\left(k\right)}$. First, we shall prove that if $f\left(\xi \right)$ obeys Equation (66), then

$$f_{\xi }^{\left(k\right)}=\sum _{m=0}^k{g}_m\left(n\right)f^{(n-k+2m)/n}.$$

(69)

In order to prove this, we mention that $f_{\xi }$ satisfies this relationship, as can be seen from Equation (59). The second, third, and fourth derivatives of $f\left(\xi \right)$

$$\begin{array}{ccc}{f}_{\xi \xi }\hfill & =\hfill & n\left[(n-1)f^{(n-2)/n}-2nf+(n+1)f^{(n+2)/2}\right],\hfill \\ f_{\xi \xi \xi }\hfill & =\hfill & n[(n^2-3n+2)f^{(n-3)/n}+(-3n^2+3n-2)F^{(n-1)/n}+\hfill \\ \hfill & \hfill & (3n^2+3n+2)f^{(n+1)/n}-(n^2+3n+2)f^{(n+3)/3}],\hfill \\ f_{\xi \xi \xi \xi }\hfill & =\hfill & n[-(n^3-6n^2+11n-6)f^{(n-4)/n}-4(n^3-3n^2+4n-2)f^{(n-2)/n}+\hfill \\ \hfill & \hfill & (6n^3+10n)f-4(n^3+3n^2+4n+2)f^{(n+2)/n}+\hfill \\ \hfill & \hfill & (n^3+6n^2+11n+6)f^{(n+4)/n}],\hfill \end{array}$$

(70)

are of the kind (69). Let us assume that the k-th derivative of $f\left(\xi \right)$ is of kind (69). We shall show that the $(k+1)$-st derivative of $f\left(\xi \right)$ is of kind (69). From Equation (69), we obtain ($q=k+1$)

$$f_{\xi }^{(k+1)}=\sum _{m=0}^{q-1}{g}_m\left(n\right)(n-q+2m+1)f^{(n-q+2m)/n}-\sum _{m=0}^{q-1}{g}_m\left(n\right)(n-q+2m+1)f^{(n-q+2m+2)/n}$$

(71)

The term ${\displaystyle \sum _{m=0}^{q-1}}{g}_m\left(n\right)(n-q+2m+1)f^{(n-q+2m)/n}$ is of kind (69). Let us split the term ${\displaystyle \sum _{m=0}^{q-1}}{g}_m\left(n\right)(n-q+2m+1)f^{(n-q+2m+2)/n}$ into two parts: ${\displaystyle \sum _{m=0}^{q-2}}{g}_m\left(n\right)(n-q+2m+1)f^{(n-q+2m+2)/n}$ and ${\displaystyle \sum _{m=q-1}^{q-1}}{g}_m\left(n\right)(n-q+2m+1)f^{(n-q+2m+2)/n}$. The first term above is of kind (69). Thus, for $f_{\xi }^{(k+1)}$ we have up to now all terms of the sum (69) except the last one (the term corresponding to $m=q$, which must contain $f^{(n+q)/n}$). But let us consider the second term above. This is exactly the missing term, as it is equal to $g_{q-1}\left(n\right)(n+q-1)f^{(n+q)/n}$, which is a term of the same kind as the k-th term of the sum in Equation (69). Thus, the derivative $f_{\xi }^{(k+1)}$ is also of the kind (69) and our proposition is proven by the method of mathematical induction.

We have shown that $f_{\xi }^{\left(k\right)}$ is of the kind (68). Then, it follows that any of the terms $\left(A\right)$-$\left(H\right)$ are of the same kind or of the kind $f^0$. Thus, P is reduced to a relationship of kind (68). Then, any nontrivial solution of the system of nonlinear algebraic equations ${\kappa }_{{\sigma }_i}=0$, $i=1,\dots$ leads to a solution of the solved nonlinear partial differential equation $\mathcal{P}=0$. □

Next, we consider examples of the use of SEsM on the basis of the simple Equation (66). The first example is connected to the following equation from the class of reaction-telegraph equations [277]:

$$u_t-a{u}_{tt}-b{u}_{xx}-c(q+2ru)u_t-(p+qu+r{u}^2)=0.$$

(72)

The application of the methodology of SEsM on the basis of a solution $u(x,t)=\sigma +\delta f\left(\xi \right)$, $\xi =\alpha x+\beta t$ (where $f\left(\xi \right)$ is a solution to the simple Equation (66)) leads to the balance equation $n=1$ and to the reduction of Equation (72) to the following system of nonlinear partial differential equations:

$$\begin{array}{c}\hfill a{\beta }^2+{\alpha }^{2}b-\beta \delta cr=0,\\ \hfill \beta (2\sigma cr+cq-1)-\delta r=0,\\ \hfill \beta \delta cr-a{\beta }^2+{\alpha }^{2}b-\sigma r-{\displaystyle \frac{1}{2}}q=0\\ \hfill \beta \delta (1-2cr\sigma -cq)-r{\sigma }^2-q\sigma -p=0.\end{array}$$

(73)

One nontrivial solution to the system of Equations (73) is

$$\begin{array}{c}\hfill \alpha =-{\displaystyle \frac{1}{2b}}{\left[b(a+c)(4pr-q^2)\right]}^{1/2};\beta =-{\displaystyle \frac{1}{2}}{\left(q^2-4pr\right)}^{1/2}\\ \hfill \sigma =-{\displaystyle \frac{q}{2r}};\delta ={\displaystyle \frac{1}{2r}}{\left(q^2-4pr\right)}^{1/2},\end{array}$$

(74)

and the corresponding solution to Equation (72) is

$$\begin{array}{c}\hfill u(x,t)=-{\displaystyle \frac{q}{2r}}-{\displaystyle \frac{1}{2r}}{\left(q^2-4pr\right)}^{1/2}tanh\{{\displaystyle \frac{1}{2b}}{\left[b(a+c)(4pr-q^2)\right]}^{1/2}x+\\ \hfill {\displaystyle \frac{1}{2}}{\left(q^2-4pr\right)}^{1/2}t\}\end{array}$$

(75)

The second example is the equation

$$u_t-a{u}_{tt}-b{u}_{xx}-F\left(u\right)=0,$$

(76)

where $F\left(u\right)={\displaystyle \sum _{j=0}^M}{b}_j{u}^j$. We apply the simple Equation (66) for the case $n=1$. SEsM leads to the balance equation

$$N(M-1)=2.$$

(77)

We consider the case $M=N=2$. In this case, SEsM transforms (76) to a system of five nonlinear algebraic equations. One nontrivial solution to his system is

$$\begin{array}{c}\hfill a_0={\displaystyle \frac{4b_0{b}_2-b_1^2-{[b_1^2-4b_0{b}_2]}^{1/2}}{4b_2{[b_1^2-4b_0{b}_2]}^{1/2}}};a_1=-{\displaystyle \frac{{[b_1^2-4b_0{b}_2]}^{1/2}}{2b_2}};a_2={\displaystyle \frac{{[b_1^2-4b_0{b}_2]}^{1/2}}{4b_2}};\\ \hfill \alpha =-{\displaystyle \frac{(1+10b){[b_1^2-4b_0{b}_2]}^{1/2}}{24a}};\beta ={\displaystyle \frac{5}{12}}{[b_1^2-4b_0{b}_2]}^{1/2}.\end{array}$$

(78)

The solution becomes

$$\begin{array}{c}\hfill u(x,t)={\displaystyle \frac{4b_0{b}_2-b_1^2-{[b_1^2-4b_0{b}_2]}^{1/2}}{4b_2{[b_1^2-4b_0{b}_2]}^{1/2}}}-{\displaystyle \frac{{[b_1^2-4b_0{b}_2]}^{1/2}}{2b_2}}tanh[-{\displaystyle \frac{(1+10b){[b_1^2-4b_0{b}_2]}^{1/2}}{24a}}x+\\ \hfill {\displaystyle \frac{5}{12}}{[b_1^2-4b_0{b}_2]}^{1/2}t]+{\displaystyle \frac{{[b_1^2-4b_0{b}_2]}^{1/2}}{4b_2}}{tanh}^2\left[-{\displaystyle \frac{(1+10b){[b_1^2-4b_0{b}_2]}^{1/2}}{24a}}x+{\displaystyle \frac{5}{12}}{[b_1^2-4b_0{b}_2]}^{1/2}t\right].\end{array}$$

(79)

Figure 4 shows the solution (79) for $t=0$ and fixed values of $b_{0,1,2}$. The basic solution is drawn in black. The solution in red shows the influence of the change in the parameter a. The solution in blue shows the influence of the change in the parameter b. All solutions represent a combination of a kink and a solitary wave. The solitary part of the solution is more influenced by the changes in the parameters a and b in comparison to the kink part of the solution.

5. Discussion

In this review article, we discuss an aspect of the Simple Equations Method (SEsM). The aspect is connected to the simple equations used in the methodology. We note the following:

1.

SEsM has a very simple algorithm, based on a transformation of the solved nonlinear differential equation to a system of nonlinear algebraic equations. The solution is constructed as a composite function of solutions of simpler differential equations. Each obtained nontrivial solution of the system of nonlinear algebraic relationships leads to a nontrivial solution of the solved equation.

2.

The methodology leads to exact solutions to many nonlinear differential equations. Some of these equations are widely used as model equations in physics, chemistry, biology, and engineering.

3.

SEsM is connected to the Inverse Scattering Transform Method and the method of Hirota. SEsM leads to the equation of Gelfand–Levitan–Marchenko for the case of the Korteweg–de Vries equation and the relationships of Zakharov and Shabat in the case of the nonlinear Schrödinger equation [231]. SEsM can be used for obtaining multisoliton solutions of integrable nonlinear differential equations.

4.

Different simple equations can be used in SEsM. Usually, one uses as simple equations the nonlinear ordinary differential equations of Riccati and Bernoulli. The equations for the elliptic functions of Weierstrass and Jacobi are much used in SEsM. The form of the simple equation influences the form of the composite function of the solution of the solved nonlinear differential equation. In this article, we studied the use of other possible simple equations and some of the nonlinear differential equations that can be solved on the basis of the application of SEsM with these simple equations.

5.

The used simple equations lead to interesting conclusions about the connection of SEsM with other methods for obtaining exact solutions of nonlinear differential equations. The use of equations of exponential functions connects SEsM to the Inverse Scattering Transform method and to the method of Hirota. The use of other simple equations connects the following methods to the methodology of SEsM [243,272,278]:

(a)

Jacobi Elliptic function Expansion method [279],

(b)

F-Expansion method [280,281,282],

(c)

Modified Simple Equation Method [283],

(d)

Trial Function Method [284,285],

(e)

General Projective Riccati Equations Method [286],

(f)

First Integral Method [287].

(g)

The Homogeneous Balance Method [288,289,290,291]

(h)

Auxiliary Equation Method [292].

(i)

the G’/G - method [293,294],

(j)

Exp-function method [295],

(k)

Tanh-method [296]

(l)

The method of Fourier series.

he list can be continued. We note, in addition, that SEsM can also deal with differential equations containing fractional derivatives [237]. This research area has been much more active in the last years (see [238,239,240,241,242] for examples).

6.

We can formulate

Conjecture:

• Any method for obtaining exact analytical solutions of (nonintegrable) nonlinear differential equations is a specific case of SEsM.
  The basis of this conjecture is as follows:

(a)

The methodology of SEsM is to construct an exact solution of a complicated nonlinear differential equation (this equation can also be fractional differential equation) by means of known solutions of simple differential equations.

(b)

Any method for obtaining exact analytical solutions to nonlinear differential equations (these equations can be integrable or nonintegrable) describes how to construct these solutions by means of known functions.

(c)

The latter known functions are the solutions to certain simple differential equations. For example, the exponential function is a solution to a linear differential equation, and the elliptic functions of Jacobi are solutions to an ordinary nonlinear differential equation with polynomial nonlinearity.

(d)

The solution to the solved equation is a function of these known functions. But this is exactly the composite function from the methodology of SEsM.

(e)

Because of all the above, if one wants to construct a method for obtaining exact solutions of nonlinear differential equations that is not a specific case of SEsM, then one has to do one of the following:

(f)

One will have to use known functions that are not solutions of any simple differential equation. This is an extremely complicated task, as one will have to find functions that are not solutions of differential equations.

(g)

One has to construct the solution of the solved equation as a function of the known solutions of simple equations, which is not a composite function. This is also an extremely complicated task.

7.

The above reasoning hints at the possibility of also extending the conjecture to the area of integrable nonlinear differential equations.

8.

SEsM is a method for obtaining exact solutions to nonlinear differential equations. Thus, SEsM is in a different category of methodology in comparison to the methods for obtaining approximate solutions to nonlinear equations, such as the Adomiam Decomposition Method (ADM) [297,298,299,300] or the Homotopy Analysis Method (HAM) [301,302,303,304]. SEsM leads to exact solutions, but its area of application is more limited than the areas of application of ADM and HAM.

9.

We can not expect to obtain an exact solution to any nonlinear differential equation by means of SEsM. We can obtain exact solutions to nonlinear equations whose solution can be represented as a composite function of exact solutions of more simple equations. Not every nonlinear differential equation belongs to this class of equations. The integrable nonlinear differential equations belong to this class of equations. Many nonitegrable nonlinear differential equations also belong to this class of equations, and SEsM allows us to obtain specific exact solutions to these equations. Thus, an interesting open question for future research is as follows: How large is the class of nonlinear differential equations for which one can obtain an exact solution(s) by means of SEsM?

10.

SEsM reduces the solved nonlinear differential equation to a system of nonlinear algebraic equations. As we search for an exact solution of the solved equation, we have to obtain an analytical solution to the corresponding system of nonlinear differential equations. Modern computer algebra systems can solve this task, if possible. We write if possible, because in some cases the number of equations is larger than the number of the unknowns in the solved algebraic system. Then, it is difficult to obtain an analytical solution to the algebraic system, and we are not able to obtain an exact solution to the solved equation, even if we manage to reduce this equation to a system of nonlinear algebraic equations.

11.

SEsM works well when the solved nonlinear differential equation only has nonlinearities of the polynomial kind. In the course of the years, we have shown that SEsM also works for nonlinear differential equations that can be reduced to nonlinear equations with polynomial nonlinearities by means of appropriate transformations (this is Step 1 in the algorithm of SEsM). An interesting open question for future research is to extend the capability of SEsM to deal with larger classes of nonlinear differential equations, where the nonlinearities are non-polynomial.

6. Concluding Remarks

In this article, we present the Simple Equations Method (SEsM) for obtaining exact solutions to nonlinear differential equations. The focus is on the variety of simple equations that can be used in SEsM. We provided here several final remarks.

• SEsM is connected to the Inverse Scattering Transform Method and to the Method of Hirota for obtaining exact solutions of nonlinear differential equations. These two methods led to a large amount of research on the symmetry properties of nonlinear differential equations and on the use of symmetries for obtaining new exact solutions of such nonlinear equations. The study of symmetries and the use of these symmetries for obtaining exact solutions of differential equations is a promising research area [305,306,307,308,309,310]. This methodology can be combined with SEsM: SEsM leads to new exact solutions, and then the symmetry methodology can be used to study obtaining additional exact solutions on the basis of solutions obtained by SEsM.
• We show in this text that the methodology of SEsM is effective. It is connected to famous methods for obtaining exact multisoliton solutions of nonlinear differential equations and contains as specific cases many methods for obtaining specific exact analytical solutions of nonintegrable equations.
• SEsM already has many applications for obtaining exact solutions to nonlinear differential equations used as model equations in the natural sciences. Examples include from the areas of population dynamics, ecology, and genetics [253,254,255,256], pattern formation [258], and fluid mechanics [259,261,263,264].
• We note the following about the use of simple equations in the methodology of SEsM: We construct a solution to the solved equation as a composite function of solutions to differential equations that are simpler than the solved equation. Then, the requirements for the simple equations are
  • To be more simple than the solved equation.
  • To have exact solutions.
  • To help to transform the solved differential equation to a system of nonlinear algebraic equations.
  In principle, any differential equation that satisfies these requirements can be used as a simple equation. Let us give an example. We want to solve a differential equation which has polynomial nonlinearities. In order to do this, we have to use as simple equations more simple differential equations that have polynomial nonlinearities or are linear equations. The simplest such equations with known solutions are the equations for the exponential function, as well as the equations of Riccati and Bernoulli. This is why these equations are much used in the methodology of SEsM and in the methodologies that are connected to SEsM. If the solved equation has polynomial nonlinearities of higher order, then we can use as simple equations differential equations such as the equation for the elliptic function of Weierstrass or the equation for the elliptic functions of Jacobi.
• The future research on SEsM and its applications is promising. For example, there are the following possible directions of research:

  (a)

  Combination of SEsM with the symmetry methods for obtaining exact solutions of nonlinear differential equations.

  (b)

  Extension of the area of application of SEsM by studying additional classes of nonlinearities and equations

  (c)

  Application of the methodology for systematically obtaining exact solutions of classes of nonlinear differential equations.