Numerical Investigation on Thermally Induced Self-Excited Thermoacoustic Oscillations in the Pipelines of Cryogenic Storage Systems
Abstract
1. Introduction
2. CFD Methodology
2.1. Model Description
2.2. Simplifications and Assumptions
2.3. Solution of the Governing Equations
2.4. Simulation Strategy and Boundary Conditions
2.5. Sensitivity Studies
2.6. Comparison with Existing Literature
3. Acoustic and Flow Characteristics of the Cryogenic Helium Pipe
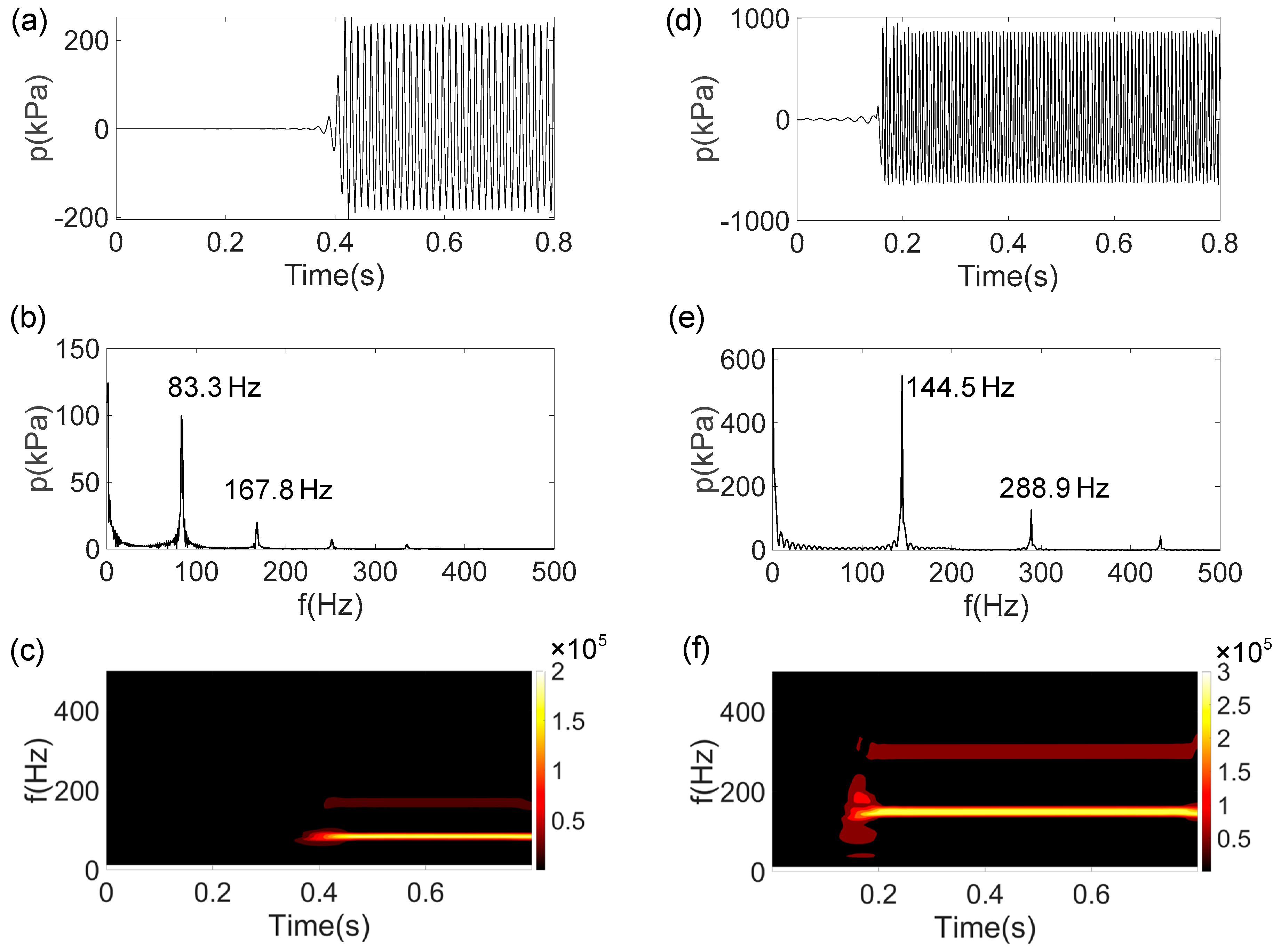
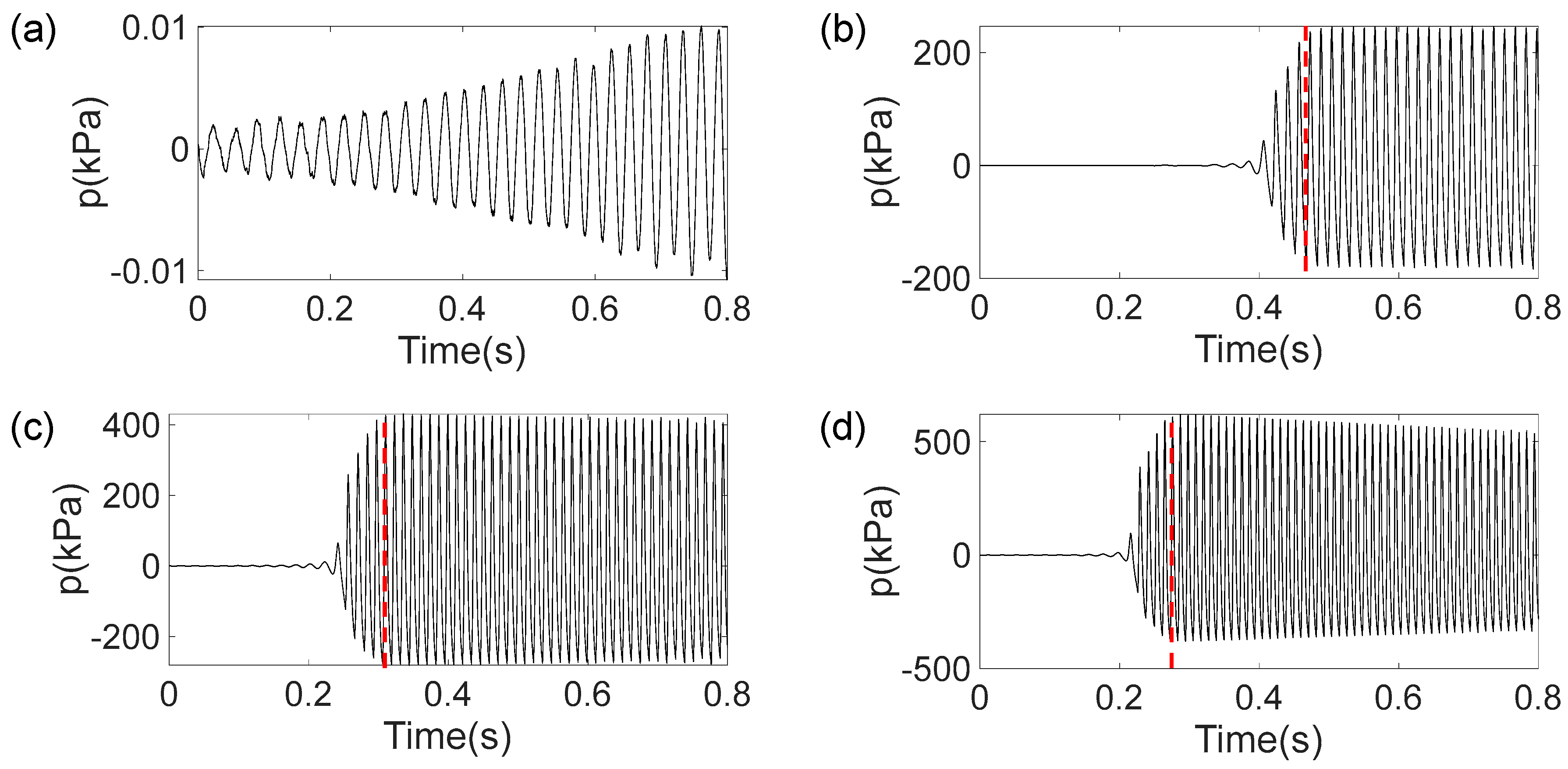
3.1. Transient Growth of Self-Excited Thermoacoustic Oscillations
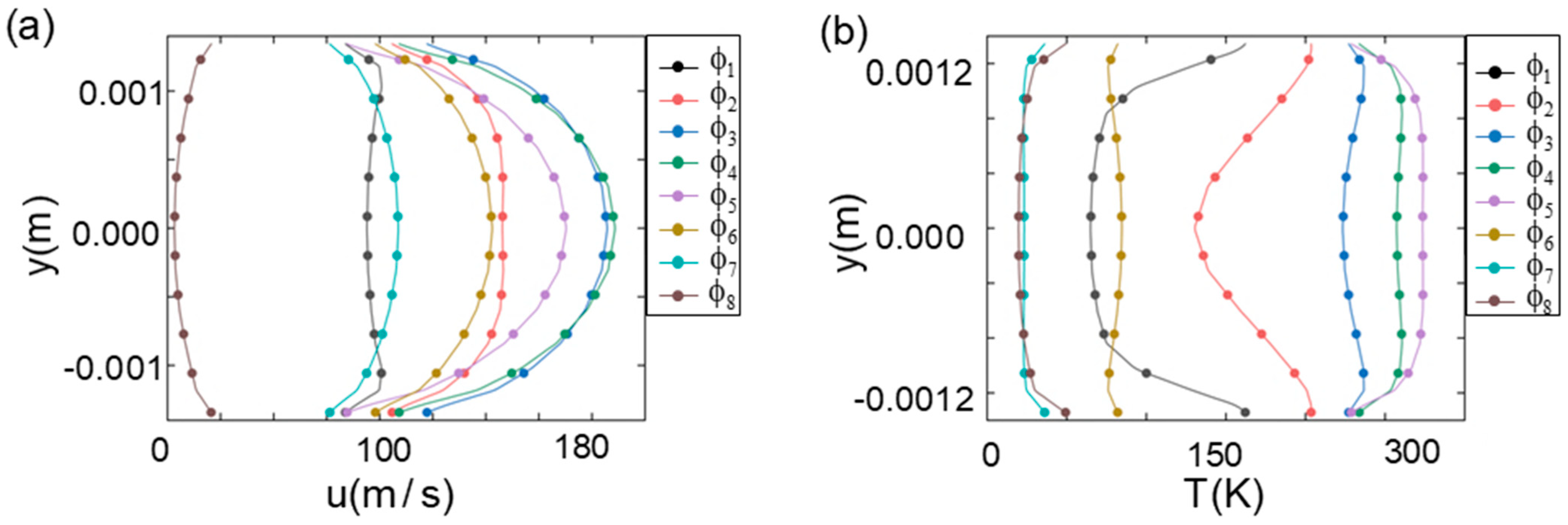
3.2. Velocity and Temperature Profiles at Steady State
4. Impact on the Dynamic Behavior of Taconis Oscillations
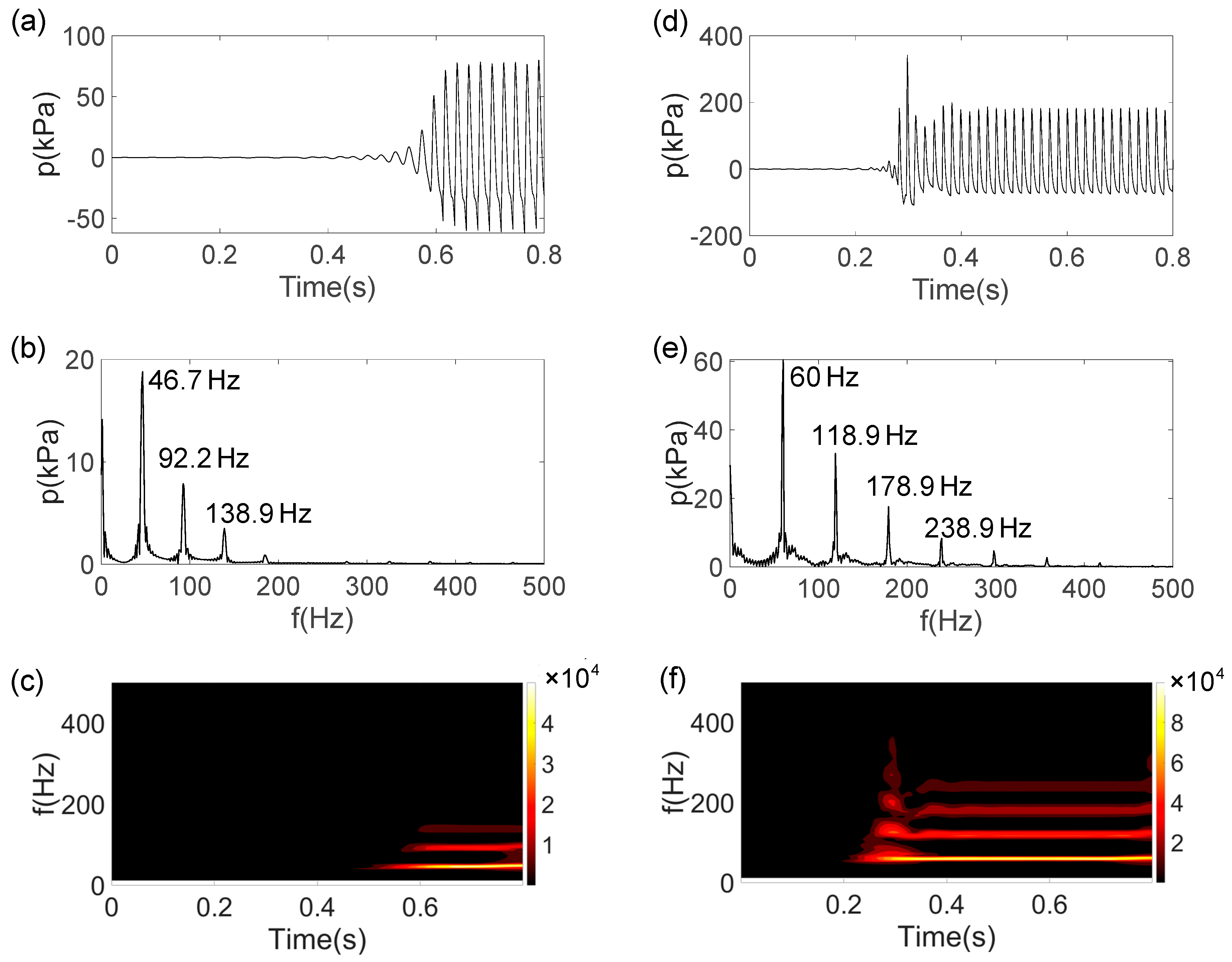
4.1. Position of Temperature Gradient
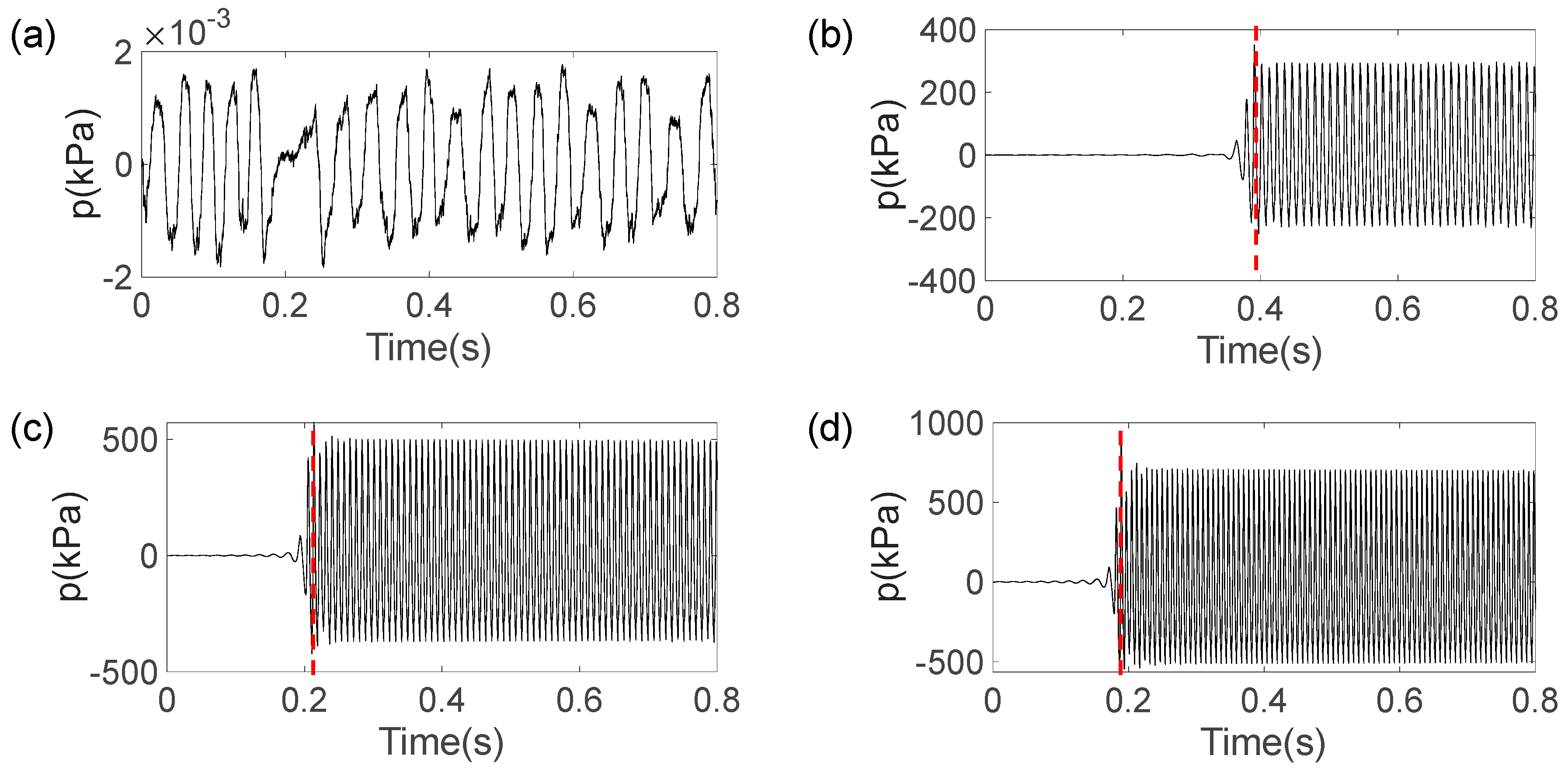
4.2. Magnitude of Temperature Gradient
5. Conclusions
- (1)
- CFD simulations on the benchmark cryogenic helium pipe indicate that when ε = 1 and Γ = 14,500 K/m, large-amplitude Taconis oscillations occur. These oscillations exhibit two distinct frequencies: a first-mode frequency of 60 Hz with an amplitude of 213 kPa and a second-mode frequency of 121 Hz with a significantly lower amplitude. The velocity profile in the y direction follows a Poiseuille pattern, whereas the helium temperature is more uniform away from the walls.
- (2)
- The position of the temperature gradient significantly affects the stability of the cryogenic helium pipe. When ε = 1, the onset temperature gradient for Taconis oscillations is relatively low, approximately 7000 K/m. This suggests that, to prevent the occurrence of Taconis oscillations, the transition between the warm and cold sections should be away from one-quarter of the cryogenic pipe. When ε = 0.5, although the pressure amplitude is lower, higher-order acoustic modes are more easily excited within the helium pipeline, leading to the coexistence of multiple acoustic modes. The natural frequencies of acoustic modes increase as ε increases due to increased average temperature as a result of a larger proportion the hot section.
- (3)
- The magnitude of the temperature gradient also has a significant impact on the dynamic behavior of Taconis oscillations. As Γ increases, the cryogenic helium tube becomes more susceptible to instability and easier to excite, resulting in a shorter time to reach steady-state periodic oscillations. In addition, the oscillation frequency of the cryogenic helium pipe rises with increasing Γ due to the increased sound speed at higher temperatures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Swift, G.W. Thermoacoustics: A Unifying Perspective for Some Engines and Refrigerators; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Chen, G.; Tang, L.; Mace, B.; Yu, Z. Multi-physics coupling in thermoacoustic devices: A review. Renew. Sustain. Energy Rev. 2021, 146, 111170. [Google Scholar] [CrossRef]
- Guo, L.; Zhao, D.; Becker, S. Temperature Difference and Stack Plate Spacing Effects on Thermodynamic Performances of Standing-Wave Thermoacoustic Engines Driven by Cryogenic Liquids and Waste Heat. J. Therm. Sci. 2022, 31, 1434–1451. [Google Scholar] [CrossRef]
- Hsu, S.-H.; Liao, Z.-Y. Impedance matching for investigating operational conditions in thermoacoustic Stirling fluidyne. Appl. Energy 2024, 374, 123973. [Google Scholar] [CrossRef]
- Niu, Y.; Hu, L.; Chen, P.; Liu, Y.; Gao, B. Numerical study of oscillation characteristics in T-shaped cryogenic helium tube. Int. Commun. Heat Mass Transf. 2023, 143, 106725. [Google Scholar] [CrossRef]
- Gu, Y.; Timmerhaus, K. Effect of Tube Temperature Profile on Thermal Acoustic Osciallations in Liquid Hydrogen Systems. In Proceedings of the Sixth International Cryocooler Conference, Plymouth, MA, USA, 25–26 October 1990; pp. 329–340. [Google Scholar]
- Matveev, K.I. Influence of Porous Inserts and Compact Resonators on Onset of Taconis Oscillations. J. Vib. Acoust. 2024, 146, 014501. [Google Scholar] [CrossRef]
- Swift, G.; Gardner, D.; Backhaus, S. Quarter-wave pulse tube. Cryogenics 2011, 51, 575–583. [Google Scholar] [CrossRef]
- Luck, H.; Trepp, C. Thermoacoustic oscillations in cryogenics. Part 2: Applications. Cryogenics 1992, 32, 698–702. [Google Scholar] [CrossRef]
- Luck, H.; Trepp, C. Thermoacoustic oscillations in cryogenics. Part 1: Basic theory and experimental verification. Cryogenics 1992, 32, 690–697. [Google Scholar] [CrossRef]
- Rott, N. Thermally driven acoustic oscillations. Part II: Stability limit for helium. Z. Angew. Math. Phys. ZAMP 1973, 24, 54–72. [Google Scholar] [CrossRef]
- Yazaki, T.; Tominaga, A.; Narahara, Y. Stability limit for thermally driven acoustic oscillation. Cryogenics 1979, 19, 393–396. [Google Scholar] [CrossRef]
- Tominaga, A. Thermodynamic aspects of thermoacoustic theory. Cryogenics 1995, 35, 427–440. [Google Scholar] [CrossRef]
- Shimizu, D.; Sugimoto, N. Numerical study of thermoacoustic Taconis oscillations. J. Appl. Phys. 2010, 107, 034910. [Google Scholar] [CrossRef]
- Sugimoto, N.; Shimizu, D. Boundary-layer theory for Taconis oscillations in a helium-filled tube. Phys. Fluids 2008, 20, 104102. [Google Scholar] [CrossRef]
- Chen, G.; Tao, S.; Wang, K.; Tang, L.; Li, Z.; Xu, J.; Yu, Z. Full-scale numerical simulations of standing-wave thermoacoustic engines with circular-pore and pin-array stacks. Int. J. Heat Mass Transf. 2024, 228, 125605. [Google Scholar] [CrossRef]
- Di Meglio, A.; Massarotti, N. CFD Modeling of Thermoacoustic Energy Conversion: A Review. Energies 2022, 15, 3806. [Google Scholar] [CrossRef]
- Sharify, E.M.; Takahashi, S.; Hasegawa, S. Development of a CFD model for simulation of a traveling-wave thermoacoustic engine using an impedance matching boundary condition. Appl. Therm. Eng. 2016, 107, 1026–1035. [Google Scholar] [CrossRef]
- Sun, D.; Wang, K.; Guo, Y.; Zhang, J.; Xu, Y.; Zou, J.; Zhang, X. CFD study on Taconis thermoacoustic oscillation with cryogenic hydrogen as working gas. Cryogenics 2016, 75, 38–46. [Google Scholar] [CrossRef]
- Putselyk, S. Thermal acoustic oscillations: Short review and countermeasures. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; p. 012080. [Google Scholar]
- Hu, L.; Yuan, P.; Niu, Y.; Liu, Y.; Gao, B. Sensitivity analysis of thermoacoustic oscillation in cryogenics system based on response surface method. Therm. Sci. 2023, 27, 3795–3804. [Google Scholar] [CrossRef]
- Matveev, K.I.; Leachman, J.W. Thermoacoustic Modeling of Cryogenic Hydrogen. Energies 2024, 17, 2884. [Google Scholar] [CrossRef]
- Rao, A.G.; Yin, F.; Werij, H.G.C. Energy Transition in Aviation: The Role of Cryogenic Fuels. Aerospace 2020, 7, 12. [Google Scholar] [CrossRef]
- Lai, C.-H.; Hsu, S.-H. Empirical Modeling of Subcritical Hopf Bifurcation of Thermoacoustic Stirling Engine. Aerospace 2024, 11, 347. [Google Scholar] [CrossRef]
- Hu, L.; Yang, P.; Liu, Y. Numerical investigation on the control of cryogenic fluid oscillations by applying an external sound source. J. Appl. Phys. 2021, 130, 054903. [Google Scholar] [CrossRef]
- Hu, L.; Yang, P.; Chen, P.; Liu, Y. Numerical study on suppression of thermoacoustic oscillation in cryogenic helium pipeline system. Cryogenics 2021, 117, 103311. [Google Scholar] [CrossRef]
- Gu, L.; Liu, L.; Li, Z.; Tang, L.; Yu, Z.; Chen, G. Suppression of Taconis oscillations in cryogenic hydrogen tubes using a Helmholtz resonator: Theoretical modelling and numerical simulations. Appl. Therm. Eng. 2025, 274, 126687. [Google Scholar] [CrossRef]
- Rao, Y. Chemical Engineering Thermodynamics; Universities Press (India) Privated Limited: Hyderabad, India, 1997. [Google Scholar]
- Alfonsi, G. Reynolds-averaged Navier–Stokes equations for turbulence modeling. Appl. Mech. Rev. 2009, 62, 040802. [Google Scholar] [CrossRef]
- Chen, G.; Tang, L.; Mace, B.R. Bistability and triggering in a thermoacoustic engine: A numerical study. Int. J. Heat Mass Transf. 2020, 157, 119951. [Google Scholar] [CrossRef]
- Guo, L.; Zhao, D.; Xu, J.; Tokhi, M.O.; Karimi, H.R. Predicting unsteady heat-fluid interaction features and nonlinear acoustic behaviors in standing-wave thermoacoustic engines using unsteady RANS, LES and hybrid URANS/LES methods. Int. Commun. Heat Mass Transf. 2023, 142, 106617. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Y. Numerical study on a thermoacoustic refrigerator with continuous and staggered arrangements. Therm. Sci. 2022, 26, 3939–3949. [Google Scholar] [CrossRef]
- Shenton, M.P.; Leachman, J.W.; Matveev, K.I. Investigating Taconis oscillations in a U-shaped tube with hydrogen and helium. Cryogenics 2024, 143, 103940. [Google Scholar] [CrossRef]
- Shenton, M.P.; Leachman, J.W.; Matveev, K. Study of Taconis-Based Cryogenic Thermoacoustic Engine with Hydrogen and Helium. Energies 2025, 18, 4114. [Google Scholar] [CrossRef]
- Shenton, M.; Matveev, K.; Leachman, J. Initiation and suppression of Taconis oscillations in tubes with junctions and variable-diameter tube segments. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2024; p. 012042. [Google Scholar]
- Chen, G.; Wang, Y.; Tang, L.; Wang, K.; Yu, Z. Large eddy simulation of thermally induced oscillatory flow in a thermoacoustic engine. Appl. Energy 2020, 276, 115458. [Google Scholar] [CrossRef]
- Yazaki, T.; Takashima, S.; Mizutani, F. Complex quasiperiodic and chaotic states observed in thermally induced oscillations of gas columns. Phys. Rev. Lett. 1987, 58, 1108. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Ma, Y.; Xie, F.; Ai, L.; Wu, S.; Li, Y. Numerical Simulation Research on Thermoacoustic Instability of Cryogenic Hydrogen Filling Pipeline. Cryo 2025, 1, 9. [Google Scholar] [CrossRef]









| Parameters | Symbols | Values and Units |
|---|---|---|
| Hot-section temperature | Th | Values: 150 K to 900 K; increment: 50 K |
| Cold-section temperature | Tc | Fixed at 10 K |
| Temperature ratio | Γ | Values: 7000 K/m to 44,500 K/m; baseline value: 14,500 K/m |
| Length of hot section | l | 1/6L, 1/4L, and 1/3L; |
| Length ratio | ε | Values: 0.5, 1, and 2; baseline value: 1 |
| Steps | Hot Section | Cold Section | Transition Section | Left End (x = 0) | Right End (x = L) |
|---|---|---|---|---|---|
| Step 1: Steady calculation | Rigid wall, T = Th | Rigid wall, T = Tc | Rigid wall, linear decrease from Th to Tc | Pressure inlet, p = 10 Pa, T = Th | Pressure outlet, p = 0 Pa, T = Th |
| Step 2: Transient calculation | Rigid wall, T = Th | Rigid wall, T = Tc | Rigid wall, linear decrease from Th to Tc | Rigid wall, u = 0, T = Th | Rigid wall, u = 0, T = Th |
| Grid Node | 91,563 | 142,531 | 241,520 | Timestep Size | 1.5 × 10−5 s | 1 × 10−5 s | 0.5 × 10−5 s |
|---|---|---|---|---|---|---|---|
| f (Hz) | 60.8 | 60 | 59.1 | f (Hz) | 58.4 | 60 | 61.3 |
| ER | 2.9% | 1.5% | N/A | ER | 4.7% | 2.1% | N/A |
| CPUhs | 431 | 545 | 631 | CPUhs | 270 | 545 | 675 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Zhuo, C.; Liu, Y.; Chen, G. Numerical Investigation on Thermally Induced Self-Excited Thermoacoustic Oscillations in the Pipelines of Cryogenic Storage Systems. Symmetry 2025, 17, 1361. https://doi.org/10.3390/sym17081361
Liu L, Zhuo C, Liu Y, Chen G. Numerical Investigation on Thermally Induced Self-Excited Thermoacoustic Oscillations in the Pipelines of Cryogenic Storage Systems. Symmetry. 2025; 17(8):1361. https://doi.org/10.3390/sym17081361
Chicago/Turabian StyleLiu, Liu, Cong Zhuo, Yongqing Liu, and Geng Chen. 2025. "Numerical Investigation on Thermally Induced Self-Excited Thermoacoustic Oscillations in the Pipelines of Cryogenic Storage Systems" Symmetry 17, no. 8: 1361. https://doi.org/10.3390/sym17081361
APA StyleLiu, L., Zhuo, C., Liu, Y., & Chen, G. (2025). Numerical Investigation on Thermally Induced Self-Excited Thermoacoustic Oscillations in the Pipelines of Cryogenic Storage Systems. Symmetry, 17(8), 1361. https://doi.org/10.3390/sym17081361







