Sim-Geometry Modal Decomposition (SGMD)-Based Optimization Strategy for Hybrid Battery and Supercapacitor Energy Storage Frequency Regulation
Abstract
1. Introduction
2. Decomposition of FM Signals and Optimization of Energy Storage Configurations
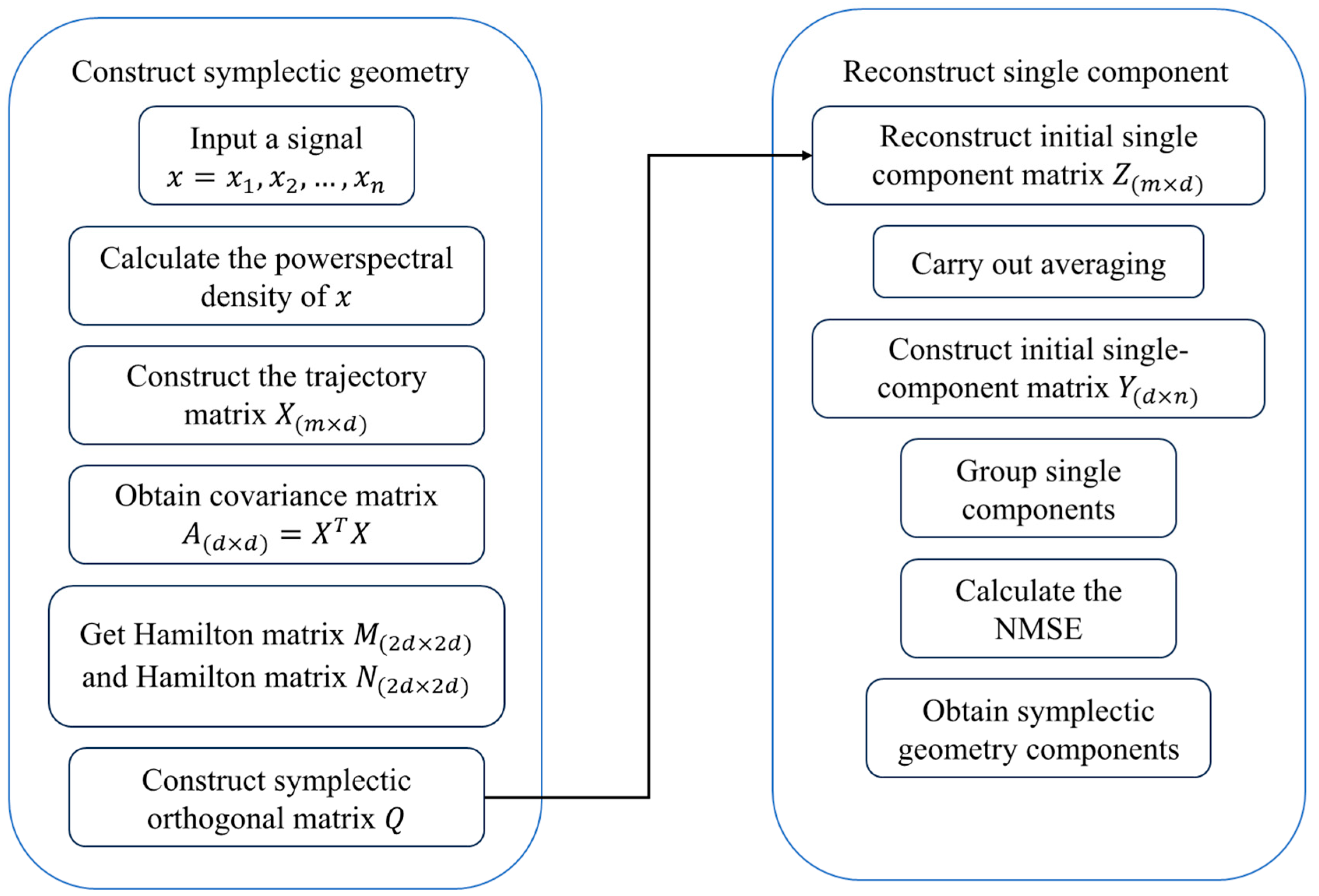
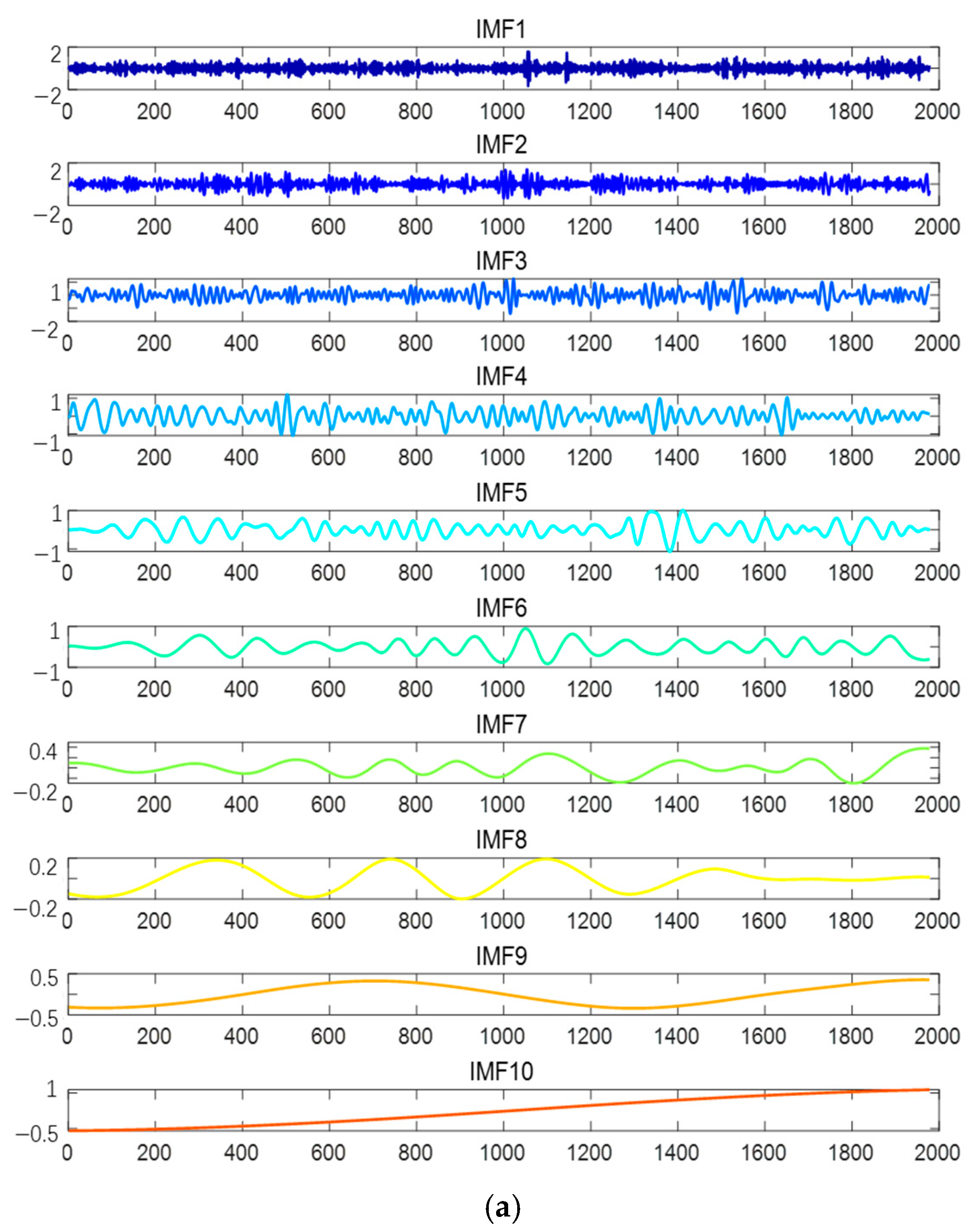
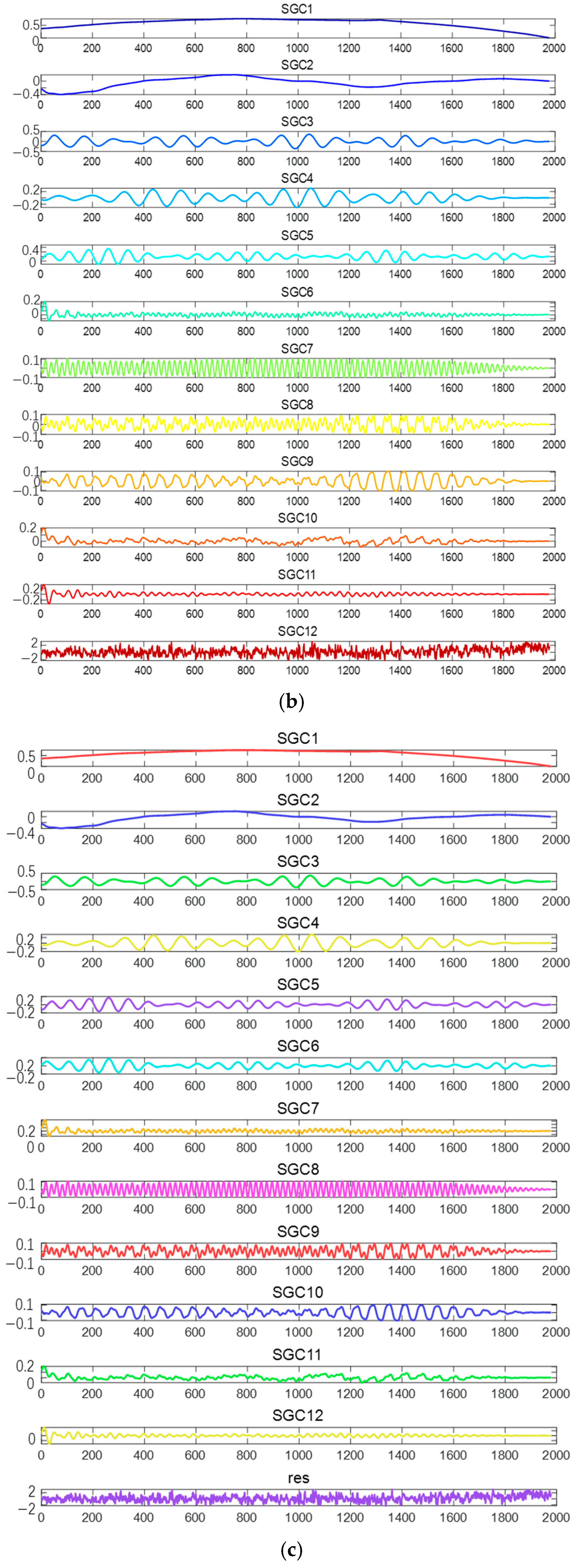
2.1. Singular Geometry Modal Decomposition
- The modal decomposition method lacks adaptive selection capabilities, is extremely sensitive to user-defined parameters, and needs them.
- When noise is present, the modal decomposition method is unable to decompose the signal efficiently.
- The modal decomposition method cannot decompose a complex waveform into several precise components.
2.2. Optimization of Hybrid Energy Storage Characteristics for FM Based on Genetic Gray Wolf Algorithm
3. FM System and Power Allocation Strategy for Wind Power Combined with Energy Storage
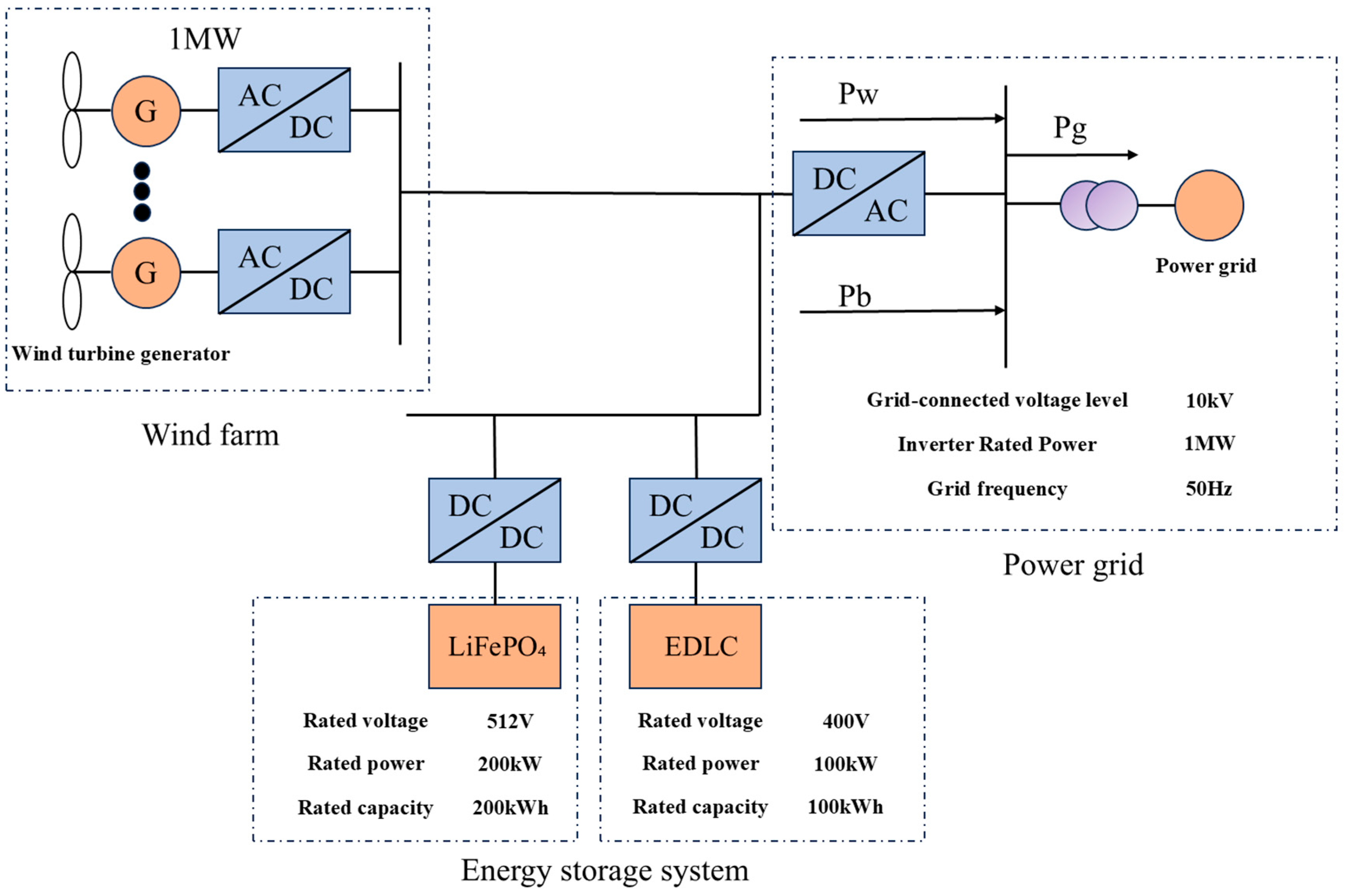
3.1. FM System for Wind Power Combined with Energy Storage
3.2. Hybrid Energy Storage FM Power Allocation Strategy
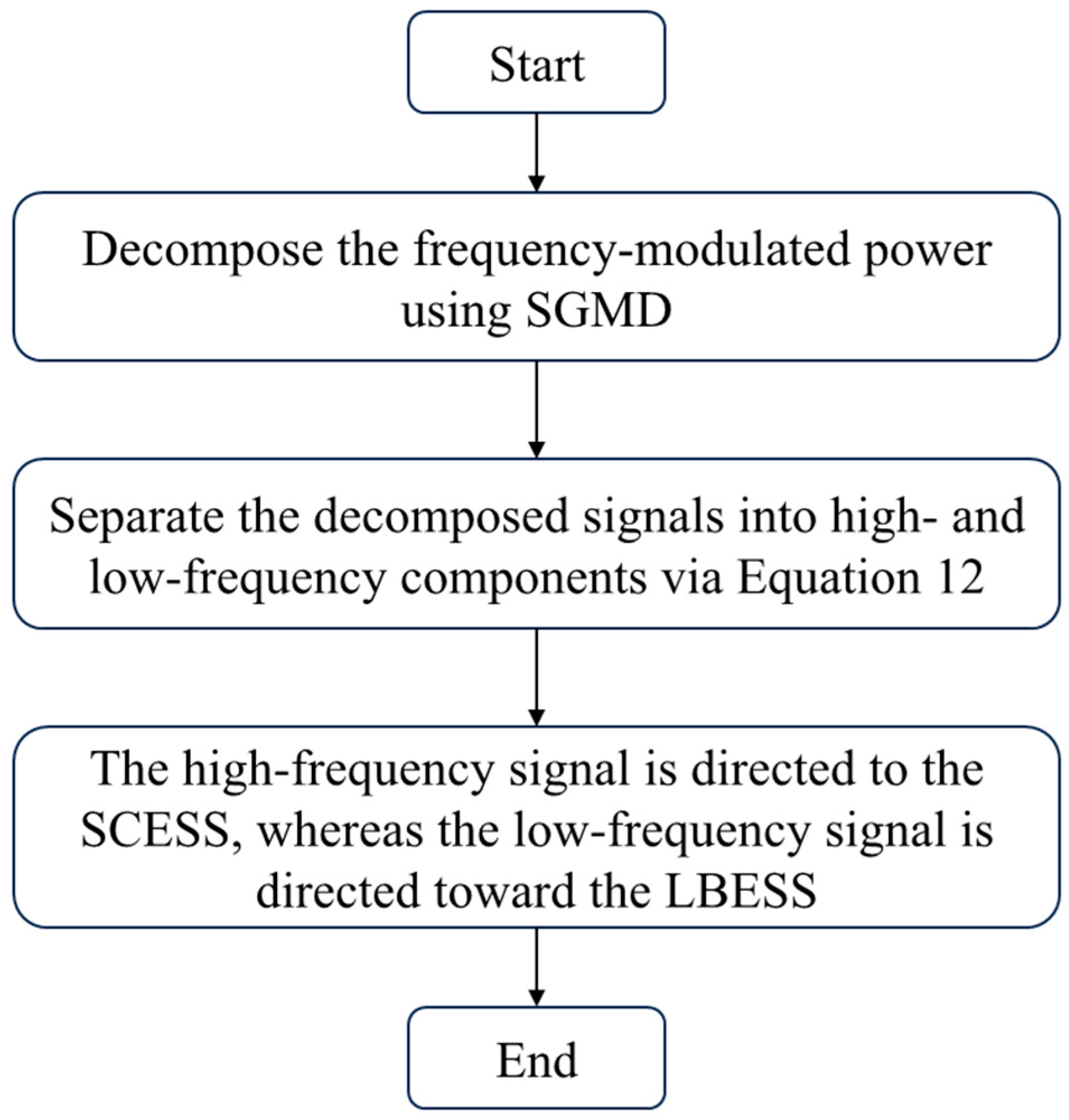
3.3. FM Power Allocation Model Based on SGMD
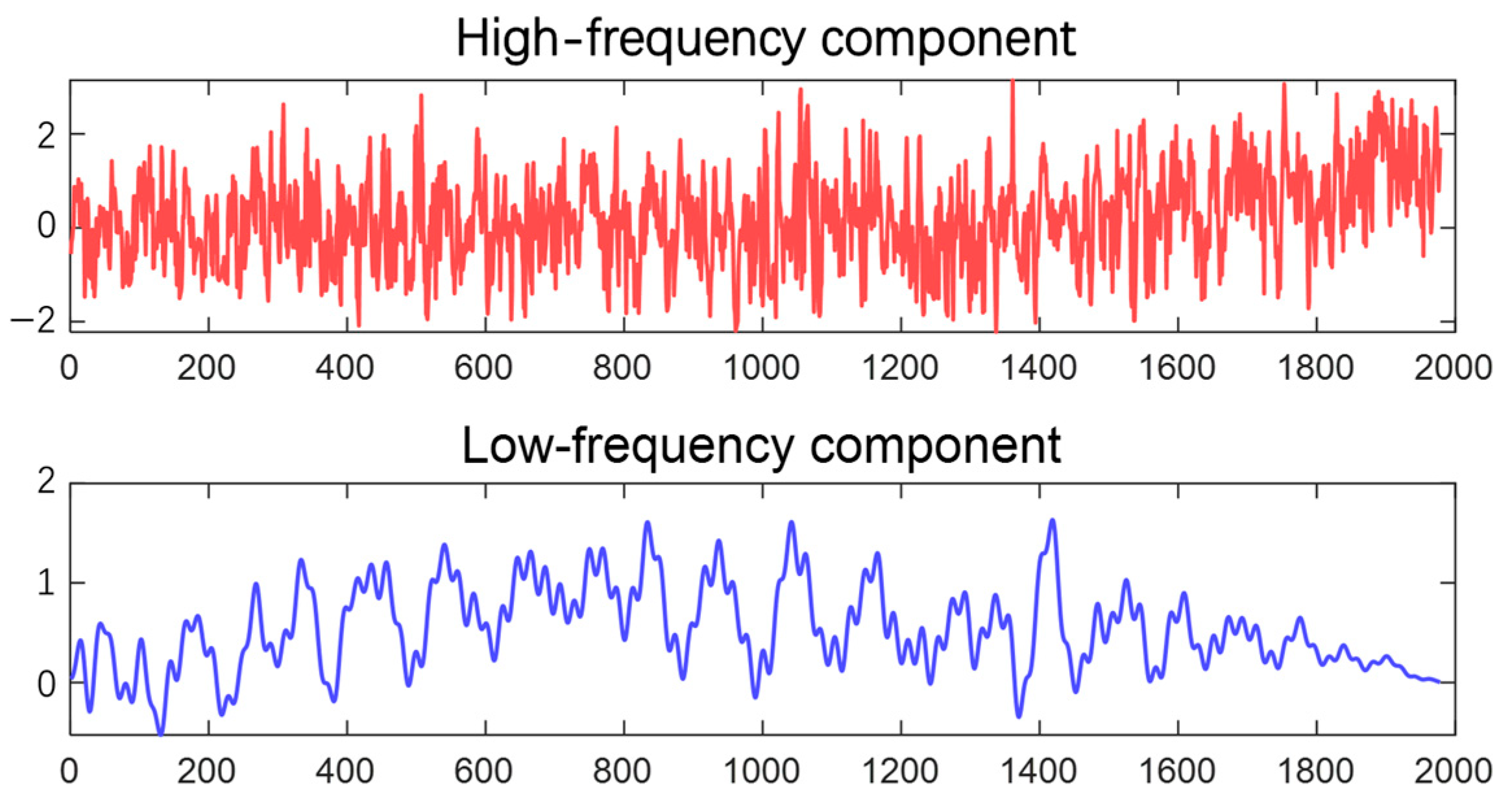
3.4. Enhanced Sinusoidal Geometry Modal Decomposition Method (SE-SGMD)
4. Energy Storage System Modeling
4.1. Constraint Function
- Power limitations in hybrid energy storage system charging and discharging are calculated as follows:
- 2.
- Hybrid energy storage SOC constraints are as follows:
- 3.
- Power balance constraints are as follows:
4.2. Lithium Battery Life Function: Hybrid Energy-Storage-Capacity Optimization Function
4.3. Modeling the Life-Cycle Cost of HESSs
4.4. Revenue Accounting Method for Energy Storage Systems
4.5. Wind-Storage Economic Model
4.6. Parameters for Energy-Storage Capacity Configuration
5. Optimized Solution Method Based on Genetic Gray Wolf Algorithm
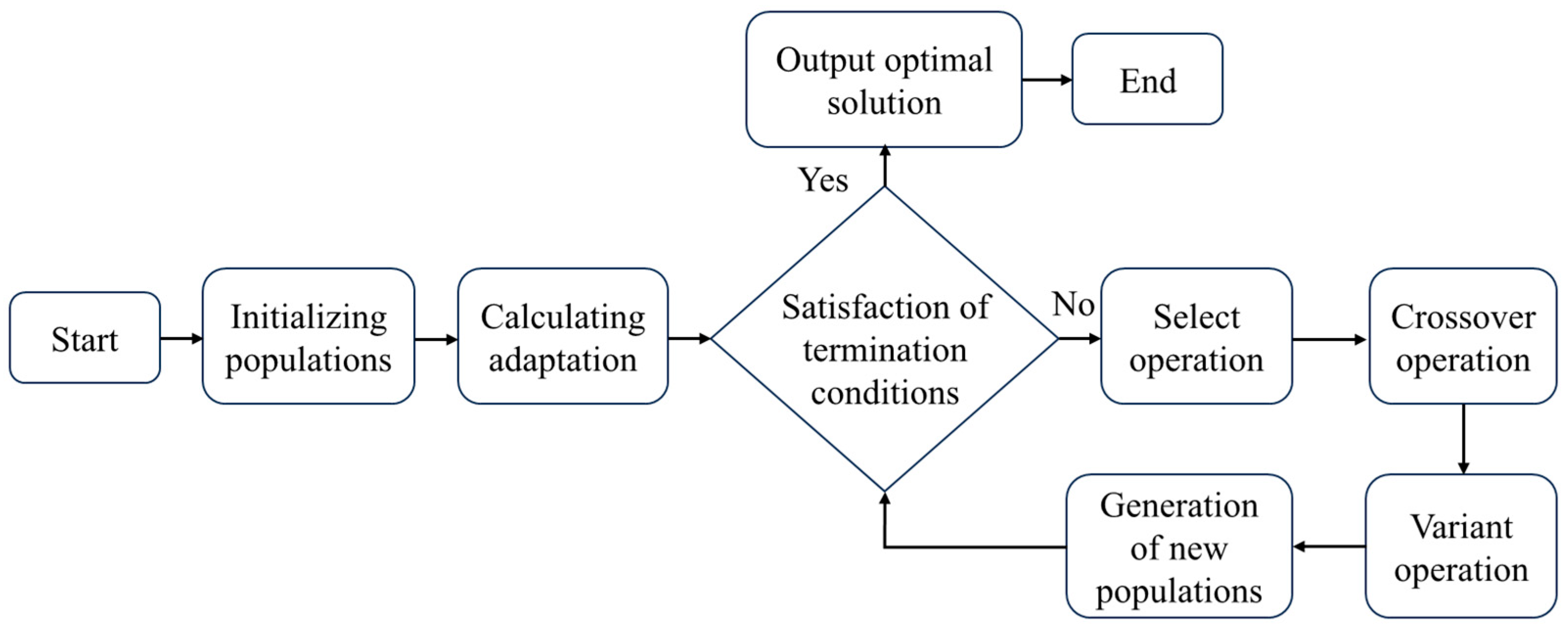
5.1. Genetic Algorithm
- (1)
- Algorithm Encoding
- (2)
- Fitness Function
- (3)
- Genetic Operations
- (4)
- Algorithm Termination Conditions
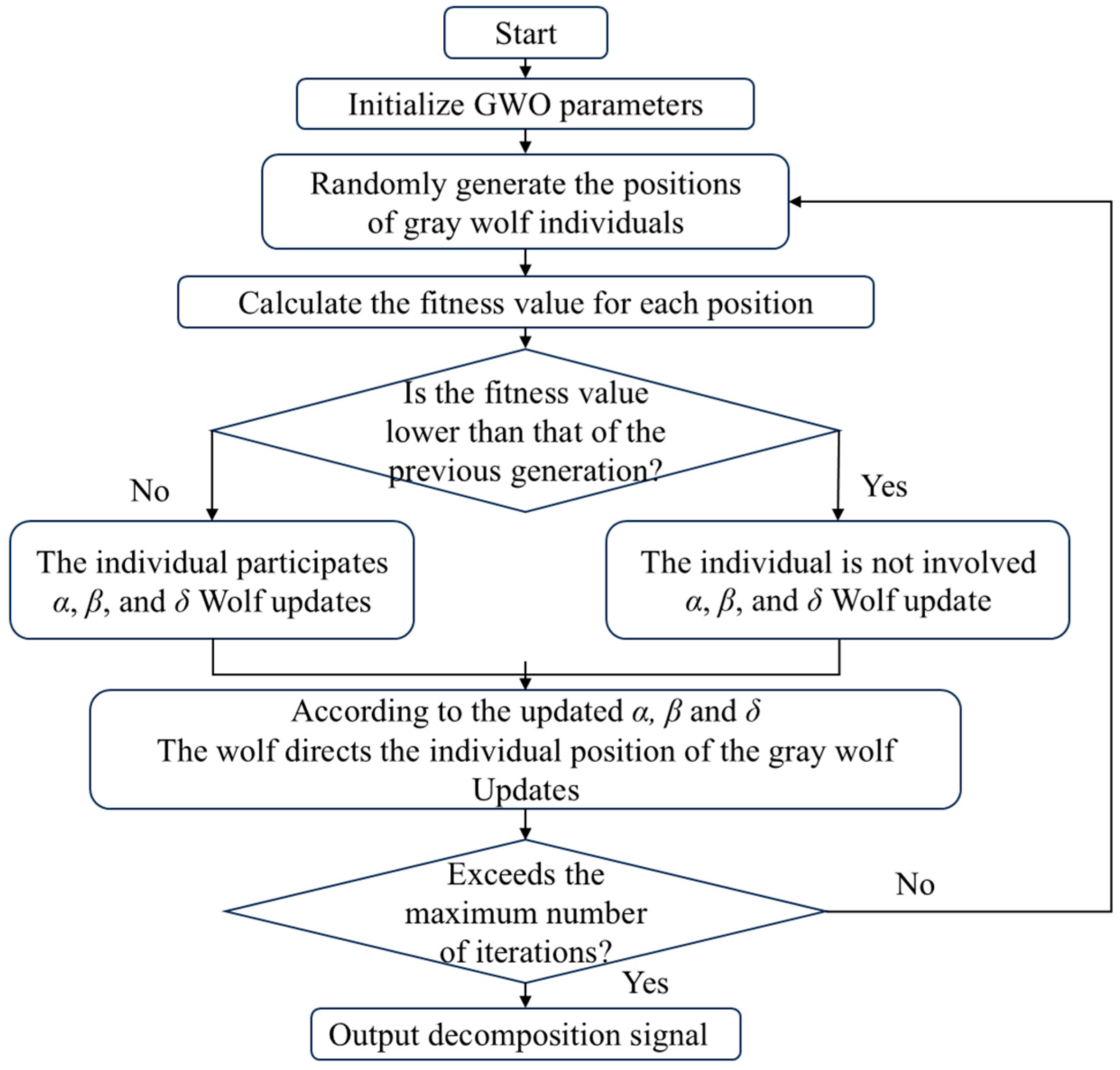
5.2. Gray Wolf Optimizer
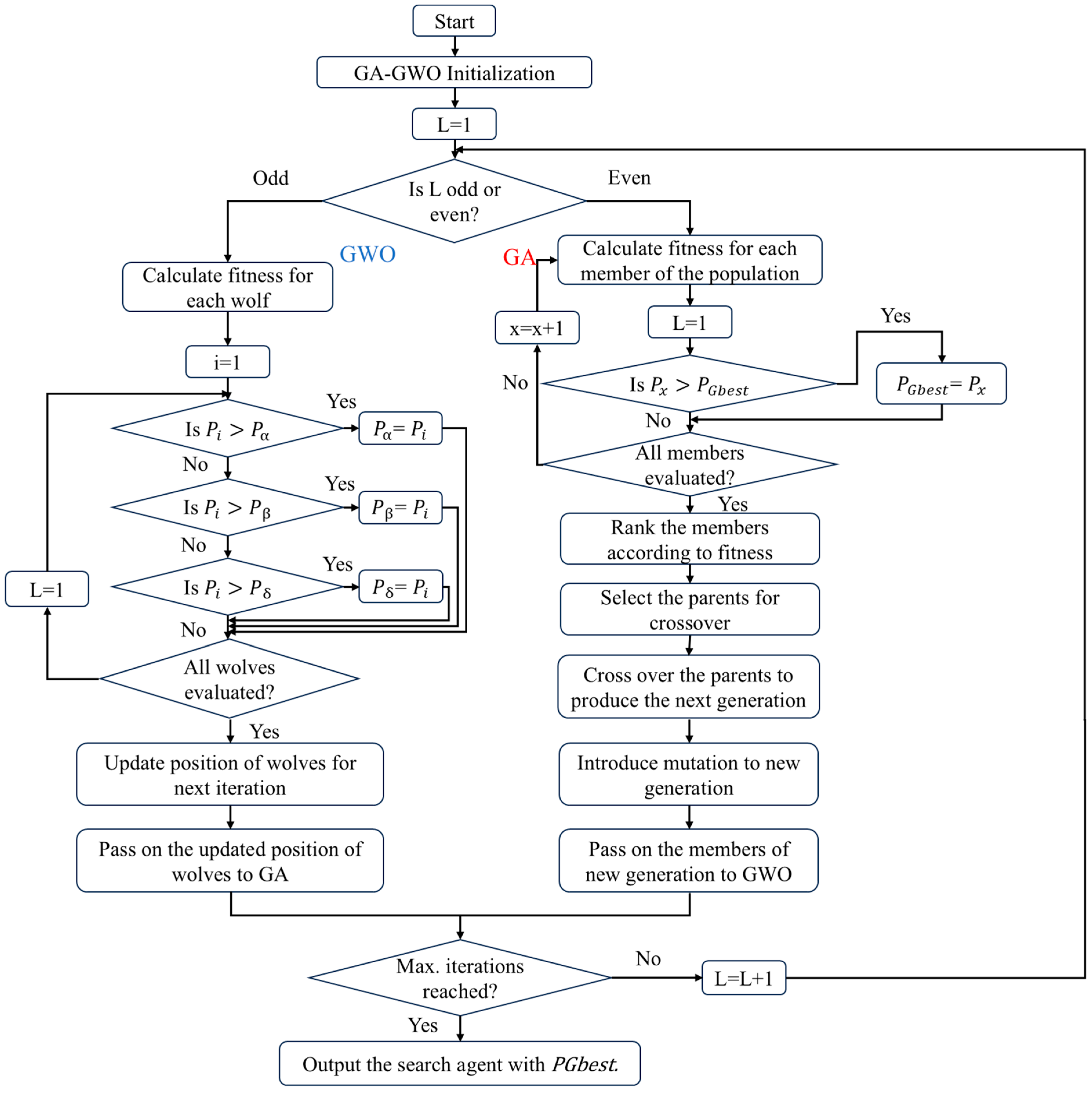
5.3. GA-GWO
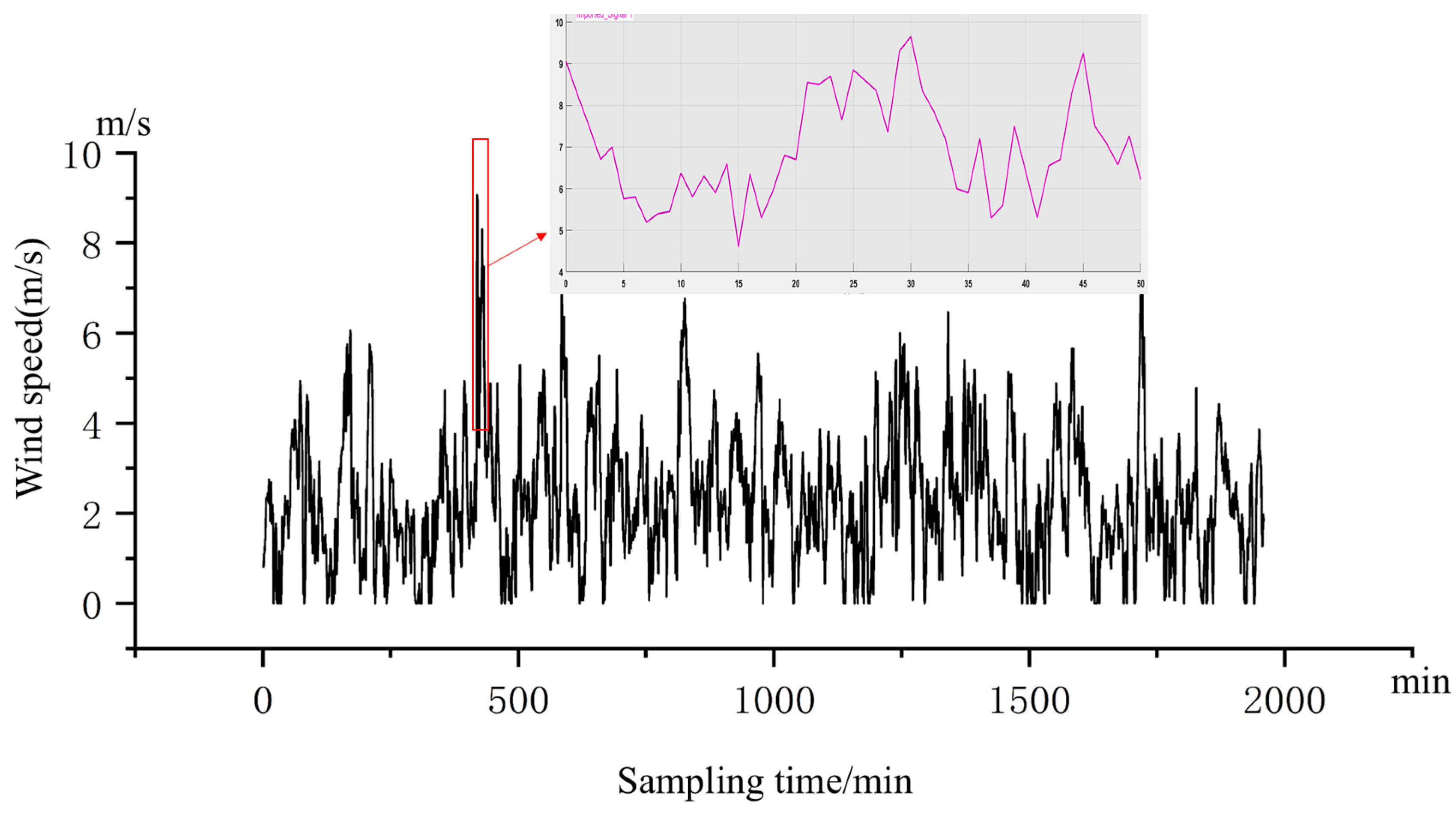
6. Simulation Verification
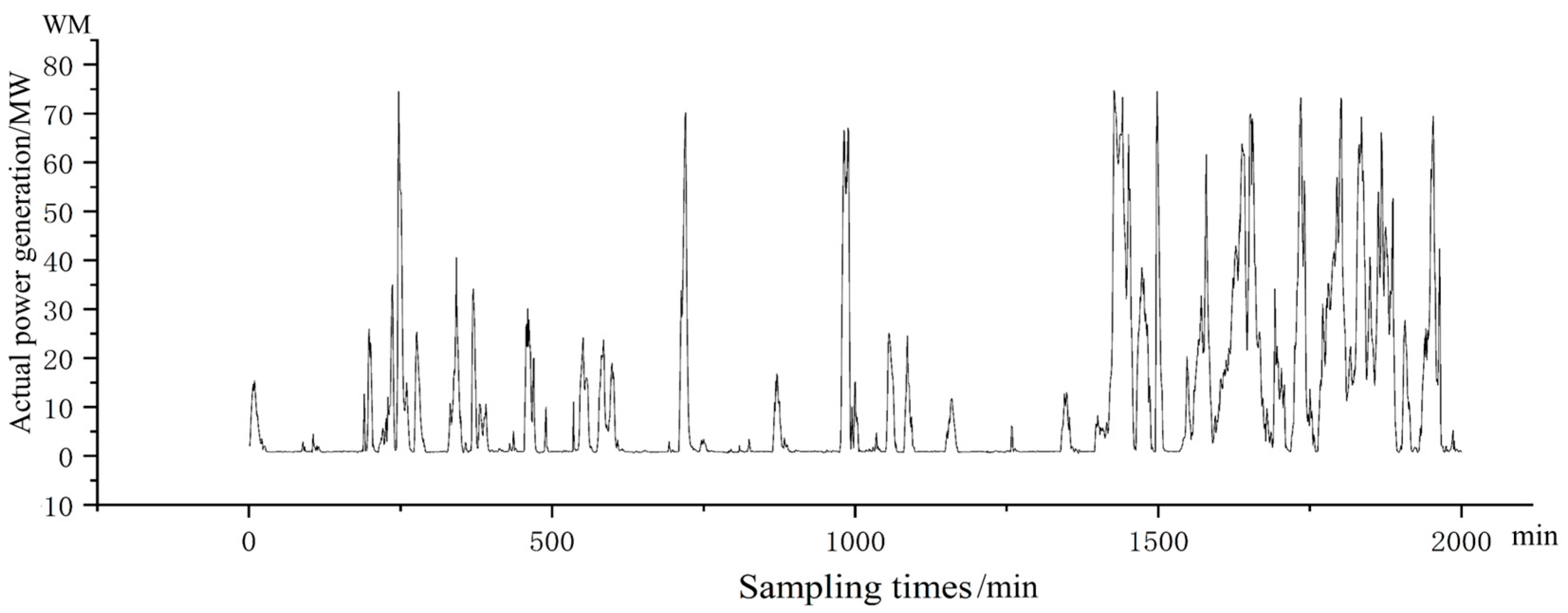
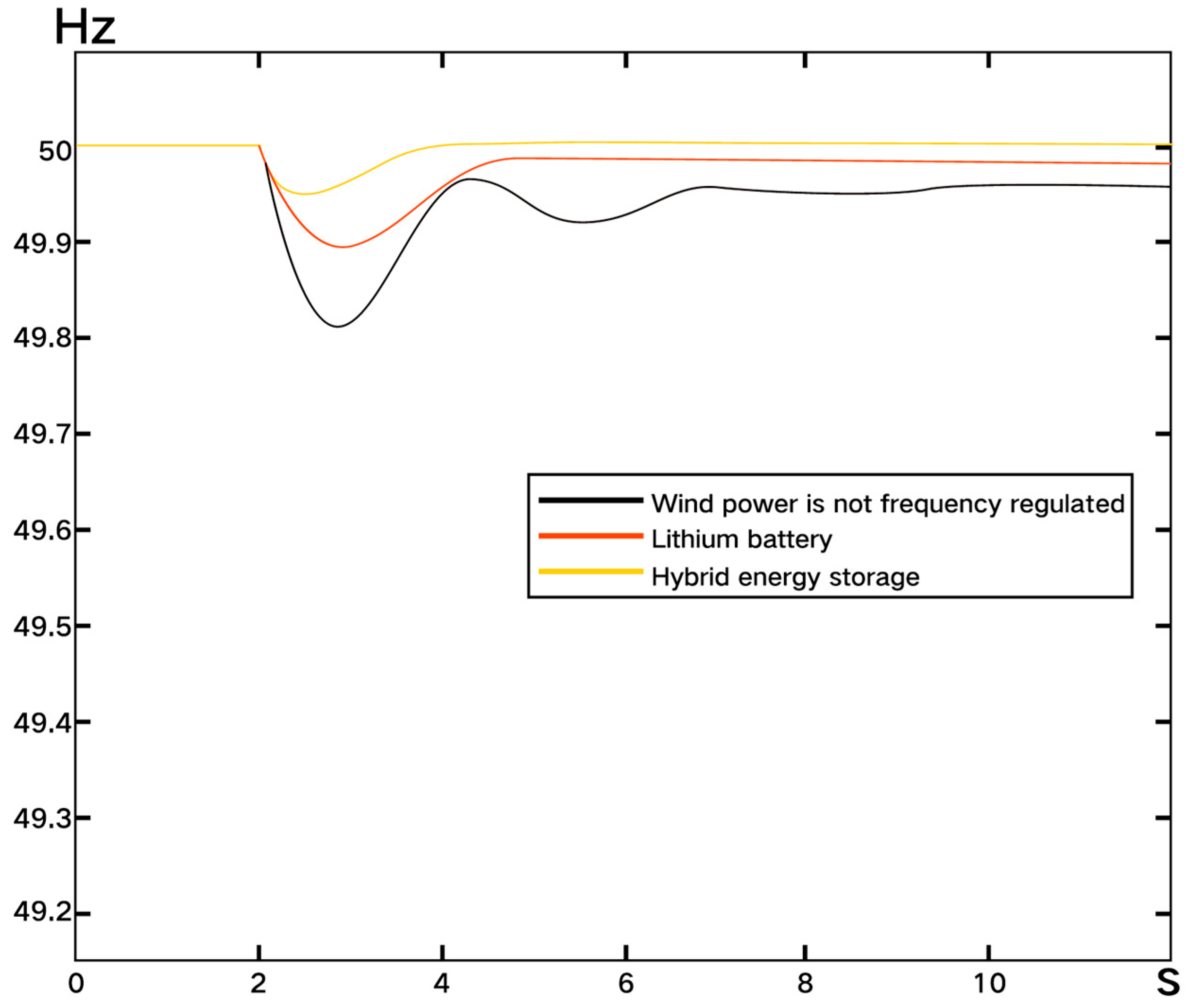
6.1. Frequency Stability Analysis Under Step-Load Disturbance
6.2. Results of Capacity Optimization Allocation
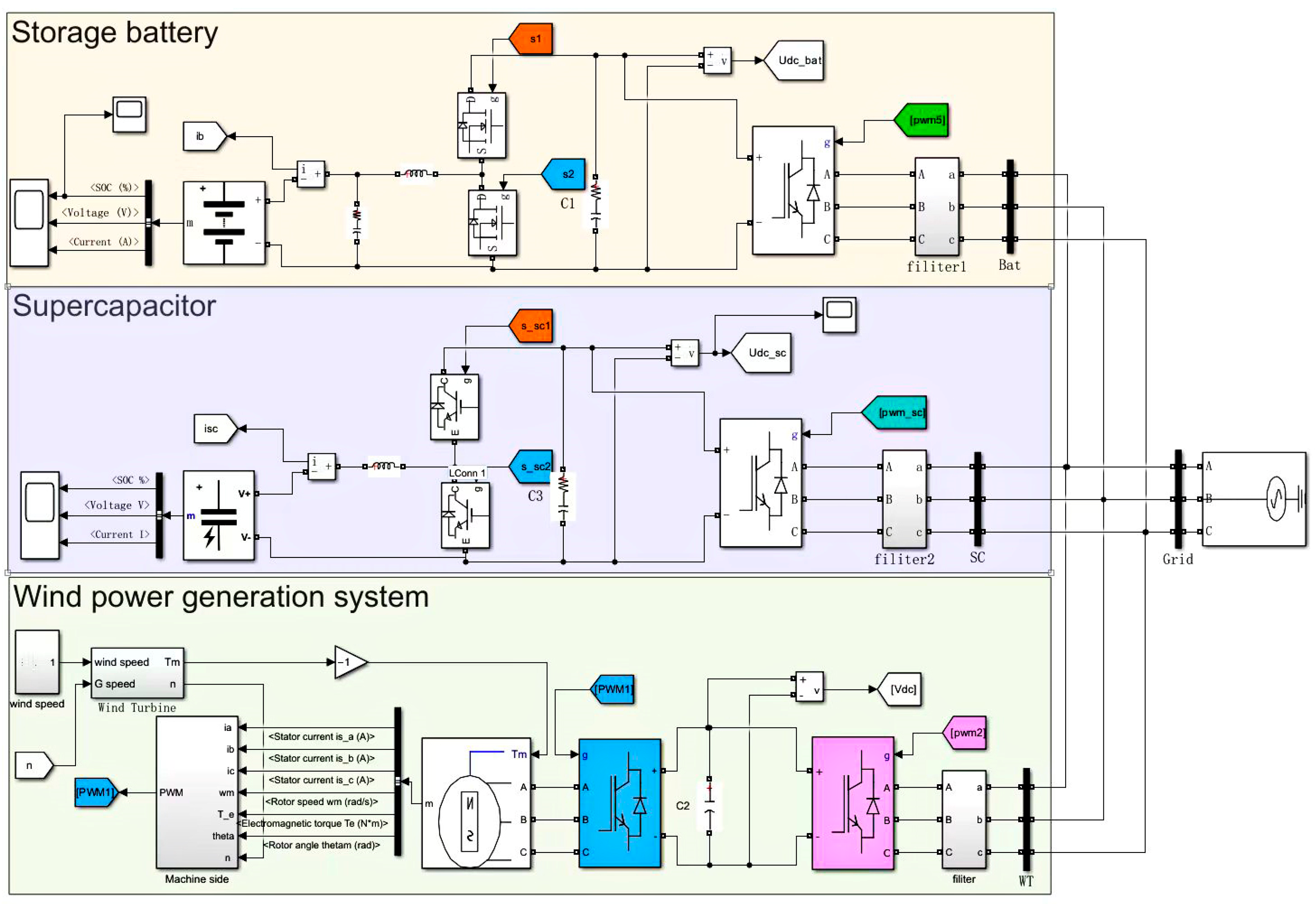
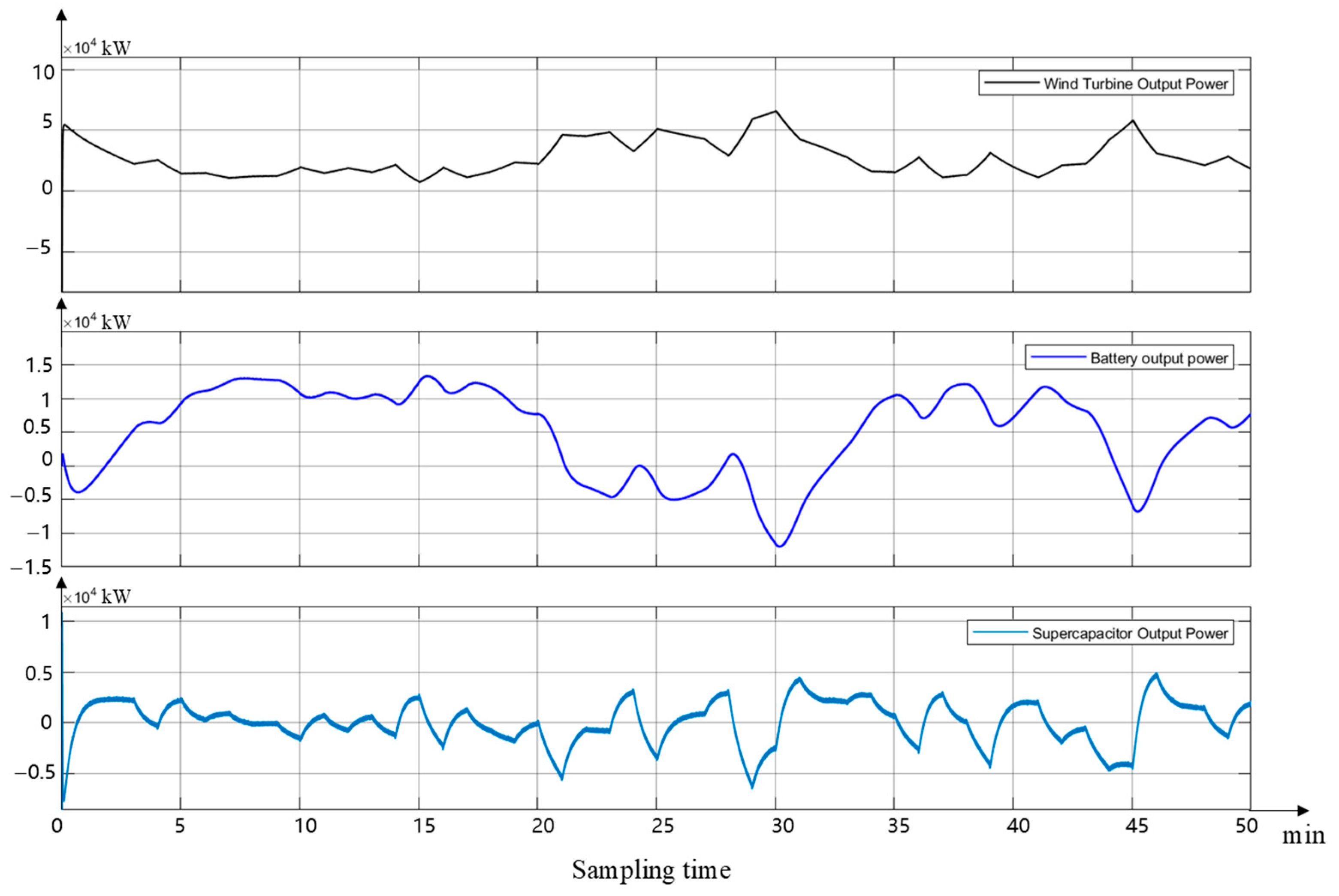
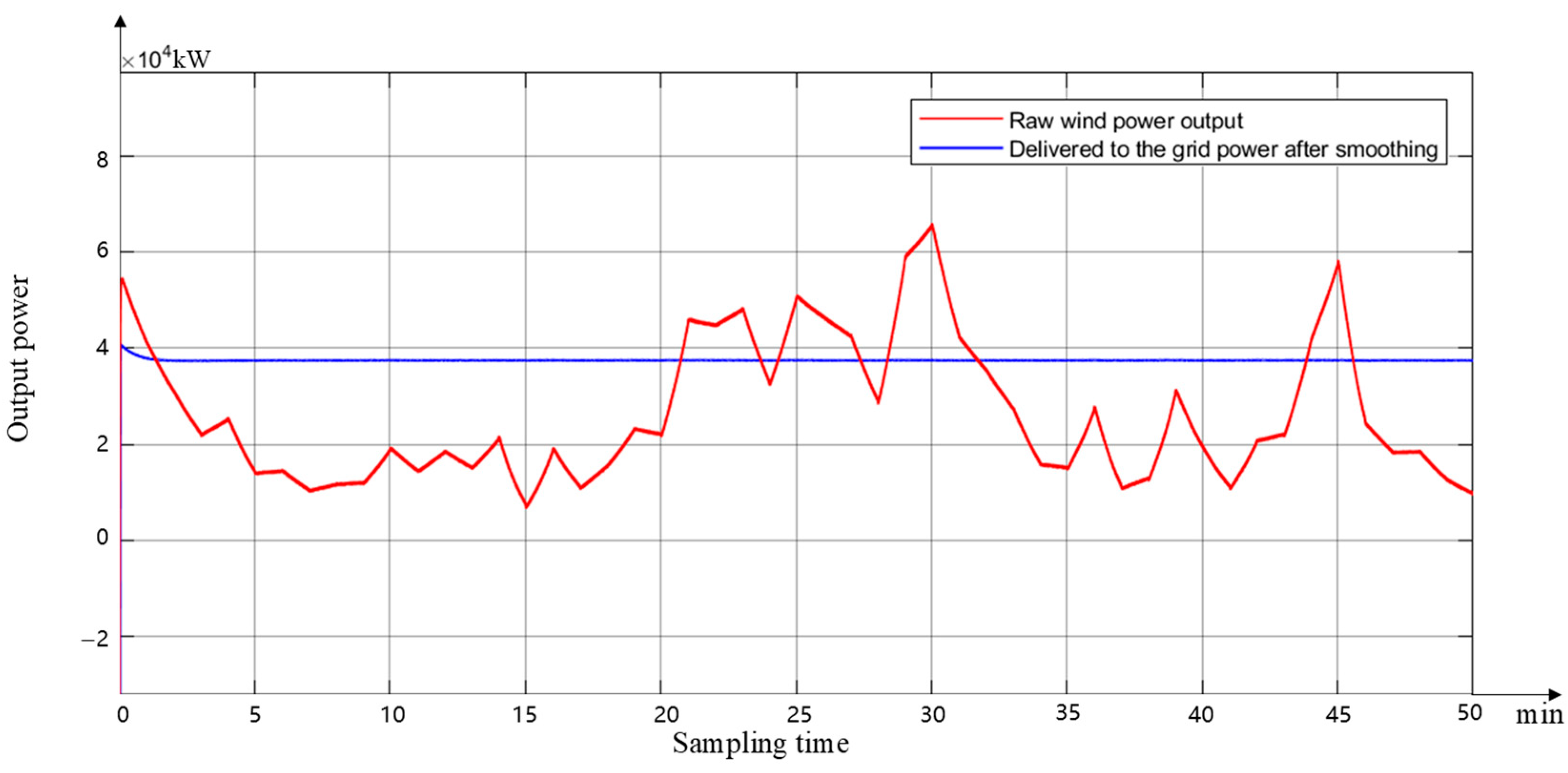
6.3. MATLAB System Simulation
6.4. Analysis of Simulation Results
7. Conclusions
- The primary frequency modulation power command is decomposed using SGC modal decomposition, which decouples the original frequency modulation command into low- and high-frequency power commands. The problem of frequent output during the FM process is successfully mitigated by the lithium battery energy storage, which distributes the low-frequency power commands. The benefits of the rapid charging and the discharge properties of the flywheel energy storage are completely realized when the supercapacitor energy storage reacts to the high-frequency part of the FM command.
- The genetic gray wolf algorithm is applied to determine the ideal configuration on the basis of typical intraday FM power characteristics. The principal frequency modulation performance of the wind power production system could effectively be improved by the hybrid energy storage. The HESS outperformed the single storage configurations in terms of frequency stability under the step-load disruption test scenario.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sepulveda, N.A.; Jenkins, J.D.; Edington, A.; Mallapragada, D.S.; Lester, R.K. The design space for long-duration energy storage in decarbonized power systems. Nat. Energy 2021, 6, 506–516. [Google Scholar] [CrossRef]
- Tewari, S.; Mohan, N. Value of NAS energy storage toward integrating wind: Results from the wind to battery project. IEEE Trans. Power Syst. 2013, 28, 532–541. [Google Scholar] [CrossRef]
- Pavlos, P.; Konstantinos, O.; Anna, T.; Georgios, C. A modified decentralized droop control method to eliminate battery short-term operation in a hybrid supercapacitor/battery energy storage system. Energies 2023, 16, 2858. [Google Scholar] [CrossRef]
- Xia, L.; Zhaoxiang, Z. The intelligent control for the battery charge in the solar lighting system. In Proceedings of the International Conference on Energy and Environmental Protection (ICEEP), Hohhot, China, 23–24 June 2012; pp. 296–300. [Google Scholar]
- Rout, T.; Maharana, M.K.; Chowdhury, A.; Samal, S. A comparative study of stand-alone photovoltaic system with battery storage system and battery-supercapacitor storage system. In Proceedings of the 2018 4th International Conference on Electrical Energy Systems (ICEES), Chennai, India, 7–9 February 2018; pp. 77–81. [Google Scholar] [CrossRef]
- Roy, P.; He, J.; Liao, Y. Cost minimization of battery-supercapacitor hybrid energy storage for hourly dispatching wind-solar hybrid power system. IEEE Access 2020, 8, 210099–210115. [Google Scholar] [CrossRef]
- Yang, F.; Ren, Y.; Yun, P.; Xue, Y.; Lian, M.; Xu, W. Coordinated control and power allocation of two-stage lithium battery-supercapacitor hybrid energy storage system. Renew. Energy Resour. 2019, 37, 361–366. [Google Scholar] [CrossRef]
- Hou, E.; Xu, Y.; Tang, J.; Wang, Z. Strategy of flywheel–battery hybrid energy storage based on optimized variational mode decomposition for wind power suppression. Electronics 2024, 13, 1362. [Google Scholar] [CrossRef]
- Peng, Y.; Lei, G.L.; Yong, Z.; Yan, C.; Shu, M.S.; Peng, Z. The review on the topology of battery-supercapacitor hybrid system applied into the real-time wind power suppression. Adv. Mater. Res. 2013, 860–863, 287–292. [Google Scholar] [CrossRef]
- Xu, H.; Zhongwen, L. Research on frequency modulation capacity configuration and control strategy of multiple energy storage auxiliary thermal power unit. J. Energy Storage 2023, 73, 109186. [Google Scholar] [CrossRef]
- Alawasa, K.M.; Malahmeh, B.K.; Almajali, Z.S. Improved Virtual Inertia Emulation for Frequency Stability Enhancement in Microgrid System. Int. J. Renew. Energy Res. (IJRER) 2022, 12, 2121–2131. [Google Scholar]
- Ma, Q.; Guo, X.; Luo, P.; Zhang, Z.W. A novel railway power conditioner based on super capacitor energy storage system. Trans. China Electrotech. Soc. 2018, 33, 1208–1218. [Google Scholar] [CrossRef]
- Pan, H.; Yang, Y.; Li, X.; Zheng, J.; Cheng, J. Symplectic geometry mode decomposition and its application to rotating machinery compound fault diagnosis. Mech. Syst. Signal Process. 2019, 114, 189–211. [Google Scholar] [CrossRef]
- Luo, F. Coordinated operational planning for wind farm with battery storage system. IEEE Trans. Sustain. Energy 2015, 6, 253–262. [Google Scholar] [CrossRef]
- Ai, X.; Dong, C. Review on the application of energy storage technology in power system with renewable energy sources. Mod. Electr. Power 2015, 32, 1–9. [Google Scholar]
- Guo, T.; Zhang, T.; Lim, E.; Lopez-Benitez, M.; Ma, F.; Yu, L. A review of wavelet analysis and its applications: Challenges and opportunities. IEEE Access 2022, 10, 58869–58903. [Google Scholar] [CrossRef]
- Chen, C.; Tang, W.; Xia, Y.; Chen, C. Hybrid-energy storage optimization based on successive variational mode decomposition and wind power frequency modulation power fluctuation. Energies 2024, 17, 4391. [Google Scholar] [CrossRef]
- Wang, F.; Ling, L.; Qi, Z. Research on data drift suppression method of gyroscope sensor based on first-order inertia and low-pass filter. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020. [Google Scholar]
- Khodarahmi, M.; Maihami, V. A review on Kalman filter models. Arch. Comput. Methods Eng. 2023, 30, 727–747. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Zheng, L.; Shen, F.; Zhao, Q.; Liu, F.; Lou, Y. Research on partial discharge location based on decision disturbance grey wolf optimization. In Proceedings of the 2020 Chinese Automation Congress (CAC2020), Shanghai, China, 6–8 November 2020; pp. 322–327. [Google Scholar] [CrossRef]
- Karan, Y.; Bhavnesh, K.; Guerrero, J.M.; Abderezak, L. A hybrid genetic algorithm and grey wolf optimizer technique for faster global peak detection in PV system under partial shading. Sustain. Comput. Inform. Syst. 2022, 35, 100770. [Google Scholar]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Pincus, S.M. Assessing serial irregularity and its implications for health. Ann. N. Y. Acad. Sci. 2001, 954, 245–267. [Google Scholar] [CrossRef]
- Sun, K. Research on Control Strategy and Capacity Configuration of Wind Power-Hybrid Energy Storage Combined System; North China Electric Power University: Beijing, China, 2021. [Google Scholar] [CrossRef]
- Dong, S.; Shuang, X. State of Health Prediction for Retired Lithium-Ion Batteries in Cascade Utilization. Trans. China Electrotech. Soc. 2018, 33, 2121–2129. [Google Scholar] [CrossRef]
- Shan, H. Research on Optimal Configuration of Battery Energy Storage Systems for Enhancing Wind Power Cluster Delivery; Northeast Electric Power University: Jilin, China, 2020. [Google Scholar] [CrossRef]
- Gbadegesin, O.A.; Sun, Y.; Nwulu, I.N. Stacked value streams of hybrid energy storage systems in prosumer microgrids. J. Eng. Des. Technol. 2020, 19, 1063–1079. [Google Scholar] [CrossRef]
- Yu, Q.; Xie, L. Optimal configuration of multi-objective hybrid energy storage system for grid-connected wind power. Mod. Electron. Technol. 2021, 44, 111–115. [Google Scholar]
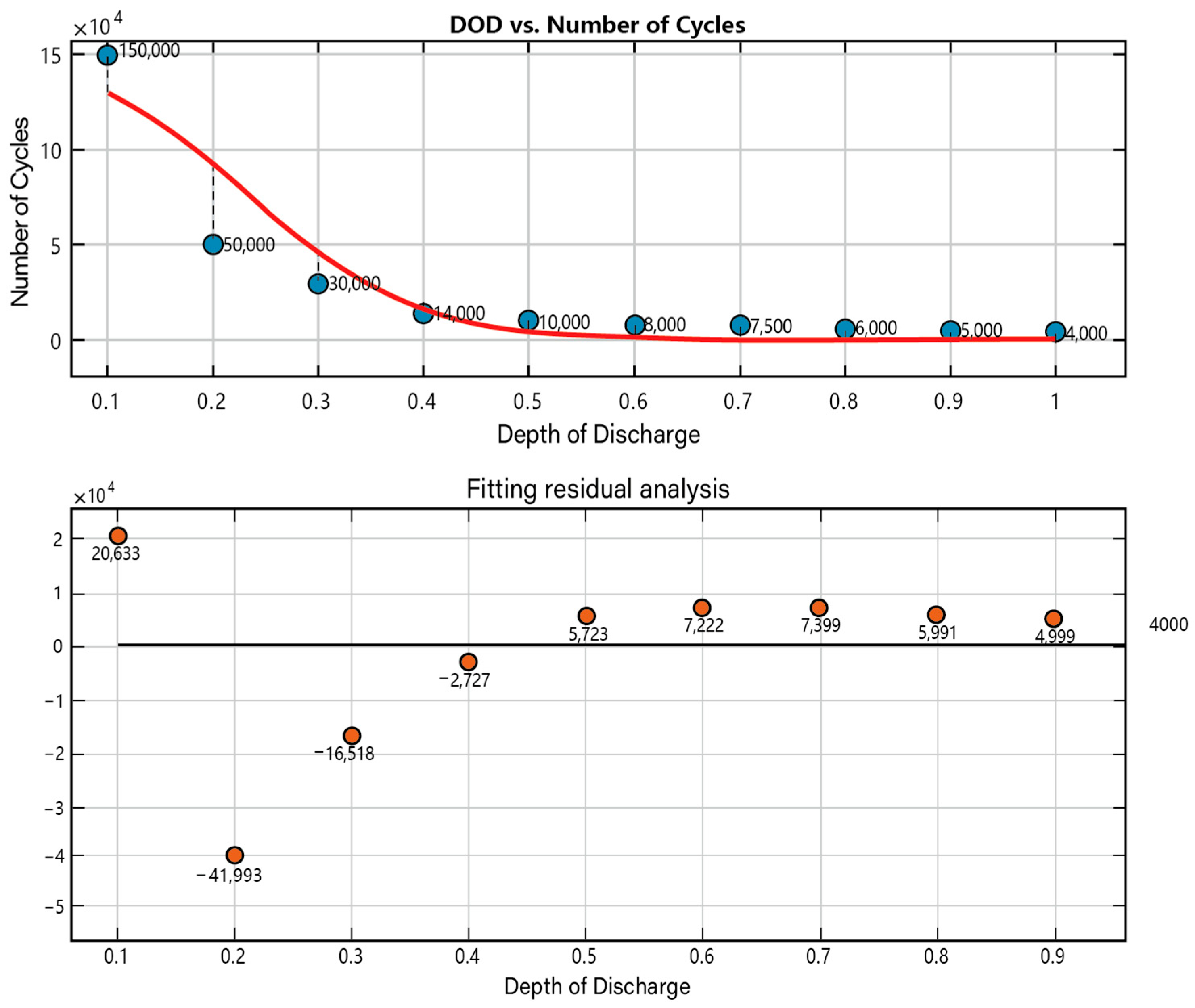
| Depth of Discharge | Number of Cycles | Depth of Discharge | Number of Cycles |
|---|---|---|---|
| 0.1 | 150,000 | 0.6 | 8000 |
| 0.2 | 50,000 | 0.7 | 7500 |
| 0.3 | 30,000 | 0.8 | 6000 |
| 0.4 | 14,000 | 0.9 | 5000 |
| 0.5 | 10,000 | 1 | 4000 |
| Parameter | Li Battery | SC |
|---|---|---|
| Unit power cost CNY/kW | 2700 | 1500 |
| Unit cost of capacity CNY/kWh | 640 | 27,000 |
| O&M costs CNY/kWh | 0.05 | 0.05 |
| Processing costs CNY/kWh | 0.04 | 0.05 |
| Charge and discharge efficiency % | 80 | 95 |
| SOC range | (0.15, 0.85) | (0.1, 0.9) |
| Cycle life/year | 3 | 15 |
| Funds discount rate | 6 | 9 |
| Other | Other | SC | |
|---|---|---|---|
| Wind farm size | 80 MW | Scale of energy storage | 3 MW |
| Daily power generation | 12 h | Recycling income | 5–10% |
| Annual running time | 3000 h | Life cycle | 20 years |
| Frequency Modulation | ||
|---|---|---|
| Wind power does not participate in frequency modulation | 0.1936 | 5.28 |
| Single lithium FM battery | 0.1072 | 2.37 |
| Lithium-ion battery with supercapacitor frequency modulation | 0.0535 | 1.76 |
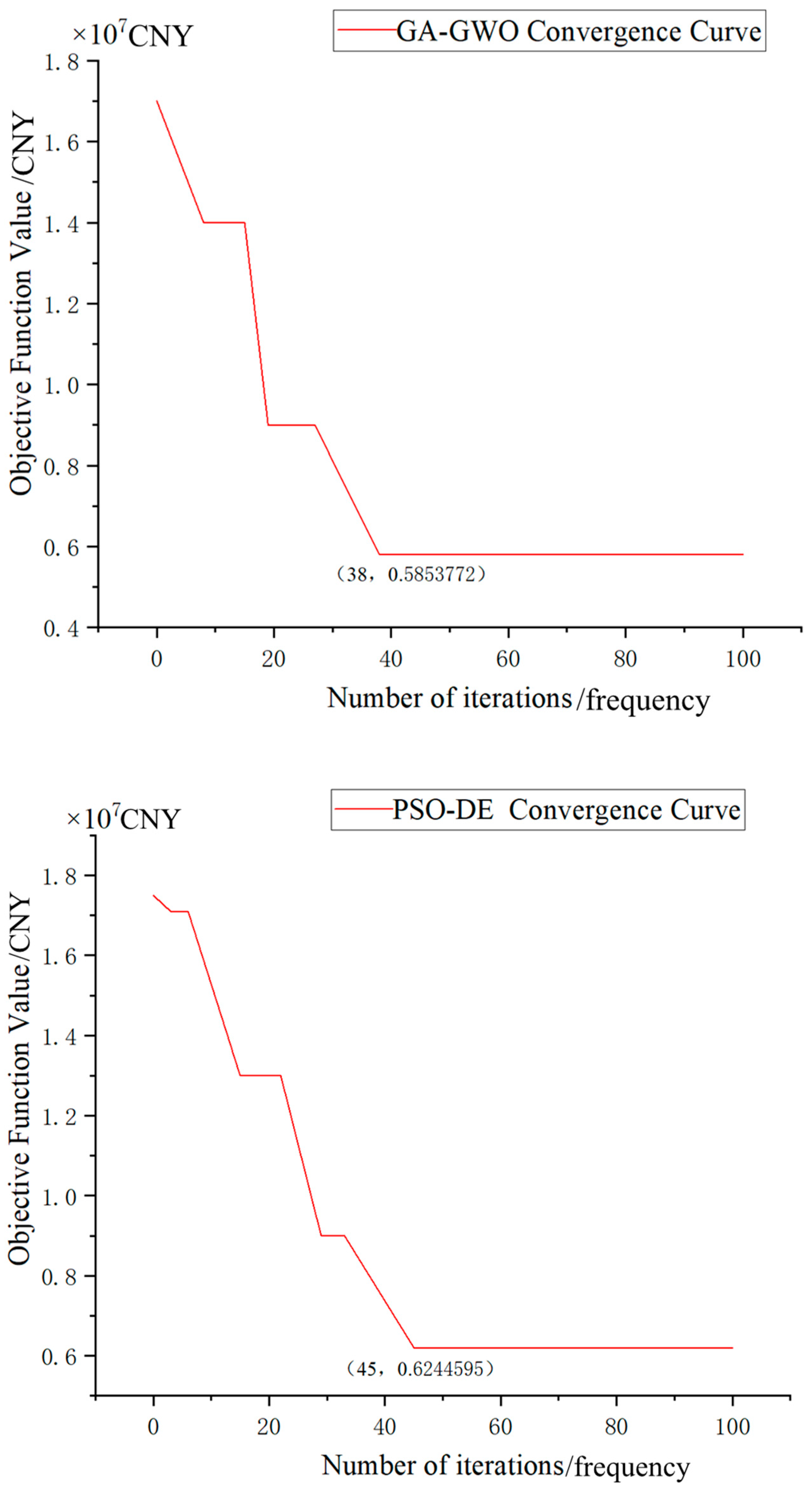
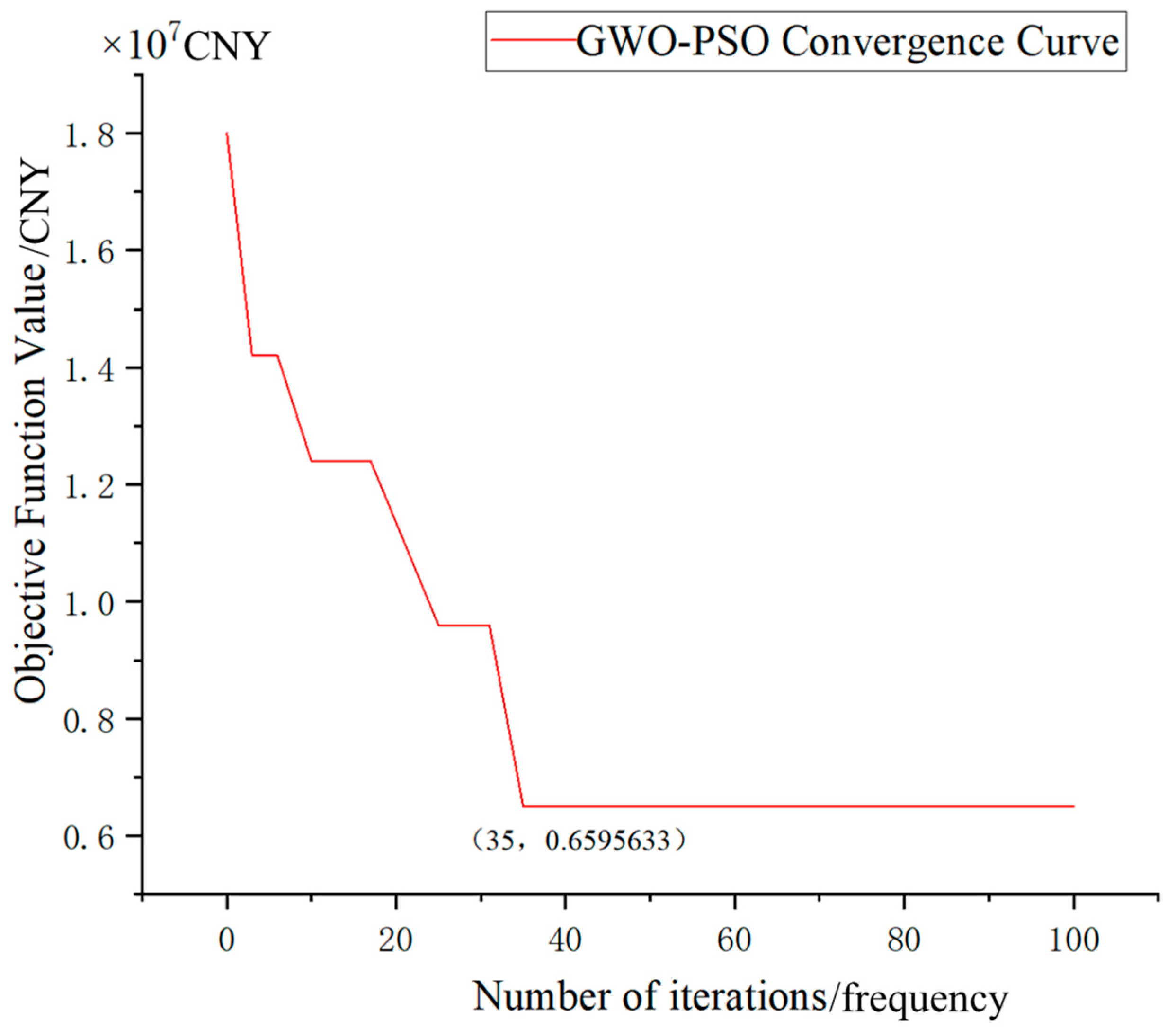
| Optimization Algorithm | GA-GWO | PSO-DE | GWO-PSO |
|---|---|---|---|
| Number of iterations | 38 | 45 | 34 |
| Running time/s | 6 | 10 | 9 |
| Cost/CNY | 5,853,772 | 6,244,595 | 6,695,633 |
| Net benefit/CNY | 3,755,140 | 3,100,866 | 3,196,547 |
| Li battery/MW | 0.62 | 0.51 | 0.57 |
| Supercapacitor/MW | 0.37 | 0.45 | 0.39 |
| Li battery/MWh | 0.59 | 0.26 | 0.31 |
| Supercapacitor/MWh | 0.42 | 1.21 | 1.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Zuo, Z.; Shen, K.; Gao, J.; Chen, Q.; Liu, J.; Liu, H. Sim-Geometry Modal Decomposition (SGMD)-Based Optimization Strategy for Hybrid Battery and Supercapacitor Energy Storage Frequency Regulation. Symmetry 2025, 17, 1356. https://doi.org/10.3390/sym17081356
He Y, Zuo Z, Shen K, Gao J, Chen Q, Liu J, Liu H. Sim-Geometry Modal Decomposition (SGMD)-Based Optimization Strategy for Hybrid Battery and Supercapacitor Energy Storage Frequency Regulation. Symmetry. 2025; 17(8):1356. https://doi.org/10.3390/sym17081356
Chicago/Turabian StyleHe, Yongling, Zhengquan Zuo, Kang Shen, Jun Gao, Qiuyu Chen, Jianqun Liu, and Haoyu Liu. 2025. "Sim-Geometry Modal Decomposition (SGMD)-Based Optimization Strategy for Hybrid Battery and Supercapacitor Energy Storage Frequency Regulation" Symmetry 17, no. 8: 1356. https://doi.org/10.3390/sym17081356
APA StyleHe, Y., Zuo, Z., Shen, K., Gao, J., Chen, Q., Liu, J., & Liu, H. (2025). Sim-Geometry Modal Decomposition (SGMD)-Based Optimization Strategy for Hybrid Battery and Supercapacitor Energy Storage Frequency Regulation. Symmetry, 17(8), 1356. https://doi.org/10.3390/sym17081356






