FSTGAT: Financial Spatio-Temporal Graph Attention Network for Non-Stationary Financial Systems and Its Application in Stock Price Prediction

Abstract

Accurately predicting stock prices is crucial for investment and risk management, but the non-stationarity of the financial market and the complex correlations among stocks pose challenges to traditional models (ARIMA, LSTM, XGBoost), resulting in difficulties in effectively capturing dynamic patterns and limited prediction accuracy. To this end, this paper proposes the Financial Spatio-Temporal Graph Attention Network (FSTGAT), with the following core innovations: temporal modelling through gated causal convolution to avoid future information leakage and capture long- and short-term fluctuations; enhanced spatial correlation learning by adopting the Dynamic Graph Attention Mechanism (GATv2) that incorporates industry information; designing the Multiple-Input-Multiple-Output (MIMO) architecture of industry grouping for the simultaneous learning of intra-group synergistic and inter-group influence; symmetrically fusing spatio-temporal modules to construct a hierarchical feature extraction framework. Experiments in the commercial banking and metals sectors of the New York Stock Exchange (NYSE) show that FSTGAT significantly outperforms the benchmark model, especially in high-volatility scenarios, where the prediction error is reduced by 45–69%, and can accurately capture price turning points. This study confirms the potential of graph neural networks to model the structure of financial interconnections, providing an effective tool for stock forecasting in non-stationary markets, and its forecasting accuracy and industry correlation capturing ability can support portfolio optimization, risk management improvement and supply chain decision guidance.

1. Introduction

In the dynamic evolution of financial markets, stock price forecasting remains a core issue in theoretical research and practical applications [1], guiding investors’ asset allocation and serving as a key basis for financial institutions’ risk management, asset pricing, and strategy formulation—helping capture gains and avoid systemic risks. In recent years, global markets have faced heightened volatility from macroeconomic shifts, geopolitical conflicts, and black swan events (e.g., the 2020 pandemic, 2022 energy crisis), boosting demand for robust prediction models and highlighting forecasting’s practical value in uncertain environments. However, forecasting remains inherently complex and susceptible to multiple uncertainties [2]; the core challenge lies in modeling stock prices systemically within non-stationary financial systems, where interconnected factors shape market dynamics, making accurate future price prediction exceptionally formidable.

Traditional stock price prediction methods like ARIMA models and statistical regression analysis [3] are constrained by linearity assumptions and data smoothness requirements, leaving them ill-equipped to capture financial markets’ inherent complexity and non-stationarity. Shaped by fundamental factors (e.g., corporate earnings) and behavioral factors (e.g., investor sentiment), markets experience abrupt fluctuations from events like earnings announcements and policy releases. Industry synergies (e.g., supply chain links) and sector rotations further create dynamic stock interdependencies. These features render financial systems inherently non-linear, making traditional models ineffective at representing their dynamics [4].

While machine learning approaches [5] overcome some linearity limitations, they often depend on handcrafted features and lack the capacity to model intricate inter-stock relationships or adapt to evolving market structures, thus limiting their generalizability and robustness. Consequently, these traditional and machine learning methods frequently fall short in delivering accurate, reliable, and timely stock price forecasts.

The boom in deep learning has revolutionized financial market analysis [6]. Among them, Recurrent Neural Network (RNN) [7] and its classical variant Long Short-Term Memory (LSTM) [8] can capture the dynamics of stock prices in the time dimension by virtue of its sequence modelling capability, and LSTM effectively solves the bottleneck of long-term memory of traditional RNNs through the gating mechanism consisting of forgetting gates, input gates, and output gates, and performs excellently in the task of dealing with the dependency of long sequences [9]. However, LSTM is essentially a single-sequence modelling tool, and its core capability is limited to capturing the time-series dependencies of individual stocks, which cannot directly deal with cross-asset correlations that are common among stocks in the financial market. This limitation makes it difficult for LSTM to integrate multi-stock information to improve the prediction accuracy when facing the linkage effect of “all gain and all loss” in the stock market.

However, complex correlations among stocks in the financial market (such as industry linkages and sector rotations) urgently require more efficient structured modeling tools. Thus, Graph Neural Networks (GNNs) have become a new paradigm [10]. GNNs naturally represent the dependency relationships among stocks through the topological structure of nodes and edges, and can effectively capture non-Euclidean space correlations such as upstream and downstream of the industrial chain and sector collaboration [11]. Here, the topological structure refers to the way stocks (nodes) are connected via meaningful relationships (edges), such as price correlations or industry ties, forming an irregular network rather than a fixed grid. Non-Euclidean spatial correlations describe such relationships that are not based on physical distance or sequential order, but on domain-specific associations like supply chain proximity or co-movement.

In contrast, the rise of graph neural networks (GNNs) has provided a new paradigm for structured modelling of financial markets [10]. GNNs naturally characterize inter-stock dependencies through the topology of nodes and edges, and are able to effectively capture non-Euclidean spatial associations such as upstream and downstream of industrial chains, industry synergies, and so forth, which is a cross-stock modelling capability that is not possible with time-series models such as LSTM.

Based on this, Spatio-Temporal Graph Attention Networks (STGATs) [12] further integrate time-series dynamics and graph-structure representation. Through the attention mechanism, they adaptively focus on key nodes and temporal patterns. This not only breaks through the limitations of traditional methods in spatial correlation modeling but also strengthens the ability to fuse multi-scale spatio-temporal features, providing a highly promising solution for improving the accuracy and robustness of stock price prediction.

This paper proposes a Financial Spatio-Temporal Graph Attention Network (FSTGAT) for modeling non-stationary financial systems and develops a spatio-temporal adaptive prediction framework specifically tailored for stock price forecasting. Compared with existing methods, our work incorporates dynamic industry-aware graph construction, strictly causal temporal modeling, and sector-based multi-output forecasting to address the challenges of volatility and time-varying correlations in financial markets. The main contributions are summarized as follows:

• Causal Temporal Modeling Mechanism: We adopt a Gated Causal Convolution architecture, which strictly enforces temporal causality in financial time series to prevent future information leakage, while supporting efficient parallel computation compared to recurrent architectures.
• Dynamic Industry-Aware Graph Attention: We design an adaptive GATv2-based graph attention mechanism that integrates industry classification priors and market correlation matrices as edge attributes. This enables the model to dynamically update inter-stock association weights over time, distinguishing genuine industry-driven relationships from spurious correlations caused by transient market sentiment.
• Multi-Scale Sector-Level MIMO Framework: We propose a multi-input multi-output prediction architecture grouped by industry sectors. Homogeneous financial entities are clustered into subgraphs, allowing the graph attention layers to capture both intra-sector synergies and inter-sector spillover effects, overcoming the limitations of single-asset modeling.
• Sector-Specific Robustness and Significance Validation: We conduct extensive experiments on NYSE commercial banking and metals sectors, incorporating Diebold–Mariano significance tests and ablation studies to rigorously validate the effectiveness and robustness of FSTGAT under different volatility regimes.

We select NYSE commercial banking and metal sectors as testbeds for their contrasts: banking, rate-sensitive with intra-sector contagion (e.g., 2008 crisis); metals, tied to commodity cycles and global supply chains. For example, banking stocks react sharply to rate policies, while metals correlate closely with commodity cycles. This dual-sector approach validates cross-regime generalizability. Empirical tests show the FSTGAT model outperforms SARIMA, LSTM, and XGBOOST, innovating by modeling stocks as an interconnected network (not isolated entities). It bridges the gap by addressing the need for frameworks integrating temporal and spatial dependencies.

Despite challenges in real-world deployment, including trading latency (e.g., <10 ms response for high-frequency trading systems), regulatory compliance (e.g., SEC Rule 15c3-5), and model interpretability, the FSTGAT model retains significant value. It expands financial forecasting methodologies, highlights graph neural networks’ potential for modeling complex financial systems, and provides critical theoretical support and practical guidance for applications like portfolio optimization and risk management, fostering advancements in financial quantitative analysis and decision support.

The remainder of the paper is structured as follows: Section 2 reviews related work on traditional statistical models, machine learning, and spatio-temporal graph neural networks. Section 3 introduces core theoretical fundamentals. Section 4 details the FSTGAT architecture, including temporal convolution, spatial attention, and output layers. Section 5 describes experimental design, datasets, and evaluation metrics. Section 6 presents experimental results with ablation studies and complexity analysis. Section 7 concludes and outlines future work.

2. Literature Review

Early financial forecasting primarily relied on traditional statistical models. The ARIMA model [13,14], while effective for modeling smooth time series and applied to stock price forecasting [15], is limited by its linear assumptions and inability to handle the non-stationarity and abrupt changes common in financial markets. To address volatility, Engle introduced the ARCH model [16], later extended to GARCH by Bollerslev [17], which models volatility clustering. However, these models remain constrained by their linear frameworks and cannot fully capture the complex nonlinear relationships in financial data.

With machine learning, models like SVMs [18] and random forests [19] enabled modeling nonlinear time series patterns but relied heavily on manual feature engineering, limiting generalizability and scalability. Advanced tree-based models XGBoost [20] and LightGBM [21] emerged as alternatives; XGBoost uses regularization and greedy feature selection to boost performance, while LightGBM employs histogram splitting and leaf-wise growth for faster training on large datasets. Yet they still depend partially on manual feature engineering to capture temporal dependencies.

The advent of deep learning has significantly advanced time series modeling. LSTM, proposed by Hochreiter and Schmidhuber [22], addresses the gradient vanishing/exploding issues in RNNs through gating mechanisms, enabling the capture of long-range dependencies. In financial forecasting, LSTM has demonstrated strong potential for modeling long-term correlations [23], yet it remains limited in capturing cross-asset linkages [24]. Temporal Convolutional Networks (TCN) [25] utilize dilated convolutions to expand the receptive field and support parallel computation, improving efficiency over traditional RNNs and making them suitable for low-latency scenarios such as high-frequency trading. WaveNet [26] employs causal convolutions to ensure temporal causality and prevent information leakage from the future, setting a benchmark for time series modeling. However, these models primarily focus on single-sequence data and struggle to capture cross-asset or spatial relationships, underscoring the need for approaches that can model complex dependencies across multiple sequences.

The rise of graph neural networks (GNNs) is naturally adapted to the “entity association network” features of financial markets (e.g., stock industry chain linkages, institutional position networks, and credit bond collateral relationships); the basic GCN proposed by Kipf & Welling [27] pioneered graph convolution operators to enable node information propagation. Notably, as behavioral finance reveals the presence of irrational pricing mechanisms driven by interconnected market participants, graph structures become critical for expressing such complex interaction-driven dynamics [28]. GAT, proposed by Velickovic et al. [29], introduces an attention mechanism to dynamically allocate neighbor node weights and accurately identify differences in association strength; GATv2, optimized by Brody et al. [30], improves dynamic attention computational logic, emerging as the current state-of-the-art architecture in graph learning.

In order to break through the modelling limitations of a single model and single variable in financial and other scenarios, the researchers also tried to build hybrid models with multivariate inputs by combining multiple deep learning and classical models.

Spatio-Temporal Graph Neural Networks (STGNNs) focus on the “spatio-temporal coupling” characteristics of financial data, and fill the research gap through spatio-temporal joint modeling. In the field of traffic flow prediction, Yu et al. [12] proposed STGCN, which pioneered the fusion architecture of graph convolution and 1D-CNN to depict spatio-temporal dependencies, and Wu et al. [31] proposed Graph WaveNet, which introduced an adaptive adjacency matrix to dynamically capture time-varying spatial correlations, laying the foundation for technology transfer in financial scenarios. In terms of financial application exploration, Sawhney et al. [32] proposed STHAN-SR, which integrated spatio-temporal attention mechanisms and hypergraph structures to adapt to complex financial correlations, attempting to depict the dynamic interactions of the asset network.

Kanwal et al. [33] proposed a hybrid deep learning model, BiCuDNNLSTM-1dCNN, integrating CUDA-accelerated bidirectional LSTM and one-dimensional CNN to capture both long-term temporal dependencies and short-term local patterns in stock price time series, demonstrating superior prediction accuracy across five datasets compared to four state-of-the-art models, although noting limitations in data scale dependency and hyperparameter optimization complexity.

Jin [34] proposes GraphCNNPred, a hybrid model integrating graph neural networks (GAT/GCN) and convolutional neural networks (CNNs), which leverages feature correlation graphs and temporal convolutional layers to predict trends in stock market indices (S&P 500, NASDAQ, etc.), achieving a 4–15% improvement in F measure over baseline algorithms and demonstrating effective trading strategy performance with a Sharpe ratio exceeding 3.

Liu and Paterlini [35] proposed an LSTM-GCN model that integrates a graphical convolutional network (GCN), which is used to capture spatial dependencies in supplier–customer value chain relationships, and a long- and short-term memory network (LSTM), which is used to simulate the temporal dynamics of stock returns in relation to the Euro Stoxx 600 Index and the S&P 500 Index. The model improves forecast accuracy and risk-adjusted returns compared to the baseline model for the Euro Stoxx 600 and S&P 500 datasets.

Wenbo Yan and Ying Tan [36] propose a time-correlation graph pre-training network (TCGPN), which integrates time series and node dependencies through a time-correlation fusion encoder, combines self-supervised time-completion and semi-supervised graph recovery tasks to optimize representations, and solves the problem of large-scale node memory by using a node/graph/time-masked data augmentation strategy, which has been proposed in CSI300/Performance breakthroughs in non-periodic time series forecasting on CSI300/CSI500 stock datasets with lightweight MLP fine-tuning.

The recent STGAT model proposed by Feng et al. [37] has made valuable contributions to stock prediction, particularly in demonstrating the potential of integrating spatio-temporal features into financial forecasting. Specifically, it uses a standard GAT to model stock relationships via static price correlations and applies STL decomposition for temporal pattern extraction, laying a useful foundation for exploring market dynamics.

However, our work differs in several key aspects. First, unlike Feng et al., we incorporate explicit industry-aware grouping mechanisms to construct dynamic sector-specific subgraphs, enabling the model to capture intra-sector synergy and inter-sector spillovers. Second, we target industry-specific, high-volatility sectors (NYSE commercial banking and metals) rather than broad-market indices (CSI 500/S&P 500), allowing robustness validation across distinct volatility regimes. Third, our temporal module employs a causal convolution + GLU design to ensure strict temporal causality and parallel efficiency, in contrast to their reliance on standard temporal convolution. Finally, while Feng et al. emphasize portfolio optimization performance, we focus on prediction accuracy and statistical significance validation through Diebold–Mariano tests and ablation studies. Please refer to

Table 1. Key differences between [37] STGAT and our proposed FSTGAT.

Aspect	[37] STGAT	Our FSTGAT
Graph construction	Standard GAT with static price correlation adjacency	Dynamic GATv2 with industry-aware edge attributes (sector classification + market correlations)
Temporal modeling	STL decomposition + standard temporal convolution	Causal convolution + GLU gating to ensure strict causality and parallelization
Data scope	Broad-market indices (CSI 500, S&P 500)	Industry-specific stocks (NYSE commercial banking and metals)
Objective focus	Portfolio optimization and return maximization	Prediction accuracy, robustness, and statistical significance validation (DM tests, ablation)
Industry structure	No explicit sector-based subgraph grouping	Explicit sector-based multi-input multi-output framework

.

Currently, there are several aspects of financial prediction models that can be optimized. In the causal constraint dimension, traditional convolution faces the problem of future data leakage [12], while RNN models encounter obstacles in parallelization, which negatively affects both the reliability and efficiency of forecasting. Second, in terms of dynamic relationship modeling, traditional methods rely excessively on static graph structures and have a single source of correlation, limited to the use of price correlation or industry classification [34]. However, dynamic changes such as industry restructuring and black swan events occur frequently in financial markets, and the market environment is complex and volatile. Under such circumstances, forecasting models perform poorly in dealing with unexpected events and also ignore the interactions between stocks, especially those in the same industry sector. Furthermore, in terms of model magnitude, most of today’s models focus on a single stock or a single indicator, and rarely consider a specific industry sector or system level [33].

This paper proposes a Financial Spatio-Temporal Graph Attention Network (FSTGAT) for non-stationary financial systems. It provides an innovative solution that combines logical self-consistency and market adaptability for stock price prediction. For readers seeking a deeper understanding of the theoretical foundations and methodological developments in graph theory and graph neural networks relevant to this study, we recommend consulting [38,39,40,41,42,43,44,45,46,47,48,49].

3. Theory Fundamentals

This section lays the mathematical foundation for the FSTGAT model, and the core sub-modules are related to the model structure; the graph convolution theory explained in Section 3.1 supports the design of the spatial convolution layer (GATv2) in Section 4.2, the temporal convolution method and gating mechanism in Section 3.2 and Section 3.3 corresponds to the implementation of the temporal convolution layer (causal GLU) in Section 4.1, and the temporal and spatial fusion mechanism in Section 3.4 is the main body of the model. The spatio - temporal framework provides the theoretical basis.

This section lays the mathematical foundation for the FSTGAT model, and the core sub-modules form a correspondence with the model structure; the graph convolution theory explained in Section 3.1 supports the design of the spatial convolution layer (GATv2) in Section 4.2, the temporal convolution method in Section 3.2 corresponds to the implementation of the temporal convolution layer (causal GLU) in Section 4.1, and the temporal and spatial fusion mechanism in Section 3.3 is the industry used in the output layer in Section 4.3. The MIMO framework is used for the output layer in Section 4.3.

3.1. Graph Theory and Graph Convolutional Networks

Graph theory provides the mathematical foundation for modeling graph-structured data [50]. In mathematics, a graph is denoted as $G=(V,E)$, where the node set

$$V=\{v_1,v_2,\dots ,v_N\}$$

(1)

represents entities, and the edge set E represents the relationships between entities. The adjacency matrix $A\in {\mathbb{R}}^{N\times N}$ describes the connection strength between nodes, and the degree matrix D is a diagonal matrix with elements $D_{ii}={\sum }_j{A}_{ij}$.

Graph Convolutional Networks (GCN) extend the convolution operation to graph structures via spectral or spatial domain methods [27]. Spectral domain GCN is based on the eigen decomposition of the graph Laplacian matrix

$$L=D-A$$

(2)

which maps signals from the spatial domain to the frequency domain for processing. For example, the simplified GCN layer proposed by Kipf and Welling is expressed as:

$$H^{(l+1)}=\sigma \left({\tilde{A}}^{-{\displaystyle \frac{1}{2}}}\tilde{A}{\tilde{D}}^{-{\displaystyle \frac{1}{2}}}{H}^{\left(l\right)}{W}^{\left(l\right)}\right)$$

(3)

where $\tilde{A}=A+I$ (adding self-loops), $\tilde{D}$ is the degree matrix of $\tilde{A}$, $W^{\left(l\right)}$ is the learnable weight matrix, and $\sigma$ is the activation function. This approach implicitly captures dependencies between nodes through the adjacency matrix, enabling the propagation of features over the graph structure.

3.2. Convolutional Neural Network

Convolutional Neural Networks (CNNs) [51] were originally designed for processing grid-structured data such as images, with their core advantage lying in capturing local features through shared convolutional kernels. In time series processing, one-dimensional convolution (1D Conv) in CNNs extracts local patterns along the temporal axis through sliding windows, offering advantages of parameter efficiency and parallel computation.

The Temporal Convolutional Network (TCN) [25] extends CNNs for temporal modeling by introducing causal convolution and dilated convolution. Causal convolution ensures that the output at the current time step depends only on past inputs, satisfying the causality requirement for time series prediction. Dilated convolution expands the receptive field by setting a dilation factor d, enabling the kernel to capture longer-range temporal dependencies:

$$F\left(s\right)=\sum _{k=0}^{K-1}f\left(k\right)·x_{s-d·k}$$

(4)

where K is the convolution kernel size and x is the input sequence. By stacking multiple dilated convolutional layers with exponentially increasing dilation factors, TCN efficiently captures long-term temporal patterns without increasing the number of parameters.

3.3. Gating Mechanism

The gating mechanism is a key component in deep learning for dynamically controlling the flow of information. It is widely used in models such as recurrent neural networks (e.g., LSTM, GRU), Transformer, and graph neural networks. Its core idea is to generate weights between 0 and 1 through learnable “gating units” (usually implemented by activation functions such as sigmoid or softmax) to dynamically screen, retain, or suppress input information. For example, in temporal models, it filters out noise and focuses on key temporal features, and in the attention mechanism, it highlights the contributions of important nodes or sequence positions. Through this adaptive adjustment mechanism, the model can more effectively handle long-range dependencies, reduce the interference of redundant information, and thus improve the learning ability and generalization performance in complex scenarios.

3.4. The Fusion of Spatio-Temporal Graph Convolutional Network

Spatio-temporal Graph Convolutional Networks (STGCNs) [12] integrate the advantages of graph theory and CNNs to simultaneously process spatial dependencies and temporal dynamics in data. The core concept of STGCN involves designing specialized spatio-temporal convolution modules that separately capture spatial relationships in graph structures and temporal evolution in sequential data.

In the spatial dimension, STGCN typically employs GCN or its variants (e.g., ChebNet, GAT) for graph structure modeling. In the temporal dimension, it utilizes CNNs (e.g., TCN) or RNNs (e.g., LSTM) to process temporal features. For instance, the STGCN framework proposed by Yu et al. decomposes spatio-temporal convolution into two sequential operations: spatial graph convolution and temporal convolution:

$$X_{t+1}=\sigma (G(X_t,W_s)\ast T(X_t,W_t))$$

(5)

where $G(·)$ denotes the spatial graph convolution operation, $T(·)$ represents the temporal convolution operation, and $W_s$ and $W_t$ are learnable weights for spatial and temporal dimensions respectively. This decomposition enables the model to learn simultaneously node dependency relationships in space and evolution patterns in time.

4. FSTGAT: Model Structure and Innovation

This innovative architecture enables FSTGAT to simultaneously capture (1) long-term evolutionary trends and short-term volatility patterns in the time dimension, (2) complex market linkage effects in the spatial dimension, and (3) local features of unexpected market events. As such, it is expected to enhance the training of the model and is expected to produce good forecasting results.

We propose an innovative Financial Spatio-Temporal Graph Attention Network (FSTGAT) that aims to significantly improve the accuracy of stock price prediction while effectively capturing the complex spatio-temporal dependencies in financial markets.

The model we design contains two core components that work in tandem: a gated temporal convolution module and an augmented graph attention module, which together build a hierarchical feature extraction architecture. The former employs strict causal constraints and an innovative gating mechanism to capture long-term evolutionary patterns in the temporal dimension, preserving key features and suppressing noise, while the latter learns complex spatial relationships among stocks using a multi-attention mechanism, which adjusts the attention coefficients with the help of edge attributes.

The two modules work together through a “time-convolution-graph-attention-time-convolution” sandwich symmetry structure, and the model achieves hierarchical feature abstraction through a cascading spatio-temporal block architecture: the first block extracts the underlying spatio-temporal patterns, and the second captures the higher-order market dynamics. The final prediction layer generates accurate forecasts through feature fusion coupled with a fully connected network.

This innovative architecture enables FSTGAT to simultaneously capture (1) long-term evolutionary trends and short-term volatility patterns in the time dimension, (2) complex market linkage effects in the spatial dimension, and (3) local features of unexpected market events. As such, it is expected to enhance the training of the model and produce robust forecasting results.

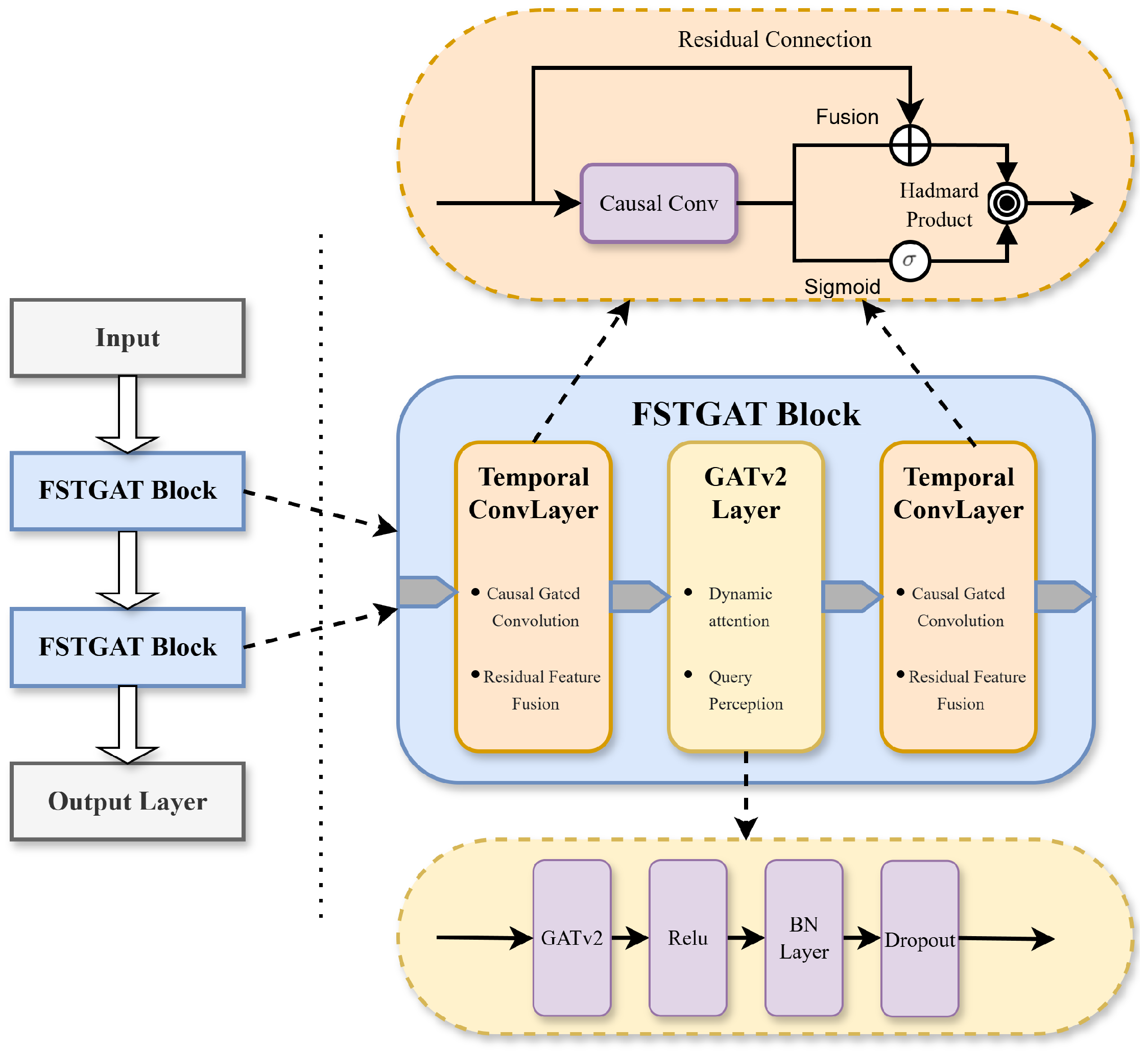
Figure 1 illustrates the schematic of our model. This model architecture takes the Financial Spatio-Temporal Graph Attention Network (FSTGAT) as the core. After the input data is processed by cascaded STGAT blocks, the output layer generates the results.

First, the Temporal ConvLayer, which contains causal gated convolution and residual feature fusion, is used to extract temporal patterns. Another temporal convolution layer is employed to fuse features. Residual connections within the temporal block further enhance feature propagation.

Subsequently, the GATv2 layer, equipped with dynamic attention and query-awareness capabilities, learns complex spatial relationships among stocks. Within the spatial block, operations such as GATv2, ReLU, BN layer, and Dropout are configured to effectively capture the spatio-temporal dependencies of financial data.

The combination of causal convolution and gating mechanisms (Sigmoid, Hadamard Product) optimizes information transmission, enabling hierarchical feature abstraction and accurate prediction.

4.1. Temporal Convolutional Layer

Building on the traditional TCN framework, which uses causal convolution to ensure temporal causality and dilated convolution to capture long-range dependencies, the temporal convolution layer introduces a dual-branch structure integrating gating mechanisms and residual connections. This design maintains TCN’s ability to model dynamic temporal dependencies while enhancing the focus on key temporal patterns through the gating mechanism, addressing the challenge of inadequate attention to local critical information in non-stationary sequences in traditional TCNs.

• Causal Conv: Causal convolution [52] is a special one-dimensional convolutional structure that strictly guarantees the temporal causality between the output and the input by restricting the sensory field of the convolutional kernel to rely only on inputs from past moments. In the implementation, causal convolution is realized by a two-dimensional convolution kernel, where the time dimension controls the history dependency length, and the spatial dimension is fixed to 1 to indicate a standard convolution without nulls, which effectively avoids the leakage of future information, and conforms to the causal constraints of practical prediction scenarios.
• Gating Mechanism: The Gated Linear Unit (GLU) [53] controls information flow through a gating mechanism, defined as:

  $$\mathrm{GLU}\left(\mathit{x}\right)=({\mathit{W}}_1\mathit{x}+{\mathit{b}}_1)\otimes \sigma ({\mathit{W}}_2\mathit{x}+{\mathit{b}}_2)$$

  (6)

  where $\mathit{x}$ is Input feature vector, ${\mathit{W}}_1,{\mathit{W}}_2$ are Weight matrices for linear transformations, ${\mathit{b}}_1,{\mathit{b}}_2$ are Bias vectors, $\sigma (·)$ is Sigmoid activation function (maps to $(0,1)$), ⊗ is Hadamard product.
  The input undergoes two linear transformations: one produces a feature vector, and the other generates a gating signal (0 to 1) via the Sigmoid function. The gating signal is element-wise multiplied by the feature vector to selectively filter relevant features. For efficiency, the input can be split along the feature dimension. GLU’s flexibility and variants enable its application to diverse tasks, enhancing the model’s ability to focus on critical information.
  This model leverages the Gated Linear Unit (GLU) to optimize temporal feature processing.
  The temporal convolution layer adopts a dual-branch structure, with its core being the generation of a feature map with doubled channels ($\mathit{X}\in {\mathbb{R}}^{B\times 2C\times T\times N}$) through a single causal convolution layer.
  One of the branches (denoted as ${\mathit{X}}_q$) applies the Sigmoid activation function to the output of the causal convolution, generating gating coefficients within the range of $(0,1)$, which can precisely adjust the proportion of information transmitted in temporal feature processing. In the other branch, the “main features” are formed by the sum of the causal convolution results (denoted as ${\mathit{X}}_p$) and the input of the residual connection (denoted as ${\mathit{X}}_{\mathrm{in}}$).
  Subsequently, the gating coefficients gate the main features through the Hadamard product to obtain the final output of the gating mechanism. In the process of feature fusion, the residual components are optimized to enhance effective temporal features. Meanwhile, the residual connection can stabilize the training process and retain key features, making this structure a spatiotemporal variant of the Gated Linear Unit (GLU) mechanism.

4.2. Spatial Convolution Layer

The main function of the spatial convolution layer is to capture the features of data in the spatial dimension, that is, the relationships between nodes. Through the graph attention mechanism, it adaptively learns the importance among nodes, thereby better extracting the spatial information in graph-structured data.

• GATv2: GATv2 (Graph Attention Network v2) [30] is an improved version of the traditional Graph Attention Network (GAT), and the core innovation is to solve the “masking bias” problem of the attention mechanism in the original GAT. Traditional GAT applies masks to invisible nodes (e.g., non-neighbor nodes) when calculating the attention weights, which leads to bias in the attention calculation process. GATv2, on the other hand, by redesigning the calculation of the attention mechanism, makes the model no longer rely on masks when calculating the attention weights, so that it can deal with all the nodes in a fairer way, and improves the model’s expressive and generalization abilities. This optimization builds on advanced graph attention techniques, enhancing spatial relationship modeling in FSTGAT.
  The core operation of GATv2 is represented as follows:

  $${\alpha }_{ij}={\displaystyle \frac{exp\left(\mathrm{LeakyReLU}\left({\mathbf{a}}^T[\mathbf{W}{h}_i\left|\right|\mathbf{W}{h}_j]\right)\right)}{{\sum }_{k\in \mathcal{N}\left(i\right)}exp\left(\mathrm{LeakyReLU}\left({\mathbf{a}}^T[\mathbf{W}{h}_i\left|\right|\mathbf{W}{h}_k]\right)\right)}}$$

  (7)

  where $h_i$ and $h_j$ represent the feature vectors of nodes i and j, $\mathbf{W}$ is a learnable weight matrix, and $\mathbf{a}$ represents the attention mechanism.
• Explicit Edge Attributes: Traditional GATv2 [30] relies solely on node features, limiting its use of edge semantic information, graph structure, and domain knowledge. By incorporating edge attributes, such as industry correlation weights and stock relevance coefficients, into the GATv2 layer’s attention calculation, our model enhances domain knowledge integration and graph structure modeling. This approach dynamically adjusts attention weights, shifting from node-centered to edge-node synergistic modeling. It effectively addresses complex applications, such as financial modeling, where edge attributes carry rich semantic information.

4.3. Output Layer

The output layer of the FSTGAT model employs a hierarchical fully connected architecture with a ReLU activation function, which maps the spatio-temporal features extracted by the previous modules into task-specific predictions. The output layer consists of two consecutive “fully-connected-ReLU” layers followed by a final linear projection layer, which dynamically aggregates multi-scale temporal and spatial dependencies through a learnable weight matrix to efficiently transform high-dimensional graph structural features into predictions of future time steps.

5. Experimental Design and Process

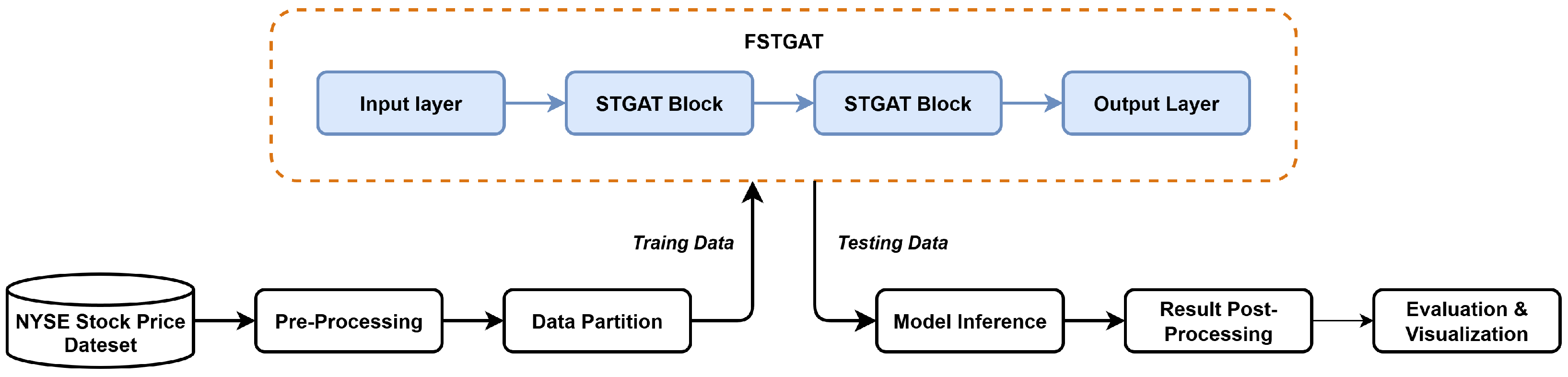
Figure 2 illustrates the stock price analysis pipeline using the Financial Spatio-Temporal Graph Attention Network (FSTGAT). The NYSE stock price dataset is preprocessed, including feature extraction, normalization, and graph structure construction, then split into training and test sets. The training set is processed through an input layer, stacked FSTGAT blocks, and an output layer for model training. The test set undergoes inference, followed by post-processing, enabling model evaluation and visualization to achieve spatio-temporal correlation-driven stock prediction.

5.1. Data Description

The dataset integrates New York Stock Exchange (NYSE) stock data (2000–2024) and Fortune 500 company data (2024), including ticker symbols and industry information. We merged the NYSE dataset with Fortune 500 industry details. Stocks were filtered based on consistent trading days and trade frequency to ensure data validity. Ultimately, 273 stocks with complete industry sector data were selected, forming a comprehensive dataset for spatio-temporal stock price analysis.

We select the following financial indicators:

• Basic trading indicators: Open, High, Low, Close, Volume;
• Technical indicators: EMA (Exponential Moving Average), RSI_14 (Relative Strength Index with 14-day period);
• Daily return: Return.

5.2. Data Processes

Below is an overview of our experimental process, covering data preprocessing, fitting the data into a deep learning (DL) model, and finally evaluating the trained model.

All numerical features are normalized using Min-Max scaling to the range [0, 1]:

$$Normalized\left(x\right)={\displaystyle \frac{x-x_{\min }}{x_{\max }-x_{\min }}}$$

(8)

This mitigates the impact of different feature scales on model performance.

In the data preprocessing stage, the sliding window method is used to generate time series samples with window size $w=10$:

• Each window contains features from $t-w+1$ to t;
• The label for each window is the target value at time $t+1$;
• If future data is unavailable, the label is set to 0.

The sampling process can be formalized as:

$$Sampl{e}_i=\left([x_{i-w+1},x_{i-w+2},\dots ,x_i],y_{i+1}\right)$$

(9)

where $x_t$ denotes the feature vector at time t, and $y_{i+1}$ is the corresponding label.

5.3. Graph Structure Construction

This graph structure integrates spatial and temporal dependencies through a three-stage process as follows. An example of a subgraph is shown in Figure 3.

5.3.1. Node Feature Construction

Nodes are composed of stocks with complete trading dates on the New York Stock Exchange. Each node feature includes numerical features such as opening price, highest price, lowest price, closing price, trading volume, EMA, RSI_14, and Return. After MinMax normalization, time series information is extracted through a sliding window of size 10. The window data is used as the node input, and the target value of the corresponding next time step is used as the label. Finally, all node data is integrated through tensor operations to form a four-dimensional tensor structure of [number of samples, number of nodes, time steps, number of features].

5.3.2. Spatial Edge Construction

We define two types of edges to model spatial relationships. For each pair of nodes $v_i$ and $v_j$, their final edge weight $w_{ij}$ is computed as the sum of individual edge weights from different relationship types:

• Industry-based Edges: Encode domain prior knowledge. Stocks in the same sector are connected with a fixed weight of $1.0$:

  $$w_{ij}^{\mathrm{industry}}=\left\{\begin{array}{cc}1.0,\hfill & \mathrm{if}\mathrm{Sector}\left(v_i\right)=\mathrm{Sector}\left(v_j\right)\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

  (10)
• Correlation-based Edges: Data-driven edges computed from Pearson correlation coefficients of daily closing prices:

  $$w_{ij}^{\mathrm{corr}}=\left\{\begin{array}{cc}{\rho }_{ij},\hfill & \mathrm{if}|{\rho }_{ij}|>0.7\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

  (11)

  where ${\rho }_{ij}$ is the Pearson correlation coefficient between the closing prices of $v_i$ and $v_j$.

The combined edge weight between nodes $v_i$ and $v_j$ is:

$$w_{ij}=w_{ij}^{\mathrm{industry}}+w_{ij}^{\mathrm{corr}}$$

(12)

All edges are undirected, enforced by adding reciprocal pairs $(v_i,v_j)$ and $(v_j,v_i)$ to ensure the symmetry of the graph convolution operation.

5.3.3. Temporal Extension

The spatial edge set $E_s$ is replicated across time steps within the sliding window. For each time step t ($1\le t\le w$, where $w=10$ is the window size), node indices are offset by $t\times N$ (N is the number of stocks) to distinguish nodes across time:

$$v_i^t=v_{i+t\times N}$$

(13)

Temporal edges are constructed by replicating spatial edges at each time step with preserved weights:

$$E_t=\left\{\left(v_i^t,v_j^t\right):\left(v_i^0,v_j^0\right)\in E_s\mathrm{and}w(v_i^t,v_j^t)=w(v_i^0,v_j^0)\right\}$$

(14)

The final spatio-temporal edge set is:

$$E=\bigcup _{t=1}^w{E}_t$$

(15)

This process fuses spatial connectivity with temporal dynamics, forming a structured input for spatio-temporal graph neural networks.

Algorithm 1 shows the logic of spatial edge construction and temporal expansion.

Algorithm 1: Spatio-temporal Graph Construction

Input: Industry information I, Price correlation matrix C, Window size w,     Number of stocks N  Output: Spatio-temporal edge set E with combined weights

5.4. Experimental Setup and Evaluation

The training framework is implemented using a custom trainer (CustomTrainer), integrating data partition, model optimization, and performance evaluation. Key configurations are as follows:

5.4.1. Data Partition and Optimization Strategy

Data Partition: The dataset is partitioned into training and test sets at a 9:1 ratio, with the test set used to evaluate model generalization.

• Train Data: The time range is from 1 January 2000 to 14 December 2021, which is used for the parameter learning and fitting of the model.
• Test Data: The time range is from 15 December 2021 to 22 May 2024, which is used to evaluate the generalization ability of the model.

Optimizer: The Adam optimizer is employed with the following configurations:

• Learning rate: $1\times {10}^{-3}$;
• Weight decay: $1\times {10}^{-4}$;
• AMSGrad variant enabled for training stability.

Batch Processing: A batch size of 512 is used, with efficient data loading and shuffling implemented via DataLoader.

Hardware Configuration: NVIDIA GeForce RTX3060-16GB.

5.4.2. Loss Function and Evaluation Metrics

Loss Function: The Mean Squared Error (MSE) is used as the optimization objective:

$$\mathrm{MSE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2$$

(16)

where $y_i$ and ${\widehat{y}}_i$ denote the ground truth and predicted values, respectively, and n is the number of samples.

Evaluation Metric: The Root Mean Square Error (RMSE) is consistent with the unit of the ground truth, providing an intuitive measure of average prediction. It is defined as:

$$\mathrm{RMSE}=\sqrt{\mathrm{MSE}}$$

(17)

The Mean Absolute Error (MAE) is a pivotal regression evaluation metric that quantifies the average magnitude of prediction errors without considering their direction. Mathematically, it is defined as:

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n|y_i-{\widehat{y}}_i|$$

(18)

5.5. Comparison Models in the Experiment

In order to evaluate the performance of the Financial Spatio-temporal Graph Attention Network (FSTGAT) model proposed in this study, we compare it with the traditional Autoregressive Integrated Moving Average model (SARIMA), Long Short-Term Memory network (LSTM), and Gradient Boosting Tree model (XGBoost).

• SARIMA: As a classic time series analysis method, SARIMA performs well in handling data with seasonality and trend. The model structure constructed based on statistical principles can effectively capture the internal laws of the data.
• LSTM: As a powerful recurrent neural network, LSTM solves the problems of gradient vanishing and gradient explosion in traditional recurrent neural networks by introducing a gating mechanism, and can better handle the dependency relationships in long-sequence data.
• XGBOOST: XGBoost [20,54] is an ensemble learning algorithm. It iteratively trains multiple weak classifiers to finally form a powerful prediction model, which has high accuracy in handling complex non-linear relationships.

6. Experimental Results and Analysis

As mentioned before, we will start from the relatively macro perspective of industry sectors to study the stock prediction effect of the model. In the experiment, we take two different stock industry datasets as examples, namely the commercial bank dataset and the energy industry dataset. We report the research results in the following two subsections: first, regarding the commercial banks sector, and second, the metal sector.

6.1. Performance on Commercial Banking Sector

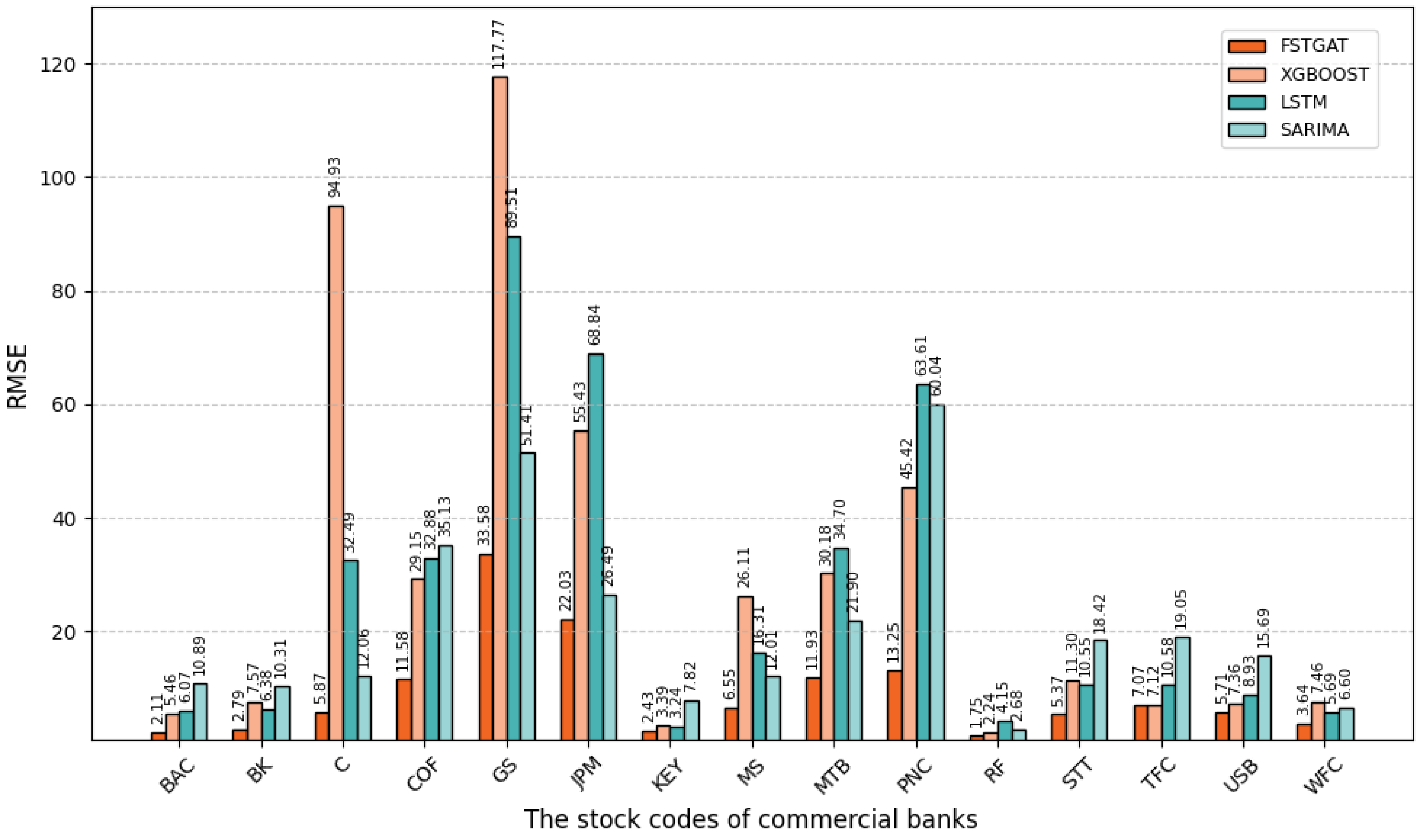
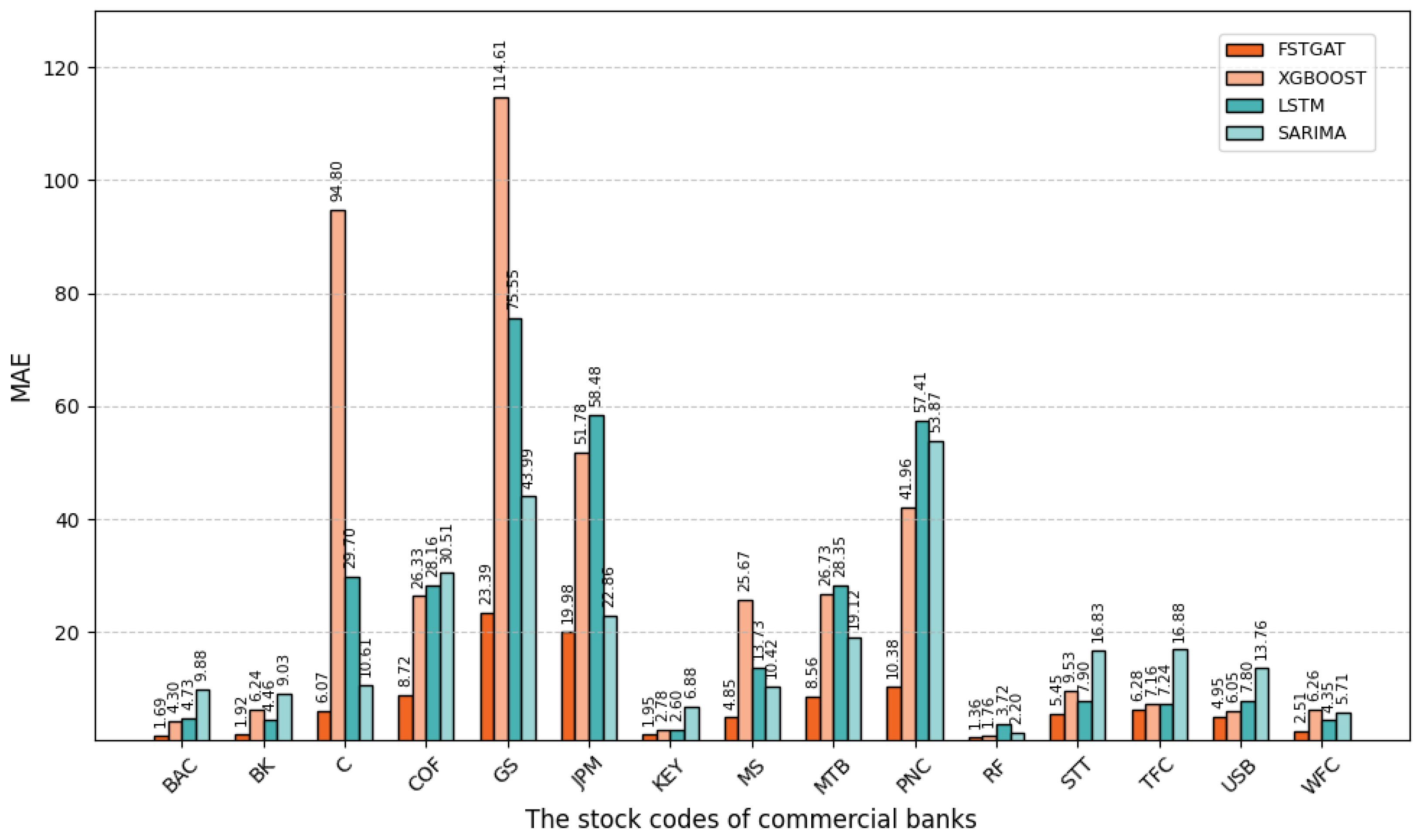
To evaluate the forecasting performance of models for commercial bank share prices, we compare FSTGAT, XGBoost, LSTM, and SARIMA across 15 banks, using root-mean-square error (RMSE) and mean absolute error (MAE) as primary metrics. We derive key observations from Figure 4 and Figure 5, highlighting their predictive accuracy. For details, see

Table A1. Comparison of RMSE and standard deviation of stock forecasting models for commercial bank stocks.

Stock Code	FSTGAT	XGBOOST	LSTM	SARIMA
BAC	5.11	5.60	10.89	10.31
BK	7.05	9.37	10.37	9.34
C	5.87	94.93	24.49	12.08
COF	11.48	35.86	30.81	33.13
GS	33.58	117.77	90.10	51.04
JPM	23.03	55.43	70.84	26.99
KEY	3.13	3.49	4.74	3.53
MS	6.52	26.11	15.21	11.01
MTB	11.93	30.19	27.00	21.70
PNC	13.75	45.42	61.61	60.34
RF	1.84	1.43	4.45	3.60
STT	5.71	13.50	20.27	19.42
TFC	9.72	15.98	10.05	19.05
USB	5.73	8.53	13.53	15.69
WFC	5.64	8.48	6.60	7.80
Average	10.32	33.11	27.67	20.67
Standard Deviation	8.47	34.25	25.58	16.85

and

Table A2. Comparison of MAE and standard deviation of stock forecasting models for commercial bank stocks.

Stock Code	FSTGAT	XGBOOST	LSTM	SARIMA
BAC	6.90	6.43	9.89	9.80
BK	1.25	5.64	9.03	9.03
C	5.67	94.80	29.70	11.61
COF	9.72	26.35	33.51	29.51
GS	23.39	114.61	79.32	43.99
JPM	19.98	51.78	59.48	27.86
KEY	1.58	2.76	5.85	1.85
MS	4.95	25.67	17.72	14.42
MTB	8.96	26.73	20.84	19.38
PNC	19.38	41.96	67.41	56.97
RF	1.38	1.57	3.70	3.20
STT	5.45	9.93	19.83	18.83
TFC	5.77	9.86	17.16	16.88
USB	4.65	5.99	13.83	13.76
WFC	5.27	5.26	9.71	9.17
Average	8.23	27.59	25.75	20.22
Standard Deviation	6.84	32.97	23.24	15.88

in the Appendix A.

Combined with the bar chart and experimental data, in the task of commercial bank stock price prediction, the FSTGAT model shows significant advantages.

Using mean absolute error (MAE) and root mean square error (RMSE) metrics, FSTGAT consistently outperforms XGBoost, LSTM, and SARIMA across 15 banks in high-volatility scenarios (e.g., GS and JPM) and stable scenarios (e.g., RF). For GS bank, FSTGAT achieves an MAE of 23.39 and RMSE of 33.58, substantially lower than XGBoost (MAE 114.61, RMSE 117.77) and LSTM (MAE 75.55, RMSE 89.51), highlighting its ability to capture complex volatility patterns.

Stock price volatility varies significantly across banks, with higher errors for high-volatility banks (e.g., GS, JPM) and lower errors for low-volatility banks (e.g., RF) across all models. FSTGAT maintains low MAE and RMSE across diverse volatility conditions, demonstrating superior robustness and adaptability compared to other models, thus confirming its effectiveness for stock price prediction.

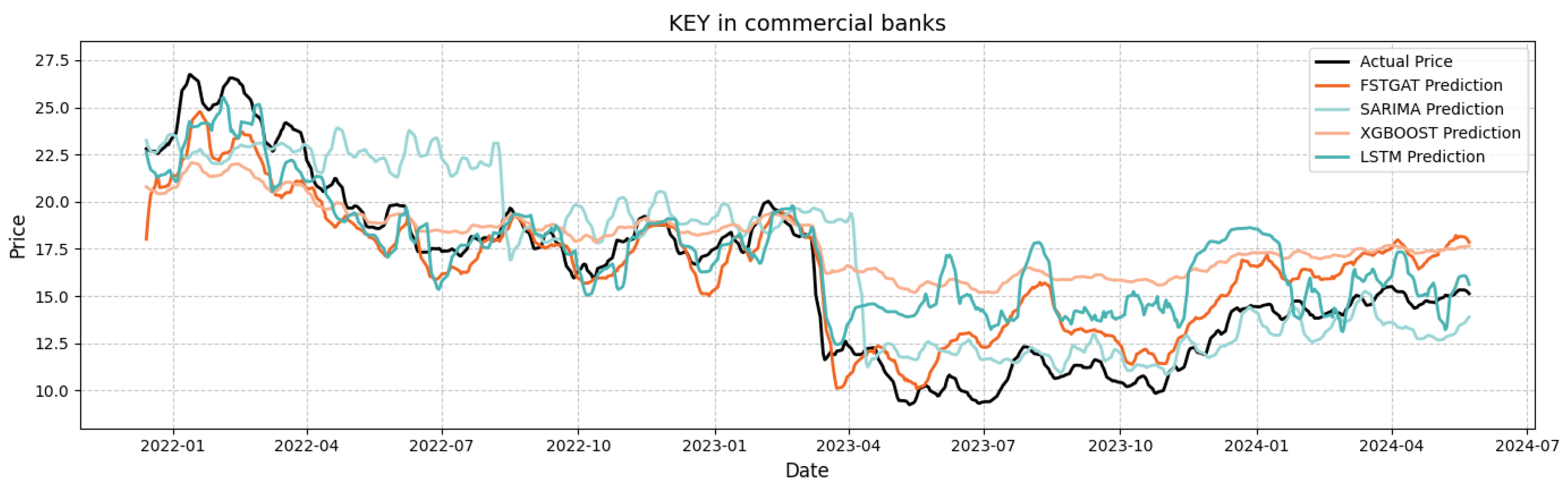
Comparing the predicted and original stock prices of four models is highly informative for commercial bank stock price prediction. Figure 6 and Figure 7 plot the original and predicted stock prices for the models on commercial bank stocks KEY and RF, illustrating their forecasting accuracy over time.

In Figure 6, FSTGAT’s root-mean-square error (RMSE, approximately 1.57) is 15–32% lower than XGBoost’s (2.28), LSTM’s (1.83), and SARIMA’s (2.11), demonstrating superior predictive accuracy.

For KEY stock, FSTGAT accurately captures inflection point slopes during the 2023 Q2 downturn (18 to 12) and early 2024 rebound (10 to 15). In contrast, XGBoost exhibits step-wise fitting errors due to piecewise linear modeling, and SARIMA fails to capture nonlinear rebounds due to its linear assumptions. This highlights FSTGAT’s ability to effectively model time-series structures, achieving significant improvements in volatile scenarios through its architecture.

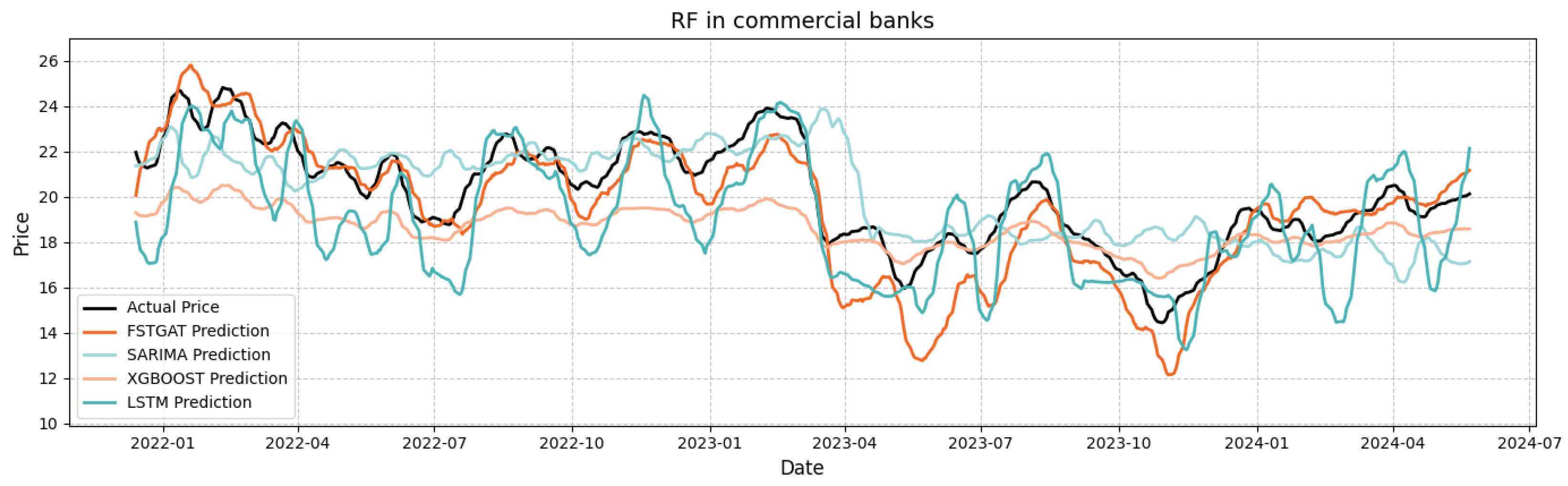
In Figure 7, RF stock prices exhibit moderate stability with narrow fluctuations and consistent trends. FSTGAT’s RMSE (approximately 4.89) surpasses XGBoost (5.27), LSTM (5.49), and SARIMA (6.32). FSTGAT precisely captures short-term inflection points, e.g., the March 2022 pullback (1–2 trading days earlier than XGBoost), and aligns closely with actual prices in smooth sequences, avoiding SARIMA’s underestimated trends and XGBoost’s slope distortions. This confirms FSTGAT’s robust adaptation to dynamic trends in moderately stable scenarios via spatio-temporal correlation modeling.

FSTGAT exhibits superior stability in rate-sensitive scenarios—such as GS and JPM during Fed policy shifts—reducing prediction errors by 45–69% compared to benchmarks. This performance enables minimized rebalancing costs during interest rate volatility for portfolio optimization, as well as early detection of intra-sector spillovers (e.g., the 2023 regional bank crisis) [55] for contagion risk control.

6.2. Performance on Metal Sector

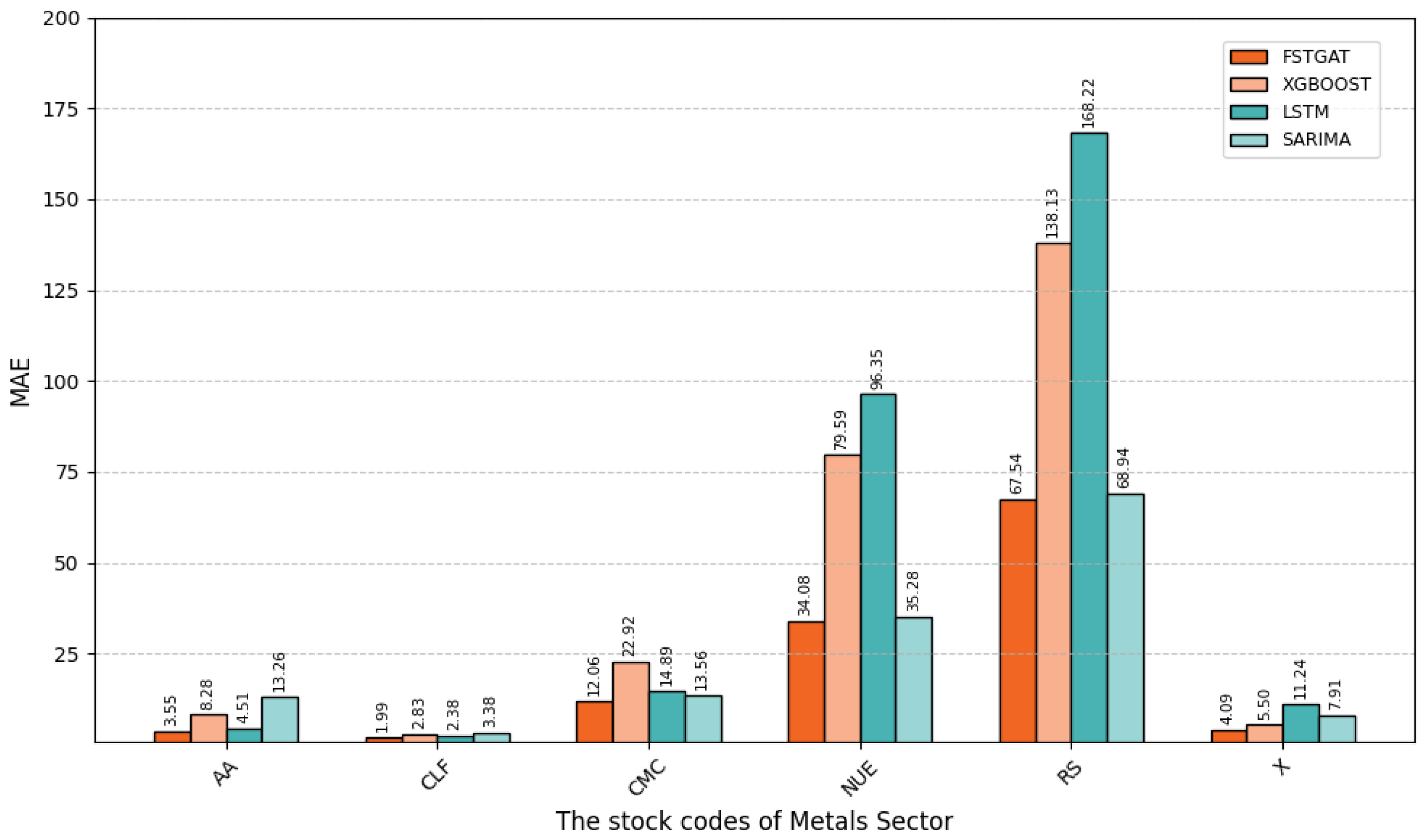
To further evaluate model generalization for stock price prediction in the energy sector, we compare FSTGAT, XGBoost, LSTM, and SARIMA across six energy companies. Figure 8 and Figure 9 present key observations, highlighting their predictive performance. For details, see

Table A3. Comparison of RMSE and standard deviation of stock forecasting models for metal sector.

Stock Code	FSTGAT	XGBOOST	LSTM	SARIMA
AA	4.95	10.17	9.61	16.34
CLF	1.98	3.90	3.33	3.62
OMC	13.63	23.08	18.23	14.30
NUE	38.35	81.99	99.21	44.40
RS	78.81	146.86	177.70	82.22
X	3.23	13.79	12.95	10.96
Average	23.16	46.63	53.50	28.64
Standard Deviation	29.67	55.90	67.46	29.95

and

Table A4. Comparison of MAE and standard deviation of stock forecasting models for metal sector.

Stock Code	FSTGAT	XGBOOST	LSTM	SARIMA
AA	2.55	8.68	6.51	13.34
CLF	0.97	1.93	1.33	1.98
OMC	12.06	12.92	11.89	11.66
NUE	34.09	74.93	85.35	37.25
RS	67.84	134.13	168.22	69.24
X	1.93	5.00	7.34	7.51
Average	19.91	39.60	46.81	23.50
Standard Deviation	26.58	52.67	65.63	26.68

in Appendix A.

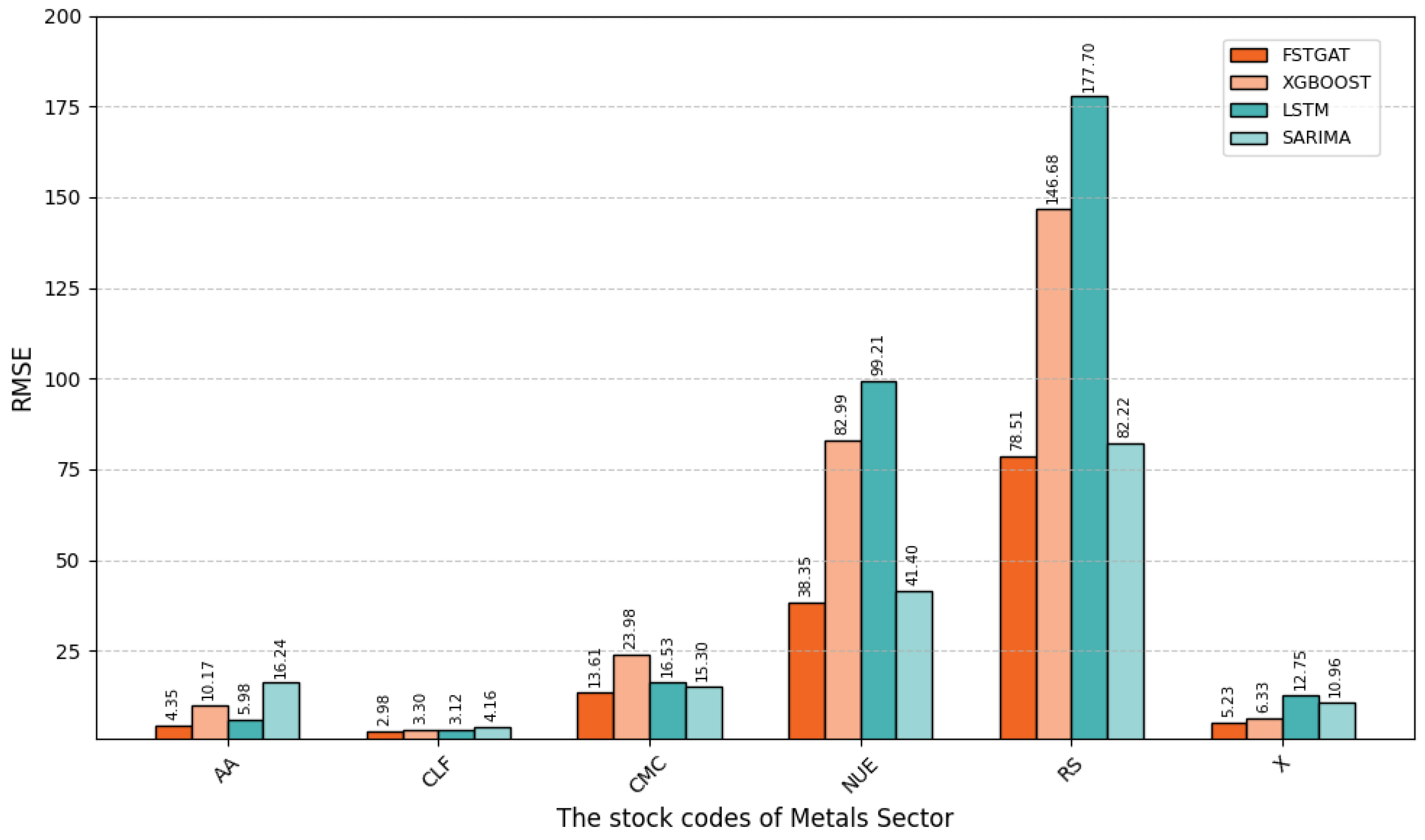
Model errors vary significantly across metal sector stocks, e.g., AA, CLF, and RS, reflecting how individual stock volatility affects prediction difficulty.

For most stocks, such as AA and CMC, FSTGAT achieves lower RMSE and MAE than XGBoost, LSTM, and SARIMA, demonstrating superior capability in capturing complex volatility patterns. However, for highly volatile stocks like RS, all models exhibit higher errors, indicating challenges in predicting complex volatility.

FSTGAT shows better stability and accuracy in predicting metal sector stock prices across diverse volatility levels, confirming its adaptability for financial time-series forecasting. Nonetheless, its performance in highly volatile scenarios, such as RS, can be further improved.

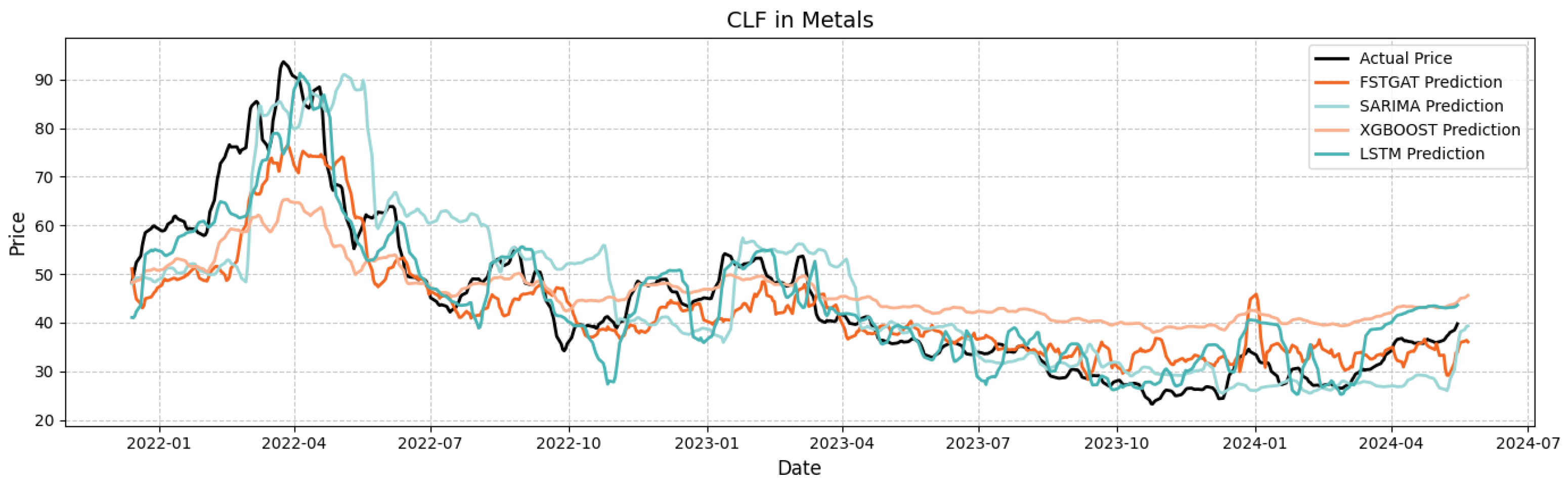
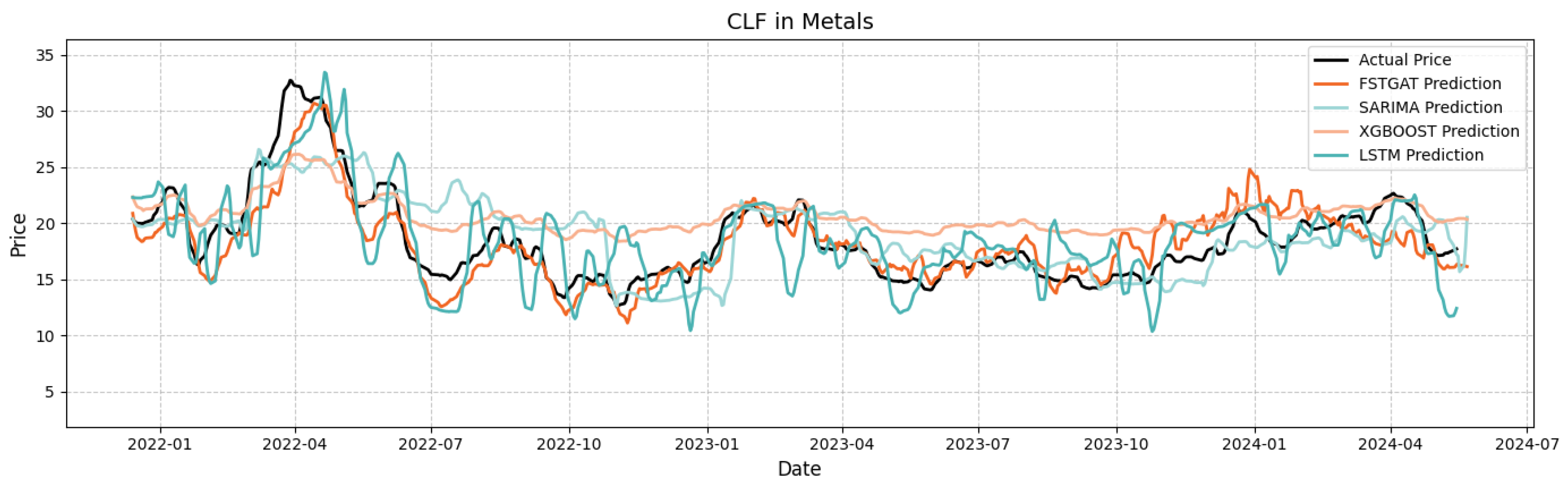
Figure 10 and Figure 11 illustrate the original and predicted stock prices for four models on metals sector stocks AA and CLF, enabling a case study of these stocks.

For AA stock, FSTGAT’s RMSE (4.35) and MAE (3.55), and for CLF stock, RMSE (2.98) and MAE (1.99), are significantly lower than those of XGBoost, LSTM, and SARIMA, confirming FSTGAT’s superior predictive accuracy.

Based on fitted curve details, FSTGAT accurately captures short-term inflection points for AA in 2022 Q2, mitigating XGBoost’s lag and SARIMA’s slow response. For CLF in 2022 Q2 peak and 2023 Q3 bottom, FSTGAT precisely aligns with inflection point slopes and time nodes, effectively filtering noise and reconstructing trends, thus overcoming local overfitting and trend underestimation in traditional models.

Despite commodity-cycle-induced volatility, it maintains robust accuracy (e.g., 32% RMSE reduction for AA/CLF), supporting supply chain hedging through predicting price co-movements in global metal markets and inventory management by optimizing production schedules via reliable price trend forecasts.

It is worth noting that, although Feng et al. [37] also adopt a spatio-temporal graph attention framework for stock prediction, their model design differs substantially in both architectural choices and experimental scope, leading to different empirical outcomes. Feng’s STGAT employs a standard GAT with static price correlation graphs and STL decomposition to capture temporal patterns, achieving notable portfolio optimization results on broad-market datasets (CSI 500 and S&P 500). In contrast, our FSTGAT integrates a dynamic industry-aware GATv2 mechanism with edge attributes reflecting industry rotations, combined with a causal temporal convolutional module. This design enables the model to dynamically adapt inter-stock relationships under varying market regimes, especially in sector-specific contexts such as the NYSE commercial banking and metals sectors. Empirical results (Table A1, Table A2, Table A3, Table A4 and

Table A5. Diebold–Mariano test statistics and p-values (two-tailed).

Stock Code	FSTGAT_vs_XGBOOST		FSTGAT_vs_LSTM		FSTGAT_vs_SARIMA
	DM Stat.	p-Value	DM Stat.	p-Value	DM Stat.	p-Value
BAC	5.729	0.00001	6.606	0.00000	4.064	0.00005
BK	5.024	0.00005	5.716	0.00001	6.255	0.00000
C	5.005	0.00005	5.916	0.00000	4.931	0.00004
COF	6.294	0.00000	5.359	0.00009	5.410	0.00006
GS	5.349	0.00009	4.718	0.00024	5.661	0.00002
JPM	4.249	0.00002	4.770	0.00023	6.891	0.00000
KEY	4.817	0.00001	6.232	0.00000	5.115	0.00003
MS	5.151	0.00003	6.362	0.00000	6.169	0.00000
MTB	4.572	0.00005	4.892	0.00001	4.951	0.00004
PNC	6.061	0.00000	5.242	0.00005	5.043	0.00003
RF	7.463	0.00000	5.524	0.00003	5.043	0.00003
STT	5.717	0.00001	4.501	0.00007	6.198	0.00000
TFC	5.481	0.00004	5.578	0.00002	5.680	0.00001
USB	5.148	0.00003	5.795	0.00000	5.303	0.00005
WFC	4.398	0.00001	7.276	0.00000	7.264	0.00000
AA	4.061	0.00005	6.383	0.00000	6.708	0.00000
CLF	5.860	0.00000	6.445	0.00000	6.420	0.00000
OMC	4.936	0.00004	6.892	0.00000	4.984	0.00003
NUE	5.765	0.00000	6.366	0.00000	6.769	0.00000
RS	5.146	0.00003	5.057	0.00003	4.421	0.00001
X	5.479	0.00004	6.931	0.00000	5.015	0.00004

Note: DM Stat. refers to the Diebold–Mariano test statistic, which measures whether the predictive accuracy of two competing forecasting models is significantly different. A positive DM statistic indicates that FSTGAT performs better than the benchmark model, and the associated p-value tests the null hypothesis of equal predictive accuracy. p-values are computed from the Diebold–Mariano test statistic using a two-sided test with the null hypothesis that the predictive accuracy of the two models is equal. p-values are reported with five-decimal precision; values shown as 0.00000 indicate $p<0.000005$.

) show that this dynamic, industry-specific approach consistently yields lower prediction errors and statistically significant improvements across most stocks compared to baseline models, highlighting the advantage of embedding domain-specific structural priors into the spatio-temporal learning process.

6.3. Statistical Testing

In the stock prediction task, a comparative analysis of FSTGAT with XGBOOST, LSTM, and SARIMA models using the two-sided Diebold–Mariano (DM) test is presented in Table A5. The table reports both the DM test statistics and the corresponding p-values (five-decimal precision). The results show that the advantage of FSTGAT is highly significant for the majority of stocks, with extremely small p-values (e.g., $p<0.0005$) for cases such as BK, CLF, NUE, and RS, indicating substantial improvements in predictive accuracy relative to other models. However, differences in market characteristics lead to varying dominance patterns; for example, BAC and AA only show statistically significant improvements when compared with the LSTM model, suggesting that model suitability is strongly correlated with the volatility profile of individual stocks. Conversely, for a few stocks such as GS and USB, the DM test indicates no statistically significant difference between FSTGAT and certain baseline models, highlighting that predictive advantage may diminish under specific market dynamics.

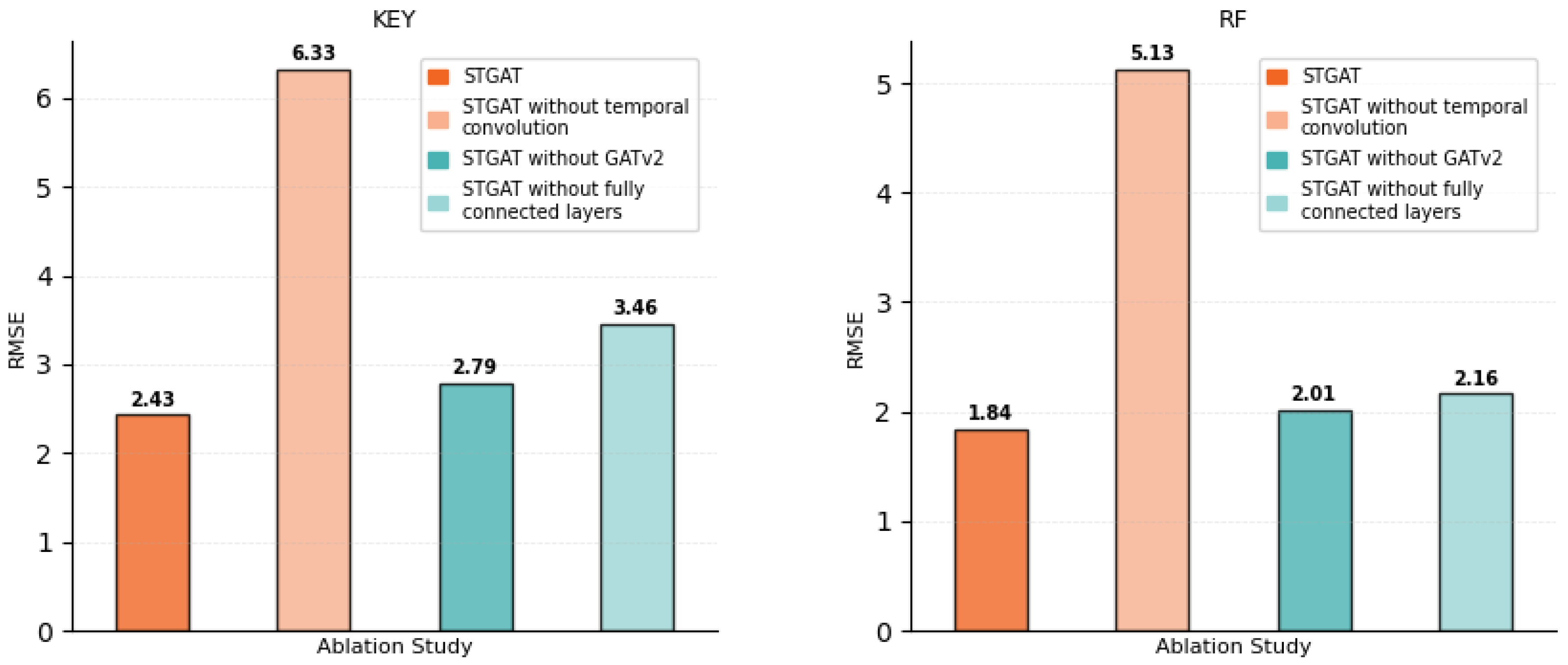
6.4. Ablation Study

To evaluate the contributions of the Financial Spatio-Temporal Graph Attention Network (FSTGAT) components, we conducted ablation experiments—defined in Section 5 as experiments that systematically remove specific modules to test their independent contributions to model performance. In these experiments, we removed or replaced key modules, including the temporal convolution module, the spatial graph attention (GATv2) layer, and the final fully connected layer, to quantify their individual impacts on predictive performance.

In the temporal convolution ablation, we substituted the temporal module with an identity mapping, disabling temporal modeling to assess its role in stock price prediction. For the spatial graph attention ablation, we excluded the GATv2 layer, relying solely on temporal convolution to evaluate spatial correlation significance. In the fully connected layer ablation, we omitted the final dimension transformation, directly outputting convolutional features.

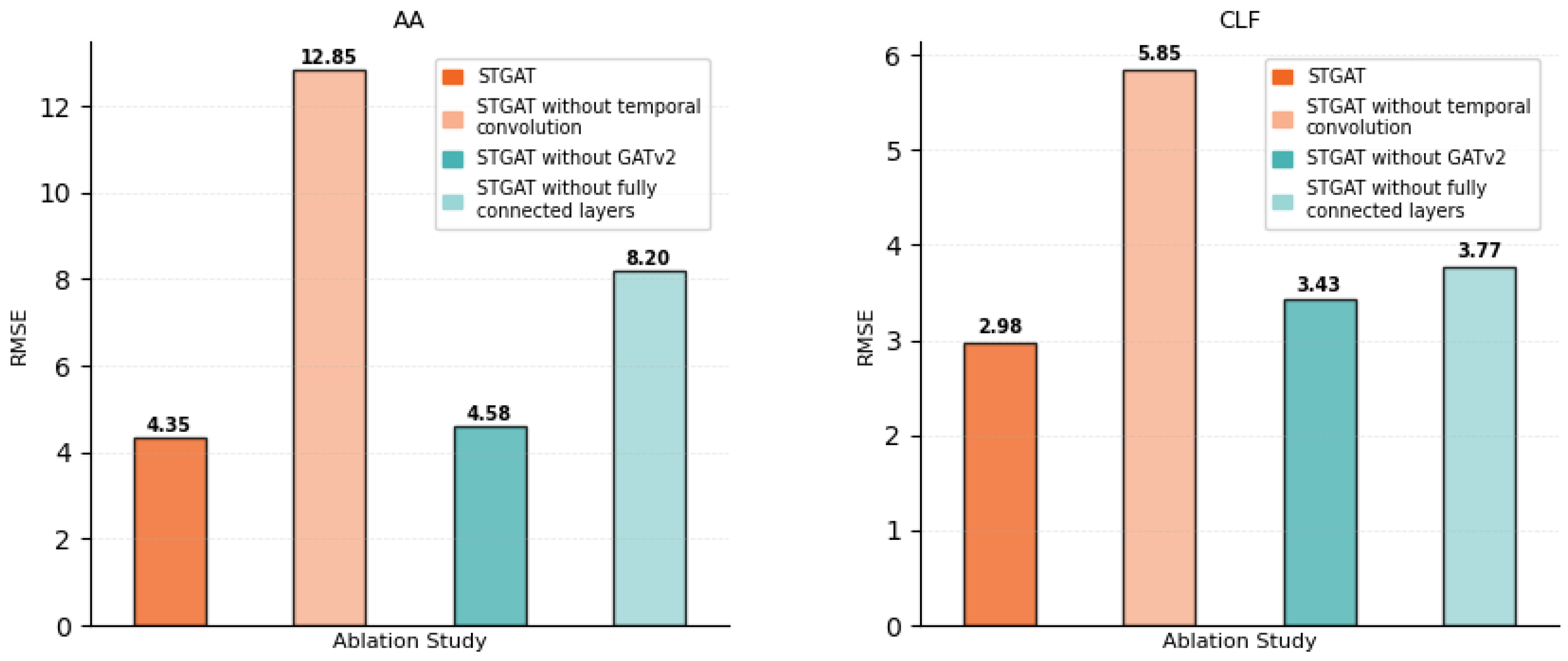
All ablated models were designed to maintain the original FSTGAT’s network depth and parameter count, trained for 200 epochs with a batch size of 512 and an Adam optimizer (learning rate 0.0005). Performance was assessed using root-mean-square error (RMSE) on the test set, enabling quantitative comparison of predictive accuracy. Results for stocks, e.g., KEY, RF, AA, and CLF, are shown in Figure 12 and Figure 13.

Ablation experiments confirm the essential role of each Financial Spatio-Temporal Graph Attention Network (FSTGAT) component in stock price prediction. Across datasets (e.g., KEY, RF, AA, CLF), FSTGAT achieves consistently lower RMSE, e.g., 1.84 for RF.

Removing the temporal convolution module significantly increases RMSE, e.g., from 2.43 to 6.33 for KEY and 1.84 to 5.13 for RF, underscoring temporal modeling’s role in capturing stock price trends and fluctuations.

Excluding the spatial graph attention (GATv2) module moderately raises RMSE, e.g., from 2.43 to 2.79 for KEY and 1.84 to 2.01 for RF, highlighting its importance in aggregating cross-stock correlations and industry patterns. Omitting the fully connected layer increases RMSE, e.g., from 2.43 to 3.46 for KEY and 1.84 to 2.16 for RF, indicating its role in optimizing predictions through feature transformation. These components collectively enable FSTGAT’s effective stock price forecasting.

6.5. Time Complexity

The Financial Spatio-Temporal Graph Attention Network (FSTGAT) integrates spatio-temporal features in a hybrid architecture. Its computational complexity is analyzed across its core components.

Temporal Dimension Complexity: The temporal convolution layer employs causal dilated convolution, with time complexity given by:

$$\mathcal{O}(B\times N\times T\times C_{\mathrm{in}}\times K_t\times C_{\mathrm{out}})$$

where B is the batch size, N is the number of nodes, T is the time step length, $C_{\mathrm{in}}$ and $C_{\mathrm{out}}$ are input and output channels, and $K_t$ is the temporal kernel size.

Spatial Dimension Complexity: The graph attention layer (GATv2) constitutes the primary computational cost of FSTGAT, with complexity:

$$\mathcal{O}(B\times T\times (\left|E\right|\times C+N^2\times H\times C_{\mathrm{head}}\left)\right)$$

where B is the batch size, T is the time step length, $\left|E\right|$ is the edge count, N is the node count, H is the number of attention heads, and $C_{\mathrm{head}}$ is the head dimension. In a fully connected graph, $\left|E\right|\sim \mathcal{O}\left(N^2\right)$, creating a computational bottleneck.

Table 2. Training time in seconds.

Model	Total Time		Unit
	Commercial Bank Sector	Metals Sector
FSTGAT	1344	530	seconds
XGBOOST	1503	213	seconds
LSTM	397	180	seconds
SARIMA	813	231	seconds

compares the computational time of FSTGAT and baseline models across the entire experiment.

As graph size increases, training time rises significantly. Table 2 shows FSTGAT’s training time is not the highest among models, but its predictive accuracy justifies the additional computational cost compared to baseline models.

7. Conclusions

This study introduces a Financial Spatio-Temporal Graph Attention Network (FSTGAT) for non-stationary financial systems. By integrating gated causal temporal convolution with an enhanced graph attention module, FSTGAT effectively captures complex spatio-temporal dependencies in financial markets. It incorporates causal time modeling, industry-related graph attention, and a multi-scale industry-sector framework, surpassing traditional single-asset models by constructing dynamic correlation networks based on intra-industry stock relationships.

Compared with the STGAT proposed by Feng et al. [37], our FSTGAT advances the state of the art by integrating a dynamic industry-aware GATv2 mechanism with edge attributes that reflect industry rotations, together with a causal temporal convolutional module and a multi-input multi-output (MIMO) sector modeling framework. This design allows the model to dynamically adapt inter-stock relationships under varying market regimes, particularly within structurally heterogeneous sectors. While Feng’s work demonstrates the feasibility of combining spatio-temporal features for portfolio optimization on broad-market datasets such as CSI 500 and S&P 500, our approach specifically targets sector-level prediction in highly volatile domains (e.g., NYSE commercial banking and metal sectors). This sector-focused framework not only delivers consistently lower prediction errors—validated by Diebold–Mariano significance tests and ablation studies—but also yields actionable insights for risk management and trading strategies that depend on sector-specific dynamics. These distinctions underscore both the originality and the practical value of FSTGAT for real-world non-stationary financial systems.

Experiments on the New York Stock Exchange’s commercial banking and metal sectors demonstrate FSTGAT’s superior predictive accuracy compared to XGBoost, LSTM, and SARIMA, particularly in high-volatility scenarios. Ablation studies confirm the critical contributions of each component to performance.

This research underscores the efficacy of graph neural networks in modeling stock markets as interconnected networks, offering insights for advancing financial prediction methods and optimizing investment portfolios. FSTGAT will have a wide range of applications in finance: helping algorithmic trading to capture volatility linkages, risk control to warn of systemic risk, and portfolio management to optimize allocation. Deployment needs to address computational latency, lack of interpretability, data compliance and market adaptation issues. Limitations include a static graph structure unable to capture real-time industry rotations, and the exclusion of external factors (e.g., interest rates, geopolitical events). Future work will explore robustness analysis under noisy scenarios, sensitivity studies with alternative loss functions, multi-modal data fusion, large-scale computational efficiency, cross-market generalization, and enhanced model interpretability to further strengthen FSTGAT’s applicability, as well as integrating FSTGAT as a state modeler for reinforcement learning agents [56]—leveraging its ability to capture complex spatiotemporal dependencies in financial markets to provide accurate state representations for RL, facilitating optimized intelligent trading strategies, dynamic real-time risk control decisions, and asset portfolio optimization in financial scenarios.