Digital Art Pattern Generation with Arbitrary Quadrilateral Tilings

Abstract

In the context of the deep integration of digital art and geometric computing, this paper proposes a digital art pattern generation method with arbitrary quadrilateral tiling. The aim is to break through the limitations of traditional fixed tiling templates in terms of adaptability to irregular tiling shapes, controllability of local deformations, and naturalness of boundary transitions. By decoupling the topological stability of quadrilaterals from deformation parameters and combining the Coons surface interpolation method, a smooth invariant mapping for the fundamental region of arbitrary quadrilaterals is constructed, solving the seamless splicing problem of irregular fundamental region. This method supports real-time editing of quadrilateral shape and colors the fundamental region based on the dynamical system model to generate periodic seamless patterns with global symmetry and controllable local details. Experiments show that the proposed method can be adapted to any quadrilateral structure, from regular rectangles to non-convex polygons. By adjusting the interpolation parameters and dynamical system functions, the symmetry, texture complexity, and visual rhythm of the patterns can be flexibly regulated. The algorithm achieves efficient computation under GPU parallel optimization (with an average generation time of 0.25 s per pattern), providing a new solution for the pattern generation and personalized design of digital art patterns.

1. Introduction

In the era of profound integration between digital technology and art, research on digital pattern generation methods rooted in nonlinear theory has sustained dual vitality in theoretical innovation and engineering transformation [1,2,3,4,5]. These approaches transcend the constraints of traditional design paradigms by leveraging efficient computational logic to generate infinite, morphologically diverse patterns. This not only significantly elevates design efficiency but also substantially enriches design resource pools. Across domains such as textile design, architectural decoration, and dynamic wallpaper creation, this technology has exhibited extensive application potential, injecting innovative impetus into industrial practices. Moreover, the massive and diversified pattern datasets generated by these methods offer high-quality training materials for machine learning models, thereby facilitating the progression of intelligent design technologies.

In existing digital pattern generation, prevalent methodologies such as fractal geometry [6], dynamical systems [7], and quasi-regular patterns [8] yield aesthetically striking designs distinguished by their characteristic styles. Nevertheless, these models often falter in providing precise spatial compositional control. Conversely, tiling-based generation methods [4,5] leverage regular geometric units to achieve seamless patterns, offering enhanced user control over spatial arrangement. However, conventional research has primarily centered on fixed tiling templates, where invariant mappings rely on explicit mathematical expressions. This restricts adaptability to irregular tiles, thereby imposing significant constraints on topological flexibility, natural boundary transitions, and localized deformation controllability.

To surmount these challenges, this paper introduces a new digital art pattern generation method founded on arbitrary quadrilateral tiling [9]. The core innovation lies in decoupling the topological stability of quadrilateral structures from the flexibility of deformation parameters, thus establishing an invariant mapping adaptable to arbitrary deformations. This effectively resolves the issue of seamless assembly. Specifically, the method employs arbitrary quadrilaterals as fundamental compositional units, enabling real-time shape editing via parametric vertex coordinate manipulation. A novel invariant mapping algorithm for arbitrary quadrilateral tiling is developed using Coons surface interpolation [10]. This algorithm maps the fundamental region to a unit square parametric domain and derives parametric coordinate calculation formulas. By predefining invariant mappings along the fundamental region’s boundaries, it interpolates a smooth invariant mapping across the interior, preserving the advantages of quadrilateral tiling in square continuity and computational efficiency while eliminating the reliance on fixed templates. Experimental results demonstrate that patterns generated by this method maintain mathematical rigor while accommodating arbitrary quadrilateral tiling structures, ranging from regular rectangles to non-convex polygons. By adjusting interpolation parameters, the method flexibly controls local details and global symmetry, offering a novel approach for dynamic generation and personalized design of digital art patterns.

2. Related Work

The mathematical models of generating digital art patterns exhibit diverse typologies. Among these, classical methods rooted in nonlinear theory hold representative significance, giving rise to paradigmatic models such as fractal graphics, dynamical system patterns, weak chaotic patterns, and quasi-regular patterns. Fractal and dynamical system models, constructed upon chaos theory, represent pioneering achievements in this field that continue to demonstrate enduring vitality [6,7]. However, the absence of fixed model parameters makes shape control inherently challenging, substantially limiting their large-scale application. In contrast, quasi-regular patterns have a relatively shorter history. They are derived from the mathematical theory of ZZSUC mappings [11] satisfying q-fold resonance conditions, which involves Hamiltonian transformations and smoothing procedures, followed by contour-based visualization [8,12]. The inherent regularity and symmetry characteristics of quasi-regular patterns stem from their relatively fixed mathematical parameters, enabling both structural diversity and distinctive aesthetic qualities. Although these pattern generation principles differ fundamentally and possess unique artistic styles, they all rely on mathematical equations and involve complex computations to ultimately achieve intricate and sophisticated visual effects.

To transcend the morphological limitations of digital art patterns and expand their variational dimensions, numerous researchers have explored and innovated models from diverse perspectives. Regarding pattern content, Chung et al. [13] pioneered the extension of dynamical systems patterns from Euclidean to hyperbolic space, opening a new dimension for pattern generation and laying the foundation for subsequent research [14]. Wang et al. [15] and Gdawiec et al. [16], respectively, expanded the theoretical frameworks of Julia sets and Newton fractals in complex fractals, establishing more universal mathematical structures that yield fractal patterns with significantly enhanced morphological diversity. Zhang et al. [17] systematically transformed and optimized fundamental models of quasi-regular pattern using various mathematical operations, deriving series of patterns with distinct symmetrical, quasi-symmetrical, and asymmetrical styles, substantially enriching their expressive forms. Jin et al. [18] achieved controllable symmetric structure generation for digital art pattern by leveraging parameter-adjustable spherical harmonic functions while integrating visualization principles of quasi-regular pattern.

Another research direction focuses on expanding digital art pattern generation through spatial composition frameworks, mainly including two types of methods based on symmetry functions and tiling constraints. The approach based on symmetry functions generates digital art patterns with local symmetric features through constructing dynamic system functions with spatial symmetry properties. Chung et al. [19] and Lu et al. [20] independently developed distinct strategies to construct dynamical systems by using wallpaper group, producing patterns conforming to various planar symmetry rules. Zou et al. [21] investigated the generation methods of digital art patterns for cyclic symmetry and dihedral symmetry based on the orbit trap method. Gdawiec et al. [22] employed fixed-point theory-based iterative algorithms, creating symmetric dynamical system patterns through multi-iteration fusion and affine combination strategies. Subsequently, they proposed an enhanced orbit trapping iterative method [7], significantly improving pattern refinement. However, this approach exhibits notable limitations: the spatial structure of the generated patterns is relatively uniform, and function design relies on manual intervention, resulting in limited flexibility.

Tiling-constrained generation methods construct tiling structures as foundational frameworks for pattern design, generating novel digital art patterns by filling seamless colors and textures. The core challenge lies in ensuring continuous of texture transitions at tiling boundaries. Chung et al. [23] pioneered research in tiling-constrained pattern, creating dynamical system patterns based on the Sphinx and Penrose aperiodic tiling structures via invariant mappings. Zou et al. [24] constructed invariant mappings for chair tiling, generating another kind of aperiodic pattern. Subsequently, Ouyang et al. [25,26] combined dynamical system patterns with fractal tilings and Archimedean tiling structures, proposing innovative pattern generation methods that expanded compositional diversity. More recently, they further integrated spiral tilings to create Escher-style patterns [27] and rose-shaped Escher tiling patterns [3], and extended these techniques to generate spherical patterns [2]. Although these approaches enhanced controllability of digital art patterns, practical limitations persist: spatial composition types remain restricted, and case-specific invariant mapping designs are often required to maintain boundary continuity, also with obvious boundary gaps in some scenarios. Recently, Yin et al. [4] proposed a symmetry-enhancement method for quasi-regular patterns, grounded in k-uniform periodic tiling of regular polygons. This approach supports hundreds of tiling configurations, enabling multi-dimensional pattern control that significantly enhances controllability and variability in digital art design. It also unifies invariant mapping construction to achieve seamless transitions across the boundaries of the fundamental region. However, these methods still exhibit some practical limitations. On one hand, all are constrained by predetermined fixed tiling templates, which restricts users’ ability to customize tile shapes according to individual creative demands, thereby restricting art freedom and expression. On the other hand, existing techniques of constructing invariant mapping universally rely on explicit function-based approaches. While these methods remain effective for structurally simple, regular fundamental regions, their complexity escalates exponentially or becomes entirely infeasible when applied to irregular, complex polygonal shapes.

3. Methods

This paper aims to generate digital art patterns with seamless textures and natural transitions across tile edges under constraints of arbitrary quadrilateral tiling, while enabling flexible spatial composition control through shape editing of quadrilateral tiles. Given the inherent arbitrariness of quadrilateral tiles that often result in irregular shapes, this paper treats quadrilateral tiles as fundamental regions and constructs invariant mappings for arbitrary quadrilateral domains using the Coons surface interpolation method [10], uses a dynamic system model to color the fundamental region, and finally realizes the generation of digital art patterns through tiling operations.

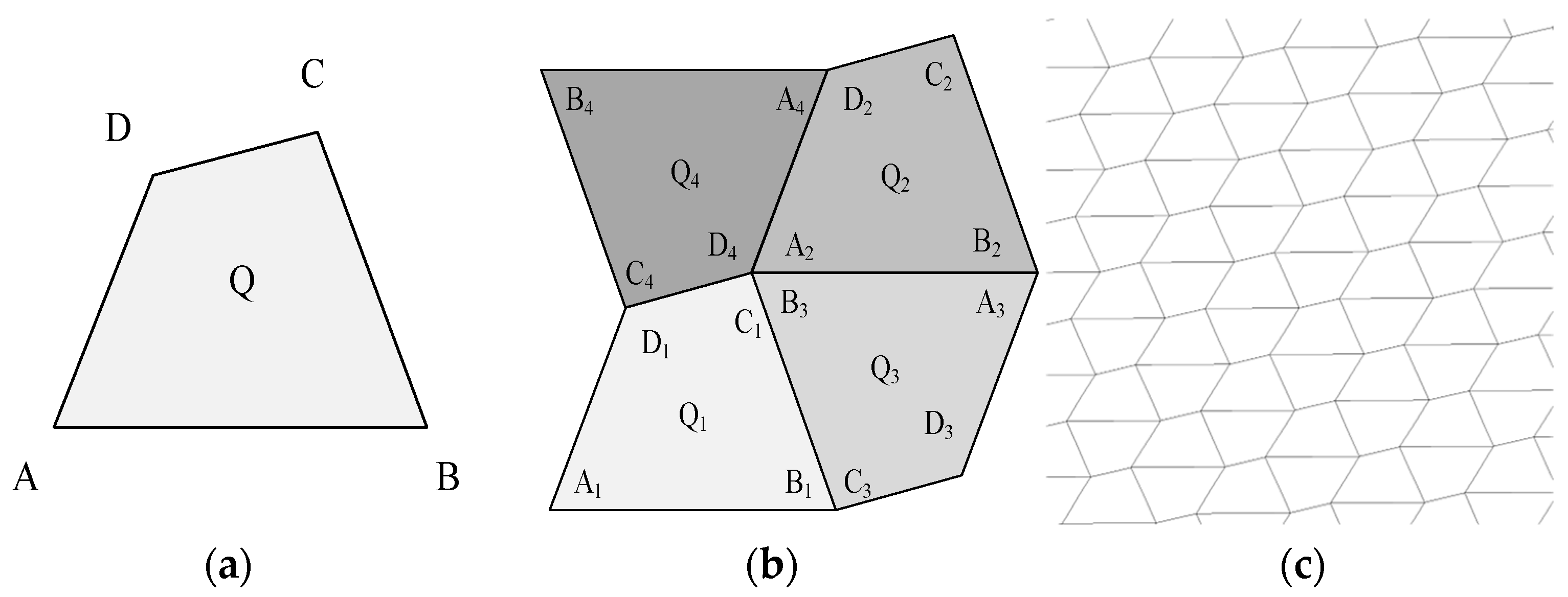
3.1. Quadrilateral Tiling

Any arbitrary quadrilateral Q = <A, B, C, D> (with vertices A, B, C, D ordered in counter-clockwise orientation) can achieve planar tiling through rigid transformations [9], where the core mechanism relies on leveraging the vertex symmetry of the quadrilateral and constructing periodic repeating units (tiles) via translational and rotational symmetry operations.

Let the coordinates of the four vertices of quadrilateral Q be denoted as P₁, P₂, P₃, P₄. Define the translation transformation T(P) = P + v, where the vector v = P₁ − P₃, and the 180° central rotation transformation R(P) = −P + O, with O representing the rotation center (which can be also selected as the centroid or a vertex of Q). Therefore, seamless and non-overlapping tiling structures can be generated through these transformations:

• Generate tile Q₂: it can be obtained by translating quadrilateral tile Q, resulting in Q₂ with coordinates of four vertex as follows: $P_i^2=T(P_i)$.
• Generate tile Q₃: it can be obtained by rotating Q with 180° around vertex B, resulting in transformed coordinates: $P_i^3=R(P_i-P_2)+P_2=-P_i+2P_2$.
• Generate tile Q₄: it can be obtained by rotating Q with 180° around vertex D, resulting in transformed coordinates: $P_i^4=R(P_i-P_4)+P_4=-P_i+2P_4$.

Let the vertices of quadrilateral tile Q_i be denoted as A_i, B_i, C_i, D_i. By combining four quadrilateral tiles through above operations, a composite unit is formed as a new polygonal complex <A₁, B₁, D₃, A₃, C₂, D₂, B₄, C₄>; translating this unit periodically can cover the entire plane without seams, as shown in Figure 1.

3.2. Invariant Mapping Construction

In the generation mechanism of digital art patterns, the fundamental region and invariant mapping play a critical role in achieving symmetry of tiles and seamless integration of textures across the boundaries of tiles.

As a subset of the plane, the fundamental region enables seamless tiling of the entire space through group transformations. For quadrilateral tiling, this paper defines the quadrilateral tile as the fundamental region Ω. Under the action of group G, transformed copies of Ω can cover the entire plane seamlessly, with overlapping occurring only at the boundaries.

Invariant mapping is used to ensure the symmetry layout of the pattern and seamless transition across the boundaries of the fundamental region. It is typically defined as a function satisfying invariance under a specific symmetry group G, i.e., for a group G, the invariant mapping f: Ω→R² maps symmetric points z and τz(τ ∈ G) on the plane to the same image:

$$f(z)=f(\tau z).$$

(1)

To ensure the generated patterns exhibit natural, seamless textures on the plane, the invariant mapping must satisfy two critical conditions: smoothness within the fundamental region and compliance with symmetry constraints on the boundary. Due to the irregular geometry of the quadrilateral tiling’s fundamental region and the complexity of symmetry constraints, the construction of traditional explicit functions presents significant challenges. This paper leverages the quadrilateral topology of the tile and proposes an invariant mapping construction method applicable to arbitrary quadrilateral fundamental regions, based on Coons surface interpolation [10]. The approach proceeds as follows: first, boundary mappings of the fundamental region are constructed according to symmetry conditions; then, guided by these boundary mapping functions, Coons surface interpolation is used to smoothly interpolate the internal invariant mapping of the domain.

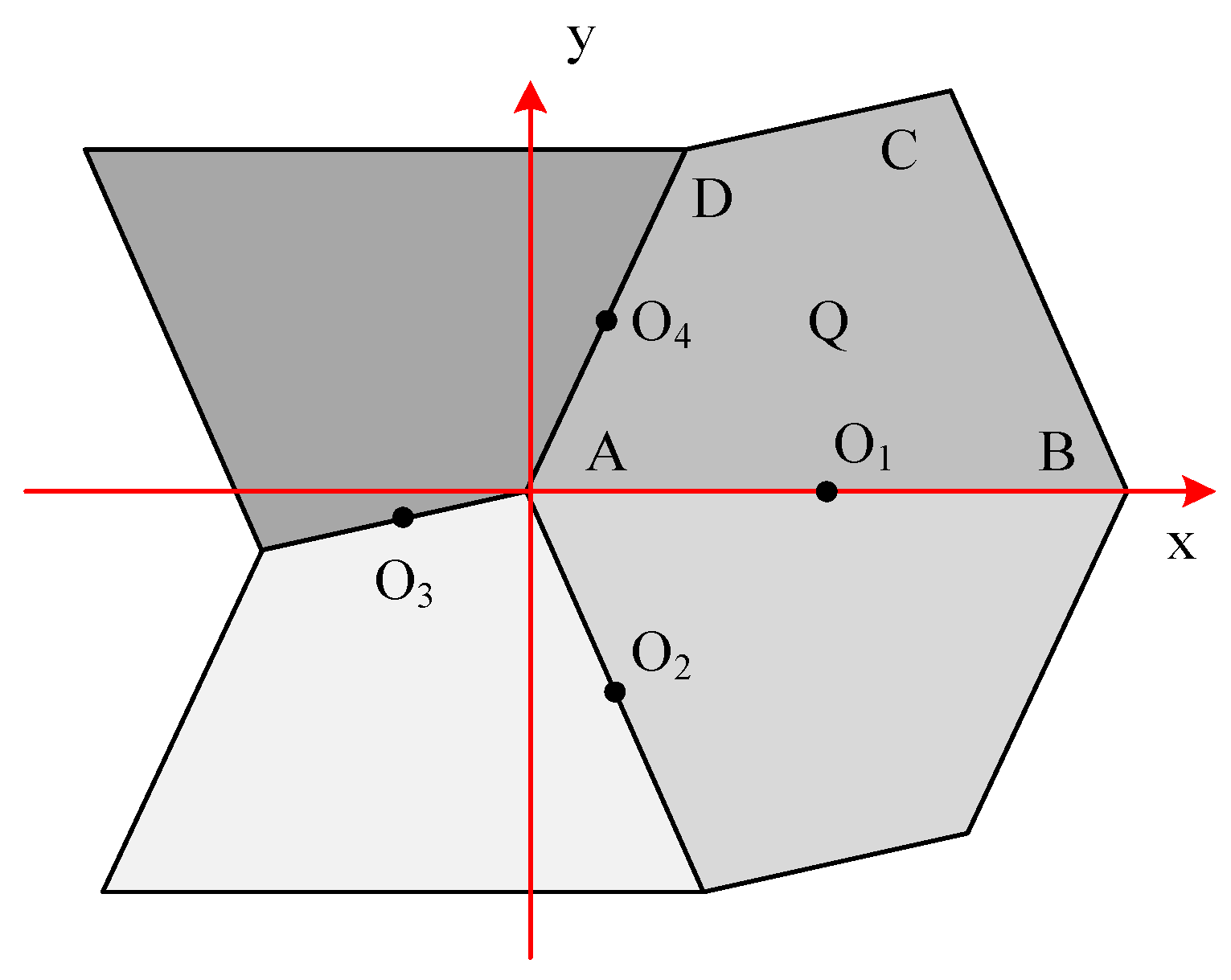
3.2.1. Boundary Mapping Construction

To ensure that adjacent copies of the fundamental region share identical color values at their boundaries, each edge of the quadrilateral tile must satisfy a central symmetry constraint. Without loss of generality, for edge AB, the points on it must be satisfied under the invariant mapping:

$$f_{\partial \Omega }(P_A+t(P_B-P_A))=f_{\partial \Omega }(P_B+t(P_A-P_B)),$$

(2)

where t ∈ [0, 1]. Under this constraint, the four vertices are mapped to the same value, and for each edge, only half of the edge needs to be constructed for the invariant mapping, with the remaining half obtained through symmetry transformations.

To construct the boundary mapping under the constraints of Equation (2), this paper first establishes a local coordinate system on the fundamental region Q as shown in Figure 2, where vertex A is set as the coordinate origin, with edge AB aligned along the x-axis; the centers of each edge are denoted as O₁, O₂, O₃, O₄. The invariant mapping $f_{\partial \Omega }:\partial \Omega \to R^2$ is then defined on edges AO₁ and AO₄. Specifically, the mapping can be expressed as follows: $f_{\partial \Omega }(x)=w(x)$, where $x\in A{O}_1\cup A{O}_4$. The function w is user-defined and can be customized as a composite transformation based on affine transformations or other operations:

$$w(x)=\phi (Ax+b),$$

(3)

where φ is a user-defined linear or nonlinear function, A is a 2 × 2 affine transformation matrix defaulting to the identity matrix, and b is a translation vector defaulting to [0, 0]^t. The invariant mappings on edges O₁B and O₄D are then computed using Equation (2).

Since four vertices of the quadrilateral tile ABCD are mapped to the same value, defining the mapping directly on edges CB and CD would result in vertex C having a distinct value from the other three vertices. To resolve this, the two edges are translated to the origin, aligning vertex C with the coordinate origin to ensure consistent mapping values across four vertices (as shown in Figure 2). Subsequently, Equation (3) is applied in this coordinate system to define the invariant mappings for the two edges.

3.2.2. Internal Mapping Construction

The invariant mapping functions on the four boundary edges of the fundamental region have been explicitly constructed under the symmetry constraints outlined above, labeled in a counterclockwise order as f₁, f₂, f₃, and f₄. Leveraging the quadrilateral topology of the fundamental region, this paper constructs the invariant mapping within the fundamental region by means of the Coons surface interpolation method.

For the convex quadrilateral fundamental region Q, a meticulously designed bijective mapping is established to map it onto the normalized parameter space [0, 1] × [0, 1], which corresponds to the unit square domain. This transformation serves as a pivotal step, enabling the application of the bilinear Coons surface interpolation method within the parameter domain. By leveraging this interpolation technique, a continuous and smooth invariant mapping is constructed, ensuring that it strictly adheres to the interpolation constraints imposed by the boundary functions. Specifically, the bijective mapping preserves the topological properties of Q during the transformation process, while the bilinear Coons surface interpolation method takes advantage of the parametric representation within the unit square to seamlessly blend the boundary conditions. This synergy between the mapping and interpolation process not only guarantees the mathematical integrity of the invariant mapping but also facilitates the generation of high-quality digital art patterns with precise control over the geometric and visual characteristics.

The physical coordinates P within the fundamental region and their parametric coordinates U = (u,v) are related by the following bilinear mapping:

$$P=(1-u)(1-v)P_1+u(1-v)P_2+uv{P}_3+(1-u)v{P}_4.$$

(4)

For any point P in the fundamental region, to obtain its parameter coordinate U, the inverse mapping needs to be calculated. Although general numerical methods such as the Newton–Raphson method can be employed for this purpose, this paper derives an analytical formula for computing U based on the characteristics of Equation (4), to improve computational efficiency and enhance numerical robustness.

Let the i-th edge vector of the quadrilateral be e_i = P_(i+1)%4 − P_i, e = P − P₀. By eliminating the v-variable in Equation (4), a function of v in terms of u is derived:

$$v={\displaystyle \frac{u{e}_{1,x}-e_x}{u(e_{1,x}+e_{3,x})+e_{4,x}}},$$

(5)

where e_x and e_i,x denote the x-components of the edge vectors e and e_i, respectively. Substituting Equation (5) into Equation (4), and through derivation, a univariate quadratic equation for the coordinate u can be further obtained:

$$A{u}^2+Bu+C=0.$$

(6)

The coefficients are as follows: $A=e_1\times e_3$, $B=e_1\times e_4-e\times (e_1+e_3)$, $C=e_4\times e$.

Based on the value of coefficient A in Equation (5), the u-coordinate can be computed in the following two cases:

Case 1: when A = 0, i.e., the first and third edges are parallel, the equation degenerates into a univariate linear equation, thus yielding $u=-{\displaystyle \frac{C}{B}}$;

Case 2: when $A\ne 0$, the equation yields two solutions, i.e., $u={\displaystyle \frac{-B\pm \sqrt{B^2-4AC}}{2A}}$, with the valid solution being the one that lies within the interval [0, 1]. The corresponding v-coordinate can then be computed using Equation (5).

After obtaining the parametric coordinates U, the invariant mapping interpolating the boundary functions is derived based on the bilinear Coons surface interpolation method [10] as follows:

$$f(x,y)=F(u,v)=(1-v)f_1(p_1)+u{f}_2(p_2)+v{f}_3(p_3)+(1-u)f_4(p_4),$$

(7)

where $p_i=P_i+u(P_{i+1}-P_i)$, i = 1, 3; $p_i=P_i+v(P_{(i+1)\%4}-P_i)$, i = 2, 4.

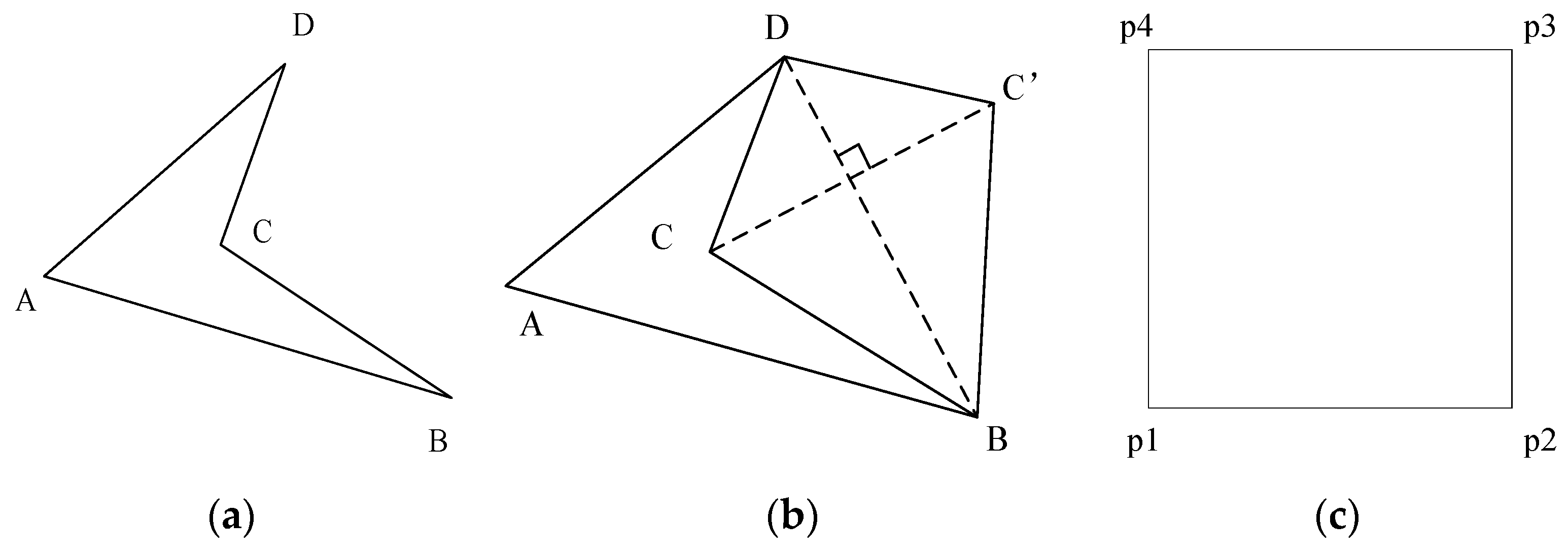
Such interpolation can lead to self-intersections of parameter lines in the vicinity of the concave regions. This geometric anomaly not only disrupts the mathematical integrity of the interpolation process but also induces distortion in the resulting interpolated surface, compromising the quality of the generated patterns.

To circumvent this challenge, a multi-step geometric transformation strategy is implemented. First, the concave vertex (C as illustrated in Figure 3a) undergoes a mirror reflection transformation along the opposite edge of the concave vertex (BD) as the reflection axis. This reflective operation effectively reconfigures the non-convex geometry into a convex quadrilateral, as depicted in Figure 3b (ABC’D), thereby eliminating the problematic concavity that causes interpolation issues. Subsequently, by leveraging generalized barycentric coordinates (Equation (8)), a smooth bijective mapping is meticulously constructed to establish a one-to-one correspondence between the original concave domain and the newly formed convex domain. Finally, the convex domain is mapped onto the parameterization domain, as shown in Figure 3c, after which the well-established Coons surface interpolation method can be applied for computation. This sequential approach not only resolves the self-intersection problem associated with direct interpolation of concave quadrilaterals but also provides a reliable and efficient solution for generating smooth and distortion-free surfaces in the context of digital art pattern creation.

Generalized barycentric coordinates extend the concept of traditional barycentric coordinates, originally defined for simple geometric primitives like triangles to arbitrary polygonal domains. This extension facilitates a unique and systematic representation of interior points within geometric spaces, providing a powerful mathematical tool for geometric processing. The underlying principle hinges on expressing a target point as a linear combination of the polygon’s vertices, achieved through a set of carefully crafted weight functions. These weight functions adhere to stringent mathematical constraints, including non-negativity, linear precision, and normalization, ensuring the geometric and algebraic consistency of coordinates. In the realm of computer graphics, geometric modeling, and physical simulations, generalized barycentric coordinates have emerged as a cornerstone technique. They enable seamless interpolation between geometric entities, precise control over shape deformations, and efficient parameterization mapping, thereby enhancing the flexibility and accuracy of digital geometric representations. Given the diverse array of generalized barycentric coordinates available in the literature [28], this paper strategically selects Mean Value Coordinates [29]. These coordinates are particularly advantageous due to their exceptional properties, which include the following:

$$P={\displaystyle {\sum }_{i=1}^4{\lambda }_i(P)P_i},$$

(8)

In the equation, λ_i denotes the generalized barycentric coordinate, which is derived from normalized Mean Value Coordinates:

$${\lambda }_i={\displaystyle \frac{w_i(P)}{{\displaystyle {\sum }_{j=1}^4{w}_j(P)}}},$$

(9)

where w_i is derived from the following formula:

$$w_i(P)={\displaystyle \frac{\tan ({\alpha }_{i-1}(P)/2)+\tan ({\alpha }_i(P)/2)}{\left|\right|P_i-P\left|\right|}},$$

(10)

where angles α_i−1(P) and α_i(P) represent the signed angles at point P formed by the two triangles <P, P_i−1, P_i> and <P, P_i, P_i+1>. To avoid angle and trigonometric function calculations in Equation (10) and enhance computational efficiency, we adopt an efficient and robust algorithm proposed by Hormann et al. [30], which is also suited for concave polygons.

With Equation (8), we can smoothly map any concave quadrilateral to its corresponding convex counterpart, as illustrated in Figure 3. The specific process is as follows: For any given point P in the concave region, the parameters {w_i} are calculated by Hormann et al. [30]. Next, based on Equation (9), the generalized barycentric coordinates {λ_i} are derived. Subsequently, point P is mapped to the corresponding point P′ by Equation (8).

3.3. Colorization

After constructing invariant mappings on the fundamental region, seamless patterns with boundary continuity are generated through colorization followed by tiling operations. Classical colorization schemes include dynamical systems and quasi-regular patterns, the latter of which are derived from contour-based visualization techniques applied to specific two-dimensional functions defined on the domain. The resulting pattern morphology is inherently determined by the function’s mathematical structure. However, due to the arbitrary shape of quadrilaterals and potential significant deformation after unit square parameterization, applying quasi-regular pattern models may induce large texture distortions that compromise aesthetic quality. To address this limitation, this paper selects the colorization scheme with a dynamical system that operates independently of the underlying function morphology.

The dynamical system is a mathematical model that describe the temporal evolution of system states through structural relationships, with the core principle lying in establishing mappings between state variables and time. These systems are typically characterized by systems of ordinary differential equations or discrete maps, the latter of which can be expressed in the following iterative form:

$$\left\{\begin{array}{c}{x}_{n+1}=x_n-g(x,y)\\ y_{n+1}=y_n-h(x,y)\end{array}\right.,$$

(11)

where (x₀,y₀)^t denotes the initial coordinate point, and g, h: R²→R represent user-defined functions that govern the iterative dynamics of the system.

The dynamic system generates a sequence of points through iterative functions, and the set of these points is termed an orbit. In this paper, based on dynamic systems, the orbit trap method is adopted to colorize the fundamental region. This involves assigning colors to pixels by determining whether the points in the orbit fall into specific geometric shapes (i.e., orbit traps), thereby achieving rendering results. The selection of color can be contingent upon the number of iterations.

To maintain symmetry and seamless tiling in the colored texture, each pixel (n_x,n_y) within the fundamental region is first transformed into the space of the dynamical system:

$$(x,y)=\left(x_t+n_x{\displaystyle \frac{s}{W_x}},y_t+n_y{\displaystyle \frac{s}{W_y}}\right),$$

(12)

where W_x and W_y represent the height values, while (x_t,y_t)^t denotes the translation vector defaulting to (0,0)^t. The parameter s controls the pattern’s scaling ratio defaulting to 1. Subsequently, the coordinate (n_x,n_y) is transformed via invariant mapping into a new coordinate (f(x),f(y)), and this mapped coordinate is then substituted as the initial point in Equation (11) to compute the corresponding pixel value, which is subsequently applied for domain coloring.

4. Results

The algorithm proposed in this paper is implemented in C++ for core computational modules, with invariant mapping calculations and colorization processes realized using OpenGL’s GLSL. The experimental setup includes a PC equipped with an Intel Core i7-12700K processor, NVIDIA GeForce RTX 3070 Ti GPU, and Windows 10 operating system.

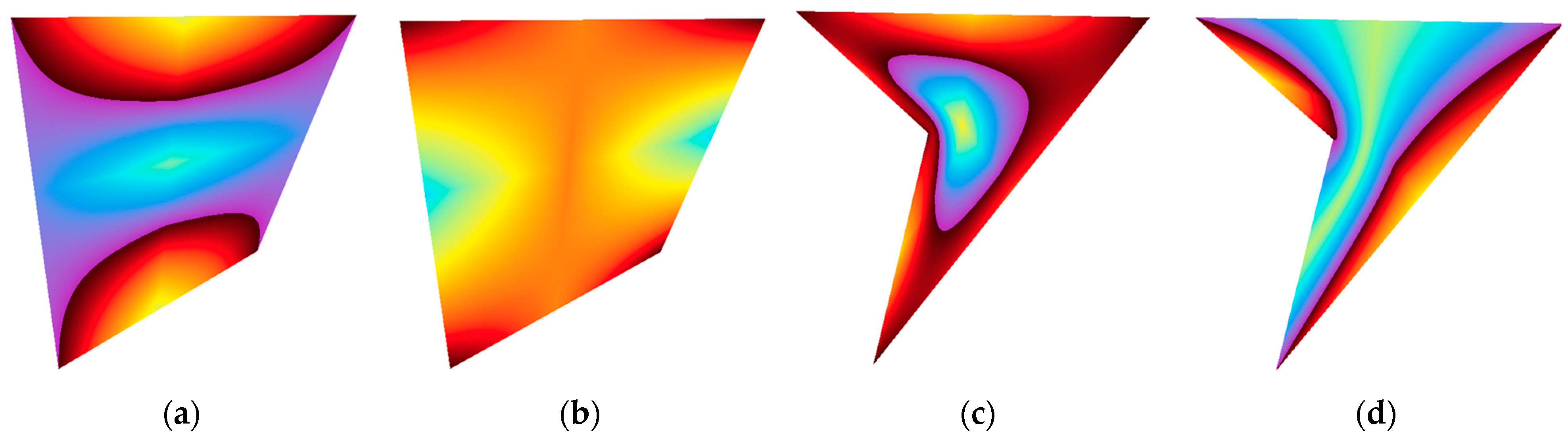
To visually demonstrate the quality of the proposed invariant mapping algorithm on quadrilateral fundamental regions, normalized heat maps illustrating the invariant mapping field distribution were generated for both convex and concave quadrilateral tiles (see Figure 4). In this example, the boundary function is defined as w(x) = sin(x + [2, 2]^t). As shown in the figure, the field under invariant mapping construction maintains strict central symmetry along the boundaries for both convex and concave quadrilaterals, while exhibiting deformation-invariant symmetry within the interior of the domains. Additionally, the field demonstrates high smoothness, effectively satisfying the construction objectives of invariant mapping and providing a robust foundation for subsequent digital pattern generation.

Based on the constructed fundamental region and invariant mapping above, the dynamical system functions are defined as g(x,y) = 0.8sinxcosy, h(x,y) = 0.6cos2xsiny. The iterative calculation yields the visualization results shown in Figure 5. For an individual tile, the symmetry inherent to the invariant mapping within the fundamental region directly influences the colored texture, resulting in patterns exhibiting corresponding symmetry characteristics. In spatial extension, the generated tiling achieves strict periodic repetition, with adjacent tiles seamlessly aligned at boundaries to form a natural, four-directional continuous pattern. This method not only satisfies translational invariance in a mathematical sense but also demonstrates strong aesthetic value. Its continuous, seam-free visual effects and rhythmic pattern arrangement provide a novel approach for decorative art design and digital pattern generation.

The invariant mappings on the fundamental region’s boundary act as “generators” for the mapping family, with their intrinsic properties directly dictating the global distribution patterns of invariant mappings across the entire fundamental region. This critical characteristic establishes the selection of invariant mapping functions as one of the core variables influencing the generation effects of digital art patterns. To systematically validate this theoretical hypothesis, we designed controlled experiments while keeping both the fundamental region structure and dynamical system functions constant (where g(x,y) = 0.4sin2xcosy + 0.1sinxcos2y, h(x,y) = 0.4cosxsin2y + 0.1cos2xsiny), and different forms of function w were selected as boundary invariant mappings under identical experimental conditions. The experimental results are presented in Figure 6, with the parameters in function w specified as follows: $A_2=\left[\begin{array}{cc}2& 1\\ 2& 1\end{array}\right]$, $A_3=\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]$, $b_1={[2,2]}^t$, $b_2={[2,3]}^t$. As illustrated in Figure 6, when different analytical forms are adopted, even under identical fundamental regions and colorization schemes, the generated patterns exhibit significant variations in symmetry properties, texture complexity, and visual periodicity. Notably, empirical results demonstrate that nonlinear formulations of the φ function can overcome the monotonicity inherent in linear transformations through iterative computation. This enables the generation of more complex textural structures, thereby enhancing both visual expressiveness and art potential in digital pattern design.

As a core control parameter, the dynamical system functions not only exert a profound influence on the textural morphology of patterns but also serve as a crucial technical means for facilitating user-interactive editing. To investigate their mechanism, we conducted controlled experiments under fixed quadrilateral fundamental regions and invariant mapping conditions by switching different dynamical system functions g and h for coloring (function 1: g(x,y) = sin(x − y) + cosx; h(x,y) = sin(x + y) + cosy; function 2: g(x,y) = 1.2cos(x + 0.2y); h(x,y) = 0.8cos(x + sin(x + y)); function 3: g(x,y) = 0.4(1.2)^sinxlog(1.5 − sinx); h(x,y) = 1.2(1 + sin(x + y))^{(0.2+1.5siny)}). The experimental results are depicted in Figure 7. Through visualization analysis, it becomes evident that despite the unchanging topological structure of fundamental regions and the symmetry constraints of invariant mappings, the incorporation of distinct dynamical system functions leads to substantial modifications in local textural characteristics. At the microscopic scale, these functions govern the parameter dynamics during iterative processes, yielding a spectrum of textural effects, from delicate gradients to stark contrasts. Conversely, at the macroscopic compositional level, the global symmetry structure and spatial arrangement retain a high degree of consistency, attributable to the continuous geometric constraints exerted by fundamental regions and invariant mappings. These discoveries underscore the pivotal role of dynamical system functions in achieving a balance between design flexibility and structural integrity, thereby offering both theoretical underpinnings and practical methodologies for parametric design in the creation of digital art patterns.

The affine transformation defined in Equation (12) performs specific mathematical mapping operations on the domain, with parameters x_t, y_t, and s playing important roles in shaping textural details of the generated patterns. To systematically investigate their influence mechanisms, we set up the dynamical system functions as follows: g(x,y) = e^(−0.1y)cosx, h(x,y) = e^(−0.1x)siny. The experimental procedure is outlined as follows: Initially, parameter s is fixed at 40. With this configuration, distinct values are assigned individually to parameters x_t and y_t, and the resulting patterns are displayed in the first row (a–d) of Figure 8. Subsequently, while maintaining x_t = y_t = 2 as constants, parameters is varied across different values, with the corresponding results shown in the second row (e–h) of Figure 8. As shown in the visualizations, variations in parameter values lead to significant differences in the textural details of the generated patterns. This phenomenon demonstrates that the dynamical system model exhibits high sensitivity to initial conditions during the iterative process, where minute changes in initial parameter values, through successive iterations, result in pronounced alterations in the final textural characteristics of the patterns.

To systematically examine the influence of fundamental region shapes on digital pattern generation, a comparative study was conducted as follows: Under strictly controlled conditions where boundary invariant mapping functions and dynamical system functions (where g(x,y) = 0.2(sinxcos2y − sin(−x)cos(−2y)) + 0.1(sin(−y)cos2x − sinycos(−2x)), h(x,y) = −0.2(sin(−y)cos2x − sinycos(−2x)) − 0.1(sin(−x)cos(−2y) − sinxcos2y)) remain identical, convex and concave quadrilaterals were selected as the fundamental region. 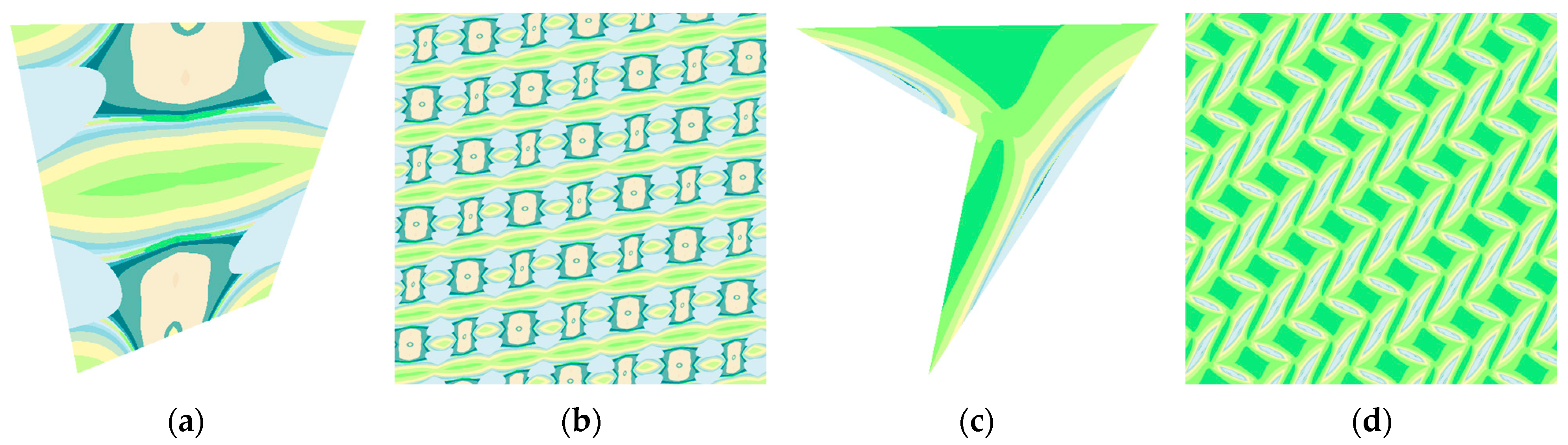Employing a meticulously designed controlled variable experimental framework, the corresponding visual representations are illustrated in Figure 9. Rigorous analysis of the experimental data reveals that, even when boundary function selections and coloring algorithm parameters remain constant, the geometric morphological disparities among quadrilaterals exert a profound influence on the spatial distribution of invariant functions within the fundamental region. At the microscale, the distinct geometries of quadrilaterals trigger disparate parameter propagation trajectories during the iterative mapping process, giving rise to notable variations in the texture density, orientation, and continuity of the generated patterns. At the macroscale, the intrinsic geometric properties of convex and concave quadrilaterals directly mold the overall pattern morphology. Notably, concave quadrilaterals, through the iterative operation of the dynamical system, manifest S-shaped distortion characteristics in dynamic textures, creating fluid curve transitions and rhythmic visual patterns that offer unparalleled aesthetic expressions in digital art pattern generation. These findings not only elucidate the pivotal role of fundamental regions in pattern formation but also pioneer innovative design methodologies for harmoniously integrating structural parameters with aesthetic objectives in the realm of parametric design.

To validate the superiority of our proposed method, we conducted comparative experiments with the traditional method of wallpaper symmetrical dynamical system [22]. Under the condition of using identical dynamical system functions g and h (corresponding to those in Figure 1 of [22]), our approach employed two distinct quadrilateral tiles as fundamental regions. The experimental results are presented in Figure 10, where panels a–d show the tiling outcomes from [22], and panels e–h and i–l, respectively, display the coloring results of our method using convex and concave quadrilateral domains. Through in-depth visual comparative analysis, it is evident that, despite identical functions of dynamical system, pronounced disparities in visual characteristics emerge. The traditional approach documented in [22], governed by wallpaper group theory, yields highly regular geometric symmetries manifested as periodically repeating grid-like patterns, embodying a mechanical precision. Conversely, our proposed methodology maintains the essential periodicity while introducing innovative geometric composition designs and mapping mechanisms, effectively transcending the constraints of conventional regularity. The experimental results showcase a wealth of spatial compositional variations, characterized by irregular texture distributions and dynamic morphological transitions. This not only sustains pattern continuity but also significantly amplifies visual tension and artistic expressiveness, demonstrating the superiority of our method in aesthetic and design innovation.

The patterns generated by our methodology possess extensive versatility, positioning them as ideal candidates for a multitude of applications spanning diverse industries. As vividly illustrated in the accompanying visual, one notable application domain is interior design (Figure 11), where our proposed approach demonstrates remarkable potential in transforming living and working spaces. By seamlessly integrating with various objects—from expansive wall surfaces that serve as a backdrop for artistic expression, to intricately designed furniture pieces that become carriers of unique patterns, and even to textiles that add texture and color to the environment, the patterns enhance the aesthetic appeal and thematic coherence of the space. Our method leverages advanced techniques such as symmetry-preserving mappings and boundary-invariant interpolation, which are pivotal in maintaining topological consistency across different surfaces and scales. This ensures that regardless of the shape, size, or curvature of the application medium, the patterns retain their structural integrity and visual harmony. The result is a series of designs that exhibit optimized color transitions, where hues blend seamlessly to create a visually pleasing gradient effect. Moreover, the parametric adaptability inherent in our approach allows for the patterns to be effortlessly customized and adapted to complex surfaces. Whether it is a uniquely contoured wall, an irregularly shaped piece of furniture, or a fabric with a specific weave, our patterns can be fine-tuned to fit the objects properly, achieving a seamless integration that elevates the overall design aesthetic. This combination of technical sophistication and artistic flexibility makes our patterns not only functional but also highly desirable for designers seeking to create innovative and visually stunning interior spaces.

The GPU-based parallel implementation of the core modules in our algorithm empowers the proposed pattern generation method with exceptional computational efficiency. Rigorous experimental evaluations reveal that, across a wide spectrum of resolutions, the average computation time for generating each pattern remains steadfastly below 0.25 s, a remarkable performance benchmark that substantially expedites the design iteration process. As meticulously documented in

Table 1. Pattern generation speed at different resolutions.

Pattern Resolution	Time Spent (s)
512 × 512	0.23483
1024 × 1024	0.25114
2048 × 2048	0.26079
4096 × 4096	0.27230
Average	0.25477

, the detailed efficiency statistics and resolution-dependent performance metrics offer a solid quantitative basis for subsequent engineering implementations. This GPU-enabled parallel strategy capitalizes on the inherent massive parallel processing capabilities of graphics processing units, enabling concurrent execution of computationally intensive tasks. By doing so, it not only guarantees the generation of high-fidelity patterns but also achieves efficient real-time rendering, striking a delicate balance between computational speed and output quality. This dual-optimization approach establishes a robust computational framework, facilitating rapid prototyping and interactive design in digital pattern creation. Notably, it proves to be especially advantageous in symmetry-based artistic applications, where the ability to swiftly visualize and modify patterns in real-time significantly enhances the creative workflow and artistic expression.

5. Conclusions

This paper introduces an innovative approach to digital art pattern generation utilizing arbitrary quadrilateral tilings. By enabling seamless adaptation of smooth invariant mappings to any quadrilateral fundamental region, the proposed method effectively decouples the topological stability of quadrilateral structures from deformation parameters. Integrating Coons surface interpolation techniques, it not only preserves the translational symmetry and computational efficiency advantages inherent in traditional tiling methods but also significantly enhances user control over spatial composition and local pattern intricacies. Rigorous experimental evaluations validate that the generated patterns excel in natural transitions across tile edges, symmetry preservation, and texture diversity. Through the strategic adjustment of dynamical system functions and boundary mapping parameters, the method facilitates the creation of a wide spectrum of artistic effects, ranging from precisely regular geometric patterns to dynamically distorted visual expressions.

Compared with existing symmetrical dynamical system approaches, our method represents a significant advancement by transcending the limitations of fixed templates. This breakthrough allows for the generation of patterns with heightened visual tension and greater artistic expression potential, all while maintaining strict mathematical rigor. Nevertheless, like many dynamical system-based methodologies, the current approach may produce aesthetically less-than-optimal results for certain arbitrary parameter inputs. As a result, manual parameter tuning is often required to achieve desirable designs in practical applications, which poses a minor challenge to the overall generation efficiency. That said, we have identified certain empirical insights: specifically, selecting a smooth nonlinear function φ (one that does not change abruptly) for constructing boundary mappings, along with employing commonly used and validated functions from dynamical systems, can help alleviate this issue.

Looking ahead, our future research endeavors will focus on exploring mapping techniques tailored to tilings with more complex curved boundaries, aiming to expand the geometric diversity of generated patterns. We also intend to develop specialized aesthetic evaluation models for digital art patterns, which will serve as a guiding framework for automated parameter adjustment and efficient design processes. Additionally, we plan to incorporate deep learning techniques, enabling style transfer and intelligent interactive design capabilities. These initiatives are expected to significantly enhance the intelligence and practical applicability of digital art pattern generation technologies, thereby opening new possibilities for creative expression in the digital art domain.