Clock Noise Suppression Techniques in Space-Borne Gravitational Wave Detection: A Review
Abstract
1. Introduction
2. Laser Interferometric Data Streams in Space-Borne GW Detection
3. Clock Noise Impact Mechanism
4. Basic Principles of Clock Noise Suppression Techniques
4.1. TDI Technique
4.2. Clock Noise Calibrated TDI Technique
4.3. Optical Comb TDI Technique
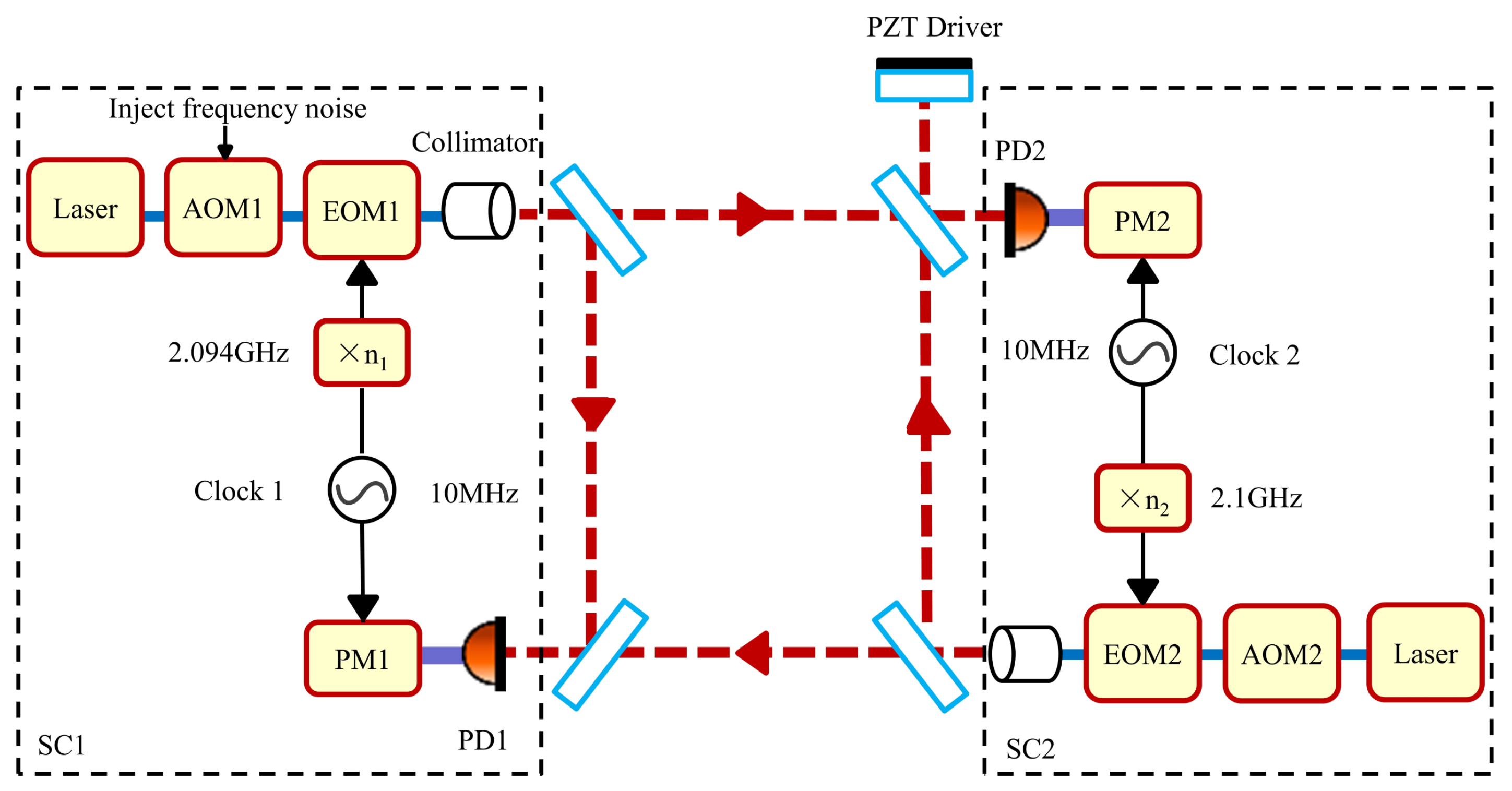
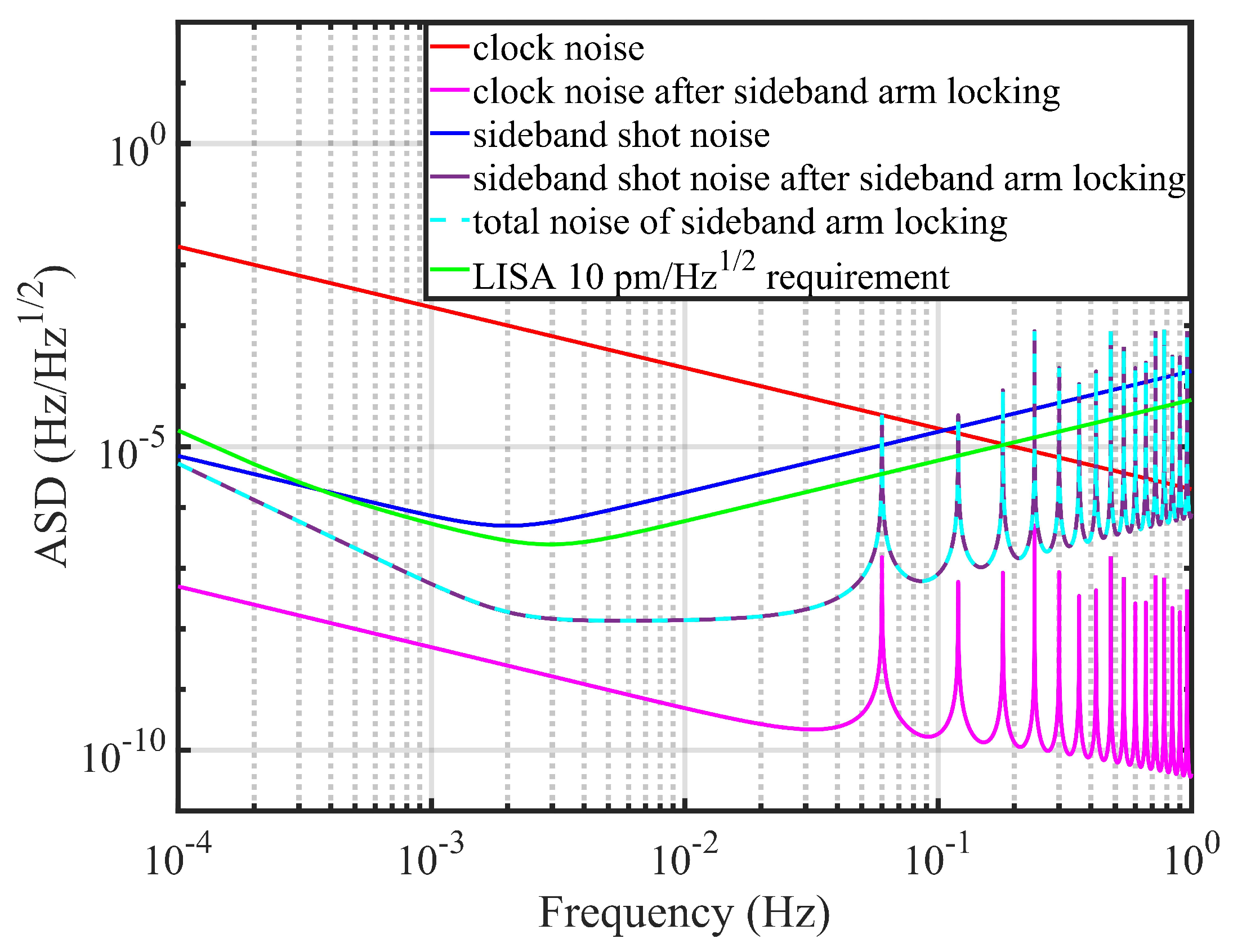
4.4. Sideband Arm Locking Technique
5. Current Research Status of Clock Noise Suppression Techniques
5.1. Clock Noise Calibrated TDI Technique
5.2. Optical Comb TDI Technique
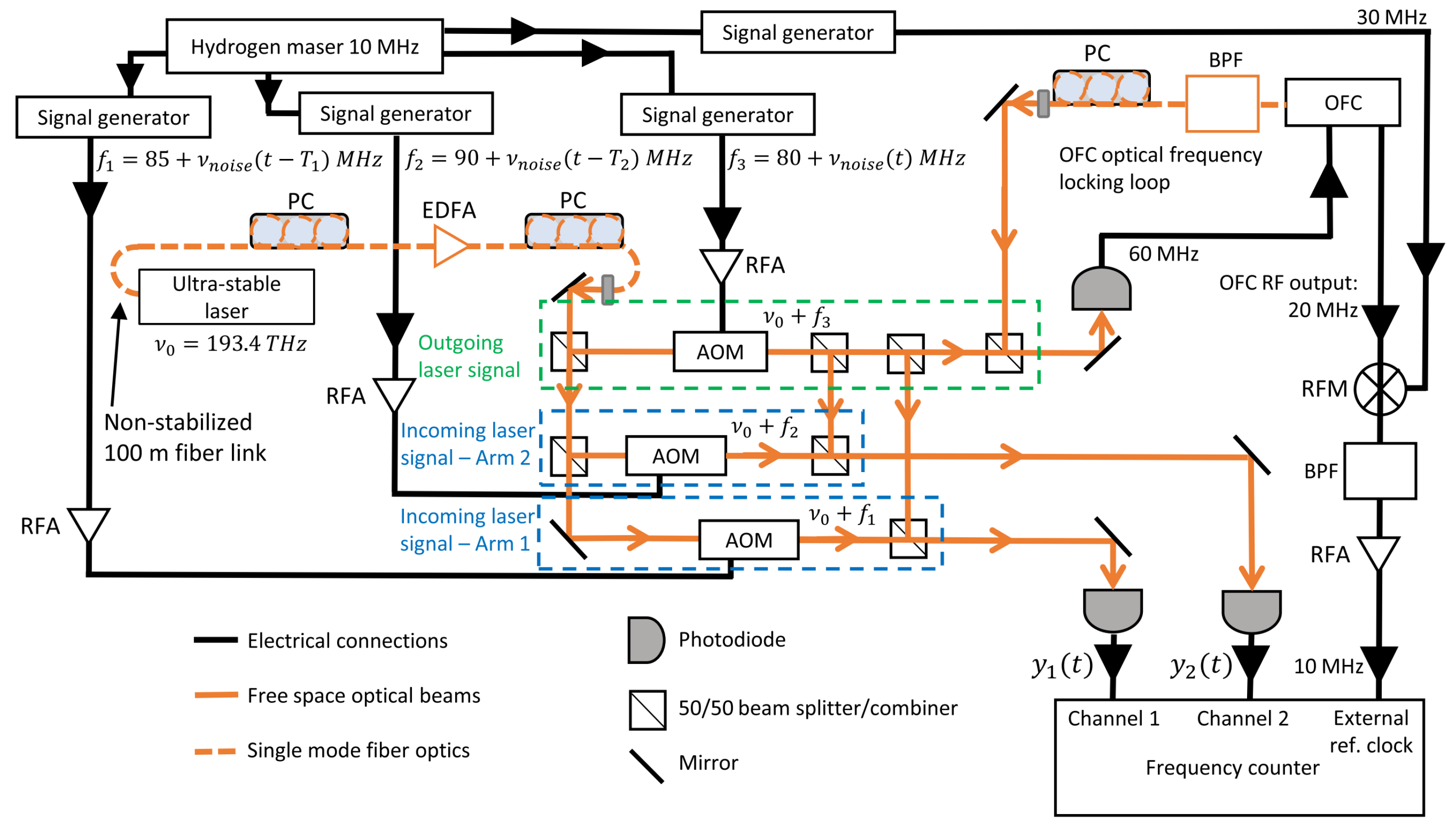
5.3. Sideband Arm Locking Technique
6. Conclusions and Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Einstein, A. Die grundlage der allgemeinen relativitätstheorie. Annalen der Physik 1916, 354, 769–822. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; LIGO Scientific Collaboration and Virgo Collaboration. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; LIGO Scientific Collaboration and Virgo Collaboration. GW151226: Observation of gravitational waves from a 22-solar-mass binary black hole coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef] [PubMed]
- Cai, R.G. Revealing the amplitude of primordial curvature perturbations on small scales from Primordial black hole binaries for gravitational wave detection. Sci. China Phys. Mech. Astron. 2023, 66, 260461. [Google Scholar] [CrossRef]
- He, S.; Li, L.; Li, Z.; Wang, S.J. Gravitational waves and primordial black hole productions from gluodynamics by holography. Sci. China Phys. Mech. Astron. 2024, 67, 240411. [Google Scholar] [CrossRef]
- Wang, C.W.Z.; Zhu, J.B.; Huang, G.Q.; Shu, F.W. Testing the first law of black hole mechanics with gravitational waves. arXiv 2024, arXiv:2304.10117. [Google Scholar] [CrossRef]
- Cervantes-Cota, J.L.; Galindo-Uribarri, S.; Smoot, G.F. A brief history of gravitational waves. Universe 2016, 2, 22. [Google Scholar] [CrossRef]
- Chen, C.M.; Nester, J.M.; Ni, W.T. A brief history of gravitational wave research. Chin. J. Phys. 2017, 55, 142–169. [Google Scholar] [CrossRef]
- Li, J.; Liu, F.; Pan, Y.; Wang, Z.; Cao, M.; Wang, M.; Zhang, F.; Zhang, J.; Zhu, Z.H. Detecting gravitational wave with an interferometric seismometer array on lunar nearside. Sci. China Phys. Mech. Astron. 2023, 66, 109513. [Google Scholar] [CrossRef]
- Shao, L. Perceiving deci-Hertz gravitational waves over the Moon. Sci. China Phys. Mech. Astron. 2023, 66, 119531. [Google Scholar] [CrossRef]
- Torres-Orjuela, A.; Huang, S.J.; Liang, Z.C.; Liu, S.; Wang, H.T.; Ye, C.Q.; Hu, Y.M.; Mei, J. Detection of astrophysical gravitational wave sources by TianQin and LISA. Sci. China Phys. Mech. Astron. 2024, 67, 259511. [Google Scholar] [CrossRef]
- Han, Z. FAST unveils a new era in the discovery of long-period pulsars in globular clusters. Sci. China Phys. Mech. Astron. 2024, 67, 269532. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar] [CrossRef]
- Luo, J.; Chen, L.S.; Duan, H.Z.; Gong, Y.G.; Hu, S.; Ji, J.; Liu, Q.; Mei, J.; Milyukov, V.; Sazhin, M.; et al. TianQin: A space-borne gravitational wave detector. Class. Quantum Gravity 2016, 33, 035010. [Google Scholar] [CrossRef]
- Hu, W.R.; Wu, Y.L. The Taiji program in space for gravitational wave physics and the nature of gravity. Natl. Sci. Rev. 2017, 4, 685–686. [Google Scholar] [CrossRef]
- Derevianko, A.; Gibble, K.; Hollberg, L.; Newbury, N.R.; Oates, C.; Safronova, M.S.; Sinclair, L.C.; Yu, N. Fundamental physics with a state-of-the-art optical clock in space. Quantum Sci. Technol. 2022, 7, 044002. [Google Scholar] [CrossRef]
- Kolkowitz, S.; Pikovski, I.; Langellier, N.; Lukin, M.; Walsworth, R.; Ye, J. Gravitational wave detection with optical lattice atomic clocks. Phys. Rev. D 2016, 94, 124043. [Google Scholar] [CrossRef]
- Wang, B.; Li, B.; Xiao, Q.; Mo, G.; Cai, Y.F. Space-based optical lattice clocks as gravitational wave detectors in search for new physics. Sci. China Phys. Mech. Astron. 2025, 68, 249512. [Google Scholar] [CrossRef]
- Weaver, G.; Garstecki, J.; Reynolds, S. The performance of ultra-stable oscillators for the Gravity Recovery and Interior Laboratory (GRAIL). In Proceedings of the Annual Precise Time & Time Interval Systems & Applications Meeting, Reston, VA, USA, 15–18 November 2010. [Google Scholar]
- Hellings, R.W. Elimination of clock jitter noise in spaceborne laser interferometers. Phys. Rev. D 2001, 64, 022002. [Google Scholar] [CrossRef]
- Tinto, M.; Armstrong, J.W.; Estabrook, F.B. Modulator noise suppression in the LISA time-delay interferometric combinations. Class. Quantum Gravity 2007, 25, 015008. [Google Scholar] [CrossRef]
- Otto, M.; Heinzel, G.; Danzmann, K. TDI and clock noise removal for the split interferometry configuration of LISA. Class. Quantum Gravity 2012, 29, 205003. [Google Scholar] [CrossRef]
- Tinto, M.; Hartwig, O. Time-delay interferometry and clock-noise calibration. Phys. Rev. D 2018, 98, 042003. [Google Scholar] [CrossRef]
- Hartwig, O.; Bayle, J.B. Clock-jitter reduction in LISA time-delay interferometry combinations. Phys. Rev. D 2021, 103, 123027. [Google Scholar] [CrossRef]
- Yang, Z.J.; Wang, P.P.; Tan, Y.J.; Shao, C.G. Clock noise reduction in geometric time delay interferometry combinations. Results Phys. 2023, 53, 106900. [Google Scholar] [CrossRef]
- Tinto, M.; Yu, N. Time-delay interferometry with optical frequency comb. Phys. Rev. D 2015, 92, 042002. [Google Scholar] [CrossRef]
- Tan, Y.J.; Xu, M.Y.; Wang, P.P.; Wu, H.Z.; Shao, C.G. Modified time-delay interferometry with an optical frequency comb. Phys. Rev. D 2022, 106, 044010. [Google Scholar] [CrossRef]
- Xu, M.Y.; Tan, Y.J.; Shao, C.G. Clock-jitter noise reduction by sideband arm locking for space-borne gravitational wave detectors. Phys. Rev. D 2024, 110, 102003. [Google Scholar] [CrossRef]
- de Vine, G.; Ware, B.; McKenzie, K.; Spero, R.E.; Klipstein, W.M.; Shaddock, D.A. Experimental demonstration of time-delay interferometry for the Laser Interferometer Space Antenna. Phys. Rev. Lett. 2010, 104, 211103. [Google Scholar] [CrossRef]
- Mitryk, S.J.; Mueller, G.; Sanjuan, J. Hardware-based demonstration of time-delay interferometry and TDI-ranging with spacecraft motion effects. Phys. Rev. D 2012, 86, 122006. [Google Scholar] [CrossRef]
- Li, X.K.; Liu, H.S.; Wu, P.Z.; Li, H.S.; Xu, P.; Luo, Z.R. Proof-of-principle experimental demonstration of Time-delay-interferometry for Chinese space-borne gravitational wave detection missions. Microgravity Sci. Technol. 2022, 34, 64. [Google Scholar] [CrossRef]
- Yamamoto, K.; Vorndamme, C.; Hartwig, O.; Staab, M.; Schwarze, T.S.; Heinzel, G. Experimental verification of intersatellite clock synchronization at LISA performance levels. Phys. Rev. D 2022, 105, 042009. [Google Scholar] [CrossRef]
- Vinckier, Q.; Tinto, M.; Grudinin, I.; Rieländer, D.; Yu, N. Experimental demonstration of time-delay interferometry with optical frequency comb. Phys. Rev. D 2020, 102, 062002. [Google Scholar] [CrossRef]
- Wu, H.Z.; Xu, M.Y.; Wang, P.P.; Zhang, Z.Q.; Fang, P.C.; Tan, Y.J.; Zhang, J.; Chen, Q.F.; Lu, Z.H.; Shao, C.G. Time delay interferometry with a transfer oscillator. Opt. Lett. 2023, 48, 9–12. [Google Scholar] [CrossRef] [PubMed]
- Klipstein, W.; Halverson, P.G.; Peters, R.; Cruz, R.; Shaddock, D. Clock noise removal in LISA. AIP Conf. Proc. 2006, 873, 312–318. [Google Scholar] [CrossRef]
- Barke, S.; Tröbs, M.; Sheard, B.; Heinzel, G.; Danzmann, K. EOM sideband phase characteristics for the spaceborne gravitational wave detector LISA. Appl. Phys. B 2010, 98, 33–39. [Google Scholar] [CrossRef]
- Zeng, H.Y.; Yan, H.; Xie, S.Y.; Jiang, S.C.; Li, Y.Z.; Pan, Y.H.; He, D.M.; Du, Y.B.; chi Yeh, H. Experimental demonstration of weak-light inter-spacecraft clock jitter readout for TianQin. Opt. Express 2023, 31, 34648–34666. [Google Scholar] [CrossRef] [PubMed]
- Sweeney, D.; Mueller, G. Experimental verification of clock noise transfer and components for space based gravitational wave detectors. Opt. Express 2012, 20, 25603–25612. [Google Scholar] [CrossRef]
- Barke, S. Inter-Spacecraft Frequency Distribution for Future Gravitational Wave Observatories. Ph.D. Thesis, Leibniz University, Hannover, Germany, 2015. [Google Scholar] [CrossRef]
- Hartwig, O.; Bayle, J.B.; Staab, M.; Hees, A.; Lilley, M.; Wolf, P. Time-delay interferometry without clock synchronization. Phys. Rev. D 2022, 105, 122008. [Google Scholar] [CrossRef]
- Reinhardt, J.N.; Staab, M.; Yamamoto, K.; Bayle, J.B.; Hees, A.; Hartwig, O.; Wiesner, K.; Shah, S.; Heinzel, G. Ranging sensor fusion in LISA data processing: Treatment of ambiguities, noise, and onboard delays in LISA ranging observables. Phys. Rev. D 2024, 109, 022004. [Google Scholar] [CrossRef]
- Yamamoto, K.; Reinhardt, J.N.; Hartwig, O. Observable-based reformulation of time-delay interferometry. Phys. Rev. D 2025, 111, 122001. [Google Scholar] [CrossRef]
- Guo, Y.; Zeng, L.; Zhang, F.; Bai, Y.; Chen, X.; Gao, Y.; Zou, D.; Lu, X. Time synchronization between satellites via inter-satellite link observations of BDS-3 Constellation: Method, experiment and analysis. Measurement 2024, 224, 113855. [Google Scholar] [CrossRef]
- Gu, X.; Qiu, Z.; Wang, Y.; Jiang, W. LSTM-based clock synchronization for satellite systems using inter-satellite ranging measurements. GPS Solut. 2024, 28, 147. [Google Scholar] [CrossRef]
- Yang, J.; Tang, C.; Hu, X.; Zhou, S.; Liu, L.; Song, Y.; Yang, Y.; Guo, R.; Liu, S.; Pan, J. Centimeter-level clock synchronization and space-borne timescale generation for BDS-3 using inter-satellite link measurements. J. Geod. 2023, 97, 77. [Google Scholar] [CrossRef]
- Xu, M.; Tan, Y.; Shao, C. Research progress on clock noise suppression technique for space-borne gravitational wave detection. Sci. Sin. Phys. Mech. Astron. 2025, 55, 230409. [Google Scholar] [CrossRef]
- Shaddock, D.A.; Tinto, M.; Estabrook, F.B.; Armstrong, J.W. Data combinations accounting for LISA spacecraft motion. Phys. Rev. D 2003, 68, 061303. [Google Scholar] [CrossRef]
- Tinto, M.; Estabrook, F.B.; Armstrong, J.W. Time-delay interferometry for LISA. Phys. Rev. D 2002, 65, 082003. [Google Scholar] [CrossRef]
- Shaddock, D.A.; Ware, B.; Spero, R.E.; Vallisneri, M. Postprocessed time-delay interferometry for LISA. Phys. Rev. D 2004, 70, 081101. [Google Scholar] [CrossRef]
- Tinto, M.; Dhurandhar, S.V. Time-delay interferometry. Living Rev. Relativ. 2021, 24, 1. [Google Scholar] [CrossRef]
- Vallisneri, M.; Bayle, J.B.; Babak, S.; Petiteau, A. Time-delay interferometry without delays. Phys. Rev. D 2021, 103, 082001. [Google Scholar] [CrossRef]
- Page, J.; Littenberg, T.B. Bayesian time delay interferometry for orbiting LISA: Accounting for the time dependence of spacecraft separations. Phys. Rev. D 2023, 108, 044065. [Google Scholar] [CrossRef]
- Tinto, M.; Dhurandhar, S.; Malakar, D. Second-generation time-delay interferometry. Phys. Rev. D 2023, 107, 082001. [Google Scholar] [CrossRef]
- Colpi, M.; Danzmann, K.; Hewitson, M.; Holley-Bockelmann, K.; Jetzer, P.; Nelemans, G.; Petiteau, A.; Shoemaker, D.; Sopuerta, C.; Stebbins, R.; et al. LISA Definition Study Report. arXiv 2024, arXiv:2402.07571. [Google Scholar] [CrossRef]
- Gerberding, O.; Diekmann, C.; Kullmann, J.; Tröbs, M.; Bykov, I.; Barke, S.; Brause, N.C.; Esteban Delgado, J.J.; Schwarze, T.S.; Reiche, J.; et al. Readout for intersatellite laser interferometry: Measuring low frequency phase fluctuations of high-frequency signals with microradian precision. Rev. Sci. Instrum. 2015, 86, 074501. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.R. Note: A new method for directly reducing the sampling jitter noise of the digital phasemeter. Rev. Sci. Instrum. 2018, 89, 036106. [Google Scholar] [CrossRef]
- Huang, X.Q.; Wang, G.F.; Yang, M.; Yang, Z.Q.; Cai, C.B.; Ming, M.; Zhang, J.Y.; Yang, S.Q.; Tu, L.C.; Duan, H.Z.; et al. Study on picometer-level laser interferometer readout system in TianQin project. Opt. Laser Technol. 2023, 161, 109185. [Google Scholar] [CrossRef]
- Zhang, Q.T.; Liu, H.S.; Dong, P.; Li, P.; Luo, Z.R. Multi-frequency signal acquisition and phase measurement in space gravitational wave detection. Rev. Sci. Instrum. 2024, 95, 054501. [Google Scholar] [CrossRef]
- Tinto, M.; Estabrook, F.B.; Armstrong, J.W. Time delay interferometry with moving spacecraft arrays. Phys. Rev. D 2004, 69, 082001. [Google Scholar] [CrossRef]
- Wang, P.P.; Shao, C.G. Time-Delay Interferometry: The Key Technique in Data Pre-Processing Analysis of Space-Based Gravitational Waves. Universe 2024, 10, 398. [Google Scholar] [CrossRef]
- Xie, X.P.; Bouchand, R.; Nicolodi, D.; Giunta, M.; Hansel, W.; Lezius, M.; Joshi, A.; Datta, S.; Alexandre, C.; Lours, M.; et al. Photonic microwave signals with zeptosecond-level absolute timing noise. Nat. Photonics 2017, 11, 44–47. [Google Scholar] [CrossRef]
- Nakamura, T.; Davila-Rodriguez, J.; Leopardi, H.; Sherman, J.A.; Fortier, T.M.; Xie, X.; Campbell, J.C.; McGrew, W.F.; Zhang, X.G.; Hassan, Y.S.; et al. Coherent optical clock down-conversion for microwave frequencies with 10-18 instability. Science 2020, 368, 889–892. [Google Scholar] [CrossRef]
- Brochard, P.; Schilt, S.; Südmeyer, T. Ultra-low noise microwave generation with a free-running optical frequency comb transfer oscillator. Opt. Lett. 2018, 43, 4651–4654. [Google Scholar] [CrossRef]
- Nardelli, N.; Fortier, T.; Pomponio, M.; Baumann, E.; Nelson, C.; Schibli, T.; Hati, A. 10 GHz generation with ultra-low phase noise via the transfer oscillator technique. APL Photonics 2022, 7, 026105. [Google Scholar] [CrossRef]
- Ma, L.S.; Bi, Z.Y.; Bartels, A.; Robertsson, L.; Zucco, M.; Windeler, R.S.; Wilpers, G.; Oates, C.; Hollberg, L.; Diddams, S.A. Optical frequency synthesis and comparison with uncertainty at the 10-19 level. Science 2004, 303, 1843–1845. [Google Scholar] [CrossRef] [PubMed]
- Sheard, B.S.; Gray, M.B.; McClelland, D.E.; Shaddock, D.A. Laser frequency stabilization by locking to a LISA arm. Phys. Lett. A 2003, 320, 9–21. [Google Scholar] [CrossRef]
- McKenzie, K.; Spero, R.E.; Shaddock, D.A. Performance of arm locking in LISA. Phys. Rev. D 2009, 80, 102003. [Google Scholar] [CrossRef]
- Ghosh, S.; Sanjuan, J.; Mueller, G. Arm locking performance with the new LISA design. Class. Quantum Gravity 2022, 39, 115009. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, M.; Wang, T.; Zhao, X.; Ma, L.; Fang, S.; Xin, M. Transient analysis of the arm locking controller. Phys. Rev. D 2024, 109, 042006. [Google Scholar] [CrossRef]
- Yu, Y.; Mitryk, S.; Mueller, G. Arm locking for space-based laser interferometry gravitational wave observatories. Phys. Rev. D 2014, 90, 062005. [Google Scholar] [CrossRef]
- Valliyakalayil, J.T.; Wade, A.; Rabeling, D.; Zhang, J.; Shaddock, D.; McKenzie, K. Experimental demonstration of the combined arm- and cavity-locking system for LISA. Phys. Rev. D 2024, 110, 062004. [Google Scholar] [CrossRef]
- Heinzel, G.; Esteban, J.J.; Barke, S.; Otto, M.; Wang, Y.; Garcia, A.F.; Danzmann, K. Auxiliary functions of the LISA laser link: Ranging, clock noise transfer and data communication. Class. Quantum Gravity 2011, 28, 094008. [Google Scholar] [CrossRef]
- Xu, M.; Tan, Y.; Liang, Y.; Zhi, J.; Guo, X.; Luo, D.; Wang, P.; Wu, H.; Shao, C. Experimental demonstration of sub-100 picometer level signal extraction with time-delay interferometry technique. Results Phys. 2024, 56, 107221. [Google Scholar] [CrossRef]
- Jiang, Q.; Dong, P.; Liu, H.; Luo, Z. Ground-based principle verification of clock noise transfer for the Taiji program. Chin. Opt. 2023, 16, 1394–1403. [Google Scholar] [CrossRef]

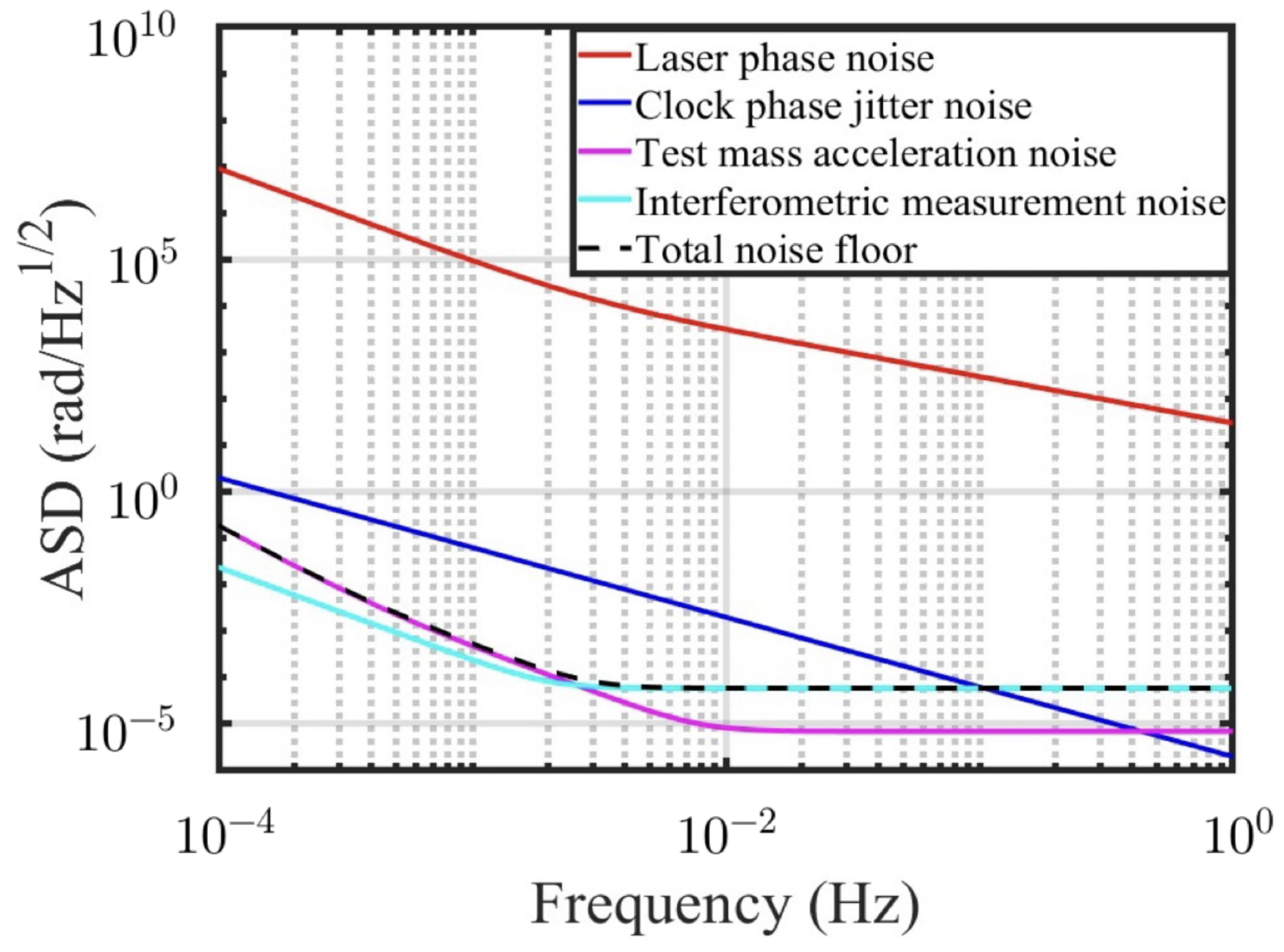
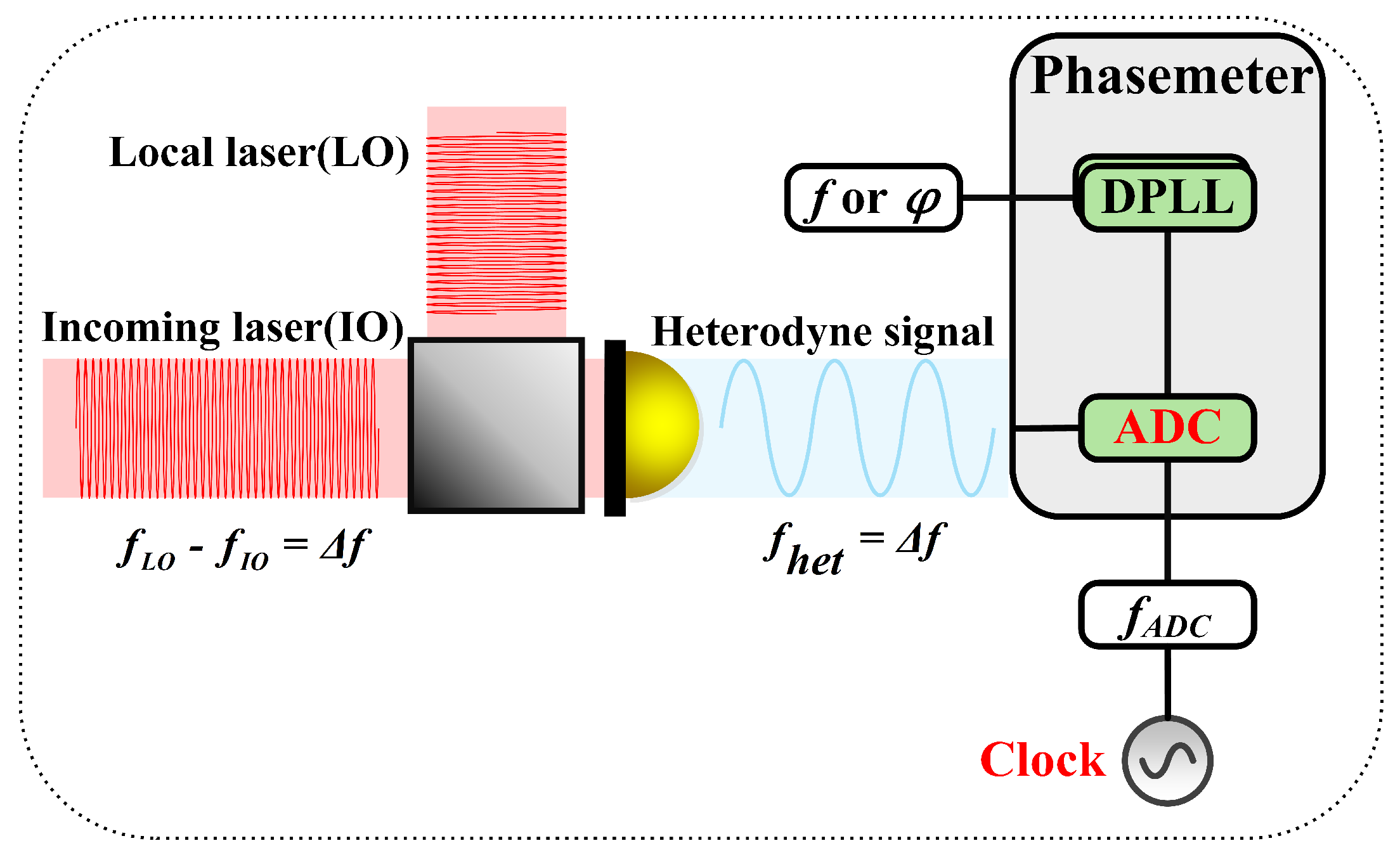
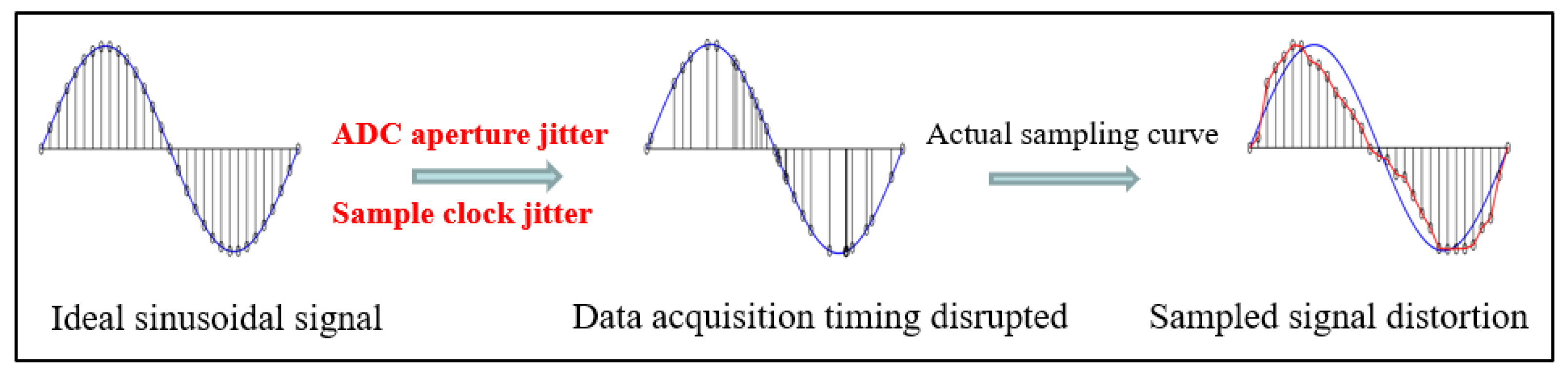
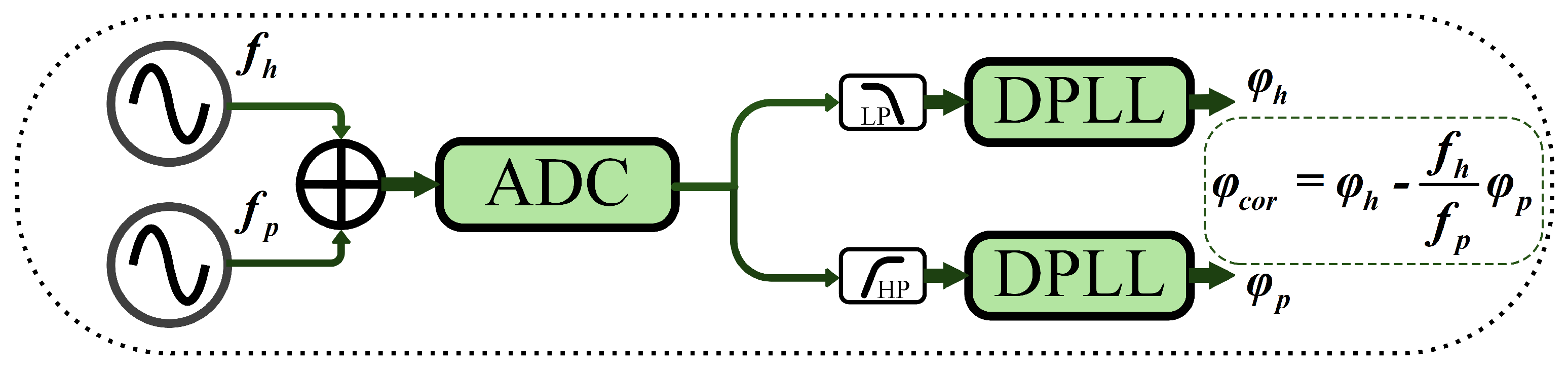
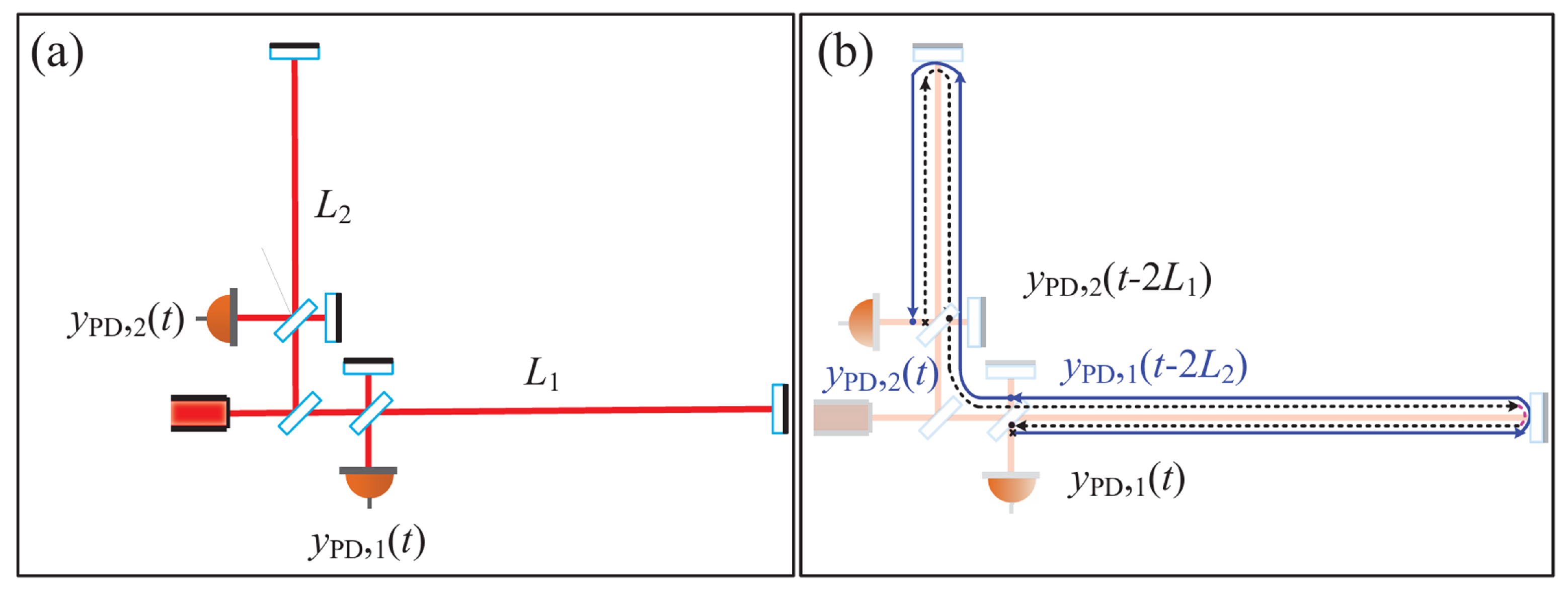

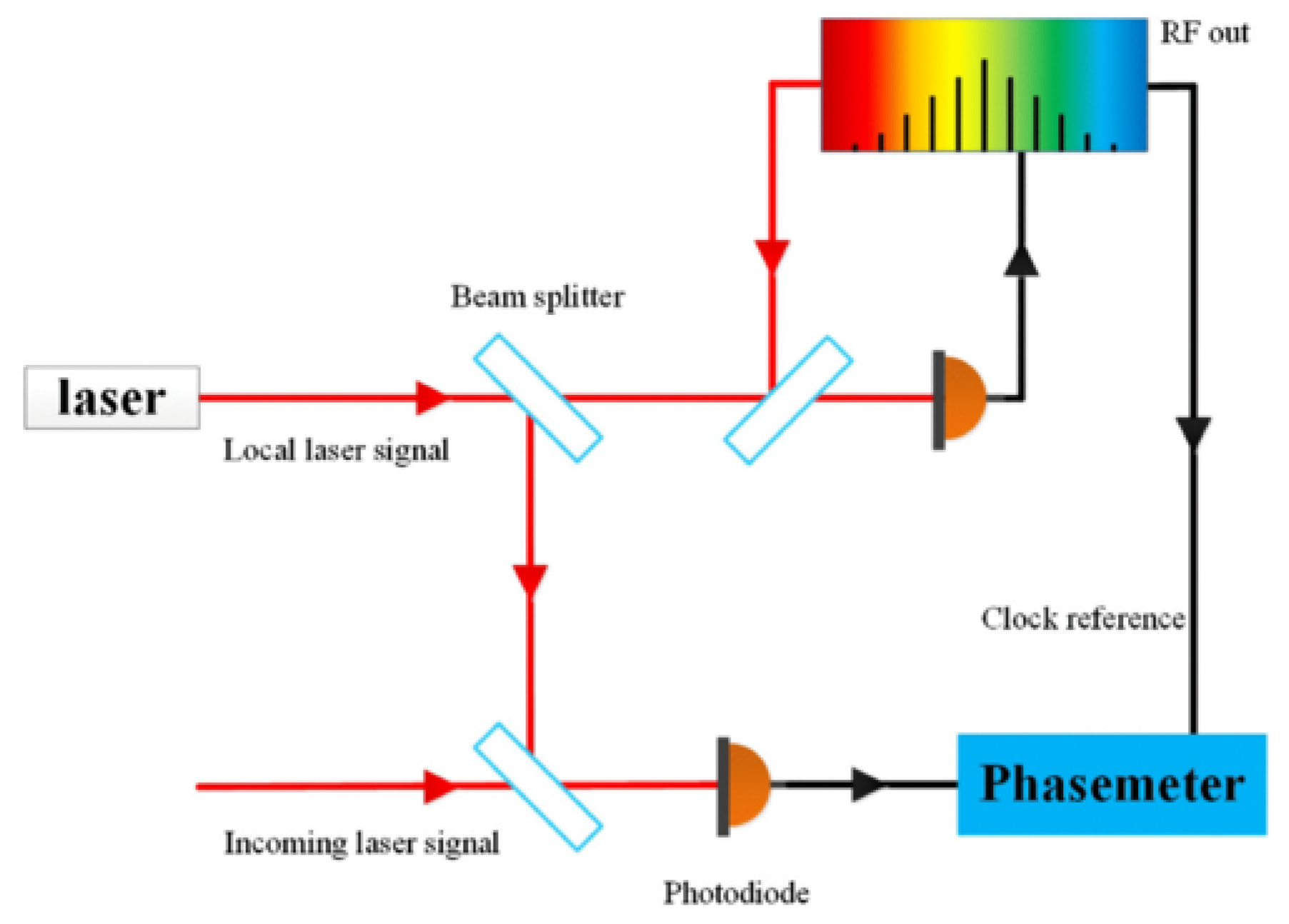
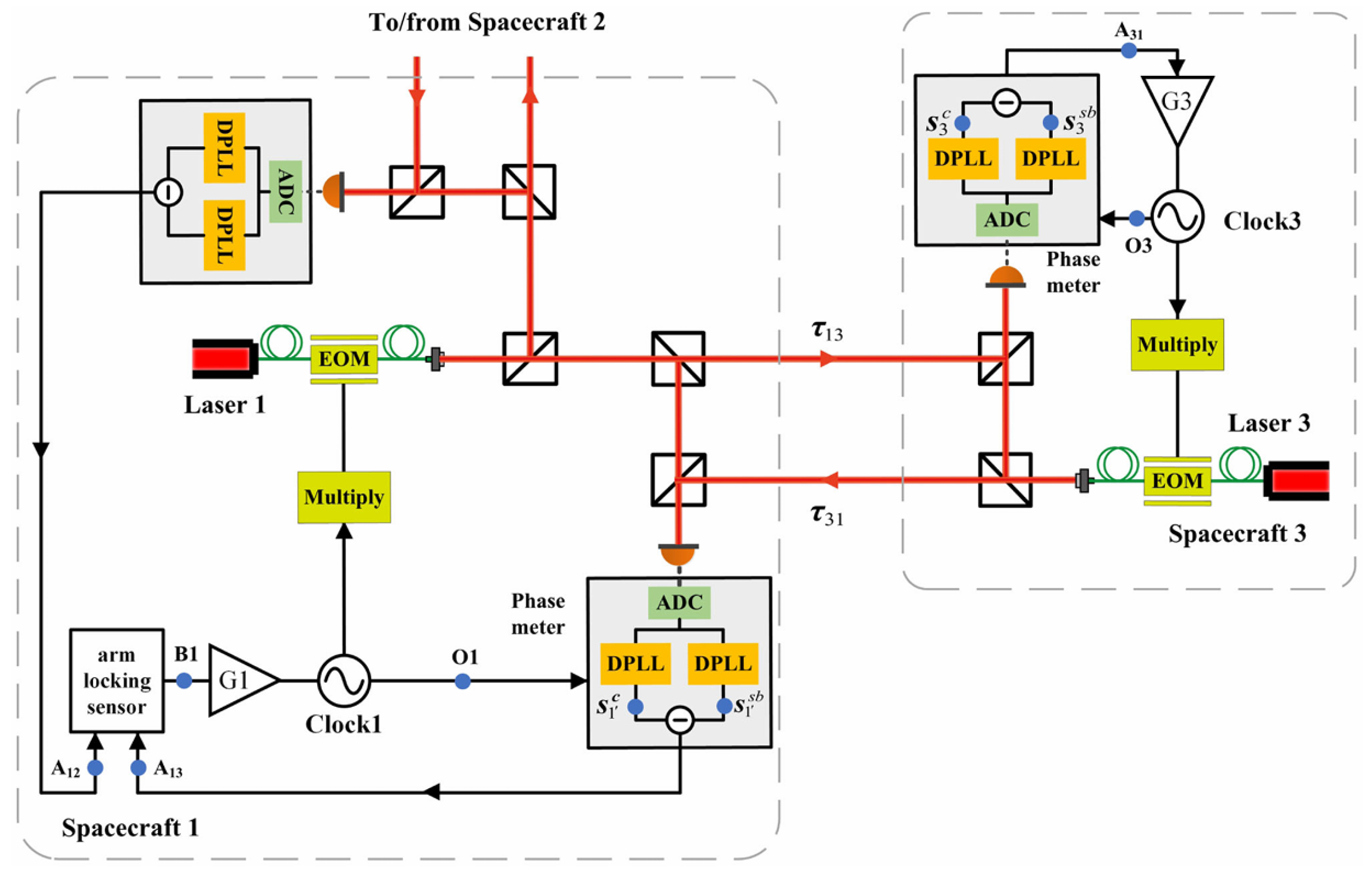
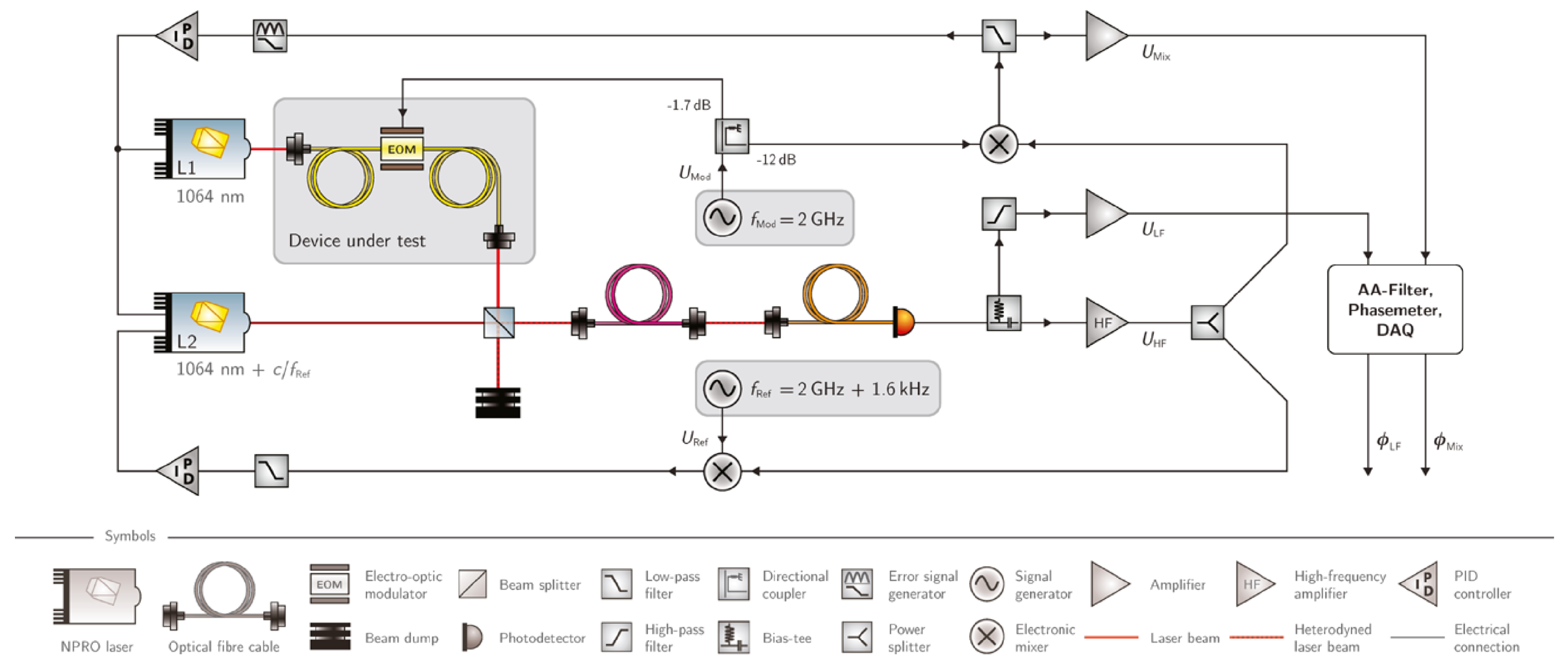
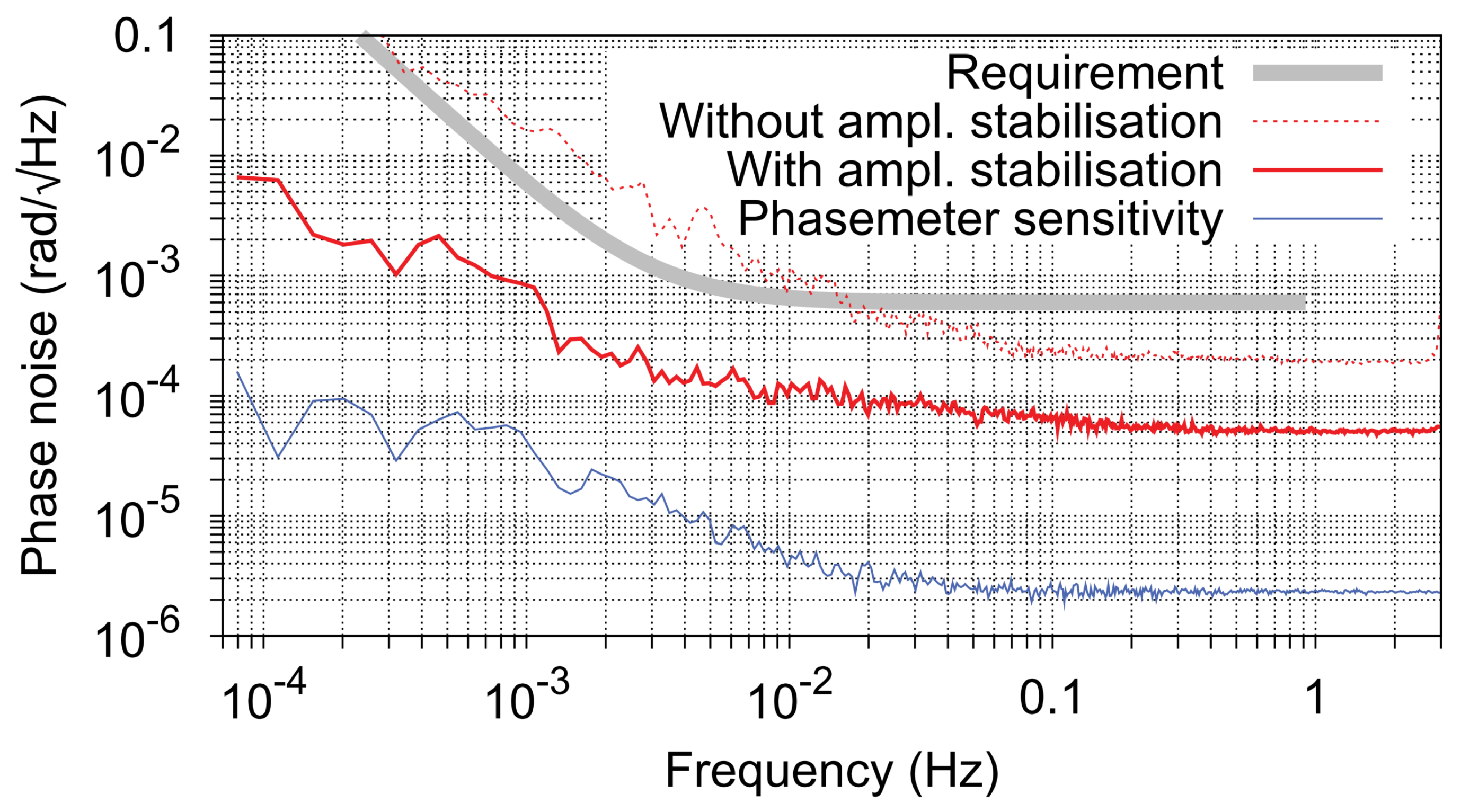
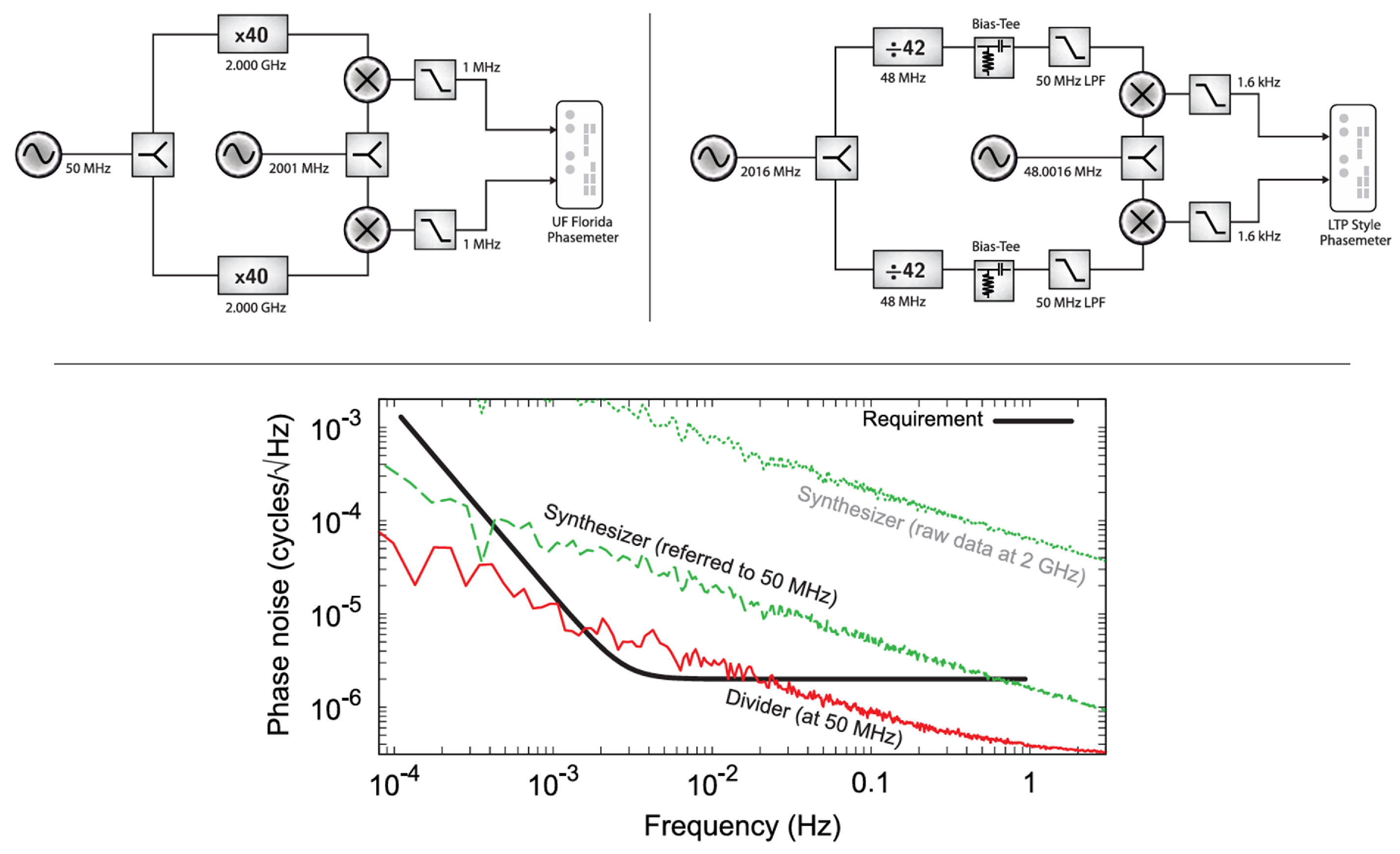
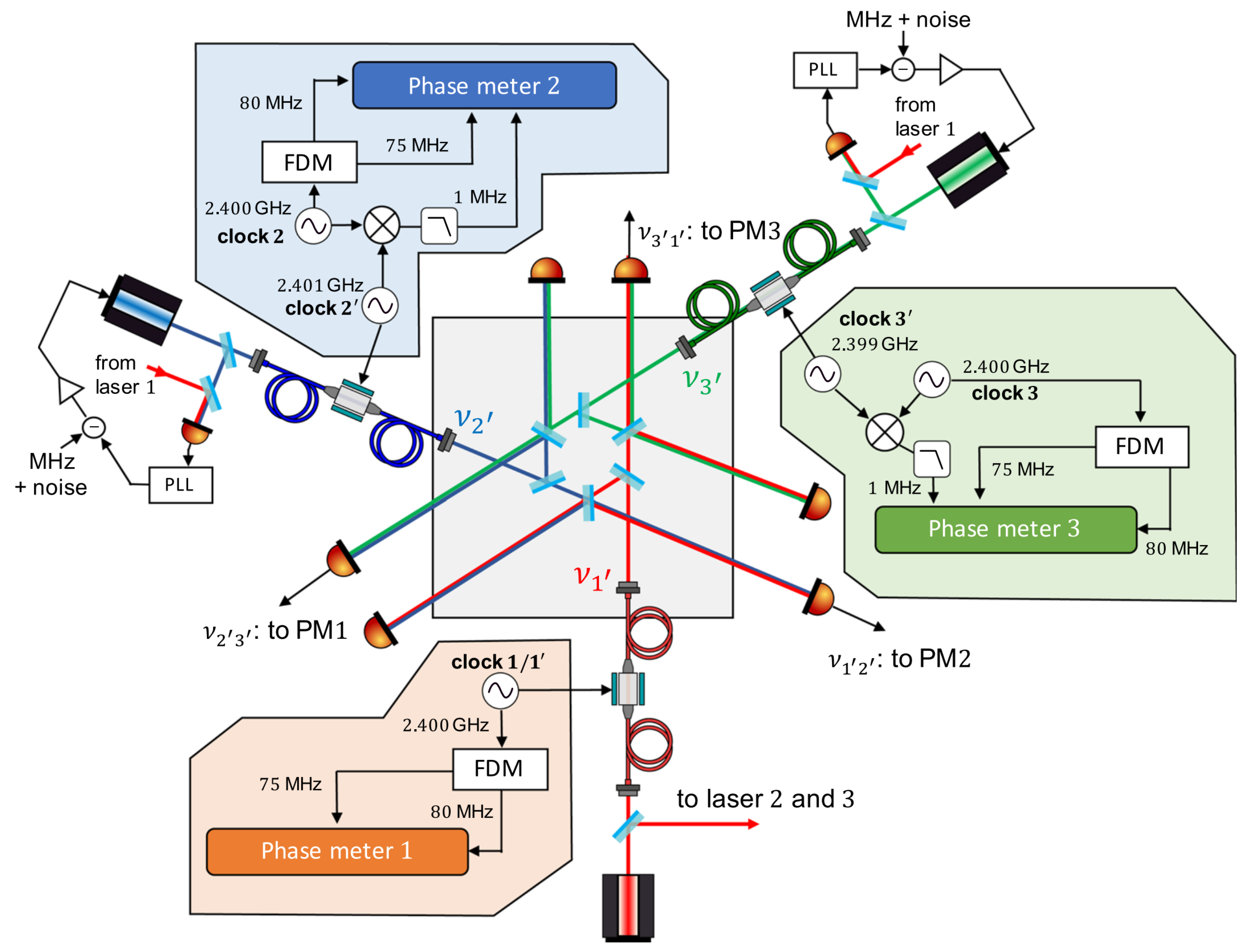
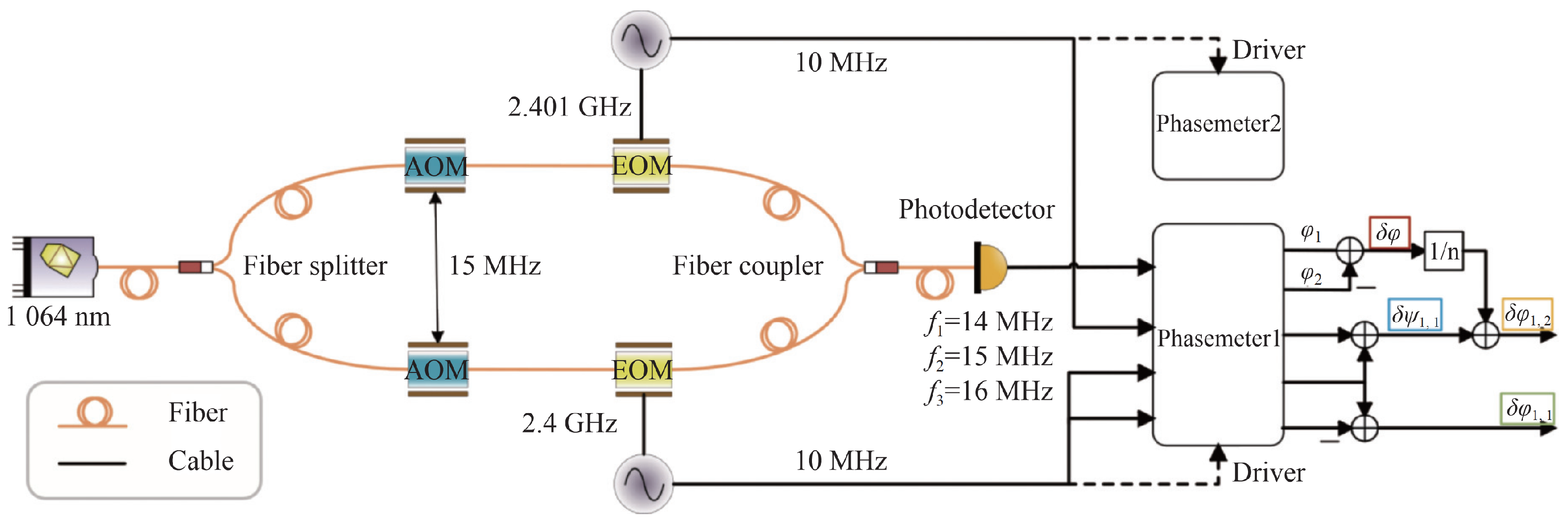


| Parameter | Symbol | Value |
|---|---|---|
| Laser phase noise | ||
| Clock phase jitter noise | ||
| Test mass acceleration noise | ||
| Interferometric measurement noise |
| Year | Team | Technical Point | Level | |
|---|---|---|---|---|
| 2010 | AEI [36] | EOM test | 1 pm@ 2 mHz | |
| 2011 | AEI [72] | frequency divider test | 1 pm@ 3 mHz | |
| 2022 | AEI [32] | synchronous of the clock between three satellites | 1 pm@ 0.1 Hz | |
| a | 2023 | UCAS [74] | clock noise transfer for Taiji | 10 pm@ 0.05 Hz |
| 2023 | SYSU [37] | clock noise transmission under weak-light conditions | 1 pm@ 6 mHz | |
| 2024 | HUST [73] | picometer-level signal extraction | 10 pm@ 1 Hz | |
| b | 2020 | JPL [33] | the repetition frequency as the clock source | 160 pm@ 0.01 Hz |
| 2023 | HUST [34] | optical comb TDI with a transfer oscillator | 30 pm@ 0.1 Hz | |
| c | 2024 | HUST [28] | sideband single-arm locking simulation | 10 pm@ 3 mHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.; Fang, A.; Xu, M.; Tan, Y.; Shao, C. Clock Noise Suppression Techniques in Space-Borne Gravitational Wave Detection: A Review. Symmetry 2025, 17, 1314. https://doi.org/10.3390/sym17081314
Xia Y, Fang A, Xu M, Tan Y, Shao C. Clock Noise Suppression Techniques in Space-Borne Gravitational Wave Detection: A Review. Symmetry. 2025; 17(8):1314. https://doi.org/10.3390/sym17081314
Chicago/Turabian StyleXia, Yijun, Aoting Fang, Mingyang Xu, Yujie Tan, and Chenggang Shao. 2025. "Clock Noise Suppression Techniques in Space-Borne Gravitational Wave Detection: A Review" Symmetry 17, no. 8: 1314. https://doi.org/10.3390/sym17081314
APA StyleXia, Y., Fang, A., Xu, M., Tan, Y., & Shao, C. (2025). Clock Noise Suppression Techniques in Space-Borne Gravitational Wave Detection: A Review. Symmetry, 17(8), 1314. https://doi.org/10.3390/sym17081314






