Abstract
The black-box nature of deep machine learning hinders the extraction of knowledge in science. To address this issue, a proposal for a neural network (k-net) based on the Kolmogorov–Arnold Representation Theorem is presented, pursuing to be an alternative to the traditional Multilayer Perceptron. In its core, the algorithmic nature of neural networks lies in the fundamental symmetry between forward-mode and reverse-mode accumulation techniques, both of which rely on the chain rule of partial derivatives. These methods are essential for computing gradients of functions, an operation that is at the core of the training process of neural networks. Automatic differentiation addresses the need for accurate and efficient calculation of derivative values in scientific computing; procedural programs are thus transformed into the computation of the required derivatives at the same numerical arguments. This work formalizes the algebraic structure of neural network computations by framing the training process within the domain of hyperdual numbers. Specifically, it defines a Kolmogorov–Arnold-inspired neural network (k-net) using dual numbers by extending the univariate functions and their compositions that appear in the representation theorem. This approach focuses on computation of the Jacobian and the ability to implement such procedures algorithmically, without sacrificing accuracy and mathematical rigor, while exploiting the inherent symmetry of the dual number formalism.
1. Introduction
Traditional neural networks have demonstrated remarkable capabilities across various application fields, from image recognition to natural language processing and generation. The main building block of these networks is the Multilayer Perceptron (MLP), grounded on the Universal Approximation Theorem. According to this theorem, MLPs can approximate any continuous function given enough neurons in the hidden layer [1,2]. However, their approximation capabilities rely on the use of nonlinear activation functions to approximate arbitrary continuous functions, which complicates the interpretability of the model [3]. One of the main limitation of MLPs, particularly when deep architectures are used, is the lack of explainability. These models are often regarded as black boxes, due to the difficulty of interpreting the way they make decisions from given inputs [4]. This lack of transparency poses significant challenges in application domains such as medicine, security, and financial decision-making, where the need to understand the process behind a decision may be as important as the prediction itself.
The field of Explainable Artificial Intelligence aims to address this issue by developing methods that enable the interpretation of deep learning models [5]. However, the complexity of their architectures and the nonlinearity of their activation functions represent a challenge for this field. While current approaches, such as activation visualizations, input attribution techniques, and surrogate models provide partial insights, they often rely on heuristics that may not guarantee complete interpretability.
The newly proposed Kolmogorov–Arnold Networks (k-nets), or simply k-nets, based on the Kolmogorov–Arnold Representation Theorem, seeks to address this issue as an alternative to traditional Multilayer Perceptron [3]. Kolmogorov published the proof in 1957 [6], including Arnold’s results [7], to solve the Hilbert’s 13th problem proving whether a solution exists for all 7th-degree equations using continuous functions of two arguments (the variant for algebraic functions is still unresolved). These networks fundamentally employ forward and reverse accumulation techniques based on the chain rule of partial derivatives to compute function gradients, which are fundamental in the optimization process. Automatic differentiation provides accurate and efficient calculations of derivative values, transforming procedural programs into derivative computations at the same numerical arguments [8].
The formal algebraic framework, for addressing rigorously such differentiation problems, lies in the algebraic structure of dual numbers. This work aims to formally define k-nets in terms of dual numbers [9] by extending their function compositions into the dual number domain. This approach focuses on the Jacobian and the implementation of these procedures algorithmically without losing accuracy and mathematical rigor. In this context, networks based on the Kolmogorov–Arnold Representation Theorem have emerged as a promising alternative to enhance the explainability of neural models. This theorem states that any continuous function of multiple variables can be expressed as a combination of univariate functions, allowing for a more interpretable decomposition of the relationship between inputs and outputs. The ability to structure inference in a more explicit manner may provide advantages in terms of interpretability and decision transparency.
This article explores the use of k-nets in the context of dual numbers, examining how this combination can contribute to both computational efficiency and model explainability. Weights on k-nets are represented by univariate functions, typically by spline functions; in terms of parameter optimization, k-nets introduce learnable optimization functions instead of fixed linear weights, which could adapt to different data patterns [10]. Recently, the Kolmogorov–Arnold theorem (KAT) has gained increased attention thanks to the work of [3]. They suggest a performance increase in these networks by introducing learnable univariate functions [3]. From this point, new research efforts in the field had followed [10]. Among neural network architectures, the Multilayer Perceptron (MLP), a fully connected network that extends the original Rosenblatt Perceptron, is the building block of current deep learning architectures [3]. The MLP approximation of nonlinear functions is supported by the Universal Approximation Theorem [2]. However, its use has significant drawbacks, and it is difficult to interpret without the use of post-analysis tools [11].
The Kolmogorov–Arnold Networks, or k-nets, mentioned since 1987 by [12] by introducing the “Kolmogorov’s Mapping Neural Network Existence Theorem” based on the work due to [13], establish that any continuous function can be represented by a neural network with two hidden layers, and are inspired by the Kolmogorov–Arnold Representation Theorem [6]. k-nets resemble an MLP because of a fully connected structure. However, instead of using fixed activation functions on each node, a k-net uses learnable activation functions on edges, replacing weights with learnable single variable functions. Each k-net node adds incoming values without adding any nonlinear function [3].
This paper is therefore organized as follows: the first part introduces Kolmogorov–Arnold Networks (k-nets) defined entirely on the Kolmogorov–Arnold Representation Theorem, as composition of linear combination of simple univariate functions. While the theorem guarantees the existence of such functions, their exact form is not specified and they are often difficult to interpret or apply in practice. Therefore, the first task is to select a suitable set of simple functions that can be used to represent and numerically approximate and implement the desired mappings. Section 2 formally defines k-nets and introduces the use of dual numbers to compute the Jacobian matrix of the network functions that is a fundamental component of the training of k-nets; that is, the method to optimize all parameters that define them. Section 4 is dedicated to an empirical evaluation of the theoretical proposal of the model, with a direct non-optimized implementation. The results are compared with other approaches inspired by the Kolmogorov–Arnold Representation Theorem, specifically the KAN model proposed by Liu et al. [3].
The contributions of this work are (i) to show the theoretical feasibility of building neural networks based on the mentioned representation theorem, and also the feasibility of implementing them, as an alternative to the traditional architecture by replacing the “activation functions” in a more flexible manner, despite current limitations in performance and efficiency that prevent their practical use yet; (ii) to introduce the algebraic expressivity of dual numbers in the training of neural networks, since it has been proven elsewhere to perform well in the calculations of the Jacobian to optimize the loss function; (iii) a practical implementation of the theoretical framework that shows the viability of the new proposal in practical applications; and finally, the possibility of practical use of splines in defining neural networks. Finally, the paper concludes with a discussion and conclusions derived from key findings.
2. Theoretical Framework
The original Kolmogorov–Arnold Representation Theorem states that if f is a multivariate continuous function on a bounded domain, then f can be rewritten as a finite composition of continuous functions of a single variable and the binary operation of addition. Being more specific, for a continuous function , Here, and are continuous real univariate functions. This means that the and the n univariate functions are enough for an exact representation of an n-variate function [14,15]. As every other function can be written using univariate functions and sum, addition becomes the only true multivariate function [3]. Although the Kolmogorov–Arnold Representation Theorem (KAN) does not explicitly specify the form of the functions and , it establishes that they can be approximated through superpositions of a fixed form involving polynomials in a single variable and summation [6]. This property guarantees the existence of such functions and suggests that effective approximations can be constructed using polynomials. Despite the theoretical power of the Kolmogorov–Arnold theorem, its practical application in neural networks has been largely overlooked due to several limitations [10]. One key challenge is that the one-dimensional functions involved in the representation can be highly non-smooth or even fractal, making them difficult to learn in practice [3]. This spurious behavior led to the theorem being regarded as formally grounded but impractical for machine learning applications [16]. Additionally, compared to Multilayer Perceptrons (MLPs), Kolmogorov–Arnold Networks (k-nets) require numerous function superpositions, resulting in significantly higher computational complexity [10]. Early attempts to leverage the theorem for neural network implementations in the late 20th century were constrained by the limited computational power and lack of efficient optimization algorithms at the time. Sprecher’s reformulation [13] proposed an alternative representation of the Kolmogorov–Arnold theorem. He demonstrated that all inner functions could be replaced by translations and scalings of a single function , such that where are constants independent of the function f, and is a small constant. Additionally, Lorentz [17] showed that all outer functions can be replaced by a single function , allowing the full representation to be rewritten as in (1):
Sprecher’s reformulation, in addition to Lorentz’s work, laid the groundwork for the result later presented by Hecht-Nielsen [12], known as the “Kolmogorov Mapping Neural Network Existence Theorem”. It states that any continuous mapping , can be implemented by a neural network structured as follows: , ; , . Here, the real constants and the continuous real monotonic increasing function are independent of f, constant is an arbitrary rational number, . The function can be chosen to satisfy a Lipschitz condition, and the outer functions depend on f and . Each hidden unit is a weighted sum of translated inputs passed through , forming a hidden layer of units. Each output is a sum of shared functional transformations applied to simple univariate compositions, Sprecher introduces a modification to the original on requirements, obtaining a representation that no longer requires the final constant q [18]. This results in the representation in Equation (1), which will serve as the foundation for experimental evaluation of the model. Although Equation (1) is a suitable starting point for defining k-nets, it relies on specific assumptions that, while potentially valid in the long term, may limit the exploration of other alternative ways for choosing inner functions. In fact, Equation (1) is the one implemented in the present study and compared against other proposals in the literature. The formal definition of k-nets is provided in the next section, adopting a more general approach.
2.1. Kolmogorov–Arnold Neural Networks (K-Nets)
All considerations discussed in previous sections are accounted for in the implementation of k-nets. However, to maintain generality, we define k-nets without imposing any specific approximation scheme, thereby preserving the possibility to select the functions ’s and in some other way. For instance, in [15], authors propose an algorithm for constructing the inner functions in a way that preserves the spirit of the original proof of the theorem by Arnold and Kolmogorov. While the authors claim that the original construction is not suitable for algorithmic implementation, they demonstrate that it is possible to define the inner functions to be Lipschitz continuous, a property that is often desirable in the design of neural network activation functions [1] in the context of deep learning algorithms.
The Kolmogorov–Arnold Representation Theorem expresses a function in terms of functions of the form . The idea is to define a neural network based on such representation. Let be a function for every k. In this composition diagram (Figure 1), simply represents the sum over the last index p and q. Index k is being used to allow the composition diagram to obtain a single output . The function corresponds to a neural network with n inputs and one output, two hidden layers, clearly represented by (or one single ) and (or one single times some constants ); this is one of the main differences with other neural networks.

Figure 1.
Composition diagram for a k-net.
Thus, for every k, we have an output vector , then we can define a neural network as follows . The mapping Z is a composition of maps in such a way that domain of must coincide with the codomain of ; some authors in the literature called property model layer structure; this is represented by a vector of integers , where L is the number of layers that define the network. In our case, is the number n, but since the number of layers is changing, it is customary to use indices.
Definition 1.
Let be a continuous function for which exists univariate function , such that , , , then a k-net is a composition mapping , where , and . The coordinates of each are , as defined in the diagram of Figure 1. The model layer structure is the vector of dimensions of the domain of every for each layer.
A neural network would not be complete without its training process. For that, we introduce the concept of dual numbers and how it can be integrated in our formulation of k-nets. The use of dual numbers is not new: it is within the area of artificial intelligence called automatic differentiation (AD), and it has been proven to be a promising technique to solve differential equations [19]. However, the algebraic representation as well as their implementation remains a challenge; firstly, because it is difficult to represent any real function in the dual domain, and secondly, it computationally lies in the realm of meta-programming that it is not always possible to achieve in any language. Dual numbers are used in the implementation of the so-called forward mode of AD [20]. The key idea relies on the fact that dual numbers can encode not only the value of a function but also its derivative, without the need for symbolic manipulation or finite difference approximations. Before introducing dual numbers, let us discuss the need for efficient calculation of gradient of functions, necessary for data training in a network. Data training consists essentially in finding the local or global minimum of a map ; that is, find such that for all . Thus, training a k-net as in Definition 1 means to find a minimum set of parameters, denoted by , which are defined by the functions and from the definition of Z. To do so, we assume some initial experimental dataset ; to fit a neural k-net , where m is well-defined and depends on the number n, which is the number of functions ’s and ’s used in defining Z. Thus, the method of gradient descent to solve the minimization problem , the preferred method to train neural networks, is to update of the following form . Just to clarify the training, consider for example, the mean square method , and therefore, the from which we can infer that training a k-net is translated into the direct calculation of the gradient of Z mapping itself. The above discussion will be elaborated in more detail in the results section, where some other functions are considered for training. Therefore, one of the main purposes of this paper is not only to define a neural network but to introduce the mechanism of calculating the gradient of k-nets by using dual numbers in forward-mode automatic differentiation, since it is required by the method of gradient descent; this is particularly challenging since it has to be repeated thousands of times. Reverse mode cannot be directly implemented using dual numbers, as they do not have a structure that allows backpropagation.
2.2. The Jacobian of Z K-Nets
Let be a differentiable function; thus, when evaluating Z on a dual number , using the Taylor expansion [21]
and the property , we obtain , where denotes the Jacobian matrix of Z; since we are assuming that image of mapping Z has dimension one, it would be more appropriate to write because the second term in Equation (2) is precisely the gradient of Z; in other words, . Let us recall that the third term in Equation (2) is known as the Hessian matrix. This result indicates that the dual component of directly contains the Jacobian or gradient (for dimension one) . Therefore, by overloading arithmetic operations to work with dual numbers, one can propagate derivatives alongside function evaluations in a computational graph, enabling efficient and exact gradient computation [19,20]. The above procedure shows a very intuitive way of looking at dual numbers and its relation to its first derivatives in several variables. However, a k-net Z is multidimensional, thus extending t to a vector; the Taylor expansion in Equation (2) contains also terms of second degree and above, and the simple substitution will be a first-degree approximation only. To consider terms of more degrees or derivatives of higher degree, for example, second degree in Equation (2), we must define hyperdual numbers as an algebra of polynomials [8].
Definition 2.
Let , be and consider the algebra , where is the ideal generated by all monomials of order . Then,
is the algebra of dual numbers (3). The degree of a monomial of type is defined as , denoted by deg.
In order to use Definition 2, it is assumed that the mappings Z are polynomials; this appears to be rather restrictive, however, as we show in the results. It is the way that this new proposal of neural network may result in a practical alternative. In the next section, it is shown that a practical k-net can be accomplished by assuming that , where and are splines of some degree. To lift to dual numbers, we must calculate ; this can always be achieved using Definition 2 and Equation (2). Now, since are splines and therefore polynomials, we can assume that is a polynomial in . From the above discussion, we can establish a proposition. The proof is incomplete; considering the purpose and the length of the paper, we sketch the proof using an example to show why the proposition is true. To sketch the proof, we make use of one of the parabolic singularities studied by Arnold [22], which is . The idea of the proof is to show that in the ring ; in other words, the coefficients of —the remainder of —for some N, are precisely the partial derivatives of .
Proposition 1.
If , then is the truncated polynomial of the Taylor series expansion of , Equation (2), up to N terms. In other words, . In particular, if , then becomes
Proof.
The proof of Proposition 1 should be straightforward from Definition 2 and Equation (2). Nevertheless, let us assume that we are interested in evaluating the following expression in the ring of dual numbers. The polynomial is taken from [22], but any polynomial should work just fine. By using as a shorthand for , we know, from direct calculation of Z, that Jacobian and the Hessian are given by (5)
After expanding quadratic and cubic polynomials, and grouping terms in ascending order by total degree (), we have that . By making , homogeneous polynomial of degree 3, we see that the homogeneous polynomial of degree 1 is , whereas the homogeneous polynomials of degree 1 and 2 correspond to ], , respectively; then, can be rewritten as
The coefficient of the third term in variable corresponds to first entry in , the coefficient of the fourth and fifth term correspond to second () and third () entry in matrix , respectively, and this will be true for any polynomial in any number of variables. Analogously, the coefficients of monomials of degree 2 in Equation (6) for Z correspond to every entry in the Hessian matrix for i, j; the residual homogeneous polynomial on variables contain monomials of total degree greater than 2; that is, with is either 3 or greater in general. From Definition 2, the ideal is the set of all monomials . Since the goal is to look at Z in the domain of hyperdual numbers, we must consider Z module the ideal ; that is, Z in the quotient corresponds to . This is true because (the remainder) is equivalent to making as long as , which is the case for all monomial of ; therefore, . By comparing (4) and Taylor expansion of Z around , we see that the coefficients of Z as polynomial on variables correspond precisely to the derivatives of the mapping Z; thus, the dual part of a polynomial function always carries the derivative of the function. □
In contrast to the more traditional numerical methods based on finite differences that are inherently prone to rounding or truncation errors, auto-differentiation is theoretically exact, and computationally inexpensive, compared to symbolic algorithms, making use of the fact that all computer calculations are executed as a series of elementary arithmetic operations and elementary functions to compute derivatives of arbitrary order by applying the chain rule.
2.3. A Practical K-Net
Based on the foundational work of Kolmogorov, Sprecher, Hecht-Nielsen, and Lorentz, a neural network architecture that explicitly reflects the structure of the representation theorem is proposed, where each layer of the network follows Definition 1 and the Hecht-Nielsen model. With a more flexible combination of the coefficients and selecting a function with enough internal variability, it is possible to simplify giving the following approximation (7):
Sprecher [18] also makes reference to the work of Kúrková, where functions and , are approximated with sums of sigmoidal functions. Following Liu’s [3] proposal for the functions, grade 3 B-splines with learnable coefficients are used, and ReLU activation with learnable parameters is used for the functions. An inner layer (8), based on units, which computes for each unit :
where is a cubic B-spline with learnable coefficients specific to the pair , and are trainable parameters. The inner layer is implemented as InnerLayer, as shown in Figure 2. An outer layer (9) that maps the inner functions to the output for :
where each is a trainable scalar weight, and is a fixed univariate nonlinear activation function such as ReLU or sigmoid. These weights determine the contribution of each transformed inner unit to the output . The outer layer module is shown in Figure 2, labeled as OuterLayer.
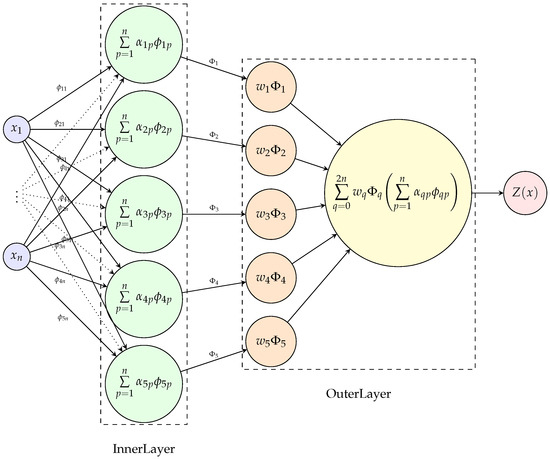
Figure 2.
Kolmogorov–Arnold representation implemented as a combination of inner and outer layers.
These two layers are grouped into a composite module called FullLayer, which realizes a full Kolmogorov–Arnold representation, yielding a single scalar output. When multiple outputs are needed, multiple instances of FullLayer are used in parallel, each receiving the same input vector . Figure 2 shows the organization of a full layer. For a single layer k-net, is the output of the model. Model layer structure is represented by an integer array , where is the number of inputs to the model, is the output dimension, and each layer is defined by , where is the number of inputs to the layer l, and is the number of outputs. The layer then will have blocks, each one combining an inner layer followed by an outer layer, realizing a Kolmogorov–Arnold representation. Making the network deeper is achieved by stacking several layers with the FullLayer module where the input of each subsequent layer is taken from the output of the previous one. This hierarchical composition helps to preserve the constructive approximation capabilities of the architecture.
3. Methods
To validate the proposed framework, the steps as shown below are followed:
- Define k-nets in the dual number and automatic differentiation framework.
- Extend function compositions to dual numbers, ensuring mathematical consistency.
- Implement gradient-based optimization using dual numbers to enhance computational efficiency.
- Compare performance and interpretability against Liu’s Kolmogorov–Arnold-inspired proposal KAN [3].
The key variables of study include model accuracy (evaluating predictive performance), gradient computation efficiency (measuring computational cost in training), and interpretability (assessing the transparency of the learned representation). The other technical consideration for the implementation is the fact that Bernstein polynomials can be evaluated over dual numbers. Samanci [23] introduced a formulation of Bernstein polynomials defined over the ring of dual numbers , enabling the simultaneous evaluation of a function and its derivative via forward-mode automatic differentiation. Note that from Definition 2, the ideal , which corresponds to polynomials of type Equation (2) modulus the ideal . The dual Bernstein basis functions are defined as , which expands to where is the classical Bernstein basis and its derivative. This formulation allows for differentiability-aware modeling using Bernstein polynomials, and serves as a foundation for our generalization of B-spline basis functions to dual inputs. Following the extension of Bernstein polynomials to dual variables as presented by Samanci [23], it is possible to generalize B-spline basis functions to operate over the ring of dual numbers . This extension enables forward-mode automatic differentiation by evaluating both the value and the derivative of a B-spline function in a single computation. Let us recall that a B-spline of degree k is defined recursively applying (10) and (11):
where is a non-decreasing knot sequence; to extend B-splines to dual inputs, let . Since each recursive step involves affine transformations and multiplication operations that are well-defined in , the recurrence relation naturally extends to the dual setting. Thus, the dual B-spline basis provides both the function value and its derivative with respect to x at a. This extension preserves the locality, partition of unity, and continuity properties of the B-spline basis, while enriching it with derivative information, making it suitable for applications in automatic differentiation and learning architectures involving differentiable programming. Since Bernstein polynomials are a special case of B-splines with fixed degree and uniform knot vector on , Samanci’s construction can be viewed as the zero-degree instance of this more general dual B-spline framework.
3.1. Training Procedure
In this implementation, the internal univariate functions of InnerLayer (Figure 2) are represented using cubic B-splines, as proposed by Liu [3]. These functions are defined by a fixed set of knots and allow flexible approximation of continuous transformations on each input coordinate. Each is represented as a linear combination of six basis B-splines (corresponding to the number of internal basis functions for degree 3 and 10 knots). For the external layer OuterLayer, each function is implemented using a nonlinear activation function, such as ReLU, sigmoid or the identity. These functions are applied after the summation over the internal spline-transformed inputs and provide the necessary nonlinearity for function approximation. To enable gradient-based training, a forward-mode automatic differentiation strategy based on dual numbers was implemented, considering the work of [23]. Each scalar or tensor value in the network is extended to a dual number of the form , where . This allows the network to compute derivatives of the loss with respect to each model parameter directly by evaluating the dual component of the forward pass. This formulation preserves the interpretable structure of the Kolmogorov–Arnold representation by explicitly modeling each intermediate transformation as a sum of univariate functions. The inner functions are applied independently to each input variable, and the summation across p introduces controlled linear mixing. The outer layer aggregates the resulting activations via nonlinear univariate mappings, enabling a flexible yet interpretable composition. The training of the Kolmogorov–Arnold Network exploits the modularity and interpretability of its architecture. Let be a dataset of N input-output pairs, where and . Each forward pass computes the hidden activations and output predictions using the defined inner and outer layers. The prediction loss is quantified using a loss function , typically cross-entropy (12) for classification or mean squared error (MSE) (13) for regression:
- Cross-entropy. Measures the difference between two probability distributions; normally, the true labels on the dataset and the predicted value produced by the classifier.
- Mean Squared Error. On regression, measures the average squared difference between the predicted value and the actual target.
For each training epoch:
- (1)
- Compute for each input via the model.
- (2)
- Use dual numbers to compute the forward-mode derivatives of regarding all learnable parameters (B-spline coefficients and weights .
- (3)
- Update parameters using gradient descent as in (14):where is the learning rate.
This training procedure is implemented in Python 3 using custom modules for dual number arithmetic, spline evaluation, and layer composition. Metrics such as loss and accuracy for both training and test datasets are recorded and visualized per epoch to monitor convergence.
3.2. Computational Complexity of the K-Net Model
The computational cost of training a Kolmogorov–Arnold Network (k-net) model using forward-mode automatic differentiation grows significantly with the architecture size. Each weight update requires a full forward pass with dual numbers, which makes the number of training steps a critical factor. The operation count can be estimated as follows: for each FullLayer in the network, the number of dual evaluations required depends on P—the number of inputs to the layer, Q—the number of outputs (i.e., number of full KA blocks), K—the number of B-spline coefficients per univariate basis function (i.e., number of basis functions, which depends on the knot vector length as , where m is the number of knots and d is the spline degree), and B—the number of training samples in the batch. Each internal function contributes operations, and each output function contributes operations. Therefore, the total number of dual forward evaluations per layer is, according to (15),
For a full network with L layers defined by dimensions , the total number of operations per epoch is
4. Results and Discussion
To evaluate the performance of the k-net architecture, experiments were conducted on regression and classification tasks. Regression was tested training two different models on the Diabetes dataset, and for classification, two distinct models were trained on the Iris dataset. Table 1 presents the model configurations used for the experiments, including model name and estimated operation counts per epoch for each configuration. Total number of operations is directly related with the dimensions of the input, and is based on Equation (16). As explained in Section 3.1, grade 3 B-splines were used (), with ten knots (), resulting in six B-spline coefficients (i.e., ), as explained in Section 3.2, and full-batch training.

Table 1.
Number of dual forward evaluations per epoch for each k-net model configuration.
For regression tasks, the mean squared error (MSE), as defined in Equation (13), is used as the loss function. To report a more interpretable performance metric, the root mean squared error (RMSE) in Equation (17) is used. RMSE is calculated as the square root of the MSE:
This value reflects the average magnitude of prediction error in the original target scale, and is particularly useful for comparing models across datasets or tasks.
For classification tasks, the softmax function shown in Equation (18) is applied to the model output vector (where m is the output dimension) to obtain class probabilities:
The loss function used is the categorical cross-entropy, defined for one-hot encoded ground truth as defined in Equation (12). To evaluate classification performance, we use accuracy as in Equation (19), computed as the proportion of correct predictions:
where is the indicator function.
4.1. Regressions
The Diabetes dataset consists of 442 samples with 10 input features and a single continuous target. Two model configurations were tested: A single-layer k-net with architecture , whose performance is shown in Figure 3, and a two-layer k-net with architecture , the performance of which can be observed in Figure 4. Loss for the first architecture is shown in Figure 3a and the mean squared error (RMSE) over epochs for this single layer k-net, equivalent to the KAT can be seen in Figure 3b. As can be observed, the model learns over epochs, loss decreases up to 0.960 as well as the training RMSE, and RMSE over the test set goes down up to 0.918. For the second configuration—a two layer k-net— Figure 4a shows loss and Figure 4b illustrates RMSE. Notice the increase in the loss and RMSE around epoch number 40. This model requires twice the number of evaluations compared to the single layer, as shown in Table 1, requiring almost four times more training time, and its results are less satisfactory, indicating that a deeper k-net does not necessarily imply better generalization.
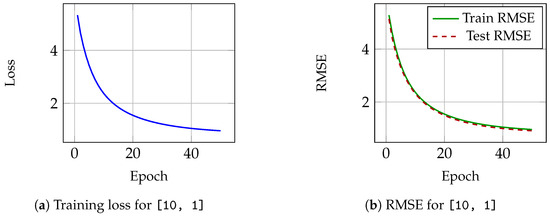
Figure 3.
Performance on the Diabetes dataset using k-net model with architecture [10, 1].
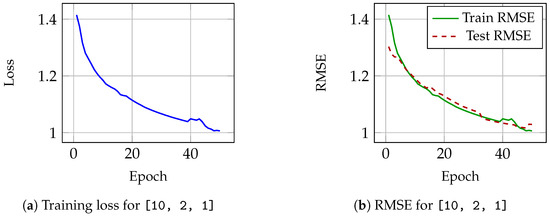
Figure 4.
Performance on the Diabetes dataset using k-net model with architecture [10, 2, 1].
The configuration used was [10, 2, 1]. Performance of KAN model is shown in Figure 5. Loss can be observed in Figure 5a; although variations of the loss during training can be observed, it is reduced consistently, and RMSE for training and test is shown in Figure 5b, behavior of the RMSE is consistent with loss.
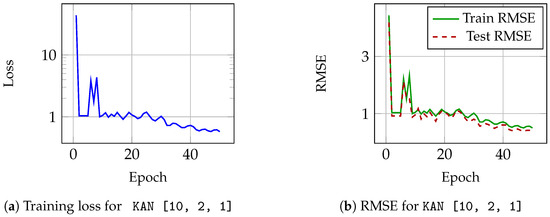
Figure 5.
Performance on the Diabetes dataset using KAN model with architecture [10, 2, 1].
For the regression task, in Figure 6, loss and error of the models are compared. Figure 6a presents the evolution of the loss for the three models evaluated on the Diabetes dataset. KAN achieves a lower loss compared to both k-net-1r and k-net-2r. Both k-net configurations exhibit an almost similar final loss. Logarithmic scale is used for better visualization. Figure 6b shows the training RMSE. Notice that KAN model is slightly better than both k-net models, with a final RMSE of 0.759. Training RMSE for the k-net models is around 1. For test RMSE, Figure 6c compares test RMSE. Here, the first k-net model has a slightly better performance than the second. The KAN model performs better than both k-net models.
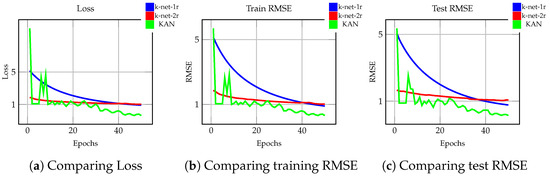
Figure 6.
Evolution of loss and RMSE for the k-net and KAN models on regression.
Table 2 summarizes results including loss, training, and testing RMSE. Training time is displayed in the last column of the table. As can be observed, both k-net models have an almost similar performance while KAN model loss is almost half of k-net and its test RMSE is 77% of the lowest k-net error, indicating a better approximation.

Table 2.
Performance comparison of k-net and KAN models on the Diabetes dataset.
4.2. Classification
The Iris dataset includes 150 samples, each with 4 input features and a categorical label for one of three classes. Two k-net architectures were tested: a two-layer k-net with shape , whose results are shown in Figure 7, and a three-layer k-net with displayed in Figure 8. Cross-entropy loss and classification accuracy are shown below for each case. For the first architecture, Figure 7a shows decreasing loss across the 50 epochs. Training and test accuracy can be observed in Figure 7b, where a lot of variation and a few plateaus occur as accuracy improves.
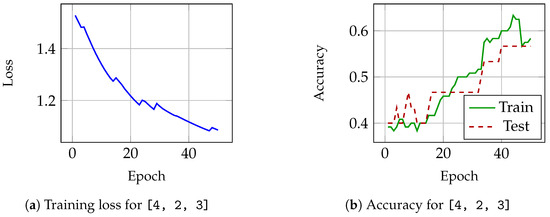
Figure 7.
Performance on the Iris dataset using k-net model with architecture [4, 2, 3].
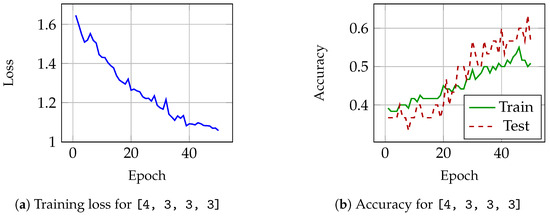
Figure 8.
Performance on the Iris dataset using k-net model with architecture [4, 3, 3, 3].
In Figure 8, results of the second k-net architecture are shown. During the 50 epochs in Figure 8a, loss is reduced with higher variation than the first model, as shown in Figure 7a. In Figure 8b, accuracy for the test set improves more than training accuracy.
The model used was [4, 3, 3, 3]. Figure 9 shows the performance of this model. For this case, Figure 9a shows that loss during training increases, and Figure 9b shows that accuracy is not improved.
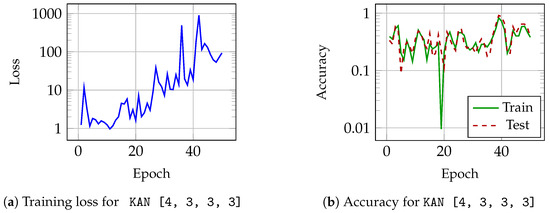
Figure 9.
Performance on the Iris dataset using KAN model with architecture [4, 3, 3, 3].
In Figure 10, evolution of loss and accuracy for the three models used on classification is presented. Figure 10a compares the change in loss during training on the Iris dataset. Both k-net models achieve a similar loss (note that k-net-2c plot overlaps k-net-1c in the graph). Interestingly, KAN loss increases over epochs. Figure 10b shows the training accuracy. k-net-1c achieves better training accuracy than k-net-2c despite having a simpler architecture, suggesting that the additional layer in k-net-2c may not contribute effectively to learning on this dataset. The KAN model exhibits high variation, with an accuracy lower than both k-net models. Figure 10c compares the test accuracy of the models. Although k-net-2c exhibits some variability across epochs, its final accuracy is similar to that of k-net-1c. KAN presents very high variability. These results indicate that, for this classification task, increasing the architectural complexity of k-net does not yield improved performance.
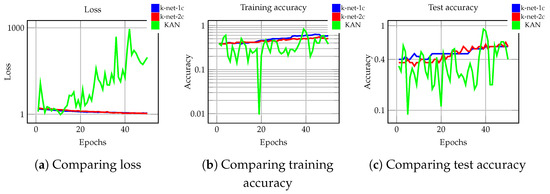
Figure 10.
Evolution of loss and accuracy for the k-net and KAN models on classification.
The performance comparison of k-net and KAN models on the Iris dataset is displayed in Table 3, which summarizes results, including loss, training, and testing accuracy. Training time is observed in the last column.

Table 3.
Performance comparison of k-net and KAN models on Iris dataset.
The comparative evaluation of Kolmogorov–Arnold Networks (k-nets) and KAN model across classification (Iris) and regression (Diabetes) tasks reveals consistent performance on both k-net models. Notably, adding depth to the k-net architecture—such as moving from a two-layer (k-net-1c) to a three-layer (k-net-2c) modeling—does not yield performance improvements, suggesting diminishing returns from increased architectural complexity under the current training setup. In regression tasks, both k-net variants and KAN achieved very similar results. Moreover, the deeper k-net model underperformed relative to the simpler one, indicating that increased depth may introduce over-parametrization or training instability when the internal transformations are constrained to a fixed functional form (e.g., B-splines). These observations highlight several limitations in the current implementation of k-net, which is based on the classical Hecht-Nielsen interpretation of the Kolmogorov–Arnold theorem. While theoretically elegant, the structured decomposition employed in k-net may impose rigidity that restricts the expressiveness or learning dynamics of the model when optimized via standard gradient descent. The performance plateau observed in deeper k-net models may also reflect suboptimal gradient flow, potentially exacerbated by the sequential structure of the spline-based inner representations. Despite these limitations, the k-net framework offers a unique architectural bias grounded in formal functional decomposition. This may be advantageous for interpretability, as the intermediate transformations are explicitly defined and independently accessible. However, such transparency appears to come at a cost in terms of representational flexibility and optimization efficiency when compared to conventional deep learning architectures.
5. Conclusions
This paper presents a mathematically grounded definition of Kolmogorov–Arnold Networks (k-nets), formulated as a neural architecture inspired by the representation theorem of Kolmogorov and Arnold. The proposed definition exploits the linearity of the representation and is independent of the specific class of univariate functions satisfying certain Lipschitz conditions employed, offering a flexible and generalizable foundation for network construction. The principal contribution of this study is twofold: (i) the formalization of k-nets as a class of neural networks derived directly from the mapping of several variable functions in terms of simpler functions of one variable, and (ii) the exploration of forward-mode automatic differentiation using dual numbers as a viable training mechanism within this framework. In addition to establishing the theoretical foundation, this study presents a practical implementation of k-nets using cubic B-splines as internal univariate functions, ReLU as external function, and evaluates their learning performance on standard classification and regression tasks.
The results show that, although k-nets are capable of learning and exhibit convergence during training, their predictive accuracy, convergence speed, and generalization performance consistently fall short when compared to standard Multilayer Perceptrons (MLPs). Furthermore, increasing the depth of k-nets did not improve the outcome, and in some cases, led to diminished performance. Despite these limitations, the structured nature of k-nets offers a valuable degree of interpretability: each internal transformation corresponds to an explicitly defined univariate function, which can be independently analyzed. This property opens new possibilities for incorporating alternative univariate function representations—beyond traditional sigmoidal activations—thereby expanding the design space of explainable neural models. Moreover, the use of dual numbers for gradient computation highlights an alternative to classical backpropagation techniques, and may be of particular interest in domains such as differential equation solving, as an alternative to traditional methods such as finite-differences.
This study also serves as a practical validation of the k-net framework, keeping its definition as close as possible to the original theorem, showing that such models are not merely theoretical constructs, but can be trained and compared to existing architectures. While their performance under standard training regimes may not yet match modern neural architectures, k-nets provide a promising direction for structured and interpretable learning frameworks, where each transformation can be analyzed independently. Future research may explore enhanced initialization schemes, dynamic adaptation of internal functions, alternative representation of the internal functions, different optimization strategies, and hybrid architectures that preserve interpretability while improving empirical performance. Ultimately, addressing the trade-off between mathematical structure and expressive power remains a central challenge in the development of this model class.
Author Contributions
Conceptualization, J.R.M.-R. and J.A.H.-S.; Software, A.S.-W.; Formal analysis, J.A.H.-S.; Investigation, A.S.-W.; Writing—original draft, A.S.-W.; Writing—review and editing, J.R.M.-R. and J.A.H.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been partially supported by the Mexican National Council of Science, Technology and Humanities (CONAHCyT) through its scholarship program for students to obtain a MSc or PhD degree, scholarship number 66c4d44c0834050f707a8789; as well as the division of National System of Researchers (SNI) that provides support for many researchers accross the country.
Data Availability Statement
The programs developed to implement the model—including the tested examples reported in this article and the result tables used—are available at http://github.com/aswinkler/k-net, accessed on 3 August 2025.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Petersen, P.; Zech, J. Mathematical Theory of Deep Learning. arXiv 2024, arXiv:2407.18384. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer Feedforward Networks Are Universal Approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. KAN: Kolmogorov-Arnold Networks. arXiv 2025, arXiv:2404.19756. [Google Scholar] [CrossRef]
- Tsimenidis, S. Limitations of Deep Neural Networks: A Discussion of G. Marcus’ Critical Appraisal of Deep Learning. arXiv 2020, arXiv:2012.15754. [Google Scholar]
- Zhao, H.; Chen, H.; Yang, F.; Liu, N.; Deng, H.; Cai, H.; Wang, S.; Yin, D.; Du, M. Explainability for Large Language Models: A Survey. arXiv 2023, arXiv:2309.01029. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. On the Representation of Contuous Functions of Several Variables as Superposition of Continuous Functions of a Smaller Number of Variables. Dokl. Akad. Nauk USR 1956, 5, 953–956. [Google Scholar]
- Arnol’d, V. On Functions of Three Variables. Dokl. Akad. Nauk USR 1957, 4, 679–681. [Google Scholar]
- Hoffmann, P.H.W. A Hitchhiker’s Guide to Automatic Differentiation. Numer. Algorithms 2016, 72, 775–811. [Google Scholar] [CrossRef]
- Kandasamy, W.B.V.; Smarandache, F. Dual Numbers; Zip Publishing: Las Vegas, NV, USA, 2012. [Google Scholar]
- Ji, T.; Hou, Y.; Zhang, D. A Comprehensive Survey on Kolmogorov Arnold Networks (KAN). arXiv 2025, arXiv:2407.11075. [Google Scholar] [CrossRef]
- Cunningham, H.; Ewart, A.; Riggs, L.; Huben, R.; Sharkey, L. Sparse Autoencoders Find Highly Interpretable Features in Language Models. arXiv 2023, arXiv:2309.08600. [Google Scholar] [CrossRef]
- Nielsen, R.H. Kolmogorov’s Mapping Neural Network Existence Theorem. In Proceedings of the IEEE First International Conference on Neural Networks, San Diego, CA, USA, 21–24 June 1987; IEEE: Piscataway, NJ, USA, 1987; Volume III, pp. 11–13. [Google Scholar]
- Sprecher, D.A. On the Structure of Continuous Functions of Several Variables. Trans. Am. Math. Soc. 1965, 115, 340–355. [Google Scholar] [CrossRef]
- Schmidt-Hieber, J. The Kolmogorov–Arnold Representation Theorem Revisited. Neural Netw. 2021, 137, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Actor, J.; Knepley, M.G. An Algorithm for Computing Lipschitz Inner Functions in Kolmogorov’s Superposition Theorem. arXiv 2017, arXiv:1712.08286. [Google Scholar] [CrossRef]
- Poggio, T.; Banburski, A.; Liao, Q. Theoretical Issues in Deep Networks: Approximation, Optimization and Generalization. arXiv 2019, arXiv:1908.09375. [Google Scholar] [CrossRef]
- Lorentz, G.G. Metric Entropy, Widths, and Superpositions of Functions. Am. Math. Mon. 1962, 69, 469–485. [Google Scholar] [CrossRef]
- Sprecher, D.A. A Numerical Implementation of Kolmogorov’s Superpositions. Neural Netw. 1996, 9, 765–772. [Google Scholar] [CrossRef] [PubMed]
- Vigliotti, A.; Auricchio, F. Automatic Differentiation for Solid Mechanics. Arch. Comput. Methods Eng. 2020, 28, 875–895. [Google Scholar] [CrossRef]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic Differentiation in Machine Learning: A Survey. arXiv 2018, arXiv:1502.05767. [Google Scholar] [CrossRef]
- Bustamante, J. Bernstein Operators and Their Properties; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Arnold, V.I. Local Normal Forms of Functions. Invent. Math. 1976, 35, 87–109. [Google Scholar] [CrossRef]
- Samanci, H.K. Generalized Dual-Variable Bernstein Polyniomials. Konuralp J. Math. 2017, 5, 56–67. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).