Exploiting Semantic-Visual Symmetry for Goal-Oriented Zero-Shot Recognition
Abstract
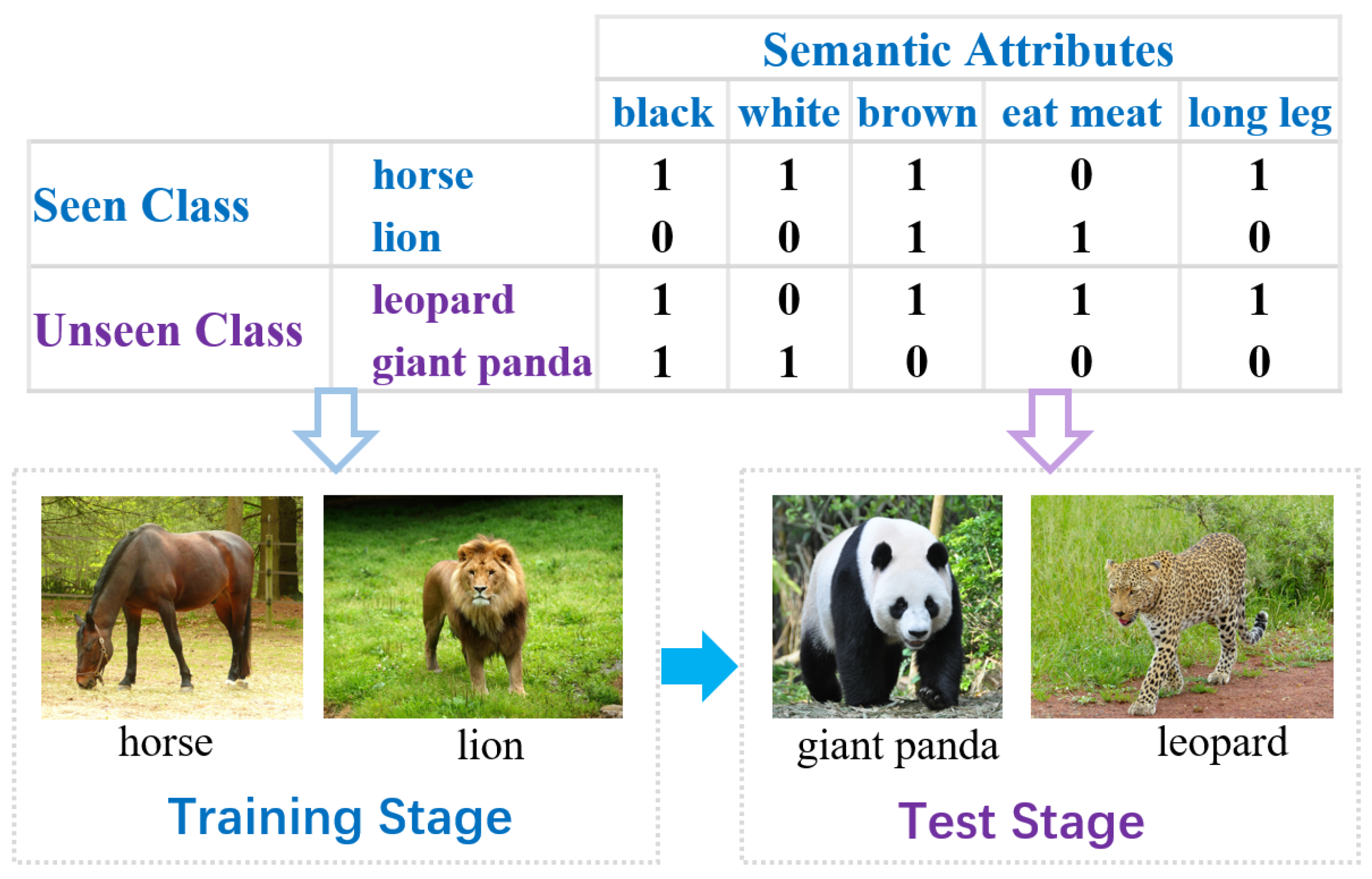
1. Introduction
- This work leverages the dictionary learning framework to model the latent feature and attribute spaces. Specifically, images are reconstructed using components from the latent feature dictionary. The original attributes are expressed as distinct combinations of elements from the latent attribute dictionary, with each combination representing a latent attribute. Additionally, the latent attributes naturally capture the correlations among different attributes.
- For the purpose of maintaining semantic information, a linear transformation is applied to establish the symmetric relationships between latent features and latent attributes. Therefore, the latent features can be regarded as various combinations of the latent attributes.
- The classifiers for seen classes are trained to enhance the discriminability of latent features, with the output probabilities being interpreted as a measure of similarity to the seen classes. As a result, the image representations are transformed from the latent feature domain to the label space.
- The experimental results are very encouraging. The proposed approach outperforms recent advanced ZSL approaches, demonstrating the power of jointly learning the symmetric alignment between images, categories and attributes.
2. Related Work
3. Methodology
3.1. Problem Definition
3.2. Formulation
- The first term represents the reconstruction error, ensuring that the learned dictionary B is able to encode the feature set X as much as possible, so that the original features X can be accurately reconstructed using the latent features E.
- The minimization of enables dictionary D to encode original attribute matrix A well, so that the semantic attributes A can be reproduced through the latent attribute elements Z.
- The symmetric alignment loss aims to maintain semantic information. The linear transformation matrix M is applied to establish the symmetric relationships between latent features E and latent attributes Z.
- The fourth term enhances the discriminability of the latent features E. Specifically, a linear mapping W is trained to transform the latent feature domain into label space, where instances belonging to the same class are clustered closely together, while instances from different classes are separated apart, enabling this mapping to effectively discriminate between different classes.
3.3. Optimization
- (1)
- Compute the codes E.
- (2)
- Compute the codes Z.
- (3)
- Update the dictionary B.
- (4)
- Update the dictionary D.
- (5)
- Fix B, E, D, Z, W and update M.
- (6)
- Fix B, E, D, Z, M and update W.
| Algorithm 1 Goal-oriented joint learning |
|
3.4. Zero-Shot Recognition
- (1)
- Recognition in the latent feature domain.
- (2)
- Recognition in the label space.
- (3)
- Recognition in the attribute domain.
- (4)
- Recognition by fusing multiple spaces.
4. Experiments
4.1. Datasets
4.2. Parameter Settings
4.3. Results and Discussion
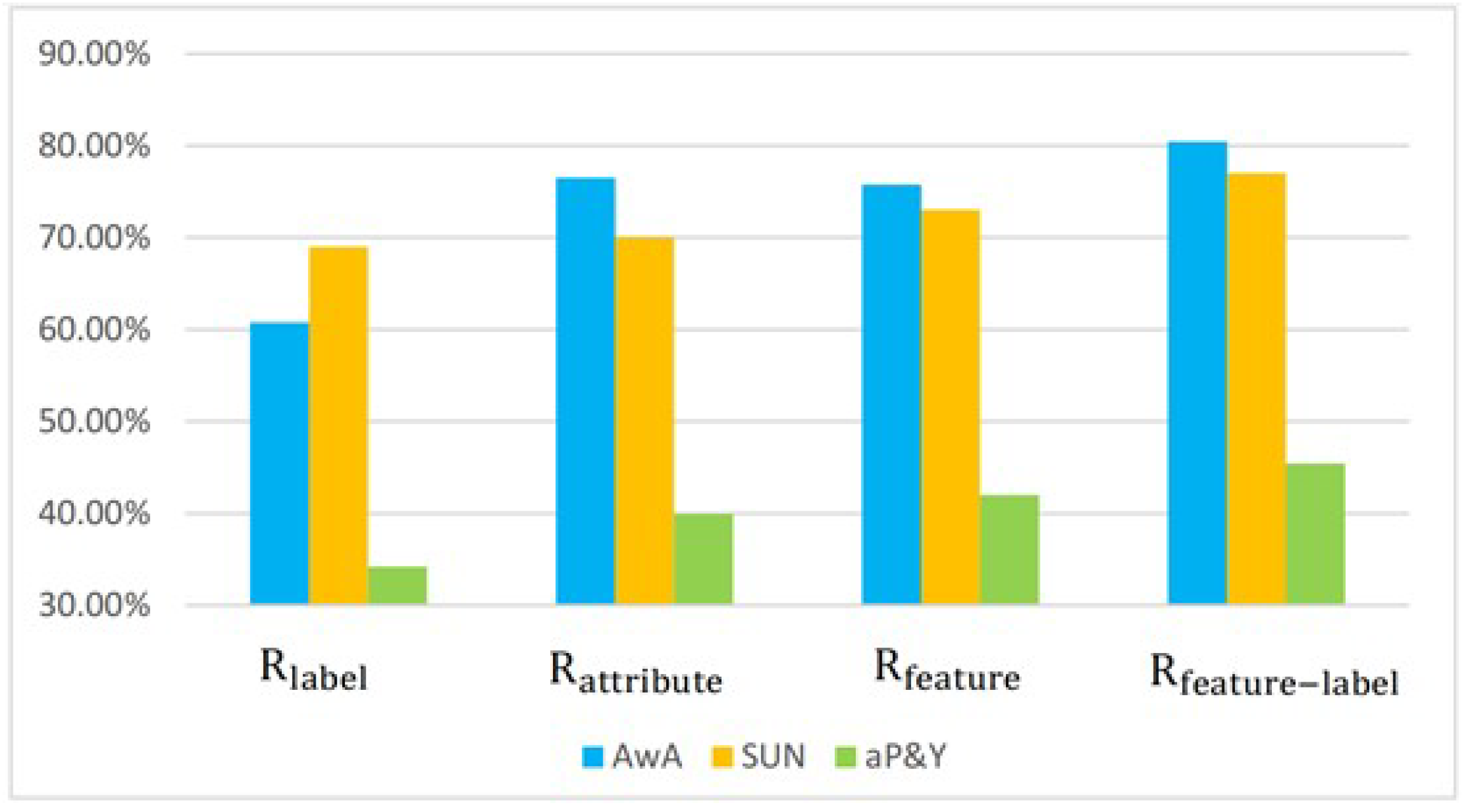
4.3.1. Component Analysis
- Recognition performance in the label space only, denoted as .
- Recognition performance in the attribute domain only, denoted as .
- Recognition performance in the latent feature domain only, denoted as .
- Recognition performance by fusing the latent feature representation and label vector, denoted as .
4.3.2. Comparison with State-of-the-Art Approaches
4.3.3. Discrimination Evaluations
4.3.4. Running Cost
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, V.W.; Hu, D.H.; Yang, Q. Cross-domain activity recognition. In Proceedings of the 11th International Conference on Ubiquitous Computing, Orlando, FL, USA, 30 September–3 October 2009; pp. 61–70. [Google Scholar]
- Venugopalan, S.; Hendricks, L.A.; Rohrbach, M.; Mooney, R.; Darrell, T.; Saenko, K. Captioning images with diverse objects. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1170–1178. [Google Scholar]
- Jiang, H.; Wang, R.; Shan, S.; Yang, Y.; Chen, X. Learning discriminative latent attributes for zero-shot classification. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 4233–4242. [Google Scholar]
- Fu, Z.; Xiang, T.A.; Kodirov, E.; Gong, S. Zero-shot object recognition by semantic manifold distance. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 2635–2644. [Google Scholar]
- Lampert, C.H.; Nickisch, H.; Harmeling, S. Learning to detect unseen object classes by between-class attribute transfer. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 951–958. [Google Scholar]
- Ba, J.L.; Swersky, K.; Fidler, S.; Salakhutdinov, R. Predicting deep zero-shot convolutional neural networks using textual descriptions. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 4247–4255. [Google Scholar]
- Socher, R.; Ganjoo, M.; Manning, C.D.; Ng, A. Zero-shot learning through cross-modal transfer. In Proceedings of the 27th International Conference on Neural Information Processing Systems (NIPS’13), Lake Tahoe, NE, USA, 5–10 December 2013; pp. 935–943. [Google Scholar]
- Xian, Y.; Akata, Z.; Sharma, G.; Nguyen, Q.; Hein, M.; Schiele, B. Latent embeddings for zero-shot classification. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 69–77. [Google Scholar]
- Karessli, N.; Akata, Z.; Schiele, B.; Bulling, A. Gaze embeddings for zeroshot image classification. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6412–6421. [Google Scholar]
- Al-Halah, Z.; Tapaswi, M.; Stiefelhagen, R. Recovering the missing link: Predicting class-attribute associations for unsupervised zero-shot learning. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 17–30 June 2016; pp. 5975–5984. [Google Scholar]
- Fu, Y.; Hospedales, T.M.; Xiang, T.; Gong, S. Transductive multi-view zeroshot learning. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 2332–2345. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhang, H.; Xiao, J.; Liu, W.; Chang, S.-F. Zero-shot visual recognition using semantics-preserving adversarial embedding networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1043–1052. [Google Scholar]
- Biswas, S.; Annadani, Y. Preserving semantic relations for zero-shot learning. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7603–7612. [Google Scholar]
- Frome, A.; Corrado, G.S.; Shlens, J.; Bengio, S.; Dean, J.; Ranzato, M.A.; Mikolov, T. Devise: A deep visual-semantic embedding model. In Proceedings of the 27th International Conference on Neural Information Processing Systems (NIPS’13), Lake Tahoe, NE, USA, 5–10 December 2013; pp. 2121–2129. [Google Scholar]
- Akata, Z.; Reed, S.; Walter, D.; Lee, H.; Schiele, B. Evaluation of output embeddings for fine-grained image classification. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 2927–2936. [Google Scholar]
- Romera-Paredes, B.; Torr, P.H.S. An embarrassingly simple approach to zeroshot learning. In Proceedings of the 32nd International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015; pp. 2152–2161. [Google Scholar]
- Akata, Z.; Perronnin, F.; Harchaoui, Z.; Schmid, C. Label-embedding for image classification. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1425–1438. [Google Scholar] [CrossRef] [PubMed]
- Kodirov, E.; Xiang, T.; Gong, S. Semantic autoencoder for zero-shot learning. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4447–4456. [Google Scholar]
- Xian, Y.; Lampert, C.H.; Schiele, B.; Akata, Z. Zero-shot learning—a comprehensive evaluation of the good, the bad and the ugly. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 2251–2265. [Google Scholar] [CrossRef] [PubMed]
- Long, Y.; Liu, L.; Shen, F.; Shao, L.; Li, X. Zero-shot learning using synthesised unseen visual data with diffusion regularisation. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 2498–2512. [Google Scholar] [CrossRef] [PubMed]
- Xian, Y.; Sharma, S.; Schiele, B.; Akata, Z. F-vaegan-d2: A feature generating framework for any-shot learning. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 10267–10276. [Google Scholar]
- Narayan, S.; Gupta, A.; Khan, F.S.; Snoek, C.G.; Shao, L. Latent embedding feedback and discriminative features for zero-shot classification. In Proceedings of the 16th European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 479–495. [Google Scholar]
- Farhadi, A.; Endres, I.; Hoiem, D.; Forsyth, D. Describing objects by their attributes. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1778–1785. [Google Scholar]
- Lampert, C.H.; Nickisch, H.; Harmeling, S. Attribute-based classification for zero-shot visual object categorization. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 453–465. [Google Scholar] [CrossRef] [PubMed]
- Norouzi, M.; Mikolov, T.; Bengio, S.; Singer, Y.; Shlens, J.; Frome, A.; Corrado, G.; Dean, J. Zero-shot learning by convex combination of semantic embeddings. In Proceedings of the 2nd International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. In Proceedings of the 27th International Conference on Neural Information Processing Systems (NIPS’13), Lake Tahoe, NE, USA, 5–10 December 2013; pp. 3111–3119. [Google Scholar]
- Jayaraman, D.; Sha, F.; Grauman, K. Decorrelating semantic visual attributes by resisting the urge to share. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1629–1636. [Google Scholar]
- Palatucci, M.; Pomerleau, D.; Hinton, G.E.; Mitchell, T.M. Zero-shot learning with semantic output codes. In Proceedings of the 23rd Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009; pp. 1410–1418. [Google Scholar]
- Bucher, M.; Herbin, S.; Jurie, F. Improving semantic embedding consistency by metric learning for zero-shot classiffication. In Proceedings of the 14th European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 730–746. [Google Scholar]
- Zhang, L.; Xiang, T.; Gong, S. Learning a deep embedding model for zero-shot learning. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3010–3019. [Google Scholar]
- Changpinyo, S.; Chao, W.L.; Sha, F. Predicting visual exemplars of unseen classes for zero-shot learning. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 3496–3505. [Google Scholar]
- Zhang, L.; Wang, P.; Liu, L.; Shen, C.; Wei, W.; Zhang, Y.; Hengel, A. Towards effective deep embedding for zero-shot learning. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 2843–2852. [Google Scholar] [CrossRef]
- Zhang, Z.; Saligrama, V. Zero-shot learning via semantic similarity embedding. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 4166–4174. [Google Scholar]
- Zhang, Z.; Saligrama, V. Zero-shot recognition via structured prediction. In Proceedings of the 14th European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 533–548. [Google Scholar]
- Changpinyo, S.; Chao, W.L.; Gong, B.; Sha, F. Synthesized classifiers for zero-shot learning. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 5327–5336. [Google Scholar]
- Akata, Z.; Malinowski, M.; Fritz, M.; Schiele, B. Multi-cue zero-shot learning with strong supervision. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 59–68. [Google Scholar]
- Gavves, E.; Mensink, T.; Tommasi, T.; Snoek, C.G.M.; Tuytelaars, T. Active transfer learning with zero-shot priors: Reusing past datasets for future tasks. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 2731–2739. [Google Scholar]
- Kodirov, E.; Xiang, T.; Fu, Z.; Gong, S. Unsupervised domain adaptation for zero-shot learning. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 2452–2460. [Google Scholar]
- Li, X.; Guo, Y.; Schuurmans, D. Semi-supervised zero-shot classification with label representation learning. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 4211–4219. [Google Scholar]
- Li, Y.; Wang, D. Zero-shot learning with generative latent prototype model. arXiv 2017. [Google Scholar] [CrossRef]
- Patterson, G.; Xu, C.; Su, H.; Hays, J. The sun attribute database: Beyond categories for deeper scene understanding. Int. J. Comput. Vis. 2014, 108, 59–81. [Google Scholar] [CrossRef]
- Everingham, M.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. The Pascal Visual Object Classes Challenge 2008 Results. Available online: http://www.pascal-network.org/challenges/VOC/voc2008/workshop/index.html (accessed on 7 May 2024).
- Jayaraman, D.; Grauman, K. Zero-shot recognition with unreliable attributes. In Proceedings of the 28th International Conference on Neural Information Processing Systems (NIPS’14), Montreal, QC, Canada, 8–13 December 2014; pp. 3464–3472. [Google Scholar]
- Vedaldi, A.; Lenc, K. Matconvnet: Convolutional neural networks for MATLAB. In Proceedings of the 23rd Annual ACM Conference on Multimedia Conference, Brisbane, Australia, 26–30 October 2015; pp. 689–692. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 2015 International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Xian, Y.; Lorenz, T.; Schiele, B.; Akata, Z. Feature generating networks for zeroshot learning. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5542–5551. [Google Scholar]
- Jiang, H.; Wang, R.; Shan, S.; Chen, X. Transferable contrastive network for generalized zero-shot learning. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9764–9773. [Google Scholar]
- Huynh, D.; Elhamifar, E. Fine-grained generalized zero-shot learning via dense attribute-based attention. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 4482–4492. [Google Scholar]
- Xie, G.S.; Liu, L.; Zhu, F.; Zhao, F.; Zhang, Z.; Yao, Y.; Qin, J.; Shao, L. Region graph embedding network for zero-shot learning. In Proceedings of the 16th European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 562–580. [Google Scholar]
- Xu, W.; Xian, Y.; Wang, J.; Schiele, B.; Akata, Z. Attribute prototype network for zero-shot learning. In Proceedings of the 34th International Conference on Neural Information Processing Systems(NIPS ’20), Vancouver, BC, Canada, 6–12 December 2020; pp. 21969–21980. [Google Scholar]
- Han, Z.; Fu, Z.; Chen, S.; Yang, J. Contrastive embedding for generalized zero-shot learning. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 2371–2381. [Google Scholar]
- Chen, S.; Hong, Z.; Xie, G.S.; Yang, W.; Peng, Q.; Wang, K.; Zhao, J.; You, X. Msdn: Mutually semantic distillation network for zero-shot learning. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 7602–7611. [Google Scholar]
- Chen, S.; Hong, Z.; Liu, Y.; Xie, G.S.; Sun, B.; Li, H.; Peng, Q.; Lu, K.; You, X. Transzero: Attribute-guided transformer for zero-shot learning. In Proceedings of the Thirty-Sixth AAAI Conference on Artificial Intelligence (AAAI), Virtual, 22 February–1 March 2022. [Google Scholar]
- Chen, Z.; Zhang, P.; Li, J.; Wang, S.; Huang, Z. Zero-shot learning by harnessing adversarial samples. In Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 4138–4146. [Google Scholar]
- Laurens, V.D.M.; Hinton, G. Visualizing data using t-sne. J. Mach. Res. 2008, 9, 2579–2605. [Google Scholar]




| Datasets | Granularity | Attributes | Classes | Images | ||||
|---|---|---|---|---|---|---|---|---|
| Total | Training | Test | Total | Training | Test | |||
| aP&Y | coarse | 64 | 32 | 20 | 12 | 15,339 | 12,695 | 2644 |
| AwA | coarse | 85 | 50 | 40 | 10 | 30,475 | 24,295 | 6180 |
| SUN | fine | 102 | 717 | 707 | 10 | 14,340 | 12,900 | 1440 |
| Methods | AwA | SUN |
|---|---|---|
| f-CLSWGAN [46] | 0.682 | 0.608 |
| TCN [47] | 0.712 | 0.615 |
| f-VAEGAN-D2 [21] | 0.711 | 0.647 |
| DAZLE [48] | 0.679 | 0.594 |
| RGEN [49] | 0.736 | 0.638 |
| APN [50] | 0.684 | 0.616 |
| TF-VAEGAN [22] | 0.722 | 0.66 |
| CE-GZSL [51] | 0.704 | 0.633 |
| MSDN [52] | 0.701 | 0.658 |
| TransZero [53] | 0.701 | 0.656 |
| HAS [54] | 0.714 | 0.632 |
| Ours | 0.756 | 0.77 |
| Training | Test | |
|---|---|---|
| aP&Y | 41.2457 | 0.021620 |
| AwA | 17.1541 | 0.038948 |
| SUN | 100.6624 | 0.010036 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, H.; Zhou, Y.; Jiang, M. Exploiting Semantic-Visual Symmetry for Goal-Oriented Zero-Shot Recognition. Symmetry 2025, 17, 1291. https://doi.org/10.3390/sym17081291
Zheng H, Zhou Y, Jiang M. Exploiting Semantic-Visual Symmetry for Goal-Oriented Zero-Shot Recognition. Symmetry. 2025; 17(8):1291. https://doi.org/10.3390/sym17081291
Chicago/Turabian StyleZheng, Haixia, Yu Zhou, and Mingjie Jiang. 2025. "Exploiting Semantic-Visual Symmetry for Goal-Oriented Zero-Shot Recognition" Symmetry 17, no. 8: 1291. https://doi.org/10.3390/sym17081291
APA StyleZheng, H., Zhou, Y., & Jiang, M. (2025). Exploiting Semantic-Visual Symmetry for Goal-Oriented Zero-Shot Recognition. Symmetry, 17(8), 1291. https://doi.org/10.3390/sym17081291





