Multi-Team Agile Software Project Scheduling Using Dual-Indicator Group Learning Particle Swarm Optimization

Abstract

Core problems in agile software project scheduling, such as resource-constrained balancing and iteration cycle optimization, embody the pursuit of symmetry. Simultaneously, optimization algorithms find extensive applications in symmetry problems, for example, in graphs and pattern recognition. Considering the cooperation among multiple teams and environmental changes in complex agile software development, a dynamic periodic scheduling model for multi-team agile software project is constructed, which includes three tightly coupled sub-problems, namely user story selection, user story-development team allocation, and task-employee allocation. To solve the model, a group learning particle swarm optimization algorithm is proposed, which includes three novel strategies. First, the population is divided into four groups based on dual indicators of objective values and potential values. Second, different learning objects are selected according to the characteristic of each group so that the search diversity can be improved. Third, to react to the environmental changes and enhance the mining ability, heuristic population initialization and local search strategies are designed by utilizing the problem-specific information. Systematic experimental results on 13 instances indicate that compared with the state-of-the-art algorithms, the proposed algorithm is able to provide a schedule with better precision for the project manager in each sprint of the agile development.

1. Introduction

The software industry is one of the important pillar industries for the national economic development. Software projects are generally characterized by long cycles, high complexities, flexible human resources, and high expertise, which increases the risk of project failure. According to a report by Standish Group, the global proportion of projects successfully delivered on time in 2023 is only 34%. One major reason for this is the unreasonable scheduling of tasks and employees by project managers [1]. Software Project Scheduling (SPS) refers to determining the development sequence of different tasks and allocating employees to each task, on the basis of the estimated task efforts and skill requirements [2]. SPS aims to optimize the project’s cost, duration, or other performance indicators, satisfying the constraints of human resources, task priorities, and so on. As an important part of software development, SPS directly affects the economic benefits and market competitiveness of enterprises.

Agile software development is a flexible methodology, which adopts “small and skilled” teams and “short time and high frequency” development cycles. It splits the software project through the iterative and incremental approach, making software development more flexible. It is able to timely respond to the requirement changes and dynamically adjust the software development plan. Compared with the traditional waterfall model, agile development addresses close cooperation with customers throughout the development process, providing a faster delivery and a higher project satisfaction. Agile development aligns better with the concept of software project management, and more and more agile software projects have appeared in recent years.

With the surge in user requirements and the ever-changing market environment, software project development has become increasingly complex. Moreover, the tasks in a project might come from different fields and need professional teams. The project development with a single team appears to be limited, making the cross-departmental and cross-team project a common occurrence, especially in agile development. Multi-team Agile Software Project Scheduling (MTASPS) refers to coordinating user stories among different sprints and teams, and assigning various tasks of user stories within teams, considering temporary changes or newly inserted requirements during agile development. Since agile development advocates communication and cooperation between teams, there are more challenges in MTASPS than regular software project scheduling, including competition of shared resources (test environment and cross-domain experts), conflicts between team autonomy and cross-team cooperation, and non-linear growth of communication cost with scale expansion, etc. Such issues will affect various development links like the release plan, sprint plan, and sprint review. By optimizing the user story allocation and resolving the resource conflict, MTASPS plays a vital role in improving the management level and success rate of the agile project. However, to the best of our knowledge, academic research on MTASPS is scarce [3]. Thus, it is urgent to study the model and algorithm for MTASPS.

SPS has been proven to be an NP-hard problem [4]. MTASPS can be regarded as an extension of SPS, where dynamic changes in the scheduling environment and allocations of user stories among and within teams need to be considered on the basis of SPS. Therefore, MTASPS is also an NP-hard problem. Core issues in MTASPS, such as resource-constrained balancing and iteration cycle optimization, embody the pursuit of symmetry. Most early studies adopted exact algorithms like dynamic programming or heuristic methods to allocate tasks in software projects. Exact algorithms are capable of finding optimal solutions theoretically but are only applicable to small-scale problems due to limitations in time and space complexity. Heuristic methods construct feasible solutions quickly but cannot guarantee the quality of solutions. With increasing problem scale and complexity of the model, search-based software engineering [5] has been rapidly developed in recent years. It models complex problems in software engineering as search-based optimization problems, where meta-heuristic algorithms [6] are employed to search the decision space, further assisting managers in making final decisions. Also, optimization algorithms are widely applied in symmetry-related problems, for instance, in graph theory and pattern recognition.

Particle Swarm Optimization (PSO) is a meta-heuristic algorithm proposed by Kennedy and Eberhart in 1995, which simulates the random search for food by a flock of birds [7]. PSO has three typical merits: (1) It finds the optimal solution through collaboration and information sharing among individuals in the population. Each individual possesses the abilities of memory, self-learning, and social learning. (2) PSO is easy to implement, with a few parameters and fast convergence. (3) PSO has been widely applied to various scheduling problems, such as berth allocation and quay crane assignment and scheduling problem [8], job-shop scheduling [9], network scheduling [10], and so on. Furthermore, compared to other swarm intelligence-based methods such as Ant Colony Optimization (ACO) and Cuckoo Search (CS), PSO demonstrates distinct advantages for the MTASPS, including superior dynamic adaptability and more efficient constraint handling. When confronted with frequent requirement changes inherent in MTASPS, PSO enables dynamic solution iteration through its real-time particle update mechanism. In contrast, ACO and CS rely heavily on pheromone accumulation or stochastic Lévy flights, respectively, making them highly sensitive to iterations and prone to becoming trapped in a local optimum. Concurrently, PSO can directly encode discrete variables associated with task assignments. While ACO is predominantly suited for path-finding problems, its application to task assignment problems necessitates the additional design of heuristic rules, thereby increasing implementation complexity. Although PSO has achieved some success, its individual updates during the evolutionary process rely too much on the personal best and the global best and fail to fully utilize the effective information of other individuals. This causes the loss of the population diversity, and the algorithm is prone to getting stuck in the local optimum.

Group learning strategy divides the population into several groups, with each group evolving separately to carry out the corresponding search task. These groups interact regularly and cooperate to solve the problem, which is beneficial to improving the search diversity of meta-heuristic algorithms [11]. Combining the advantages of PSO and group learning, this paper proposes a dual-indicator group learning particle swarm optimization (DGLPSO)-based dynamic periodic scheduling method to solve MTASPS, with the aim of producing the most suitable schedule efficiently in each sprint during the agile software project development.

This work mainly has two contributions: (1) focusing on the three tightly coupled sub-problems, including user story selection, story-team allocation, and task-employee allocation, a multi-team agile software project scheduling model, termed MTASPS, is established, which considers the additions of user stories and uncertainties of employees’ working hours. Moreover, the development experiences and preferences of each team for different types of user stories are also introduced. The model simultaneously maximizes the user story values, employees’ time utilization rates, team efficiency, and team satisfaction under the constraints of team speed and maximum working hours. (2) A DGLPSO-based dynamic periodic scheduling approach is proposed to solve the constructed model MTASPS. First, for the three coupled sub-problems, each individual is encoded by a variable-length chromosome with three layers. Second, we group the population based on dual indicators of objective values and potential values and use different learning objects to guide individuals with distinct characteristics to diversify their learnings. Third, in order to respond to environmental changes and enhance mining abilities, heuristic population initialization and local search strategies are designed using information derived from objectives.

The remainder is organized as follows. Section 2 discusses the related work. Section 3 constructs the mathematical model for MTASPS. Section 4 describes the proposed algorithm, DGLPSO. Section 5 presents the experimental studies. This work is summarized in Section 6.

2. Related Work

In this section, the existing studies on the agile software project scheduling (ASPS) and the multi-team task allocation problem are briefly reviewed. We also summarize the existing work on the PSO.

2.1. Models for Agile Software Project Scheduling

As far as we know, only the literature [12,13,14,15,16] has studied SPS with the agile development mode. Lucas et al. [12] proposed an ASPS model to minimize the duration and cost of the agile software project based on task similarities. However, the dynamic periodic scheduling feature of the agile project was not considered. Michael et al. [13] combined scheduling with Scrum, an agile development framework, to establish a resource-constrained ASPS model, but the dynamic characteristics of requirement changes were not considered. Nigar et al. [14] constructed an SPS model with a hybrid Scrum framework, where the project duration, cost, stability, and robustness were regarded as the optimization objectives. Nevertheless, its scheduling was essentially based on the waterfall model of software development and did not provide a solution method. Zapotecas et al. [15] built a scrum-based ASPS model and used the decomposition-based multi-objective evolutionary algorithm MOEA/D to solve it. However, the model directly took the development speed as the project cost and the number of sprints as the duration without considering other factors affecting the cost or duration. In addition, the model did not take dynamic factors into account, like changes in user requirements or employees’ attributes, which made the schedule lack adaptability to environmental changes. Nilay et al. [16] constructed a multi-objective hybrid model based on the Scrum framework and employed two multi-objective evolutionary algorithms named NSGA-II and SPEA2 for solving it. However, the hybrid model failed to address the allocation of user story-decomposed tasks to employees and ignored dynamic factors like user story insertion or removal. Consequently, the resulting schedule exhibits limited adaptability to real-world dynamics.

In summary, there are still some problems with the existing studies on the ASPS model. First, the characteristic of periodic development in each sprint of the agile project was not reflected in the existing models. Second, during the process of real-world agile development, changes in user requirements and employees’ or user stories’ attributes often occur, while the existing models did not account for such dynamic factors. Third, the existing models only optimized the resource allocation problem, while the actual ASPS involves multiple coupled sub-problems. Last, the existing research has not considered the situation that complex agile software projects need to be completed through multi-team collaboration. In order to overcome the above difficulties, we establish a dynamic periodic multi-team agile software project scheduling model named MTASPS, which focuses on three tightly coupled sub-problems.

2.2. Multi-Team Task Allocation Problem

Mathieu et al. [17] were the first to introduce the concept of multi-team systems in 2001. So far, a number of scholars have conducted research on the theoretical issues and influence factors in multi-team systems. Carter et al. [18] discussed the influence of leadership on collaborative innovation in multi-team systems. Davision et al. [19] investigated the issue of effective collaboration in multi-team systems. Berg et al. [20] studied the moderating role of emotions in a multi-team system. Matusik et al. [21] considered the impact of multiple identities of sub-teams on multi-team systems after constructing relational network linkages. Ziegert et al. [22] explored how to balance the dual identities of the sub-team and the system in a multi-team system and the impact it has on inter-team interactions. Xie et al. [23] discussed the relationship between management entropy and system network and constructed an evaluation system for multi-team system knowledge. Wu et al. [24] discussed the impact of diverse knowledge and resources on sub-team productivity.

However, there is limited research on resource scheduling for multi-team systems. Maarten et al. [25] investigated the impact of cross-sub-team collaboration on sub-team resources and on the performance of the multi-team system. Si et al. [26] proposed a multi-center collaborative maintenance strategy to optimize the serving route of each group based on dynamic maintenance costs and geographic locations of the centers.

The above studies on multi-team systems or multi-team resource scheduling have only paid attention to the interactions between teams and several influencing factors on system operations. Moreover, only the task assignment problem among teams is considered. Our model MTASPS introduces the development experience and preferences of each team. In addition to two indicators of user story values and employees’ time utilization rates, we also optimize the team efficiency and team satisfaction. Besides assigning the selected user stories to each team, a task-employee allocation is further implemented within the team.

2.3. The PSO Algorithm and the Group Learning Strategy

PSO uses information sharing to evolve the population from disorder to order in the solution space by observing the behavior of bird flocking, and, thus, the optimal solution is obtained. It achieves population evolution by generating better offspring through the initialization and individual evaluation, as well as the speed and position updating. Each individual in the population not only learns from their own “optimal experience” but also learns from the “global optimal experience” of the population so as to adjust direction and speed of the next movement. So far, a lot of studies have been conducted on improving PSO.

In terms of parameter optimization, Eberhart et al. [27] were the first to present a maximum speed limit to ensure controllable particle trajectories. Cai et al. [28] designed a dynamic adjustment of the maximum speed to improve the algorithm performance. For the learning factor, Ratnaweera et al. [29] introduced an adaptive strategy that tuned the learning factor with the evolutionary generations. Jacques et al. [30] designed a negative learning factor to increase the population diversity. For the inertia weight, Li et al. [31] proposed a “three-variable iterative” inertia weighting strategy with a multi-information fusion, considering the simultaneous changes in time, particles, and dimensions. Wang et al. [32] devised a self-adjusting nonlinear strategy for the inertia weight by combining the search levels of different subgroups.

In terms of neighborhood topology, PSO can be classified into global and local models based on whether the particle neighborhood encompasses the whole population. Particles in the global model exchange individuals with other particles in the whole population, resulting in a faster convergence speed, but they are easier to fall into the local optimum. Therefore, a variety of local models have emerged. Some scholars have generated static neighborhood topologies named ring topology, star topology, Von Neumann topology, random topology, etc., depending on particle numbers [32]. Others have designed dynamic neighborhood topologies. Li et al. [33] employed a local update strategy with a neighborhood difference mutation to enhance the population diversity. Anh et al. [34] presented a variable neighborhood search strategy, where particles from different neighborhoods could also exchange information.

In terms of hybrid strategies, many scholars have combined PSO with other algorithms to improve the population diversity and search capability of PSO. Hybrid strategy-based PSO approaches can be categorized into three types: integration with evolutionary algorithms, integration with neural networks, and integration with reinforcement learning. For integration with evolutionary algorithms, Beyene et al. [35] hybridized PSO with genetic algorithms to dynamically adapt optimization performance, thereby obtaining higher-quality solutions for islanded microgrid problems. For integration with neural networks, Bi et al. [36] combined PSO with neural networks to propose a new method for predicting the trend of biofuel slagging. And Roy et al. [37] integrated PSO with artificial neural networks to design a control method for degasser parameters in recirculating aquaculture systems. For integration with reinforcement learning, Zhang et al. [38] integrated PSO with reinforcement learning, proposing a novel approach to optimize the power allocation strategy for hybrid electric vehicles. These studies have greatly enriched the learning forms of particles in PSO.

Some studies introduced the group learning strategy into the metaheuristic algorithm to divide the population into several groups, which searched the decision space cooperatively. Zou et al. [39] proposed a dynamic sparse grouping evolutionary algorithm, which dynamically grouped the non-zero decision variables so that the sub-population evolved stably towards a sparser Pareto optimal population. Wichaya et al. [40] presented a hybrid method combining PSO and the sine–cosine algorithm. The particles were sorted by fitness values from the best to the worst, and then sequentially divided into three groups in the ratios of 20%, 40%, and 40%, respectively. Each group of particles shared the same motion equation. Song et al. [41] randomly grouped the population into three subgroups of equal size at each generation. Each subgroup adopted different search operators. In this way, different search strategies were performed on each individual with the same probability, which enhanced the population diversity. Hu et al. [42] grouped the population based on fitness values and particle activity level and improved the original speed and position update methods in PSO. In this way, the grouping mechanism enhanced the efficiency of information exchange between particles.

In this paper, DGLPSO is designed as a dynamic periodic scheduling method, which differs from the previous studies in that: (1) By employing dual indicators of objective values and self-defined potential values, the PSO population is divided into four groups with different characteristics. In contrast, the existing studies commonly grouped the population based on one indicator. (2) For each group, learning objects are chosen based on characteristics of the individuals it contains, and personalized learning is performed, while most previous work focused on devising different search operators in different groups. (3) A dynamic response mechanism and heuristic local search operators are, respectively, designed based on domain knowledge, which aim to increase the search efficiency. In contrast, the existing work underutilized the problem features.

3. Mathematical Modeling of MTASPS

In this section, the agile development process based on Scrum is introduced at first. Then we construct the mathematical model of MTASPS.

3.1. Agile Development Process Based on Scrum

Agile development is a collective term for a series of methods and frameworks with common characteristics, including extreme programming (XP), crystal family development, adaptive software development, feature-driven development, lean development, Scrum, and so on [43]. Scrum is the most widely adopted agile development framework globally. Its utilization of fixed-length iterations aligns more closely with the phased work planning characteristic of real-world software engineering. Furthermore, Scrum’s standardized processes facilitate the clear and effective establishment of problem models. In contrast, other prevalent agile frameworks, such as XP and lean development, demonstrate a mismatch with the requirements of scheduling problems. XP places greater emphasis on technical practices (e.g., pair programming, test-driven development) and exhibits weaker capabilities for the structured management of tasks and resources, posing significant challenges for constructing the problem model. Lean development lacks explicit standardized guidelines for task and resource utilization, relying heavily on team experiential judgment and lacking widely accepted evaluation metrics; consequently, it fails to provide quantifiable parameters essential for modeling. As a result, Scrum is adopted as the agile development framework, and its development process is illustrated in Figure 1.

Scrum divides the entire development process into multiple short iteration cycles (sprints) [43]. The development team breaks down the entire project into modules (user stories) with different software product features and functionality based on user requirements, with the aim of facilitating communication between the team and the users. These user stories, either independently or with dependencies, form a list of product requirements that changes as user requirements change. The development team estimates the story points (difficulty, workload, etc.) and value points of the user stories using a planning poker and measures the team’s speed by the number of story points completed in each sprint. At the beginning of each sprint, the team selects the user stories that will be completed in the current sprint, i.e., the sprint to-do list, based on the updated list of product requirements, user story priorities, and team speed. Once constructed, this list remains unchanged until the current sprint is completed. The development team collaborates to complete a user story, which needs to be further broken down into a number of separate modular tasks. The team clearly identifies the working hours and skill requirements needed to complete each task and assigns the right employee to the task accordingly.·

3.2. A Dynamic Periodic Scheduling Model for MTASPS

The considered multi-team agile software project scheduling problem can be seen as a dynamic periodic process, formed by a sequence of software project scheduling problems with different sets of user stories, teams, tasks, and employees to be scheduled. This process continues until all the sprints in the project have been completed. A dynamic periodic scheduling method is employed. At the beginning of each sprint, the scheduling method is triggered to generate a new schedule based on the current project state. Considering the above features, the mathematical model of MTASPS is established at a specific sprint.

3.2.1. Dynamic and Uncertain Factors

In the proposed model, the agile software project has a predetermined delivery time, which is set through negotiation between the user and the development team before the project starts. During the actual development, new user stories can be generated at any time due to changes in user requirements. Moreover, software employees often switch positions with many uncontrollable factors, so the maximum working hours of the same employee might change in different sprints. To reflect the dynamic nature of the agile development, the proposed model considers two types of dynamic factors: (1) introduction of new user stories; (2) uncertainties of employees’ maximum working hours.

In our model, different types of dynamic factors might occur at the same time, and each dynamic factor is allowed to occur more than once.

3.2.2. Properties Related to the Model

Properties of the user story, task, team, and sprint involved in the constructed model MTASPS are shown in

Table 1. Properties in the MTASPS model.

Name	Description
User story	The user requirements, i.e., desired functional modules to be implemented
$u{s}_i$	The ith user story, $i=1,2,\dots ,n$ (n is the total number of user stories at the initial time).
$t{p}_i$	The category of the ith user story.
$s{p}_i$	Story points of the ith user story (an estimated value of the story’s workload, difficulty, etc.).
$v{p}_i$	Value points of the ith user story (value obtained from completing the user story).
Task	A user story is decomposed into a number of tasks. It is assumed that a task is completed by only one employee.
$t{n}_i$	The number of tasks decomposed from $u{s}_i$ (the number of tasks varies from story to story)
$t{h}_{ij}$	The effort of the jth task in $u{s}_i$ (time required to complete the task), $j=1,2,\dots ,t{n}_i$.
$t{s}_{ij}$	The skill required by the jth task in $u{s}_i$ (assume only one skill is required to complete a task).
Sprint	A project is completed in L sprints.
$L$	The limited number of sprints to complete the project.
$T$	Each sprint has the same and fixed period T.
$p{b}_l$	The to-do user story set at the beginning of the lth sprint (including newly inserted stories), $l=1,2,\dots ,L$.
Team	A team is comprised of several employees who cooperate to work.
$D$	The number of teams.
$m_d$	The number of employees in the dth team, $d=1,2,\dots ,D$.
$hi{s}_d^{t{p}_i}$	The development experience of the dth team on user stories with the category $t{p}_i$.
$pr{e}_d^{t{p}_i}$	The preference of the dth team on user stories with the category $t{p}_i$.
$e_{dk}$	The kth employee in the dth team, $k=1,2,\dots ,m_d$
$e{s}_{dk}$	The set of skills possessed by the kth employee in the dth team.
$e{h}_{dkl}$	The maximum working hours of the employee $e_{dk}$ at the lth sprint.
$v_{dl}$	Speed of the dth team at the lth sprint (the maximum number of user story points that can be completed)

.

3.2.3. Changes in the Team Speed

Since the maximum working hours of an employee in each sprint may vary, the speed $v_{dl}$ of each team in each sprint will also vary. For the d^th team consisting of $m_d$ employees, assume the initial team speed in the first sprint be $v_{d1}$ ($v_{d1}$ can be taken as the team’s average development speed in historical projects). The speed $v_{dl}$ of the d^th team at the l^th sprint ($l\ge 2$) is estimated by the following two factors: (1) the ratio of the sum of the maximum working hours of each employee in the current sprint and the previous one, (2) the total number of story points completed by the team in the previous sprint. The estimation for $v_{dl}$ is shown in Equation (1).

$$v_{dl}=\left\{\begin{array}{l}{V}_{d1},l=1\\ {\displaystyle \frac{{\displaystyle \sum _{k=1}^{m_d}e{h}_{dkl}}}{{\displaystyle \sum _{k=1}^{m_d}e{h}_{dk(l-1)}}}}·{\displaystyle \sum _{u{s}_i\in p{b}_{(l-1)}}{y}_{id(l-1)}}·s{p}_i,2\le l\le L\end{array}\right.$$

(1)

where ${\displaystyle \sum _{u{s}_i\in p{b}_{(l-1)}}{y}_{id(l-1)}}·s{p}_i$ denotes the sum of user story points accomplished by the d^th team in the (l − 1)^th sprint; $y_{id(l-1)}$ is a binary variable defined as in Equation (2).

$$y_{id(l-1)}=\left\{\begin{array}{c}1, \mathrm{the} i^{\mathrm{th}} \mathrm{story} \mathrm{is} \mathrm{assigned} \mathrm{to} \mathrm{the} d^{\mathrm{th}} \mathrm{team} \hfill \\ \hfill \mathrm{in} \mathrm{the} (l-1{)}^{\mathrm{th}} \mathrm{sprint} \hfill \\ 0, \mathrm{others}\hfill \end{array}\right.$$

(2)

3.2.4. Mathematical Model

Before the start of a software project, n initial user stories $u{s}_i\left(i=1,2,\mathrm{\dots },n\right)$ of the project are obtained through discussion of the development team, including the story points $s{p}_i$, the value points $v{p}_i$ and priorities among the stories. At the beginning of the l^th sprint ($l=1,2,\dots ,L$), the first step is to select the user stories that will be completed in the current sprint, including unfinished stories and newly added ones, to form the sprint to-do list (assume each sprint has at most one newly added story). The user stories of the to-do list are decomposed into tasks, obtaining the effort $t{h}_{ij}$ and skill $t{s}_{ij}$ required for each task. Then, the user stories that would be completed by each team are determined based on team speed and story category. At last, task-employee allocation is performed based on skills and the maximum working hours of the employees in the team. According to the above process, focusing on three tightly coupled sub-problems of user story selection, story-team allocation, and task-employee allocation, the dynamic periodic scheduling model MTASPS is constructed at the initial time of the l^th sprint, which introduces development experiences and preferences of teams for different categories of user stories.

The decision variables $x_{il}$, $y_{idl}$, and $z_{ijdkl}$ of the constructed model MTASPS are shown in Equations (3)–(5), respectively.

$$x_{il}=\left\{\begin{array}{l}1, \mathrm{select} \mathrm{the} i^{\mathrm{th}} \mathrm{user} \mathrm{story} \mathrm{in} \mathrm{the} l^{\mathrm{th}} \mathrm{sprint} \\ 0, \mathrm{others}\end{array}\right.$$

(3)

$$y_{idl}=\left\{\begin{array}{l}1, \mathrm{allocate} \mathrm{the} i^{\mathrm{th}} \mathrm{story} \mathrm{to} \mathrm{the} d^{t\mathrm{h}} \mathrm{team} \mathrm{in} \mathrm{the} l^{\mathrm{th}} \mathrm{sprint}\\ 0, \mathrm{others}\end{array}\right.$$

(4)

$$z_{ijdkl}=\left\{\begin{array}{c}1, \mathrm{allocate} \mathrm{the} j^{\mathrm{th}} \mathrm{task} \mathrm{of} \mathrm{the} i^{\mathrm{th}} \mathrm{story} \mathrm{to} \mathrm{the} \hfill \\ \hfill k^{\mathrm{th}} \mathrm{employee} \mathrm{of} \mathrm{the} d^{\mathrm{th}} \mathrm{team} \mathrm{in} \mathrm{the} l^{\mathrm{th}} \mathrm{sprint} \hfill \\ 0, \mathrm{others}\hfill \end{array}\right.$$

(5)

At the initial time of the l^th sprint, the objective of the model is defined as Equations (6)–(9), with constraints provided in Equations (10)–(17), respectively.

$$\max F_l={\omega }_1·F_{1l}+{\omega }_2·F_{2l}+{\omega }_3·F_{3l}$$

(6)

$$F_{1l}={\displaystyle \sum _{u{s}_i\in p{b}_l}{x}_{il}·v{p}_i}$$

(7)

$$F_{2l}={\displaystyle \frac{1}{D}}·{\displaystyle \sum _{d=1}^D\left(\frac{{\displaystyle \sum _{u{s}_i\in p{b}_l}{y}_{idl}·s{p}_i}}{v_{dl}}+\frac{{\displaystyle \sum _{u{s}_i\in p{b}_l}{y}_{idl}·pr{e}_d^{t{p}_i}·hi{s}_d^{t{p}_i}}}{{\displaystyle \sum _{u{s}_i\in p{b}_l}{y}_{idl}}}\right)}$$

(8)

$$F_{3l}={\displaystyle \frac{1}{{\displaystyle \sum _{d=1}^D{m}_d}}}·{\displaystyle \sum _{d=1}^D{\displaystyle \sum _{k=1}^{m_d}\frac{{\displaystyle \sum _{u{s}_i\in p{b}_l}{\displaystyle \sum _{j=1}^{t{n}_i}{x}_{il}·y_{idl}·z_{ijdkl}·t{h}_{ij}}}}{e{h}_{dkl}}}}$$

(9)

s.t.

$${\displaystyle \sum _{u{s}_i\in p{b}_l}{x}_{il}·s{p}_i}\le {\displaystyle \sum _{d=1}^D{v}_{dl}}$$

(10)

$${\displaystyle \sum _{u{s}_i\in p{b}_l}{y}_{idl}·s{p}_i}\le v_{dl}\hspace{0.33em},\hspace{0.33em}\forall d=1,2,\dots ,D$$

(11)

$${\displaystyle \sum _{u{s}_i\in p{b}_l}{\displaystyle \sum _{j=1}^{t{n}_i}{y}_{idl}·t{h}_{ij}}}\le {\displaystyle \sum _{k=1}^{m_d}e{h}_{dkl}}\hspace{0.33em},\hspace{0.33em}\forall d=1,2,\dots ,D$$

(12)

$${\displaystyle \sum _{u{s}_i\in p{b}_l}{x}_{il}·y_{idl}}\ge 1\hspace{0.33em},\hspace{0.33em}\forall d=1,2,\dots ,D$$

(13)

$$\begin{array}{r}{\displaystyle \sum _{u{s}_i\in p{b}_l}{\displaystyle \sum _{j=1}^{t{n}_i}{y}_{idl}·z_{ijdkl}·t{h}_{ij}}}\le e{h}_{dkl}\hspace{0.33em},\hspace{0.33em}\forall d=1,2,\dots ,D\hspace{0.33em},\hspace{0.33em}\\ k=1,2,\dots ,m_d\hspace{0.33em}\end{array}$$

(14)

$${\displaystyle \sum _{u{s}_i\in p{b}_l}{\displaystyle \sum _{j=1}^{t{n}_i}{y}_{idl}·z_{ijdkl}}}\ge 1\hspace{0.33em},\hspace{0.33em}\forall d=1,2,\dots ,D\hspace{0.33em},\hspace{0.33em}k=1,2,\dots ,m_d$$

(15)

$${\displaystyle \sum _{d=1}^D{\displaystyle \sum _{k=1}^{m_d}{y}_{idl}·z_{ijdkl}}=1}\hspace{0.33em},\hspace{0.33em}\forall u{s}_i\in p{b}_l\hspace{0.33em},j=1,2,\dots ,t{n}_i\hspace{0.17em}$$

(16)

$$\begin{array}{l}\mathrm{if} y_{idl}·z_{ijdkl}=1,\hspace{0.33em}then t{s}_{ij}\in e{s}_{dk},\\ \forall u{s}_i\in p{b}_l\hspace{0.33em},j=1,2,\dots ,t{n}_i\hspace{0.17em},d=1,2,\dots ,D\hspace{0.33em},\hspace{0.33em}k=1,2,\dots ,m_d\end{array}$$

(17)

where the optimization objective $F_l$ in Equation (6) is defined as the weighted sum of the three sub-objectives $F_{il}$ (i = 1, 2, 3), with ${\omega }_i$ representing the weights. Equation (7) is the sum of the value points $v{p}_i$ of the selected user stories, with $v{p}_i$ being the integer between 0 and 20 [43]. Equation (8) is the sum of average team efficiency and team satisfaction. Team efficiency is calculated as the ratio of the assigned story points to the team speed, while team satisfaction is defined as the product of the team’s experiences and preferences for different categories of user stories, both of which belong to $\left[0, 1\right]$. Equation (9) represents the average time utilization rates of all employees across all teams, also belonging to $\left[0, 1\right]$. In order to make the three weighted terms in the same order of magnitude, the weights are set as ${\omega }_1=0.01$, ${\omega }_2=1$, ${\omega }_3=1$, respectively. Equations (10)–(17) are the constraints. Equation (10) indicates that for each sprint, the sum of story points of the selected user stories must not exceed the sum of all team speeds. Equation (11) means that the story points assigned to each team must not exceed the speed of that team. Equation (12) indicates that the total task efforts of each team shall not exceed the working hours of all team employees. Equation (13) indicates that each team completes at least one user story. Equation (14) indicates that the task efforts assigned to each employee in the team must not exceed his/her maximum working hours. Equation (15) indicates that each employee completes at least one task. Equation (16) indicates that each task of each story is performed by only one employee in a particular team. Equation (17) indicates that the employee responsible for the task must have the skill required by that task.

Both our model MTASPS and the existing software project dynamic scheduling models [44,45,46] address the task allocation problem, but they are different in several aspects: (1) In terms of the scheduling mode, our model adopts periodic dynamic scheduling aligned with the characteristics of agile project development, performing scheduling at the beginning of each sprint. In contrast, most existing models utilize event-driven dynamic scheduling, which relies on the immediacy of event response and lacks periodic planning essential for multi-team collaboration. (2) In terms of subproblems, our model includes three tightly coupled sub-problems, better reflecting actual software project scheduling, while the exiting models only solve the task-employee allocation, overlooking the impact of teams on project scheduling. (3) In terms of task properties, our model adheres to agile project scheduling principles by decomposing user stories into modular tasks of short working hours, each requiring only one skill and completed by one employee in a particular team. Each employee can develop only one task at the same time. In contrast, each task in the traditional waterfall software projects typically requires more than one skill, developed collaboratively by multiple employees. An employee is allowed to work on multiple tasks at the same time. (4) In terms of decision variables, the constructed model decides which user stories to select for each sprint and which employee from which team develops each of the tasks contained in each story. However, the existing model determines the dedication of each employee to each task (the ratio of the hours for which an employee works on a task to his/her maximum working hours). (5) In terms of delivery time, the constructed model adheres to agile scheduling principles by establishing a negotiated fixed delivery time beforehand, whereas a traditional waterfall software project minimizes project duration by searching for the task–employee allocation matrix.

4. A Dynamic Periodic Scheduling Method for MTASPS

In order to solve the formulated model MTASPS, a dynamic periodic scheduling method based on a dual-indicator group learning particle swarm optimization algorithm (DGLPSO) is proposed. Framework of the scheduling method and the procedure of DGLPSO are introduced.

4.1. Framework of the Dynamic Periodic Scheduling

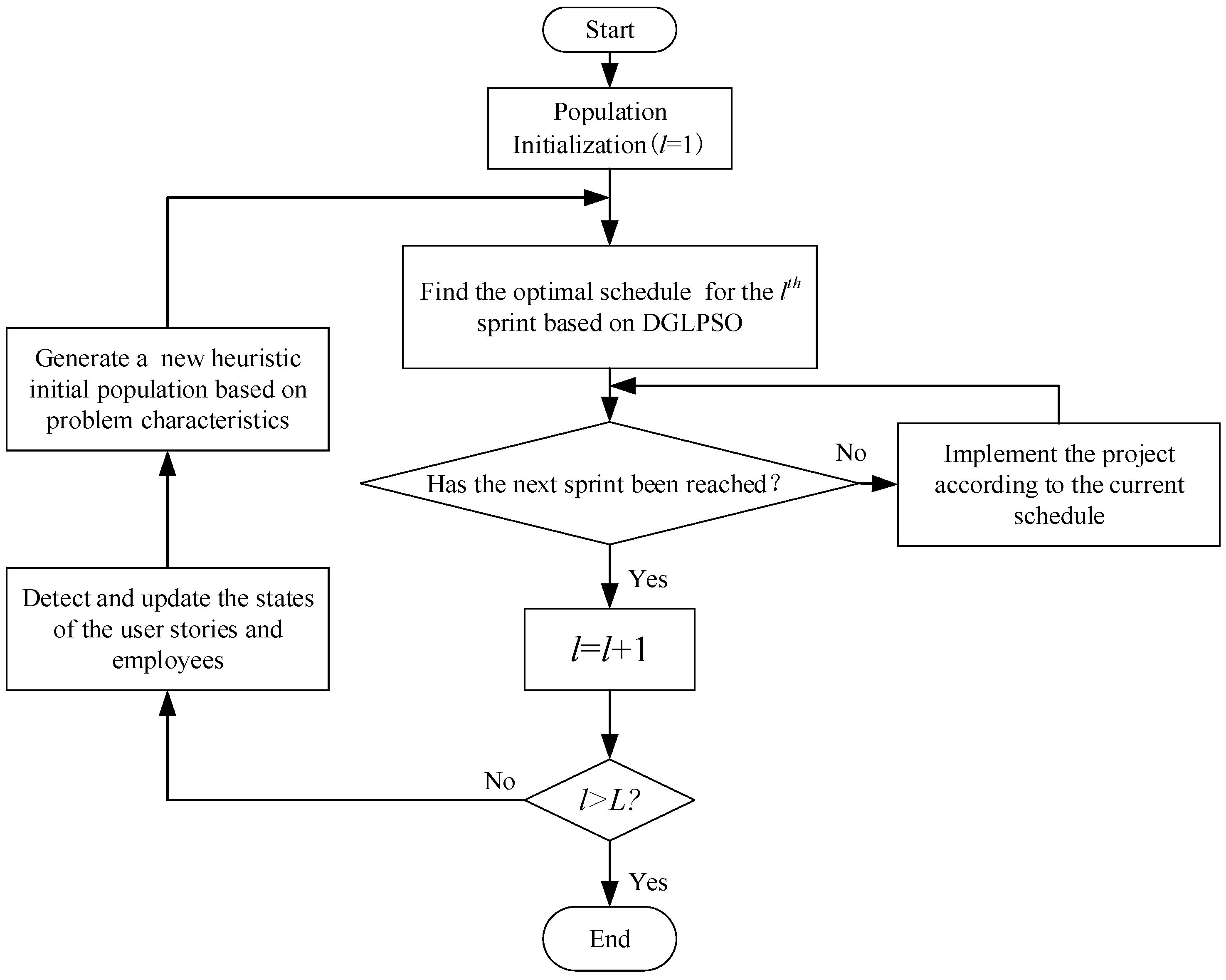
The initial scheduling–periodic rescheduling approach is used to solve the model MTASPS, and the scheduling framework is shown in Figure 2.

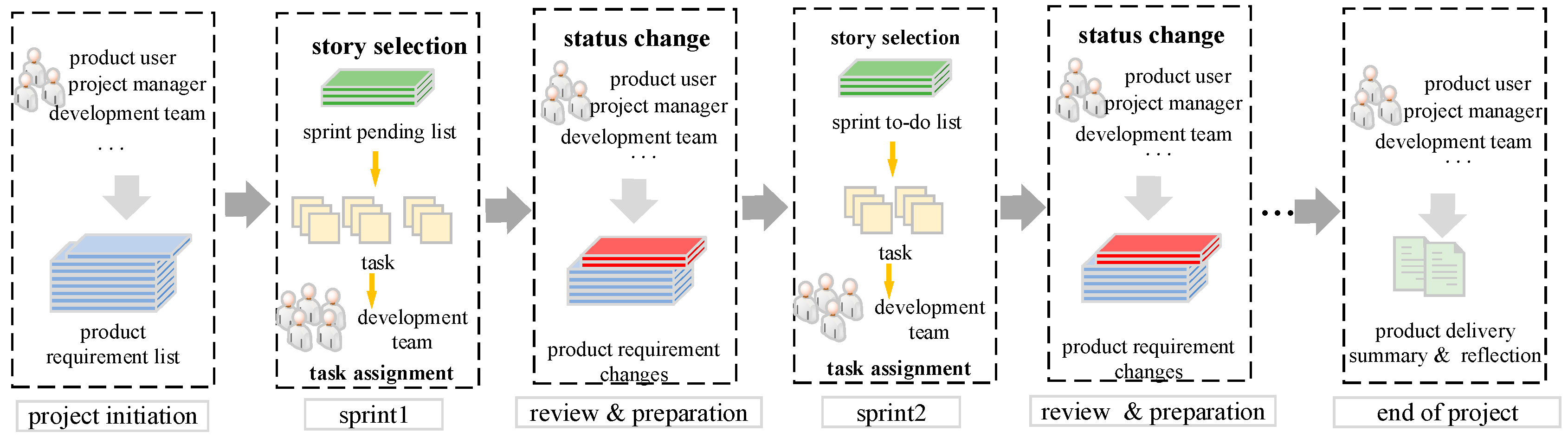
The scheduling has three steps.

Step 1: At the initial time of the project, the project manager specifies key project properties, including user stories to implement, decomposed tasks from user stories, effort estimates, task skill requirements, and employees’ maximum working hours. For example, the project manager may decompose 12 tasks from a user story, like requirements analysis, solution design, UI design, and software testing. After decomposition of user stories, the project manager specifies required skills for each task and estimates effort using techniques such as planning poker or function point analysis. Additionally, the project manager is required to specify team and employee properties, like team development experience and employee maximum working hours. These properties are derived from the project manager’s practical experience, project-specific knowledge, and historical project data. Then, an initial population is generated based on the properties of user stories and employees. The optimal schedule for the first sprint (l = 1), including the user story selection, story-team assignment, and task-employee allocation, is determined by the proposed algorithm DGLPSO. The algorithm optimizes the object while adhering to constraints like each employee must be assigned at least one task, and task skill requirements must be fulfilled.

Step 2: Determine whether the next sprint has been reached. If not, execute the project according to the current schedule. If yes, let l = l + 1, then detect and update the states of user stories and employees at the beginning of the l^th sprint through the sprint retrospective and sprint review mechanisms. All the states serve as inputs to DGLPSO. After that, generate a new heuristic initial population based on domain knowledge and obtain the optimal schedule for the sprint by DGLPSO.

Step 3: Step 2 is repeated until the end of the last sprint (l > L).

4.2. The Procedure of DGLPSO

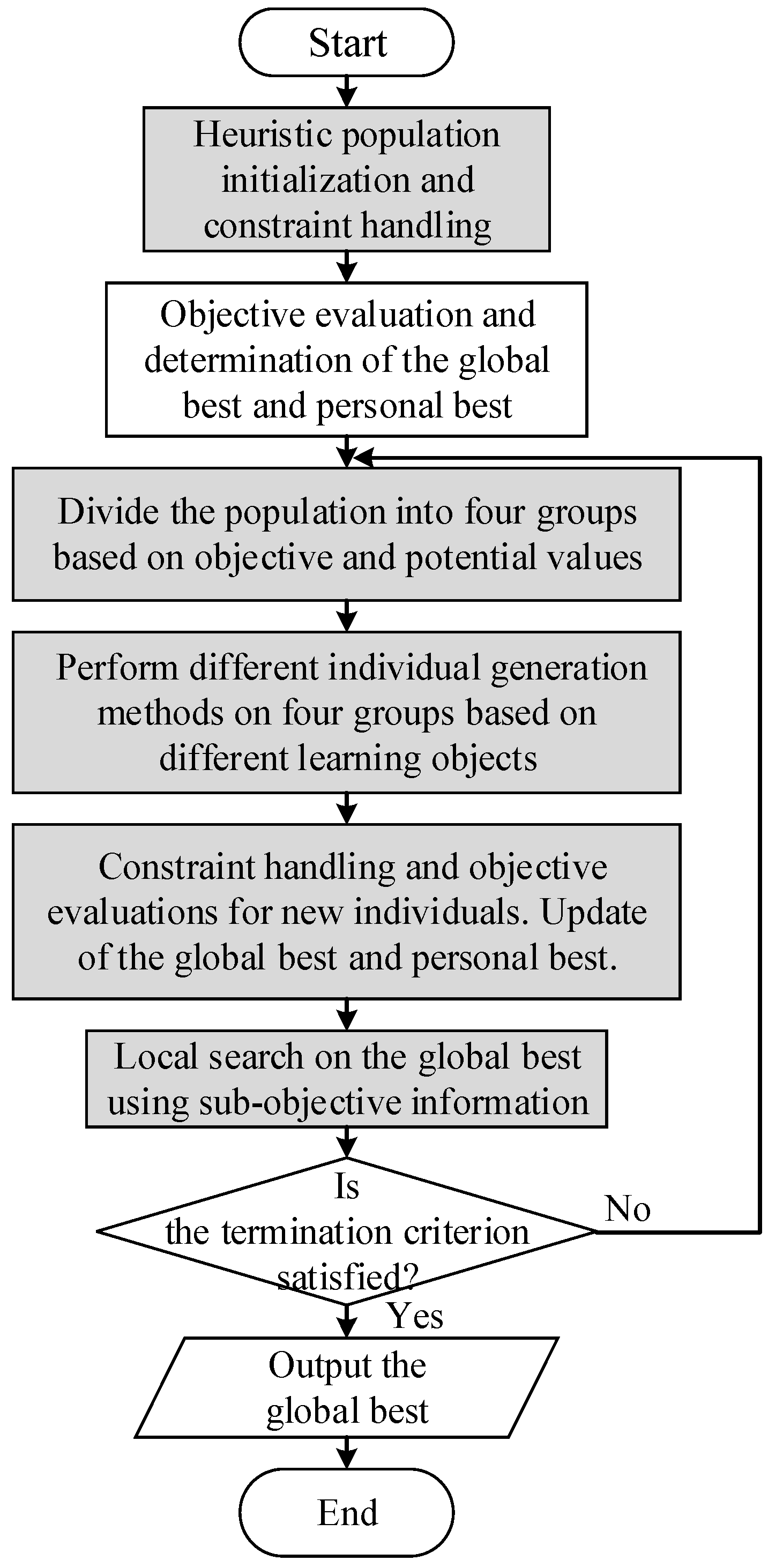
The procedure of DGLPSO is shown in Figure 3, where the new strategies are marked in gray. The algorithm consists of seven steps: (1) Initialize the population by heuristic information and handle the constraints. (2) Evaluate the objective values and obtain the personal best and the global best. (3) Divide the population into four subgroups based on the objective values and potential values. (4) Update the individuals by selecting different learning objects for different subgroups. (5) Perform constraint handling and objective evaluation on the updated individuals and update the personal and the global best. (6) Conduct local search on the global best by the knowledge derived from the sub-objectives. (7) Check the termination criterion.

4.3. Encoding and Decoding

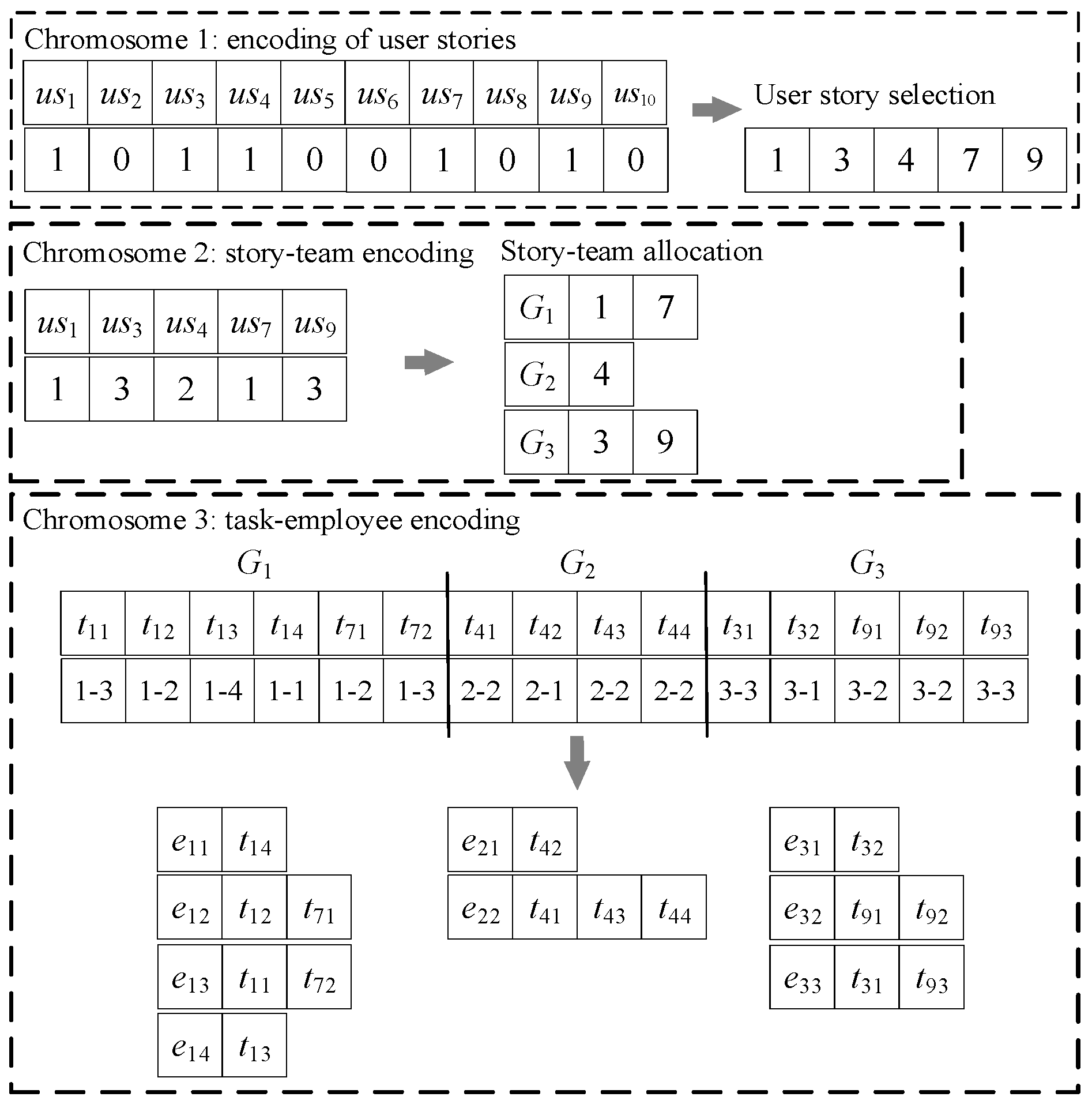
For the three tightly coupled sub-problems of MTASPS, an encoding method with variable-length three-layer chromosomes is designed. Figure 4 presents an encoding and decoding illustration.

The project in Figure 4 has ten initial user stories and three teams. The number of employees in each team is four, two, and three, respectively. Chromosome 1 encodes the user stories by a 0/1 string, with “1” and “0” indicating selection or non-selection of the corresponding story. The length of chromosome 1 is the number of initial user stories n in the first sprint, and it changes with the customer’s requirements in subsequent sprints (user stories have been completed, added, or cancelled), i.e., the length is not fixed. By decoding, the user stories us₁, us₃, us₄, us₇, and us₉ are selected in the current sprint. Chromosome 2 is the story team encoding, indicating the assignment of the user stories to the teams. The code represents the team number. After decoding, team G₁ will complete the user stories us₁ and us₇, G₂ will complete us₄, and G₃ will complete us₃ and us₉. Each user story is decomposed into several tasks, which are assigned to the employees of the corresponding team, taking into account the skill constraints and the employees’ working time constraints. Chromosome 3 is such a task-employee encoding. Take team G₂ as an example. The user story us₄ is decomposed into four tasks, which are assigned to the two employees in G₂. Among them, employee e₂₁ performs task t₄₂, and the remaining tasks t₄₁, t₄₃, and t₄₄ are assigned to employee e₂₂.

4.4. Heuristic Population Initialization Based on Objective Information

According to the step (1) in Section 4.2, in the l^th sprint ($l=1,2,\dots ,L$), with the aim of improving quality of the initial population and providing the algorithm with a good starting point, heuristic information is extracted from the sub-objective related to each of the three sub-problems. Four selection strategies are designed: value point-based roulette selection, team satisfaction-based roulette selection, team speed-based roulette selection, and working hours-based roulette selection. The greater the value points, the higher the probability of selecting the user story to be executed in the current sprint. The greater a team’s satisfaction or speed, the higher the probability of selecting the team to conduct the current user story. The greater an employee’s maximum working hours in the current sprint, the higher the probability of selecting the employee to execute a task. Figure 5 shows the heuristic population initialization strategy. For the initial population of size N, N/2 individuals are randomly generated in all the three sub-problems to introduce randomness. For the other N/2 individuals, one of the four roulette selection strategies mentioned above is randomly selected, based on which the corresponding sub-problem is heuristically generated. Meanwhile, the remaining two sub-problems are still randomly initialized.

4.5. Constraint Handling

According to Section 4.2, new individuals are generated in both steps (1) and (5). To ensure the feasibility of individuals and avoid the reduction in search efficiency and computational resource waste caused by discarding infeasible solutions during the initialization and individual updating, we design some constraint handling methods to process individuals according to the constraints shown in Equations (10)–(17). On one hand, it mitigates the appearances of infeasible solutions. On the other hand, if generated, such infeasible solutions can be transformed into feasible ones while preserving part of their original information.

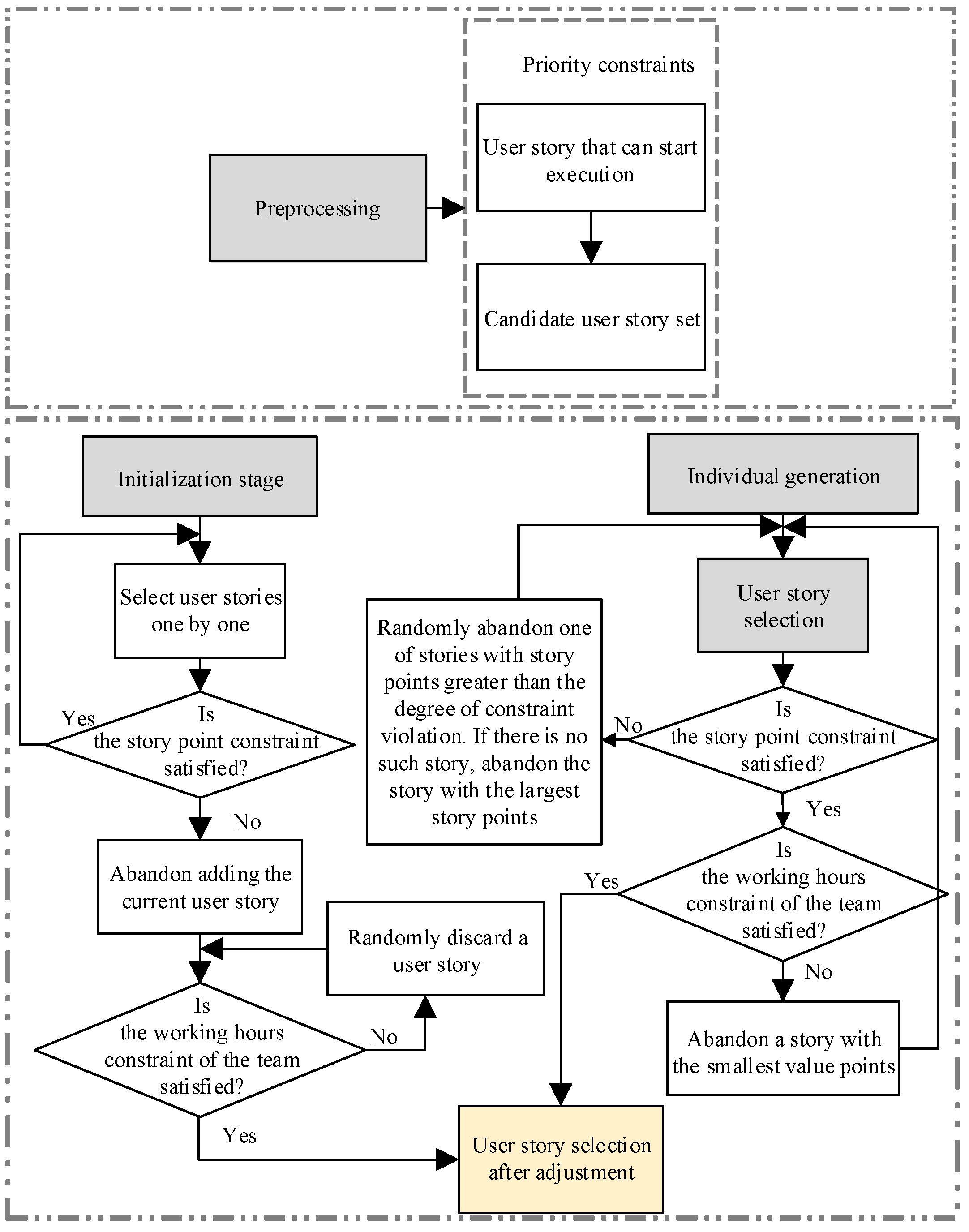
Constraint handling for user story selection in both the initialization and individual generation is shown in Figure 6. Pre-processing is conducted at the beginning of each sprint, and the user stories that can start executing constitute the candidate story set based on the story priorities.

In the population initialization, one user story is selected each time and added to the current schedule based on value point-based roulette selection or random selection. This process iterates until the story point constraint defined in Equation (10) is violated, at which point the last added story is removed. Then, check whether the total task efforts decomposed from the selected user stories satisfy the working hours constraint of the entire team (Equation (12)). If yes, the schedule of user story selection is determined. Otherwise, a user story is randomly discarded until Equation (12) is satisfied.

In the individual generation during evolution, first, check the story point constraint (Equation (10)) for the selected user stories of the newly generated individual. If not satisfied, a story with story points larger than the constraint violation degree is randomly discarded, and in the case that there is no such story, the story with the largest story point is discarded until the constraint is satisfied. Second, check whether the total task efforts decomposed from the selected user stories satisfy the working hours constraint of the entire team (Equation (12)). If not satisfied, discard a user story with the smallest value points (retaining the stories with higher value points as much as possible) until it satisfies the constraint.

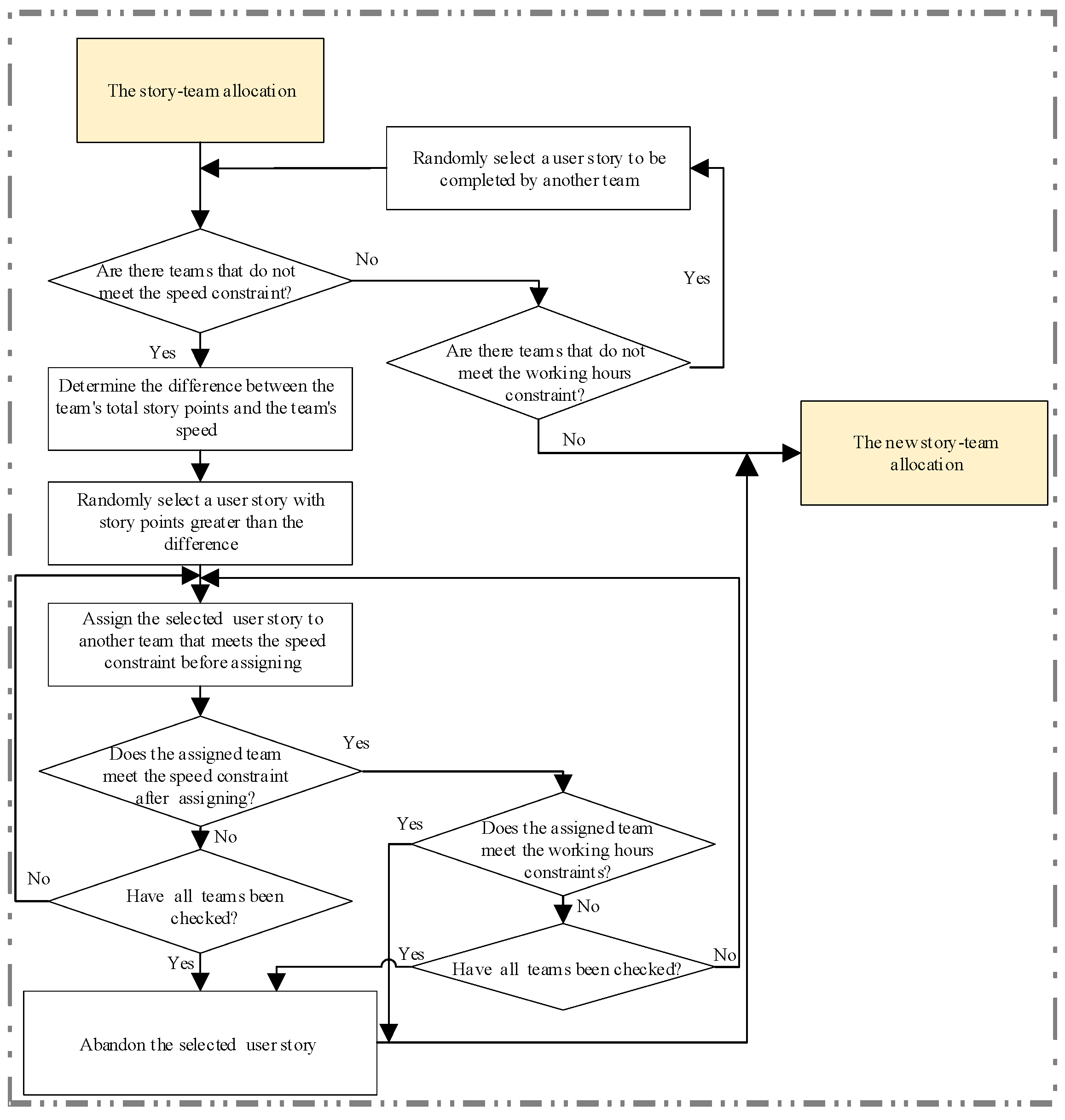
Figure 7 shows the constraint handling for story-team allocation. For a newly generated individual, first, find out the teams not satisfying the speed constraint (Equation (11)). Determine the difference between the team’s total story points and the team’s speed and randomly select a user story with story points greater than the difference. Assign the selected user story to another team that meets the speed constraint. Next, check whether the assigned team satisfies the working hours constraint (Equation (12)). If yes, the process ends. Otherwise, if none of the teams are able to complete the selected story subject to the constraints, the story is abandoned in the current sprint.

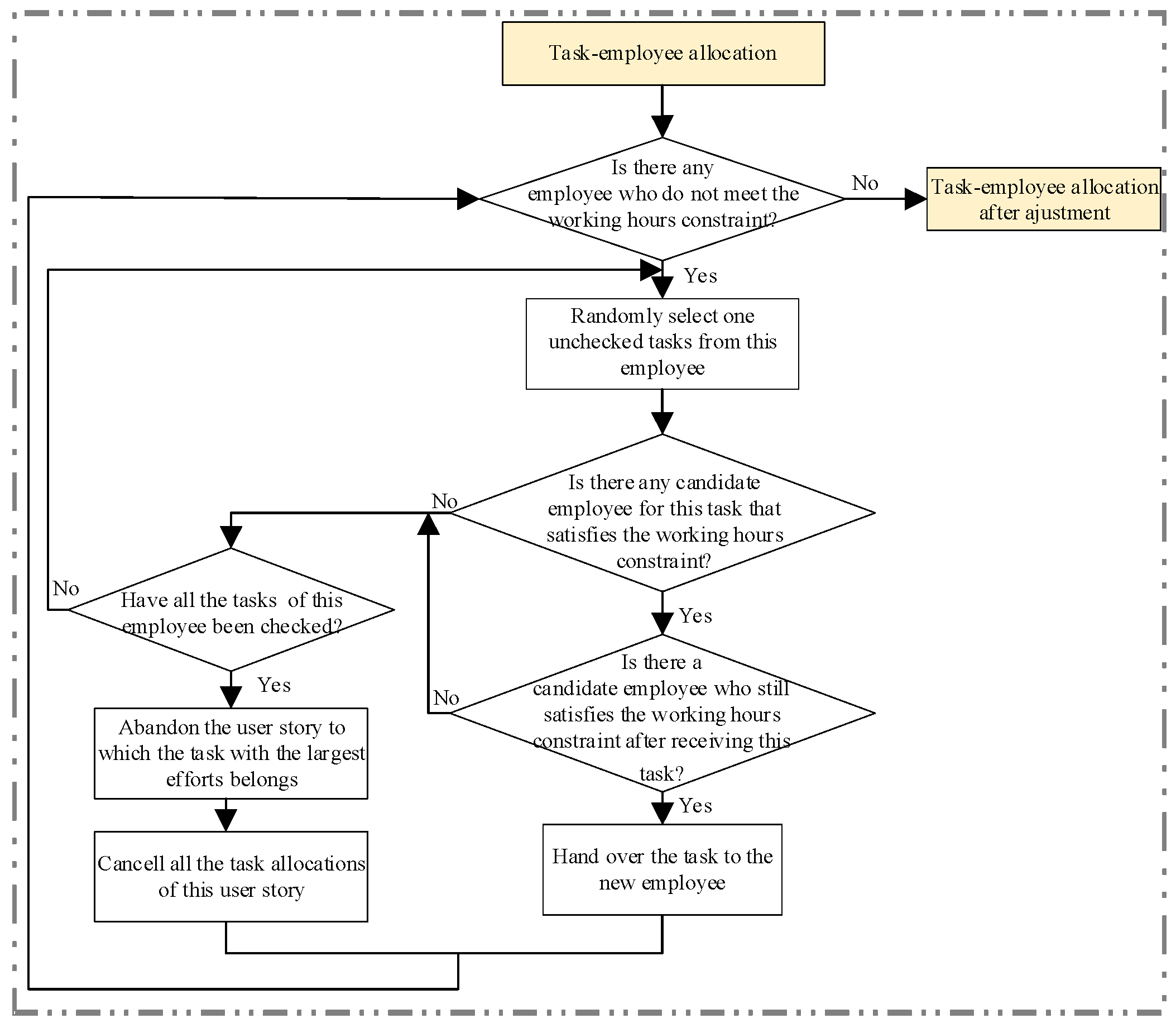
Figure 8 shows the constraint handling for task–employee allocation. After assigning employees to each task, check whether each employee satisfies the working hours constraint (Equation (14)). If there is an employee A not satisfying this constraint, test if assigning a particular task to another employee B would allow employee B to still satisfy the working hours constraint. If so, the task is reassigned to employee B. If not, the story that employee A’s task with the largest efforts belongs to is abandoned.

4.6. The Dual-Indicator Group Learning Strategy

According to steps (3), (4), and (5) in Section 4.2, individuals are grouped and updated. Most existing population grouping methods classify population into better and worse individuals only based on a single indicator, such as the objective value or degree of improvement [47]. However, this kind of method ignores the potential for individual evolution and promotion space. To address this issue, a population grouping approach that considers both the objective value and the potential value is proposed. By integrating both the objective value F_l and evolutionary potential value Q_l (as shown in Equation (18)) of individuals in the current l^th sprint, this approach can not only avoid the mis-discarding of high-potential individuals, thereby maintaining the population diversity, but also implements differentiated learning strategies based on combined characteristics, thereby achieving a dynamic balance between exploitation and exploration.

$$Q_l={\alpha }_1·\left({\displaystyle \sum _{d=1}^D{v}_{dl}-{\displaystyle \sum _{u{s}_i\in p{b}_l}{x}_{il}·s{p}_i}}\right)+{\alpha }_2·\left(2-F_{2l}\right)+{\alpha }_3·\left(1-F_{3l}\right)$$

(18)

where the first term of Q_l represents that after executing the schedule at the l^th sprint, the user story points that can still be developed in the remaining time. The second term denotes the value that can be increased in the team efficiency and team satisfaction. The third term means the value that can be increased in the employee’s average time utilization rates. The coefficients ${\alpha }_1=0.1$, ${\alpha }_2=1$, and ${\alpha }_3=1$ make the three weighted terms in the same order of magnitude.

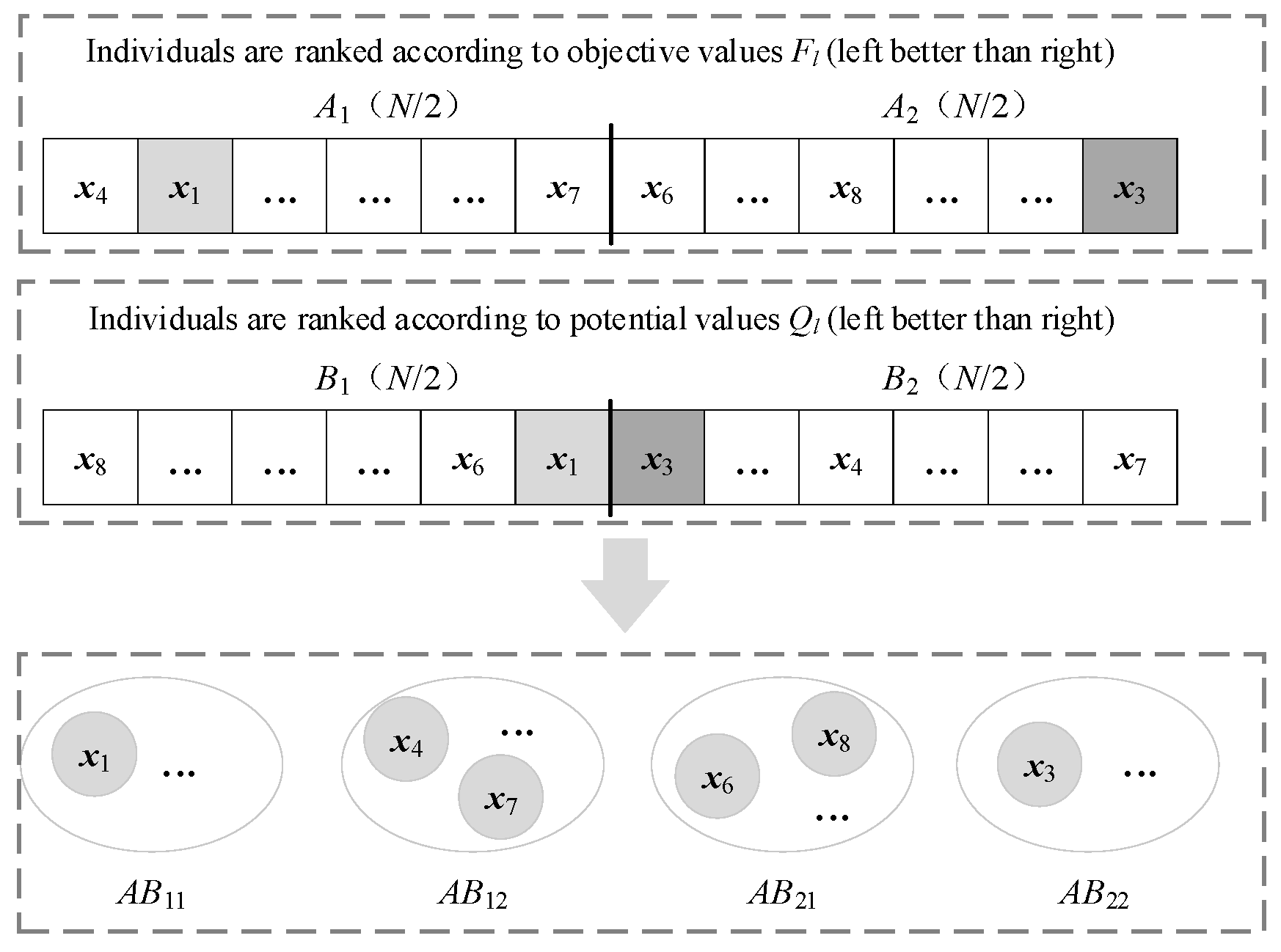
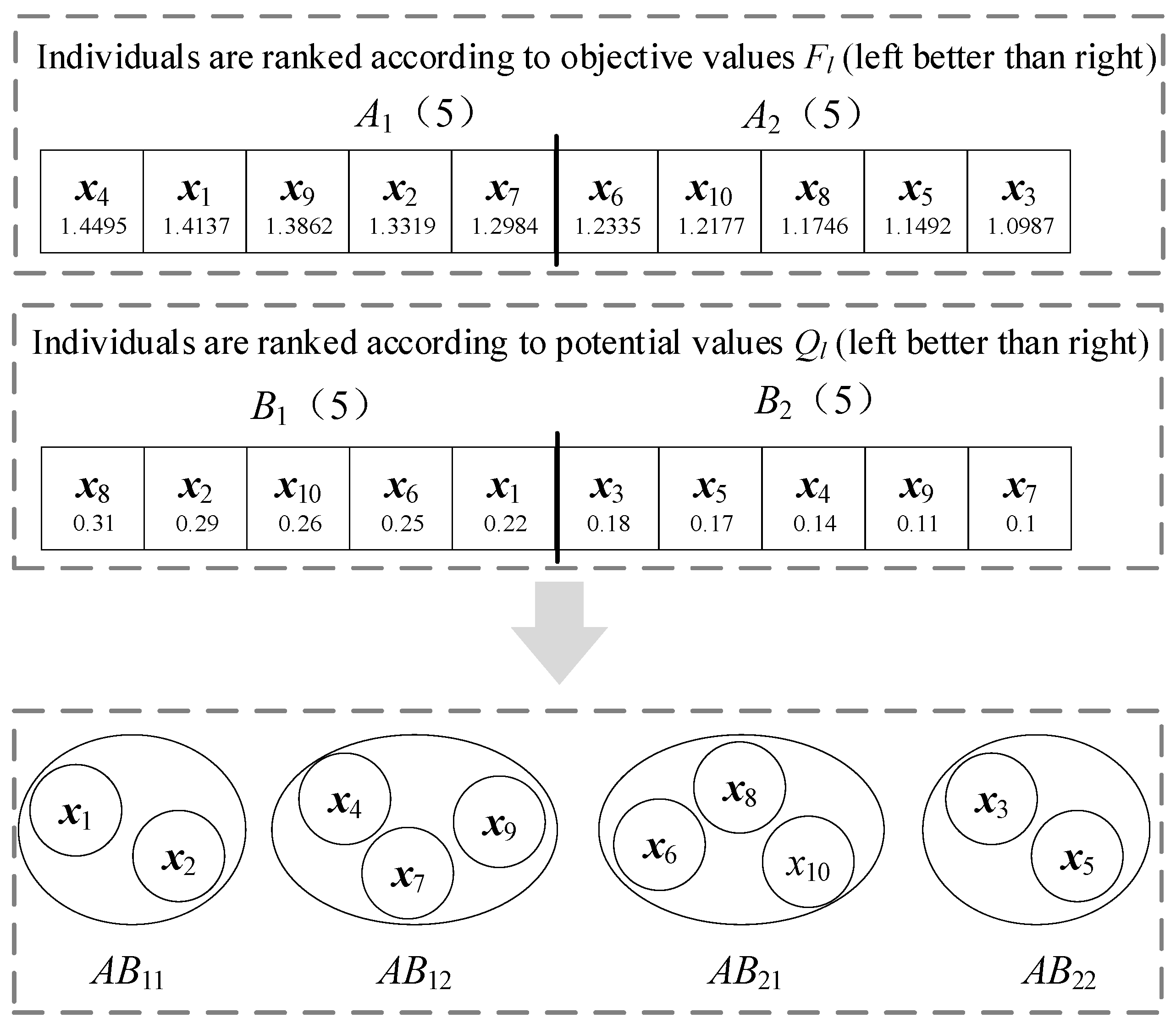
Figure 9 illustrates the dual-indicator group learning strategy. First, N individuals in the population are, respectively, sorted according to the objective value F_l and the potential value Q_l, obtaining two sequences of population. For the convenience of understanding, A₁ and A₂, respectively, denote the top N/2 individuals and the last N/2 individuals according to F_l, and B₁ and B₂, respectively, denote those according to Q_l. Selecting N/2 as the grouping criterion ensures a uniform distribution, thereby mitigating potential biases arising from uneven group sizes and striking a balance between exploration and exploitation in individual evolution. Then, according to the sorting position of each individual on F_l and Q_l, the whole population is divided into four groups, named AB₁₁, AB₁₂, AB₂₁, and AB₂₂, respectively.

Take Figure 10 as an example. There are a total of 10 individuals, so A₁, A₂, B₁, and B₂ each contain 5 individuals. The numerical values below the individual ${\mathit{x}}_i(i=1,2\dots \dots 10)$ in each box represent corresponding F_l or Q_l. A₁ and A₂ are sorted in descending order based on F_l, and B₁ and B₂ are sorted in descending order according to Q_l. Thus, it can be seen that A₁ includes the ${\mathit{x}}_4$, ${\mathit{x}}_1$, ${\mathit{x}}_9$, ${\mathit{x}}_2$, ${\mathit{x}}_7$, A₂ includes the ${\mathit{x}}_6$, ${\mathit{x}}_{10}$, ${\mathit{x}}_8$, ${\mathit{x}}_5$, ${\mathit{x}}_3$, B₁ includes the ${\mathit{x}}_8$, ${\mathit{x}}_2$, ${\mathit{x}}_{10}$, ${\mathit{x}}_6$, ${\mathit{x}}_1$, and B₂ includes the ${\mathit{x}}_3$, ${\mathit{x}}_5$, ${\mathit{x}}_4$, ${\mathit{x}}_9$, ${\mathit{x}}_7$. ${\mathit{x}}_1$ is sorted in A₁ based on F_l and sorted in B₁ based on Q_l; thus, it will be divided into group AB₁₁. Grouping of other individuals can be obtained in the same way. Ultimately, AB₁₁ comprises ${\mathit{x}}_1$ and ${\mathit{x}}_2$, AB₁₂ comprises ${\mathit{x}}_4$,${\mathit{x}}_9$, AB₂₁ comprises ${\mathit{x}}_6$, ${\mathit{x}}_8$, and ${\mathit{x}}_{10}$, and AB₂₂ comprises ${\mathit{x}}_3$ and ${\mathit{x}}_5$.

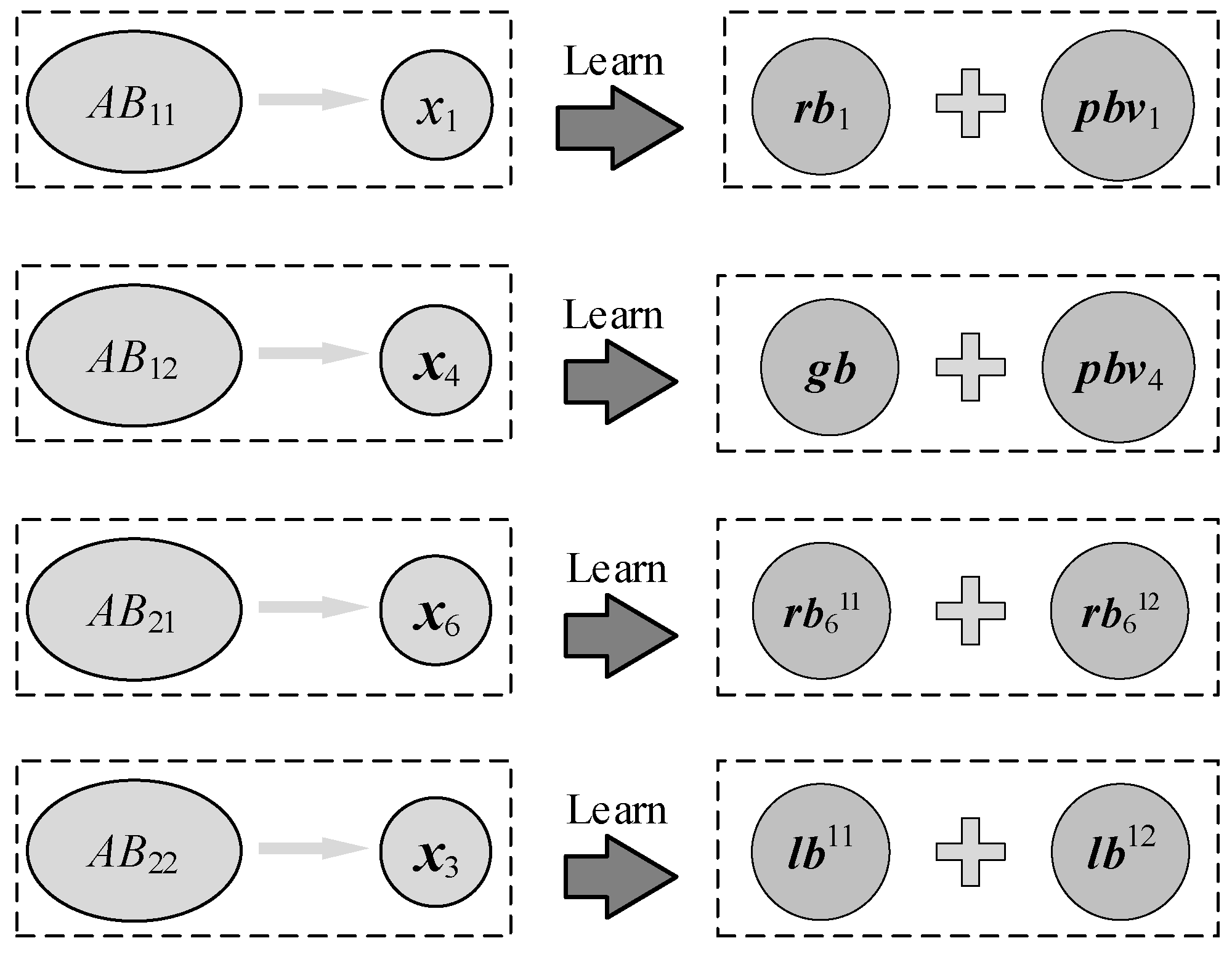
In classical PSO, the current individual learns respectively from the personal best and the global best to generate a new individual. We improve this individual generation method by selecting two appropriate learning objects based on the characteristics of different groups.

Figure 11 illustrates the learning object selection method for different groups. For the individual ${\mathit{x}}_1$ in group AB₁₁, it has not only a good fitness value but also a great improvement potential. Select the personal best value ${\mathit{pbv}}_1$ of ${\mathit{x}}_1$, and any individual $\mathit{r}{\mathit{b}}_1$ in group AB₁₁ or AB₁₂ whose objective value is better than ${\mathit{x}}_1$ as the learning object. This method ensures ${\mathit{x}}_1$ to learn from the better individual while increasing the population diversity to a certain extent. For the individual ${\mathit{x}}_4$ in group AB₁₂, the personal best value ${\mathit{pbv}}_4$ of ${\mathit{x}}_4$ and the current global best $\mathit{gb}$ are selected as learning objects. Compared to group AB₁₁, the individuals in group AB₁₂ have less improvement room. Thus, the current global best $\mathit{gb}$ is used to guide the learning in order to further improve their qualities. Individual ${\mathit{x}}_6$ is located in group AB₂₁, indicating that it has a poor objective value but a lot of room for improvement. Individuals in this group have a high chance of evolving into better solutions. Therefore, individuals in this group are guided to diversify their learning in order to enhance the population diversity. Individuals $\mathit{r}{\mathit{b}}_6^{11}$ and $\mathit{r}{\mathit{b}}_6^{12}$ are, respectively, selected from groups AB₁₁ and AB₁₂ uniformly at random as their learning objects, ensuring that the individuals learn from the better individuals while also making full use of the effective information from other individuals. Individual ${\mathit{x}}_3$ is located in group AB₂₂, which has poor objective and potential values. The individuals $\mathit{l}{\mathit{b}}^{11}$ and $\mathit{l}{\mathit{b}}^{12}$, with the optimal objective values in groups AB₁₁ and AB₁₂, are, respectively, selected as its learning objects. $\mathit{l}{\mathit{b}}^{11}$ or $\mathit{l}{\mathit{b}}^{12}$ is definitely the current global best $\mathit{gb}$, which ensures that the individual moves in a better direction.

4.7. Objective-Driven Local Search Operators

After updating the individuals, as depicted in step (6) of Section 4.2, the local search is conducted. To further improve the search accuracy of the algorithm, three enhanced local search operators are designed to mine around the neighborhood of global best based on the information of each sub-objective.

4.7.1. The Greedy Insertion Operator Based on the Team Speed Constraint

For the subproblem of user story selection, a greedy insertion operator based on team speed constraint is designed to maximize the total value points of user stories in the current sprint, as shown in Figure 12. Chromosome 1 of individual ${\mathit{x}}_p$ represents the schedule of user stories in the current sprint, based on which the unselected user story is inserted one by one, and the team speed constraint (Equation (10)) is checked. If it is satisfied, the story is added and the current operation ends. If not, the search continues for the next story that satisfies the speed constraint. If the constraint is still not satisfied after traversing all the unselected stories, the operation ends, and the original chromosome 1 remains unchanged. The updated chromosome 1 (${\mathit{x}}_{p1}^{*}$) of ${\mathit{x}}_p$ in the illustration of Figure 12 newly selects the user story us₇.

4.7.2. Local Search Operators Based on Team Efficiency or Team Satisfaction

For the subproblem of story–team allocation, two local search operators based on team efficiency or team satisfaction are, respectively, designed, as shown in Figure 13. The newly selected user stories generated by the greedy insertion operator (Section 4.7.1) are allocated to the team with the lowest development efficiency or team satisfaction to complete, and the new story–team allocation schedule, i.e., the updated chromosome 2 (${\mathit{x}}_{p2}^{*}$), is obtained. In Figure 13, if the local search operator based on team efficiency is used, the newly selected user story us₇ is assigned to team G₃. If the local search based on team satisfaction is used, us₇ is assigned to team G₁.

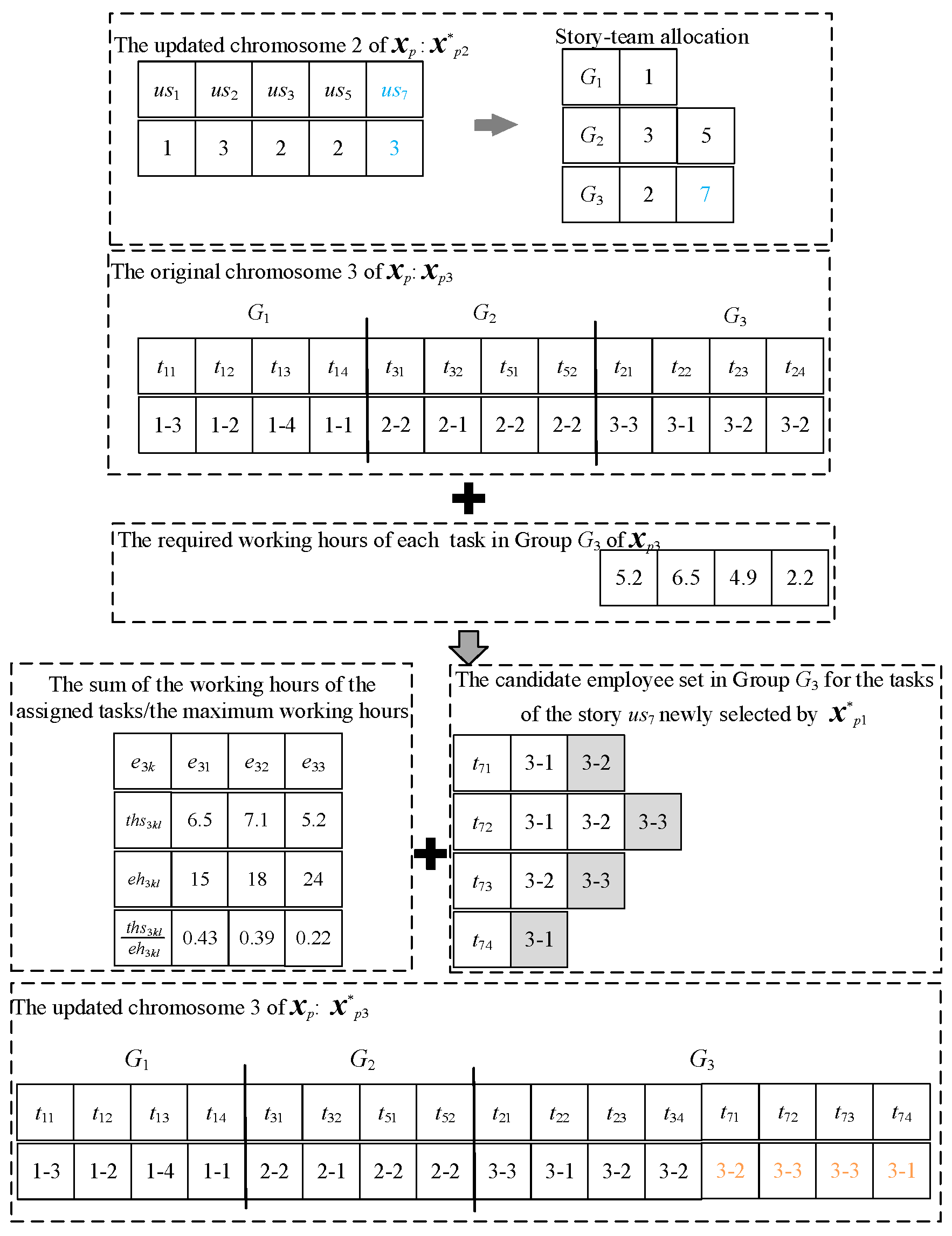
4.7.3. The Local Search Operator Based on the Time Utilization Rate

For the subproblem of task–employee allocation within each team, a local search operator based on the time utilization rate is designed to assign the tasks of the newly selected user stories to the candidate employees in the team with low time utilization rates, as in Figure 14. The time utilization rate $ET{A}_{dkl}$ of the k^th employee in the d^th team at the l^th sprint is defined in Equation (19).

$$ET{A}_{dkl}={\displaystyle \frac{{\displaystyle \sum _{u{s}_i\in p{b}_l}{\displaystyle \sum _{j=1}^{t{n}_i}{x}_{il}·y_{idl}·z_{ijdkl}·t{h}_{ij}}}}{e{h}_{dkl}}}$$

(19)

Assume that Figure 13 employs a team-efficiency-based local search operator to assign the newly selected user story us₇ to team G₃. So, it is necessary to assign each task $t_{7j}$ in us₇ to each employee $e_{3k}$ in G₃. As shown in Figure 14, for the originally assigned story us₂ in G₃, its task–employee allocation is kept unchanged. From this, we can obtain the sum of task durations $th{s}_{3kl}$ that each employee $e_{3k}$ has undertaken at the l^th sprint. Together with the maximum working hours $e{h}_{3kl}$, we can calculate the current time utilization rate $ET{A}_{3kl}={\displaystyle \frac{th{s}_{3kl}}{e{h}_{3kl}}}$ of employee $e_{3k}$. For each task of the newly selected user story us₇, the employee with the lowest time utilization rate is selected from the set of candidate employees who grasp the skill required by the task. For example, task $t_{71}$ is completed by employee $e_{32}$, $t_{72}$ is completed by employee $e_{33}$, and so on. In this way, an updated chromosome 3 (${\mathit{x}}_{p3}^{*}$) is generated. If the new individual ${\mathit{x}}_p^{*}$ consisting of ${\mathit{x}}_{p1}^{*}$, ${\mathit{x}}_{p2}^{*}$, and ${\mathit{x}}_{p3}^{*}$, is infeasible, it is adjusted using the constraint handling method of Section 4.5.

5. Experimental Studies

With the aim of verifying the effectiveness of the proposed strategies and algorithm, we conducted all the experiments in PyCharm 3.9 on a personal computer with an Intel (R) core (TM) i5-7200u CPU @2.50 GHz made in China, and 8 GB Samsung operating memory made in China. Four groups of experiments were performed: (1) Validating the heuristic population initialization strategy. (2) Validating the dual-indicator group learning strategy. (3) Performance verification of the objective-driven local search operators. (4) Validating the overall performance of the DGLPSO-based dynamic periodic scheduling method by comparing it with five state-of-the-art algorithms.

5.1. Instance Generation and Parameter Settings

Across all experiments, the algorithm parameters were set as follows: the population size N, maximum number of fitness evaluations, and maximum number of iterations were assigned values of 100 [46], 100,000 [46], and 1000, respectively. These values represent widely adopted settings in existing literature. Furthermore, other parameters, such as the individual learning factor $c_1$ and social learning factor $c_2$, were both set to 2. This parameter configuration was determined through systematic tuning: each parameter was adjusted within the corresponding range while fixing others constant, with performance observed across experimental process.

With reference to various data of Beta, one of Norway’s largest large-scale agile development projects [47], and the estimation and plan of agile software development practice by agile expert Mike [43], 12 MTASPS instances with different sizes were generated. Each instance is named US#1_G#2_V#3, where US#1 denotes the initial number of user stories, G#2 indicates the number of teams, and V#3 denotes the initial speed of each team. Take US100_G3_V20 as an example. It indicates that a project with 100 user stories is completed by three teams, with an initial team speed being 20 story points each. Referring to the literature [15,43], the parameter settings (corresponding to Table 1) of MTASPS instances are shown in

Table 2. Parameter settings for MTASPS instances.

Parameters	Descriptions
$n$	$n=\left\{100,200,300\right\}$
$t{p}_i$	$t{p}_i=\left\{1,2,\dots ,10\right\}$
$s{p}_i$	$s{p}_i=\left\{1,2,3,5,8,13,20\right\}$ (approximate Fibonacci series)
$v{p}_i$	$v{p}_i=\left\{1,2,3,5,8,13,20\right\}$ (approximate Fibonacci series)
$t{h}_{ij}$	Follow the normal distribution of mean $\mu =4$ and variance $\sigma =0.1·\mu$ in $\left(0,8\right]$
$t{s}_{ij}$	$t{s}_{ij}\in \left\{1,2,\dots ,S\right\}$, $S=5$ is the total number of skills required for the project
$L$	$L=6$ (Assume twice a month, and there are a total of six sprints in a quarter of a year.)
$T$	$T=80$ h (A sprint has two weeks, and there are five working days a week and eight hours a day.)
$D$	$D=\left\{3,5\right\}$
$m_d$	$m_d=\left\{5,6,7,8,9,10\right\}$
$pr{e}_d^{t{p}_i}$	$pr{e}_d^{t{p}_i}\in \left(0,1\right)$
$hi{s}_d^{t{p}_i}$	$hi{s}_d^{t{p}_i}\in \left(0,1\right)$
$e{s}_{dk}$	$e{s}_{dk}\subseteq \left\{1\hspace{0.33em},2\hspace{0.33em},\dots ,\hspace{0.33em}S\right\}$
$e{h}_{dkl}$	Follow the normal distribution of mean $\mu =3T/4$ and variance $\sigma =0.1·\mu$ in $\left[T,T/2\right]$
$v_{dl}$	$v_{dl}\in \left\{20,40\right\}$

. In addition, a real instance is gathered from the IT department of a private bank [16]. The real instance is referred to as a medium-sized problem instance containing 60 user stories and 10 sprints. The instance is named Real60_D3_V20. In the Real60_D3_V20 dataset, the number of user stories, story points, story categories, and number of sprints are provided by the instance. The remaining parameters related to teams and staff members are generated based on [43,47]. The population size of the proposed DGLPSO is set to 100, the maximum number of local search iterations is set to 5, and the algorithm terminates after the number of objective evaluations reaches the maximum value of 20,000.

5.2. The Experimental Procedure

In the experiments, each instance includes L sprints (iterations). Eleven algorithms are used to solve the scheduling problems in each sprint, including the proposed algorithm DGLPSO, the five algorithms used to validate effectiveness of the new strategies, and the five comparison algorithms in validating the proposed algorithm. Since the overall performance evaluation of each algorithm across all sprints is different from that at a single scheduling point, the experimental procedures of multi-team agile software project dynamic periodic scheduling are described below.

Step 1: At the beginning of the l^th sprint, each of the 11 algorithms runs 20 times, and it terminates until the number of objective evaluations reaches a maximum value of 20,000 in each run. Then, the obtained 220 results are combined, from which the optimal schedule corresponding to the maximum objective value is determined.

Step 2: In the l^th sprint, the project is developed according to the selected new optimal schedule. This approach ensures that all the 11 algorithms are compared in the same working environment in each sprint.

Step 3: Determine whether l is equal to the maximum number L. If not, collect the attributes of user stories (including new stories, unfinished stories, etc.), tasks, teams, and employees at the initial time of the (l + 1)^th sprint and update the scheduling environment. Then let l = l + 1 and go to step 1. If l is equal to L, then perform step 4.

Step 4: Compare the overall performance of each algorithm across different runs and sprints. As shown in Figure 15, for the kth run $\left(k=1,2,\dots ,20\right)$ of the q^th algorithm $\left(q=1,2,\dots ,11\right)$, the optimal objective values in L sprints are averaged to obtain $mea{n}_k^q$. The 20 average values obtained from 20 runs form a vector $\mathit{v}\mathit{e}{\mathit{c}}^{\mathit{q}}$. The average and best values of the vector $\mathit{v}\mathit{e}{\mathit{c}}^{\mathit{q}}$ are recorded as $\mathrm{Avg}{.}^q$ and ${\mathrm{Best}}^q$, respectively, which are treated as the overall average and best values of the q^th algorithm. In addition, the Wilcoxon rank sum tests with the significance level of 0.05 are adopted to statistically test the vector $\mathit{v}\mathit{e}{\mathit{c}}^1$ of the proposed algorithm DGLPSO against the vectors ($\mathit{v}\mathit{e}{\mathit{c}}^{\mathit{k}},k=2,\dots ,11$) of the other 10 algorithms. Experimental results are shown in

Table 3. Comparison results between the proposed algorithm and the algorithm that replaces a single strategy.

Instances	US100_D3_V20		US100_D3_V40		US100_D5_V20		US100_D5_V40
	Avg.	Best	Avg.	Best	Avg.	Best	Avg.	Best
DGLPSO	2.41	2.55	3.61	3.75	2.63	2.87	4.05	4.25
DGLPSO-RI	2.30+	2.41	3.63=	3.67	2.52+	2.65	3.97+	4.07
DGLPSO-PVG	2.39=	2.50	3.57+	3.69	2.58+	2.73	3.98+	4.15
DGLPSO-OVG	2.31+	2.43	3.60=	3.68	2.55+	2.75	3.95+	4.09
DGLPSO-GL	2.38=	2.49	3.56+	3.68	2.57+	2.69	3.93+	4.04
DGLPSO-LS	2.27+	2.38	3.49+	3.63	2.45+	2.61	3.85+	3.82
Instances	US200_D3_V20		US200_D3_V40		US200_D5_V20		US200_D5_V40
	Avg.	Best	Avg.	Best	Avg.	Best	Avg.	Best
DGLPSO	2.49	2.75	3.57	3.82	2.78	2.94	4.01	4.36
DGLPSO-RI	2.40+	2.49	3.53+	3.65	2.74=	2.89	4.03=	4.19
DGLPSO-PVG	2.45+	2.68	3.54+	3.73	2.77=	2.90	3.95+	4.32
DGLPSO-OVG	2.43+	2.62	3.52+	3.70	2.76=	2.85	3.96+	4.26
DGLPSO-GL	2.45+	2.61	3.52+	3.70	2.77=	2.88	3.91+	4.30
DGLPSO-LS	2.36+	2.52	3.42+	3.51	2.64+	2.80	3.81+	4.05
Instances	US300_D3_V20		US300_D3_V40		US300_D5_V20		US300_D5_V40
	Avg.	Best	Avg.	Best	Avg.	Best	Avg.	Best
DGLPSO	2.37	2.58	3.34	3.40	2.88	3.13	4.44	4.71
DGLPSO-RI	2.35=	2.48	3.17+	3.30	2.80+	2.94	4.39+	4.57
DGLPSO-PVG	2.34+	2.50	3.26+	3.33	2.83+	3.00	4.40+	4.61
DGLPSO-OVG	2.33+	2.52	3.22+	3.28	2.81+	3.06	4.36+	4.59
DGLPSO-GL	2.34+	2.49	3.12+	3.21	2.83+	2.95	4.38+	4.49
DGLPSO-LS	2.23+	2.23	3.03+	3.17	2.72+	3.05	4.24+	4.51
Instances	Real60_D3_V20		+/=/−
	Avg.	Best
DGLPSO	2.28	2.42
DGLPSO-RI	2.22+	2.32	9/4/0
DGLPSO-PVG	2.23+	2.39	11/2/0
DGLPSO-OVG	2.19+	2.35	11/2/0
DGLPSO-GL	2.23+	2.38	11/2/0
DGLPSO-LS	2.14+	2.28	13/0/0

and

Table 4. Experimental results of the proposed algorithm and the comparison algorithms.

Instances	US100_D3_V20		US100_D3_V40		US100_D5_V20		US100_D5_V40
	Avg.	Best	Avg.	Best	Avg.	Best	Avg.	Best
DGLPSO	2.41	2.55	3.63	3.75	2.63	2.87	4.05	4.25
GA-HC	2.13+	2.18	3.30+	3.33	2.32+	2.35	3.61+	3.66
DQPSO	2.33+	2.48	3.55+	3.68	2.53+	2.70	3.90+	4.03
TLPSO	2.28+	2.40	3.68=	3.69	2.55+	2.70	3.87+	4.00
EDPSO	2.34+	2.43	3.54+	3.70	2.51+	2.62	3.93+	4.07
SW-OBLCSO	2.27+	2.36	3.46+	3.61	2.51+	2.73	3.82+	3.92
iACO4iNRP	2.35+	2.49	3.57+	3.72	2.57+	2.68	3.89+	3.99
Instances	US200_D3_V20		US200_D3_V40		US200_D5_V20		US200_D5_V40
	Avg.	Best	Avg.	Best	Avg.	Best	Avg.	Best
DGLPSO	2.49	2.75	3.57	3.82	2.78	2.94	4.03	4.36
GA-HC	2.20+	2.24	3.25+	3.26	2.54+	2.59	3.68+	3.74
DQPSO	2.51=	2.56	3.52+	3.67	2.80=	2.84	3.88+	3.95
TLPSO	2.45+	2.66	3.51+	3.54	2.71+	2.89	3.88+	4.05
EDPSO	2.40+	2.60	3.51+	3.73	2.66+	2.78	3.88+	4.13
SW-OBLCSO	2.35+	2.58	3.47+	3.67	2.66+	2.79	3.85+	4.05
iACO4iNRP	2.44+	2.55	3.50+	3.64	2.74+	2.86	3.91+	4.18
Instances	US300_D3_V20		US300_D3_V40		US300_D5_V20		US300_D5_V40
	Avg.	Best	Avg.	Best	Avg.	Best	Avg.	Best
DGLPSO	2.37	2.58	3.14	3.40	2.88	3.13	4.44	4.71
GA-HC	2.07+	2.09	2.96+	3.02	2.53+	2.57	3.95+	4.04
DQPSO	2.29+	2.41	3.11=	3.27	2.76+	2.95	4.34+	4.47
TLPSO	2.31+	2.49	3.09+	3.26	2.89=	2.95	4.37+	4.52
EDPSO	2.28+	2.46	3.07+	3.24	2.82+	3.02	4.41+	4.67
SW-OBLCSO	2.25+	2.39	3.04+	3.15	2.71+	2.89	4.32+	4.58
iACO4iNRP	2.30+	2.43	3.09+	3.31	2.78+	2.86	4.39+	4.62
Instances	Real60_D3_V20		+/=/−
	Avg.	Best
DGLPSO	2.28	2.42
GA-HC	2.12+	2.25	13/0/0
DQPSO	2.15+	2.26	10/3/0
TLPSO	2.23+	2.34	11/2/0
EDPSO	2.21+	2.32	13/0/0
SW-OBLCSO	2.22+	2.29	13/0/0
iACO4iNRP	2.23+	2.38	13/0/0

, respectively, where “+/=/−” denotes the number of instances in which the proposed algorithm is significantly better than/not significantly different from/significantly worse than the corresponding comparison algorithm.

5.3. Validating the New Strategies

This section validates the effectiveness of the proposed heuristic population initialization strategy (Section 4.4), the dual-indicator group learning strategy (Section 4.6), and the objective-driven local search operators (Section 4.7). The comparison results are listed in Table 3.

5.3.1. Validating the Heuristic Population Initialization Strategy

With the purpose of verifying whether the heuristic population initialization strategy in DGLPSO helps to generate better initial individuals in new sprints and improves the search efficiency of the dynamic scheduling algorithm, it is replaced by a random initialization strategy, obtaining the algorithm named DGLPSO-RI (the DGLPSO algorithm that adopts random initialization). The other parts of DGLPSO-RI are kept unchanged with DGLPSO.

It can be seen from Table 3 that compared with DGLPSO-RI, DGLPSO finds better values of “Avg.” on 10 of the 13 instances and better values of “Best” on all the 13 instances. The Wilcoxon statistical test result of “9/4/0” demonstrates that DGLPSO significantly outperforms DGLPSO-RI on nine instances, and there is no significant difference between the two algorithms on the remaining four instances, including one small-scale, two medium-scale, and one large-scale instances. According to the objective information of the three subproblems, four kinds of selection strategies are designed for initialization of DGLPSO. It is able to quickly generate initial solutions adapted to the new environment at the beginning of each sprint. Meanwhile, by randomly generating a portion of the population, a better diversity is introduced, which balances the exploring scope and the search efficiency of the algorithm. In contrast, the population of DGLPSO-RI is completely randomly initialized without utilizing any knowledge on the problem, leading to a lower search performance in most problems compared with DGLPSO.

5.3.2. Validating the Dual-Indicator Group Learning Strategy

In order to validate the effectiveness of the dual-indicator population grouping strategy and the way to generate individuals in different groups of DGLPSO, it is, respectively, replaced with the grouping strategy that divides the population by only the objective value F_l and the strategy that only uses the potential value Q_l as the grouping criterion, obtaining two algorithms DGLPSO-OVG (the DGLPSO algorithm that adopts the objective value for grouping) and DGLPSO-PVG (the DGLPSO algorithm that adopts the potential value for grouping). Both algorithms divide the population into two groups. The top $⌊N/2⌋$ ($⌊·⌋$ indicates rounding down) individuals form the first subgroup, in which individuals learn from the global best and the personal best, the same as the standard PSO. The last $⌈N/2⌉$ ($⌈·⌉$ indicates rounding up) N/2 individuals constitute the second subgroup, in which individuals learn from the global best and a randomly selected individual with a better ranking number. Meanwhile, the DGLPSO-GL (the DGLPSO algorithm that removes group learning) algorithm is obtained by removing the group learning strategy, which does not group the population, and all individuals learn from the global best and the personal best. The parameter settings, encoding, decoding, and the rest of the three comparison algorithms are the same as DGLPSO.

It can be seen from Table 3 that compared with DGLPSO-PVG, DGLPSO-OVG, and DGLPSO-GL, DGLPSO achieves better values of “Avg.” and “Best” on all the 13 instances. The Wilcoxon statistical test results are all “11/2/0”, indicating that DGLPSO significantly outperforms the three comparison algorithms on 11 instances, respectively, and there is no significant difference between them in two small-scale or medium-scale instances. The proposed dual-indicator group learning strategy consists of both a dual-indicator-based population grouping method and the use of different learning mechanisms in different groupings. Compared with DGLPSO-PVG and DGLPSO-OVG, which only adopt a single indicator, the dual-indicator grouping makes DGLPSO not only focus on the objective value but also take each individual’s improvement room into account. As a result, the individual measurement is more comprehensive, and the population division is more specified. DGLPSO-GL does not perform the group learning, and the search direction of the population is single, which causes individuals to become assimilated and get trapped in the local optimum. In contrast, the group learning of DGLPSO diversifies the learning objects of individuals. Considering that different grouped individuals own different characteristics on two indicators and undertake different search functions, DGLPSO chooses applicable learning objects for them. In this way, a better guidance is provided to the search direction of each individual, increasing the population diversity and assisting to escape the local optimum.

5.3.3. Validating the Objective-Driven Local Search Operators

To verify the effectiveness of the objective-driven local search operators in DGLPSO, it is removed to obtain the algorithm DGLPSO-LS (the DGLPSO algorithm that removes local search), while other parts are kept unchanged with DGLPSO. It can be seen from Table 3 that compared with DGLPSO-LS, DGLPSO achieves better values of “Avg.” and “Best” on all the 13 instances. The Wilcoxon statistical test result of “13/0/0” indicates that DGLPSO significantly outperforms DGLPSO-LS on all the instances. These results show that the objective-driven local search operators designed in Section 4.7 can fully exploit the neighborhood information of the global optimal solution and significantly improve the search accuracy of the algorithm. Thus, it can select more appropriate user stories in each sprint. Meanwhile, the efficiency of story–team allocation and task–employee assignment within the team is also improved.

5.4. Validating the DGLPSO-Based Dynamic Periodic Scheduling Method

As far as we know, there is no multi-team agile software project scheduling model that is the same as this paper and the corresponding solution methods. The distinctions between the proposed model MTASPS and existing software project dynamic scheduling models are detailed in Section 3.2.4. In order to validate the performance of the proposed algorithm DGLPSO, six representative and recent algorithms are selected for comparisons. Genetic algorithm—Hill climbing (GA-HC) [48] is a hybrid algorithm combining the genetic algorithm and the hill climbing method, which has been applied to dynamic software project scheduling considering variations of employees’ productivity, a similar problem to our work. As in this paper, GA-HC also deals with multiple objectives through a weighted sum method. GA-HC is chosen to validate whether the proposed algorithm can achieve better accuracy compared to the existing dynamic software project scheduling approach. In addition, since the proposed algorithm is a particle swarm optimization (PSO) algorithm, four improved PSO algorithms that have been applied to the combinatorial optimization problems in recent years are also selected for comparisons. Diversity-preserving Quantum Particle Swarm Optimization (DQPSO) [49] utilizes the marginal analysis and the clustering method. It incorporates a distance-based diversity maintenance strategy and is applied to the classical 0–1 multidimensional knapsack problem. Three-learning Strategy Particle Swarm Optimization (TLPSO) [50] contains three hybrid learning strategies and has been validated as efficient in function optimization, as well as several combinatorial optimization problems. Extended Discrete Particle Swarm Optimization (EDPSO) [51] solves the remanufacturing scheduling problem. It employs a new population updating mechanism, where the learning directions of individuals are guided according to the optimal solution of each sub-objective. Moreover, the crossover and mutation operators are designed to keep the individuals away from the local optimum. Soils and wets—Opposition-based Learning and Competitive Swarm Optimizer (SW-OBLCSO) [52] is a multi-swarm PSO that adopts the competitive learning and inverse learning, which has been applied to the electric vehicle charging scheduling problem. In addition, through the research, the Next Release Problem (NRP) is very similar to the ASPS problem, so an improved ACO algorithm applied to the NRP problem is selected for comparison. iACO4iNRP [53] is an interactive ACO algorithm that considers that the user can interact with the algorithm at the priori moments and at in-the-loop moments, which has been effectively applied to the NRP problem. All the six comparison algorithms are encoded and decoded in the same way as described in this paper. The population grouping, the update strategy, and other parameters are the same as their original literature. Each algorithm solves the proposed model following the initial scheduling-dynamic periodic rescheduling approach, as detailed in Section 4.1. The experimental results of the proposed algorithm and the comparison ones are listed in Table 4.

It can be seen from Table 4 that compared with the six comparison algorithms, DGLPSO achieves the optimal values of “Best” on all the instances and the best values of “Avg.” on most of the instances. Wilcoxon statistical test results show that DGLPSO is significantly better than GA-HC, EDPSO, iACO4iNRP, and SW-OBLCSO on all the 13 instances, significantly outperforms DQPSO on ten instances, and significantly outperforms TLPSO on 11 instances. The superior performance of the proposed algorithm is attributed to the combined use of various improved strategies. First, the population initialization strategy provides a good starting point for the algorithm by generating the initial feasible solutions utilizing the features of each sub-objective. Second, the dual-indicator group learning strategy increases the search diversity and reduces the possibility of falling into the local optimum. Last, the objective-driven local search operators mine the neighborhood of the elitist, which further improves the search accuracy of the algorithm. Particularly, DGLPSO performs better than the comparison algorithms in the real-world application (instance Real60_D3_V20). That is to say, in real production, it can assign more valuable user stories and tasks while the team and employees all remain efficient and highly satisfied and, thus, obtain a scheduling solution that is close to the global optimum. This demonstrates the practical utility of the proposed algorithm DGLPSO. In summary, DGLPSO achieves better performance for solving the constructed model MTASPS than the comparison algorithms, and it demonstrates good scalability to problems of different sizes. At the initial stage of each sprint, DGLPSO can automatically provide the project manager with a schedule that behaves well in story value points, team efficiency, team satisfaction, and employees’ time utilization rates, facilitating the manager to make an informed decision.

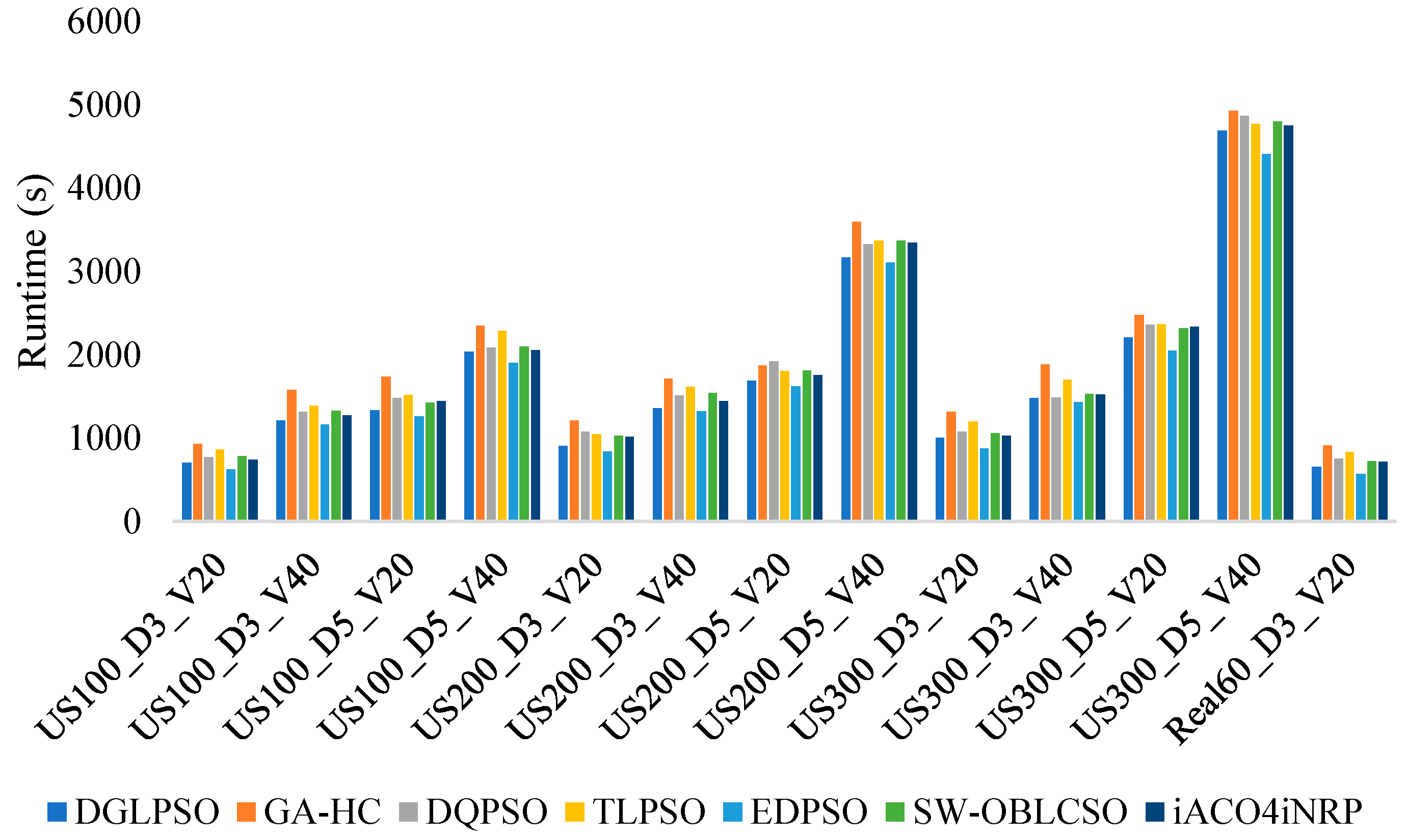
The runtime of the proposed algorithm was compared against the six algorithms introduced in this section across 13 instances of varying scales. Figure 16 illustrates the average runtime (in seconds) of each algorithm over all instances. It can be observed that the runtime of the proposed DGLPSO is only marginally slower than EDPSO across all instances. This is attributed to EDPSO’s population update mechanism, which accelerates information propagation and enhances computational efficiency. Furthermore, as evidenced by Table 4, DGLPSO significantly outperforms EDPSO on all instances in terms of solution quality, indicating that the generated scheduling solutions are superior. Thus, the computational overhead of DGLPSO is justifiable. Additionally, both Figure 16 and Table 4 demonstrate that DGLPSO achieves shorter runtimes than all other algorithms across all instances while also delivering significantly better performance metrics on the vast majority of instances. This further validates the efficacy of the proposed DGLPSO.

6. Conclusions

This work aims to study a practical agile software project schedule in which multiple teams cooperate to complete the project. To achieve this, first, we consider the speed, experience, and preferences of each team for developing different types of user stories, which has an effect on the development efficiency and team satisfaction. To capture the dynamic characteristics during the agile project development, we also introduce the insertion of new user stories and the uncertainty of maximum working hours. Then, we construct a multi-team agile software project scheduling model, where, in each sprint, the objectives of user story value, time utilization rates of employees, team efficiency, and team satisfaction are simultaneously optimized subject to the constraints. Next, we propose a DGLPSO-based dynamic periodic scheduling method to solve MTASPS. A three-layer encoding method with variable length is designed for the three tightly coupled subproblems. A dynamic reaction policy is presented to generate an appropriate initial population to adapt to the environmental changes. The population is divided into four groups by dual indicators. In each group, specific learning objects are chosen according to the features of individuals it contains. Heuristic local search operators are also designed.

An experimental study of the proposed strategies and algorithm is performed on 13 instances. Simulation results show that the dynamic reaction policy is capable of guiding the algorithm to better respond to new environments. The dual-indicator-based group learning strategy can help the population to search along different directions so that the population diversity is maintained. The heuristic local search operators further improve the mining ability around the elitists. The proposed algorithm DGLPSO can produce the schedule with higher accuracy in most instances compared to the five state-of-the-art algorithms. Therefore, DGLPSO is more effective in solving the established model MTASPS and exhibits a better scalability to the problem size.

Overall, we capture the uncertainties and dynamic events that might take place during agile project development and consider the user story allocations among multiple sprints and teams. However, several factors remain unaddressed in this research. Specifically, first, the intra-team communication cost and its transmission mechanism during the dynamic adjustments of agile projects, along with the quantitative relationship to collaboration effectiveness, have not been adequately revealed. Second, the influence of leadership on multi-team agile software project scheduling models remains unexplored. Furthermore, how differences in inter-team learning mechanisms impact teams’ adjustment capabilities during agile implementation lacks investigation. These factors not only shape collaborative patterns among multi-teams but also exert profound effects on the overall project through complex interactions. Consequently, in future research, we will conduct multi-case empirical investigations on real-world agile projects. Utilizing methodologies such as in-depth interviews and participant observation, we will systematically examine the relationship between these underexplored factors and the proposed model. This will further validate the mathematical model’s efficacy in practical projects, refine optimization strategies for multi-team collaboration, and advance the research. Moreover, we will further relax the constraints, eliminating restrictions such as single-skill tasks and one-task-per-employee limitations, thereby enhancing the model’s alignment with real-world scenarios.