Abstract
Multidimensional clustering of large-scale multi-view data is an important topic because it makes possible to combine a variety of manifestations of a complex information set. Nevertheless, comparing and selecting the most suitable deep clustering method is not an easy task, especially when several opposing criteria are applied. Multi-criteria decision-making (MCDM) techniques provide systematic approaches to making such judgments, although they are often limited in their ability to handle uncertainty, imprecise judgments, and interdependencies in practice. To solve these problems, this paper suggests a circular Fermatean fuzzy technique order preference by similarity to ideal solution (CFF-TOPSIS) method, which combines improved fuzzy modeling with MCDM to make the decision-making process accurate and sound. By exploiting the intrinsic symmetry of TOPSIS, where distances to positive and negative ideal solutions are treated symmetrically, the proposed model integrates five evaluation criteria for assessing clustering adequacy, including clustering accuracy, scalability, computational complexity, robustness, and interpretability, to critically evaluate five alternative clustering methods based on the input of three decision-makers. This measurement is performed efficiently by the CFF-TOPSIS method based on the uncertainty and subjective judgment contained within circular Fermatean fuzzy sets (CFFSs). The model is reliable and superior to existing models, as confirmed by sensitivity and comparative analyses. The suggested approach provides a systematic and flexible method for making decisions in complex big-data settings, while maintaining symmetry in the evaluation of alternatives and criteria.
1. Introduction
The current data environment features objects with multiple modalities, such as text, images, sensor streams, gene expressions, or financial indicators, all of which are commonly called multi-view data. Deep multi-view clustering (DMVC) describes a group of unsupervised learning methods where deep neural networks generate latent representations of each view and identify shared structures among views to cluster objects most effectively. DMVC learns the complementary information of view-specific embeddings together, resulting in clusters that are more semantically meaningful and better suited for subsequent downstream analytical tasks with increased accuracy. This process inherently reflects the principle of symmetry, as it seeks balanced and consistent representation across diverse data views.
This becomes more challenging in large-scale environments because millions of examples and high-dimensional feature spaces quickly render traditional clustering methods impractical. Recent DMVC models overcome this scalability issue using shared encoders, graph neural architectures, variational fusion schemes, or ensemble agreement networks, but each approach involves different trade-offs in accuracy, training efficiency, and robustness. As a result, practitioners must compare a set of candidate algorithms systematically, rather than relying on random trial and error.
Choosing one technique among many competing DMVC methods is inherently a multi-criteria decision. Cluster metrics, such as compactness, cross-view consistency, computation cost, and interpretability, often conflict with each other, and priorities vary depending on stakeholders. MCDM thus provides the framework for analyses needed to balance conflicting evidence and expert opinions into a justified ranking of alternatives, ensuring the final model chosen is not only technically sound but also aligns with strategic (even if informal) goals. The implementation of fuzzy MCDM into the clustering process, primarily the CFF-TOPSIS method, provides a robust approach to enhancing the accuracy and reliability of clustering in large-scale multi-view environments. This integration helps model uncertainty, reluctance, and partial concurrence with views, as well as more constructive decision-making over widely varied and frequently noisy data. For example, when using complex image-text datasets, some views may present redundant or noisy information; however, the fuzzy weighting incorporated in CFF-TOPSIS can help overcome this issue. The framework achieves this by prioritizing the importance of several views using fuzzy logic, thereby allotting proportionately more weight in the clustering process to the most stable and informative representations, which makes the clustering results more robust and interpretable.
The performance of any MCDM process depends on the degree to which it addresses such issues as uncertainty. Zadeh [1] introduced classical fuzzy sets (FSs) with degrees of membership (MDs) in the range of as an extension of traditional fuzzy sets, but they cannot be used to express multiple and concurrent non-membership degrees (NMDs). In Atanassov [2], intuitionistic fuzzy sets (IFSs) extend further, as they allow NMD to be added, and in Yager [3] Pythagorean fuzzy sets (PyFSs) can be even more flexible by way of the square-sum constraint in . Fermatean sets of fuzzy sets [4] are a further generalization, the exponent being slackened to three to further improve expressive power, in very ambiguous applications. Introducing modifications to these concepts, CFFS [5] restricts MD and NMD to the interior of a unit circle, which makes it possible to represent the component of hesitation, a feature that is especially desirable when using an expert to assess complex deep learning models.
There is a voluminous list of MCDM techniques, including EDAS [6], WASPAS [7], DEMATEL [8], SWARA [9], and COCOSO [10], among others. In this present study, however, TOPSIS is used, which was initially introduced by Hwang and Yoon [11]. TOPSIS sorts the alternatives based on their geometric proximity to an imaginary perfect and their distance from an imaginary worst, a rationale that smoothly scales with additional criteria and also maintains common interpretation even when embedded in complex fuzzy settings. By incorporating TOPSIS into the CFFS, an established ranking mechanism is combined with a model of uncertainty that is adjusted to subtle expert assessments used in selecting DMVCs.
To demonstrate the strength of the suggested method, the analysis compares it to each of the previously discussed MCDM methods and includes a wide range of sensitivity tests that modify the values of decision-maker weights across numerous scenarios. These checks provide a good overview of how the method performs under real variations and how stable the rankings are, a crucial aspect when decisions have significant operational consequences. The evaluation also highlights the symmetry in the decision-making structure, ensuring balanced consideration of both ideal and anti-ideal alternatives across different weighting schemes.
To conclude, the paper presents a CFF-TOPSIS framework for evaluating large-scale deep multi-view clustering methods, demonstrating its empirical benefit through a methodological comparison and sensitivity analysis. It also introduces a decision-support workflow that integrates expert knowledge with rigorous mathematical reasoning. The following paragraphs detail the theoretical background, empirical case study, and managerial implications of the contribution, thereby guiding researchers and practitioners toward more informed model selection in a multi-view massive data context.
1.1. Objectives and Contributions of the Study
The primary goal of this research is to develop a reliable decision-making framework for comparing and choosing the most suitable deep multi-view clustering method for large-scale multi-view data analysis. Because multi-view data are inherently complex and varied, with multiple, often conflicting evaluation criteria, this study aims to fill the gaps in existing decision-making methods by introducing a new multi-view CFF-TOPSIS. This approach considers uncertainty and imprecision while capturing subjective preferences, offering greater accuracy in decision-making than current techniques.
The most essential study contributions are as follows:
- Development of a combined decision framework dedicated to the analysis of deep multi-view clustering strategies in terms of real-world criteria of performance.
- CFFS combined with TOPSIS to cope with greater levels of reluctance and vagueness in the expert judgments.
- Implementation of a case scenario with more specific details that comprise five alternatives, five criteria, and three decision-makers to prove that the suggested model can be applied.
- Running the sensitivity analysis in ten scenarios to determine the robustness and symmetry of the method.
- Comparative study showing how the proposed CFF-TOPSIS is better than some of the well-established techniques of MCDM, such as EDAS, WASPAS, DEMATEL, SWARA, and COCOSO.
1.2. Research Gap and Motivations
DMVC has been proposed as a powerful method for analyzing large datasets that contain a mixture of diverse views. Given its growing importance, there are no specific decision-making methods that select the best clustering techniques in an uncertain and fuzzy environment. Existing literature often overlooks the multi-criteria nature of evaluating clustering models, which includes accuracy, scalability, robustness, computational cost, and interpretability, especially when multiple decision-makers are involved. Additionally, most classical MCDM methods are ineffective because they fail to adequately represent the high level of uncertainty, imprecision, and hesitation that are naturally expressed in expert ratings in such complex scenarios.
Such a gap motivates the development of a more adaptable and uncertainty-resistant decision-making model. This approach offers promising potential for CFFS, which already has enhanced capabilities in modeling vagueness and opposing views. By integrating these fuzzy sets with the well-known TOPSIS method, more accurate ranking of alternatives can be achieved in environments with large-scale data. Therefore, the core reasoning behind the proposed research is driven by the need for a more sophisticated, precise, and context-specific decision-making process that can effectively facilitate the selection of a deep multi-view clustering method in an integrative and interpretive manner.
1.3. Layout of the Study
The rest of the paper is organized as follows: Section 2 reviews recent developments in deep multi-view clustering and fuzzy MCDM approaches. Section 3 discusses the preliminaries related to CFFS. Section 4 proposes the CFF-TOPSIS MCDM approach, outlining its detailed steps. Section 5 applies the proposed approach for selecting the best deep multi-view clustering technique for large-scale multi-view data and discusses its results. Section 6 performs a comparison and sensitivity analysis to assess the superiority of the proposed approach, discussing its practical and managerial implications and highlighting the advantages and limitations of the study. Finally, Section 7 concludes with key findings and discusses future research directions.
2. Literature Review
This section reviews recent developments in deep multi-view clustering and fuzzy MCDM approaches. It highlights existing methods for handling large-scale multi-view data and explores the role of fuzzy MCDM, especially TOPSIS, in enhancing clustering decisions.
2.1. Deep Multi-View Clustering Technique for Large-Scale Multi-View Data
DMVC is a new type of unsupervised learning that is effective in dealing with multi-view and heterogeneous data sets by learning sample-level related representations and exploring the underlying cluster patterns. It attempts to leverage the complementarity across views to reduce noise and redundancy, thereby enhancing the symmetry in the representation of multi-view data. Conventional clustering methods have been extended to multi-view designs, which handle large-scale data by building low-redundant representations. These designs include multi-view multiple clustering models, which optimize objective functions to reduce redundancy [12]. On the same note, scalable regression-based models of clustering view bipartite graph weights as features, incorporating structural data provided as input to the clustering model [13]. Scalability is also supported with the anchor-based techniques by lowering the complexity of computation and aligning the more important characteristics between viewpoints [14], along with cross-view anchor alignment, which can maintain the consistency of the dataset globally across high-dimensional space [15]. The innovations play a crucial role in enhancing the clustering performance of large-scale and real-world applications. The importance of deep multi-view clustering is even more accentuated when integrated into decision-making frameworks. As an example, in a fault diagnosis in electric cars, clustering categories on the scale of failure are then used to generate an MCDM procedure [16]. This kind of integration indicates that multi-view clustering is helpful not only in the preprocessing and learning of the data structure, but also at an underlying level in complex assessments of expert consensus and risk prioritization. Moreover, more powerful frameworks, such as the pseudo-labeled enhanced fuzzy clustering, offer additional possibilities for the conventional understanding of Fuzzy C-Means by leveraging deep features and multi-view flexibility, thereby improving the quality of cluster labels in large-scale datasets [17]. In general, the DMVC method has become a vital skill, and these methods are applied in the areas of pattern identification and intelligent decision systems.
2.2. MCDM TOPSIS Approach
The MCDM TOPSIS method has become an indispensable resource for complex decision-making processes when assessing numerous criteria that conflict with each other. TOPSIS provides an objective and structured methodology for decision analysis, ranking alternatives based on their geometric proximity to the ideal solution and the anti-ideal solution. Recent works have already implemented fuzzy TOPSIS to some varied fields like credit rating assessment, wherein an interaction of criteria is deemed to improve consistency of results [18], and in the medical diagnostic systems like fibromyalgia prediction prognosis, wherein fusion with fuzzy logic has made it more robust and easier to interpret [19]. The flexibility of TOPSIS has also contributed to not only offering superior adaptations but also providing more refined fuzzy extensions, such as intuitionistic and circular intuitionistic fuzzy sets, as a measure to help deal with the high levels of uncertainty within the decision-making setup [20]. Adapted versions of TOPSIS have been used in the sports industry for assessing the quality of sports and planning infrastructure with circular pythagorean and Fermatean fuzzy data exhibiting greater amounts of precision and situational awareness [21], [22]. In addition, the decision-making process is further bolstered through hybrid frameworks, which integrate multiple methods, such as AHP and TOPSIS, and associate weight extraction with ranking models, deciphered in healthcare technology selection [23]. It is safe to say that all the components referenced make TOPSIS a versatile and potent MCDM method applicable to both structured and uncertain decision environments.
2.3. Studies Applying the CFFS
The CFFS framework has emerged as a potential model for managing complex and imprecise information in decision-making settings, particularly in cases of advanced uncertainty, uncertainty in hesitancy, and flexibility. CFFS are further extensions of the classical Fermatean fuzzy sets by adding circular membership, non-membership, and hesitancy values that improve interpretability and information retention. CFFS has also been examined in various applications. Specifically in the area of higher education, particularly in physical education decision-making, a proposal was put forward concerning a general IVF-FS framework with circular fuzzy logic to effectively handle uncertainties in evaluation [24]. The features of CFFS, namely a circular form of the boundary by the center of which the average values are stored, make it a superior alternative to Fermatean and Interval-Valued FFS, which offer a better aggregation and comparison process in the constructs of MCDM [25]. Researchers have further developed assemblage methods, such as the Einstein operator in a CFF environment, which solidifies the applicability of CFFS to real-world applications [26]. Additionally, the CFFS-based similarity measure has been advantageous for modern pattern recognition problems, which underscores its potential to add strength and confidence to the decision-making process under uncertain and multidimensional conditions.
3. Preliminaries and Theoretical Background
An addition to the PyFS is a developed Senapati [4] FFS. In this section, the literature on FFS, CFFS, and related concepts is reviewed comprehensively.
Definition 1
([4]). An FFS, indicated by on a universal set , is fixed by where and denots the MD and NMD of the element to respectively. These functions always cover the range of [0, 1], and such functions satisfy the following condition:
Additionally, the hesitation degree (HD) is defined as
Definition 2
([5]). A CFFS, indicated by on a universal set, is fixed by , where and are the MD and NMD of the element to respectively. These functions always cover the range of [0, 1], and such functions satisfy the following condition:
Also, the HD is defined as
and is the radius of the circle.
Definition 3
([5]). For any two circular Fermatean fuzzy values (CFFVs), we address a variety of algebraic laws, including
Moreover, we find the score value to simplify two CFFVs through these techniques.
Definition 4.
For any CFFV, we state the scoring technique as follows:
4. Circular Fermatean Fuzzy TOPSIS Approach
CFF-TOPSIS is an improved version of the TOPSIS method that incorporates the CFF model, resolving ambiguities in decision-making premises and their interdependencies. CFFS also introduces an optional radius parameter, providing a more precise representation of uncertain data compared to common MD and NMD methods. To enhance the accuracy of MCDM, this study develop CFF-TOPSIS, which considers expert opinions based on circular Fermatean fuzzy weighted averaging operator (CFFWA), enabling a proper combination of estimates without the need to eliminate data fuzziness during evaluation. The Euclidean distance uses normalized values to distinguish an alternative from the most desirable one and captures variations in MD, NMD, and radius readings. The ranking improves when based on distances and integrated with CFFWA, offering better performance under data variation and uncertainty. Both TOPSIS and CFFS address the challenge of uncertainty in fuzzy MCDM models, which often rely heavily on subjective evaluation standards and inaccurate ratings. Figure 1 illustrates the methodology and the entire flowchart.
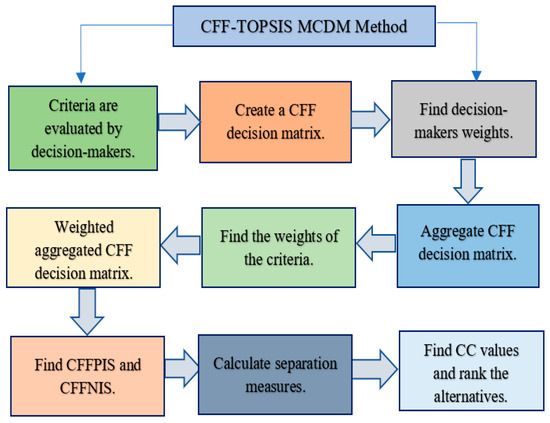
Figure 1.
Flowchart of the CFF-TOPSIS methodology.
Algorithms
- Step 1: Determine the decision matrix and locate the weights of the decision-maker.
- Using the alternatives and the criterion , build a decision matrix for the following problem.
- Express decision matrix elements comprising radius, MD, and NMD as CFFS.
- Utilizing the formula below, determine the decision-maker weights φⱥ:
- Step 2: Aggregate the decision matrix and calculate weights.
Consider a collection of CFFVs, . After that, the CFFWA operators are detailed as follows:
where is the set of weights of vector and .
The opinions of the experts were integrated using the CFFWA operator adapted from [4], which facilitates the aggregation of individual assessments while preserving the uncertainty structure of CFF fuzzy information. The weights assigned to each expert were determined using Equation (4) in Step 1, ensuring a proportional influence based on their expertise. This approach provides a consistent and robust mechanism for fusing expert knowledge in the MCDM process.
- Step 3: Determine the weighted aggregated decision matrix.
To arrive at the weighted aggregated decision matrix, multiply each of the aggregated CFFVs by the weights which were defined in the previous step.
The weighted aggregated decision matrix is represented by , and .
- Step 4: Determine the ideal solution (CFFPIS) and the ideal solution (CFFNIS) for the CFF.
Given that the sets of benefit and cost criteria are B and C, respectively, and
and
where
The suggested approach addresses both benefit type and cost type criteria in a pretty explicit manner. In solving the ideal and anti-ideal solutions, CFFPIS and CFFNIS, the benefit () and cost () criteria sets are considered separately as represented by Equations (7)–(12). Hence, cost criteria do not require inversion or transformation, which implies their eminently applicable use in various decision contexts.
- Step 5: Find out the distances between each alternative and CFFPIS and CFFNIS.
The prescribed CFFPIS and CFFNIS determine the values of decision-making and . The normalized Euclidean distance is executed according to the reason that it controls the MD, NMD, and degree of radius in CFFVs. The following formula can be used to achieve the two separation values of each alternative system:
- Step 6: To calculate the closeness coefficient (CC) of every alternative with respect to the ideal solution, use the formula below:The value of CC is between 0 and 1, and a bigger value of CC means that it is nearer to the ideal solution.
- Step 7: Rank the alternatives according to CC.
5. Case Study: Selecting the Best Deep Multi-View Clustering Technique for Large-Scale Multi-View Data
Multi-view data is a type of dataset used in data-driven organizational environments; it refers to datasets that employ more than one representation or modality to describe the same entities. For example, these can include pictures described by words, sensor inputs, readings from various sources, or financial data from different departments. To extract meaningful patterns from such diverse data, DMVC methods have become effective. These solutions leverage deep learning to understand complex, non-linear relationships across views, achieving higher clustering accuracy compared to earlier methods. However, it is essential to acknowledge that numerous models exist, each with distinct architectures, fusion techniques, and optimization steps. Therefore, conducting a systematic comparison and selecting the most suitable DMVC approach for a specific large-scale task is crucial. This selection process must also consider various performance and practicality factors, making it a multi-dimensional decision problem.
The use of MCDM methods in such complex selection environments is not only practical but also helpful in comparing alternatives based on various criteria. It is not just the clustering performance that matters when choosing the best DMVC model; resource efficiency, quantitative interpretability, and alignment with organizational objectives are also important considerations. MCDM techniques help formalize this decision-making process by capturing the preferences of different professionals and combining these preferences into a sequence of preferred alternatives. This approach allows not only for selecting one metric to base decisions on, but also for viewing the overall suitability of the model. Especially when trade-offs exist between accuracy, computational cost, and consistency, which are common challenges in deep clustering, MCDM provides a systematic way to achieve balanced and logical judgments.
The literature presents various MCDM methods for evaluating algorithms, includincludeding AHP, VIKOR, PROMETHEE, and TOPSIS. However, traditional MCDM approaches are challenging to follow because they tend to obscure the uncertainty and hesitation involved in experts’ judgments, especially when assessing large datasets related to deep learning algorithms. To address this, this study employs a superior method called the CFF-TOPSIS approach. This method leverages the power of CFFS, which allows for greater flexibility in expressing uncertain or hesitant opinions with varying MD and NMD, albeit within the confines of circular conditions. The CFF-TOPSIS technique ranks alternatives based on their closeness to the optimal solution and effectively manages expert uncertainty. Therefore, it is highly suitable for selecting deep multi-view clustering models, where both objective measures and expert feedback are crucial.
To illustrate how the proposed methodology works, we consider a three-expert decision-making scenario. The lead data scientist is familiar with various clustering techniques and model evaluation methods. The second expert is experienced in the domain, with a deep understanding of the nature of the data and the requirements for its interpretability. The third expert is an IT infrastructure specialist who assesses technical feasibility, computational costs, and deployment speed. This group of experts is deliberately selected to demonstrate the varying but interrelated perspectives on technical, practical, and operational aspects that are vital in the rigorous evaluation of deep multi-view clustering. Such expert configuration is validated in recent MCDM research, where three experts provide sufficient expertise and a range of opinions, ensuring that the resulting decision is trustworthy and reliable [27].
To ensure a comprehensive and practically relevant evaluation, the five deep multi-view clustering methods are selected to represent a diverse range of learning paradigms, including a shared encoder-based K-means clustering model , a co-training spectral clustering method , a variational autoencoder-based clustering model with late fusion , a graph convolutional clustering technique , and an ensemble autoencoder-based consensus clustering approach . These models are widely recognized for their distinct strengths in handling complex multi-view data.
Five benefit criteria are carefully chosen to capture essential aspects of clustering performance, interpretability, and applicability in real-world large-scale settings.
- The former criterion is the coefficient of the silhouette that gauges the level of segmentation of the clusters. The higher coefficient indicates that the data are closely fitted within their respective clusters and are independent in other adjacent clusters; hence, they are effectively grouped.
- The second (somewhat indirect) criterion is the adjusted mutual information, which measures the extent to which the clustering performance aligns with the known ground truth, controlling for chance. AMI is especially pertinent in situations where partial validation of the labeled data is at hand, and with its assistance, the guaranteed outcome of clustering is significant within the assigned context of the application.
- The third criterion is the cross-view consistency score which measures the consistency of how well a clustering technique works across views of a data set. A more considerable consistency score indicates that the framework effectively accumulates multi-modal information and is able to provide consistent results.
- The fourth criterion is the training efficiency of a training algorithm, and it refers to the inverse of the average time it takes to train all epochs. Whereas training time is a historical cost criterion, it is standardized here by considering that the more efficient the models, the higher the scores; therefore, this aspect can be regarded as a benefit criterion.
- The fifth criterion is the clustering robustness score where the score decides on how the model would perform when there is data or parameter perturbation. A robust model is also preferred in large-scale settings where data variability and noise are frequent.
All decision-makers compare the five options using five benefit criteria with linguistic expressions, such as very high, high, medium, and low. These judgments are then converted into CFFVs to develop personal decision matrices. These matrices are combined to form a single group opinion master matrix, considering the three experts as one entity. Since the categories are all related to benefits, normalization is performed while maintaining the preference direction. The case study demonstrates the practical importance of the CFF-TOPSIS approach for managing uncertainty, integrating expert opinions, and providing an organized solution to selecting the best clustering methods in a high-dimensional, large-scale multi-view data context. The implementation process of the CFF-TOPSIS method follows the steps outlined in the methodology section. Decision-makers also provide their linguistic scores related to the criteria using CFFVs, as illustrated in Table 1.

Table 1.
Linguistic values for decision-makers and criteria.
Table 2 presents some linguistic terminologies that help compare the level of achievement of different alternatives in the CFFS structure. The MD, NMD, and radius of the CFFVs clarify the distinctions between the decision-making options.

Table 2.
Linguistic values of alternatives.
The values of the importance of the five criteria within the scope of three decision-makers () and the equations are illustrated in Table 3. The language with which the values are described is biased towards linguistics, in which all the decision-makers themselves produce the coefficients of importance against those criteria.

Table 3.
Values of the criteria.
The weights of the decision-makers were also determined based on Equation (4), i.e., the weights are obtained as an outcome of their inputs. Weights assigned to individual decision-makers are as shown in Table 4 below. These weights are required because they indicate how the various assessments by other decision-makers influence the ultimate conclusion.

Table 4.
Decision-makers weights.
The weights of the different criteria are assessed and introduced in Table 5, starting with Equation (5), to the CFFWA operator. Weights such as MD, NMD, and radius are shown below. These values underscore the significance of each requirement in decision-making and demonstrate that the remaining requirements serve a secondary role.

Table 5.
Aggregation of the criteria.
Table 6 shows an evaluation of the differing choices ( to ) proposing a course of action on the grounds of pertinent assessments. Two additional decision-makers’ ratings are also provided on the verbal-linguistic scale.

Table 6.
Assessment of alternatives.
Table 7 presents the CFF decision matrix, the CFFWA, and the transformed linguistic multidimensional questions from Table 6.

Table 7.
Circular Fermatean fuzzy aggregated decision matrix.
Table 8 indicates the weighted CFF decision matrix of CFFS that is calculated by multiplying the numbers in Table 7 by the corresponding weights of Table 5 in the CFF methodology rules.

Table 8.
Weighted aggregated circular Fermatean fuzzy decision matrix.
Table 9 decomposes the CFF-TOPSIS, which is calculated based on CFFPIS and CFFNIS values. The ideal positive and negative solutions can be exhibited by the total weighted CFF decision table.

Table 9.
Circular Fermatean fuzzy positive ideal solution and negative ideal solution.
Table 10 presents the solutions for the separation measures and the CC for each of the discussed alternatives. The closer the alternative to the ideal solution and the farther the negative solution, the higher the CC.

Table 10.
Separation and closeness coefficient of each alternative.
5.1. Result Discussion
Based on the implementation of the CFF-TOPSIS method, the five deep multi-view clustering techniques were ranked as follows: , as shown in Figure 2. This ranking results from the closeness coefficients calculated for each alternative relative to the CFFPIS and CFFNIS, considering input from three decision-makers and five benefit-based evaluation criteria. emerged as the most preferred deep multi-view clustering technique, consistently receiving high scores across all criteria. It performed exceptionally well in terms of clustering quality, as indicated by a high silhouette coefficient and adjusted mutual information. Additionally, its robustness across various data conditions and strong cross-view consistency reinforced its position as the best choice for large-scale multi-view data analysis. ranked second due to its strong performance in robustness and cross-view consistency. It delivered reliable clustering results even under data variability and maintained coherence across multiple views. Although slightly less efficient in training and in producing compact clusters than remains a competitive and practical option. , in third place, demonstrated strengths in training efficiency and showed moderate performance in other areas. Its architecture is suitable for scalable learning, making it an appealing choice when computational resources and time are limited. However, it has slightly lower clustering effectiveness compared to and , affecting its overall ranking.
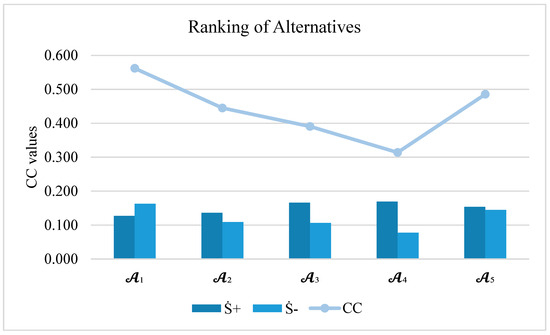
Figure 2.
Ranking of alternatives.
received balanced, average scores on five criteria, which helped it secure fourth position. It did not perform exceptionally well in any particular aspect, and thus, although it can be considered a reliable choice in scenarios where a general-purpose clustering model is needed, it does not appear to outperform various other alternatives in any aspect. With the lowest ranking, was found to be relatively weaker in aspects of clustering accuracy, consistency across views, and robustness. Although conceptually sound, its practical application has so far not been as effective as the rest of the alternatives; hence, discretion is attached to its usage, specifically regarding readjustments or upgrading requirements before applying it in large-scale, multi-view clustering applications. Overall, the outcome suggests the appropriateness of the suggested CFF-TOPSIS technique in managing complex decision-making situations with uncertain outcomes and multiple facets of assessment, incorporating expert opinions. It also provides a logical and systematic basis, helping to choose a more suitable clustering model when conducting multi-view data analysis on a large scale.
5.2. Theoretical Implications
The results of the proposed study have several important theoretical implications in the fields of MCDM, fuzzy logic, and deep multi-view clustering. By combining the CFFS and TOPSIS methods, the research broadens understanding of the theoretical foundations of decision analysis under uncertainty and imprecision in large-scale, complex, high-dimensional decisions. The CFFS scheme also offers a less rigid and more responsive approach to interpreting human judgment, especially when hesitation, indeterminacy, and dual uncertainty are involved. This marks significant progress beyond traditional fuzzy, intuitionistic fuzzy, and even Pythagorean extensions. Additionally, implementing the CFF-TOPSIS algorithm into a deep multi-view clustering task creates a new intersection between soft computing and unsupervised learning. Although clustering methods are usually data-dependent heuristics, the integration of expert-driven criteria via fuzzy MCDM provides a hybrid decision-support approach. This not only bridges the gap between high performance and interpretability but also offers new insights into how subjective preferences can be systematically incorporated when evaluating machine learning models. The proposed framework also highlights CFFS as a foundational element for future MCDM models in complex and uncertain environments. Importantly, the study emphasizes these methods’ ability to handle multidimensional trade-offs involving clustering quality, robustness, consistency, and computational efficiency. In doing so, it paves the way for future research to explore issues related to deep learning combined with advanced fuzzy decision-making systems, particularly in big data analytics, intelligent systems, and multi-modal educational contexts.
6. Sensitivity Analysis
To examine the sensitivity of the upper-level decision-maker preference output, weights attributed to the three decision-makers were overall perturbed in logically versatile situations of ten. In the most extreme environments, the map value of ranged between and with the and varying in an opposing balancing manner. Closeness coefficients of the five alternatives were recalculated for every weight vector. The findings are presented in Figure 3. Although the extent of influence of experts varied conspicuously, the rank order of the alternatives was the same: . The narrow numerical range of and a distinct gap between it and explain why no reversal of the ranking took place as the weight of surpassed half of the total sum or sank to the level of less than thirty percent. The same was true of against , which was consistently better by approximately , well beyond any perturbation created by the ten weight settings, and of the lower-rank alternatives too, which also maintained their own internal ranking. The above observations verify that the provided CFF-TOPSIS model has rank-stable decisions relative to reasonable changes in stakeholder weighting. Such dominance of is not an artefact of any single weighting scheme but a property that is robust over a very broad range of expert-preference settings, making the point that the methodology is robust against weighting schemes.
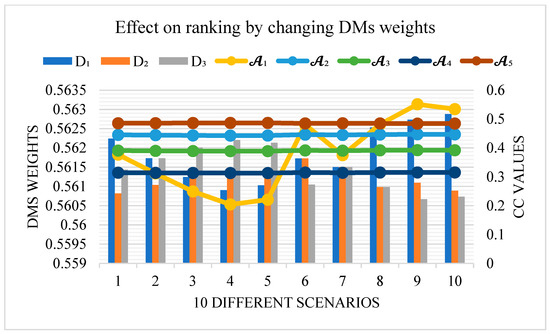
Figure 3.
Sensitivity analysis.
6.1. Comparison with Existing MCDM Approaches
The comparative analysis presented in Table 11 shows that the overall performance of the CFF-TOPSIS approach is higher across multiple decision-support dimensions. Notably, unlike traditional MCDM methods such as EDAS [6], WASPAS [7], DEMATEL [8], SWARA [9], and COCOSO [10], the current version of the CFF-TOPSIS method excels at handling uncertainty and hesitation due to its advanced fuzzy expression. It demonstrates that it is well suited for large-scale, high-dimensional, multi-view data, supporting the robust inclusion of disparate criteria weights based on any subjective or objective scheme. Additionally, it ensures rank stability even when there are significant changes in the decision-maker’s preferences, a quality shown through sensitivity analysis. Although techniques like DEMATEL and SWARA can be useful for weighting criteria, they are either inapplicable or yield poor results in complex, data-intensive applications involving ranking large numbers of alternatives. Therefore, because the CFF-TOPSIS tool is more theoretically and practically prepared for reliable, high-scale decision-making in deep multi-view clustering applications (as shown in Table 11), it is more relevant for applications requiring dependable and large-scale decision support in deep multi-view clustering.

Table 11.
Comparison analysis.
6.2. Practical and Managerial Implications
In practice, the suggested fuzzy MCDM model can be used to systematically assess and select deep multi-view clustering models in fields like healthcare analytics, customer behavioral insights, or large-scale recommendation systems. For example, an organization dealing with multi-source data, such as sensor networks or user activity logs, could apply this methodology to compare clustering methods based on performance, interpretability, and resource usage. With expert knowledge enabled by CFFWA, all domain-specific information, technical limitations, and deployment priorities are considered during the final decision. This approach helps practitioners choose models that are not only statistically sound but also meet operational requirements. The structured steps of aggregation and ranking make the methodology time-efficient, with low computational complexity, and capable of scaling to real-time or high-volume operations. Consequently, this enhances decision reliability without sacrificing speed.
6.3. Advantages of the Study
This research offers several methodological and practical benefits. First, it introduces a new combination of the CFF environment with the TOPSIS method, which enhances decision-making processes and increases levels of uncertainty, indecisiveness, and imprecision in expert estimates. This makes it particularly useful in complex, large-scale data environments where precise judgments are often impractical. Second, the methodology supports multi-criteria decision-making related to deep multi-view clustering, increasingly relevant in fields like healthcare analytics, image recognition, finance, and big data processing. An additional advantage is the model’s scalability and flexibility; it can incorporate any number of decision-makers, weighting schemes, and a large set of alternatives without sacrificing computational efficiency. Moreover, the CFF-TOPSIS model demonstrates high rank stability, as confirmed by sensitivity analysis, and maintains consistent symmetry in preference evaluation, making it suitable for critical decision-making scenarios. Finally, by providing a mechanized framework for evaluating clustering models, the research helps researchers, data scientists, and organizational leaders make informed, transparent, and defensible decisions in data-driven contexts.
6.4. Limitations of the Study
Although the proposed CFF-TOPSIS method is both quite robust and practically useful, several limitations should be noted. First, the approach heavily depends on expert opinion to determine the decision matrix and criteria weights, which introduces subjectivity and potential bias, especially in areas lacking consensus among experts. While the fuzzy environment helps address uncertainty, initial judgments are still human-based. Second, the current research was conducted using a hypothetical case study that involves a limited number of alternatives, criteria, and decision-makers. Although this effectively demonstrates the methodology, it may not accurately reflect real-world applications involving hundreds of data points and high-dimensional data. Additionally, the model assumes all criteria are benefit-type, which is not always true, as many applications include mixed or cost-type criteria. Furthermore, while the CFF setting offers increased flexibility in managing uncertainty, it is mathematically complex and may pose challenges for practitioners who are not experienced in fuzzy logic. Lastly, the paper does not consider the integration of dynamic data or real-time clustering assessments, which are increasingly important in time-dependent decision-making scenarios. These limitations highlight areas for further research and development.
7. Conclusions
The present study proposed an integrated decision-making approach using the CFF-TOPSIS model to evaluate the most suitable deep multi-view clustering method in the context of large-scale multi-view data analysis. This methodology was designed to handle the uncertainty and complexity involved in selecting among several high-performing clustering models, considering diverse data sources and expert opinions. To demonstrate the relevance of the proposed method, a real-life-inspired scenario was created, considering five clustering techniques, five evaluation criteria, and three decision-makers. Each criterion, such as clustering accuracy, scalability, convergence speed, interpretability, and robustness, was clearly defined based on key performance factors for large-scale deep clustering. The CFFS enabled the model to account for varying levels of uncertainty and hesitation in professional judgments, while TOPSIS provided a coherent ranking of options. Results show that the approach effectively ranked the alternatives, and sensitivity analysis confirmed the stability of these rankings under different decision-maker weightings. Furthermore, a comparative study with existing MCDM methods highlighted that the CFF-TOPSIS approach offers greater flexibility, accuracy, and support for decision-making. Overall, this study introduced a robust and adaptable approach that enhances stability, symmetry, and appropriateness in multi-view data clustering decision processes. The findings have significant practical and theoretical implications for data scientists, researchers, and managers involved in the selection and implementation of large-scale clustering models.
Further research on the current CFF-TOPSIS model can explore more complex fuzzy environments. For example, spherical fuzzy sets [28] and interval-valued picture fuzzy AHP with the Frank operator [29] can offer improved uncertainty modeling. Aggregation robustness could be strengthened by using complex picture fuzzy Dombi aggregation [30] and prioritized Muirhead means in complex neutrosophic values [31]. Combining Pythagorean fuzzy rough sets with Schweizer–Sklar norms [32] and interval-valued T-spherical fuzzy information [33] can also improve decision-making in large-scale uncertain situations. Finally, the effectiveness of the proposed approach in various fields might be validated by comparing it with circular intuitionistic fuzzy EDAS [34].
Author Contributions
Conceptualization, Y.L. and B.W.; Methodology, Y.L. and B.W.; Software, Y.L. and B.W.; Validation, B.W.; Formal analysis, Y.L.; Investigation, B.W.; Resources, Y.L.; Data curation, B.W.; Visualization, B.W.; Project administration, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
This study did not involve human participants, human data, or human tissue.
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets. In Intuitionistic Fuzzy Sets; Studies in Fuzziness and Soft Computing; Physica-Verlag HD: Heidelberg, Germany, 1999; Volume 35, pp. 1–137. ISBN 978-3-7908-2463-6. [Google Scholar]
- Yager, R.R. Pythagorean Fuzzy Subsets. In Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 24–28 June 2013; pp. 57–61. [Google Scholar]
- Senapati, T.; Yager, R.R. Fermatean Fuzzy Weighted Averaging/Geometric Operators and Its Application in Multi-Criteria Decision-Making Methods. Eng. Appl. Artif. Intell. 2019, 85, 112–121. [Google Scholar] [CrossRef]
- Aruchsamy, R.; Velusamy, I.; Dhandapani, P.B.; Nasiru, S.; Chesneau, C. Modern Approach in Pattern Recognition Using Circular Fermatean Fuzzy Similarity Measure for Decision Making with Practical Applications. J. Math. 2024, 2024, 6503747. [Google Scholar] [CrossRef]
- Aggarwal, A.; Choudhary, C.; Mehrotra, D. Evaluation of Smartphones in Indian Market Using EDAS. Procedia Comput. Sci. 2018, 132, 236–243. [Google Scholar] [CrossRef]
- Akram, M.; Ali, U.; Santos-García, G.; Niaz, Z. 2-Tuple Linguistic Fermatean Fuzzy MAGDM Based on the WASPAS Method for Selection of Solid Waste Disposal Location. Math. Biosci. Eng. 2023, 20, 3811–3837. [Google Scholar] [CrossRef] [PubMed]
- Abdullah, L.; Rahim, N. The Use of Fuzzy DEMATEL for Urban Sustainable Development. In Intelligent and Fuzzy Techniques in Big Data Analytics and Decision Making; Kahraman, C., Cebi, S., Cevik Onar, S., Oztaysi, B., Tolga, A.C., Sari, I.U., Eds.; Advances in Intelligent Systems and Computing; Springer International Publishing: Cham, Switzerland, 2020; Volume 1029, pp. 722–729. ISBN 978-3-030-23755-4. [Google Scholar]
- Ahmed, O.S.; Al-Gahtani, K.S.; Altuwaim, A. Cost–Benefit Framework for Selecting a Highway Project Using the SWARA Approach. Buildings 2025, 15, 439. [Google Scholar] [CrossRef]
- Cui, A.; Liu, Z. Utilizing CoCoSo and Interval Neutrosophic MAGDM with SuperHyperSoft for Competitiveness Assessment in Rural Tourism of Surrounding Cities. Neutrosophic Sets Syst. 2025, 78, 10. [Google Scholar]
- Yoon, K.P.; Kim, W.K. The Behavioral TOPSIS. Expert. Syst. Appl. 2017, 89, 266–272. [Google Scholar] [CrossRef]
- Xiong, X.; Cui, J.; Xie, R.; Guo, S.; Zhou, J. Large-Scale Multi-View Multiple Clustering. In Proceedings of the ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 6205–6209. [Google Scholar]
- Zhao, X.; Fan, J.; Chang, X.; Nie, F.; Zhang, Q.; Guo, J. Scalable Multi-View Regression Clustering for Large-Scale Data. IEEE Trans. Circuits Syst. Video Technol. 2025, 1. [Google Scholar] [CrossRef]
- Moujahid, A.; Dornaika, F. Advanced Unsupervised Learning: A Comprehensive Overview of Multi-View Clustering Techniques. Artif. Intell. Rev. 2025, 58, 234. [Google Scholar] [CrossRef]
- Wang, S.; Liu, X.; Liao, Q.; Wen, Y.; Zhu, E.; He, K. Scalable Multi-View Graph Clustering With Cross-View Corresponding Anchor Alignment. IEEE Trans. Knowl. Data Eng. 2025, 37, 2932–2945. [Google Scholar] [CrossRef]
- Liang, D.; Li, F.; Chen, X. Failure Mode and Effect Analysis by Exploiting Text Mining and Multi-View Group Consensus for the Defect Detection of Electric Vehicles in Social Media Data. Ann. Oper. Res. 2024, 340, 289–324. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, H.; Deng, Z.; Zhang, W.; Luo, C.; Wang, G.; Ge, Y.; Hu, S. Pseudolabel Enhanced Multiview Deep Concept Factorization Fuzzy Clustering. IEEE Trans. Fuzzy Syst. 2024, 32, 5334–5347. [Google Scholar] [CrossRef]
- Hajek, P.; Sahut, J.-M.; Olej, V. Credit Rating Prediction Using a Fuzzy MCDM Approach with Criteria Interactions and TOPSIS Sorting. Ann. Oper. Res. 2024. [Google Scholar] [CrossRef]
- Devadas, R.M.; Hiremani, V.; Gujjar, P. Aiding in Prognosis of Fibromyalgia Syndrome Utilizing MCDM TOPSIS Method in Fusion with Fuzzy Logic. In Ubiquitous Computing and Technological Innovation for Universal Healthcare; IGI Global Scientific Publishing: Hershey, PA, USA, 2024; pp. 127–152. ISBN 9798369322680. [Google Scholar]
- Bozyiğit, M.C.; Ünver, M. Parametric Circular Intuitionistic Fuzzy Information Measures and Multi-Criteria Decision Making with Extended TOPSIS. Granul. Comput. 2024, 9, 43. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y. A Modified TOPSIS Algorithm for the Assessment of Sports Quality in Higher Education Using Circular Pythagorean Fuzzy Information. Sci. Rep. 2025, 15, 18846. [Google Scholar] [CrossRef] [PubMed]
- Dharmalingam, M.; Mahapatra, G.S.; Vijayakumar, R. Environment-Aware Multi-Criteria Decision-Making for Selecting a Site for a Mobile Tower Installation Using the Fermatean Fuzzy TOPSIS Technique. Int. J. Fuzzy Syst. 2025. [Google Scholar] [CrossRef]
- Boonsothonsatit, G.; Vongbunyong, S.; Chonsawat, N.; Chanpuypetch, W. Development of a Hybrid AHP-TOPSIS Decision-Making Framework for Technology Selection in Hospital Medication Dispensing Processes. IEEE Access 2024, 12, 2500–2516. [Google Scholar] [CrossRef]
- Luo, H.J. Decision Algorithm for Physical Education in Higher Education and Circular Fermatean Fuzzy Framework. IEEE Access 2025, 13, 29122–29133. [Google Scholar] [CrossRef]
- Revathy, A.; Inthumathi, V.; Krishnaprakash, S.; Anandakumar, H.; Arifmohammed, K.M. The Characteristics of Circular Fermatean Fuzzy Sets and Multicriteria Decision-Making Based on the Fermatean Fuzzy t-Norm and t-Conorm. Appl. Comput. Intell. Soft Comput. 2024, 2024, 6974363. [Google Scholar] [CrossRef]
- Aruchsamy, R.; Velusamy, I.; Dhandapani, P.B.; Radwan, T. Einstein Aggregation Operator Technique in Circular Fermatean Fuzzy Environment for MCDM. Symmetry 2024, 16, 1243. [Google Scholar] [CrossRef]
- Duan, Y.; Stević, Ž.; Novarlić, B.; Hashemkhani Zolfani, S.; Görçün, Ö.F.; Subotić, M. Application of the Fuzzy MCDM Model for the Selection of a Multifunctional Machine for Sustainable Waste Management. Sustainability 2025, 17, 2723. [Google Scholar] [CrossRef]
- Mahmood, T.; Ullah, K.; Khan, Q.; Jan, N. An Approach toward Decision-Making and Medical Diagnosis Problems Using the Concept of Spherical Fuzzy Sets. Neural Comput. Appl. 2019, 31, 7041–7053. [Google Scholar] [CrossRef]
- Mahmood, T.; Waqas, H.M.; Ali, Z.; Ullah, K.; Pamucar, D. Frank Aggregation Operators and Analytic Hierarchy Process Based on Interval-valued Picture Fuzzy Sets and Their Applications. Int. J. Intell. Syst. 2021, 36, 7925–7962. [Google Scholar] [CrossRef]
- Nazeer, M.S.; Imran, R.; Amin, M.; Rak, E. An Intelligent Algorithm for Evaluating Martial Arts Teaching Skills Based on Complex Picture Fuzzy Dombi Aggregation Operator. J. Innov. Res. Math. Comput. Sci. 2024, 3, 44–70. [Google Scholar] [CrossRef]
- Imran, R.; Ullah, K.; Ali, Z.; Akram, M.; Senapati, T. The Theory of Prioritized Muirhead Mean Operators under the Presence of Complex Single-Valued Neutrosophic Values. Decis. Anal. J. 2023, 7, 100214. [Google Scholar] [CrossRef]
- Hussain, A.; Pamucar, D. Multi-Attribute Group Decision-Making Based on Pythagorean Fuzzy Rough Set and Novel Schweizer-Sklar T-Norm and T-Conorm. J. Innov. Res. Math. Comput. Sci. 2022, 1, 2. [Google Scholar]
- Nazeer, M.S.; Ullah, K.; Hussain, A. A Novel Decision-Making Approach Based on Interval-Valued T-Spherical Fuzzy Information with Applications. J. AppliedMath 2023, 1, 79. [Google Scholar] [CrossRef]
- Imran, R.; Ullah, K. Circular Intuitionistic Fuzzy EDAS Approach: A New Paradigm for Decision-Making in the Automotive Industry Sector. Spectr. Eng. Manag. Sci. 2025, 3, 76–92. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).