Symmetry-Driven Two-Population Collaborative Differential Evolution for Parallel Machine Scheduling in Lace Dyeing with Probabilistic Re-Dyeing Operations

Abstract

In lace textile manufacturing, the dyeing process in parallel machine environments faces challenges from sequence-dependent setup times due to color family transitions, machine eligibility constraints based on weight capacities, and probabilistic re-dyeing operations arising from quality inspection failures, which often lead to increased tardiness. To tackle this multi-constrained problem, a stochastic integer programming model is formulated to minimize total estimated tardiness. A novel symmetry-driven two-population collaborative differential evolution (TCDE) algorithm is then proposed. It features two symmetrically complementary subpopulations that achieve a balance between global exploration and local exploitation. One subpopulation employs chaotic parameter adaptation through a logistic map for symmetrically enhanced exploration, while the other adjusts parameters based on population diversity and convergence speed to facilitate symmetry-aware exploitation. Moreover, it also incorporates a symmetrical collaborative mechanism that includes the periodic migration of top individuals between subpopulations, along with elite-set guidance, to enhance both population diversity and convergence efficiency. Extensive computational experiments were conducted on 21 small-scale (optimally validated via CVX) and 15 large-scale synthetic datasets, as well as 21 small-scale (similarly validated) and 20 large-scale industrial datasets. These experiments demonstrate that TCDE significantly outperforms state-of-the-art comparative methods. Ablation studies also further verify the critical role of its symmetry-based components, with computational results confirming its superiority in solving the considered problem.

1. Introduction

The lace textile industry encounters significant pressures in optimizing its dyeing processes, where both efficiency and product quality are critical concerns [1,2]. This process is characterized by sequence-dependent setup times, such as the extensive cleaning necessitated when switching between dark and light color families. Additionally, machine eligibility, dictated by varying weight capacities, adds another layer of complexity. Compounding these two elements, the stochastic nature of re-dyeing operations, frequently triggered by quality inspection failures introduces significant variability. Such rework, implemented to salvage imperfect products, is not unique to textiles and is prevalent in manufacturing sectors like panel furniture processing [3], bearing production [4], and automotive parts manufacturing [5]. Actually, these combined factors can lead to substantial production delays [6] and increased operational costs in the lace dyeing process.

The dyeing optimization process is vital for tackling chronic tardiness issues in the lace textile industry. This research is motivated by a significant challenge faced by a major lace manufacturing facility in Fuzhou, China, which is the nation’s second-largest producer. The factory employs parallel automatic dyeing vessels. Effective scheduling of these vessels requires the simultaneous consideration of deterministic constraints, such as sequence-dependent setups and machine eligibility, as well as the inherent stochasticity of re-dyeing operations. The latter introduces considerable variability in processing times, which can lead to significant delays. The primary challenge lies in scheduling parallel machines to minimize the tardiness criterion under these complex and uncertain conditions.

This recognition has elevated rework operations to a prominent research theme within manufacturing systems. Recent advancements in rework-aware scheduling have focused on single-machine and job-shop issues, with hybrid metaheuristic algorithms emerging as powerful tools to address their complexities.

Table 1. Summary of related works on rework-aware scheduling.

Reference	Authors & Year	Problem	Solution Method
[7]	Zhu et al. (2021)	Single-machine scheduling with rework	Mixed-integer programming, Tabu search
[8]	Mahmoud et al. (2023)	Stochastic job shop with rework costs	Markovian modeling framework
[9]	Zhang et al. (2023)	Uncertain re-manufacturing with rework	Hybrid DE-particle swarm optimization
[10]	Albayrak et al. (2024)	Flexible job shop with rework & energy	Enhanced NSGA-II, Local search
[4]	Wang et al. (2024)	Green re-entrant job shop with rework	Multi-objective hybrid algorithm
[11]	Quan et al. (2024)	Flexible job shop with rework	Adaptive evolutionary algorithm
[12]	Kim et al. (2025)	Dynamic hybrid flow shop with rework	genetic programming-based reinforcement learning algorithm
[13]	Peng et al. (2025)	Multi-skill project with rework risks	Improved gazelle optimization algorithm
[14]	Kao et al. (2018)	Unrelated parallel batching machines	Mixed-integer programs
[15]	Wang et al. (2020)	Unrelated parallel machines with rework	Genetic algorithm, Simulated annealing
[16]	Rezaeian et al. (2023)	Parallel machines with eligibility	Sensitivity analysis
[17]	Wang et al. (2025)	Parallel machines with rework and pre-emption	Two-stage heuristic
	This work	Parallel machines with probabilistic re-dyeing operations	Symmetry-driven TCDE

summarizes the key characteristics of representative studies related to scheduling problems with rework operations and parallel machine environments.

Zhu et al. [7] investigated a single-machine resource-constrained multi-project scheduling problem that focuses on detection and rework. They adopted a mixed-integer programming model and a tabu search framework with a chain-based baseline scheme to satisfy both online and offline scheduling. Mahmoud et al. [8] tackled a stochastic job-shop problem by introducing a Markovian modeling framework that incorporates both job-specific costs and success probability distributions. Zhang et al. [9] proposed a hybrid optimization algorithm that integrates differential evolution (DE) and particle swarm optimization to solve an uncertain re-manufacturing scheduling model with rework risk. This algorithm outperformed baseline algorithms in 17 out of 18 test instances by utilizing enhanced population diversity mechanisms.

In the past two years, Albayrak et al. [10] employed an enhanced non-dominated sorting genetic algorithm-II (NSGA-II), a hybrid metaheuristic that combines evolutionary strategies with local searches, to address an energy-sensitive flexible job shop problem considering rework processes and new job arrival. The optimization objectives included minimizing energy consumption, workload, and makespan. To tackle green re-entrant job-shop scheduling with job reworking, Wang et al. [4] designed a multi-objective hybrid algorithm based on a local neighborhood search. Quan et al. [11] proposed a two-level virtual workflow model combined with an adaptive evolutionary algorithm to address scheduling challenges in flexible job shop scheduling with rework. Additionally, Kim et al. [12] developed a genetic programming-based reinforcement learning algorithm for dynamic hybrid flow shop scheduling with reworks, which can achieve superior total tardiness minimization by integrating variable neighborhood search with deep Q-networks. Peng et al. [13] applied an improved gazelle optimization algorithm with dynamic operators and mutation strategies to address multi-skill project scheduling with rework risks.

While these studies contribute to the broader field of rework scheduling, fewer have focused specifically on parallel machine environments. Kao et al. [14] developed mixed-integer programs for unrelated parallel batching machines, comparing static and dynamic equipment health indicators. Wang et al. [15] used a modified genetic algorithm and simulated annealing for unrelated parallel machine scheduling with random rework. They demonstrated that simulated annealing outperformed the genetic algorithm in terms of computational efficiency for minimizing the expected total weighted tardiness. Rezaeian et al. [16] studied unrelated parallel machines with eligibility constraints and release times, optimizing makespan through sensitivity analysis. Wang et al. [17] investigated the problem with random rework and limited pre-emption, and proposed a two-stage heuristic algorithm to balance makespan with earliness–tardiness costs. Few of these studies consider the deterministic–stochastic nature of the problem, such as deterministic setup times and probabilistic re-dyeing operations in textile manufacturing. Notably, Table 1 synthesizes these key contributions, revealing a critical gap: none of the existing studies simultaneously consider deterministic setup times, machine eligibility, and probabilistic re-dyeing operations in parallel machine scheduling for textile manufacturing.

Moreover, to effectively deal with stochastic rework in parallel machine scheduling, the concept of total estimated processing time ($TEPT$) has emerged as a pivotal metric for tardiness prediction. Building on previous research that minimizes total estimated tardiness ($TET$) in stochastic environments [17,18,19], $TEPT$ employs Bayesian estimation to integrate probabilistic processing times and rework cycles. By embedding $TEPT$ into the scheduling model, we directly target $TET$ minimization in parallel dyeing vessel coordination.

This work examines the above issue as a parallel machine scheduling problem with sequence-dependent setup times, machine eligibility, and probabilistic re-dyeing operations, which is strongly NP-hard [20]. Therefore, metaheuristics are frequently applied in the related literature to address practical instances of these problems [21,22,23,24,25,26]. Among metaheuristics, DE [27] is selected for its simplicity, efficiency, and robustness in solving complex optimization problems. Compared to genetic algorithms, DE typically exhibits faster convergence and better performance in continuous and high-dimensional search spaces, making it particularly suitable for scheduling problems with stochastic components [28,29,30,31,32,33]. Its capacity to balance exploration and exploitation further enhances its applicability to the considered problem. To the best of our knowledge, DE has not yet been applied to lace dyeing scheduling with $TET$ minimization, which motivates this study.

On the other hand, the hybrid metaheuristic advancements above highlight the efficacy of combining complementary optimization mechanisms to tackle stochasticity and complexity in scheduling. However, existing frameworks often lack symmetry-driven coordination between exploration and exploitation [34], which is critical for parallel machine environments with probabilistic re-dyeing. In the context of metaheuristics like DE or symmetry can be leveraged to design algorithms that efficiently explore the search space while effectively exploiting promising solutions. Motivated by this gap, our work builds on the hybrid metaheuristic paradigm by introducing a symmetry-based dual-subpopulation collaborative structure to address lace dyeing scheduling challenges.

Expanding upon our previous work [35], this study introduces a symmetry-driven optimization paradigm for parallel machine scheduling. The novelty and main contributions of our work are highlighted as follows:

• To minimize $TET$, a stochastic integer programming model is developed. This model captures uncertainty in lace manufacturing rework cycles and is validated optimally via CVX (a MATLAB, R2024-based convex optimization toolbox) on small-scale synthetic and industrial datasets.
• A novel symmetry-driven TCDE algorithm is designed, where symmetrically structured subpopulations collaborate to balance exploration and exploitation. Unlike conventional hybrid metaheuristics for rework scheduling, Subpopulation A employs chaotic parameter adaptation to ensure ergodic symmetry in global search, while Subpopulation B uses diversity-convergence adaptive control to maintain convergence symmetry in local exploitation.
• A symmetrical collaborative mechanism is proposed, which involves periodic exchange of migrants between subpopulations and guidance from an elite set to facilitate knowledge sharing among subpopulations. This mechanism addresses the lack of symmetry-driven coordination in existing hybrid metaheuristics.
• Extensive computational experiments conducted on both synthetic and industrial datasets comprehensively evaluate the performance of TCDE. Ablation studies provide further evidence of the critical role played by the novel components of TCDE, with computational results solidly confirming its advantages in addressing the problem.

The remainder of this paper is organized as follows. The problem description is presented in Section 2. Section 3 outlines the proposed TCDE for solving the problem. Numerical experiments on TCDE are reported in Section 4, and the conclusions are summarized in the final section, which also includes suggestions for future research topics.

2. Problem Description

2.1. Problem Statement

In this paper, the dyeing optimization problem is defined as a parallel machine scheduling problem with sequence-dependent setup times, machine eligibility, and probabilistic re-dyeing operations. The notations used for this problem are presented in

Table 2. A summary of notations used in the mathematical model.

Notations	Description
n	The number of jobs
m	The number of machines
c	The number of color families
H	The number of operations for each job
$d{p}_{j,h}$	Defective probability of the h-th operation of job j, $d{p}_{j,H}=0$,
	it is assumed that job j is allowed to be processed at most $H-1$ times
$m{p}_j$	The processing time of the main dyeing operation of the job j
$l_j$	The color family of the job j,$l_j\in \{1,2,\dots ,c\}$
${\alpha }_{j,h}$	The decreasing coefficient of the processing time in the rework process of the h-th
	operation of the job j($0\le {\alpha }_{j,h}\le 1$)
$p_{j,h}$	The processing time of the h-th operation of the job j, $p_{j,1}=m{p}_j$,
	$p_{j,h}=p_{j,(h-1)}\times {\alpha }_{j,h}(h\in \{2,\dots ,H\})$
$S_{l_i,l_j}$	The sequence-dependent setup time when $l_j$ is preceded by $l_i$
$g_j$	The weight of the job j
$G_k$	The capacity of the machine k
$E{T}_j$	The expected tardiness of the job j
$d_j$	The due date of the job j
$E\left(C_j\right)$	The expected completion time of the job j
M	A problem-specific upper bound
Decision Variables	Description
$X_{j,h}$	The setup completion time of the h-th operation of the job j
$C_{j,h}$	The completion time of the h-th operation of the job j
$Y_{i{h}^{\prime },jh,k}$	Binary variable, $Y_{i{h}^{\prime },jh,k}=1$, of the h-th operation of the job j is immediately
	preceded by the $h^{\prime }$th operation of the job i on machine k; otherwise, it is 0

.

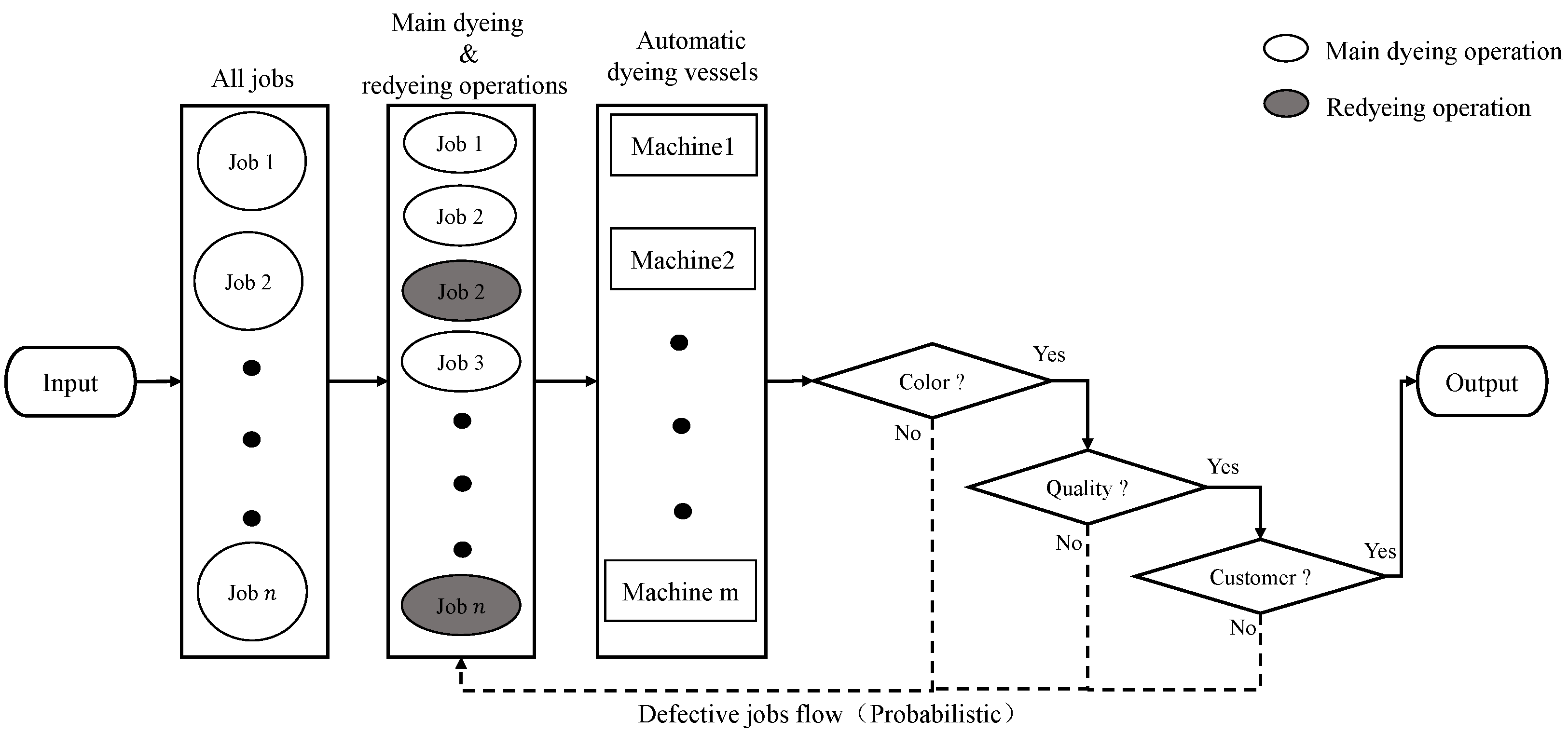
Once the main dyeing operation is completed, the job undergoes three sequential inspections: color, quality, and customer inspection. If a job fails any of these inspections, it is returned for re-dyeing until it passes, with no further inspections required after passing. The number of re-dyeing processes is finite ($d{p}_{j,H}=0$), and the imperfect production probability $d{p}_{j,h}$ is estimated from historical data. Each re-dyeing operation reduces the dyeing time linearly via a decreasing coefficient ${\alpha }_{jh}$ ($0\le {\alpha }_{j,h}\le 1$), where $p_{j,1}=m{p}_j$ and $p_{j,h}=m{p}_{j,(h-1)}\times {\alpha }_{jh}$. The first operation is the main dyeing process, while subsequent operations are probabilistic processes. Figure 1 illustrates the configuration of the problem.

Each job is defined by four attributes: color family ($l_j$), weight ($g_j$), main dyeing time ($m{p}_j$), and due date ($d_j$). In the factory, eight color families are split into light and dark depths, which influence $m{p}_j$ (see

Table 3. The relationship between color depth and processing time.

${\mathit{l}}_{\mathit{j}}$	Color Family	Color Depth	${\mathit{mp}}_{\mathit{j}}$
1	White	Light	2
2	Flesh Color	Light	6
3	Pink	Light	6
4	Gray	Light	6
5	Blue	Dark	8
6	Purple	Dark	8
7	Green	Dark	8
8	Red	Dark	8

). No setup time is needed between successive jobs of the same color family. However, when transitioning between different color families, setup involves cleaning, with the thoroughness (either rough or thorough) determined by the color depth of the preceding job. Setup times demonstrate asymmetric properties based on color depth transitions: thorough cleaning (from dark to light) requires three times the duration of rough cleaning (from light to dark).

Moreover, each vessel $k\in \{1,2,\dots ,m\}$ can process only one job at a time without pre-emption and has a capacity limit of $G_k$. Job j can be assigned to vessel k only if $g_j\le G_k$. Jobs cannot be merged, even within the same color family. There are also additional constraints, including the absence of pre-emption or insertion.

2.2. Mathematical Model

The proposed mathematical model for minimizing $TET$ is as follows:

$$\begin{array}{c}\hfill minTET=\sum _{j=1}^{n}E{T}_j.\end{array}$$

(1)

This is subject to the following:

$$\begin{array}{cc}\hfill & E{T}_j=max\{E\left(C_j\right)-d_j,0\},\forall j,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & E\left(C_j\right)=C_{j,1}(1-d{p}_{j,1})+\sum _{h=2}^H{C}_{j,h}\prod _{h^{\prime }}^{H}d{p}_{j,h^{\prime }}(1-d{p}_{j,h^{\prime }}),\forall j,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & \sum _{k=1}^m\sum _{i=0}^n\sum _{h^{\prime }}^H{Y}_{i{h}^{\prime },jh,k}=1,\forall j,h,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & \sum _{j=1}^n\sum _{h=1}^H{Y}_{00,jh,k}=1,\forall k,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & \sum _{j=1}^n\sum _{h=1}^H{Y}_{i{h}^{\prime },jh,k}\le \sum _{i^{\prime }=0}^n\sum _{h^{″}=1}^H{Y}_{i^{\prime }{h}^{″},i{h}^{\prime },k},\forall k,\in \{1,2,\dots ,n\},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & X_{j,h}\le M·(1-Y_{00,jh,k}),\forall j,h,k,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & M=\sum _{j=1}^n\sum _{h=1}^H{p}_{j,h}+\underset{i,j}{max}\{S_{l_i,l_j}\}·(n-1),\forall j,h,k,\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & X_{j,h}\le C_{i,h^{\prime }}+S_{l_i,l_j}+M·(1-Y_{i{h}^{\prime },jh,k}),\forall j,h,h^{\prime },k,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & C_{j,h}\ge p_{j,h}+M·(Y_{00,jh,k}-1),\forall j,h,k,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & C_{j,h}\ge C_{i,h^{\prime }}+p_{j,h}+M·(Y_{i{h}^{\prime },jh,k}-1),\forall i,j,h,h^{\prime },k,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & C_{j,h}\ge X_{j,h}+p_{j,h},\forall j,h,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & C_{j,h}\ge C_{j,(h-1)}+p_{j,h},\forall j,h,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & G_k\ge g_j\times \sum _{i=0}^n\sum _{h^{\prime }}^H{Y}_{i{h}^{\prime },jh,k},\forall i,j,h,h^{\prime },k,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & Y_{i{h}^{\prime },jh,k}\in \{0,1\},\forall i,j,h,h^{\prime },k.\hfill \end{array}$$

(15)

The goal is to minimize $TET$, as demonstrated in Equation (1). The estimated tardiness for job j, denoted as $E{T}_j$, is calculated as the maximum of the difference between $E\left(C_j\right)$ and $d_j$, or zero, as defined in Equation (2). Equation (3) calculates $E\left(C_j\right)$ within a probabilistic framework. Equation (4) ensures that each job is assigned to one machine and processed in a sequential manner. A dummy operation $Y_{00,jh,k}$ Equation (5) initializes each machine. Equation (6) allows the hth operation of job j to be empty if the $h^{\prime }$th operation of job i is the last on a machine for three consecutive jobs. Equation (7) establishes the setup completion time of the first operation on each machine as 0. Equation (8) ensures that M scales linearly with the problem size and avoids arbitrarily large values, thereby improving both numerical stability and computational efficiency. Equation (9) links the setup completion time $X_{j,h}$ to the preceding operation’s completion time $C_{i,h^{\prime }}$, incorporating setup time $S_{l_i,l_j}$ controlled by a large number M and binary variable $Y_{i{h}^{\prime },jh,k}$. Equation (10) ensures that the setup completion time $C_{j,h}$ is at least the processing time $p_{j,h}$. Equation (11) relates $C_{j,h}$ to $C_{i,h^{\prime }}$ with setup and processing times. Equation (12) ensures $C_{j,h}$ is at least $X_{j,h}+p_{j,h}$. Equation (13) ensures $C_{j,h}$ is at least the previous operation’s completion time $C_{j,(h-1)}$ plus $p_{j,h}$. Equation (14) enforces machine capacity constraints. The decision variable is binary, as stated in Equation (15).

It is important to note that we use problem-specific upper bounds derived from actual production constraints, which enhances numerical stability and mitigates the issues associated with large constant values. Furthermore, the maximum number of re-dyeing operations (denoted as H) is fixed based on practical considerations observed in the dyeing factory under investigation. Historical production data and expert insights indicate that excessive re-dyeing is strictly limited in practice, as it can lead to fabric damage, increased energy consumption, and higher production costs. Therefore, setting a fixed upper bound H is both realistic and essential to ensure model tractability and industrial applicability.

2.3. Illustrative Example

To make the problem and constraints concrete, consider the instance summarized in

Table 4. Data of the illustrative instance.

Job	Operations	Color Family	Weight (kg)	Main Time (h)	Due Date (h)	${\mathit{dp}}_{\mathit{j},1}$
1	$1,2,3$	White (light)	5	2	6	0.61
2	$4,5,6$	Pink (light)	15	6	12	0.54
3	$7,8,9$	Blue (dark)	20	8	24	0.56

. Three jobs must be processed on two parallel dyeing vessels. Each job is characterized by color family, weight, main processing time and due date. Vessel capacities are $G_1=15$ kg and $G_2=25$ kg. The maximum number of dyeing operations (main + reworks) is set to $H=3$; the processing-time reduction coefficient for any rework is ${\alpha }_{j,h}=0.5$. Sequence-dependent setup times follow the following rule: dark-to-light requires 3 h, light-to-dark 1 h, and identical color families need 0 h.

A feasible schedule obtained by the proposed TCDE algorithm is depicted in Figure 2. The Gantt chart reveals the following key observations:

• Machine eligibility: Job 3 (20 kg) can only be assigned to $M_2$, whereas jobs 1 and 2 fit both vessels.
• Sequence-dependent setup: Three hours of cleaning are required on $M_2$ when the color changes from dark (job 3) to light (job 2).
• Probabilistic reworks: Job 1 fails the first inspection with probability $d{p}_{1,1}=0.61$ and returns for a 1-h rework (operation 1–2). The expected completion time is $E\left(C_1\right)=7.67$ h, yielding tardiness of 1.67 h.

The fitness of each chromosome is evaluated using the expected job completion time, with the first operation as the main dyeing process and subsequent operations as probabilistic re-dyeing processes. All chromosomes satisfy the precedence constraints. In Figure 2, $E\left(C_1\right)=C_{1,1}(1-d{p}_{1,1})+C_{1,2}d{p}_{1,1}(1-d{p}_{1,2})+C_{1,3}d{p}_{1,1}d{p}_{1,2}(1-d{p}_{1,3})=7.6730$. Similarly, $E\left(C_2\right)=7.8447$ and $E\left(C_3\right)=23.6208$. Thus, $TET$ for this solution is 1.6730.

3. TCDE for the Considered Problem

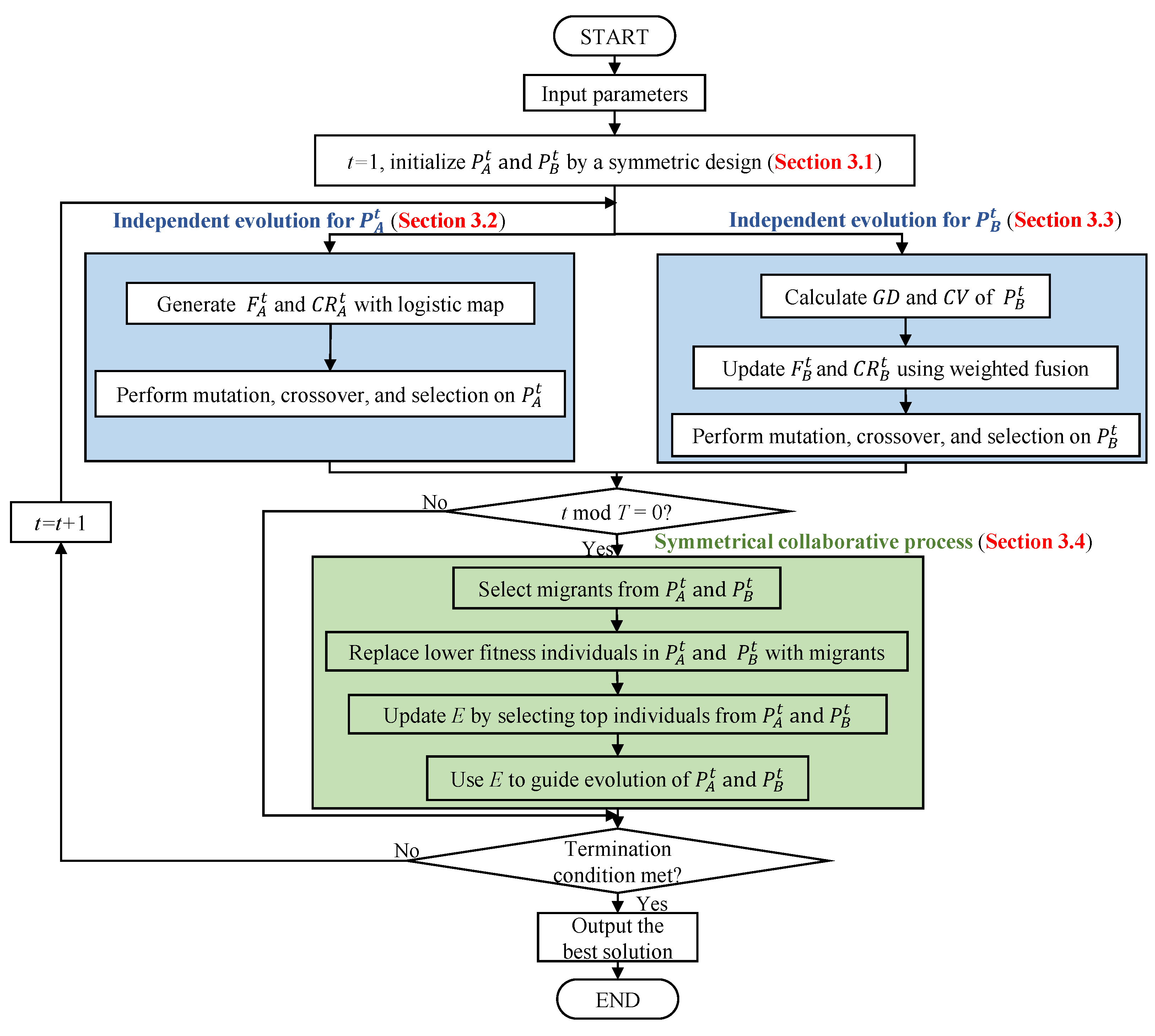
Usually, metaheuristics are favored over mathematical models (e.g., mixed-integer programming models) for their efficiency in solving complex problems within practical timeframes [26]. Therefore, we propose symmetry-driven TCDE to tackle the scheduling problem. To provide a clear and intuitive understanding of the proposed TCDE algorithm, we present a flowchart and pseudocode that illustrate its workflow. Specifically, Figure 3 depicts the flow chart, while Algorithm 1 details the step-by-step implementation of TCDE. The key components and their interactions are detailed in subsequent subsections.

Algorithm 1 Symmetry-driven TCDE

Input: parameters   1: $t=1$   2: randomly initialize population $P_A^t$ and $P_B^t$ by a symmetric design (Section 3.1)   3: while termination condition not met do   4:     /******Independent evolution for ${\mathit{P}}_{\mathit{A}}^{\mathit{t}}$ (Section 3.2)******/   5:     update $P_A^t$ using chaos theory:   6:        generate chaotic parameters $F_A^t$ and $C{R}_A^t$ using logistic map   7:        perform mutation, crossover, and selection on $P_A^t$ with $F_A^t$ and $C{R}_A^t$   8:     /******Independent evolution for ${\mathit{P}}_{\mathit{B}}^{\mathit{t}}$ (Section 3.3)******/   9:     update $P_B^t$ by population diversity and convergence speed:  10:        calculate population diversity $GD$ and convergence speed $CV$ of $P_B^t$  11:        update $F_B^t$ and $C{R}_B^t$ using weighted fusion  12:        perform mutation, crossover, and selection on $P_B^t$ with $F_B^t$ and $C{R}_B^t$  13:     /****Symmetrical collaborative process (Section 3.4)****/  14:     if $tmodT=0$ then  15:         select migrants from $P_A^t$ and $P_B^t$ based on solution quality  16:         replace lower fitness individuals in $P_A^t$ and $P_B^t$ with migrants  17:        update elite set E by selecting the top individuals from $P_A^t$ and $P_B^t$  18:         use elite set E to guide the evolution of $P_A^t$ and $P_B^t$  19:     end if  20:     $t=t+1$  21: end while  Output: the best solution

The TCDE algorithm operates through a structured workflow, as illustrated in Figure 2 and Algorithm 1. It begins with the initialization of two subpopulations, $P_A^t$ and $P_B^t$, using a symmetric design as described in Section 3.1. Throughout the iterative process on generation t, $P_A^t$ evolves using parameters $F_A^t$ (scaling factor of $P_A^t$) and $C{R}_A^t$ (crossover rate of $P_A$), which are dynamically generated via a logistic map rooted in chaos theory (Section 3.2). Correspondingly, $P_B^t$ adjusts its parameters $F_B^t$ (scaling factor of $P_B$) and $C{R}_B^t$ (crossover rate of $P_B^t$) by evaluating population diversity $GD$ and convergence speed $CV$, as depicted in Section 3.3. This process creates parameter symmetry through distinct but equivalent adaptation mechanisms. At every T generation, migrants are exchanged between $P_A^t$ and $P_B^t$ to introduce new diversity, replacing lower fitness individuals and updating the elite set E, which guides subsequent evolution (Section 3.4). This symmetrical interactive and collaborative mechanism used in Section 3.4 not only enriches population diversity but also enhances global search capabilities and improves convergence speed.

3.1. Population Initialization

Given predefined population sizes N and L (where $L=n\times H$), the population is represented by a $q\times L$ matrix ${\mathbf{A}}^t$, with t indicating the generation number. Matrix ${\mathbf{A}}^t$ is composed of rows ${\mathbf{a}}_1^t,{\mathbf{a}}_2^t,\dots ,{\mathbf{a}}_q^t$, each consisting of L real numbers. These rows are decoded into scheduling solutions. To ensure the feasibility of initial solutions, a random key-based encoding scheme is used [1]. Each entry $a_{ej}^t$ is assigned a value within ${\cup }_{k\in {\Omega }_j}(k-1,k]$, where ${\Omega }_j$ is the set of machines capable of processing job j.

Moreover, the operation sequence employs structured encoding, where each job’s main dyeing and re-dyeing operations are marked by a unique symbol. Each job appears exactly H times, representing its H operations. This method ensures every chromosome corresponds to a feasible solution. For instance, job $J_1$ is represented by the number 1, with its re-dyeing operations numbered sequentially up to H. Similarly, job $J_2$ is denoted by $H+1$, and its re-dyeing processes are numbered from $H+2$ to $2H$, and so on.

An illustrative example is presented above in Section 2.3. The initial population is shown as Matrix ${\mathbf{A}}^1$ in Equation (16). For clarity, matrix values are rounded to four decimal places, and $N=5$. Given $g_1\le G_1$, $g_2\le G_1$ and $g_3\ge G_1$, the intervals for the matrix elements are $a_{e1}^1,a_{e2}^1,a_{e3}^1,a_{e4}^1,a_{e5}^1,a_{e6}^1\in (0,2]$ and $a_{e7}^1,a_{e8}^1,a_{e9}^1\in (1,2]$.

$${\mathbf{A}}^1=\left(\begin{array}{c}\begin{array}{ccccccccc}1.1154& 0.6489& 1.3413& 0.2246& 1.1468& 0.1421& 1.8632& 1.5537& 1.4683\\ 0.7886& 1.2993& 1.8899& 0.9001& 1.1882& 1.9021& 1.8922& 1.2561& 1.2903\\ 0.4724& 1.5662& 1.1299& 0.3674& 0.2276& 1.8996& 1.7892& 1.9002& 1.2442\\ 0.5552& 1.1783& 1.5621& 1.7821& 0.2788& 1.8991& 1.9001& 1.3442& 1.5672\\ 1.6729& 1.8901& 1.1436& 0.9416& 1.9823& 1.0811& 1.8001& 1.1788& 1.1123\end{array}\end{array}\right).$$

(16)

Algorithm 2 illustrates the decoding procedure. During decoding, the machine assignment for the h-th operation of job j is determined by $\lceil a_{ej}^t\rceil$, and the operation sequence on each machine is sorted by the decimal part $a_{ej}^t-\lfloor a_{ej}^t\rfloor$. Operations of the same job are unified in symbol representation to form a feasible schedule based on operation order. The fitness of each chromosome is evaluated using the expected value method for calculating job completion times, considering the first operation as the main dyeing process and subsequent operations as probabilistic re-dyeing processes.

Algorithm 2 Decoding process

Input:  ${\mathbf{a}}_e^t\in {\mathbf{A}}^t$   1: for  $k=1$ to m do   2:     decide all operations assigned to machine $M_k$ by using the ceiling value $\lceil a_{ej}^t\rceil$, and obtain the operation sequence ${\mathrm{\Psi }}_k$ on $M_k$ is sorted according to the decimal part $a_{ej}^t-\lfloor a_{ej}^t\rfloor$   3:     all operations of a job are unified under the same job symbol, that is, each ${\mathrm{\Psi }}_k$ is changed to ${\mathrm{\Psi }}_k^{\prime }$   4: end for   5: ${\phi }_1={\phi }_2=\dots ={\phi }_m=1$, $k=1$, $u=1$   6: while   $u\le {\sum }_{k=1}^m{\mathrm{\Psi }}_k^{\prime }$ do   7:     while $k\le m$ do   8:         if ${\phi }_k\le H_k$ then   9:            find the ${\phi }_k$ unassigned job j, $J_{k,{\phi }_k}\in {\mathrm{\Psi }}_k^{\prime }$, process it on machine $M_k$, and its operation sequence is then interpreted based on its job order of occurrence  10:             ${\phi }_k={\phi }_k+1$, $u=u+1$  11:         end if  12:         $k=k+1$, $k=1$ if $k>m$  13:     end while  14: end while  Output:  $TET$ of the solution ${\mathbf{a}}_e^t$

In the decoding process, each chromosome ensures a feasible solution. For example, take the first row ${\mathbf{a}}_1^1$ of ${\mathbf{A}}^1$. The ceiling values $a_{1j}^1=[2,1,2,1,2,1,2,2,2]$ assign operations 2, 4, and 6 to machine 1, and the rest to machine 2. The decimal parts $a_{1j}^1-\lfloor a_{1j}^1\rfloor$ then order operations on each machine. For machine 1, the sequence is ${\mathrm{\Psi }}_1=(6,4,2)$; for machine 2, it is ${\mathrm{\Psi }}_2=(1,5,3,9,8,7)$. To maintain feasibility, the operations of the same job follow their predefined order. Finally, unifying all operations under the same job symbol provides ${\mathrm{\Psi }}_1^{\prime }=(1,2,1,3,3,3)$ and ${\mathrm{\Psi }}_2^{\prime }=(2,2,1)$, which are used to construct a feasible schedule. The Gantt chart for this decoded solution is shown in Figure 2, where $TET$ for ${\mathbf{a}}_1^1$ is 1.6730.

In TCDE, the symmetric design of the two-population structure is evident right from the initialization stage. Subpopulations $P_A^1$ and $P_B^1$, each of size $N/2$, are randomly initialized to establish a symmetrical duality. This balanced configuration allows the two subpopulations to complement each other, mirroring interactions in symmetric systems.

3.2. Independent Evolution for $P_A^t$

The evolution of $P_A^t$ is independently driven by parameters dynamically adjusted via a chaos theory-based logistic map. This approach leverages the chaotic properties of ergodicity and stochasticity to enhance global exploration and prevent local optima trapping, resulting in enhanced algorithmic performance and efficiency in solving complex optimization problems.

3.2.1. Generate Chaotic Parameters $F_A^t$ and $C{R}_A^t$ Using the Logistic Map

In basic DE [27], the parameters (including scaling factor F and crossover rate $CR$) are constant, yet they significantly impact the performance of DE. To improve this, a self-adaptive mechanism using chaotic theory can be embedded into DE [35]. Chaotic sequences, known for ergodicity, stochasticity, and irregularity, enhance the algorithm’s exploitation and convergence in the search space.

In this work, the logistic map, a simple dynamic system exhibiting chaotic behavior, is used as the self-adaptive mechanism for $F_A^t$ and $C{R}_A^t$ in $P_A^t$. Updating these parameters is based on the logistic map, as shown in Equation (17).

$$y^{t+1}=\mu \times y^t\times (1-y^t),$$

(17)

where $y^t$ is the chaotic number used for $F_A^t$ and $C{R}_A^t$, with $\mu$ as a control parameter, where $0\le \mu \le 4$. Equation (14) generates a deterministic chaotic dynamic number in the range $(0,1)$, ensuring $y^1\in (0,1)$ and, when $\mu =4$, $y^0\notin \{0,0.25,0.5,0.75,1\}$. During evolution, $F_A^t$ and $C{R}_A^t$ are initialized and then dynamically adjusted each iteration via this chaotic mechanism. This strategy diminishes the initial values’ influence on the algorithm’s performance, enhances global convergence and improves its capacity to avoid local optima.

3.2.2. Mutation

In $P_A^t$, the ‘DE/rand/1’ mutation operator is applied to generate the mutant vector ${\mathbf{V}}_e^{t+1}$. For each target vector ${\mathbf{a}}_e^t$, the mutant vector ${\mathbf{V}}_e^{t+1}$ is generated using the scaling factor $F_A^t$ and three distinct randomly selected target vectors, ${\mathbf{a}}_{r_1}^t$, ${\mathbf{a}}_{r_2}^t$, and ${\mathbf{a}}_{r_3}^t$, as shown in Equation (18):

$${\mathbf{V}}_e^{t+1}={\mathbf{a}}_{r_1}^t+F_A^t\times ({\mathbf{a}}_{r_2}^t-{\mathbf{a}}_{r_3}^t),r_1\ne r_2\ne r_3\ne e.$$

(18)

Here, the scaling factor $F_A^t$ controls the amplification of differential variation ${\mathbf{a}}_{r_2}^t-{\mathbf{a}}_{r_3}^t$, with $F_A^t\in (0,2)$ [27].

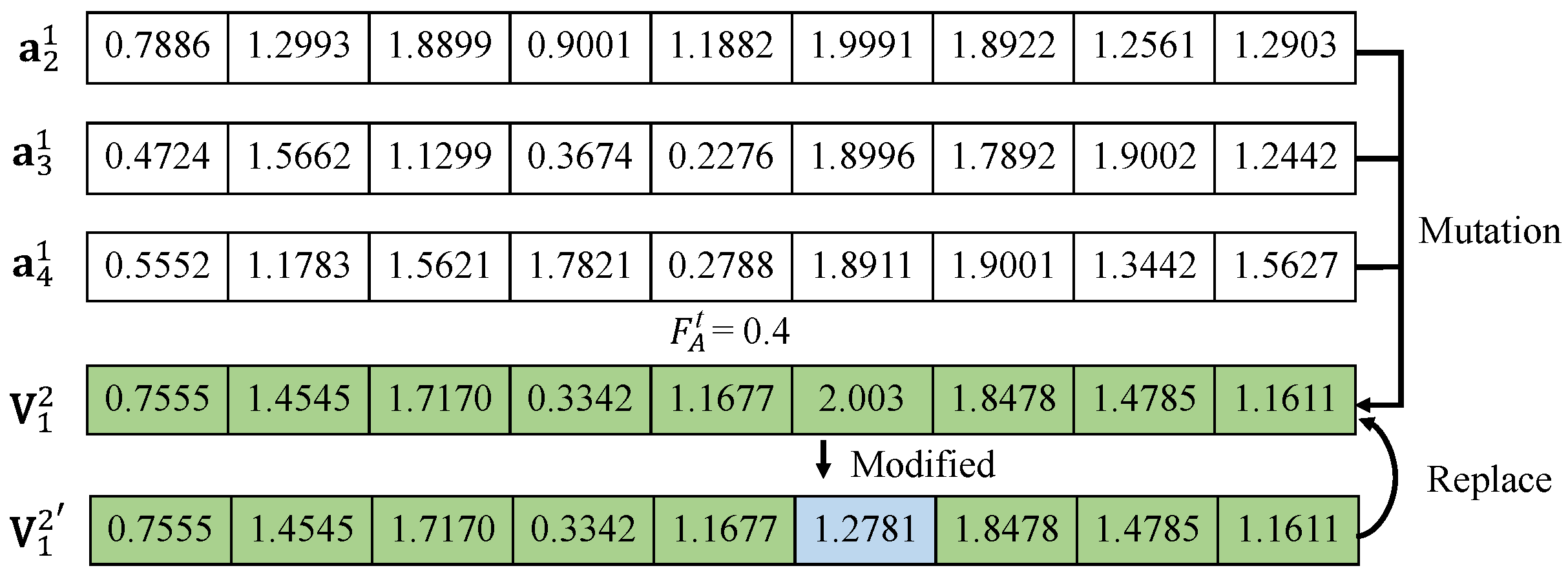
However, the mutation operator may generate vectors that violate capacity constraints, requiring a repair modification. In this process, only the elements that violate the constraints are regenerated. For example, in matrix ${\mathbf{A}}^1$, the mutation operator and repair modification are illustrated in Figure 4. With $e=1$, $r_1=2$, $r_2=3$, $r_3=4$, and $F_A^t=0.4$, the initial mutant vector ${\mathbf{V}}_1^2$ obtained from Equation (18) is $[0.7555,1.4545,1.7170,0.3342,1.1677,2.003,1.8478,1.4785,1.1611]$. Since $w_2>g_1$, $v_{e2}^1$ must fall within the range $(1,2]$. The element $v_{16}^2=2.003$ exceeds this range and is thus infeasible. A new value of 1.2781 is randomly selected from $(1,2]$ to replace $v_{12}^2$. The repaired vector ${\mathbf{V}}_1^{2^{\prime }}$ becomes $[0.7555,1.4545,1.7170,0.3342,1.1677,1.2781,1.8478,1.4785,1.1611]$, with all other elements satisfying the capacity constraints as defined by Equation (14).

3.2.3. Crossover

After the mutation phase, a crossover operator is applied to obtain a trial vector ${\mathbf{U}}_e^{t+1}=[u_{e1}^{t+1},u_{e2}^{t+1},\dots ,u_{en}^{t+1}]$, controlled by the crossover rate $C{R}_A^t\in [0,1]$. The trial vector ${\mathbf{U}}_e^{t+1}$ is formed by selecting elements from the mutant vector ${\mathbf{V}}_e^{t+1}$ and the target vector ${\mathbf{a}}_e^t$. The trial element $u_{ej}^{t+1}$ is generated using Equation (19):

$$u_{ej}^{t+1}=\left\{\begin{array}{cc}{v}_{ej}^{t+1}\hfill & \mathrm{if}r\left(j\right)\le C{R}_A^t\mathrm{or}j=rnb\left(e\right)\hfill \\ a_{ej}^t\hfill & \mathrm{otherwise}\hfill \end{array}\right..$$

(19)

Here, $r\left(j\right)$ is a random number between (0, 1), and $rnb\left(e\right)$ is a randomly chosen index from $\{1,2,\dots ,n\}$, ensuring that ${\mathbf{U}}_e^{t+1}$ includes at least one element from ${\mathbf{V}}_e^{t+1}$. For instance, using the example from Section 3.2.2 with $C{R}_A^t=0.9$, $rnb\left(e\right)=3$, and the given $r\left(j\right)$ values, the trial elements $u_{1j}^2$ are calculated via Equation (19), resulting in ${\mathbf{U}}_1^2=[0.7555,0.6489,1.717,0.2246,1.1677,1.2781,1.8478,1.5537,1.1611]$, as depicted in Figure 5.

3.2.4. Greedy Selection

After the crossover phase, a selection process is performed to update the target vector ${\mathbf{a}}_e^{t+1}=[a_{e1}^{t+1},a_{e2}^{t+1},\dots ,a_{en}^{t+1}]$. The target vector ${\mathbf{a}}_e^t$ is compared to its corresponding trial vector ${\mathbf{U}}_e^{t+1}$ using a one-to-one greedy criterion. If the objective value of ${\mathbf{U}}_e^{t+1}$ is no larger than that of ${\mathbf{a}}_e^t$, then ${\mathbf{a}}_e^{t+1}$ is updated to ${\mathbf{U}}_e^{t+1}$; otherwise, ${\mathbf{a}}_e^t$ is retained. This selection process is formalized in Equation (20).

$${\mathbf{a}}_e^{t+1}=\left\{\begin{array}{cc}{\mathbf{U}}_e^{t+1}\hfill & iff\left({\mathbf{U}}_e^{t+1}\right)\le f\left({\mathbf{a}}_e^t\right)\hfill \\ {\mathbf{a}}_e^t\hfill & otherwise\hfill \end{array}\right..$$

(20)

3.3. Independent Evolution for $P_B^t$

The evolution of $P_B^t$ is driven by the dynamic adjustment of $F_B^t$ and $C{R}_B^t$ based on population diversity ($GD$) and convergence speed ($CV$). This adaptive mechanism balances exploration and exploitation, with an emphasis on enhancing local search efficiency. Mutation, crossover, and selection operations on $P_B^t$ use the updated parameters to enhance local exploitation, similar to those on $P_A^t$.

3.3.1. Population Diversity Metric

The population diversity ($GD$) is measured using the following formula:

$$GD={\displaystyle \frac{1}{N}}\sum _{i=1}^N{D}_i,$$

(21)

where $D_i={\sum }_{j=1,j\ne i}^N\sqrt{{\sum }_{k=1}^D{(x_{i,k}-x_{j,k})}^2}$. Here, $GD$ represents the average distance between individuals in the subpopulation $P_B^t$, which can reflect the overall diversity.

3.3.2. Convergence Speed Metric

The convergence speed ($CV$) is assessed using the following formula:

$$CV={\displaystyle \frac{f_{\mathrm{best},t}-f_{\mathrm{best},t-1}}{f_{\mathrm{best},t-1}}},$$

(22)

where $f_{\mathrm{best},t}$ and $f_{\mathrm{best},t-1}$ are the best fitness values in the current and previous generations, respectively. A smaller $CV$ indicates faster convergence.

3.3.3. Parameter Adjustment Strategy

Based on the population diversity $GD$ and convergence speed $CV$, the parameters $F_B^t$ and $C{R}_B^t$ are adaptively adjusted as follows:

$$\Delta F_{GD}=\left\{\begin{array}{cc}-\Delta F,\hfill & \mathrm{if}GD>G{D}_{\mathrm{threshold}\_\mathrm{high}}\hfill \\ +\Delta F,\hfill & \mathrm{if}GD<G{D}_{\mathrm{threshold}\_\mathrm{low}}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.,$$

(23)

$$\Delta F_{CV}=\left\{\begin{array}{cc}+\Delta F,\hfill & \mathrm{if}CV<C{V}_{\mathrm{threshold}}\hfill \\ -\Delta F,\hfill & \mathrm{if}CV>C{V}_{\mathrm{threshold}}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.,$$

(24)

$$\Delta F_{\mathrm{final}}=w_{GD}·\Delta F_{GD}+w_{CV}·\Delta F_{CV},$$

(25)

$$F_B^t=F_B^{t-1}+\Delta F_{\mathrm{final}}.$$

(26)

Similarly, the adjustment formula for $C{R}_B^t$ can be derived. This strategy dynamically adjusts $F_B^t$ and $C{R}_B^t$ based on the current state of the population. When diversity is high ($GD>G{D}_{\mathrm{threshold}\_\mathrm{high}}$), $F_B^t$ is decreased to enhance local search ability. Conversely, when diversity is low ($GD<G{D}_{\mathrm{threshold}\_\mathrm{low}}$), $F_B^t$ is increased to improve global search ability. Additionally, $F_B^t$ is adjusted based on convergence speed: it is increased if convergence is fast ($CV<C{V}_{\mathrm{threshold}}$) to prevent premature convergence, and it is decreased if convergence is slow ($CV>C{V}_{\mathrm{threshold}}$) to accelerate the process. The weights $w_{GD}$ and $w_{CV}$ are set to 0.5 to balance the influences of diversity and convergence speed.

To simplify the parameter space, a relative diversity threshold $r_{GD}\in (0,0.5)$ is introduced to unify $G{D}_{\mathrm{threshold}\_\mathrm{high}}$ and $G{D}_{\mathrm{threshold}\_\mathrm{low}}$:

$$G{D}_{\mathrm{threshold}\_\mathrm{high}}=(1+r_{GD})·{\overline{GD}}_t,$$

(27)

$$G{D}_{\mathrm{threshold}\_\mathrm{low}}=(1-r_{GD})·{\overline{GD}}_t,$$

(28)

where ${\overline{GD}}_t$ is the average genetic diversity over the past t generations. This ensures $G{D}_{\mathrm{threshold}\_\mathrm{low}}$ remains positive and $G{D}_{\mathrm{threshold}\_\mathrm{high}}$ does not exceed $2·{\overline{GD}}_t$, maintaining a reasonable diversity window around the historical average.

By dynamically adjusting $F_B^t$ and $C{R}_B^t$ based on the population’s diversity and convergence speed, this self-adaptive mechanism enhances the algorithm’s local search ability while maintaining a balance between global and local search capabilities. This ensures more efficient exploration of the search space and improves the overall performance.

3.4. Symmetrical Collaborative Process

In the symmetrical collaborative process, TCDE employs a coevolution mechanism to strengthen the global search capability and accelerate convergence speed. This mechanism promotes information exchange and and maintains diversity through individual bidirectional migration and information sharing between $P_A^t$ and $P_B^t$.

3.4.1. Individual Bidirectional Migration

Individual bidirectional migration is conducted at specific intervals, referred to as migration intervals, to facilitate information exchange between $P_A^t$ and $P_B^t$. In detail, the process is as follows: at each migration interval T, a fixed number of individuals, denoted as $N{P}_m$, are selected from each subpopulation based on their fitness values. The top $N{P}_m$ individuals with the highest fitness values in $P_A^t$ are migrated to $P_B^t$, replacing the $N{P}_m$ individuals with the lowest fitness values in $P_B^t$. Similarly, the top $N{P}_m$ individuals from $P_B^t$ are migrated to $P_A^t$ to replace the $N{P}_m$ individuals with the lowest fitness values in $P_A^t$. This bidirectional migration ensures that both subpopulations maintain a high fitness level while introducing fresh genetic material.

Mathematically, the migration process can be described as follows:

$$P_A^{\prime t}=(P_A\setminus {low\_fitness\_subset}_A^t)\cup {high\_fitness\_subset}_B^t,$$

(29)

$$P_B^{\prime t}=(P_B\setminus {low\_fitness\_subset}_B^t)\cup {high\_fitness\_subset}_A^t,$$

(30)

where ${low\_fitness\_subset}_A^t$ and ${low\_fitness\_subset}_B^t$ are the subsets of $N{P}_m$ individuals with lower fitness in $P_A^t$ and $P_B^t$, respectively. ${high\_fitness\_subset}_A^t$ and ${high\_fitness\_subset}_B^t$ are the subsets of $N{P}_m$ individuals with higher fitness. To balance simplicity and effectiveness, $N{P}_m$= $⌊0.1\times N⌋$. This setting ensures an appropriate exchange of individuals between subpopulations, which promotes diversity while keeping computational efficiency.

3.4.2. Information-Sharing Mechanism

The information-sharing mechanism aims to increase subpopulation diversity and prevent premature convergence. It consists of two key components:

• Update the elite set E by selecting top individuals from $P_A^t$ and $P_B^t$: A shared elite set E is formed by selecting elite individuals from each subpopulation. These elite individuals guide the evolution of both subpopulations, ensuring high-quality genetic information is propagated.
• Use the elite set E to guide the evolution of $P_A^t$ and $P_B^t$: During the guide phase, individuals from the shared elite set E are introduced into each subpopulation’s guide operation. This helps maintain diversity and improves the overall search capability.

To ensure the elite set size is adaptive, we propose a self-adaptive mechanism. The size of the elite set $\left|E\right|$ is dynamically calculated based on $GD$:

$$\left|E\right|=⌊{\displaystyle \frac{N}{2}}\times \left(1-{\displaystyle \frac{GD}{G{D}_{\max }}}\right)⌋,$$

(31)

$$G{D}_{\max }=max\left({\displaystyle \frac{1}{N(N-1)}}\sum _{i=1}^N\sum _{j=1,j\ne i}^N\sqrt{\sum _{k=1}^D{(x_{i,k}-x_{j,k})}^2}\right),$$

(32)

where $G{D}_{\max }$ is the maximum possible diversity. This formula ensures that the elite set size decreases as the population diversity increases, which helps to maintain balance between exploration and exploitation.

The guide operation for an individual x in either subpopulation is modified as follows:

$$x^{\prime }=x+F^t\times (e-x),$$

(33)

where e is an individual randomly selected from E, and $F^t$ is the scaling factor. If $e\in P_A^t$, then $F^t=F_A^t$; otherwise, $F^t=F_B^t$.

The symmetrical coevolution process, facilitated by individual bidirectional migration and information sharing, enables the coordinated evolution of both subpopulations. This process not only maintains structural equilibrium through reciprocal knowledge transfer but also enriches diversity and accelerates convergence.

In summary, the proposed TCDE algorithm embodies the concept of symmetry through its dual-subpopulation structure. The two subpopulations, $P_A^t$ and $P_B^t$, represent two symmetrical yet distinct exploration strategies. $P_A^t$ focuses on global exploration using chaotic parameter adaptation, while $P_B^t$ emphasizes local exploitation with adaptive control based on population diversity and convergence speed. The symmetrical collaboration between $P_A^t$ and $P_B^t$ is further enhanced by the periodic migration of top individuals and the guidance of an elite set, which facilitates the exchange of genetic information and maintains population diversity. This symmetrical design enables the algorithm to efficiently navigate the complex search space and converge on high-quality solutions.

3.5. Computational Complexity Analysis

The computational complexity of the TCDE algorithm is analyzed through its core components. Population initialization involves creating two subpopulations, $P_A^t$ and $P_B^t$, each of size $N/2$, with $L=n\times H$ operations per individual. This results in a complexity of $O(N\times L)$. During the independent evolution phase, $P_A^t$’s chaotic parameter adaptation via logistic maps requires $O(N/2)$ operations per generation. The mutation, crossover, and selection steps for $P_A^t$ contribute $O(N/2\times L)$ operations per generation. For $P_B^t$, calculating the population diversity ($GD$) and convergence speed ($CV$) involves $O({(N/2)}^2\times L)$ operations. Parameter adaptation and evolution in $P_B^t$ add $O(N/2\times L)$ operations per generation. The symmetrical collaboration mechanism, including migrant selection and elite-set updates, contributes $O(NlogN)$ operations at each migration interval T. Over G generations, the overall computational complexity simplifies to $O(G\times N^2\times L)$ for sufficiently large N. This places TCDE in the same complexity class as other population-based metaheuristics, making it suitable for large-scale instances with parallelization.

4. Computational Experiments and Results

The experiments were conducted in MATLAB R2023a using the CVX solver (version 3.0) for exact solutions in small-scale instances. All tests ran on a workstation with an Intel Core i9-13900K CPU (3.0 GHz) and 64 GB RAM.

MATLAB R2024 was selected for implementation primarily due to its strengths in handling the problem’s key components: (1) efficient matrix operations for population-based metaheuristic (TCDE) iterations; (2) seamless integration with the CVX toolbox (used for validating small-scale instances via convex optimization); (3) built-in functions for statistical analysis. These features align well with the needs of our scheduling model, which involves complex numerical computations and comparative experiments.

4.1. Data Description and Comparative Algorithms

The dataset is grounded in the industrial data characteristics from our prior study [35], which analyzed a lace textile factory in Fuzhou, China. Drawing upon factory records and worker expertise, the re-dyeing constraints are modeled to reflect real-world operational limits, allowing up to three re-dyeing operations per job ($H=3$). The re-dyeing probabilities $d{p}_{j,h}$ follow a uniform distribution $U[0.1,0.6]$, while processing time-reduction coefficients ${\alpha }_{j,h}$ are set to $U[0.8,0.9]$ based on operator feedback during repeated rework.

To comprehensively evaluate the performance of TCDE, computational experiments are designed using two types of datasets: industrial-derived synthetic data and real-world industrial data, each in small and large scales. For synthetic data, their instances are constructed by abstracting empirical patterns from real industrial operations. Real-world industrial datasets are collected from the lace textile factory to validate the practical applicability of TCDE. Additionally, all small-scale instances are solved via CVX to obtain optimal benchmarks.

There are currently no existing methods for the considered parallel machine scheduling problem with probabilistic re-dyeing operations, sequence-dependent setup times, and machine eligibility constraints. To demonstrate the advantages and benefits of the proposed TCDE algorithm, three comparative algorithms are selected: the hybrid differential evolution algorithm (HDE, [35]), the fuzzy genetic algorithm (FGA, [36]), and the modified metaheuristics for random rework (MMRR, [17]).

Both HDE and FGA are utilized to address parallel machine scheduling problems with some constraints. HDE focuses on minimizing total tardiness in deterministic environments, whereas FGA targets minimizing total weighted tardiness by integrating fuzzy logic. These two algorithms have been successfully applied to deal with multi-constraint scheduling problems; thus, they can be adapted to the considered problem. Meanwhile, MMRR is designed to handle the unrelated parallel machine scheduling problem with random rework. For this study, MMRR has been adapted to include color-family constraints and sequence-dependent setup times, with its rework model adjusted to reflect the finite number of re-dyeing operations and processing time reduction patterns.

To guarantee a fair comparison, all compared algorithms, HDE, FGA and MMRR, were re-implemented by the authors strictly according to the parameter settings and procedural descriptions in their original papers. No third-party or built-in solver routines were used for any of the metaheuristics.

4.2. Parameter Settings

In this study, the stopping criterion for all algorithms was set to $n\times m$ non-improving iterations. This decision was based on testing that showed TCDE and other comparison algorithms converge effectively within this number of iterations.

The other parameters of TCDE, namely population size N, migration interval T, diversity threshold $r_{GD}$, chaos control parameter $\mu$, initial scaling factor $F^1$, and initial crossover rate $C{R}^1$, were optimized using the Taguchi method [37] in the instance $30\times 5\times 5\times 2$. For fairness, $F_A^1$ and $F_B^1$ were both initialized to $F^1$, and $C{R}_A^1$ and $C{R}_B^1$ to $C{R}^1$.

Table 5. Level of the parameters.

Parameters	Factor Level
	1	2	3
N	60	80	100
T	20	30	40
$r_{GD}$	0.2	0.3	0.4
$\mu$	3	4	5
$F^1$	0.40	0.45	0.50
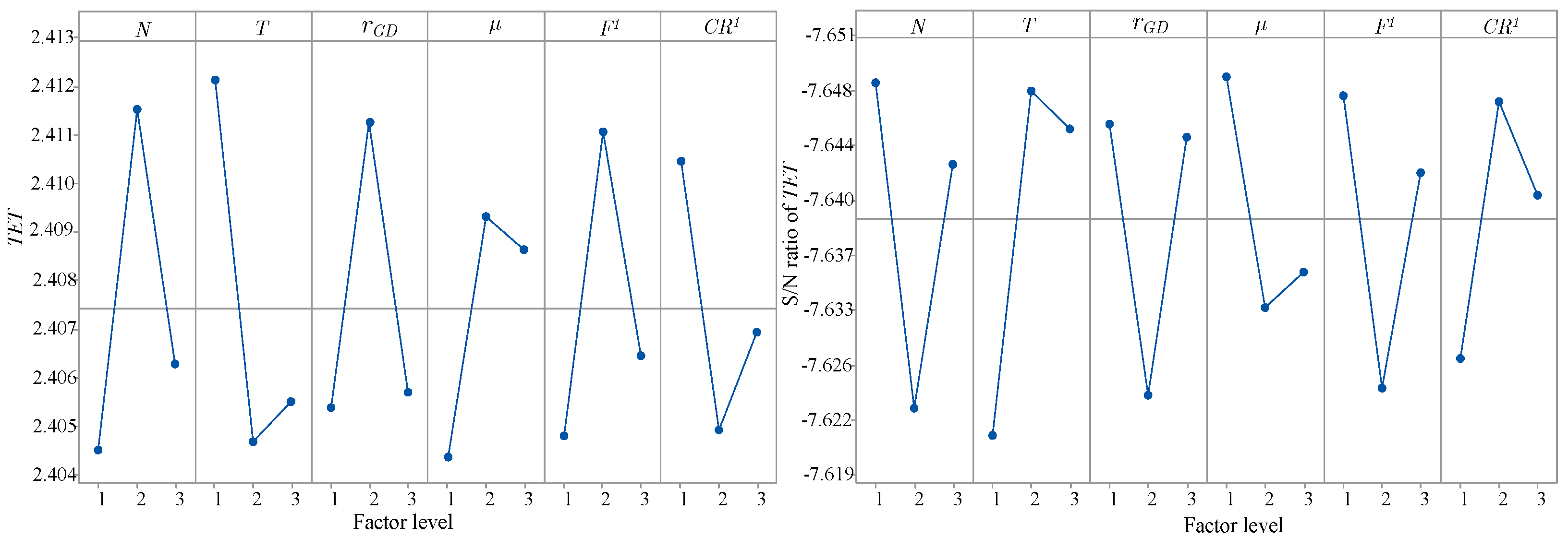
$C{R}^1$	0.85	0.90	0.95

lists three reasonable levels for each parameter using the orthogonal array $L_{27}\left(3^6\right)$. Each parameter combination was tested independently 10 times, with mean $TET$ values collected as response variables. Figure 6 shows the mean $TET$ and corresponding S/N ratios, defined as $-10{log}_{10}\left(TE{T}^2\right)$.

As shown in Figure 6, when the levels of N, T, $r_{GD}$, $\mu$, $F^1$, and $C{R}^1$ are set to 2, 1, 2, 2, 2, and 1, respectively, TCDE generates a smaller mean $TET$ and a larger S/N ratio than other level combinations. Consequently, the optimal parameter combination is adopted as $N=80$, $T=20$, $r_{GD}=0.3$, $\mu =4$, $F^1=0.45$, and $C{R}^1=0.85$.

Regarding HDE, FGA, and MMRR, all parameters except for the stopping condition are directly obtained from [17,35,36]. These parameter settings, validated via Taguchi-based analysis, have been proven to deliver optimal performance in most instances.

4.3. Ablation Experiment on Synthetic Datasets

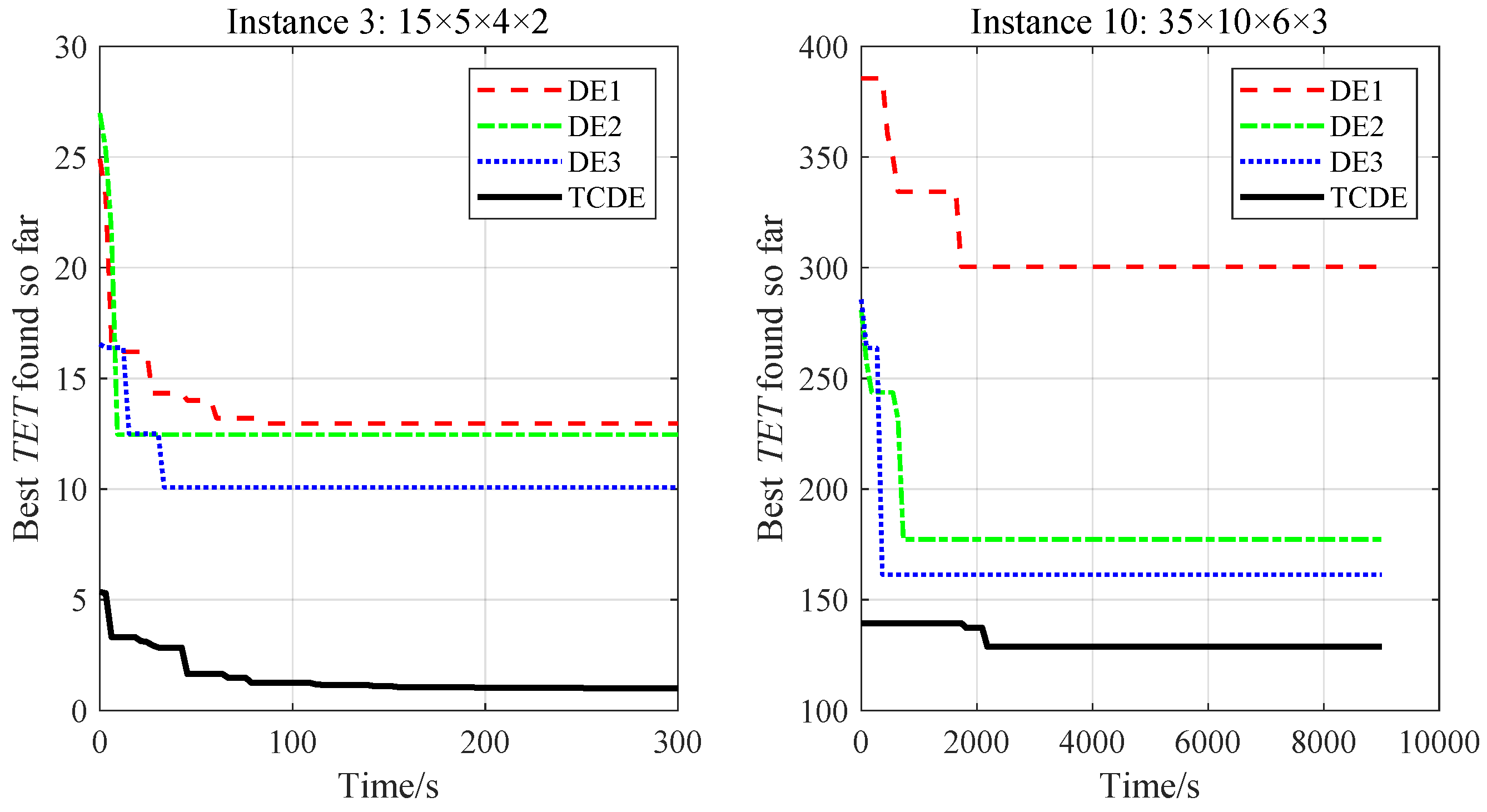
To test the effectiveness of the proposed TCDE and its components, an ablation experiment was performed on both small-scale and large-scale synthetic datasets. Three variants of TCDE were designed to evaluate the contribution of each key component. DE1 removes the chaotic parameter adaptation in subpopulation $P_A^t$, specifically disabling the logistic map-driven dynamic adjustments of $F_A^t$ and $C{R}_A^t$. The comparison between TCDE and DE1 aims to isolate the impact of chaotic exploration on global search performance. DE2 eliminates the diversity-convergence adaptive control mechanism in subpopulation $P_B^t$, freezing the parameter update rules based on $GD$ and $CV$. This variant serves to quantify how local exploitation prevents premature convergence. DE3 entirely disables the periodic exchange of elite individuals between $P_A^t$ and $P_B^t$, along with the guidance from the adaptive elite set E. By contrasting TCDE with DE3, the experiment reveals the synergistic effects of knowledge transfer and coevolution across subpopulations.

4.3.1. Small-Scale Synthetic Datasets

Table 6. Computational results of CVX, DE1, DE2, DE3, and TCDE on small-scale synthetic datasets.

No.	$\mathit{n}\times \mathit{m}\times \mathit{c}\times \mathit{H}$	CVX		DE1		DE2		DE3		TCDE
		Optimal	Time	Best	Time	Best	Time	Best	Time	Best	Time
1	2 × 2 × 2 × 2	2.7	2.8	2.7 *	2.3	2.7 *	1.7	2.7 *	2.1	2.7 *	2.0
2	2 × 2 × 2 × 3	0.4	3.3	0.4 *	1.5	0.4 *	2.3	0.4 *	1.8	0.4 *	2.4
3	2 × 3 × 2 × 2	2.6	3.0	2.6 *	1.6	2.6 *	1.8	2.6 *	2.6	2.6 *	2.3
4	2 × 3 × 2 × 3	2.1	3.5	2.1 *	1.1	2.1 *	2.5	2.1 *	2.1	2.1 *	3.3
5	3 × 2 × 2 × 3	6.2	4.2	10.6	6.2	6.2 *	2.2	6.2 *	6.3	6.2 *	3.2
6	3 × 2 × 3 × 2	0.4	3.3	1.0	0.4	0.4 *	1.9	0.4 *	1.0	0.4 *	2.2
7	3 × 2 × 3 × 3	5.0	4.4	5.0 *	5.0	5.0 *	2.7	5.0 *	5.3	5.0 *	3.4
8	3 × 3 × 2 × 2	2.3	3.5	2.3 *	2.6	2.3 *	2.5	2.3 *	2.7	2.3 *	3.5
9	3 × 3 × 2 × 3	5.5	4.6	5.5 *	3.4	5.5 *	4.6	5.5 *	5.1	5.5 *	6.3
10	3 × 3 × 3 × 2	3.2	3.7	3.2 *	4.1	3.2 *	2.5	3.2 *	2.2	3.2 *	5.3
11	3 × 3 × 3 × 3	0.6	4.5	0.6 *	2.6	0.6 *	3.6	0.6 *	0.6	0.6 *	6.1
12	4 × 2 × 2 × 3	0.2	6.8	0.8	3.2	0.2 *	3.2	0.2 *	0.6	0.2 *	5.1
13	4 × 3 × 3 × 3	4.9	12.2	4.9 *	5.0	4.9 *	7.2	4.9 *	5.0	4.9 *	12.1
14	5 × 3 × 3 × 2	2.3	6.6	5.2	2.3	2.3 *	4.3	2.3 *	3.4	2.3 *	8.2
15	5 × 3 × 3 × 3	1.1	12.3	1.1 *	10.2	1.3	10.5	1.1 *	2.3	1.1 *	11.8
16	5 × 4 × 3 × 3	7.8	58.0	7.8 *	10.6	7.8 *	14.0	7.8 *	11.4	7.8 *	12.9
17	6 × 3 × 3 × 2	0.8	16.0	0.8 *	6.8	0.8 *	4.9	0.8 *	6.8	0.8 *	8.5
18	6 × 4 × 3 × 2	4.8	12.8	6.3	8.8	4.8 *	8.0	4.8 *	4.8	4.8 *	10.4
19	6 × 4 × 3 × 3	1.6	2120.1	1.6 *	2.4	1.6 *	38.2	1.6 *	3.7	1.6 *	28.0
20	7 × 4 × 3 × 2	3.2	238.8	3.2 *	13.3	3.5	16.8	3.2 *	3.6	3.2 *	20.2
21	7 × 4 × 3 × 3	-	-	10	5.9	5.6	53.6	5.9	6.5	5.6	47.0

Note: * indicates the optimal value.

shows the optimal solutions, computation times for CVX, and best objective values on small-scale synthetic datasets for TCDE and its three variants. $TET$ is measured in hours, and computation time in seconds. The data size is denoted as $n\times m\times c\times H$, with a gradual increase. Each algorithm was run independently 10 times. Notably, Instance 21 is specifically marked as lacking a CVX solution, where CVX is unable to find the optimal solution within two hours.

As depicted in Table 6, TCDE matches the optimal solutions derived by CVX in all instances, while DE1 fails to achieve optimality in five cases (e.g., Instances 5, 6, and 12), exhibiting a 10.67% higher average $TET$ compared to TCDE. DE2 struggles with premature convergence, particularly in complex setups like Instance 15, resulting in a 1.57% higher average $TET$. While DE3 achieves optimality in all 20 small-scale instances, its performance deteriorates for larger configurations (e.g., Instance 21), yielding a higher average $TET$ than TCDE. Therefore, it can be concluded that TCDE achieves the best objective values, despite it requiring a relatively longer computational time.

4.3.2. Large-Scale Synthetic Datasets

Table 7. Average objective values (with standard deviations) and computational times for large-scale synthetic datasets.

Instance	$\mathit{n}\times \mathit{m}\times \mathit{c}\times \mathit{H}$	Average Objective Value (±Std)				Average Computational Time
		DE1	DE2	DE3	TCDE	DE1	DE2	DE3	TCDE
1	10 × 5 × 4 × 2	34.8 ± 5.2	38.2 ± 6.1	34.8 ± 4.9	34.8 ± 3.7	63.5	70.5	47.4	48.2
2	10 × 5 × 4 × 3	21.4 ± 3.8	20.8 ± 4.2	20.9 ± 3.5	20.2 ± 2.9	214.2	127.2	146.0	177.9
3	15 × 5 × 4 × 2	13.4 ± 2.7	18.1 ± 3.3	12.7 ± 2.5	1.0 ± 0.8	206.2	159.6	145.6	253.9
4	15 × 5 × × 3	17.2 ± 3.1	53.2 ± 7.6	12.6 ± 2.8	0.0 ± 0.0	358.4	502.1	261.3	326.7
5	20 × 5 × 5 × 2	24.0 ± 4.5	18.6 ± 3.9	23.5 ± 4.2	4.2 ± 1.5	220.4	315.7	143.8	672.6
6	20 × 5 × 5 × 3	6.7 ± 1.9	26.2 ± 5.1	6.6 ± 1.7	0.1 ± 0.1	581.4	599.8	289.6	434.6
7	30 × 5 × 5 × 2	77.6 ± 10.2	41.1 ± 6.8	51.2 ± 8.3	2.4 ± 1.1	598.7	858.3	269.9	1426.2
8	10 × 10 × 5 × 2	16.0 ± 3.2	13.4 ± 2.9	16.2 ± 3.0	12.1 ± 2.4	276.5	258.4	277.5	580.3
9	15 × 10 × 5 × 2	31.2 ± 5.3	39.8 ± 6.5	31.2 ± 4.9	23.6 ± 3.8	701.4	562.5	656.9	580.3
10	35 × 10 × 6 × 3	330.7 ± 42.5	196.5 ± 31.2	194.0 ± 28.7	131.1 ± 18.3	5998.0	5519.6	3209.1	8186.3
11	55 × 15 × 8 × 3	421.3 ± 48.6	478.2 ± 52.1	398.5 ± 44.7	345.6 ± 38.2	9800.3	10,200.5	9500.2	12,000.4
12	100 × 20 × 8 × 3	512.3 ± 58.1	578.9 ± 64.7	489.6 ± 55.3	398.4 ± 42.6	12,450.6	13,200.3	11,800.7	15,000.2
13	120 × 25 × 10 × 3	687.5 ± 79.2	769.4 ± 82.5	654.8 ± 73.1	532.7 ± 58.9	18,760.9	19,500.7	18,200.4	22,000.3
14	150 × 30 × 10 × 3	789.4 ± 88.3	865.7 ± 92.1	748.2 ± 81.5	612.3 ± 67.4	22,000.8	23,500.2	21,000.5	28,000.1
15	200 × 40 × 12 × 3	1025.6 ± 112.4	1120.3 ± 118.7	978.5 ± 105.2	798.1 ± 89.3	35,000.5	37,000.9	33,500.7	42,000.6

Note: The objective values of the best performing algorithm are marked in bold.

presents the average objective values and computational times of TCDE, DE1, DE2, and DE3 for large-scale synthetic datasets. As shown in Table 7, TCDE significantly outperforms its variants, achieving a 59.94%, 50.74%, and 43.15% reduction on average $TET$ compared to DE1, DE2, and DE3, respectively. For example, in Instance 3, TCDE achieves a $TET$ of 1.0 h, whereas DE1, DE2, and DE3 yield 13.4, 18.1, and 12.7 h, respectively. Although TCDE takes 27.33%, 29.26%, and 57.06% longer to compute than DE1, DE2, and DE3 on average, it still maintains superior solution quality. Especially in complex scenarios like Instance 10, TCDE reduces $TET$ by 32.42% compared to DE3.

Overall, the integration of chaos-driven exploration, diversity-convergence exploitation, and the collaborative mechanism of TCDE addresses the limitations of TCDE variants. These results highlight the effectiveness of the strategies incorporated into TCDE, such as chaotic parameter adaptation, diversity-convergence adaptive control, and symmetrical collaborative mechanism, in enhancing the comprehensive performance of the algorithm. While computational costs increase moderately, these strategies collectively ensure that near-optimal solutions can be achieved with manageable computational overhead.

Although TCDE occasionally requires more computational time than some competitors (e.g., DE3), this increase is marginal and well-justified by the significant improvement in solution quality. In practical applications such as lace-dyeing production, a reduction in TET by just one hour can save approximately USD 1200 in penalty costs, while the additional computational expense remains below USD 0.10 per hour. Thus, the trade-off strongly favors TCDE in terms of overall economic efficiency.

Figure 7 illustrates the convergence behavior of TCDE and its variants in two representative large-scale instances. TCDE shows a rapid decrease in the early stage, reflecting strong global exploration capability, and stabilizes quickly in the later stage. It outperforms other algorithms in terms of convergence speed, further confirming that TCDE effectively balances exploration and exploitation.

4.4. Comparative Experiment on Industrial Datasets

The industrial datasets used in this study are derived from a lace textile factory in Fuzhou, China. The industrial solutions are currently generated manually based on the first-in-first-out (FIFO) rule or the earliest due date (EDD) rule. In the industrial sample tests, the proposed TCDE algorithm is compared against three state-of-the-art algorithms: HDE, FGA, and MMRR, as well as industrial solutions.

4.4.1. Small-Scale Industrial Datasets

Table 8. Computational results of CVX, HDE, FGA, MMRR, and TCDE, along with an industrial method for small-scale industrial datasets.

No.	$\mathit{n}\times \mathit{m}\times \mathit{c}\times \mathit{H}$	Industrial	CVX		HDE		FGA		MMRR		TCDE
			Optimal	Time	Best	Time	Best	Time	Best	Time	Best	Time
1	2 × 2 × 2 × 2	0.53	0.53	4.65	0.53 *	1.35	0.53 *	1.57	0.53 *	1.33	0.53 *	1.89
2	2 × 2 × 2 × 3	1.64	1.64	4.99	1.64 *	1.34	1.64 *	1.55	1.64 *	1.41	1.64 *	3.85
3	3 × 2 × 2 × 2	2.52	2.52	5.22	2.52 *	1.33	2.52 *	1.79	2.52 *	1.57	2.52 *	3.85
4	3 × 2 × 2 × 3	6.28	6.28	5.90	6.38	1.61	6.28 *	1.77	6.28 *	1.68	6.28 *	5.97
5	3 × 2 × 3 × 3	3.34	2.84	6.75	2.87	1.45	2.84 *	1.56	2.84 *	1.46	2.84 *	5.79
6	3 × 3 × 2 × 2	2.53	2.53	5.51	2.53 *	1.37	2.53 *	1.56	2.53 *	1.39	2.53 *	3.90
7	3 × 3 × 2 × 3	5.83	5.83	7.49	5.83 *	1.50	5.83 *	1.61	5.83 *	1.50	5.83 *	4.40
8	3 × 3 × 3 × 2	3.60	3.60	5.94	3.60 *	1.49	3.60 *	1.54	3.60 *	1.46	3.60 *	3.16
9	3 × 3 × 3 × 3	0.19	0.19	7.58	0.19 *	1.43	0.19 *	1.55	0.19 *	1.35	0.19 *	4.94
10	4 × 2 × 2 × 3	9.14	8.02	21.44	8.47	1.73	8.02 *	1.74	8.02 *	1.68	8.02 *	7.66
11	4 × 3 × 3 × 3	4.58	0.14	8.88	0.41	1.78	0.14 *	1.63	0.14 *	1.57	0.14 *	6.73
12	5 × 3 × 3 × 2	1.09	0.17	7.07	4.20	1.69	0.17 *	1.61	0.17 *	1.46	0.17 *	5.47
13	5 × 3 × 3 × 3	0.69	0.00	10.06	0.62	2.06	0.00 *	1.64	0.00 *	1.79	0.00 *	7.76
14	5 × 4 × 3 × 3	7.13	6.63	12.64	7.15	2.57	6.63 *	1.78	6.63 *	2.35	6.63 *	8.56
15	6 × 3 × 3 × 2	17.08	17.08	8.87	28.16	1.85	17.08 *	1.79	17.08 *	1.99	17.08 *	7.08
16	6 × 3 × 3 × 3	32.53	29.33	664.20	45.73	1.82	29.92	8.53	30.04	2.12	29.33 *	10.64
17	6 × 4 × 3 × 2	13.09	11.69	8.85	12.54	1.62	11.69	1.66	11.69	1.79	11.69 *	12.82
18	6 × 4 × 3 × 3	7.61	4.51	4.51	4.82	1.30	4.51 *	2.01	4.75	1.68	4.51 *	10.05
19	7 × 4 × 3 × 2	13.65	12.32	14.41	14.32	1.05	12.38	1.82	13.44	1.57	12.32 *	8.54
20	7 × 4 × 3 × 3	26.04	12.25	595.13	16.14	1.23	13.84	1.92	13.85	1.79	12.25 *	14.94
21	8 × 4 × 3 × 3	28.74	-	-	29.59	1.53	24.53	2.29	27.15	2.01	22.42	15.03

* indicates the optimal value.

displays the optimal solutions and computation times for CVX, HDE, FGA, MMRR, TCDE, and the industrial solutions across small-scale industrial datasets. Figure 8 presents a bar chart comparing each algorithm’s results (HDE, FGA, MMRR, TCDE, and industrial) against the CVX optimal solution for each dataset instance. In Figure 8, ‘CVX Optimal’ denotes the optimal solution obtained via CVX, while ‘CVX N/A’ indicates instances where CVX failed to derive an optimal solution within the time limit.

As outlined in Table 8, TCDE consistently matches the optimal solutions derived by CVX in all instances. In contrast, industrial solutions exhibit significantly higher $TET$ values, particularly in more complex instances. HDE and FGA also achieve optimal solutions in many cases, but show variability in computation time. Although TCDE requires longer computational time than some algorithms, such as FGA, in certain instances, it exhibits remarkable performance in obtaining optimal solutions. This relatively longer computation time is justified by its effectiveness. MMRR, while effective in some cases, generally underperforms compared to TCDE. As visually summarized in Figure 8, TCDE consistently matches the CVX optimal solutions across all instances, whereas the industrial method exhibits significantly higher $TET$ values. Therefore, TCDE consistently outperforms the industrial solutions and shows better overall performance than HDE, FGA, and MMRR in small-scale industrial datasets.

In summary, TCDE emerges as the most effective algorithm for small-scale industrial datasets due to its consistent ability to match CVX’s optimal solutions. While it may require longer computational time than some algorithms like FGA, its superior solution quality makes it the preferred choice. The industrial solutions, despite their simplicity, are not competitive in terms of solution quality, particularly as the problem complexity increases.

4.4.2. Large-Scale Industrial Datasets

Table 9. Computational results of HDE, FGA, MMRR, and TCDE, along with an industrial method for large-scale industrial datasets.

No.	Instance	I	Average Objective Value (±std)				Average Computational Time
			HDE	FGA	MMRR	TCDE	HDE	FGA	MMRR	TCDE
1	10 × 4 × 3 × 2	37.49	19.13 ± 16.23	23.96 ± 15.08	30.27 ± 15.49	19.13 ± 15.75	20.15	8.74	7.21	24.70
2	10 × 4 × 3 × 3	154.28	80.46 ± 58.97	78.42 ± 56.21	81.89 ± 60.44	72.06 ± 31.72	28.54	14.78	9.31	36.27
3	15 × 4 × 3 × 2	345.95	182.31 ± 78.45	288.42 ± 74.88	280.22 ± 75.26	182.31 ± 50.12	31.13	19.72	15.67	38.26
4	15 × 4 × 3 × 3	30.86	15.40 ± 59.82	27.85 ± 57.02	22.70 ± 48.32	5.39 ± 25.13	43.33	35.98	27.94	57.67
5	20 × 5 × 4 × 2	287.00	97.72 ± 57.48	225.49 ± 54.61	207.16 ± 50.79	91.03 ± 26.31	50.10	33.72	18.19	66.24
6	20 × 5 × 4 × 3	127.16	67.33 ± 115.62	38.59 ± 112.97	31.96 ± 133.30	0.67 ± 46.54	56.30	57.18	56.90	96.53
7	25 × 5 × 5 × 2	532.86	174.56 ± 70.53	439.31 ± 67.60	488.08 ± 81.17	164.87 ± 25.45	79.11	45.99	24.50	102.15
8	25 × 5 × 5 × 3	254.32	134.61 ± 190.34	214.05 ± 185.69	201.71 ± 133.90	74.74 ± 80.91	95.46	109.41	86.05	156.09
9	30 × 8 × 6 × 2	873.20	356.76 ± 62.47	767.56 ± 59.70	707.28 ± 70.30	352.06 ± 27.21	95.61	58.47	94.00	165.59
10	30 × 8 × 6 × 3	589.05	313.97 ± 116.83	636.98 ± 113.00	590.69 ± 98.53	256.99 ± 30.86	184.33	105.98	226.35	306.61
11	35 × 8 × 6 × 2	1082.55	363.47 ± 110.25	919.87 ± 106.59	919.82 ± 130.78	362.66 ± 41.89	118.33	63.10	172.17	190.20
12	35 × 8 × 6 × 3	570.35	300.72 ± 125.67	424.43 ± 120.43	502.23 ± 99.74	213.93 ± 44.83	210.54	120.51	212.31	394.69
13	40 × 10 × 7 × 2	1066.71	408.72 ± 68.92	949.30 ± 65.67	861.83 ± 36.67	361.90 ± 24.49	138.19	124.94	279.15	232.14
14	40 × 10 × 7 × 3	617.13	329.69 ± 126.88	574.51 ± 121.32	561.98 ± 54.30	279.36 ± 67.08	206.42	205.37	284.38	358.54
15	45 × 10 × 7 × 2	1009.80	537.42 ± 178.93	804.89 ± 172.47	916.86 ± 27.68	512.20 ± 73.40	118.49	84.72	148.64	200.16
16	45 × 10 × 7 × 3	570.35	301.81 ± 153.47	397.46 ± 148.87	422.08 ± 44.47	261.32 ± 13.45	197.59	306.97	254.92	381.55
17	50 × 10 × 8 × 2	495.55	263.08 ± 73.68	536.44 ± 70.01	444.62 ± 110.51	218.49 ± 24.31	117.94	184.70	399.21	221.94
18	50 × 10 × 8 × 3	1388.16	366.93 ± 101.45	1078.80 ± 97.01	1054.09 ± 111.94	309.99 ± 14.19	269.48	379.78	491.32	520.11
19	55 × 10 × 8 × 2	1538.65	393.05 ± 75.24	922.15 ± 71.19	896.57 ± 60.02	354.81 ± 61.77	144.83	179.80	363.76	272.65
20	55 × 10 × 8 × 3	1640.78	607.72 ± 73.05	886.97 ± 69.82	846.63 ± 9.20	555.58 ± 5.57	227.99	391.27	492.89	535.62

Note: The objective values of the best-performing algorithm are marked in bold.

presents the average objective value and average computational times for HDE, FGA, MMRR, and TCDE, along with the industrial method, on large-scale industrial datasets. “I” denotes the industrial solution. Figure 9 provides a boxplot comparison of TCDE, HDE, FGA, MMRR, and the industrial method. The standard deviation results of HDE, FGA, MMRR, and TCDE across 20 large-scale industrial datasets are effectively visualized in Figure 10. Figure 10a displays a bar chart where each group of bars corresponds to a specific dataset instance, and Figure 10b depicts a line chart where each line represents the standard deviation of one algorithm across the 20 dataset instances.

As described in Table 9, TCDE consistently outperforms HDE, FGA, MMRR, and traditional industrial methods in minimizing $TET$ while maintaining acceptable computational efficiency. Compared to real industrial solutions, HDE, FGA, MMRR, and the proposed TCDE algorithm reduce the $TET$ by an average of 59.77%, 22.53%, 23.79%, and 64.81%, respectively. The results also demonstrate that TCDE achieves lower average objective values across all 20 dataset instances. Although TCDE incurs longer computational times than HDE, FGA, and MMRR, its solution quality justifies this trade-off. For example, in Instance 4, TCDE achieves a $TET$ of 5.39 h in 57.67 s, whereas HDE requires 43.33 s to produce a $TET$ three times higher at 15.40 h. This balance between runtime and performance aligns with industrial requirements, where minimizing tardiness outweighs marginal time savings. As shown in Figure 9, TCDE consistently demonstrates lower median $TET$ and narrower interquartile ranges, further confirming its robust performance across all test instances.

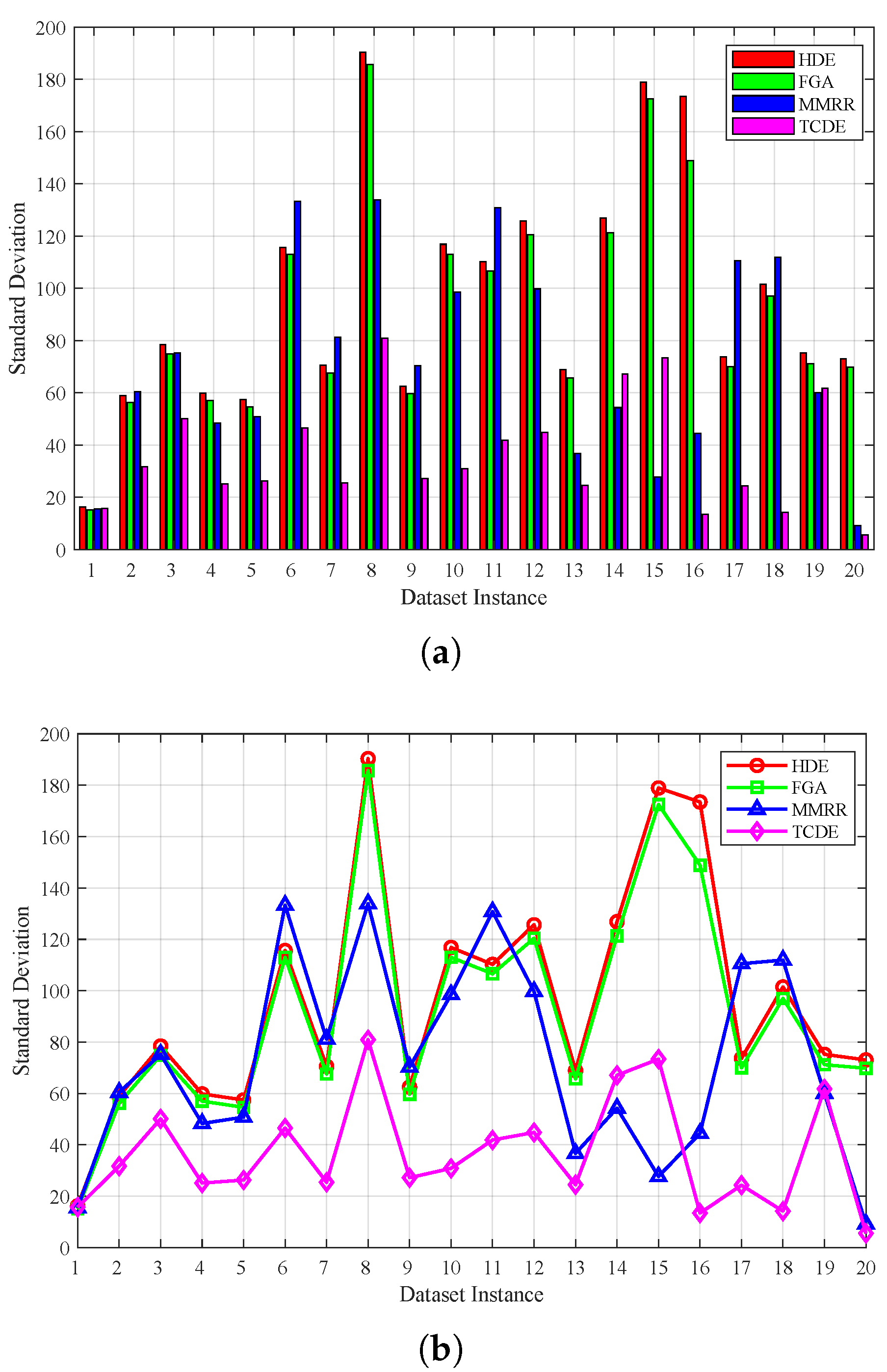
The standard deviation comparison provided in Figure 10 further solidifies the proposed algorithm’s position as a reliable solution. Its stability is evident from its low standard deviation, which is 27% lower than that of HDE, 57% lower than that of FGA, and 49% lower than that of MMRR. Furthermore, both the bar chart and line chart indicate that the algorithm exhibits lower variability in its performance across different dataset instances. The bar chart in Figure 10a reveals that TCDE’s average objective values are not only lower but also exhibit less fluctuation, suggesting a more robust optimization process. Similarly, the line chart in Figure 10b illustrates that TCDE maintains a tighter performance range, which minimizes the likelihood of obtaining suboptimal solutions in diverse scenarios.

On the whole, TCDE demonstrates a high level of robust performance in reducing $TET$ for large-scale industrial scheduling problems. It achieves significant $TET$ reductions while ensuring stability and reasonable runtimes. Moreover, its strong capacity to address complex scheduling challenges makes it an invaluable instrument for practical manufacturing systems, offering a reliable solution for optimizing production efficiency and minimizing delays in real-world applications.

4.5. Comprehensive Performance Summary

To systematically compare the performance of TCDE with benchmark algorithms across all datasets, Table 9 summarizes key metrics, including average $TET$, average computational time, and relative improvement ($RI$), compared to industrial solutions.

As shown in

Table 10. Comprehensive performance comparison of algorithms across datasets.

Dataset Type	Scale	Metric	TCDE	HDE	FGA	MMRR	Industrial
Synthetic	Small (21)	Average $TET$ (h)	3.2 ± 1.8	5.7 ± 2.3	4.9 ± 2.1	5.3 ± 2.2	12.6 ± 4.5
		Average Time (s)	8.7 ± 3.2	6.2 ± 2.8	5.9 ± 2.5	7.1 ± 3.0	-
		$RI$ (%)	74.6%	54.8%	61.1%	57.9%	-
	Large (15)	Average $TET$ (h)	42.3 ± 15.6	105.6 ± 32.1	85.1 ± 28.7	74.4 ± 25.3	238.5 ± 67.2
		Average Time (s)	587.2 ± 142.5	452.6 ± 110.3	410.8 ± 98.7	376.3 ± 89.5	-
		$RI$ (%)	82.3%	55.7%	64.3%	68.8%	-
Industrial	Small (21)	Average $TET$ (h)	2.1 ± 1.5	3.8 ± 1.9	3.2 ± 1.7	3.5 ± 1.8	9.7 ± 3.6
		Average Time (s)	7.5 ± 2.9	4.8 ± 2.3	4.5 ± 2.1	5.3 ± 2.6	-
		$RI$ (%)	78.4%	60.8%	67.0%	63.9%	-
	Large (20)	Average $TET$ (h)	189.6 ± 52.3	456.2 ± 108.7	532.7 ± 124.5	498.3 ± 116.2	538.2 ± 142.8
		Average Time (s)	215.4 ± 68.7	142.3 ± 45.6	138.5 ± 41.2	156.8 ± 50.3	-
		$RI$ (%)	64.8%	15.2%	0.8%	7.4%	-

Note: Values are presented as mean ± standard deviation. “$RI$ (%)” is calculated as [(Industrial $TET$ − Algorithm $TET$)/Industrial $TET$] × 100%.

, TCDE outperforms all benchmark algorithms across all dataset types and scales. For synthetic datasets, TCDE achieves the lowest average $TET$ (3.2 h for small-scale and 42.3 h for large-scale) and the highest improvement over industrial solutions (74.6% and 82.3%, respectively), demonstrating its robustness in both simple and complex artificial scenarios.

In industrial datasets, TCDE maintains its superiority: it reduces the average $TET$ to 2.1 h (small-scale) and 189.6 h (large-scale), with improvements over industrial solutions reaching 78.4% and 64.8%. Notably, in large-scale industrial datasets, where real-world complexity is highest, TCDE outperforms HDE by 58.4%, FGA by 64.4%, and MMRR by 61.9%, highlighting its practical applicability.

While TCDE exhibits slightly longer computational times compared to HDE, FGA, and MMRR, this trade-off is justified by its significantly better solution quality, which aligns with industrial priorities of minimizing tardiness over marginal time savings. The low standard deviation values across all metrics further confirm TCDE’s stability across diverse scheduling scenarios.

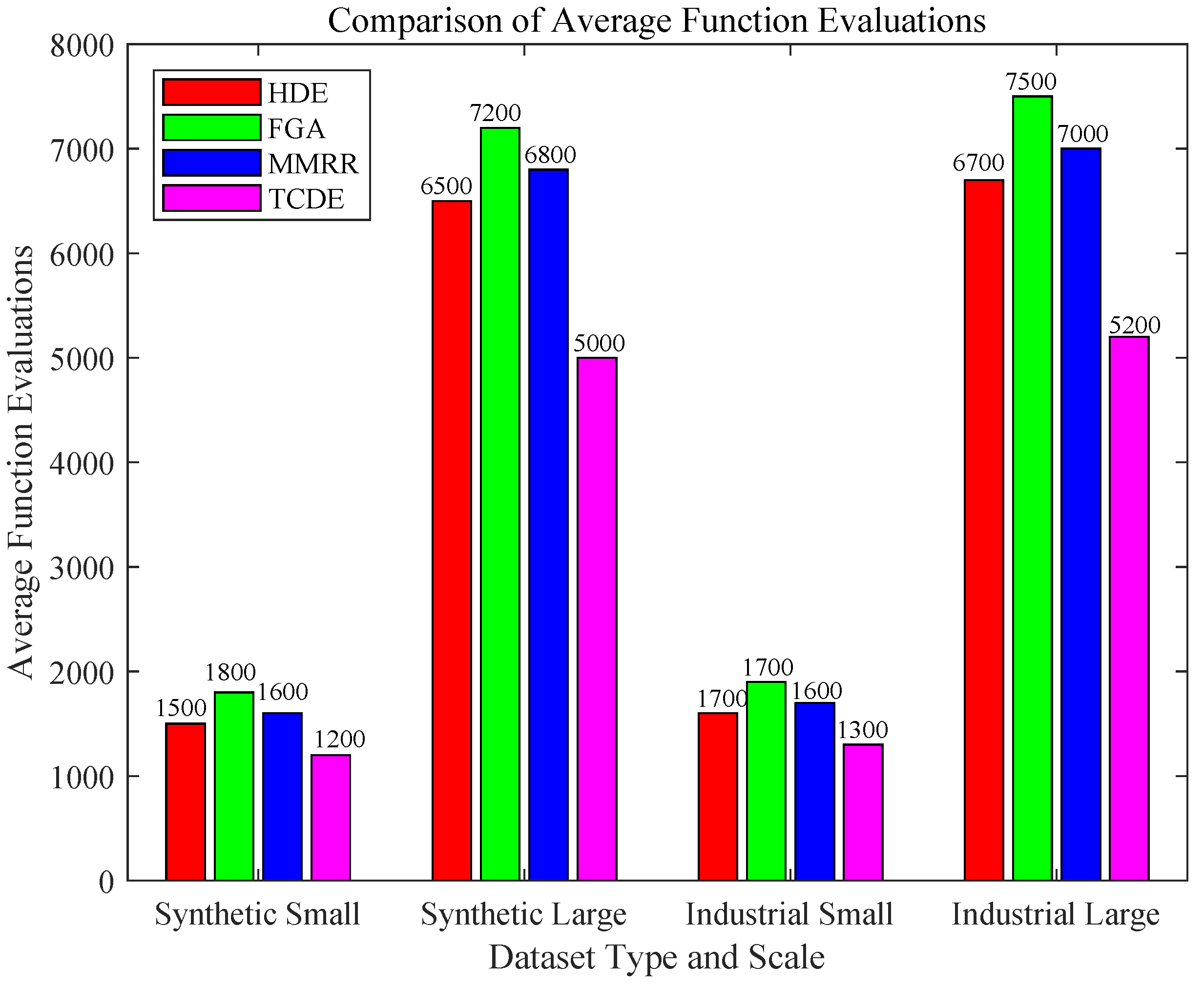
In addition to computational time, algorithmic efficiency was assessed using the number of function evaluations (FEs). This hardware-agnostic metric reflects the optimization effort necessary to achieve convergence. Figure 11 illustrates the comparison of the average number of function evaluations needed by each algorithm across different dataset instances.

Table 11. Average number of function evaluations for each algorithm.

Dataset Type	Scale	HDE	FGA	MMRR	TCDE
Synthetic	Small	1500 ± 300	1800 ± 400	1600 ± 350	1200 ± 200
Synthetic	Large	6500 ± 1000	7200 ± 1200	6800 ± 1100	5000 ± 800
Industrial	Small	1600 ± 300	1900 ± 400	1700 ± 350	1300 ± 250
Industrial	Large	6700 ± 1100	7500 ± 1300	7000 ± 1200	5200 ± 900

presents the average number of function evaluations required by each algorithm across various dataset instances.

As shown in Table 11 and Figure 11, TCDE consistently requires fewer function evaluations compared to HDE, FGA, and MMRR across all dataset types and scales. This indicates that TCDE achieves better solution quality with higher computational efficiency in terms of function evaluations. In summary, the additional experiments demonstrate that TCDE not only outperforms other algorithms in terms of solution quality but also requires fewer function evaluations, making it a more efficient and effective choice for solving the considered scheduling problem.

4.6. Statistical Significance Analysis

To statistically validate the significance of TCDE’s performance superiority, the Friedman test, a non-parametric method suitable for comparing multiple algorithms across diverse datasets, was conducted on the average $TET$ values. The test rejects the null hypothesis of equal performance among all algorithms, which can indicate statistically significant differences.

Table 12. Post-hoc pairwise comparisons (Holm–Bonferroni corrected p-values).

Comparison	Adjusted p-Value	Result
TCDE vs. HDE	0.002	TCDE is significantly better
TCDE vs. FGA	0.001	TCDE is significantly better
TCDE vs. MMRR	0.003	TCDE is significantly better
HDE vs. FGA	0.124	No significant difference
HDE vs. MMRR	0.087	No significant difference
FGA vs. MMRR	0.632	No significant difference

summarizes the adjusted p-values and conclusions for all pairwise comparisons.

Post-hoc pairwise comparisons were performed using the Holm–Bonferroni correction to identify specific differences between TCDE and each comparative algorithm. As shown in Table 12, TCDE exhibits significantly lower average $TET$ than HDE, FGA, and MMRR at the 95% confidence level (p-values < 0.05). In contrast, no significant differences were found among the comparative algorithms themselves. These results confirm that the performance advantages of TCDE are statistically robust and are not attributable to random variation.

4.7. Practical Applicability

The proposed TCDE algorithm is designed with practical manufacturing environments in mind. The scheduling problem addressed in this study originates from a real-world lace dyeing factory in Fuzhou, China, where sequence-dependent setup times, machine eligibility, and probabilistic re-dyeing operations are daily challenges.

In addition to minimizing $TET$, machine utilization ($MU$) is another critical performance indicator in practice. It measures how efficiently the available machine capacity is used. The machine utilization is defined as follows:

$$MU={\displaystyle \frac{{\sum }_{k=1}^m{\sum }_{j=1}^n{\sum }_{h=1}^H{p}_{j,h}·Z_{j,h,k}}{{\sum }_{k=1}^m{C}_{\max ,k}}},$$

(34)

where $Z_{j,h,k}\in \{0,1\}$ indicates whether the operation h of job j is assigned to machine k; $C_{\max ,k}$ is the completion time of the last job on machine k.

A higher machine utilization indicates a more compact schedule with less idle time, which is desirable in manufacturing environments to reduce operational costs and improve throughput.

Table 13. Performance comparison of scheduling methods in industrial settings.

Method	Avg. $\mathit{TET}$ (h)	$\mathit{MU}$ (%)	Avg. Runtime (s)
Industrial	538.2	72.1	–
HDE	456.2	78.5	142.3
FGA	532.7	75.3	138.5
MMRR	498.3	76.8	156.8
TCDE	189.6	85.4	215.4

summarizes the key performance indicators across different scheduling methods, including average tardiness, machine utilization, and average runtime. These results demonstrate the practical value of TCDE in improving the production efficiency and reducing operational costs.

5. Conclusions, Limitations, and Future Work

5.1. Conclusions

The symmetry-driven TCDE algorithm has demonstrated exceptional effectiveness in minimizing $TET$. This can be attributed to the effective symmetrical collaboration between the two subpopulations. The chaotic parameter adaptation in $P_A^t$ equips the algorithm with strong global exploration capabilities, while the adaptive control in $P_B^t$ ensures refined local exploitation. The periodic exchange of individuals between the subpopulations further strengthens the symmetry of the algorithm, enabling it to maintain a good balance between exploration and exploitation throughout the optimization process. Extensive experimental validation on both industrial and synthetic datasets has shown that TCDE outperforms current state-of-the-art methods, showcasing its significant potential for real-world applications in enhancing sustainable manufacturing within the textile industry. This symmetrical approach is particularly advantageous in handling the complex and uncertain scheduling problem under consideration. Its ability to handle the inherent complexity and variability of the lace dyeing process with probabilistic re-dyeing operations makes it a valuable asset for promoting sustainable and intelligent manufacturing practices.

5.2. Research Limitations

Despite its strengths, the TCDE framework has some key limitations. First, it focuses on static scheduling and lacks efficient mechanisms to handle real-time disruptions like unexpected job arrivals or machine failures. Second, its execution times for large-scale instances (typically minutes to hours) may not meet the subsecond response requirements of real-time cloud-based production systems, especially for rapid rescheduling. Third, it assumes input data (e.g., re-dyeing probabilities, processing times) are accurate, but adversarial noise or data corruption (e.g., erroneous sensor measurements) could degrade performance, as the algorithm lacks explicit mechanisms to detect or mitigate such perturbations. In practice, adversarial noise (e.g., maliciously altered due dates or erroneous re-dyeing probabilities) or data corruption (e.g., sensor errors in job weight measurements) could degrade performance. Additionally, the fixed H assumption for reworks, while simplifying the model, may limit adaptability in highly dynamic or uncertain environments.

5.3. Recommendation for Future Research

Future research will prioritize bridging these gaps through several interconnected pathways. Most notably, deploying TCDE within real-time cloud/edge architectures offers compelling potential for dynamic scheduling. A proposed edge-cloud collaborative framework would position lightweight TCDE variants on edge devices for low-latency response to local disruptions (e.g., machine breakdowns, urgent job insertions), while leveraging cloud resources for heavy computations like predictive scenario analysis and parameter tuning. To handle dynamic job arrivals, we will develop an event-triggered TCDE variant that performs incremental rescheduling instead of full recomputations. This variant will incorporate a dynamic prioritization module that adjusts job weights based on real-time factors such as due date urgency, customer priority, and production bottlenecks. For instance, urgent jobs with tight deadlines could be assigned higher priority weights, guiding the symmetry-driven exploration-exploitation balance in TCDE to prioritize their timely completion.

Moreover, although TCDE is demonstrated in the context of lace dyeing, its core mechanisms, such as symmetry-driven dual-population collaboration, chaotic parameter adaptation, and elite-based migration, are designed to address general scheduling challenges. These include probabilistic operations, sequence-dependent setups, and machine eligibility constraints, which are common in various manufacturing systems (e.g., automotive parts, panel furniture, and electronics). Thus, TCDE is highly portable and can be adapted to other scheduling domains with appropriate modeling.

Further extensions include applying TCDE’s symmetry-driven framework to green manufacturing contexts with energy/carbon constraints and multi-factory supply chain scheduling. Hybridization with complementary metaheuristics like artificial bee colony algorithms could expand its cross-domain applicability. Throughout these developments, maintaining robust security protocols for Cloud–Edge communication and implementing fail-safe mechanisms will be essential for industrial adoption. Collectively, these advancements position TCDE as a cornerstone for responsive, data-driven manufacturing within Industry 4.0 ecosystems, transforming theoretical optimization capabilities into tangible productivity gains for complex production environments like lace dyeing.

Additionally, to address vulnerabilities to adversarial noise and corrupted inputs, adaptive mechanisms will be integrated into TCDE. This includes enhancing the diversity metrics in the second subpopulation to detect outliers in input data (e.g., implausible re-dyeing probabilities), triggering adjusted parameter settings to increase exploration and reduce reliance on noisy parameters. Additionally, during the decoding process, job attributes such as color family and weight will be cross-checked against historical distributions, with ambiguous values replaced by consensus from the elite set to preserve feasibility. TCDE will also be trained on synthetic noisy datasets (e.g., perturbed due dates or machine capacities) to enable dynamic adjustment of migration intervals under high noise, accelerating knowledge exchange between subpopulations to maintain performance in minimizing total estimated tardiness.

Finally, TCDE’s framework shows promise for energy-aware scheduling. By integrating real-time power consumption models, it can optimize both tardiness and energy efficiency. Adaptive parameter control can balance throughput with energy constraints, while edge deployment reduces computational and cloud data transfer costs. In addition, future work will extend the TCDE framework to handle multi-objective optimization by incorporating factors such as energy consumption and machine utilization into the fitness function. A Pareto-based selection mechanism will be developed to balance trade-offs among conflicting objectives, enabling more comprehensive and sustainable scheduling solutions in real-world industrial settings. To address the fixed rework limit H, dynamic modeling is introduced. Real-time quality feedback and Bayesian updating adjust expected reworks per job based on observed defect rates and history.