Two-Dimensional Reproducing Kernel-Based Interpolation Approximation for Best Regularization Parameter in Electrical Tomography Algorithm
Abstract
1. Introduction
2. Related Work
2.1. ET Principle and Related Imaging Algorithm
- (1)
- L-curve (LC): The LC method selects the optimal parameter of λ by identifying the corner of the L-curve plot, characterized by the pair (||σ||, ||Sσ-U||). This corner can be pinpointed using the second-order difference index within the plot [21]. Since the L-curve is commonly represented in a log-log coordinate system, the second-order difference is computed as follows
- (2)
- Generalized cross validation (GCV): The GCV method [19] generalizes cross validation as follows:
- (1)
- Extreme points on their curves are often uncertain, and encountering multiple points may prevent algorithms from correctly identifying them. Efforts had been made to overcome these problems, but the effectiveness and efficiency of those studies are conditional.
- (2)
- Both of the two algorithms are time-consuming, requiring numerous candidates for optimal values to be evaluated by the objective function to find the extreme point. Hence, they are not suitable for most engineering applications requiring real-time and rapid responses.
2.2. Interpolation Approximation in Reproducing Kernel Space
- (1)
- The optimality of pk cannot be assured in any mathematical sense; thus, the generalization of the approximation form used in Equation (9) is also not guaranteed.
- (2)
- The weighting scheme applied in Equation (9) renders it sensitive to noise and unable to reflect the typicality or compatibility of each interpolated image [25].
3. The Best Interpolation Approximation for the Hypermeter in TR
3.1. Feature Reduction by Multidimensional Scaling
- (1)
- There are feasible two-dimensional BIAO methods in practice, and the upper bound of their approximation errors is estimable [29]. Specially, the generalization of the BIAO within a two-dimensional Hilbert space based on a reproducing kernel is both theoretically demonstrated and practically validated. Inversely, these properties in other typical interpolation approximation cannot be assured.
- (2)
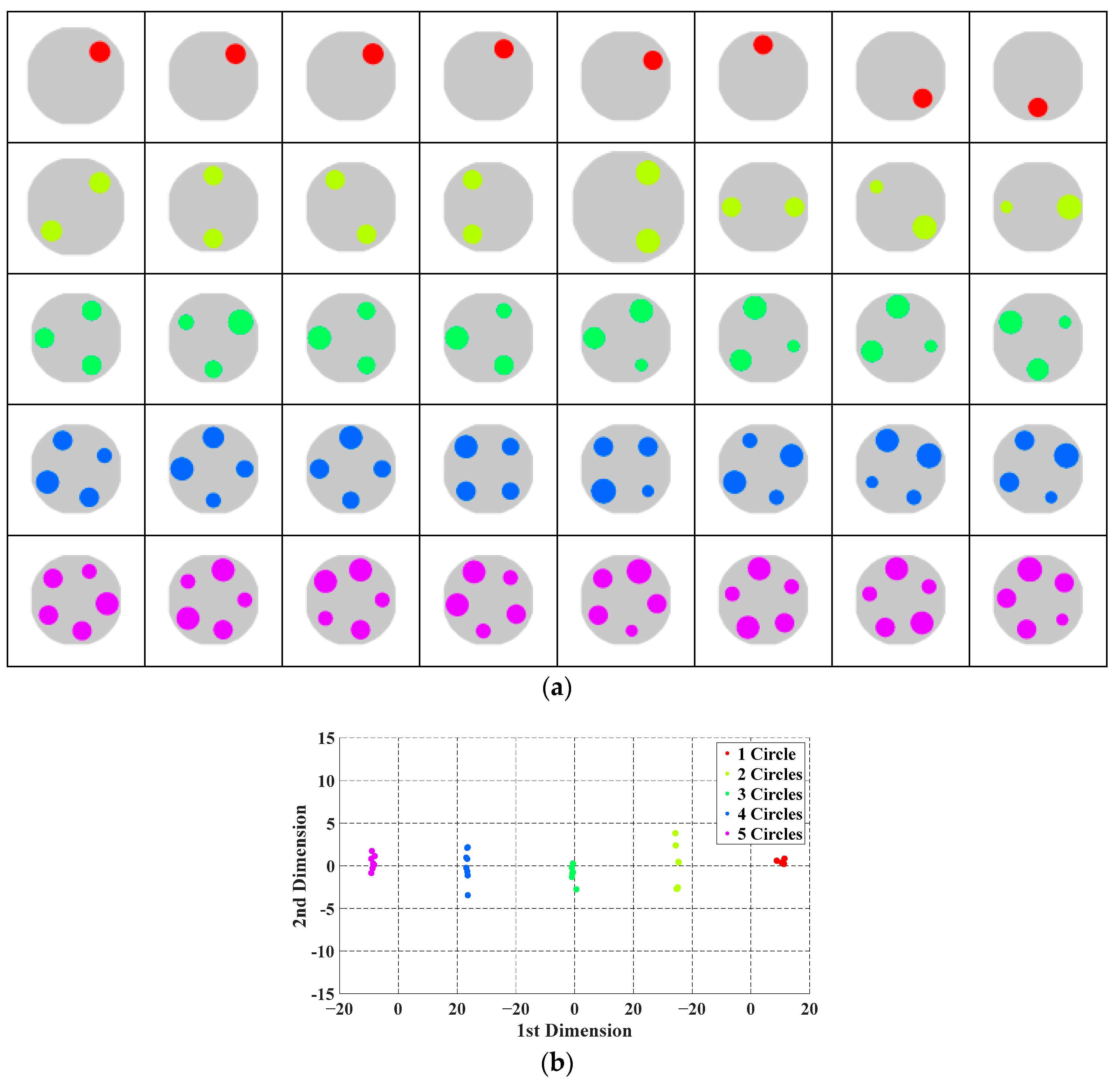
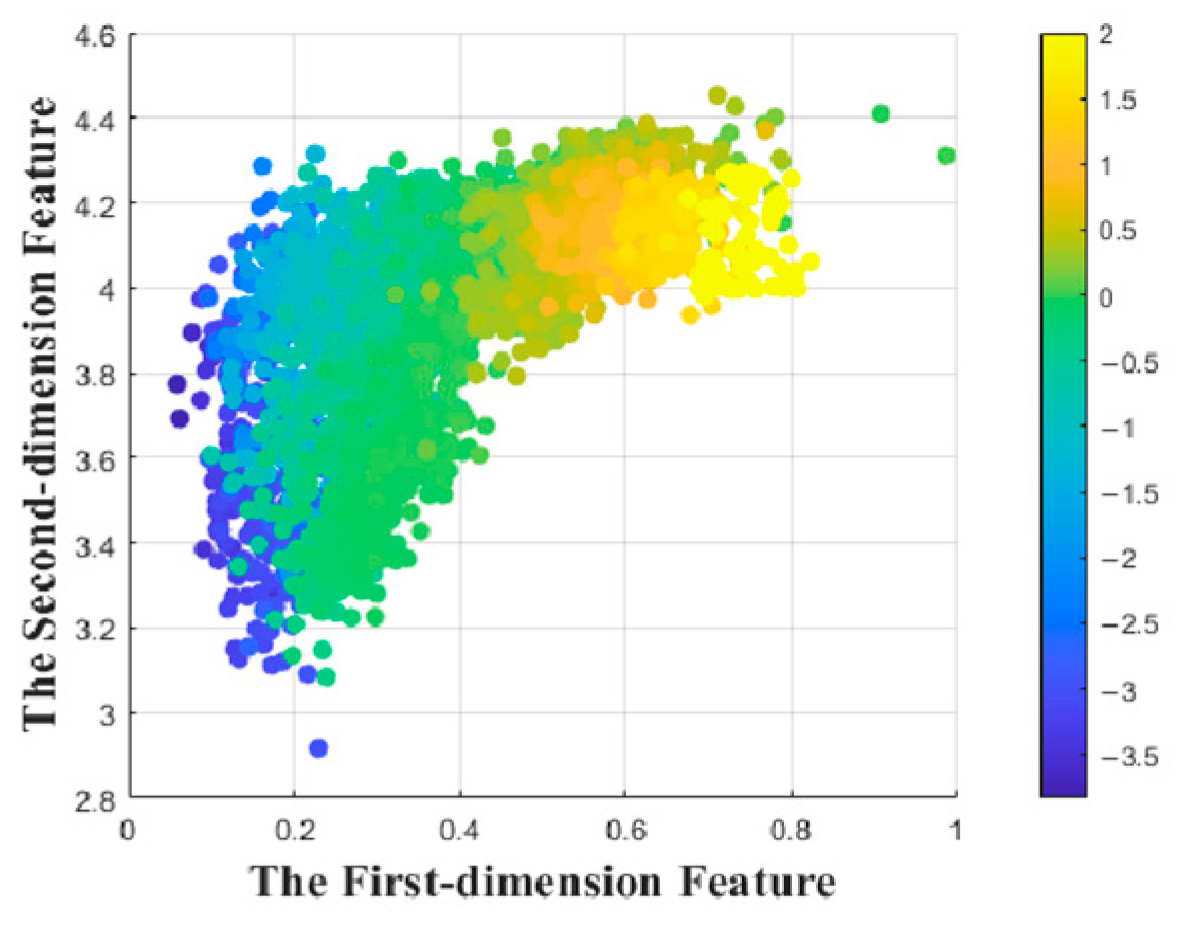
- The topological structure of the original data remains unchanged after MDS mapping. MDS preserves the distances between points as unchanged as possible then maps from a high-dimensional space to a selected low-dimensional space. Specially, if L is small, the mapped distances are nearly unchanged. Hence, the distribution of all data points can be visually observed and further be interpolated and computed in the two-dimensional data space.
3.2. Representative Sample and Best Interpolation Approximation
- (1)
- If Yp and Yq in S are similar/dissimilar, λp and λq must be nearly same/different, satisfying the principle “similar problem has a similar solution” [31]. Specifically, it must be prohibited that the same value of Y corresponds to two different values of λ, and else the determined output will be contradictory.
- (2)
- Each representative sample Yp is centralized in a neighborhood, so that, when any Y falls in the neighborhood of Yp, the corresponding λ will fall into the neighborhood of λp. Hence, it is necessary that neighborhoods from different representative samples in Y should be separated to each other.
4. Experiment
4.1. CT-Based ET Simulation
- (1)
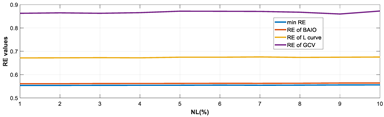
- Imaging quality. These images from BIAO are very close to the best ones in terms of shapes and positions, essentially in M13, M14, and M15. Because BAIO is based on the principle that similar measurements yield similar outputs, it is data-driven and stable. In contrast, these images from LC have large errors in M13, M14, and M15; some tissues cannot be found at all. This is because the corner of the L-curve can become blurred or even disappear. And the images from GCV are the worst. This is because GCV assumes Gaussian noise, while noise in ERT measurements, particularly model noise, is often non-Gaussian.
- (2)
- RE value. The RE value of each reconstructed image from BIAO is lower than those from LC and GCV. Both LC and GCV have very similar RE values since they have similar mechanisms, which is consistent with the results of the reconstructed images. The L-curve and GCV methods do not perform well in this context. The L-curve relies on the existence of a clear corner, which is not theoretically guaranteed. GCV assumes a specific type of noise, but in practice, the noise includes both model noise and measurement system noise, which do not satisfy the assumptions underlying GCV. The reproducing kernel method is data-driven and can maintain stability when applied to data of the same distribution.
- (3)
- HE value. The HE value of each reconstructed image is different from their RE value; partial values of HE are closer to optimal value λ* from BIAO than that from LC and GCV such as M11, M13, and M16. We conclude the reason results from the nonlinear relation of f(•). For example, the distribution of objects affects the optimal parameter differently. Adding an object at the center causes little change in measured values but a large change in the optimal regularization parameter. In contrast, adding an object at the boundary leads to large changes in measured values but only minor changes in the optimal parameter.
- (4)
- Runtime. Except for the time to find the representative samples and build the BIAO, the run time of BIAO is significantly shorter than those of LC and GCV in which each of them takes a group of discrete values in the interval [10−8, 10−1]. Although BIAO requires prior calibration, this does not affect its implementation or application.
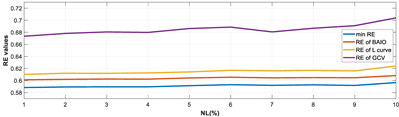
4.1.1. Experiments Under Various Noise Levels
4.1.2. Sensitivity Analysis of Cluster Number
4.1.3. Real Models with Various Features
- (1)
- Imaging quality. The imaging results from the three methods can be visually evaluated by comparing the shapes and positions of all target objects with those of the real models. Even though there are different sizes and shapes in M21–M26, these images from BIAO are closer to the best ones. In contrast, the images from GCV exhibit large errors with numerous artifacts present in all models. Also, the images from LC and BIAO show that the shapes and positions of the target objects are similar, but those from LC have slightly more artifacts than those from BIAO. However, for the models with small or central objects, the reconstructed images from BIAO and LC are unclear, and the edge information is not obvious. However, the images from both LC and GCV are similar in edge information to the target objects.
- (2)
- RE value. The RE value of each reconstructed image from BIAO is lower than those from LC and GCV. The result is consistent with that shown in their imaging quality. Both LC and GCV have very similar RE values since they have similar mechanisms. The RE values of all images are shown below those images in Table 5. The reconstructed images obtained by both algorithms with different measurement numbers show the shape and position of the objects, and the quality of the reconstructed images varies. The reconstructed images obtained by the LC of the multi-objective distribution model have large artifacts. It can only confirm the approximate position and shape of the targets. The M25 model can distinguish the number and shape of the targets, while the M22 model can only roughly distinguish the number of targets but not the shape.
- (3)
- HE value. The HE value of each reconstructed image is different from their RE value; partial values of HE are closer to the optimal value λ* from BIAO than that from LC and GCV. We conclude that the optimal value usually exists within a small interval and is not positively corrected with its own distance due to the nonlinear relation of f(•).
- (4)
- Runtime. Except for the time to find the representative samples and building the BIAO, the run time of BIAO is an order of magnitude less than those from LC and GCV in which each of them takes a group of discrete values in the interval [10−8, 10−1]. Thus, when a set of representative samples is available, the BIAO can find the correct parameter in real-time when using the TR algorithm.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peng, L.; Yang, Y.; Li, Y.; Zhang, M.; Wang, H.; Yang, W. Deep learning-based image reconstruction for electrical capacitance tomography. Meas. Sci. Technol. 2025, 36, 062003. [Google Scholar] [CrossRef]
- York, T. Status of electrical tomography in industrial applications. J. Electron. Imaging 2001, 10, 608. [Google Scholar] [CrossRef]
- Tan, Y.; Yue, S.; Cui, Z.; Wang, H. Measurement of Flow Velocity Using Electrical Resistance Tomography and Cross-Correlation Technique. IEEE Sens. J. 2021, 21, 20714–20721. [Google Scholar] [CrossRef]
- Wang, J.; Deng, J.; Liu, D. Deep prior embedding method for electrical impedance tomography. Neural Netw. 2025, 188, 107419. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhang, T.; Wang, Q. DELTA: Delving into high-quality reconstruction for electrical impedance tomography. IEEE Sens. J. 2025, 25, 13618–13631. [Google Scholar] [CrossRef]
- Sun, B.; Yue, S.; Hao, Z.; Cui, Z.; Wang, H. An Improved Tikhonov Regularization Method for Lung Cancer Monitoring Using Electrical Impedance Tomography. IEEE Sens. J. 2019, 19, 3049–3057. [Google Scholar] [CrossRef]
- Vauhkonen, M. Electrical Impedance Tomography and Prior Information. Ph.D. Thesis, Department of Physics, University of Kuopio, Kuopio, Finland, 1997. [Google Scholar]
- Antoni, J.; Idier, J.; Bourguignon, S. A Bayesian interpretation of the L-curve. Inverse Probl. 2023, 39, 065016. [Google Scholar] [CrossRef]
- Bellec, P.C.; Du, H.; Koriyama, T.; Patil, P.; Tan, K. Corrected generalized cross-validation for finite ensembles of penalized estimators. J. R. Stat. Soc. Ser. B Stat. Methodol. 2025, 87, 289–318. [Google Scholar] [CrossRef]
- Vogel, C.R. Non-convergence of the l-curve regularization parameter selection method. Inverse Probl. 1996, 12, 535. [Google Scholar] [CrossRef]
- Buccini, A.; Reichel, L. Generalized cross validation for lp − lq minimization. Numer. Algorithms 2021, 88, 1595–1616. [Google Scholar] [CrossRef]
- Hanke, M. Limitations of the L-curve method in ill-posed problems. BIT Numer. Math. 1996, 36, 287–301. [Google Scholar] [CrossRef]
- Calvetti, D.; Reichel, L.; Shuibi, A. L-curve and curvature bounds for Tikhonov regularization. Numer. Algorithms 2004, 35, 301–314. [Google Scholar] [CrossRef]
- Mc Carthy, P.J. Direct analytic model of the L-curve for Tikhonov regularization parameter selection. Inverse Prob. 2003, 19, 643–663. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.; Esmaeili, F.; Lindenbergh, R. Least squares B-spline approximation with applications to geospatial point clouds. Measurement 2025, 221, 116887. [Google Scholar] [CrossRef]
- Gasca, M.; Sauer, T. Polynomial interpolation in several variables. Adv. Comput. Math. 2000, 12, 377–410. [Google Scholar] [CrossRef]
- Berlinet, A.; Thomas-Agnan, C. Reproducing Kernel Hilbert Spaces in Probability and Statistics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Li, F.; Cui, M. A best approximation for the solution of one-dimensional variable-coefficient burgers’ equation. Numer. Methods Partial Differ. Equ. 2009, 25, 1353–1365. [Google Scholar] [CrossRef]
- Polydorides, N. Image Reconstruction Algorithm for Soft-Field Tomography. Ph.D. Thesis, Department of Electrical Engineering and Electronics, UMIST, Manchester, UK, 2002. [Google Scholar]
- Huang, P.; Bao, Z.; Guo, J. Detection of magnetic samples by electromagnetic tomography with PID controlled iterative L1 regularization method. IEEE Sens. J. 2025, 25, 15477–15488. [Google Scholar] [CrossRef]
- Li, J.; Yue, S.; Ding, M.; Wang, H. Choquet Integral-Based Fusion of Multiple Patterns for Improving EIT Spatial Resolution. IEEE Trans. Appl. Supercond. 2019, 29, 0603005. [Google Scholar] [CrossRef]
- Wang, X.; Chen, J.; Richard, C. Tuning-free plug-and-play hyperspectral image deconvolution with deep priors. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5506413. [Google Scholar] [CrossRef]
- Rezghi, M.; Hosseini, S.M. A new variant L-curve for Tikhonov regularization. J. Comput. Appl. Math. 2009, 231, 914–924. [Google Scholar] [CrossRef]
- Barbour, A.D.; Holst, L.; Janson, S. Poisson Approximation; Oxford Studies in Probability; Clarendon Press: Oxford, UK, 1992; Volume 2. [Google Scholar]
- Chen, L.H.Y.; Goldstein, L.; Shao, Q.-M. Normal Approximation by Stein’s Method: Probability and Its Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Cui, M.G.; Deng, Z.X. On the best operator of interpolation in W21. Math. Numer. Sin. 1986, 8, 209–216. [Google Scholar]
- Fasshauer, G.E.; Hickernell, F.J.; Ye, Q. Solving support vector machines in reproducing kernel Banach spaces with positive definite functions. Appl. Comput. Harmon. Anal. 2015, 38, 115–139. [Google Scholar] [CrossRef]
- Borg, I.; Groenen, P. Modern Multidimensional Scaling: Theory and Applications; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Paulsen, V.I.; Raghupathi, M. An Introduction to the Theory of Reproducing Kernel Hilbert Spaces; Cambridge Studies in Advanced Mathematics; Cambridge University Press: Cambridge, UK, 2016; Volume 152. [Google Scholar]
- Wang, Q.; Heng, Z. Near MDS codes from oval polynomials. Discrete Math. 2021, 344, 112277. [Google Scholar] [CrossRef]
- Girosi, F.; Jones, M.; Poggio, T. Regularization Theory and Neural Networks Architectures. Neural Comput. 1995, 7, 219–269. [Google Scholar] [CrossRef]
- Liu, W.K.; Jun, S.; Zhang, Y.F. Reproducing kernel particle methods. Int. J. Numer. Methods Fluids 1995, 20, 1081–1106. [Google Scholar] [CrossRef]
- Wang, Z.; Yue, S.; Li, Q. Unsupervised Evaluation and Optimization for Electrical Impedance Tomography. IEEE Trans. Instr. Meas. 2021, 70, 4506312. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Maulik, U. An evolutionary technique based on k-means algorithm for optimal clustering in RN. Inf. Sci. 2022, 146, 221–237. [Google Scholar] [CrossRef]
- Yue, S.; Wu, T.; Cui, L.; Wang, H. Clustering mechanism for electric tomography imaging. Sci. China Inf. Sci. 2012, 55, 2849–2864. [Google Scholar] [CrossRef]

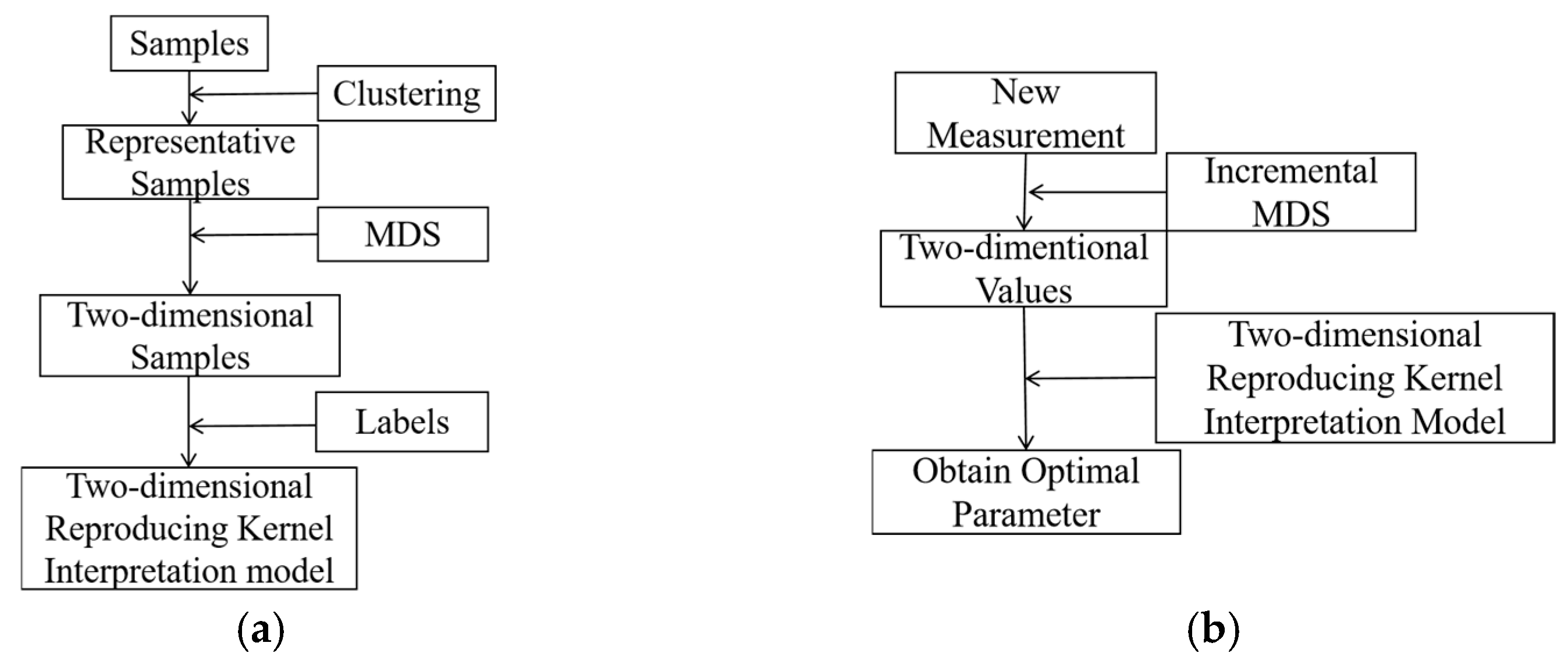


| Input: A set of samples on the ET image and relative parameter, {(Uk, λk)} (0≦k≦L). Output: BIAO for f(.) from U to λ. Method: 1. Solve {(Yk, λk)} (0≦k≦L) from {(Uk, λk)} (0≦k≦L) by MDS map; 2. Calculate the distance of any two samples after in {(Yk, λk)} (0≦k≦L) using the kernel trial; 3. Determine the number of clusters c* by DB along the value of c when c ∈ [2, n1/2]; 4. Cluster (Yk, λk)} (0≦k≦L) by the CM algorithm to obtain c cluster centers, v1, v2, …, vc; 5. Take v1, v2, …, vc as the representative samples; 6. Construct BAIO by v1, v2, …, vc. |
| Representative Sample | ||||||||
| CT |  V11 | 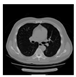 V12 | 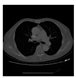 V13 |  V14 |  V15 |  V16 |  | |
| ET |  |  |  |  |  |  | ||
| λ* | 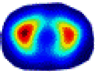 | 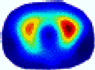 | 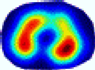 | 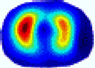 |  | 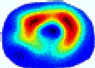 | ||
| RE | 0.5751 | 0.6115 | 0.5642 | 0.5882 | 0.5756 | 0.6214 | ||
| LC |  |  | 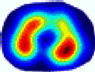 | 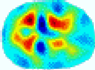 |  | 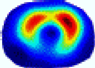 | ||
| Re | 0.7189 | 0.7640 | 0.5642 | 0.7329 | 0.7373 | 0.6417 | ||
| HE/T | 3/4.44 | 3/4.21 | 0/4.30 | 4/4.18 | 3/4.56 | 1/4.33 | ||
| GCV |  |  |  | 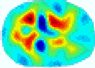 |  | 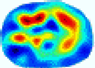 | ||
| RE | 0.8025 | 0.8190 | 0.6906 | 0.7484 | 0.8300 | 0.6868 | ||
| HE/T | 5/4.31 | 7/4.35 | 6/4.12 | 8/4.19 | 8/3.99 | 6/4.27 | ||
| BIAO |  |  |  | 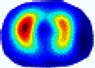 |  |  | ||
| RE | 0.5751 | 0.6115 | 0.5642 | 0.5882 | 0.5756 | 0.6214 | ||
| HE/T | 0/0.77 | 0/0.59 | 0/0.66 | 0/0.72 | 0/0.68 | 0/0.75 | ||
| Testing sample |  | |||||||
| CT | 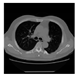 M11 |  M12 | 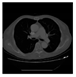 M13 |  M14 | 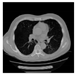 M15 | 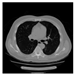 M16 | ||
| ET |  |  |  |  |  |  | ||
| λ* |  |  |  |  |  |  | ||
| RE | 0.6150 | 0.5721 | 0.5932 | 0.6096 | 0.5799 | 0.6719 | ||
| LC | 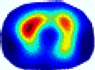 | 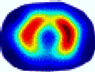 |  | 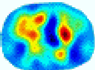 | 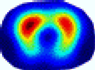 | 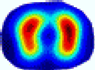 | ||
| RE | 0.6554 | 0.6193 | 0.6434 | 0.7218 | 0.6009 | 0.6856 | ||
| HE/T | 2/4.05 | 1/4.39 | 2/4.18 | 4/4.35 | 2/4.21 | 2/4.23 | ||
| GCV | 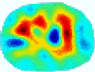 |  |  | 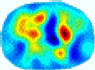 |  |  | ||
| RE | 0.6622 | 0.6588 | 0.6821 | 0.7370 | 0.6045 | 0.8555 | ||
| HE/T | 6/4.12 | 6/4.28 | 6/4.61 | 8/4.45 | 5/4.38 | 9/4.31 | ||
| BIAO |  |  | 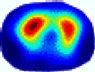 | 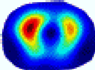 | 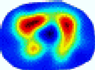 | 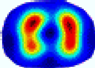 | ||
| RE | 0.6125 | 0.5716 | 0.5953 | 0.6108 | 0.5771 | 0.6850 | ||
| HE/T | 0/0.72 | 0.30/0.77 | 0.24/0.79 | 0.57/0.70 | 1.21/0.68 | 0.04/0.73 | ||
| Conductivity | Right Lung | Left Lung | |||
|---|---|---|---|---|---|
| Upper Lobe | Middle Lobe | Down Lobe | Upper Lobe | Lower Lobe | |
| Range | 0.265~0.32 | 0.26~0.30 | 0.24~0.28 | 0.197~0.275 | 0.22~0.267 |
| Mean | 0.30 | 0.28 | 0.26 | 0.25 | 0.24 |
| Model | RE Curves |
|---|---|
 |  |
 | 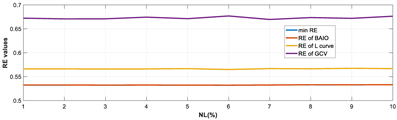 |
 |  |
 |  |
| Representative Sample | |||||||
| Model |  V21 |  V22 |  V23 |  V24 |  V25 |  V26 |  |
| λ* |  |  | 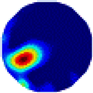 |  |  | 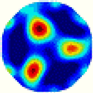 | |
| RE | 0.3011 | 0.2412 | 0.2022 | 0.2522 | 0.2023 | 0.2340 | |
| LC |  | 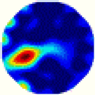 |  | 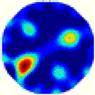 | 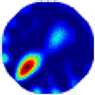 | 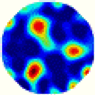 | |
| Re | 0.3549 | 0.2870 | 0.2289 | 0.3033 | 0.2582 | 0.3023 | |
| HE/T | 1/0.15 | 2/0.22 | 1/0.18 | 2/0.19 | 2/0.21 | 2/0.20 | |
| GCV | 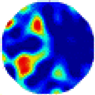 |  |  | 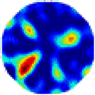 |  | 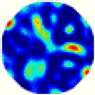 | |
| RE | 0.4249 | 0.3532 | 0.2822 | 0.3522 | 0.3028 | 0.3840 | |
| HE/T | 2/0.12 | 3/0.09 | 3/0.10 | 4/0.14 | 3/0.12 | 3/0.14 | |
| BIAO |  |  |  |  |  |  | |
| RE | 0.3011 | 0.2412 | 0.2022 | 0.2522 | 0.2023 | 0.2340 | |
| HE/T | 0/0.058 | 0/0.060 | 0/0.053 | 0/0.062 | 0/0.055 | 0/0.071 | |
| Testing sample | |||||||
| Model |  M21 |  M22 |  M23 |  M24 |  M25 |  M26 |  |
| λ* | 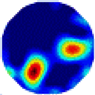 |  |  | 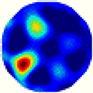 |  |  | |
| RE | 0.1836 | 0.2072 | 0.1980 | 0.2238 | 0.2122 | 0.2123 | |
| LC | 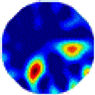 | 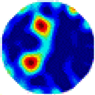 | 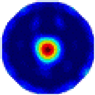 | 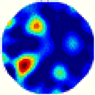 | 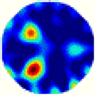 | 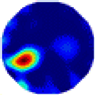 | |
| RE | 0.2304 | 0.2802 | 0.2502 | 0.2809 | 0.2333 | 0.2345 | |
| HE/T | 2/0.21 | 2/0.19 | 2/0.18 | 2/0.17 | 1/0.15 | 1/0.16 | |
| GCV |  | 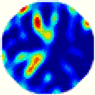 | 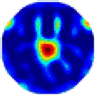 |  |  | 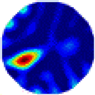 | |
| RE | 0.2702 | 0.3230 | 0.3201 | 0.3149 | 0.3182 | 0.2823 | |
| HE/T | 3/0.11 | 4/0.10 | 5/0.12 | 3/0.16 | 3/0.12 | 3/0.13 | |
| BIAO |  | 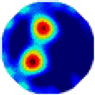 | 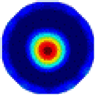 |  | 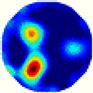 |  | |
| RE | 0.2102 | 0.2102 | 0.1980 | 0.2308 | 0.2233 | 0.2123 | |
| HE/T | 0.4304/0.059 | 0.49/0.060 | 0.15/0.061 | 1.17/0.056 | 1.07/0.058 | 0.10/0.061 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, F.; Yue, S. Two-Dimensional Reproducing Kernel-Based Interpolation Approximation for Best Regularization Parameter in Electrical Tomography Algorithm. Symmetry 2025, 17, 1242. https://doi.org/10.3390/sym17081242
Dong F, Yue S. Two-Dimensional Reproducing Kernel-Based Interpolation Approximation for Best Regularization Parameter in Electrical Tomography Algorithm. Symmetry. 2025; 17(8):1242. https://doi.org/10.3390/sym17081242
Chicago/Turabian StyleDong, Fanpeng, and Shihong Yue. 2025. "Two-Dimensional Reproducing Kernel-Based Interpolation Approximation for Best Regularization Parameter in Electrical Tomography Algorithm" Symmetry 17, no. 8: 1242. https://doi.org/10.3390/sym17081242
APA StyleDong, F., & Yue, S. (2025). Two-Dimensional Reproducing Kernel-Based Interpolation Approximation for Best Regularization Parameter in Electrical Tomography Algorithm. Symmetry, 17(8), 1242. https://doi.org/10.3390/sym17081242






