Dual Chaotic Diffusion Framework for Multimodal Biometric Security Using Qi Hyperchaotic System
Abstract
1. Introduction
- Design of a novel dual-chaos encryption algorithm that leverages double Qi hyperchaotic systems, significantly enhancing randomness and security beyond single-chaotic methods. The algorithm implements distinct rotation diffusion methods that adapt based on input images, enhancing resistance to selected plaintext attacks. This innovative method addresses limitations of traditional chaotic systems while substantially improving the algorithm’s cryptographic strength and resistance to cryptanalysis.
- The research introduces a novel secure biometric framework that establishes a robust cryptographic relationship between active user biometric identification information and encrypted templates in the system database. This framework ensures continuous encryption of biometric data in storage, with decryption occurring only during authentication processes, effectively preventing unauthorized acquisition, tampering, and exploitation of sensitive biometric.
- The proposed framework integrates multimodal biometric authentication—combining left iris, right iris, and facial characteristics—with dual chaotic encryption, establishing a multi-layered security architecture that significantly increases the computational complexity required for successful compromise. This approach necessitates simultaneous decryption of multiple biometric modalities for user identification, thereby enhancing the system’s overall security through the principle of multi-factor authentication.
- Experimental results and performance analysis demonstrate that the proposed scheme offers significant advantages across multiple performance metrics. The system successfully passes all the 15 NIST Test Suites. Notable strengths include an expansive key space dimension of 10320, indicating robust encryption characteristics, while maintaining an efficient computational overhead despite its dual-encryption architecture.
2. Theoretical Framework
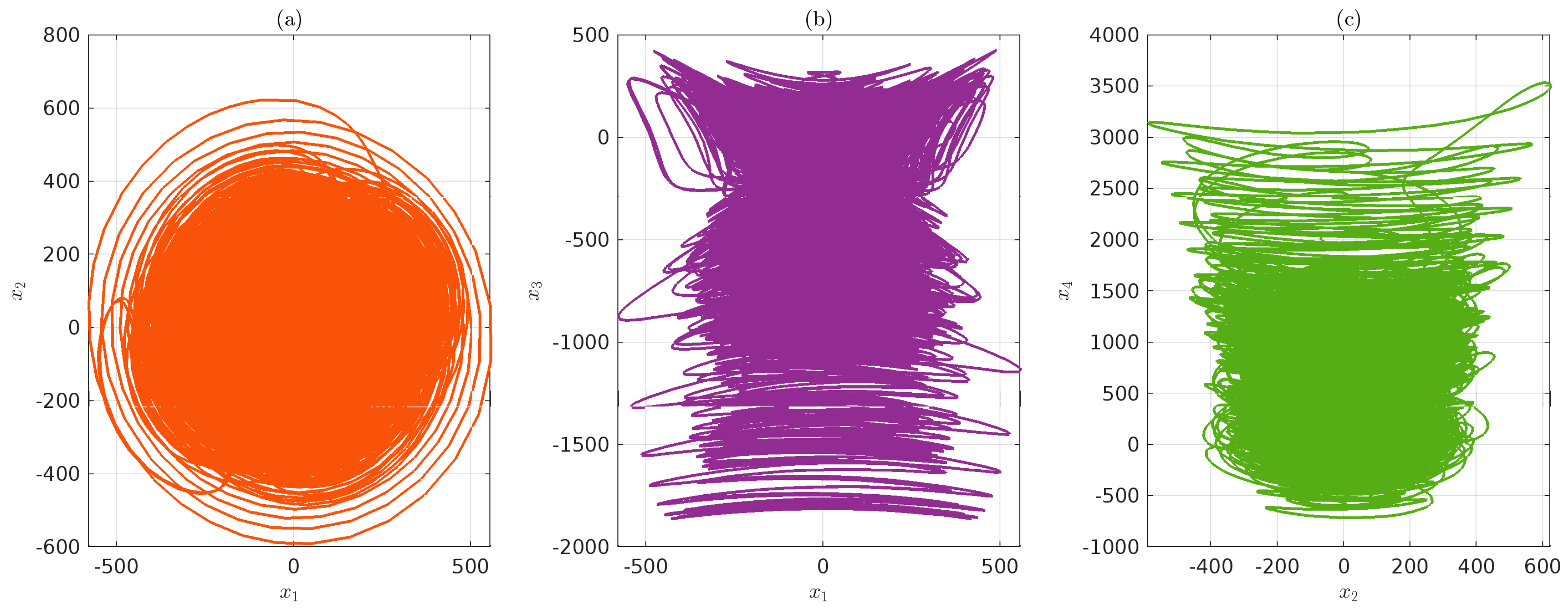
2.1. Four-Dimensional Qi Hyperchaos System
2.2. Key Generation and Binary Sequence Transformation
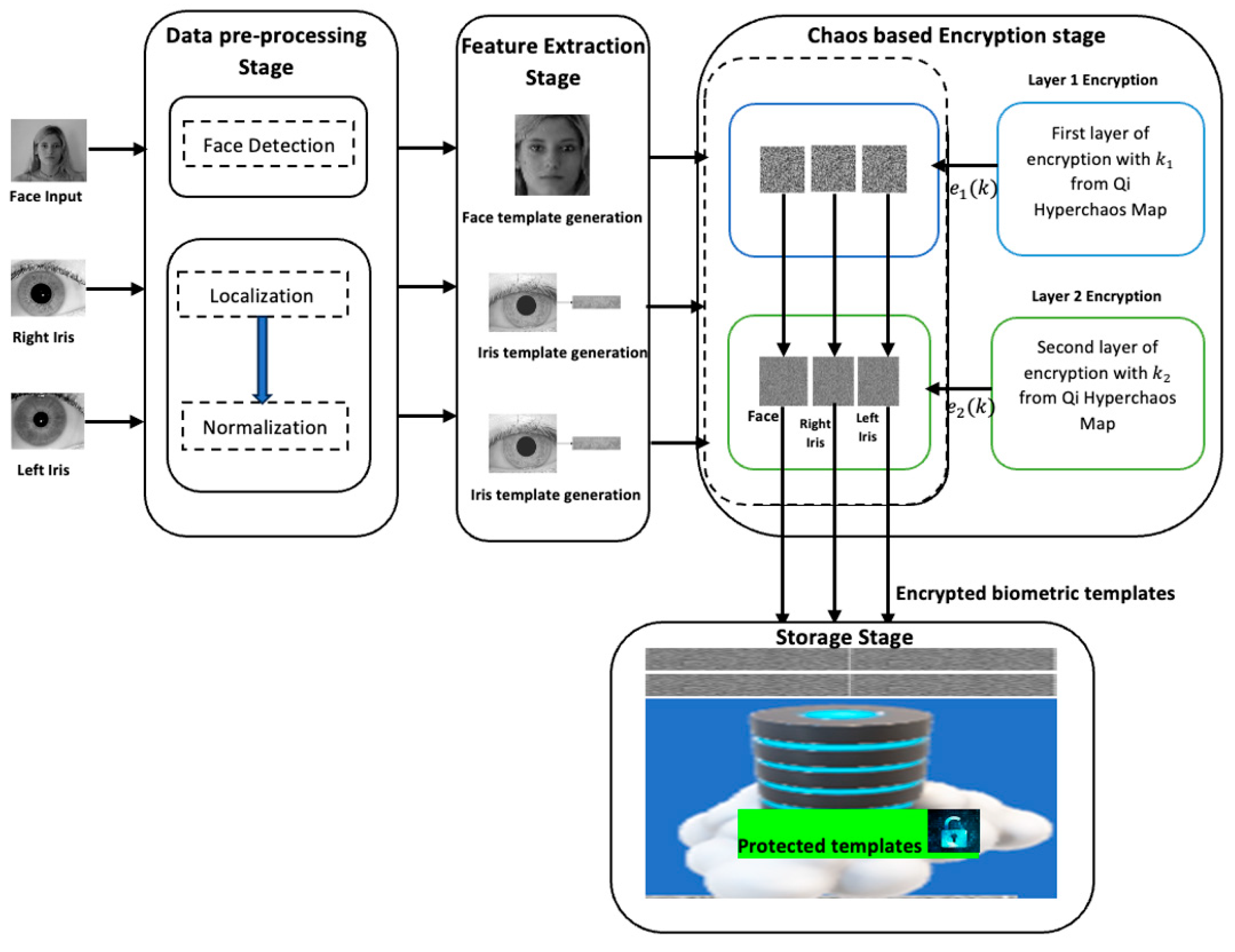
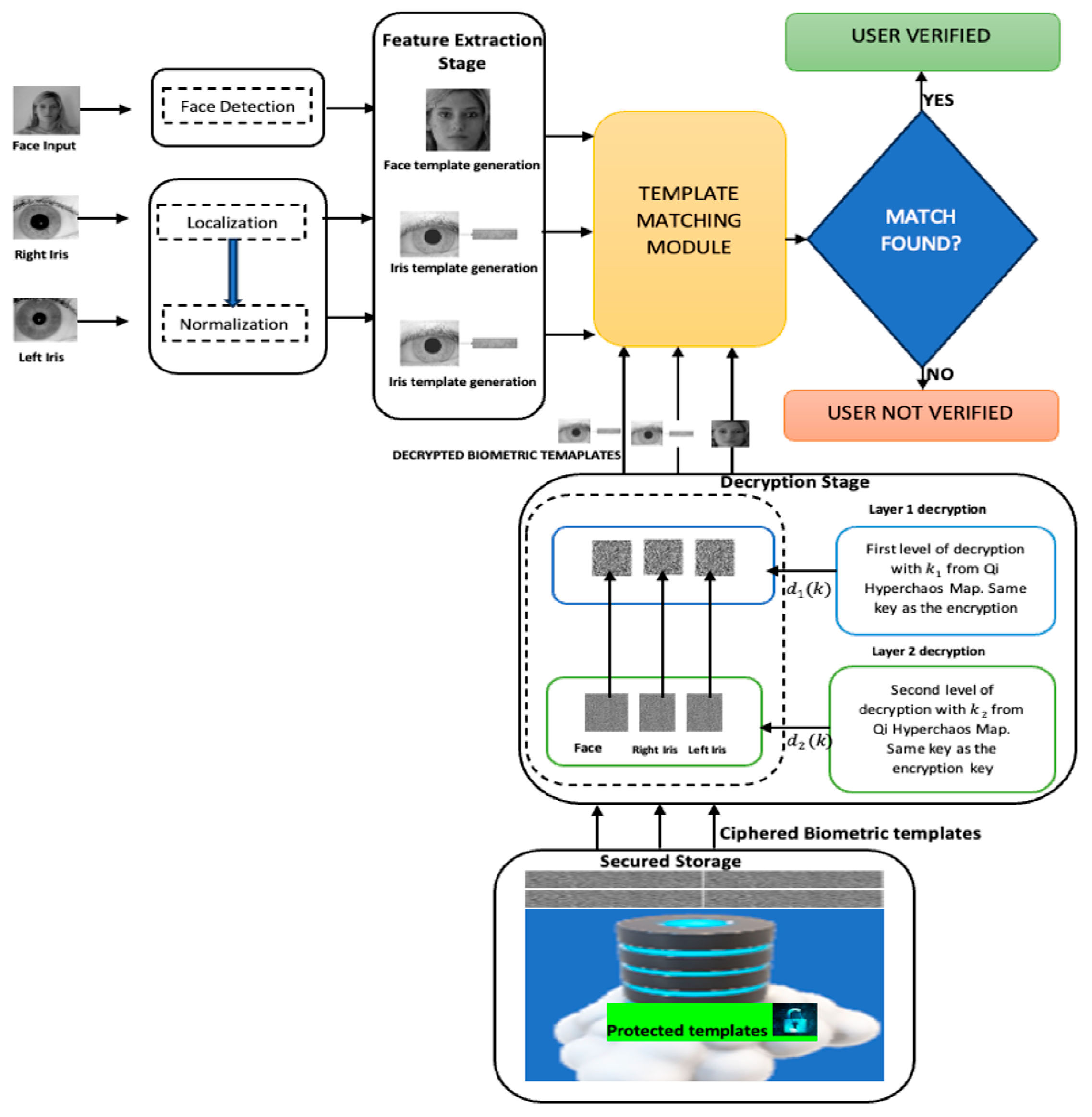
3. Our Proposed Secure Biometric Protection Framework
3.1. Encryption Algorithm
| Algorithm 1: Image Pixel-Shuffling Algorithm |
| Input: Get the image dimensions rng (seed) = PixelIndices = = ; = ; = ; End Output |
| Algorithm 2: Double-Encryption Algorithm Pseudocode |
Input:
|
3.2. Decryption Algorithm
| Algorithm 3: Image Pixel-Reverse-Shuffling Algorithm |
| Input: Get the shuffled image of dimensions Set random see to original value rng (seed) Recreate the same number of iterations PixelIndices = Create the inverse permutation = ; = ; Apply the inverse permutation = ; = ; Output recovered Biometric image |
| Algorithm 4: Decryption Algorithm Pseudocode | |
| Input: | |
| |
4. Experimental and Performance Analyses
4.1. Qi Hyperchaos System Randomness Test
4.2. Key Space Analysis
4.3. Key Sensitivity Analysis
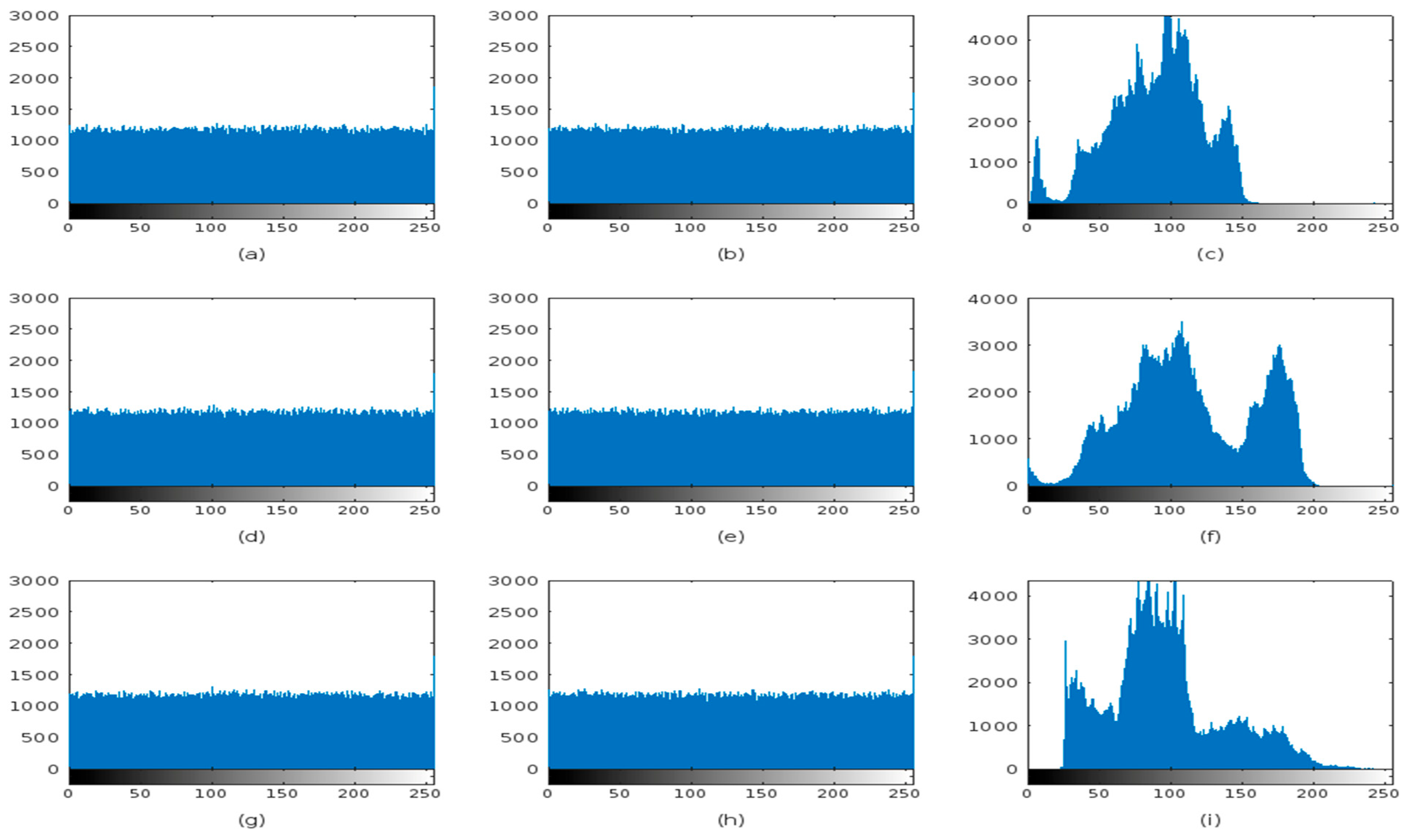
4.4. Histogram Analysis
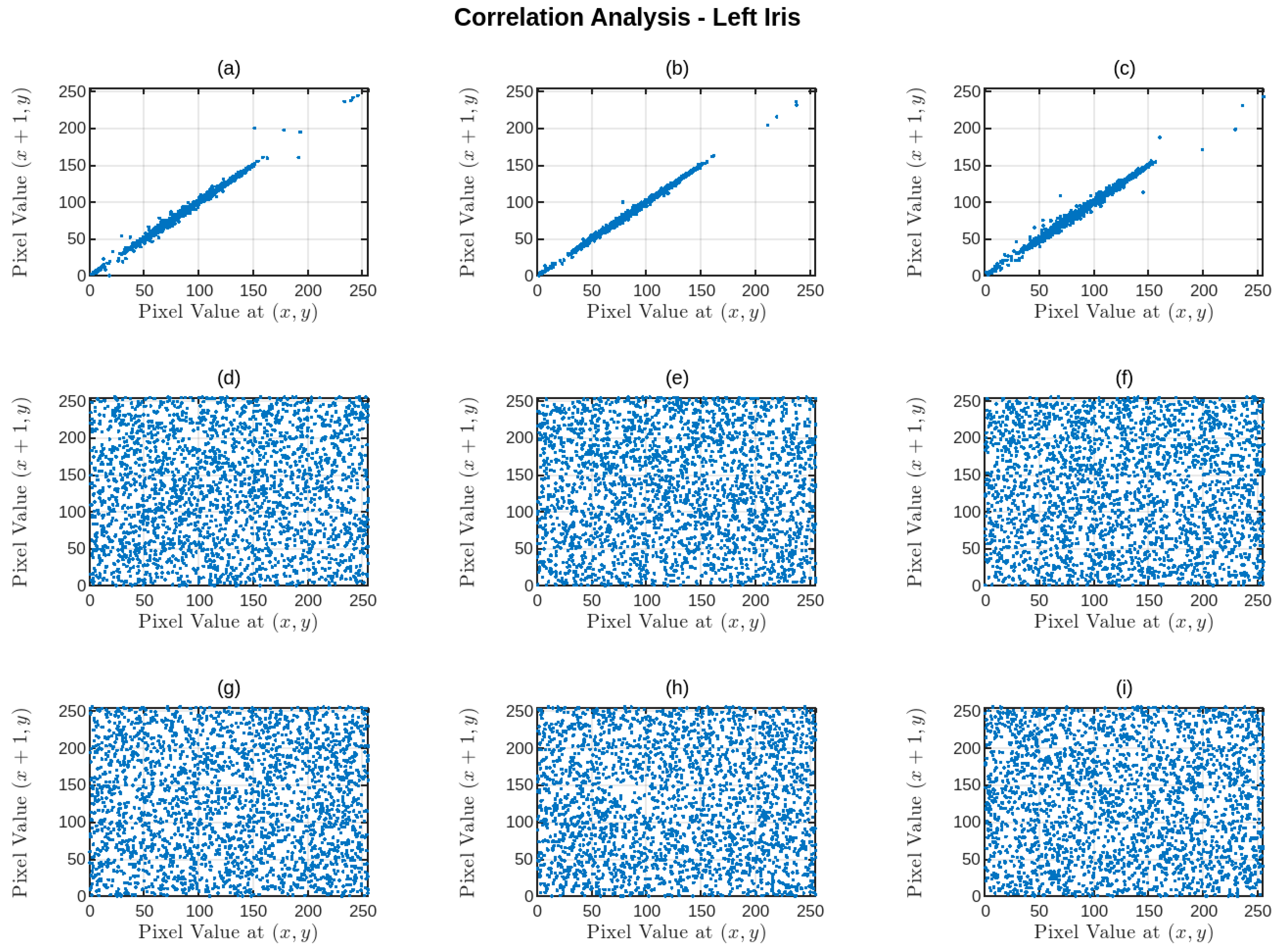
4.5. Pixels Correlation Analysis
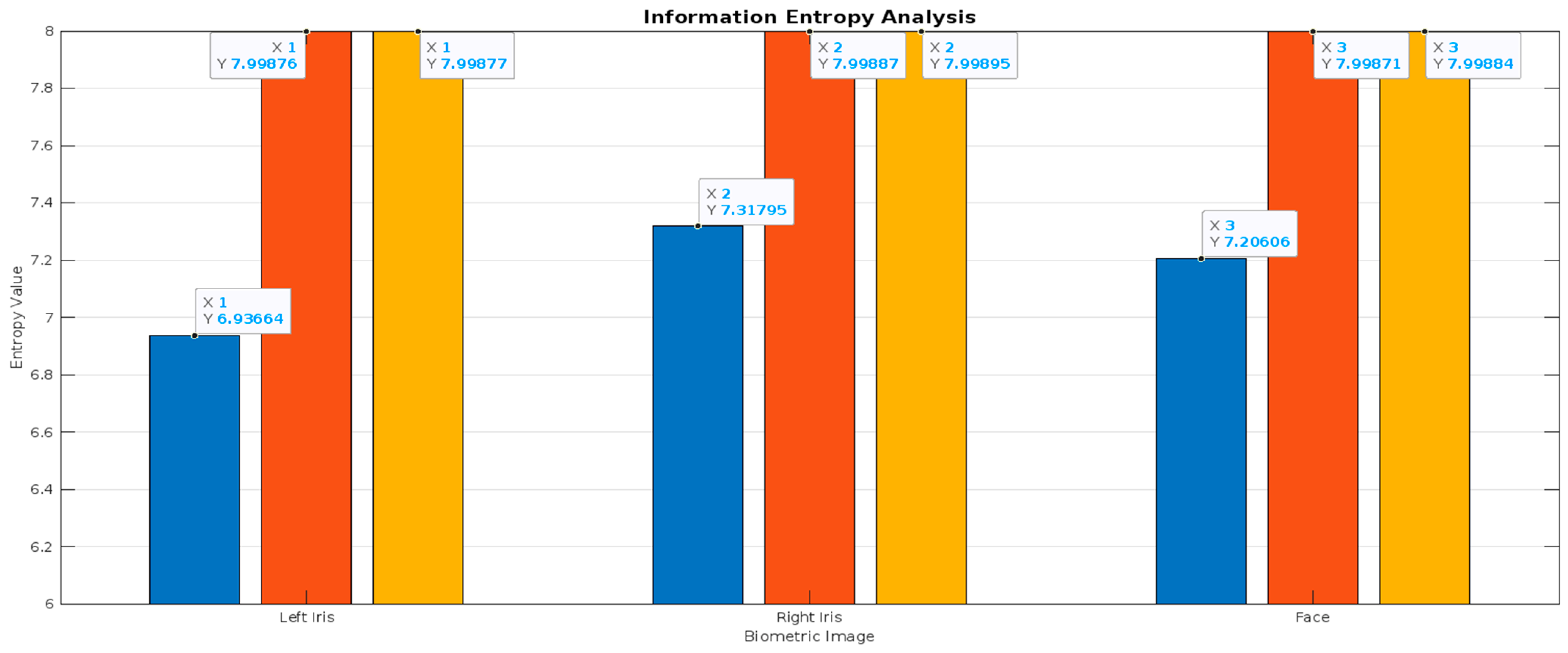
4.6. Information Entropy Analysis
4.7. Diferential Attacks Analysis
4.8. Time Efficiency Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, E. A Review of the Comparative Studies on Traditional and Intelligent Face Recognition Methods. In Proceedings of the 2020 International Conference on Computer Vision, Image and Deep Learning, CVIDL 2020, Chongqing, China, 10–12 July 2020; pp. 11–15. [Google Scholar] [CrossRef]
- Sumalatha, U.; Prakasha, K.K.; Prabhu, S.; Nayak, V.C.A. Comprehensive Review of Unimodal and Multimodal Fingerprint Biometric Authentication Systems: Fusion, Attacks, and Template Protection. IEEE Access 2024, 12, 64300–64334. [Google Scholar] [CrossRef]
- Yang, W.; Wang, S.; Hu, J.; Zheng, G. SS symmetry Security and Accuracy of Fingerprint-Based Biometrics: A Review. Symmetry 2019, 11, 141. [Google Scholar] [CrossRef]
- Kaur, G. Multimodal Biometrics Feature Level Fusion for Iris and Hand Geometry Using Chaos-based Encryption Technique. In Proceedings of the IEEE International Conference Image Information Processing, Taipei, Taiwan, 22–25 September 2019; Volume 2019, pp. 304–309. [Google Scholar] [CrossRef]
- Vallabhadas, D.K.; Sandhya, M.; Sarkar, S.; Chandra, Y.R. Multimodal biometric authentication using Fully Homomorphic Encryption. In Proceedings of the 2023 2nd International Conference on Paradigm Shifts in Communications Embedded Systems, Machine Learning and Signal Processing, PCEMS 2023, Nagpur, India, 5–6 April 2023. [Google Scholar] [CrossRef]
- Chen, H.; Ding, D.; Su, S.; Yin, J. Biometrics-based cryptography scheme for E-Health systems. J. Phys. Conf. Ser. 2020, 1550, 022039. [Google Scholar] [CrossRef]
- Singla, S.K.; Singh, M.; Kanwal, N. Biometric system—Challenges and future trends. In Proceedings of the 2021 8th International Conference on Computing for Sustainable Global Development, INDIACom 2021, New Delhi, India, 17–19 March 2021; pp. 647–651. [Google Scholar]
- Nita, S.L.; Mihailescu, M.I.; Pau, V.C. Security and Cryptographic Challenges for Authentication Based on Biometrics Data. Cryptography 2018, 2, 39. [Google Scholar] [CrossRef]
- Devi, R.; Sujatha, P. A study on biometric and multi-modal biometric system modules, applications, techniques and challenges. In Proceedings of the Emerging Devices and Smart Systems, ICEDSS 2017, Mallasamudram, India, 3–4 March 2017; pp. 267–271. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, Z.; Lei, Z.; Yi, D.; Li, S.Z. Face liveness detection by exploring multiple scenic clues. In Proceedings of the 2012 12th International Conference on Control, Automation, Robotics and Vision, ICARCV 2012, Guangzhou, China, 5–7 December 2012; Volume 2012, pp. 188–193. [Google Scholar] [CrossRef]
- Kulkarni, N.A.; Sankpal, L. Efficient Approach Determination for Fake Biometric Detection. In Proceedings of the 2017 International Conference on Computing, Communication, Control and Automation, ICCUBEA 2017, Pune, India, 7–18 August 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Saranya, S.; Sherline, S.V.; Maheswari, M. Fake biometric detection using image quality assessment: Application to iris, fingerprint recognition. In Proceedings of the 2016 2nd International Conference on Science Technology Engineering and Management, ICONSTEM 2016, Chennai, India, 30–31 March 2016; pp. 98–103. [Google Scholar] [CrossRef]
- He, X.; Lu, Y.; Shi, P. A fake iris detection method based on FFT and quality assessment. In Proceedings of the 2008 Chinese Conference on Pattern Recognition, CCPR 2008, Beijing, China, 22–24 October 2008; pp. 316–319. [Google Scholar] [CrossRef]
- Makrushin, A.; Uhl, A.; Dittmann, J. A Survey on Synthetic Biometrics: Fingerprint, Face, Iris and Vascular Patterns. IEEE Access 2023, 11, 33887–33899. [Google Scholar] [CrossRef]
- Ammour, B.; Bouden, T.; Amira-Biad, S. Multimodal biometric identification system based on the face and iris. In Proceedings of the 2017 5th International Conference on Electrical Engineering—Boumerdes, ICEE-B 2017, Boumerdes, Algeria, 29–31 October 2017; Volume 2017, pp. 1–17. [Google Scholar] [CrossRef]
- Ammour, B.; Bouden, T.; Boubchir, L. Face-Iris Multimodal Biometric System Based on Hybrid Level Fusion. In Proceedings of the 2018 41st International Conference on Telecommunications and Signal Processing, TSP 2018, Athens, Greece, 4–6 July 2018; pp. 298–302. [Google Scholar] [CrossRef]
- Rodrigues, R.N.; Kamat, N.; Govindaraju, V. Evaluation of biometric spoofing in a multimodal system. In Proceedings of the IEEE 4th International Conference on Biometrics: Theory, Applications and Systems, BTAS 2010, Washington, DC, USA, 28–30 September 2010. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Xie, E.Y. When an attacker meets a cipher-image in 2018: A year in review. J. Inf. Secur. Appl. 2019, 48, 102361. [Google Scholar] [CrossRef]
- Feng, W.; Qin, Z.; Zhang, J.; Ahmad, M. Cryptanalysis and improvement of the image encryption scheme based on Feistel network and dynamic DNA encoding. IEEE Access 2021, 9, 145459–145470. [Google Scholar] [CrossRef]
- Belazi, A.; Talha, M.; Kharbech, S.; Xiang, W. Novel Medical Image Encryption Scheme Based on Chaos and DNA Encoding. IEEE Access 2019, 7, 36667–36681. [Google Scholar] [CrossRef]
- Zahid, A.Z.; Al-Kharsan, I.H.M.S.; Bakarman, H.A.; Ghazi, M.F.; Salman, H.A.; Hasoon, F.N. Biometric Authentication Security System Using Human DNA. In Proceedings of the 2019 1st International Conference of Intelligent Computing and Engineering: Toward Intelligent Solutions for Developing and Empowering our Societies, ICOICE 2019, Hadhramout, Yemen, 15–16 December 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Ajeethra, B.; Prasath, S.G.; Balaji, R.A.; Kumar, K.A. A Cryptography based Face Authentication System for Secured Communication. In Proceedings of the IEEE 2022 4th International Conference on Advances in Electronics, Computers and Communications, ICAECC 2022, Bengaluru, India, 10–11 January 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Jiang, M.; Yang, H. Image Encryption Using a New Hybrid Chaotic Map and Spiral Transformation. Entropy 2023, 25, 1516. [Google Scholar] [CrossRef]
- Sun, S.; Guo, Y.; Wu, R. A novel image encryption scheme based on 7D hyperchaotic system and row-column simultaneous swapping. IEEE Access 2019, 7, 28539–28547. [Google Scholar] [CrossRef]
- Yu, F.; Tan, B.; He, T.; He, S.; Huang, Y.; Cai, S.; Lin, H. A Wide-Range Adjustable Conservative Memristive Hyperchaotic System with Transient Quasi-Periodic Characteristics and Encryption Application. Mathematics 2025, 13, 726. [Google Scholar] [CrossRef]
- Man, Z. Biometric information security based on double chaotic rotating diffusion. Solitons Fractals 2023, 172, 113614. [Google Scholar] [CrossRef]
- Feng, W.; Yang, J.; Zhao, X.; Qin, Z.; Zhang, J.; Zhu, Z.; Wen, H.; Qian, K. A Novel Multi-Channel Image Encryption Algorithm Leveraging Pixel Reorganization and Hyperchaotic Maps. Mathematics 2024, 12, 3917. [Google Scholar] [CrossRef]
- Ye, C.; Tan, S.; Wang, J.; Shi, L.; Zuo, Q.; Feng, W. Social Image Security with Encryption and Watermarking in Hybrid Domains. Entropy 2025, 27, 276. [Google Scholar] [CrossRef]
- Yu, F.; He, S.; Yao, W.; Cai, S.; Xu, Q. Bursting Firings in Memristive Hopffeld Neural Network with Image Encryption and Hardware Implementation. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2025. early access. [Google Scholar] [CrossRef]
- Rashik, A.; Priya, C.V. A Secure Application of Multi_Biometric Recognition and QR Coding System. In Proceedings of the 2022 International Conference on Innovative Trends in Information Technology (ICITIIT), Kottayam, India, 12–13 February 2022. [Google Scholar]
- Eid, M.M.; Mohamed, M.A. A secure multimodal authentication system based on chaos cryptography and fuzzy fusion of iris and face. In Proceedings of the ACCS/PEIT 2017—2017 Intl Conf on Advanced Control Circuits Systems and 2017 Intl Conf on New Paradigms in Electronics and Information Technology, Alexandria, Egypt, 5–8 November 2017; Volume 2018, pp. 163–171. [Google Scholar] [CrossRef]
- Arulalan, V.; Joseph, K.S.; Premanand, V. Securing Digital Data using 256-bit Multimodal Biometrics based Cryptographic Key. In Proceedings of the IEEE Sponsored World Conference on Futuristic Trends in Research and Innovation for Social Welfare (WCFTR’16), Coimbatore, India, 29 February–1 March 2016. [Google Scholar]
- Wen, H.; Lin, Y. Cryptanalysis of an image encryption algorithm using quantum chaotic map and DNA coding. Expert Syst. Appl. 2024, 237, 121514. [Google Scholar] [CrossRef]
- Feng, W.; He, Y.; Li, H.; Li, C. Cryptanalysis and improvement of the image encryption scheme based on 2D logistic-adjusted-sine map. IEEE Access 2019, 7, 12584–12597. [Google Scholar] [CrossRef]
- Qi, G.; van Wyk, M.A.; van Wyk, B.J.; Chen, G. On a new hyperchaotic system. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2008, 372, 124–136. [Google Scholar] [CrossRef]
- Tresor, L.O.; Sumbwanyambe, M. A selective image encryption scheme based on 2D DWT, henon map and 4D Qi hyper-chaos. IEEE Access 2019, 7, 103463–103472. [Google Scholar] [CrossRef]
- Zhu, H.; Zhao, Y.; Song, Y. 2D Logistic-Modulated-Sine-Coupling-Logistic Chaotic Map for Image Encryption. IEEE Access 2019, 7, 14081–14098. [Google Scholar] [CrossRef]
- Rajan, P.K.; Reddy, H.C. Hyper chaos: Laboratory experiment and numerical confirmation. IEEE Trans. Circuits Syst. 1986, 33, 1143–1147. [Google Scholar]
- Liu, L.; Zhang, Z.; Chen, R. Cryptanalysis and Improvement in a Plaintext-Related Image Encryption Scheme Based on Hyper Chaos. IEEE Access 2019, 7, 126450–126463. [Google Scholar] [CrossRef]
- Tamang, J.; Nkapkop, J.D.D.; Ijaz, M.F.; Prasad, P.K.; Tsafack, N.; Saha, A.; Kengne, J.; Son, Y. Dynamical Properties of Ion-Acoustic Waves in Space Plasma and Its Application to Image Encryption. IEEE Access 2021, 9, 18762–18782. [Google Scholar] [CrossRef]
- Inzunza-González, E.; Cruz-Hernández, C. Double Hyperchaotic Encryption for Security in Biometric Systems. Nonlinear Dyn. Syst. Theory 2013, 13, 55–68. [Google Scholar]
- Zhu, C.; Wang, G.; Sun, K. Cryptanalysis and improvement on an image encryption algorithm design using a novel chaos based s-box. Symmetry 2018, 10, 399. [Google Scholar] [CrossRef]
- Nkapkop, J.D.; Effa, J.Y.; Borda, M.; Terebes, R. A Novel Fast and Secure Chaos-Based Algorithm for Image Encryption. In Innovative Security Solutions for Information Technology and Communications; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2015; pp. 87–101. [Google Scholar] [CrossRef]
- Alawida, M.; Teh, J.S.; Samsudin, A.; Alshoura, W.H. An image encryption scheme based on hybridizing digital chaos and finite state machine. Signal Process. 2019, 164, 249–266. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y. Image encryption using 2D Logistic-adjusted-Sine map. Inf. Sci. 2016, 339, 237–253. [Google Scholar] [CrossRef]
- Gupta, K.; Silakari, S. New Approach for Fast Color Image Encryption Using Chaotic Map. J. Inf. Secur. 2011, 2, 139–150. [Google Scholar] [CrossRef]
- Gao, X.; Mou, J.; Xiong, L.; Sha, Y.; Yan, H.; Cao, Y. A fast and efficient multiple images encryption based on single-channel encryption and chaotic system. Nonlinear Dyn. 2022, 108, 613–636. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Q. A novel image encryption algorithm based on dynamic S-boxes constructed by chaos. Nonlinear Dyn. 2014, 75, 567–576. [Google Scholar] [CrossRef]
- Nalini, M.K.; Radhika, K.R. Encryption on Multimodal Biometric using Hyper Chaotic Method and Inherent Binding Technique. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 630–642. [Google Scholar]
- Nestor, T.; De Dieu, N.J.; Jacques, K.; Yves, E.J.; Iliyasu, A.M.; El-Latif, A.A.A. A multidimensional hyperjerk oscillator: Dynamics analysis, analogue and embedded systems implementation, and its application as a cryptosystem. Sensors 2020, 20, 83. [Google Scholar] [CrossRef] [PubMed]
- Gupta, M.; Singh, V.P.; Gupta, K.K.; Shukla, P.K. An efficient image encryption technique based on two-level security for internet of things. Multimed. Tools Appl. 2023, 82, 5091–5111. [Google Scholar] [CrossRef]
- Bao, H.; Hua, Z.Y.; Liu, W.B.; Bao, B.C. Discrete memristive neuron model and its interspike interval-encoded application in image encryption. Sci. China Technol. Sci. 2021, 64, 2281–2291. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Q.; Liu, H.; Ren, Y.; Zhang, J.; Zhang, S.; Qian, K.; Wen, H. Exploiting Newly Designed Fractional-Order 3D Lorenz Chaotic System and 2D Discrete Polynomial Hyper-Chaotic Map for High-Performance Multi-Image Encryption. Fractal Fract. 2023, 7, 887. [Google Scholar] [CrossRef]
- Jithin, K.C.; Sankar, S. Colour image encryption algorithm combining Arnold map, DNA sequence operation, and a Mandelbrot set. J. Inf. Secur. Appl. 2020, 50, 102428. [Google Scholar] [CrossRef]
- Ma, K.; Lin, T.; Xingyuan, W.; Juan, M. Color image encryption scheme based on the combination of the fisher-yates scrambling algorithm and chaos theory. Multimed. Tools Appl. 2021, 80, 24737–24757. [Google Scholar] [CrossRef]
- Biometrics Ideal Test. Available online: http://biometrics.idealtest.org/dbDetailForUser.do?id=4 (accessed on 9 April 2023).








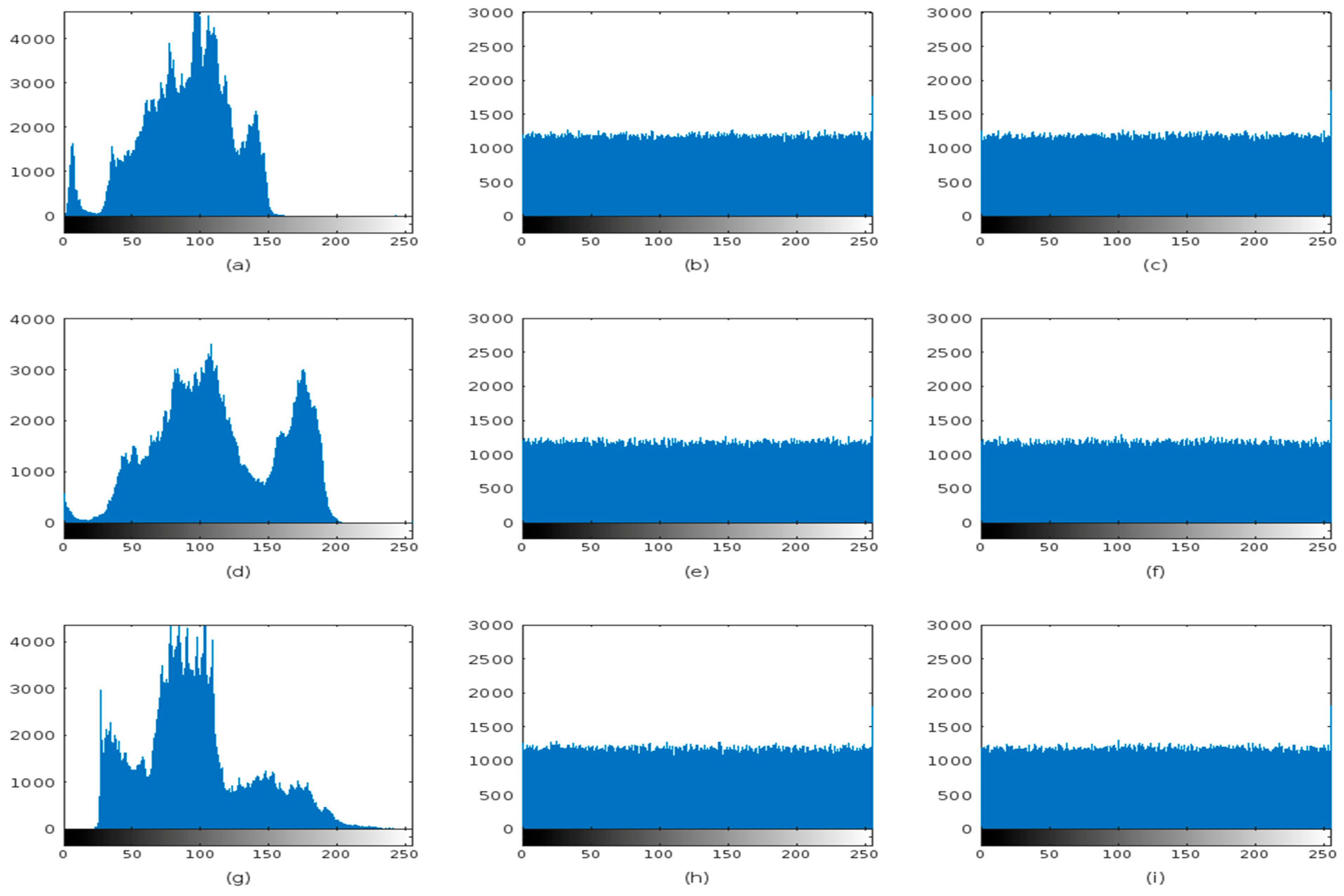



| Test Name | Result | ||
|---|---|---|---|
| Frequency (Monobit) Test | 0.0375 | 0.8103 | Pass–Random |
| Block Frequency Test | 0.7509 | 0.3084 | Pass–Random |
| Runs Test | 0.7632 | 0.4023 | Pass–Random |
| Longest Run of Ones in a Block Test | 0.4252 | 0.0215 | Pass–Random |
| Binary Matrix Rank Test | 0.6883 | 0.5895 | Pass–Random |
| Discrete Fourier Transform (Spectral) Test | 0.5318 | 0.7420 | Pass–Random |
| Non-overlapping Template Matching Test | 0.4654 | 0.8026 | Pass–Random |
| Overlapping Template Matching Test | 0.6917 | 0.9102 | Pass–Random |
| Maurer’s Universal Statistical Test | 0.4965 | 0.5782 | Pass–Random |
| Linear Complexity Test | 0.8346 | 0.7831 | Pass–Random |
| Serial Test | 0.0491 | 0.1749 | Pass–Random |
| Approximate Entropy Test | 0.9704 | 0.1690 | Pass–Random |
| Cumulative Sums (Cusum) Test | 0.9998 | 0.1045 | Pass–Random |
| Random Excursions Test | 0.9992 | 0.0916 | Pass–Random |
| Random Excursions Variant Test | 0.9985 | 0.8342 | Pass–Random |
| Chaotic System | Precision | Number of Parameter and Initial Conditions | Key Space |
|---|---|---|---|
| Ours | 20 | ||
| Ref. [40] | 8 | ||
| Ref. [36] | 10 | ||
| Ref. [26] | 5 | ||
| Ref. [41] | 14 |
| Chaotic System | Correlation Coefficients | ||
|---|---|---|---|
| Horizontal | Vertical | Diagonal | |
| Ours | 0.0072 | 0.0046 | 0.0063 |
| Ref. [36] | 0.0105 | −0.0019 | −0.0019 |
| Ref. [40] | 0.0206 | 0.0003 | −0.0141 |
| Ref. [41] | −0.0082 | 0.0073 | 0.0089 |
| Ref. [44] | 0.0003 | 0.0009 | 0.019 |
| Ref. [45] | 0.0011 | 0.0012 | 0.016 |
| Ref. [46] | 0.004 | 0.007 | 0.037 |
| Proposed | Ref. [36] | Ref. [40] | Ref. [43] | Ref. [47] | Ref. [48] | Ref. [49] |
|---|---|---|---|---|---|---|
| 7.9988 | 7.9983 | 7.9998 | 7.9996 | 7.9993 | 7.9971 | 7.7795 |
| Proposed | Ref. [26] | Ref. [36] | Ref. [40] | Ref. [44] | Ref. [47] | Ref. [49] | Ref. [51] | |
|---|---|---|---|---|---|---|---|---|
| NPCR (%) | 99.629 | 99.658 | 99.810 | 99.715 | 99.603 | 99.614 | 99.510 | 99.630 |
| UACI (%) | 33.441 | 33.459 | 33.400 | 33.511 | 33.692 | 33.466 | 33.160 | 33.480 |
| Algorithms | Image Size | Encryption Time in s | Decryption Time in s |
|---|---|---|---|
| Ours | 512 × 512 | 0.8763 | 1.0910 |
| 256 × 256 | 0.50913 | 0.5219 | |
| Ref. [26] | 512 × 512 | 2.727 | 2.708 |
| 256 × 256 | 0.941 | 0.902 | |
| Ref. [39] | 512 × 512 | 0.951 | - |
| - | - | - | |
| Ref. [44] | 512 × 512 | 0.5156 | - |
| 256 × 256 | 0.1272 | - | |
| Ref. [45] | 512 × 512 | - | - |
| 256 × 256 | 0.8342 | - | |
| Ref. [54] | 512 × 512 | 16.43 | - |
| 256 × 256 | 8.2 | - | |
| Ref. [55] | 512 × 512 | 25.867 | 24.564 |
| 256 × 256 | 6.494 | 6.471 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lisungu Oteko, T.; Ogudo, K.A. Dual Chaotic Diffusion Framework for Multimodal Biometric Security Using Qi Hyperchaotic System. Symmetry 2025, 17, 1231. https://doi.org/10.3390/sym17081231
Lisungu Oteko T, Ogudo KA. Dual Chaotic Diffusion Framework for Multimodal Biometric Security Using Qi Hyperchaotic System. Symmetry. 2025; 17(8):1231. https://doi.org/10.3390/sym17081231
Chicago/Turabian StyleLisungu Oteko, Tresor, and Kingsley A. Ogudo. 2025. "Dual Chaotic Diffusion Framework for Multimodal Biometric Security Using Qi Hyperchaotic System" Symmetry 17, no. 8: 1231. https://doi.org/10.3390/sym17081231
APA StyleLisungu Oteko, T., & Ogudo, K. A. (2025). Dual Chaotic Diffusion Framework for Multimodal Biometric Security Using Qi Hyperchaotic System. Symmetry, 17(8), 1231. https://doi.org/10.3390/sym17081231







