Truncation Error Bounds for Branched Continued Fraction Expansions of Some Appell’s Hypergeometric Functions F2
Abstract
1. Introduction
2. Truncation Error Bounds
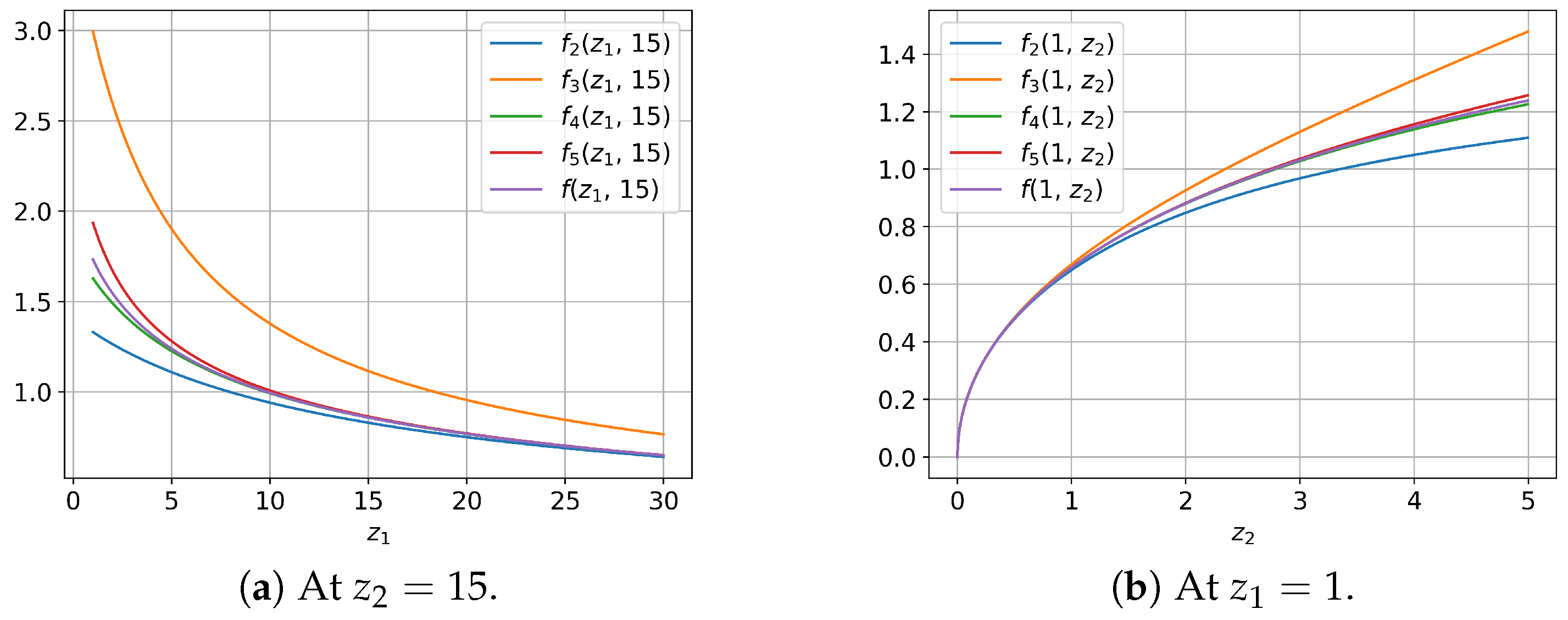
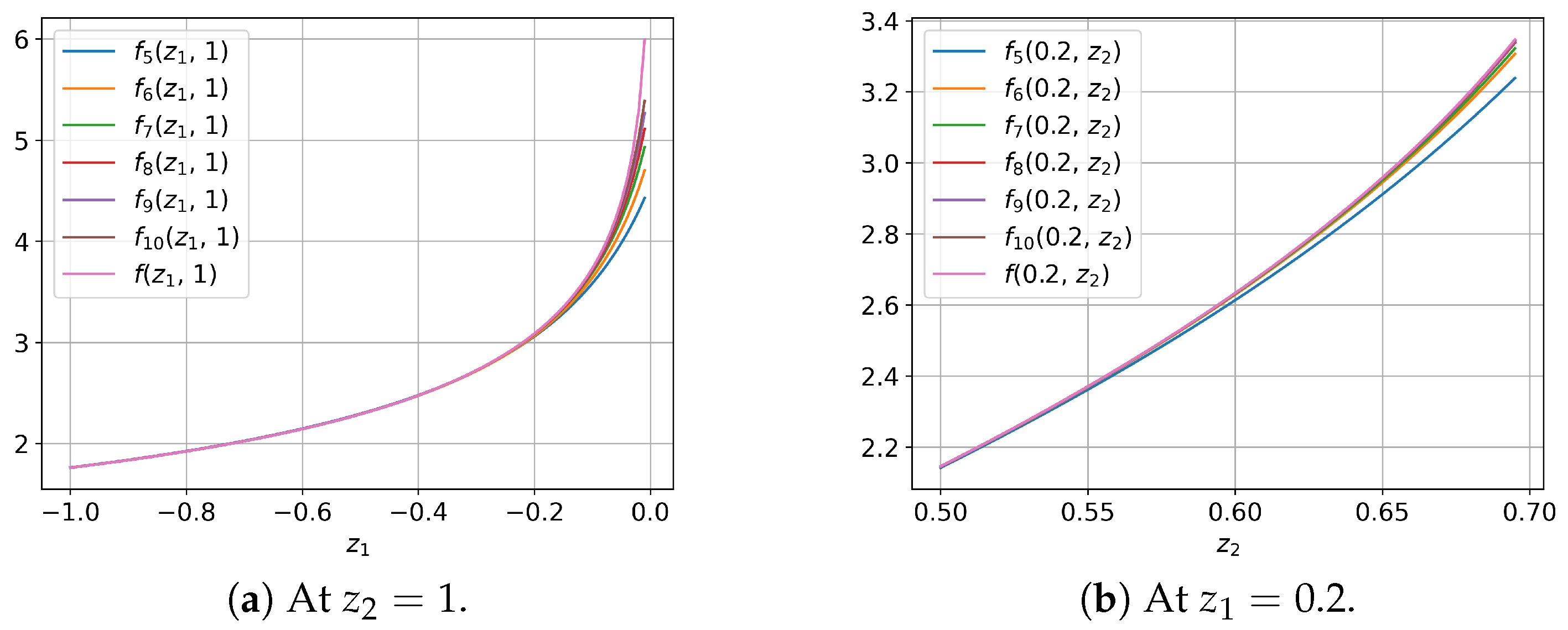
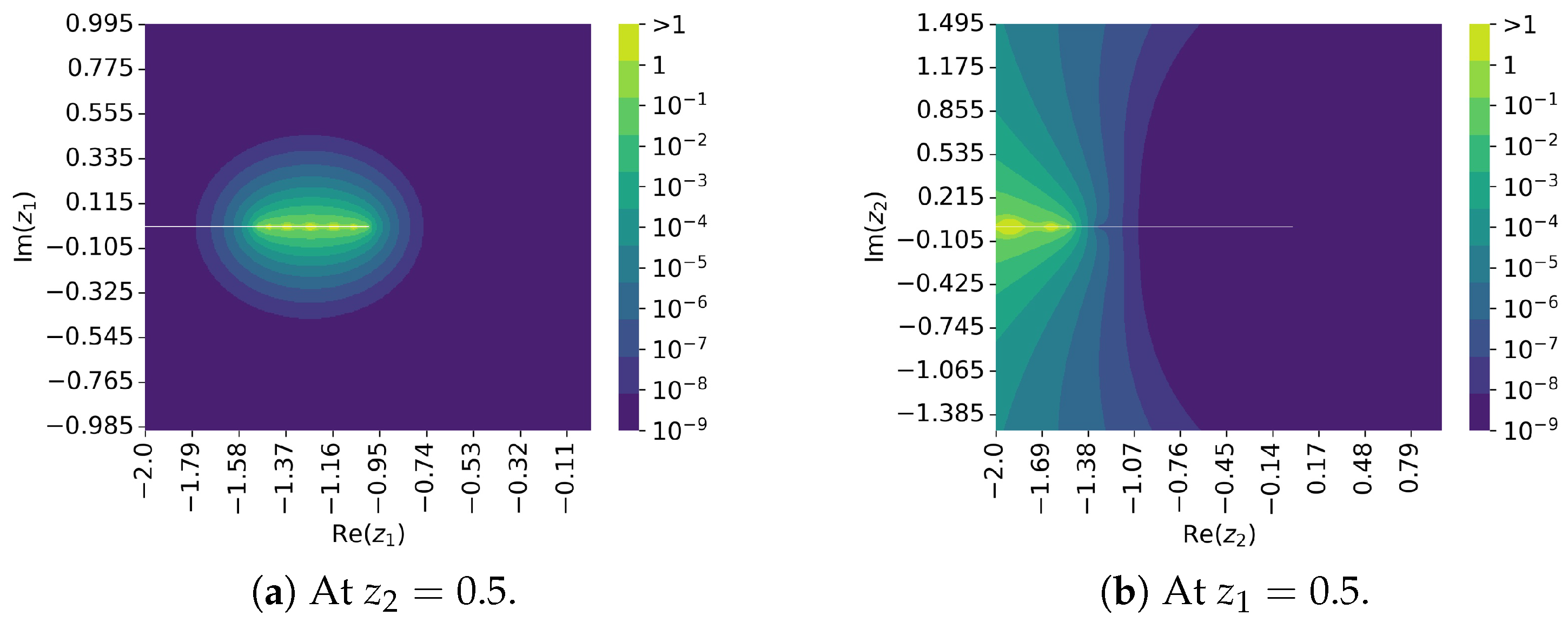
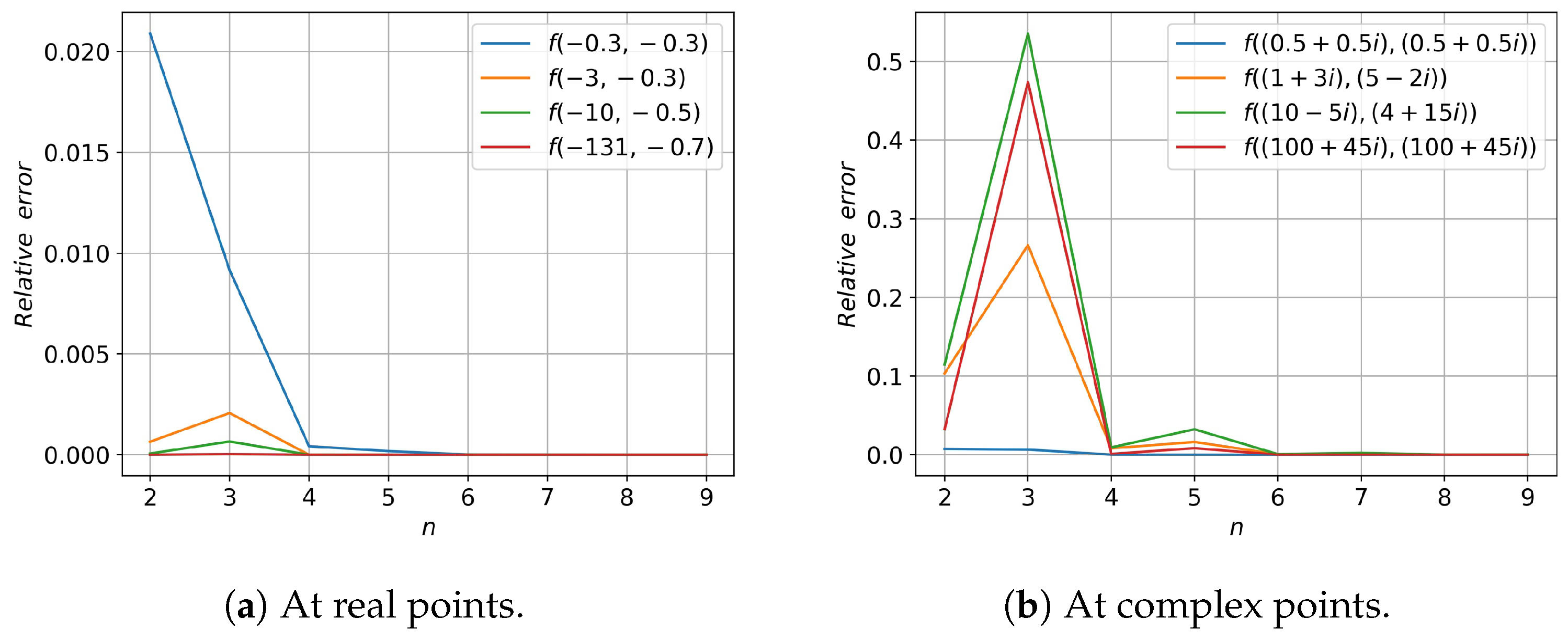
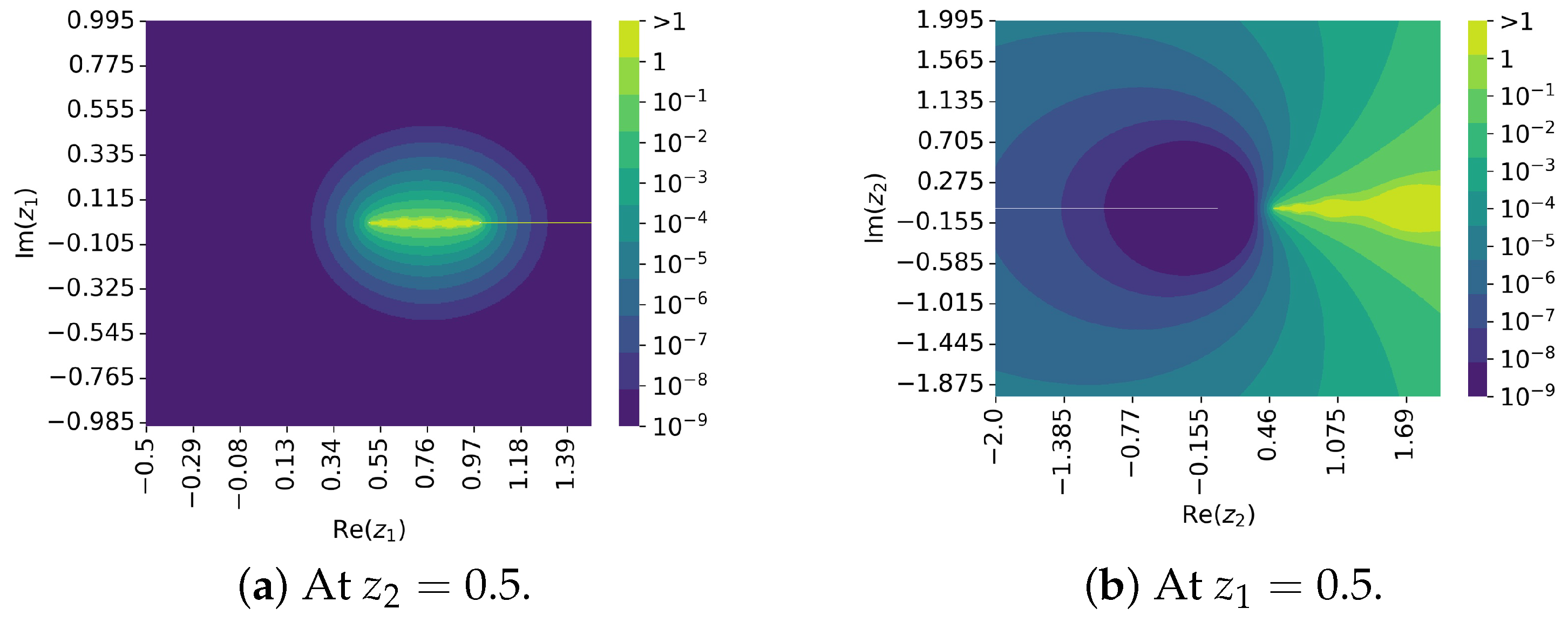
3. Numerical Experiments
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Exton, H. Multiple Hypergeometric Functions and Applications; Horwood, E., Ed.; Halsted Press: Chichester, UK, 1976. [Google Scholar]
- Seaborn, J.B. Hypergeometric Functions and Their Applications; Springer: New York, NY, USA, 1991. [Google Scholar]
- Appell, P. Sur les séries hyper géométriques de deux variables et sur des équations différentielles lineaires aux dérivées partielles. C. R. Acad. Sci. 1880, 90, 296–298+731–734. [Google Scholar]
- Appell, P. Sur les fonctions hyper géométriques de deux variables. J. Math. Pures Appl. 1982, 8, 173–216. [Google Scholar]
- Hang, P.-C.; Luo, M.-J. Asymptotics of Saran’s hypergeometric function FK. J. Math. Anal. Appl. 2025, 541, 128707. [Google Scholar] [CrossRef]
- Muneera, A.Q.; Sarah, A.Q. Solution of fractional kinetic equations involving new extended incomplete second Appell hypergeometric matrix functions. J. Funct. Spaces 2025, 2025, 9578749. [Google Scholar] [CrossRef]
- Bentalha, Z. A new formula for Coulomb matrix elements in the lowest Landau level in disk geometry. Phys. Scr. 2025, 100, 051501. [Google Scholar] [CrossRef]
- Caamaño-Carrillo, C.; Bevilacqua, M.; Zamudio-Monserratt, M.; Contreras-Reyes, J.E. Bivariate Pareto-Feller distribution based on Appell hypergeometric function. Axioms 2024, 13, 701. [Google Scholar] [CrossRef]
- Gauss, C.F. Disquisitiones generales circa seriem infinitam In Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores; Classis Mathematicae, 1812; H. Dieterich: Gottingae, Germany, 1813; Volume 2, pp. 3–46. [Google Scholar]
- Dmytryshyn, R.; Cesarano, C.; Lutsiv, I.-A.; Dmytryshyn, M. Numerical stability of the branched continued fraction expansion of Horn’s hypergeometric function H4. Mat. Stud. 2024, 61, 51–60. [Google Scholar] [CrossRef]
- Hladun, V.; Rusyn, R.; Dmytryshyn, M. On the analytic extension of three ratios of Horn’s confluent hypergeometric function H7. Res. Math. 2024, 32, 60–70. [Google Scholar] [CrossRef] [PubMed]
- Bodnar, D.I. Expansion of a ratio of hypergeometric functions of two variables in branching continued fractions. J. Math. Sci. 1993, 64, 1155–1158. [Google Scholar] [CrossRef]
- Bilanyk, I.B.; Bodnar, D.I.; Vozniak, O.G. Convergence criteria of branched continued fractions. Res. Math. 2024, 32, 53–69. [Google Scholar] [CrossRef] [PubMed]
- Bodnar, D.I.; Bodnar, O.S.; Dmytryshyn, M.V.; Popov, M.M.; Martsinkiv, M.V.; Salamakha, O.B. Research on the convergence of some types of functional branched continued fractions. Carpathian Math. Publ. 2024, 16, 448–460. [Google Scholar] [CrossRef]
- Antonova, T. On structure of branched continued fractions. Carpathian Math. Publ. 2024, 16, 391–400. [Google Scholar] [CrossRef]
- Antonova, T.; Cesarano, C.; Dmytryshyn, R.; Sharyn, S. An approximation to Appell’s hypergeometric function F2 by branched continued fraction. Dolomites Res. Notes Approx. 2024, 17, 22–31. [Google Scholar] [CrossRef]
- Dmytryshyn, R. On the analytic continuation of Appell’s hypergeometric function F2 to some symmetric domains in the space . Symmetry 2024, 16, 1480. [Google Scholar] [CrossRef]
- Antonova, T.; Dmytryshyn, R.; Sharyn, S. Branched continued fraction representations of ratios of Horn’s confluent function H6. Constr. Math. Anal. 2023, 6, 22–37. [Google Scholar] [CrossRef]
- Hladun, V.R.; Dmytryshyn, M.V.; Kravtsiv, V.V.; Rusyn, R.S. Numerical stability of the branched continued fraction expansions of the ratios of Horn’s confluent hypergeometric functions H6. Math. Model. Comput. 2024, 11, 1152–1166. [Google Scholar] [CrossRef]
- Antonova, T.M.; Dmytryshyn, R.I. Truncation error bounds for branched continued fraction whose partial denominators are equal to unity. Mat. Stud. 2020, 54, 3–14. [Google Scholar] [CrossRef]
- Bodnar, D.I. Branched Continued Fractions; Naukova Dumka: Kyiv, Ukraine, 1986. [Google Scholar]
- Jones, W.B.; Thron, W.J. Continued Fractions: Analytic Theory and Applications; Addison-Wesley Pub. Co.: Reading, MA, USA, 1980. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables; U.S. Government Printing Office, NBS: Washington, DC, USA, 1964.
- Schlosser, M.J. Multiple Hypergeometric Series: Appell Series and Beyond. In Computer Algebra in Quantum Field Theory: Integration, Summation and Special Functions; Schneider, C., Blümlein, J., Eds.; Springer: Vienna, Austria, 2013; pp. 305–324. [Google Scholar] [CrossRef]
- Hladun, V.R.; Bodnar, D.I.; Rusyn, R.S. Convergence sets and relative stability to perturbations of a branched continued fraction with positive elements. Carpathian Math. Publ. 2024, 16, 16–31. [Google Scholar] [CrossRef]
- Hladun, V.R. Some sets of relative stability under perturbations of branched continued fractions with complex elements and a variable number of branches. J. Math. Sci. 2016, 215, 11–25. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dmytryshyn, R. Truncation Error Bounds for Branched Continued Fraction Expansions of Some Appell’s Hypergeometric Functions F2. Symmetry 2025, 17, 1204. https://doi.org/10.3390/sym17081204
Dmytryshyn R. Truncation Error Bounds for Branched Continued Fraction Expansions of Some Appell’s Hypergeometric Functions F2. Symmetry. 2025; 17(8):1204. https://doi.org/10.3390/sym17081204
Chicago/Turabian StyleDmytryshyn, Roman. 2025. "Truncation Error Bounds for Branched Continued Fraction Expansions of Some Appell’s Hypergeometric Functions F2" Symmetry 17, no. 8: 1204. https://doi.org/10.3390/sym17081204
APA StyleDmytryshyn, R. (2025). Truncation Error Bounds for Branched Continued Fraction Expansions of Some Appell’s Hypergeometric Functions F2. Symmetry, 17(8), 1204. https://doi.org/10.3390/sym17081204