Voxel-Based Asymptotic Homogenization of the Effective Thermal Properties of Lattice Materials with Generic Bravais Lattice Symmetry
Abstract
1. Introduction
2. Methodology
2.1. Representative Volume Element
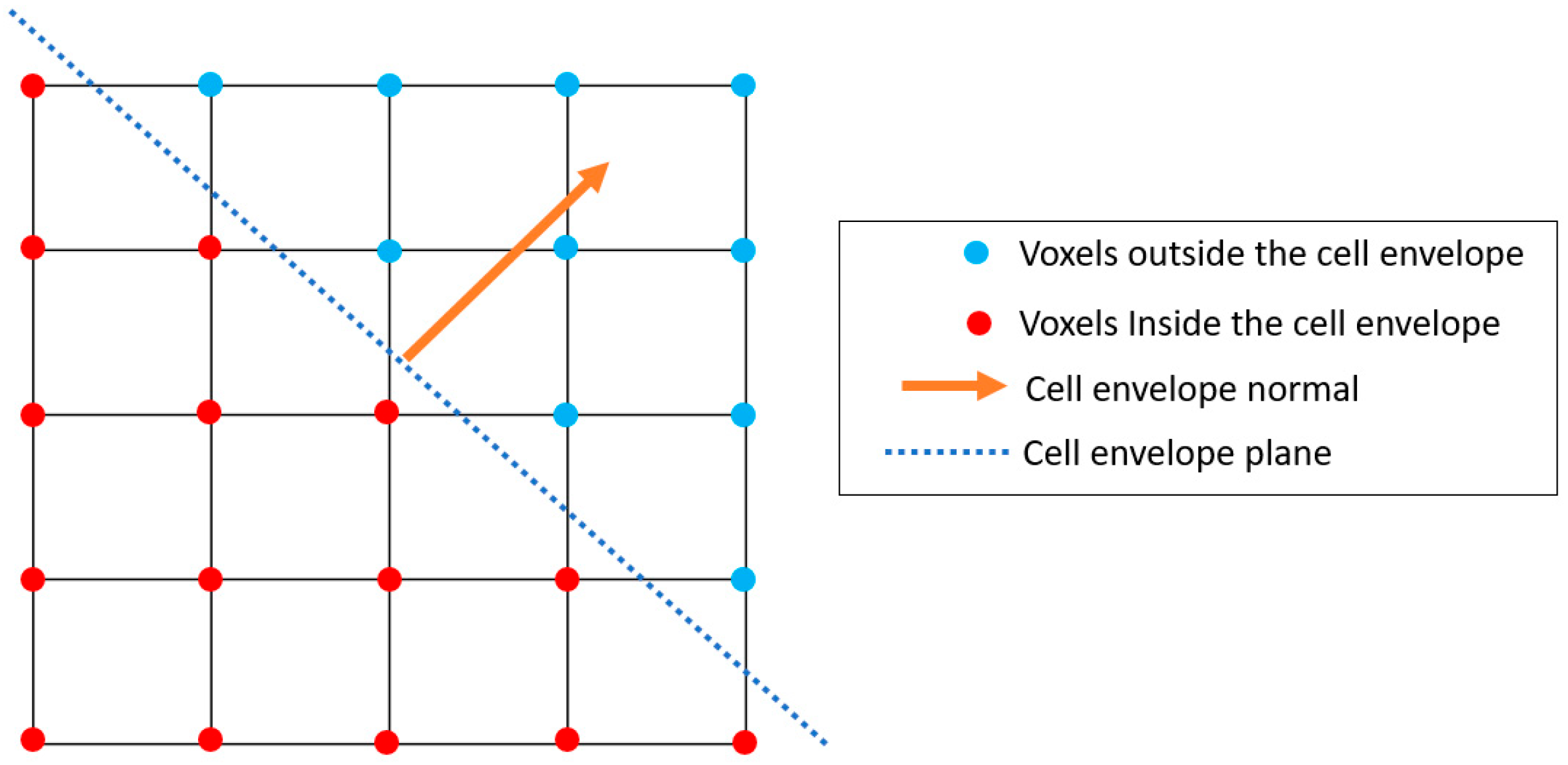
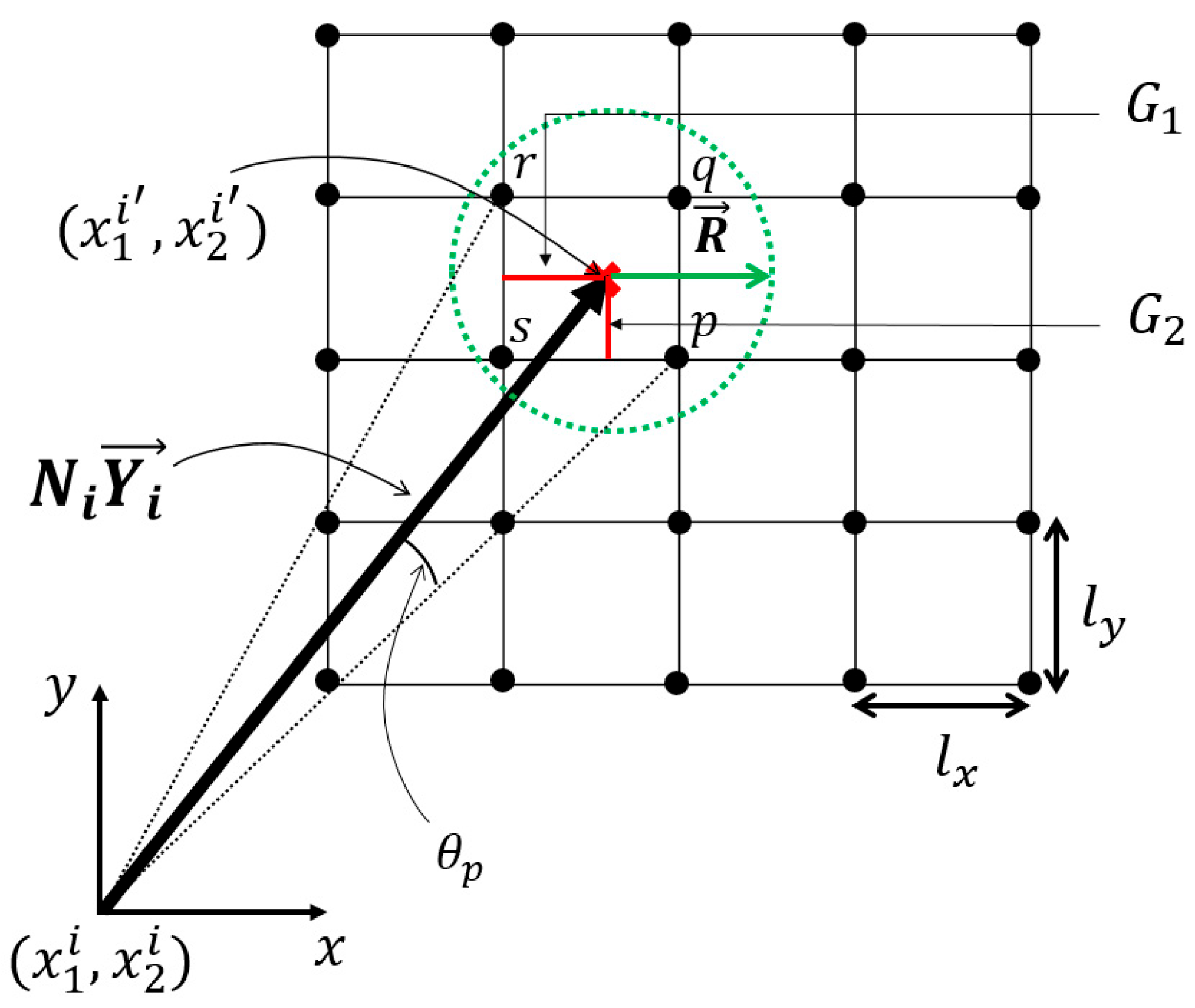
2.2. Discretization and Approximation of the Periodic Boundary Condition
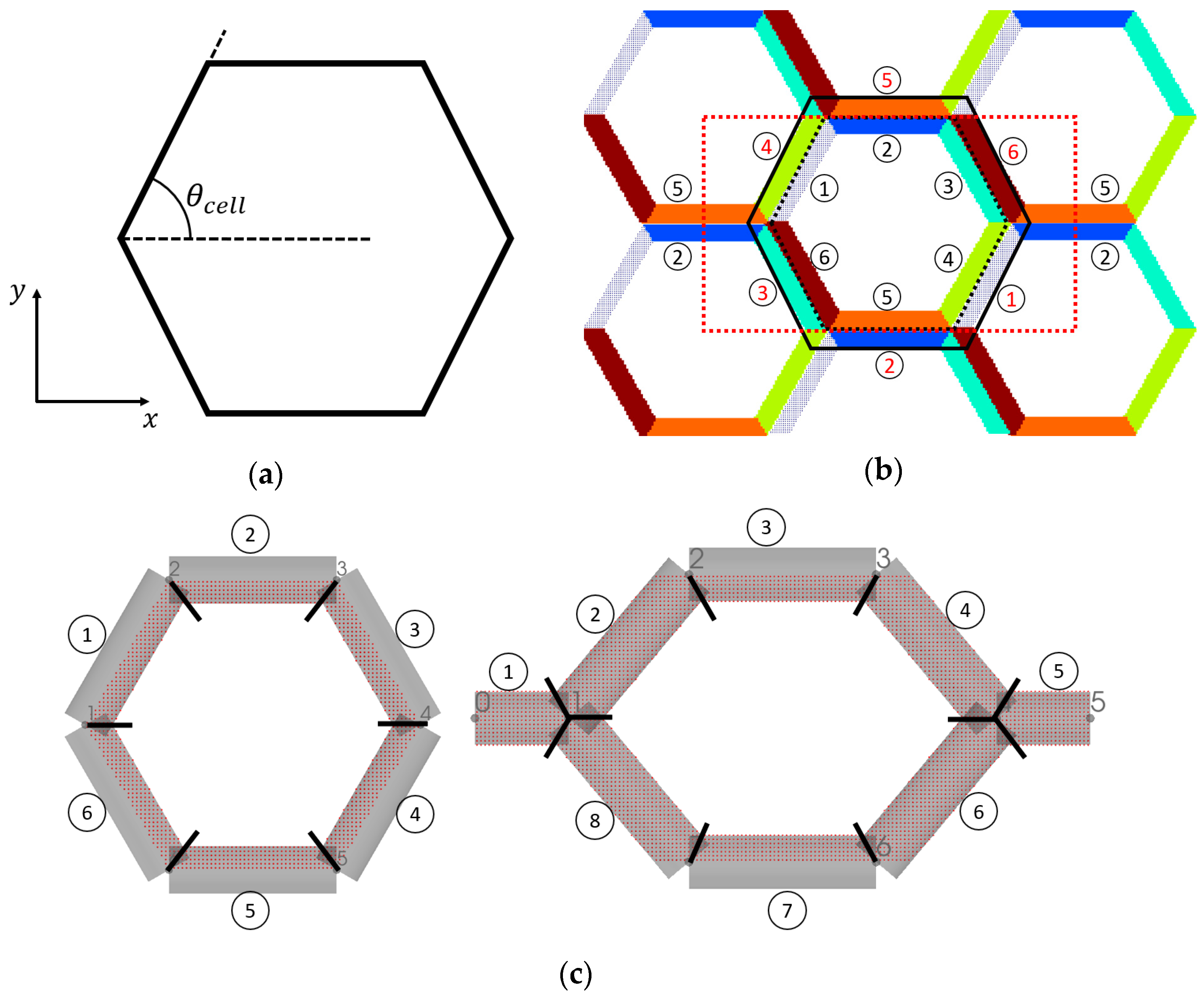
2.3. Multi-Material Assignment to a Discretized Lattice Structure
2.4. Asymptotic Homogenization
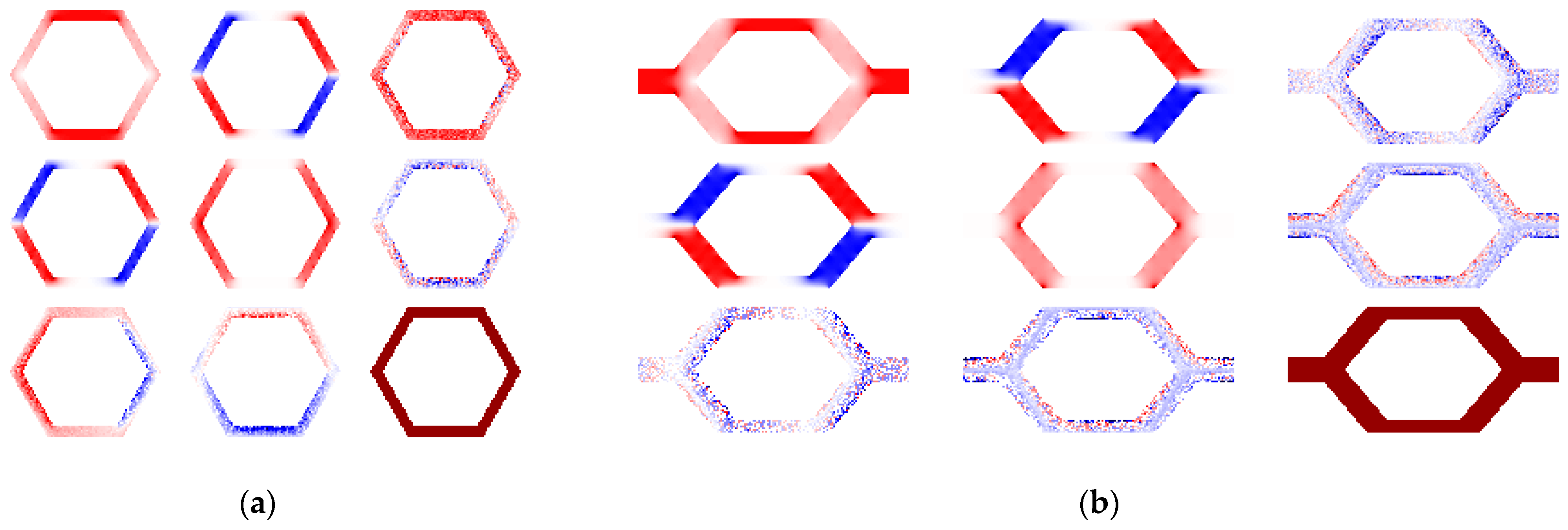
2.4.1. Thermal Expansion Homogenization
2.4.2. Thermal Conduction Homogenization
3. Verification and Validation
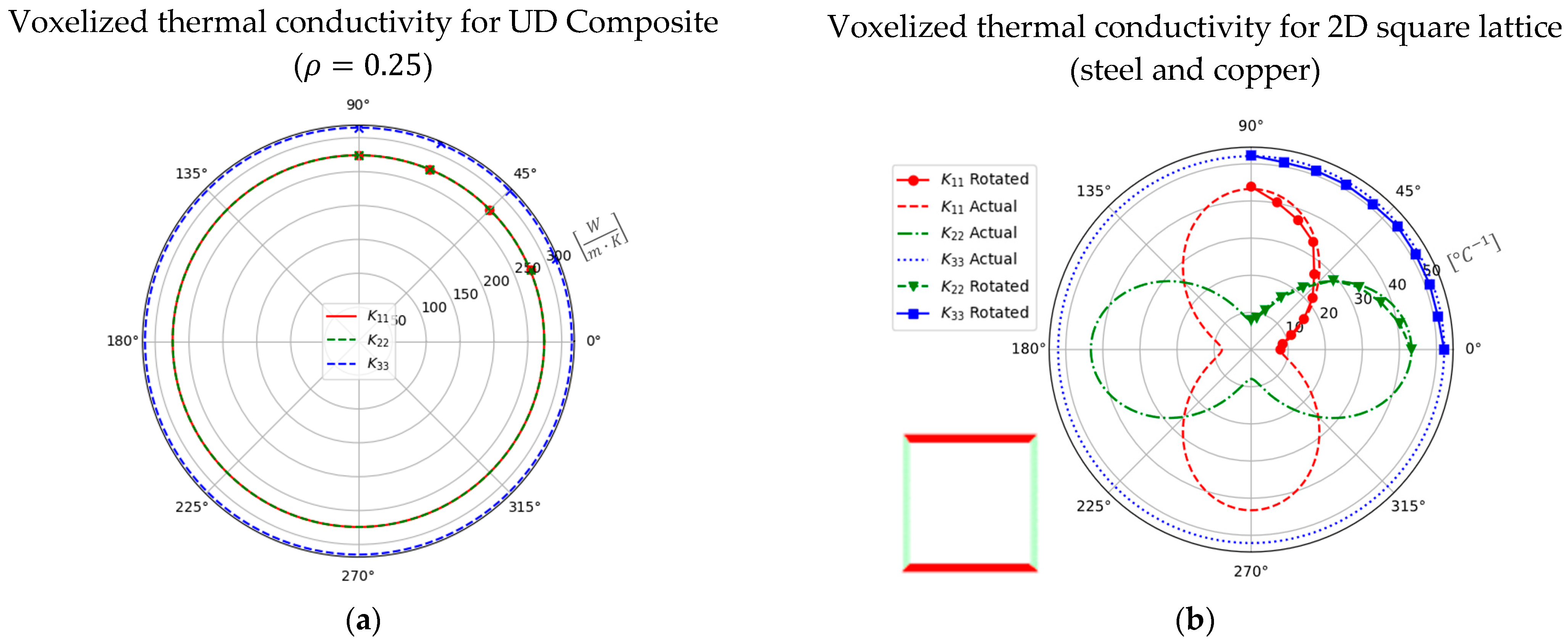
3.1. Uni-Directional Composite
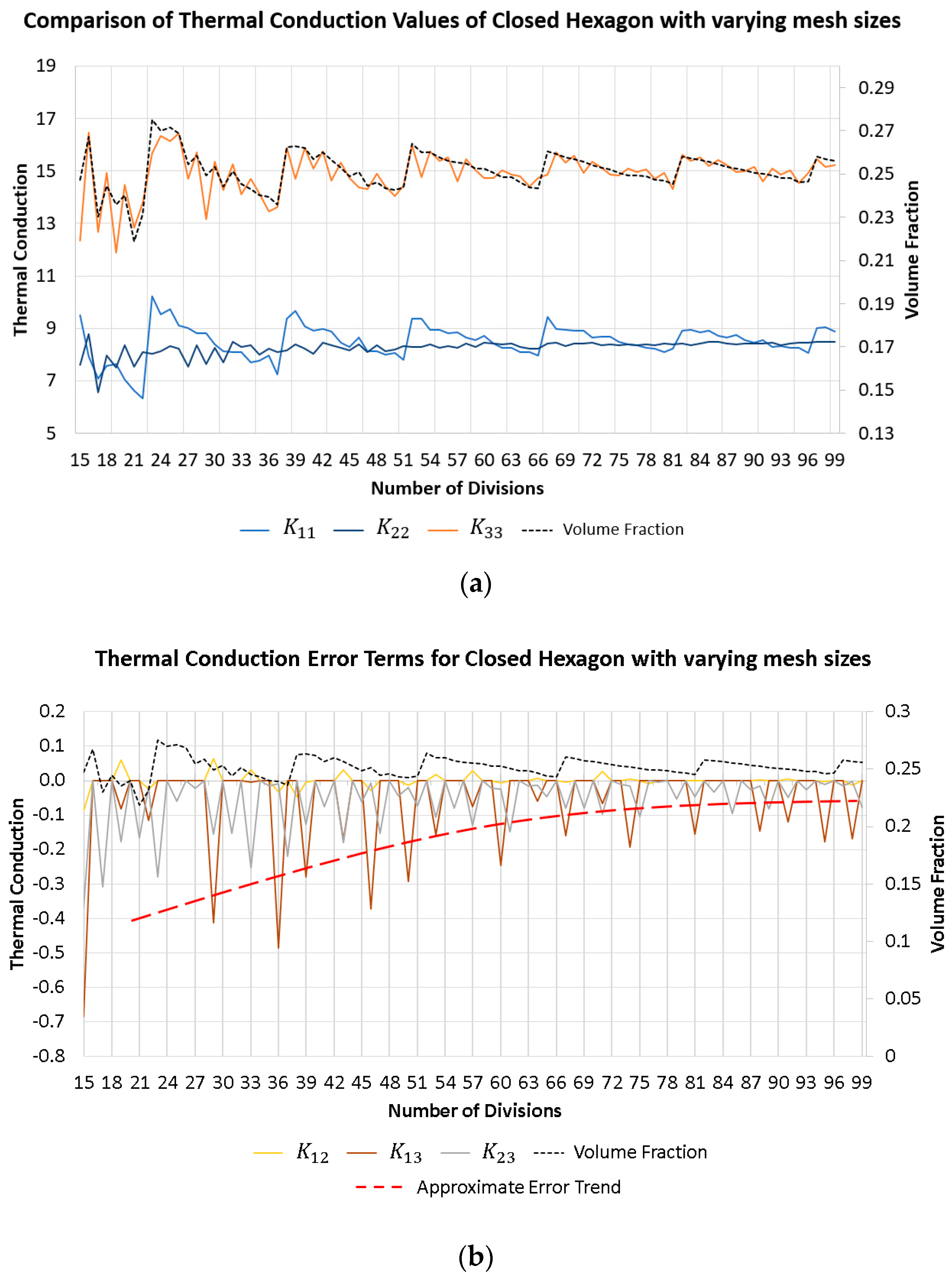
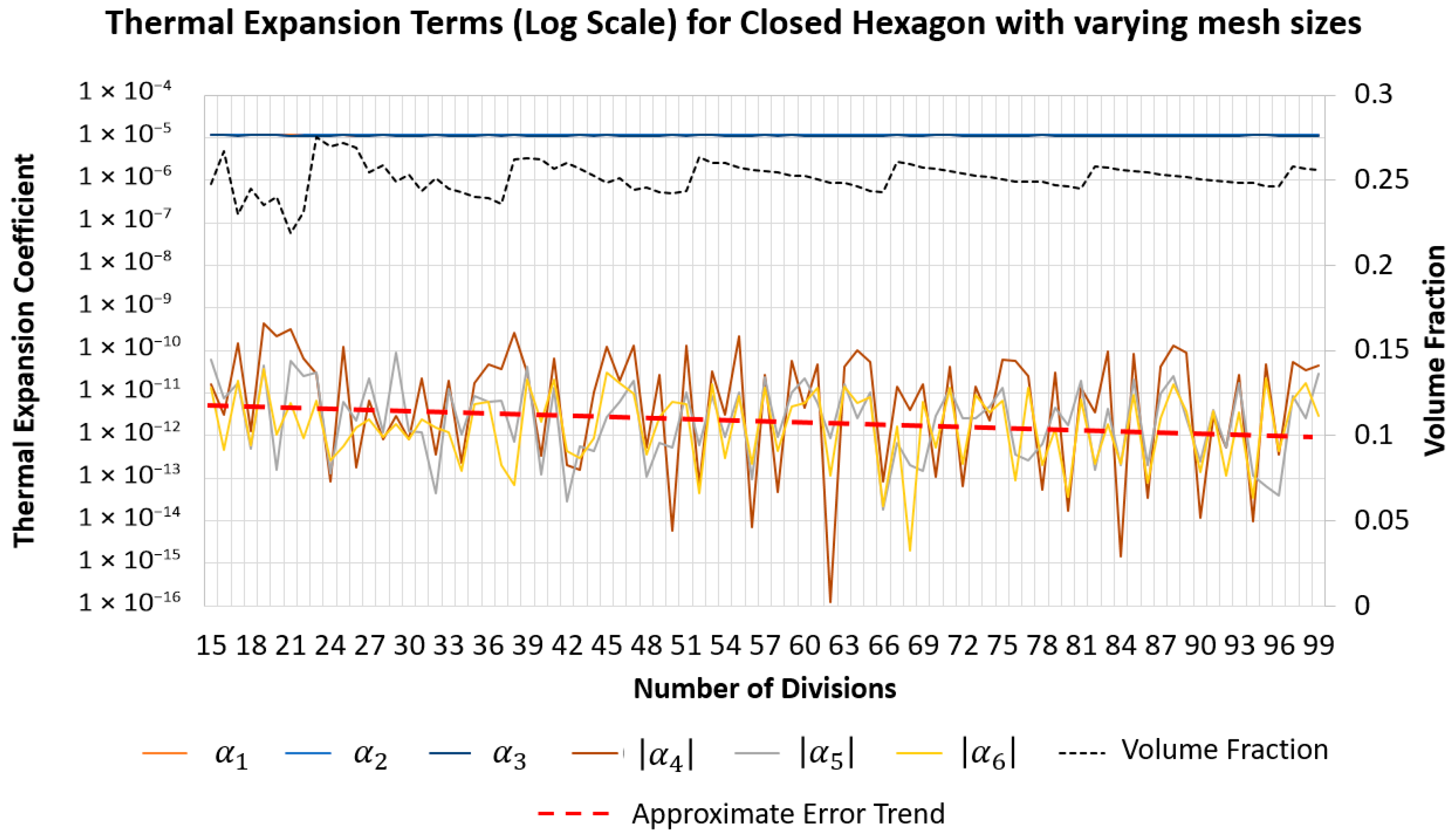
3.2. Grid Convergence
3.3. Numerical Errors Due to Approximating Periodicity
4. Results and Discussion
4.1. Variation in Thermal Expansion w.r.t Cell Angle for Multiple Material Configuration
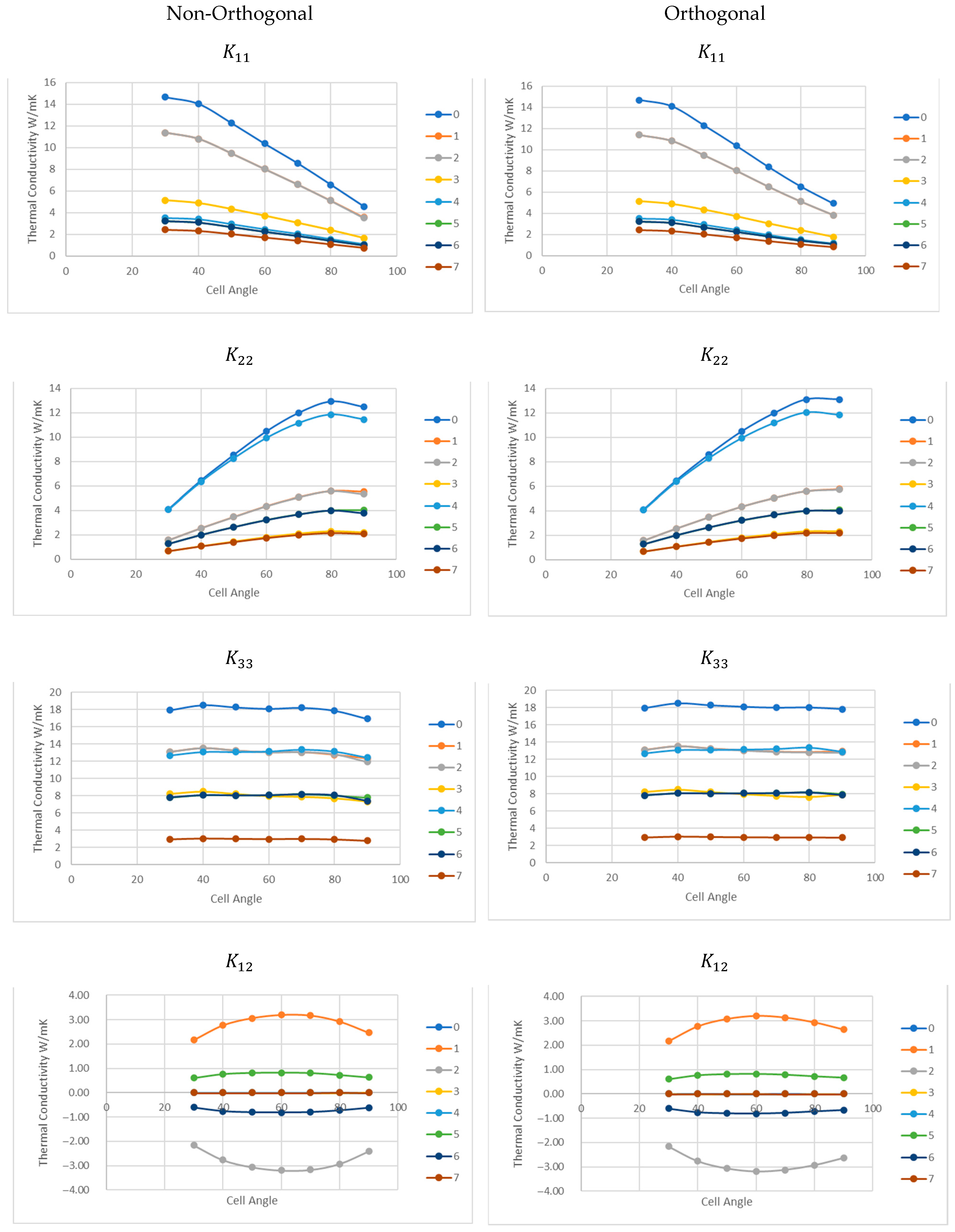
4.2. Variation in Thermal Conduction w.r.t Cell Angle for Multiple Material Configuration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sigmund, O.; Torquato, S. Design of Materials with Extreme Thermal Expansion Using a Three-Phase Topology Optimization Method. J. Mech. Phys. Solids 1997, 45, 1037–1067. [Google Scholar] [CrossRef]
- Xu, H.; Pasini, D. Structurally Efficient Three-Dimensional Metamaterials with Controllable Thermal Expansion. Sci. Rep. 2016, 6, 34924. [Google Scholar] [CrossRef]
- Chen, J.; Xu, W.; Wei, Z.; Wei, K.; Yang, X. Stiffness Characteristics for a Series of Lightweight Mechanical Metamaterials with Programmable Thermal Expansion. Int. J. Mech. Sci. 2021, 202–203, 106527. [Google Scholar] [CrossRef]
- Grima, J.N.; Farrugia, P.S.; Gatt, R.; Zammit, V. A System with Adjustable Positive or Negative Thermal Expansion. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 1585–1596. [Google Scholar] [CrossRef]
- Holmén, A. Multi-Metamaterial Composites: Kelvin Cell Derivatives in Pursuit of Low Thermal Expansion and Poisson’s Ratio. Master’s Thesis, KTH, Royal Institute of Technology, Stockholm, Sweden, 2025. [Google Scholar]
- Wang, Q.; Jackson, J.A.; Ge, Q.; Hopkins, J.B.; Spadaccini, C.M.; Fang, N.X. Lightweight Mechanical Metamaterials with Tunable Negative Thermal Expansion. Phys. Rev. Lett. 2016, 117, 175901. [Google Scholar] [CrossRef]
- Dubey, D.; Mirhakimi, A.S.; Elbestawi, M.A. Negative Thermal Expansion Metamaterials: A Review of Design, Fabrication, and Applications. J. Manuf. Mater. Process. 2024, 8, 40. [Google Scholar] [CrossRef]
- Ni, X.; Guo, X.; Li, J.; Huang, Y.; Zhang, Y.; Rogers, J.A. 2D Mechanical Metamaterials with Widely Tunable Unusual Modes of Thermal Expansion. Adv. Mater. 2019, 31, e1905405. [Google Scholar] [CrossRef]
- Askar, A.; Cakmak, A.S.S. A Structural Model of a Micropolar Continuum. Int. J. Eng. Sci. 1968, 6, 583–589. [Google Scholar] [CrossRef]
- Chen, J.Y.; Huang, Y.; Ortiz, M. Fracture Analysis of Cellular Materials: A Strain Gradient Model. J. Mech. Phys. Solids 1998, 46, 789–828. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Christensen, M. Analogy between Micropolar Continuum and Grid Frameworks under Initial Stress. Int. J. Solids Struct. 1972, 8, 327–346. [Google Scholar] [CrossRef]
- Kumar, R.S.; McDowell, D.L. Generalized Continuum Modeling of 2-D Periodic Cellular Solids. Int. J. Solids Struct. 2004, 41, 7399–7422. [Google Scholar] [CrossRef]
- van Tuijl, R.A.; Remmers, J.J.C.; Geers, M.G.D. Multi-Dimensional Wavelet Reduction for the Homogenisation of Microstructures. Comput. Methods Appl. Mech. Eng. 2019, 359, 112652. [Google Scholar] [CrossRef]
- Vigliotti, A.; Pasini, D. Mechanical Properties of Hierarchical Lattices. Mech. Mater. 2013, 62, 32–43. [Google Scholar] [CrossRef]
- Hutchinson, R.G.; Fleck, N.A. The Structural Performance of the Periodic Truss. J. Mech. Phys. Solids 2006, 54, 756–782. [Google Scholar] [CrossRef]
- Elsayed, M.S.A.; Pasini, D. Analysis of the Elastostatic Specific Stiffness of 2D Stretching-Dominated Lattice Materials. Mech. Mater. 2010, 42, 709–725. [Google Scholar] [CrossRef]
- Vigliotti, A.; Pasini, D. Linear Multiscale Analysis and Finite Element Validation of Stretching and Bending Dominated Lattice Materials. Mech. Mater. 2012, 46, 57–68. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, W. Energy-Based Homogenization Method for Lattice Structures with Generalized Periodicity. Comput. Struct. 2024, 302, 107478. [Google Scholar] [CrossRef]
- Yu, B.; Xu, Z.; Mu, R.; Wang, A.; Zhao, H. Design of Large-Scale Space Lattice Structure with Near-Zero Thermal Expansion Metamaterials. Aerospace 2023, 10, 294. [Google Scholar] [CrossRef]
- Florence, C.; Sab, K. A Rigorous Homogenization Method for the Determination of the Overall Ultimate Strength of Periodic Discrete Media and an Application to General Hexagonal Lattices of Beams. Eur. J. Mech. A/Solids 2006, 25, 72–97. [Google Scholar] [CrossRef]
- Assidi, M.; Dos Reis, F.; Ganghoffer, J.-F. Equivalent Mechanical Properties of Biological Membranes from Lattice Homogenization. J. Mech. Behav. Biomed. Mater. 2011, 4, 1833–1845. [Google Scholar] [CrossRef]
- Dos Reis, F.; Ganghoffer, J.F. Equivalent Mechanical Properties of Auxetic Lattices from Discrete Homogenization. Comput. Mater. Sci. 2012, 51, 314–321. [Google Scholar] [CrossRef]
- Wicht, D.; Schneider, M.; Böhlke, T. Computing the Effective Response of Heterogeneous Materials with Thermomechanically Coupled Constituents by an Implicit Fast Fourier Transform-Based Approach. Int. J. Numer. Methods Eng. 2020, 122, 1307–1332. [Google Scholar] [CrossRef]
- Lu, X.; Fu, X.; Lu, J.; Sun, R.; Xu, J.; Yan, C.; Wong, C.P. Numerical Homogenization of Thermal Conductivity of Particle-Filled Thermal Interface Material by Fast Fourier Transform Method. Nanotechnology 2021, 32, 12. [Google Scholar] [CrossRef]
- To, Q.D.; Bonnet, G. FFT Based Numerical Homogenization Method for Porous Conductive Materials. Comput. Methods Appl. Mech. Eng. 2020, 368, 113160. [Google Scholar] [CrossRef]
- Lages, E.N.; Pereira, S.; Marques, C. Thermoelastic Homogenization of Periodic Composites Using an Eigenstrain-Based Micromechanical Model. Appl. Math. Model. 2020, 85, 1–18. [Google Scholar] [CrossRef]
- Schneider, M.; Merkert, D.; Kabel, M. FFT-Based Homogenization for Microstructures Discretized by Linear Hexahedral Elements. Int. J. Numer. Methods Eng. 2017, 109, 1461–1489. [Google Scholar] [CrossRef]
- Hassani, B.; Hinton, E. A Review of Homogenization and Topology Optimization I—Homogenization Theory for Media with Periodic Structure. Comput. Struct. 1998, 69, 707–717. [Google Scholar] [CrossRef]
- Hollister, S.J.; Kikuehi, N. A Comparison of Homogenization and Standard Mechanics Analyses for Periodic Porous Composites. Comput. Mech. 1992, 10, 73–95. [Google Scholar] [CrossRef]
- Guedes, J.J.M.J.; Kikuchi, N. Preprocessing and Postprocessing for Materials Based on the Homogenization Method with Adaptive Finite Element Methods. Comput. Methods Appl. Mech. Eng. 1990, 83, 143–198. [Google Scholar] [CrossRef]
- Andreassen, E.; Andreasen, C.S. How to Determine Composite Material Properties Using Numerical Homogenization. Comput. Mater. Sci. 2014, 83, 488–495. [Google Scholar] [CrossRef]
- Dong, G.; Tang, Y.; Zhao, Y.F. A 149 Line Homogenization Code for Three-Dimensional Cellular Materials Written in MATLAB. J. Eng. Mater. Technol. Trans. ASME 2019, 141, 011005. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Y. Multi-Scale Analysis Method for Thermal Conductivity of Porous Material with Radiation. Multidiscip. Model. Mater. Struct. 2006, 2, 327–344. [Google Scholar] [CrossRef]
- Hill, R. A Self-Consistent Mechanics of Composite Materials. J. Mech. Phys. Solids 1965, 13, 213–222. [Google Scholar] [CrossRef]
- Chou, T.-W.; Nomura, S.; Taya, M. A Self-Consistent Approach to the Elastic Stiffness of Short-Fiber Composites. J. Compos. Mater. 1980, 14, 178–188. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average Stress in Matrix and Average Elastic Energy of Materials with Misfitting Inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Dasgupta, A.; Agarwal, R.K.; Bhandarkar, S.M. Three-Dimensional Modeling of Woven-Fabric Composites for Effective Thermo-Mechanical and Thermal Properties. Compos. Sci. Technol. 1996, 56, 209–223. [Google Scholar] [CrossRef]
- Zhai, H.; Wu, Q.; Yoshikawa, N.; Xiong, K.; Chen, C. Space-Time Asymptotic Expansion Method for Transient Thermal Conduction in the Periodic Composite with Temperature-Dependent Thermal Properties. Comput. Mater. Sci. 2021, 194, 110470. [Google Scholar] [CrossRef]
- Dasgupta, A.; Agarwal, R.K. Orthotropic Thermal Conductivity of Plain-Weave Fabric Composites Using a Homogenization Technique. J. Compos. Mater. 1992, 26, 2736–2758. [Google Scholar] [CrossRef]
- Bowles, D.E.; Tompkins, S.S. Prediction of Coefficients of Thermal Expansion for Unidirectional Composites. J. Compos. Mater. 1989, 23, 370–388. [Google Scholar] [CrossRef]
- Berger, H.; Gabbert, U.; Köppe, H.; Rodriguez-Ramos, R.; Bravo-Castillero, J.; Guinovart-Diaz, R.; Otero, J.A.; Maugin, G.A. Finite Element and Asymptotic Homogenization Methods Applied to Smart Composite Materials. Comput. Mech. 2003, 33, 61–67. [Google Scholar] [CrossRef]
- Mirabolghasemi, A. Thermal Conductivity of Architected Cellular Metamaterials. Master’s Thesis, McGill University, Montreal, QC, Canada, 2018. [Google Scholar]
- El Moumen, A.; Kanit, T.; Imad, A.; El Minor, H. Computational Thermal Conductivity in Porous Materials Using Homogenization Techniques: Numerical and Statistical Approaches. Comput. Mater. Sci. 2015, 97, 148–158. [Google Scholar] [CrossRef]
- Kalamkarov, A.L.; Andrianov, I.V.; Danishevs’kyy, V.V. Asymptotic Homogenization of Composite Materials and Structures. Appl. Mech. Rev. 2009, 62, 030802. [Google Scholar] [CrossRef]
- Masoumi, E.; Abad, K.; Khanoki, S.A.; Pasini, D. Fatigue Design of Lattice Materials via Computational Mechanics: Application to Lattices with Smooth Transitions in Cell Geometry. Int. J. Fatigue 2012, 47, 126–136. [Google Scholar] [CrossRef]
- Cheng, G.D.; Cai, Y.W.; Xu, L. Novel Implementation of Homogenization Method to Predict Effective Properties of Periodic Materials. Acta Mech. Sin./Lixue Xuebao 2013, 29, 550–556. [Google Scholar] [CrossRef]
- Liu, P.; Liu, A.; Peng, H.; Tian, L.; Liu, J.; Lu, L. Mechanical Property Profiles of Microstructures via Asymptotic Homogenization. Comput. Graph. 2021, 100, 106–115. [Google Scholar] [CrossRef]
- Arabnejad, S.; Pasini, D. Mechanical Properties of Lattice Materials via Asymptotic Homogenization and Comparison with Alternative Homogenization Methods. Int. J. Mech. Sci. 2013, 77, 249–262. [Google Scholar] [CrossRef]
- Peng, X.; Cao, J. A Dual Homogenization and Finite Element Approach for Material Characterization of Textile Composites. Compos. Part B Eng. 2002, 33, 45–56. [Google Scholar] [CrossRef]
- Guinovart-Daz, R.; Rodrguez-Ramos, R.; Bravo-Castillero, J.; Sabina, F.J.; Dario Santiago, R.; Martinez Rosado, R. Asymptotic Analysis of Linear Thermoelastic Properties of Fiber Composites. J. Thermoplast. Compos. Mater. 2007, 20, 389–410. [Google Scholar] [CrossRef]
- Visrolia, A.; Meo, M. Multiscale Damage Modelling of 3D Weave Composite by Asymptotic Homogenisation. Compos. Struct. 2013, 95, 105–113. [Google Scholar] [CrossRef]
- Takano, N.; Zako, M.; Kubo, F.; Kimura, K. Microstructure-Based Stress Analysis and Evaluation for Porous Ceramics by Homogenization Method with Digital Image-Based Modeling. Int. J. Solids Struct. 2003, 40, 1225–1242. [Google Scholar] [CrossRef]
- Dong, K.; Liu, K.; Zhang, Q.; Gu, B.; Sun, B. Experimental and Numerical Analyses on the Thermal Conductive Behaviors of Carbon Fiber/Epoxy Plain Woven Composites. Int. J. Heat Mass Transf. 2016, 102, 501–517. [Google Scholar] [CrossRef]
- Hashin, Z. Analysis of Composite Materials—A Survey. J. Appl. Mech. 1983, 50, 481–505. [Google Scholar] [CrossRef]
- Rosen, B.W.; Hashin, Z. Effective Thermal Expansion Coefficients and Specific Heats of Composite Materials. Int. J. Eng. Sci. 1970, 8, 157–173. [Google Scholar] [CrossRef]
- Chamis, C.C.; Sendeckyj, G.P. Critique on Theories Predicting Thermoelastic Properties of Fibrous Composites. J. Compos. Mater. 1968, 2, 332–358. [Google Scholar] [CrossRef]
- Mirabolghasemi, A.; Akbarzadeh, A.H.; Rodrigue, D.; Therriault, D. Thermal Conductivity of Architected Cellular Metamaterials. Acta Mater. 2019, 174, 61–80. [Google Scholar] [CrossRef]
- Zhang, Y.; Shang, S.; Liu, S. A Novel Implementation Algorithm of Asymptotic Homogenization for Predicting the Effective Coefficient of Thermal Expansion of Periodic Composite Materials. Acta Mech. Sin./Lixue Xuebao 2017, 33, 368–381. [Google Scholar] [CrossRef]
- Material Designer User’s Guide. Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v194/acp_md/acp_md.html (accessed on 16 December 2020).
- Hassani, B.; Hinton, E. A Review of Homogenization and Topology Opimization II—Analytical and Numerical Solution of Homogenization Equations. Comput. Struct. 1998, 69, 719–738. [Google Scholar] [CrossRef]
- Hassani, B.; Hinton, E. A Review of Homogenization and Topology Optimization III—Topology Optimization Using Optimality Criteria. Comput. Structures 1998, 69, 739–756. [Google Scholar] [CrossRef]
- Rajakareyar, P. Thermo-Elastic Mechanics of Morphing Lattice Structures with Applications in Shape Optimization of BLI Engine Intakes. Master’s Thesis, Carleton University, Ottawa, ON, Canada, 2023. [Google Scholar]
- Rajakareyar, P.; ElSayed, M.S.A.; Abo El Ella, H.; Matida, E. Effective Mechanical Properties of Periodic Cellular Solids with Generic Bravais Lattice Symmetry via Asymptotic Homogenization. Materials 2023, 16, 7562. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Logan, D.L. A First Course in the Finite Element Method, SI ed.; Cengage Learning: Boston, MA, USA, 2016. [Google Scholar]
- SPACEMATDB—Space Materials Database. Materials Details. Available online: https://www.spacematdb.com/spacemat/datasearch.php?name=Invar 36 (accessed on 30 July 2022).
- Van Der Walt, S.; Colbert, S.C.; Varoquaux, G. The NumPy Array: A Structure for Efficient Numerical Computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef]
- SciPy, Scipy.Spatial.CKDTree—SciPy v1.5.4 Reference Guide. 2022. Available online: https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.cKDTree.html (accessed on 11 December 2020).
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Ramachandran, P.; Varoquaux, G. Mayavi: 3D Visualization of Scientific Data. Comput. Sci. Eng. 2011, 13, 40–51. [Google Scholar] [CrossRef]
- Gaillac, R.; Pullumbi, P.; Coudert, F.-X. ELATE: An Open-Source Online Application for Analysis and Visualization of Elastic Tensors. J. Phys. Condens. Matter 2016, 28, 275201. [Google Scholar] [CrossRef] [PubMed]
- Kermode, J.; Pastewka, L. Matscipy/Elasticity.Py at Master · LibAtoms/Matscipy. Available online: https://github.com/libAtoms/matscipy/blob/master/matscipy/elasticity.py (accessed on 11 December 2020).
- Hoogendoorn, E.; van Golen, K. Numpy-Indexed · PyPI. Available online: https://pypi.org/project/numpy-indexed/. (accessed on 11 December 2020).
- Lam, S.K.; Pitrou, A.; Seibert, S. Numba: A LLVM-Based Python JIT Compiler. In Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC-LLVM ’15, Austin, TX, USA, 15 November 2015; pp. 1–6. [Google Scholar]



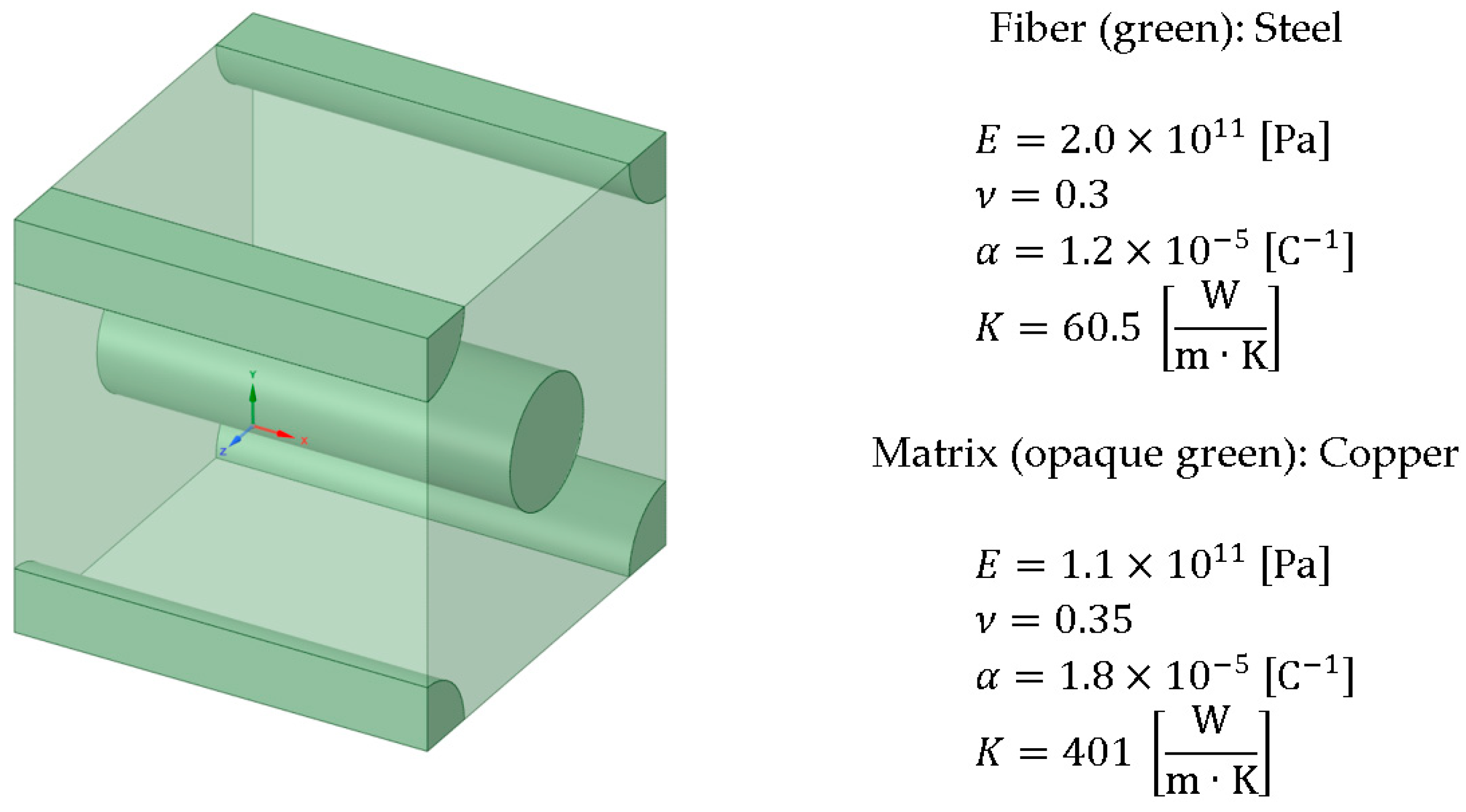




| Configuration Number | Group 1 | Group 2 | Group 3 |
|---|---|---|---|
| 0 | Steel | Steel | Steel |
| 1 | Steel | Steel | Invar |
| 2 | Steel | Invar | Steel |
| 3 | Steel | Invar | Invar |
| 4 | Invar | Steel | Steel |
| 5 | Invar | Steel | Invar |
| 6 | Invar | Invar | Steel |
| 7 | Invar | Invar | Invar |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rajakareyar, P.; Abo El Ella, H.; ElSayed, M.S.A. Voxel-Based Asymptotic Homogenization of the Effective Thermal Properties of Lattice Materials with Generic Bravais Lattice Symmetry. Symmetry 2025, 17, 1197. https://doi.org/10.3390/sym17081197
Rajakareyar P, Abo El Ella H, ElSayed MSA. Voxel-Based Asymptotic Homogenization of the Effective Thermal Properties of Lattice Materials with Generic Bravais Lattice Symmetry. Symmetry. 2025; 17(8):1197. https://doi.org/10.3390/sym17081197
Chicago/Turabian StyleRajakareyar, Padmassun, Hamza Abo El Ella, and Mostafa S. A. ElSayed. 2025. "Voxel-Based Asymptotic Homogenization of the Effective Thermal Properties of Lattice Materials with Generic Bravais Lattice Symmetry" Symmetry 17, no. 8: 1197. https://doi.org/10.3390/sym17081197
APA StyleRajakareyar, P., Abo El Ella, H., & ElSayed, M. S. A. (2025). Voxel-Based Asymptotic Homogenization of the Effective Thermal Properties of Lattice Materials with Generic Bravais Lattice Symmetry. Symmetry, 17(8), 1197. https://doi.org/10.3390/sym17081197





