Stability Analysis of Biological Systems Under Threshold Conditions

Abstract

In biological models exhibiting symmetric interactions within each compartmental group, threshold dynamics are typically governed by a key parameter known as the basic reproduction number $R_0$. The stability of an equilibrium often hinges on whether $R_0$ is greater than or less than one. However, general results for stability at the critical threshold—when $R_0$ equals one—remain scarce. In this paper, we establish two theorems to analyze the stability of both trivial and boundary equilibria under this threshold condition. Our results provide explicit expressions for the threshold parameters in terms of partial derivatives of the nonlinear reaction function, making them readily applicable to a wide range of biological systems.

1. Introduction

In many biological systems exhibiting symmetry in birth and death rates across subpopulations, one should define the basic reproduction number based on the Jacobian matrix obtained by linearizing the system about an equilibrium point. For instance, consider a multigroup or multistage ecological model.

$$u^{\prime }\left(t\right)=f\left(u\left(t\right)\right),$$

(1)

where $u\left(t\right)\in {\mathbb{R}}_{+}^n$ denotes the population densities at $t \ge 0$, and $f\in C^2({\mathbb{R}}_{+}^n,{\mathbb{R}}^n)$ with $f\left(0\right)=0$. The Jacobian matrix of the system about the trivial equilibrium 0 is given by

$$A=f^{\prime }\left(0\right)\in {\mathbb{R}}^{n\times n}.$$

(2)

Assume that A is cooperative: all off-diagonal entries of A are non-negative. Furthermore, assume that A is irreducible: there does not exist a permutation matrix $P\in {\mathbb{R}}^{n\times n}$ such that $P^{T}AP$ is a block upper triangular matrix, or equivalently, for any $j,k=1,\dots ,n$, there exists m such that the $(j,k)$ entry of $A^m$ is nonzero, namely, ${\left(A^m\right)}_{jk}\ne 0$. Let

$$A=F-V$$

(3)

be a regular splitting Section 3.6 of ref. [1] in the sense that $F\in {\mathbb{R}}_{+}^{n\times n}$ is a non-negative matrix containing the birth/growth rates of the species and the transition/development rates between different groups/stages, and $V\in {\mathbb{R}}^{n\times n}$ is an invertible matrix that includes the death/removal rates of species with a non-negative inverse matrix $V^{-1}\in {\mathbb{R}}_{+}^{n\times n}$. We can define the basic reproduction number as the spectral radius of the next-generation matrix $F{V}^{-1}$; that is,

$$R_0:=\rho \left(F{V}^{-1}\right)=\rho \left(V^{-1}F\right);$$

(4)

see [2,3]. It is well known that the following threshold dynamics holds:

(i)

if $R_0<1$, then the spectral bound $s\left(A\right)$ is negative and the trivial equilibrium 0 is locally asymptotically stable;

(ii)

if $R_0>1$, then $s\left(A\right)>0$ and the trivial equilibrium 0 becomes unstable.

The biological interpretation of this result is that the species will survive if the basic reproduction number $R_0$ exceeds the threshold value 1 and will be extinct if $R_0<1$. A natural question is what if $R_0=1$. Will the trivial equilibrium 0 be stable or unstable under the threshold condition when the basic reproduction number is equal to one? The objective of this work is to provide a criterion for the stability of 0 under threshold conditions. Note that if $R_0=1$ then $s\left(A\right)=0$ is the principal eigenvalue of A with a non-trivial and non-negative eigenvector $u_0\in {\mathbb{R}}_{+}^n$. In this case, the linearized system $u^{\prime }\left(t\right)=Au\left(t\right)$ possesses infinitely many equilibrium points $c{u}_0$ with $c\ge 0$. Thus, a linear approximation is not sufficient to determine the stability of 0 for the original system. To resolve this issue, we shall consider the second-order approximation of the function f and investigate the normal form of (1) in the center manifold of the equilibrium point 0.

In many applications, in particular for disease models or predator-prey systems, we shall linearize the system about the disease-free equilibrium or predator-free equilibrium to define the basic reproduction number $R_0$. We will also investigate the stability of the boundary equilibrium point under the threshold condition $R_0=1$.

Throughout this paper, we say a vector (or matrix) is non-negative if each component of the vector (or matrix) is non-negative. We use ${\mathbb{R}}_{+}^n$ and ${\mathbb{R}}_{+}^{n\times n}$ to denote the sets of non-negative (column) vectors and non-negative square matrices, respectively. We say a vector (or matrix) is positive if each component of the vector (or matrix) is positive. Given $f\in C^2({\mathbb{R}}_{+}^n,{\mathbb{R}}^n)$, the first-order (Fréchet) derivative of f is denoted as $f^{\prime }\in C^1({\mathbb{R}}_{+}^n,{\mathbb{R}}^{n\times n})$ such that

$$f_{ij}^{\prime }\left(x\right)={\displaystyle \frac{\partial f_i}{\partial x_j}}\left(x\right),$$

for any $x\in {\mathbb{R}}_{+}^n$ and $i,j=1,\dots ,n$. For each component $f_i\in C^2({\mathbb{R}}^n,\mathbb{R})$, the second-order (Fréchet) derivative of $f_i$ is denoted as $f_i^{\prime \prime }\in C({\mathbb{R}}_{+}^n,{\mathbb{R}}^{n\times n})$ such that

$$f_{ijk}^{\prime \prime }\left(x\right)={\displaystyle \frac{{\partial }^2{f}_i}{\partial x_j\partial x_k}}\left(x\right),$$

for any $x\in {\mathbb{R}}_{+}^n$ and $i,j,k=1,\dots ,n$. For any square matrix $M\in {\mathbb{R}}^{n\times n}$, the spectral radius $\rho \left(M\right)$ is defined as the maximum of the absolute values of its eigenvalues, while the spectral bound $s\left(M\right)$ is the maximum of the real parts of its eigenvalues. For any $x\in {\mathbb{R}}^n$ and $\epsilon >0$, we defined $B_{\epsilon }\left(x\right)$ the open ball of all vectors whose Euclidean distance to x is less than $\epsilon$.

For a mathematical model in biological systems, we provide a rigorous definition for the local asymptotic stability of the trivial equilibrium or a boundary equilibrium.

Definition 1. 

Consider the system (1) with $f\in C({\mathbb{R}}_{+}^n,{\mathbb{R}}^n)$ and an equilibrium point $\overline{u}\in {\mathbb{R}}_{+}^n$ satisfying $f\left(\overline{u}\right)=0$. Assume that ${\mathbb{R}}_{+}^n$ is positively invariant; that is, $u\left(0\right)\in {\mathbb{R}}_{+}^n$ implies $u\left(t\right)\in {\mathbb{R}}_{+}^n$ for all $t\ge 0$. We say $\overline{u}$ is locally asymptotically stable (in ${\mathbb{R}}_{+}^n$) if the following conditions are satisfied:

1.

(stability) For any $\epsilon >0$ there exists $\delta >0$ such that $u\left(0\right)\in B_{\delta }\left(\overline{u}\right)\cap {\mathbb{R}}_{+}^n$ implies $u\left(t\right)\in B_{\epsilon }\left(\overline{u}\right)$ for all $t\ge 0$.

2.

(attractivity) There exists $\delta >0$ such that $u\left(0\right)\in B_{\delta }\left(\overline{u}\right)\cap {\mathbb{R}}_{+}^n$ implies that $u\left(t\right)\to \overline{u}$ as $t\to \infty$.

We say $\overline{u}$ is unstable if there exists $\epsilon >0$ such that for any $\delta >0$, we can find an initial value $u\left(0\right)\in B_{\delta }\left(\overline{u}\right)\cap {\mathbb{R}}_{+}^n$ and a time $t_1\ge 0$ such that $u\left(t_1\right)\notin B_{\epsilon }\left(\overline{u}\right)$.

Remark 1. 

Comparing with the traditional definition of local asymptotic stability of an equilibrium, we have used $B_{\delta }\left(\overline{u}\right)\cap {\mathbb{R}}_{+}^n$, instead of $B_{\delta }\left(\overline{u}\right)$, in Definition 1. If $\overline{u}$ is an interior equilibrium with positive components, then it is unnecessary to make this modification because $B_{\delta }\left(\overline{u}\right)\subset {\mathbb{R}}_{+}^n$ for sufficiently small $\delta >0$. However, if $\overline{u}$ is the trivial equilibrium or a boundary equilibrium with some components being zero, then we should replace $B_{\delta }\left(\overline{u}\right)$ with $B_{\delta }\left(\overline{u}\right)\cap {\mathbb{R}}_{+}^n$. This is because, in biological systems, we are only interested in the non-negative solutions.

2. Stability of Trivial Equilibrium

In this section, we consider the system (1) with the following biologically reasonable assumptions:

(A1)

$f\in C^2({\mathbb{R}}_{+}^n,{\mathbb{R}}^n)$ with $f\left(0\right)=0$.

(A2)

${\mathbb{R}}_{+}^n$ is positively invariant; that is, $u\left(0\right)\in {\mathbb{R}}_{+}^n$ implies $u\left(t\right)\in {\mathbb{R}}_{+}^n$ for all $t\ge 0$.

(A3)

$A=f^{\prime }\left(0\right)\in {\mathbb{R}}^{n\times n}$ is cooperative and irreducible.

(A4)

There exists a regular splitting $A=F-V$, where $F\in {\mathbb{R}}_{+}^{n\times n}$ is non-negative and V is invertible with a non-negative inverse $V^{-1}\in {\mathbb{R}}_{+}^{n\times n}$.

The following lemma plays a crucial role in the proof of our theorem.

Lemma 1. 

Consider a scalar equation

$$y^{\prime }\left(t\right)=h\left(y\left(t\right)\right),$$

(5)

where $h\in C^2\left({\mathbb{R}}_{+}\right)$ with $h\left(0\right)=0$ and $h^{\prime }\left(0\right)=0$. Then 0 is locally asymptotically stable (in ${\mathbb{R}}_{+}$) if $h^{\prime \prime }\left(0\right)<0$ and unstable if $h^{\prime \prime }\left(0\right)>0$.

Proof. 

It is readily seen from $f\left(0\right)=0$ that ${\mathbb{R}}_{+}$ is positively invariant; that is, $y\left(0\right)\ge 0$ implies $y\left(t\right)\ge 0$ for all $t\ge 0$.

If $h^{\prime \prime }\left(0\right)<0$, then there exist $\alpha >0$ and $\delta >0$ such that $h^{\prime \prime }\left(y\right)\le -2\alpha$ for all $y\in [0,\delta ]$. By Taylor expansion, we obtain

$$\begin{array}{c}\hfill h\left(y\right)={\displaystyle \frac{h^{\prime \prime }\left(\xi \right)}{2}}{y}^2\le -\alpha y^2,\end{array}$$

for all $y\in [0,\delta ]$, where $\xi \in [0,y]$ depends on y. If $y\left(0\right)\in (0,\delta ]$, then

$$\begin{array}{c}\hfill y^{\prime }\left(0\right)=h\left(y\left(0\right)\right)\le -\alpha y{\left(0\right)}^2<0.\end{array}$$

The positive invariance of ${\mathbb{R}}_{+}$ implies that $y\left(t\right)>0$ for all $t\ge 0$. We claim that $y^{\prime }\left(t\right)<0$ for all $t\ge 0$. If not, there exists $t_1>0$ such that $y^{\prime }\left(t\right)<0$ for all $t\in [0,t_1)$ and $y^{\prime }\left(t_1\right)=0$. Hence, we obtain $0<y\left(t_1\right)<y\left(0\right)\le \delta$, which implies

$$\begin{array}{c}\hfill y^{\prime }\left(t_1\right)=h\left(y\left(t_1\right)\right)\le -\alpha y{\left(t_1\right)}^2<0,\end{array}$$

a contradiction to $y^{\prime }\left(t_1\right)=0$. Therefore, we have proved that if $y\left(0\right)\in (0,\delta ]$, then $y\left(t\right)$ is always positive and strictly decreasing in t. Denote

$$\begin{array}{c}\hfill c:=\underset{t\to \infty }{lim}y\left(t\right)\in [0,\delta ].\end{array}$$

It follows from

$$\begin{array}{c}\hfill 0=\underset{t\to \infty }{lim}{y}^{\prime }\left(t\right)=h\left(c\right)\le -\alpha c^2\le 0\end{array}$$

that $c=0$. Thus, 0 attracts the interval $[0,\delta ]$. Moreover, since the interval $[0,\alpha ]$ is positively invariant for any $\epsilon \in (0,\delta )$, 0 is locally asymptotically stable.

Now we assume $h^{\prime \prime }\left(0\right)>0$. A similar application of the continuity of $h^{\prime \prime }$ and Taylor expansion guarantees the existence of two small positive numbers $\beta >0$ and $\sigma >0$ such that

$$\begin{array}{c}\hfill h\left(y\right)\ge \beta y^2,\end{array}$$

for all $y\in [0,\sigma ]$. For any $\epsilon >0$, we choose $y\left(0\right)=min\{\epsilon ,\sigma \}>0$ and prove by contradiction that $y\left(t_2\right)>\sigma$ for some $t_2>0$. Assume $y\left(t\right)\le \sigma$ for all $t\ge 0$. The positive invariance of $R_{+}$ implies $y\left(t\right)>0$ for all $t\ge 0$. Hence,

$$\begin{array}{c}\hfill y^{\prime }\left(t\right)=h\left(y\left(t\right)\right)\ge \beta y{\left(t\right)}^2,\end{array}$$

for all $t\ge 0$. Solving the above differential inequality yields

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{y\left(0\right)}}-{\displaystyle \frac{1}{y\left(t\right)}}\ge \beta t.\end{array}$$

The left-hand side is bounded by $1/y\left(0\right)$ while the right-hand side can be arbitrarily large. This leads to a contradiction. Therefore, 0 is unstable. □

Remark 2. 

In Lemma 1, we say 0 is locally asymptotically stable (in ${\mathbb{R}}_{+}$) when it satisfies the conditions given in Definition 1. Note that if $f^{\prime \prime }\left(0\right)<0$, then 0 attracts solutions from the interval $(0,\delta )$ for sufficiently small $\delta >0$ while repelling those in the interval $(-\epsilon ,0)$ for sufficiently small $\epsilon >0$. This phenomenon is called semi-stable or half-stable in some literature or textbooks [4]. However, since we are only interested in the non-negative solutions in biological systems, it is more convenient and common to say that 0 is locally asymptotically stable (in ${\mathbb{R}}_{+}$); see Remark 1.

Now, we are ready to state our first main theorem.

Theorem 1. 

Consider the system (1) under the assumptions (A1)–(A4). Define $R_0=\rho \left(F{V}^{-1}\right)=\rho \left(V^{-1}F\right)$. If $R_0=1$, then we have $s\left(A\right)=0$ and it is a simple eigenvalue of A with a positive left eigenvector $\alpha \in {\mathbb{R}}^n$ and a positive right eigenvector $\beta \in {\mathbb{R}}^n$ such that

$${\alpha }^{T}A=0,A\beta =0,{\alpha }^T\beta =1.$$

Denote

$$\lambda :=\sum _{i=1}^n\sum _{j=1}^n\sum _{k=1}^n{\alpha }_i{f}_{ijk}^{\prime \prime }\left(0\right){\beta }_j{\beta }_k.$$

Then the trivial equilibrium 0 is locally asymptotically stable (in ${\mathbb{R}}_{+}^n$) if $\lambda <0$ and unstable if $\lambda >0$.

Proof. 

By (A4), the matrix $F{V}^{-1}$ is non-negative. Hence, the Perron–Frobenius theorem implies that $R_0=\rho \left(F{V}^{-1}\right)=1$ is an eigenvalue of $F{V}^{-1}$ with a non-negative left eigenvector $\alpha \in {\mathbb{R}}_{+}^n$; namely,

$${\alpha }^{T}F{V}^{-1}=R_0{\alpha }^T.$$

From $R_0=1$, we have ${\alpha }^{T}F={\alpha }^{T}V$ and hence

$${\alpha }^{T}A={\alpha }^T(F-V)=0.$$

Since A is cooperative by (A3), there exists $c>0$ such that $B:=cI+A$ is non-negative. The above equation shows that $c>0$ is an eigenvalue of B with a non-negative left eigenvector c. Again, by Perron–Frobenius theorem, $c=\rho \left(B\right)$ is a simple eigenvalue of B and c is a positive left eigenvector. Consequently, 0 is a simple eigenvector of A. If $\mu \in \mathbb{C}$ is any eigenvalue of A, then $\mu +c$ is an eigenvalue of B and $|\mu +c|\le c$. Therefore, we have Re $(\mu +c)\le c$ and Re $\mu \le 0$; namely, $s\left(A\right)=0$.

Now, we restrict the dynamics of (1) to the center manifold that is locally represented by

$$w={\alpha }^{T}u={\alpha }_1{u}_1+\dots +{\alpha }_n{u}_n.$$

Assume $u_i={\beta }_{i}w+O\left(w^2\right)$. Then we have from (1) and Taylor expansion

$$w^{\prime }=\sum _{i=1}^n{\alpha }_i{f}_i\left(u\right)=\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{f}_{ij}^{\prime }\left(0\right){\beta }_{j}w+O\left(w^2\right).$$

Recall that $A=f^{\prime }\left(0\right)$ and ${\alpha }^{T}A=0$, the first/linear term on the right-hand side of the above equation vanishes. Hence, we have $w^{\prime }=O\left(w^2\right)$. To determine the coefficient of the quadratic term, we shall make use of (1) and Taylor expansion again to obtain for each $i=1,\dots ,n$,

$$u_i^{\prime }=f_i\left(u\right)=\sum _{j=1}^n{f}_{ij}^{\prime }\left(0\right){\beta }_{j}w+O\left(w^2\right).$$

From $u_i={\beta }_{i}w+O\left(w^2\right)$ and $w^{\prime }=O\left(w^2\right)$, we have $u_i^{\prime }=O\left(w^2\right)$. Hence, the first/linear term on the right-hand side of the above equation should be zero; that is,

$$\sum _{j=1}^n{f}_{ij}^{\prime }\left(0\right){\beta }_j=0,i=1,\dots ,n.$$

This implies that $\beta ={({\beta }_1,\dots ,{\beta }_n)}^T\in {\mathbb{R}}^n$ is a right eigenvector of A with respect to the eigenvector 0. From non-negativeness of u and positiveness of $\alpha$, we obtain $w\ge 0$. Hence, we shall choose $\beta$ to be positive. Moreover, since $w={\alpha }^{T}u={\alpha }^T\beta w+O\left(w^2\right)$, the left eigenvector $\alpha$ and the right eigenvector $\beta$ are normalized by the condition ${\alpha }^T\beta =1$.

Finally, we obtain from (1) and $f\in C^2({\mathbb{R}}_{+}^n,{\mathbb{R}}^n)$ that

$$w^{\prime }=\sum _{i=1}^n{\alpha }_i{f}_i\left(u\right)={\displaystyle \frac{1}{2}}\sum _{i=1}^n\sum _{j=1}^n\sum _{k=1}^n{\alpha }_i{f}_{ijk}^{\prime \prime }\left(0\right){\beta }_j{\beta }_k{w}^2+o\left(w^2\right).$$

The result is a direct application of Lemma 1 and the equivalence of the dynamics of (1) and its restriction on the center manifold [5,6]. □

Remark 3. 

In real applications, the normalization condition ${\alpha }^T\beta =1$ can be released because any multiplication by a positive constant does not affect the sign of the stability parameter λ.

3. Stability of Boundary Equilibrium

In this section, we consider the following system

$$\begin{array}{cc}\hfill u^{\prime }\left(t\right)=& f\left(u\right(t),v(t\left)\right),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill v^{\prime }\left(t\right)=& g\left(u\right(t),v(t\left)\right),\hfill \end{array}$$

(7)

where $u\left(t\right)\in {\mathbb{R}}_{+}^n$, $v\left(t\right)\in {\mathbb{R}}_{+}^m$, $f\in C^2({\mathbb{R}}_{+}^{n+m},{\mathbb{R}}^n)$ and $g\in C^2({\mathbb{R}}_{+}^{n+m},{\mathbb{R}}^m)$. Assume $(0,\overline{v})\in {\mathbb{R}}_{+}^{n+m}$ is a boundary equilibrium such that $f(0,\overline{v})=0$ and $g(0,\overline{v})=0$. Denote the partial derivative of f with respect to u and v at the boundary equilibrium $(0,\overline{v})$ by

$$A=D_{u}f(0,\overline{v})\in {\mathbb{R}}^{n\times n},B=D_{v}f(0,\overline{v})\in {\mathbb{R}}^{n\times m}$$

(8)

such that

$$A_{ij}={\displaystyle \frac{\partial f_i}{\partial u_j}}(0,\overline{v}),i,j=1,\dots ,n,$$

(9)

and

$$B_{ip}={\displaystyle \frac{\partial f_i}{\partial v_p}}(0,\overline{v}),i=1,\dots ,n,p=1,\dots ,m.$$

(10)

Denote the partial derivative of g with respect to u and v at the boundary equilibrium $(0,\overline{v})$ by

$$C=D_{u}g(0,\overline{v})\in {\mathbb{R}}^{m\times n},D=D_{v}g(0,\overline{v})\in {\mathbb{R}}^{m\times m}$$

(11)

such that

$$C_{pi}={\displaystyle \frac{\partial g_p}{\partial u_i}}(0,\overline{v}),p=1,\dots ,m,i=1,\dots ,n,$$

(12)

and

$$D_{pq}={\displaystyle \frac{\partial g_p}{\partial v_q}}(0,\overline{v}),p,q=1,\dots ,m.$$

(13)

Similarly to Assumptions (A1)–(A4), we make the following assumptions.

(B1)

$f\in C^2({\mathbb{R}}_{+}^{n+m},{\mathbb{R}}^n)$ and $g\in C^2({\mathbb{R}}_{+}^{n+m},{\mathbb{R}}^m)$ with $f(0,\overline{v})=0$, where $\overline{v}\in {\mathbb{R}}_{+}^m$.

(B2)

${\mathbb{R}}_{+}^{n+m}$ is positively invariant; that is, $u\left(0\right)\in {\mathbb{R}}_{+}^n$ and $v\left(0\right)\in {\mathbb{R}}_{+}^m$ implies $u\left(t\right)\in {\mathbb{R}}_{+}^n$ and $v\left(t\right)\in {\mathbb{R}}_{+}^m$ for all $t\ge 0$.

(B3)

$A=D_{u}f(0,\overline{v})\in {\mathbb{R}}^{n\times n}$ is cooperative and irreducible.

(B4)

There exists a regular splitting $A=F-V$, where $F\in {\mathbb{R}}_{+}^{n\times n}$ is non-negative and V is invertible with a non-negative inverse $V^{-1}\in {\mathbb{R}}_{+}^{n\times n}$.

In addition to (B1)–(B4), we also assume that

(B5)

$B=D_{v}f(0,\overline{v})=0\in {\mathbb{R}}^{n\times m}$; namely,

$${\displaystyle \frac{\partial f_i}{\partial v_p}}(0,\overline{v})=0,$$

for any $i=1,\dots ,n$ and $p=1,\dots ,m$.

(B6)

$D=D_{v}g(0,\overline{v})\in {\mathbb{R}}^{m\times m}$ is invertible.

Our second main theorem is presented below.

Theorem 2. 

Consider the system (6) and (7) under the assumptions (B1)–(B6). Define $R_0=\rho \left(F{V}^{-1}\right)=\rho \left(V^{-1}F\right)$. If $R_0=1$, then we have $s\left(A\right)=0$ and it is a simple eigenvalue of A with a positive left eigenvector $\alpha \in {\mathbb{R}}^n$ and a positive right eigenvector $\beta \in {\mathbb{R}}^n$ such that

$${\alpha }^{T}A=0,A\beta =0,{\alpha }^T\beta =1.$$

Denote $\delta :=-D^{-1}C\beta \in {\mathbb{R}}^m$ and

$$\begin{array}{cc}\hfill \lambda :=\sum _{i=1}^n{\alpha }_i[\sum _{j=1}^n\sum _{k=1}^n{\displaystyle \frac{{\partial }^2{f}_i}{\partial u_j\partial u_k}}(0,\overline{v}){\beta }_j{\beta }_k& +2\sum _{j=1}^n\sum _{p=1}^m{\displaystyle \frac{{\partial }^2{f}_i}{\partial u_j\partial v_p}}(0,\overline{v}){\beta }_j{\delta }_p\hfill \\ & +\sum _{p=1}^m\sum _{q=1}^m{\displaystyle \frac{{\partial }^2{f}_i}{\partial v_p\partial v_q}}(0,\overline{v}){\delta }_p{\delta }_q].\hfill \end{array}$$

Then the boundary equilibrium $(0,\overline{v})$ is locally asymptotically stable (in ${\mathbb{R}}_{+}^n$) if $\lambda <0$ and unstable if $\lambda >0$.

Proof. 

Similarly as in the proof of Theorem 1, we can show that $s\left(A\right)=0$ and it is a simple eigenvalue of A with a positive left eigenvector $\alpha \in {\mathbb{R}}^n$ such that ${\alpha }^{T}A=0$.

Now, we restrict the dynamics of (6) and (7) to the center manifold that is locally represented by

$$w={\alpha }^{T}u={\alpha }_1{u}_1+\dots +{\alpha }_n{u}_n,$$

with $u_i={\beta }_{i}w+O\left(w^2\right)$ for $i=1,\dots ,n$ and $v_p={\overline{v}}_p+{\delta }_{p}w+O\left(w^2\right)$ for $p=1,\dots ,m$. Applying the Taylor expansion to (6) yields

$$u_i^{\prime }=\sum _{j=1}^n{\displaystyle \frac{\partial f_i}{\partial u_j}}(0,\overline{v})u_j+\sum _{p=1}^m{\displaystyle \frac{\partial f_i}{\partial v_p}}(0,\overline{v})(v_p-{\overline{v}}_p)+O\left(w^2\right).$$

By (B3), we have $D_{u}f(0,\overline{v})=A$. By (B5), we have $D_{v}f(0,\overline{v})=0$. It then follows from ${\alpha }^{T}A=0$ and $w={\alpha }^{T}u$ that

$$w^{\prime }=\sum _{i=1}^n{\alpha }_i{u}_i^{\prime }=O\left(w^2\right).$$

A combination of $u_i={\beta }_{i}w+O\left(w^2\right)$ and the above two equations gives

$$\sum _{j=1}^n{\displaystyle \frac{\partial f_i}{\partial u_j}}(0,\overline{v}){\beta }_j=0,i=1,\dots ,n.$$

This implies that $\beta ={({\beta }_1,\dots ,{\beta }_n)}^T\in {\mathbb{R}}^n$ is a right eigenvector of A with respect to the eigenvector 0. We choose $\beta$ to be positive and normalize it such that ${\alpha }^T\beta =1$.

Next, we apply the Taylor expansion to (7) and find

$$v_p^{\prime }=\sum _{i=1}^n{\displaystyle \frac{\partial g_p}{\partial u_i}}(0,\overline{v})u_i+\sum _{q=1}^m{\displaystyle \frac{\partial g_p}{\partial v_q}}(0,\overline{v})(v_q-{\overline{v}}_q)+O\left(w^2\right).$$

Since $u_i={\beta }_{i}w+O\left(w^2\right)$ and $v_q={\overline{v}}_q+{\delta }_{q}w+O\left(w^2\right)$, we rewrite the above equation as

$$v_p^{\prime }=\sum _{i=1}^n{\displaystyle \frac{\partial g_p}{\partial u_i}}(0,\overline{v}){\beta }_{i}w+\sum _{q=1}^m{\displaystyle \frac{\partial g_p}{\partial v_q}}(0,\overline{v}){\delta }_{q}w+O\left(w^2\right).$$

In view of $v_p={\overline{v}}_p+{\delta }_{p}w+O\left(w^2\right)$ and $w^{\prime }=O\left(w^2\right)$, the left-hand side of the above equation is of order $O\left(w^2\right)$. Hence, the linear term on the right-hand side of the above equation vanishes, that is,

$$\sum _{i=1}^n{\displaystyle \frac{\partial g_p}{\partial u_i}}(0,\overline{v}){\beta }_i+\sum _{q=1}^m{\displaystyle \frac{\partial g_p}{\partial v_q}}(0,\overline{v}){\delta }_q=0,$$

for all $p=1,\dots ,m$. On account of the definitions of matrices C and D in (11), the above system can be written in matrix form:

$$C\beta +D\delta =0.$$

By (B6), D is invertible and we have

$$\delta =-D^{-1}C\beta .$$

Finally, we obtain from (6) and $f\in C^2({\mathbb{R}}_{+}^{n+m},{\mathbb{R}}^n)$ that

$$\begin{array}{cc}\hfill w^{\prime }=& \sum _{i=1}^n{\alpha }_i{f}_i(u,v)\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}\sum _{i=1}^n{\alpha }_i[\sum _{j=1}^n\sum _{k=1}^n{\displaystyle \frac{{\partial }^2{f}_i}{\partial u_j\partial u_k}}(0,\overline{v}){\beta }_j{\beta }_k+2\sum _{j=1}^n\sum _{p=1}^m{\displaystyle \frac{{\partial }^2{f}_i}{\partial u_j\partial v_p}}(0,\overline{v}){\beta }_j{\delta }_p\hfill \\ & +\sum _{p=1}^m\sum _{q=1}^m{\displaystyle \frac{{\partial }^2{f}_i}{\partial v_p\partial v_q}}(0,\overline{v}){\delta }_p{\delta }_q]w^2+o\left(w^2\right).\hfill \end{array}$$

Since the dynamics of (6) and (7) is equivalent to the dynamics of its restriction on the center manifold [5,6], we obtain our desired result from a direct application of Lemma 1. □

Remark 4. 

Similar as in Remark 3, we may release the normalization condition ${\alpha }^T\beta =1$ in real applications. It is also noted that Theorem 1 is a special case of Theorem 2 if we set $m=0$.

4. Applications

We consider the age structure model of a biological species that exhibits asymmetry between the immature and mature population densities, denoted by $u_1$ and $u_2$, respectively. The dynamics of these two compartments are governed by the equations

$$\begin{array}{cc}\hfill u_1^{\prime }\left(t\right)=& {\displaystyle \frac{r{u}_2\left(t\right)}{1+u_2\left(t\right)/H}}-d_1{u}_1\left(t\right)-\sigma u_1\left(t\right),\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill u_2^{\prime }\left(t\right)=& \sigma u_1\left(t\right)-d_2{u}_2\left(t\right),\hfill \end{array}$$

(15)

where r is the intrinsic birth rate, $\sigma$ is the maturation rate, and $d_1$ and $d_2$ are the death rates of immature and mature population, respectively. Note that asymmetry is introduced by assuming different death rates for the immature and mature groups. The nonlinear birth function is modeled by the Holling type function $r{u}_2/(1+u_2/H)$, which is a decreasing function of the mature population $u_2$, where H denotes the density of mature population when the birth rate is reduced to half the intrinsic birth rate $r/2$. Denote the right-hand side of the above system by a vector-valued function $f\in C^2({\mathbb{R}}_{+}^2,{\mathbb{R}}^2)$. Linearizing the above system about the trivial equilibrium $0\in {\mathbb{R}}^2$, we obtain the Jacobian matrix

$$A=f^{\prime }\left(0\right)=\left(\begin{array}{cc}-d_1-\sigma & r\\ \sigma & -d_2\end{array}\right).$$

We use the regular splitting $A=F-V$, where

$$F:=\left(\begin{array}{cc}0& r\\ 0& 0\end{array}\right)$$

is the matrix of birth, while

$$V:=\left(\begin{array}{cc}{d}_1+\sigma & 0\\ -\sigma & d_2\end{array}\right)$$

is the matrix of death and maturation. Hence, the basic reproduction number $R_0$ is defined as the spectral radius of the next-generation matrix

$$F{V}^{-1}=\left(\begin{array}{cc}r\sigma /\left[(d_1+\sigma )d_2\right]& r/d_2\\ 0& 0\end{array}\right);$$

that is,

$$R_0=r·{\displaystyle \frac{\sigma }{d_1+\sigma }}·{\displaystyle \frac{1}{d_2}},$$

where r is the intrinsic birth rate, $\sigma /(d_1+\sigma )$ is the probability of maturation, and $1/d_2$ is the average lifespan of the mature population. It is easily seen that (A1)–(A4) are satisfied. Now, we assume that $R_0=1$, that is, $r\sigma =(d_1+\sigma )d_2$. The spectral bound of the Jacobian matrix A is 0 and it is an eigenvalue associated with a positive left eigenvector $\alpha ={(d_2,r)}^T$ and a positive right eigenvector $\beta ={(d_2,\sigma )}^T$. As mentioned in Remark 3, we do not need to normalize the inner product ${\alpha }^T\beta$. A simple calculation gives

$$f_{2jk}^{″}\left(0\right)=0,j=1,2,k=1,2,$$

and

$$f_{111}^{″}\left(0\right)=f_{112}^{″}\left(0\right)=f_{121}^{″}\left(0\right)=0,$$

and

$$f_{122}^{″}\left(0\right)=-{\displaystyle \frac{r}{H}}.$$

Consequently,

$$\lambda =\sum _{i=1}^2\sum _{j=1}^2\sum _{k=1}^2{\alpha }_i{f}_{ijk}^{″}\left(0\right){\beta }_j{\beta }_k={\alpha }_1{f}_{122}^{″}{\beta }_2^2=-{\displaystyle \frac{d_2{\sigma }^{2}r}{H}}<0.$$

Based on Theorem 1, we have the following result.

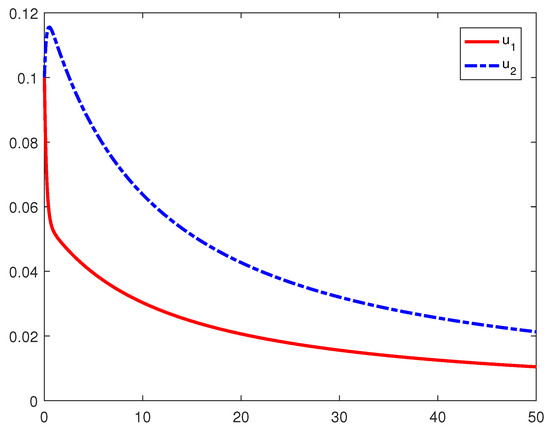
Proposition 1. 

If $R_0=1$, then the trivial equilibrium $0\in {\mathbb{R}}^2$ of the system (14) and (15) is locally asymptotically stable in ${\mathbb{R}}_{+}^2$.

The above result is illustrated in Figure 1.

Figure 1. The trivial equilibrium 0 of the system (14) and (15) is locally asymptotically stable for $R_0=1$. The model parameters are chosen as $H=1,r=2,d_1=2,\sigma =2,d_2=1$.

Next, we consider the infectious disease model with four compartments: susceptible (S), exposed (E), infectious (I) and recovered (R) populations. The dynamical system is given by

$$\begin{array}{cc}\hfill S^{\prime }\left(t\right)=& b-d_{S}S\left(t\right)-h(S\left(t\right),I\left(t\right))+\eta R\left(t\right),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill E^{\prime }\left(t\right)=& h(S\left(t\right),I\left(t\right))-\sigma E\left(t\right)-d_{E}E\left(t\right),\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill I^{\prime }\left(t\right)=& \sigma E\left(t\right)-d_{I}I\left(t\right)-\gamma I\left(t\right),\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill R^{\prime }\left(t\right)=& \gamma I\left(t\right)-d_{R}R\left(t\right)-\eta R\left(t\right),\hfill \end{array}$$

(19)

where b is the birth rate, $d_S$, $d_E$, $d_I$, and $d_R$ are the death rates that characterize the asymmetry among the four compartmental groups, and $h\in C^2({\mathbb{R}}_{+}^2,{\mathbb{R}}_{+})$ is the nonlinear function of infection satisfying

$$h(x_1,0)=h(0,x_2)=0,$$

for any $x_1,x_2\in {\mathbb{R}}^{+}$. For convenience, we denote the partial derivatives of h as

$$h_j\left(x\right)={\displaystyle \frac{\partial h}{\partial x_j}}\left(x\right),h_{jk}\left(x\right)={\displaystyle \frac{{\partial }^{2}h}{\partial x_j\partial x_k}}\left(x\right)$$

for $j=1,2$, $k=1,2$, and $x={(x_1,x_2)}^T\in {\mathbb{R}}_2^{+}$. Clearly,

$$h_1(x_1,0)=h_{11}(x_1,0)=0$$

for any $x_1\ge 0$. The progression rate from exposed to infectious is denoted by $\sigma$, while the recovery rate is $\gamma$. We also denote by $\eta$ the rate of immunity loss. The disease-free equilibrium is given by $E_0=(\overline{S},0,0,0)$, where $\overline{S}=b/d_S$. We choose $n=2$ and $m=2$, and define

$$u\left(t\right)=\left(\begin{array}{c}E\left(t\right)\\ I\left(t\right)\end{array}\right)\in {\mathbb{R}}_{+}^2,v\left(t\right)=\left(\begin{array}{c}S\left(t\right)\\ R\left(t\right)\end{array}\right)\in {\mathbb{R}}_{+}^2.$$

Hence, the infectious disease model (16)–(19) is equivalent to (6) and (7) with

$$\begin{array}{cc}\hfill f(u,v)=& \left(\begin{array}{c}h(v_1,u_2)-(\sigma +d_E)u_1\\ \sigma u_1-(d_I+\gamma )u_2\end{array}\right),\hfill \\ \hfill g(u,v)=& \left(\begin{array}{c}b-d_S{v}_1-h(v_1,u_2)+\eta v_2\\ \gamma u_2-(d_R+\eta )v_2\end{array}\right).\hfill \end{array}$$

The boundary equilibrium is $(0,\overline{v})$, with $\overline{v}=(\overline{S},0)\in {\mathbb{R}}_{+}^2$. A simple calculation gives

$$\begin{array}{cc}\hfill A=& D_{u}f(0,\overline{v})=\left(\begin{array}{cc}-(\sigma +d_E)& h_2(\overline{S},0)\\ \sigma & -(d_I+\gamma )\end{array}\right)\in {\mathbb{R}}^{2\times 2},\hfill \\ \hfill B=& D_{v}f(0,\overline{v})=0\in {\mathbb{R}}^{2\times 2},\hfill \\ \hfill C=& D_{u}g(0,\overline{v})=\left(\begin{array}{cc}0& -h_2(\overline{S},0)\\ 0& \gamma \end{array}\right)\in {\mathbb{R}}^{2\times 2},\hfill \\ \hfill D=& D_{v}g(0,\overline{v})=\left(\begin{array}{cc}-d_S& \eta \\ 0& -(d_R+\eta )\end{array}\right)\in {\mathbb{R}}^{2\times 2}.\hfill \end{array}$$

Now, we introduce the regular splitting $A=F-V$, where

$$F=\left(\begin{array}{cc}0& h_2(\overline{S},0)\\ 0& 0\end{array}\right)$$

is the matrix of infection, and

$$V=\left(\begin{array}{cc}\sigma +d_E& 0\\ -\sigma & d_I+\gamma \end{array}\right)$$

is the matrix of transition and death. The basic reproduction number is defined as the spectral radius of the next-generation matrix

$$R_0=\rho \left(F{V}^{-1}\right)=\rho \left(V^{-1}F\right)=h_2(\overline{S},0)·{\displaystyle \frac{\sigma }{\sigma +d_E}}·{\displaystyle \frac{1}{d_I+\gamma }},$$

(20)

where $h_2(\overline{S},0)$ is the transmission rate, $\sigma /(\sigma +d_E)$ is the probability of progression from exposed to infectious, and $1/(d_I+\gamma )$ is the average infectious duration. It is easily seen that (B1)–(B6) are satisfied.

If $R_0=1$, then $h_2(\overline{S},0)\sigma =(\sigma +d_E)(d_I+\gamma )$ and $s\left(A\right)=0$ is a simple eigenvalue of A with a positive left eigenvector $\alpha ={(\sigma ,\sigma +d_E)}^T$ and a positive right eigenvector $\beta ={(d_I+\gamma ,\sigma )}^T$. As commented in Remark 4, it is unnecessary to normalize the inner product ${\alpha }^T\beta$. A simple calculation gives

$$\delta =-D^{-1}C\beta =\left(\begin{array}{cc}1/d_S& \eta /\left[d_S(d_R+\eta )\right]\\ 0& 1/(d_R+\eta )\end{array}\right)\left(\begin{array}{c}-h_2(\overline{S},0)\sigma \\ \gamma \sigma \end{array}\right)=\left(\begin{array}{c}{\delta }_1\\ {\delta }_2\end{array}\right),$$

where

$${\delta }_1={\displaystyle \frac{\eta \gamma \sigma }{d_S(d_R+\eta )}}-{\displaystyle \frac{h_2(\overline{S},0)\sigma }{d_S}},{\delta }_2={\displaystyle \frac{\gamma \sigma }{d_R+\eta }}.$$

Next, we evaluate the non-zero partial derivatives

$${\displaystyle \frac{{\partial }^2{f}_1}{\partial u_2^2}}(0,\overline{v})=h_{22}(\overline{S},0),$$

and

$${\displaystyle \frac{{\partial }^2{f}_1}{\partial v_1\partial u_2}}(0,\overline{v})=h_{12}(\overline{S},0).$$

Finally, we compute

$$\lambda ={\alpha }_1[h_{22}(\overline{S},0){\beta }_2^2+2h_{12}(\overline{S},0){\delta }_1{\beta }_2]={\sigma }^3\left[h_{22}(\overline{S},0)+2h_{12}(\overline{S},0){\displaystyle \frac{\eta \gamma -h_2(\overline{S},0)(d_R+\eta )}{d_S(d_R+\eta )}}\right].$$

An application of Theorem 2 gives the following result.

Proposition 2. 

Assume $R_0=1$. Denote a threshold parameter

$$\xi :=d_S(d_R+\eta )h_{22}(\overline{S},0)+2[\eta \gamma -h_2(\overline{S},0)(d_R+\eta )]h_{12}(\overline{S},0).$$

The boundary equilibrium $E_0=(\overline{S},0,0,0)\in {\mathbb{R}}^4$ of system (16)–(19) is locally asymptotically stable (in ${\mathbb{R}}_{+}^4$) if $\xi <0$ and unstable if $\xi >0$.

Proof. 

Note that

$$\lambda d_S(d_R+\eta )=\xi {\sigma }^3.$$

The signs of $\lambda$ and $\xi$ are the same. Hence, the results follow from a direct application of Theorem 2. □

Corollary 1. 

Assume $h_{12}(\overline{S},0)>0$ and $h_{22}(\overline{S},0)\le 0$. If $R_0=1$, then the boundary equilibrium $E_0=(\overline{S},0,0,0)\in {\mathbb{R}}^4$ of system (16)–(19) is locally asymptotically stable in ${\mathbb{R}}_{+}^4$.

Proof. 

Since $\eta <d_R+\eta$ and

$$h_2(\overline{S},0)={\displaystyle \frac{(\sigma +d_E)(d_I+\gamma )}{\sigma }}>\gamma ,$$

we obtain $\xi <0$. The result then follows from a direct application of Proposition 2. □

Remark 5. 

The condition in Corollary 1 is satisfied by many commonly used disease transmission functions $h(S,I)$, including the mass-action/bilinear function $cSI$, the standard incidence function $cSI/(S+I)$, the Holling type function $cSI/(1+aI)$, and the media impacted function $cSI{e}^{-mI}$; see [7,8].

We consider the following air pollution model [9]

$$\begin{array}{cc}\hfill G^{\prime }\left(t\right)=& \mathsf{\Lambda }-aG\left(t\right)P\left(t\right)+b_{4}C\left(t\right)-\mu G\left(t\right),\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill P^{\prime }\left(t\right)=& aG\left(t\right)P\left(t\right)-b_{1}P\left(t\right)+b_{3}C\left(t\right),\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill C^{\prime }\left(t\right)=& b_{1}P\left(t\right)-(b_2+b_3)C\left(t\right),\hfill \end{array}$$

(23)

where $G\left(t\right)$, $P\left(t\right)$, and $C\left(t\right)$ denote the general air class, the polluted air class, and the clean air class, respectively. The pollution-free equilibrium is given by $E_0=(\overline{G},0,0)$, where $\overline{G}=\mathsf{\Lambda }/\mu$. According to [9] (Theorem 3), $E_0$ is locally asymptotically stable if $R_0<1$ and unstable if $R_0>1$, where $R_0$ is the basic reproduction number defined as

$$R_0={\displaystyle \frac{a\overline{G}(b_2+b_3)}{b_1{b}_2}}$$

(24)

We choose $n=2$ and $m=1$, and define

$$u\left(t\right)=\left(\begin{array}{c}P\left(t\right)\\ C\left(t\right)\end{array}\right)\in {\mathbb{R}}_{+}^2,v\left(t\right)=G\left(t\right)\in {\mathbb{R}}_{+}^1.$$

Consequently, the air pollution model (21)–(23) can be rewritten as (6) and (7) with

$$\begin{array}{cc}\hfill f(u,v)=& \left(\begin{array}{c}av{u}_1-b_1{u}_1+b_3{u}_2\\ b_1{u}_1-(b_2+b_3)u_2\end{array}\right),\hfill \\ \hfill g(u,v)=& \mathsf{\Lambda }-av{u}_1+b_4{u}_2-\mu v.\hfill \end{array}$$

The boundary equilibrium is $(0,\overline{v})$, where $\overline{v}=\overline{G}=\mathsf{\Lambda }/\mu$. It is easy to verify that

$$A=D_{u}f(0,\overline{v})=\left(\begin{array}{cc}a\overline{v}-b_1& b_3\\ b_1& -(b_2+b_3)\end{array}\right)$$

has a regular splitting $A=F-V$ with

$$F=\left(\begin{array}{cc}a\overline{v}& 0\\ 0& 0\end{array}\right),V=\left(\begin{array}{cc}{b}_1& -b_3\\ -b_1& b_2+b_3\end{array}\right).$$

A simple calculation gives the explicit formula of the basic reproduction number $R_0=\rho \left(F{V}^{-1}\right)$ as in (24), which is consistent with Section 3.3 of ref. [9]

If $R_0=1$, then $a\overline{v}(b_2+b_3)=b_1{b}_2$ and $s\left(A\right)=0$ is a simple eigenvalue of A with a positive left eigenvector $\alpha ={(b_2+b_3,b_3)}^T$ and a positive right eigenvector $\beta ={(b_2+b_3,b_1)}^T$. Furthermore, we compute

$$\delta =-{\left[D_{v}g(0,\overline{v})\right]}^{-1}\left[D_{u}g(0,\overline{v})\right]\beta =-{\displaystyle \frac{(-a\overline{v}s.b_4)}{-\mu }}\left(\begin{array}{c}{b}_2+b_3\\ b_1\end{array}\right)={\displaystyle \frac{b_1(b_4-b_2)}{\mu }}.$$

The only non-zero second-order partial derivative of f is

$${\displaystyle \frac{{\partial }^2{f}_1}{\partial u_1\partial v}}(0,\overline{v})=a.$$

Hence, we obtain

$$\lambda =2{\alpha }_{1}a{\beta }_1\delta ={\displaystyle \frac{2a{b}_1{(b_2+b_3)}^2(b_4-b_2)}{\mu }}.$$

Proposition 3. 

Assume $R_0=1$. The boundary equilibrium $E_0=(\overline{G},0,0)\in {\mathbb{R}}^3$ of system (21)–(23) is locally asymptotically stable (in ${\mathbb{R}}_{+}^3$) if $b_4<b_2$ and unstable if $b_4>b_2$.

Proof. 

Since the sign of $\lambda$ coincides with that of $b_4-b_2$, the conclusion follows directly from Theorem 2. □

Remark 6. 

Note that $\lambda =0$ if $b_4=b_2$. Theorem 2 is not applicable in this critical case. It would be interesting and more challenging to extend our results to the general models when both $R_0=1$ and $\lambda =0$ hold.

5. Conclusions and Discussion

In this work, we establish a simple criterion for determining the stability of biological equilibrium when the basic reproduction number equals one. We examine two distinct scenarios based on whether the equilibrium is trivial or located on the boundary. By applying the center manifold theorem, we reduce the original dynamical system to a scalar equation that preserves the local dynamics. For each case, we derive an explicit expression for the threshold parameter in terms of the partial derivatives of the nonlinear reaction term evaluated at the equilibrium. Our results have broad applications in the stability analysis of ecological and epidemiological models.

It is important to note a limitation in applying our results. When $R_0=1$, we define a threshold parameter $\lambda$ based on second-order approximations of the nonlinear system. We prove that the relevant equilibrium is locally asymptotically stable for $\lambda <0$ and unstable for $\lambda >0$. However, the critical case $\lambda =0$ remains unresolved. Third-order or even higher-order approximations of the nonlinear system are required to derive the normal form equation. The scenario where both $R_0=1$ and $\lambda =0$ hold simultaneously is left for future study.