Abstract
Herein, a matrix representation of the Hamilton quaternion group by 4 × 4 square matrices with entries equal to −1, 0, or 1 is defined. It is proven that this group, denoted as , is a group of rotational symmetries of the four-dimensional hypercube that is, a subgroup of the special orthogonal group As a consequence, is a group of rotational symmetries for each of the biological hypercubes RNY, YNY, YNR, and RNR. It is also proven that is a group of permutations of the eight cubes contained in the four-dimensional hypercube The latter is a novel result. It is also proven that the matrix quaternion group is a normal subgroup of and that the latter is a semidirect product of with a copy of the special orthogonal group also called an octahedral group because it is a group of rotational symmetries of a regular octahedron or of a three-dimensional cube.
1. Introduction
Francis Crick proposed that the almost universal genetic code could be nothing more than a frozen accident [1]. He contrasted his theory with the stereochemical theory [2] and with theories that the code was selected to minimize the effects of mutations [3,4]. It has recently been proven that Crick’s hypothesis of the freezing of the genetic code is no longer a metaphor but rather a feasible path of freezing the code [5]. Yet, the SGC exhibits several special features: it can be partitioned exactly into the two classes of aminoacyl-tRNA synthetases (aaRSs) across six dimensions [6]; it displays four equal symmetry groups when the polar requirement is used; it can be broken down into a product of simpler groups reflecting the pattern of degeneracy observed; and the salient fact that it retains clear signatures of its own evolutionary history.
There are mathematical models on the symmetries [7], optimality, and evolution [8,9,10], degeneracy [11], and uniqueness [12] of the genetic code. The distribution of the two classes of aaRSs in the genetic code obeys symmetrical patterns [13].
The search for symmetries in the SGC has been made by examining algebraic models that seek to unveil hidden symmetries [7,14,15]. For example, the SGC has been theoretically derived from a primeval RNY (R means purines, Y pyrimidines, and N any of them) genetic code [14,15] under a model of sequential symmetry breaking. Universal vestiges of these evolutionary steps have been found in the current genomes of both Eubacteria and Archaea [16,17].
A mathematical object is said to be symmetrical if it is invariant under a transformation. A symmetry group is a group of symmetry-preserving operations, e.g., rotations, reflections, and roto-reflections. The study of symmetries of the standard genetic code (SGC) provides insights into its structure, functioning, and evolution.
The table of the genetic code can be arranged in four columns: RNY, YNY, YNR, and RNR (R stands for purines, Y for pyrimidines, and N for any of them). In previous works, we have demonstrated that each column of the table can be represented in a four-dimensional hypercube [13,14,15]. We have also shown that starting from the RNY hypercube, or any hypercube, the remaining three hypercubes can be obtained by transversions in the first or third nucleobase. The whole genetic code can be represented in a six-dimensional hypercube, where each triplet is represented as a sextuple of zeros and ones.
Hamilton quaternions have been employed to represent the genetic code [16]. However, their use was not justified, as these authors made arbitrary assignments of prime quaternions to both nucleotides and amino acids [16]. Furthermore, the use of quaternions was not exploited to search for symmetries in the genetic code. Quadruplet symmetry and the supersymmetry of the genetic code have been proposed [17].
The complex plane is equivalent to the real plane Likewise, is equivalent to Hence, 4D hypercubes live in the complex space of In this space, Sir William Rowan Hamilton defined, in the 19th century, quaternion numbers. Hamilton discovered the fundamental formula for quaternion multiplication: where are the unitary vectors.
The quaternion group is a finite group generated by two elements (i and j) such that
The elements and are taken as the quadruples and respectively, the second and the third vectors of the canonical basis of the four-dimensional vector space , being the set of real numbers. Equation (1) defines a product in the four-dimensional vector space of all the quadruples of real numbers.
Taking as the vector the fourth of the canonical basis, and as the neutral element of the product, the quadruple may be represented as the linear combination The group product is extended to the vector space that becomes a noncommutative unitary ring where every non-null element is invertible. Then, it is a division ring or noncommutative body, which is called the Algebra of Hamilton Quaternions. A Cayley table describes the structure of a finite group by arranging all the possible products/operations of all the group’s elements in a square table (see Table 1).

Table 1.
A Cayley table of the quaternion group.
Herein, a matrix representation of the Hamilton quaternion group by 4 × 4 square matrices with entries equal to −1, 0, or 1 is defined. It is proven that this group, denoted as is a group of rotational symmetries of the four-dimensional hypercube that is, a subgroup of the special orthogonal group As a consequence, is a group of rotational symmetries of each of the biological hypercubes RNY, YNY, YNR, and RNR. Consequently, we extract a novel algebraic structure of the genetic code. The latter is a novel result, unsuspected in Hamilton’s time, when the genetic code was unknown. It is also proven that the matrix quaternion group is a normal subgroup of and that the latter is a semidirect product of with a copy of the special orthogonal group also called an octahedral group because it is a group of rotational symmetries of a regular octahedron or of a three-dimensional cube. It is also proven that is a group of permutations of the eight cubes contained in the four-dimensional hypercube There are 48 symmetries in each hypercube. Until now, this type of symmetry was unsuspected in the SGC. These symmetries are not hidden; they can be seen in plain sight. The article is organized as follows: We start with a unitary cube with the lattice of all triples of whole numbers. We deal with the conversion of the unitary cube [0, 1]3 onto a cube of edges of length 2 and vertices with coordinates 1 or −1. Then, we study the group of symmetries of the cube Next, the notion of the matrix quaternion group is introduced. It turns out that the matrix form of the quaternion group is a group of symmetries of the hypercube and of the lattice We arrive at 2 salient theorems: 1. The special orthogonal group, as a semidirect product of the matrix quaternion group , with a copy of the special orthogonal group and 2. The special orthogonal group is the semidirect product of its subgroups the matrix quaternion group, and the stabilizer subgroup of the point We illustrate the biological hypercubes, highlighting their 3D cubes and their possible rotations under the matrix quaternion group. Finally, we discuss the results and generalize the matricial quaternion group for the whole SGC.
2. Materials and Methods
- Unitary cube
A unitary cube, or unitary regular hexahedron, of vertices
is the Cartesian product where is the closed interval Its set of vertices is the Cartesian product , where is the binary set whose elements are 0 and 1. The set of vertices is a subset of the lattice being the set of integers (see Figure 1). The lattice is the set of points of the Abelian free group the subgroup of the additive group of the 3-dimensional vector space The center of the cube is the point obtained from the component-wise sum of the eight vertices divided by 8.
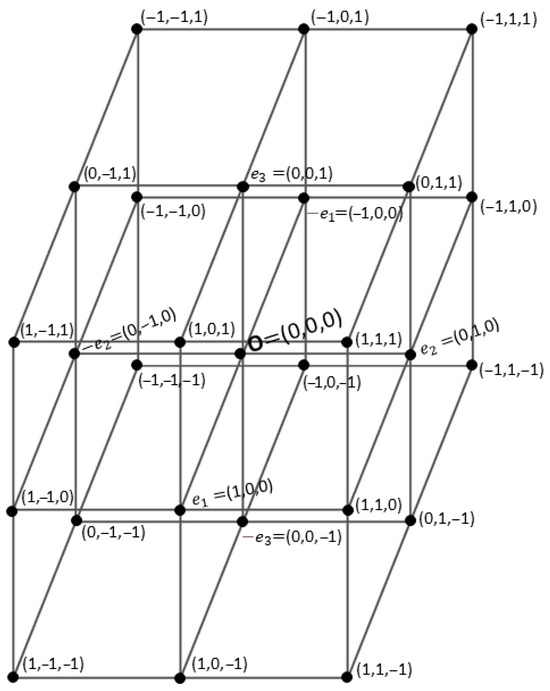
Figure 1.
The intersection of the cube with the lattice of all triples of whole numbers, which is equal to the Cartesian product (27 triples, which include the 8 vertices of the cube and the 19 inner points).
The cube is called unitary because its twelve edges have lengths equal to 1. The eight vertices are at the same distance from the center This means that the cube is inscribed into the sphere of center , and the radius is equal to whose Cartesian equation is or, equivalently,
The binary set is represented as hence, the set of vertices is represented as In it, the binary operations the so-called module 2 addition and product, respectively, are defined in such a way that the ordered triplet is a field, the smallest possible, that contains only the neutral elements of both operations. It is called the binary field, and it is the homomorphic image of the integral domain of the whole numbers under the module 2 reduction such that, for every integer being the entire part, by defect, of the fraction or, equivalently,
Conversion of the unitary cube [0, 1]3 onto a cube of edges of length 2 and vertices with coordinates 1 or −1.
Consider the affine transformation , such that which is equal to the dilatation followed by the translation This affine transformation converts the cube of center onto the cube of center the origin of coordinates. It also converts the set of vertices onto the set Notice that the affine transformation when acting over the set of vertices which is the set of all triplets of zeros and ones, converts each 0 into −1 and each 1 into itself.
3. Results
3.1. The Group of Symmetries of the Cube
In the lattice of all of the triples , where belong to the set of the integers, the only unitary vectors are those of the canonical basis and their opposites whose extremal points are the central points of the six faces of the cube. Then, the linear symmetries of the set are represented by the orthogonal 3 × 3 matrices whose columns are associated with three linearly independent vectors selected from these six. The number of such orthogonal matrices is equal to the number of orthonormal bases whose components belong to the set of these six vectors. Thus, the following takes place:
Theorem 1.
The number of orthonormal bases in the Euclidean three-dimensional vector space is equal to 48.
Proof.
As is well known, an orthogonal basis is called orthonormal if its components are unitary vectors.
- Let be any of the orthonormal bases. It is a basis whose components are pairwise orthogonal and belong to the set To form this basis, the first component, may be selected in six ways because it is any of the vectors of the set. For the second component, there are four different possibilities because it may be any of the five remaining vectors, except the opposite of the selected Additionally, for the third, it may be selected in two ways because it may be any of the four remainders, except the two opposites of the selected and Hence the total number of possibilities is equal to □
It is known that the number of orthogonal matrices is equal to the number of orthonormal bases. In fact, if an orthogonal matrix has columns C1, C2, and C3, they correspond to unitary vectors that are pairwise orthogonal and form an orthonormal basis. Conversely, if is an orthonormal basis, its three components correspond to the columns of an orthogonal matrix.
Definition of a Normal Subgroup
A subgroup H of the group G is called a normal subgroup if, for all x elements of G and all h elements of H, the conjugate xhx−1 belongs to H.
We have confirmation of the number of orthonormal bases with entire components by the following:
Theorem 2.
The number of orthogonal matrices with entries in is equal to 48.
Proof.
An orthogonal 3 × 3 matrix is named a permutation matrix if its columns are permutations of the canonical basis Its number is equal to If some of the columns are replaced by their opposites, that is, if the number 1 is replaced by −1, the matrix remains orthogonal. This may be achieved in ways because this is the number of subsets of the set of the three columns; hence, the total number of orthogonal matrices is .
- Generalization: By similar arguments, it may be shown that the number of orthogonal matrices, or orthonormal bases in the n-dimensional Euclidean vector space , is equal to The matrix variant approach:
- Consider the matrix , which represents a rotation of , or radians, around the -axis, generated by the vector
- Consider now the matrix , which also represents a rotation of , or radians, around the -axis, generated by the vector
- Next, consider the matrix which represents a rotation of , or radians, around the line generated by the vector
- Finally, consider the matrix which represents a rotation of , or radians, around the line generated by the vector The four matrices satisfy the equalitiesFrom these equalities, it follows that the group generated by and is the set of products of the form where and This is the group of all the rotational symmetries of the cube, and its number is It is the group of all the orthogonal 3 × 3 matrixes with entries in whose determinant is equal to 1. It is the group called the special orthogonal group of all the 3 × 3 orthogonal matrices with entries in and determinant equal to 1. It is the group of all the rotational symmetries of the cube , as well as the group of all the rotational symmetries of the lattice , which is the set of all the triplets of the whole numbers, and it is the free Abelian group generated by the three unitary triplets The group has an order equal to 24. The special orthogonal group is also called an octahedral group of rotations because it is a group of rotational symmetries of a regular octahedron. However, not all the symmetries of the cube are rotations. For example, the orthogonal matrix of determinants equal to −1, represents a reflection by the YZ plane, which is not a rotational symmetry. Then, the set which is a left coset of the group also has 24 elements, and they represent roto-reflections, as orthogonal matrices of determinant −1. Then, the disjoint union is the orthogonal group of all the orthogonal 3 × 3 matrices with entries in and its order is as we have seen before using different arguments. The subgroup of the group has index two. Then, it is a normal subgroup of
- Note: If we have a physically constructed cube, like the well-known cube of Rubik, it may be placed over any plane square of a size equal to any of its six faces. However, rotating it around the center of this face, it has four different positions over each of the six faces. Hence, the total number of different positions over the square is equal to 6 × 4 = 24. This confirms the fact that the number of rotational symmetries is equal to 24. □
3.2. The Matrix Quaternion Group
The four elements which are the members of the canonical basis of the vector space operate over themselves in the following way:
The quadruple of course, operates as the identity function, whose matrix, with respect to the canonical basis is the identity matrix below.
A previous note: We remind the reader that, in the plane XY, the two-dimensional Euclidean vector space a rotation of angle has a matrix, with respect to the canonical base, of the form Hence, if the matrix takes the form
How do the unitary vectors 1, i, j, and k operate over themselves? The element operates as the linear function such that,
whose matrix, with respect to the canonical basis, is
This matrix represents a double rotation: a rotation of angle in the plane XY, generated by the vectors and and another rotation, also of angle in the plane ZT, generated by the vectors and
The element operates as the linear function such that,
whose matrix, with respect to the canonical basis, is
This matrix also represents a double rotation: a rotation of angle in the plane XZ, generated by the vectors and ; and another rotation of angle in the plane YT, generated by the vectors and
The element operates as the linear function such that
whose matrix, with respect to the canonical basis, is
This matrix represents a double rotation: a rotation of angle , in the plane XZ, generated by the vectors and and another rotation, also of angle in the plane YT, generated by the vectors and
The matrices , and are orthogonal; that is, their inverses are their transposes, and they have determinants equal to 1. Additionally, and satisfy the following equalities, being
which are the defining relations of a quaternion group. Hence, the matrix group generated by the matrices and is a quaternion group, isomorphic to the quaternion group generated by the elements and In addition, each of the orthogonal transformations has, as the only fixed point, the origin of coordinates. A Cayley table of the matrix quaternion group is shown in Table 2.

Table 2.
The Cayley table of the matrix quaternion group.
Observation: The matrices , and have as columns the associated unitary vectors, members of the set Clearly, the group is a subgroup of the special orthogonal group Then, it is a group of symmetries of the four-dimensional hypercube
We now prove remarkable:
Theorem 3.
The matrix form of the quaternion group is a group of symmetries of the hypercube and of the lattice
Proof.
- Note: The lattice defines a subgroup of the additive group of the Algebra of the numerical Hamilton quaternions. The members of the lattice are the Hamilton quaternions of whole components. □
3.3. The Special Orthogonal Group, as a Semidirect Product of the Matrix Quaternion Group , with a Copy of the Special Orthogonal Group
Consider the following four orthogonal matrices:
They generate a subgroup of the special orthogonal group which is, obviously, isomorphic to the orthogonal group the group of the rotational symmetries of the three-dimensional cube We denote this group as The upper bar means the immersion of into The former is a subgroup of order 3! × 23 = 48, of the group of order 4! × 24 = 24 × 16 = 384; its index, that is, the number of its left or of its right cosets, is which is the order of the matrix quaternion group . The group is the group of all linear isometries of the four-dimensional hypercube that fix the point which is the associated vector, to the fourth column of each of the generator matrices. This means that the group is the stabilizer subgroup of the point as well as the group of all linear isometries of the cube contained in the set of all quadruples whose fourth component is equal to 1.
The intersection is the trivial unitary subgroup whose unique element is the identity matrix Hence, the product defines a group of order 48 × 8 = 384, which is the whole orthogonal group
A previous definition: A group is a semidirect product of its subgroups and if
being the neutral element of
S3: One of the subgroups is a normal subgroup. In this case,
If is normal, it is expressed as If is normal, then we write
If both subgroups are normal, it is said that is the direct product of both subgroups and is expressed as
It takes place as follows:
Theorem 4.
The special orthogonal group is the semidirect product of its subgroups the matrix quaternion group, and the stabilizer subgroup of the point However, it is not a direct product.
Proof.
- First, we prove that the matrix quaternion group is a normal subgroup of the special orthogonal group
- For this, we prove that the conjugated
- and all belong to the matrix quaternion group meaning it is invariant under the action of inner automorphisms. This is because and are generators of and , and are generators of
- Initially, we observe that the matrices and are their own inverses. This is because and are diagonal and is symmetric, meaning that they are their own transposes, which are their own inverses. □
Proof of Normality.
- (1)
- Conjugate of the generator
- Consider the following product:Then, it is proven that QM.
- Now consider the following product:Then, it is proven that
- Now consider the following product:Then, it is proven that QM.
- Now consider the following product:Then, it is proven that
- (2)
- Conjugate of the generator .
- Consider the following product:Then, it is proven that
- Now consider the following product:Then, it is proven that
- Now consider the following product:Then, it is proven that
- Now consider the following product:Then, it is proven that
- Now, the proof of the normality of the subgroup of the special orthogonal group is complete.
- Now, we have proven that the product is not direct because the orthogonal subgroup is not normal.
- That the orthogonal subgroup is not normal is seen from the fact that the conjugated matrixdoes not belong to the subgroup because its fourth column is not associated with the vector □
3.4. The Action of the Matrix Quaternion Group over the Four-Dimensional Hypercube
The set with the module 2 operations of addition and multiplication respectively, is a field or commutative division ring, and the four-dimensional hypercube with the component-wise addition and the product of the scalars 0 and 1 by the quadruples is a binary vector space, that is, a vector space, or a vector space over the field
It contains eight three-dimensional cubes: The first four are three-dimensional subspaces—solution spaces of linear systems consisting of a single equation in four unknowns, with a rank of 1 and a dimension of 4 − 1 = 3. The last four are affine three-dimensional subspaces obtained by translating the first four.
Analogously, the hypercube contains the following eight three-dimensional cubes:
Observations:
The cube is the complementary set of the cube .
It is also clear that is a subgroup of the multiplicative group , and is its only different coset. Notice that the group is a group of order 16, while its subgroup has order 8. Hence, its index is .
Now, we examine the action of the matrix
over the three-dimensional cubes contained in the hypercube
First, we observe that the action of over a quadruple is expressed as the product of the matrix by the column vector . Then, F = .
From this equality, it is deduced that the operator converts the cubes in the following way:
From this, it follows that the operator F represents a permutation of the eight three-dimensional cubes.
Let us now see the action of the matrix
over the eight three-dimensional cubes contained in the hypercube
First, let us see how acts over any quadruple . In fact, From this equality, it is deduced that the operator converts the cubes in the following way:
From this, it follows that the operator represents a permutation of the eight three-dimensional cubes.
We arrive at the following:
Theorem 5.
The matrix quaternion group is a group of permutations of the eight three-dimensional cubes contained in the hypercube
Proof.
As F and G are generators of the matrix quaternion and both represent permutations of the eight cubes, then is obviously a group of permutations of the eight three-dimensional cubes. □
3.5. Biological Hypercubes
The standard RNA genetic code defines a correspondence between the set of 64 triplets where —the set of the four RNA nucleotides (or RNA nitrogenated bases), where C = Cytosine, U = Uracil, A = Adenine, and G = Guanine—and the set of the 20 known amino acids, extended to the set where is the so-called stop signal. In such correspondence, each triplet is associated with one amino acid or the stop signal and each amino acid or the stop signal may be associated with one or more triplets. Therefore, the genetic code can be seen as a surjective function The triplets are called codons because each encodes an amino acid or the stop signal. The function is not injective, which means that an amino acid or the stop signal S may be coded by several triplets. This is why it is said that the genetic code is degenerate.
We now illustrate the actions of in 4D hypercubes. The operator converts the cubes and into the cubes and respectively. A 360-degree rotation around the center of the hypercube would match each cube into itself. A rotation of 45 degrees clockwise would convert the pair into the pair which is the result of applying the operator to the 16 quartets of −1 and 1 (Figure 2).
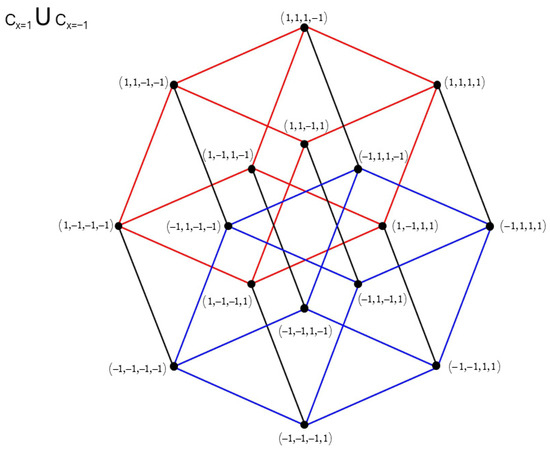
Figure 2.
The hypercube with edges of length 2 and center The cube is in red, and the cube is in blue.
The operator converts the cubes and into the cubes and respectively. A 360-degree rotation around the center of the hypercube would match each cube into itself. A rotation of 90 degrees clockwise would convert the pair into the pair which is the result of applying the operator to the 16 quadruples of −1 and 1 (Figure 3).
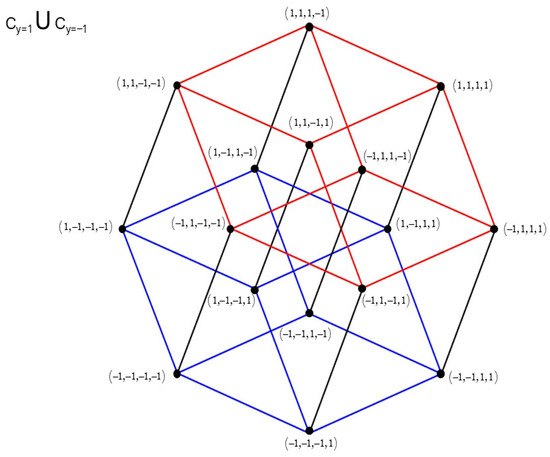
Figure 3.
The hypercube with edges of length 2 and center The cube is in red, and the cube in blue.
The operator converts the cubes and into the cubes and respectively. A 360-degree rotation around the center of the hypercube would match each cube with itself. A rotation of 90 degrees clockwise would convert the pair into the pair which is the result of applying the operator to the 16 quadruples of −1 and 1 (Figure 4).
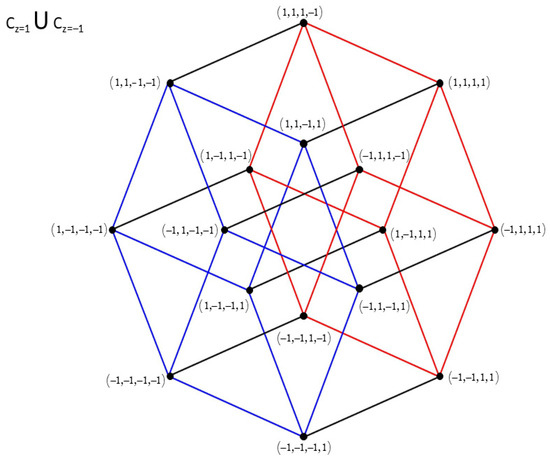
Figure 4.
The hypercube with edges of length 2 and center The cube is in red, and the cube is in blue.
The operator converts the cubes and into the cubes and respectively. A 360-degree rotation around the center of the hypercube would match each cube into itself. A rotation of 90 degrees clockwise would convert the pair into the pair which is the result of applying the operator to the 16 quadruples of −1 and 1 (Figure 5).
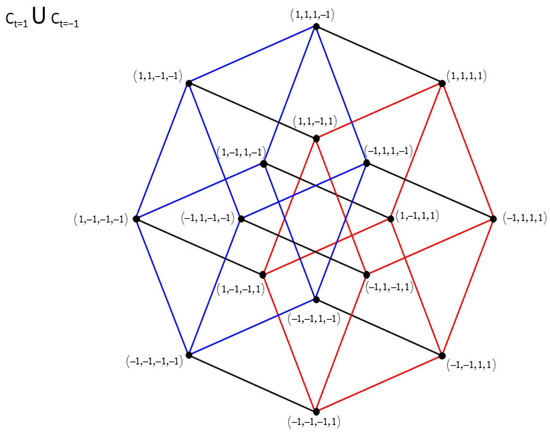
Figure 5.
The hypercube with edges of length 2 and center The cube in red, and the cube in blue.
4. Conclusions
The genetic code can be characterized by a new group of rotational symmetries. It was proven that this group, denoted as , is a group of rotational symmetries of the four-dimensional hypercube that is, a subgroup of the special orthogonal group The matrix quaternion group is a group of permutations of the eight three-dimensional cubes contained in the hypercube Consequently, is a group of rotational symmetries for each of the biological hypercubes RNY, YNY, YNR, and RNR.
It was also proven that the matrix quaternion group is a normal subgroup of and that the latter is a semidirect product of , with a copy of the special orthogonal group also called an octahedral group because it is a group of rotational symmetries of a regular octahedron or of a three-dimensional cube. It was also proven that is a group of permutations of the eight cubes contained in the four-dimensional hypercube
The quaternion group may be a factor behind the robustness and flexibility of the SGC to mutations. Quaternions are a powerful mathematical tool for representing and manipulating rotations and orientations in the three-dimensional space of the sub-cubes of 4D hypercubes representing sets of codons of RNY, YNY, YNR, and RNR.
Regarding the amino acids, let us consider the set of triplets RNY (usually the first column of the table of the genetic code). In Figure 6, the red 3D cube comprises the amino acids {Gly, Val, Ser, Ile}, and the blue 3D cube consists of the set {Asp, Ala, Asn, Thr}. A clockwise rotation of 90 degrees converts one cube into the other. Similarly, in Figure 3, Figure 4 and Figure 5, the corresponding rotations are {Gly, Val, Asp, Ala}{Ser, Ile, Asn, Thr}, {Gly, Ser, Asp, Asn}{Val, Ile, Asn, Thr}, and {Gly, Asp, Val, Ala, Ser, Asn, Ile Thr}{Gly, Asp, Val, Ala, Ser, Asn, Ile, Thr}, respectively.
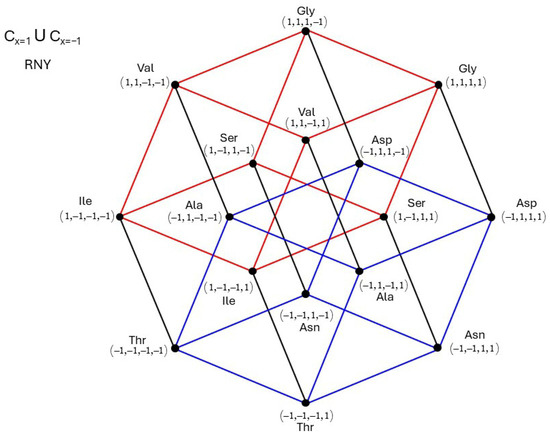
Figure 6.
The RNY hypercube indicating its 8 amino acids at the vertices.
The same exercise can be done for the YNR, YNY, and RNR triplet sets.
Matrices F and G cannot operate over the triplets because they are equivalent to sextuples of ones and minus ones. However, they can be extended to 6 × 6 matrices, adding two new rows above and two new columns to the left, in the following way:
and
These new types of matrices generate a quaternion group, isomorphic to which are rotational symmetries of the six-dimensional hypercube These matrices leave invariant the first component of a triplet and operate as the matrices F and G over the duplet NY, which is equivalent to a quadruple of ones and minus ones. In a forthcoming work, we explore the relationship between our quaternions, which are quadruplets, with the proposed quadruplet classification of the 64 codons of the genetic code [17].
Author Contributions
Conceptualization, M.V.J. and E.R.M.M.; methodology, M.V.J. and E.R.M.M.; formal analysis, E.R.M.M. and M.V.J.; investigation, M.V.J. and E.R.M.M.; writing—original draft preparation, E.R.M.M. and M.V.J.; writing—review and editing, M.V.J. and E.R.M.M.; analysis and visualization, J.R.B. All authors have read and agreed to the published version of the manuscript.
Funding
M.V.J. was financially supported by Dirección General de Asuntos del Personal Académico (DGAPA), Universidad Nacional Autónoma de México, and UNAM (PAPIIT-IN200823).
Data Availability Statement
The manuscript is theoretical, and therefore, there are no data.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Crick, F.H.C. The origin of the genetic code. J. Mol. Biol. 1968, 38, 367–379. [Google Scholar] [CrossRef] [PubMed]
- Woese, C.R. The Genetic Code: The Molecular Basis for Genetic Expression; Harper and Row: New York, NY, USA, 1967. [Google Scholar]
- Woese, C.R. Order in the Genetic Code. Proc. Natl. Acad. Sci. USA 1965, 54, 71–75. [Google Scholar] [CrossRef] [PubMed]
- Woese, C.R.; Dugre, D.H.; Saxingern, W.C.; Dugre, S.A. The molecular basis for the genetic code. Proc. Natl. Acad. Sci. USA 1966, 55, 966–974. [Google Scholar] [CrossRef] [PubMed]
- Lenstra, R.; Lenstra, C.L.; José, M.V. Crick’s “Frozen accident theory” of the genetic code explored by Ising models. J. Theor. Biol. 2025, 609, 112146. [Google Scholar] [CrossRef] [PubMed]
- José, M.V.; Zamudio, G.S.; Morgado, E.R. A unified model of the standard genetic code. R. Soc. Open Sci. 2017, 4, 160908. [Google Scholar] [CrossRef] [PubMed]
- Hornos, J.E.M.; Hornos, Y.M.M. Algebraic model for the evolution of the genetic code. Phys. Rev. Lett. 1993, 71, 4401–4404. [Google Scholar] [CrossRef] [PubMed]
- Novozhilov, A.S.; Wolf, Y.I.; Koonin, E. Evolution of the genetic code: Partial optimization of a random code for robustness to translation error in a rugged fitness landscape. Biol. Direct 2007, 2, 24. [Google Scholar] [CrossRef] [PubMed]
- José, M.V.; Zamudio, G.S. Symmetrical properties of graph representations of genetic codes: From genotype to phenotype. Symmetry 2018, 10, 388. [Google Scholar] [CrossRef]
- Wnętrzak, M.; Błażej, P.; Mackiewicz, D.; Mackiewicz, P. The optimality of the standard genetic code assessed by an eight-objective evolutionary algorithm. BMC Evol. Biol. 2018, 18, 192. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, D.L.; Giannerini, S.; Rosa, R. On the origin of degeneracy in the genetic code. Interface Focus 2019, 9, 20190038. [Google Scholar] [CrossRef] [PubMed]
- Zamudio, G.S.; Jose, M.V. On the uniqueness of the standard genetic code. Life 2017, 7, 7. [Google Scholar] [CrossRef] [PubMed]
- José, M.V.; Morgado, E.R.; Bobadilla, J.R. Groups of symmetries of the two classes of synthetases in the four-dimensional hypercubes of the Extended Code type II. Life 2023, 13, 2002. [Google Scholar] [CrossRef] [PubMed]
- José, M.V.; Morgado, E.R.; Govezensky, T. An extended RNA code and its relationship to the standard genetic code: An algebraic and geometrical approach. Bull. Math. Biol. 2007, 69, 215–243. [Google Scholar] [CrossRef] [PubMed]
- Palacios-Pérez, M.; José, M.V. The evolution of proteome: From the primeval to the very dawn of LUCA. Biosystems 2019, 181, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Carlevaro, C.M.; Irastorza, R.M.; Vericat, F. Quaternionic representation of the genetic code. Biosystems 2016, 141, 10–19. [Google Scholar] [CrossRef] [PubMed]
- Rosandić, M.; Paar, V. The Evolution of Life Is a Road Paved with the DNA Quadruplet Symmetry and the Supersymmetry Genetic Code. Int. J. Mol. Sci. 2023, 24, 12029. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).