Transient Dynamic Analysis of Composite Vertical Tail Structures Under Transportation-Induced Vibration Loads

Abstract

The potential damage to aviation products caused by vibration and shock during road transportation has long been overlooked, despite structural failure under dynamic loading emerging as a critical technical challenge affecting product reliability. For aviation components, both stress and vibration analysis are essential prerequisites prior to formal assembly. This study investigates a symmetric vertical tail, a common aviation structure, employing an innovative model group analysis method to characterize its dynamic stress and strain distributions under real transportation conditions. Experimental measurements of vibration acceleration and impact loads during transport served as input data for constructing a numerical model based on stress and vibration theory. The model elucidates the mechanical responses of the tail in both modal and vibrational states, enabling effectively evaluation of dynamic vibrations on the tail and its critical subcomponents during road transport. The findings provide actionable insights for optimizing aviation component packaging design, mitigating vibration-induced damage, and enhancing transportation safety.

1. Introduction

As key components of aviation equipment, the safety and reliability of structural parts during transportation directly impact overall system performance and mission success. With the rapid advancement of aviation technology, structural components are increasingly designed to be larger, more precise, and lighter [1,2,3]. For instance, typical parts—such as titanium alloy frames combined with carbon fiber-reinforced composite panels—require micron-level surface accuracy and stringent control of residual stress control withstand extreme operational conditions [4,5,6]. Consequently, quantitative analysis of stress and strain distributions during transportation is critical for evaluating product performance.

Large packaging containers are transported via land, sea, or air, each subjecting cargo to varying levels of vibration and shock. Among these, land transportation induces the most severe vibrations, particularly under poor road conditions. Thus, the structural design of aviation component packaging must account for complex and dynamic vibration environments, including random vibrations, cyclic shocks, and low-frequency, high-amplitude oscillations [7,8,9]. Statistical data indicate that approximately 30% of transportation-related damage in aerostructures stems from vibration-induced fatigue crack propagation and interfacial debonding [10,11,12]. Notably, during land transport, the cumulative effect of vibrational loads can cause irreversible alterations in the dynamic behavior of structural components. As a result, developing packaging systems with high-performance vibration damping has emerged as a critical technical challenge in land transportation engineering [13,14].

In conventional vibration-absorbing packaging design, passive cushioning materials such as foam and rubber remain the primary solution. Inspired by grapefruit peels, Hu [15] developed a biomimetic multifunctional composite material capable of resisting diverse external impacts, thereby improving product durability. However, this approach relies heavily on intrinsic material properties for vibration damping and suffers from inherent limitations, including inefficient energy absorption and narrow frequency-band adaptability. To address these issues, Lee [16] proposed a topology-optimized foam cushioning design to enhance vibration resistance while minimizing packaging volume. Although effective for low-velocity impacts, such materials exhibit stress hardening under high-frequency vibrations, leading to over 50% attenuation in damping performance.

Vibration isolators incorporating spring-damping elements are widely adopted for large packaging due to their adaptability and reliability. Qu [17] introduced a parallel air spring isolation system for precision equipment transport across varying road conditions, achieving high isolation efficiency and lateral stability. Huang [18] designed a compact transmission-blocking structure integrating piezoelectric actuators and rubber isolators to suppress vibration propagation, demonstrating harmonic reduction alongside broadband attenuation. Li [19] developed a self-induced vibration suppression device using a solid-liquid friction nanogenerator, where a liquid-tuned damper unit improved damping efficiency by 19.6%. Dynamic dampers leveraging anti-resonance characteristics are another effective solution. Hu [20] replaced conventional dampers with an inertial mechanical network, achieving superior damping performance. To simultaneously mitigate transverse, torsional, and axial vibrations in rotor systems, He [21] designed a bionic spider-web dynamic damper, which not only meets multi-axis damping requirements but also reduces size, mass, and component count. Kakou [22] and Joubaneh [23] demonstrated that electromagnetically grounded sensors offer optimal damping performance. Liu [24] reviewed advances in inertial vibration isolators across automotive, civil, marine, and power transmission engineering, highlighting their potential to enhance performance and reduce costs.

Enhancing the safety of aerostructural components during transport also hinges on rational packaging design. By analyzing dynamic characteristics, the safety performance of these components can be more intuitively assessed. Lee et al. [25] employed finite element simulations to predict peak accelerations in packaging under real-world impact and vibration. Bernad et al. [26] studied deformation in multilayer stacked packages under mechanical excitation, identifying external loads and system properties as key influencing factors. For complex-shaped products with uneven mass distribution, empirical cushioning design methods often fail to ensure sufficient energy absorption. Kim [27] proposed an analytical-experimental optimization process, reducing package volume by 22% and maximum acceleration by 25%. Zhang et al. [28] investigated random vibration effects on cargo safety, using stacking height and road unevenness as critical factors to optimize multilayer packaging. Pan [29] analyzed road-transport vibration characteristics at launch sites and developed a virtual instrument-based monitoring system.

The demand for lightweight structures to improve fuel efficiency has elevated composites for their high specific strength and stiffness as core materials for load-bearing components [30,31,32,33,34]. However, composite structures are more susceptible to manufacturing defects and in-service damage than metals [35,36,37,38,39], necessitating rigorous damage studies to ensure reliability. Vertical tail structures, comprising composites and metal parts, require precise stress–strain evaluation during transport to guarantee safety. Current mechanical testing methods, such as contact sensors and optical nondestructive testing, lack real-time monitoring capabilities for transport processes [40,41,42], limiting accurate assessment of dynamic structural evolution.

Combining experimental tests with finite element simulations has emerged as a robust tool for analyzing transport-induced vibrations. Vibration data collection typically involves laboratory-based virtual tests or real-world transport trials [43]. To evaluate the dynamic response of a symmetric vertical tail (SVT) in a wooden packaging box (WPB) under actual transport conditions, this study employed triaxial accelerometers to monitor impact loads throughout the transport chain. A refined finite element model was developed using measured load spectra to elucidate stress and strain evolution in critical substructures, revealing damage mechanisms in stress-concentration zones. By correlating transport loads with structural safety at the mechanical response level, this work provides theoretical support for WPB optimization.

2. Materials and Testing

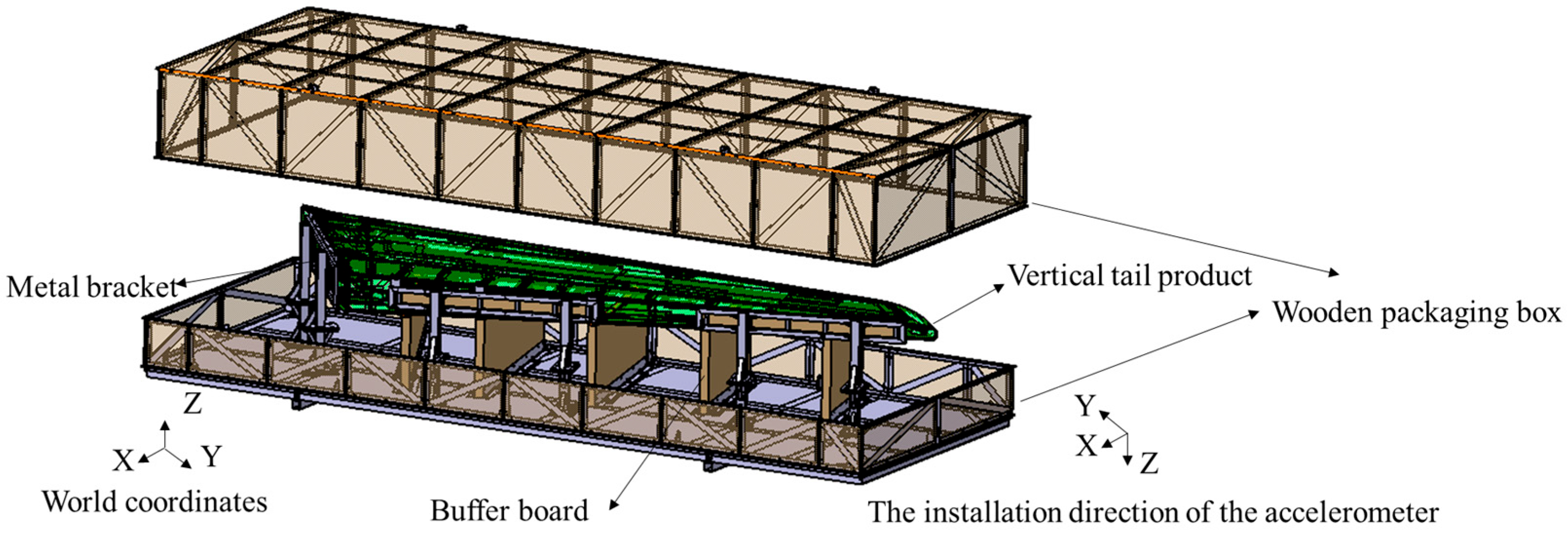
2.1. Geometry Models

Figure 1 illustrates an assembly model comprising four primary components: the symmetric vertical tail (SVT), wooden packaging box (WPB), metal support structure, and buffer boards. The SVT has approximate dimensions of 8650 mm (length) × 3700 mm (width) × 600 mm (height) and a mass of 429 kg. Its construction primarily includes metal structural elements, composite sandwich panels, and composite laminates.

2.2. Material Properties

For flakeboard, metal, and bufferboard, key parameters include density (ρ) and elastic modulus (E). The WPB flakeboard is fabricated by gluing and compressing renewable wood chips to minimize the inherent anisotropy of natural wood. Consequently, the flakeboard is treated as isotropic in this study, with material properties detailed in

Table 1. Material parameters of flakeboard, metal, and bufferboard.

Name	ρ/(kg/m3)	E/(N/m2)	v
Metal	2.7 × 103	6.9 ×1010	0.33
Flakeboard	4 × 102	9.8 × 109	0.35
Bufferboard	1 × 103	6.1 × 106	0.49

.

The plain composite laminate (PCL) is a 17-ply laminate and the variable-thickness laminate (VTL) is 43-ply laminate. Their stacking sequence and mechanical properties are listed in

Table 2. Stacking sequence of composite laminates.

Name	Stacking Sequence
Plain composite laminates (PCL)	[45/−45/0/45/90/−45/45/0/−45/90/45/−45/−45/−45/−45/−45/45]
Variable-thickness laminates (VTL)	[45/90/90/−45/0/−45/0/−45/45/45/90/−45/−45/−45/013/−45/05/−45/0/0/45/0/0/45/−45/−45/45]
Aramid honeycomb sandwich	[45/−45/0/45/90/−45/45/0/45/90/−45/45]

,

Table 3. CFRP matrix composite materials elastic parameters.

Name	Ex/GPa	Ey/GPa	Ez/GPa	Gxy/GPa	Gxz/GPa	Gyz/GPa	Vxy
CFRP	120	8.9	8.9	4.53	4.53	4.53	0.32

and

Table 4. CFRP matrix composite materials strength parameters.

Name	XT/MPa	XC/MPa	YT/MPa	YC/MPa	ZT/MPa	ZC/MPa	Sxy/MPa	Sxz/MPa	Syz/MPa
CFRP	2380	1236	216	133	216	133	133	86	200

. For carbon fiber reinforced plastics (CFRP) laminates, E_x, E_y, and E_z are the elastic moduli along in-plane fiber direction, transverse to fiber direction and thickness direction, respectively. G_xy, G_xz, and G_yz are the three shear moduli, and v_xy is the in-plane Poisson’s ratio. X_T, Y_T, and Z_T are the longitudinal, transverse, and interlaminar tensile strengths. X_C, Y_C, and Z_C are the longitudinal, transverse, and interlaminar compressive strengths, respectively. S_xy, S_xz, and S_yz represent the XY, XZ, and YZ shear strengths.

The aramid honeycomb sandwich panel consists of skin layers and core structure. The skin layer is a 12-ply laminate with the stacking sequence listed in Table 2. The hexagonal aramid honeycomb core is inserted between the 90° and −45° plies (i.e., penultimate and third layers), where L, W are parallel, perpendicular to the honeycomb strip direction, and T is along to honeycomb thickness direction. The strength and modulus in each direction are listed in

Table 5. Aramid honeycomb material parameters.

Name	Grid Material Thickness/mm	Grid Length/mm	T-Directional Modulus/MPa	L-Directional Modulus/MPa	W-Directional Modulus/MPa	L-Directional Shear Strength/MPa	W-Directional Shear Strength/MPa
Aramid honeycomb	0.084	2.75	4.48	15.17	31.03	0.62	0.66

.

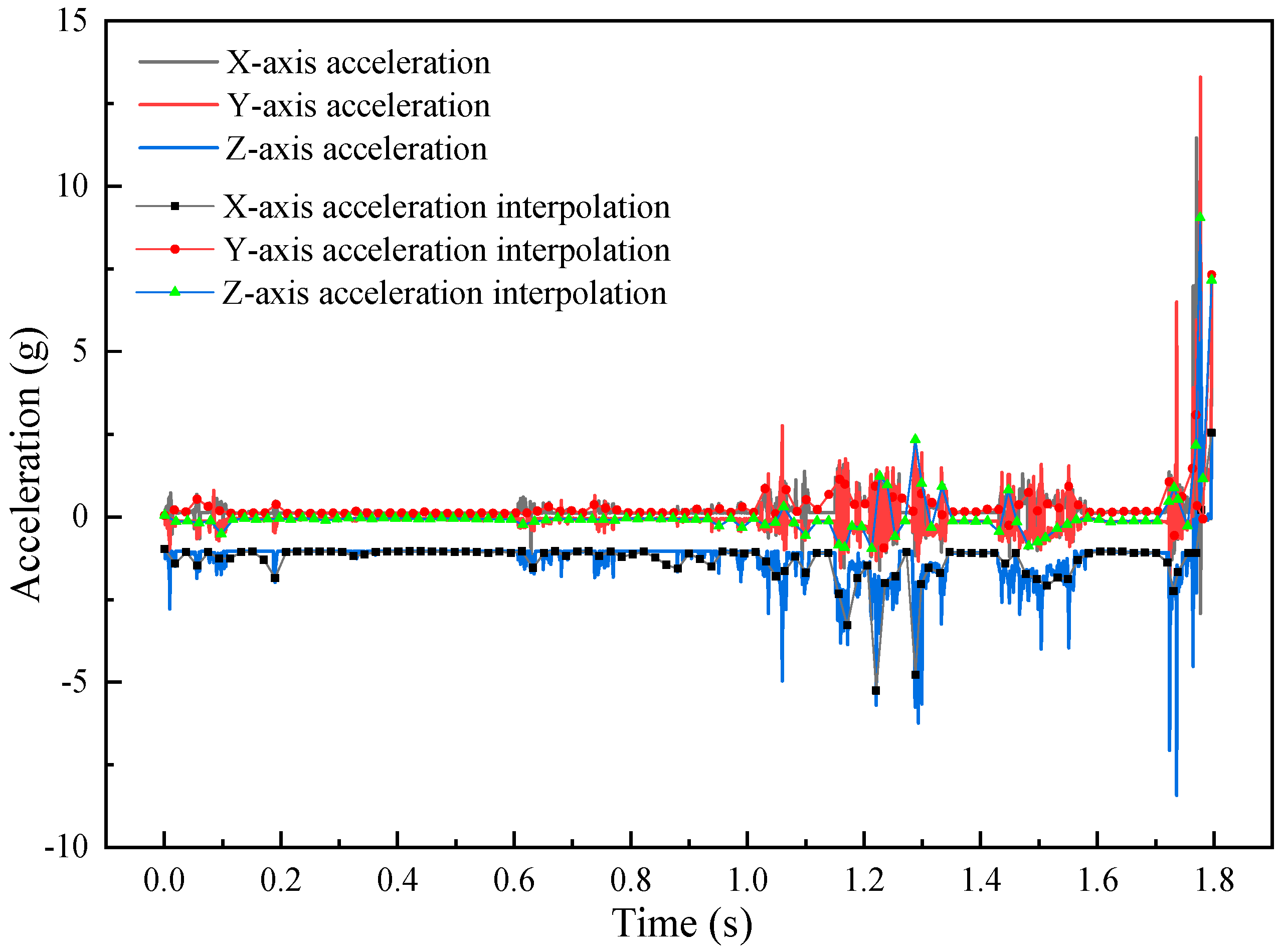
2.3. Transportation Vibration and Shock Testing

Aircraft structural components are typically transported from manufacturing facilities in specialized packaging systems equipped with internal sensors to monitor vibration and shock profiles. The vibrational response of aircraft components during road transport is influenced by multiple factors, including road surface conditions, vehicle mechanical status, transportation speed, and driver operation techniques. The primary vibration and shock excitation sources in road transportation can be classified into four fundamental types: sinusoidal vibration, periodic vibration, random vibration, and discrete shock events [26]. During actual transport operations, the SVT experiences complex vibrational loading resulting from the vector superposition of multiple shock types acting simultaneously in all three orthogonal axes (X, Y, and Z). This superposition effect is particularly pronounced due to road surface turbulence and vehicle dynamics.

To precisely characterize the SVT’s dynamic response during transportation, a triaxial accelerometer (model MT-Shock300-EB, Nanjing Meditech Technology Co., Ltd., Najing, China) was installed inside the packaging structure. This instrumentation serves to record shock impulses, vibration spectra, and acceleration transients providing quantitative data for assessing the SVT’s transport-induced dynamic loading. The accelerometer was configured with a sampling frequency of 1000 Hz (sufficient to resolve all relevant frequency components), a measurement range of ±300 g (adequate for transport loading scenarios), and a temperature stability of ±0.5% over −40 °C to +85 °C (ensuring reliability under varying environmental conditions). The acquired acceleration data (Figure 2) provide peak acceleration magnitudes, shock duration characteristics, frequency domain profiles, and root-mean-square vibration levels. This comprehensive dataset enables rigorous evaluation of packaging system performance, structural response characteristics, and potential damage mechanisms during the complete transportation cycle. The experimental setup and data collection protocol were designed to meet ASTM D4169 standards [44] for transportation simulation testing.

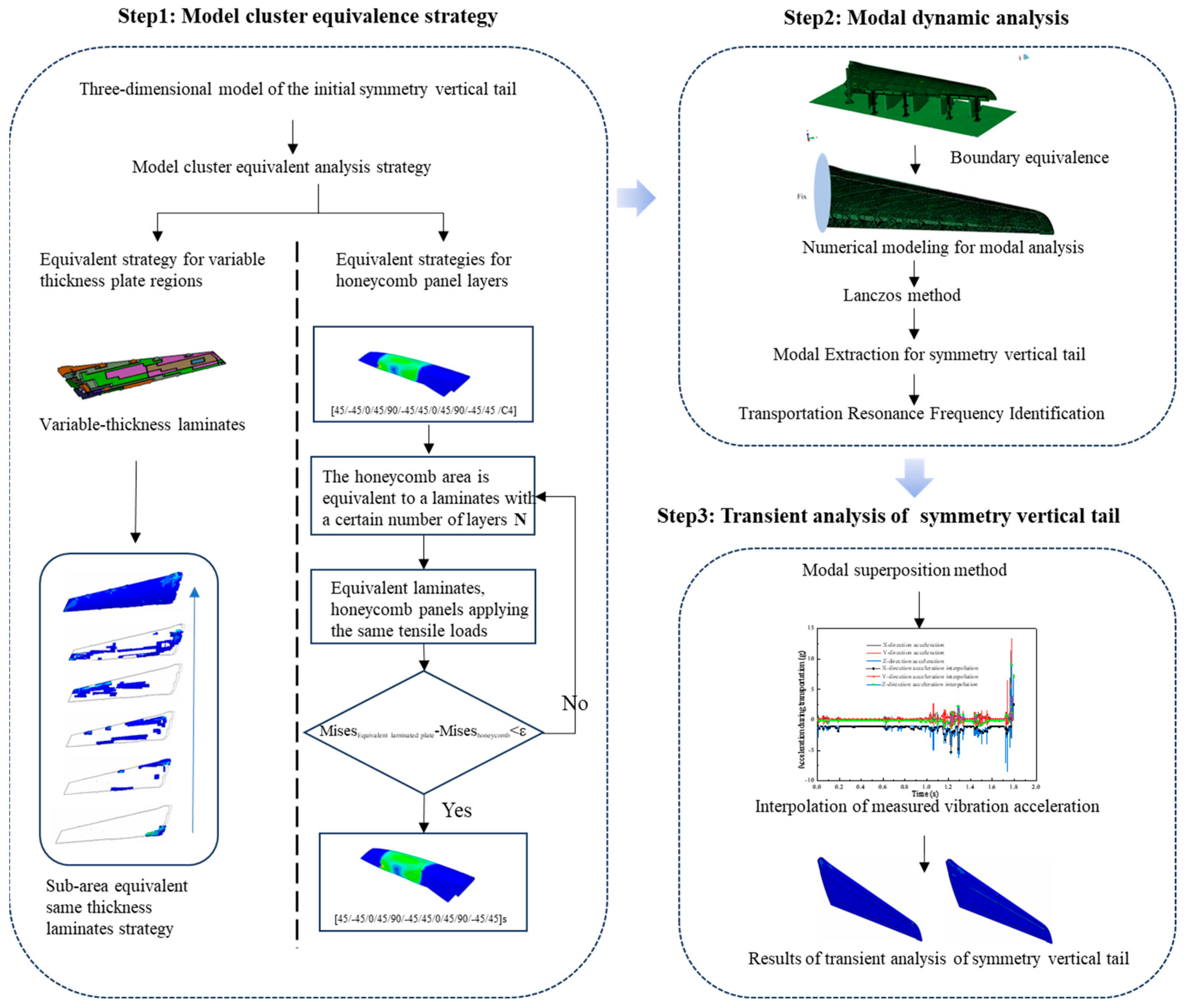
3. Methods and Numerical Modeling

This study investigates the dynamic characteristics of the SVT in the air transportation environment through a full-scale analysis system, as illustrated in Figure 3. Based on stress and vibration theory, a high-fidelity finite element model of the physical specimen was established, and a novel model group equivalent (MGQ) method was proposed for the characteristics of complex assemblies, as described below.

Firstly, in the MGO method, the thickness regionalization equivalent method was used to analyze the variable-thickness composite components, and it is named as variable-thickness laminates (VTLs). The honeycomb sandwich structure was analyzed by calculating the stress difference between the equivalent laminate and the honeycomb sandwich structure within an acceptable error threshold (0.1 MPa) to obtain an equivalent laminate strategy. It is named as honeycomb-equivalent laminates (HELs).

Secondly, to address computational bottleneck in transportation-condition analysis, a three-phase optimization scheme was implemented, including (a) the equivalent replacement of the packing box supports by fixed-end constraints at endpoints (Boundary Conditions), (b) the deployment of a 20 mm hexahedral-dominant meshes in critical stress zone and the verification of mesh independence to confirm convergence at 560,875 nodes (Meshing Strategy), and (c) the construction of a general contact system with tangential Coulomb friction coefficient of 0.3 and normal hard contact with a Lanczos eigenvalue solver to obtain the first 20 modal parameters (Contact Algorithm).

Finally, to account for the non-stationary road spectrum, a cubic spline interpolation algorithm was used to spatiotemporally reconstruct the measured acceleration time histories, generating 100 equivalent load nodes. The solid line in Figure 2 represents the actual collected vibration acceleration, and the dashed points represent the interpolated inputs for numerical modeling. The transient analysis was performed via the modal superposition method to resolve the transient stress and strain distribution. All simulations were conducted in ABAQUS 2022, providing a robust framework for aviation equipment airworthiness verification.

In order to ensure SVT safety during transportation and operational reliability, the minimum stress of the SVT during transportation is taken as the standard for the evaluation of the transportation process. According to the permissible requirements of safety factor verification, composite assemblies are required to meet 1.5 times the safety factor. In this study, the design allowable value was obtained by dividing the strength parameters of CFRP materials in Table 4 of the manuscript by the safety factor (1.5). For the transportation safety of the SVT, the base limit value of 65 MPa was selected as the design’s allowable strength to further improve the safety. Taking the SVT fixation within the wooden packaging box (WPB) as the modeling objective, the SVT stress concentration zones were identified to provide design guidelines for WPB optimization and safe transit protocols.

4. Results and Discussion

4.1. Modal Analysis

The Lanczos method has been widely adopted in structural eigenvalue extraction due to its computational accuracy and efficiency [45,46,47]. In this study, this method was employed to obtain the first 20 orders of constrained modal parameters for the SVT, as summarized in

Table 6. Results of constrained modal analysis of SVT.

Modal Order	Frequency (Hz)	Effective Mass Fraction
		X-Flat	Y-Flat	Z-Flat	X-Turn	Y-Turn	Z-Turn
1	9.0452	1.34 × 10−7	1.65 × 10−8	4.34 × 10−2	5.31 × 105	5.85 × 107	18.693
2	16.476	1.34 × 10−2	9.52 × 10−3	9.42 × 10−8	1.8007	140.01	1.78 × 107
3	24.901	9.64 × 10−8	9.00 × 10−10	1.77 × 10−2	1.58 × 105	2.60 × 107	7.3503
4	25.256	2.87 × 10−5	6.35 × 10−7	2.86 × 10−5	252.99	41,797	1867.4
5	25.759	1.27 × 10−6	1.56 × 10−6	1.28 × 10−3	4052.4	1.59 × 106	3374.5
6	29.389	8.32 × 10−5	1.86 × 10−5	8.35 × 10−3	1.52 × 105	1.20 × 107	56,150
7	31.573	6.12 × 10−5	5.08 × 10−5	3.38 × 10−2	7.43 × 105	4.95 × 107	1.03 × 105
8	32.691	3.76 × 10−6	1.65 × 10−7	4.56 × 10−2	7.53 × 105	6.55 × 107	659.21
9	36.57	1.79 × 10−5	8.20 × 10−6	1.40 × 10−2	4.69 × 105	2.16 × 107	23,295
10	37.039	1.82 × 10−6	1.03 × 10−5	6.62 × 10−3	1.89 × 105	1.00 × 107	13,985
11	39.906	1.08 × 10−5	1.31 × 10−6	4.72 × 10−2	2.47 × 105	6.60 × 107	67.868
12	42.094	1.54 × 10−5	5.44 × 10−7	0.26379	3.59 × 106	3.86 × 108	290.97
13	45.362	1.37 × 10−6	2.00 × 10−8	2.20 × 10−3	27,981	3.14 × 106	34.003
14	45.434	1.76 × 10−6	5.70 × 10−8	4.41 × 10−3	56,916	6.31 × 106	9.7166
15	47.225	7.21 × 10−7	3.96 × 10−6	3.39 × 10−4	3790.3	5.00 × 105	723.14
16	53.528	6.71 × 10−4	3.16 × 10−4	3.23 × 10−4	12,441	4.99 × 105	9.97 × 105
17	55.737	1.46 × 10−3	9.56 × 10−4	3.77 × 10−5	456.57	52,979	2.66 × 106
18	59.981	5.45 × 10−5	1.79 × 10−5	7.80 × 10−5	588.49	1.08 × 105	35,943
19	65.175	2.19 × 10−5	8.42 × 10−6	1.68 × 10−3	168.09	1.97 × 106	18,513
20	65.524	2.26 × 10−5	1.69 × 10−5	1.14 × 10−4	35,069	2.38 × 105	34,218

.

It can be seen that the first 20 modal frequencies range from 9.0452 Hz to 65.524 Hz. The Z-direction translational effective mass ratio (0.49/0.52 = 94%) exceeds the 90% threshold, confirming the sufficiency of 20 modes for transient analysis. The contribution of the rotational degrees of freedom is higher in the first six order modes. Specifically, Z-axis rotation dominates in the 1st mode; X- and Y-axis rotation dominates in the 2nd mode; Z-axis rotation dominates in the 3rd mode; Y- and Z-axis rotation dominates in the 4th mode; X- and Z-axis rotation dominates in the 5th mode; and Z-axis rotation dominates in the 6th mode. Among the first 20 modes, the maximum rotational response occurs in the 18th mode (59.981 Hz), and the maximum Z-direction translational response occurs in the 12th mode (42.094 Hz). The analysis of effective mass fractions reveals the dominant vibration directions for each modal order, providing critical insights into the structure’s dynamic behavior. This modal decomposition forms the foundation for subsequent transient response analysis.

Figure 4 demonstrates the SVT stress and strain evolution at different modal orders. Both stress and strain exhibit a non-monotonic increasing trend with higher modal orders and the distinct peaks occur at the 11th, 15th, and 18th modal orders.

Figure 5 illustrates the SVT stress distribution at the 11th, 12th, 15th, and 18th order modes. The stress concentration occurs in the upper-right region at the 11th mode (39.906 Hz), and it shifts to the upper-left region at the 18th mode (59.981 Hz). At the 12th and 15th modes, there is a broader stress distribution, which helps to reduce the stress concentration effects. Nevertheless, it shows significantly higher stress–strain magnitudes than other modes.

Therefore, considering the trends of effective mass fraction and stress–strain, special attention should be paid to avoid the resonance phenomenon with 39.906 Hz (11th mode), 42.094 Hz (12th mode), 47.225 Hz (15th mode), and 59.981 Hz (18th mode) during transportation to improve the safety of SVT during transportation.

To better characterize the structural deformation patterns at natural frequencies, this study examines the first six orders of constrained mode shapes for the SVT, as illustrated in Figure 6 and Figure 7. The analysis reveals several key findings regarding stress and strain distribution.

It is observed that in the 1st to 6th modes, the evolution of stress concentration is progressive, merging from dual concentration regions to a single dominant region, and the affected area is gradually expanding with increasing mode order. The strain distribution patterns consistently correlate with stress concentration regions.

In the 1st and 2nd modes, the stress concentration is localized at the SVT upper section. In the 3rd and 4th modes, the stress concentration shifts to the SVT base region. In the 5th and 6th modes, the stress concentration returns to the SVT upper structure. It indicated that the natural frequency excitation during transport significantly alters the spatial distribution of stress–strain fields and magnitude of localized deformation. Therefore, reducing the resonance phenomenon during transportation can further reduce the stress–strain values of the symmetric droop tail structure.

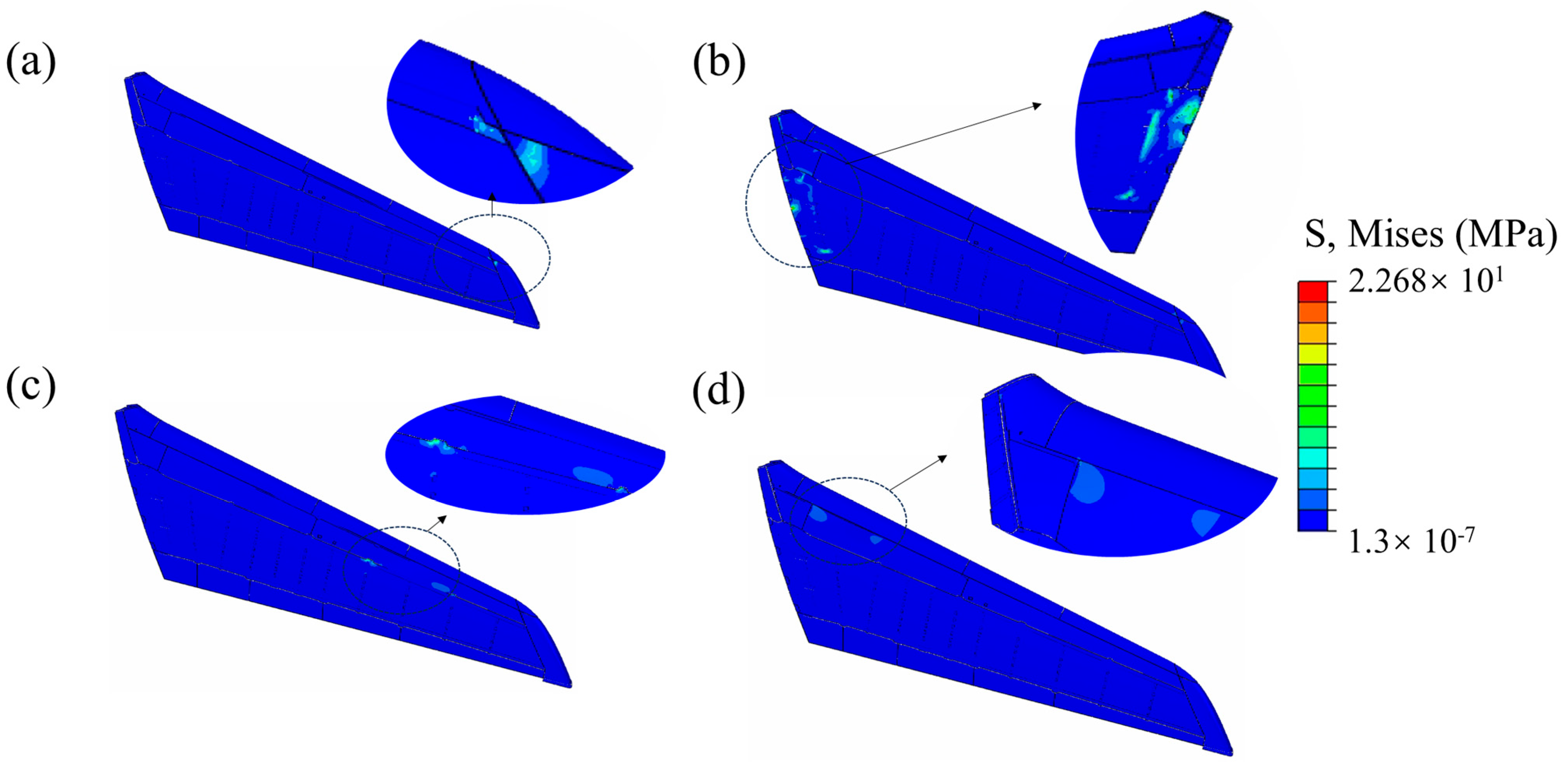
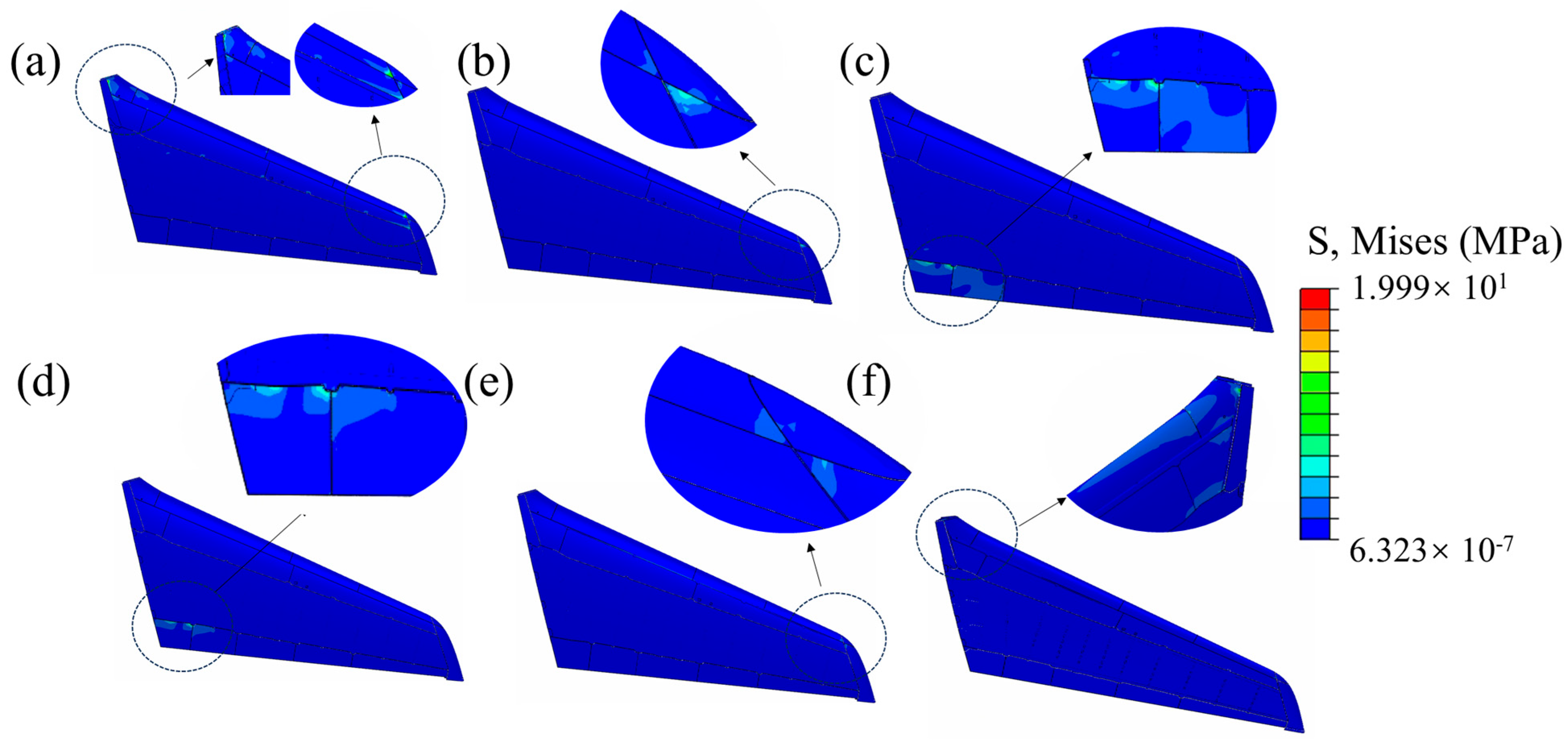
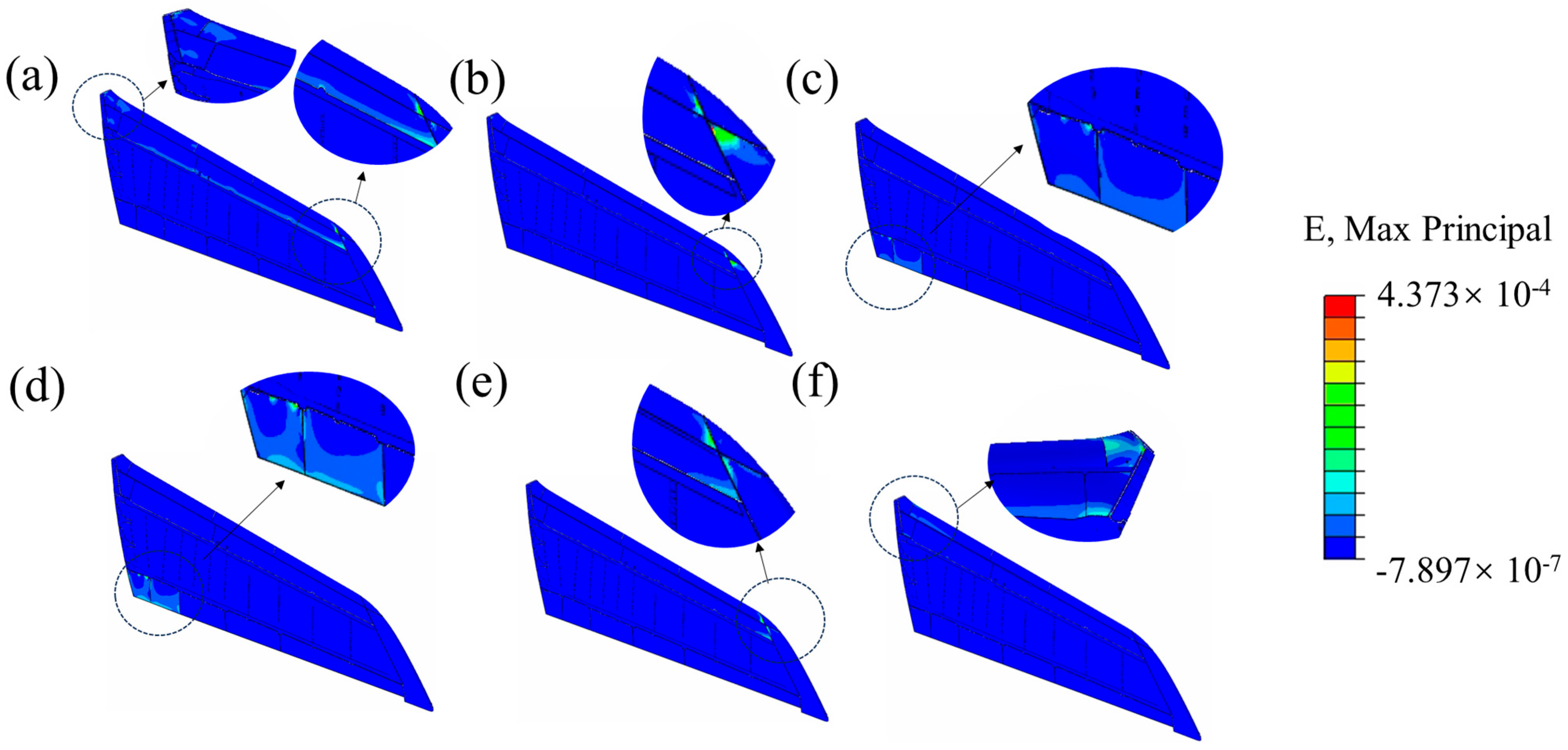
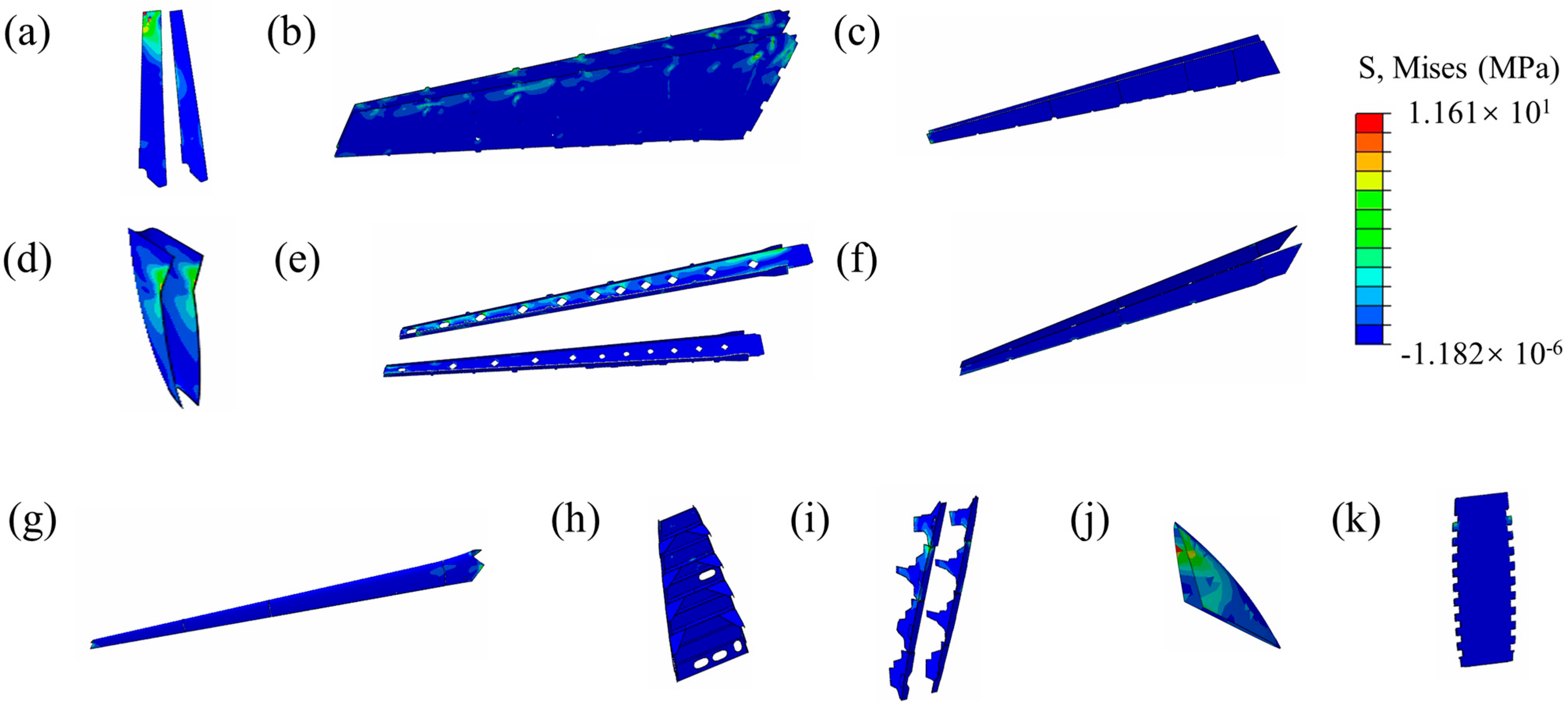
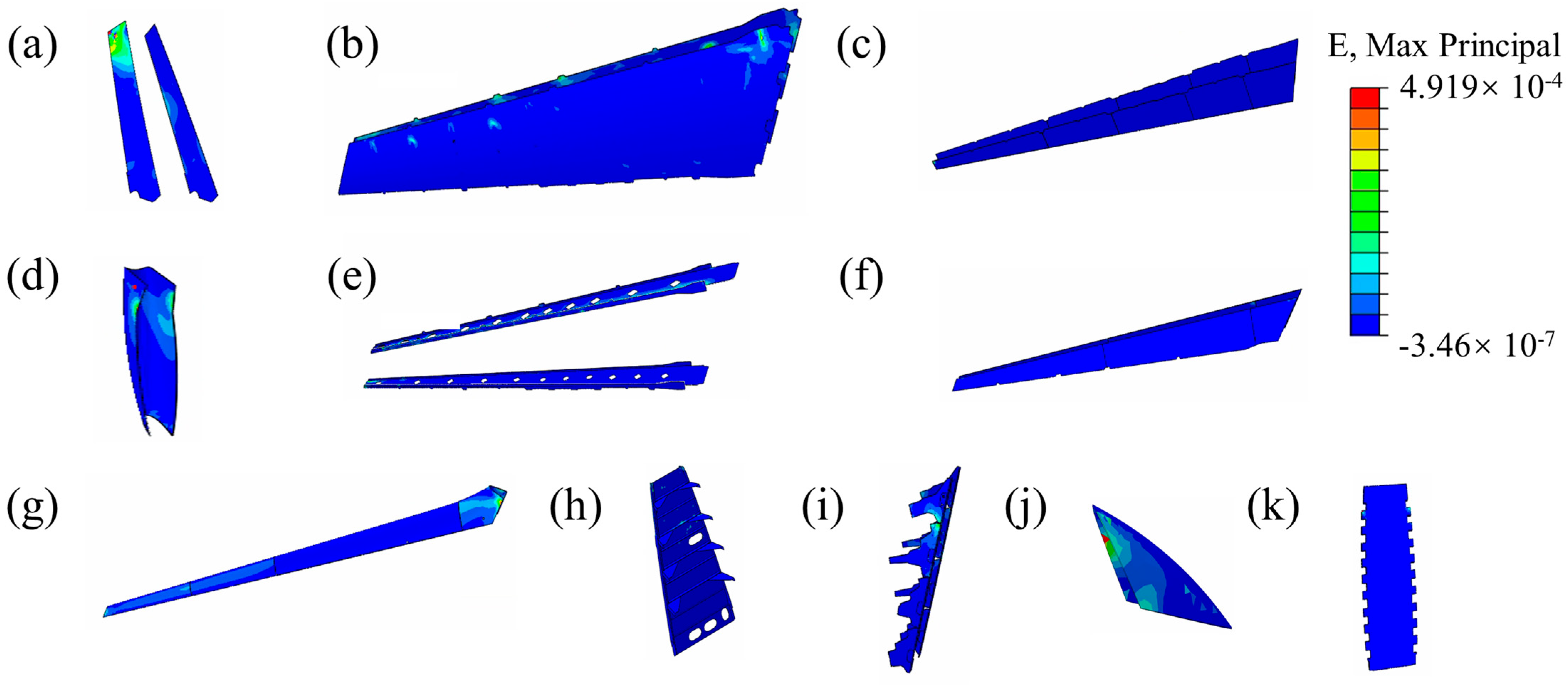
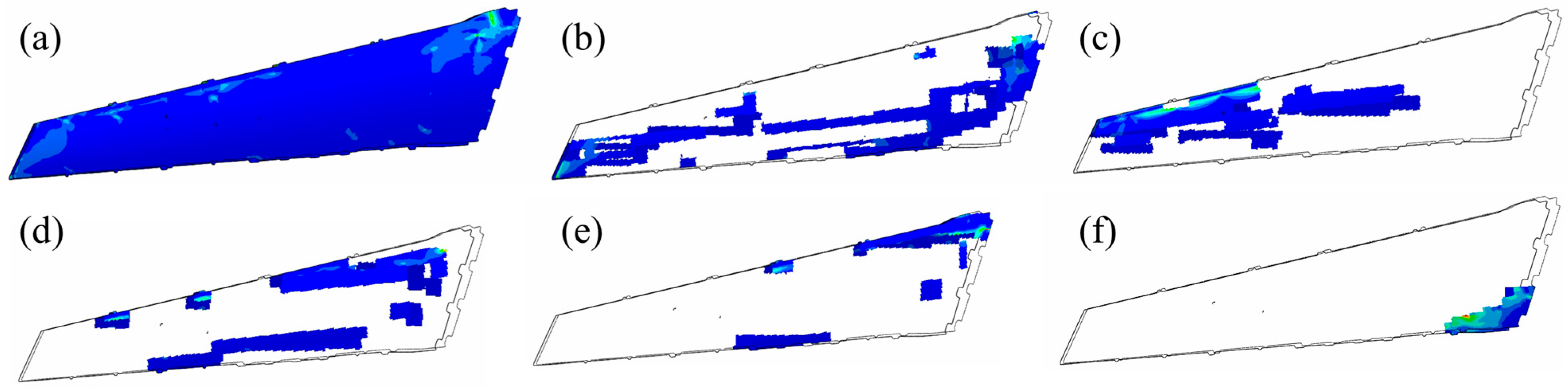
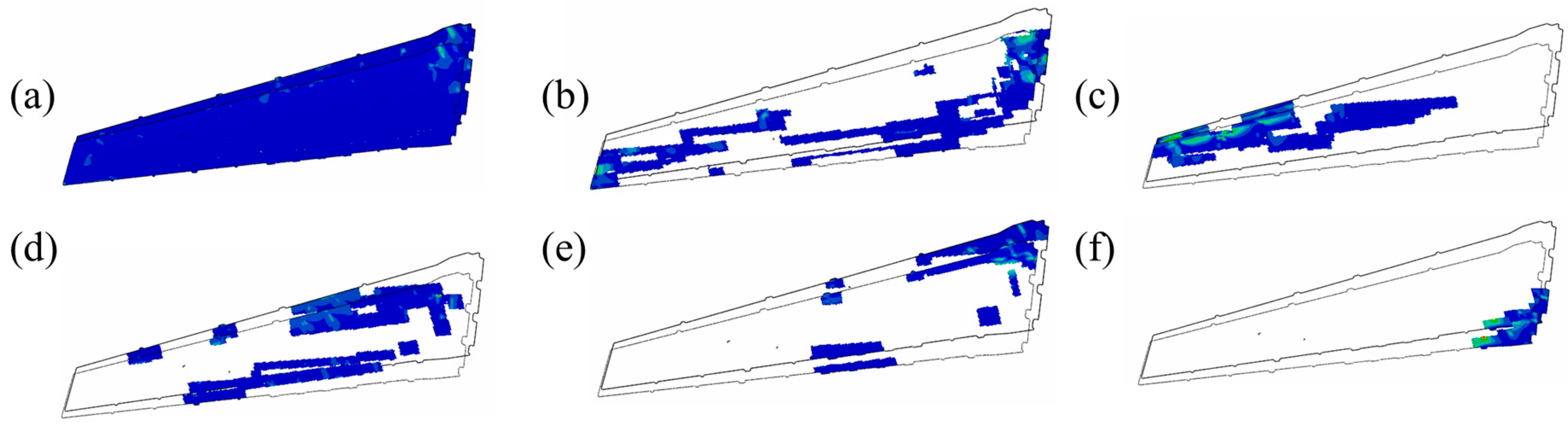
4.2. Transient Dynamics Analysis of SVT

Based on the modal analysis results (Table 6), the highest frequency among the first 20 modes of the SVT during transportation is 65.524 Hz, corresponding to a period of 0.015 s (1/65.524). To ensure numerical accuracy in the transient analysis, the time increment was smaller than the period value and set to 0.005 s (1/3 of the minimum period). The total analysis duration was 5 s to adequately capture vibration decay. A damping ratio of 0.09 was applied for the 1–100 Hz frequency range [48], because the lower damping ratios prolong vibration decay and the higher damping reduces peak stress amplitudes.

(1)

Stress–strain response to transportation shock

According to the calculation results of the modal superposition method, the SVT’s dynamic response is shown in Figure 8. The stress–strain distribution shows that during transportation, the maximum stress of 11.61 MPa and the maximum strain of 491.9 με are induced by triaxial vibration acceleration impacts. The peak stress is 82% below the 65 MPa threshold specified in aviation transportation standards. This confirms the adequacy of the packaging box design, the structural integrity during transport, and absence of fatigue-critical stress concentrations.

To comprehensively characterize the transient response of the SVT during transportation, this study analyzed the stress–strain distribution across typical structural components, as illustrated in Figure 9 and Figure 10.

For the composite components (Figure 9a–g), the peak stress (11.61 MPa) is located in the upper component of Figure 9g. For the metal metallic components (Figure 9h–k), the peak stress (8.026 MPa) is located in the upper component of Figure 9h. Accordingly, targeted reinforcement of upper packaging regions with enhanced cushioning materials could reduce peak stresses during transport. The components (Figure 9b,d,e,i,j) have relatively uniform stress distribution, while the stress concentration is observed on the components (Figure 9a,c,f,k). Although the overall stress is less than the permissible requirement, the service life of the structure can be significantly extended by alleviating the stress concentration phenomenon.

Figure 10 illustrates the strain distribution of typical components, being moderate correlation with stress patterns. However, the peak strains for the composite components are found in the member of Figure 10f, followed by the member of Figure 10g, and the same for the metallic structural members are found in Figure 10h. It can be seen that the strain distribution does not exactly correspond to the stress concentration point, and the member shape and the layup sequence will have an effect on the stress transfer, which in turn affects the strain distribution.

(2)

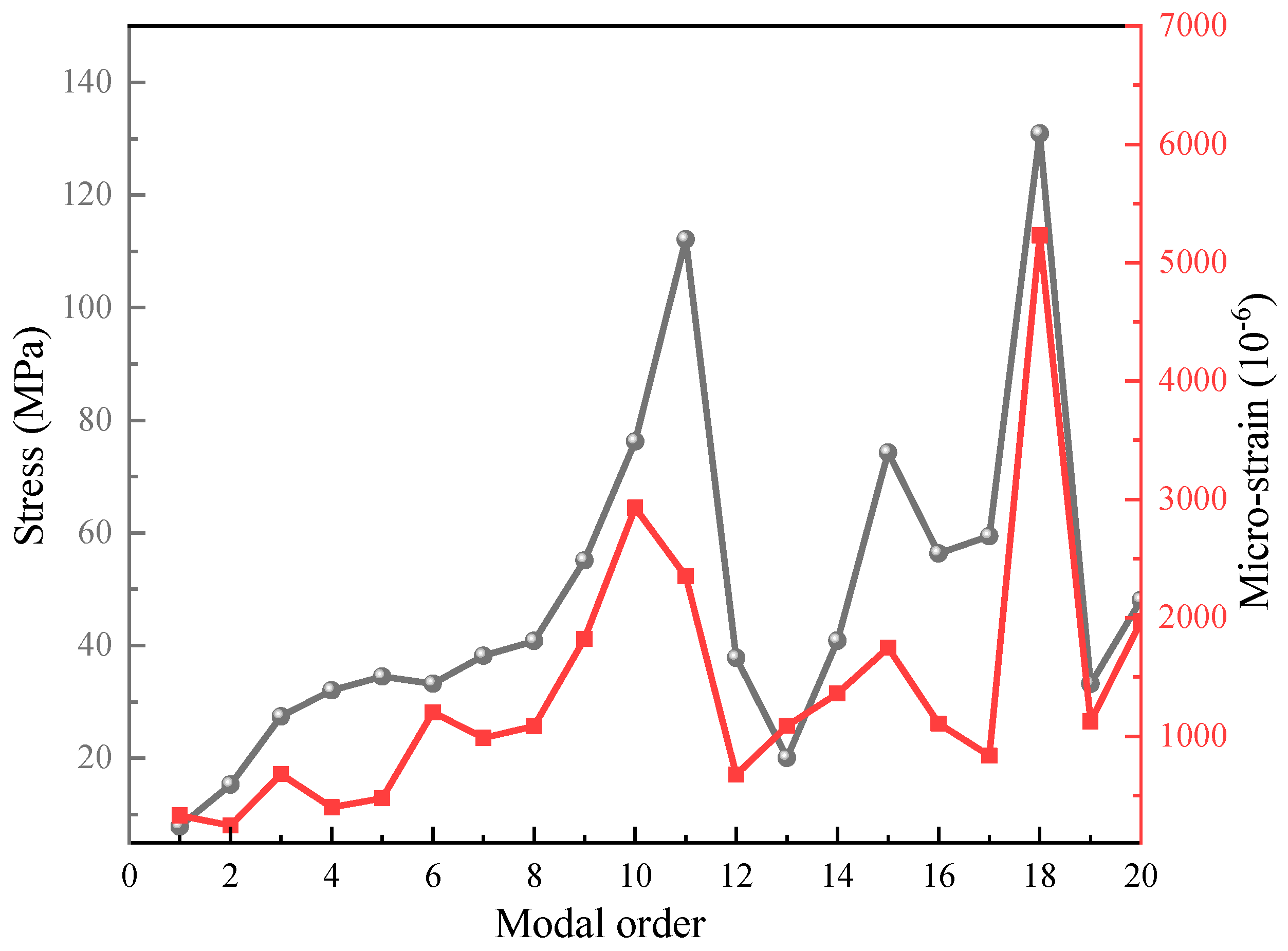
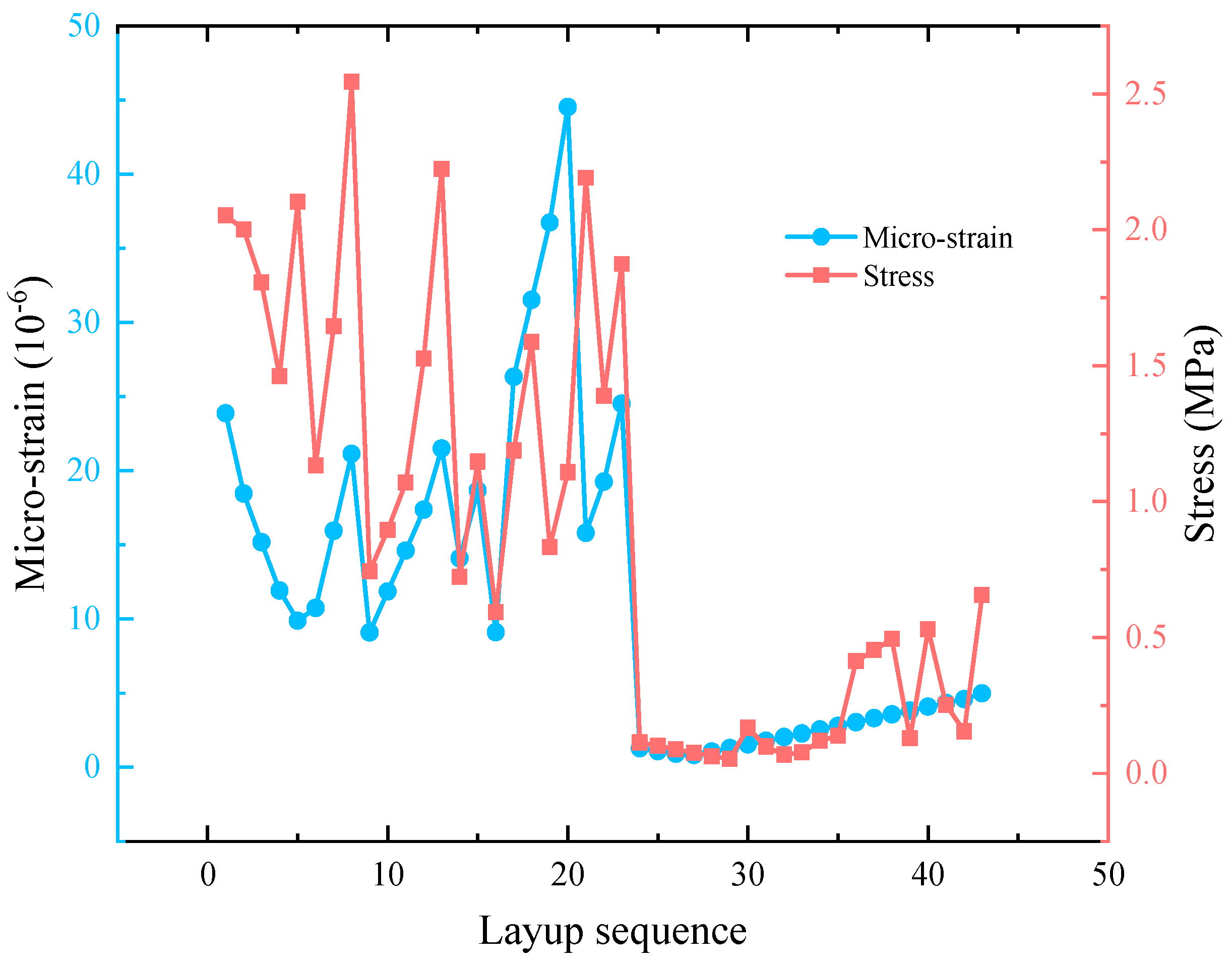
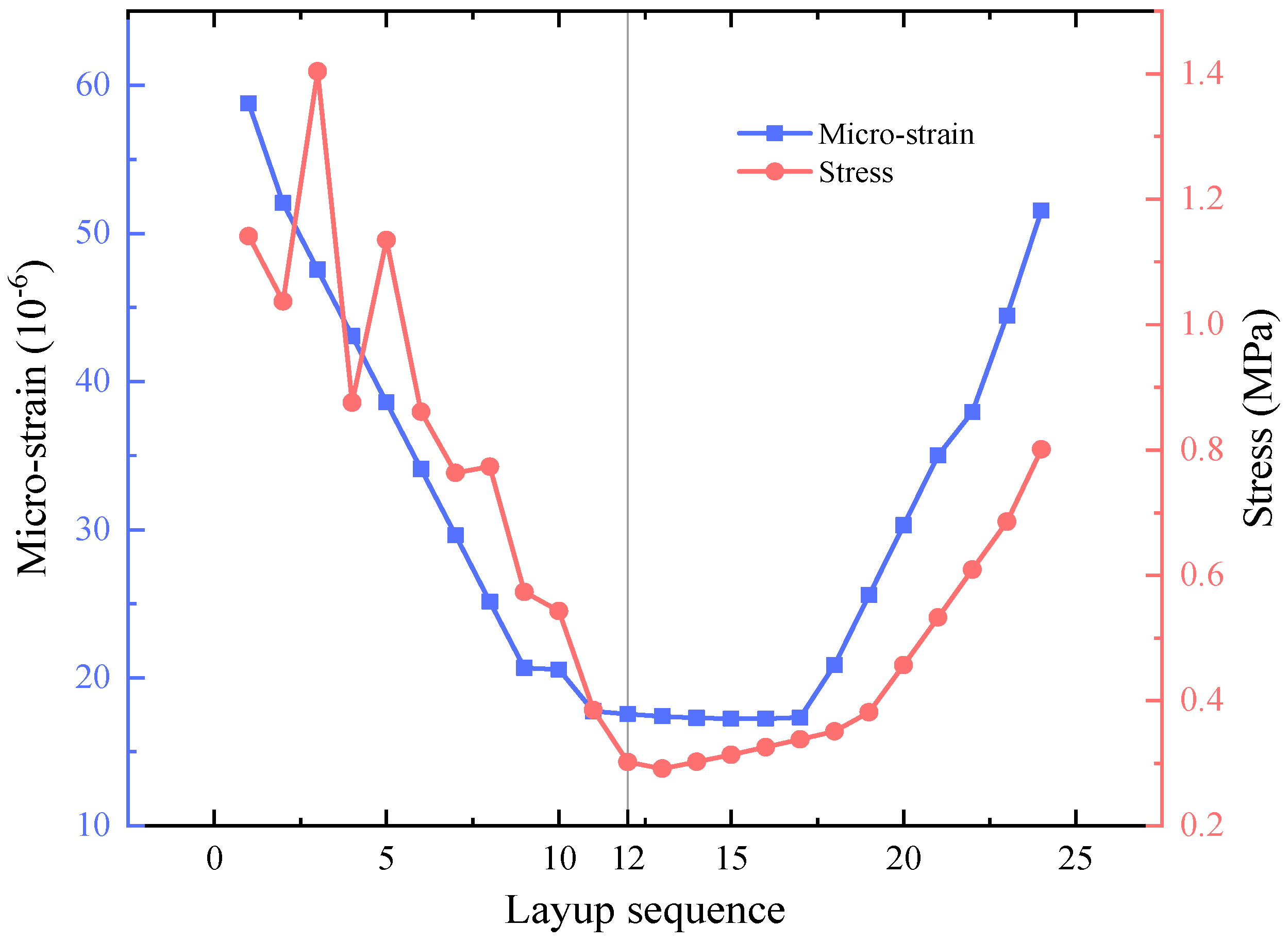
Interlaminar stress–strain response of typical substructures

Compared to metallic components, composite materials exhibit more complex damage evolution mechanisms during transportation. This study examines three representative composite substructures in SVT, aiming to investigate the effects of acceleration impacts on composite laminations during transportation.

The composites damage is usually characterized by transverse, longitudinal, and shear stresses. By comparative analysis, all interlaminar stress components during transportation remain below the von Mises stress level. Therefore, the von Mises stress criterion provides a conservative damage assessment. Composite damage is typically characterized by three stress components of plain composite laminates (PCLs, Figure 9a), variable-thickness laminates (VTLs, Figure 9b) and honeycomb-equivalent laminates (HELs, Figure 9d), respectively. The interlaminar stress–strain behavior of these typical substructures are discussed as follows.

⮚

Interlaminar stress–strain behavior of PCL

The typical PCL consists of 17 plies with the layup sequence listed in Table 2. Figure 11 illustrates the through-thickness stress–strain evolution. The stress and strain exhibit a slight decrease followed by a significant increase with plies. During transportation, the stress is less than 1.5 MPa, and the strain is less than 70 με in the whole layup range, which greatly satisfies the requirements of the allowable values.

The stress and strain cloud maps of the 5th and 17th layers are plotted in the small graph in Figure 11. It shows that the stress and strain distributions in the 5th layer are more homogeneous than those in the 17th layer, because the 5th layer is located in the middle of the PCL. The area of stress distribution in the 17th layer is less than that of the 5th layer, especially the area of strain distribution where it is reduced abruptly. This is because the 17th layer is located on the outer side of the PCL, which is not only affected by the stress between the 16th layer, but also by its connection structure. Therefore, the risk of damage to the outer 17th layer of the PCL is higher compared to the inner layer.

⮚

Interlaminar stress–strain behavior in VTL

The typical VTL has 43-ply with the layup sequence listed in Table 2. Figure 12 shows the trend of stress and strain with ply for the VTL. It can be found that in the first 24 plies, the stress and strain show obvious fluctuating trends with the increase in plies. In the 24th to 43rd layers, the strain gradually increases with the increase in layers, while the stress shows a fluctuating increasing trend. During transportation, the stresses in all layers were less than 3 MPa, and the strains were less than 45 με over the entire range of layers, which complied with the specified permissible values. The sudden decrease in stress–strain in the 24th ply is due to the area decrease in the variable-thickness layup area from the 23rd ply to the 24th ply. Comparing with the PCL, it can be found that the overall stress–strain variations of the VTL are more drastic, but their strain extremes are lower than those of the PCL. The extreme distribution of VTL interlaminar strains increases the risk of composite delamination damage.

The distribution of stress and strain for the VTL is plotted in Figure 13 and Figure 14. It can be found that the stress and strain distributions are well compatible, which explains their lower strains during transportation. Through the use of variable-thickness paving technology, it can effectively transfer the stress concentration area from the low layup to the high layup, thus further reducing the overall stress concentration effect and making the stress distribution more uniform. Nevertheless, the maximum strain values appear in Figure 14d, while the minimum strain values appear in Figure 14f. It indicates that the extreme values of the strains are not directly related to the layup area of the composite, but closely related to the position and angle of the layup.

⮚

Interlaminar stress–strain behavior in HEL

The typical HEL consists of 12 layers of composite with the layup sequence listed in Table 2. Unlike PCL and VTL, the stress–strain trend of HEL shows a U-shaped distribution, first decreasing, then flattening, and finally increasing, as shown in Figure 15. On the one hand, because HEL has symmetrical layups, this reduces the risk of interlaminar stress and internal delamination. During transportation, the stresses in each layer of the HEL are less than 1.5 MPa, and the strains are less than 60 με throughout the range of composite layers, which satisfy the allowable values. Comparing the strain changes of the three typical sub-structures, there is a correlation between the transient stress–strain trends during transportation and the layup angle.

The stress–strain distribution in the 10th, 11th, 17th, and 18th plies of the HEL is plotted in Figure 16. By comparing the stress distribution regions in Figure 16c,d with Figure 16g,h and Figure 16a,b with Figure 16e,f, it can be found that the stress distribution of the symmetric equivalent layer shows an increasing trend compared to the original layup. This phenomenon coincides with the trend of the stress values changing with the layup in Figure 15, which is mainly due to the large stress extremes, thus affecting the range of the surrounding high-strain distribution. Meanwhile, the stress–strain distribution of the honeycomb-equivalent laminates shows some compatibility, and the location of the high stress–strain distribution of the symmetric equivalent layer and the original ply layer remains the same.

5. Conclusions

This study developed an innovative model group collaborative analysis strategy to address the computational challenges posed by mesh proliferation in numerical simulations of complex assemblies. By integrating experimentally measured transportation vibration spectra with advanced numerical modeling, the nonlinear dynamic response of the symmetric vertical tail (SVT) under transport conditions is systematically elucidated. The key findings are summarized as follows:

(1)

The spatial-temporal reconstruction of 100 equivalent acceleration nodes enabled quantitative determination of stress–strain distribution patterns. The SVT dynamic response characterization reveals the critical stress concentration zones, which is helpful to the optimal packaging design and the safe transportation. The SVT vibration modal analysis identified four resonant frequency bands (39.906 Hz, 42.094 Hz, 47.225 Hz, and 59.981 Hz) requiring mitigation of stress concentration.

(2)

The transient response assessment obtained using the modal superposition method showed that the peak equivalent stress (11.61 MPa) during transportation is 82% below the threshold stress of land transportation standards. This indicates that the existing packaging solution has sufficient safety margins. Further analysis of the distribution characteristics of typical structural components reveals that by optimizing the stiffness distribution of the cushioning pads in the upper part of the SVT, the stress level in the critical region can be further reduced, which provides a clear direction for packaging improvement.

(3)

The stress distribution of a typical composite structure showed a quasi-periodic evolution pattern concerning the layup angle, while the strain response shows non-monotonic characteristics due to the stress redistribution effect of the variable-thickness design. This heterogeneous response mechanism reveals the physical nature of variable-thickness layups to effectively reduce the stress concentration effect and inhibit the strain development by improving the stress transfer path, which provides new theoretical support for the impact-resistant design of composite structures.

(4)

The established “load reconstruction-modal synthesis-transient solution” framework can provide fundamental understanding of composite structure transport dynamics, delivers a complete workflow for aviation packaging design, reduces computational costs through model group equivalence, and offers direct applicability to other aerospace transport systems.