Analysis of Stability of Delayed Quaternion-Valued Switching Neural Networks via Symmetric Matrices
Abstract
1. Introduction
- (1)
- The combination of quaternions and switching neural networks has been rarely studied, so in this paper, we try to explore the stability of QVSNNs by analysing the properties of some symmetric matrices in an undecomposed approach.
- (2)
- The QVSNN discussed in this paper has a global asymptotic stability under arbitrary switching laws and a global exponential stability under a given switching sequence and switching condition;
- (3)
- The Wirtinger-based inequality is generalized to the domain of quaternions and used in the analysis of stability, where the method of proof differs from the existing literature.
2. Preliminaries
2.1. Quaternion Algebra
- (i)
- Additive operation:
- (ii)
- Multiplication operation:
2.2. Model Description
3. Main Results
3.1. Global Asymptotic Stability
3.2. Global Exponential Stability
3.3. State Decay Estimate
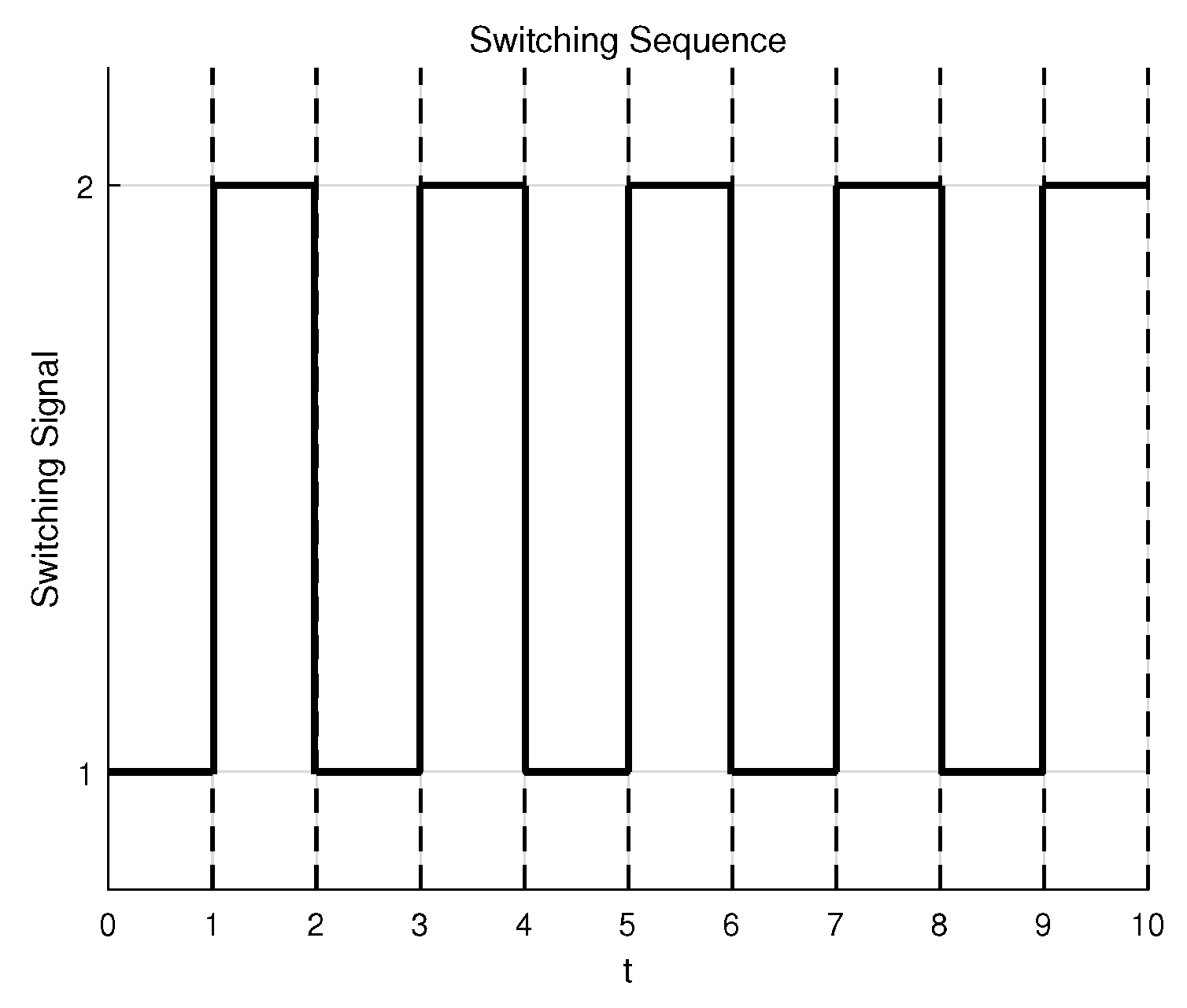
Switching Condition
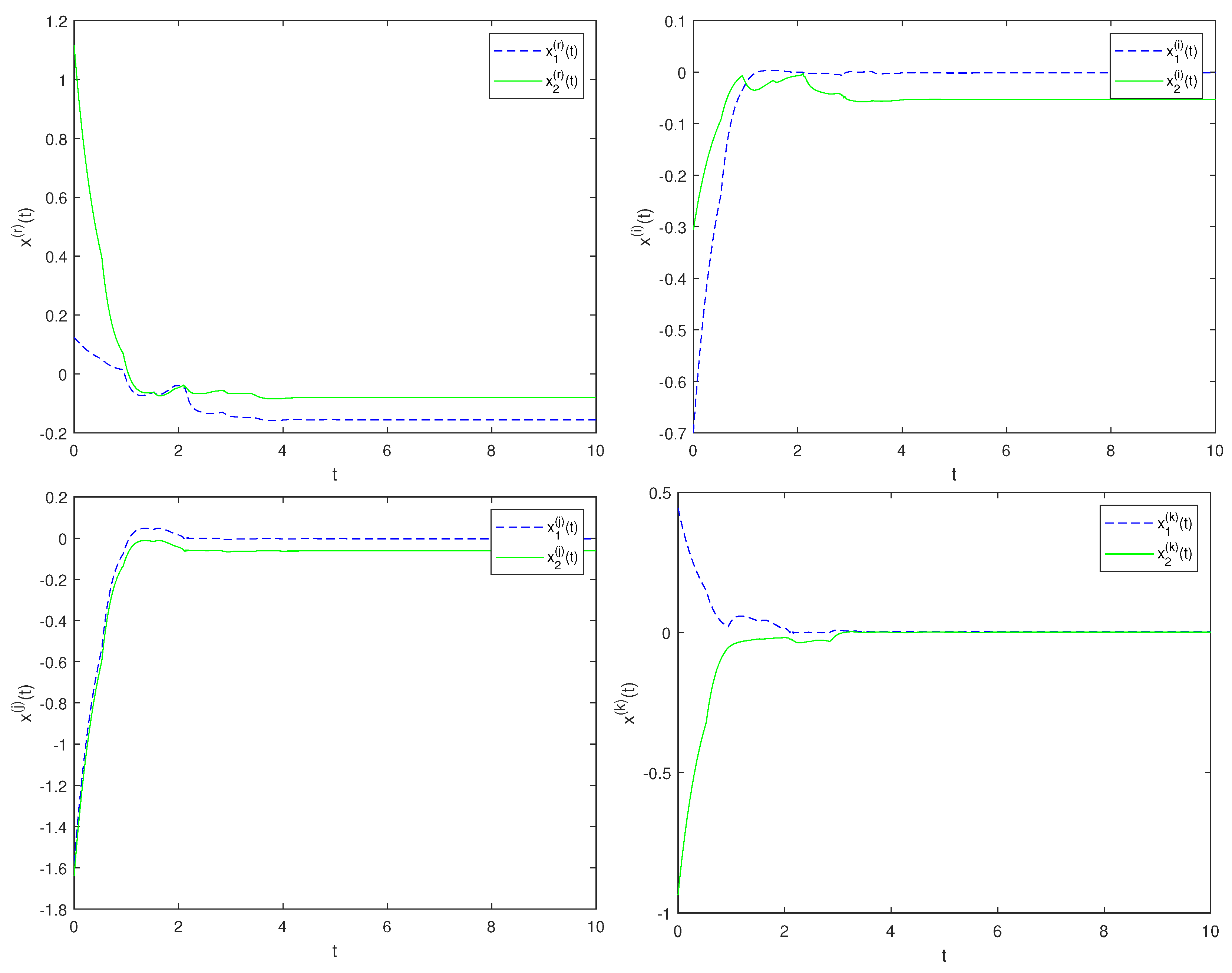
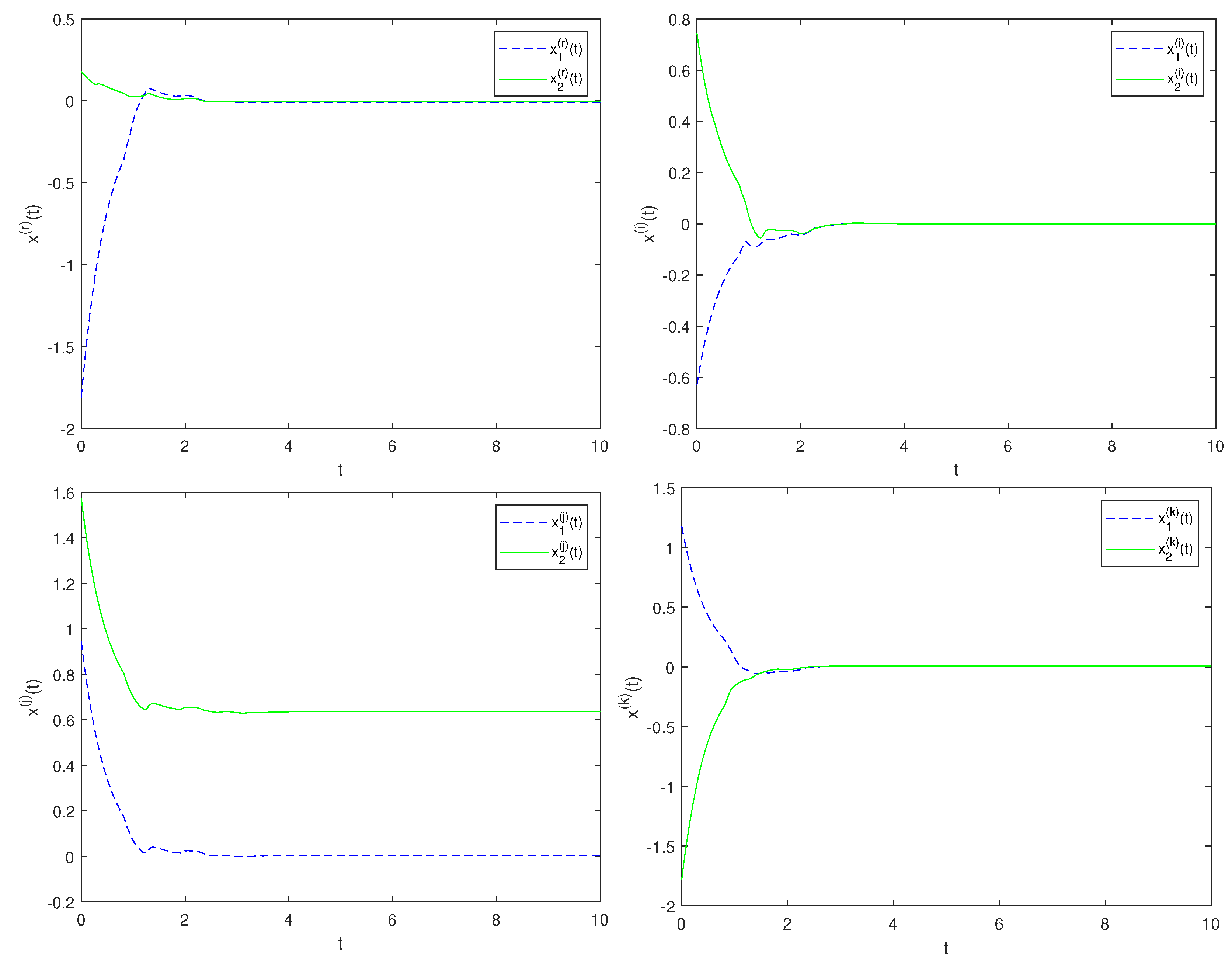
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QVNNs | Quaternion-valued neural networks |
| QVSNNs | Quaternion-valued switching neural networks |
| GAS | Global asymptotic stability |
| GES | Global exponential stability |
References
- Zou, A.M.; Kumar, K.D.; Hou, Z.G. Quaternion-based adaptive output feedback attitude control of spacecraft using Chebyshev neural networks. IEEE Trans. Neural Netw. 2010, 21, 1457–1471. [Google Scholar] [PubMed]
- Rochefort, D.; De Lafontaine, J.; Brunet, C.A. A new satellite attitude state estimation algorithm using quaternion neural networks. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005; p. 6447. [Google Scholar]
- Song, Q.; Wu, Q.; Liu, Y. Stabilization of chaotic quaternion-valued neutral-type neural networks via sampled-data control with two-sided looped functional approach. Nonlinear Anal. Model. Control 2024, 29, 1150–1166. [Google Scholar] [CrossRef]
- Peng, T.; Wu, Y.; Tu, Z.; Alofi, A.; Lu, J. Fixed-time and prescribed-time synchronization of quaternion-valued neural networks: A control strategy involving Lyapunov functions. Neural Netw. 2023, 160, 108–121. [Google Scholar] [CrossRef]
- Takahashi, K. Remarks on quaternion neural networks with application to trajectory control of a robot manipulator. In Proceedings of the 2019 Australian & New Zealand Control Conference (ANZCC), Auckland, New Zealand, 27–29 November 2019; pp. 116–121. [Google Scholar]
- Altamirano-Gomez, G.; Gershenson, C. Quaternion Convolutional Neural Networks: Current Advances and Future Directions. Adv. Appl. Clifford Algebr. 2024, 34, 42. [Google Scholar] [CrossRef]
- Miao, J.; Kou, K.I.; Yang, Y.; Yang, L.; Han, J. Quaternion matrix completion using untrained quaternion convolutional neural network for color image inpainting. Signal Process. 2024, 221, 109504. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, X.; Zhang, C.; Ma, Q. Quaternion convolutional neural networks for hyperspectral image classification. Eng. Appl. Artif. Intell. 2023, 123, 106234. [Google Scholar] [CrossRef]
- Kumar, S.; Rastogi, U. A comprehensive review on the advancement of high-dimensional neural networks in quaternionic domain with relevant applications. Arch. Comput. Methods Eng. 2023, 30, 3941–3968. [Google Scholar] [CrossRef]
- Hirose, A.; Shang, F.; Otsuka, Y.; Natsuaki, R.; Matsumoto, Y.; Usami, N.; Song, Y.; Chen, H. Quaternion Neural Networks: A physics-incorporated intelligence framework [Hypercomplex Signal and Image Processing]. IEEE Signal Process. Mag. 2024, 41, 88–100. [Google Scholar] [CrossRef]
- Wang, H.; Tan, J.; Wen, S. Exponential stability analysis of mixed delayed quaternion-valued neural networks via decomposed approach. IEEE Access 2020, 8, 91501–91509. [Google Scholar] [CrossRef]
- Humphries, U.; Rajchakit, G.; Kaewmesri, P.; Chanthorn, P.; Sriraman, R.; Samidurai, R.; Lim, C.P. Stochastic memristive quaternion-valued neural networks with time delays: An analysis on mean square exponential input-to-state stability. Mathematics 2020, 8, 815. [Google Scholar] [CrossRef]
- Yang, X.; Li, C.; Song, Q.; Li, H.; Huang, J. Effects of state-dependent impulses on robust exponential stability of quaternion-valued neural networks under parametric uncertainty. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 2197–2211. [Google Scholar] [CrossRef] [PubMed]
- Shu, J.; Wu, B.; Xiong, L. Stochastic stability criteria and event-triggered control of delayed Markovian jump quaternion-valued neural networks. Appl. Math. Comput. 2022, 420, 126904. [Google Scholar] [CrossRef]
- Chen, X.; Li, Z.; Song, Q.; Hu, J.; Tan, Y. Robust stability analysis of quaternion-valued neural networks with time delays and parameter uncertainties. Neural Netw. 2017, 91, 55–65. [Google Scholar] [CrossRef]
- Song, Q.; Chen, Y.; Zhao, Z.; Liu, Y.; Alsaadi, F.E. Robust stability of fractional-order quaternion-valued neural networks with neutral delays and parameter uncertainties. Neurocomputing 2021, 420, 70–81. [Google Scholar] [CrossRef]
- You, X.; Song, Q.; Liang, J.; Liu, Y.; Alsaadi, F.E. Global μ-stability of quaternion-valued neural networks with mixed time-varying delays. Neurocomputing 2018, 290, 12–25. [Google Scholar] [CrossRef]
- Wu, L.; Feng, Z.; Lam, J. Stability and synchronization of discrete-time neural networks with switching parameters and time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1957–1972. [Google Scholar] [CrossRef]
- Shen, W.; Zeng, Z.; Wang, L. Stability analysis for uncertain switched neural networks with time-varying delay. Neural Netw. 2016, 83, 32–41. [Google Scholar] [CrossRef]
- Liu, C.; Yang, Z.; Sun, D.; Liu, X.; Liu, W. Stability of switched neural networks with time-varying delays. Neural Comput. Appl. 2018, 30, 2229–2244. [Google Scholar] [CrossRef]
- Tu, Z.; Zhao, Y.; Ding, N.; Feng, Y.; Zhang, W. Stability analysis of quaternion-valued neural networks with both discrete and distributed delays. Appl. Math. Comput. 2019, 343, 342–353. [Google Scholar] [CrossRef]
- Wang, Y.; Niu, B.; Wang, H.; Alotaibi, N.; Abozinadah, E. Neural network-based adaptive tracking control for switched nonlinear systems with prescribed performance: An average dwell time switching approach. Neurocomputing 2021, 435, 295–306. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Cao, J.; Rutkowski, L. Synchronization of coupled time-delay neural networks with mode-dependent average dwell time switching. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 5483–5496. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Han, J.; Liu, P.; Wang, Y. Memristor-based neural network circuit of pavlov associative memory with dual mode switching. AEU-Int. J. Electron. Commun. 2021, 129, 153552. [Google Scholar] [CrossRef]
- Chen, Z.; Niu, B.; Zhang, L.; Zhao, J.; Ahmad, A.M.; Alassafi, M.O. Command filtering-based adaptive neural network control for uncertain switched nonlinear systems using event-triggered communication. Int. J. Robust Nonlinear Control 2022, 32, 6507–6522. [Google Scholar] [CrossRef]
- Dong, Z.; Wang, X.; Zhang, X.; Hu, M.; Dinh, T.N. Global exponential synchronization of discrete-time high-order switched neural networks and its application to multi-channel audio encryption. Nonlinear Anal. Hybrid Syst. 2023, 47, 101291. [Google Scholar] [CrossRef]
- Wang, H.; Yang, X.; Xiang, Z.; Tang, R.; Ning, Q. Synchronization of switched neural networks via attacked mode-dependent event-triggered control and its application in image encryption. IEEE Trans. Cybern. 2022, 53, 5994–6003. [Google Scholar] [CrossRef]
- Bao, Y.; Zhang, Y.; Zhang, B. Resilient fixed-time stabilization of switched neural networks subjected to impulsive deception attacks. Neural Netw. 2023, 163, 312–326. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Liu, L.; Wang, J. Multistability of switched neural networks with piecewise linear activation functions under state-dependent switching. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 2052–2066. [Google Scholar] [CrossRef]
- Jiao, T.; Park, J.H.; Zong, G.; Zhao, Y.; Du, Q. On stability analysis of random impulsive and switching neural networks. Neurocomputing 2019, 350, 146–154. [Google Scholar] [CrossRef]
- Yang, D.; Li, X. Robust stability analysis of stochastic switched neural networks with parameter uncertainties via state-dependent switching law. Neurocomputing 2021, 452, 813–819. [Google Scholar] [CrossRef]
- Wu, L.; Feng, Z.; Zheng, W.X. Exponential stability analysis for delayed neural networks with switching parameters: Average dwell time approach. IEEE Trans. Neural Netw. 2010, 21, 1396–1407. [Google Scholar]
- Tu, Z.; Yang, X.; Wang, L.; Ding, N. Stability and stabilization of quaternion-valued neural networks with uncertain time-delayed impulses: Direct quaternion method. Phys. A Stat. Mech. Its Appl. 2019, 535, 122358. [Google Scholar] [CrossRef]
- Zeng, H.B.; He, Y.; Wu, M.; Xiao, S.P. Stability analysis of generalized neural networks with time-varying delays via a new integral inequality. Neurocomputing 2015, 161, 148–154. [Google Scholar] [CrossRef]
- Chen, Z.W.; Yang, J.; Zhong, S.M. Delay-partitioning approach to stability analysis of generalized neural networks with time-varying delay via new integral inequality. Neurocomputing 2016, 191, 380–387. [Google Scholar] [CrossRef]
- Peng, T.; Qiu, J.; Lu, J.; Tu, Z.; Cao, J. Finite-time and fixed-time synchronization of quaternion-valued neural networks with/without mixed delays: An improved one-norm method. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 7475–7487. [Google Scholar] [CrossRef]
- Syed Ali, M.; Hymavathi, M.; Saroha, S.; Krishna Moorthy, R. Global asymptotic stability of neutral type fractional-order memristor-based neural networks with leakage term, discrete and distributed delays. Math. Methods Appl. Sci. 2021, 44, 5953–5973. [Google Scholar] [CrossRef]
- Subramanian, K.; Muthukumar, P. Global asymptotic stability of complex-valued neural networks with additive time-varying delays. Cogn. Neurodynamics 2017, 11, 293–306. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, D.; Lu, J. Global exponential stability for quaternion-valued recurrent neural networks with time-varying delays. Nonlinear Dyn. 2017, 87, 553–565. [Google Scholar] [CrossRef]
- Xia, Y.; Chen, X.; Lin, D.; Li, B.; Yang, X. Global exponential stability analysis of commutative quaternion-valued neural networks with time delays on time scales. Neural Process. Lett. 2023, 55, 6339–6360. [Google Scholar] [CrossRef]
- Li, X.; Pal, N.R.; Li, H.; Huang, T. Intermittent event-triggered exponential stabilization for state-dependent switched fuzzy neural networks with mixed delays. IEEE Trans. Fuzzy Syst. 2021, 30, 3312–3321. [Google Scholar] [CrossRef]
- Zhan, T.; Ma, S.; Li, W.; Pedrycz, W. Exponential stability of fractional-order switched systems with mode-dependent impulses and its application. IEEE Trans. Cybern. 2021, 52, 11516–11525. [Google Scholar] [CrossRef]
- Xiao, H.; Zhu, Q.; Karimi, H.R. Stability of stochastic delay switched neural networks with all unstable subsystems: A multiple discretized Lyapunov-Krasovskii functionals method. Inf. Sci. 2022, 582, 302–315. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Peng, T.; Tu, Z.; Duan, H.; Tan, W. Analysis of Stability of Delayed Quaternion-Valued Switching Neural Networks via Symmetric Matrices. Symmetry 2025, 17, 979. https://doi.org/10.3390/sym17070979
Dong Y, Peng T, Tu Z, Duan H, Tan W. Analysis of Stability of Delayed Quaternion-Valued Switching Neural Networks via Symmetric Matrices. Symmetry. 2025; 17(7):979. https://doi.org/10.3390/sym17070979
Chicago/Turabian StyleDong, Yuan, Tao Peng, Zhengwen Tu, Huiling Duan, and Wei Tan. 2025. "Analysis of Stability of Delayed Quaternion-Valued Switching Neural Networks via Symmetric Matrices" Symmetry 17, no. 7: 979. https://doi.org/10.3390/sym17070979
APA StyleDong, Y., Peng, T., Tu, Z., Duan, H., & Tan, W. (2025). Analysis of Stability of Delayed Quaternion-Valued Switching Neural Networks via Symmetric Matrices. Symmetry, 17(7), 979. https://doi.org/10.3390/sym17070979



