Dual-Domain Joint Learning Reconstruction Method (JLRM) Combined with Physical Process for Spectral Computed Tomography (SCT)
Abstract
1. Introduction
2. Preliminary Knowledge
3. Method
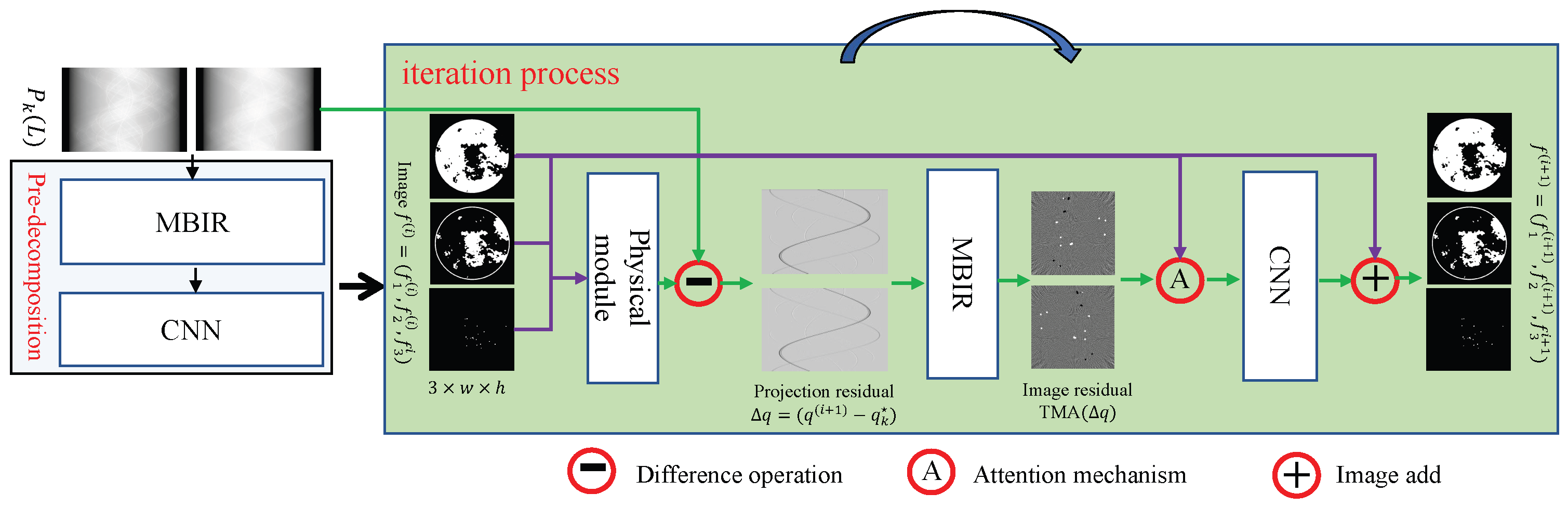
3.1. JLRM Architecture
- Step 1. Obtain initial value:
- Step 2. Nonlinear physical process:
- Step 3. Residual increment: CNN(MBIR
- Step 4. Update: .
| Algorithm 1 Training stage |
|
| Algorithm 2 Test stage |
|
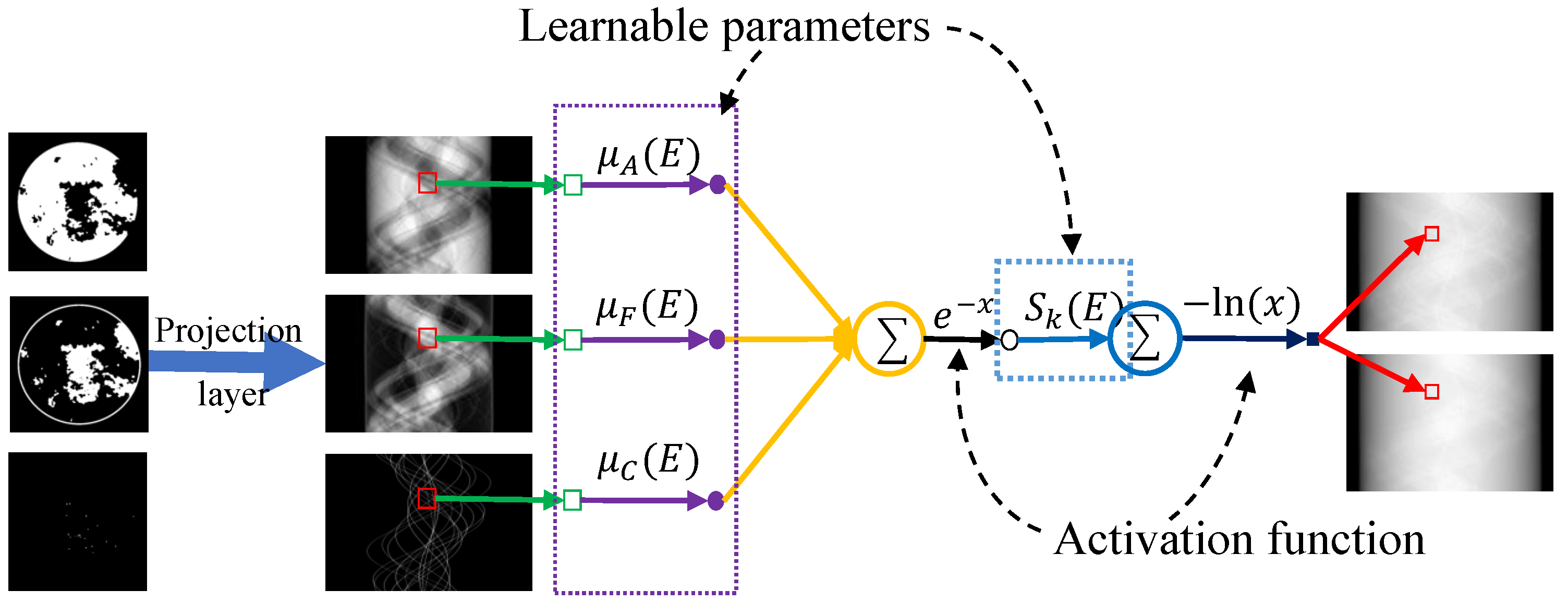
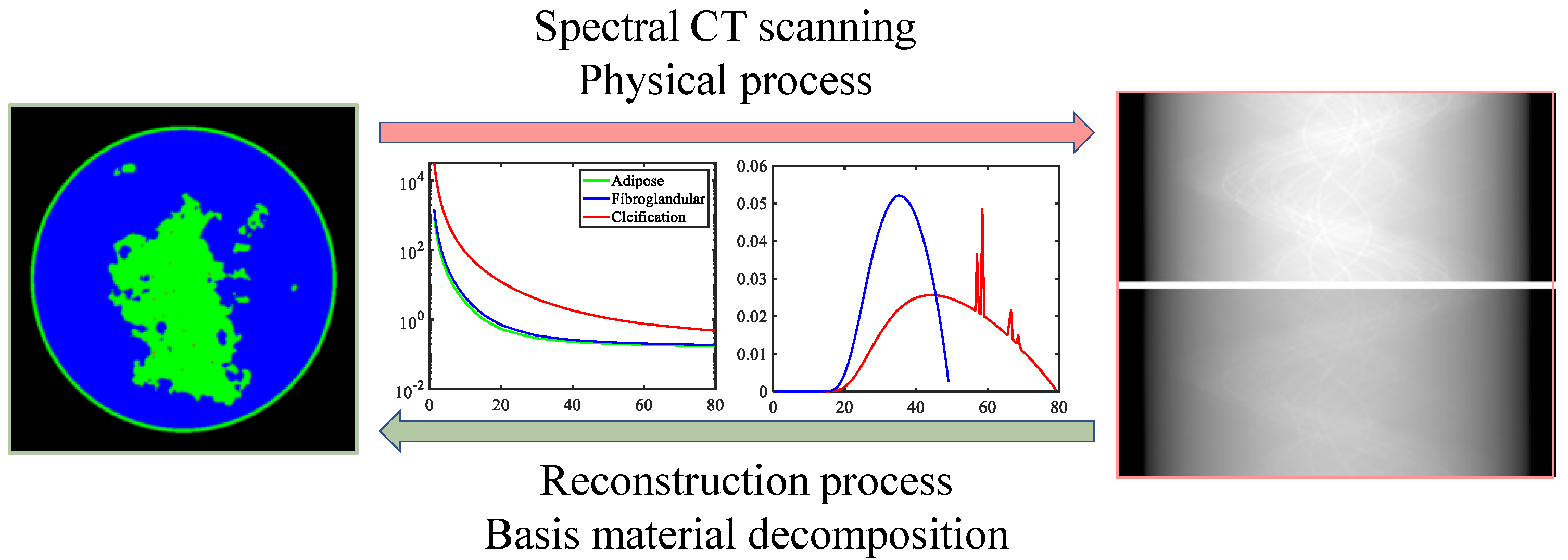
3.1.1. Physical Module for Nonlinear Physical Process
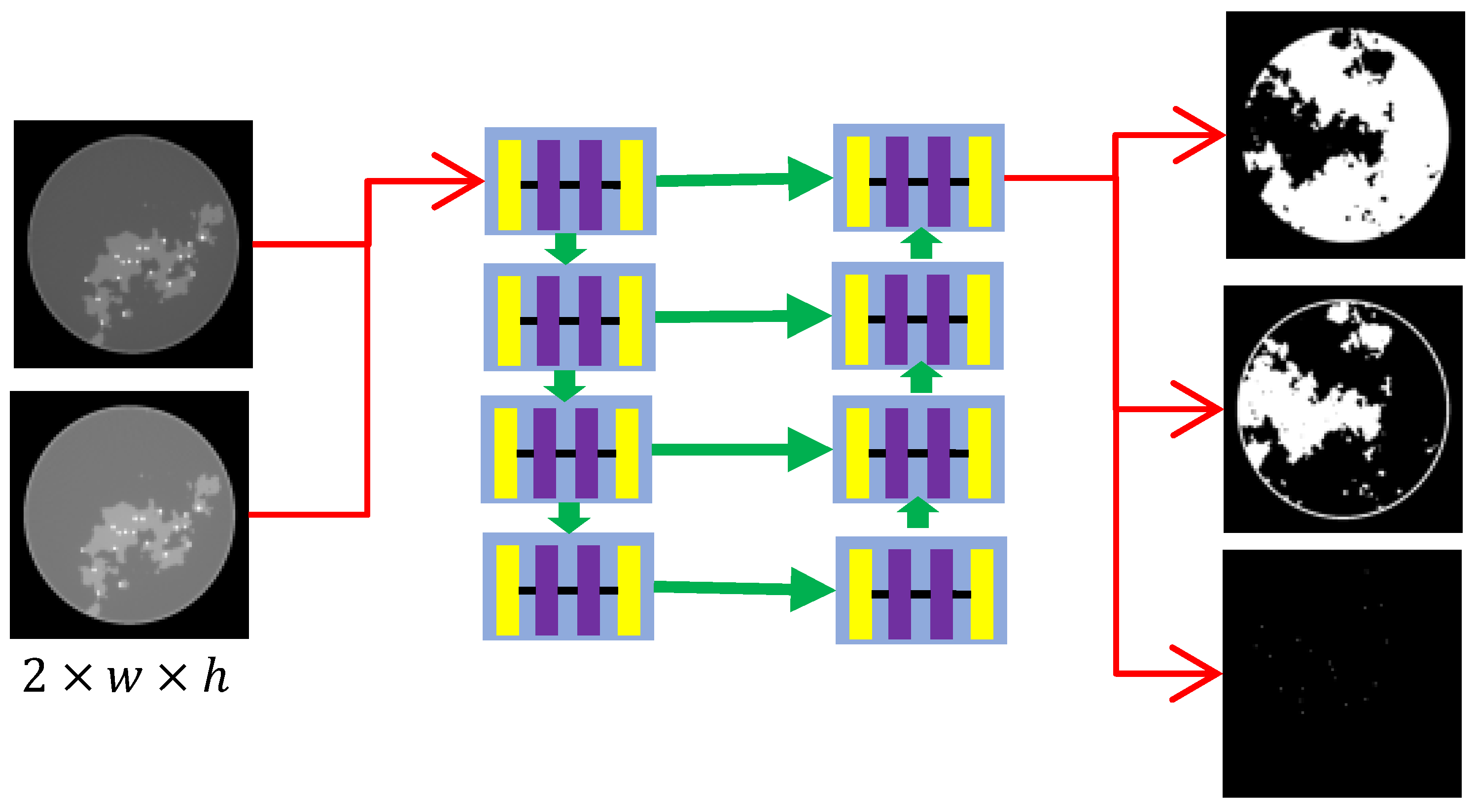
3.1.2. CNN Network Structure Design
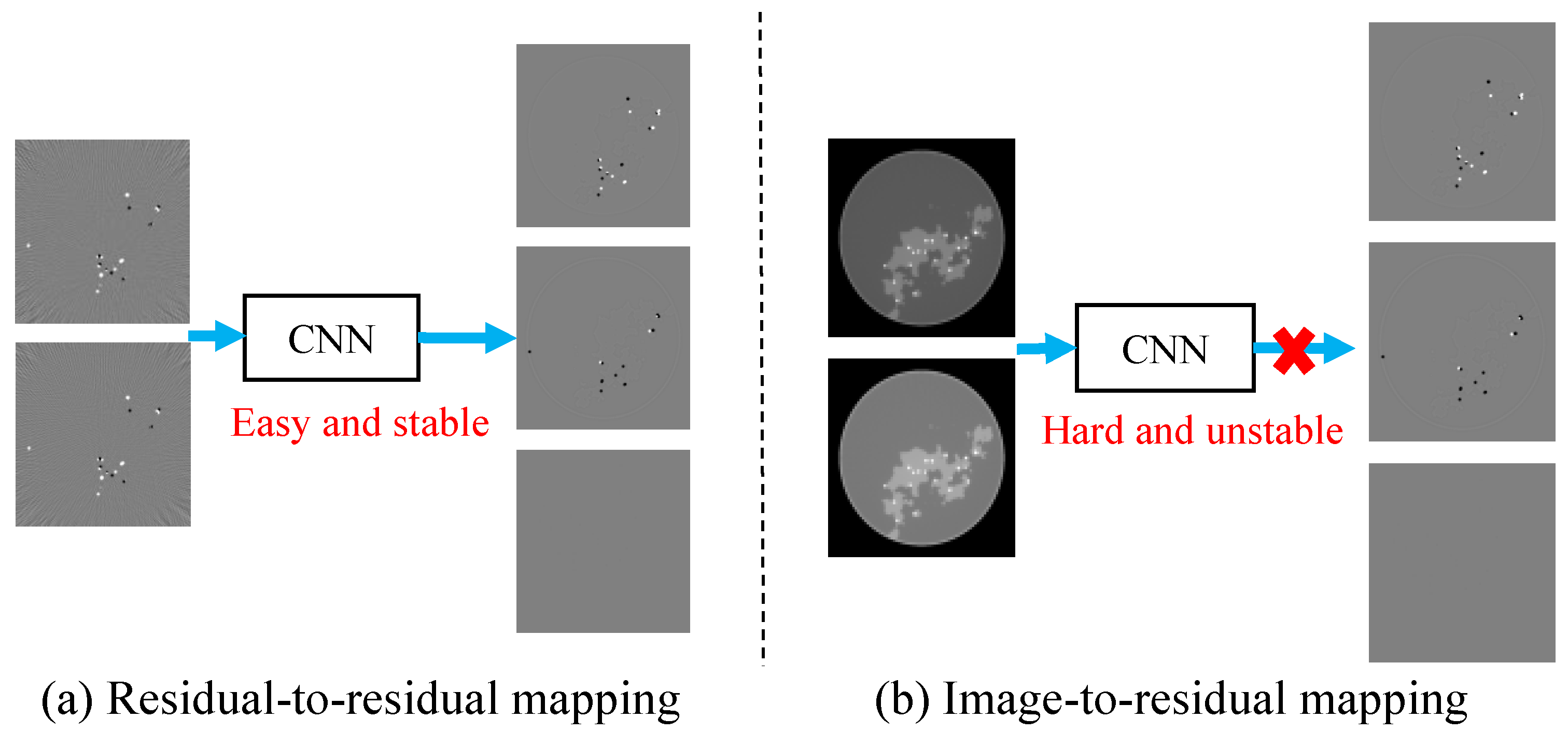
3.1.3. Residual-to-Residual Strategy
3.2. Network Training
- Input: EART-decomposed basis material images
- Processing: Three dedicated networks individually process the inputs
- Output: Refined images of three basis materials
- Condition: Activated when spectral information is unknown
- Input: Polychromatic projection data paired with reference labels
- Function: Updates the spectral information through physics-constrained learning
- Input: Reconstructed images from projection residual and current basis material images
- Processing: Three separate networks generate material-specific residuals
- Output: Corrected residual images for each basis material
4. Results
4.1. DL-Spectral CT Setup of AAPM Challenge
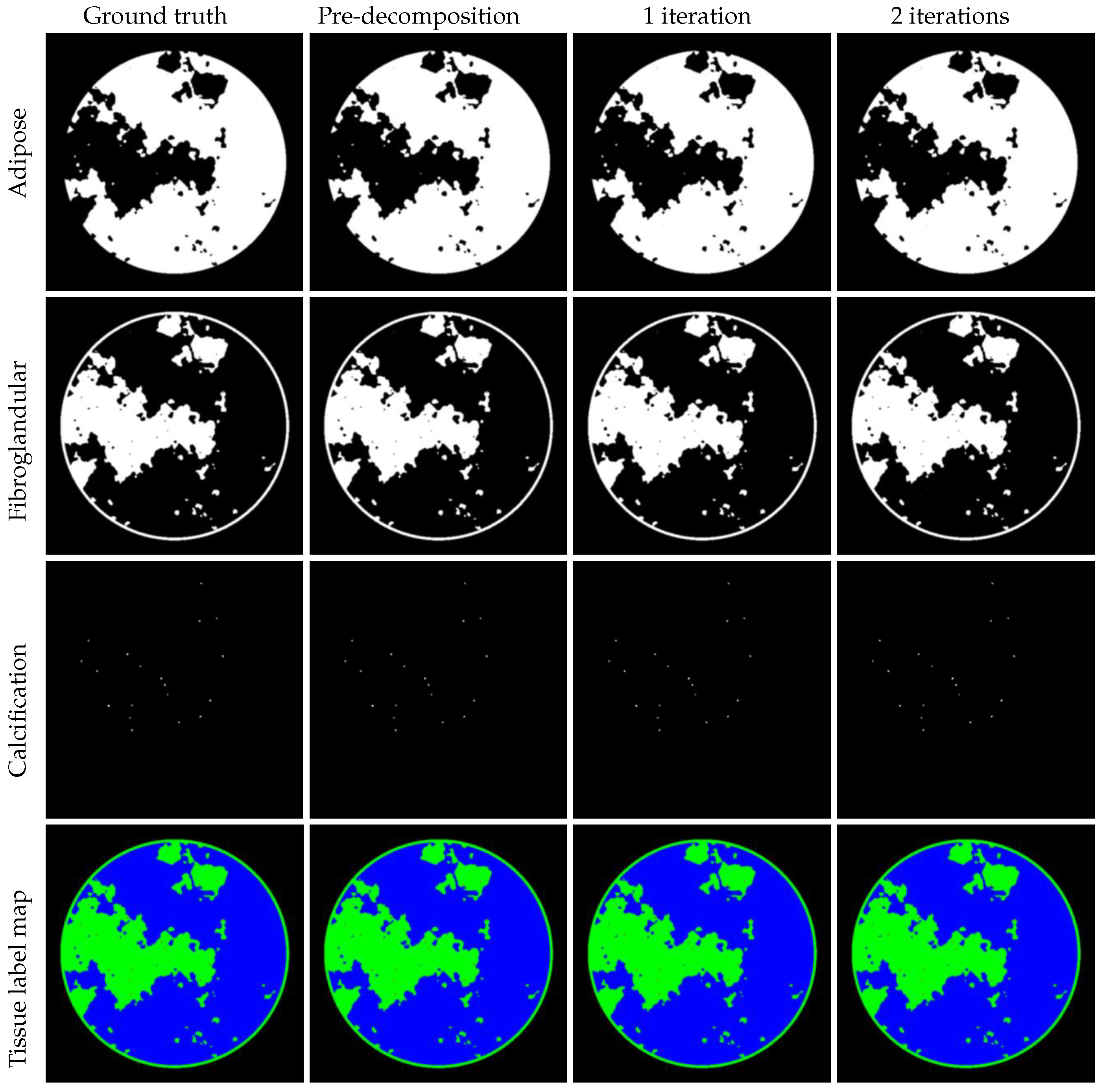
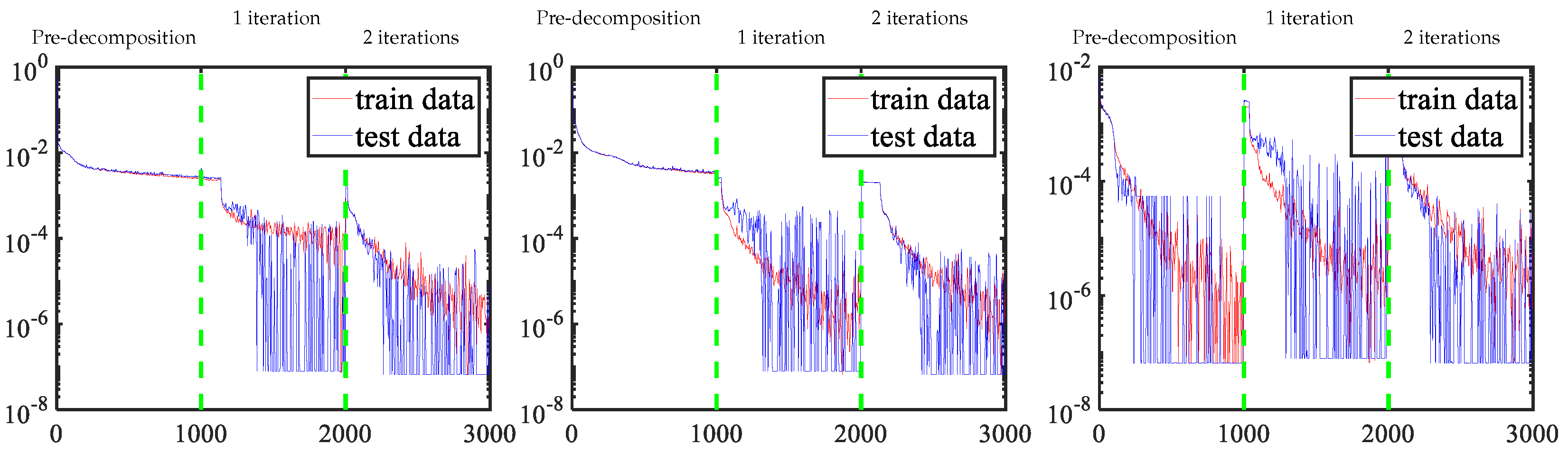
4.2. Performance and Analysis of JLRM
4.3. Residual Analysis
4.4. Performance of JLRM in Noise Suppression
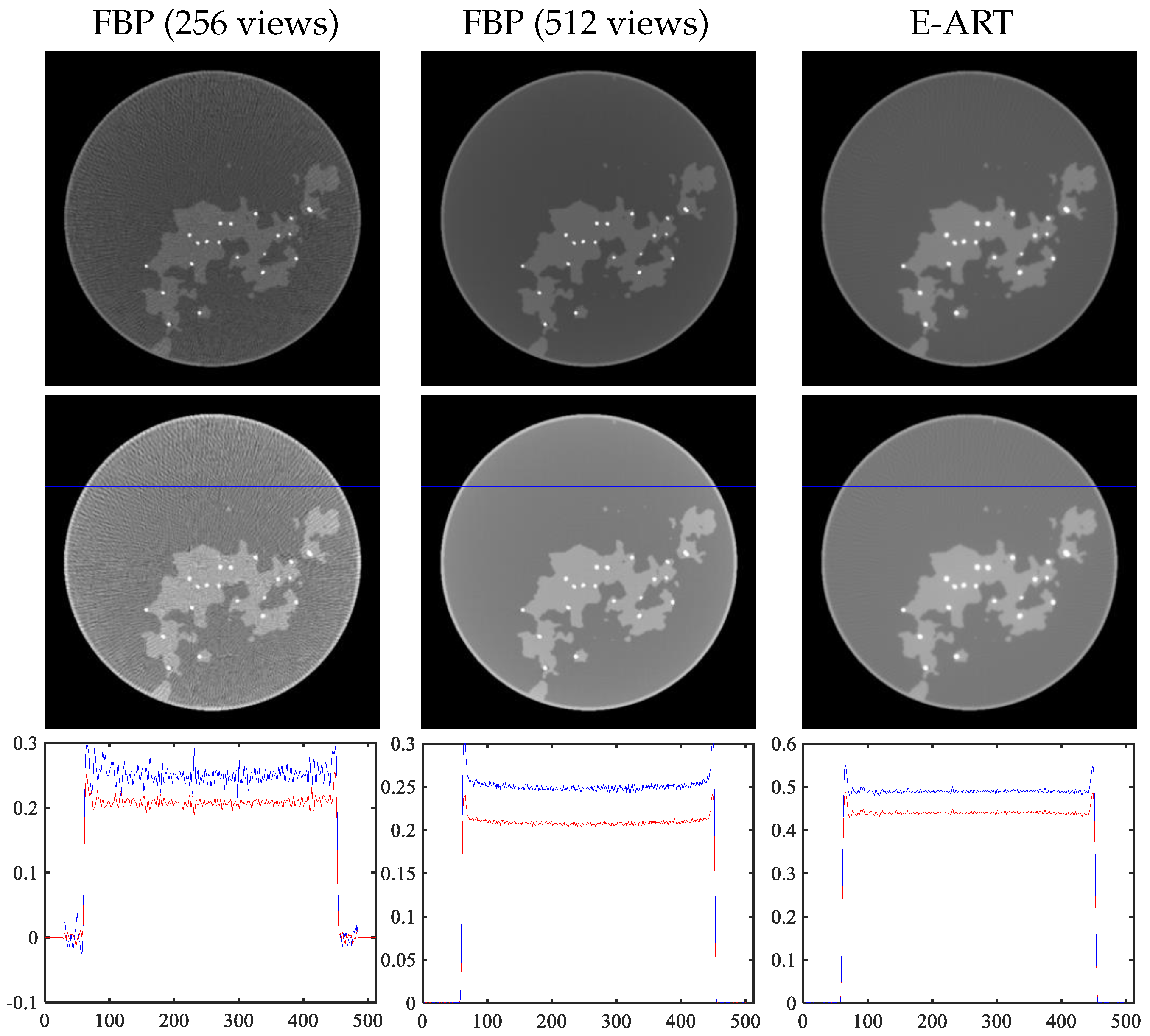
4.5. Reconstruction Method: FBP vs. E-ART
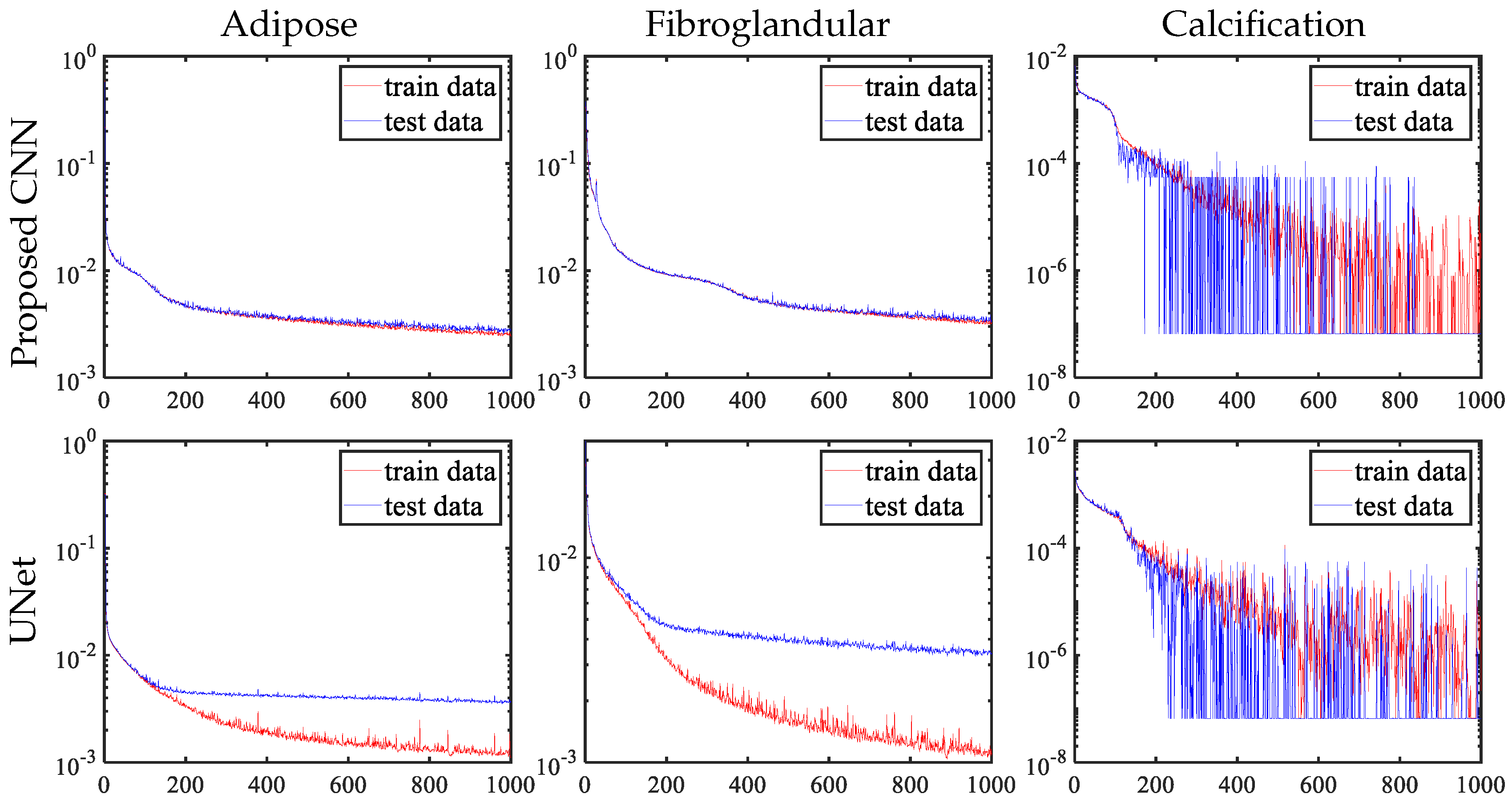
4.6. Receptive Field: Small or Large
4.7. Residual-to-Residual vs. Image-to-Residual
5. Summary
- Synergistic integration of complementary components: By integrating physical processing (for nonlinear SCT physics), MBIR (for stable domain transformations), and deep learning (for material decomposition), the proposed method combines the interpretability of physics-driven models with the adaptability of neural networks. The physical component ensures fidelity to fundamental X-ray interactions, MBIR provides robustness against noise and incomplete data, and the neural network resolves ambiguities in material-specific attenuation profiles.
- Network-embedded physical model: A network-integrated physical model governs SCT projection data generation, enabling more accurate representation of SCT physical processes. The iterative process progressively enhances reconstruction accuracy through comprehensive physical modeling, where the SCT physical framework is implemented as a network module with learnable parameters including X-ray spectra and attenuation coefficients .
- Residual-to-residual training: The training paradigm employs residual-to-residual mapping rather than conventional image-to-image or image-to-residual approaches. This strategy focuses on error-sensitive regions that are visually identifiable in residual images but indistinguishable in original reconstructions. This is a novel training paradigm that prioritizes error-sensitive regions by mapping residual projections to residual images.
- Network structure design: The network architecture addresses practical constraints through domain-specific design by (1) accounting for limited spatial correlations between SCT projection data and reconstructed images under inconsistent projections and (2) optimizing CNN receptive field size to balance feature extraction capability with prevention of overfitting and robustness degradation.
6. Limitations
- Modular disconnection in network training: The current framework adopts a modular reassembly strategy in which the physical model, MBIR, and deep learning components are trained in a distributed manner. Although this design simplifies implementation (e.g., pretraining the physics module independently), it restricts synergistic interactions between modules. For example, updates to the physical parameters (e.g., X-ray spectra ) are based on localized loss functions rather than global feedback from the downstream decomposition task. This fragmented optimization prevents end-to-end error propagation, potentially underutilizing the physical model’s capacity to guide holistic reconstruction. A fully-integrated organic training framework in which modules co-evolve through shared gradients could better harmonize physics constraints with data-driven priors, likely improving reconstruction accuracy.
- Narrow data scope and limited spectral diversity: Validation relied primarily on the AAPM Challenge dataset, which uses synthetic projections generated from a single known X-ray spectrum. While effective for proof-of-concept, this setup overlooks real-world complexities such as spectral drift, detector nonlinearity, and patient-specific anatomical variations. Material decomposition accuracy may degrade when applied to clinical data with unknown or mixed spectra (e.g., dual-energy CT with vendor-specific beam hardening corrections), highlighting the need for validation across diverse scanner configurations and patient populations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, D.; Langan, D.A.; Wu, X.; Pack, J.D.; Benson, T.M.; Tkaczky, J.E.; Schmitz, A.M. Dual energy CT via fast kVp switching spectrum estimation. In Medical Imaging 2009: Physics of Medical Imaging; SPIE: Bellingham, WA, USA, 2009; Volume 7258, pp. 1198–1207. [Google Scholar]
- Petersilka, M.; Bruder, H.; Krauss, B.; Stierstorfer, K.; Flohr, T.G. Technical principles of dual source CT. Eur. J. Radiol. 2008, 68, 362–368. [Google Scholar] [CrossRef] [PubMed]
- Willemink, M.J.; Persson, M.; Pourmorteza, A.; Pelc, N.J.; Fleischmann, D. Photon-counting CT: Technical Principles and Clinical Prospects. Radiology 2018, 289, 293–312. [Google Scholar] [CrossRef]
- Leng, S.; Bruesewitz, M.; Tao, S.; Rajendran, K.; Halaweish, A.F.; Campeau, N.G.; Fletcher, J.G.; McCollough, C.H. Photon-counting Detector CT: System Design and Clinical Applications of an Emerging Technology. Radiographics 2019, 39, 729–743. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, R.E.; Macovski, A. Energy-selective reconstructions in X-ray computerised tomography. Phys. Med. Biol. 1976, 21, 733. [Google Scholar] [CrossRef]
- Alvarez, R.; Seppi, E. A comparison of noise and dose in conventional and energy selective computed tomography. IEEE Trans. Nucl. Sci. 1979, 26, 2853–2856. [Google Scholar] [CrossRef]
- Alvarez, R.E.; Seibert, J.A.; Thompson, S.K. Comparison of dual energy detector system performance. Med. Phys. 2004, 31, 556–565. [Google Scholar] [CrossRef]
- Kalender, W.A.; Perman, W.; Vetter, J.; Klotz, E. Evaluation of a prototype dual-energy computed tomographic apparatus. I. Phantom studies. Med. Phys. 1986, 13, 334–339. [Google Scholar] [CrossRef]
- Yu, L.; Leng, S.; McCollough, C.H. Dual-energy CT–based monochromatic imaging. Am. J. Roentgenol. 2012, 199, S9–S15. [Google Scholar] [CrossRef]
- Brooks, R.A.; Di Chiro, G. Beam hardening in X-ray reconstructive tomography. Phys. Med. Biol. 1976, 21, 390. [Google Scholar] [CrossRef] [PubMed]
- Coleman, A.; Sinclair, M. A beam-hardening correction using dual-energy computed tomography. Phys. Med. Biol. 1985, 30, 1251. [Google Scholar] [CrossRef]
- Cardinal, H.N.; Fenster, A. An accurate method for direct dual-energy calibration and decomposition. Med. Phys. 1990, 17, 327–341. [Google Scholar] [CrossRef]
- Dong, X.; Niu, T.; Zhu, L. Combined iterative reconstruction and image-domain decomposition for dual energy CT using total-variation regularization. Med. Phys. 2014, 41, 051909. [Google Scholar] [CrossRef]
- Zeng, D.; Huang, J.; Zhang, H.; Bian, Z.; Niu, S.; Zhang, Z.; Feng, Q.; Chen, W.; Ma, J. Spectral CT image restoration via an average image-induced nonlocal means filter. IEEE Trans. Biomed. Eng. 2015, 63, 1044–1057. [Google Scholar] [CrossRef] [PubMed]
- Stenner, P.; Berkus, T.; Kachelriess, M. Empirical dual energy calibration (EDEC) for cone-beam computed tomography. Med. Phys. 2007, 34, 3630–3641. [Google Scholar] [CrossRef] [PubMed]
- Maaß, N.; Sawall, S.; Knaup, M.; Kachelrieß, M. Empirical multiple energy calibration (EMEC) for material-selective CT. In Proceedings of the 2011 IEEE Nuclear Science Symposium Conference Record, Valencia, Spain, 23–29 October 2011; pp. 4222–4229. [Google Scholar]
- Ying, Z.; Naidu, R.; Crawford, C.R. Dual energy computed tomography for explosive detection. J. X-ray Sci. Technol. 2006, 14, 235–256. [Google Scholar] [CrossRef]
- Maaß, C.; Meyer, E.; Kachelrieß, M. Exact dual energy material decomposition from inconsistent rays (MDIR). Med. Phys. 2011, 38, 691–700. [Google Scholar] [CrossRef]
- Feng, C.; Shen, Q.; Kang, K.; Xing, Y. An empirical material decomposition method (EMDM) for spectral CT. In Proceedings of the 2016 IEEE Nuclear Science Symposium, Medical Imaging Conference and Room-Temperature Semiconductor Detector Workshop (NSS/MIC/RTSD), Strasbourg, France, 29 October–6 November 2016; pp. 1–5. [Google Scholar]
- Sukovic, P.; Clinthorne, N.H. Penalized weighted least-squares image reconstruction for dual energy X-ray transmission tomography. IEEE Trans. Med. Imaging 2000, 19, 1075–1081. [Google Scholar] [CrossRef]
- Elbakri, I.A.; Fessler, J.A. Statistical image reconstruction for polyenergetic X-ray computed tomography. IEEE Trans. Med. Imaging 2002, 21, 89–99. [Google Scholar] [CrossRef]
- Xu, Q.; Mou, X.; Tang, S.; Hong, W.; Zhang, Y.; Luo, T. Implementation of penalized-likelihood statistical reconstruction for polychromatic dual-energy CT. In Medical Imaging 2009: Physics of Medical Imaging; SPIE: Bellingham, WA, USA, 2009; Volume 7258, pp. 1666–1674. [Google Scholar]
- Long, Y.; Fessler, J.A. Multi-material decomposition using statistical image reconstruction for spectral CT. IEEE Trans. Med. Imaging 2014, 33, 1614–1626. [Google Scholar] [CrossRef]
- Niu, T.; Dong, X.; Petrongolo, M.; Zhu, L. Iterative image-domain decomposition for dual-energy CT. Med. Phys. 2014, 41, 041901. [Google Scholar] [CrossRef]
- Zhang, R.; Thibault, J.B.; Bouman, C.A.; Sauer, K.D.; Hsieh, J. Model-based iterative reconstruction for dual-energy X-ray CT using a joint quadratic likelihood model. IEEE Trans. Med. Imaging 2013, 33, 117–134. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Zhao, X.; Zhang, P. An extended algebraic reconstruction technique (E-ART) for dual spectral CT. IEEE Trans. Med. Imaging 2014, 34, 761–768. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Zhao, X.; Wang, F. An extended simultaneous algebraic reconstruction technique (E-SART) for X-ray dual spectral computed tomography. Scanning 2016, 38, 599–611. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Zhang, Z.; Sidky, E.Y.; Xia, D.; Pan, X. Image reconstruction and scan configurations enabled by optimization-based algorithms in multispectral CT. Phys. Med. Biol. 2017, 62, 8763. [Google Scholar] [CrossRef]
- Li, M.; Zhao, Y.; Zhang, P. Accurate iterative FBP reconstruction method for material decomposition of dual energy CT. IEEE Trans. Med. Imaging 2018, 38, 802–812. [Google Scholar] [CrossRef]
- Zhao, S.; Pan, H.; Zhang, W.; Xia, D.; Zhao, X. An oblique projection modification technique (OPMT) for fast multispectral CT reconstruction. Phys. Med. Biol. 2021, 66, 065003. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, S.; Pan, H.; Zhao, Y.; Zhao, X. An iterative reconstruction method based on monochromatic images for dual energy CT. Med. Phys. 2021, 48, 6437–6452. [Google Scholar] [CrossRef]
- Sawatzky, A.; Xu, Q.; Schirra, C.O.; Anastasio, M.A. Proximal ADMM for multi-channel image reconstruction in spectral X-ray CT. IEEE Trans. Med. Imaging 2014, 33, 1657–1668. [Google Scholar] [CrossRef]
- Barber, R.F.; Sidky, E.Y.; Schmidt, T.G.; Pan, X. An algorithm for constrained one-step inversion of spectral CT data. Phys. Med. Biol. 2016, 61, 3784. [Google Scholar] [CrossRef]
- Touch, M.; Clark, D.P.; Barber, W.; Badea, C.T. A neural network-based method for spectral distortion correction in photon counting X-ray CT. Phys. Med. Biol. 2016, 61, 6132. [Google Scholar] [CrossRef]
- Liao, Y.; Wang, Y.; Li, S.; He, J.; Zeng, D.; Bian, Z.; Ma, J. Pseudo dual energy CT imaging using deep learning-based framework: Basic material estimation. In Medical Imaging 2018: Physics of Medical Imaging; SPIE: Bellingham, WA, USA, 2018; Volume 10573, pp. 1190–1194. [Google Scholar]
- Zhao, W.; Vernekohl, D.; Han, F.; Han, B.; Peng, H.; Yang, Y.; Xing, L.; Min, J.K. A unified material decomposition framework for quantitative dual-and triple-energy CT imaging. Med. Phys. 2018, 45, 2964–2977. [Google Scholar] [CrossRef]
- Xu, Y.; Yan, B.; Chen, J.; Zeng, L.; Li, L. Projection decomposition algorithm for dual-energy computed tomography via deep neural network. J. X-ray Sci. Technol. 2018, 26, 361–377. [Google Scholar] [CrossRef]
- Xu, Y.; Yan, B.; Zhang, J.; Chen, J.; Zeng, L.; Wang, L. Image decomposition algorithm for dual-energy computed tomography via fully convolutional network. Comput. Math. Methods Med. 2018, 2018, 2527516. [Google Scholar] [CrossRef] [PubMed]
- Hu, D.; Wu, W.; Xu, M.; Zhang, Y.; Liu, J.; Ge, R.; Chen, Y.; Luo, L.; Coatrieux, G. SISTER: Spectral-image similarity-based tensor with enhanced-sparsity reconstruction for sparse-view multi-energy CT. IEEE Trans. Comput. Imaging 2019, 6, 477–490. [Google Scholar] [CrossRef]
- Wu, X.; He, P.; Long, Z.; Guo, X.; Chen, M.; Ren, X.; Chen, P.; Deng, L.; An, K.; Li, P.; et al. Multi-material decomposition of spectral CT images via Fully Convolutional DenseNets. J. X-ray Sci. Technol. 2019, 27, 461–471. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Li, S.; Zhu, M.; Gao, Q.; Bian, Z.; Huang, H.; Zhang, S.; Huang, J.; Zeng, D.; Ma, J. Unsupervised data fidelity enhancement network for spectral CT reconstruction. In Medical Imaging 2020: Physics of Medical Imaging; SPIE: Bellingham, WA, USA, 2020; Volume 11312, pp. 1081–1088. [Google Scholar]
- Yao, L.; Li, S.; Li, D.; Zhu, M.; Gao, Q.; Zhang, S.; Bian, Z.; Huang, J.; Zeng, D.; Ma, J. Leveraging deep generative model for direct energy-resolving CT imaging via existing energy-integrating CT images. In Medical Imaging 2020: Physics of Medical Imaging; SPIE: Bellingham, WA, USA, 2020; Volume 11312, pp. 1190–1195. [Google Scholar]
- Primak, A.; Ramirez Giraldo, J.; Liu, X.; Yu, L.; McCollough, C.H. Improved dual-energy material discrimination for dual-source CT by means of additional spectral filtration. Med. Phys. 2009, 36, 1359–1369. [Google Scholar] [CrossRef] [PubMed]
- Flohr, T.G.; McCollough, C.H.; Bruder, H.; Petersilka, M.; Gruber, K.; Süβ, C.; Grasruck, M.; Stierstorfer, K.; Krauss, B.; Raupach, R.; et al. First performance evaluation of a dual-source CT (DSCT) system. Eur. Radiol. 2006, 16, 256–268. [Google Scholar] [CrossRef]
- Shan, H.; Padole, A.; Homayounieh, F.; Kruger, U.; Khera, R.D.; Nitiwarangkul, C.; Kalra, M.K.; Wang, G. Competitive performance of a modularized deep neural network compared to commercial algorithms for low-dose CT image reconstruction. Nat. Mach. Intell. 2019, 1, 269–276. [Google Scholar] [CrossRef]
- Sidky, E.Y.; Pan, X. Report on the AAPM deep-learning spectral CT Grand Challenge. Med. Phys. 2024, 51, 772–785. [Google Scholar] [CrossRef]
- Genzel, M.; Gühring, I.; Macdonald, J.; März, M. Near-Exact Recovery for Tomographic Inverse Problems via Deep Learning. In Proceedings of the 39th International Conference on Machine Learning, PMLR, Baltimore, MD, USA, 17–23 July 2022; pp. 7368–7381. [Google Scholar]
- Wu, D.; Kim, K.; Li, Q. Computationally efficient deep neural network for computed tomography image reconstruction. Med. Phys. 2019, 46, 4763–4776. [Google Scholar] [CrossRef]
- Adler, J.; Öktem, O. Learned primal-dual reconstruction. IEEE Trans. Med. Imaging 2018, 37, 1322–1332. [Google Scholar] [CrossRef]
- Dhar, P.; Singh, R.V.; Peng, K.C.; Wu, Z.; Chellappa, R. Learning without memorizing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5138–5146. [Google Scholar]
- Li, Z.; Hoiem, D. Learning without forgetting. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 2935–2947. [Google Scholar] [CrossRef]
- Würfl, T.; Hoffmann, M.; Christlein, V.; Breininger, K.; Huang, Y.; Unberath, M.; Maier, A.K. Deep learning computed tomography: Learning projection-domain weights from image domain in limited angle problems. IEEE Trans. Med. Imaging 2018, 37, 1454–1463. [Google Scholar] [CrossRef]
- Syben, C.; Michen, M.; Stimpel, B.; Seitz, S.; Ploner, S.; Maier, A.K. PYRO-NN: Python reconstruction operators in neural networks. Med. Phys. 2019, 46, 5110–5115. [Google Scholar] [CrossRef]
- Reiser, I.; Nishikawa, R. Task-based assessment of breast tomosynthesis: Effect of acquisition parameters and quantum noise a. Med. Phys. 2010, 37, 1591–1600. [Google Scholar] [CrossRef]







| X-ray source to rotation center (mm) | 500 |
| X-ray source to detector distance (mm) | 1000 |
| Scanning angle (deg) | [0°, 360°] |
| Scanning angular interval (deg) | |
| Number of detector units | 1024 |
| Detector unit size (mm) | 0.3574 |
| Reconstructed image size (pixel) |
| Pre-Decomposition | 1 Iteration | 2 Iterations | ||
|---|---|---|---|---|
| adipose | training set | |||
| test set | ||||
| fibroglandular | training set | |||
| test set | ||||
| calcification | training set | |||
| test set |
| Noise Level | ||||
|---|---|---|---|---|
| adipose | training set | |||
| test set | ||||
| fibroglandular | training set | |||
| test set | ||||
| calcification | training set | |||
| test set |
| Proposed CNN | UNet | ||
|---|---|---|---|
| adipose | training set | ||
| test set | |||
| fibroglandular | training set | ||
| test set | |||
| calcification | training set | ||
| test set |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, G.; Yang, P.; Zhao, X. Dual-Domain Joint Learning Reconstruction Method (JLRM) Combined with Physical Process for Spectral Computed Tomography (SCT). Symmetry 2025, 17, 1165. https://doi.org/10.3390/sym17071165
Ma G, Yang P, Zhao X. Dual-Domain Joint Learning Reconstruction Method (JLRM) Combined with Physical Process for Spectral Computed Tomography (SCT). Symmetry. 2025; 17(7):1165. https://doi.org/10.3390/sym17071165
Chicago/Turabian StyleMa, Genwei, Ping Yang, and Xing Zhao. 2025. "Dual-Domain Joint Learning Reconstruction Method (JLRM) Combined with Physical Process for Spectral Computed Tomography (SCT)" Symmetry 17, no. 7: 1165. https://doi.org/10.3390/sym17071165
APA StyleMa, G., Yang, P., & Zhao, X. (2025). Dual-Domain Joint Learning Reconstruction Method (JLRM) Combined with Physical Process for Spectral Computed Tomography (SCT). Symmetry, 17(7), 1165. https://doi.org/10.3390/sym17071165





