Energy-Efficient Bipedal Locomotion Through Parallel Actuation of Hip and Ankle Joints

Abstract

Achieving energy-efficient, human-like gait remains a major challenge in bipedal humanoid robotics, as traditional serial actuation architectures often lead to high instantaneous power peaks and uneven load distribution. This study addresses the lack of research on how mechanical symmetry, achieved through parallel actuation, can improve power management in lower-limb joints. We developed a 14-degree-of-freedom (DOF) hip-sized bipedal robot model and conducted simulations comparing a conventional serial configuration—using single-DOF rotary actuators—with a novel parallel configuration that employs paired linear actuators at the hip pitch, hip roll, ankle pitch, and ankle roll joints. Simulation results over a standardized walking cycle show that the parallel configuration reduces peak hip-pitch power by 80.4% and peak ankle-pitch power by 53.5%. These findings demonstrate that incorporating actuator symmetry through parallel joint design significantly reduces actuator stress, improves load sharing, and enhances overall energy efficiency in bipedal locomotion.

1. Introduction

Achieving stable and energy-efficient bipedal locomotion remains a central challenge in humanoid robotics due to the complexity of coordinating multiple joints under dynamic loads. Traditional bipedal configurations often rely on serial actuation, where each joint is powered independently by a rotary actuator. While this approach simplifies control, it leads to high instantaneous power peaks and poor load distribution, especially at key joints such as the hip and ankle. These limitations hinder overall system efficiency and increase actuator stress. Consequently, there is a growing interest in exploring alternative actuation strategies that can enhance energy performance while maintaining gait stability and coordination [1].

Bipedal gaits in humanoid robots are typically classified as either bird-like or human-like [2]. Early developments between 1972 and 2000 focused on establishing fundamental bipedal motion using serially actuated configurations. Robots like WABOT [3], WASUBOT [4], Honda’s E and P series [5], and Hadaly 1 and 2 [6] featured primarily serial architectures with limited joint coordination, often emphasizing basic gait feasibility over energy efficiency. Saika [7] extended this effort through improved mechanical design but still followed a serial approach. In the 2000s, more sophisticated platforms emerged. Bird-like robots such as CASSIE [8,9] and BirdBot [10] introduced compliant legs with reduced degrees of freedom, optimized for dynamic agility. In contrast, human-like robots including ASIMO [11], Sony’s Qrio [12], Fujitsu’s HOAP-1 [13], and the KHR series [14,15] adopted higher degree-of-freedom (DOF) architectures, particularly at the hip and ankle, to better replicate human gait. These robots, while mechanically advanced, continued to rely on single-actuator serial joints, often resulting in high torque requirements and peak power consumption at key joints. Subsequent platforms like HRP-4 [16], WABIAN-2 [17,18], and REEM-A [19] introduced improvements in joint placement and stability, targeting more human-like posture and step transitions. Notably, LOLA [20] implemented partial parallel elements for improved control accuracy, though not focused on energy reduction. More recent humanoids—REEM-B [21], NAO [22], HUBO-2 PLUS [23], REEM-C [24,25], TOPIO 1.0, ATLAS [26], and TaeMu [27]—explored diverse actuation strategies, including electric and hydraulic systems. Several control strategies have also been proposed to enhance gait coordination and energy efficiency. Notable among them are Arena et al.’s bioinspired motor neuron and nullcline-based control models [28,29], which enable advanced synchronization and adaptability. However, these approaches remain limited by the underlying mechanical architecture. Despite the technological maturity of recent humanoid platforms, most continue to rely on serial actuation, with little emphasis on leveraging mechanical symmetry or parallel configurations for improved energy efficiency.

Parallel mechanisms, though widely recognized for their advantages in industrial robotics, have been underutilized in humanoid locomotion. Studies by Pandilov and Dukovski [30] emphasized their potential for better load handling and power efficiency, albeit with added control complexity. Applications in surgical and humanoid arms [31,32] have demonstrated the effectiveness of hybrid serial–parallel configurations for improving dexterity. Further, works by Briot et al. [33] and Assoumou Nzue et al. [34] have confirmed that parallel systems can surpass serial ones in precision and repeatability. Despite these benefits, humanoid bipedal robots have seldom integrated parallel actuators—often only at isolated joints. Notable examples include LOLA [20] and WABIAN-2 [17,18], but even these remain predominantly serial in architecture. As a result, joint control remains localized, and high-torque joints continue to experience elevated power demands. Although some energy-optimized control strategies have been proposed [35,36], their effectiveness is limited by the inherent inefficiencies of the mechanical structure.

This study addresses the existing gap by proposing a novel bipedal robot architecture that incorporates parallel actuation at the hip pitch, hip roll, ankle pitch, and ankle roll joints—four of the most energy-intensive joints during walking. Unlike previous approaches that either selectively implemented parallel mechanisms or focused solely on control strategies, this work introduces a fully integrated 7-DOF parallel actuation system for each leg. In this configuration, conventional single-actuator serial joints are replaced with pairs of linear actuators operating in parallel, allowing for more effective torque distribution, improved mechanical symmetry, and substantial reductions in peak power demand. We hypothesize that by symmetrically distributing joint forces through paired actuators, it is possible to significantly lower instantaneous power loads and actuator stress, ultimately enhancing both energy efficiency and mechanical performance in bipedal locomotion. The proposed architecture also offers several advantages: improved power-to-weight ratio via load sharing, reduced actuator fatigue, and more stable, precise joint control due to distributed actuation. Additionally, the design reduces energy expenditure during static phases and promotes smoother motion by maintaining actuator operation within optimal performance ranges. To test this hypothesis, the study compares serial and parallel actuation schemes through simulations that analyse torque and power performance. The analysis is supported by forward and inverse kinematic models, along with the trajectory planning method, detailed in Section 2 and Section 3.

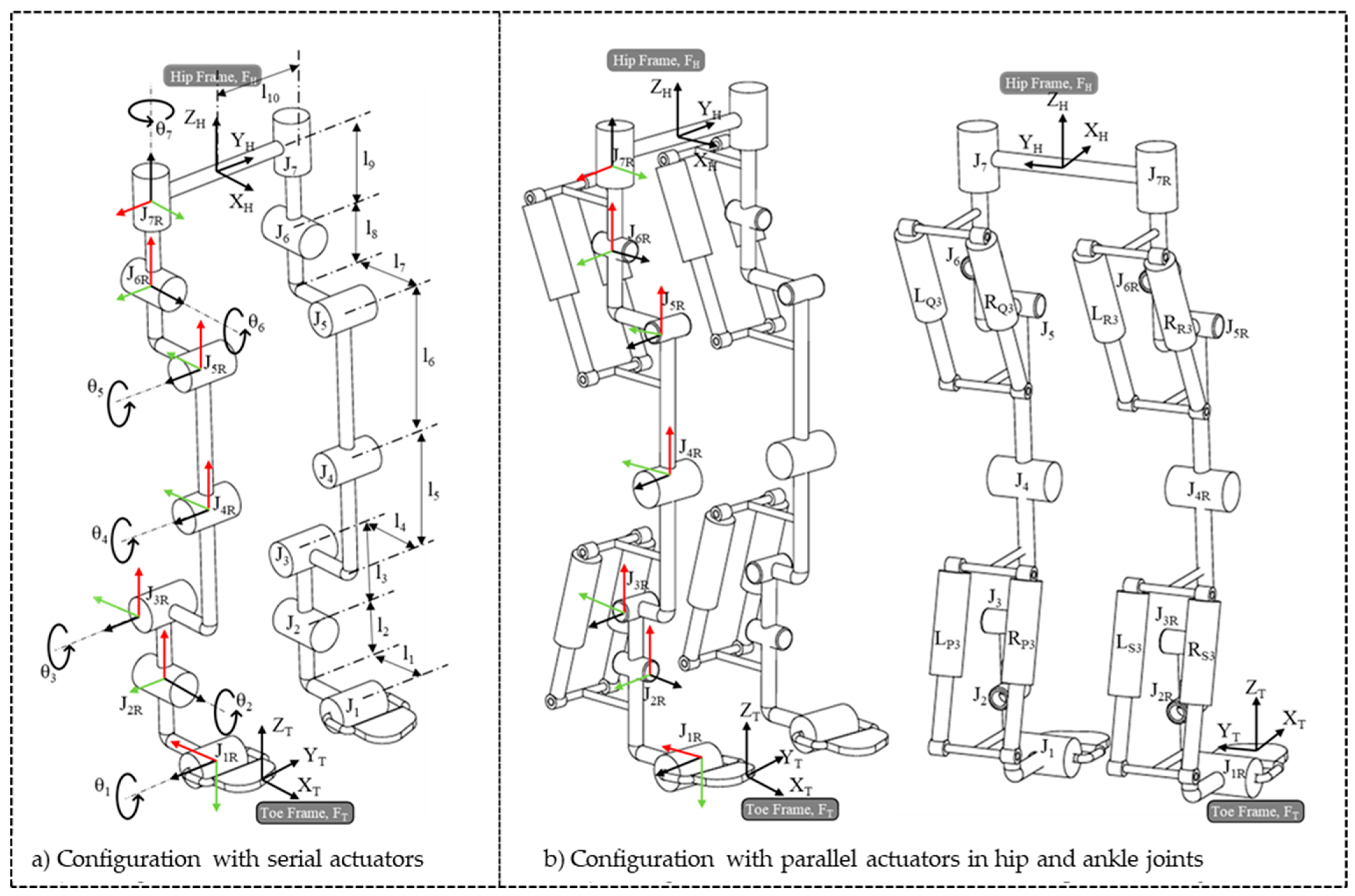
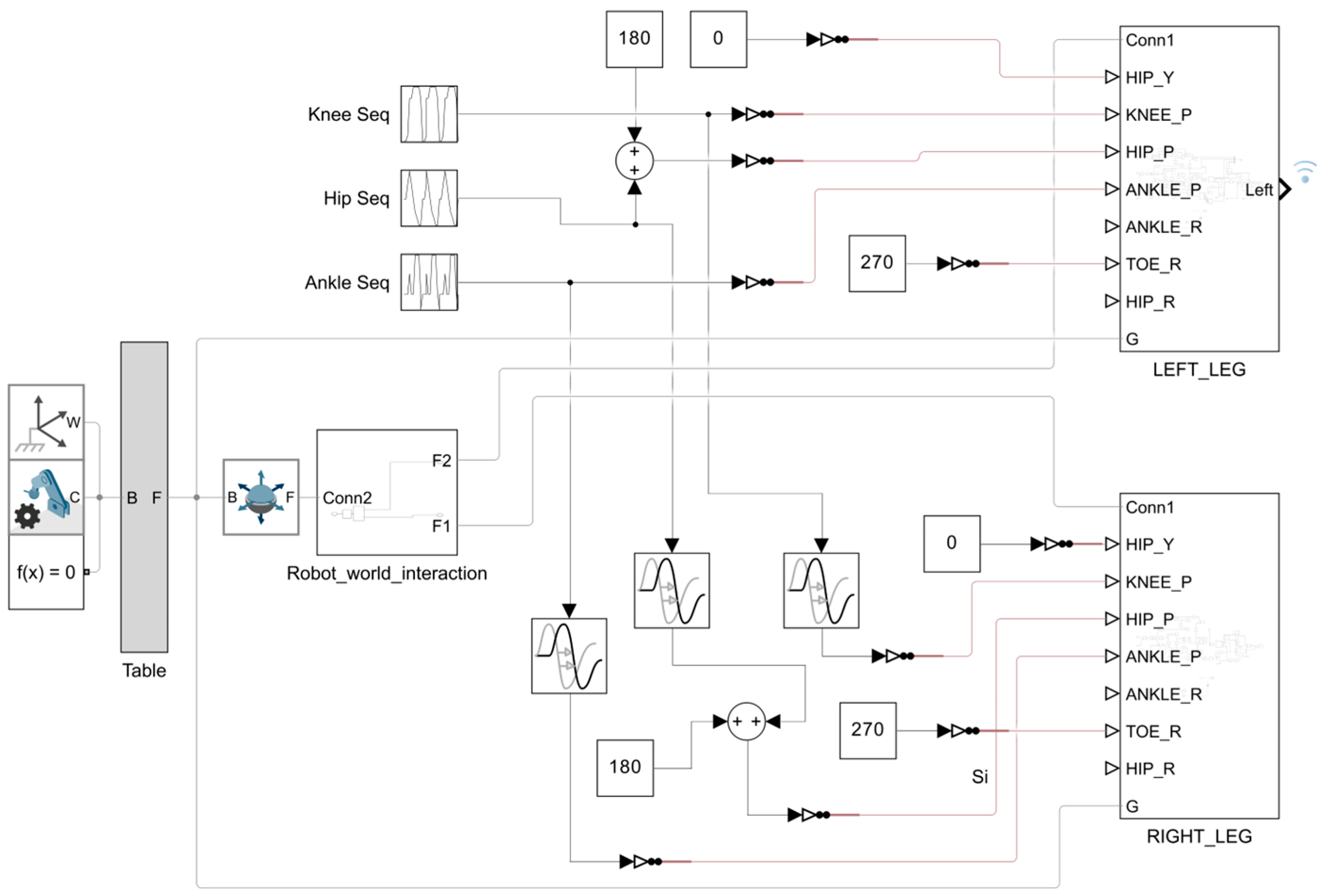
2. Methodology

The proposed bipedal robot consists of two legs, with each leg having seven degrees of freedom (DOF) from the hip to the toe. The kinematic diagram of both the serial configuration and parallel configuration is shown in Figure 1, where all joints are labelled for clarity. The robot’s joints are structured as follows:

• F_T—Frame representing the toe link
• F_H—Frame representing the hip link
• J₁ (toe pitch joint): Provides pitch motion at the toe.
• J₂ & J₃ (ankle joints): Two revolute joints enabling independent roll and pitch movements at the ankle.
• J₄ (knee pitch joint): A single revolute joint allowing pitch motion at the knee.
• J₅, J₆ & J₇ (hip joints):

  ▪

  J₅ & J₆: Provide pitch and roll motion at the hip.

  ▪

  J₇: Controls yaw motion at the hip.

To enhance power efficiency, we implement parallel actuators L_P3 and R_P3 for left leg ankle joint J₂ and J₃, L_S3 and R_S3 for right leg ankle joint J_2R and J_3R, L_Q3 and R_Q3 for left leg hip joint J₅ and J₆, L_R3 and R_R3 for right leg hip joint J_5R and J_6R, as shown in Figure 1b. Instead of actuating those serial joints independently, each joint pair shares two actuators working in parallel.

Also, in Figure 1b. the hip yaw (J₇ & J_7R), knee pitch (J₄ & J_4R), and toe pitch (J₁ & J_1R) remain in a serial configuration, as they are not the focus of this study. Our analysis is limited to evaluating power efficiency improvements specifically due to parallel actuation at the hip and ankle joints. This design choice is based on prior findings that hip and ankle joints typically experience the highest torque and power demand during walking and balance control in humanoid robots [34,37]. By introducing parallel actuation specifically at these joints, the system can benefit from improved mechanical symmetry and load sharing, which reduces peak actuator effort and enhances energy efficiency. In contrast, joints such as the hip yaw, knee pitch, and toe pitch are retained in a serial configuration, as their motion is either limited or contributes less significantly to power consumption. This selective implementation helps balance complexity with performance gain and is aligned with the goal of achieving more efficient joint-level actuation.

2.1. Forward Kinematics

The forward kinematics of the robot were derived using a homogeneous transformation matrix-based approach. Each joint frame was defined through direct application of rotation and translation matrices, where fixed link lengths and joint angles were substituted with known values, and variable joints were assigned symbolic joint angles (θ₁, θ₂, …) for formulation. This method offers a straightforward framework for modelling the forward kinematics of the 14-DOF robot. Assuming, toe frame “F_T” as joint “J₀” and hip frame “F_H” as joint “J₈”, the position and the orientation of the ith joint “J_i” from the toes “J₀” can be obtained by multiplying the transformation matrices from the toe joint to the ith joint shown in (1).

$${\mathrm{T}}_{\mathrm{Toe}}^{\mathrm{Hip}}{=\mathrm{T}}_{\mathrm{Toe}}^1\times {\mathrm{T}}_1^2\times {\mathrm{T}}_2^3\times \dots \times {\mathrm{T}}_{(\mathrm{i}-1)}^{\mathrm{i}}\times \dots \times {\mathrm{T}}_6^7\times {\mathrm{T}}_7^{\mathrm{Hip}}$$

(1)

where ${\mathrm{T}}_{(\mathrm{i}-1)}^{\mathrm{i}}$ is the homogeneous transformation matrix from (I − 1)^th joint to ith joint. Each homogeneous transformation matrix is constructed as a product of multiple rotation and translation matrices, used to align the coordinate frames and joint axes appropriately. For example, the transformation matrix from joint 1 to joint 2 is constructed by sequentially multiplying two rotation matrices—one about the z-axis by −π/2 and another about the x-axis by +π/2 followed by two translation matrices along the x-axis and y-axis by distances l₁ and l₂, respectively. Similar sequences of rotation and translation matrices are used to construct the transformation matrices between all successive joints. The final positions of the hip frame can be calculated from the forward kinematic equation given in (2):

P_x = −l₂S₁ − l₁C₁ − C₂l₃S₁ − S₄l₆C₃C₁ + S₄l₆C₂S₁ − S₃l₆C₂C₃S₁ − S₃l₆S₃C₁ + S₆l₉S₂S₁ − S₆l₉C₅C₂C₃S₄S₁ + S₆l₉C₅S₃C₃C₁ − S₆l₉C₅S₃S₄C₁ + S₆l₉C₅C₂S₁ + S₆l₉S₅ (−C₃S₄C₁ − C₂S₃C₃S₁ + C₂S₃S₄S₁ + C₁) + C₆l₉C₅ (−C₃S₄S₁C₁ − C₂S₃C₃S₁ + C₂S₃S₄S₁ + C₂C₁) + C₆l₉S₅ (C₂C₃S₄S₁ − S₃C₃C₁ + S₃S₄C₁ − C₂S₁) − lS₆ − C₂S₁S₃l₄ − C₂S₁l₅C₃ + C₁l₄C₃ − C₁S₃l₅ + (C₅l₈ − l₇S₅) (−C₃S₄S₁C₁ − C₂S₃C₃S₁ + C₂S₃S₄S₁ + C₂C₁) + (C₅l₇ + l₈S₅) (C₂C₃S₄S₁ − S₃C₃C₁ + S₃S₄C₁ − C₂S₁)

P_y = S₃S₂C₅l₈ − S₃S₂C₅l₇S₅ − S₃S₂C₃l₈ + S₃S₂S₄l₇ + S₃S₂S₄S₅ + S₂C₃C₅l₇ − S₂C₃C₅ + S₂C₃S₄l₈ − S₂C₃l₈ + S₂C₅l₇ + S₂S₅l₈ − S₂S₅ − S₂l₃ − S₂S₃l₄ − S₂l₅C₃ − S₂S₃C₃l₆ + S₂S₄l₆ − S₆l₉S₂C₅C₃S₄ + S₆l₉S₂C₅ + S₆l₉S₂S₅C₃ − S₆l₉S₂S₅ − S₆l₉C₂ − C₆l₉S₂C₅C₃S₄ + C₆l₉S₂C₅ + C₆l₉S₂S₅C₃ − C₆l₉S₂S₅

P_z = l₂C₁ + l₁S₁ − C₂l₃C₁ + S₄l₆C₃S₁ − S₄l₆C₂S₃C₁ − S₃l₆C₂C₃C₁ + S₃l₆S₃ + S₆l₉S₂C₁ − S₆l₉C₅C₂C₃S₄C₁ − S₆l₉C₅S₃C₃S₁ + S₆l₉C₅S₃S₄S₁ − S₆l₉C₅C₂C₁ + S₆l₉S₅C₃S₄S₁ − S₆l₉S₅C₂S₃C₃C₁ − S₆l₉S₅C₂S₃S₄C₁ − S₆l₉S₅S₁ + C₆l₉C₅C₃S₄S₁ − C₆l₉C₅C₂S₃C₃C₁ − C₆l₉C₅C₂S₃S₄C₁ − C₆l₉C₅S₁ + C₆l₉S₅C₂C₃S₄C₁ + C₆l₉S₅S₃C₃S₁ − C₆l₉S₅S₃S₄S₁ + C₆l₉S₅C₂C₁ − S₁l₄C₃+S₁S₃ − C₂C₁S₃l₄ − C₂C₁l₅C₃ + (C₅l₈C₃S₄S₁ − C₅l₈C₂S₃C₃C₁ − C₅l₈C₂S₃S₄C₁ − C₅l₈S₁) + (l₇S₅C₃S₄S₁ − l₇S₅C₂S₃C₃C₁ − l₇S₅C₂S₃S₄C₁ − l₇S₅S₁) + (C₅l₇C₂C₃S₄C₁ + C₅l₇S₃C₃S₁ − C₅l₇S₃S₄S₁ + C₅l₇C₂C₁) + (l₈S₅C₂C₃S₄C₁ + l₈S₅S₃C₃S₁ − l₈S₅S₃S₄S₁ + l₈S₅C₂C₁)

(2)

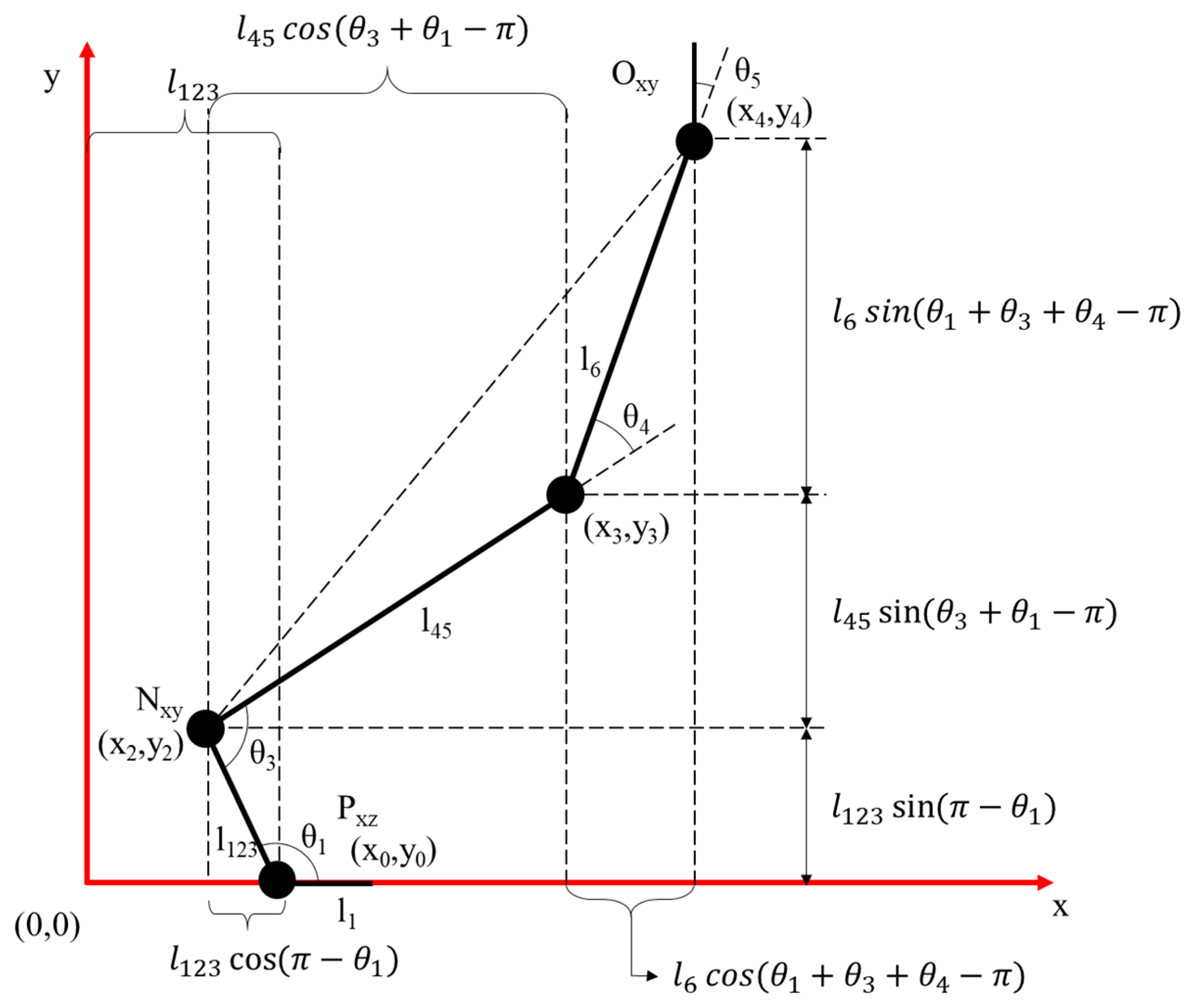
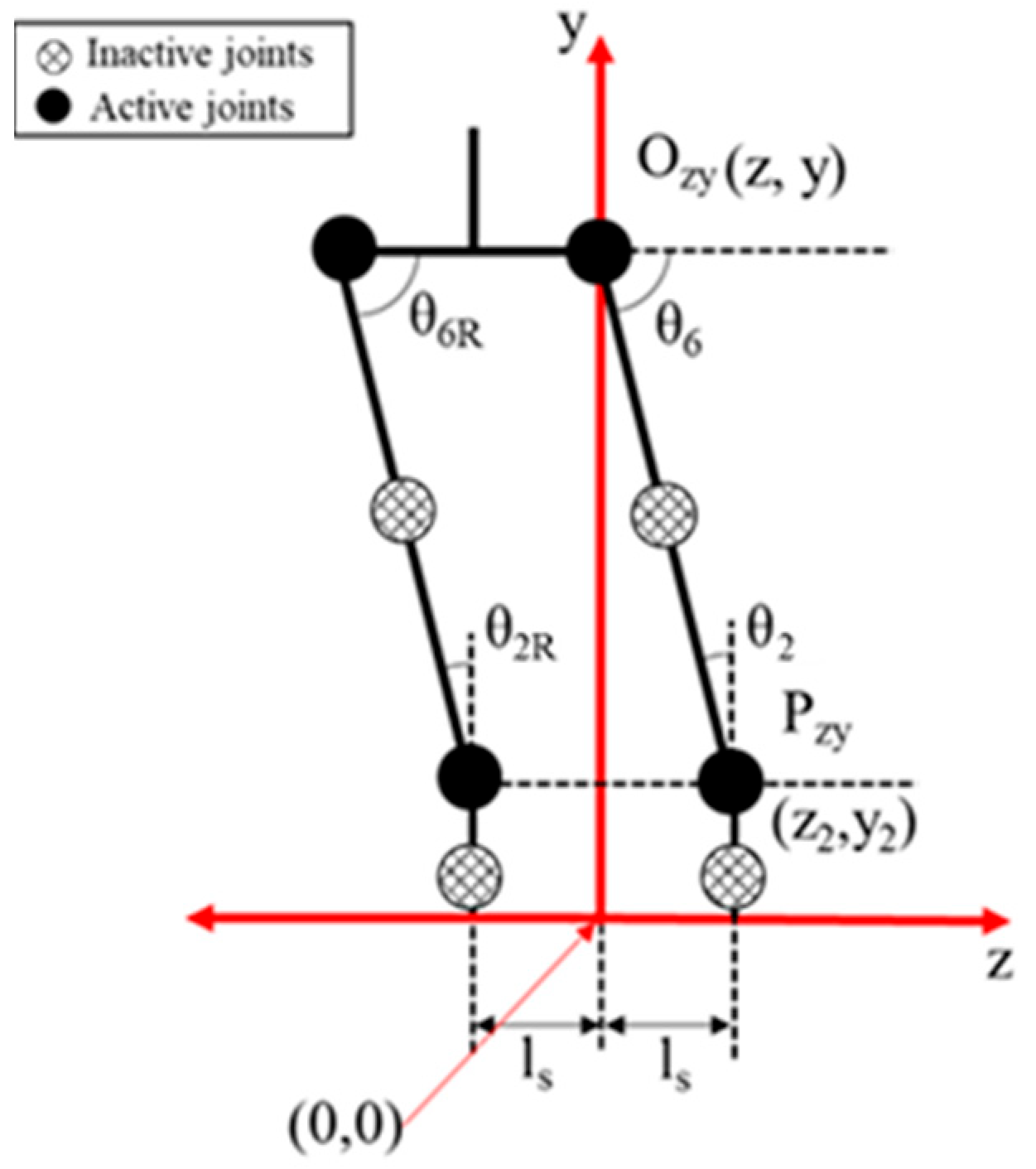
2.2. Theory on Inverse Kinematics

2.2.1. Inverse Kinematics in Sagittal Plane

The sagittal plane of the robot shown in Figure 2 gives the pitching angles θ₁, θ₃, θ₄, and θ₅ of the left leg of the bipedal robot.

Here θ₁—angle of toe joint J₁; θ₃—angle of ankle joint J₃; θ₄—angle of knee joint J₄; θ₅—angle of hip joint J₅. The system in undetermined and thus has infinitely many solutions. So, the angle between toes and ankle can be provided as ∅, which can be applied to obtain x₄, y₄. From the Figure 2, the triangle bound by “l₆” and “l₄₅”, the distance “d” between N_xy and O_xy is given in (3):

$$\mathrm{d}=\sqrt{{\left({\mathrm{x}}_4-{\mathrm{l}}_{123}\left(1-\cos \mathrm{\varphi }\right)\right)}^2+{\left({\mathrm{y}}_4-{\mathrm{l}}_{123}\sin \mathrm{\varphi }\right)}^2}$$

(3)

Using the law of cosines, “θ₄” can be found as shown in (4), and Angle “θ₃” is given in (5):

$${\mathrm{\theta }}_4=\left\{\begin{array}{c}\mathrm{\pi }-{\cos }^{-1}\left({\displaystyle \frac{{\mathrm{l}}_{45}^2+{\mathrm{l}}_6^2-{\mathrm{d}}^2}{2{\mathrm{l}}_{45}{\mathrm{l}}_6}}\right)\\ {\cos }^{-1}\left({\displaystyle \frac{{\mathrm{d}}^2-{\mathrm{l}}_{45}^2-{\mathrm{l}}_6^2}{2{\mathrm{l}}_{45}{\mathrm{l}}_6}}\right)\end{array}\right.$$

(4)

$${\mathrm{\theta }}_3={\tan }^{-1}\left({\displaystyle \frac{{\mathrm{y}}_4-{\mathrm{l}}_{123}\sin \mathrm{\varphi }}{{\mathrm{x}}_4-\left({\mathrm{l}}_{123}+{\mathrm{l}}_{123}\cos \mathrm{\varphi }\right)}}\right)-{\tan }^{-1}\left({\displaystyle \frac{{\mathrm{l}}_6\sin {\mathrm{\theta }}_4}{{\mathrm{l}}_{45}+{\mathrm{l}}_6\cos {\mathrm{\theta }}_4}}\right)+\mathrm{\pi }-\mathrm{\varphi }$$

(5)

The hip of the robot must be always retained at a specific angle so that the vertical component of the hip and the surface of the floor will be perpendicular to each other. Thus, the θ₄ makes an angle π/2 radian to the horizontal component parallel to the floor. The θ₅ is given in (6):

$${\mathrm{\theta }}_5={\displaystyle \frac{3\mathrm{\pi }}{2}}-{\mathrm{\theta }}_1-{\mathrm{\theta }}_3-{\mathrm{\theta }}_4$$

(6)

Similarly, the right leg of the robot can be solved as θ_1R—angle of toe joint of right leg; θ_3R—angle of ankle joint of right leg; θ_4R—angle of knee joint of right leg; θ_5R—angle of hip joint of right leg, as shown in (7):

$$\begin{array}{l}{\mathrm{\theta }}_{4\mathrm{R}}=\left\{\begin{array}{c}\mathrm{\pi }-{\cos }^{-1}\left({\displaystyle \frac{{\mathrm{l}}_{45}^2+{\mathrm{l}}_6^2-{\mathrm{d}}^2}{2{\mathrm{l}}_{45}{\mathrm{l}}_6}}\right)\\ {\cos }^{-1}\left({\displaystyle \frac{{\mathrm{d}}^2-{\mathrm{l}}_{45}^2-{\mathrm{l}}_6^2}{2{\mathrm{l}}_{45}{\mathrm{l}}_6}}\right)\end{array}\right.;\\ {\mathrm{\theta }}_{3\mathrm{R}}={\tan }^{-1}\left({\displaystyle \frac{{\mathrm{y}}_4-{\mathrm{l}}_{123}\sin \mathrm{\varphi }}{{\mathrm{x}}_4-\left({\mathrm{l}}_{123}+{\mathrm{l}}_{123}\cos \mathrm{\varphi }\right)}}\right)-{\tan }^{-1}\left({\displaystyle \frac{{\mathrm{l}}_6\sin {\mathrm{\theta }}_4}{{\mathrm{l}}_{45}+{\mathrm{l}}_6\cos {\mathrm{\theta }}_4}}\right)+\mathrm{\pi }-\mathrm{\varphi };\\ {\mathrm{\theta }}_{5\mathrm{R}}={\displaystyle \frac{3\mathrm{\pi }}{2}}-{\mathrm{\theta }}_{1\mathrm{R}}-{\mathrm{\theta }}_{3\mathrm{R}}-{\mathrm{\theta }}_{4\mathrm{R}}\end{array}$$

(7)

2.2.2. Inverse Kinematics in Frontal Plane

The kinematic diagram of the robot in frontal plane is shown in Figure 3. Here θ₂—angle of frontal ankle joint of right leg; θ_2R—angle of frontal ankle joint of left leg; θ₆—angle of frontal hip joint of right leg; θ_6R—angle of frontal hip joint of left leg; l_s—distance between feet. Since the angle “∅” is provided the point “P_zy” can be represented as shown in (8), where θ₂ is shown in (9):

$${\mathrm{P}}_{\mathrm{z}\mathrm{y}}=\left[\begin{array}{c}{\mathrm{z}}_2\\ {\mathrm{y}}_2\end{array}\right]=\left[\begin{array}{c}{\mathrm{l}}_{\mathrm{s}}\\ {\mathrm{l}}_2\sin \mathrm{\varphi }\end{array}\right]$$

(8)

From Figure 3, similar to the sagittal plane, the hip of the robot has to be kept at a certain angle at all times so that the vertical component of the hip and the surface of the floor will be perpendicular to each other. Thus, the sum of angles θ₆ and θ₂ are equal to π/2 radian. The same procedures can be followed for solving the right leg.

$${\mathrm{\theta }}_2=\mathrm{atan}\left({\displaystyle \frac{\left|{\mathrm{l}}_{\mathrm{z}}-\mathrm{z}\right|}{\mathrm{y}-{\mathrm{l}}_{\mathrm{z}}\sin \mathrm{\varphi }}}\right)$$

(9)

$${\mathrm{\theta }}_6={\displaystyle \frac{\mathrm{\pi }}{2}}-{\mathrm{\theta }}_2$$

(10)

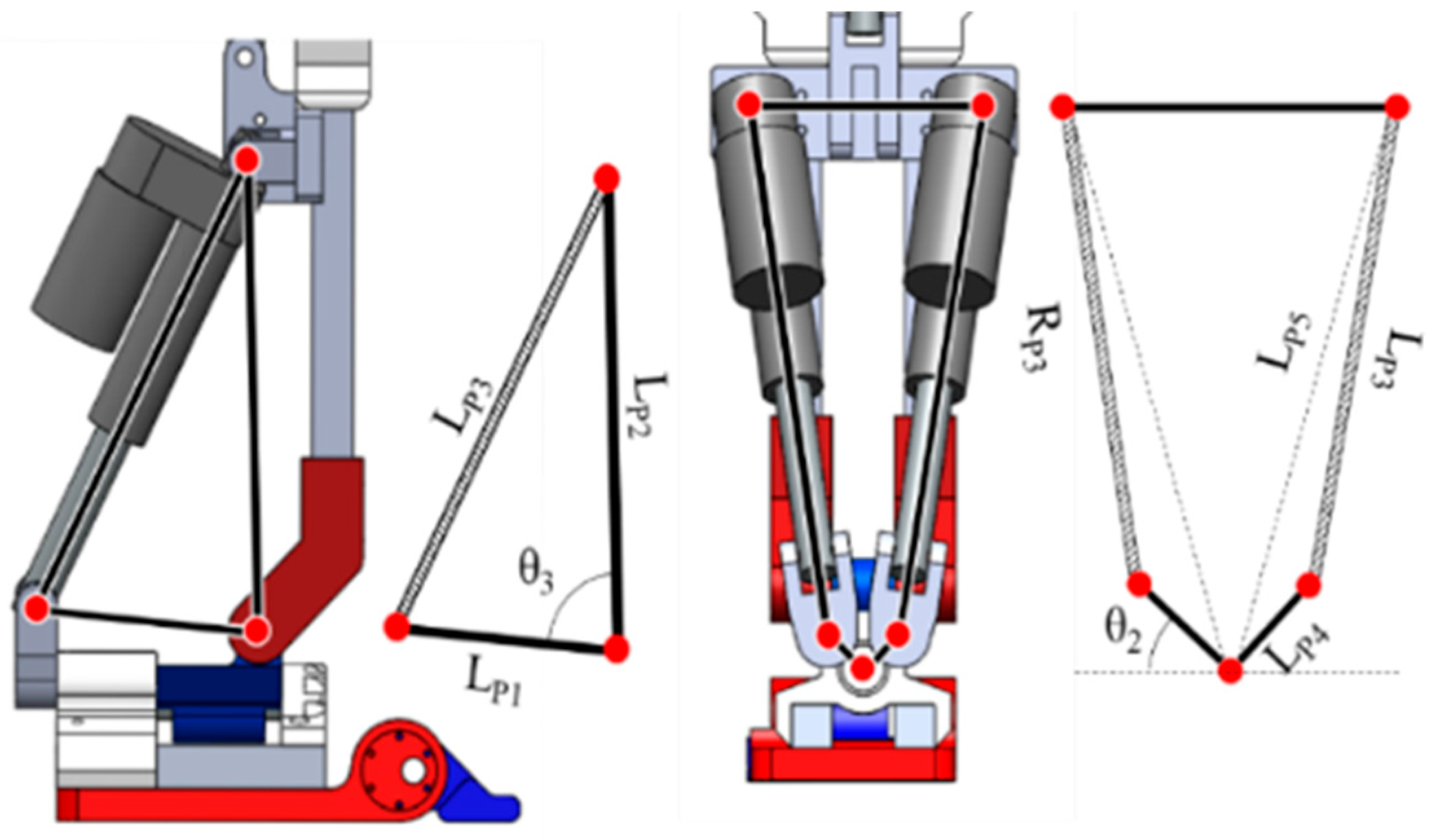
2.2.3. Inverse Kinematics for Linear Actuator Positions

The mathematical relationship between joint angles and actuator positions is formulated using the geometry of the joints, as depicted in the Figure 4. Assuming L_p1, L_p2, L_p4, and L_p5 are the length of the links connected by the joints J₂ and J₃, the desired lengths L_p3 and R_p3 of the linear actuators can be calculated using trigonometric relations.

$$\begin{array}{l}{\mathrm{R}}_{\mathrm{P}3}=\sqrt{{\mathrm{R}}_{\mathrm{P}1}^2+{\mathrm{R}}_{\mathrm{P}2}^2}-2{\mathrm{R}}_{\mathrm{P}1}{\mathrm{R}}_{\mathrm{P}2}\cos {\mathrm{\theta }}_3-\sqrt{{\mathrm{R}}_{\mathrm{P}4}^2+{\mathrm{R}}_{\mathrm{P}5}^2}-2{\mathrm{R}}_{\mathrm{P}4}{\mathrm{R}}_{\mathrm{P}5}\cos {\mathrm{\theta }}_2\\ {\mathrm{L}}_{\mathrm{P}3}=\sqrt{{\mathrm{L}}_{\mathrm{P}1}^2+{\mathrm{L}}_{\mathrm{P}2}^2}-2{\mathrm{L}}_{\mathrm{P}1}{\mathrm{L}}_{\mathrm{P}2}\cos {\mathrm{\theta }}_3-\sqrt{{\mathrm{L}}_{\mathrm{P}4}^2+{\mathrm{L}}_{\mathrm{P}5}^2}-2{\mathrm{L}}_{\mathrm{P}4}{\mathrm{L}}_{\mathrm{P}5}\cos {\mathrm{\theta }}_2\end{array}$$

(11)

Equation (11) gives us the inverse kinematics of the 2-DOF ankle joints, where the positions of the linear actuator can be derived using the angle of the joints.

3. Trajectory Planning

To achieve statically stable walking, we define the Cartesian trajectories for the feet and hip of the robot using piecewise continuous wave-based equations. These trajectories are designed to ensure that at least one foot is always in contact with the ground while the other swings forward and that the centre of mass stays within the support polygon.

The trajectory planner takes three primary input parameters:

• Step length (s)—the forward distance moved in each step;
• Step time (T)—the duration of one complete step;
• Step height (s_h)—the maximum vertical displacement of the foot during swing.

Let ‘n’ be the current step number and ‘t’ the continuous time variable. The equations can be derived as follows.

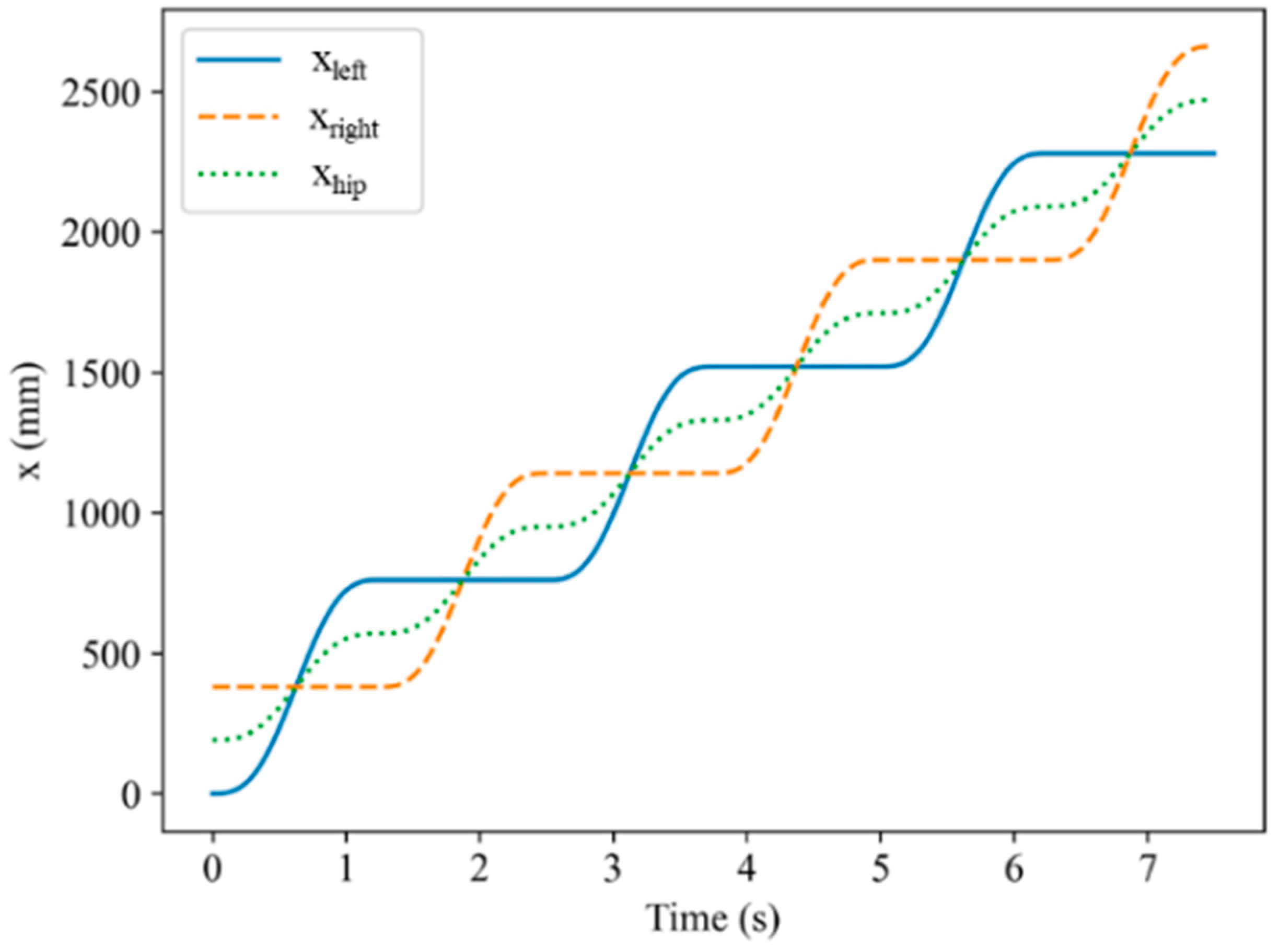
3.1. Deriving x_left and x_right for Toe Frame

During walking, each foot undergoes a stance phase and a swing phase. To emulate human-like gait patterns, the trajectory for foot motion must maintain constant velocity during the stance phase and sinusoidal smoothing in the swing phase. The velocity ‘v’ is the ratio of the step distance ‘s’ to the time taken ‘T/2’ considering only the swing phase. The x(t) can be represented using the inputs ‘s’ and ‘t’ as shown in (12):

$$\mathrm{x}\left(\mathrm{t}\right)=\mathrm{v}\mathrm{t}\Rightarrow \mathrm{x}\left(\mathrm{t}\right)={\displaystyle \frac{2\mathrm{s}}{\mathrm{T}}}\mathrm{t}$$

(12)

The Equation (12) gives purely linear motion, which though functionally sufficient, lacks smoothness in acceleration transitions and may induce abrupt changes in actuator torque. To introduce natural acceleration and deceleration around toe-off and heel strike, a sinusoidal modulation term is superimposed on the linear motion. This modifier, derived from a rectified quarter-wave sine function, subtracts from the linear component, ensuring that the foot velocity begins and ends at zero during the swing phase. This creates a smooth bell-shaped velocity curve, preventing jerky transitions. Equation (13) shows the resulting swing trajectory:

$$\mathrm{x}\left(\mathrm{t}\right)={\displaystyle \frac{2\mathrm{s}\mathrm{t}}{\mathrm{T}}}-{\displaystyle \frac{\mathrm{s}}{2\mathrm{\pi }}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\displaystyle \frac{4\mathrm{\pi }\mathrm{t}}{\mathrm{T}}}\right)$$

(13)

To synchronize successive steps, the trajectory is offset in space by subtracting the term ‘ns’ where ‘n’ denotes the current step number. This ensures that each swing trajectory initiates from a new foot placement, effectively creating a step-by-step progression in the sagittal plane. Equation (14) shows the x trajectory of the foot with function of time ‘t’.

$${\mathrm{x}}_{\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t}}\left(\mathrm{t}\right)={\displaystyle \frac{2\mathrm{s}\mathrm{t}}{\mathrm{T}}}-\mathrm{n}\mathrm{s}-{\displaystyle \frac{\mathrm{s}}{2\mathrm{\pi }}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\displaystyle \frac{4\mathrm{\pi }\mathrm{t}}{\mathrm{T}}}\right)$$

(14)

Now apply piecewise logic:

• During the stance phase, the foot is fixed: x = (n + 1)s;
• During the swing phase, the foot moves using the wave-based equation.

$${\mathrm{x}}_{\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t}}=\left\{\begin{array}{lll}{\displaystyle \frac{2\mathrm{s}\mathrm{t}}{\mathrm{T}}}-\mathrm{n}\mathrm{s}-{\displaystyle \frac{\mathrm{s}}{2\mathrm{\pi }}}\sin \left({\displaystyle \frac{4\mathrm{\pi }\mathrm{t}}{\mathrm{T}}}\right)\hfill & \mathrm{f}\mathrm{o}\mathrm{r}\hfill & \left(\mathrm{n}\right)\mathrm{T}\le \mathrm{t}\le \left(\mathrm{n}+{\displaystyle \frac{1}{2}}\right)\mathrm{T}\hfill \\ \left(\mathrm{n}+1\right)\mathrm{s}\hfill & \mathrm{f}\mathrm{o}\mathrm{r}\hfill & \left(\mathrm{n}+{\displaystyle \frac{1}{2}}\right)\mathrm{T}\le \mathrm{t}\le \left(\mathrm{n}+1\right)\mathrm{T}\hfill \end{array}\right.$$

(15)

To achieve alternating leg motion, the right foot trajectory follows the same formulation but is temporally shifted by T/2 and spatially offset by −s/2 to reflect mid-step staggering:

$${\mathrm{x}}_{\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}}=\left\{\begin{array}{lll}{\displaystyle \frac{2\mathrm{s}\mathrm{t}}{\mathrm{T}}}-\mathrm{n}\mathrm{s}-{\displaystyle \frac{\mathrm{s}}{2\mathrm{\pi }}}\sin \left({\displaystyle \frac{4\mathrm{\pi }\mathrm{t}}{\mathrm{T}}}\right)-{\displaystyle \frac{\mathrm{s}}{2}}\hfill & \mathrm{f}\mathrm{o}\mathrm{r}\hfill & \left(\mathrm{n}+{\displaystyle \frac{1}{2}}\right)\mathrm{T}\le \mathrm{t}\le \left(\mathrm{n}+1\right)\mathrm{T}\hfill \\ \left(\mathrm{n}+{\displaystyle \frac{3}{2}}\right)\mathrm{s}\hfill & \mathrm{f}\mathrm{o}\mathrm{r}\hfill & \left(\mathrm{n}+1\right)\mathrm{T}\le \mathrm{t}\le \left(\mathrm{n}+{\displaystyle \frac{3}{2}}\right)\mathrm{T}\hfill \end{array}\right.$$

(16)

These wave-based functions were crafted to ensure smooth foot transitions. The sinusoidal term introduces gentle accelerations and decelerations during swing, avoiding a jerky motion. When one foot is in the swing phase, the other remains stationary, mimicking a realistic gait.

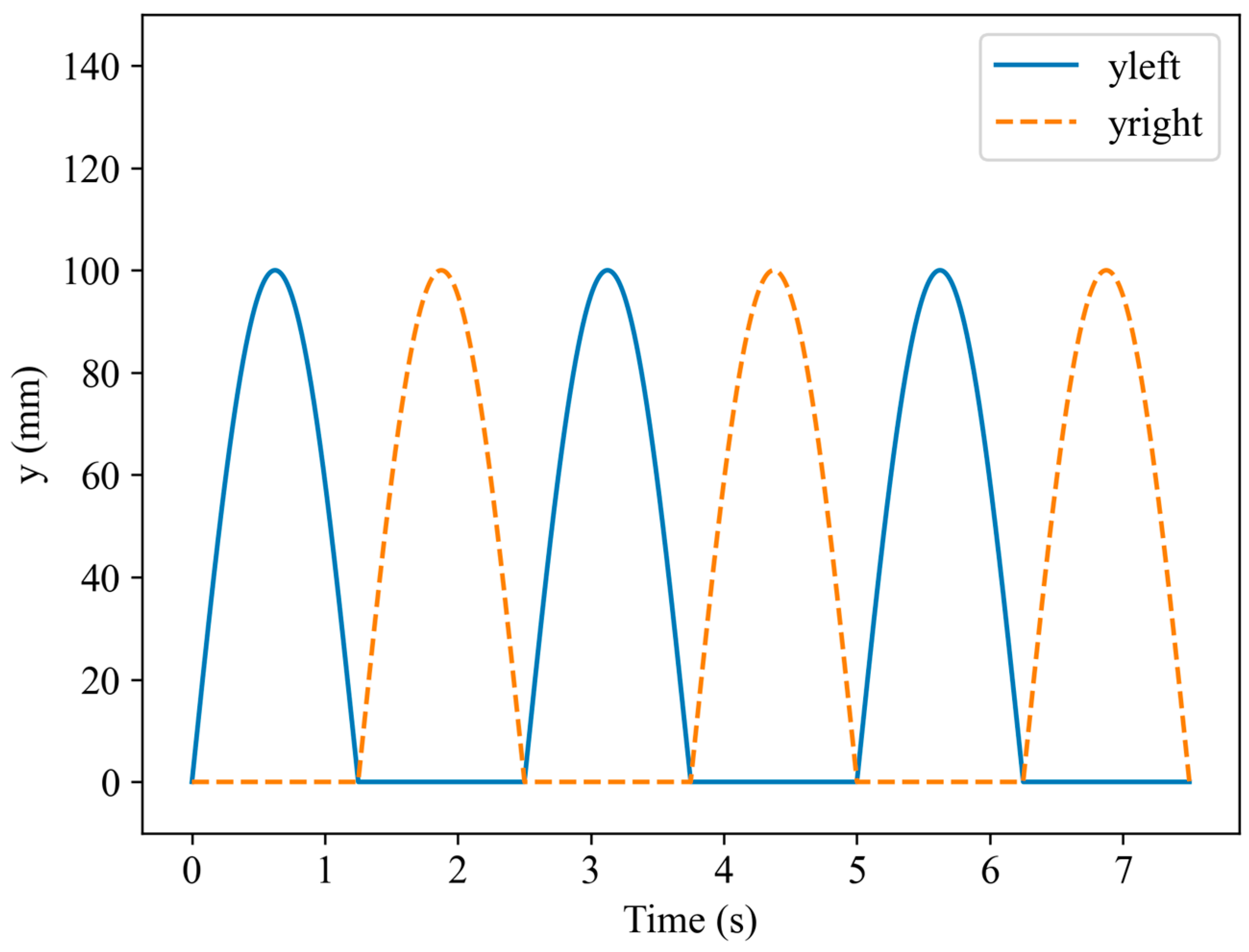
3.2. Deriving Y_left and Y_right

The foot should lift and land smoothly. We define the vertical position using sinusoidal arcs. To ensure that each foot remains grounded during its stance phase and lifts only during its swing phase, the vertical foot trajectory is defined using a half-sine function activated only during the swing interval. The trajectory reaches a maximum height of sh at the midpoint of the swing and returns to zero at touchdown, ensuring a smooth toe-off and landing. Outside of this swing phase, the vertical foot position remains zero, signifying ground contact. This piecewise definition reflects physical leg behaviour in walking and maintains consistency with statically stable gait patterns. Assuming swing occurs from t = nT to t = (n + 1/2)T and stance from t = (n + 1/2)T to t = (n + 1)T, the vertical trajectory of the left foot should be

$${\mathrm{y}}_{\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t}}=\left\{\begin{array}{lll}{\mathrm{s}}_{\mathrm{h}}.\sin \left({\displaystyle \frac{2\mathrm{\pi }\left(\mathrm{t}-\mathrm{n}\mathrm{T}\right)}{\mathrm{T}}}\right)\hfill & \mathrm{f}\mathrm{o}\mathrm{r}\hfill & 0\le \left(\mathrm{t}-\mathrm{n}\mathrm{T}\right)\le {\displaystyle \frac{\mathrm{T}}{2}}\hfill \\ 0\hfill & \mathrm{f}\mathrm{o}\mathrm{r}\hfill & {\displaystyle \frac{\mathrm{T}}{2}}\le (\mathrm{t}-\mathrm{n}\mathrm{T})\le \mathrm{T}\hfill \end{array}\right.$$

(17)

and the right foot, which swings during the second half of the step cycle, becomes

$${\mathrm{y}}_{\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}}=\left\{\begin{array}{lll}0\hfill & \mathrm{f}\mathrm{o}\mathrm{r}\hfill & 0\le \left(\mathrm{t}-\mathrm{n}\mathrm{T}\right)\le {\displaystyle \frac{\mathrm{T}}{2}}\hfill \\ {\mathrm{s}}_{\mathrm{h}}.\sin \left({\displaystyle \frac{2\mathrm{\pi }\left(\left(\mathrm{t}-\mathrm{n}\mathrm{T}\right)-\raisebox{1ex}{$\mathrm{T}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)}{\mathrm{T}}}\right)\hfill & \mathrm{f}\mathrm{o}\mathrm{r}\hfill & {\displaystyle \frac{\mathrm{T}}{2}}\le \left(\mathrm{t}-\mathrm{n}\mathrm{T}\right)\le \mathrm{T}\hfill \end{array}\right.$$

(18)

3.3. Deriving Hip Trajectory

In addition to foot trajectories, the trajectory of the hip plays a critical role in maintaining balance, especially in statically stable walking. The hip movement must be coordinated in all three dimensions—sagittal (forward), coronal (lateral), and vertical—to ensure that the centre of mass (CoM) remains within the support polygon throughout the gait cycle. To maintain smooth and balanced forward progression, the x-direction motion of the hip is computed as the average of the horizontal positions of both feet. This averaging approach ensures that the hip remains equidistant between the supporting and swinging foot, promoting CoM alignment over the base of support:

$${\mathrm{x}}_{\mathrm{h}\mathrm{i}\mathrm{p}}={\displaystyle \frac{{\mathrm{x}}_{\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t}}+{\mathrm{x}}_{\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}}}{2}}$$

(19)

This formulation not only keeps the CoM near the midline of the robot but also minimizes abrupt changes in momentum, which is crucial for quasi-static or statically stable walking:

$${\mathrm{y}}_{\mathrm{h}\mathrm{i}\mathrm{p}}=\mathrm{H}$$

(20)

The vertical trajectory of the hip is held at a constant height throughout the walking cycle. This simplification reflects a quasi-static walking assumption where changes in gravitational potential energy are minimized, thereby reducing the energy demand. To replicate natural pelvic sway observed in human locomotion and to ensure dynamic weight shifting, a sinusoidal function is used for lateral hip motion. This oscillation mimics the lateral displacement of the pelvis during single-leg support phases and helps shift the CoM toward the stance leg, improving balance:

$${\mathrm{z}}_{\mathrm{h}\mathrm{i}\mathrm{p}}={\mathrm{l}}_{\mathrm{s}}\sin \left({\displaystyle \frac{2\mathrm{\pi }\mathrm{t}}{\mathrm{T}}}\right)$$

(21)

where ‘l_s’ is the lateral distance between the legs (hip width), and ‘T’ is the step period. The sinusoidal profile ensures periodic motion aligned with the step cycle, reaching lateral extremes at mid-stance and returning to the centre during the double-support phase.

The generated trajectories are then sent to the joint angle generator which uses inverse kinematics to find the position and angle of the actuators. These generated positions are fed to the linear actuator by means of a controller, and encoders are used to obtain the feedback to control the system. The control flow diagram of the robot is shown in Figure 5:

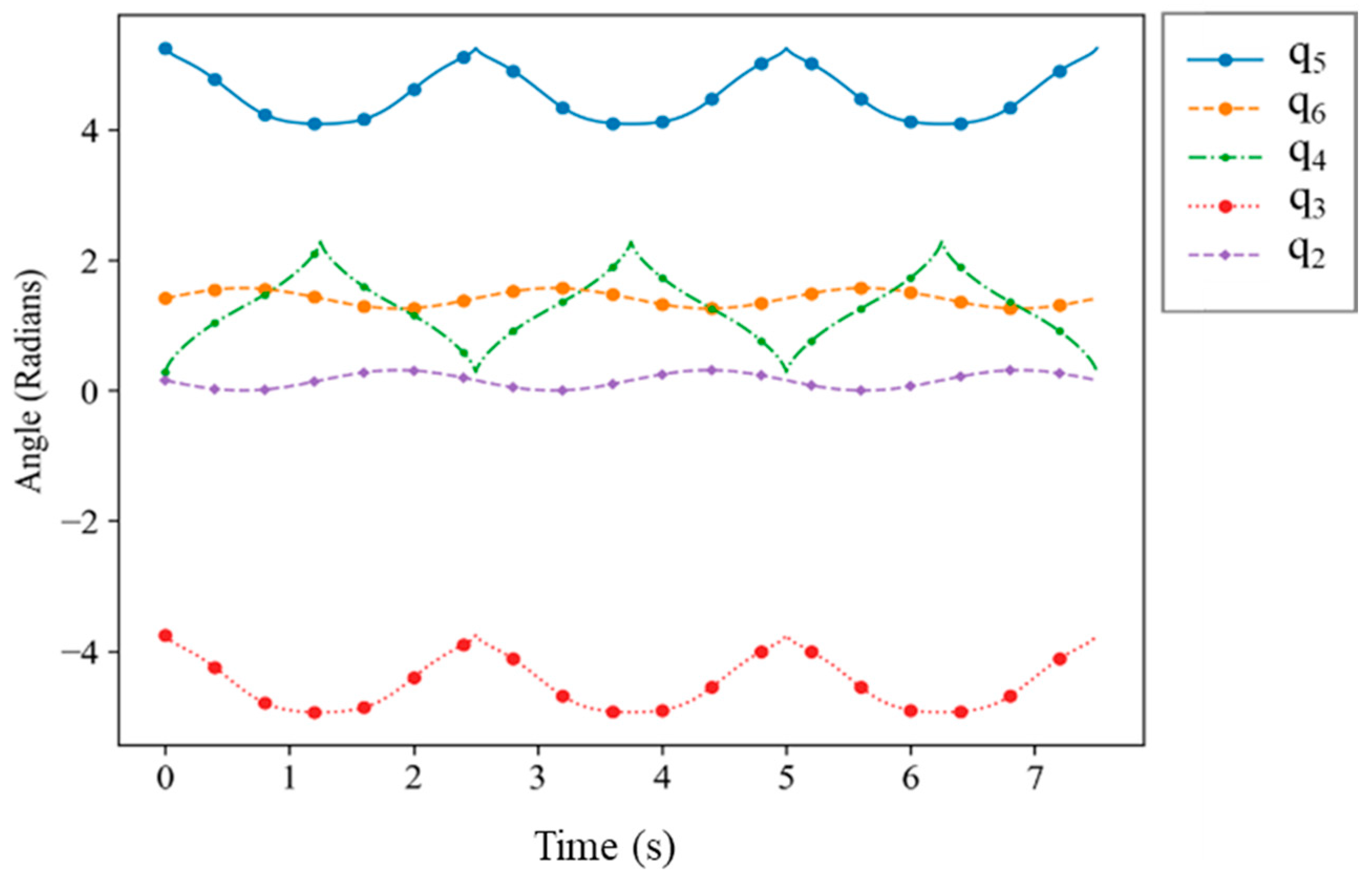
4. Results and Discussion

The trajectory equations for the knee, hip, and ankle joint angles were calculated for both legs. A detailed design model of the bipedal robot was created, incorporating precise material specifications to support accurate inertial parameter calculations during simulation. All components were assigned real-world material properties, enabling accurate mass computation using CAD-based mass property analysis. The robot’s total mass was calculated as 18.2 kg. To ensure stable locomotion and balanced motion, the robot’s key physical characteristics were established as follows: it stands 808 mm tall, with its centre of mass positioned 464 mm above the ground—just above the knees. Each foot measures 210 mm in length and 100 mm in width, ensuring full-ground contact during the stance phase and forming a stable support polygon. These dimensions are consistent with established bipedal robot models, such as those described by Ogura et al. [17,18] and the wider foot dimensions used in WABIAN-2R, reinforcing their effectiveness for stable, human-like gait generation.

The model was simulated in MATLAB R2019a Simulink using the backward Euler solver with a 0.001 s time step. This implicit method offers strong numerical stability under stiff dynamic conditions, such as those involving rapid actuator responses. It was selected for its balance between computational efficiency and stability, making it well suited for accurate simulation of the robot’s transient dynamics. The bipedal robot design includes link dimensions defined as [l1, l2, l3, l4, l5, l6, l7, l8, l9, l10, H] = [95, 28, 36, 32.6, 310, 318, 33, 36, 53.5, 94, 600] mm. To simulate a realistic walking motion, gait parameters—step length, step height, and step time—were selected based on average values derived from the human walking cycle. According to Inman et al. [38], typical human step lengths range from 650 mm to 800 mm depending on speed and height. A step length of 760 mm was chosen to optimize stability and energy efficiency, avoiding the drawbacks of both shorter steps (which require more steps for a given distance) and longer steps (which can increase joint torque requirements and compromise balance). A step height of 100 mm ensures adequate ground clearance for obstacle-free swing leg motion while minimizing energy usage. As shown by [39], step heights between 80 mm and 120 mm offer a balance between terrain clearance and energy efficiency.

A step time of 2.5 s (approximately 24 steps per minute) was used, resulting in a walking speed of 0.3–0.4 m/s with a 760 mm step length. This speed corresponds to quasi-static walking, suitable for robots without active dynamic stability mechanisms. The control strategy focused on maintaining the centre of mass within the support polygon to preserve balance [40], which is typical for early-stage humanoid robots or when testing new mechanical features like parallel joint actuation. Collins et al. [37] noted that walking speeds of 0.2–0.5 m/s are standard for such designs, enabling safe, energy-efficient assessment of joint mechanics. Moreover, the slower gait speed allows sufficient time for accurate inverse kinematics computation and real-time control, which is especially important when coordinating parallelly actuated hip and ankle joints. Future research will incorporate dynamic stability control, enabling higher walking speeds and agility while extending the energy-saving benefits observed in this study. the parameters of the robot’s leg links and joints are given in

Table 1. Trajectory parameters.

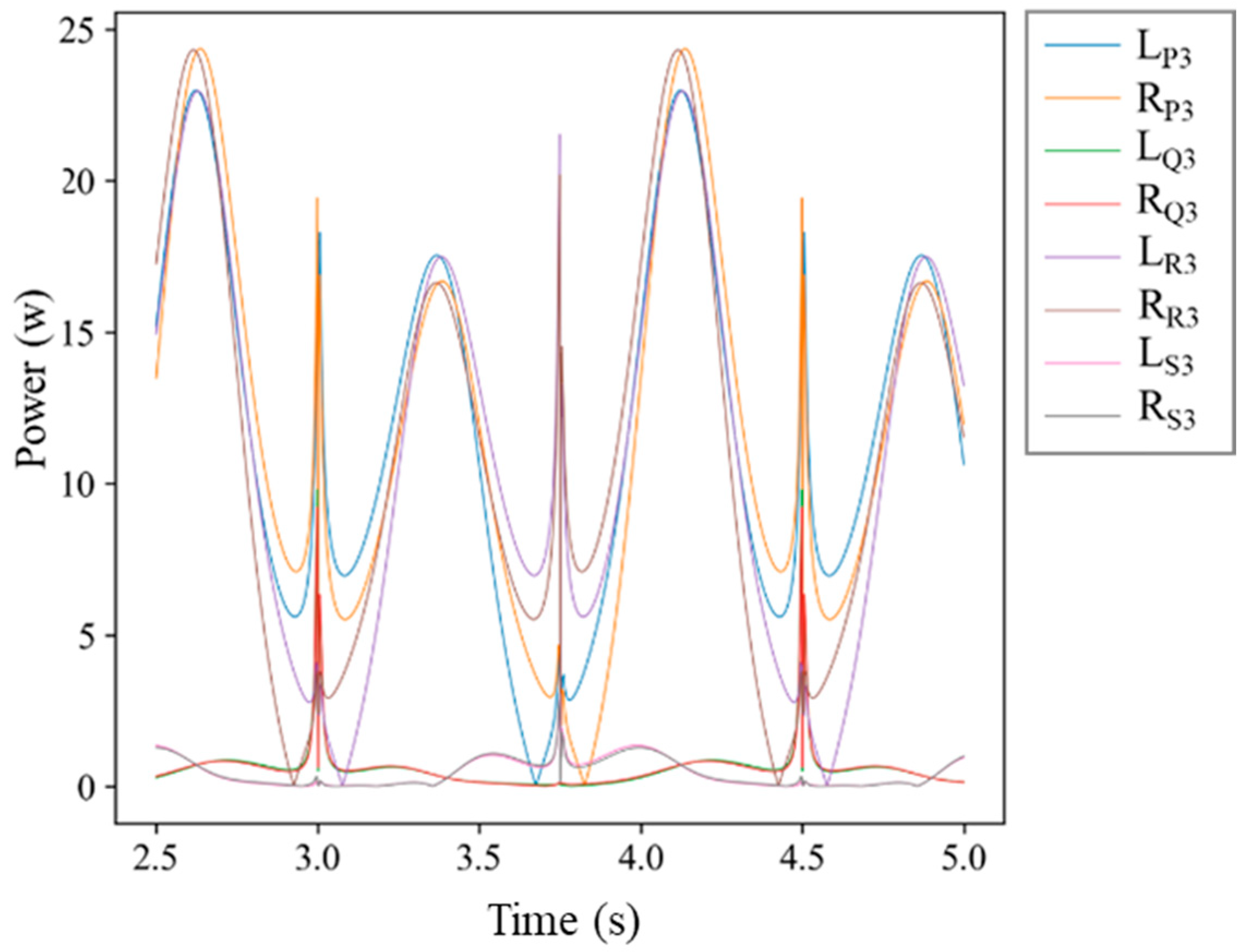
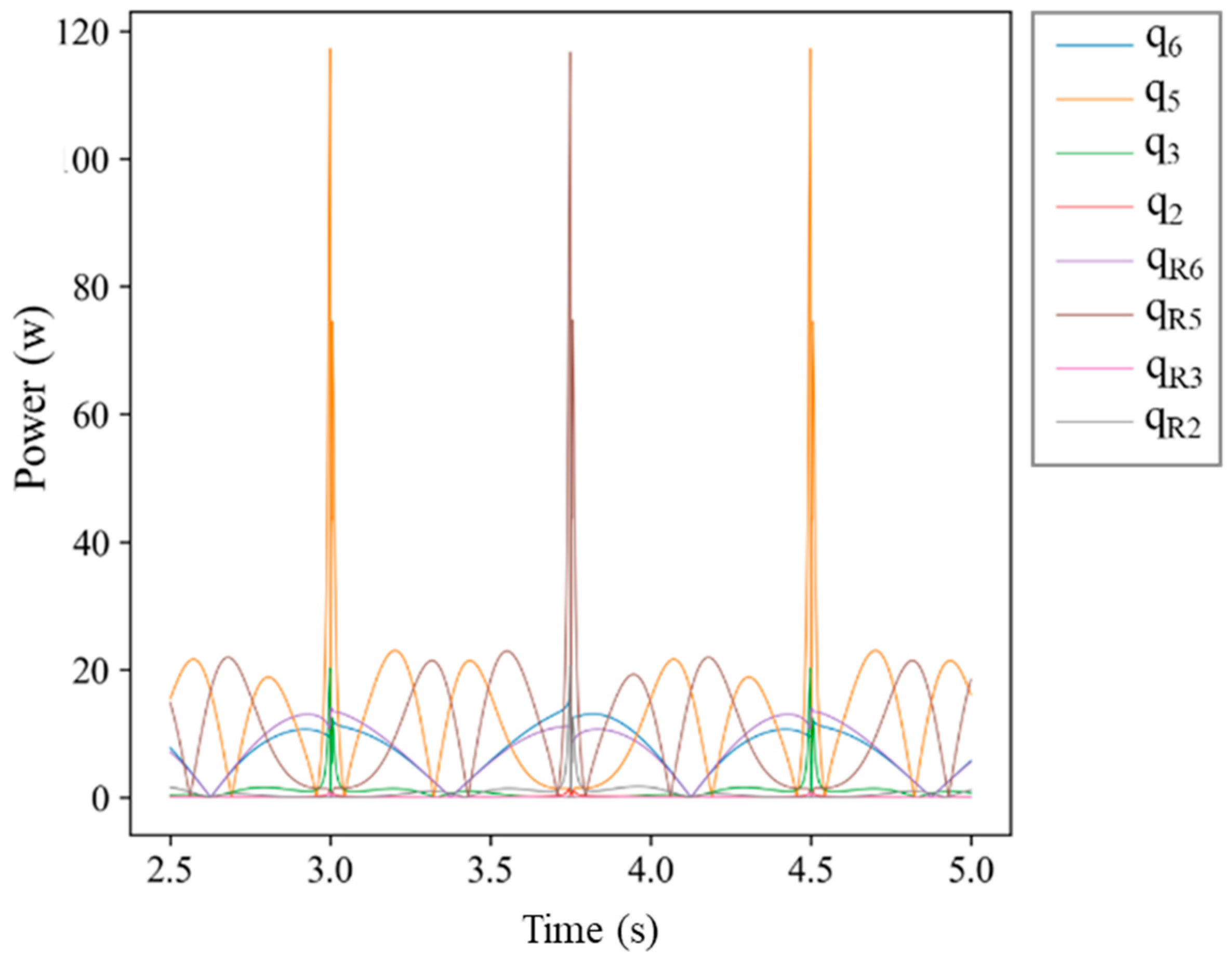
S. No	Parameters	Values
1	Step length	760 mm
2	Step height	100 mm
3	Step time	2.5 s
4	Distance between two centres of the foot in ‘z’ axis	93.96 mm

.

The trajectory of the left leg and right leg in x-axis for three steps with above parameters is plotted in Figure 6. The continuous line shows the trajectory of the left leg in the X axis, the dotted line gives the trajectory of the hip in the X axis, and the dashed line shows the trajectory of the right leg in the X axis.

The trajectory of the left leg and right leg in the y-axis for three cycles were plotted with the above parameters. In Figure 7, the continuous line shows the trajectory of the left leg in the Y axis, and the dotted line gives the trajectory of the right leg in the Y axis.

The robot’s frontal plane trajectory plot is a sine wave for all the roll angles in the frontal plane since the movement on the front plane solely involves shifting the robot’s weight towards the stance leg to get the centre of mass aligned inside the support polygon of the stance leg. The plot of all the angles for one leg is shown in Figure 8. For the left leg, let us assume that the ankle output angle q₂ and q₃ are controlled by linear actuators L_P3 and R_P3 by parallel configuration. Similarly, the hip output angles q₅ and q₆ are controlled by the linear actuators L_Q3 and R_Q3. The position displacement of the linear actuators for the left leg is shown in Figure 9. A screenshot of the simulation model was created in MATLAB-Simulink and is shown in Figure 10.

The inputs were given in a repeating sequence block set, which outputs a repeating sequence of numbers specified in a table of time–value pairs with monotonically increasing time. The inputs are then fed to the input port of the revolute joint block and input port of the prismatic joint block, which represent joints and linear actuators of the robot model. The torque at each joint was observed and recorded and is shown in Figure 11. To ensure the reliability of the results, simulations were conducted multiple times. After the initial transient phase (0–2.5 s), where the robot transitions from a standing posture to walking, the gait trajectory stabilizes and becomes periodic. The interval from 2.5 to 5 s captures a complete steady-state gait cycle and was selected for detailed analysis. As subsequent cycles exhibited nearly identical behaviour, this segment is representative of the robot’s sustained walking pattern and forms the basis for the results discussed in this section. The outputs are taken from the linear position, linear velocity, linear acceleration, and force ports of the prismatic joint blocks, whereas the angular position, angular velocity, angular acceleration, and torque outputs are obtained from the revolute joint blocks.

The torque required to achieve the prescribed joint displacements was recorded, and the corresponding power consumption was computed and shown in Figure 12 and Figure 13. Figure 12 illustrates the power usage for the parallel configuration (linear actuators), while Figure 13 represents the serial configuration.

These plots show that the highest peak power demands occur at the hip and ankle pitch joints. In the parallel setup, power is distributed across paired actuators, resulting in noticeably reduced loads compared to the serial configuration. The observed improvements are attributed to better load sharing and smoother actuator transitions. A summary of these results is provided in

Table 2. Inferences from the simulation results.

S. No	Joint			Maximum Instantaneous Power (W)
1	Left Leg	Hip roll	q6	15.26021
2		Hip pitch	q5	117.245
3		Ankle pitch	q3	20.26243
4		Ankle roll	q2	1.395065
5		Hip parallel	Lq3	22.98631
6			Rq3	24.3601
7		Ankle parallel	Lp3	9.795821
8			Rp3	9.206407
9	Right Leg	Hip roll	q6r	13.96714
10		Hip pitch	q5r	116.6731
11		Ankle pitch	q3r	20.49206
12		Ankle roll	q2r	0.722933
13		Hip parallel	Lr3	22.95801
14			Rr3	24.32176
15		Ankle parallel	Ls3	3.036088
16			Rs3	3.066172

.

5. Conclusions

The simulation outcomes demonstrate that the proposed parallel actuation configuration for the hip and ankle joints significantly reduces instantaneous power and torque demands compared to conventional serial configurations. In addition to peak power analysis, total energy consumption over a full gait cycle was also evaluated. The robot consumed approximately 104.0 W in the serial configuration and 103.2 W in the parallel configuration, indicating a small but measurable improvement in overall energy usage. This slight difference can be attributed to factors such as linkage arrangement and actuator distribution. While the reduction in total power is not as dramatic as the drop observed in peak power, this is expected because in the parallel configuration, the power is distributed across two actuators. As observed in Figure 12 and Figure 13, the serial configuration shows three sharp power peaks (up to 117.2 W), while the parallel setup exhibits more distributed peaks (up to 24.36 W) across seven smaller crests. This illustrates that while peak loads are significantly reduced due to parallel actuation and load sharing, the overall power draw remains stable throughout the gait cycle, contributing to smoother performance and a potentially longer actuator lifespan. In reporting peak power reductions, comparisons are made between individual actuators. For instance, the serial hip pitch joint requires 117.2 W, while each parallel actuator (Lq3 and Rq3) handles only 22.99 W and 24.36 W, corresponding to an approximate 80.4% reduction in peak power per actuator. Similarly, for the ankle pitch joint, the peak power drops from 20.26 W in the serial configuration to 9.80 W and 9.21 W in the parallel setup, representing a reduction on average of 53.5%. Since the objective is to reduce per-actuator load, these comparisons are made on a per-actuator basis, highlighting how parallel actuation allows for the use of smaller, lighter actuators without sacrificing joint performance, while significantly lowering peak demand.

Additionally, it is important to note that direct comparison of total power consumption with other robots such as ASIMO or CASSIE, which each consume approximately 200 W during locomotion, is not appropriate since those platforms are full-sized humanoids, whereas the robot in this study is hip-sized and lighter (18.2 kg). Naturally, the absolute energy consumption scales with size, so the focus here is on relative performance gains and architectural advantages rather than raw power values.

One limitation of this architecture is the reduction in joint range of motion due to the spatial layout of paired linear actuators—estimated at about 30% compared to serial joints. However, this can be mitigated by optimizing actuator placement and linkage geometry. In this study, the joints were designed specifically for quasi-static walking, and the reduced range did not hinder task performance. A dedicated study on the relationship between workspace and joint design is planned for future development.

It is also important to note that the simulation assumes perfect synchronization between actuator pairs. In practice, manufacturing tolerances typically introduce 2–5% variations in actuator response times and force outputs. These discrepancies can affect load-sharing efficiency and may lead to localized stress or imbalance. To address this, real-time sensor feedback and closed-loop control systems will be explored in future prototypes to improve actuator coordination and dynamic robustness under practical operating conditions.

The findings are based on simulations conducted under idealized conditions, without accounting for actuator non-linearities, mechanical backlash, or control delays. Moreover, gait planning was limited to quasi-static walking. Future work will address these limitations through experimental validation using a physical prototype, integrating dynamic locomotion strategies, sensor feedback, and energy optimization under varied walking conditions.