1. Introduction
Basis functions are a powerful tool in numerical simulations of problems arising from science and engineering. The aim of the present article is to introduce new basis functions and develop a new collocation method. Basis functions are used for two reasons: (1) to approximate scattered data in the arbitrary domain and (2) to be used for solving ordinary differential equations (ODEs) or partial differential equations (PDEs). The ideal numerical method for solving PDE problems should be highly accurate (preferably of high order), flexible in handling piecewise smooth initial or boundary conditions, complex geometries, computationally efficient, and easy to implement. However, commonly used methods typically satisfy only one or two of these criteria, but rarely all of them simultaneously. Hence, more research is necessary in this field. In this study, we try to fill this gap by introducing Legendre delta-shaped base functions. We show in this current study that when the delta-shaped functions are used in the interpolation of partially smooth functions, such as the rectangular pulse, the resulting Gibbs oscillations decay rapidly. This leads to significantly improved accuracy in the smooth regions. This represents a major development in the field, which had previously been studied extensively by Tadmor and colleagues [
1,
2,
3,
4,
5] Also, this is the continuation of another original study in this area. Previously, we explored the Chebyshev delta-shaped base functions [
6].
In recent decades, researchers have made intensive efforts to develop and introduce new high-order numerical methods, owing to their superior accuracy and reduced numerical diffusion and dissipation compared to conventional second-order methods. Several such studies can be found in [
7,
8,
9,
10,
11]. There are several outstanding advantages of using a higher-order accurate method [
12,
13].
Meshfree methods represent a rapidly evolving area of research, built on a variety of methodological foundations. These approaches have gained considerable attention in recent years due to their key advantages, most notably, their simplicity, ease of implementation, and potential for super-convergence. They have successfully applied a wide range of problems, showing strong promise for solving complex, real-world challenges. One of their major strengths lies in their flexibility when dealing with complex geometries in the computational domain.
Generally, meshfree methods can be divided into two main categories. The first category includes weak-form-based methods, such as the element-free Galerkin (EFG) method [
14], spectral Galerkin method [
15], Galerkin radial basis function method [
16], local Petrov–Galerkin meshless method [
17], and the direct meshless local Petrov–Galerkin (DMLPG) method [
18]. The second category consists of strong-form-based methods, including the pseudospectral method [
19], Kansa method (also known as the radial basis collocation method) [
20], meshfree methods based on Pascal polynomials [
21], and the moving least squares method [
22,
23], along with other related techniques discussed in [
24]. In addition to the aforementioned studies, mesh-dependent methods have also been utilized. For instance, Govindarao et al. [
25] solved a singularly perturbed delay parabolic problem arising in population dynamics using the implicit Euler scheme. Anand et al. [
26] addressed various parabolic equations in non-convex domains using the finite element method. Elango et al. [
27] tackled Fredholm integro-differential equations of convection–diffusion type with integral boundary conditions using an upwind scheme combined with a Shishkin mesh. Mohapatra et al. [
28] solved two-dimensional time-dependent singularly perturbed reaction–diffusion problems using a splitting-based higher-order numerical scheme. Moreover, Sekar Elango et al. [
29] also studied singularly perturbed Fredholm integro-differential equations by employing a second-order scheme for the derivatives and the trapezoidal rule for the integral terms.
Reutskiy [
30] derived a delta-shaped basis function from the Fourier series representation of the Dirac delta function, which was successfully used to simulate scattered data in both regular and irregular domains. More recently, Akyildiz, Alshammari, and Tunç [
6] employed Chebyshev polynomials to construct Chebyshev delta-shaped basis functions, which were then applied to solve the Poisson equation.
In the present study, we introduced a new class of basis functions, termed Legendre delta-shaped basis functions, and used them to obtain approximate solutions to various linear and nonlinear differential equations. It is worth noting that other basis functions can also be employed to interpolate partially smooth functions, potentially yielding improved performance in mitigating Gibbs oscillations (see, for example, [
31,
32]). Moreover, the application of these basis functions to differential equations with partially smooth initial or boundary conditions will be explored in our forthcoming work.
Novel Contributions
The novel contributions of this paper to the scientific community are as follows:
I-Theoretical Foundation:
The completeness and orthogonality relations of the eigenfunctions of the regular Sturm–Liouville–Legendre problem are expressed, in the distributional sense, via the Dirac delta function. By taking regularized finite sums from this infinite expansion, we prove that the resulting set of functions forms a basis for a Haar space—that is, the interpolation matrix constructed using Legendre delta-shaped basis functions (LDSBFs) is non-singular.
II-Introduction of LDSBF-Based Interpolation:
We introduce the Legendre delta-shaped interpolation method, in which interpolation is performed using LDSBFs at collocation points. It is also shown that interpolation using Legendre polynomials is a special case of interpolation using LDSBFs.
III-Application to Test Functions:
The proposed interpolation method is applied to obtain approximate analytical solutions of benchmark functions.
IV-Application to PDEs and Nonlinear Systems:
The LDSBF-based collocation method is used to solve the Poisson equation and a system of nonlinear differential equations arising from heat transfer induced by a convectively heated stretching sheet—a well-known benchmark problem in thermal analysis.
V-Novel Error Bounds:
We derive new error bounds in the discrete norm and the Sobolev norm for a special case, confirming that the LDSBF-based collocation method exhibits spectral accuracy.
VI-Numerical Validation:
Numerical results demonstrate that the proposed method is accurate, efficient, and highly competitive with existing, well-established numerical methods.
Section 2 introduces the Legendre delta-shaped function. In
Section 3, we demonstrate that the Legendre delta-shaped functions form a basis for a Haar space. In other words, interpolation using these functions at collocated points is well-posed. We also compare interpolation using the Legendre delta-shaped basis functions (LDSBF) with that using classical Legendre polynomials. Additionally, Franke’s function [
33] and the Heaviside step function [
34] are reconstructed using the Legendre delta-shaped interpolation method. In
Section 4, the collocation method is applied to solve Poisson’s equation and a heat transfer problem induced by a convectively heated stretching sheet. Error estimates for the interpolation polynomials are presented in
Section 5. Numerical results are discussed in
Section 6. Finally, the conclusions of our study are given in the
Section 7.
2. Legendre Delta-Shaped Functions
In this section, we introduce some fundamental properties of Legendre polynomials and the delta-shaped functions constructed from them. We also present the definition of Sobolev spaces, which will be useful in the subsequent analysis. We begin by defining the Legendre polynomials. For any nonnegative integer
, we assign
to be a space of polynomials of degree
or less. For
, we assume
. Legendre polynomial
is defined as the unique degree
that is orthogonal to
and
, so then these polynomials have the following property [
35]
A function
defined on [−1, 1] may be approximated by Lagrange polynomials as
where
, it is obvious that Equation (1) is exact when
is the
degree of the polynomial, at most. We can express Equation (1) in matrix form as
where
and
Using Equation (2) and keeping in mind that
is the degree of polynomial
, which can be written as
and using Equation (2), we have
again, we can express this equation in matrix norm:
where
is called the differential matrix or derivative matrix. The subscript
in
stands for dimension. From the last two equations, we get
. According to [
36,
37,
38,
39], we have
Also, it can be shown that where superscripts represent the power of the matrix in .
Let
be an integer and
. The set of all functions in
whose distributional derivatives up to order
also belong to
is called a Sobolev space, denoted by
, and is defined as follows:
where norm is defined as
In a special case, for
, Sobolev norm becomes
and the square integrable space defined by
Let us consider now the following real second-order linear differential operator in a regular Sturm–Liouville problem Legendre operator:
Define the eigenvalue problem for
as
or
with separated homogeneous boundary conditions
Non-zero solutions
of the Sturm–Liouville problem are called eigenfunctions, and the corresponding values of
are referred to as eigenvalues. The theory after the report of Sturm and Liouville [
40] has been vastly developed. Among the many authors, we need to mention notable studies of Titchmarsh [
41,
42] and Weyl [
43]. It is well known that, for a given Sturm–Liouville problem, there exists a family of real eigenfunctions forming a complete orthogonal set under the weighted inner product in the Hilbert space
.
These eigenfunctions can be ordered such that their corresponding real eigenvalues
form a strictly increasing sequence tending to infinity. The completeness and orthogonality of the eigenfunctions can be expressed in the sense of distributions through the Dirac delta function, as follows
For a given
, the infinite sum does not converge [
30]. Our main objective here is to construct basis functions by smoothing this formal expansion using regularization techniques [
30]. In the literature, there are mainly three different regularization methods [
44,
45]. However, in this study, we focus solely on the Riesz regularization scheme [
45]. Accordingly, we obtain the regularized delta-shaped functions from Equation (6) as follows:
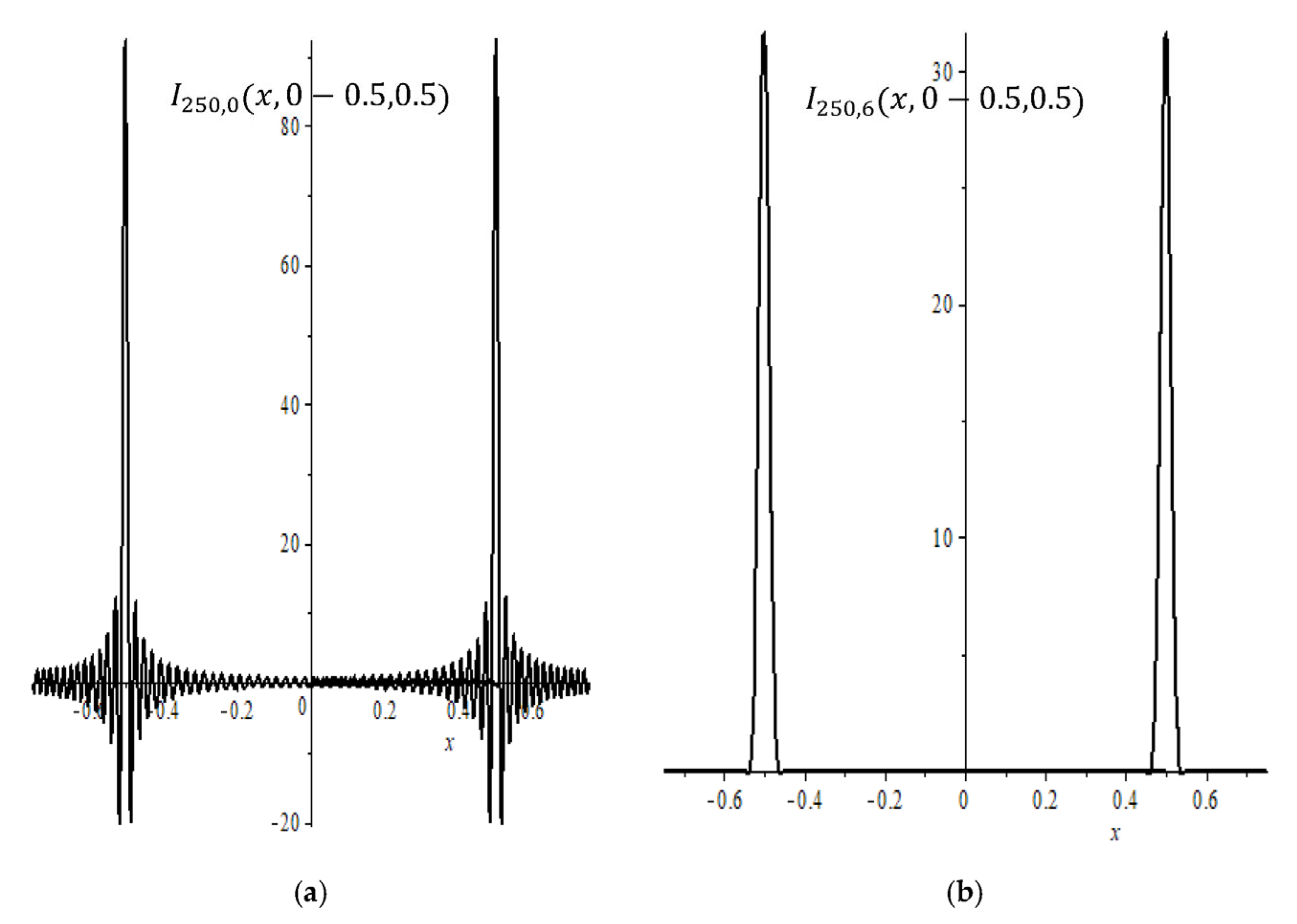
From now on, we call Equation (7) Legendre delta-shaped functions.
where
scaler, and
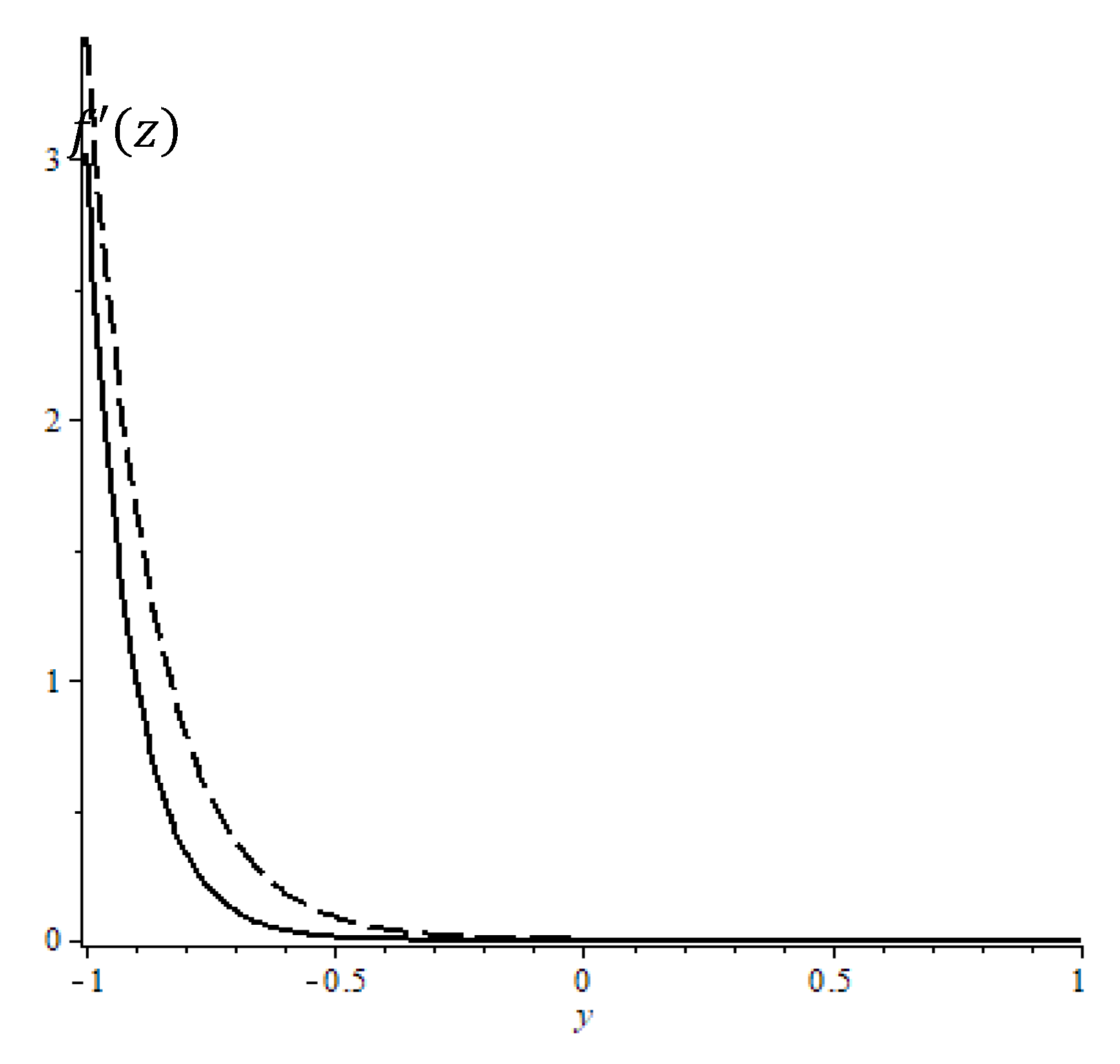
Figure 1a,b show the delta-shaped functions before and after regularization, where
and for the number of digits, we used 80 in Maple.
It can be shown easily that
The elements of this set are linearly independent (this can be performed by using Wronskian with mathematical induction principles). In the following section, we show that the interpolation matrix formed by Legendre delta-shaped functions is non-singular.
3. Approximation
Legendre delta-shaped functions, interpolating the following data
take the form
Then, unknown coefficient
was obtained from the data:
which can be written as
where
is the
matrix. Since the number of basis elements must be greater than or equal to the number of unknowns to ensure the uniqueness of the solution, we require
. In this case, the matrix
can be expressed as follows:
In the following, we establish that the matrix is non-singular. One of the key challenges in this work is the selection of appropriate collocation points. In this study, we utilize both Chebyshev and Gauss–Legendre points as collocation points.
Proposition 1. If the parameter, and the center points are chosen as the collocation points in Equation (9), then the coefficient matrix defined in Equation (10) is guaranteed to be positive definite.
Proof of Proposition 1. We have from (17) and (18) at
which can be written as
which can be written as
where
,
and
is a diagonal matrix,
then the matrix
is written as
Where for , the
matrix is given by
if the center points are chosen as collocation points in (8), then matrices,
, setting
; hence,
, then
is a symmetric matrix; furthermore, we demonstrate that
is not only symmetric but also positive definite. Consider any real row vector,
, then
So let us say,
, then
; then, it is easy to see that
because
; on the other hand,
is zero if and only if
, or
, which is
. This homogeneous linear system admits only the trivial solution as
is an
matrix with
, and we thus showed that
is positive definite, on the other hand matrix
can be written as
It is now evident that is positive definite, and thus nonsingular, completing the proof. Therefore, the set in the equation forms a basis for a Haar space. This proposition guarantees that interpolation with Legendre delta-shaped basis functions is well-posed. We can now state the following proposition. □
Proposition 2. The maximal absolute error can be reduced by increasing the value of the parameter
This is a new interpolation scheme by Legendre delta-shaped base functions. Now, we are ready to test the interpolation by the new Legendre delta-shaped interpolation method on the famous benchmark problems. Here, we used the collocation technique to find the unknown coefficient. We will show in the
Section 6 that an increase in the value of the parameter
causes a decrease in the value of the error.
Conjecture 1. The question is what the difference is between interpolation by using Legendre polynomials and Legendre delta-shaped basis functions; the answer is the following.
Interpolation by using the Legendre delta-shaped base functions if where are constants. On the other hand, the expansion of with Legendre base functions yieldsand matching Equation (12) with (14), we have We examined the condition number of the coefficient matrix for M = 10 and M = 15 and found that it is very large and highly sensitive to the choice of collocation points. Therefore, the two approaches under consideration are not identical, but only slightly different.
With regard to the formulation in Equation (13), applying the Galerkin method leads to an overdetermined system, which is not acceptable. In general, there is no direct connection between the two collocation-based approaches; however, in the special case where M = N, Equation (13) reduces to Equation (12). In the next section, we demonstrate through a specific example that these two approaches are not equivalent.
Another notable advantage of the LDSBF method, as illustrated in
Figure 1, is that increasing the number of terms in the delta-shaped basis functions results in more compact support. Moreover, choosing the centers of the delta-shaped functions as the collocation points leads to a diagonally dominant matrix in the interpolation problem. This observation may help answer the question of how many terms should be included in the delta-shaped basis functions to minimize the error in solving PDEs or ODEs.
We now proceed to recover two well-known functions using the LDSBF approach.
Example 1. We start with the reconstruction of Franke’s function, a widely used benchmark problem in numerical analysis (c.f. [46,47,48,49]). Franke’s function was originally defined on the unit square [0, 1] × [0, 1], this region was transferred to the , then Franke’s function after transformation becomes Let us now approach Franke’s function in terms of our new Legendre delta-shaped base function; for this, we define the approximate function as follows:
substituting collocation points
and the center
, we obtain the following system of linear equations:
For a given
, we obtain a system of linear equations, which can be solved easily for several values of
and the results are discussed in
Section 4.
For interpolation with Gaussian radial base functions, we write
where the used Gaussian radial function is defined as
with
also,
is again determined by interpolation;
We used the standard MATLAP routine. We have seen that the error in LDSBF interpolation is always less than the result of Gaussian radial function interpolation. Some results are also given in the Tables in the last section.
Example 2. Our second test function is the rectangular pulse function:where there is a jump discontinuity at If we approximate this function using the orthogonal interpolation technique, we observe overshoots and undershoots (oscillations) near the point where the function is discontinuous. This is known as the Gibbs phenomenon [50]. The oscillations gradually decay as we move away from the discontinuity. However, as we will demonstrate in later sections, if our proposed basis functions are used, the oscillations (Gibbs phenomenon) are rapidly damped. This small example demonstrates that the basis functions we defined are indeed significant in this field. 4. Meshless Collocation Method for Differential Equations
Legendre delta-shaped basis functions can be used for solving partial differential equations in the context of the collocation method as well. Choose the set of collocation points on the domain ; let us say are interior points in the domain , and the remaining collocation points (depending on the order of the differential equations) on the boundary (). The selection of the center point of each delta-shaped base function is crucial to the success of the method; here, we used both Chebyshev points and Gauss–Legendre points as the center points, let us say .
Example 3. Let us now consider the following Poisson problem as in the famous paper of Shen [15] and Haidvogel and Zang [51]:which has singularities at the four corners. It is not difficult to see that the exact solution of this equation is We now seek the approximate solution of the above equation in the form
or using matrix and Kronecker product, we rewrite the above equations as
,
and
substituting (43) and (44) into the Poisson problem, we obtain
We can now collocate the above equation in
. Note that these collocation points are not lying in boundary conditions; for boundary conditions, we have
Combining Equation (18) with Equation (19), we obtain the following matrix equations:
Lagrange delta-shaped base functions have compact support; hence, the coefficient matrix becomes a band and non-singular, and once we solve Equation (20), substituting it into Equation (17), we obtain an approximate analytical solution of the Poisson equation. Since we used Lagrange delta-shaped base functions in the solution, we call it the Lagrange delta-shaped collocation method.
Since we compared the prediction of the new collocation method with the Legendre pseudospectral method, we now show how to use this method for the Poisson problem; briefly, for this method, we need to define an approximate solution as follows:
where
and
are the Gauss–Legendre nodes. Using Equation (3), we obtain
and now we can collocate the above equation in
:
where
is the
row
identity matrix. Further, these equations can be represented in the following matrix form:
where
is a submatrix of
such that it contains the
th rows of
. Hence, we can rewrite the above equations as
for the discretization of boundary conditions, first using Equation (3) for Equation (15), we have
using the boundary conditions in (15), we obtain:
By collocating the above first equation in
and the second one in
, we obtain
In the matrix equation, they become
Therefore, Equations (21) with (23) constitute a system of linear equations; here, we used the least squares method to solve the unknown coefficient. The results are documented in the following section.
Example 4. In this example, we solve the system of nonlinear differential equations that describe heat transfer in a convectively heated stretching sheet [52,53]:whererepresent the dimensionless velocity, temperature, and concentration distributions, respectively. The dimensionless boundary conditions become Here, also,
are material constants described in [
52]. To use the method, we must again transform the independent variables
; afterward, we introduce a new dependent variable as
, then we get from (24–26)
Now, assume the solution in the form:
and
where
,
and
Collocating the points
and applying the predictor–corrector scheme, we obtain
This system of equations is solved for different values of parameters, and numerical results are given in the
Section 6.
6. Numerical Results and Discussion
In
Section 3, we demonstrated that our interpolation method is well-posed. In the application phase, we now numerically reconstruct Franke’s function, as described in the first example. Numerical results are presented in
Table 1 and
Table 2, where the accuracy is measured using the root mean square error (RMSE) as
where
are the test points.
From
Table 1, it is evident that increasing the number of points (N) leads to a decrease in error. Another important observation is the effect of the regularization constant (σ) on the error. For certain values of σ, interpolation using the Legendre delta-shaped basis functions yields more accurate results than interpolation using classical Legendre polynomials. In
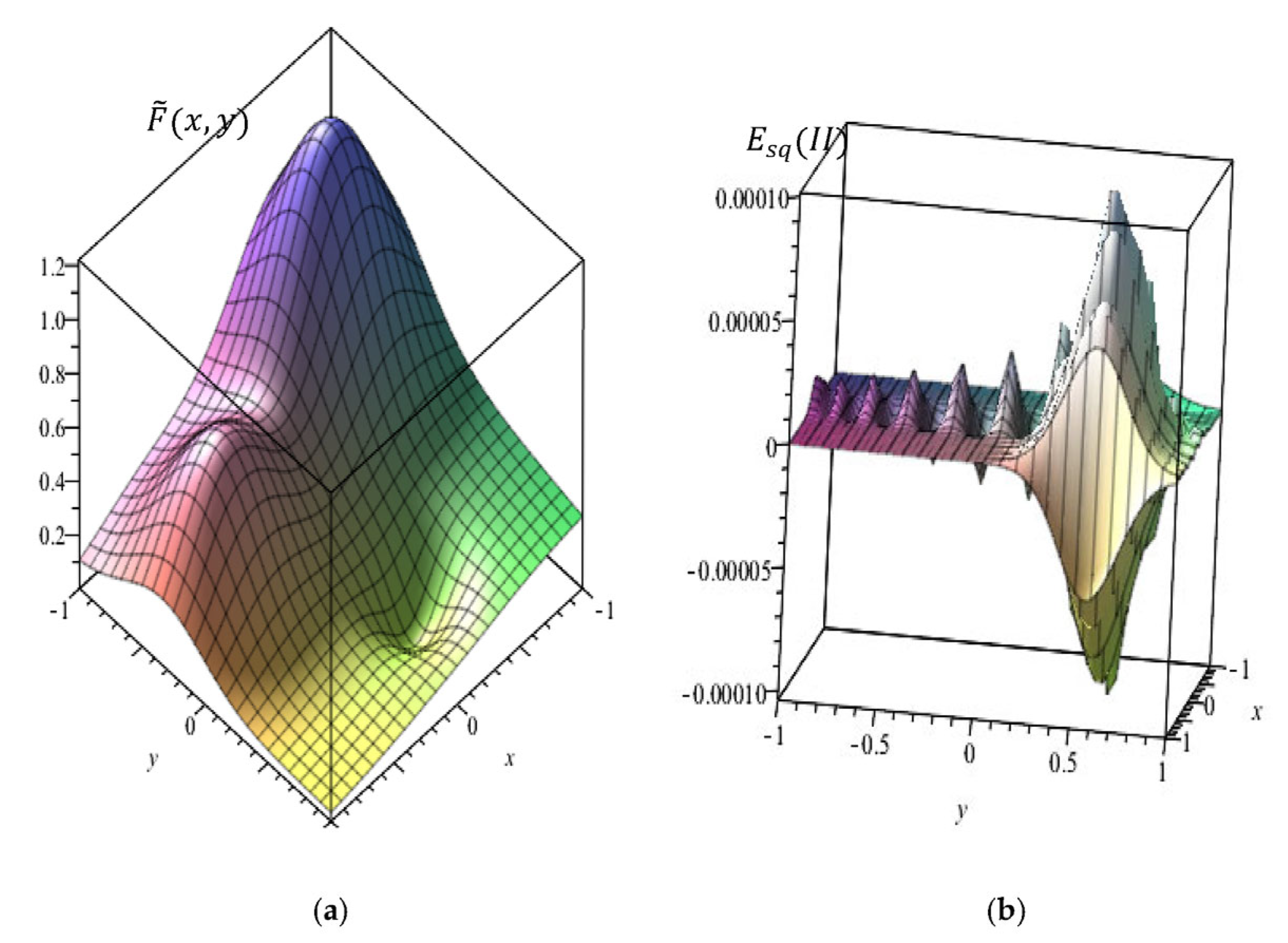
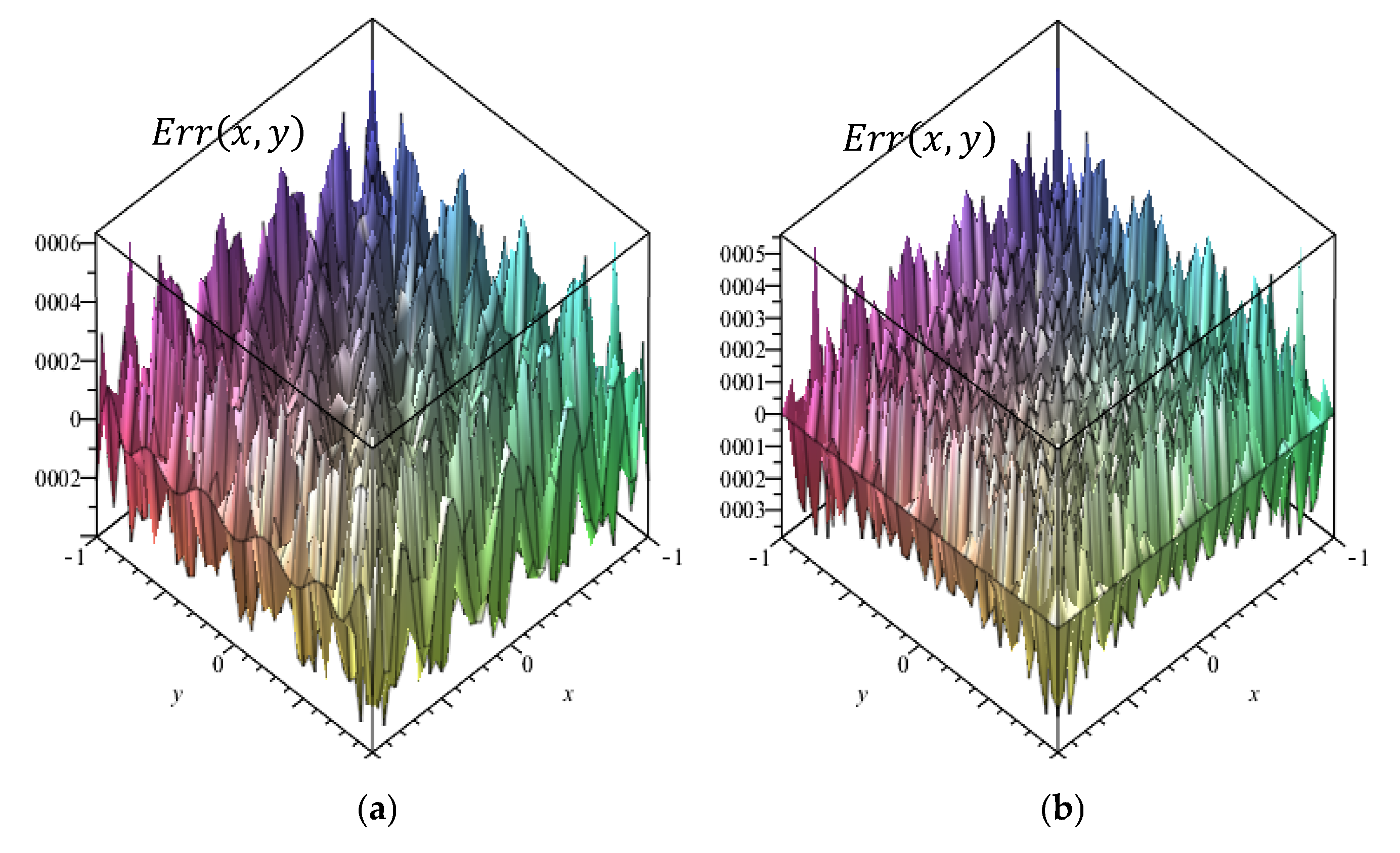
Figure 2a, we present the numerical reconstruction of the Franke function using the new Legendre delta-shaped basis functions. The corresponding error—defined as the difference between the exact and approximate solutions—is shown in
Figure 2b.
For the collocation points, we used Chebyshev points as well as a central point. Alternatively, Gauss–Legendre points can also be employed as collocation nodes. The results, presented in
Table 2, indicate that Chebyshev collocation points outperform Gauss–Legendre points in terms of accuracy when the same number of points is used.
From
Table 1 and
Table 2, we can state that the Legendre delta-shaped interpolation method is well-posed and reliable, and we have more adjustable parameters
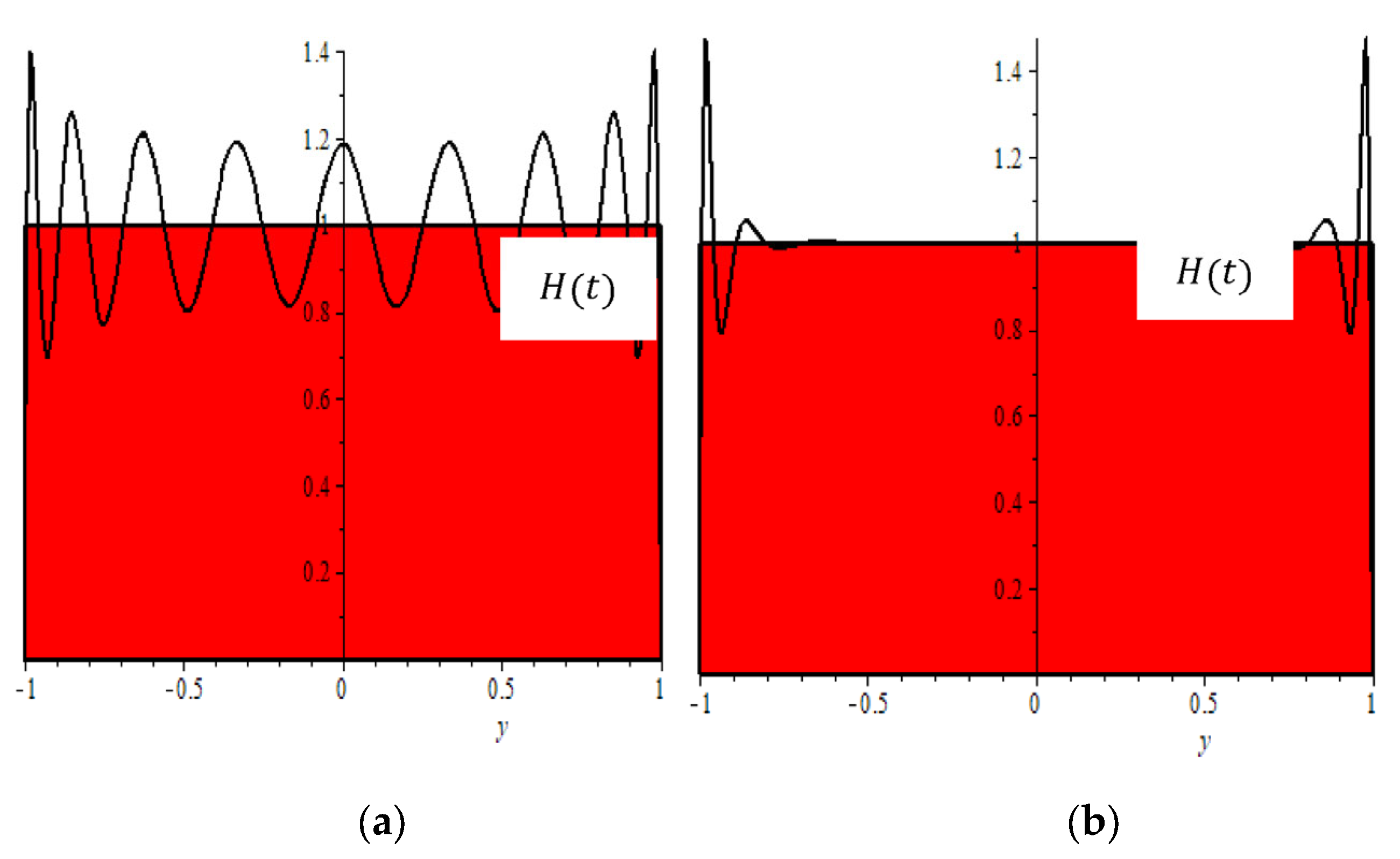
more competitive than interpolation by Legendre polynomials. Now, consider rectangular pulse and approach to rectangular pulse both by using both Legendre polynomial and LDSBF (where
, as expected, Gibbs phenomenon occurs, but oscillation damped shortly for the approach with LDSBF, as shown
Figure 3 for
; from the figure, we see that error in approximation with LDSBF much smaller than approximation with Legendre polynomials. This example provides enough motivation for us to study the delta-shaped base functions.
From
Table 1 and
Table 2, we observe that the Legendre delta-shaped interpolation method is well-posed and reliable. Moreover, due to the presence of additional adjustable parameters (namely,
and
; see Equation (5)), it is more competitive than classical interpolation using Legendre polynomials.
Now, consider the rectangular pulse function and its approximation using both Legendre polynomials and the Legendre Delta-Shaped Basis Functions (LDSBF) with
. As expected, the Gibbs phenomenon occurs in both cases. However, the oscillations decay more rapidly in the LDSBF approximation, as illustrated in
Figure 3 for (a)
. The figure clearly shows that the approximation error with LDSBF is significantly smaller than that obtained with Legendre polynomials. This example strongly motivates our further investigation into delta-shaped basis functions.
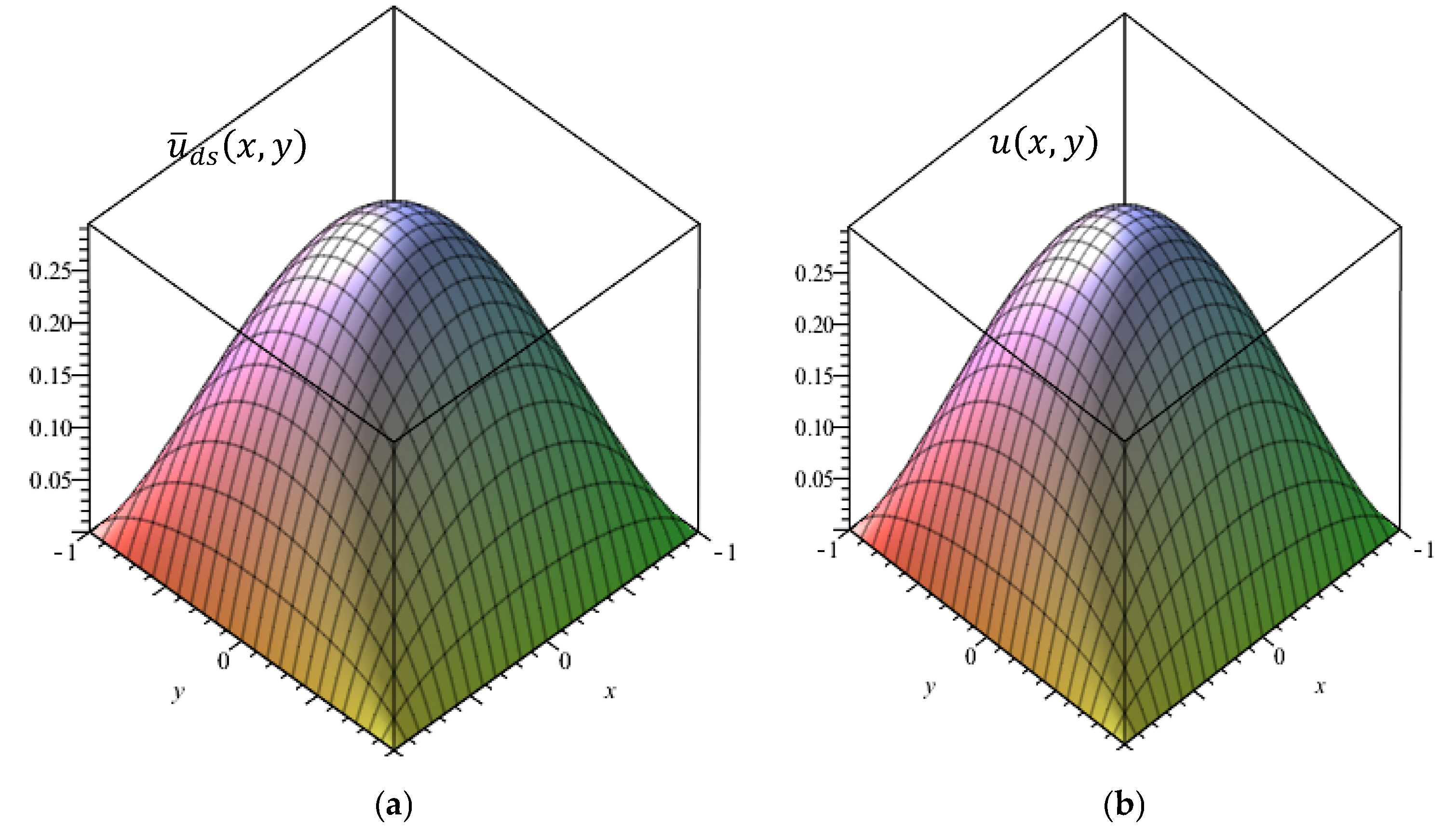
For the collocation method, we first tested our new base function for the approximate solution of the Poisson equation in Equation (15); the results are given in
Figure 4a,b, which show the approximate solution obtained from the Legendre delta-shaped collocation method (LDSCM) for
and
and the exact solution of Equation (16), respectively. Since the exact solution of the Poisson problem is known, then the pointwise error is defined as
. We observed once again that the results obtained using LDSCM are more accurate than those produced by the Legendre Pseudospectral Method (LPM), as illustrated in
Figure 5a,b. The maximum pointwise errors are summarized in
Table 3, where comparisons are made with the Legendre–Galerkin Method (LGM), Chebyshev–Tau Method (CTM), Chebyshev–Collocation Method (CCM), Second-Order Finite Difference (FD2), Fourth-Order Finite Difference (FD4), and collocation schemes using both Chebyshev Points (CP) and Gauss–Legendre Points (GLP).
From
Table 3, it can be observed that our results are slightly less accurate than those obtained using other spectral methods under smooth conditions. However, as demonstrated in Example 3, when the initial or boundary conditions of the differential equation involve piecewise continuous functions, the basis functions proposed in this study yield significantly lower errors compared to those used in the methods summarized in
Table 3. As expected, increasing the number of basis elements improves the accuracy of the solution. For instance, when
N = 24, the maximum pointwise error obtained using Gauss–Legendre Points (GLP) was found to be less than
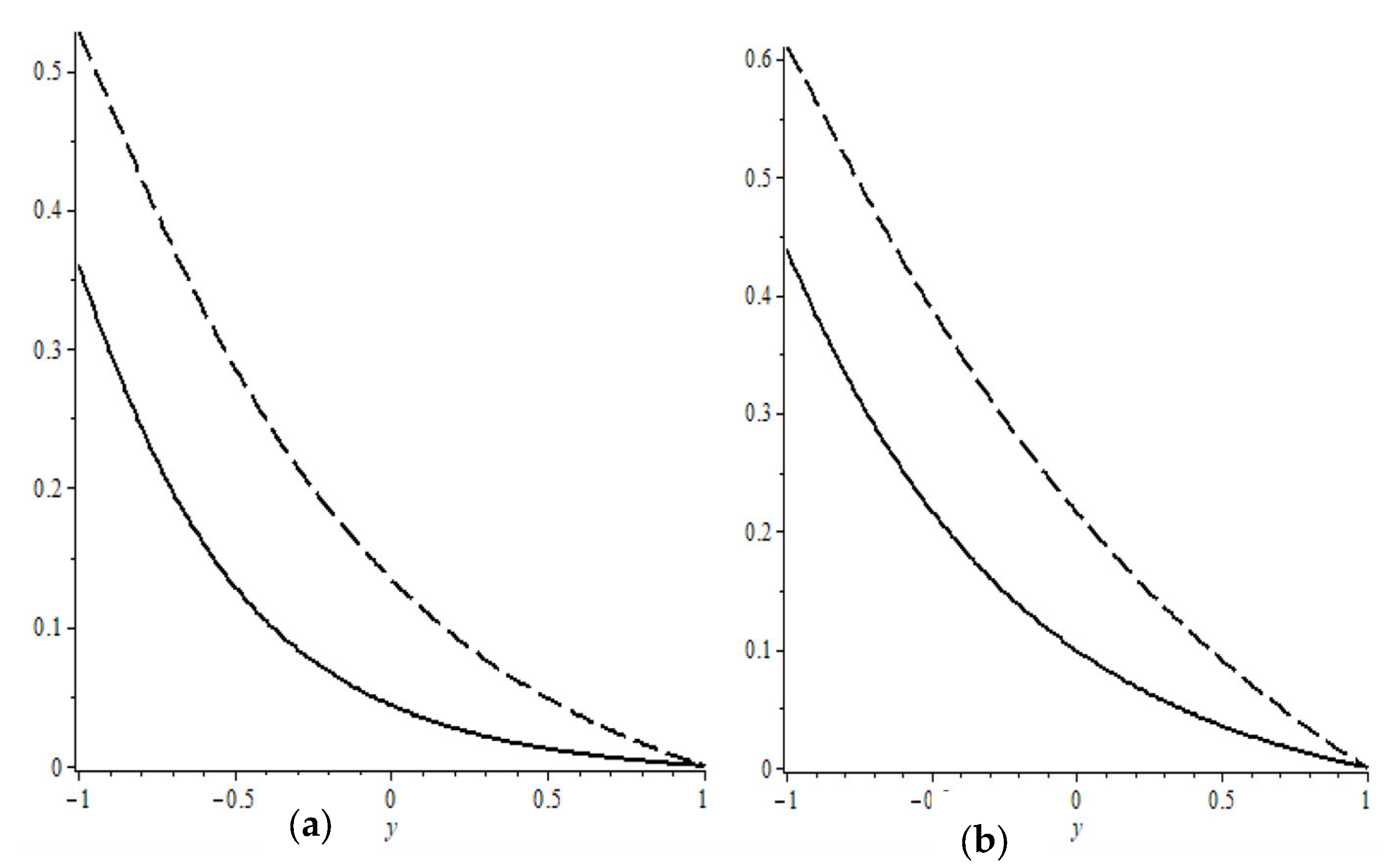
. The solution of example 4 for the derivative of dimensionless velocity distribution is given in
Figure 6 for
, where the other parameters are fixed. We used same parameters to obtain the dimensionless temperature and concentrations distributions; these graph are given in
Figure 7a,b at
, where we used only 20 base elements and Legendre– Gauss collocation points. We also note that our solution technique, by reducing the order of differential equations, is also original.
Table 4 is provided to demonstrate that our results are consistent with those of previous studies on this problem.