Abstract
The reliability and safety of five-axis CNC abrasive water jet machining are critical for many industries. This study employs Failure Mode and Effects Analysis (FMEA) to identify and mitigate potential failures in this machining system. Traditional FMEA, which relies on crisp numerical values, often struggles with handling uncertainty in risk assessment. To address this limitation, this paper introduces an Interval-Valued Spherical Fuzzy FMEA (IVSF-FMEA) approach, which enhances risk evaluation by incorporating membership, non-membership, and hesitancy degrees. The IVSF-FMEA method leverages the inherent rotational symmetry of interval-valued spherical fuzzy sets and the permutation symmetry among severity, occurrence, and detectability criteria, resulting in a transformation-invariant and unbiased risk assessment framework. Applying IVSF-FMEA to seven periodic failure (PF) modes in five-axis CNC water jet machining achieves a more precise prioritization of risks, leading to improved decision-making and resource allocation. The findings highlight improper fixturing of the workpiece (PF6) as the most critical failure mode, with the highest RPN value of −0.54, followed by mechanical vibrations (PF2) and tool wear and breakage (PF1). This indicates that ensuring proper fixturing stability is essential for maintaining machining accuracy and preventing defects. Comparative analysis with traditional FMEA demonstrates the superiority of the proposed fuzzy-based approach in handling subjective assessments and reducing ambiguity. The findings highlight improper fixturing, mechanical vibrations, and tool wear as the most critical failure modes, necessitating targeted risk mitigation strategies. This research contributes to advancing risk assessment methodologies in complex manufacturing environments.
1. Introduction
Five-axis computer numerical control (CNC) abrasive water jet machining is crucial in various industries, including aerospace, automotive, and healthcare. Its ability to cut complex shapes from different materials makes it a critical manufacturing method [1,2]. However, achieving high levels of precision and accuracy in water jet cutting comes with challenges.
Machine errors can generally be divided into three main categories. The first type is mechanical errors, which pertain to issues within the machine tool, such as vibrations and wear on the nozzles [3]. The second type involves control system errors, which relate to restrictions or limitations inherent in the control system utilized by the machine [4]. Lastly, thermal errors involve heat-related effects that can significantly affect the machining process [5]. Understanding these categories is essential for diagnosing and resolving issues during operation.
These errors can negatively impact the quality, safety, and dependability of the end product. A thorough risk assessment method, such as Failure Mode and Effects Analysis (FMEA), is crucial for addressing these challenges. FMEA is a structured approach that helps identify potential failures, assess their impact, and develop effective mitigation strategies [6,7]. By implementing FMEA, organizations can improve system safety and reliability by proactively managing potential issues before they escalate into serious problems [8].
While traditional FMEA is a helpful tool, it has meaningful limitations in handling the uncertainties and imprecision of risk analysis, especially within complex systems such as five-axis CNC water jet machining. Traditional FMEA primarily relies on exact numerical values to consider risk factors, which may not accurately capture the subjective nuances of expert evaluations. This dependence on crisp data may result in an oversimplified interpretation of risk, potentially overlooking critical failure modes [9,10].
A considerable drawback of traditional FMEA is its inadequacy in addressing the inherent ambiguity and vagueness of linguistic assessments. It typically assigns identical Risk Priority Numbers (RPNs) to different failure modes, despite significant differences in their associated risk implications [11,12]. Such ambiguity may block practical decision-making when prioritizing and mitigating these failure modes.
Adopting spherical fuzzy sets (SFSs) in applications like FMEA offers significant advantages over traditional fuzzy sets. SFSs enhance uncertainty representation by incorporating membership, non-membership, and hesitancy degrees, providing a comprehensive framework that better captures expert opinions. This leads to an improved understanding of uncertainty, which is vital in subjective decision-making contexts. Integrating SFSs with multi-criteria decision-making methods allows for more balanced conclusions, accommodating diverse perspectives and enhancing flexibility in complex assessments. Additionally, SFSs improve risk assessments by minimizing biases and discrepancies, facilitating expert consensus. SFSs also enable the use of advanced analytical techniques, making them valuable for analyzing complex systems with intricate relationships [13,14,15].
The research employs an Interval-Valued Spherical Fuzzy FMEA (IVSF-FMEA) method, which enhances traditional FMEA approaches by incorporating fuzzy logic to better manage uncertainties in risk analysis. The interval-valued spherical fuzzy sets locate membership, non-membership, and hesitancy on the unit sphere, so that the space of uncertainty has complete rotational symmetry. FMEA introduces permutation symmetry by assigning the same weights to severity, occurrence, and detectability. These permutations and geometric symmetries form a transformation-invariant, unbiased assessment system reflecting the multidisciplinary nature of symmetry. The choice of IVSF-FMEA as opposed to traditional fuzzy sets (e.g., type 1 fuzzy sets, intuitionistic fuzzy sets, hesitant fuzzy sets) is justified primarily by the enhanced capability of IVSF to represent uncertainty. While conventional fuzzy methods address uncertainty to some extent, IVSF-FMEA is particularly advantageous because it allows experts to represent their judgments as intervals rather than single points. This flexibility is critical in complex manufacturing scenarios like CNC machining, where precise numerical evaluations are challenging. IVSF captures the hesitancy, variability, and nuanced assessments of domain experts more realistically, improving risk evaluation accuracy. Moreover, IVSF provides a structured means to manage and quantify expert uncertainty more robustly than other fuzzy methods. A comparative analysis between the proposed IVSF-FMEA and traditional FMEA methods, as aforementioned, supported these advantages.
The literature highlights the need for a more robust risk assessment framework to address the inherent fuzziness and vagueness intrinsic in failure mode evaluations [6,16]. This research explicitly presents the challenge of assessing and contrasting various risk assessment methodologies in the context of five-axis CNC abrasive water jet machining, supporting a more effective FMEA approach. The objective is to apply a method that can (i) more effectively manage subjective assessments of failure modes, (ii) generate a more precise and thorough risk profile, and (iii) enrich the decision-making process concerning the prioritization and mitigation of failure modes.
In light of this information, the originality of this research is underlined by its application of IVSF-FMEA to evaluate compensation strategies within a five-axis water jet machining system—an innovative approach not currently documented in the literature.
- This study proposes a novel IVSF-FMEA method tailored specifically for five-axis CNC water jet machining. This approach extends traditional FMEA by incorporating interval-valued spherical fuzzy sets, which effectively capture uncertainty, hesitancy, and variability in expert evaluations.
- The IVSF-FMEA method improves the differentiation between failure modes by considering membership, non-membership, and hesitancy degrees as intervals rather than crisp values. It leads to more precise and reliable RPNs, which surpass traditional FMEA’s limitations in handling ambiguity [6,9,14].
- The method is applied to seven critical failure modes in five-axis CNC water jet machining, demonstrating its practical relevance in a complex and high-precision manufacturing environment where risk assessment is inherently challenging [17,18].
- This paper provides a comprehensive comparison between the proposed IVSF-FMEA and traditional crisp FMEA, highlighting significant differences in risk ranking and emphasizing how the fuzzy-based approach avoids oversimplification and equal treatment of distinct risks [19,20].
- Based on the analysis, actionable strategies for risk mitigation, such as improved fixture, vibration control, and tool maintenance, are proposed to enhance operational safety and product quality.
This paper is structured into several key sections. Section 2 reviews existing studies on FMEA in CNC machining, discusses traditional and fuzzy-based risk assessment methods, and justifies the need for IVSF-FMEA. Section 3 explains the theoretical foundation of IVSF-FMEA, including fuzzy risk prioritization, and outlines the steps taken to compare it with traditional FMEA. Section 4 presents the process of calculating Interval-Valued Spherical Fuzzy RPNs. Section 5 shows an application of the proposed IVSF-FMEA approach in assessing failure modes in five-axis CNC water jet machining. Section 6 gives the results of traditional FMEA for comparison purposes. Section 7 provides actionable recommendations based on the study’s findings. Finally, Section 8 concludes the paper.
2. Literature Review
Five-axis CNC abrasive water jet machining is widely used across industries due to its high precision and flexibility. However, like any machining process, it is susceptible to periodic failures (PFs) affecting productivity and quality [17]. Several studies have examined the recurring failures in CNC machining systems, particularly in water jet cutting, where high-pressure abrasive flow and thermal expansion introduce significant challenges.
Two of the most common periodical failures in water jet machining are tool wear and nozzle erosion, which directly impact cutting accuracy and surface finish quality. Prolonged exposure to high-speed abrasive particles causes nozzle deformation, leading to deviations in jet trajectory and inconsistent material removal rates [21]. Studies have shown that nozzle wear can significantly increase kerf width and reduce machining precision, necessitating periodic replacements and condition monitoring techniques [22].
Another frequent issue is mechanical vibrations resulting from machine structure instability or imbalances in rotating components. Vibrations cause deviations in the tool path, leading to reduced dimensional accuracy and potential surface defects [18]. Research indicates that excessive vibrations, if left unaddressed, can propagate through the machine frame, affecting long-term system performance [23].
Thermal deformation is another periodical failure mode observed in CNC machining, particularly in long-duration operations. The heat generated by prolonged cutting can cause thermal expansion of machine components, leading to positional errors and misalignment of the cutting head [24]. Advanced cooling mechanisms and thermal compensation models have been proposed in recent studies to mitigate these effects and maintain machining accuracy [25].
Furthermore, recurring control system errors have been identified as a significant issue in automated machining. These failures often stem from software glitches, sensor malfunctions, or miscalibrations in CNC programming. Studies highlight the importance of real-time monitoring and adaptive control algorithms to detect and correct such errors before they impact production quality [26].
Addressing these periodical failures is essential for maintaining the reliability and efficiency of five-axis CNC water jet machining. Recent advancements in predictive maintenance, machine learning-driven fault detection, and adaptive compensation strategies provide effective solutions for mitigating these recurring issues. By integrating these approaches with fuzzy risk assessment models, manufacturers can proactively manage failure risks and improve overall machining performance.
Table 1 summarizes the FMEA studies in CNC machining. FMEA is a systematic tool used to identify potential failure modes within a system and evaluate their impact on overall performance. In CNC machining, traditional FMEA has been utilized to detect issues such as tool wear, failures of machine components, and inaccuracies in the machining process [27,28]. This process typically involves a detailed analysis where each component of the machining process is assessed for its likelihood of failure, the severity of its consequences, and the likelihood of its detection. Moreover, as industries evolve and technology advances, the application of FMEA in CNC machining is becoming increasingly sophisticated [28,29]. Modern techniques often incorporate advanced data analytics and machine learning, allowing for real-time monitoring and predictive maintenance. Incorporating FMEA into the design and operational stages of CNC machining can significantly improve productivity and cost-effectiveness [30,31]. By fostering a culture of continuous improvement and regular review of processes, manufacturers can stay ahead of potential challenges, streamline operations, and ultimately deliver better products to their customers [32].

Table 1.
FMEA studies in CNC machining.
Traditional FMEA methods, while commonly used to identify potential failures, often suffer from drawbacks, including vague definitions of risk factors [34,35,36], equal treatment of all risk factors [19,37,38], and a lack of clear guidance on mitigating weaknesses [20,39]. Researchers increasingly focus on developing more robust and data-driven FMEA approaches to address these limitations, incorporating refined risk factor definitions [15,40], weighting schemes based on expert judgment and objective data [11,12], and advanced analytical techniques [41]. This shift towards more sophisticated FMEA techniques aims to enhance the accuracy, effectiveness, and value of FMEA in ensuring the reliability and performance of CNC machine tools [33].
Table 2 summarizes fuzzy extensions of FMEA research. Fuzzy sets have become a valuable tool in FMEA, allowing for more nuanced risk assessments by accommodating uncertainty and imprecision in expert evaluations [11,14]. Ervural and Ayaz [42] and Cardiel-Ortega and Baeza-Serrato [43] provided fuzzy numbers to experts for evaluating failure modes and expressing their opinions based on their knowledge and experience as interpretations of criteria can vary. Among the various types of fuzzy sets, SFSs have gained attention for their ability to enhance traditional FMEA methodologies [13]. This is achieved by integrating SFSs with multi-criteria decision-making (MCDM) methods, thereby addressing the subjective nature of expert judgments and providing a more flexible framework for evaluating risk factors, ultimately leading to improved accuracy and robustness in risk assessments.
Several studies have shown the effectiveness of SFSs in enhancing FMEA across various applications. Chang [15] integrated SFSs with FMEA to propose a new emergency risk evaluation approach, specifically addressing uncertain or ambiguous information that often arises during emergencies or emerging disease outbreaks. Gündoğdu and Shishavan [36] utilized SFSs to develop a two-stage risk assessment method for shipyards, combining it with AHP (Analytical Hierarchy Process) and VIKOR (VIekriterijumsko KOmpromisno Rangiranje) methods. This approach is particularly relevant for industries like shipbuilding, which is known for complex processes and a high degree of uncertainty, highlighting the adaptability of SFSs to different contexts. Ma et al. [44] incorporated SFSs into FMEA along with a projection model, entropy, and a correlation coefficient to improve the accuracy of failure mode prioritization. This multi-faceted approach demonstrates the versatility of SFSs in integrating various analytical tools, further enhancing the robustness of FMEA. Huang et al. [45] presented an FMEA model using T-spherical fuzzy sets, focusing on addressing flexibility limitations in expert preference expression and improving the reliability of weight allocation and risk ranking results. Their approach involved incorporating a divergence-based maximizing deviation method and a combined compromise solution method, further enhancing the analytical capabilities of FMEA.
While all these studies highlight the benefits of SFSs in FMEA, they differ in their specific applications and methodological choices. For instance, Chang [15] focused on emergency risk evaluation, while Gündoğdu and Shishavan [36] targeted the shipbuilding industry. Ma et al. [44] prioritized failure modes, and Huang et al.’s [45] work focused on the flexibility and reliability of expert judgments. These variations reflect the adaptability of SFSs to diverse contexts and problem formulations within FMEA.
However, a potential drawback of the standard SFS method is its reliance on precise membership, non-membership, and hesitancy degrees, which might be difficult for experts to provide, especially when dealing with complex systems or limited data. Interval-valued spherical fuzzy sets (IVSFSs) offer a solution to this limitation by allowing experts to express their judgments as intervals rather than single points, providing greater flexibility and accommodating a wider range of uncertainty in expert evaluations. This approach can lead to more robust and realistic risk assessments, especially when precise estimations are challenging. To the author’s knowledge, two sources directly address the application of IVSFSs in FMEA. Gul and Ak [9] proposed a modified FMEA model using an interval-valued spherical fuzzy extension of the TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) method. They applied this model to a marble manufacturing facility, demonstrating its effectiveness in prioritizing failure modes based on six risk parameters, including cost, prevention, and effectiveness, in addition to the traditional severity, occurrence, and detection. Their work highlights the practicality of IVSFSs in handling real-world FMEA scenarios where precise estimations are often challenging. Zhao et al. [35] developed a time-varying FMEA method based on IVSFSs, focusing on incorporating the dynamic nature of risk factors over time. They introduced the concept of cumulative failure intensity to capture changes in occurrence probability and applied their method to a case study of a motorized spindle. Their research emphasizes the importance of considering the temporal dimension in FMEA, particularly for systems with varying failure rates over their life cycle. Both studies demonstrate the advantages of IVSFSs in enhancing the flexibility and robustness of FMEA, but they differ in their specific focus and application area.

Table 2.
Fuzzy FMEA studies.
Table 2.
Fuzzy FMEA studies.
| Study | Year | Fuzzy Set | Application Area | Fuzzified Element |
|---|---|---|---|---|
| [35] | 2017 | IFS | Steel production process | Expert evaluations |
| [20] | 2021 | HFS | Photovoltaic cell manufacturing | Expert evaluations |
| [46] | 2019 | IFS | Healthcare | Expert evaluations |
| [47] | 2021 | PyFS | Super-twisted nematic | Expert evaluations |
| [48] | 2022 | HFS | Gear grinding machining | Expert evaluations |
| [49] | 2014 | IFS | Horizontal directional drilling machining | Expert evaluations |
| [50] | 2016 | HFS | Healthcare | Expert evaluations |
| [51] | 2017 | Z-numbers | Geothermal power plant | Expert evaluations |
| [52] | 2016 | IFS | Healthcare | Expert evaluations |
| [40] | 2021 | z-numbers | Automotive parts manufacturing | RPN |
| [15] | 2022 | IFS | Healthcare | RPN |
| [53] | 2023 | SFS | New product design | Expert evaluations |
| [39] | 2024 | SFS | Smart grid | Expert evaluations |
| [54] | 2023 | SFS | Roadway | Expert evaluations |
| [36] | 2021 | SFS | Ship production | Expert evaluations |
| [55] | 2021 | T2FS | CNC machining | Expert evaluations |
| [56] | 2022 | T1FS | Petroleum pipeline | Rule base |
| [34] | 2024 | SFS | Railway | Expert evaluations |
| [38] | 2021 | T1FS | Industrial centrifugal pump | Rule base |
| [37] | 2021 | T1FS | Automotive parts manufacturing | Rule base |
| [57] | 2021 | T1FS | Refinery | Rule base |
| [58] | 2024 | T1FS | Aeronautical | Rule base |
| [59] | 2023 | T1FS | Test and calibration laboratories | Rule base |
| [19] | 2023 | T1FS | Shipboard compressor system | Rule base |
| [60] | 2024 | T1FS | Water supply | Rule base |
| [61] | 2023 | T1FS | Safety | RPN |
| [62] | 2023 | T1FS | Construction | RPN |
| [63] | 2022 | T1FS | Healthcare | Rule base |
IFS: intuitionistic fuzzy set; T1FS: type 1 fuzzy set; T2FS: type 2 fuzzy sets; HFS: hesitant fuzzy set; PyFS: Pythagorean fuzzy set; SFS: spherical fuzzy set.
No previous study has combined interval-valued spherical fuzzy sets with FMEA and applied this approach to a multi-axis water jet machining system. This machining system exhibits unique characteristics, including high levels of operational complexity, precise motion control requirements, and sensitivity to variations in abrasive nozzle conditions, workpiece stability, and mechanical vibrations. The interaction between multiple machine axes and the abrasive water jet stream creates dynamic and intricate risk profiles, significantly different from conventional machining processes. Therefore, a specialized FMEA approach is essential to adequately capture and assess the unique uncertainties and risks associated with multi-axis water jet systems. Utilizing IVSFS within FMEA specifically addresses these nuanced challenges, enabling more robust and precise evaluations of potential failures and thereby enhancing decision-making and risk mitigation strategies tailored explicitly to the distinct operational environment of multi-axis water jet machining.
3. Methodological Background
The paper focuses on the risk assessment of five-axis CNC water jet machining, a complex manufacturing process frequently used in industries such as aerospace, automotive, and healthcare. Precision and reliability in these sectors are crucial, as any failures can lead to significant safety risks, financial loss, or compromised product quality. Traditional FMEA methods, while helpful, inadequately handle uncertainty and ambiguity in expert evaluations, often oversimplifying risks and neglecting subtle but critical differences in potential failures. Given the complexity and precision demands of five-axis CNC machining, an improved approach to handling uncertainty in failure mode assessment is essential, thus motivating this research.
Figure 1 depicts the framework of the steps followed. This section provides a brief explanation of the Risk Priority Number, method, and basic definitions and concepts.
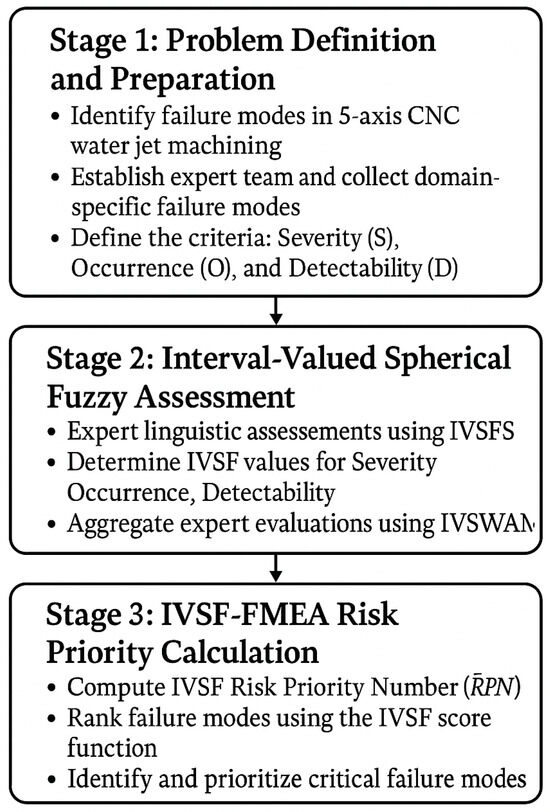
Figure 1.
Framework for the methodology.
3.1. Risk Priority Number (RPN)
Failure Mode and Effects Analysis stands as the predominant risk assessment technique utilized across various sectors; this approach originated within the aerospace field during the 1950s and has gained widespread adoption in different industries since then [64]. The FMEA methodology ranks potential failure risks using the Risk Priority Number (RPN). The RPN is determined by multiplying three equally weighted risk factors: severity (S), occurrence (O), and detection (D). The calculation of the RPN is carried out using Equation (1).
The risk factor S indicates the intensity of a failure’s occurrence, O refers to the likelihood of a failure, and D represents the chance that a failure cannot be identified. These risk factors, S, O, and D, utilize risk assessment ratings ranging from 1 to 10. A potential failure mode with a greater RPN value signifies that this FM poses a higher risk of failure, necessitating a greater priority to be assigned to avoid such failures.
3.2. Spherical Fuzzy Sets (SFSs)
Spherical fuzzy sets are founded on intuitionistic and neutrosophic fuzzy sets [65]. They include membership degree (MD), non-membership degree (NMD), and hesitancy degree (HD) The fundamental concepts associated with spherical fuzzy sets and their calculation are outlined as follows:
Definition 1.
The depiction of a spherical fuzzy set established on the universe of discourse U is illustrated in Equation (2).
where and .
The MD, NMD, and HD of element u in relation to the spherical fuzzy set are denoted as , , and , respectively, for each individual u.
Definition 2.
The fundamental arithmetic operations for SVSFSs are outlined as follows.
Definition 3.
The Spherical Weighted Arithmetic Mean (SWAM) considers a weight vector , where each is in the interval , and the total of all equals 1, as represented by the following formulation [66].
The definition of the SWAM operation is provided in Equation (7).
Definition 4.
The score function used for sorting SVSFSs is specified by Equation (8).
3.3. Interval-Valued Spherical Fuzzy Sets (IVSFSs)
Interval-valued spherical fuzzy sets extend the concept of spherical fuzzy sets to address uncertainty more effectively by using intervals rather than precise numerical values for the membership degrees. They are beneficial in applications where exact MD, NMD, and HD cannot be determined precisely. MD () indicates the extent to which an element is part of the fuzzy set. In IVSFSs, this is represented as an interval , where and represent the lower and upper limits of membership, respectively. NMD () signifies the extent to which an element is not part of the fuzzy set. Like MD, it is defined as an interval . HD () reflects the uncertainty or doubt related to membership and non-membership. It is also represented as an interval .
Kutlu Gündogdu and Kahraman [67] formulated IVSFSs, along with specific definitions and mathematical operations, as shown below.
Definition 5.
For every element x, the values , , and represent the upper MD, NMD, and HD of x in relation to , respectively.
As outlined below, certain operations are specified over the IVSFS, where is greater than 0. In order to simplify the calculations, a more streamlined formulation has been created as outlined below: .
Definition 6.
The Interval-Valued Spherical Weighted Geometric Mean (IVSWAM) is an aggregation operator intended for IVSFSs. It integrates several spherical fuzzy values by considering their significance (weights) while adhering to the spherical constraint. Thus, the resulting aggregation stays within the bounds of the spherical fuzzy domain.
Here, ; .
Functions for scoring in ranking spherical fuzzy numbers are established as Equation (15).
4. Interval-Valued Spherical Fuzzy RPNs
This study proposes integrating IVSFSs into the RPN framework to improve risk assessment. SFSs enhance traditional methods by incorporating membership, non-membership, and hesitancy, while IVSFSs offer interval-based quantification, allowing for more flexible evaluations when experts struggle to assign exact numerical values.
This integration improves the handling of uncertainty in risk assessment. By incorporating fuzzy logic, the model allows for better differentiation of failure modes and provides a range of possible values to reflect hesitancy in evaluations. This combination enhances decision-making capabilities by enabling more precise prioritization of risks, ultimately leading to more effective risk management strategies.
The three elements of FMEA, namely severity, probability, and detectability, are considered to be IVSF values: , , . The IVSF Risk Priority Number () is subsequently computed as indicated in Equations (16) and (17).
where and are given by and , respectively.
The IVSF scales for severity, occurrence, and detectability were determined based on expert input, industry standards, and previous research. Three domain experts in CNC machining and risk assessment provided linguistic evaluations, ensuring realistic and practical scale values. The scales were adapted from standard FMEA rating systems, modified using fuzzy logic principles to handle uncertainty. Severity reflects the impact of failure, occurrence represents the frequency of failure, and detectability indicates the likelihood of identifying failures before disruptions occur.
Using interval-based values instead of crisp numbers allows for greater flexibility, capturing expert hesitancy and variability in risk perception. The final IVSF scales, as presented in Table 3, were validated through expert consensus, ensuring their reliability in CNC water jet machining risk assessment.

Table 3.
IVSF scale for severity, occurrence, and detectability.
5. An Illustrative Application on Five-Axis CNC Machining
This part demonstrates the proposed approach for a five-axis CNC machining application. Seven failure modes in five-axis CNC machining were considered in this study. One significant problem is tool wear and breakage (PF1), which can occur due to prolonged use or improper handling of tools. This issue often leads to diminished machining accuracy and poor surface finish quality. Another concern is mechanical vibrations (PF2), which can occur within the machine structure or the tool. These vibrations can adversely affect dimensional accuracy and heighten the likelihood of defects in the finished parts. Thermal deformation (PF3) is also critical, as the heat generated during lengthy operations can cause distortions in various machine components, compromising precision. Control system errors (PF4) are another potential failure mode. These can emerge from limitations or malfunctions within the CNC control unit, negatively impacting the machine’s ability to follow designed tool paths accurately. For water jet systems, abrasive nozzle wear (PF5) significantly affects cutting accuracy and can inflate operational costs. Improper fixturing of the workpiece (PF6) can also create significant issues. If the fixturing is inadequate or unstable, it can lead to movement during machining, which results in misalignment and dimensional inaccuracies. Lastly, programming errors (PF7) can occur when CNC programming contains inaccuracies or omissions, which may lead to collisions, over-cutting, or undercutting of components.
These experts evaluated these seven potential failures, and evaluations are given in Table 4.

Table 4.
IVSF assessments of three experts for the potential failure modes.
Table 4 is aggregated with Equation (6), and Table 5 is obtained. The IVFS FMEA results indicate the relative importance of different failure modes in five-axis CNC machining. The failure modes with values closer to zero are considered more critical. Based on this ranking, improper fixturing of the workpiece (PF6) is the highest-priority issue (−0.54). If the workpiece is not securely fixed, it can shift during machining, leading to misalignment and dimensional inaccuracies. Ensuring stable and precise fixturing is essential to maintaining machining accuracy and preventing defects.

Table 5.
Aggregated IVSF expert assessments.
The second most critical failure mode is mechanical vibrations (PF2) (−0.63), which can arise from machine structure or tool instability. These vibrations negatively affect dimensional accuracy and can increase the likelihood of surface defects. Implementing proper vibration-damping techniques and ensuring machine rigidity can help mitigate these effects. Tool wear and breakage (PF1) (−0.68) also ranks high in priority, as excessive tool wear can degrade machining precision and surface quality. Regular tool inspections and timely replacements are necessary to prevent disruptions.
Further down the priority list, programming errors (PF7) (−0.75) present a significant risk, as inaccuracies in CNC programming can lead to tool collisions, over-cutting, or undercutting. Strict validation of programming before execution can help minimize these issues. Thermal deformation (PF3) (−0.83) is another concern, particularly in prolonged machining operations where excessive heat can cause dimensional distortions in machine components. Implementing cooling strategies and thermal compensation mechanisms is essential to maintaining precision.
Abrasive nozzle wear (PF5) (−0.87) is particularly relevant for water jet systems, as it significantly impacts cutting accuracy and increases operational costs. Regular maintenance and timely nozzle replacements are necessary to mitigate this issue. Finally, control system errors (PF4) (−0.94) rank as the lowest-priority failure mode, though they still present risks. Malfunctions in the CNC control system can disrupt tool path accuracy, but their impact is comparatively lower than that of other failure modes.
6. Experimental Results
This section includes some additional results to highlight the proposed methodology’s usefulness.
6.1. Comparison with Traditional FMEA
Table 6 is obtained when the IVSF scale for severity, occurrence, and detectability given in Table 3 is converted into a crisp scale (from Extremely High to Non-detection, taking values from 10 to 1). The experts’ linguistic evaluations given in Table 4 are transferred into traditional S, O, and D scores to calculate . Then, the assessments of three experts are aggregated in the same way: calculation of the geometric means. Table 7 presents the results.

Table 6.
Traditional FMEA.

Table 7.
Traditional FMEA results.
The traditional FMEA results provide a different perspective on the criticality of failure modes by using RPNs. In this evaluation, higher RPN values indicate more critical failure modes that require urgent attention. PF4 (control system errors) is the most critical failure mode, with an RPN of 295.95. This shows that control system malfunctions pose the highest risk due to their high occurrence and low detectability, making them a priority for corrective measures. The second most critical issue is PF5 (abrasive nozzle wear) with an RPN of 271.02, emphasizing the need for frequent nozzle maintenance to ensure cutting accuracy.
Following these, PF1 (tool wear and breakage) and PF2 (mechanical vibrations) have RPN values of 153.67 and 144.61, respectively. These values suggest they pose significant risks but are more manageable than PF4 and PF5. PF3 (thermal deformation) has an RPN of 119.69, highlighting its moderate impact on machining precision, particularly in prolonged operations.
At the lower end, PF6 (improper fixturing) and PF7 (programming errors) have the lowest RPN values, 87.72 and 55.93, respectively. While still relevant, their lower scores suggest they pose less risk than the other failure modes. However, improper fixturing can still affect machining accuracy, and programming errors should be minimized through proper verification.
In the comparative analysis of risk prioritization methods for five-axis CNC water jet machining, distinct differences emerged among traditional FMEA, fuzzy FMEA, and the proposed IVSF-FMEA. The order of risk prioritization revealed that traditional FMEA identified control system errors (PF4) as the most critical failure mode, with a risk priority number of 296. This was closely followed by abrasive nozzle wear (PF5) at 271.
In contrast, the IVSF-FMEA ranked improper fixturing (PF6) as the highest risk, with a value of −0.54, followed by mechanical vibrations (PF2) at −0.63. Control system errors (PF4) ranked the lowest in this analysis at −0.94. This variation suggests that traditional FMEA, which relies on crisp numerical values, may overemphasize detectability issues, as seen in PF4. On the other hand, IVSF-FMEA effectively captures the true impact of failures through expert uncertainty modeling.
Regarding failure mode sensitivity, traditional FMEA assigned very close RPN values to various failure modes, leading to minimal differentiation among critical failures. For instance, failure modes PF1, PF2, and PF3 had RPNs of 154, 145, and 120, respectively. Conversely, IVSF-FMEA provided a wider risk score spread, distinguishing the most critical risks from the least vital. This capability allows for more precise prioritization when allocating resources.
Additionally, the handling of uncertainty further separates these methodologies. Traditional FMEA does not account for expert hesitancy and uncertainty, while fuzzy FMEA improves upon this limitation by incorporating linguistic terms. IVSF-FMEA takes this a step further by utilizing interval-valued spherical fuzzy numbers. This approach reduces ambiguity and offers a more realistic risk assessment in complex machining environments.
6.2. Aggregated Expert Assessment
Figure 2 shows the grouped bar chart of the aggregated expert scores for severity (blue), occurrence (green), and detectability (red) for each failure mode (PF1–PF7). These values are the geometric mean of three experts’ assessments converted to a 1–10 scale. Higher numbers indicate greater severity, higher failure frequency, or poorer detectability. The chart highlights failure modes with relatively high or low S, O, and D values.
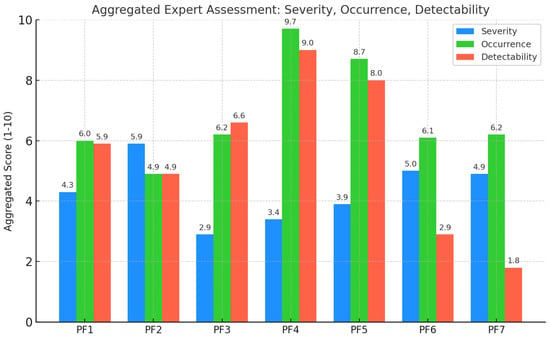
Figure 2.
Aggregated expert assessment of S, O, and D.
PF4 (control system errors) stands out with an extremely high occurrence (9.7) and poor detectability (9.0), meaning these errors happen frequently and are hard to detect before causing issues. Its severity is comparatively moderate (3.4), suggesting that while control errors happen often, they do not always severely damage the process. In contrast, PF7 (programming errors) shows a moderate severity (4.9) and occurrence (6.2), but the lowest detectability rating (1.8), indicating such errors are relatively easy to catch early. PF6 (improper fixturing) has a fairly high severity (5.0) and occurrence (6.1) paired with very low detectability (2.9). It means an unsecured workpiece can significantly and frequently impact quality. Yet, these issues might not be noticed until defects occur, aligning with PF6 being flagged as critical in the fuzzy FMEA.
6.3. Failure Mode Impact
Figure 3 gives the schematic of a five-axis CNC water jet machining system with labeled zones for each potential failure mode. The diagram highlights the tool system (cutting head/nozzle) with PF1 and PF5, the machine structure (gantry, frame) with PF2, areas prone to thermal effects (motors/drive components) with PF3, the CNC controller unit with PF4, the workpiece fixture (clamps, table) with PF6, and the CNC programming input with PF7. Arrows indicate how each failure mode impacts the process.
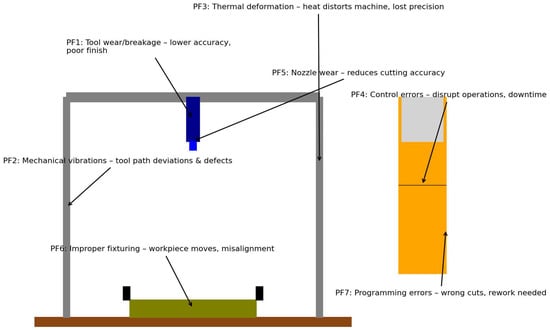
Figure 3.
Aggregated expert assessment of S, O, and D.
Tool System (Cutting Head/Nozzle): The water jet cutting head components, including the orifice and mixing tube, are susceptible to wear or breakage due to extended use or mishandling, resulting in diminished machining accuracy and poor surface finish quality. Moreover, the abrasive nozzle gradually erodes because of continuous exposure to high-pressure abrasive slurry, enlarging the jet stream and decreasing cutting precision over time, leading to tapered or oversized cuts and increased operational costs. Regular inspections, maintenance, and timely replacement of worn nozzles are essential for optimal cutting performance and precision.
Machine Structure (Gantry, Frame): Instability or imbalances within the machine’s structural components, such as the frame, gantry, or moving axes, can induce mechanical vibrations during the cutting process. These vibrations cause deviations in the tool path, negatively affecting dimensional accuracy and increasing the likelihood of surface defects on the workpiece. Implementing vibration-damping solutions and ensuring proper machine leveling and balance significantly reduce these risks.
Heat Zones (Motors/Drive Components): Even though water jet cutting is considered a “cold” process, prolonged operation can generate heat in motors, ball screws, and other drive components. This heat can cause thermal deformation, such as expansion or bending of machine elements, compromising precision and potentially causing misalignments over extended periods. Employing cooling systems or allowing pauses in extended operations helps manage these thermal effects effectively.
CNC Controller Unit: Malfunctions or software bugs in the CNC controller unit can cause control system errors, such as misinterpretation of G-code or loss of positional feedback. These issues disrupt the commanded tool paths and machining operations, potentially leading to missed cuts, collisions, downtime, and costly rework until corrected. Ensuring robust control hardware and regularly validating software updates can mitigate these risks.
Workpiece Fixture (Clamps, Table): Improper or insecure fixturing of the workpiece can result in unwanted shifting or vibration during machining. Such movements cause misalignment and dimensional inaccuracies, significantly compromising precision. Secure and precise fixturing is critical, as even minor displacements can lead to severe defects in finished parts. A robust and stable work-holding setup is therefore essential for maintaining accuracy.
CNC Programming Input—PF7: Errors within CNC programming, such as incorrect G-code or flawed path planning, can result in unintended tool movements, leading to collisions, over-cutting, or under-cutting. These programming mistakes often produce scrapped parts and cause downtime for corrections. Comprehensive offline simulation and meticulous code verification before actual machining are necessary to minimize these risks.
7. Results and Discussion
By implementing the following managerial strategies, companies can enhance the reliability, precision, and efficiency of five-axis CNC water jet machining operations while reducing downtime and operational costs.
The study identifies improper fixturing (PF6), mechanical vibrations (PF2), and tool wear (PF1) as the most critical failure modes in five-axis CNC water jet machining. Managers should prioritize these issues by implementing robust fixturing systems, vibration-damping techniques, and regular tool inspections. Investing in precision work-holding solutions and real-time monitoring systems can significantly reduce these risks.
Abrasive nozzle wear (PF5) and thermal deformation (PF3) reduce machining accuracy over time. Maintenance teams should implement predictive maintenance using condition monitoring technologies to mitigate these effects. Scheduled nozzle replacements and temperature control measures, such as cooling systems or thermal compensation algorithms, will help sustain machining precision.
Control system errors (PF4) and programming errors (PF7) can disrupt machining operations, leading to costly rework and downtime. Managers should emphasize robust CNC programming verification procedures and adopt adaptive control systems that detect and correct deviations in real time. Training personnel in best practices for CNC programming and investing in software that minimizes human errors will further reduce risks.
This study demonstrates the advantages of IVSF-FMEA over traditional FMEA in handling uncertainties. Organizations should integrate fuzzy logic-based risk assessment tools into their decision-making processes. These methods enable a more precise ranking of failure modes, improving resource allocation for risk mitigation.
The IVSF-FMEA methodology enhances risk assessment by incorporating IVSFSs, which capture expert uncertainty and reduce subjectivity. Unlike traditional FMEA, which relies on crisp numerical inputs, IVSF-FMEA allows experts to express membership, non-membership, and hesitancy degrees, ensuring a more balanced risk evaluation. Systematically aggregating expert opinions minimizes variability between different teams. Integrating real-time sensor data and historical failure records can enhance consistency. While it does not eliminate subjectivity, IVSF-FMEA provides a more structured, reliable, and adaptable risk assessment framework for complex manufacturing environments. Manufacturers should continuously leverage historical failure data and expert assessments to refine risk models. Organizations can enhance their predictive capabilities by integrating machine learning algorithms and big data analytics and pre-emptively addressing potential failures before they escalate.
In practice, SFS typically focuses on identifying known potential failure modes, but it may not predict new or unexpected failure modes. It heavily depends on historical data and previous experiences. The proposed IVSF-FMEA can be enhanced by integrating machine learning and real-time monitoring systems to alleviate SFS’s limitation in predicting new or unexpected failure modes. The methodology can identify emerging failure patterns beyond historical records by incorporating sensor data, predictive analytics, and anomaly detection techniques. Additionally, expert knowledge can be supplemented with AI-driven insights, reducing reliance on subjective experience. A hybrid approach, combining IVSF-FMEA with data-driven models, would enable dynamic risk assessment, allowing continuous updates and adaptation to previously unknown failure modes.
Establishing a culture of continuous improvement is essential for minimizing risks in CNC machining operations. Regular training programs for operators, engineers, and maintenance personnel on emerging risk factors and best practices will ensure sustained operational efficiency and product quality improvements.
8. Conclusions
This study presents a comprehensive risk analysis of five-axis CNC water jet machining using the Interval-Valued Spherical Fuzzy Failure Mode and Effects Analysis (IVSF-FMEA) method. The findings identify improper fixturing (PF6), mechanical vibrations (PF2), and tool wear (PF1) as the most critical failure modes, significantly affecting machining accuracy and reliability. This study demonstrates that traditional FMEA, which relies on crisp numerical values, may oversimplify risk evaluations. In contrast, IVSF-FMEA provides a more nuanced and precise risk prioritization framework by incorporating expert hesitancy and uncertainty.
From a practical perspective, the findings provide actionable insights for improving machining reliability. Managers should prioritize proactive maintenance strategies, such as predictive maintenance for tool wear and thermal compensation for heat-induced distortions. Improving control systems and CNC programming verification can minimize human and system-related errors. Fuzzy-based risk assessment techniques can enhance resource allocation, reducing operational downtime and production costs.
The comparative analysis between IVSF-FMEA and traditional FMEA highlights key differences. Traditional FMEA treats all risk factors equally and relies on deterministic values, which may lead to ambiguous prioritization. In contrast, IVSF-FMEA provides a more refined evaluation by effectively handling uncertainty, leading to better differentiation among failure modes. This makes it a superior tool for decision-making in high-precision manufacturing.
Despite its advantages, this study has some limitations. The analysis is based on expert assessments, which may introduce subjective biases. Future research could integrate real-time sensor data and machine learning algorithms to enhance risk prediction accuracy. An adaptive control system that dynamically adjusts machining parameters based on real-time risk evaluations could improve process stability and efficiency.
Author Contributions
Conceptualization, U.C., U.S., and O.D.; methodology, O.D.; formal analysis, O.D.; investigation, U.S. and O.D.; writing—original draft preparation, U.C., U.S., and O.D.; writing—review and editing, U.C., U.S., and O.D.; supervision, U.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data supporting the conclusions of this article can be made available from the corresponding author upon reasonable request.
Conflicts of Interest
Author Ugur Simsir was employed by the company Milteksan CNC A.S. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Wu, S.; Dong, Z.; Qi, F.; Fan, Z. Prediction of the comprehensive error field in the machining space of the five-axis machine tool based on the “S”-shaped specimen family. Machines 2022, 10, 408. [Google Scholar] [CrossRef]
- Lu, Z.; Huo, G.; Jiang, X. A new method to minimize the five-axis CNC machining error around singular points based on NC program interpolation. J. Manuf. Process. 2024, 131, 1263–1281. [Google Scholar] [CrossRef]
- Sun, X.; Qian, Z.; Xu, Y.; Huang, J. Meshing Characteristic Analysis of CBR Reducer Considering Tooth Modification and Manufacturing Error. Machines 2024, 12, 915. [Google Scholar] [CrossRef]
- Brtiš, J.; Ždánsky, J.; Hrbček, J.; Rástočnỳ, K. Development and Application of a Safety-Related Control System Implementing a Safety Function for a CNC Milling Machine. Electronics 2024, 13, 4870. [Google Scholar] [CrossRef]
- Sun, G.; Fan, K.; Yang, J. Digital-driven in-situ monitoring for thermally-induced volumetric errors of CNC machine tools. J. Manuf. Process. 2024, 131, 2000–2015. [Google Scholar] [CrossRef]
- Haktanir, E.; Kahraman, C. A literature review on fuzzy FMEA and an application on infant car seat design using spherical fuzzy sets. In Customer Oriented Product Design: Intelligent and Fuzzy Techniques; Springer: Berlin/Heidelberg, Germany, 2020; pp. 429–449. [Google Scholar]
- Wang, N.; Wang, W.; Yu, S.; Chen, J.; Yang, X. Efficiency Assessment Method for Evoking Cultural Empathy in Symbolic Cultural and Creative Products Based on Fuzzy-FMEA. Appl. Sci. 2024, 15, 221. [Google Scholar] [CrossRef]
- Dogan, O.; Cebeci, U. An Integrated Quality Tools Approach for New Product Development. In Techniques, Tools and Methodologies Applied to Quality Assurance in Manufacturing; Springer: Berlin/Heidelberg, Germany, 2021; pp. 3–22. [Google Scholar]
- Gul, M.; Ak, M.F. A modified failure modes and effects analysis using interval-valued spherical fuzzy extension of TOPSIS method: Case study in a marble manufacturing facility. Soft Comput. 2021, 25, 6157–6178. [Google Scholar] [CrossRef]
- Arslan, Ö.; Karakurt, N.; Cem, E.; Cebi, S. Risk analysis in the food cold chain using Decomposed fuzzy set-based FMEA approach. Sustainability 2023, 15, 13169. [Google Scholar] [CrossRef]
- Ilbahar, E.; Kahraman, C.; Cebi, S. Risk assessment of renewable energy investments: A modified failure mode and effect analysis based on prospect theory and intuitionistic fuzzy AHP. Energy 2022, 239, 121907. [Google Scholar] [CrossRef]
- Karasan, A.; Ilbahar, E.; Cebi, S.; Kahraman, C. A new risk assessment approach: Safety and Critical Effect Analysis (SCEA) and its extension with Pythagorean fuzzy sets. Saf. Sci. 2018, 108, 173–187. [Google Scholar] [CrossRef]
- Pirbalouti, R.G.; Dehkordi, M.K.; Mohammadpour, J.; Zarei, E.; Yazdi, M. An advanced framework for leakage risk assessment of hydrogen refueling stations using interval-valued spherical fuzzy sets (IV-SFS). Int. J. Hydrogen Energy 2023, 48, 20827–20842. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, W.; Yang, Z.; Deveci, M.; Delen, D. Evaluating risk of IoT adoption in the food supply chain using an integrated interval-valued spherical fuzzy generalised TODIM method. Int. J. Prod. Econ. 2024, 277, 109386. [Google Scholar] [CrossRef]
- Chang, K.H. A new emergency-risk-evaluation approach under spherical fuzzy-information environments. Axioms 2022, 11, 474. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, W.; Nie, W. Literature review and prospect of the development and application of FMEA in manufacturing industry. Int. J. Adv. Manuf. Technol. 2021, 112, 1409–1436. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, J.; Dai, Q.; Huang, W.; Wang, X. Recent Advances and Status of Abrasive Jet Machining Technology. Surf. Technol. 2022, 51, 80–98. [Google Scholar]
- Apostolou, G.; Ntemi, M.; Paraschos, S.; Gialampoukidis, I.; Rizzi, A.; Vrochidis, S.; Kompatsiaris, I. Novel framework for quality control in vibration monitoring of CNC machining. Sensors 2024, 24, 307. [Google Scholar] [CrossRef]
- Ceylan, B.O. Shipboard compressor system risk analysis by using rule-based fuzzy FMEA for preventing major marine accidents. Ocean Eng. 2023, 272, 113888. [Google Scholar] [CrossRef]
- Wen, T.C.; Chung, H.Y.; Chang, K.H.; Li, Z.S. A flexible risk assessment approach integrating subjective and objective weights under uncertainty. Eng. Appl. Artif. Intell. 2021, 103, 104310. [Google Scholar] [CrossRef]
- Chen, X.; Yu, H.; Pan, H.; Chen, L.; You, H.; Liang, X. Nozzle Wear in Abrasive Water Jet Based on Numerical Simulation. Materials 2024, 17, 3585. [Google Scholar] [CrossRef]
- Golovin, K.; Pushkarev, A.; Kovaleva, A. Determination of the wear limit value, the optimal operating time, and the consumption of jet-forming elements made of different materials when implementing water jet technologies. Transp. Res. Procedia 2021, 57, 210–219. [Google Scholar] [CrossRef]
- Kim, J.G.; Song, J.J. Abrasive water jet cutting methods for reducing blast-induced ground vibration in tunnel excavation. Int. J. Rock Mech. Min. Sci. 2015, 75, 147–158. [Google Scholar] [CrossRef]
- Zhou, Z.D.; Gui, L.; Tan, Y.G.; Liu, M.Y.; Liu, Y.; Li, R.Y. Actualities and development of heavy-duty CNC machine tool thermal error monitoring technology. Chin. J. Mech. Eng. 2017, 30, 1262–1281. [Google Scholar] [CrossRef]
- Reddy, T.N.; Shanmugaraj, V.; Vinod, P.; Krishna, S.G. Real-time thermal error compensation strategy for precision machine tools. Mater. Today Proc. 2020, 22, 2386–2396. [Google Scholar] [CrossRef]
- Sun, J.; Liu, Z.; Qiu, C.; Luo, J.; He, L.; Liu, H.; Sa, G.; Jiang, Z.; Tan, J. Machining accuracy prediction and adaptive compensation method of CNC machine tool under absence of machining process sensing. J. Intell. Manuf. 2024, 1–18. [Google Scholar] [CrossRef]
- Dwianda, Y. Failure mode and effect analysis (FMEA) of pneumatic system of cnc milling machine. J. Ocean Mech.-Aerosp.-Sci. Eng. 2021, 65, 14–18. [Google Scholar] [CrossRef]
- Tian, H.; Sun, Y.; Chen, C.; Zhang, Z.; Liu, T.; Zhang, T.; He, J.; Yu, L. A novel FMECA method for CNC machine tools based on D-GRA and data envelopment analysis. Sci. Rep. 2024, 14, 26596. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, T.; Tian, H.; Yang, Z.; Liu, A.; Zhang, F. FMECA of CNC machine tool design stage based on CBWM and DEA. Qual. Reliab. Eng. Int. 2024, 40, 154–169. [Google Scholar] [CrossRef]
- Jiang, S.; Liu, Z.; Chen, J. A dynamic failure mode and effect analysis (FMEA) method for CNC machine tool in service. J. Phys. Conf. Ser. 2023, 2483, 012047. [Google Scholar] [CrossRef]
- Patil, R.; Kothavale, B. Failure modes and effects analysis (FMEA) of computerized numerical control (CNC) turning center. Int. Rev. Mech. Eng. 2018, 12, 78–87. [Google Scholar] [CrossRef]
- Zhang, K.; Jia, Z.; Bian, R.; He, K.; Jia, Z. Reliability Prediction and FMEA of Loading and Unloading Truss Robot for CNC Punch. Appl. Sci. 2023, 13, 4951. [Google Scholar] [CrossRef]
- Yang, H.; Li, G.; He, J.; Wang, L.; Zhou, X. Improved FMEA based on IVF and fuzzy VIKOR method: A case study of workpiece box system of CNC gear milling machine. Qual. Reliab. Eng. Int. 2021, 37, 2478–2498. [Google Scholar] [CrossRef]
- Ak, M.F.; Demir, E. A novel qualitative risk assessment using the interval-valued spherical fuzzy extension of TOPSIS method: A case study in rail transit systems. Neural Comput. Appl. 2024, 36, 5109–5132. [Google Scholar] [CrossRef]
- Zhao, H.; You, J.X.; Liu, H.C. Failure mode and effect analysis using MULTIMOORA method with continuous weighted entropy under interval-valued intuitionistic fuzzy environment. Soft Comput. 2017, 21, 5355–5367. [Google Scholar] [CrossRef]
- Gündoğdu, F.K.; Seyfi-Shishavan, S.A. Occupational Risk Assessment Using Spherical Fuzzy Safety and Critical Effect Analysis for Shipyards. J. ETA Marit. Sci. 2021, 9, 110–119. [Google Scholar] [CrossRef]
- Godina, R.; Silva, B.G.R.; Espadinha-Cruz, P. A DMAIC integrated fuzzy FMEA model: A case study in the Automotive Industry. Appl. Sci. 2021, 11, 3726. [Google Scholar] [CrossRef]
- Gupta, G.; Ghasemian, H.; Janvekar, A.A. A novel failure mode effect and criticality analysis (FMECA) using fuzzy rule-based method: A case study of industrial centrifugal pump. Eng. Fail. Anal. 2021, 123, 105305. [Google Scholar] [CrossRef]
- Maghami, M.R.; Vahabzadeh, S.; Mutambara, A.G.O.; Ghoushchi, S.J.; Gomes, C. Failure analysis in smart grid solar integration using an extended decision-making-based FMEA model under uncertain environment. Stoch. Environ. Res. Risk Assess. 2024, 38, 3543–3563. [Google Scholar] [CrossRef]
- Abbaspour Onari, M.; Yousefi, S.; Jahangoshai Rezaee, M. Risk assessment in discrete production processes considering uncertainty and reliability: Z-number multi-stage fuzzy cognitive map with fuzzy learning algorithm. Artif. Intell. Rev. 2021, 54, 1349–1383. [Google Scholar] [CrossRef]
- Vaysi, A.; Rohani, A.; Tabasizadeh, M.; Khodabakhshian, R.; Kolahan, F. Using Fuzzy FMEA approach to improve decision-making process in CNC machine Electrical and control equipment failure prediction. Int. J. Ind. Eng. Prod. Res. 2018, 29, 359–376. [Google Scholar]
- Ervural, B.; Ayaz, H.I. A fully data-driven FMEA framework for risk assessment on manufacturing processes using a hybrid approach. Eng. Fail. Anal. 2023, 152, 107525. [Google Scholar] [CrossRef]
- Cardiel-Ortega, J.J.; Baeza-Serrato, R. Failure mode and effect analysis with a Fuzzy Logic approach. Systems 2023, 11, 348. [Google Scholar] [CrossRef]
- Ma, Q.X.; Zhu, X.M.; Bai, K.Y.; Zhang, R.T.; Liu, D.W. A novel failure mode and effect analysis method with spherical fuzzy entropy and spherical fuzzy weight correlation coefficient. Eng. Appl. Artif. Intell. 2023, 122, 106163. [Google Scholar] [CrossRef]
- Huang, G.; Xiao, L.; Pedrycz, W.; Zhang, G.; Martinez, L. Failure mode and effect analysis using T-spherical fuzzy maximizing deviation and combined comparison solution methods. IEEE Trans. Reliab. 2022, 72, 552–573. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Duan, C.Y. An integrated approach for failure mode and effect analysis under interval-valued intuitionistic fuzzy environment. Int. J. Prod. Econ. 2019, 207, 163–172. [Google Scholar] [CrossRef]
- Akram, M.; Luqman, A.; Alcantud, J.C.R. Risk evaluation in failure modes and effects analysis: Hybrid TOPSIS and ELECTRE I solutions with Pythagorean fuzzy information. Neural Comput. Appl. 2021, 33, 5675–5703. [Google Scholar] [CrossRef]
- Wang, Z.C.; Ran, Y.; Chen, Y.; Yang, X.; Zhang, G. Group risk assessment in failure mode and effects analysis using a hybrid probabilistic hesitant fuzzy linguistic MCDM method. Expert Syst. Appl. 2022, 188, 116013. [Google Scholar] [CrossRef]
- Liu, H.C.; Liu, L.; Li, P. Failure mode and effects analysis using intuitionistic fuzzy hybrid weighted Euclidean distance operator. Int. J. Syst. Sci. 2014, 45, 2012–2030. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Li, P.; Su, Q. Failure mode and effect analysis under uncertainty: An integrated multiple criteria decision making approach. IEEE Trans. Reliab. 2016, 65, 1380–1392. [Google Scholar] [CrossRef]
- Mohsen, O.; Fereshteh, N. An extended VIKOR method based on entropy measure for the failure modes risk assessment–A case study of the geothermal power plant (GPP). Saf. Sci. 2017, 92, 160–172. [Google Scholar] [CrossRef]
- Wang, L.E.; Liu, H.C.; Quan, M.Y. Evaluating the risk of failure modes with a hybrid MCDM model under interval-valued intuitionistic fuzzy environments. Comput. Ind. Eng. 2016, 102, 175–185. [Google Scholar] [CrossRef]
- Chang, K.H. Integrating spherical fuzzy sets and the objective weights consideration of risk factors for handling risk-ranking issues. Appl. Sci. 2023, 13, 4503. [Google Scholar] [CrossRef]
- Jafarzadeh Ghoushchi, S.; Shaffiee Haghshenas, S.; Memarpour Ghiaci, A.; Guido, G.; Vitale, A. Road safety assessment and risks prioritization using an integrated SWARA and MARCOS approach under spherical fuzzy environment. Neural Comput. Appl. 2023, 35, 4549–4567. [Google Scholar] [CrossRef] [PubMed]
- Boral, S.; Chakraborty, S. Failure analysis of CNC machines due to human errors: An integrated IT2F-MCDM-based FMEA approach. Eng. Fail. Anal. 2021, 130, 105768. [Google Scholar] [CrossRef]
- Hassan, S.; Wang, J.; Kontovas, C.; Bashir, M. Modified FMEA hazard identification for cross-country petroleum pipeline using Fuzzy Rule Base and approximate reasoning. J. Loss Prev. Process. Ind. 2022, 74, 104616. [Google Scholar] [CrossRef]
- Ivančan, J.; Lisjak, D. New FMEA risks ranking approach utilizing four fuzzy logic systems. Machines 2021, 9, 292. [Google Scholar] [CrossRef]
- Resende, B.A.d.; Dedini, F.G.; Eckert, J.J.; Sigahi, T.F.; Pinto, J.d.S.; Anholon, R. Proposal of a facilitating methodology for fuzzy FMEA implementation with application in process risk analysis in the aeronautical sector. Int. J. Qual. Reliab. Manag. 2024, 41, 1063–1088. [Google Scholar] [CrossRef]
- Testik, O.M.; Unlu, E.T. Fuzzy FMEA in risk assessment for test and calibration laboratories. Qual. Reliab. Eng. Int. 2023, 39, 575–589. [Google Scholar] [CrossRef]
- Beiranvand, B. Development of modified fuzzy FMEA method in environmental risk assessment of earth dams. Sci. Rep. 2024, 14, 17585. [Google Scholar] [CrossRef]
- Kamsefidi, M.M.; Shahraki, A.; Saljooghi, F.H. Improving the Calculation of RPN in the FMEA Method by Combining a Nonlinear Model with Revised TOPSIS and Fuzzy Logic. J. Health Saf. Work. 2023, 12, 854–871. [Google Scholar]
- ul Hassan, F.; Nguyen, T.; Le, T.; Le, C. Automated prioritization of construction project requirements using machine learning and fuzzy Failure Mode and Effects Analysis (FMEA). Autom. Constr. 2023, 154, 105013. [Google Scholar] [CrossRef]
- Jin, G.; Meng, Q.; Feng, W. Optimization of logistics system with fuzzy FMEA-AHP methodology. Processes 2022, 10, 1973. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, Z.; Qian, H.; Su, X. Failure Mode and Effects Analysis Based on Z-Numbers and the GradedMean Integration Representation. CMES-Comput. Model. Eng. Sci. 2023, 134, 1005–1019. [Google Scholar]
- Kutlu Gündoğdu, F.; Kahraman, C. Spherical fuzzy sets and spherical fuzzy TOPSIS method. J. Intell. Fuzzy Syst. 2019, 36, 337–352. [Google Scholar] [CrossRef]
- Gundogdu, F.K.; Kahraman, C. A novel spherical fuzzy analytic hierarchy process and its renewable energy application. Soft Comput. 2020, 24, 4607–4621. [Google Scholar] [CrossRef]
- Gundogdu, F.K.; Kahraman, C. A novel fuzzy TOPSIS method using emerging interval-valued spherical fuzzy sets. Eng. Appl. Artif. Intell. 2019, 85, 307–323. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).