Establishment and Identification of Fractional-Order Model for Structurally Symmetric Flexible Two-Link Manipulator System
Abstract
1. Introduction
- A fractional differential operator is introduced to characterize the viscoelastic potential energy and viscous friction of the FTLM system, which is more consistent with the dynamic characteristics of the FTLM system.
- A fractional-order model of the FTLM system is established based on a fractional-order Euler–Lagrange equation and the symmetry of the system structure; this model is used to describe the flexible oscillation process of the system accurately.
- A fractional-order system identification algorithm based on the MIOM is proposed. The multi-innovation technique is combined with the least-squares method to solve the FTLM system’s operational matrix and improve system identification accuracy.
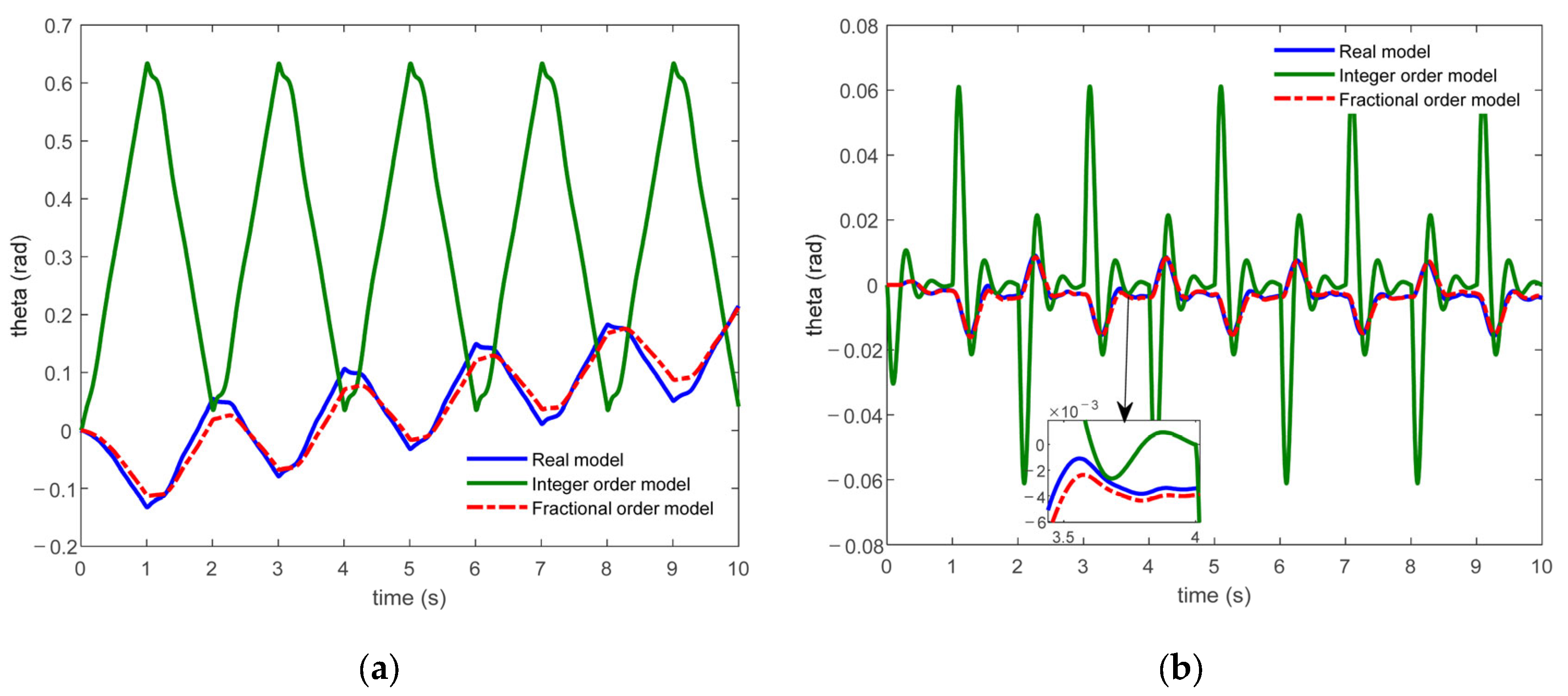
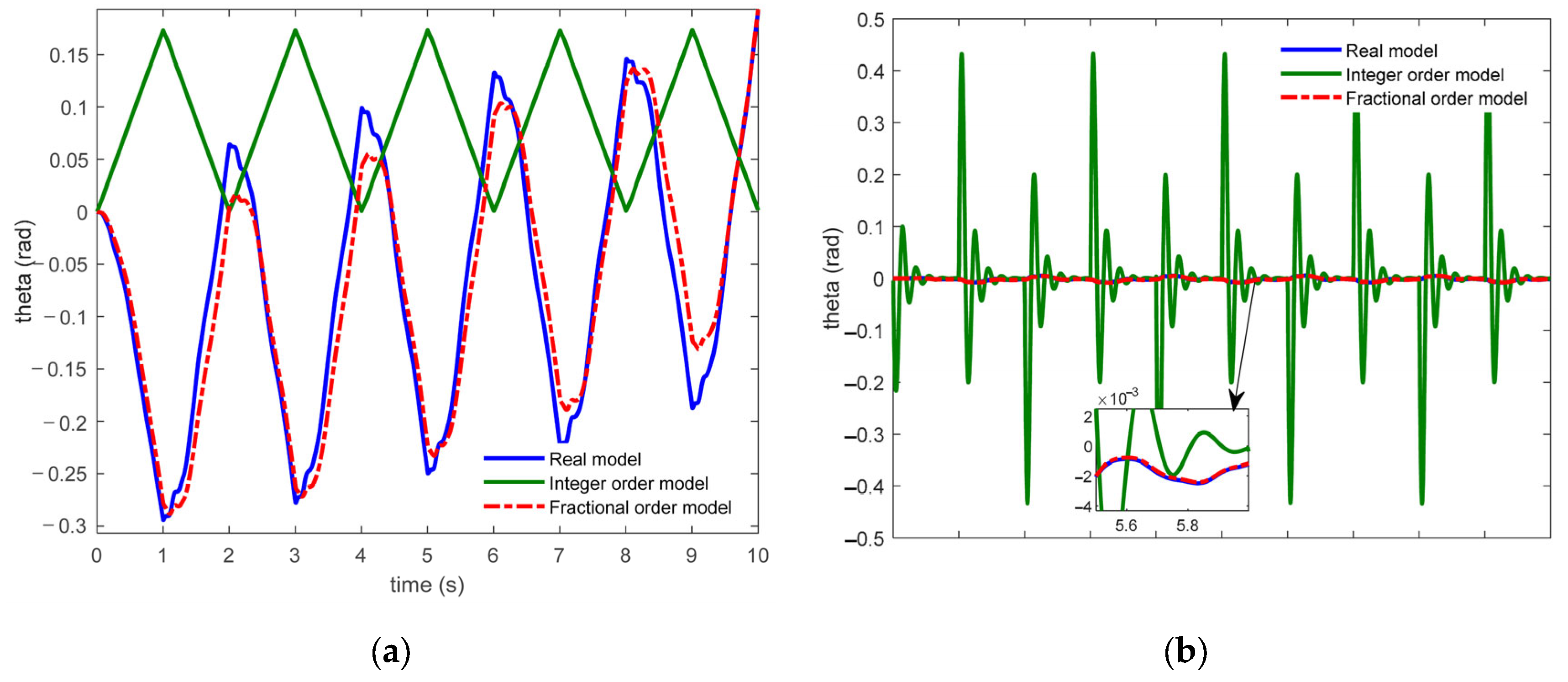
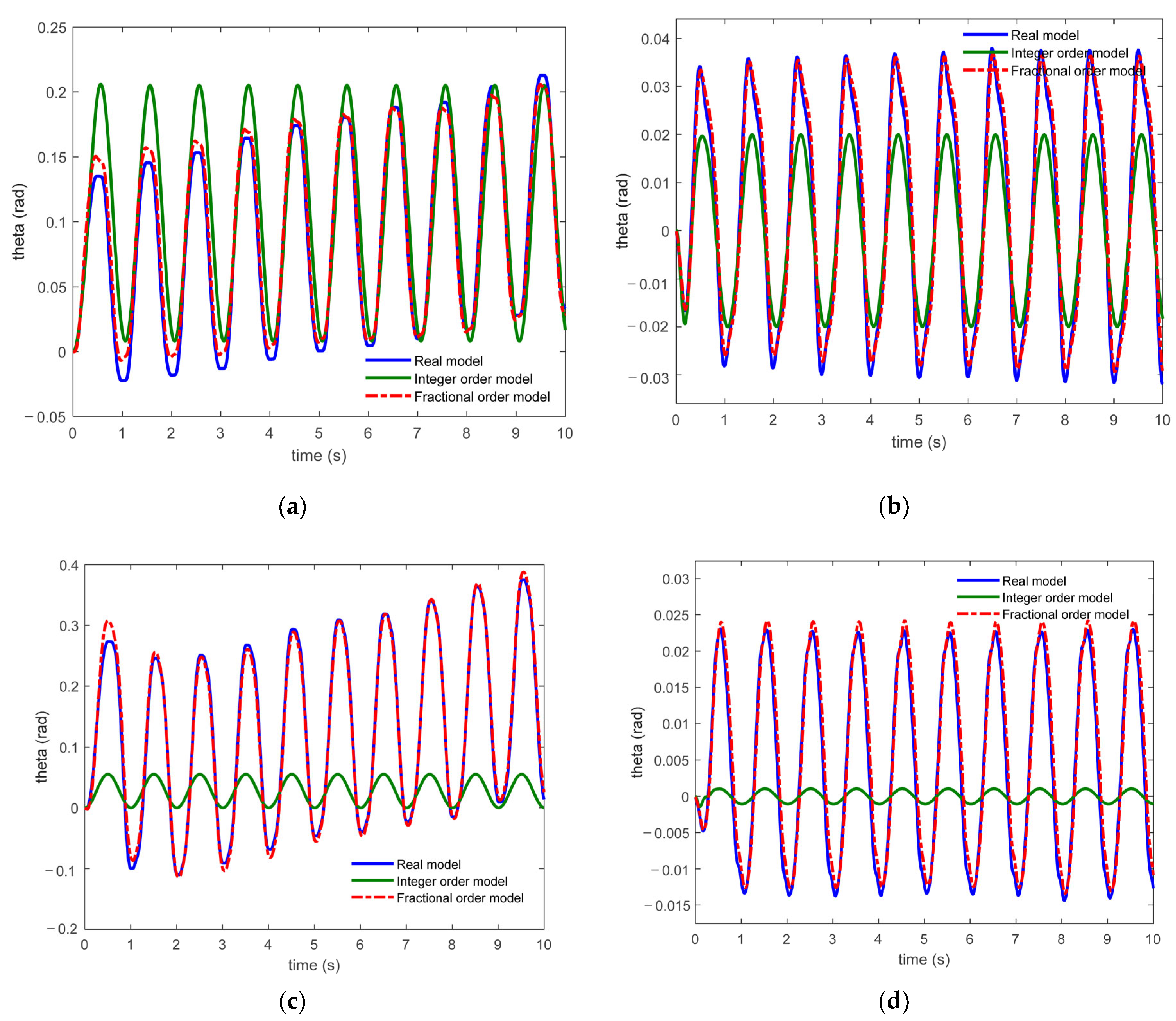
- The established fractional-order model can describe the dynamic characteristics of the system more accurately than integer-order models and is more suitable for engineering applications. It can provide an accurate model for fast, accurate, and stable control of the FTLM system.
2. Theory of Fractional Calculus
- 1.
- Grünwald–Letnikov (G-L) definition:
- 2.
- Riemann–Liouville (R-L) definition
- 3.
- Caputo definition
3. Establishment of the FTLM System’s Fractional-Order Model
4. Identification of Fractional-Order FTLM System Model
4.1. Haar Wavelet-Based Integration Operational Matrix
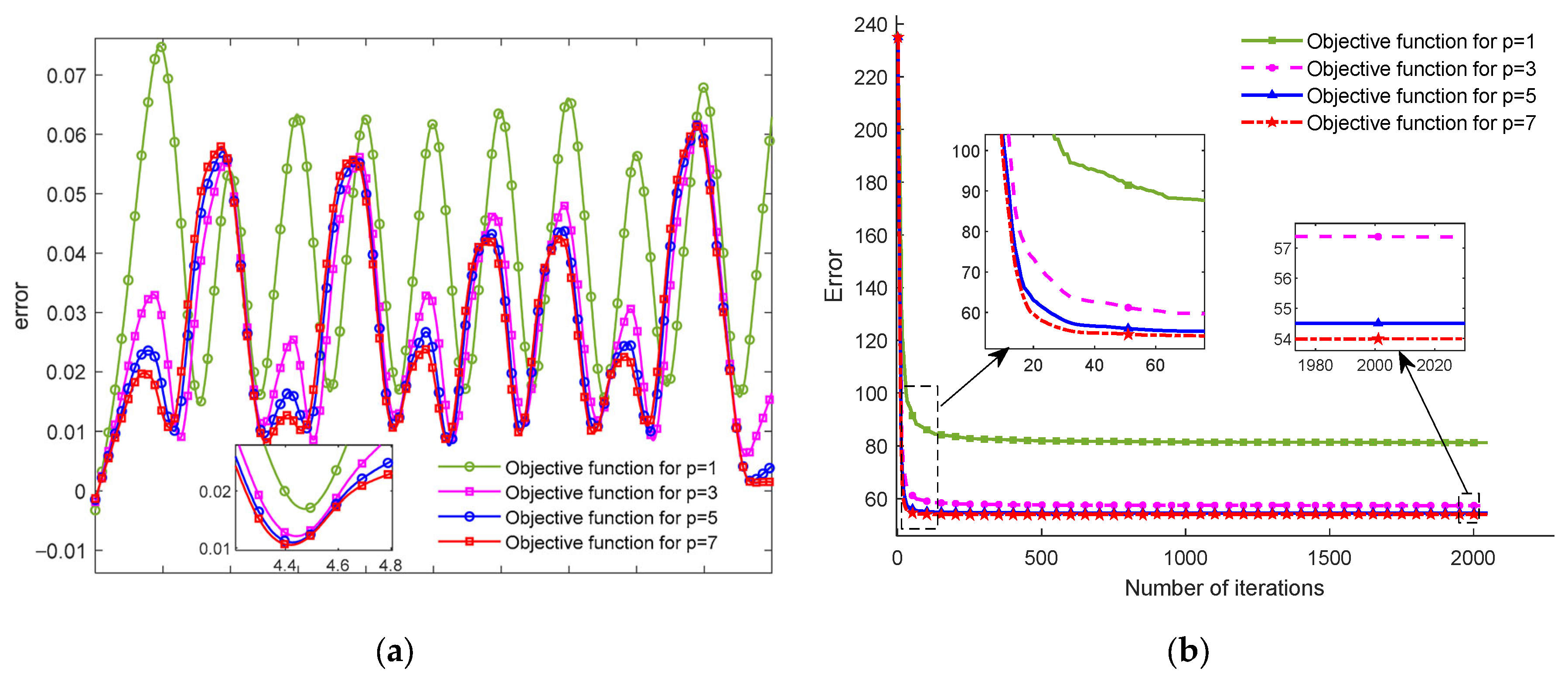
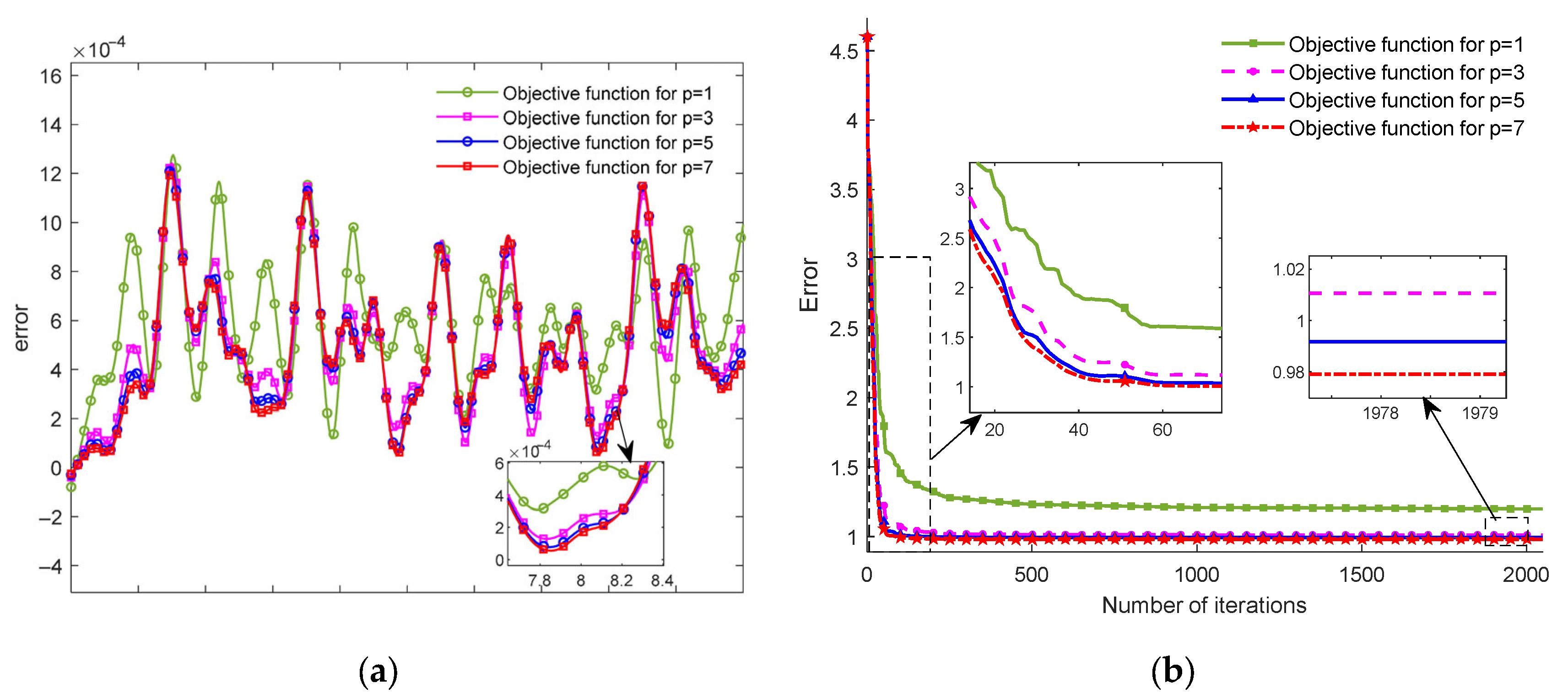
4.2. Fractional-Order FTLM System Model Identification
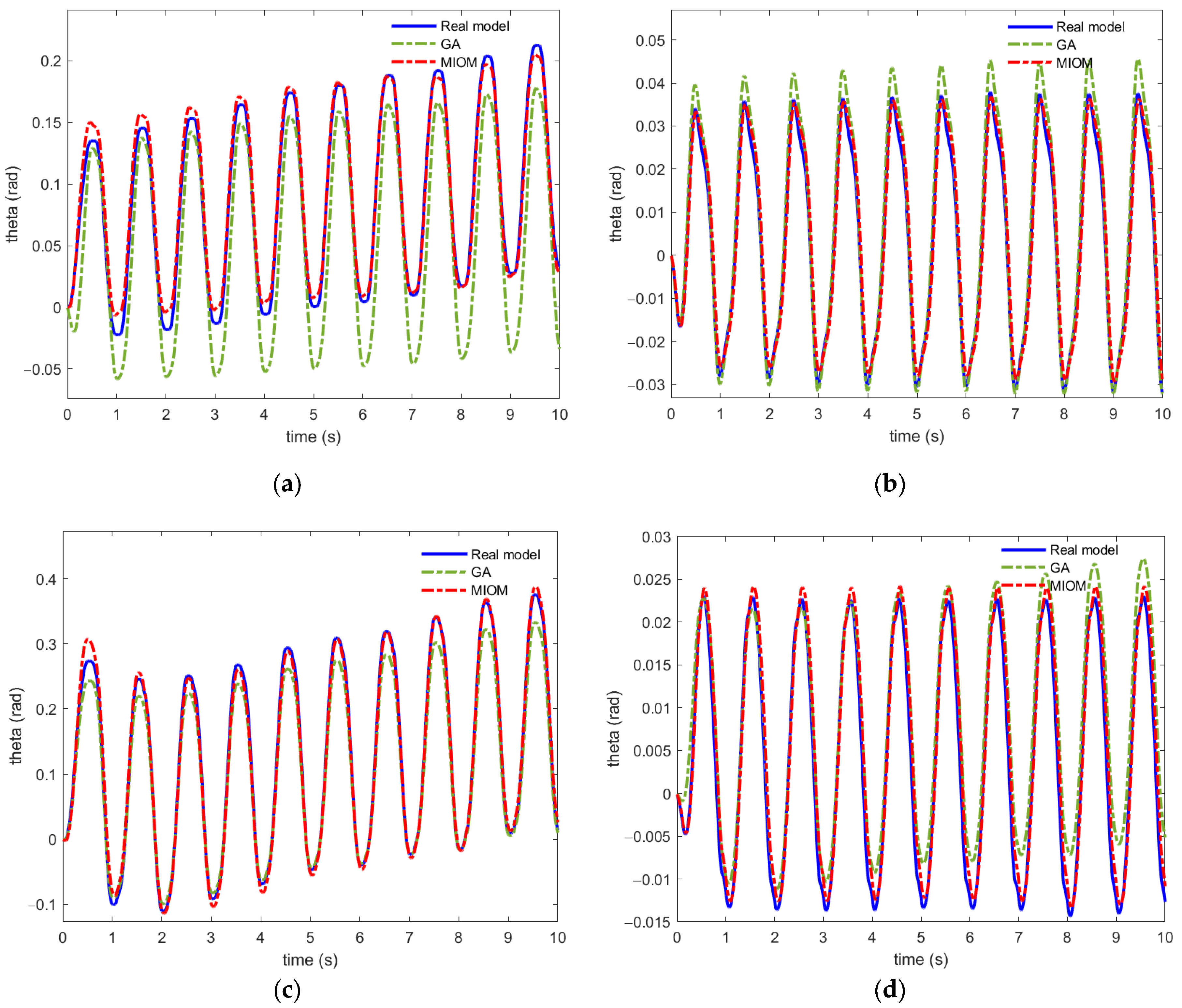
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dehkordi, S.F. Dynamic analysis of flexible-link manipulator in underwater applications using Gibbs-Appell formulations. Ocean Eng. 2021, 241, 110057. [Google Scholar] [CrossRef]
- Pu, Y.X.; Li, X.B.; Zhang, F. Hybrid control of piezoelectric flexible manipulator based on Volterra filtered-xLMS algorithm. J. Vib. Control 2023, 29, 185–199. [Google Scholar] [CrossRef]
- Mo, H.J.; Wei, R.F.; Bo, O.Y.; Xing, L.X.; Shan, Y.H.; Liu, Y.H.; Sun, D. Control of a flexible continuum manipulator for laser beam steering. IEEE Rob. Autom. Lett. 2021, 6, 1074–1081. [Google Scholar] [CrossRef]
- Chen, X.A. The computational design of a fractal-inspired soft robotic. Alex. Eng. J. 2023, 84, 37–46. [Google Scholar] [CrossRef]
- Ma, X.; Wang, P.; Ye, M.X.; Chiu, P.W.Y.; Li, Z. Shared autonomy of a flexible manipulator in constrained endoluminal surgical tasks. IEEE Rob. Autom. Lett. 2019, 4, 3106–3112. [Google Scholar] [CrossRef]
- Mehedi, I.M.; Rao, K.P. Surgical robotic arm control for tissue ablation. J. Robot. Surg. 2020, 14, 881–887. [Google Scholar] [CrossRef]
- Kim, J.; de Mathelin, M.; Ikuta, K.; Kwon, D.S. Advancement of flexible robot technologies for endoluminal surgeries. Proc. IEEE 2022, 110, 909–931. [Google Scholar] [CrossRef]
- Qiao, J.Z.; Wu, H.; Yu, X. High-precision attitude tracking control of space manipulator system under multiple disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 4274–4284. [Google Scholar] [CrossRef]
- Ranjan, R.; Dwivedy, S.K. Dynamic analysis of flexible manipulators, a literature review. Mech. Mach. Theory 2006, 41, 749–777. [Google Scholar] [CrossRef]
- Subudhi, B.; Morris, A.S. Dynamic modelling, simulation and control of a manipulator with flexible links and joints. Rob. Auton. Syst. 2002, 41, 257–270. [Google Scholar] [CrossRef]
- Nejad, F.H.; Fayazi, A.; Zadeh, H.G.; Marj, H.F.; HosseinNia, S.H. Precise tip-positioning control of a single-link flexible arm using a fractional-order sliding mode controller. J. Vib. Control 2020, 26, 1683–1696. [Google Scholar] [CrossRef]
- Alandoli, E.A.; Lee, T.S.; Lin, Y.J.; Vijayakumar, V. Dynamic model and intelligent optimal controller of flexible link manipulator system with payload uncertainty. Arab. J. Sci. Eng. 2021, 46, 7423–7433. [Google Scholar] [CrossRef]
- Liu, J.Q.; Li, X.P.; Yin, M.; Wei, L.; Wang, H.Z. Modeling and Rotation Control Strategy for Space Planar Flexible Robotic Arm Based on Fuzzy Adjustment and Disturbance Observer. Mathematics 2024, 12, 2513. [Google Scholar] [CrossRef]
- Huang, J.; Ji, J.C. Vibration control of coupled Duffing oscillators in flexible single-link manipulators. J. Vib. Control 2021, 27, 2058–2068. [Google Scholar] [CrossRef]
- Loudini, M.; Boukhetala, D.; Tadjine, M.; Boumehdi, M.A. Application of Timoshenko beam theory for deriving motion equations of a lightweight elastic link robot manipulator. Int. J. Autom. Robot. Auton. Systems. 2006, 5, 11–18. [Google Scholar]
- Yin, H.B.; Li, Y.G.; Li, J.F. Decomposed dynamic control for a flexible robotic arm in consideration of nonlinearity and the effect of gravity. Adv. Mech. Eng. 2017, 9, 1687814017694104. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, X.N.; Liu, Z.J.; Li, Q. Boundary torque control of a flexible two-link manipulator and its experimental investigation. IEEE Trans. Ind. Electron. 2020, 68, 8708–8717. [Google Scholar] [CrossRef]
- Abdoon, M.A.; Saadeh, R.; Berir, M.; EL Guma, F.; Ali, M. Analysis, modeling and simulation of a fractional-order influenza model. Alex. Eng. J. 2023, 74, 231–240. [Google Scholar] [CrossRef]
- Biswas, D.; Sharma, K.D. Real-time fractional order φ1 adaptive control strategy for fractional order two link manipulator. Phys. Scr. 2024, 99, 075272. [Google Scholar] [CrossRef]
- Bueno, A.M.; Daltin, D.C.; Serni, P.J.A.; Balthazar, J.M.; Tusset, A.M. Suboptimal State Tracking Control Applied to a Nonlinear Fractional-Order Slewing Motion Flexible Structure. J. Comput. Nonlinear Dyn. 2022, 17, 091005. [Google Scholar] [CrossRef]
- Cheng, C.; Shen, H.k. Fractional-order dynamics and adaptive dynamic surface control of flexible-joint robots. Asian J. Control 2023, 25, 3029–3044. [Google Scholar] [CrossRef]
- Haro-Olmo, M.I.; Tejado, I.; Vinagre, B.M.; Feliu-Batlle, V. Fractional-Order Models of Damping Phenomena in a Flexible Sensing Antenna Used for Haptic Robot Navigation. Fractal Fract. 2023, 7, 621. [Google Scholar] [CrossRef]
- Muresan, C.I.; Folea, S.; Birs, I.R.; Ionescu, C. A novel fractional-order model and controller for vibration suppression in flexible smart beam. Nonlinear Dyn. 2018, 93, 525–541. [Google Scholar] [CrossRef]
- Xu, Y.Q.; Wei, P.J. Dynamic response of fractional-order viscoelastic high-order shear beam based on nonlocal strain gradient elasticity. Acta Mech. Solida Sin. 2023, 36, 875–883. [Google Scholar] [CrossRef]
- Wei, J.T.; Wu, Y.H. Improved Fractional Order Single Optimization Parameter Grey Model. J. Grey System. 2023, 35, 154–171. [Google Scholar]
- Danca, M.F.; Feckan, M. Mandelbrot set and Julia sets of fractional order. Nonlinear Dyn. 2023, 111, 9555–9570. [Google Scholar] [CrossRef]
- Cattani, C. Haar wavelet fractional derivative. Proc. Est. Acad. Sci. 2022, 71, 55–64. [Google Scholar] [CrossRef]
- Arafa, H.M.; Ramadan, M.A.; Althobaiti, N.A. Numerical Technique Based on Bernoulli Wavelet Operational Matrices for Solving a Class of Fractional Order Differential Equations. Fractal Fract. 2023, 7, 604. [Google Scholar] [CrossRef]
- Shree, R.V.; Mallikarjun, B.P.; Souayeh, B.; Bhattacharya, S. Application of fibonacci wavelet frame operational matrix for the analysis of arrhenius-controlled heat transfer flow in a microchannel. Case Stud. Therm. Eng. 2024, 63, 105326. [Google Scholar] [CrossRef]
- Wang, Z.S.; Liang, S.N.; Chen, B.C.; Sun, H.L. Identification of fractional order time delay system with measurement noise using variable period integration operational matrix. Mech. Syst. Sig. Process. 2025, 223, 111930. [Google Scholar] [CrossRef]
- Shiralashetti, S.C.; Pala, V.R.; Hanaji, S.I. Legendre wavelet integration operational matrix method for the numerical solution of unsteady MHD nanofluid flow between moving parallel plates. Numer. Heat Transfer, Part B 2024, 1–24. [Google Scholar] [CrossRef]
- Wang, Y.X.; Zhu, L.; Hu, D.L. Euler wavelets operational matrix of integration and its application in the calculus of variations. Int. J. Comput. Math. 2024, 101, 386–406. [Google Scholar] [CrossRef]
- Turan-Dincel, A.; Tural-Polat, S.N. Operational matrix method approach for fractional partial differential-equations. Phys. Scr. 2024, 99, 125254. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Podlubny, I. Geometrical and physical interpretation of fractional integration and fractional diggerentiation. Fract. Calc. Appl. Anal. 2002, 5, 357–366. [Google Scholar]
- Chen, B.; Li, C.Y.; Wilson, B.; Huang, Y.J. Fractional modeling and analysis of coupled MR damping system. IEEE/CAA J. Autom. Sin. 2016, 3, 288–294. [Google Scholar] [CrossRef]
- Zhu, J.W.; Chen, D.Y.; Zhao, H.; Ma, R.F. Nonlinear dynamic analysis and modeling of fractional permanent magnet synchronous motors. J. Vib. Control 2016, 22, 1855–1875. [Google Scholar] [CrossRef]
- Lazarevic, M.P.; Mandić, P.D.; Ostojic, S. Further results on advanced robust iterative learning control and modeling of robotic systems. J. Mech. Eng. Sci. 2021, 235, 4719–4734. [Google Scholar] [CrossRef]
- Lavin-Delgado, J.E.; Solis-Perez, J.E.; Gomez-Aguilar, J.F.; Escobar-Jimenez, R.F. Trajectory tracking control based on non-singular fractional derivatives for the PUMA 560 robot arm. Multibody Sys. Dyn. 2020, 50, 259–303. [Google Scholar] [CrossRef]
- Jiang, G.; Ke, T.; Deng, M.T. Least square method based on Haar wavelet to solve multi-dimensional stochastic Itô-Volterra integral equations. Appl. Math. Serb. 2023, 38, 591–603. [Google Scholar] [CrossRef]
- Tang, Y.G.; Li, N.; Liu, M.M.; Lu, Y.; Weng, W.W. Identification of fractional-order systems with time delays using block pulse functions. Mech. Syst. Sig. Process. 2017, 91, 382–394. [Google Scholar] [CrossRef]
- Wu, J.L.; Chen, C.H.; Chen, C.F. Numerical inversion of Laplace transform using Haar wavelet operational matrices. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 120–122. [Google Scholar] [CrossRef]
- Hsiao, C.H. A Haar wavelets method of solving differential equations characterizing the dynamics of a current collection system for an electric locomotive. Appl. Math. Comput. 2015, 265, 928–935. [Google Scholar] [CrossRef]
- Ding, F. Several multi-innovation identification methods. Digit. Signal Process. 2010, 20, 1027–1039. [Google Scholar] [CrossRef]
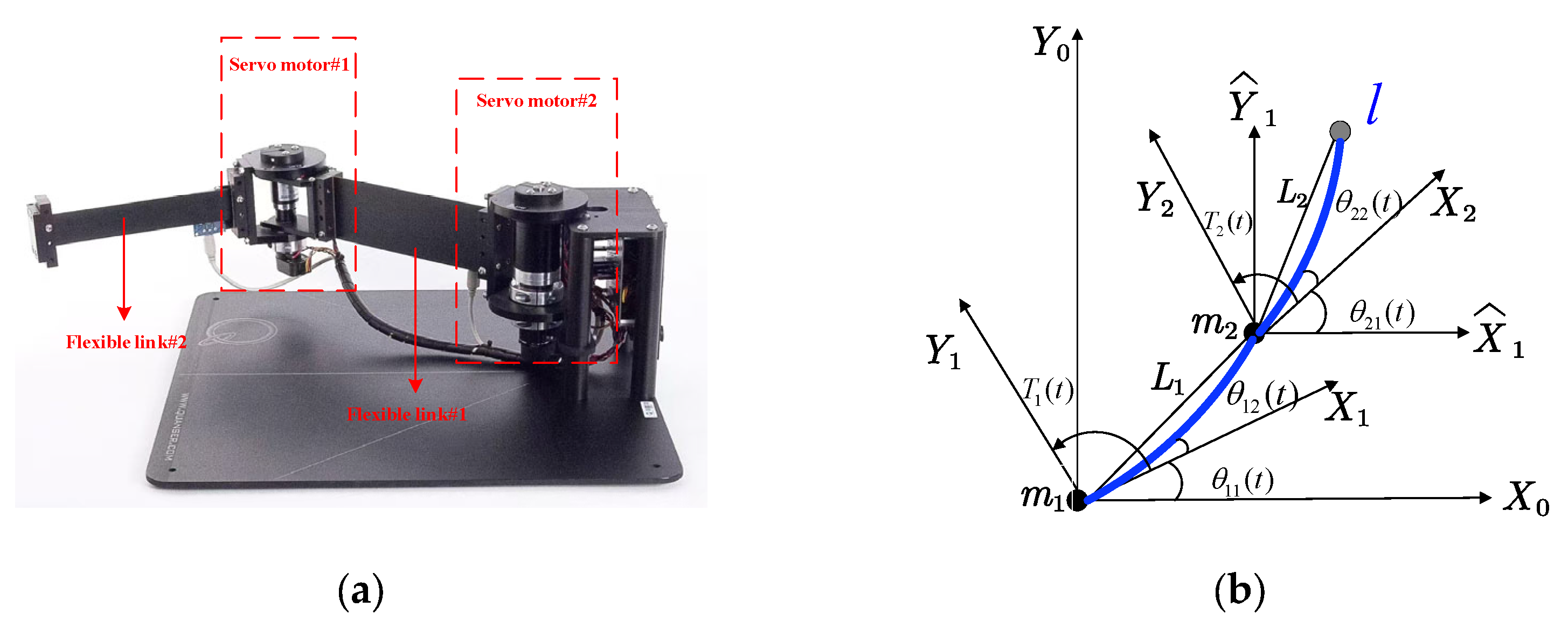

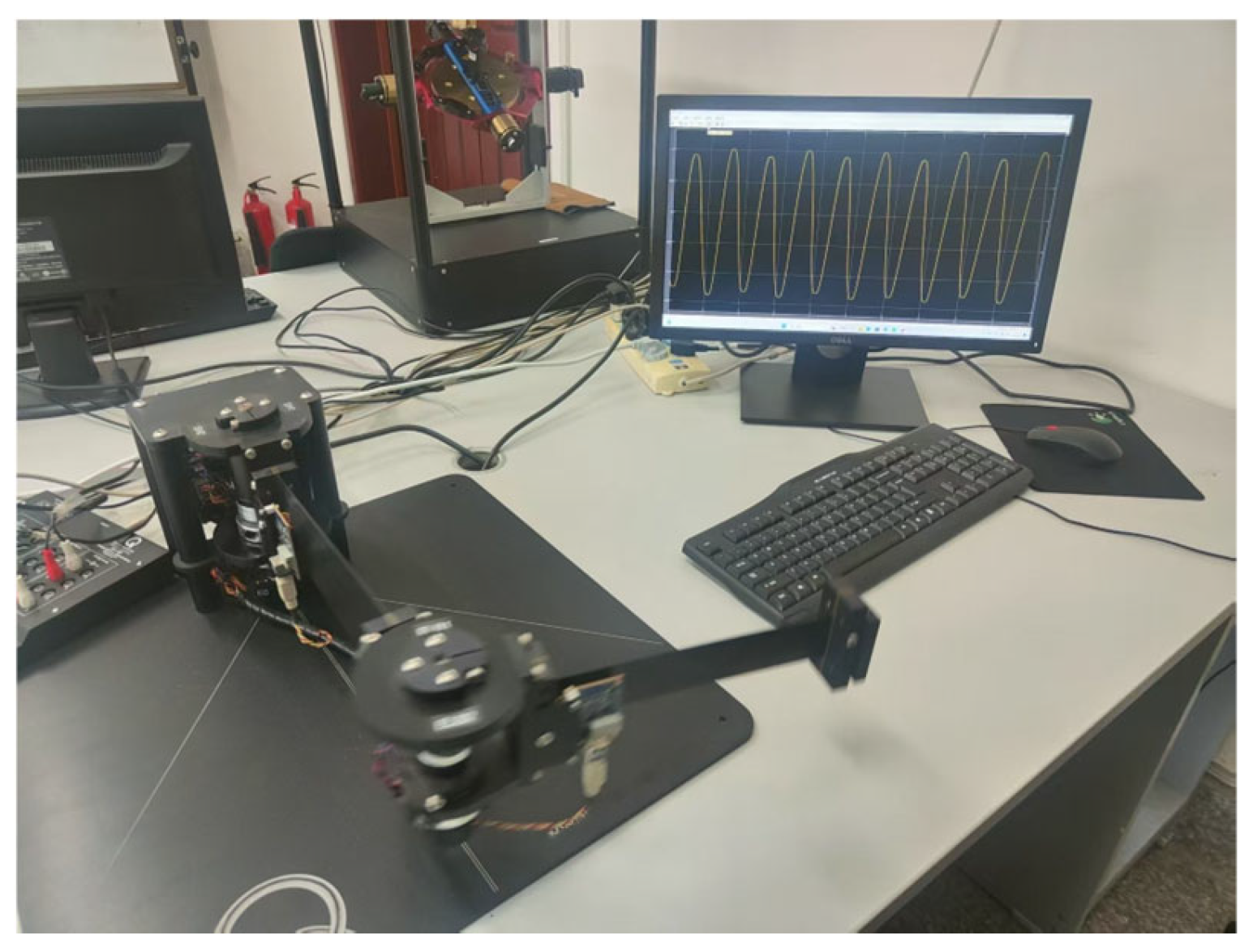

| Symbol Name | Description |
|---|---|
| first-stage servo angle | |
| first-stage oscillation deflection angle | |
| second-stage servo angle | |
| second-stage oscillation deflection angle | |
| input current of the first-stage servo motor | |
| input current of the second-stage servo motor | |
| torque produced by first-stage servo motor | |
| torque produced by second-stage servo motor | |
| viscoelastic potential energy of the first-stage flexible link | |
| kinetic energies of the first-stage servo motor | |
| kinetic energies of the first-stage flexible link | |
| total kinetic energy of the first-stage flexible oscillation deflection subsystem | |
| non-conservative generalized force of the first-stage servo motor | |
| non-conservative generalized force of the first-stage flexible link | |
| -order fractional differential of the first-stage oscillation deflection angle | |
| -order fractional differential of the second-stage servo angle | |
| -order fractional differential of the second-stage oscillation deflection angle | |
| -order fractional differential of the first-stage oscillation deflection angle | |
| -order fractional differential of the second-stage oscillation deflection angle | |
| -order fractional differential of the first-stage oscillation deflection angle | |
| -order fractional differential of the second-stage oscillation deflection angle |
| Algorithm | Identification Algorithm Based on MIOM for FTLM System |
|---|---|
| Step 1 | Collect input, and , and output, , , , and , data. |
| Step 2 | Determine the Haar wavelet matrix dimension, M, and generate the Haar wavelet integral operation matrix. |
| Step 3 | Convert the FTLM system’s fractional-order model into a fractional-order integral equation using Equation (38). |
| Step 4 | Use Equation (39) to expand the input and output data into Haar wavelets. |
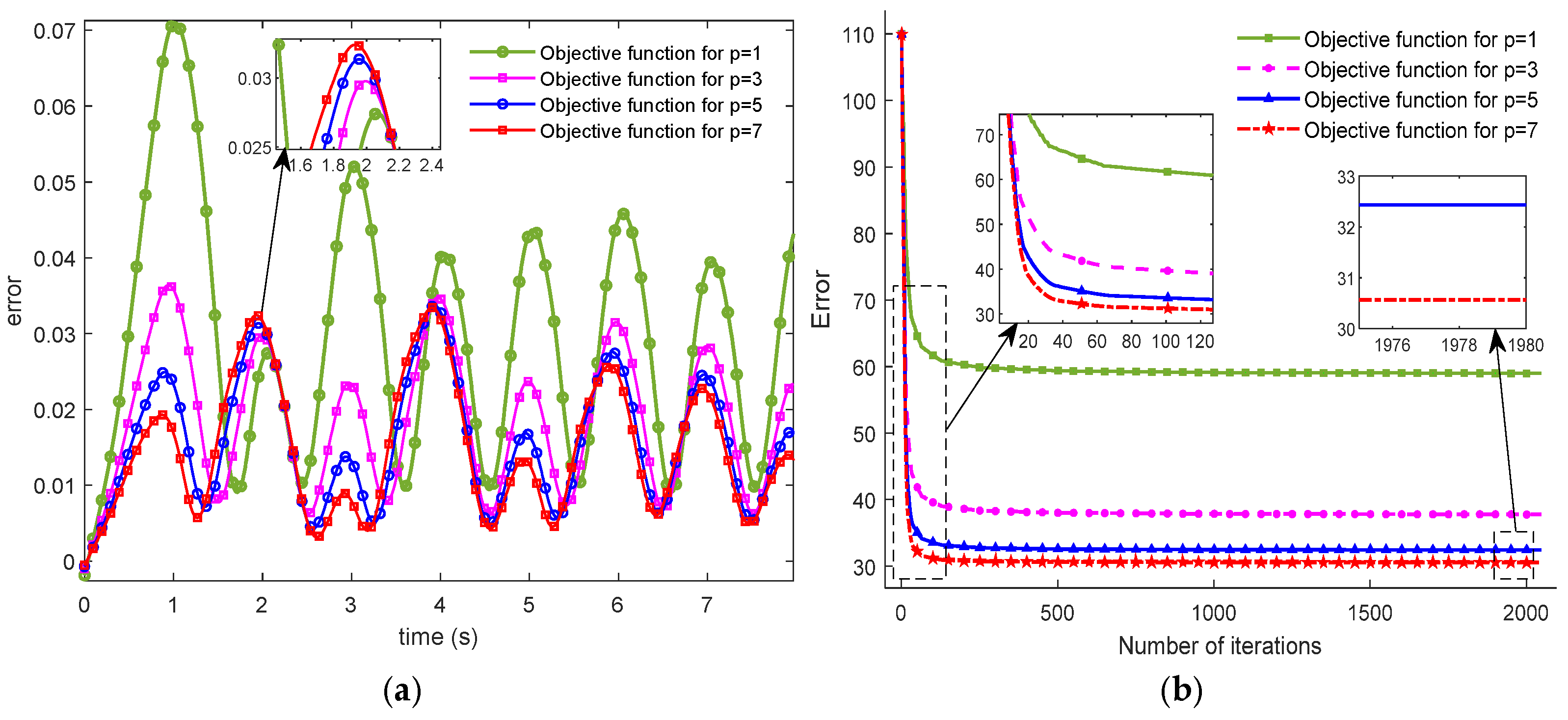
| Step 5 | Determine the system parameters to be identified, including the model parameters, fractional order, and identification interval. Cyclically change the fractional order of the system within the identification interval and use Equation (44) to identify the FTLM model parameter, . |
| Step 6 | Substitute the model parameters and fractional orders into the fractional-order FTLM model (Equation (26)) and then calculate the error between and using Equation (45). |
| Step 7 | Select the fractional order and model parameters corresponding to the minimum error as the optimal solution for the FTLM model. |
| Parameter Name | Description | Value | Unit |
|---|---|---|---|
| length of the first-stage flexible link | 0.3493 | m | |
| length of the second-stage flexible link | 0.2975 | ||
| moment of inertia of the first-stage servo motor | 0.0635 | ||
| moment of inertia of the first-stage flexible link | 0.1704 | ||
| rotational friction coefficient of the first-stage servo motor | 4.0 | ||
| viscous friction coefficient of the first-stage flexible link | 0.421 | ||
| moment of inertia of the second-stage servo motor | 0.003 | ||
| moment of inertia of the second-stage flexible link | 0.0064 | ||
| rotational friction coefficient of the second-stage servo motor | 1.5 | ||
| viscous friction coefficient of the second-stage flexible link | 0.856 | ||
| viscoelastic coefficient of the first-stage flexible link | 2.69 | ||
| viscoelastic coefficient of the second-stage flexible link | 0.463 | ||
| torque constant of the first-stage servo motor | 0.119 | ||
| torque constant of the second-stage servo motor | 0.0234 |
| Parameters and Orders | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Integer-order models [17] | 1 | 2 | - | 1 | 628.89 | −62.956 | - | 140.47 | 640.31 | 0.3829 | 4.2028 |
| FOM with p = 1 | 1.9 | 2 | 1.85 | 1.8 | −0.5002 | 0.0253 | 0.0186 | 0.0345 | 58.973 | 0.0336 | 0.3683 |
| FOM with p = 3 | 1.9 | 2 | 1.85 | 1.8 | −0.7798 | 0.0339 | 0.0214 | 0.0115 | 37.764 | 0.0212 | 0.2323 |
| FOM with p = 5 | 1.9 | 2 | 1.85 | 1.8 | −0.8789 | 0.0321 | 0.0155 | 0.0029 | 32.426 | 0.0186 | 0.2045 |
| FOM with p = 7 | 1.9 | 2 | 1.85 | 1.8 | −0.9302 | 0.0277 | 0.0077 | −0.0015 | 30.561 | 0.0180 | 0.1974 |
| Parameters and Orders | |||||||||||
| Integer-order models [17] | 1 | 2 | - | 1 | −863.33 | 62.956 | - | −140.47 | 23.764 | 0.0205 | 3.4665 |
| FOM with p = 1 | 1.95 | 2 | 1.9 | 1.85 | −0.7308 | 0.0039 | −0.4494 | −0.0016 | 1.5643 | 0.00097 | 0.1653 |
| FOM with p = 3 | 1.95 | 2 | 1.9 | 1.85 | −0.9449 | 0.0016 | −0.2617 | −0.0018 | 1.4834 | 0.00092 | 0.1559 |
| FOM with p = 5 | 1.95 | 2 | 1.9 | 1.85 | −1.1164 | 0.0011 | −0.0825 | −0.0018 | 1.3957 | 0.00087 | 0.1465 |
| FOM with p = 7 | 1.95 | 2 | 1.9 | 1.85 | −1.2655 | 0.0008 | 0.0779 | −0.0017 | 1.3136 | 0.00081 | 0.1378 |
| Parameters and Orders | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Integer-order models [17] | 1 | 2 | - | 1 | 2271.12 | −496.76 | 28.35 | 288.12 | 242.16 | 0.2312 | 1.6330 |
| FOM with p = 1 | 1.9 | 2 | 1.85 | 1.8 | −0.8114 | 0.0108 | 0.0067 | 0.0228 | 81.229 | 0.0447 | 0.3155 |
| FOM with p = 3 | 1.9 | 2 | 1.85 | 1.8 | −1.0049 | 0.0043 | −0.0028 | 0.0395 | 57.369 | 0.0329 | 0.2322 |
| FOM with p = 5 | 1.9 | 2 | 1.85 | 1.8 | −1.0556 | 0.0048 | −0.0146 | 0.0439 | 54.504 | 0.0321 | 0.2267 |
| FOM with p = 7 | 1.9 | 2 | 1.85 | 1.8 | −1.0791 | 0.0144 | −0.0266 | 0.0459 | 53.989 | 0.0320 | 0.2266 |
| Parameters and Orders | |||||||||||
| Integer-order models [17] | 1 | 2 | - | 1 | −3336.18 | 496.76 | −41.65 | −288.12 | 244.79 | 0.1045 | 29.967 |
| FOM with p = 1 | 1.95 | 2 | 1.9 | 1.85 | −0.5149 | 0.0053 | −0.4219 | −0.0006 | 1.1985 | 0.00072 | 0.2051 |
| FOM with p = 3 | 1.95 | 2 | 1.9 | 1.85 | −0.6531 | 0.0026 | −0.4494 | −0.0009 | 1.0105 | 0.00062 | 0.1781 |
| FOM with p = 5 | 1.95 | 2 | 1.9 | 1.85 | −0.7226 | 0.0019 | −0.4173 | 0.0010 | 0.9917 | 0.00061 | 0.1756 |
| FOM with p = 7 | 1.95 | 2 | 1.9 | 1.85 | −0.7787 | 0.0017 | −0.3759 | 0.0010 | 0.9791 | 0.00060 | 0.1737 |
| Identification Results of GA | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1.9299 | 1.9722 | 1.8977 | 1.8655 | −0.2832 | 4.8206 | −4.1504 | 0.0112 | |
| 1.9621 | 1.9722 | 1.9299 | 1.8977 | −0.0159 | 0.0238 | 0.5145 | 0.0172 | |
| 1.9299 | 1.9722 | 1.8977 | 1.8655 | −0.4537 | −9.0544 | 9.5132 | 0.0006 | |
| 1.9621 | 1.9722 | 1.9299 | 1.8977 | −0.0231 | −0.0009 | 0.2365 | 0.0012 |
| Comparison of Performance Indicators | ||||||
|---|---|---|---|---|---|---|
|
Name of Performance Indicators | ||||||
| 70.844 | 30.561 | 0.0401 | 0.0180 | 0.3554 | 0.1974 | |
| 6.8453 | 1.3136 | 0.0042 | 0.0008 | 0.1812 | 0.1378 | |
| 65.306 | 53.989 | 0.0395 | 0.0320 | 0.2270 | 0.2266 | |
| 7.3449 | 0.9791 | 0.0042 | 0.0006 | 0.3058 | 0.1737 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Li, Y.; Li, J.; Liang, S.; Gao, X. Establishment and Identification of Fractional-Order Model for Structurally Symmetric Flexible Two-Link Manipulator System. Symmetry 2025, 17, 1072. https://doi.org/10.3390/sym17071072
Wang Z, Li Y, Li J, Liang S, Gao X. Establishment and Identification of Fractional-Order Model for Structurally Symmetric Flexible Two-Link Manipulator System. Symmetry. 2025; 17(7):1072. https://doi.org/10.3390/sym17071072
Chicago/Turabian StyleWang, Zishuo, Yijia Li, Jing Li, Shuning Liang, and Xingquan Gao. 2025. "Establishment and Identification of Fractional-Order Model for Structurally Symmetric Flexible Two-Link Manipulator System" Symmetry 17, no. 7: 1072. https://doi.org/10.3390/sym17071072
APA StyleWang, Z., Li, Y., Li, J., Liang, S., & Gao, X. (2025). Establishment and Identification of Fractional-Order Model for Structurally Symmetric Flexible Two-Link Manipulator System. Symmetry, 17(7), 1072. https://doi.org/10.3390/sym17071072





