Abstract
The electroosmotic flow (EOF) of non-Newtonian fluids plays a significant role in microfluidic systems. The EOF of Powell–Eyring fluid within a parallel-plate microchannel, under the influence of both electric field and pressure gradient, is investigated. Navier’s boundary condition is adopted. The velocity distribution’s approximate solution is derived via the homotopy perturbation technique (HPM). Optimized initial guesses enable accurate second-order approximations, dramatically lowering computational complexity. The numerical solution is acquired via the modified spectral local linearization method (SLLM), exhibiting both high accuracy and computational efficiency. Visualizations reveal how the pressure gradient/electric field, the electric double layer (EDL) width, and slip length affect velocity. The ratio of pressure gradient to electric field exhibits a nonlinear modulating effect on the velocity. The EDL is a nanoscale charge layer at solid–liquid interfaces. A thinner EDL thickness diminishes the slip flow phenomenon. The shear-thinning characteristics of the Powell–Eyring fluid are particularly pronounced in the central region under high pressure gradients and in the boundary layer region when wall slip is present. These findings establish a theoretical base for the development of microfluidic devices and the improvement of pharmaceutical carrier strategies.
1. Introduction
With the rapid advancement of manufacturing technologies, including Micro-Electro-Mechanical Systems (MEMSs), biological sensors, and chemical sensors, microscale fluid flow control has become a key research area in microfluidics [1,2,3]. To achieve more efficient and stable microflow control, researchers are increasingly investigating fluid flow in nanochannels or microfluidic systems.
Microfluidic technology is predominantly employed in the study of non-Newtonian fluids, including biofluids [4,5,6,7] and polymeric solutions [8,9]. As a result, many academics have redirected their interest towards investigating non-Newtonian fluids. Heydari et al. [10,11,12,13] systematically investigated the ion transport regulation mechanisms in smart nanochannels through multidisciplinary approaches, including bipolar diffuse soft layer modulation, Joule heating suppression via AC/DC field optimization, comparative analysis of electric field configurations, and geometric nanostructure design. This work establishes a comprehensive framework for performance enhancement in nanofluidic systems. Separately, Aminnia et al. [14] demonstrated the mechanistic basis of electric field-assisted antifouling in nanofluidic membranes, culminating in the development of innovative separation technologies. Khatibi et al. [15] investigated ion concentration polarization effects in nanofluidic membranes and developed a novel multi-nanochannel array configuration for enhanced salt rejection. Ashrafizadeh et al. [16] reviewed the Pinch Flow Fractionation method in microfluidic technology from 2004 to 2024, highlighting its widespread application in particle separation and its immense potential for future development. Seifollahi et al. [17,18] enhanced the understanding of ion and fluid transport in confined spaces through improved micro-nanostructure design and interfacial physicochemical regulation. These studies provide the theoretical foundation and design paradigms for next-generation nanofluidic chips.
The unique transport mechanism of electroosmotic flow (EOF) renders it indispensable in microfluidic chips, biosensor development, and microscale chemical analysis systems [19,20,21]. Upon application of an electric field, mobile ions in the electric double layer (EDL) experience Coulomb forces, inducing bulk liquid motion and generating EOF [22]. Understanding the electrokinetic transport phenomena of non-Newtonian fluids in confined micro/nanochannels presents significant challenges in soft matter physics while offering new opportunities for lab-on-a-chip applications.
Prior studies have systematically investigated both analytical and numerical approaches for characterizing EOF velocity profiles of power-law fluids in diverse microchannel geometries, with comprehensive analysis of their non-Newtonian flow behavior [23,24,25]. Other studies have investigated the EOF of Bingham fluids, with particular emphasis on analyzing the effects of viscoelastic properties on velocity profiles [26,27]. Tan et al. [28,29] delved into the EOF of Eyring fluids within parallel microchannels and circular tubes, all while considering slip boundary conditions. They came up with both precise and approximate solutions, meticulously analyzing how different factors impacted the velocity profiles. Extensive studies have examined advanced non-Newtonian fluid models, including Maxwell fluids [30,31], Oldroyd-B fluids [32,33,34], and Burgers fluids [35,36]. In a seminal study, Ali et al. [37] rigorously characterized the electrokinetic transport phenomena of the Walters-B fluid, deriving closed-form analytical solutions for both velocity profiles and thermal distributions. Khan et al. [38] made significant contributions by formulating a groundbreaking analytical framework to address entropy generation in electroosmosis-assisted peristaltic transport of Williamson fluids through curvilinear microconduits. Bhattacharyya and Bag [39] investigated the EOF of the Herschel–Bulkley fluid in a parallel-plate microchannel. They focused on how the fluid’s motion interacts with the channel walls, which have a unique structure featuring slippery, uncharged patches alternating with charged areas where the fluid exhibits strong adhesion and resists slipping. To delve into the mathematical complexities, they employed a control volume method, enhancing it with a pressure correction technique to derive the necessary solutions.
The intricate and highly variable rheological properties of non-Newtonian fluids cannot be sufficiently described by a straightforward shear stress–shear rate relationship. As a result, numerous studies have adopted various constitutive models to describe their distinct rheological behaviors. Based on liquid kinetic theory, the Powell–Eyring model establishes a robust constitutive relationship that effectively captures shear-thinning and shear-thickening phenomena throughout all shear rate regimes [40,41]. Compared with other fluid models, the Powell–Eyring formulation demonstrates several distinct advantages:
- At low shear rates, it exhibits Newtonian characteristics; at high shear rates, its apparent viscosity diminishes in a manner akin to power-law fluids [41]. The hyperbolic sine function enables a natural transition of shear behavior without requiring piecewise modeling.
- Based on Eyring’s molecular activation energy theory, it treats flow as a transition process where molecules overcome energy barriers. This provides clear physical interpretation and makes it suitable for mechanistic studies (e.g., polymer chain dynamics).
- It simultaneously incorporates Newtonian viscosity, shear-thinning, and viscoelasticity, allowing comprehensive description of flow behavior.
- Without yield stress limitations, it applies to continuously varying flow behaviors such as those of biological fluids or polymer solutions.
Owing to these characteristics, the Powell–Eyring fluid model finds extensive applications in geophysics, industrial processes, and natural phenomena, including but not limited to thermal insulation optimization, environmental pollution control, drying processes of porous materials, and subsurface energy transport. Consequently, this model has attracted considerable attention from researchers worldwide.
Substantial progress has been made in understanding Powell–Eyring fluids in recent years. Goswami et al. [41,42] analyzed Powell–Eyring fluid flow within microchannels, and their findings revealed substantial interaction between rheology and boundary conditions. The coupled magneto-rheological behavior of Powell–Eyring fluids has attracted growing research interest. Hayat et al. [43] established a three-dimensional magnetohydrodynamic (MHD) model with radiation effects, deriving an exact analytical solution. Bhatti et al. [44] extended this framework by including nonlinear thermal radiation to analyze entropy generation in flow through permeable surfaces. Experimental validation by Hayat et al. [45] demonstrated that Newtonian heating enhances thermal boundary layer development in inclined magnetic fields. In nanofluid heat transfer, Jamshed et al. [46,47] demonstrated that the thermal performance of Powell–Eyring fluids is markedly improved by nanoparticle doping. Considering the geometric configuration, Nazeer et al. [48] conducted an analytical investigation of MHD flow of variable-viscosity Eyring–Powell fluids in circular tubes, using the Reynolds–Vogel model. In their comprehensive research, Krishna et al. [49] explored the complex interplay of heat and mass distribution within a Powell–Eyring fluid as it flowed erratically across a sloping, elongated surface. The study factored in the impact of radiation, varying heating and cooling agents, and chemical exchanges, all while considering the effects of suction and injection mechanisms. To tackle the problem computationally, they utilized a Runge–Kutta shooting method. Halim et al. [50] conducted an investigation into the mixed convection dynamics of Powell–Eyring nanofluid adjacent to the stagnation point along a vertically stretched surface.
The inherent mathematical complexity of the Powell–Eyring fluid model poses significant challenges in obtaining closed-form analytical solutions. As a result, the homotopy perturbation method (HPM) has been predominantly employed in existing studies to obtain approximate solutions [41,42], with subsequent validation through numerical simulations. Among the most widely implemented numerical techniques are the shooting method [41,42] and finite element analysis [47,51]. Ongoing developments in computational methodologies have facilitated the continuous refinement of numerical algorithms to enhance both accuracy and computational efficiency for complex non-Newtonian fluid systems. Liu et al. [52] implemented an innovative hybrid approach combining spectral collocation methods with accelerated computational algorithms to resolve MHD transport phenomena in fractional Oldroyd-B fluids confined between parallel plates. Bai et al. [53] made seminal contributions by introducing a novel finite difference–spectral hybrid method for analyzing unsteady stagnation point flow characteristics in fractional Burgers fluids over stretching surfaces. In recent years, the spectral local linearization method (SLLM) has garnered increasing attention from researchers. The SLLM is a numerical approach integrating spectral techniques with local linearization, designed to solve nonlinear differential equations. Developed by Motsa, this method demonstrates advantages such as straightforward implementation, computational efficiency, robust stability, and exceptional precision [54]. Shateyi and Marewo [55] utilized the SLLM to delve into how the Hall effect affects MHD flow and heat transfer dynamics. They examined the behavior of a fluctuating, stretching porous boundary under the influence of thermal radiation, as well as the presence of a heat source or sink. Ghulam and Abderrahim [56] developed a flow model for second-grade nanofluid adjacent to a vertical Riga plate, incorporating Lorentz forces, the Cattaneo–Christov heat conduction model, and thermal boundary conditions, with the solution obtained through the SLLM.
Although extensive research exists on Powell–Eyring fluids, studies investigating their electroosmotic flow behavior under combined electrohydrodynamic conditions remain remarkably limited, particularly regarding comprehensive parametric interaction analyses. To bridge this knowledge gap, we systematically examine Powell–Eyring fluid dynamics in parallel microchannels subjected to coupled electric field- and pressure-driven flows, incorporating Navier slip boundary conditions. Our methodology combines the HPM for approximate analytical solutions with a modified SLLM for numerical velocity profile determination, with rigorous validation of the enhanced SLLM’s superior performance. Through multidimensional parameter space analysis, we quantitatively evaluate individual and synergistic parameter influences on velocity distributions, with particular emphasis on comparative electrokinetic- versus pressure-driven flow contributions. These findings significantly advance the fundamental understanding of complex non-Newtonian fluid rheology while providing practical design guidelines for microfluidic chip architectures, precision drug delivery systems, and targeted therapeutic applications.
2. Governing Equations
The EOF of Powell–Eyring fluid within a parallel microchannel is presented. A Cartesian coordinate framework is set up parallel to the pipe’s central axis. The two plates are positioned at and , respectively, separated by a distance of . Moreover, the assumed electric field is , with the pressure gradient remaining a fixed constant. Geometrical symmetry dictates that solely the channel’s upper segment is taken into account, i.e., the region . Figure 1 depicts the problem’s schematic. Table 1 outlines the variables and parameters applied in the current investigation.
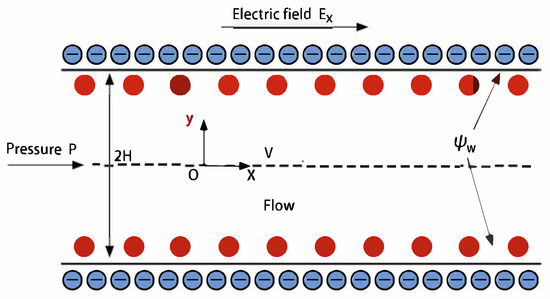
Figure 1.
Diagram of flow in a micro-parallel pipe.

Table 1.
Nomenclature.
2.1. Assumptions
The following assumptions are in place:
- The fluid is assumed to be incompressible.
- The flow is considered fully developed, resulting in time-independent velocity profiles.
- Gravitational effects on the EOF are negligible.
- The zeta potential exhibits a consistent distribution along the channel’s surface.
- The parallel-plate microchannel configuration is assumed to be homogeneous and symmetric.
- The applied external electric field strength remains within a range that justifies neglecting Joule heating effects.
2.2. Governing Equation
Under the above conditions, the continuity equation is
Assuming the velocity field takes the form , the continuity equation is automatically satisfied.
The gravity of the fluid is neglected. The fluid satisfies the modified Cauchy momentum equation:
where is the shear stress, represents the EDL’s spatial charge concentration along the channel boundary, represents the intensity of the external electric field, is the electric field force density, and represents the pressure.
The shear stress of Powell–Eyring fluid [40] satisfies the following equation:
where and denote the fluid’s material parameters. When , Equation (3) can be approximated as [41]
By incorporating Equation (4) into Equation (2), the resulting expression is derived:
The boundary condition of Equation (5) is described by the linear Navier’s relation [57] as follows:
The condition of symmetry along the channel’s midline is expressed as
2.3. Electric Potential
In accordance with electrostatic laws, the potential fulfills Poisson’s equation
where stands for EDL potential, and represents the fluid’s dielectric constant. The distribution of electrostatic charge density equals the aggregate of all ions present in the solution, i.e., . Here, is the volumetric concentration of ions in the fluid, is the elementary electronic charge, is the valence of the ions, is the Boltzmann constant, and is the absolute temperature.
Applying the Debye–Hückel linearization, ionic potential energy is considered minimal compared to thermal energy, i.e., , which gives . The potential distribution then satisfies the following linear Poisson–Boltzmann equation:
where is called the Debye–Hückel parameter, and represents the EDL thickness, which is called the Debye length.
Equation (9) satisfies the following boundary conditions:
2.4. Dimensionless Processing
The subsequent nondimensionalized quantities are utilized to render the aforementioned equations dimensionless:
where denotes the ratio of the pressure gradient to the electric field, the Reynolds number denotes the ratio of the inertial force to the viscous force, and are the material parameters of the Powell–Eyring fluid, and denotes the ratio of the viscosity of the Powell–Eyring fluid to that of a Newtonian fluid.
Omitting the ‘-’ mark for dimensionless variables, Equations (9) and (10) can be written as
Here, is called the dimensionless electric width.
Solving Equations (12) and (13), the potential distribution is obtained as
To nondimensionalize Equations (5)–(7), the following equations are obtained:
where , , , and . By substituting Equation (14) into Equation (15), the dimensionless equation of velocity can be obtained, which is strongly nonlinear.
3. Approximate and Numerical Solutions
3.1. Approximate Solution
The HPM is a numerical technique that combines homotopy theory with perturbation theory, primarily used for solving nonlinear equations [58]. This method introduces an embedding parameter , constructing a parameterized equation such that the solution can be expressed as a power series in terms of the parameter . As the parameter varies from 0 to 1, the equation transitions gradually from an initial simple form to the target nonlinear equation, thereby solving the original problem. Its calculation process is simple and has high accuracy, so it is widely used to solve various types of integer- and fractional-order nonlinear differential equations and integral equations.
We examine a nonlinear differential equation, presented as follows:
In this model, denotes the linear component, signifies the nonlinear component, and is a given function or constant.
A small, artificial parameter is introduced. Consequently, the perturbation equation takes the following form:
The estimated solution for Equation (19) is posited to be presented in the given form
By inserting Equation (20) into Equation (19) and matching the powers of on both sides, the solutions , , , , are derived.
As , Equation (19) corresponds to Equation (18), with Equation (20) being the corresponding solution.
An approximate solution for Equations (15)–(17) is derived by using the HPM. The perturbation equation is constructed as
It is assumed that the solution to Equation (21) has the same form as Equation (20). Therefore, the exact solution of Equation (15) is given by:
Take the first two terms, i.e., , and bring them into Equation (21). Compare the powers of parameter
By incorporating the boundary conditions Equations (16) and (17), the solutions can be obtained as follows:
Thus, the approximate solution of Equations (15)–(17) is
A comparison with Reference [41] reveals that this approximate solution achieves high accuracy with only the first two terms retained, while maintaining a concise form. This demonstrates that the selected initial guess solution exhibits superior accuracy and closer proximity to the true solution. Consequently, it significantly improves the convergence of the HPM, reduces the required number of iterations, and enhances computational efficiency.
3.2. Numerical Solution
We now briefly introduce the SLLM [54]. The nonlinear system of equations is presented below:
Here, represents the unknown functions.
The nonlinear terms are linearized as follows:
Thus, at the current iteration with , Equation (28) becomes
where and denote the current and prior iteration’s approximations of , respectively.
After the above processing, the equation in matrix form can be obtained as follows:
By incorporating a convergence control parameter , the SLLM can be adjusted to enhance its convergence efficiency [54]. Then the modified SLLM is defined as
Evidently, when the convergence parameter , it degenerates into the SLLM. By selecting an appropriate , the efficiency and accuracy of the iteration can be significantly enhanced.
Subsequently, the Chebyshev pseudospectral collocation technique is utilized to tackle the iterative process outlined in Equation (32).
To assess the accuracy of the approximate solution, the modified SLLM is utilized to derive the numerical velocity profile for the Powell–Eyring fluid. First, a coordinate transformation is performed on Equations (15)–(17), changing the range of from to . Let ; the following is obtained:
Let ; the following nonlinear differential equations can be obtained:
Let the nonlinear term be
Substituting Equation (35) into Equation (34), the following is obtained:
This can be represented in matrix form as
where is the Chebyshev differential matrix [54], denotes the configuration point on , and
Using the modified SLLM, Equation (37) is corrected as follows:
A suitable initial guess is paramount for effectively solving nonlinear problems. An appropriate starting point significantly facilitates the iterative process. Typically, the initial guess should satisfy the boundary conditions of the problem. In this study, we have refined the initial guess from a simple to a more informed , which better aligns with the problem’s characteristics. MATLAB (https://www.mathworks.com) plots demonstrate that this refined initial guess enhances the stability of the numerical solution. Newton’s iterative method is used to solve Equation (39), and finally the numerical solution to the equation can be obtained.
4. Results and Discussion
The correctness of both the approximate and numerical solutions is confirmed through a comparison with the findings in Reference [41]. Throughout this analysis, we maintained fixed parameter values [29,33,41]: , , , and . Unless explicitly stated otherwise, all subsequent parameter values used in this study corresponded to and . With the convergence parameter , the velocity is numerically solved using the modified SLLM. Figure 2 demonstrates a high degree of concordance between the approximate and numerical solutions and the outcomes presented in Reference [41]. This strong alignment serves as compelling evidence of the robustness and reliability of our approaches. When applying the HPM, the improved initial solution enables achieving desirable approximation accuracy by retaining only second-order expansion terms. In contrast to the more complex formulations requiring third-order or higher expansions in the existing literature (e.g., Equations (26), (29), and (32) in Reference [41]), the concise analytical expressions proposed in this study (Equations (25) and (26)) significantly reduce computational complexity while maintaining equivalent solution accuracy. Therefore, when employing the HPM to solve nonlinear differential equations, the selection of an optimal initial solution is of paramount importance.
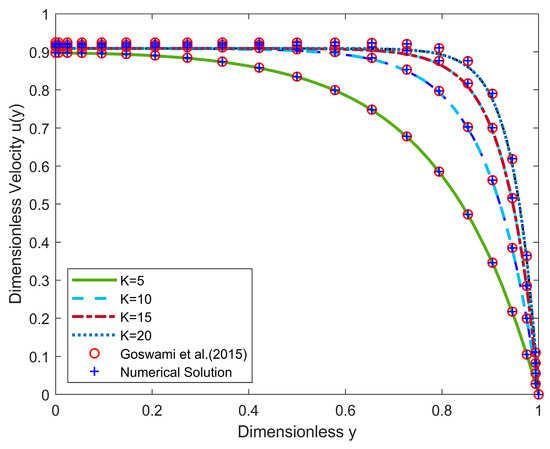
Figure 2.
Comparison between numerical solution, approximate solution, and the approximate solution of Goswami et al. (2015) [41].
To validate the superiority of the modified SLLM, we compare it with the SLLM, the finite difference method (FDM), and the finite element method (FEM). With the parameters and fixed, we compare the number of iterations and residuals of the four numerical methods when the parameter and , and the results are shown in Table 2. When , the SLLM requires the highest number of iterations (26), while the modified SLLM and the FDM both require 6 iterations, and the FEM necessitates only 4 iterations. However, under these conditions, the modified SLLM demonstrates the smallest residual (). When , the SLLM still requires a higher number of iterations (20), whereas the modified SLLM needs 4 iterations, and both the FDM and the FEM require only 2 iterations. Similarly, under these circumstances, the modified SLLM maintains the smallest residual (). In summary, the modified SLLM exhibits the smallest residuals under both tested parameter values ( and ), corroborating its superiority in terms of solution accuracy. Although the modified SLLM is not optimal in terms of iteration count, the difference compared to the optimal number of iterations is marginal. Overall, considering the optimal combination of number of iterations and accuracy, the modified SLLM presents a distinct advantage.

Table 2.
Comparison of different numerical methods.
A comparative analysis of the computational efficiency and accuracy between the HPM and the modified SLLM is presented in Table 3. With parameters set as , , , , and , , , , the results obtained from both the HPM and the modified SLLM are benchmarked against Reference [41], with residual errors, root mean square errors (RMSEs), and computational time being evaluated. The results demonstrate that the modified SLLM yields smaller residual errors and shows better agreement with the findings of Reference [41], indicating superior accuracy. In contrast, while the HPM exhibits lower accuracy, its computational time is significantly shorter, rendering it more efficient in terms of computational performance.

Table 3.
Comparison of modified SLLM () with HPM.
Based on the above analysis, the modified SLLM demonstrates high efficiency and accuracy. Therefore, in the subsequent analysis, the modified SLLM is employed to investigate the influence of various parameters on velocity distribution.
Figure 3 demonstrates the dependence of the velocity distribution on the pressure gradient-to-electric field ratio . When , the image of velocity change is given in Figure 3a. When , the image of velocity change is shown in Figure 3b. Observation reveals that when , i.e., the pressure gradient satisfies , the flow is exclusively influenced by the electric field force. At this point, except for the boundaries, the flow velocity is similarly linearly distributed. When is small, electroosmosis plays a dominant role, and the nonlinear effects are mainly manifested within the EDL, having a smaller impact on the overall velocity distribution. Figure 3a demonstrates considerable EDL thickness and substantial velocity distribution alteration due to the EDL’s impact. At this point, the velocity profile is parabolic in shape. In Figure 3b, it is evident that the thickness of the EDL is small, and the velocity is less influenced by the EDL. As increases, i.e., the pressure gradient increases, the Powell–Eyring fluid’s shear-thinning effect becomes more pronounced in the central region. The shear rate increases, viscosity decreases, flow resistance decreases, fluid fluidity enhances, and the top of the velocity profile becomes flatter (similar to “plug flow”).
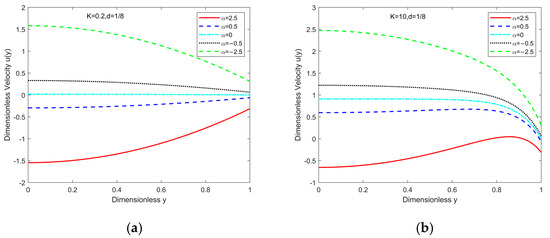
Figure 3.
(a): Dimensionless velocity distribution with different for ; (b): dimensionless velocity distribution with different for .
The influence of the electrokinetic width on the velocity profile under various parameter combinations is investigated, as shown in Figure 4. When , , , , nondimensional velocity plots are shown in Figure 4a,c. When is small, the EDL exhibits a larger thickness, indicating a stronger influence of the EDL on theflow. Under these conditions, although a pressure gradient is present, the electrokinetic force dominates the flow dynamics, resulting in a parabolic velocity profile. The velocity increases sharply near the channel walls before plateauing, suggesting that the fluid experiences significant resistance in the near-wall region while flowing more freely in the bulk region. Conversely, when , , , , Figure 4b,d depict the nondimensional velocity distributions. At elevated , the reduced EDL thickness diminishes its hydrodynamic influence, resulting in greater predominance of pressure-driven flow. In this regime, pressure-driven effects become more pronounced. Notably, as increases, the velocity profile progressively approaches a plug-like shape, with a relatively uniform distribution across the channel except in the near-wall region. At the boundaries, the higher shear rate reduces the local viscosity, diminishing wall resistance and leading to a sharp velocity increase.
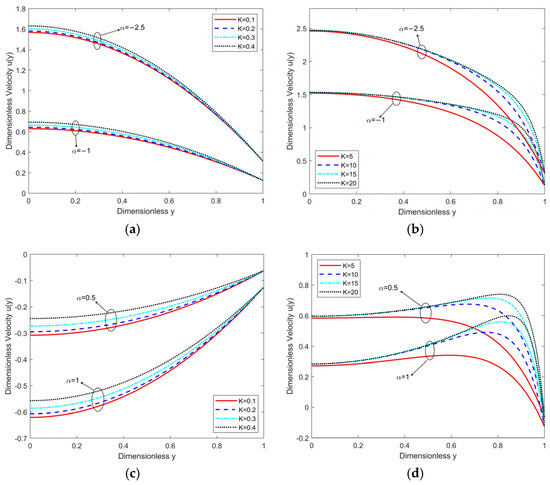
Figure 4.
(a): Dimensionless velocity distribution with , , , , for and ; (b): dimensionless velocity distribution with , , , for and ; (c): dimensionless velocity distribution with , , , for and ; (d): dimensionless velocity distribution with , , , for and .
Figure 5 highlights how the slip length affects the velocity for , , , . Under the condition of and , , the velocity trends are shown in Figure 5a. Additionally, the velocity trends for scenarios , and , are illustrated in Figure 5b. These images reveal that the velocity displays a high degree of self-similarity across various parameters. When other parameters remain constant, the velocity increases in proportion to the slip length . This occurs because the slip at the channel boundary introduces additional shear forces into the flow, which then propagate through adjacent fluid layers, ultimately enhancing the velocity. In Figure 5a, it is observed that for a constant , a smaller corresponds to a lower velocity, indicating a thicker EDL and consequently a weaker driving force for the EOF, reducing the flow’s sensitivity to boundary slip. In Figure 5b, when (electroosmosis-dominated regime), wall slip primarily affects near- wall flow dynamics. This weakens the restraining effect of the EDL on fluid motion, resulting in a more pronounced “plug-like” velocity profile. Conversely, when (pressure-gradient-dominated regime), wall slip induces significant modifications to the global velocity distribution. Here, shear-thinning effects amplify the influence of slip, leading to enhanced centerline velocity and a more symmetric parabolic profile. When an external pressure gradient is present, it interacts with the EOF. The pressure gradient alters the overall velocity profile, prominently affecting the region close to the wall. This modification affects the distribution and thickness of the EDL, thereby modulating the EOF intensity. Specifically, the pressure gradient can weaken the restrictive effect of the EDL on fluid motion, making the near-wall slip more pronounced.
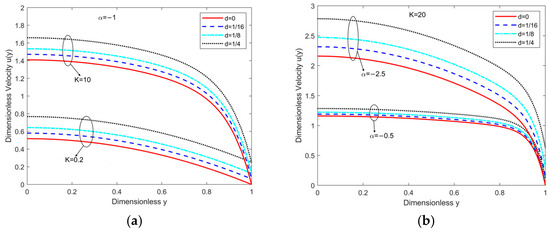
Figure 5.
(a): Dimensionless velocity distribution with different for and when , ; (b): dimensionless velocity distribution with different for and when , .
5. Conclusions
This study investigates the electrohydrodynamic (EOF) characteristics of Powell–Eyring fluids within a parallel-plate microchannel subjected to simultaneous electric field and pressure gradient actuation. Within the slip boundary framework of Navier, both approximate analytical and numeric methods are employed to illustrate the velocity profile for the Powell–Eyring fluid. An extensive study has meticulously explored the interplay between the pressure gradient and the electric field, the thickness of the EDL, and the magnitude of the slip length, all of which significantly influence the velocity distribution. Several key findings emerge from this analysis.
- (1)
- The modified SLLM demonstrates significant superiority in terms of both the number of iterations and accuracy.
- (2)
- The pressure gradient-to-electric field ratio exhibits a nonlinear modulating effect on the EOF velocity.
- (3)
- A thicker EDL significantly constrains flow development, maintaining a parabolic velocity distribution. Conversely, a thinner EDL allows pressure-driven effects to dominate, leading to a velocity profile that approaches the ideal “plug flow” shape.
- (4)
- The shear-thinning characteristics of the Powell–Eyring fluid are particularly pronounced in the central region under high pressure gradients and in the boundary layer region when wall slip is present.
Funding
This research was funded by the Dongying Natural Science Foundation Project (No. 2023ZR041).
Data Availability Statement
All data generated or analyzed during this study are included in this published article.
Acknowledgments
The author is grateful to her advisor, Tian, for his guidance and assistance.
Conflicts of Interest
The author declares no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the readability of Table 1. This change does not affect the scientific content of the article.
Abbreviations
The following abbreviations are used in this manuscript:
| HPM | Homotopy perturbation method |
| SLLM | Spectral local linearization method |
| EOF | Electroosmotic flow |
| EDL | Electric double layer |
| MEMSs | Micro-Electro-Mechanical Systems |
| MHD | Magnetohydrodynamic |
| RMSEs | Root mean square errors |
References
- Li, Z.; Zhang, B.; Dang, D.; Yang, X.; Yang, W.; Liang, W. A review of microfluidic-based mixing methods. Sens. Actuators A-Phys. 2022, 344, 113757. [Google Scholar] [CrossRef]
- Heydari, A.; Khatibi, M.; Ashrafizadeh, S.N. Fine-tuning ionic transport through hybrid soft nanochannels: The role of polyelectrolyte charge density distribution. Phys. Fluids 2023, 35, 082006. [Google Scholar] [CrossRef]
- Karimzadeh, M.; Khatibi, M.; Ashrafizadeh, S.N. Boost ionic selectivity by coating bullet-shaped nanochannels with dense polyelectrolyte brushes. Phys. Fluids 2022, 34, 122008. [Google Scholar] [CrossRef]
- Ponalagusamy, R. Particulate suspension Jeffrey fluid flow in a stenosed artery with a particle-free plasma layer near the wall. Korea Aust. Rheol. J. 2016, 28, 217–227. [Google Scholar] [CrossRef]
- Ramakrishna, M.; Ponalagusamy, R. Modeling of pulsatile EMHD flow of au-blood in an inclined porous tapered atherosclerotic vessel under periodic body acceleration. Arch. Appl. Mech. 2021, 91, 3421–3447. [Google Scholar] [CrossRef]
- Ponalagusamy, R. Electro-rheological flow of seminal fluid (K-L MODEL) induced by movement of cilia in a circular conduit. Proc. Inst. Mech. Eng. E J. Process Mech. Eng. 2023, 1–18. [Google Scholar] [CrossRef]
- Ponalagusamy, R.; Murugan, D. Effect of electro-magneto-hemodynamic environs on dispersion of solute in the peristaltic motion through a channel with chemical reaction, wall properties and porous medium. Korea Aust. Rheol. J. 2022, 34, 69–90. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, W.; Liu, Y.; Yu, X.; Chen, Z. Polydopamine-functionalized Poly(ether Ether Ketone) tube for capillary electrophoresis-eass spectrometry. Anal. Chim. Acta 2017, 987, 64–71. [Google Scholar] [CrossRef]
- Roshanak, S.; Reinhard, I.B.; Basil, D.; Yuanzhong, Y.; Kei, S.; Milton, T.W.H. Application of pH-Responsive Poly(2-Dimethyl-aminoethylmethacrylate)-block-poly(acrylic Acid) coatings for the open-tubular capillary electrochromatographic analysis of acidic and basic compounds. Anal. Chim. Acta 2016, 917, 117–125. [Google Scholar] [CrossRef]
- Heydari, A.; Khatibi, M.; Ashrafizadeh, S.N. Manipulation of ionic transport behavior in smart nanochannels by diffuse bipolar soft layer. Phys. Fluids 2024, 36, 112026. [Google Scholar] [CrossRef]
- Khatibi, M.; Ashrafizadeh, S.N. Mitigating Joule heating in smart nanochannels: Evaluating the efficacy of AC vs. DC fields. Int. Commun. Heat Mass Transf. 2024, 154, 107448. [Google Scholar] [CrossRef]
- Khatibi, M.; Ashrafizadeh, S.N. Ion transport in intelligent nanochannels: A comparative analysis of the role of electric field. Anal. Chem. 2023, 95, 18188–18198. [Google Scholar] [CrossRef] [PubMed]
- Heydari, A.; Khatibi, M.; Ashrafizadeh, S.N. Smart nanochannels: Tailoring ion transport properties through variation in nanochannel geometry. Phys. Chem. Chem. Phys. 2023, 25, 26716. [Google Scholar] [CrossRef]
- Aminnia, A.; Khatibi, M.; Ashrafizadeh, S.N. Fouling minimization with nanofluidic membranes; How electric field may help. Sep. Purif. Technol. 2023, 325, 124698. [Google Scholar] [CrossRef]
- Khatibi, M.; Aminnia, A.; Ashrafizadeh, S.N. The role of ionic concentration polarization on the behavior of nanofluidic membranes. Chem. Eng. Process.-Process Intensif. 2024, 202, 109849. [Google Scholar] [CrossRef]
- Ashrafizadeh, S.N.; Zare, M.; Khatibi, M. A comprehensive review of pinch flow fractionation in microfluidics: From principles to practical applications. Chem. Eng. Process.-Process Intensif. 2025, 208, 110087. [Google Scholar] [CrossRef]
- Seifollahi, Z.; Khatibi, M.; Ashrafizadeh, S.N. Ionic transport behavior of soft nanochannels for Newtonian and Non-Newtonian electrolytes. Ind. Eng. Chem. Res. 2024, 63, 10812–10824. [Google Scholar] [CrossRef]
- Khatibi, M.; Mojavezi, A.; Pourjafarabadi, E. Harvesting blue energy: pH-regulated nanochannels inspired by carbon nanostructures. Phys. Fluids 2023, 35, 102017. [Google Scholar] [CrossRef]
- Yu, X.R.; Cui, J.F.; Chen, X.G.; Mu, J.Y.; Qiao, Y.R. Time period electroosmotic flow of a class of incompressible micropolar fluid in parallel plate microchannels under high Zeta potential. Acta Phys. Sin. 2024, 73, 164701. [Google Scholar] [CrossRef]
- Wang, Y.N.; Fu, L.M. Micropumps and biomedical applications-A review. Microelectron. Eng. 2018, 195, 121–138. [Google Scholar] [CrossRef]
- Yang, R.J.; Hou, H.H.; Wang, Y.N.; Fu, L.M. Micro-magnetofluidics in microfluidic systems: A review. Sens. Actuators B-Chem. 2016, 224, 1–15. [Google Scholar] [CrossRef]
- Polevoi, V.V.; Bilova, T.E.; Shevtsov, Y.I. Electroosmotic phenomena in plant tissues. Biol. Bull. 2003, 30, 133–139. [Google Scholar] [CrossRef]
- Ng, C.O.; Qi, C. Electroosmotic flow of a Power-Law fluid in a non-uniform microchannel. J. Non-Newton. Fluid Mech. 2014, 208, 118–125. [Google Scholar] [CrossRef]
- Ellahi, R.; Sait, S.M.; Shehzad, N.; Mobin, N. Numerical simulation and mathematical modeling of Electro-osmotic couette–poiseuille flow of MHD Power-Law nanofluid with entropy generation. Symmetry 2019, 11, 1038. [Google Scholar] [CrossRef]
- Halifi, A.S.; Shafie, S.; Amin, N.S.S. Numerical solution of biomagnetic Power-Law fluid flow and heat transfer in a channel. Symmetry 2020, 12, 1959. [Google Scholar] [CrossRef]
- Tanveer, A.; Khan, M.; Salahuddin, T.; Malik, M. Numerical simulation of electroosmosis regulated peristaltic transport of Bingham nanofluid. Comput. Methods Programs Biomed. 2019, 180, 105005. [Google Scholar] [CrossRef]
- Hosham, H.A.; Thabet, E.N.; Abd-Alla, A.M.; El-Kabeir, S.M.M. Dynamic patterns of electroosmosis peristaltic flow of a Bingham fluid model in a complex wavy microchannel. Sci. Rep. 2023, 13, 8686. [Google Scholar] [CrossRef]
- Tan, Z.; Liu, J. Electro-osmotic flow of Eyring fluids in a circular microtube with Navier’s slip boundary condition. Phys. Lett. A 2017, 381, 2573–2577. [Google Scholar] [CrossRef]
- Jiang, Y.T.; Qi, H.T. Electroosmotic slip flow of Eyring fluid in a slit microchannel. Acta Phys. Sin. 2015, 64, 174702. [Google Scholar] [CrossRef]
- Wang, X.P.; Qiao, Y.L.; Qi, H.T.; Xu, H.Y. Effect of magnetic field on electroosmotic flow of viscoelastic fluids in a microchannel. Electrophoresis 2021, 42, 2347–2355. [Google Scholar] [CrossRef]
- Yang, X.; Xiao, Y.; Wang, S.W.; Zhao, M.L. Electroosmotic flow of fractional Maxwell fluid in a microchannel of isosceles right-triangular cross-section. Mech. Time-Dependent Mater. 2022, 28, 449–468. [Google Scholar] [CrossRef]
- Jiang, Y.T.; Qi, H.T.; Xu, H.Y.; Jiang, X.Y. Transient electroosmotic slip flow of fractional Oldroyd-B fluids. Microfluid. Nanofluidics 2017, 21, 7. [Google Scholar] [CrossRef]
- Wang, X.P.; Xu, H.Y.; Qi, H.T. Transient magnetohydrodynamic flow and heat transfer of fractional Oldroyd-B fluids in a microchannel with slip boundary condition. Phys. Fluids 2020, 32, 103104. [Google Scholar] [CrossRef]
- Peng, L.; Zhang, Z.H.; Tang, L.; Hao, Y.; Li, J. Electrokinetic ion transport of viscoelastic fluids in a pH-regulated nanochannel. Surf. Interfaces 2024, 46, 103957. [Google Scholar] [CrossRef]
- Hayat, T.; Afzal, S.; Hendi, A. Exact solutions of electroosmotic flow in generalized Burgers fluid. Appl. Math. Mech.-Engl. 2011, 32, 1119–1126. [Google Scholar] [CrossRef]
- Abdulhameed, M.; Adamu, G.T.; Dauda, G.Y. Modeling electro-osmotic flow and thermal transport of Caputo fractional Burgers fluid through a micro-channel. Proc. Inst. Mech. Eng. E J. Process Mech. Eng. 2021, 235, 2254–2270. [Google Scholar] [CrossRef]
- Ali, F.; Iftikhar, M.; Khan, I.; Sheikh, N.A.; Nisar, K.S. Time fractional analysis of electro-osmotic flow of Walters’s-B fluid with time-dependent temperature and concentration. Alex Eng. J. 2020, 59, 25–38. [Google Scholar] [CrossRef]
- Khan, A.A.; Zahra, B.; Ellahi, R.; Sait, S.M. Analytical solutions of peristalsis flow of non-Newtonian Williamson fluid in a curved micro-channel under the effects of electro-osmotic and entropy generation. Symmetry 2023, 15, 889. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Bag, N. Enhanced electroosmotic flow of Herschel-Bulkley fluid in a channel patterned with periodically arranged slipping surfaces. Phys. Fluids 2019, 31, 072007. [Google Scholar] [CrossRef]
- Powell, R.E.; Eyring, H. Mechanism for the relaxation theory of viscosity. Nature 1944, 154, 427–428. [Google Scholar] [CrossRef]
- Goswami, P.; Mondal, P.K.; Dutta, S.; Chakraborty, S. Electroosmosis of Powell-Eyring fluids under interfacial slip. Electrophoresis 2015, 36, 703–711. [Google Scholar] [CrossRef] [PubMed]
- Dutta, S.; Mondal, P.K.; Goswami, P. Slipping hydrodynamics of Powell-Eyring fluid in a cylindrical microchannel under electrical double layer phenomenon. Phys. Scr. 2019, 94, 025002. [Google Scholar] [CrossRef]
- Hayat, T.; Awais, M.; Asghar, S. Radiative effects in a three-dimensional flow of MHD Eyring-Powell fluid. J. Egypt. Math. Soc. 2013, 21, 379–384. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.-S.; Yang, Z. Entropy generation on MHD Eyring-Powell nanofluid through a permeable stretching surface. Entropy 2016, 18, 224. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, Z.; Farooq, M.; Alsaedi, A. Magnetohydrodynamic flow of Powell-Eyring fluid by a stretching cylinder with Newtonian heating. Therm. Sci. 2018, 22, 371–382. [Google Scholar] [CrossRef]
- Jamshed, W.; Eid, M.R.; Nisar, K.S.; Nasir, N.A.A.M.; Edacherian, A.; Saleel, C.A.; Vijayakumar, V. A numerical frame work of magnetically driven Powell-Eyring nanofluid using single phase model. Sci. Rep. 2021, 11, 16500. [Google Scholar] [CrossRef]
- Ibrahim, W.; Lamesse, T. Powell-Eyring nanofluid analysis with finite element method when past stretching sheet with convective heating and passive control of nanoparticle. Int. J. Thermofluids 2023, 19, 100388. [Google Scholar] [CrossRef]
- Nazeer, M.; Ahmad, F.; Saeed, M.; Saleem, A.; Naveed, S.; Akram, Z. Numerical solution for flow of a Eyring-Powell fluid in a pipe with prescribed surface temperature. J. Braz. Soc. Mech. Sci. 2019, 41, 518. [Google Scholar] [CrossRef]
- Krishna, P.M.; Sandeep, N.; Reddy, J.V.R.; Sugunamma, V. Dual solutions for unsteady flow of Powell-Eyring fluid past an inclined stretching sheet. J. Nav. Archit. Mar. Eng. 2016, 13, 89–99. [Google Scholar] [CrossRef]
- Halim, N.A.; Noor, N.F.M. Mixed convection flow of Powell-Eyring nanofluid near a stagnation point along a vertical stretching sheet. Mathematics 2021, 9, 364. [Google Scholar] [CrossRef]
- Ponnalagarsamy, R.; Kawahara, M. A finite element analysis of laminar unsteady flow of viscoelastic fluids through channels with non-uniform cross-sections. Int. J. Numer. Methods Fluids 1989, 9, 1487–1501. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Jiang, X. Fast evaluation for magnetohydrodynamic flow and heat transfer of fractional Oldroyd-B fluids between parallel plates. ZAMM-J. Appl. Math. Mech. 2021, 101, 11–26. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, X.; Zhang, Y.; Liu, C.Y. Unsteady stagnation point flow of fractional burgers’ fluid based on finite difference-spectral method. Chin. J. Comput. Mech. 2024, 41, 458–466. [Google Scholar] [CrossRef]
- Motsa, S.S. A new spectral local linearization method for nonlinear boundary layer flow problems. J. Appl. Math. 2013, 2013, 423628. [Google Scholar] [CrossRef]
- Shateyi, S.; Marewo, G.T. On a new numerical analysis of the Hall effect on MHD flow and heat transfer over an unsteady stretching permeable surface in the presence of thermal radiation and heat source/sink. Bound. Value Probl. 2014, 2014, 170. [Google Scholar] [CrossRef]
- Ghulam, R.; Abderrahim, W. Numerical spectral examination of EMHD mixed convective flow of second-grade nanofluid towards a vertical Riga plate using an advanced version of the revised Buongiorno’s nanofluid model. J. Therm. Anal. Calorim. 2021, 143, 2379–2393. [Google Scholar] [CrossRef]
- Thompson, P.A.; Troian, S.M. A general boundary condition for liquid flow at solid surfaces. Nature 1997, 389, 360–362. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method for solving boundary value problems. Phys. Lett. A 2006, 350, 87–88. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).